Abstract
Despite countless studies on autism spectrum disorder (ASD), diagnosis relies on specific behavioral criteria and neuroimaging biomarkers for the disorder are still relatively scarce and irrelevant for diagnostic workup. Many researchers have focused on functional networks of brain activities using resting‐state functional magnetic resonance imaging (rsfMRI) to diagnose brain diseases, including ASD. Although some existing methods are able to reveal the abnormalities in functional networks, they are either highly dependent on prior assumptions for modeling these networks or do not focus on latent functional connectivities (FCs) by considering discriminative relations among FCs in a nonlinear way. In this article, we propose a novel framework to model multiple networks of rsfMRI with data‐driven approaches. Specifically, we construct large‐scale functional networks with hierarchical clustering and find discriminative connectivity patterns between ASD and normal controls (NC). We then learn features and classifiers for each cluster through discriminative restricted Boltzmann machines (DRBMs). In the testing phase, each DRBM determines whether a test sample is ASD or NC, based on which we make a final decision with a majority voting strategy. We assess the diagnostic performance of the proposed method using public datasets and describe the effectiveness of our method by comparing it to competing methods. We also rigorously analyze FCs learned by DRBMs on each cluster and discover dominant FCs that play a major role in discriminating between ASD and NC. Hum Brain Mapp 38:5804–5821, 2017. © 2017 Wiley Periodicals, Inc.
Keywords: autism spectrum disorder, functional magnetic resonance imaging, discriminative restricted Boltzmann machine, multiple clusters, hierarchical clustering, functional network analysis
INTRODUCTION
Autism spectrum disorder (ASD) is a heritable neurodevelopmental disorder [Bailey et al., 1995] characterized by the impaired development of social interactions and repetitive patterns of behavior and restricted interests [Amaral et al., 2008]. According to a recent report [CDC, 2014], 1 in 68 American children is identified as having ASD. Even though many researchers have devoted their efforts to developing a neurodevelopmental model [Baron‐Cohen, 2009] and identifying disease‐specific genes [Levy et al., 2009] for ASD, its etiology remains unknown. Thus, ASD diagnosis continues to rely on the identification of behavioral symptoms, which can cause it to be confused with other psychological and psychiatric disorders [Guilmatre et al., 2009].
Recently, many researchers have focused on revealing the abnormalities in functional networks of brain activities caused by brain diseases such as Alzheimer's disease [Greicius et al., 2004; Li et al., 2002], Parkinson's disease [Gao and Wu, 2016; Sang et al., 2015], schizophrenia [Garrity et al., 2007; Liang et al., 2006; Lynall et al., 2010; Zhou et al., 2007], and ASD [Iidaka, 2015; Monk et al., 2009] using resting‐state functional magnetic resonance imaging (rsfMRI). rsfMRI focuses on spontaneous low frequency fluctuations (<0.1 Hz) in blood‐oxygen‐level dependent (BOLD) signals while subjects are not performing any explicit cognitive, language, or motor tasks [Biswal et al., 1995; Lee et al., 2013]. Numerous studies have been conducted to discover resting‐state functional networks [Biswal et al., 1995; Raichle et al., 2001; Smith et al., 2009; Tomasi and Volkow, 2012; Vincent et al., 2008] and significant evidence exists connecting some of these networks to certain brain diseases, such as ASD [Hadjikhani, 2007; Monk et al., 2009; Price et al., 2014; Rudie et al., 2012].
The conventional method [Fox et al., 2006; Vincent et al., 2008] for functional network construction is a seed‐based approach [Biswal et al., 1995]. A region of interest (ROI) is selected as a seed and correlations between the averaged time courses of BOLD signals on voxels within the seed and other ROIs are calculated to determine functional connectivities (FCs). Based on this approach, some functional networks related to ASD are revealed [Verly et al., 2014]. The main drawback of this approach is that results are highly dependent on seeds, which should be selected in advance. To overcome this limitation, several data‐driven methods, specifically, single matrix factorization models such as principal component analysis (PCA), independent component analysis (ICA), and non‐negative matrix factorization were examined [Assaf et al., 2010; Carbonell et al., 2011; Eavani et al., 2015; Murdaugh et al., 2015; Price et al., 2014; Zhang et al., 2015]. However, the flexibility and representational capacity of these methods are limited and no empirical evidence exists that supports certain assumptions, such as orthogonality and the independence of source signals for solving linear‐mixing problems [Hjelm et al., 2014; Liu et al., 2012].
To address the limitations of conventional approaches, dictionary learning‐based methods have been widely used for analyzing functional networks [Lee et al., 2016; Lv et al., 2015a, 2015b]. Unlike conventional approaches such as PCA and ICA, dictionary learning does not impose that source signals are orthogonal or independent, allowing more flexibility in adapting the representation to the data [Mairal et al., 2010]. Specifically, Lv et al. [2015b] proposed a novel framework, holistic atlases of functional networks and interaction (HAFNI), which seeks out functional networks based on sparse representation and dictionary learning for whole‐brain fMRI data.
As an another alternative to conventional approaches, a graph theory‐based method has been widely used for analyzing functional networks [Bullmore and Sporns, 2009; van den Heuvel et al., 2008]. It considers ROIs and their FCs as nodes and edges, respectively, of a graph and represents functional networks with attributes of the graph [van den Heuvel et al., 2008]. Based on this approach, some researchers have attempted to identify altered graph topologies in ASD [Itahashi et al., 2014; Martino et al., 2013; Redcay et al., 2013].
Generative stochastic models for analyzing neuroimaging data also have garnered great attention [Hjelm et al., 2014; Iidaka, 2015; Plis et al., 2014; Suk et al., 2014, 2015]. Specifically, the restricted Boltzmann machine (RBM) [Hinton, 2002] and its extended version, the discriminative RBM (DRBM) [Larochelle and Bengio, 2008] has been widely used to model functional networks [Hjelm et al., 2014; Suk et al., 2014, 2015]. However, only a few studies have applied them to diagnosing brain diseases [Plis et al., 2014; Suk et al., 2014, 2015].
In this study, we propose a novel framework designed to model functional networks of rsfMRI in a data‐driven manner for ASD diagnosis. We first consider that a seed‐based FC becomes a basic unit of the functional networks as it represents temporal synchronization between the BOLD signals of respective seed and those of other ROIs and characterizes how they are functionally associated. The seed‐based FCs in which similar connectivity patterns represent that their respective seeds are similarly associated to other ROIs and they are highly engaged in the network level. For example, in Figure 1, we can see that the seed‐based FCs (row vectors) in each group A and B, respectively, show similar connectivity patterns to other ROIs. In that case, we consider the seed‐based FCs in each group are functionally associated, and then construct multiple functional networks by clustering the seed‐based FCs in each group. For each cluster, we learn the features of FCs and classifiers through DRBMs. The rationale for using DRBMs is that they can learn latent discriminative features while considering relations among FCs in a nonlinear way, and then classify these features in a probabilistic manner. Although deep architecture models that use RBMs as a building block show promise in various fields, we adapt this basic model in order to improve the model's interpretative network analysis capabilities. By combining the clustering approach with an ensemble of DRBMs in a unified framework, the proposed method performs effective diagnosis on public datasets in comparison with competing methods. We also analyze discriminative functional connectivities and learned DRBM weights on each cluster to identify potential biomarkers of ASD.
Figure 1.
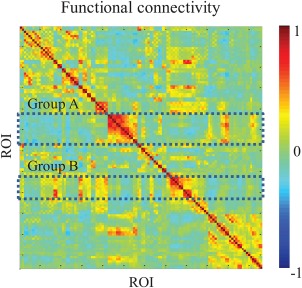
An example of a functional connectivity map. Each element of the map represents connectivity between each pair of ROIs and a row vector represents seed‐based FCs. [Color figure can be viewed at http://wileyonlinelibrary.com]
MATERIALS AND METHODS
Materials and Preprocessing
We acquired preprocessed rsfMRI data1 from the University of Michigan (UM) and the New York University (NYU) Langone Medical Center; these are the largest number of samples (149 subjects from UM and 184 subjects from NYU, in total) in the Autism Brain Imaging Data Exchange (ABIDE) [Martino et al., 2014]. Table 1 shows the scan environment for each dataset. From each dataset, we considered only subjects under 20 years old2 and then removed subjects rejected by the manual inspection conducted by ABIDE.3 In the end, we used 133 subjects (61 ASD and 72 NC) from the UM dataset and 130 subjects (58 ASD and 72 NC) from the NYU dataset.
Table 1.
Scanners and scan parameters for the UM and NYU datasets
| UM dataset | NYU dataset | |
|---|---|---|
| Scanner | 3.0 T GE Signa scanner | 3.0 T Siemens Allegra scanner |
| Repetition Time (TR) (ms) | 2,000 | 2,000 |
| Echo Time (TE) (ms) | 30 | 15 |
| Flip angle (°) | 90 | 90 |
| The number of slices | 40 | 33 |
| The number of volumes | 300 | 180 |
| Voxel thickness (mm) | 4 | 3 |
During preprocessing, the first five volumes were discarded to ensure magnetization equilibrium and the remaining volumes were spatially normalized to MNI space with a voxel size of . Nuisance signals including ventricle, white matter, global signals, and head motion are regressed out of the data with the Friston 24‐parameter model [Fristonand et al., 1996]. Using the Automated Anatomical Labeling (AAL) atlas [Tzourio‐Mazoyer et al., 2002], the regressed rsfMRI images were parcellated into 116 ROIs and the time courses of the BOLD signals in voxels of each ROI were averaged. Table 2 shows the names of the ROIs in the AAL template. The mean signals were then band‐pass filtered from 0.01 to 0.1 Hz resulting in 116‐dimensional vectors for each subject (or sample).
Table 2.
The indices and names of the ROIs in the AAL template
| Index | ROI label | Index | ROI label |
|---|---|---|---|
| 1,2 | Precentral gyrus (PreCG) | 3,4 | Superior frontal gyrus (dorsal) (SFGdor) |
| 5,6 | Orbitofrontal cortex (superior) (ORBsup) | 7,8 | Middle frontal gyrus (MFG) |
| 9,10 | Orbitofrontal cortex (middle) (ORBmid) | 11,12 | Inferior frontal gyrus (opercular) (IFGoperc) |
| 13,14 | Inferior frontal gyrus (triangular) (IFGtriang) | 15,16 | Orbitofrontal cortex (inferior) (ORBinf) |
| 17,18 | Rolandic operculum (ROL) | 19,20 | Supplementary motor area (SMA) |
| 21,22 | Olfactory (OLF) | 23,24 | Superior frontal gyrus (medial) (SFGmed) |
| 25,26 | Orbitofrontal cortex (medial) (ORBmed) | 27,28 | Rectus gyrus (REC) |
| 29,30 | Insula (INS) | 31,32 | Anterior cingulate gyrus (ACG) |
| 33,34 | Middle cingulate gyrus (MCG) | 35,36 | Posterior cingulate gyrus (PCG) |
| 37,38 | Hippocampus (HIP) | 39,40 | Parahippocampal gyrus (PHG) |
| 41,42 | Amygdala (AMYG) | 43,44 | Calcarine cortex (CAL) |
| 45,46 | Cuneus (CUN) | 47,48 | Lingual gyrus (LING) |
| 49,50 | Superior occipital gyrus (SOG) | 51,52 | Middle occipital gyrus (MOG) |
| 53,54 | Inferior occipital gyrus (IOG) | 55,56 | Fusiform gyrus (FFG) |
| 57,58 | Postcentral gyrus (PoCG) | 59,60 | Superior parietal gyrus (SPG) |
| 61,62 | Inferior parietal lobule (IPL) | 63,64 | Supramarginal gyrus (SMG) |
| 65,66 | Angular gyrus (ANG) | 67,68 | Precuneus (PCUN) |
| 69,70 | Paracentral lobule (PCL) | 71,72 | Caudate (CAU) |
| 73,74 | Putamen (PUT) | 75,76 | Pallidum (PAL) |
| 77,78 | Thalamus (THA) | 79,80 | Heshl gyrus (HES) |
| 81,82 | Superior temporal gyrus (STG) | 83,84 | Temporal pole (superior) (TPOsup) |
| 85,86 | Middle temporal gyrus (MTG) | 87,88 | Temporal pole (middle) (TPOmid) |
| 89,90 | Inferior temporal gyrus (ITG) | 91–94 | Crus I–II of cerebellar hemisphere (CRBLCrus) |
| 95–108 | Lobule III–X of cerebellar hemisphere (CRBL) | 109–116 | Lobule I–X of vermis (Vermis) |
Frontal = (1–16, 19–28, 69–70); insula = (29:30); temporal = (79–90); parietal = (17–18, 57–68); occipital = (43–56).
Limbic = (31–40); subcortical = (41–42, 71–78); cerebellum = (91–108); vermis = (109–116).
The odd and even indices refer to the left‐ and right‐hemispheric regions, respectively.
Overview of Methodology
We propose a novel method to model discriminative functional networks in multiple clusters with data‐driven approaches for ASD diagnosis. Figure 2 illustrates the overall framework of our method. We first calculate FC by means of Pearson's correlation on each pair of ROIs and construct group‐mean FC matrices by averaging the FCs over training samples of each group (i.e., ASD and NC). Note that in the group‐mean FC matrices, each row vector denotes a seed‐based FC that represents connectivity patterns between the respective seed and other ROIs. We consider the seed‐based FC becomes a basic unit of the functional networks and hypothesize that the seed‐based FCs in which similar connectivity patterns should be considered as units to improve ASD diagnostic performance. Based on this hypothesis, we cluster the seed‐based FCs to better characterize functional networks. We extract discriminative FCs from each cluster as features and learn nonlinearly transformed features and classifiers through DRBMs. In the testing phase, given FCs from the testing sample, each DRBM probabilistically determines whether a test sample is an example of ASD or NC. We then consider the probability of outputs to be the decisional confidence of DRBMs. Based on the DRBMs’ confidence, we determine a final clinical decision using an ensemble of outputs from the DRBM models.
Figure 2.
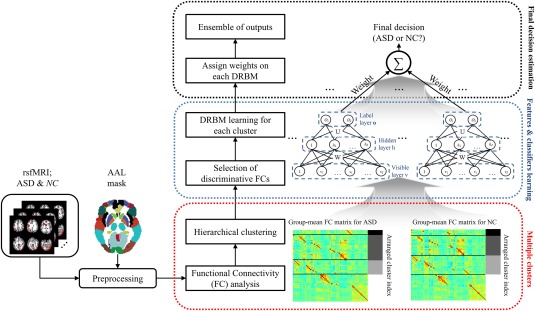
Illustration of the proposed framework for ASD diagnosis. [Color figure can be viewed at http://wileyonlinelibrary.com]
Multiple Network Construction and Feature Extraction
We first calculate FCs for each ROI pair using the Pearson's correlation of the averaged time courses of BOLD signals for each sample. We then construct FC matrices , where R denotes the number of ROIs and t denotes the training sample index. By averaging the FC matrices of each group, we construct group‐mean FC matrices , where . As brain diseases, including ASD, alter functional networks [Rudie et al., 2013; Verly et al., 2014; Wang et al., 2007], we consider each group‐mean FC matrix separately in the following steps. In each group‐mean FC matrix, the rth row vector denotes a seed‐based FC N r in which the ROI r is a seed. The seed‐based FC represents associations between the seed ROI and other ROIs, and the connectivity patterns illustrate how the FCs cooperate with each other. Thus, we believe that seed‐based FCs that show similar patterns can be characterized in a large‐scale network, by which it is expected for the network analysis to be robust to noise. For this, we cluster the seed‐based FCs by adopting hierarchical clustering [Rokach and Maimon, 2005] with a bottom–up approach. In this method, each seed‐based FC starts in its own cluster, and pairs of clusters are merged as one moves up the hierarchy based on their inter‐cluster distance. Then, the higher hierarchies gradually construct large‐scale networks by enhancing their functional roles. In order to measure the intercluster distance for each pair of clusters, we adopt the average linkage method [Sokal and Michener, 1958], which is commonly used in other research areas such as ecology and bioinformatics. In the average linkage method, we compute the distance E(a,b) between clusters a and b as follows:
| (1) |
where Q a and Q b are the number of seed‐based FCs and that belong to clusters a and b, respectively, and represents their similarity as calculated by means of Pearson's correlation. A seed‐based FC is represented with an R‐dimensional vector, as the seed‐based FC consists of FCs between a seed and R ROIs, including the seed ROI. To cluster the seed‐based FCs, we adopt a method [Liu et al., 2012] that was designed to analyze functional networks acquired by rsfMRI in anesthetized rats. Liu et al. [2012] constructed spatial maps by averaging the clustered seed‐based FCs, and illustrated the effectiveness of the method by comparing with probabilistic independent component analysis [Beckmann and Smith, 2005]. However, their study examined the distribution of brain activities in spatial maps for only a single group, and thus is not applicable to diagnostic applications.
Hierarchical clustering generates a dendrogram for each of the two groups (i.e., ASD and NC). We first decompose the dendrograms to a predefined number of clusters C, which is determined from data (details are provided in the section “Results”),4 and then we construct 2 × C clusters.
After constructing 2 × C large‐scale functional networks (C functional networks per group), we then use these for feature extraction from rsfMRI. A cluster a consists of Q a seed‐based FCs and each seed‐based FC is represented with an R‐dimensional vector. Thus, we have features for a training sample t in the cluster. Among these features, we select discriminative features between ASD and NC by performing a two‐sample t‐test with only training samples. The selected features are normalized by z‐score transformation, and then fed into a DRBM for classification as depicted below.
Classifier Learning
We adopt the DRBM [Larochelle and Bengio, 2008], which is an extended version of the RBM [Hinton, 2002], to find nonlinear relations among the selected features in each cluster and design an ensemble classifier with which we can enhance the diagnostic accuracy of ASD.
An RBM is an energy‐based undirected graphical model consisting of a visible and a hidden layer. Each layer consists of I visible units and J hidden units . An RBM can be represented with a parameter set , where and represent bias terms of the visible and hidden layers, respectively, and denotes an interlayer connection. Figure 3A shows the architecture of an RBM. This architecture notably assumes restricted symmetric connections with no within‐layer connections and models interactions between visible and hidden units. Because the hidden units h are unobservable, the objective function is defined as the marginal distribution of the visible units v as follows:
| (2) |
where Z is a partition function that can be obtained by summing all possible pairs of v and h [Hinton, 2002] and denotes an energy function. In this study, as the FCs that become observations of the visible units are real values, we adopt a Gaussian‐Bernoulli energy function [Hinton and Salakhutdinov, 2006]5 defined by
| (3) |
where denotes a standard deviation of the ith visible unit. In this case, the conditional distributions of visible and hidden units are, respectively, computed by
| (4) |
| (5) |
where sigm(·) denotes a logistic sigmoid function. To learn the parameters of Eq. (3), the contrastive divergence algorithm [Hinton, 2002] is used, maximizing the log‐likelihood of the marginal distribution of visible units.
Figure 3.
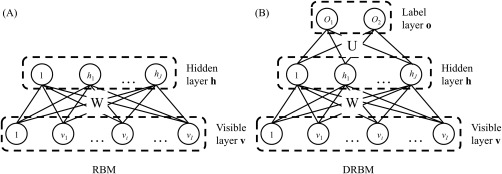
Architectures of (A) RBM and (B) DRBM.
Compared to the RBM, a DRBM has one additional layer, called a label layer, which is injected at the hidden layer to indicate the label of inputs , where S denotes the number of groups or classes [Larochelle and Bengio, 2008]. Figure 3B shows the architecture of a DRBM. As the hidden layer is connected to both the visible and label layers, the DRBM models discriminative feature representations by integrating the processes of input feature discovery and classification [Larochelle and Bengio, 2008]. The probability of an observation is defined as:
| (6) |
The conditional distribution of the hidden units is computed by
| (7) |
where denotes an interlayer connection between hidden and label layers.
For the label layer, we adopt a softmax function defined as follows:
| (8) |
We also learn DRBM parameters by using the contrastive divergence algorithm [Hinton, 2002] to maximize the log‐likelihood of the observed data (v,o). In our method, the discriminative FCs are the input to the visible units and their discriminative relations are modeled in each hidden unit of a DRBM. Thus, the connection weights W between the visible and hidden units can be interpreted as discriminative functional networks.
As described in the section “Multiple Network Construction and Feature Extraction,” multiple clusters are constructed with different functional roles, and we learn the features of FCs and classifiers for each cluster through DRBMs. Because of their different functional roles, different DRBMs estimate different outputs. To make a clinical decision, we combine the DRBM outputs using a weighted voting strategy. Note that each DRBM outputs a decision with its own confidence in terms of the probability of a test sample being an example of ASD or NC. We regard the probabilities as weights for their corresponding models and the final decision is determined using a weighted sum of the models’ outputs.
Experimental Setting
To validate the effectiveness of the proposed method, we compared it with a baseline model, for which we used a support vector machine (SVM), which is one of the most widely used classifiers for brain disease diagnosis in the literature [Chen et al., 2016; Craddock et al., 2009; Fan et al., 2011], and two other competing methods, recursive feature elimination‐based SVM (RSVM) [Chen et al., 2015; Plitt et al., 2015], and a graph theory‐based SVM (GSVM) [Barttfeld et al., 2012; Khazaee et al., 2015]. In this work, all the competing methods also used FCs with Pearson's correlation as basic features and a linear SVM6 as a classifier. However, the methods utilized different feature selection strategies. While the SVM simply used discriminative FCs selected by t‐test (P < 0.05) to construct classifier, the RSVM adopted a recursive feature elimination strategy, a pruning technique that eliminates original input features by using feature ranking coefficients as classifier weights, and retains a minimum subset of features that yields best classification performance ]Guyon et al., 2002]. We also designed the GSVM by applying graph theory [Itahashi et al., 2014; Uehara et al., 2014] to FCs and used network topologies as features. In this comparison, we used “clustering coefficient,” commonly used in the literature, which is defined as the ratio of the number of edges between the neighbors of a node and the total number of possible edges between its neighbors. The clustering coefficient expresses the level of connectedness of the direct neighbors of a node [van den Heuvel et al., 2008]. The proposed DRBM‐based method used the t‐test (P < 0.05), the same measure as the SVM to select discriminative FCs, and the number of hidden units J was set to half the number of visible units I (i.e., J = I/2). Figure 4 presents the differences between the methods by focusing on their discriminative feature and classifier learning strategies.
Figure 4.
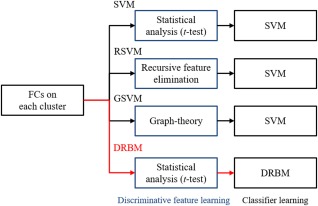
The differences between the proposed and competing methods by focusing on their discriminative feature and classifier learning strategies. [Color figure can be viewed at http://wileyonlinelibrary.com]
Note that all the methods adopted both single cluster (sc) and multiple cluster (mc) approaches. Compared to the multiple cluster approach, the single cluster method constructed a network in a single cluster; thus, it is a special case of the multiple clusters approach with C = 1.
RESULTS
For performance evaluation, diagnostic performance was computed by the following quantitative measurements
Accuracy (ACC) = (TP + TN)/(TP + TN + FP + FN)
Sensitivity (SEN) = TP/(TP + FN)
Specificity (SPEC) = TN/(TN + FP)
Positive predictive value (PPV) = TP/(TP + FP)
Negative predictive value (NPV) = TN/(TN + FN)
where TP, TN, FP, and FN denote true positive, true negative, false positive, and false negative, respectively.
UM Dataset
For evaluation, a 10‐fold cross‐validation technique was adopted in all the step of the proposed method. In Table 3, we compared the performance of the proposed and competing methods on the UM dataset. For the multiple cluster approach, we tested performance with different numbers of clusters and chose the best performance for each method. Figure 5 shows the performance change of the proposed and competing methods based on the number of clusters.
Table 3.
Performance comparison of the proposed and competing methods on the UM dataset
| Method | ACC (%) | SEN (%) | SPEC (%) | PPV (%) | NPV (%) | |
|---|---|---|---|---|---|---|
| Single cluster (sc) | SVM | 74.20* (ES: 0.53) | 70.71 | 76.78 | 73.21 | 76.74 |
| RSVM | 67.39* (ES: 0.56) | 65.48 | 68.57 | 64.28 | 71.35 | |
| GSVM | 58.17** (ES: 0.63) | 52.62 | 62.32 | 55.69 | 60.75 | |
| DRBM | 67.70* (ES: 0.57) | 67.14 | 67.68 | 64.08 | 72.07 | |
| Multiple cluster (mc) | SVM | 73.49* (ES: 0.48) | 72.14 | 74.46 | 70.67 | 76.36 |
| RSVM | 73.32* (ES: 0.57) | 65.48 | 79.64 | 75.45 | 73.61 | |
| GSVM | 69.23* (ES: 0.50) | 50.95 | 84.11 | 73.83 | 68.25 | |
| DRBM | 80.82 | 75.48 | 85.00 | 81.12 | 81.37 | |
SVM: support vector machine; RSVM: recursive feature elimination‐based SVM; GSVM: graph theory‐based SVM; DRBM: discriminative restricted Boltzmann machine; ACC: accuracy; SEN: sensitivity; SPEC: specificity; PPV: positive predictive value; NPV: negative predictive value. Asterisks represent the results of the Wilcoxon signed‐rank test (*P < 0.05, **P < 0.01) with the proposed mcDRBM and ES denotes the effect size.
Figure 5.
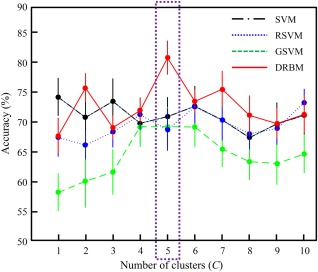
The diagnostic accuracy of the proposed (DRBM: discriminative restricted Boltzmann machine) and competing methods (SVM: support vector machine; RSVM: recursive feature elimination‐based SVM; GSVM: graph theory‐based SVM) based on the number of clusters for the UM dataset. Points and bars show the mean and standard error of the mean, respectively, over 10‐fold cross‐validation. [Color figure can be viewed at http://wileyonlinelibrary.com]
In accuracy evaluation, the proposed mcDRBM showed the best accuracy of 80.82% which is higher performance than that of scDRBM with a 13.12% improvement. Compared to the competing methods, the proposed method improved by 6.62%, 13.43%, 22.65%, 7.33%, 7.50%, and 11.59% over the scSVM, scRSVM, scGSVM, mcSVM, mcRSVM, and mcGSVM, respectively. For statistical validation between classification accuracies of the proposed and competing methods, we adopted the Wilcoxon signed rank test [Gibbons and Chakraborti, 2011], which is a nonparametric statistical hypothesis test and widely known to validate cross‐validation‐based classification results. According to the test, the classification accuracy of proposed method showed significant differences compared to that of all the competing methods (details are provided in Table 3).
Regarding sensitivity and specificity, the mcDRBM also had the best performance on the UM dataset. It achieved a sensitivity of 75.48% and specificity of 85.00%, which were improvements, respectively, of 4.77% and 8.22% over the scSVM, 10.00% and 16.43% over the scRSVM, 22.86% and 22.68% over the scGSVM, 8.34% and 17.32% over the scDRBM, 3.34% and 10.54% over the mcSVM, 10.00% and 5.36% over the mcRSVM, and 24.53% and 0.89% over the mcGSVM. Note that the higher the sensitivity, the lower the chance of misdiagnosing ASD, whereas the higher the specificity, the lower the chance of misdiagnosing NC.
We also computed positive/negative predictive values (PPV/NPV), which represent the proportion of ASD/NC correctly diagnosed. The mcDRBM had a PPV of 81.12% which was an improvement of 7.91%, 16.84%, 25.43%, 17.04%, 10.45%, 5.67%, and 7.29% in comparison with the scSVM, scRSVM, scGSVM, scDRBM, mcSVM, mcRSVM, and mcGSVM, respectively. For NPV, the mcDRBM achieved 81.37%, an improvement of 4.63%, 10.02%, 20.62%, 9.30%, 5.01%, 7.76%, and 13.12% over the scSVM, scRSVM, scGSVM, scDRBM, mcSVM, mcRSVM, and mcGSVM, respectively.
NYU Dataset
For evaluation, a 10‐fold cross‐validation technique was adopted in all the step of the proposed method. Table 4 shows the performance of the proposed and competing methods and Figure 6 shows the performance change of the methods based on the number of clusters for the NYU dataset.
Table 4.
Performance comparison of the proposed and competing methods on the NYU dataset
| Method | ACC (%) | SEN (%) | SPEC (%) | PPV (%) | NPV (%) | |
|---|---|---|---|---|---|---|
| Single cluster (sc) | SVM | 67.34** (ES: 0.58) | 53.33 | 77.32 | 70.71 | 68.38 |
| RSVM | 63.54* (ES: 0.53) | 55.67 | 69.11 | 62.33 | 66.51 | |
| GSVM | 64.24 (ES: 0.38) | 55.67 | 70.71 | 56.90 | 68.54 | |
| DRBM | 68.23* (ES: 0.47) | 59.00 | 74.82 | 69.71 | 70.03 | |
| Multiple cluster (mc) | SVM | 71.97 (ES: 0.34) | 61.00 | 80.00 | 74.93 | 72.02 |
| RSVM | 70.42 (ES: 0.33) | 57.33 | 80.00 | 74.05 | 70.71 | |
| GSVM | 68.10 (ES: 0.31) | 32.67 | 95.71 | 80.83 | 64.94 | |
| DRBM | 75.24 | 61.33 | 85.71 | 82.10 | 73.73 | |
SVM: support vector machine; RSVM: recursive feature elimination‐based SVM; GSVM: graph theory‐based SVM; DRBM: discriminative restricted Boltzmann machine; ACC: accuracy; SEN: sensitivity; SPEC: specificity; PPV: positive predictive value; NPV: negative predictive value. Asterisks represent the results of the Wilcoxon signed‐rank test (*P < 0.05, **P < 0.01) and with the proposed mcDRBM ES denotes the effect size.
Figure 6.
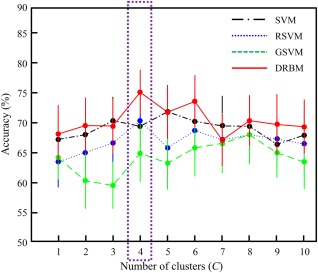
The diagnostic accuracy of the proposed (DRBM: discriminative restricted Boltzmann machine) and competing methods (SVM: support vector machine; RSVM: recursive feature elimination‐based SVM; GSVM: graph theory‐based SVM) based on the number of clusters for the NYU dataset. Points and bars show the mean and standard error of the mean, respectively, over 10‐fold cross‐validation. [Color figure can be viewed at http://wileyonlinelibrary.com]
The proposed mcDRBM showed the best accuracy, 75.24%, which was higher than that of the scDRBM, with a 7.01% improvement. Compared to the competing methods, the proposed method improved by 7.90% over the scSVM, 11.70% over the scRSVM, 11.00% over the scGSVM, 3.27% over the mcSVM, 4.82% over the mcRSVM, and 7.14% over the mcGSVM. The accuracy of the proposed method showed significant differences compared to that of scSVM, scRSVM, and scDRBM (details are provided in Table 4).
The mcDRBM also achieved the best sensitivity, 61.33%, which was an improvement of 8.00% over the scSVM, 5.66% over the scRSVM, 5.66% over the scGSVM, 2.33% over the scDRBM, 0.33% over the mcSVM, 4.00% over the mcRSVM, and 28.66% over the mcGSVM. The mcDRBM achieved a specificity of 85.71%, which was an improvement of 8.39% over the scSVM, 16.60% over the scRSVM, 15.00% over the scGSVM, 10.89% over the scDRBM, 5.71% over the mcSVM and the mcRSVM. This was, however, a 10.00% decline in specificity compared with the mcGSVM. In the case of the mcGSVM, which showed the best specificity, a severe imbalance between sensitivity and specificity is seen compared to other methods.
As for PPV and NPV, the mcDRBM had a PPV of 82.10% which was an improvement of 11.39% over the scSVM, 19.77% over the scRSVM, 25.20% over the scGSVM, 12.39% over the scDRBM, 7.17% over the mcSVM, 8.05% over the mcRSVM, and 1.27% over the mcGSVM. For NPV, mcDRBM achieved 73.73% which was an improvement of 5.35% over the scSVM, 7.22% over the scRSVM, 5.19% over the scGSVM, 3.70% over the scDRBM, 1.71% over the mcSVM, 3.02% over the mcRSVM, and 8.79% over the mcGSVM.
(UM + NYU) Combined Dataset
We combined the two datasets using half of the samples from each dataset for training and the other half for testing. Table 5 summarizes the performance of the proposed and competing methods and Figure 7 shows the performance change of the methods according to the number of clusters for the (UM+ NYU) combined dataset.
Table 5.
Performance comparison of the proposed and competing methods on the (UM + NYU) combined dataset
| Method | ACC (%) | SEN (%) | SPEC (%) | PPV (%) | NPV (%) | |
|---|---|---|---|---|---|---|
| Single cluster (sc) | SVM | 65.15 | 56.67 | 72.22 | 62.96 | 66.67 |
| RSVM | 57.58 | 53.33 | 61.11 | 53.33 | 61.11 | |
| GSVM | 62.88 | 50.00 | 73.61 | 61.22 | 63.86 | |
| DRBM | 64.39 | 58.33 | 69.44 | 61.40 | 66.67 | |
| Multiple cluster (mc) | SVM | 65.15 | 50.00 | 77.78 | 65.22 | 65.12 |
| RSVM | 64.39 | 53.33 | 73.61 | 62.75 | 65.43 | |
| GSVM | 65.91 | 56.67 | 73.61 | 64.15 | 67.09 | |
| DRBM | 67.42 | 58.33 | 75.00 | 66.04 | 68.35 | |
SVM: support vector machine; RSVM: recursive feature elimination‐based SVM; GSVM: graph theory‐based SVM; DRBM: discriminative restricted Boltzmann machine; ACC: accuracy; SEN: sensitivity; SPEC: specificity; PPV: positive predictive value; NPV: negative predictive value.
Figure 7.
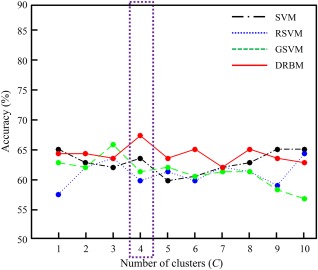
The diagnostic accuracy of the proposed (DRBM: discriminative restricted Boltzmann machine) and competing methods (SVM: support vector machine; RSVM: recursive feature elimination‐based SVM; GSVM: graph theory‐based SVM) based on the number of clusters on the (UM + NYU) combined dataset. [Color figure can be viewed at http://wileyonlinelibrary.com]
In the accuracy evaluation, the proposed mcDRBM performed best with an accuracy of 67.42%, which is higher than that of scDRBM with a 3.03% improvement. Compared to the other competing methods, the mcDRBM improved on the performance of the scSVM, scRSVM, scGSVM, mcSVM, mcRSVM, and mcGSVM by 2.27%, 9.84%, 4.54%, 2.27%, 3.03%, and 1.51%, respectively.
Table 6 shows the diagnostic performance of the mcSVM and mcDRBM, and the number of FCs for each cluster with C = 4. Note that, we constructed C clusters per group in the section “Multiple Network Construction and Feature Extraction” (i.e., eight clusters with C = 4, in total).
Table 6.
Comparison of diagnostic accuracy of the mcSVM and mcDRBM, and the number of features for each cluster with C =4 per group (i.e., eight clusters, in total) for the (UM + NYU) combined dataset
| Cluster index | mcSVM (%) | mcDRBM (%) | Number of features |
|---|---|---|---|
| 1 | 62.88 | 62.88 | 133 |
| 2 | 60.60 | 59.09 | 77 |
| 3 | 61.36 | 65.91 | 336 |
| 4 | 59.09 | 66.67 | 273 |
| 5 | 62.88 | 66.67 | 248 |
| 6 | 67.42 | 65.15 | 370 |
| 7 | 58.33 | 60.61 | 341 |
| 8 | 56.82 | 58.33 | 338 |
The mcDRBM achieved a sensitivity of 58.33%, which was again the best performance of all methods, representing an improvement of 1.66%, 5.00%, 8.33%, 8.33%, 5.00%, and 1.66% over the scSVM, scRSVM, scGSVM, mcSVM, mcRSVM, and mcGSVM, respectively. The mcDRBM achieved a specificity of 75.00%, which was an improvement of 2.78%, 13.89%, and 5.56% compared to the scSVM, scRSVM, and scDRBM, respectively, and an improvement of 1.39% over each of the scGSVM, mcRSVM, and mcGSVM, but a decline of 2.78% compared with the mcSVM.
Regarding PPV and NPV, the mcDRBM achieved 66.04% and 68.35%, respectively, which improved by 3.08% and 1.68% in comparison with the scSVM, 12.71% and 7.24% with the scRSVM, 4.82% and 4.49% with the scGSVM, 4.64% and 1.68% with the scDRBM, 0.82% and 3.23% with the mcSVM, 3.29% and 2.92% with the mcRSVM, and 1.89% and 1.26% with the mcGSVM.
DISCUSSION
Analysis of Selected FCs on Multiple Clusters
We analyze how multiple clusters are constructed and the functional roles of the clusters in classification with the (UM + NYU) combined dataset. Figure 8 shows the clustering results based on C = 4 per group (i.e., eight clusters, in total) and selected FCs by conducting t‐test (P < 0.05), respectively.
Figure 8.
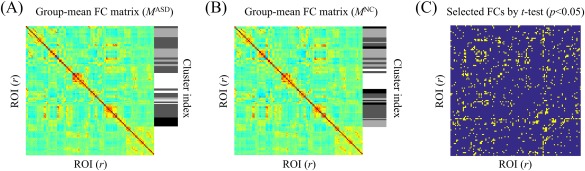
Clustering results based on C =4 with group‐mean FC matrices for (A) ASD and (B) NC are shown, respectively. (C) Selected FCs by means of a t‐test (P < 0.05). [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 9 shows th erepresentative selected FCs by conducting t‐test on each cluster. The brain networks are drawn with the BrainNet Viewer software [Xia et al., 2013]. In the figure, edges denote connections and nodes represent ROIs with different colors based on their functional modules.7 We present only the thirty edges that have the largest statistical differences between ASD and NC (i.e., the smallest P value of t‐test) and their nodes to improve visibility. The FCs on each cluster become observations of the visible units of DRBMs, and the DRBMs find latent FCs by considering discriminative relations among the FCs. The results of DRBMs that are independently conducted on each cluster with the FCs are fused by a weighted sum strategy for final decision.
Figure 9.

Selected FCs by conducting t‐test on each cluster with their sagittal (left/right), axial (top/bottom), and coronal (front/back) views. Nodes denote ROIs and edges represent connections between ROIs. Only the 30 edges that have the largest statistical differences between ASD and NC (i.e., the smallest P value of t‐test) are presented to improve visibility. The FCs on each cluster become observations of the visible units of DRBMs, and the DRBMs find latent FCs by considering discriminative relations among the FCs. [Color figure can be viewed at http://wileyonlinelibrary.com]
Clusters 4 and 5 showed the best performance, 66.67%, in Table 6, so we considered these clusters to have important roles in classification and focused them for further analysis.
Figure 10 provides additional details for Clusters 4 and 5. In Figure 10B, Cluster 5 primarily shows FCs in the regions of the default‐mode network (DMN), including the bilateral SFGdor/SFGmed/ORBsup/ORBmed/ACG/REC, the left ORBmid, and the right PCG. These regions are also connected with various posterior regions, including the bilateral IPL, the left IFGtriang/ITG/CAU/SPG/TPOsup/SOG/CRBL45, the right SMG/TPOmid, and the Vermis3/6/7. It is widely known that changes to FCs in frontal regions play important roles in diagnosing ASD [Belmonte et al., 2004; Courchesne and Pierce, 2005; Geschwind and Levitt, 2007; Hadjikhani et al., 2007; Patriquin et al., 2016; Rudie et al., 2012; Shih et al., 2010].
Figure 10.
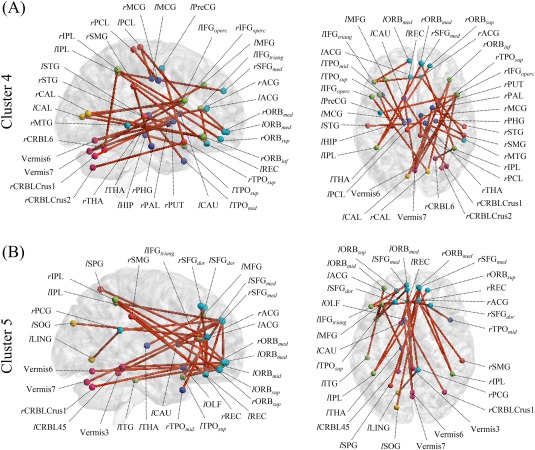
Selected FCs in Clusters 4 and 5 with their right sagittal (left) and top axial (right) views. Nodes denote ROIs, the names of the ROIs are given in their abbreviated forms (refer to Table 2 for their full names), and edges represent connections between ROIs. Only the 30 edges that have the largest differences between group‐mean FCs of ASD and NC (i.e., the smallest P value of a t‐test) are presented to improve visibility. [Color figure can be viewed at http://wileyonlinelibrary.com]
Cluster 4 mainly shows that not only FCs in frontal brain regions, but also FCs in the regions of the subcortical nuclei, including the bilateral MCG/THA, the left HIP/CAU/TPOmid, and the right PAL/PUT/PHG connected with regions of the cerebellum and sensorimotor cortex in Figure 10A. Note that the regions are closely related to the “Mirror Neuron System (MNS)” [Likowski et al., 2012]. The MNS is a brain system that is active when subjects perform an action themselves and when they observe another person performing the same action [Rizzolatti and Craighero, 2004]. The MNS is understood to be critically involved in perceiving other people's intentions and forming empathy during social interactions, and a dysfunction of this system has been identified in ASD [Gu et al., 2015; Hadjikhani, 2007].
Analysis of DRBM Weights
To investigate the role of DRBMs in the proposed method, we analyze the learned DRBM weights of hidden layer units (i.e., W in each cluster). As mentioned in the section “Classifier Learning,” the DRBM weights discover latent relations among discriminative FCs, and hidden units show different representations of these relations. We selected the 30 learned weights that have the largest absolute values and their FCs for each DRBM. We then counted the number of times FCs appear in the representations and select those from the top 10 that most frequently appear, labeling them “dominant FCs.”
Figure 11 shows the dominant FCs of DRBMs from Clusters 4 and 5. Compared to the selected FCs by conducting t‐test in Figure 10B, the learned DRBM from Cluster 5 focuses on FCs in cerebellar regions including the Vermis6/7 and the left CRBL45/10, connected to the regions of the DMN, including the bilateral OLF and the left SFGmed/ORBsup/MTG/PCG in Figure 11B. Additionally, FCs in the bilateral OLF, which have recently become known as ASD‐related regions [Ashwin et al., 2014; Rozenkrantz et al., 2015], are dominantly shown as connected with the left FFG/MTG. Finally, FCs in the right MFG connected with the right PCL/TPOmid are shown in the learned DRBM weights from Cluster 5.
Figure 11.
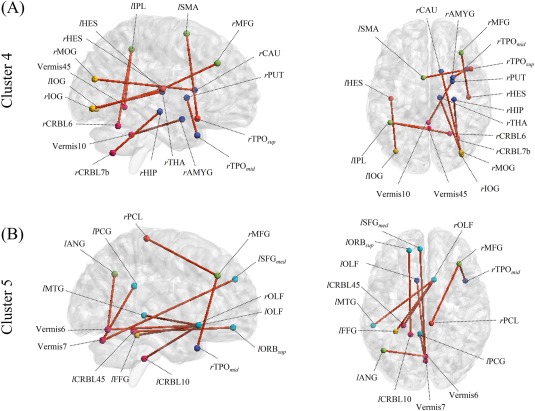
Frequently appearing FCs (top 10) from DRBM weights from Clusters 4 and 5 with their right sagittal (left) and top axial (right) views. Nodes denote ROIs, the names of the ROIs are given in their abbreviated forms (refer to Table 2 for their full names), and edges represent connections between ROIs. [Color figure can be viewed at http://wileyonlinelibrary.com]
Regarding the learned DRBM weights from Cluster 4, FCs in the right subcortical nuclei, including the TPOsup/TPOmid/AMYG/THA/HIP/CAU/PUT are connected with cerebellar regions, including the Vermis10 and the right CRBL7b, and regions of the visual cortex, including the right IOG/MOG in Figure 11A. Dominant FCs also appear in the left IPL/SMG/MFG, which are involved in attention and execution control in the learned DRBM weights from Cluster 4.
Compared to the FCs selected by focusing on the statistical differences of individual FCs, the DRBM finds latent FCs by considering the discriminative relations among the FCs (i.e., the DRBM concentrates more on FCs that conduct their functional roles in company with other FCs to enhance its discriminative power). As a result, the DRBM found FCs that are important for ASD diagnosis, even though the FCs are not remarkable in statistical analysis.
Diagnostic Performance
As mentioned in the section “RESULT,” the proposed method shows the best performance on all the measurements except for the metric of specificity. On the NYU and (UM + NYU) combined dataset, other methods, GSVM and SVM, respectively, show higher specificity (details are provided in Tables 4 and 5) compared to the proposed method. However, in these cases, the competing methods show severe imbalances between sensitivity and specificity (i.e., low sensitivity while high specificity). To interpret the relevance of the sensitivity and specificity for clinical diagnosis, we consider the likelihood ratios (LRs) [Hayden and Brown, 1999]. Two types of LRs exist, the positive LR (LR+) and negative LR (LR−) described as follows:
LR+ = SEN/(1 − SPEC)
LR− = (1 − SEN)/SPEC
The LR+ is the ratio of the probability that an individual with the disease tested positive to the probability that an individual without the disease tested positive while the LR− is the ratio of the probability that an individual with the disease tested negative to the probability that an individual without the disease tested negative. The larger the LR+, the better test to use for ruling in a disease while the smaller the LR−, the better test for ruling out a disease.
Figure 12 shows the LRs of the competing and the proposed methods on each dataset, respectively. In Figure 12A,C, the proposed method has the largest LR+ (5.03 and 2.33) and the smallest LR− (0.29 and 0.56) on the UM dataset and the (UM + NYU) dataset, respectively. In Figure 12B, the proposed method has the smallest LR− (0.45) and the second largest LR+ (4.29) on the NYU dataset. Even though the mcGSVM has the largest LR+ on NYU dataset, it shows imbalance between the LR+ and LR− (i.e., it also has the largest LR−). From this perspective, not only just comparing the accuracy, the proposed method showed better performance than all the competing methods. Nevertheless, all the methods including the proposed one showed low reliability across different datasets (i.e., the decreased performance on the (UM + NYU) combined dataset compared to individual datasets). We further discuss some limitations of the proposed method in the next subsection.
Figure 12.
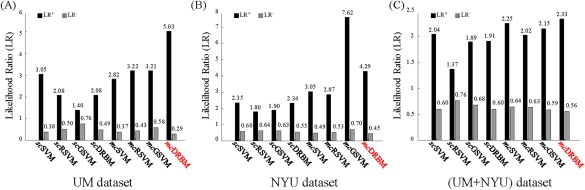
Positive and negative likelihood ratios (LR+ and LR−) of the competing and proposed methods for each dataset, respectively. (A) UM dataset, (B) NYU dataset, and (C) (UM + NYU) dataset. [Color figure can be viewed at http://wileyonlinelibrary.com]
Limitations
Many studies have adopted anatomical ROIs to estimate functional networks of the brain [Challis et al., 2015; Glasser et al., 2016; Iidaka, 2015; Plitt et al., 2015; Rudie et al., 2012; Wee et al., 2014], as we did in this work. However, it would also be intuitive to use data‐driven methods to obtain functional ROIs, as functional signals within ROIs detected by data‐driven methods are more consistent than the ROIs detected by anatomical segmentation. Nonetheless, the proposed method is valuable for automatically finding latent FCs by considering discriminative relations among FCs in a nonlinear way from data.
We estimated functional networks using Pearson's correlation, which is one of most widely used and simple approaches, to focus on the effects of multiple clusters and DRBMs. However, the estimation of functional networks is one of major issues in neuroimaging research. Geerligs et al. [2016] proposed an alternative method based on distance correlation [Szekely et al., 2007], which estimates the multivariate dependence between high dimensional vectors, allowing for both linear and nonlinear dependencies. Many researchers have also devoted their efforts to modeling functional networks by accounting for intersubject variability [Eavani et al., 2015; Liu et al., 2014]. In addition, it is worth noting that recent studies have focused on the dynamics of functional networks [Hutchison et al., 2013; Price et al., 2014; Yu et al., 2015; Zhou et al., 2016]. The high‐order functional connectivity [Zhang et al., 2016] that considers dynamics of low‐order connectivity was proposed as another alternative. It will be beneficial to consider more elaborate functional network estimation methods with our multiple cluster approach.
Recently, necessity of multisite data analysis is increased to diagnose brain diseases including ASD [Abraham et al., 2016; Chen et al., 2016; Nielsen et al., 2013] as the brain diseases are highly heterogeneous and larger datasets will be helpful to better assess individual differences. However, multisite data analysis contains inherent limitations owing to large inhomogeneities in scanning parameters, subject populations, and research protocols that limit the sensitivity for detecting abnormalities [Nielsen et al., 2013]. As the reasons, most of the methods in our experiments showed the decreased diagnostic performance on the (UM + NYU) combined dataset compared to that on the individual datasets. Although we adopted a basic RBM model to improve interpretative capabilities, deep architecture models by stacking RBMs will be helpful for multisite data analysis as they can extract high‐level and complex abstractions as data representations through a hierarchical learning process [Najafabadi et al., 2015].
Finally, the number of clusters is empirically determined in this study even though diagnostic performance depends on it. A nested cross‐validation technique will be one of the solutions to determine the number of clusters in a data‐driven manner. It will also be worthwhile to analyze multiple clusters according to some criteria for unraveling the hierarchical clusters [Alzate and Suykens, 2010; Mall et al., 2015; Tibshirani et al., 2001].
CONCLUSION
In this study, we proposed a novel method to model discriminative functional networks from rsfMRI data in multiple clusters by combining a clustering approach with an ensemble of DRBMs in a unified framework. We first constructed multiple clusters to represent various patterns of discriminative functional networks between ASD and NC using hierarchical clustering of networks and learned latent high‐level features and classifiers for each cluster in a probabilistic manner with DRBMs. The final decision was determined using an ensemble of outputs from the DRBM models. We assessed the diagnostic performance of the proposed method on public datasets and validated its effectiveness by comparing it with competing methods. In our analysis of multiple clusters and DRBM weights, we showed that the proposed method effectively estimates biomarkers of ASD by identifying latent FCs that play a major role in discriminating ASD and NC. It is noteworthy that the proposed method can also be applied to the diagnosis of other brain diseases, such as Alzheimer's disease and schizophrenia. Moreover, it can be extended to other neuroimaging research that analyzes functional networks of the brain.
Footnotes
ABIDE (http://fcon_1000.projects.nitrc.org/indi/abide) provides preprocessed rsfMRI datasets for ASD and NC with four different preprocessing pipelines. In this work, we used datasets preprocessed by the data processing assistant for resting‐state fMRI (DPARSF), convenient plug‐in software based on SPM and REST.
ASD diagnosis mainly occurs for children and adolescents. Additionally, the age of subjects highly affects ASD diagnosis, as the brains of children and adolescents are not fully developed, unlike those of adults. Thus, we only adopted data acquired from subjects aged <20 years.
In this work, we rejected data rated as “fail” for the “Rater 1” item, which examines the general quality of the preprocessed functional data and was conducted by ABIDE.
In this work, we assume that ASD and NC have the same number of clusters.
Conventional RBM defines the state of each neuron to be binary, which seriously limits their application area and one popular approach to address this problem is to replace the binary visible neurons with the Gaussian ones (Cho et al., 2011).
To optimize the SVM parameter, we utilized a nested 10‐fold cross‐validation technique. That is, the training samples from outer cross‐validation were further partitioned into 10 subsets. In an inner cross‐validation of the 10 subsets, 9 were used for training and the remaining subset was used for validation by changing the value of the parameter , whose space was defined with 10 values evenly spaced between 2−10 and 210. After 10 repetitions (i.e., one validation per subset), we chose the value of that achieved the maximal average performance. This chosen value was used to train the SVM on the training samples from outer cross‐validation.
The ROIs of the default‐mode network are shown in cyan. The module in green comprises the ROIs predominantly involved in attention and execution control. The module in red comprises the ROIs of the sensorimotor cortex. The module in yellow comprises the regions of the visual cortex. The module in blue comprises the ROIs of the subcortical nuclei. Finally, magenta nodes represent the regions of the cerebellum.
REFERENCES
- Abraham A, Milham M, Martino AD, Craddock RC, Samaras D, Thirion B, Varoquaux G (2016): Deriving reproducible biomarkers from multi‐site resting‐state data: An autism‐based example. NeuroImage 147:736–745. [DOI] [PubMed] [Google Scholar]
- Alzate C, Suykens JAK (2010): Multiway spectral clustering with out‐of‐sample extensions through weighted kernel PCA. IEEE Trans Pattern Anal Mach Intell 32:335–347. [DOI] [PubMed] [Google Scholar]
- Amaral DG, Schumann CM, Nordahl CW (2008): Neuroanatomy of autism. Trends Neurosci 31:137–145. [DOI] [PubMed] [Google Scholar]
- Ashwin C, Chapman E, Howells J, Rhydderch D, Walker I, Baron‐Cohen S (2014): Enhanced olfactory sensitivity in autism spectrum conditions. Mol Autism 5:1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Assaf M, Jagannathan K, Calhoun VD, Miller L, Stevens MC, Sahl R, O'Boyle JG, Schultz RT, Pearlson GD (2010): Abnormal functional connectivity of default mode sub‐networks in autism spectrum disorder patients. NeuroImage 53:247–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bailey A, Le Couteur A, Gottesman I, Bolton P, Simonoff E, Yuzda E, Rutter M (1995): Autism as a strongly genetic disorder: Evidence from a British twin study. Psychol Med 25:63–77. [DOI] [PubMed] [Google Scholar]
- Baron‐Cohen S (2009): Autism: The empathizing‐systemizing (e‐s) theory. Ann N Y Acad Sci 1156:68–80. [DOI] [PubMed] [Google Scholar]
- Barttfeld P, Wicker B, Cukier S, Navarta S, Lew S, Leiguarda R, Sigman M (2012): State‐dependent changes of connectivity patterns and functional brain network topology in autism spectrum disorder. Neuropsychologia 50:3653–3662. [DOI] [PubMed] [Google Scholar]
- Beckmann CF, Smith SM (2005): Tensorial extensions of independent component analysis for multisubject fMRI analysis. NeuroImage 25:294–311. [DOI] [PubMed] [Google Scholar]
- Belmonte MK, Allen G, Beckel‐Mitchener A, Boulanger LM, Carper RA, Webb SJ (2004): Autism and abnormal development of brain connectivity. J Neurosci 24:9228–9231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS (1995): Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magn Reson Med 34:537–541. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O (2009): Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:186–198. [DOI] [PubMed] [Google Scholar]
- Carbonell F, Bellec P, Shmuel A (2011): Global and system‐specific resting‐state fMRI fluctuations are uncorrelated: Principal component analysis reveals anti‐correlated networks. Brain Connect 1:496–510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CDC (2014): Community Report on Autism 2014. Centers for Disease Control and Prevention. [Google Scholar]
- Challis E, Hurley P, Serra L, Bozzali M, Oliver S, Cercignani M (2015): Gaussian process classification of Alzheimer's disease and mild cognitive impairment from resting‐state fMRI. NeuroImage 112:232–243. [DOI] [PubMed] [Google Scholar]
- Chen CP, Keown CL, Jahedi A, Nair A, Pflieger ME, Bailey BA, Müller R‐A (2015): Diagnostic classification of intrinsic functional connectivity highlights somatosensory, default mode, and visual regions in autism. NeuroImage Clin 8:238–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H, Duan X, Liu F, Lu F, Ma X, Zhang Y, Uddin LQ, Chen H (2016): Multivariate classification of autism spectrum disorder using frequency‐specific resting‐state functional connectivity ‐ A multi‐center study. Progr Neuro‐Psychopharmacol Biol Psychiatry 64:1–9. [DOI] [PubMed] [Google Scholar]
- Cho K, Ilin A, Raiko T (2011): Improved Learning of Gaussian‐Bernoulli Restricted Boltzmann Machines. Proceeding of the 21st International Conference on Artificial Neural Networks, Espoo, Finland, June 14–17, 2008.
- Courchesne E, Pierce K (2005): Why the frontal cortex in autism might be talking only to itself: Local over‐connectivity but long‐distance disconnection. Curr Opin Neurobiol 15:225–230. [DOI] [PubMed] [Google Scholar]
- Craddock RC, Holtzheimer PE, Hu XP, Mayberg HS (2009): Disease state prediction from resting state functional connectivity. Magn Reson Med 62:1619–1628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eavani H, Satterthwaite TD, Filipovych R, Gur RE, Gur RC, Davatzikos C (2015): Identifying sparse connectivity patterns in the brain using resting‐state fMRI. NeuroImage 105:286–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan Y, Liu Y, Wu H, Hao Y, Liu H, Liu Z, Jiang T (2011): Discriminant analysis of functional connectivity patterns on grassmann manifold. NeuroImage 56:2058–2067. [DOI] [PubMed] [Google Scholar]
- Fox MD, Corbetta M, Snyder AZ, Vincent JL, Raichle ME (2006): Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proc Natl Acad Sci USA 103:10046–10051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fristonand KJ, Williams S, Howard R, Frackowiak RS, Turner R (1996): Movement‐related effects in fMRI time‐series. Magn Reson Med 35:346–355. [DOI] [PubMed] [Google Scholar]
- Gao L‐l, Wu T (2016): The study of brain functional connectivity in Parkinson's disease. Transl Neurodegen 5:18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrity AG, Pearlson GD, McKiernan K, Lloyd D, Kiehl KA, Calhoun VD (2007): Aberrant “default mode” functional connectivity in schizophrenia. Am J Psychiatry 164:450–457. [DOI] [PubMed] [Google Scholar]
- Geerligs L, Cam CAN, Henson RN (2016): Functional connectivity and structural covariance between regions of interest can be measured more accurately using multivariate distance correlation. NeuroImage 135:16–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geschwind DH, Levitt P (2007): Autism spectrum disorders: Developmental disconnection syndromes. Curr Opin Neurobiol 17:103–111. [DOI] [PubMed] [Google Scholar]
- Gibbons JD, Chakraborti S (2011): Nonparametric Statistical Inference, 5th ed. Chapman and Hall/CRC. [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M, Smith SM, Van Essen DC (2016): A multi‐modal parcellation of human cerebral cortex. Nature 536:171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Srivastava G, Reiss AL, Menon V (2004): Default‐mode network activity distinguishes Alzheimer's disease from healthy aging: Evidence from functional MRI. Proc Natl Acad Sci USA 101:4637–4642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu X, Eilam‐Stock T, Zhou T, Anagnostou E, Kolevzon A, Soorya L, Hof PR, Friston KJ, Fan J (2015): Autonomic and brain responses associated with empathy deficits in autism spectrum disorder. Hum Brain Mapp 36:3323–3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guilmatre A, Dubourg C, Mosca AL, Legallic S, Goldenberg A, Drouin‐Garraud V, Layet V, Rosier A, Briault S, Bonnet‐Brilhault F, Laumonnier F, Odent S, Le Vacon G, Joly‐Helas G, David V, Bendavid C, Pinoit JM, Henry C, Impallomeni C, Germano E, Tortorella G, Di Rosa G, Barthelemy C, Andres C, Faivre L, Frébourg T, Saugier Veber P, Campion D (2009): Recurrent rearrangements in synaptic and neurodevelopmental genes and shared biologic pathways in schizophrenia, autism, and mental retardation. Arch Gen Psychiatry 66:947–956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guyon I, Weston J, Barnhill S, Vapnik V (2002): Gene selection for cancer classification using support vector machines. Mach Learn 46:389–422. [Google Scholar]
- Hadjikhani N. (2007) Progress in Autism Research: Mirror Neuron System and Autism. Nova Science Publishers, Inc. [Google Scholar]
- Hadjikhani N, Joseph RM, Snyder J, Tager‐Flusberg H (2007): Abnormal activation of the social brain during face perception in autism. Hum Brain Mapp 28:441–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayden SR, Brown MD (1999): Likelihood ratio: A powerful tool for incorporating the results of a diagnostic test into clinical decisionmaking. Ann Emerg Med 33:575–580. [DOI] [PubMed] [Google Scholar]
- Hinton GE (2002): Training products of experts by minimizing contrastive divergence. Neural Comput 14:1771–1800. [DOI] [PubMed] [Google Scholar]
- Hinton GE, Salakhutdinov RR (2006): Reducing the dimensionality of data with neural networks. Science 313:504–507. [DOI] [PubMed] [Google Scholar]
- Hjelm RD, Calhoun VD, Salakhutdinov R, Allen EA, Adali T, Plis SM (2014): Restricted Boltzmann machines for neuroimaging: An application in identifying intrinsic networks. NeuroImage 96:245–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, Penna SD, Duyn JH, Glover GH, Gonzalez‐Castillo J, Handwerker DA, Keilholz S, Kiviniemi V, Leopold DA, de Pasquale F, Sporns O, Walter M, Chang C (2013): Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage 80:360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iidaka T (2015): Resting state functional magnetic resonance imaging and neural network classified autism and control. Cortex 63:55–67. [DOI] [PubMed] [Google Scholar]
- Itahashi T, Yamada T, Watanabe H, Nakamura M, Jimbo D, Shioda S, Toriizuka K, Kato N, Hashimoto R (2014): Altered network topologies and hub organization in adults with autism: A resting‐state fMRI study. PLoS One 9:e94115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khazaee A, Ebrahimzadeh A, Babajani‐Feremi A (2015): Identifying patients with Alzheimer's disease using resting‐state fMRI and graph theory. Clin Neurophysiol 126:2132–2141. [DOI] [PubMed] [Google Scholar]
- Larochelle H, Bengio Y (2008): Classification Using Discriminative Restricted Boltzmann Machines. Proceedings of the 25th international conference on Machine learning, Helsinki, Finland, July 5–9, 2008.
- Lee MH, Smyser CD, Shimony JS (2013): Resting state fMRI: A review of methods and clinical applications. Am J Neuroradiol 34:1866–1872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee Y‐B, Lee J, Tak S, Lee K, Na DL, Seo SW, Jeong Y, Ye JC (2016): Sparse SPM: Group sparse‐dictionary learning in SPM framework for resting‐state functional connectivity MRI analysis. NeuroImage 125:1032–1045. [DOI] [PubMed] [Google Scholar]
- Levy SE, Mandell DS, Schultz RT (2009): Autism. Lancet 374:1627–1638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S‐J, Li Z, Wu G, Zhang M‐J, Franczak M, Antuono PG (2002): Alzheimer disease: Evaluation of a functional mr imaging index as a marker. Radiology 225:253–259. [DOI] [PubMed] [Google Scholar]
- Liang M, Zhou Y, Jiang T, Liu Z, Tian L, Liu H, Hao Y (2006): Widespread functional disconnectivity in schizophrenia with resting‐state functional magnetic resonance imaging. Neuroreport 17:209–213. [DOI] [PubMed] [Google Scholar]
- Likowski KU, Muehlberger A, Gerdes AB, Wieser MJ, Pauli P, Weyers P (2012): Facial mimicry and the mirror neuron system: Simultaneous acquisition of facial electromyography and functional magnetic resonance imaging. Front Hum Neurosci 6:Article 214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu W, Awate SP, Anderson JS, Fletcher PT (2014): A functional network estimation method of resting‐state fMRI using a hierarchical markov random field. NeuroImage 100:520–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Zhu X‐HZ, Qiu P, Chen W (2012): A correlation‐matrix‐based hierarchical clustering method for functional connectivity analysis. J Neurosci Methods 211:94–102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lv J, Jiang X, Li X, Zhu D, Chen H, Zhang T, Zhang S, Hu X, Han J, Huang H, Zhang J, Guo L, Liu T (2015a): Sparse representation of whole‐brain fMRI signals for identification of functional networks. Med Image Anal 20:112–134. [DOI] [PubMed] [Google Scholar]
- Lv J, Jiang X, Li X, Zhu D, Zhang S, Zhao S, Chen H, Zhang T, Hu X, Han J, Ye J, Guo L, Liu T (2015b): Holistic atlases of functional networks and interactions reveal reciprocal organizational architecture of cortical function. IEEE Trans Biomed Eng 62:1120–1131. [DOI] [PubMed] [Google Scholar]
- Lynall M‐E, Bassett DS, Kerwin R, McKenna PJ, Kitzbichler M, Muller U, Bullmore E (2010): Functional connectivity and brain networks in schizophrenia. J Neurosci 30:9477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mairal J, Bach F, Ponce J, Sapiro G (2010): Online learning for matrix factorization and sparse coding. J Mach Learn Res 11:19–60. [Google Scholar]
- Mall R, Mehrkanoon S, Suykens JAK (2015): Identifying intervals for hierarchical clustering using the gershgorin circle theorem. Pattern Recogn Lett 55:1–7. [Google Scholar]
- Martino AD, Yan C‐G, Li Q, Denio E, Castellanos FX, Alaerts K, Anderson JS, Assaf M, Bookheimer SY, Dapretto M, Deen B, Delmonte S, Dinstein I, Ertl‐Wagner B, Fair DA, Gallagher L, Kennedy DP, Keown CL, Keysers C, Lainhart JE, Lord C, Luna B, Menon V, Minshew NJ, Monk CS, Mueller S, Müller RA, Nebel MB, Nigg JT, O'Hearn K, Pelphrey KA, Peltier SJ, Rudie JD, Sunaert S, Thioux M, Tyszka JM, Uddin LQ, Verhoeven JS, Wenderoth N, Wiggins JL, Mostofsky SH, Milham MP (2014): The autism brain imaging data exchange: Towards a large‐scale evaluation of the intrinsic brain architecture in autism. Mol Psychiatry 19:659–667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martino AD, Zuo X‐N, Kelly C, Grzadzinski R, Mennes M, Schvarcz A, Rodman J, Lord C, Castellanos FX, Milham MP (2013): Shared and distinct intrinsic functional network centrality in autism and attention‐deficit/hyperactivity disorder. Biol Psychiatry 74:623–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monk CS, Peltier SJ, Wiggins JL, Weng S‐J, Carrasco M, Risi S, Lord C (2009): Abnormalities of intrinsic functional connectivity in autism spectrum disorders. NeuroImage 47:764–772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murdaugh DL, Maximo JO, Kana RK (2015): Changes in intrinsic connectivity of the brain's reading network following intervention in children with autism. Hum Brain Mapp 36:2965–2979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Najafabadi MM, Villanustre F, Khoshgoftaar TM, Seliya N, Wald R, Muharemagic E (2015): Deep learning applications and challenges in big data analytics. J Big Data 2: [Google Scholar]
- Nielsen JA, Zielinski BA, Fletcher PT, Alexander AL, Lange N, Bigler ED, Lainhart JE, Anderson JS (2013): Multisite functional connectivity MRI classification of autism: Abide results. Front Hum Neurosci 7:599. Article [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patriquin MA, DeRamus T, Libero LE, Laird A, Kana RK (2016): Neuroanatomical and neurofunctional markers of social cognition in autism spectrum disorder. Hum Brain Mapp 37:3957–3978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plis SM, Hjelm D, Salakhutdinov R, Allen EA, Bockholt HJ, Long JD, Johnson HJ, Paulsen J, Turner JA, Calhoun VD (2014): Deep learning for neuroimaging: A validation study. Front Neurosci 8:229. Article [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plitt M, Barnes KA, Martin A (2015): Functional connectivity classification of autism identifies highly predictive brain features but falls short of biomarker standards. NeuroImage Clin 7:359–366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price T, Wee C‐Y, Gao W, Shen D (2014): Multiple‐network classification of childhood autism using functional connectivity dynamics. Medical Image Computing and Computer‐Assisted Intervention, Boston, USA, September 14–18, 2014. [DOI] [PubMed]
- Raichle ME, MacLeod AM, Snyder AZ, Powers WJ, Gusnard DA, Shulman GL (2001): A default mode of brain function. Proc Natl Acad Sci USA 98:676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Redcay E, Moran JM, Mavros PL, Tager‐Flusberg H, Gabrieli JDE, Whitfield‐Gabrieli S (2013): Intrinsic functional network organization in high‐functioning adolescents with autism spectrum disorder. Front Hum Neurosci 7:e573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzolatti G, Craighero L (2004): The mirror‐neuron system. Annu Rev Neurosci 27:169–192. [DOI] [PubMed] [Google Scholar]
- Rokach L, Maimon O (2005): Data Mining and Knowledge Discovery Handbook: Clustering Methods. Springer. [Google Scholar]
- Rozenkrantz L, Zachor D, Heller I, Plotkin A, Weissbrod A, Snitz K, Secundo L, Sobel N (2015): A mechanistic link between olfaction and autism spectrum disorder. Curr Biol 25:1904–1910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudie JD, Brown JA, Beck‐Pancer D, Hernandez LM, Dennis EL, Thompson PM, Bookheimer SY, Dapretto M (2013): Altered functional and structural brain network organization in autism. NeuroImage Clin 2:79–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudie JD, Shehzad Z, Hernandez LM, Colich NL, Bookheimer SY, Iacoboni M, Dapretto M (2012): Reduced functional integration and segregation of distributed neural systems underlying social and emotional information processing in autism spectrum disorders. Cereb Cortex 22:1025–1037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sang L, Zhang J, Wang L, Zhang J, Zhang Y, Li P, Wang J, Qiu M (2015): Alteration of brain functional networks in early‐stage Parkinson's disease: A resting‐state fMRI study. PLoS One 10:e0141815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shih P, Shen M, Öttl B, Keehn B, Gaffrey MS, Müller RA (2010): Atypical network connectivity for imitation in autism spectrum disorder. Neuropsychologia 48:2931–2939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF (2009): Correspondence of the brain's functional architecture during activation and rest. Proc Natl Acad Sci USA 106:13040–13045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokal RR, Michener CD (1958): A statistical method for evaluating systematic relationships. Univ Kansas Sci Bull 38:1409–1438. [Google Scholar]
- Suk H‐I, Lee S‐W, Shen D (2014): Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. NeuroImage 101:569–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suk H‐I, Lee S‐W, Shen D (2015): Latent feature representation with stacked auto‐encoder for AD/MCI diagnosis. Brain Struct Funct 220: 841–859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szekely GJ, Rizzo ML, Bakirov NK (2007): Measuring and testing dependence by correlation of distances. Ann Stat 35:2769–2794. [Google Scholar]
- Tibshirani R, Walther G, Hastie T (2001): Estimating the number of clusters in a data set via the gap statistic. J R Stat Soc Ser B 63:411–423. [Google Scholar]
- Tomasi D, Volkow ND (2012): Resting functional connectivity of language networks: Characterization and reproducibility. Mol Psychiatry 17:841–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzourio‐Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M (2002): Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single‐subject brain. NeuroImage 15:273–289. [DOI] [PubMed] [Google Scholar]
- Uehara T, Yamasaki T, Okamoto T, Koike T, Kan S, Miyauchi S, Kira J‐I, Tobimatsu S (2014): Efficiency of a ‘small‐world’ brain network depends on consciousness levels: A resting‐state fMRI study. Cereb Cortex 24:1529–1539. [DOI] [PubMed] [Google Scholar]
- van den Heuvel MP, Stam CJ, Boersma M, Hulshoff Pol HE (2008): Small‐world and scale‐free organization of voxel‐based resting‐state functional connectivity in the human brain. NeuroImage 43:528–539. [DOI] [PubMed] [Google Scholar]
- Verly M, Verhoeven J, Zink I, Mantini D, Peeters R, Deprez S, Emsell L, Boets B, Noens I, Steyaert J, Lagae L, Cock PD, Rommel N, Sunaert S (2014): Altered functional connectivity of the language network in ASD: Role of classical language areas and cerebellum. NeuroImage Clin 4:374–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vincent JL, Kahn I, Snyder AZ, Raichle ME, Buckner RL (2008): Evidence for a frontoparietal control system revealed by intrinsic functional connectivity. J Neurophysiol 100:328–3342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K, Liang M, Wang L, Tian L, Zhang X, Li K, Jiang T (2007): Altered functional connectivity in early Alzheimer's disease: A resting‐state fMRI study. Hum Brain Mapp 28:967–978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee C‐Y, Zhao Z, Yap P‐T, Wu G, Shi F, Price T, Du Y, Xu J, Zhou Y, Shen D (2014): Disrupted brain functional network in internet addiction disorder: A resting‐state functional magnetic resonance imaging study. PLoS One 9:e107306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia M, Wang J, He Y (2013): Brainnet Viewer: A network visualization tool for human brain connectomics. PLoS One 8:e68910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Q, Erhardt EB, Sui J, Du Y, He H, Hjelm D, Cetin MS, Rachakonda S, Miller RL, Pearlson G, Calhoun VD (2015): Assessing dynamic brain graphs of time‐varying connectivity in fMRI data: Application to healthy controls and patients with schizophrenia. NeuroImage 107:345–355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Chen X, Shi F, Li G, Kim M, Giannakopoulos P, Haller S, Shen D (2016): Topographical information‐based high‐order functional connectivity and its application in abnormality detection for mild cognitive impairment. J Alzheimers Dis 54:1095–1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J, Zhou L, Wang L, Li W (2015): Functional brain network classification with compact representation of SICE matrices. IEEE Trans Biomed Eng 62:1623–1634. [DOI] [PubMed] [Google Scholar]
- Zhou L, Wang L, Liu L, Ogunbona P, Shen D (2016): Learning discriminative Bayesian networks from high‐dimensional continuous neuroimaging data. IEEE Trans Pattern Anal Mach Intell 38:2269–2283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Y, Liang M, Tian L, Wang K, Hao Y, Liu H, Liu Z, Jiang T (2007): Functional disintegration in paranoid schizophrenia using resting‐state fMRI. Schizophrenia Res 97:194–205. [DOI] [PubMed] [Google Scholar]


