Impact of correction factors in human brain lesion‐behavior inference

Abstract

Statistical voxel‐based lesion‐behavior mapping (VLBM) in neurological patients with brain lesions is frequently used to examine the relationship between structure and function of the healthy human brain. Only recently, two simulation studies noted reduced anatomical validity of this method, observing the results of VLBM to be systematically misplaced by about 16 mm. However, both simulation studies differed from VLBM analyses of real data in that they lacked the proper use of two correction factors: lesion size and “sufficient lesion affection.” In simulation experiments on a sample of 274 real stroke patients, we found that the use of these two correction factors reduced misplacement markedly compared to uncorrected VLBM. Apparently, the misplacement is due to physiological effects of brain lesion anatomy. Voxel‐wise topographies of collateral damage in the real data were generated and used to compute a metric for the inter‐voxel relation of brain damage. “Anatomical bias” vectors that were solely calculated from these inter‐voxel relations in the patients' real anatomical data, successfully predicted the VLBM misplacement. The latter has the potential to help in the development of new VLBM methods that provide even higher anatomical validity than currently available by the proper use of correction factors. Hum Brain Mapp 38:1692–1701, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

To identify critical brain regions representing cognitive functions in the human brain, early neuroscience had to rely on posthumous autopsy of individual brain damage [Broca, 1861; Wernicke, 1874]. Today, modern imaging methods in combination with new statistical procedures allow to infer lesion‐behavior relationship at a group level. Voxel‐based lesion‐behavior mapping (VLBM) techniques with either parametric [Bates et al., 2003] or non‐parametric [Rorden et al., 2007] statistics is frequently used for this purpose (overview cf. table 1 in [Karnath and Rennig, 2016]). The central aspect of this inferential method is the attempt to control for regions that are not critical for the behavioral deficit under consideration; that is, they aim to rule out regions of the brain that are simply vulnerable to damage and thus commonly damaged in stroke patients. The statistical procedure allowed numerous new insights and replaced the simple lesion overlap strategy, which included marked anatomical biases [cf., Rorden and Karnath, 2004].

One technical assumption of the VLBM method is statistical independence of all voxels, that is, that the lesion status of a voxel is treated independently of the lesion status of adjacent voxels. In reality, however, the anatomy of stroke follows typical patterns that are defined by the vascular trees [Phan et al., 2005; Lee et al.,2009; Sperber and Karnath, 2015]. Two recent studies thus have assessed the localization accuracy of the VLBM method [Inoue et al., 2014; Mah et al., 2014]. Both studies used a simulation approach based on large neurological patient samples with brain damage. They observed a bias within the lesion‐deficit maps, displacing inferred critical regions from their true anatomical locations by about 16 mm toward areas of greater general lesion affection. Mah et al. [2014] speculated that “the pattern of mislocalization across the brain will depend on the complex interaction between the multivariate lesion distribution and brain functional architecture.” They suggested to use novel machine learning techniques—such as multivariate pattern analysis [Smith et al., 2013; Mah et al., 2014; Zhang et al., 2014]—that use high‐dimensional inference to accurately describe the true locus. Multivariate pattern analysis indeed appears to be an enrichment of modern lesion analysis to train and then test predictive models based on the pattern of damage to multiple regions [Karnath and Smith, 2014]. However, this does not necessarily need to rule out the value of VLBM for certain scientific approaches per se.

In fact, the two previous simulation studies [Inoue et al., 2014; Mah et al., 2014] computed the VLBM analyses without the proper use of two commonly used correction factors, which might have led to underestimation of anatomical accuracy. Despite of the very large sample size included by Mah et al. [2014] the authors did not control for lesion size. However, for most behavioral deficits lesion size—independent from lesion location—is the best predictor for severity of the behavioral deficit; larger lesions are more likely to affect critical anatomical structures [Karnath et al., 2004]. If a sufficiently large dataset is available, VLBM studies of real datasets thus control this effect, typically by regressing out lesion size from the behavioral scores. The simulation study by Inoue et al. [2014] indeed corrected for lesion size. Surprisingly, they found VLBM with a correction for lesion size to produce a larger bias than without correction. However, the study by Inoue et al. [2014] was based on a lesion sample very different from the typical stroke samples used in VLBM studies of real datasets. The authors did not only include patients with stroke but also with other etiologies, such as, for example, encephalitis or surgical resections. It appears as if the proportion of non‐stroke patients was very high in that the lesion overlay with frontal and fronto‐temporal maxima markedly differed from the typical topography of unselected strokes with a maximum of overlap in the center of the territory of the middle cerebral artery [Phan et al., 2005; Mah et al., 2014; Sperber and Karnath, 2015]. Thus, it remains to be tested in which way a VLBM study based on only stroke etiology is modified by a correction for lesion size.

A further discrepancy between the simulation study by Inoue et al. [2014] and VLBM studies of real datasets is that the latter typically restrict statistical analysis to voxels that are affected by a certain proportion of lesions. This restriction to only voxels with “sufficient lesion affection” prevents that results are biased by brain regions that are only rarely affected by stroke and thus do not carry sufficient information. In contrast to this common practice, the simulation study by Inoue et al. [2014] did not control for this factor. In the study of Mah et al. [2014], “sufficient lesion affection” was controlled with a criterion of n = 4, equivalent to 0.7% of the total sample. Real VLBM studies usually apply such correction in the range of 5 ≤ n ≤ 10, equivalent to roughly 5–10% of the whole sample [e.g. Goldenberg and Randerath, 2015; Mirman et al., 2015; Tarhan et al., 2015; Timpert et al., 2015; Watson and Buxbaum, 2015].

Taken together, it remains an open question whether or not a VLBM bias occurs under the proper control for lesion size and for “sufficient lesion affection” in a stroke patient sample. If indeed a considerable misplacement remains, it would be interesting to find out the origin of this bias. Mah et al. [2014] speculated that such bias might originate from systematic “parasitic” voxel‐voxel relations of collateral brain damage in the general anatomy of stroke and the lesion‐deficit relation itself, which inevitably stays a black box in real settings. To clarify this question, we aimed to quantify the inter‐voxel relations and experimentally test if these alone are able to predict the size of possible VLBM misplacement.

METHODS

Patients with acute first unilateral, right hemispheric stroke admitted to the Centre of Neurology at the University of Tübingen were recruited. Patients with diffuse, bilateral, or cerebellar lesions, with tumors, marked anatomical distortion due to intracerebral hemorrhage, or patients without obvious lesion in MRI or spiral CT were excluded. A sample of 274 patients (mean age = 61.2 years; SD = 13.5) was recruited. Of these patients, 233 had an infarct and 41 a hemorrhage. Patients or their relatives gave informed consent to participate in our study, which was performed according to the ethical standards laid down in the 1964 Declaration of Helsinki.

Brain lesions were demonstrated by MRI in 144 cases and by spiral CT in 130 cases. On average, imaging was acquired 4.5 days (SD = 7.4 days) after stroke onset. Binary lesion maps were created by manual delineation of lesion boundaries on axial slices of the patient's individual scan using MRIcron (http://www.mccauslandcenter.sc.edu/mricro/mricron). For patients who underwent MR scanning, diffusion‐weighted imaging in the hyper acute stage until 48 hours after stroke onset and T₂‐weighted fluid attenuated inversion recovery imaging in later stages after stroke onset were used to delineate the lesions. If available, these scans were co‐registered with a high‐resolution T₁‐weighted structural scan using SPM8 (http://www.fil.ion.ucl.ac.uk/spm). Brain scans were warped into MNI space with 1 × 1 × 1 mm³ resolution using SPM8 spatial normalization algorithms and the Clinical Toolbox [Rorden et al., 2012], which provides age‐specific templates both for MRI and CT scan normalization. Delineation of lesion borders and quality of normalization were verified by consensus of two experienced investigators.

EXPERIMENT 1: THE SPATIAL BIAS OF VLBM IN A REALISTIC ANALYSIS SETTING

To investigate the performance of VLBM, two previous studies [Inoue et al., 2014; Mah et al., 2014] used simulated “behavioral” scores instead of the patients' real behavior to avoid circular reasoning. A priori, a so called “truth model” which was thought to be the neural substrate of the simulated behavior was selected. The “truth model” was defined by a brain region taken from a brain atlas [Inoue et al., 2014; Mah et al., 2014] or was even as simple as a single voxel [Mah et al., 2014]. Subsequently, an algorithm to compute continuous simulated “behavioral” scores from damage to the truth model brain regions was implemented. Based on this algorithm “behavioral” scores were calculated as a function of damage to these brain regions. As a final step, these truth model brain regions were compared to the voxel‐wise, three‐dimensional statistical map that was obtained in a VLBM analysis. The present experiment used a simulation procedure analogous to these previous simulation procedures. The aim was to test the impact of additional control for lesion size and for “sufficient lesion affection.”

Simulation of “Behavioral” Scores

To define our truth model, we chose the Automatic Anatomic Labeling atlas (AAL) [Tzourio‐Mazoyer et al., 2002] distributed with MRIcron, providing 45 right hemisphere cortical and subcortical regions. As the AAL atlas is slightly larger (few voxels at the borders) than the templates used for normalization, overlaying voxels were manually removed from the AAL. In line with the two previous simulation studies [Inoue et al., 2014; Mah et al., 2014], we chose a simple algorithm to compute continuous simulated scores from damage to the truth model. This strategy appears convincing as (a) no realistic mathematic model of lesion‐score relationship exists and (b) a simple simulation model should be affected by a bias genuine to VLBM the same way as a complex model. The simplest model to compute continuous scores based on damage to brain areas is a linear model, that is, a model that computes “behavioral” scores s as a linear function of the proportion of the damage to a truth model area x: $s\left(x\right)=a\ast x$.

The “behavioral” scores were set between 0 (no deficit) and 100 (maximal deficit). For example, a patient without any damage to a given area received a simulated “behavioral” score of 0 and a patient with 27% damage of all voxels in this area received a score of 27. For each of the 45 AAL regions, we performed three simulation runs, each with randomly drawn samples of 100 lesions, resulting in 135 simulations per condition. Limiting sample size to 100 lesions allowed us to draw conclusions for real VLBM settings. The simulation was implemented using custom scripts in MATLAB 2009 and the “Tools for NIFTI and ANALYZE image” toolkit (http://www.mathworks.com/matlabcentral/fileexchange/8797-tools-for-nifti-and-analyze-image).

Comparison of the Statistical VLBM Map and Truth Model

To reduce computational demands, we chose a mass‐univariate t‐test with false discovery rate (FDR) correction, implemented in Nii‐Stat software (http://www.nitrc.org/projects/niistat/). This test is commonly used in modern VLBM studies and requires only minimal computational power. All statistical analyses were tested for a P = 0.05 level. One of our hypotheses was that limiting the analysis to only voxels with sufficient “general lesion affection” should improve the performance of VLBM. In accordance with a widely accepted criterion, we defined the threshold for “sufficient affection” as 5% of the whole sample. We contrasted the effect of data restriction to voxels with “sufficient affection” to the procedure without this restriction by setting Nii‐Stat to only test voxels at least damaged in n = 5 patients (equal to 5%) versus to test all voxels at least damaged in n = 1 patient. In particular, the latter condition has been used in the simulation study by Inoue et al. [2014]. However, if voxels with less than 5% lesion affection were still included in our simulation as a part of truth model brain regions—while excluding the same from the analysis—this would a priori cause inability of any lesion analysis method to identify the truth model. Therefore, we not only applied the 5%‐criterion in the analysis as a correction factor but we also introduced a further condition were we applied the 5%‐criterion in the analysis as well as the simulation. For this condition, we simulated scores based on an alternative set of truth model brain regions that only covered aforementioned voxels. In detail, we created a modified version of the AAL by simply removing all voxels that did not fulfill the 5%‐criterion. Seven regions were eliminated completely (supplementary motor area, medial superior frontal gyrus, orbital part of middle frontal gyrus, anterior cingulum, middle cingulum, posterior cingulum, paracentral lobule). This modified AAL offered a second, alternative set of truth models that considered “sufficient lesion affection” already in the simulation.

Our second hypothesis was that controlling for lesion size improves VLBM performance. We thus carried out a VLBM analysis on each subsample once without controlling for lesion size and once with controlling for lesion size. To implement a control for lesion size, we used the built‐in default procedure of Nii‐Stat: before the mass‐univariate test is computed, lesion size is linearly regressed on the behavioral scores. Following this regression, we used the residuals for the actual VLBM analysis.

As dependent variables we included the same measurement of spatial misplacement defined by the centers of mass of truth model and statistical map as used in the two previous simulation studies by Mah et al. [2014] and Inoue et al. [2014]. In detail, for each simulation step an a priori truth model region and a statistical map were available. For both these three‐dimensional binary images, the center of mass was calculated and the Euclidean distance was measured. Additionally, we calculated “sensitivity” (true positive rate: hits/(hits + false negatives)) and “precision” (positive predictive value: hits/(hits + false positives)). The advantage of these parameters is that they do not rely on correct rejections, as these might be inflated due to the size of the image bounding box. In fact, the study by Inoue et al. [2014] found this parameter to be close to ceiling level across all groups.

Results

The sample of 274 lesions covered nearly the total right hemisphere and 770,556 voxels were damaged in at least one patient (Fig. 1A). A majority of lesions lay in the territory of the middle cerebral artery with a center of affection around putamen and insula. The topography closely resembled the one on stroke patients provided in the supplementary material in Mah et al. [2014]. Of these 770,556 voxels, 81.4% were covered by at least 5% of all lesions (equivalent to 14 lesions) (Fig. 1B).

Figure 1.

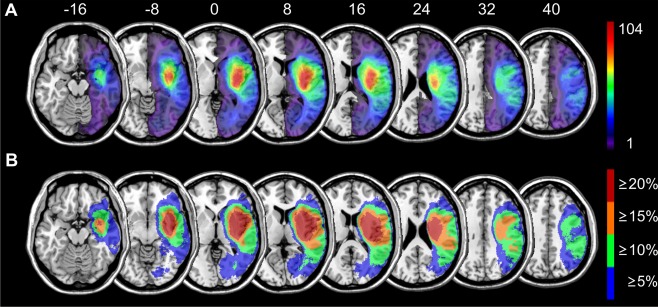
Topography of brain lesions. Lesion topography for all 274 patients with (A) continuous color scaling and (B) with an alternative step‐wise color scaling to show all voxels that were damaged in at least x% of all patients. Numbers above the slices indicate z‐coordinate in MNI space. [Color figure can be viewed at http://wileyonlinelibrary.com]

Our two hypotheses were tested in a 3 × 2 design, with factors “control for sufficient lesion affection” (not controlled with n = 1 criterion; controlled in the analysis only with n = 5 criterion; controlled in analysis and simulation with n = 5 criterion) and “control for lesion size” (controlled; not controlled). Over 97% of all VLBM analyses yielded significant results and were included into the final analysis. As both factors were only partially paired, a repeated measure ANOVA could not be computed. Therefore, as often done in this situation [e.g., Samawi and Vogel, 2013], we here calculated and report results of an independent ANOVA. In addition, we performed repeated measures ANOVA only using available paired data; all significant results of the repeated measures ANOVA turned out to be significant again and thus are not reported here. In case of significant effects, Bonferroni‐corrected post hoc tests were calculated. Averaged over all groups, the misplacement was 18.6 mm (SD = 11.3 mm). The ANOVA revealed that misplacement was affected by “control for sufficient lesion affection” (F(2,739) = 14.02; P < 0.001) and “control for lesion size” (F(1,739) = 88.73; P < 0.001) (Fig. 2A). Both factors did not interact (F(2,739) = 1.55; P = 0.21). Post hoc tests showed that misplacement was lower if VLBM analyses were controlled for lesion size and for “sufficient lesion affection” both in the analysis and simulation. Under these conditions, misplacement was reduced to 11.5 mm (SD = 6.3 mm). Sensitivity was generally high (Sens. = 0.73; SD = 0.33) (Fig. 2B). Factor “control for sufficient lesion affection” had a significant impact on sensitivity (F(2,739) = 130.88; P< 0.001) with the n = 5 criterion in both simulation and analysis outperforming the other groups. Factor “control for lesion size” neither affected sensitivity as a main effect (F(1,739) = 1.21; P = 0.27) nor in an interaction with “control for sufficient lesion affection” (F(2,739) = 0.67; P = 0.51). “Precision” was generally very low (prec. = 0.12; SD = 0.11) and was affected both by “control for lesion size” (F(1,739) = 186.84; P < 0.001) and “control for sufficient lesion affection” (F(2,739) = 8.09; P < 0.001) (Fig. 2C). Again, the interaction was not significant (F(2,739) = 0.73; P = 0.48). “Control for lesion size” improved “precision”; post hoc tests revealed that “control for sufficient lesion affection” with the n = 5 criterion in both simulation and analysis was inferior to the general n = 1 criterion. These two groups did not significantly differ from the condition with the n = 5 criterion in the analysis only.

Figure 2.

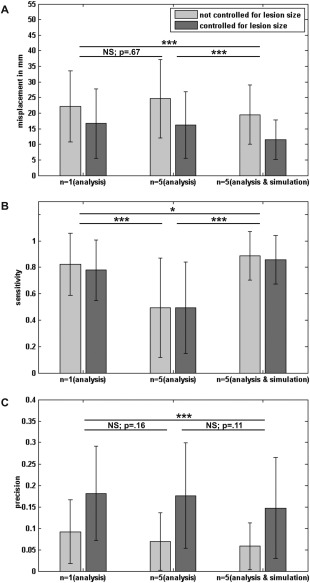
Effects of factors “control for lesion size” and “control for sufficient lesion affection” in VLBM analysis. Results of the 3 × 2 ANOVA conducted in Experiment 1 addressing the effects of factors “control for lesion size” and “control for sufficient lesion affection” in VLBM for (A) misplacement, (B) sensitivity, and (C) precision. Error bars represent standard deviation. Asterisks indicate significance in post hoc tests on the effects of “sufficient lesion affection” control (*P < 0.05, ***P < 0.001).

The simulated behavioral scores correlated with lesion size both in the condition with the full AAL simulation (average correlation r = 0.43; SD = 0.21) and with the modified AAL simulation (for “sufficient lesion affection”; average correlation r = 0.47; SD = 0.22). This is in the range of behavior‐lesion size correlations in real patient data, that may range from low, non‐significant correlations to high correlations of r = 0.7 [e.g., Kertesz and Ferro, 1984; Brott et al., 1989; Wittmann et al., 2004]. The average peak t‐values of statistical maps were t = 8.51 (SD = 0.72) for all simulations and t = 7.99 (SD = 0.62) for simulations both controlled for lesion size and “sufficient lesion affection” (see Fig. 3 for example t‐maps). Thus, our simulation‐based peak t‐values were in the high upper range of peak t‐values in real VLBM studies [e.g., Verdon et al., 2010].

Figure 3.

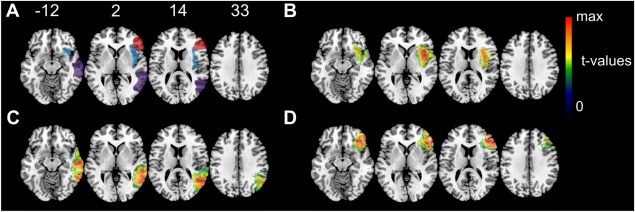
Example t‐maps. For three regions of interest example t‐maps from Experiment 1 are shown. All maps originate from the condition with both control for lesion size and “control for sufficient lesion affection” in simulation and analysis. (A) Three regions of interest taken from the AAL atlas: insula (blue), middle temporal gyrus (purple), and inferior frontal gyrus, triangular (red) (B) VLBM results for the insula with t(max) = 7.35 (C) VLBM results for the middle temporal gyrus with t(max) = 7.91 (D) VLBM results for the inferior frontal gyrus, triangular with t(max) = 8.04. Color coding in B–D indicate t‐values thresholded to only show voxels with significant t‐values P < 0.05. Numbers above the slices indicate z‐coordinate in MNI space. [Color figure can be viewed at http://wileyonlinelibrary.com]

Discussion

Simulation Experiment 1 revealed that misplacement of VLBM results can be minimized by the use of lesion size as a covariate and the exclusion of voxels with low lesion affection. Under these conditions, the misplacement could be reduced by 48% compared to uncorrected VSLM, adding up to only 11.5 mm (Fig. 2A). The following experiment should clarify whether this bias is due to natural stroke anatomy determined by the vascular architecture and systematically biased inter‐voxel relations of collateral damage, that is, if it represents an “anatomical bias.”

EXPERIMENT 2: EFFECTS OF STROKE ANATOMY ON VLBM

Mah et al. [2014] computed voxel‐wise VLBM misplacement vectors, that is, vectors based on the misplacement of statistical VLBM results compared to a truth model region/voxel, indicating that such results were systematically biased. In contrast, we here aimed to calculate voxel‐wise vectors based on the patients' anatomical data, that is, on the data before any statistical analyses were applied. Therefore, we generated voxel‐wise topographies of collateral damage in the real data and used them to compute a metric for the inter‐voxel relation of brain damage. If indeed inter‐voxel relations should be the cause for the misplacement in lesion mapping, the VLBM‐misplacement vectors observed by Mah et al. [2014] should be reliably predictable by our “anatomical bias” vectors based on anatomy.

A Voxel‐Wise Vector for “Anatomical Bias”

For each simulation run, first a voxel (truth model voxel) was chosen. To define the target point of an anatomical bias vector, that is, a center of anatomical affection, we identified all lesions that included this truth model voxel to create a “voxel overlay” (Fig. 4A). This topography already offers information on the anatomy of stroke that affects the truth model voxel. However, it neglects lesions that do not include the truth model voxel. Therefore, we calculated an element‐wise division of the voxel overlay divided by the overlay of the whole 274 patient sample (Fig. 1A) to produce topographies of inter‐voxel relation. This results in a single topography for each chosen truth voxel individually (Fig. 4B). The values in this topography indicate how many lesions that lie in any voxel also include the truth voxel. The proportional values vary between 0 (0% of all lesions in this voxels also contain the truth model voxel) and 1 (100% of all lesions in this voxel also contain the truth model voxel). For example, if in the topography for a certain truth model voxel any voxel contains the value 0.27, this means that 27% of all lesions in this voxel also damaged the truth model voxel. To prevent a high impact of voxels that are generally rarely affected by stroke and to stay close to the study by Mah et al. [2014], we limited this analysis to voxels that were damaged in at least four patients. The center of mass of this topography was identified (Fig. 4B) and used to define a vector of “anatomical bias” (purple vector in Fig. 4D). Due to high computational demands, this analysis was not carried out for the whole brain, but for 100 randomly chosen voxels.

Figure 4.

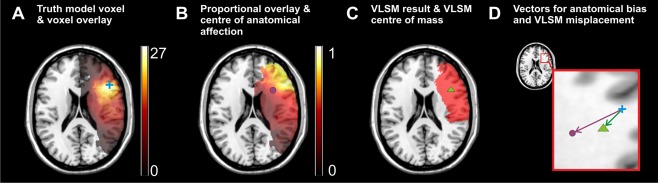
Example for the computation of voxel‐wise anatomical bias and VLBM misplacement. For one exemplary truth model voxel (MNI coordinates x = 47, y = 24, z = 20), the procedures in Experiment 2 are illustrated. (A) All lesions that include the chosen truth model voxel (blue cross) are identified to create a “voxel overlay.” (B) For each voxel damaged in at least four patients, the “voxel overlay” is element‐wisely divided by the total overlay of all 274 patients (see Fig. 1A) to produce a topography of inter‐voxel relation. The center of mass of the resulting topography (purple circle) offers a voxel‐wise center of anatomical affection. (C) The truth model voxel is used to simulate a binary “behavioral” deficit. A lesion analysis computes a statistical map (red area) and the center of mass of this map (green triangle) provides the center of VLBM results. (D) The previously defined coordinates and the truth model voxel (blue) are used to define a vector of “anatomical bias” (purple arrow) and a vector of misplacement (green arrow). All illustrations are shown on slice z = 20. Note that for the present figure the resulting centers are projected back to same z‐slice for illustration purposes. [Color figure can be viewed at http://wileyonlinelibrary.com]

A Voxel‐Wise Vector for Misplacement

The creation of a voxel‐wise VLBM misplacement vector was implemented analogous to the study by Mah et al. [2014]. Given a truth model voxel, a binary “behavioral” score was simulated. If the lesion of a patient also included damage to the truth model voxel, the patient received a behavioral score of “1” (present deficit); else he received a “0” (no deficit). These “behavioral” scores were used in a lesion analysis on the whole 274 patients data sample in Nii‐Stat, using the Liebermeister test [Rorden et al., 2007] and FDR correction. Only voxels damaged in at least four patients were investigated. This analysis of simulation data yielded a binary statistical map for each truth model voxel (Fig. 4C). The misplacement was defined as the vector from the truth model voxel to the center of mass of this statistical map (green vector in Fig. 4D).

Results

The 100 randomly chosen voxels were damaged in at least 13 and maximally 96 of all 274 patients (mean = 32.7; SD = 18.1). For each of these voxels, we calculated the VLBM misplacement vectors (Fig. 5A) and anatomical misplacement vectors (Fig. 5B). On average the anatomical misplacement vector was 25.7 mm (SD = 7.7 mm) long. Using a FDR correction at P = 0.05, the average VLBM misplacement vector for the same voxels was 18.3 mm (SD = 6.1 mm) long and thus significantly smaller than the anatomical misplacement vectors (t(99) = 16,66; P< 0.001). As the length of the VLBM misplacement vectors depended solely on false alarms—and thus on how conservative a test is—we ran a second simulation on the same voxels, but with a FDR correction at P = 0.01. For this more conservative test, the misplacement was 16.3 mm (SD = 5.5 mm) and significantly lower than with the less conservative test (t(99) = 15,98; P < 0.001). The length of vectors for VLBM misplacement and for anatomical bias correlated highly both for FDR correction at P = 0.05 (Pearson's R = 0.82; P < 0.001) and P = 0.01 (R = 0.76; P < 0.001). To measure directional similarity, we computed the cosine similarity that ranges between 1 if two vectors have the same direction and −1 if they point into the opposite direction. If two vectors are exactly orthogonal, cosine similarity is 0. Cosine similarity was cos(θ) = 0.91 (SD = 0.12) for P = 0.05 and cos(θ) = 0.88 (SD = 0.15) for P = 0.01. Thus, although anatomical vectors were significantly larger than misplacement vectors, both sets of vectors appeared to be highly similar.

Figure 5.

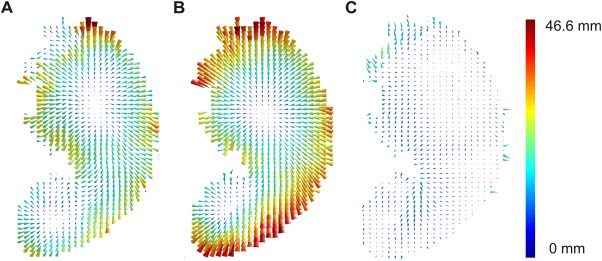
Vector maps for “anatomical bias,” VLBM misplacement, and corrected VLBM misplacement. The vector graphics visualize the results of Experiment 2 exemplarily for slice z = 17. (A) Vector map for the misplacement of statistical VLBM results at P = 0.05. (B) Vector map for “anatomical bias.” Voxel‐wise vectors here were based on the inter‐voxel relation in the anatomical data, that is, on the data before any statistical analyses were applied. (C) Vector map for “corrected misplacement vectors” using the minimization factor k = 0.6495. For illustration purposes, the length of the vectors does not show the real vector length, but is scaled using the same factor in all graphics. Color‐coding indicates the length of the vectors in mm. [Color figure can be viewed at http://wileyonlinelibrary.com]

Considering the similarity of the vectors and the assumption, that an “anatomical bias” is the reason for a VLBM misplacement, one should be able to predict VLBM misplacement with the “anatomical bias” and thus correct the VLBM misplacement. Therefore, we computed the position vector of the VLBM center of mass and subtracted the “anatomical bias” vector, that is, we corrected the VLBM center by the information provided from inter‐voxel relation of brain damage in the anatomical data. The distance between the truth model voxel and this new corrected center of VLBM results was expressed as “corrected misplacement vectors.” On average the corrected misplacement vector was 11.2 mm (SD = 3.2 mm) long for P = 0.05 and 13.1 mm (SD = 4.0 mm) long for P = 0.01. Given the different sets of misplacement vectors for varying P‐levels and the larger vectors for anatomical misplacement, we expected lower “corrected misplacement vectors” for more optimal correction with vectors individualized for the chosen P‐level. Therefore, for both P‐levels, we looked at every pair of misplacement vector $\overrightarrow{m}$ and anatomical bias vector $\overrightarrow{ab}$ and searched via minimization function for a factor k for which the corrected misplacement $c=|\overrightarrow{m}-k\ast \overrightarrow{ab}|$ was minimal. For a significance level of P = 0.05, the corrected misplacement was minimized by an average factor of k = 0.6495. This minimization factor was applied to the “corrected misplacement vectors” (Fig. 5C). On average, these “corrected misplacement vectors” had a length of 6.8 mm (SD = 2.9 mm), which was a significant improvement compared to the uncorrected misplacement (t(99) = 19,48; P< 0.001). For a significance level of P = 0.01, we found k = 0.5655 to be the average optimal factor that significantly reduced uncorrected misplacement to 7.0 mm (SD = 3.0 mm) (t(99) = 17,38; P< 0.001. Cosine similarity between the original misplacement vector and this corrected misplacement vector was cos(θ) = 0.34 (SD = 0.42) for P = 0.05 and cos(θ) = 0.40 (SD = 0.41) for P = 0.01.

Discussion

Experiment 2 tested if VLBM misplacement can be predicted by its underlying stroke anatomy. In fact, we revealed that the “anatomical bias” based on the inter‐voxel relation affected the VLBM results. In other words, measurable aspects of stroke anatomy indeed appear to be the source of VLBM misplacement. The VLBM‐misplacement vectors observed by Mah et al. [2014] thus can be reliably predicted by our “anatomical bias” vectors based on anatomy.

GENERAL DISCUSSION

The concept of a correction for lesion size by linear regression has recently been criticized on a theoretical level [Nachev, 2015]: as lesion size varies with anatomical location, it was argued that the correction would confound the anatomical interference and could even amplify the misplacement of VLBM results. In contrast to this assumption, we here observed in a large sample of stroke patients that lesion size in fact has a significant impact on VLBM accuracy. A closer look at the inter‐voxel relation explains this effect: larger lesions inflate the number of “parasitic” inter‐voxel relations over long distance (see Fig. 4A,B) and thus enlarge the bias in VLBM. Beyond, the present simulation demonstrated that the VLBM misplacement is reduced by controlling for rarely affected brain areas (control for sufficient lesion affection). In combination, the use of factors “correction for lesion size” and “sufficient lesion affection” markedly reduced the misplacement of VLBM results compared to uncorrected VSLM. The two variables reduced VLBM misplacement in an additive manner, that is, both correction factors independently improved VLBM accuracy.

The correction factors “lesion size” and “sufficient lesion affection” also increased variables “sensitivity” and “precision.” Variable “sensitivity” was very high in general, thus the actual anatomical correlate of a simulated behavior was correctly identified together with a high number of false alarms that were spatially oriented in the direction of the misplacement. The operationalization of “misplacement” used in the present as well as the two previous simulation studies [Inoue et al., 2014; Mah et al., 2014] thus could be criticized, as the simple Euclidean distance between two centers of mass omits such information and can result from an infinite number of different configurations that can differ in sensitivity, precision, and so forth. This problem is underlined by the fact that many VLBM studies provided results that were not located primarily in subcortical structures but rather at cortical gray matter regions [e.g., Karnath et al., 2004; Kalénine et al., 2010; Karnath et al., 2011; Manuel et al., 2013; Mirman et al., 2015], although a pure misplacement effect should shift cortical structures toward the center of the vascular territories.

Although the control for “sufficient lesion affection” improved performance of VLBM analyses, it is important to note that this method at the same time limits VLBM analyses. In the literature, VLBM studies usually provide a simple overlay topography of all lesions and display results on a template for the whole brain. The fact that such studies actually did not test parts of the brain is often not referred to explicitly. However, VLBM analyses self‐evidently do not provide any information about brain areas that are not tested, that is, that fall below the criterion for “sufficient lesion affection.” Therefore, we included the non‐realistic experimental condition with control for “sufficient lesion affection” in analysis and simulation into Experiment 1. This condition simulated behavioral scores only based on areas that were above the criterion for “sufficient lesion affection.” With this condition, Experiment 1 has shown that control for “sufficient lesion affection” improves performance of VLBM within the area of tested voxels. At the same time, the condition with control for “sufficient lesion affection in the analysis only” has shown that this correction also impairs VLBM if related to the whole brain. While misplacement was not significantly affected, sensitivity was decreased. This is not surprising, as positive signals could not be identified in voxels that were not tested and misses thus were inflated. To conclude, limiting VLBM for “sufficient lesion affection” trades in spatial extent of the analysis (i.e., less voxels are tested) for a more valid VLBM performance in voxels that are tested. This conclusion can be transferred to real VLBM studies. Contrary to the present condition with “sufficient lesion affection in simulation and analysis,” in real VLBM studies brain regions relevant to behavior might also lie in brain areas that are not tested, that is, that are removed from the analysis due to correction for “sufficient lesion affection.” Such areas thus should be considered as a black box that still could contribute to behavior. Following this principle, the condition with “sufficient lesion affection in simulation and analysis” in our present study is transferrable to real VLBM studies.

The misplacement of statistical VLBM maps apparently is due to physiological effects of brain lesion anatomy. Lesion anatomy here includes the lesion‐deficit relationship as well as the inter‐voxel relation. While the lesion‐deficit relationship describes the relationship between the lesion of a certain region and its behavioral consequences, inter‐voxel relation is the voxel‐wise topographies of collateral damage. In a simple simulation setting that was comparable to the simple simulation settings in the two previous studies [Inoue et al., 2014; Mah et al., 2014], we successfully corrected the VLBM misplacement by “anatomical bias” vectors, solely calculated from inter‐voxel relations in the patients' real anatomical data. However, in the present as well as in the two previous simulation studies [Inoue et al., 2014; Mah et al., 2014] the lesion‐deficit relationship only played an intermediate role as it was used to compute simulated “behavioral” scores—based on a stroke anatomy with systematically biased inter‐voxel relations. A systematic bias in the lesion‐deficit relationship itself (e.g., higher impact of subcortical voxels inside a single truth model region on simulated behavioral scores) was not introduced. Thus, the biased inter‐voxel relation alone was the reason for VLBM misplacement. Furthermore, magnitude of VLBM misplacement was affected by the VLBM's P‐level; however, the correlation between misplacement and “anatomical bias” was high in both tested P‐values.

In VLBM studies of real datasets, it is unlikely that systematically biased lesion‐deficit relations itself generally contribute to the VLBM misplacement. The black box of lesion‐deficit relations rather plays a mediating role, as it determines the severity of a deficit based on lesions that suffer from biased inter‐voxel relations. Given that the inter‐voxel relation data is the main source of VLBM misplacement, magnitude and direction of VLBM misplacement could be estimated and new correction algorithms that even further improve validity of VLBM results are imaginable. A possibility for such prospective correction could be an anatomical parcellation atlas that incorporates the anatomy of stroke and the underlying inter‐voxel relation—at the cost of data resolution compared to a voxel‐wise analysis. Also, the development of retrospective correction algorithms is imaginable. Using a valid anatomical reference sample such algorithms could be applied post hoc on previous VLBM studies. As Experiment 2 was based on a simple simulation model and “anatomical bias” depended on VLSM parameters, more complex algorithms will be required for such purpose. Possible candidates for such corrections that are able to identify spurious results versus true results are, for example, voxel‐wise vectorial algorithms or a seed‐based approach that directly uses the inter‐voxel relations (analogous to, e.g., resting state analyses [Fox and Raichle, 2007]).

To conclude, the misplacement bias in VLBM results is in fact much smaller if appropriate correction factors are used. Although such correction might be biased by the variability of lesion size across the brain [Nachev, 2015], positive effects obviously prevail. The misplacement appears to be due to physiological effects of brain lesion anatomy. The latter has the potential to help in the development of new VLBM methods providing even higher validity than currently available by the proper use of correction factors.