The functional architectures of addition and subtraction: Network discovery using fMRI and DCM

Abstract

The neuronal mechanisms underlying arithmetic calculations are not well understood but the differences between mental addition and subtraction could be particularly revealing. Using fMRI and dynamic causal modeling (DCM), this study aimed to identify the distinct neuronal architectures engaged by the cognitive processes of simple addition and subtraction. Our results revealed significantly greater activation during subtraction in regions along the dorsal pathway, including the left inferior frontal gyrus (IFG), middle portion of dorsolateral prefrontal cortex (mDLPFC), and supplementary motor area (SMA), compared with addition. Subsequent analysis of the underlying changes in connectivity – with DCM – revealed a common circuit processing basic (numeric) attributes and the retrieval of arithmetic facts. However, DCM showed that addition was more likely to engage (numeric) retrieval‐based circuits in the left hemisphere, while subtraction tended to draw on (magnitude) processing in bilateral parietal cortex, especially the right intraparietal sulcus (IPS). Our findings endorse previous hypotheses about the differences in strategic implementation, dominant hemisphere, and the neuronal circuits underlying addition and subtraction. Moreover, for simple arithmetic, our connectivity results suggest that subtraction calls on more complex processing than addition: auxiliary phonological, visual, and motor processes, for representing numbers, were engaged by subtraction, relative to addition. Hum Brain Mapp 38:3210–3225, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Neuroimaging studies have shown that mental arithmetic is not only a basic daily faculty but provides a powerful paradigm for characterizing fundamental cognitive processes underlying abstract problem solving in a variety of domains, such as magnitude representation, executive control, verbal processes, and sensorimotor concepts [Ansari, 2008; Houde et al., 2010; Nieder and Dehaene, 2009, for a review]. Moreover, pragmatically, an explicit understanding of the neural mechanisms of arithmetic calculations may also provide new pointers for education [De Smedt et al., 2011]. With an increasing knowledge of the human brain's functional anatomy, the core processes of arithmetic calculations that support mental manipulation of numerical quantities (e.g., magnitude comparison) have been associated with the bilateral intraparietal sulci (IPS) [Ansari, 2008; Dehaene et al., 2003]. Another breakthrough in mental arithmetic – in neuroimaging – is the finding of the dissociation of cognitive processes that underlie mental subtraction and multiplication [Yi‐Rong et al., 2011; Zhou et al., 2006]. Nevertheless, with respect to the two simplest operations we learn early in life, little is known about whether addition and subtraction employ shared or separate cognitive procedures or neuronal processes. Against this background, we conducted a functional magnetic resonance imaging (fMRI) study of mental arithmetic and examined the neuronal correlates of addition and subtraction – and how they were related.

Converging evidence has identified the fronto‐parietal network – including the parietal and prefrontal cortices – as the main cortical frame that supports mental arithmetic [Arsalidou and Taylor, 2011]. However, dissociations have been observed between arithmetic operations, especially between subtraction and multiplication. Functional neuroimaging data in healthy adults have revealed that the intraparietal sulcus and the posterior superior parietal lobe are more active during subtraction than during multiplication; whereas the left angular and supramarginal gyri are modulated to a greater degree by multiplication relative to subtraction [Chochon et al., 1999; Ischebeck et al., 2006]. The engagement of different strategies has been proposed to account for this dissociation [Barrouillet et al., 2008; Campbell and Xue, 2001; Dehaene et al., 2003]. Multiplication is being attributed to rote arithmetical fact retrieval, which engages the left perisylvian language areas and modularizes phonological associations between a digit pair and their answer. In contrast, subtraction requires quantitative procedural strategies (i.e., an analogue mental number line) that rely on the intraparietal sulci. This hypothesized recruitment of distinct neural networks is supported by (double dissociation) lesion studies: lesions in the left perisylvian cortex result in impairments in multiplication but not subtraction, whereas lesions to regions of the intraparietal cortex lead to difficulties with subtraction but not multiplication [Dehaene and Cohen, 1997; Dehaene et al., 2003].

By contrast, neuroimaging studies focusing on the relationship between addition and subtraction are relatively scarce. Behavioral studies have shown significantly longer reaction times and lower accuracy in subtraction than in addition [Campbell et al., 2006; Klein et al., 2014]. However, it remains unclear how neuronal processes contributes to these differences. Three kinds of hypotheses can be invoked to explain these differences: (1) strategic differences; (2) differences in hemispheric lateralization; and (3) differential processing complexity. First, compared to the consensus about the use of quantity‐based (quantitative) processes in subtraction, the computational strategies involved in addition are still debated. Some studies have suggested that addition, like multiplication, depends on a strategy based on retrieval of rote arithmetic facts, rather than a “subtraction strategy” [Schmithorst and Brown, 2004]. A recent study using fiber tractography supported the shared strategy of fact retrieval in both multiplication and addition, in view of the positive correlation observed in arithmetic competency (for both multiplication and addition) and the fractional anisotropy in the left anterior portion of the arcuate fasciculus – that was considered to subserve phonological processing and link the frontal and inferior parietal cortices [Van Beek et al., 2014]. Further evidence endorsing the retrieval hypothesis comes from studies of children. De Smedt et al. [2011] reported a dissociable pattern in children aged 10‐12 years who engaged the fronto‐parietal network during subtraction but only activated the left hippocampus during addition. This suggests reliance on the hippocampus for arithmetic fact retrieval during addition in the early stages of learning arithmetic facts. Cho et al. [2012] reported a consistent activation of prefrontal and hippocampal regions during mental addition in 7‐9‐year‐old children. However, there are some observations that cannot be explained by a common strategy hypothesis for addition and multiplication, such as common activation by both addition and subtraction in the parietal regions associated with procedural calculation [Yi‐Rong et al., 2011], and evidence suggesting distinct cerebral processes between addition and multiplication [Rosenberg‐Lee et al., 2011; Zhou et al., 2006; Zhou et al., 2007]. Furthermore, individual growth and functional maturation might result in a shift from a memory‐based frontal activation to the quantity‐specific parietal activation during arithmetic processing [Rivera et al., 2005]. Secondly, hemispheric asymmetries in parietal were distinguished by operation types: the intraparietal activation was more prominent in the right hemisphere during a quantity‐related comparison task [Chochon et al., 1999]. A triple‐code model suggested quantity manipulation in bilateral hemispheres during subtraction, relative to left‐lateralized reliance of verbal arithmetic facts during addition and multiplication [Dehaene and Cohen, 1997]. This dissociable pattern was supported by laterality indices from a meta‐analysis [Arsalidou and Taylor, 2011]. Nevertheless, recent evidence has demonstrated that this lateralized dominance might not be fixed: children with developmental dyslexia accompanied by reading disability and subtle deficits in retrieval‐based arithmetic engaged the right parietal regions for both addition and subtraction – and showed no significant difference in performance compared with healthy controls [Evans et al., 2014]. Third, a new theory challenging the former hypotheses has been proposed, claiming that differences between different mathematical operations, reported in prior studies, may have emerged due to invalid measures of complexity, rather than dissociable strategies or neuronal circuits [Tschentscher and Hauk, 2014]. Klein et al. [2010] investigated addition with different levels of difficulty (larger sum vs. smaller sum, carry vs. non‐carry) and proposed a flexible use of strategies based on the difficulty or complexity level. Easier problems (with smaller sums) appear to engage the ventral pathway, associated with the temporo‐parietal areas and subcortical‐limbic areas, which are thought to subserve a fact‐retrieval strategy. More difficult problems (with larger sums) activated the dorsal pathway associated with the fronto‐parietal areas, which appears to subserve magnitude‐related (quantitative) procedural processing. A recent fiber tracking study suggested a predominance of ventral fiber tracks for easy arithmetic, and dorsal as well as ventral streams for complex arithmetic tasks [Klein et al., 2013].

To address the ambiguity about the neuronal processes underlying addition and subtraction, effective connectivity analysis can be used to characterize distributed and context‐sensitive neuronal processing by estimating the influence that one neural system exerts over another at a neuronal level [Friston, 2011]. In this study, we examined the directed (effective) connectivity among brain regions during addition and subtraction with dynamic causal modeling (DCM) [Friston et al., 2003]. This biophysical model of the underlying neuronal interactions among an a priori selected set of brain regions (nodes) is based on a system of bilinear differential state equations with coupling parameters specified by three matrices (A matrix, B matrix, and C matrix) [Friston et al., 2003]. These parameters correspond to the effective connectivity. The purpose of DCM is to estimate the coupling parameters of a model and evaluate how well a particular model explains the observed data. In other words, one first identifies the best model, in terms of which parameters exist – and then one examines the parameter estimates to make inferences about directed coupling among regions. This involves inferring which nodes receive average (or fixed) connections from other nodes (encoded by the A matrix parameters), which specific connections are modulated (i.e., enhanced or reduced transmission between nodes) by experimental conditions (encoded by the B matrix parameters), and which nodes receive driving inputs (stimuli) from experimental manipulations (encoded by the C matrix parameters). Typically, several pre‐specified models can be compared, and one model that represents the best explanation for the data among hypothesized models can be identified by Bayesian model selection (BMS) [Penny et al., 2004]. Alternatively, one can perform an exhaustive search over all possible combinations of connections to identify the best model – all average the parameter estimates over models to produce the Bayesian parameter average. In this work, we will use Bayesian model reduction to perform exhaustive searches over all combinations of connections (and how they change between addition and subtraction) to identify the underlying functional architecture. This is known as structure learning or network discovery.

In this study, we invited healthy subjects to solve simple addition and subtraction problems. Blood‐oxygen‐level‐dependent changes were measured during addition and subtraction. After establishing regionally specific activations using standard whole brain (SPM) analyses, DCM network discovery was performed to identify the optimum operation‐specific model, and the associated intrinsic (within‐node) and extrinsic (between‐node) connections. The resulting coupling parameters were used to interpret the context‐sensitive changes in connectivity imposed by each arithmetic operation. We used simple (as opposed to complicated) arithmetic problems to increase the likelihood that the patterns of activations – and the implicit connections between different brain systems – would dissociate. In other words, by keeping the cognitive operations simple, we hoped to engage the extra cognitive processes required for subtraction that were not needed for simple addition.

MATERIALS AND METHODS

Participants

Data from 20 Chinese college graduates (9 females) with a mean age of 25.76 (SD = 3.76) years were included in the final analysis. Data from 3 participants were excluded due to unacceptable head movements within the scanning sessions. All of the participants were right‐handed, educated with identical schooling, had normal or corrected‐to‐normal vision, and reported no history of neurological or psychiatric disorders. Prior to their participation in the study, written informed consent was obtained from each participant after the nature and possible consequences of the studies were explained. This study was approved by the Ethics committee of Xuanwu Hospital, Capital Medical University, Beijing.

Stimuli and Procedure

We used a block‐designed fMRI experiment involving 2‐digit simple addition and subtraction problems. Participants were asked to complete three types of tasks – in a sequential pattern – during scanning, including an addition task (AT), a subtraction task (ST), and a number matching task (NT) that served as the baseline. Signs of “+”, “‐”, and “#” denote the three conditions, respectively. All of the visual stimuli were presented in a partitioned format and in the sequential order of “first operand”, “second operand”, “operation sign”, and “proposed solution” within each trial. Units and tens in the first operand were always larger than the corresponding digits in the second operand, for all three conditions. This controlled for the “unit‐decade compatibility effect” observed in number comparison tasks (e.g., faster and more accurate response to 56 vs. 32, which is compatible because 5 > 3 and 6 > 2; slower and less accurate response to 43 vs. 34, which is incompatible because 4 > 3 but 3 < 4) [Nuerk et al., 2001; Nuerk et al., 2004].

Participants were required to compute “the first operand plus the second” in the AT, or “the first operand minus the second” in the ST, or judge whether the “proposed solution” was the same as one of the two previous operands in the NT. Subjects then pressed one of two response keys using the left and right thumbs to report the validity of the “proposed solution” as quickly and accurately as possible. Reaction times and accuracy were obtained for each trial. The difficulty of the implicit mental arithmetic is associated with carrying or borrowing manipulations. Whenever such operations were required, response latencies, error rates, and functional brain activation increases considerably [Imbo et al., 2007a; Imbo et al., 2007b]. Therefore, carrying and borrowing were excluded to ensure that all of the problems were relatively simple. So far, few studies have tried to examine the arithmetic processes with 2‐digit simple problems. In fact, 2‐digit stimuli provide some advantages: (1) they are more likely to activate the prefrontal cortex than small single‐digit problems [De Pisapia et al., 2007; Rosenberg‐Lee et al., 2011; Zhou et al., 2007], and (2) they elicit neuronal responses in wider brain areas, in both hemispheres [Ratinckx et al., 2006]. In this way, an unbiased comparison can be implemented by using simple problems to test whether addition and subtraction differ, when both the operations elicit activation in the bilateral frontal and parietal cortices. Consequently, when considering the parallel processing of units and tens separately for 2‐digit numbers [Nuerk et al., 2001; Nuerk et al., 2004], number size and the distance for each digit of a problem varied from 1 to 9 and 1 to 8, respectively. The frequency of occurrence of each number was balanced across the three conditions. Neither “tie” problems (e.g., 32 + 32, 67 ‐ 67) that involved different operand encoding [Blankenberger, 2001; Zhou et al., 2007], nor repeated problems were used. False proposed solutions deviated by ± 1 or ± 10 from the correct solutions in 50% of all the trials. Each trial lasted for 6 s, resulting in an exposure time of 250 ms for the first operand, 250 ms for the second operand, 500 ms for operation sign, and 2000 ms for the proposed answer. Every two stimuli were separated by a 500‐ms mask (background only). The inter‐trial interval was 1500 ms. Four successive trials of the same condition were presented in one block that lasted for 24 s. Blocks of three conditions were mixed and counterbalanced, and every two task blocks were separated by a 24‐second rest block. Data were acquired in two functional runs with a total of 32 trials for each type of task.

MR Data Acquisition

The fMRI data were acquired with a 3.0 Tesla MRI scanner (Siemens Trio Tim, Siemens Medical System, Erlanger, Germany) using a 12‐channel phased array head coil. Foam padding and headphones were used to limit head motion and reduce scanning noise. One hundred ninety two slices of anatomical images with a thickness of 1 mm were obtained using a T1 weighted 3D magnetization prepared rapid gradient echo (MPRAGE) sequence (TR = 1600 ms, TE = 3.28 ms, TI = 800 ms, FOV = 256 mm, flip angle = 9°, voxel size = 1 × 1 × 1 mm³). Functional images were collected using an echo‐planar imaging (EPI) sequence (TR = 2000 ms, TE = 31 ms, flip angle = 90°, FOV = 240 × 240 mm², matrix size = 64 × 64). Thirty axial slices with a thickness of 4 mm and an inter‐slice gap of 0.8 mm were acquired.

Data Preprocessing

The preprocessing of fMRI data was performed with SPM8 software (Wellcome Trust Centre for Neuroimaging, London, UK, http://www.fil.ion.ucl.ac.uk). The first two images were discarded to allow the magnetization to approach dynamic equilibrium. The data were converted to make the fMRI data compatible with the SPM software. Functional images were corrected for slice‐timing differences and realigned to the median image to correct rigid body motion. Cases with head movement exceeding 2 mm or 2 degrees were excluded from further analysis. The high resolution anatomical image was co‐registered with the mean image of the EPI series and then spatially normalized to the MNI template. After applying the spatial normalization parameters to the EPI images, all volumes were re‐sampled into 3 × 3 × 3 mm³ and smoothed with an 8‐mm FWHM isotropic Gaussian kernel.

Statistical Parametric Mapping

Regional responses were analyzed using SPM8. After specifying the design matrix, each participant's hemodynamic responses – induced by trial blocks – were modeled with a box‐car function convolved with a hemodynamic response function. The parameters for the effects of the addition task (AT), subtraction task (ST), and number matching task (NT) were estimated – including head motion as confounding regressors of no interest. Contrast images were constructed for each individual based on the ensuing parameter estimates. At the group‐level (i.e., random‐effects analysis), one‐sample t‐tests were applied to the contrast images with the effects of sex and age modeled as confounds. To test for common cognitive processes across the three conditions (i.e., basic visual encoding, digit maintenance, matching judgment, and button pressing, as shown in Figure 1), we assessed the conjunction of addition and subtraction using (group level) contrasts of AT > NT and ST > NT. To test whether subtraction differed from addition we tested for ST > AT. All the resulting statistical parametric maps were presented using a FDR‐corrected threshold of p < 0.05 using a cluster extent threshold of 10 contiguous voxels.

Figure 1.

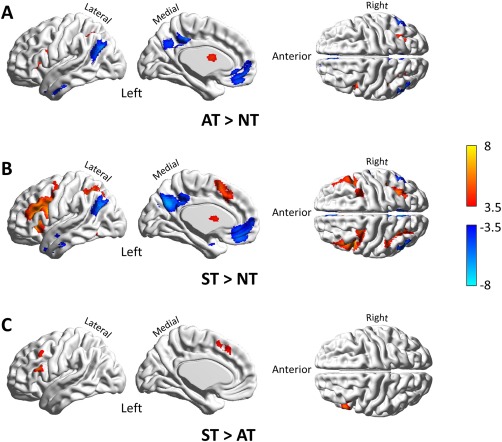
Regions with significant activation revealed by comparing AT > NT, ST > NT, and ST > AT. (A) Regions responding specifically to addition processing were revealed by comparing AT > NT. (B) Regions specific to subtraction processing were revealed by comparing ST > NT. (C) Compared with addition, greater activation during subtraction was revealed by comparing ST > AT. No significant difference resulted from the contrast of AT > ST. All contrasts are set at a threshold of p < 0.05 voxel‐wise with FDR correction and cluster size >10 voxels. Warm color bars indicate the t‐scores specific to activation, whereas cold color bars indicate the t‐scores specific to deactivation. Abbreviation: AT, addition task; ST, subtraction task; NT, number matching task. [Color figure can be viewed at http://wileyonlinelibrary.com]

Dynamic Causal Modeling and Network Discovery

In this analysis, we examined the directive connectivity among the brain regions identified by the whole brain analysis above using dynamic causal modeling (DCM) [Friston et al., 2003]. DCM analyses generally focus on a subgraph or limited number of brain regions to reduce the number of extrinsic connections and their conditional dependencies [Daunizeau et al., 2011]. Studying a few key regions also reduces computational load [Ma et al., 2015]. Although, we used a relatively small number of regions, the number of potential architectures or models entailed by each DCM is potentially enormous. However, recent advances in DCM (Bayesian model reduction) have been introduced that can be used for structure learning or network discovery. This approach searches for an optimum model by identifying the sparsity structure (i.e., absence of connections, or modulatory effects) using an efficient form of model comparison [Friston et al., 2011]. In what follows, we described the specification of the regions or nodes and how regional activities were summarized. We then describe the connectivity architectures of two (full) models that were subsequently used to explore (reduced) variants with one or more connections (changes in connections) removed.

Regions of interest and time series extraction

Three components are necessary for specifying a DCM: (i) a design matrix of external or experimental inputs and (ii) the time series stored in volume‐of‐interest (VOI) files and (iii) on an adjacency matrix or graph specifying which connections at present, and how they are affected by experimental condition. The design matrix that is optimal for a given DCM is sometimes subtly different than the one used for fMRI univariate analysis, since the regressors of the design matrix need to be recombined to define the explanatory variables and inputs for the DCM. However, this re‐combination does not change the underlying general model, simply the way in which the explanatory variables are combined to explain neuronal responses in the DCM.

Here, we used an experimental input that covered all number processing and (as above) two distinct inputs for addition and subtraction: in detail, we used three experimental inputs (1) “Number processing” that comprised all conditions with visual number input, i.e., AT, ST, and NT; (2) “Addition” that was exclusively involved in addition‐specific blocks and (3) “Subtraction” that modelled subtraction blocks. Regions or volumes of interest (VOIs) showing addition and subtraction effects were identified using the group‐level random effects in the aforementioned whole brain analysis (see Figure 2). To characterize the differences between addition and subtraction within the same distributed network, it was necessary to define nodes that were engaged by both mathematical operations. On the basis of the separate analysis of addition and subtraction, the ensuing overlap motivated a conjunction analysis to identify regions involved in both operations. The peaks of the conjunction analysis were then used as centers of VOIs, summarizing both addition and subtraction effects for dynamic causal modelling. Other common regions with deactivation overlapped the default mode network (DMN) [Fox et al., 2005], and thus were considered as task‐negative areas and not included in DCM analysis. Subtraction‐specific regions – with activation that could only be observed when comparing subtraction to the control task – were selected to represent subtraction‐specific areas. Most of these overlapped the dorsal pathway associated with magnitude or quantitative processing [Klein et al., 2013]. With the help of the VOI tool in SPM8, time series were taken from 8 mm spheres centered on each region, using the principal eigenvariate across all suprathreshold voxels for each participant (uncorrected P < 0.05), with the mean and other confounds removed from the measured time‐series [Stephan et al., 2010]. Please see the results section and Figure 2 for the (average) location of the ensuing regions.

Figure 2.

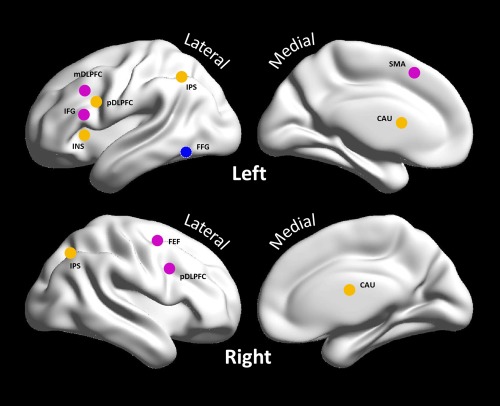
Volumes‐of‐interest (VOIs) selected for the DCM analysis. Orange spots denote brain regions with common activation during both addition and subtraction processes; purple spots denote brain regions with activation during subtraction only; the blue spot denotes where the number processing experimental input entered the brain. Abbreviation: IFG, inferior frontal gyrus; mDLPFC, middle portion of dorsolateral frontal cortex; pDLPFC, posterior portion of dorsolateral prefrontal cortex; INS, insula; IPS, intraparietal sulcus; FFG, fusiform gyrus; CAU, caudate; SMA, supplementary motor area; FEF, frontal eye field. [Color figure can be viewed at http://wileyonlinelibrary.com]

DCMs specification and network discovery

As implemented in DCM 12 in SPM12 (http://www.fil.ion.ucl.ac.uk/spm), we then specified full connectivity models: all within‐node (intrinsic) and between‐node (extrinsic) connections for both the endogenous (fixed) connectivity and modulation effects were considered. The term “modulation effect” denotes bilinear modulation effects in the context of a deterministic DCM. These bilinear effects model the change in connectivity attributable to addition or subtraction. The number processing experimental input entered at the hierarchically lowest region above the fusiform gyrus [Dehaene and Cohen, 1997; Schmithorst and Brown, 2004]. This driving input was modeled in terms of the C matrix. The remaining (addition and subtraction) inputs exerted only modulatory effects on intrinsic and extrinsic connections. These modulatory effects were modeled using two B matrices.

We investigated two distinct networks comprising six and eight nodes respectively. The first network comprised nodes that showed both addition and subtraction effects, while the second network focused on subtraction – comprising nodes that showed significant subtraction effects, relative to the number task. These two networks correspond to the ventral and dorsal pathway regions implicated in arithmetic computations. We will refer to them as the ventral pathway (first) and dorsal pathway (second) DCMs respectively.

Finally, the resulting models were pruned to discover the most likely model of connections and their modulation by addition and subtraction. These procedures rely upon Bayesian model reduction [Friston et al., 2011]. This reduction searched over all possible reduced models of our fully connected models and returned a discovered network that best explained the observed fMRI data. Changes in connectivity were quantified using Bayesian model averages over the reduced model space. These changes are expressed in hertz – because connection strengths in DCM can be regarded as rate constants, i.e., the rate of change in a target area produced by unit activity in another.

RESULTS

Behavioral Results

The behavioral results are shown in Table 1. We performed one‐way repeated‐measures analyses of variance on the accuracy (ACC) and reaction time (RT) using AT, ST and NT as the experimental conditions. The average ACC was 94.47 ± 4.59% (mean ± SD) for the addition task, 90.67 ± 6.33% for the subtraction task, and 95.51 ± 5.98% for the number matching task. The main effect of condition was significant, F (2, 57) = 4.009, p = 0.024. Post‐hoc paired t‐tests indicated that the accuracy of AT and NT were significantly higher than that of ST after a Bonferroni correction (p = 0.039, and p = 0.009, respectively). The difference between AT and NT did not reach significance.

Table 1.

In‐scanner behavioral results

	Accuracy (% correct)				Reaction Time (ms)
	M	SD	F (2,57)	P	M	SD	F (2,57)	p
Addition	94.47	4.59	4.009	0.024	1216.04	105.34	0.667	0.517
Subtraction	90.67	6.33			1259.51	140.17
Number Matching	95.51	5.98			1244.99	115.21

The average RT was 1216.04 ± 105.34 ms for the addition task, 1259.51 ± 140.17 ms for the subtraction task, and 1244.99 ± 115.21 ms for the number matching task. No significant differences were found for the RT among the three conditions (F (2, 57) = 0.667, p = 0.517).

To ensure that behavioral results were not influenced by age or sex effects, we examined the Pearson correlations among age, response speed, and accuracy for all subjects, and then implemented independent‐samples t‐tests on the behavioral performance, comparing male and female sub‐groups. No significant effect was found.

Results of Whole Brain Analyses

Specific neuronal correlates of addition and subtraction processes were revealed by the contrasts of AT > NT and ST > NT, respectively (see Table 2). As shown in Figure 1A and 1B, regions that showed activation during addition were found in the bilateral intraparietal sulci (IPS), bilateral caudate nuclei, left insula, as well as posterior portion of dorsolateral prefrontal cortex (pDLPFC, BA9) in the left hemisphere. Regions that showed activation during subtraction were detected in the left frontal cortex covering dorsolateral and inferior portions, left supplementary motor area (SMA, BA 6/32), left fusiform gyrus (FFG, BA37), right pDLPFC, right precentral gyrus/middle frontal gyrus (frontal eye field, FEF, BA 6), and bilateral insula, in addition to the common areas shared with addition in the bilateral IPS, and bilateral caudate nuclei. Regions with decreased activation were also revealed by tests for both addition and subtraction effects, which were located in the areas that overlapped with the DMN [Fox et al., 2005], including the bilateral inferior temporal gyri (ITG), bilateral angular gyri (AG), medial portions of the prefrontal cortex (mPFC), and posterior cingulate cortex (PCC).

Table 2.

Regions with significant activation and deactivation elicited by contrasts of AT > NT and ST > NT. Threshold was set at p < 0.05 voxel‐wise with FDR correction and cluster size >10 voxels. Abbreviation: AT, addition task; ST, subtraction task; NT, number matching task; IPS, intraparietal sulcus; pDLPFC, posterior portion of dorsolateral prefrontal cortex; FFG, fusiform gyrus; FEF, frontal eye field; SMA, supplementary motor area; AG, angular gyrus; ITG, inferior temporal gyrus; PCC, posterior cingulate cortex; mPFC, medial portions of the prefrontal cortex; L, left; R, right; BA, Brodmann area

Contrast	Region	BA	Cluster	MNI Coordinates			T‐score
				x	y	z
Activation
AT > NT	L. IPS	7	28	−27	−54	45	4.72
	R. IPS	7	33	27	−54	45	5.45
	L. pDLPFC	9	11	−45	9	30	5.15
	L. Caudate		19	−9	3	18	5.94
	R. Caudate		32	9	9	15	4.81
	L. Insula	13	35	−30	24	6	5.90
ST > NT	L. FFG	37	18	−48	−51	−18	4.04
	L. IPS	40	144	−27	−54	48	6.76
	R. IPS	7	151	27	−63	45	6.05
	L. pDLPFC	9	354	−42	9	30	6.66
	R. pDLPFC	46	225	48	3	30	6.23
	R. FEF	6	26	33	0	54	4.75
	L. SMA	6/32	106	−3	12	54	5.82
	L. Caudate		115	−6	9	12	4.58
	R. Caudate		151	15	−15	21	4.83
	L. Insula	13	85	−30	24	3	7.11
	R. Insula	13	47	33	21	3	6.31
Deactivation
AT > NT	L. AG	39	409	−54	−69	21	8.85
	R. AG	39	360	51	−66	24	6.06
	L. ITG	20	181	−54	3	−24	7.74
	R. ITG	20	246	45	3	−45	7.05
	L. PCC	31	495	−3	−33	42	7.15
	L. mPFC	11	389	−9	54	0	6.68
ST > NT	L. AG	39	238	−51	−66	30	6.83
	R. AG	39	186	45	−60	24	6.73
	L. ITG	21	75	−57	−3	−24	5.36
	R. ITG	20	83	51	−9	−33	6.68
	R. PCC	31	535	12	−45	36	7.36
	L. mPFC	11	363	−6	39	−18	5.88

Differences between addition and subtraction were tested with a contrast of ST > AT, as shown in Figure 1C. Compared with addition, subtraction induced greater activation in the left SMA and lower frontal area that consisted of inferior frontal gyrus (IFG, BA45/44) and the middle portion of dorsolateral frontal cortex (mDLPFC) (see Table 3). No significant differences resulted from the contrast of AT > ST.

Table 3.

Regions with significant activation detected by contrasts of ST > AT. Thresholds were set at p < 0.05 voxel‐wise with FDR correction and cluster size >10 voxels. Abbreviation: AT, addition task; ST, subtraction task; SMA, supplementary motor area; IFG, inferior frontal gyrus; mDLPFC, middle portion of dorsolateral frontal cortex; L, left; R, right; BA, Brodmann area

Contrast	Region	BA	Cluster	MNI Coordinates			T‐score
				x	y	z
ST > AT	L. SMA	8	51	−6	18	48	3.78
	L. IFG	45/44	28	−57	24	21	4.82
	L. mDLPFC	8/9	21	−51	21	42	4.49

The axial view of brain activation revealed by contrasts of AT > NT, ST > NT, and ST > AT are provided in Figure S1, S2, and S3, respectively.

Results of DCM Analysis

Six regions corresponding to areas activated by both addition and subtraction were included in the first DCM. These regions were identified as maxima in the corresponding SPM testing for the joint activation under addition and subtraction. The regions selected comprised the bilateral IPS, bilateral caudate nuclei, left pDLPFC, and left insula. The second DCM corresponded to the dorsal pathway network for subtraction and included eight regions showing subtraction effects, including the right pDLPFC, right FEF, left SMA, left IFG, left mDLPFC, in addition to the bilateral IPS and left pDLPFC that were also included in the common network. The left FFG was chosen as the entrance where the driving inputs were allowed to elicit responses initially. The location and coordinates of the ensuing nodes comprising the two networks are shown in Figure 2 and Table 4.

Table 4.

VOIs selected for DCM analysis. Abbreviation: IPS, intraparietal sulcus; pDLPFC, posterior portion of dorsolateral prefrontal cortex; FEF, frontal eye field; SMA, supplementary motor area; IFG, inferior frontal gyrus; mDLPFC, middle portion of dorsolateral frontal cortex; FFG, fusiform gyrus; L, left; R, right; BA, Brodmann area

Region	BA	MNI Coordinates
		x	y	z
Common
L. IPS	40	−27	−54	42
R. IPS	7	33	−57	48
L. pDLPFC	9	−45	6	30
L. Caudate		−12	3	18
R. Caudate		15	−3	21
L. Insula	13	−30	21	3
Subtraction‐Specific
L. IPS	40	−27	−54	42
R. IPS	7	33	−57	48
L. pDLPFC	9	−45	6	30
R. pDLPFC	9	48	3	30
R. FEF	6	33	0	54
L. SMA	6/32	−3	12	54
L. IFG	45/44	−57	24	21
L.mDLPFC	8/9	−51	21	42
Driving Input
L. FFG	37	−48	−51	−18

The network discovery identified optimal sparse model structures from initial full models by pooling model evidence over subjects. Redundant connections (and changes) with low posterior probability are effectively eliminated. The remaining connectivity and modulatory effects with nonzero posterior probability (and a mean of 91.02%) constitute the key structure of the discovered networks.

With respect to the six‐node (ventral pathway) DCM comprising addition and subtraction nodes, the connectivity matrix (A matrix) exhibited a highly interconnected (dense) infrastructure (see Figure 3A). All nodes were linked by bidirectional connections with the exception of connections from the left IPS to the left caudate, from the right IPS to the right caudate, from the left IPS to the right caudate, and from the left pDLPFC to the left caudate.

Figure 3.

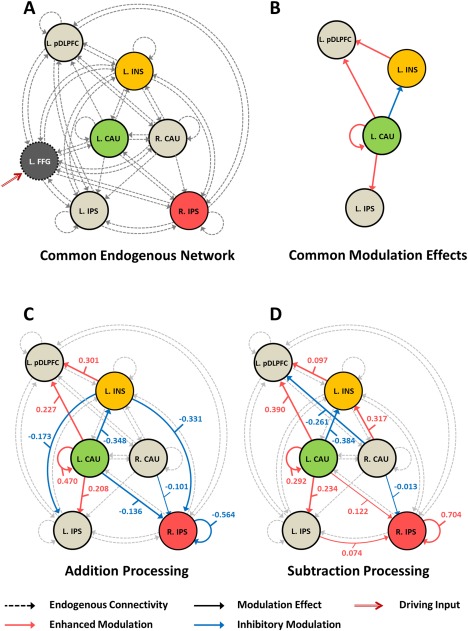
Networks discovered for arithmetic operations based on six (ventral pathway) regions showing addition and subtraction effects. (A) Addition and subtraction processes shared a network with common endogenous (or fixed) connectivity revealed by non‐redundant parameters in the A matrix; (B) a core network with identical nodes, connections, and modulatory directions (enhancement or suppression with addition and subtraction) was identified; (C) modulatory effects elicited by addition processing; (D) modulatory effects elicited by subtraction processing; Abbreviation: FFG, fusiform gyrus; IPS, intraparietal sulcus; pDLPFC, posterior portion of dorsolateral prefrontal cortex; INS, insula; CAU, caudate; L, left; R, right. [Color figure can be viewed at http://wileyonlinelibrary.com]

In terms of the modulatory effects of addition and subtraction, several connections showed enhanced or inhibitory effects to facilitate arithmetic processing. For addition (see Figure 3C), enhanced effects were imposed on connections from the left caudate to the left pDLPFC, from the left caudate to the left IPS, from the left insula to the left pDLPFC, and the self‐connection in the left caudate. Inhibitory effects were inferred on connections from the left insula to the left IPS, from the left insula to the right IPS, from the left caudate to the left insula, from the left caudate to the right IPS, from the right caudate to the right IPS, and the self‐connection in the right IPS. For subtraction (see Figure 3D), enhanced connections were found from the left caudate to the left pDLPFC, from the left IPS to the right IPS, from the left caudate to the left IPS, from the left caudate to the right IPS, from the left insula to the left pDLPFC, from the right caudate to the left insula, as well as from the left caudate and right IPS to themselves. Inhibitory effects were exerted on connections from the left caudate to the left insula, from the right caudate to the left pDLPFC, and from the right caudate to the right IPS. As shown in Figure 3B, a core component of the network with overlapping nodes, connections, and modulatory effects (enhancement or suppression) between addition and subtraction processes was identified. Posterior probabilities and connection strengths (or coupling parameters in units of Hz) of remaining bilinear modulation effects are listed in Supplementary Table S1.

With respect to the extended subtraction network used to characterize effective connectivity in the magnitude‐related dorsal pathway, most of the eight nodes were bidirectionally connected (see Figure 4A). Absences of fixed connections were all afferent connections associated with the left IFG, from the left mDLPFC, right FEF, and right IPS, respectively. A few of the connections were enhanced by subtraction (see Figure 4B), including those from the left IFG to the left SMA, left pDLPFC, and right IPS, respectively, in addition to the connection from the left IPS to the right IPS and self‐connections in the left SMA and right IPS. Inhibitory effects of subtraction were seen on connections from the left pDLPFC to the right IPS, from the right FEF to the right IPS, and from the left mDLPFC to itself. Parameters of modulations in the extended subtraction network are shown in Supplementary Table S2.

Figure 4.

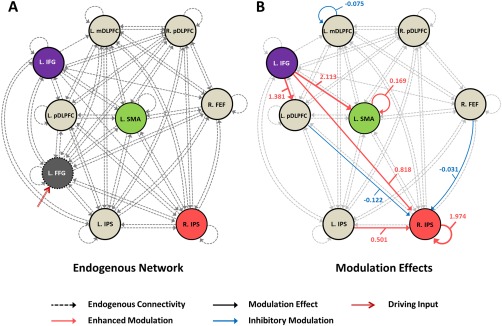
Optimal model for the extended subtraction (dorsal pathway) network. (A) The endogenous (or fixed) connectivity was revealed by non‐redundant entries in the A matrix; (B) modulatory effects of subtraction encoded by the B matrix were shown with corresponding changes in connectivity (in hertz). Abbreviation: FFG, fusiform gyrus; IPS, intraparietal sulcus; pDLPFC, posterior portion of dorsolateral prefrontal cortex; IFG, inferior frontal gyrus; FEF, frontal eye field; SMA, supplementary motor area; mDLPFC, middle portion of dorsolateral frontal cortex; L, left; R, right. [Color figure can be viewed at http://wileyonlinelibrary.com]

DISCUSSION

In the present study, we compared the neuronal processes involved in mental arithmetic, specifically addition and subtraction, in 20 normal healthy subjects by using simple calculation problems – with a special focus on the differences between addition and subtraction. To examine distributed processing during addition and subtraction, we conducted effective connectivity analysis using DCM, in a structured learning or discovery mode by identifying optimum architectures. Our results disclosed a ventral‐pathway‐dependent addition network and a subtraction network comprising both ventral and dorsal pathways. Moreover, the distributed nature of differences between addition and subtraction – in terms of strategies and laterality were also revealed by examining the connectivity between brain regions.

Simple mental arithmetic problems induced activation in a wide range of brain regions that were consistent with most previous studies on mental arithmetic [Arsalidou and Taylor, 2011], such as the bilateral IPS and insula, the left DLPFC, IFG, SMA, FFG, and caudate nuclei, and induced decreased activation located in the regions of the default mode network (DMN) [Fox et al., 2005], including the bilateral ITG, AG, mPFC, and PCC. As Klein et al. [2013] proposed, the bilateral IPS, posterior IPS, SMA, FEF, and the left IFG (BA44, 45, 47) and the right IFG (BA45) constituted the dorsal pathway; whereas the perisylvian, occipito‐temporal, and subcortical areas appeared to be connected entirely via the ventral route. Thus, many of resulting regions were specific to subtraction calculation (see Figure 2), and demonstrated a recruitment of a network comprising ventral and dorsal areas during subtraction – and only ventral areas during addition.

Subtraction produced significantly greater activation in the inferior frontal areas covering the left IFG (BA45/44) and middle part of DLPFC (mDLPFC), as well as the left SMA than addition (as shown in Figure 1C). The left IFG is well known as one part of Broca's area that is an important locus for linguistic processing and working memory [D'Esposito et al., 1999; Gabrieli et al., 1998; Mainy et al., 2007; Poldrack et al., 1999]. Subdivisions of Broca's area have been specified and implicated in disparate functions. It has been proposed that the superior and posterior portions of the IFG (BA45/44) are related to phonological and syntactic processing, while the ventral and anterior portions of the IFG (BA47/45) are more dedicated to semantic processing [Hagoort, 2005; Poldrack et al., 1999]. Studies of the relationship between working memory and arithmetic (with dual tasks) have suggested the involvement of phonological processes in procedural strategy‐based calculations as phonological load interfered with performance on arithmetic trials [Hecht, 2002; Imbo and Vandierendonck, 2007c]. Hence, the activation in the left IFG during subtraction, especially in the superior and posterior part detected in this study, is likely to correspond to extra phonological processes that contribute to a temporary storage of verbal information, such as subvocal rehearsal of operands or intermediate results. Another key part of the frontal area is the mDLPFC. A large body of evidence associates this area with visual working memory [Petrides, 2000; Stern et al., 2000]. It has been suggested that the mDLPFC is related to the active monitoring of multiple events in working memory, such as the executive process of monitoring and manipulation of spatial information [Owen et al., 1996], self‐ordered processes of visual stimuli [Petrides et al., 1993], and so forth. In the current study, therefore, a putative role of the mDLPFC in active monitoring of operands displayed sequentially can be plausibly inferred, providing a visual support to subserve working memory together with the phonological support contributed by the left IFG. With regard to the left SMA, this area has been associated with movement sequencing for a series of mental manipulations during calculation [Clower and Alexander, 1998; Nieder and Dehaene, 2009]. However, recent experiments have demonstrated the great reliance on finger‐counting‐related perception during mental calculation in 8‐13‐year‐old children, particularly during larger subtraction problems requiring numerical quantity processing [Berteletti and Booth, 2015]. Studies of adult subjects also provide evidence for overlapping brain circuits that are shared between arithmetic and finger representation [Andres et al., 2012]. Given the crucial role of SMA in representations for finger movements [Diedrichsen et al., 2013], the converging results indicate the possibility that the SMA underlies finger perception when subjects engage in arithmetic problem solving. Although our results do not allow us to ask whether the SMA is involved in goal decomposing/sequencing or finger counting, it is plausible that subtraction calls on an auxiliary process of motor representation, compared to addition. Collectively, significantly greater activation observed in the frontal areas in subtraction, relative to addition processes, is consistent with their specialization for procedural processing that implicates working memory and numeric representations in multiple forms.

To address the question of whether calculation differences exist in strategic application and cerebral laterality, we performed a DCM analysis of networks based on six regions engaged by addition and subtraction. Our rationale was that addition and subtraction entail differential switching on or off (or modulating) connections within a distributed system. Effective connectivity describes the directed propagation of activity from one neuronal system to another in a context‐sensitive fashion.

As suggested in many studies, the bilateral IPS may be the core neural substrate underlying magnitude representation [Ansari, 2008; Dehaene et al., 2003]. The left posterior portion of DLPFC (BA 9) is specialized for working memory [Baddeley, 2003; Smith et al., 1998], and related to information segregation and integration [De Pisapia et al., 2007]. We speculate that the left pDLPFC subserved the integration of sporadic information received from other nodes within the network, given the multiple afferent connections observed in our data. Compared with the fronto‐parietal areas, the left caudate nucleus and left insula – which were categorized as fact‐retrieval related ventral areas [Arsalidou and Taylor, 2011; Klein et al., 2013] – also played a crucial part in both addition and subtraction. As part of the basal ganglia, the caudate is implicated in higher‐order motor control [Menon et al., 1998] as well as learning and memory [Graybiel, 2005; Nomura and Reber, 2008]. The triple‐code model suggests that the left caudate is involved in the retrieval of rote arithmetic facts since lesions to this area impair arithmetic fact retrieval from memory, irrespective of the particular arithmetic operation [Dehaene and Cohen, 1995, 1997]. The insula may act as a toggle system that switches between outward processes (i.e., integration) and inward processes (i.e., mental representation) in line with its role as a network hub (i.e., salience network), responsible for switching between the executive control network and the default mode network during information processing [Arsalidou and Taylor, 2011; Sridharan et al., 2008].

Addition and subtraction specific networks were constructed on basis of the regions identified above (see Figure 3C and D), in which differential addition and subtraction modulation effects were quantified. Within both networks, connections for propagating signals (i.e., retrieved arithmetic facts) from the left caudate nucleus to the left IPS and pDLPFC were increased, indicating the contribution of fact retrieval to numeric processes and the final stage of information integration, not only in addition but also subtraction processes. However, modulated efferent connections from the left insula to the bilateral IPS distinguished the two networks. In terms of addition effects, connections from the left insula to the bilateral IPS were inhibited. In view of the established co‐activation associated with the anterior portion of insula (as activated in this study) and fronto‐parietal cognitive processing areas and the causality of salience detection and executive processing [Uddin, 2015], it is possible that observed inhibitory connections suppressed the functioning of the bilateral IPS during addition. Conversely, such inhibition was not seen in the effects of subtraction on network connectivity, suggesting more reliance on magnitude‐related processing in subtraction compared to prior selection of retrieved facts in addition. Another apparent difference between subtraction and addition comes from the distinct changes in afferent connections to the right IPS. Dissociations of the modulation effects on self‐connections of the right IPS were revealed, reflecting suppression for addition and enhancement for subtraction processes, respectively. Due to the inhibitory properties of the self‐connection, the suppression (decreased self‐connection) indicates unlocking of neuronal excitability of sensitivity, while the enhancement (increased self‐connection) suggests more rigorous limitation of the neural fluctuations. The former is more likely to associate with regions showing reduced activity, e.g., the right IPS in addition network, and the later might be related to regions showing greater activity, e.g., the right IPS in subtraction network and the left caudate in both networks. In addition to the inhibitory effects received from the left insula, the afferent signal from the left caudate to the right IPS for transferring arithmetic facts was also suppressed in addition network, whereas the same connection was intensified in subtraction network.

The right IPS is considered to play a particularly important role in the quantitative processing of numbers. Although bilateral parietal areas are involved in manipulating magnitude information, number comparison‐related task performance has been found to rely more on the right parietal lobule, while numerical processing, requiring access to linguistic code, is more strongly associated with the left hemisphere [Chochon et al., 1999]. A right intraparietal lesion creates difficulties in quantitative processing of numbers, even when knowledge about arithmetic facts is unimpaired [Dehaene and Cohen, 1997]. Evidence from intraoperative cortical electro‐stimulation also demonstrates impaired performance on simple subtraction problems, compared to multiplication problems when receiving stimulation at right parietal areas [Yu et al., 2011].

Cues from dynamic interactions within the networks indicate how the nodes were differentially mobilized in addition and subtraction. We tentatively propose that subtle differences in use of computational strategies, rather than a double dissociation between simple multi‐digit addition and subtraction processes. Based on a common frontal‐subcortical‐parietal circuit (as shown in Figure 3B) specialized for basic numeric representation, fact retrieval, and information integration, mental addition is more likely to employ a retrieval‐based approach, while mental subtraction is likely to draw on the magnitude processing capabilities in the parietal cortex, especially the right IPS. With respect to the operation‐specific laterality, our ventral pathway DCM analysis emphasizes the role of the right IPS and right caudate nucleus. It has been proposed that the right caudate is involved in assigning priority values or sequence to information that needs to be processed in number tasks [Arsalidou and Taylor, 2011]. Enhanced coupling of the right caudate and the left insula during subtraction suggests that this region might take a similar role to the insula in coordinating competing neuronal systems. More active participations of the right IPS and caudate in subtraction network suggest that, unlike the addition processes relying primarily on the left hemisphere, mental subtraction calls on the bilateral neural systems.

To substantiate our hypothesis that subtraction engages bilateral cerebral regions, we optimized an extended fully‐connected network based on dorsal pathway (see Figure 1B and 4). A bilateral architecture is clearly seen. However, only a few fixed connections were modulated, which were largely associated with the right IPS. In line with aforementioned roles, the left IFG may support subtraction by transmitting phonological information to the left SMA, pDLPFC, and the right IPS. Enhancement under subtraction was seen for these connections. Connections from the left IPS to its right counterpart were also increased, suggesting a greater role of the right IPS than the left IPS in selecting the final answers in subtraction tasks. Inhibited afferent connections to the right IPS came from the left pDLPFC and right FEF. The former reduction is plausibly associated with restraints on spontaneous impulses for checking computations undertaken by the left pDLPFC – to ensure efficiency. The latter inhibition is likely to result from the particular saccade direction during multi‐digit subtraction processing against the normal rightward reading habits of Chinese subjects. Since the right FEF was responsible for eye movement, and subtraction lead to leftward and downward shifts of spatial attention, which are opposite in addition [Fischer and Shaki, 2014]. Regarding modulations of self‐connections, the left SMA and right IPS were inhibited, whereas activity in the visual monitoring‐related left mDLPFC was disinhibited. Taken together, the right IPS showed responses to mental subtraction across the ventral and dorsal networks. In short, compared with the left‐lateralized addition, subtraction is characterized by recruitment of bilateral circuits.

As for simple multi‐digit arithmetic problems, our DCM results disclosed key differences between mental addition and subtraction in strategic application, laterality, and engagement of neuronal circuits. However, we speculate that such differences are not absolute. As the co‐activation in both ventral and dorsal regions (that overlap with the subtraction pattern in current study) are also observed in complex addition [Klein et al., 2013; Stanescu‐Cosson et al., 2000]. It has been suggested that brain activation induced by addition shifts from subcortical and perisylvian language areas into dorsal regions, with the increasing difficulty of the problem [Klein et al., 2013]; and previously reported differences between arithmetic operations probably emerged due to differential task complexity but not different types per se [Tschentscher and Hauk, 2014]. Our data also support the possibility of context‐sensitive neuronal couplings and available circuits in addition, given that addition and subtraction processes shared the same (fixed) network infrastructures. Nevertheless, when solving simple multi‐digit arithmetic, we propose that addition presents easy problems that only engage the ventral pathway; whereas subtraction requires difficult mental arithmetic that calls on hybrid pathways. Our findings suggest that, on this occasion, mental subtraction is inherently more complex than mental addition. This perspective can also explain our behavioral results, in which subtraction was performed with significantly lower accuracy than addition (p < 0.05). To investigate whether subtraction is always more difficult than addition, further experiments may be necessary.

In our study, significantly greater activation in the frontal cortex (e.g., left IFG) that was related to more general (non‐numerical) cognitive processes reflected the higher task demands of subtraction. Nevertheless, Katzev et al. [2013] suggest that activation in the left IFG is mediated not only by task demands but also by individual ability. In this study, all of the subjects can be considered as skilled in solving simple mental arithmetic – due to their identical experience of at least 16 years of education in China. Further research is necessary to test whether the differences we found can be observed in individuals with low arithmetic ability. In addition, considering that the effect of abacus‐based mental calculation training might be to enhance motor and visuospatial processes [Hu et al., 2011], we excluded subjects who had experience with an abacus using questionnaires.

Limitations

Several limitations of the present study deserve comment. First, we only focused on the neural basis of differences between simple addition and subtraction processes. Therefore, we failed to provide direct evidence for the orthogonal effects of difficulty. Secondly, to ensure computability under the computational loads of network discovery procedures on data from 20 subjects, regions showing deactivation during both addition and subtraction calculations were excluded from DCM analyses. These included the bilateral AG, ITG, the left mPFC, and the right PCC, which responded in line with task‐unrelated difficulty effects associated with the default mode network (DMN) [Buckner et al., 2008; McKiernan et al., 2003]. Among these regions, the left AG has been repeatedly implicated in mental arithmetic, although its precise functional role has not been well established. Possible functions of the left AG have been linked with task‐specific processes, such as arithmetic fact retrieval [Dehaene et al., 2003; Jost et al., 2011] and automatic mapping between mathematical symbols and their semantic referents [Ansari, 2008; Grabner et al., 2013]. However, no evidence has demonstrated that the left AG plays a distinct role from other components of the DMN or that it facilitated calculation in this study. Further study will be necessary to explore whether operation effects exist between the left AG and other calculation‐related regions.

CONCLUSION

Differential cognitive processing during simple multi‐digit mental addition and subtraction were examined by means of univariate and multivariate DCM analyses. By exploring information propagation among neuronal systems, our findings endorse earlier hypotheses about differences between mental addition and subtraction in strategic application, laterality, and engagement of neural circuits. Specifically, mental addition mainly relied on the so‐called ventral circuit that includes temporo‐parietal and subcortical‐limbic areas; whereas subtraction depended on ventral as well as dorsal pathways, including extra fronto‐parietal regions. Although a common frontal‐subcortical‐parietal network was recruited by both operations for processing basic numeric quantity and retrieval of arithmetic facts, addition appears to employ a retrieval‐based approach based on the left hemisphere, while subtraction shows tendency to draw on magnitude or quantitative processing in bilateral parietal cortex, especially the right IPS. At the easy level of difficulty, mental subtraction is inherently more complex than mental addition. Auxiliary phonological, visual, and motor processes for representing numbers are also needed to complete the calculation of subtraction problems.

Supporting information

Figure S1 Axial view of regions with significant activation revealed by comparing addition task vs. number matching task. All contrasts are set at a threshold of p < 0.05 voxel‐wise with FDR correction and cluster size >10. Warm color bars indicate the t‐scores specific to activation, whereas cold color bars indicate the t‐scores specific to deactivation.

Figure S2 Axial view of regions with significant activation revealed by comparing subtraction task vs. number matching task. All contrasts are set at a threshold of p < 0.05 voxel‐wise with FDR correction and cluster size >10. Warm color bars indicate the t‐scores specific to activation, whereas cold color bars indicate the t‐scores specific to deactivation.

Figure S3 Axial view of regions with significant activation revealed by comparing subtraction task vs. addition task. All contrasts are set at a threshold of p < 0.05 voxel‐wise with FDR correction and cluster size >10. The color bars indicate the t‐scores specific to activation.

Table S1 Posterior probabilities and connection strengths of remaining bilinear modulation effects in the six‐node (ventral pathway) DCM. Abbreviation: IPS, intraparietal sulcus; CAU, caudate; pDLPFC, posterior portion of dorsolateral prefrontal cortex; INS, insula; L, left; R, right.

Table S2 Posterior probabilities and connection strengths of remaining bilinear modulation effects in the extended subtraction‐specific (dorsal pathway) DCM. Abbreviation: IPS, intraparietal sulcus; pDLPFC, posterior portion of dorsolateral prefrontal cortex; FEF, frontal eye field; SMA, supplementary motor area; IFG, inferior frontal gyrus; mDLPFC, middle portion of dorsolateral frontal cortex; L, left; R, right.