Degree‐based statistic and center persistency for brain connectivity analysis

Abstract

Brain connectivity analyses have been widely performed to investigate the organization and functioning of the brain, or to observe changes in neurological or psychiatric conditions. However, connectivity analysis inevitably introduces the problem of mass‐univariate hypothesis testing. Although, several cluster‐wise correction methods have been suggested to address this problem and shown to provide high sensitivity, these approaches fundamentally have two drawbacks: the lack of spatial specificity (localization power) and the arbitrariness of an initial cluster‐forming threshold. In this study, we propose a novel method, degree‐based statistic (DBS), performing cluster‐wise inference. DBS is designed to overcome the above‐mentioned two shortcomings. From a network perspective, a few brain regions are of critical importance and considered to play pivotal roles in network integration. Regarding this notion, DBS defines a cluster as a set of edges of which one ending node is shared. This definition enables the efficient detection of clusters and their center nodes. Furthermore, a new measure of a cluster, center persistency (CP) was introduced. The efficiency of DBS with a known “ground truth” simulation was demonstrated. Then they applied DBS to two experimental datasets and showed that DBS successfully detects the persistent clusters. In conclusion, by adopting a graph theoretical concept of degrees and borrowing the concept of persistence from algebraic topology, DBS could sensitively identify clusters with centric nodes that would play pivotal roles in an effect of interest. DBS is potentially widely applicable to variable cognitive or clinical situations and allows us to obtain statistically reliable and easily interpretable results. Hum Brain Mapp 38:165–181, 2017. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Over the last decade, a systemic approach has led to a magnificent improvement in our understanding of the organization and functioning of the brain. For example, the application of graph theory has revealed conspicuous network characteristics of the brain, such as the small‐world properties, modular structure, hierarchical organization, and rich‐club organization [Bullmore and Sporns, 2009, 2012]. The functional and structural networks of the brain are associated with intellectual performance [Van den Heuvel et al., 2009] and development [Dosenbach et al., 2010; Supekar et al., 2009]. Furthermore, brain networks are altered by various disorders [Bassett and Bullmore, 2009; Buckner et al., 2008]. Within the brain network, there are a few highly connected nodes, known as hubs [Achard et al., 2006; Tomasi and Volkow, 2011; Van den Heuvel and Sporns, 2011]. The importance of a hub in a network is strongly supported by recent studies. In the brain network, a hub region is thought to improve brain function by interacting with many other regions to integrate the associated information [Sridharan et al., 2008; Van den Heuvel et al., 2012]. Recent studies have reported characteristics of hub regions such as high cerebral blood flow [Liang et al., 2012], high metabolism [Buckner et al., 2009; Drzezga et al., 2011], intensive accumulation of amyloid proteins [Buckner et al., 2009; Jagust and Mormino, 2011], and a significant association with pathophysiological mechanisms [Buckner et al., 2009].

In addition to the network approach, the localized connectivity analysis of networks has also been of interest. Connectivity analysis involves the construction of a connectivity matrix and a statistical analysis without a priori selection of specific brain regions of interest. The connectivity matrix of the brain contains a huge number of elements, that is, individual connections (links or edges) of a network (a graph). For an undirected network of N nodes, the number of edge elements in the connectivity matrix is N(N − 1)/2. Consequentially, an investigation of group differences or correlates of cognitive function or behavioral performance using the connectivity matrix requires a very large number of univariate hypothesis tests. The use of a simple P‐value such as 0.05 for multiple testing, in turn, induces the critical multiple testing problem (MTP) leading to a large number of false positives (type I error). Therefore, correction for this MTP is necessary.

Conventional analysis of functional brain imaging data is also associated with mass‐univariate hypothesis testing. For example, analysis of functional activation associated with a certain context or task has also been performed using voxel‐by‐voxel comparisons [Kennedy et al., 2015]. In this situation, a large number of voxels are simultaneously compared, which inevitably leads to the MTP. Many methods have been employed to resolve this problem, including common multiple comparison correction procedures, such as the Bonferroni correction, which control the family‐wise error rate (FWER), false discovery rate (FDR) control procedures, and nonparametric permutation‐based correction (marginal statistic). Other methods have been specifically designed for brain imaging analysis, such as random field theory‐based inference controlling the FWER [Worsley et al., 1992] and Monte–Carlo simulation [Forman et al., 1995], implemented in AFNI AlphaSim (http://afni.nimh.nih.gov/afni/doc/manual/AlphaSim). These methods can be subdivided further based on the level of inference, that is, voxel‐level or cluster‐level [Nichols, 2012]. Voxel‐wise inference retains voxels above a certain threshold, whereas cluster‐wise inference includes clusters of voxels larger than a certain cluster‐level threshold. Cluster‐wise inference has become particularly popular, since it provides more power owing to its higher sensitivity (higher true positive rate [TTR]) than voxel‐wise inference, which has less power although with higher spatial specificity.

In connectivity analysis, the number of false positive errors can be reduced by employing common correction methods, such as the Bonferroni correction, FDR control procedures, or permutation‐based correction. As mentioned, these voxel‐wise inference methods are, however, very stringent and conservative; thus, they reveal results with somewhat low sensitivity. Furthermore, in contrast to traditional brain imaging analysis, few MTP‐correction methods have been specifically proposed for connectivity analysis. They are all based on the principle of conventional cluster‐wise statistics, which has been applied to traditional MRI analysis [Han et al., 2013; Hipp et al., 2011; Ing and Schwarzbauer, 2014; Zalesky et al., 2010, 2012b]. The main difference among these studies is the definition of a cluster (Table 1). Thus, these methods differ with respect to the estimation of cluster size. The definition of a cluster in cluster‐wise statistics depends on the underlying assumption that a specific type of cluster is significantly associated with an effect of interest (a hypothesis). Network‐based statistic (NBS) uses the term “network” to consider connected components in a graph as a cluster. NBS is used to detect the connected set of edges associated with an effect of interest [Han et al., 2013; Zalesky et al., 2010]. NBS controls for the FWE by comparing the observed size of a connected component with the empirical null distribution of the maximum size of connected component obtained by permutations. Spatial pairwise clustering (SPC) uses a delicate definition of a cluster [Hipp et al., 2011; Zalesky et al., 2012b]. It defines two clusters in a pairwise manner. In SPC, pairs of voxels ({u ₁, v ₁}, …, {u _i , v _i}) form a pair of spatially distinct nodes (n and m, a pair of two clusters). Each pair of voxels, u and v (belong to the nodes n and m, respectively), has a connection (edge {u, v}) between them. Thus, these two nodes n and m are considered to have a significant association by having a set of inter‐node voxel‐wise connections ({{u ₁ , v ₁}, …, {u _i , v _i}}). Recently, one study suggested two methods, cluster mass statistic (CMS) and cluster size statistic (CSS), defining cluster mass, and cluster size, respectively [Ing and Schwarzbauer, 2014]. CMS considers the total number of connections of a spatially continuous voxel cluster with the rest of the brain, whereas CSS considers the spatial extent of this cluster. All of these methods are based on the concept of cluster‐extent‐based correction. However, only NBS defines a cluster as a connected set of edges among spatially distinct regions, whereas other methods treat it as a mass of spatially continuous voxels or parallel connections.

Table 1.

Comparison of cluster‐wise correction methods in connectivity analysis

	NBS, CBS	SPC	CMS, CSS	DBS (Current study)
Cluster Definition	A set of connected edges	A pair of two spatially distinct areas containing contiguous voxels	A set of spatially contiguous voxels having connection with other voxels	A set of edges connected through a centric node
Proper node	Voxel (small) or region (large)	Voxel (small)	Voxel (small)	Region (large or small)
Network module	Yes	No	No	Yes
Localization	No	Yes (semi)	Yes (semi)	Yes (semi)
Initial threshold	Arbitrary selection	Arbitrary selection	Arbitrary selection	Independent (Center Persistency)

Although cluster‐wise inference was shown to work successfully with higher sensitivity, this approach suffers from two innate common drawbacks: the lack of spatial specificity (localization power) and the arbitrariness of an initial cluster‐forming threshold. First, a result from cluster‐wise inference cannot be used to infer and compare the significance of smaller elements such as nodes and edges in a cluster. Cluster‐wise inference only enables us to make a statement about a cluster itself, rather than about one specific element in the cluster [Nichols, 2012; Poldrack et al., 2011]. This would not be problematic for small‐sized clusters. However, when a widely extended cluster presents itself, it is an important matter. The only way to address the problem is to raise the initial cluster‐forming threshold to obtain a smaller cluster. Raising the initial threshold is directly related to the second drawback, namely that cluster‐wise inference requires an initial cluster‐forming threshold, which is needed to define the cluster in the first place. In both MRI and connectivity analysis, an initial cluster‐forming threshold is chosen and applied to acquire a set of suprathreshold elements (voxels in MRI and edges in a connectivity matrix). The selection of the threshold depends on researchers' arbitrary decision and there is no widely accepted criterion [Woo et al., 2014; Zalesky et al., 2012a]. This arbitrary threshold problem also occurs during network construction in network analysis. Construction of a sparse network requires us to apply a certain threshold and to use only the set of edges exceeding this threshold. Researchers have addressed this problem by constructing networks across various thresholds, a technique known as “multithresholding.” The network characteristics for two or more groups, for example, were compared for a range of these threshold values [Sanz‐Arigita et al., 2010; Stam et al., 2007; Supekar et al., 2008]. Recently, graph filtration and persistent homology concepts have been applied to brain network analysis [Lee et al., 2011a, 2011b]. In these studies, a multi‐scale framework was proposed to investigate the topological changes of brain networks for every possible threshold, instead of determining one proper threshold that might not be optimal for different cognitive and/or clinical conditions. Within this framework, they could identify the persistent topological features of the brain networks over various thresholds [Lee et al., 2012]. A method, named threshold‐free cluster enhancement (TFCE), was introduced to address the above‐mentioned two problems in MR analysis [Smith and Nichols, 2009]; however, no method has yet been proposed for connectivity analysis.

In this study, we propose a novel MTP correction method for connectivity analysis, named degree‐based statistic (DBS). This method takes advantage of cluster‐wise statistics, an approach that is less conservative and more sensitive. In DBS, a cluster is defined as a set of edges connected through one single node. This is beneficial for detecting a center node which is a potential hub. In addition, we adopted the concept of “persistence” (the multi‐scale invariant) from algebraic topology [Horak et al., 2009; Zomorodian and Carlsson, 2005] to overcome (or at least minimize) the arbitrariness in an initial cluster‐forming threshold. Hence, DBS identifies persistent clusters associated with an effect of interest. We tested DBS in many different simulation settings. Finally, we applied DBS to two real cases of connectivity analysis: two imaging modalities (resting fMRI and DTI) and two neurodegenerative diseases (Alzheimer's disease and Parkinson's disease). We demonstrated that DBS is a powerful MTP correction method. DBS is expected to be sensitive and further to provide reliable and easily interpretable statistical results of connectivity analyses in variable conditions.

METHODS

Overview

In statistical analysis, controlling the FWER is of critical importance. Connectivity analysis of the human brain entails mass‐univariate hypothesis testing and, therefore, MTP inevitably occurs. The proposed DBS is designed to mitigate the increased risk of false positive errors from MTP in the connectivity analysis by using the idea of cluster‐wise correction in functional brain imaging analysis. In this method, a cluster is defined as a set of edges connected through one node (i.e., a one‐node‐centered cluster). Defining a cluster in this way allows DBS to detect clusters and their center nodes that are associated with an effect of particular interest. DBS uses one of two measures to estimate the significance of clusters: the first is based on the binary degree (representation of cluster‐size) and the other is based on the weighted degree (representation of cluster‐mass) which could be considered as a generalization of the binary degree. In addition, to resolve, at least partially, the arbitrariness of an initial cluster‐forming threshold, we propose two strategies. First, DBS is performed repeatedly across multiple initial cluster‐forming thresholds. This enables us to represent clusters of edges that are considered significantly associated with an effect of interest over successive initial cluster‐forming thresholds. Second, a new measure of clusters, center persistency (CP) is introduced. The CP score represents the extent to which cluster centers are persistently associated with an effect of interest independent of an initial cluster‐forming threshold. As a result, DBS provides two measures of clusters for significance testing, “degree” and “CP” score. The significance of the degree is estimated for multiple thresholds and reported for each threshold, whereas the persistency score and its significance is estimated independent of the thresholds as an inclusive measure.

Principle and Underlying Assumptions

DBS is based on two assumptions: (1) a cluster of connections serves a certain brain function and (2) a node that mediates this function exists in the center of the cluster. In other words, a node is centric and interacts with all regions of the cluster to process and integrate information. Based on these assumptions, DBS defines a cluster as a set of edges connected through one single node, where the weights of the edges are above a certain threshold (Fig. 1). In hypothesis testing, a cluster $E_{{\mathrm{v}}_{\mathrm{i}}}\left(s\right)$ is an edge set of a node v _i with an initial threshold s such that

$$E_{{\mathrm{v}}_{\mathrm{i}}}\left(s\right)=\left\{e=\left\{v_{\mathrm{i}},a\right\} \right| s_{\mathrm{e}}>s, \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{n}\mathrm{y} \mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e} a \mathrm{i}\mathrm{n} \mathrm{a} \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{m}\mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{x}\},$$

where s _e is the weight (a statistical value from the tested hypothesis) of edge e.

Figure 1.

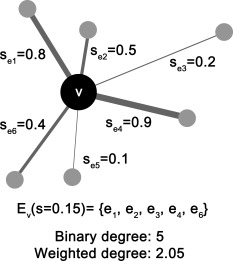
Illustration of a cluster in degree‐based statistic (DBS). A cluster is defined as a set of edges connected through one node where the edge weights are above a threshold (here, the threshold s is 0.15). In other words, this set of edges forms a one‐node‐centered cluster.

Consequently, every edge in the cluster $E_{v_i}\left(s\right)$ is an edge of this centric node v _i; thus, the size and mass of a cluster is equal to the binary and weighted degree of the centric node, respectively. Hence, in the proposed DBS, the degree of the centric node is used to determine the significance of the association between the cluster and an effect of interest.

Construction of a Connectivity Matrix

A graph or network consists of nodes and edges with a connectivity matrix forming the basis of the graph. Construction of a connectivity matrix first requires the definition of a set of nodes and edges. Nodes and edges are subjective and therefore vary across studies. In the network analysis of MR‐based brain imaging data, there have been many suggestions regarding node selection. First, every voxel in a brain image can be defined as a node, yet this approach results in a very large number of nodes. These voxel nodes themselves are not related to brain functions or anatomical brain regions and computational cost is high. To overcome these shortcomings, several parcellation schemes have been suggested, such as Brodmann areas [Brodmann, 1909], cytoarchitectonics [Schleicher and Zilles, 1990], Talairach atlas [Lancaster et al., 2000], automated anatomical labeling [Tzourio‐Mazoyer et al., 2002], Harvard‐Oxford atlas distributed with FSL (http://www.fmrib.ox.ac.uk/fsl/), or data‐driven methods [Blumensath et al., 2013; Tononi et al., 1998; Zhu et al., 2012]. These approaches divide the brain into dozens to thousands of small regions. This set of regions can be used as nodes.

After determining the nodes, edges representing pairwise interactions among the nodes should be defined. Edges can represent structural or functional associations [Papo et al., 2014]. In the case of white matter structures, diffusion tensor imaging measures the structural connectivity, whereas magnetoencephalography (MEG), electroencephalography (EEG), and fMRI can be used to measure functional synchronization indicating functional connectivity. Many concepts and mathematical methods have been developed and applied to estimate functional connectivity [Bowman, 2014; Sakkalis, 2011]. For example, the Pearson product–moment correlation coefficient and coherence estimate linear relationships, whereas rank correlation coefficients and mutual information describe nonlinear interactions. Pairwise connectivity among nodes are elements of the connectivity matrix. If the number of nodes is N and a graph is undirected, N(N − 1)/2 elements should be measured. A connectivity matrix can be weighted or binary. Hypothesis testing typically involves a comparison among groups or a correlation between connectivity and a particular brain function. In either case, a weighted matrix is generally assumed to be appropriate.

Mass‐Univariate Hypothesis Testing of the Connectivity Matrix: Suprathreshold Edges with Multiple Initial Cluster‐Forming Thresholds

Hypothesis testing of the connectivity matrix is performed to estimate a set of statistical values for every element in the connectivity matrix with an effect of interest. In general, an initial cluster‐forming threshold is then applied to define a matrix of suprathreshold edges. In DBS, multiple thresholds with a narrow step size are repeatedly applied to avoid arbitrary selection of the threshold (Fig. 2). For one initial cluster‐forming threshold s, sets of suprathreshold edges with higher statistics than the threshold s are obtained and used to define clusters E _v(s). Then, when the cluster size is chosen to determine the significance of clusters, the binary degrees, d _v(s), of the centric nodes in each cluster are measured. Here, d _vi(s) is the number of edges in edge set $E_{{\mathrm{v}}_{\mathrm{i}}}\left(s\right)$. When the cluster mass is chosen, the weighted degree $w_{{\mathrm{v}}_{\mathrm{i}}}\left(s\right)$ is calculated instead of d _vi(s). The weighted degree w _vi(s) of the node v _i for a threshold s is the sum of the h _e, intensity of suprathreshold edges, which is defined by “s _e – s,” of the node v _i:

$$w_{{\mathrm{v}}_{\mathrm{i}}}\left(s\right)={\sum }_{e\in E_{{\mathrm{v}}_{\mathrm{i}}}\left(s\right)}{h}_{\mathrm{e}}\left(s\right),$$

where h _e(s) = s _e – s.

Figure 2.

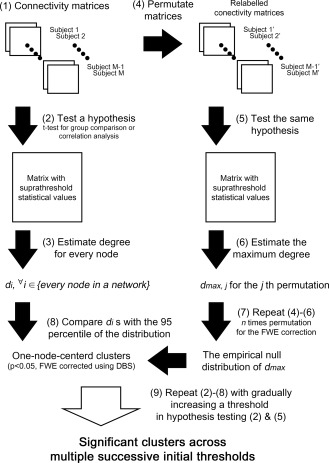
Procedure of degree‐based statistic (DBS). The observed real data and the permuted data are tested for the same hypothesis (using an equal threshold). In DBS, a cluster is defined as a set of edges connected through one node. Hence, the size of a cluster equals the degree of the centric node in the cluster. The maximum degree is measured for each permuted set and a number of permutations are used to estimate an empirical null distribution of the maximum degree. In real data, several clusters can be obtained from the hypothesis testing. The significance of each cluster is estimated by comparing its size with the 95th percentile of the null distribution of the maximum degree (cluster‐wise corrected P‐value of 0.05). Finally, one‐node‐centered clusters that are significantly associated with an effect of interest are obtained.

As described above, to avoid arbitrariness in initial thresholding, DBS calculates d _vi(s) or w _vi(s) across multiple initial cluster‐forming thresholds increasing gradually in narrow increments: the initial cluster‐forming threshold s is raised from the statistical value at P = 0.05 for the tested hypothesis, which is the conventional threshold value in one univariate hypothesis test. This is to provide a resulting set of significant clusters capable of surviving over multiple successive thresholds. As a cluster is a set of edges connected through one node, we can easily use the centric node of this cluster to detect the same cluster from different thresholds.

The significance of the degree, d _vi(s) or w _vi(s) is estimated by comparing these values with a null distribution of the maximum degree, which is acquired empirically in the following step (Fig. 3, as an example). The comparison process is explained in the next section “Degree‐based statistic (DBS): a correction procedure.”

Figure 3.

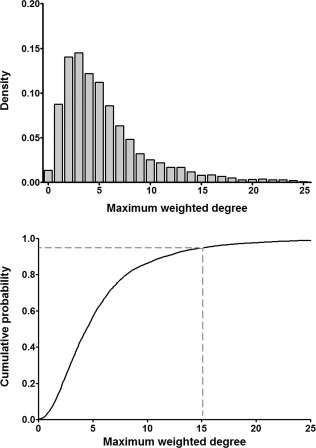
Example of an empirical null distribution of the maximum weighted degree from permutations. These density and cumulative probability distributions are empirically acquired from 5,000 permutations. The value of the 95th percentile (gray dashed line) in a distribution would be used for the DBS corrected P‐value of 0.05.

DBS: A Correction Procedure

The main step to control the FWER is permutation‐based cluster‐wise inference. We performed cluster‐wise inference by employing permutation testing, which has often been used in previous studies [Han et al., 2013; Zalesky et al., 2010]. Permutation testing consists of random labeling of data and hypothesis testing, repeated many times. We performed 5,000 permutations in Simulation and Applications of this study. For each permutation, we measure the maximum binary degree (for a cluster size), d _max,j, where j indicates the jth permutation. This d _max,j is the maximum size of the one‐node‐centered cluster in the jth permutation. From all permutations, an empirical null distribution of d _max is acquired. In the previous step, degrees, d _vi s, were measured from the observed data. A comparison of d _i with the 95th percentile of the empirical null distribution of d _max enables estimation of the significance of observed clusters (cluster‐wise corrected P < 0.05). When the weighted degree is used (as a cluster mass), the same procedure is followed to determine w _max and w _vi. The empirical maximum distribution is acquired for each of multiple initial cluster‐forming thresholds with a narrow increment as in section 2.4. Thus, DBS obtains the empirical null distribution of d _max(s) or w _max(s) and the observed d _vi(s) or w _vi(s) is compared with the 95th percentile of the empirical null distribution of d _max(s) or w _max(s) for each threshold s (Fig. 2).

Center Persistency (CP)

Above, we described how DBS functions across initial cluster‐forming thresholds. Although this approach was intended to avoid selecting one arbitrary threshold, the result still depends on a specific range of thresholds. This prompted us to define a new measure, center persistency (CP), by borrowing the concept of persistence from algebraic topology [Horak et al., 2009; Zomorodian and Carlsson, 2005]. This CP score represents the persistent and significant association of a cluster center with an effect of interest in a wide possible range of initial cluster‐forming thresholds. This persistency score is estimated for each cluster. The CP is calculated by obtaining the sum of the weighted degrees for the entire possible range of thresholds.

$${\mathrm{C}\mathrm{P}}_{{\mathrm{v}}_{\mathrm{i}}}=\int w_{{\mathrm{v}}_{\mathrm{i}}}\left(s\right)ds\approx {\sum }_n{w}_{{\mathrm{v}}_{\mathrm{i}}}\left(s\right)\Delta s$$

The threshold range is determined in a data‐driven way. At first, the lower boundary of the threshold is set to the statistical value at a P‐value of 0.05 (P = 0.05 for the tested hypothesis is the conventional threshold value in univariate hypothesis testing). Then, the initial threshold is gradually raised to the value before the binary degree threshold becomes 2, which was acquired in the previous permutation step for the cluster‐wise inference in section “Degree‐based statistic (DBS): a correction procedure.” The reason for this range is that (1) the P‐value of 0.05 for the lower boundary is a commonly selected statistical threshold in one univariate hypothesis testing and (2) the higher boundary guarantees the minimum possibility of a cluster formation having three edges. Then, the CP score of the v _i node‐centered cluster, CP_vi, is measured for this range.

The significance of CP_vi is estimated by comparison with a null distribution of the maximum persistency score, CP_max. The null distribution is acquired empirically from permutation similar to the degree described in section “Degree‐based statistic (DBS): a correction procedure.” We measure CP_max from the same permutation set (e.g., CP_max,j is for the jth permutation). Then, the observed CP_vi is compared with the 95th percentile of the empirical null distribution of CP_max. Clusters with CP scores higher the 95th percentile are persistent clusters with a corrected significance of P < 0.05. In other words, the CP score represents the extent to which the persistent association of a cluster center with an effect of particular interest is significant, independent of the initial threshold selection. In addition, the normalized CP can be used for further comparison among clusters.

$$\mathrm{n}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{d} {\mathrm{C}\mathrm{P}}_{{\mathrm{v}}_{\mathrm{i}}}={\mathrm{C}\mathrm{P}}_{{\mathrm{v}}_{\mathrm{i}}}/\{\mathrm{t}\mathrm{h}\mathrm{e} 95 \mathrm{p}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{l}\mathrm{e} \mathrm{o}\mathrm{f} {\mathrm{C}\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\}$$

We suggest the use of a normalized CP to compare clusters among studies based on different imaging modalities (such as DTI and fMRI) or connectivity measures (such as mean FA and fiber number for DTI, and different correlations and coherences for fMRI). Because the weighted degree value, even its order of magnitude, could be different across studies, the original CP scores of clusters were not easily compatible. However, as shown in the above equation, this normalized CP is estimated by the ratio of the CP score of a cluster to the threshold selected for the significance. Thus, the above equation would enable us to determine which of the clusters (estimated from different imaging modalities and connectivity measures) is more persistent for the effect of interest with a fixed threshold.

SIMULATION

This section describes the performance evaluation of DBS to detect a known “ground truth” contrast from simulations. The simulated data comprising “signal contrast + noise” were used to test the gain in power and efficacy of the DBS in a situation which is suited to the DBS. The contrast was defined by a set of edges sharing one single node as represented in Figure 1. Receiver operator characteristic (ROC) curves were constructed from simulated data and presented to validate the specificity and sensitivity of the DBS. In this simulation, we tested DBS with the weighted degree (DBSwd) and CP score.

Data Simulation

We simulated “known” differences between two groups of undirected connectivity matrices. Each of the two groups consisted of 20 subjects and the number of nodes was 100. First, one connectivity matrix was constructed by sampling from a normal distribution of zero mean and 0.3 standard deviation, N(0, 0.3²), and assigned as the first subject of the group A. Then, the other 19 subjects in group A were constructed by adding noise N(0, 0.1²) to each of the edges of the first connectivity matrix to perturb them. For group B, we defined a contrast, which is a set of edges sharing one single node. One centric node was first determined and then a set of edges with this centric node was randomly selected. Then, for every other edge without contrast, noise N(0, 0.1²) was added to the edges of the first connectivity matrix by using the same procedure as for the creation of group A. However, for the contrast edges, a signal contrast with noise N(c, 0.1²) was added. In this step, the same signal contrast c across the edges and subjects was used. We tested our method under different conditions with a varying cluster size (the number of edges comprising a contrast) and varying contrast to noise ratio (CNR, the ratio of c to 0.1). All the CNRs we tested were relatively low in agreement with the purpose of cluster‐wise correction. We tested CNRs of 0.75, 1, 1.25, and 1.5 and cluster sizes of 5, 10, 20, and 30. As a result, we simulated and tested our method for a total of 4 × 4 = 16 conditions. The same process of a simulation was repeated by changing the number of nodes within a network with proportional cluster sizes; (1) 150 nodes: cluster sizes of 10, 15, 30, and 45 and (2) 50 nodes: cluster sizes of 5, 10, and 15. The same four CNRs were used across the simulations.

Performance Evaluations Using Simulated Data

A ROC curve was used to evaluate the performance of the DBS. An ROC curve plots the TPR against the false positive rate (FPR) of contrast detection as the discrimination threshold varies. Standard ROC was designed for a single inference. As DBS deals with mass‐univariate hypothesis testing in a cluster‐wise way, we employed the alternative free‐response receiver‐operator characteristic (AFROC) curve as in similar previous studies [Ing and Schwarzbauer, 2014; Smith and Nichols, 2009]. In AFROC, the TPR is the same as in standard ROC, that is, the proportion of true positives among all positive tests. However, in AFROC FPR is defined as the probability of false positives anywhere in the image (in this study, connectivity matrix) [Chakraborty and Winter, 1990]. As the purpose of DBS is to control the FWER, a more stringent AFROC curve would be more appropriate. ROC curves were constructed for a range of FPR from 0.001 to 0.05, since an FPR exceeding 0.05 is not of interest in a typical analysis.

The complete process to construct ROC curves of 100 nodes is as follows:

1. Connectivity matrices of two groups with the known ground truth were created. The first connectivity matrix of 100 nodes of group A was constructed by sampling from N(0, 0.3²). The remaining 19 connectivity matrices in group A were created by adding noise N(0, 0.1²) to every edge of the first connectivity matrix. A contrast is first defined in group B. Twenty connectivity matrices were created by adding a signal contrast with noise N(c, 0.1²) for contrast edges, otherwise only noise N(0, 0.1²) was added. Each group consisted of 20 subjects.

2. The two groups of the connectivity matrix underwent mass‐univariate two‐sample hypothesis testing to obtain the P‐value and t‐statistics for every edge.

3. DBSwd, CP score, and permutation‐based element‐wise marginal statistics were applied for the statistical matrix results from step 2 above. For w, four different initial thresholds were tested: 0.05, 0.01, and 0.005.

4. TPR was calculated as |T∩ĥ|/|T|, where T is the contrast set of edges and ĥ is the set of edges which form clusters. FPR = 1 if |ĥ − T| ≥ 1, otherwise FPR = 0. For the CP score, as CP is assigned to each node which forms the centric of each cluster, T was differently defined; T is the centric node of the contrast set of edges.

5. Steps 1–4 were repeated 1,000 times and the average TPR and FPR values over 1,000 simulations were estimated. Then, the ROC curves were constructed using these TPR and FPR values over the range of the discrimination threshold.

6. Steps 1–5 were performed under different conditions: four different cluster sizes (4, 10, 20, and 30) and four different CNR values (0.75, 1, 1.25, and 1.5) were used. As a result, ROC curves for the CP score, DBSwd with four different initial thresholds (an initial cutoff P‐value of 0.05, 0.01, and 0.005), and element‐wise correction were constructed for these 4 × 4 = 16 different conditions.

Simulation Results

Figure 4 (and Supporting Information Figs. 1 and 2) illustrate the performances of DBS, CP score, as well as element‐wise correction and NBS from simulations under the different conditions. Overall, DBS with initial thresholds of P‐value 0.01 and 0.005 outperformed the element‐wise correction method as well as the NBS, one of cluster‐wise correction method. However, when the initial threshold of P‐value 0.05 was applied in DBS, its performance was not better than that of element‐wise correction, especially for CNR of 1.25 or higher (Fig. 4, Supporting Information Figs. 1 and 2).

Figure 4.

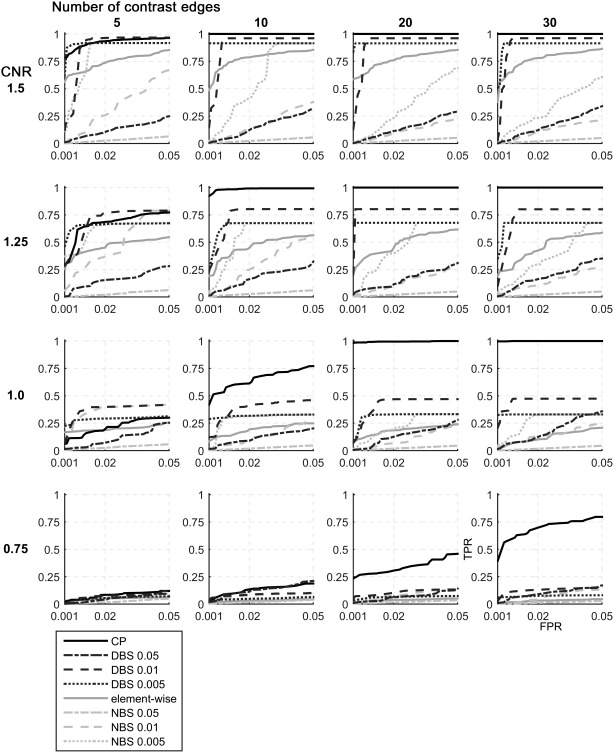
ROC curves constructed from simulations under different conditions in 100 nodes network. The performance of DBS was evaluated for the detection of a known “ground truth” contrast under different conditions. Four CNR values (0.75, 1, 1.25, and 1.5) and four cluster sizes (5, 10, 15, and 20) were applied. In general, DBS and CP worked better with larger cluster size. However, the performance of element‐wise correction was not different across multiple cluster sizes when CNR is fixed. (The number following DBS or NBS represents the applied initial threshold of P‐value.).

The CP score showed the highest power under the most conditions. When a cluster comprised a large number of edges (more than 20 edges), the CP was exceptionally effective even with a very low CNR such as 1.0 or below (Fig. 4, Supporting Information Fig. 1). However, in the case of small clusters such as five edges, CP did not outperform DBS with an initial threshold of 0.01 or 0.005. Both DBS and the CP score were more effective for larger cluster sizes in contrast to the element‐wise correction of which the performance was unlikely to be affected by the cluster size.

APPLICATIONS

For the following two applications, we used the weighted degree and CP score for significance estimation with correction.

Structural Connectivity Difference in Alzheimer's Disease: A DTI Study

Subject recruitment and MR acquisition and preprocessing

We applied DBS to analyze the difference in structural connectivity between patients with Alzheimer's disease (AD) and healthy controls. Twenty‐seven patients with probable AD dementia with a Clinical Dementia Rating score of 1 and 30 age‐matched healthy controls were recruited (Table 2). Structural MRI and diffusion‐weighted images were obtained using a 3.0 T MRI scanner (Philips 3.0 T Achieva) at Samsung Medical Center. DTI preprocessing was performed using the diffusion toolbox of the FSL package (http://www.fmrib.ox.ac.uk/fsl/fdt) and fiber tracking was performed using the TrackVis [Wang et al., 2007, http://www.trackvis.org/] following procedures described in a previous study [Kim et al., 2015] with minor modifications in network edge definition. Briefly, fiber tracking was terminated when the angle between two orientation vectors was greater than 45° or the FA of consecutive voxels was below 0.15. Additionally, fibers shorter than 20 mm and longer than 200 mm were disregarded [Guevara et al., 2011; Kim et al., 2015; Yoo et al., 2015a, 2015b]. Whole‐brain white matter fiber tracts were reconstructed in native diffusion space for each subject via the FACT algorithm [Mori et al., 1999]. The participants provided written informed consent to participate in this study. This study was approved by the Institutional Review Board of Samsung Medical Center, Seoul, Korea.

Table 2.

Demographics

	HC	AD
Subjects (sex)	30 (21F)	27 (17F)
Age	70.9 (±5.5)	70.2 (±8.2)
CDR sum of boxes (SNSB)	0.6 (±0.4)	5.8 (±1.2)*
Mini‐mental state examination	28.8 (±1.2)	17.6 (±3.8)*

*Significantly different at P < 0.001.

Network construction

We employed 90 brain regions of an AAL parcellation scheme [Tzourio‐Mazoyer et al., 2002] as a set of nodes for the network. Two nodes were considered to be structurally connected when there are fiber tracts that pass through these nodes. Both ends of fibers that pass through the nodes were truncated, whereas fibers between two nodes were left intact. The edge weights for every pair of 90 regions were calculated. The weight of an edge was defined as the mean FA of the fiber tracts between two nodes when tracts existed, and the weight was set to zero if tracts did not exist between two nodes.

Degree‐based statistic (DBS)

We investigated the difference of structural connectivity between patients with AD and age‐matched healthy controls (unpaired two‐sample t‐test). We re‐labeled each of the 57 connectivity matrices with one of two groups (AD or HC) and applied DBS with 5,000 permutations. Then, the weighted degrees and persistency score for each cluster and their significance were estimated (P < 0.05 corrected using DBS).

Results

We found two clusters centered on, respectively, the right middle cingulate gyrus and the left caudate as persistent clusters significantly altered in the AD group (Fig. 5, corrected P < 0.05; normalized CP 1.96 and 1.37, respectively). The cluster of the right middle cingulate gyrus, especially, was shown to be significant across the entire range of initial thresholds (corrected P < 0.05). In addition, another cluster of edges centered on the right amygdala was shown to be significantly altered in the AD group at a range of initial threshold t‐value below 2.2, but it did not have significant CP.

Figure 5.

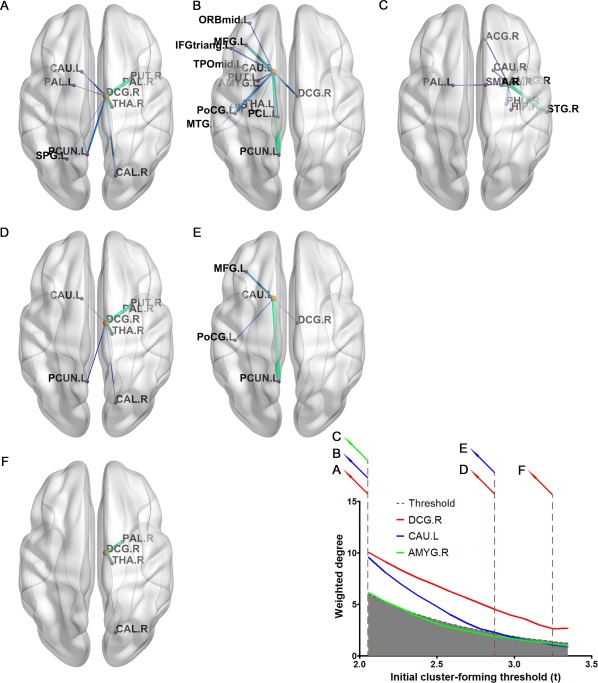
Clusters of edges significantly different in patients with Alzheimer's disease. Three clusters of edges are significantly different in patients with Alzheimer's disease compared with healthy controls over a range, at least a restricted range, of initial cluster‐forming thresholds. Only two clusters centered on the right middle cingulate gyrus (A, D, and F) and the left caudate (B and E) were shown as persistent clusters (significant CP score). A cluster of edges centered on the right amygdala was not a persistent cluster, but detected significantly different at a liberal initial threshold (C). The white area (contrasting the gray area) above the dashed line represents a significant result (P < 0.05 FWE corrected using DBS). Clusters overlaid with the brain are illustrated using BrainNet Viewer [Xia et al., 2013].

Comparison with other correction methods

Application of the Bonferroni correction to the hypothesis testing of 4,005 elements from a matrix of 90 nodes (α = 0.05 for a P‐value of 0.05/4,005 for each individual connection), did not reveal any significant changes in connectivity. For the permutation‐based marginal statistic, we estimated the empirical null distribution of the minimum P‐value from 5,000 permutations. Then, we applied thresholds of α = 0.05. After this correction, two connections were found to be significantly different, one between the right middle cingulate gyrus and putamen, and the other between the right middle cingulate gyrus and thalamus. For NBS, we applied a range of primary cut‐off thresholds, the same as the cut‐off used for DBS, and then applied an NBS threshold of corrected P = 0.05 to identify connected components. For the entire range of initial threshold that were tested, this method identified one large connected component including every connection and region identified by DBS.

Functional Connectivity with Non‐Motor Symptoms in Parkinson's Disease Regarding Motor Laterality: A Resting fMRI Study

Subject recruitment and MR acquisition and preprocessing

Secondly, we applied DBS to analyze the correlation between resting state functional connectivity and the severity of non‐motor symptoms in patients with Parkinson's disease (PD). This dataset is the same as in our previous study [Yoo et al., 2015a, 2015b]. Eighty‐seven consecutive patients with PD were recruited in the Department of Neurology at Asan Medical Center (AMC) in Seoul, Korea (Table 3). The diagnosis was made based on the United Kingdom Parkinson's Disease Society brain bank clinical diagnostic criteria [Gibb and Lees, 1998]. Structural and functional MRI data were obtained using a 3T MRI scanner (Philips Healthcare, Best, The Netherlands) at AMC. Functional MRI preprocessing was performed using Statistical Parametric Mapping 8.0 in MATLAB R2011b (7.13) (Natick, MA) following procedures described in a previous study [Yoo et al., 2015a, 2015b]. The participants provided written informed consent to participate in this study. This study was approved by the Institutional Review Board of AMC, Seoul, Korea. Detailed information is described in the previous study [Yoo et al., 2015a, 2015b].

Table 3.

Demographics

		Left‐more‐affected LPD	Right‐more‐affected PD
Subjects (sex)		44 (27F)	37 (23F)
Age		64.4(±9.3)	62.2 (±12.7)
	Part I	5.6 (±4.8)	6.0 (±4.3)
MDS‐UPDRS	Part III	29.6 (±11.9)	29.6 (±11.9)
	Total	46.9 (±18.5)	48.2 (±20.0)
S&E ADL		79.8 (±6.2)	79.1 (±9.9)
H&Y stages		2.1 (±0.6)	2.1 (±0.7)
Motor laterality		6.5 (±3.5)	7.5 (±3.5)

Network construction

The procedure that was performed was similar to that in 4.1.2, with the difference that brain regions were considered as ipsilateral or contralateral to the body side of dominant motor symptoms for each PD. For example, in the case of patients who experience several motor symptoms in the left side of their body, the left and right hemispheric regions were considered as the ipsilateral and contralateral brain regions, respectively.

Degree‐based statistic (DBS)

We investigated the correlation of resting state functional connectivity with the severity of non‐motor symptoms in PD with regards to the motor laterality (correlation analysis with Pearson product–moment correlation). We re‐labeled each of the 81 connectivity matrices with one of their severity scores and applied DBS with 5,000 permutations. Then, the weighted degrees and persistency score for each cluster and their significance were estimated (P < 0.05 corrected using DBS).

Results

We found a cluster of a centric node, the ipsilateral inferior orbitofrontal area, to be a persistent cluster significantly correlated with the severity of non‐motor symptoms of PD (Fig. 6, corrected P < 0.05; normalized CP 1.05). Regarding the specific range of the initial thresholds, this cluster was shown to be significant in a lower threshold range (corrected P < 0.05).

Figure 6.

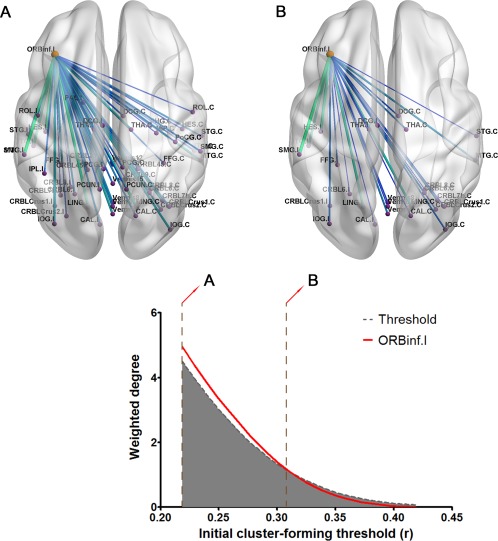
Cluster of edges significantly correlated with the severity of non‐motor symptoms in Parkinson's disease. One cluster of edges centered on the ipsilateral inferior orbitofrontal area was shown as a persistent cluster (significant CP score). The white area (contrasting the grey area) above the dashed line represents a significant result (P < 0.05 FWE corrected using DBS). Cluster overlaid with the brain is illustrated using BrainNet Viewer [Xia et al., 2013]. [Color figure can be viewed at http://wileyonlinelibrary.com.]

Comparison with other correction methods

Application of the Bonferroni correction to the hypothesis testing of 6,670 elements from a matrix of 116 nodes (α = 0.05 for a P‐value of 0.05/6,670 for each individual connection) did not reveal any significant changes in connectivity. For the permutation‐based marginal statistic, we estimated the empirical null distribution of the minimum P‐value from 5,000 permutations. Then, we applied thresholds by using α = 0.05. Again, this correction did not lead to any significant changes in connectivity. For CBS, we applied a range of primary cut‐off thresholds, the same as the cut‐off used for DBS, and then applied a CBS threshold of corrected P = 0.05 to identify connected components. For the entire range of initial thresholds that were tested, this method could not identify any connected component.

DISCUSSION

The accurate analysis of brain connectivity requires accurate statistical approaches. Connectivity analysis involves the examination of a massive number of edge elements, which is an MTP. Therefore, it is necessary to control the false positive error rate appropriately and carefully. This led us to propose a novel method, DBS, to control the FWER by adapting the principles of cluster‐wise correction and the graph theoretical concept of “degree.” DBS, which uses cluster‐wise inference, is designed to overcome two innate drawbacks of cluster‐wise inference.

The unsuitability of element‐wise corrections, such as the Bonferroni correction, permutation‐based marginal statistic, and other FDR control procedures, has resulted in the introduction of cluster‐wise approaches, because the element‐wise methods are too stringent for the analysis of MR data with low signal‐to‐noise ratios. Since then, many cluster‐wise correction methods have been developed and have become the preferred approach [Woo et al., 2014]. The use of cluster‐wise statistics to make inferences first requires a cluster to be defined. In traditional MR imaging analysis, a cluster comprises a set of neighboring voxels that clump together to form a spatially continuous mass in a physical sense. However, it is not easy to apply cluster‐wise statistics to a connectivity analysis because the definition of a cluster is not as obvious. In the case of voxel elements in an MR image, voxels within a specified proximity could simply be considered to be neighboring, for the purposes of defining a cluster. However, the situation is somewhat different for edge elements in a connectivity matrix. Two neighboring edge elements in the connectivity matrix are connected; thus, they could be assumed to form a cluster. In addition, edge elements that are not neighboring in the matrix could be connected when they share a common node. This is the case for NBS [Zalesky et al., 2010]. In these methods, a cluster is defined as a connected component and the size of a cluster is considered to be the number of connections in the component. Another method, named SPC, defines a cluster as a set of edges for which ending points, that is, two nodes, adjoin each other [Hipp et al., 2011; Zalesky et al., 2012b]. In SPC, edges are not required to share a common node; instead, nodes are required to be located nearby. In another study that introduced two methods, CSS and CMS, a cluster was defined as a set of spatially continuous voxels having connections with other voxels [Ing and Schwarzbauer, 2014]. The last two methods, SPC and CSS/CMS, might be more suitable for connectivity matrices of networks consisting of a large number of small‐sized nodes, such as voxels themselves, whereas NBS would be appropriate for a connectivity matrix with relatively large‐sized nodes. In addition, only NBS defines a cluster as a connected set of edges, literally, among spatially distinct regions, whereas the other methods consider a mass of spatially continuous voxels as a cluster.

In this study, we defined a cluster as a set of edges connected through one node, that is, a one‐node‐centered cluster. The underlying assumption for this definition is the existence of a pivotal node playing the main role in mediating brain function by interacting with every other region to integrate information in the center of the module. Based on this definition and set of assumptions, we were able to estimate the size of every suppositional cluster by calculating the degree of every node. In other words, the size of a one‐node‐centered cluster is simply the degree of the centric node of the cluster. We tested the significance of a cluster using the graph theoretical concept of degree; therefore, we named our method DBS. The definition of a cluster in DBS naturally provides several advantages. Cluster‐wise inference involves low spatial specificity. Although the edges in a DBS cluster are of interest, it is possible to point out the centric node of the cluster similar to local peaks of a cluster in MRI analysis. Another point is that we might consider the centric node to play a pivotal role as a hub of the cluster for the brain function of interest. In graph theory, hubs are nodes with high degree or high centrality [Bullmore and Sporns, 2009]. The centric node of a cluster in DBS might be considered as a hub region for a specific brain function of interest for the purpose of being tested with many significantly associated edges. Finally, our definition of a cluster facilitates location of the same cluster over multiple initial cluster‐forming thresholds. DBS extends over a range of initial cluster‐forming thresholds. Identification of a persistent cluster requires confirmation that two clusters defined by different thresholds are in fact the same cluster. In DBS, every cluster has its own unique centric node, thus it is very the way the cluster is defined does not prevent the same cluster from being found across the different thresholds.

One major limitation of cluster‐wise inference is the arbitrary decision regarding the primary threshold to acquire a set of suprathreshold edges. Cluster‐wise inference requires the use of an initial cluster‐forming threshold to define a cluster. As of yet, there is no solution for this arbitrariness issue. There has been growing consensus that too liberal a threshold should be avoided. In the case of fMRI activation, one study has suggested that a primary P‐value of 0.001 yields a reliable result [Woo et al., 2014]. Applying a similar primary threshold might be appropriate in connectivity analysis. However, there is no guarantee that the same result will be obtained for different initial thresholds, as is the case with MRI analysis. We resolved this uncertainty by borrowing the concept of persistence from algebraic topology and suggested a new measure, center persistency (CP) [Horak et al., 2009; Zomorodian and Carlsson, 2005]. This score is estimated collectively from an entire possible range of initial thresholds. The concept of persistent homology has been previously applied in medical imaging and brain network analysis [Chung et al., 2009; Lee et al., 2011a, 2011b; Pachauri et al., 2011; Singh et al., 2008]. This approach in network analysis was essentially implemented to avoid having to test every possible threshold or having to determine the optimal threshold in network construction or modeling. Adaptation of this concept enabled us to further improve DBS to reveal persistent clusters associated with an effect of interest. As a result, it was possible to identify the centers of persistent threshold‐independent clusters. The formula for CP is quite similar to that of TFCE, which is implemented in the FMRIB software library [Smith and Nichols, 2009]. Similar to the CP in DBS, TFCE is intended to avoid arbitrary primary thresholding in MR analysis. However, the difference between CP in DBS and TFCE, besides CP being proposed for connectivity analysis and TFCE being used for the analysis of MRI, is that CP in DBS is calculated for each cluster, whereas TFCE is estimated for each element (voxel). In other words, CP is a cluster‐wise method, whereas TFCE is a cluster‐like element‐wise method. The formula of the CP score could be modified should it be necessary to assign a higher weighting to the higher initial thresholds. For example, the weighted degree could be multiplied by the initial threshold on which the weighted degree is estimated before the CP score is calculated:

$${\mathrm{C}\mathrm{P}}_{\mathrm{i}}=\int s*w_{\mathrm{i}}\left(s\right)ds\approx {\sum }_{n}s*w_{\mathrm{i}}\left(s\right)\Delta s$$

This would provide higher sensitivity for revealing a cluster with a small number of edges, but which has a very significant association with an effect of interest. However, this arbitrary weighting may not be desirable in every case. A further improvement could be achieved by raising the initial threshold s and the weighted degree w _i to a certain power:

$${\mathrm{C}\mathrm{P}}_{\mathrm{i}}=\int s^{\mathrm{a}}*{w_{\mathrm{i}}\left(s\right)}^{\mathrm{b}}ds\approx {\sum }_n{s}^{\mathrm{a}}*{w_{\mathrm{i}}\left(s\right)}^{\mathrm{b}}\Delta s,$$

where a and b should be defined.

In the case of TFCE, the authors raised the cluster extent and initial threshold to a certain power in the TFCE estimation, although TFCE is calculated using the cluster extent, which is analogous to the binary degree, rather than the weighted degree in DBS. They determined the powers of an initial threshold and cluster extent from many simulations and tests to ensure an acceptable level of sensitivity. However, the result obtained by using these powers would still depend on the specific case.

We validated the power of our method, DBS, over element‐wise correction or NBS under the assumed circumstances using simulations with a known ground truth contrast. We simulated various conditions with different CNRs and cluster sizes as well as the different sizes of a network (Fig. 4 and Supporting Information Figs. 1 and 2). The performances of DBS and CP were better for higher CNR and/or larger cluster size. In contrast, the performance of element‐wise correction remained unchanged when the cluster size was varied for the same CNR, as expected. Under the most circumstances, DBS with relatively conservative initial threshold (a cut‐off P‐value of 0.01 or 0.005) was more powerful than element‐wise correction. In addition, CP scores in DBS showed the highest power for detecting high‐degree nodes. Given low signal‐to‐noise ratio of resting fMRIs and their connectivity [Fox and Grecius, 2010], better performance of DBS compared with the element‐wise method is pertinent.

We want to mention that DBS with an initial threshold of P‐value 0.05 showed poor performance in the most cases (Fig. 4, Supporting Information Figs. 1 and 2). This finding can be attributed to the too liberal initial threshold leading accidental survival of non‐contrast edges. These edges were revealed by DBS even when the cluster‐wise threshold was stringent. In contrast, DBS with an initial threshold of P‐value 0.01 or 0.005 was shown to reach saturated TPR before FPR becomes 0.05. Our results accord with the emerging consensus about the avoidance of too liberal initial threshold in cluster‐wise inference [Woo et al., 2014]. Out of initial thresholds of 0.01 and 0.005, P‐value 0.01 showed higher TPR at FPR 0.05. This finding is attributed to preventing the survival of contrast edges having low signals by more conservative threshold. However, it is worthnoting that the differences between the saturated TPRs of initial threshold 0.01 and 0.005 were decreased as CNR increases from 1.0 to 1.5 (Fig. 4, Supporting Information Figs. 1 and 2). One can expect that when higher CNRs are tested, the performance of DBS with an initial threshold P‐value 0.005 would be better than that of initial threshold 0.01. Thus, it would be beneficial if one uses more conservative initial threshold when higher CNR is ensured. However, it would not be possible to know CNR before analysis in real situations

We also applied DBS to two real datasets with different imaging modalities, resting fMRI and DTI, to demonstrate the effectiveness of DBS in real variable situations. The first analysis was intended to determine the alteration of structural connectivity by Alzheimer's disease using DTI. We found that two clusters of edges centered on the right middle cingulate gyrus and left caudate, respectively, are persistent clusters that are significantly different in AD compared with healthy controls. The disruption or alteration of the middle of the cingulate gyrus is evident. One study reported hypoperfusion in the right middle cingulate gyrus in subjects who converted to dementia compared with non‐converters [Chao et al., 2010]. Another study analyzing DTI data showed that the bilateral cingulum has reduced FA in patients with AD compared with healthy controls or patients with mild cognitive impairment [Liu et al., 2009]. In addition, other studies have shown that disruption (hypometabolism and reduced FA) of the middle cingulate gyrus is correlated with hippocampal atrophy in AD [Canu et al., 2013; Villain et al., 2008]. One network analysis study using a structural cortical network and graph theoretical approach found changes in the interregional correlation of the right middle cingulate gyrus with other areas in AD [Yao et al., 2010]. Alteration of the left caudate in AD has also been reported. One study found the volume of the left caudate to be significantly reduced in AD compared with controls [Barber et al., 2001]. A recent study reported a volume reduction in the bilateral caudate even at the presymptomatic stage, with increased fractional anisotropy of the left caudate [Ryan et al., 2013]. The second dataset to which we applied DBS contained the resting fMRI results of subjects with Parkinson's disease with the aim of performing a correlation analysis between functional connectivity and the severity of symptoms. We showed that, in patients with PD, a cluster of edges of the ipsilateral inferior orbitofrontal area was significantly correlated with the severity of non‐motor symptoms (corrected P < 0.05). We reported in our previous study that a set of connectivity of this area was significantly correlated with the severity of non‐motor symptoms [Yoo et al., 2015a, 2015b]. In this previous study, we performed a correlation analysis for one specific threshold of P = 0.001 and reported the uncorrected results. In our current study, by applying DBS, we improved the accuracy of the results by using DBS for correction and further demonstrated that this is independent of the initial threshold selection. Thus, whereas the results of traditional brain connectivity analyses are affected by statistical issues, such as MTP or the arbitrariness of the initial threshold, and would not be easily interpretable [Fornito and Bullmore, 2010], DBS can provide a relatively straightforward result in respect to a hub‐like node with resolving, at least partially, the previously mentioned statistical problems.

Nevertheless, some points need to be addressed. First, the underlying assumptions may not be applicable to certain situations. Because DBS is targeted at and optimized to discover a cluster of edges connected through one node, it cannot be used to detect a cluster that does not contain a centric hub‐like node. If any particular node of a cluster, for example, does not have many edges and if every node of a cluster is evenly connected, DBS would be unable to identify it as a cluster. This indicates that DBS is not a replacement for other cluster‐wise correction methods, but should be considered a complementary method. Second, DBS does not account for the smoothness of fMRI data. The application of cluster‐wise correction methods to the analysis of MRI data, such as fMRI with task‐activation, entails the use of image smoothness to estimate the significance of a cluster [e.g., random field theory, Worsley et al., 1992]. In DBS, the use of nodes with an insufficient size would be inappropriate. Because of the smoothness in functional imaging, neighboring voxels and/or areas have similar patterns of temporal signals and would be estimated being synchronized and connected. Hence, nodes that are defined to have a small size would produce a result that would be incorrectly affected by connections among spatially connected nodes.

CONCLUSION

In this article, we present a novel method, DBS, to control the FWER in connectivity analysis. DBS can be used to identify a set of edges connected through a single hub‐like node. The application of DBS enabled us to detect one‐node‐centered clusters that are significantly associated with an effect of particular interest. Furthermore, we suggested a new cluster measure to overcome the arbitrary selection of an initial cluster‐forming threshold and the lack of spatial specificity. We demonstrated the effectiveness of DBS in diverse situations with multiple imaging modalities, for patients affected by different neurodegenerative disorders. We believe that DBS is widely applicable to cognitive or clinical studies and yields statistically robust and easily interpretable results.