Transition of the functional brain network related to increasing cognitive demands

Abstract

Network neuroscience provides tools that can easily be used to verify main assumptions of the global workspace theory (GWT), such as the existence of highly segregated information processing during effortless tasks performance, engagement of multiple distributed networks during effortful tasks and the critical role of long‐range connections in workspace formation. A number of studies support the assumptions of GWT by showing the reorganization of the whole‐brain functional network during cognitive task performance; however, the involvement of specific large scale networks in the formation of workspace is still not well‐understood. The aims of our study were: (1) to examine changes in the whole‐brain functional network under increased cognitive demands of working memory during an n‐back task, and their relationship with behavioral outcomes; and (2) to provide a comprehensive description of local changes that may be involved in the formation of the global workspace, using hub detection and network‐based statistic. Our results show that network modularity decreased with increasing cognitive demands, and this change allowed us to predict behavioral performance. The number of connector hubs increased, whereas the number of provincial hubs decreased when the task became more demanding. We also found that the default mode network (DMN) increased its connectivity to other networks while decreasing connectivity between its own regions. These results, apart from replicating previous findings, provide a valuable insight into the mechanisms of the formation of the global workspace, highlighting the role of the DMN in the processes of network integration. Hum Brain Mapp 38:3659–3674, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Researchers have long been intrigued by the organization and dynamical reorganization of the human brain networks during performance of cognitive tasks requiring conscious processing. From the perspective of cognitive neuroscience, the question that is particularly interesting is whether the functional network architecture may adapt to the increasing demands of a cognitive task. According to global workspace theory (GWT), conscious perception requires coherent activity of multiple distributed brain regions [Baars, 1997; Dehaene et al., 1998]. Tasks that can be performed automatically and effortlessly mobilize processing within a limited number of functionally specialized modular subsystems. Conversely, effortful cognitive tasks, which require focused attention and conscious control, engage a set of long‐distance connections coordinating the activity of multiple distributed cortical areas [Dehaene et al., 1998].

In the context of functional brain network organization, activity within the global workspace can be illustrated using graph theory and verified by studying global and local topological properties of networks for different cognitive demands. These networks are typically modeled as a set of nodes (corresponding to pre‐defined brain structures) and edges (representing functional connectivity; e.g., temporal correlations of blood oxygen level‐dependent [BOLD] signal fluctuations between brain areas) [Bullmore and Bassett, 2011; Bullmore and Sporns, 2009]. Researchers have shown that the network of the brain is complex but organized in a way that minimizes wiring cost while preserving high efficiency and adaptability of its topological features [Achard et al., 2006; Achard and Bullmore, 2007; Bullmore and Sporns, 2009; Latora and Marchiori, 2001; Simon, 1962]. Several network characteristics, such as small‐worldness (high clustering and short path length), modularity and the existence of connector hubs, allow a network to dynamically switch from states of segregated (specialized) information processing to states of integrated (distributed) processing [Bullmore and Sporns, 2012; Hagmann et al., 2008; Meunier et al., 2010; Sporns et al., 2004; Watts and Strogatz, 1998]. The key question is how the trade‐off between segregated and integrated information processing is re‐negotiated to adapt to changing cognitive demands in a way that supports behavioral outcomes.

The vast majority of fMRI studies have investigated the relationship between human cognitive performance and overall network organization at rest—in the absence of any externally directed tasks [Arnemann et al., 2015; Gamboa et al., 2014; Stevens et al., 2012; van den Heuvel et al., 2009]. For example, van den Heuvel et al. [2009] found that global efficiency correlates positively with intelligence, while other studies showed a relationship of resting‐state network modularity with working memory scores [Gamboa et al., 2014], working memory capacity [Stevens et al., 2012], or improvement in behavioral performance in response to cognitive training [Arnemann et al., 2015].

Recent studies on the task‐based network reorganization support GWT by showing that automatic, unconscious, and low‐demand cognitive processes are related to high levels of network segregation, whereas tasks engaging higher cognitive functions are related to high levels of network integration. For example, in an MEG study, Kitzbichler et al. [2011] found that greater effort during a working memory n‐back task caused network reconfiguration into a more globally efficient, less clustered and less modular architecture. In an fMRI study, Vatansever et al. [2015a] found a decrease of modularity during an n‐back task and its association to behavioral performance when comparing the low‐demand (0‐back) to the high demand (3‐back) condition. Another study by Godwin et al. [2015] showed that conscious perception is associated with increased global integration and decreased modularity of the network.

According to the global neuronal workspace theory, neurons with long‐range connections in prefrontal, parietal and cingulate areas may participate in the process of global integration [Dehaene and Changeux, 2011; Dehaene and Naccache, 2001]. These assumptions are based on multiple neuroimaging studies showing consistent activation of the fronto‐parietal network (FPN) during effortful task execution [Duncan, 2010; Dux et al., 2006; Klein et al., 2007; Landmann et al., 2007]. However, regional brain activation during tasks does not provide exact information whether activated areas actually integrate distinct brain modules [Gratton et al., 2016]. In terms of the network science, entire network integration can be potentially achieved through connector hubs—highly central nodes that are connected to multiple modules [Guimera and Amaral, 2005]. Indeed, some recent network neuroscience studies showed that FPN nodes may facilitate network integration during effortful tasks [Braun et al., 2015; Cole et al., 2013], while other studies assign this role to highly inter‐connected default mode network (DMN) nodes [Fornito et al., 2012; Vatansever et al., 2015a]. Although DMN regions routinely deactivate during cognitive task performance [Mazoyer et al., 2001; Raichle et al, 2001; Shulman et al., 1997], they show a high flexibility to switch their modular membership [Vatansever et al., 2015a], to integrate with other brain regions [Fornito et al., 2012] and to increase their number of connector hubs [Stanley et al., 2014] when cognitive demands increase. Based on this evidence, more studies are needed to resolve the problem of the involvement of specific subnetworks in the integrated workspace formation, focusing on a potential role of FPN, DMN and FPN‐DMN interactions.

In the present fMRI study, we sought to provide both a replication and an extension of the previous findings by a comprehensive description of network transitions during effortful cognitive task performance. We asked healthy young adult participants to perform a working memory n‐back task with two levels of difficulty—1‐back (low demand) and 2‐back (high demand). First, we investigated whether the expectations of GWT are confirmed by effort‐dependent changes in the modularity of whole‐brain network. If they are, then performing the more demanding task (2‐back) should be associated with an increased integration of information processing reflected by a decreased level of network modularity, and a greater network integration should be beneficial for behavioral outcomes.

Going beyond the network description on the global level, we sought to identify large scale networks and specific brain regions that may play a critical role in forming the global workspace. We hypothesized that network integration may be achieved by an increased coupling between distinct brain subnetworks through long‐distance connections. Therefore, we examined changes in the number of provincial (intra‐modular) and connector (inter‐modular) hubs. According to GWT, higher cognitive demands should lead to an increase in the number of connector hubs supporting global integration. Finally, we examined potential clusters of connections that change their strength with increasing cognitive demands using network‐based statistic (NBS)—a nonparametric statistical method introduced by Zalesky et al. [2010].

METHOD

Subjects

Thirty‐five healthy volunteers (17 females; mean age 22.6 ± 3.1; range 19–31 years) with normal or corrected‐to‐normal vision participated in this study. All were right‐handed as defined by the Edinburgh Handedness Inventory [Oldfield, 1971], and without a history of neurological or psychiatric disorders. Participants were recruited from the local community through word‐of‐mouth and social networks. Written informed consent was collected from each participant, and ethical approval for the study was obtained from the Ethics Committee of the Nicolaus Copernicus University Ludwik Rydygier Collegium Medicum in Bydgoszcz, Poland, in accordance with the Declaration of Helsinki.

fMRI Paradigm

To assess working memory, we used a visual n‐back task based on letters [Gevins and Cutillo, 1993], which requires participants to constantly monitor, update and manipulate memorized information [Owen et al., 2005]. The effort required for the performance of the task increases with n number of elements that have to be traced during different working memory load task conditions (e.g., 1‐, 2‐, or 3‐back). In this study, stimulus consisted of the first five letters of the Roman alphabet (A–E) [Kearney‐Ramos et al., 2014], presented in a pseudorandom order in two working memory load conditions, 1‐ and 2‐back. The presentation of each letter (500 ms) was preceded by a fixation cross (1,500 ms) presented in the centre of the screen. Each session of the task consisted of 10 blocks (30 s per block; 12 trials with 25% of targets) of alternating 1‐ and 2‐back conditions. A short instruction screen (2,000 ms) was displayed before each block, informing the participant of the condition. The whole task consisted of three sessions and the total length of 16 min resulting in 480 functional scans. During the 1‐back condition, the participants were asked to indicate if the currently presented letter was the same or different from the letter immediately preceding it. During the 2‐back condition, the participants had to indicate if the currently presented letter was the same as or different from the letter presented two trials before. The participants had 2,000 ms for each response. The experimental protocol execution and control (stimulus delivery and response registration) were controlled by the Presentation® software (Neurobehavioral Systems, Albany, NY), version 17.2. Visual stimuli were displayed using MRI compatible NNL goggles (NordicNeuroLab, Bergen, Norway). Behavioral responses were collected using MRI compatible NNL response grips (NordicNeuroLab, Bergen, Norway), which were connected together and held in the right hand by each participant. The participants were instructed to respond as quickly and accurately as possible by pressing one of the two buttons using the thumb of the right hand (target letter—right button; non‐target—left button).

Data Acquisition

Neuroimaging data were collected using a GE Discovery MR750 3 Tesla MRI scanner (General Electric Healthcare) with a standard 8‐channel head coil. Functional scans were obtained using a T2*‐weighted gradient‐echo, echo‐planar imaging (EPI) sequence sensitive to BOLD contrast (TR = 2,000 ms, TE = 30 ms, FOV = 192 mm, flip angle = 90 degrees, matrix size = 64 × 64, voxel size = 3 × 3 × 3 mm, no gap). For each of the three sessions, 5 dummy scans (10 s) and 160 volumes (5 min 20 s) of 42 axial oblique slices were acquired in an interleaved acquisition scheme. Structural images were collected using three‐dimensional high resolution T1‐weighted gradient‐echo (FSPGR 3D) sequence (TR = 8.2 s, TE = 3.2 ms, FOV = 256 mm, flip angle = 12 degrees, matrix size = 256 × 256, voxel size = 1 × 1 × 1 mm, 206 axial oblique slices).

Node Definition

To define nodes we used a functional brain parcellation consisting of 264 functionally relevant ROIs defined on the basis of a meta‐analysis [Power et al., 2011]. The functional ROIs were modeled using the MarsBaR toolbox (http://marsbar.sourceforget.net) as 10 mm diameter spheres with centers around the coordinates provided by Power et al. [2011]. Brain coverage of all 264 ROIs was evaluated and confirmed as complete for the brain mask of each subject. Given that the use of different parcellation schemes for node definition may significantly affect the graph theory measures [Fornito et al., 2013; Wang et al., 2009], we cross‐validated our findings using Automated Anatomical Labelling atlas (AAL)—an anatomical parcellation scheme that divides the brain into 90 regions [Tzourio‐Mazoyer et al., 2002]. The AAL has been used in many previous studies linking network modularity and behavioral performance [Arnemann et al., 2015; Gamboa et al., 2014; Ginestet and Simmons, 2011]. Detailed results for the AAL parcellation scheme are presented in Supporting Information.

Data Processing

The data pre‐processing pipeline can be divided into two major steps: (1) standard pre‐processing of the functional time series; and (2) denoising of the data to perform functional connectivity analysis. We used the SPM12 toolbox to perform functional data pre‐processing (Wellcome Department of Imaging Neuroscience, Institute of Neurology, London, UK) running on MATLAB 8.3 (R2014a) (Mathworks, Natick, MA). Functional images were corrected for acquisition time and spatially realigned to the mean image to correct for interscan head motions. The structural T1‐weighted image was co‐registered to the mean functional image. Functional, gray matter, white matter and cerebrospinal fluid (CSF) images were spatially normalized to the MNI template using new unified normalization‐segmentation [Ashburner and Friston, 2005]. Additionally, we identified outlier scans with a frame‐wise displacement above 0.5 mm using Artifact Detection Toolbox (ART; http://www.nitrc.org/projects/artifact_detect/). Two participants were excluded from further analysis due to excessive head motion (more than 10 outlier scans); thus, the final sample consisted of 33 subjects (17 females; mean age 22.7 ± 3.2; range 19–31 years). There was no significant difference between the 1‐back and 2‐back conditions in the number of outlier scans (t(32) = 1.61, P = 0.1166).

The non‐smoothed functional volumes were further investigated to avoid spuriously high correlations between time‐series from the neighboring ROIs [Alavash et al., 2015; Cole et al., 2013; Fornito et al., 2010]. We used CONN Functional Connectivity Toolbox v. 15.f (http://www.nitrc.org/projects/conn/, [Whitfield‐Gabrieli and Nieto‐Castanon, 2012]) to perform the denoising of the functional time series and to create pairwise correlation matrices. This toolbox implements the anatomical component correction (aCompCor) strategy to estimate and remove physiological noise [Behzadi et al., 2007]. First, we divided functional time‐series into 1‐back and 2‐back conditions according to the onset and duration times of each block. Then, principal components of subject‐specific white matter, CSF, six rigid‐body movement parameters and outlier scans were removed by means of covariate regression analysis. To take into account the hemodynamic delay and avoid possible between‐condition crosstalk, separate block regressors for each task condition convolved with canonical hemodynamic response function and their first‐derivative terms were included in covariate regression analysis [Whitfield‐Gabrieli and Nieto‐Castanon, 2012]. The procedure of regressing out task effects separately for each task condition has been shown to yield the highest test‐retest reliability of graph theoretical properties during task‐based and resting‐state paradigms [Cao et al., 2014].

The resulting time series were filtered using 0.008 Hz high‐pass filter to remove low‐frequency drift. To preserve potentially valuable task‐relevant information from higher frequency bands, we did not apply low‐pass filter, which is commonly used in resting‐state analyses [Cao et al., 2014; Cole et al., 2013; Shirer et al., 2012].

For each condition, 225 volumes (7 min 30 s) of the task‐induced time series were used for signal extraction. Correlation matrices were created by first extracting the time course from each region of Power ROIs; then, Pearson's correlation coefficients were computed for each pair of ROIs. Fisher's transformation was then used to convert correlation coefficient to normally distributed z‐scores. This resulted in one correlation matrix (264 × 264 size) for each condition and each subject (see Fig. S1 in Supporting Information for data processing and network construction flowchart).

Functional Brain Networks

Functional connectivity networks represent nonzero values of time‐series correlations between brain regions. To focus only on the strongest connections, several thresholding approaches and further matrix binarization have been introduced and used in previous studies [Fornito et al., 2016]. However, these procedures are arbitrary and their use may not lead to meaningful representation of real networks [Ginestet et al., 2011]. Moreover, many network measures applicable to weighted networks have not been adapted to networks with negative weights, which in the case of functional brain networks often requires transforming them to positive values. Therefore, in this study, we focused both on fully connected, weighted graphs with positive and negative weights to calculate global network properties, and on thresholded and binarized versions for hub detection analysis.

Every weighted graph G can be represented by a real square matrix W, where element w_ij represents the strength of the association between nodes i and j. Here, we used functional connectivity matrices described earlier as representations of fully connected weighted graphs with N_V = 264 nodes and N_E = (½)N_V(N_V– 1) connections. In our case, associations were measured as correlation coefficients, thus w_ij ∊ [–1,1] and w_ij = w_ji. Signed networks can also be described as a difference of positive and negative weights W = W⁺ – W^–, where W⁺ = [ $w_{ij}^{+}$ ] and W^– = [ $w_{ij}^{-}$ ]. Note that for positive associations between nodes i and j we had $w_{ij}^{+}$ = w_ij and $w_{ij}^{-}$ = 0, while for negative $w_{ij}^{+}$ = 0 and $w_{ij}^{-}$ = –w_ij. We can also assign each node with a positive/negative strength defined as the sum of its positive or negative connection weights $s_i^{\pm }$ = ∑ _j $w_{ij}^{\pm }$ and total strength s _i = ∑_j w _ij. The positive/negative weight of a network is the sum of its node strengths v ^± = ∑_i $s_i^{\pm }$.

Binary networks in hub detection analysis were constructed by first applying threshold to weighted correlation networks and then setting all remaining non‐zero connection weights to one. Here, we used proportional threshold approach, which leads to fixed connection density across networks, thus allowing for direct comparison of cost‐dependent network measures. We performed our analysis using thresholds that produced networks with connection densities ranging from 5 to 15% (with a step of 1%) by integrating hub scores over that range. We chose a proportional threshold, retaining 5% of the strongest connections as a lower bound for connection density after examining the fracturing of sparse networks. For that density value, the mean size of the gigantic component (largest connected subgraph) across all functional networks exceeded 95% of the total number of network nodes (mean_GCsize = 253.5).

Graph Measures

In weighted networks analysis, cost constitutes the most fundamental and meaningful graph metric. The cost of weighted graph G is simply a mean value of the connection strength between every possible pair of nodes K(G) = (1/N_E)∑_i∑_j>iw_ij. As graph metrics are usually highly cost‐dependent, we included cost parameter in our analysis to ensure that network topology changes and their possible associations with behavioral outcomes are driven solely by network reorganization, rather than being a simple consequence of overall changes in the connectivity level.

To quantify the extent of the divisibility of the network into non‐overlapping communities, defined as subsets of densely interconnected nodes with sparse connections with the rest of the network [Newman and Girvan, 2004], we implemented an approach introduced by Newman [2006] and further extended by Gómez et al. [2009] for networks of correlated data. This method introduces the so‐called modularity quality function defined independently for positive and negative connection weights as:

$$Q^{\pm }=\pm (1/v^{\pm }){\sum }_{ij}\left(w_{ij}{}^{\pm }-\left(s_i{}^{\pm }{s}_j{}^{\pm }\right)/v^{\pm }\right){\delta }_{CiCj,}$$

where δ_CiCj = 1 when nodes i and j belong to the same community, and 0 otherwise. There are several ways to combine Q⁺ and Q^‐ into a single measure of modularity for signed networks [Rubinov and Sporns, 2011]. Here, we used asymmetric treatment of positive and negative weights, as we assume that despite the fact that the role of the negative correlations can be biologically relevant, they are not as important as the stronger positive associations. In line with that assumption, we used a single measure of network modularity Q defined as:

$$Q=Q^{+}+Q^{-}{v}^{-}/\left(v^{-}+v^{+}\right).$$

Finding a network community structure belongs to the NP‐hard (non‐deterministic polynomial‐time hard) class of problems [Brandes et al., 2006]. There are several algorithms developed to divide networks into communities in a manageable computational time. For large networks, it is recommended to use greedy optimization methods. Here, the Louvain algorithm was used for both weighted and binary networks, incorporating the heuristics that reduce running time to O(Nlog(N)) [Blondel et al., 2008]. Due to the stochastic nature of the algorithm, its outputs typically vary from run to run. To address this problem, for each weighted and binary network, we used the Louvain algorithm 1,000 times and chose the run that produced a network partition with the highest Q value. We considered that partition to be the network‐optimal community structure and the corresponding Q value—as the network modularity.

Hub Detection

To detect hub regions in functional brain networks, we adopted methods of functional cartography [Guimera and Amaral, 2005]. In this approach, the role of a node is determined by its position in two‐dimensional parameter space, which is particularly useful in analyzing modular networks. Both parameters depend on the community structure of a given network, therefore we used the optimal community structure for each binary network described in the previous paragraph.

The first parameter is a degree‐based centrality measure called within‐module degree z‐score z_i. It reflects the strength of within‐module connectivity of a node in comparison to other nodes from the same module. Therefore, it allows to detect highly central nodes called hubs. If k_i is the number of connections of node i to other nodes in its own module C, <k _C> is the average of k over all the nodes in module C, and σ_kC is the standard deviation of k in C, then we can define z_i of node i as:

$$z_i= (k_i\hspace{0.17em}-<k_C>)/{\sigma }_{kC}.$$

Note that z_i is close to zero for nodes with an intra‐modular degree close to modular average. Here, we considered nodes with z_i > 1 as hubs and nodes with z_i < 1 as non‐hubs.

The second parameter of a node, called participation coefficient pc_i, captures its inter‐module connectivity. Participation coefficient is specified by the formula:

$${\text{pc}}_i=1-{{\displaystyle \sum _{s=1}^{N_{\mathrm{m}}}\left(\frac{k_{is}}{k_i}\right)}}^2,$$

where N _m is the number of modules, k _i is the degree of node i, and k_is is the number of connections between node i and module s. Participation coefficient quantifies how a given node shares its connections with nodes in other modules. It ranges from 0 to 1, where the pc_i values close to 1 indicates nodes that share their connections evenly across modules, whereas nodes with pc_i values close to 0 share their connections exclusively within their own module. Participation coefficient can be used to determine the function of hub and non‐hub nodes. Originally hub nodes were divided into three different classes [Guimera et al., 2005], but here we considered only two of them: (1) provincial hubs defined as nodes with z_i > 1 and pc_i < 0.3; and (2) connector hubs defined as nodes with z_i > 1 and pc_i > 0.3. The third type of hubs, called kinless hubs (nodes with z_i > 1 and pc _i > 0.75), was not included in our analysis due to their absence in large‐scale brain networks (we only identified five nodes satisfying the criteria for a kinless hub among all the analyzed networks). Provincial hubs share connections mostly within their own module, and thus support local processing, whereas connector hubs link different communities, enhancing integration between modules.

In our analysis, we calculated both parameters for all nodes in each network thresholded at different levels described earlier. Then, we integrated these values over analyzed connection density range and assumed these scores as the representative values of the nodes' z‐score and participation coefficient in a given network.

Network‐Based Statistic

Performing statistical testing on connectivity values for large networks suffers from multiple comparisons problem. To overcome this issue, the NBS approach has been developed [Zalesky et al., 2010]. NBS makes it possible to find a set of connections forming a subnetwork associated with an experimental effect or an inter‐group difference. In contrast to the false discovery rate (FDR) or Bonferroni techniques, NBS has greater power to detect a whole cluster of regions spanning multiple connections associated with a hypothesis of interest [for detailed information see Zalesky et al., 2010].

In this study, we used NBS to find differences in connectivity resulting from changing cognitive demands. To this purpose, we used full, weighted connectivity matrices described earlier. The first step was computation of paired t‐test statistic (T; N = 33; df = 32), individually, for every connection. In this study, we focused on two possibilities: connection enhancement and connection weakening resulting from increased cognitive demands. We referred to a subnetwork consisting of enhanced connections as a strengthened network and to a subnetwork consisting of weakened connections as a weakened network. In the next step, a threshold (τ) selected by the user was applied to T values, and only connections exceeding this threshold (T > τ) were retained in the network. In the main text, we show the results for τ = 2.5; however, the structure of our findings is robust and extends to different τ values (see Supporting Information). Next, the algorithm searched for connected subsets of nodes among the suprathreshold connections and assigned to them a cluster size, that is, the number of their connections. The last step consisted in assigning P‐value to each cluster found. This was done by randomly permuting data labels over 10,000 iterations and creating null distribution of the largest cluster size. This null distribution was then used to assign family‐wise corrected P‐value to each previously found cluster.

To characterize strengthened and weakened networks in terms of commonly known functional brain systems, we used the network division introduced by Power et al. [2011], based on a meta‐analysis of resting state data, which has been shown to overlap with community structure revealed in task‐based networks [Cole et al., 2014]. That division consists of 11 well‐established large‐scale brain functional systems: default mode, frontoparietal, cingulo‐opercular, dorsal attention, ventral attention, memory, auditory, visual, salience, somatomotor, and subcortical. The partition also includes nodes unrelated to any known brain system. We divided the connections of each subnetwork detected by NBS into groups according to the systems that they link to. This gave us 11 types of intra‐module connections corresponding to all the systems, as well as 55 types of intra‐module connections reflecting all possible system pairs. That division can concisely be represented by 11 × 11 matrix M, in which entry m_ij is the total number of links connecting i‐th and j‐th module. Note that the diagonal entries of M reflect intra‐module connections, while the off‐diagonal entries represent the subnetworks' links connecting different systems.

Measure of n‐Back Performance

There are several measures of performance in n‐back task paradigms. One of them, called d‐prime (d′) is based on signal detection theory [Swets et al., 1961] and requires calculating hit rate and false‐alarm rate of a subject's responses. In this study, we used a measure of performance introduced by Ginestet and Simmons [2011] called penalized reaction time (pRT). In contrast to d′, pRT combines measures of speed and accuracy [Ginestet and Simmons, 2011]. For every subject and task condition, pRT was defined as:

$$\text{pRT}:\hspace{0.17em}= {\sum }_{i=1}{x}_i,$$

where the index i denotes all possible responses, and x _i is obtained from the following formula:

$$x_i=\{\begin{array}{c}{\text{RT}}_i\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{if}\hspace{0.17em}\text{subject}\hspace{0.17em}\text{answered}\hspace{0.17em}\text{correctly};\\ 2000\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{otherwise},\end{array}$$

where RT_i is the reaction time of i‐th possible response. In the formula above, the penalty for an incorrect answer or no answer is equal to a maximum possible time to respond. In contrast to d′, higher scores of pRT indicate worse performance on the n‐back task, as they are related to longer RT and more incorrect answers.

Statistical Testing

To determine if topological properties of functional brain networks change with increasing cognitive load, we performed a paired‐sample Student's t‐test for both cost and modularity metric. Subsequently, we used multiple linear regression (MLR) to test for possible correlations between the change in behavioral performance measured as ΔpRT and the change in network modularity. Formally, the MLR model takes a standard form:

$$y = {\beta }_1{x}_1+ {\beta }_2{x}_2+ e.$$

Here, y is a vector of estimated ΔpRT values, x₁ is the variable of interest—the change in modularity (ΔQ) between task conditions, x₂ is a nuisance variable—mean cost <K> = ½(K _1‐back + K _2‐back), β's represents associated parameters, and e is an error term. To verify whether the model exhibited a statistically significant effect on the change of modularity, we applied a one‐sample t‐test to estimated β values.

To ascertain if the number of functional hubs is regulated by the cognitive demand, we calculated the number of provincial and connector hubs in the 1‐back and 2‐back conditions for each participant. Next, we used a one‐sample Student's t‐test with a null hypothesis that the number of provincial and connector hubs does not change between the task conditions. We calculated the number of both types of hubs in all large‐scale brain systems described earlier. For each system, we used one‐sample Student's t‐test to determine which specific systems displayed increased or decreased number of provincial and connector hubs when subjects switched from 1‐back to 2‐back. As we tested 11 hypotheses for each brain system, we corrected the obtained P‐values for multiple comparisons using the FDR approach [Benjamini and Hochberg, 1995]. In all the t‐tests, we rejected the null hypothesis; we considered the test significant when the associated P‐value was smaller than P _crit = 0.05.

RESULTS

Behavioral Performance

We observed a significant decrease in working memory performance measured as a pRT from 1‐back to 2‐back, t(32) = 8.62, P < 0.0001 (Fig. 1A). Participants showed a higher pRT in the 2‐back (pRT_2‐back = 833.2 ms, SD = 202.9 ms) than in the 1‐back condition (pRT_1‐back = 681.7 ms, SD = 157.5 ms). As expected, these results showed that the 2‐back task condition was more cognitively demanding than the 1‐back condition.

Figure 1.

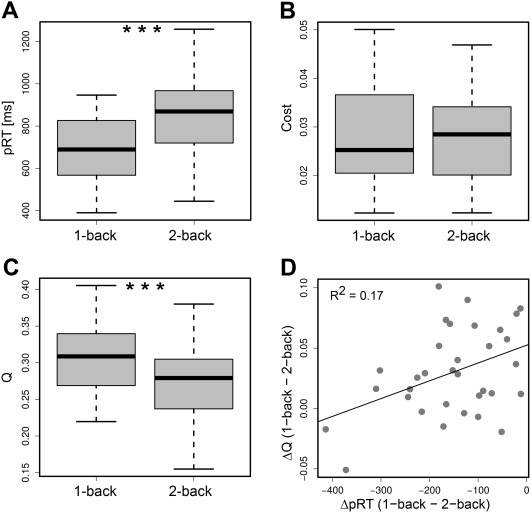
Differences in network measures and behavioral outcomes between task conditions. A presents levels of performance measured as pRT. In B and C, mean cost and mean modularity (Q) of functional networks are shown for both task conditions. Symbol *** indicates a significant difference in the corresponding measure between the task conditions (P < 0.05). In D, individual differences in modularity (ΔQ) are plotted against individual differences in pRT between 1‐back and 2‐back. Positive correlation between these measures is reflected by a solid line of best fit.

Network Modularity and Increasing Cognitive Demands

The cost of functional networks varied from 0.012 to 0.1 (mean = 0.03, SD = 0.016). We found no significant difference in network cost between the 1‐back and 2‐back conditions, thus the overall level of connectivity was preserved across both task conditions (Fig. 1B).

Network modularity varied from 0.14 to 0.405 (mean = 0.289, SD = 0.058). Individual values of modularity in 1‐back and 2‐back were positively correlated (r = 0.79, P < 0.0001), indicating that a high value of modularity in one condition was associated with a high value of modularity in another. We observed a significant difference in modularity between the two conditions (t(32) = 4.8, P < 0.0001; Fig. 1C). Functional networks in 2‐back were less modular (Q _2‐back = 0.274, SD = 0.055) than in 1‐back (Q _1‐back = 0.304, SD = 0.056).

Network Modularity and Behavioral Outcomes

MLR model fitted to the change in pRT between the task conditions proved to be statistically significant (P < 0.05) and revealed that greater deterioration in behavioral performance was associated with a smaller decrease in functional network modularity (Fig. 1D). In other words, we observed a strong decrease of functional network modularity in participants with high behavioral scores in 2‐back compared to 1‐back. For the modularity effect, the estimated beta value was equal to β ₁ = −1,075.1, SEM = 478.3, P < 0.05, while the effect of the nuisance variable <K> was statistically insignificant.

Number of Provincial and Connector Hubs

Our analysis revealed an average number of 43.06 hubs per functional network. We observed that there was no significant difference in the overall number of hubs between the task conditions (P = 0.94). However, after specifying the roles of hubs, we found differences between the working memory conditions. There was a significant decrease in the number of provincial hubs (t(32) = −4.54, P < 0.0001) accompanied by a significant increase in the number of connector hubs (t(32) = 3.67, P < 0.0001) when subjects switched from the 1‐back to the 2‐back condition. Increasing working memory load resulted in a decrease in the number of provincial hubs from 15.79 to 10.70 and an increase in the number of connector hubs from 27.30 to 32.33. The change in the number of provincial and connector hubs, with the overall number of hubs preserved across the task conditions, suggests a functional role shift of the most central brain regions, caused by a higher cognitive demand. A greater number of connector hubs in the 2‐back condition (Fig. 2A) may indicate an increased inter‐module communication traded off for a decreased intra‐module communication, which is reflected by a smaller number of provincial hubs in the 2‐back condition (Fig. 2B).

Figure 2.

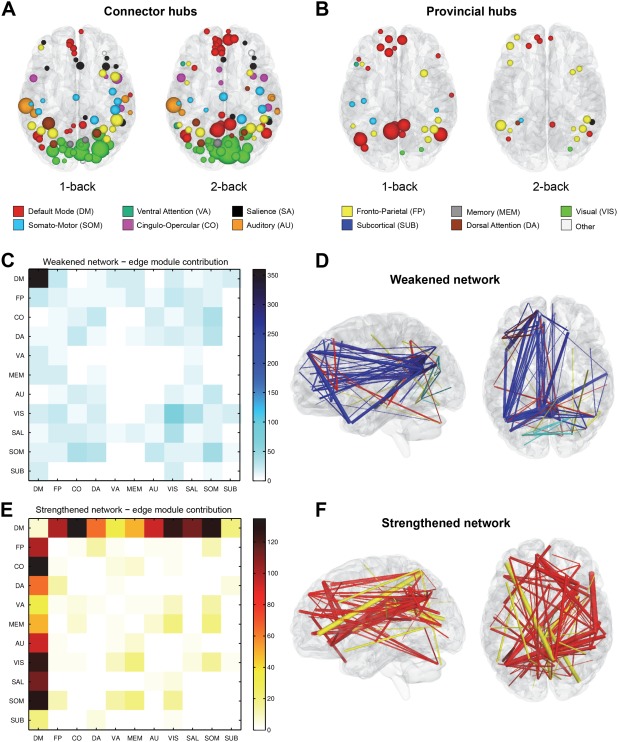
Top panel: connector hubs (A) and provincial hubs (B) drawn in the brain space. The size of the hub region reflects the frequency of occurrence of this region as a hub in a population of functional networks; thus, the largest spheres indicate regions identified as hubs for most participants. The colors of hubs reflect the regions' assignment to well‐established functional brain systems described by Power et al. [2011]. Bottom panel: weakened and strengthened networks in terms of predefined brain systems. The left panels show matrices reflecting the total number of edges linking different communities. Note that the largest group of weakened network (C) edges consists of edges within the DMN, while the vast majority of the strengthened network (E) edges link the DMN to other brain systems. The right panels show weakened (D) and strengthened networks (F) in the brain space for an NBS threshold τ = 4.0. The size of the edge reflects the value of the statistical test on that edge; thus, the thickest lines represent the edges with the largest differences in the connectivity strength between the task conditions. The edges are color‐coded in the following way: blue = within‐DMN edges, light blue = within‐community edges (not including the DMN), red = edges linking the DMN to other systems, yellow = edges linking different communities (not including the DMN).

Considering the membership of hubs in large‐scale brain systems revealed that with increased working memory load the number of provincial hubs decreased significantly only within the DMN (t(32) = −5.15; P = 0.001; FDR corrected), while the number of connector hubs increased within the DMN (t(32) = 5.41; P = 0.001; FDR corrected) and the ventral attention network (t(32) = 3.24; P = 0.015; FDR corrected). These results suggest that the change in the function of hubs occurs primarily within the DMN, which is reflected by an increased number of connector hubs supporting integration of the functional network in the cognitively demanding 2‐back condition. The numbers of both types of hubs within each large‐scale system are given in Table 1.

Table 1.

The number of connector and provincial hubs for large‐scale brain systems [Power et al., 2011]

Large‐scale networks	Connector hubs			Provincial hubs
	1‐back	2‐back	P (FDR)	1‐back	2‐back	P (FDR)
Defaut mode	4.82	8.33	0.0001	6.45	3.03	0.0001
Fronto‐parietal	3.45	3.39	0.9803	2.42	3.03	0.3148
Cingulo‐opercular	1.52	1.61	0.9803	0.48	0.24	0.2165
Dorsal attention	1.64	1.64	1.0000	0.42	0.48	0.7116
Ventral attention	0.55	0.97	0.0152	0.30	0.15	0.3148
Memory	0.64	0.67	0.9803	0.24	0.06	0.2165
Auditory	1.64	1.76	0.9803	0.36	0.15	0.2165
Visual	6.52	6.97	0.9803	2.36	1.18	0.0590
Salience	2.21	1.91	0.9803	0.42	0.52	0.5731
Somato‐motor	3.06	3.39	0.9803	2.06	1.52	0.2165
Subcortical	0.21	0.27	0.9803	0.06	0.00	0.2522

Bold P‐values reflect significant changes (P < 0.05) in the number of a certain type of hubs between task conditions. All P‐values were corrected for multiple comparisons using false discovery rate (FDR) method.

We also tested for a possible relationship between a change in the participation coefficient of the DMN nodes and changes in the modularity and behavioral performance (pRT) from the 1‐back to the 2‐back condition. We found that an increase in the mean of the participation coefficient of the DMN nodes was associated with a decrease in the modularity (rho = −0.59; P < 0.0001) (Fig. 3A) and decrease in behavioral performance (rho = −0.39; P < 0.05). This finding may suggest that an increase in inter‐module connectivity between highly centralized DMN regions may facilitate a modularity breakdown of the functional brain network and support behavioral performance.

Figure 3.

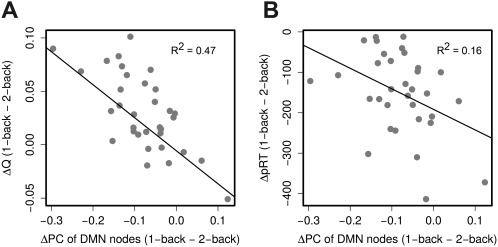
Individual differences in the change in participation coefficient (PC) of the DMN nodes and the change in modularity (ΔQ) and behavioral performance (ΔpRT) between the task conditions (1‐back minus 2‐back). Individuals who exhibited substantial increases in participation coefficient of the DMN nodes from 1‐back to 2‐back tended to have larger decline in modularity (A) and smaller decline in behavioral performance (B).

NBS Results

When considering the 1‐back > 2‐back contrast, a total of 1,364 connections forming a weakened network were identified (P < 0.0001; FWE corrected). In terms of the previously defined functional systems, the largest group among these connections consisted of 360 edges between the DMN regions (Fig. 2C). We found that 39% of connections in the weakened network were intra‐modular, while the remaining 61% connected different brain systems. The strongest disconnections were mainly located in the left hemisphere and involved functional links between the posterior cingulate cortex, medial prefrontal cortex, and left temporal lobe (Fig. 2D). These results suggest that with increasing working memory load, many brain systems reduced their internal connectivity.

When we studied connections with increased strength of connectivity in the 1‐back < 2‐back contrast, we found a cluster of 1,206 edges (P < 0.0001; FWE corrected) forming a strengthened network. The vast majority of that network consisted of connections between the DMN and other brain systems—we found the total of 915 connections between the DMN regions and the rest of the brain for which connectivity increased in the 2‐back condition (Fig. 2E). Moreover, only 1.6% of strengthened network connections were intra‐modular, which indicates that increased memory load leads almost exclusively to intra‐modular connectivity enhancement. The most strongly enhanced connections were often long‐range and inter‐hemispheric (Fig. 2F). These results suggest that the strengthened connectivity between the DMN and the rest of the brain provides additional functional integration between distinct functional systems. Although here we present, the results for t‐test threshold τ = 2.5, weakened and strengthened networks with similar properties were also present for τ = {3, 3.5, 4, 4,5}.

To examine a possible relationship between the shift of the DMN connectivity detected by NBS and graph theoretical results, we used a MLR model with decrease in modularity as the response variable and changes in inter and intra‐DMN connectivity between the task conditions as explanatory variables. Intra‐DMN connectivity (S _intra‐DMN) was simply a sum of the weights of connections linking any two DMN regions, while inter‐DMN connectivity (S _inter‐DMN) was a sum of the weights of connections linking the DMN with any other region. As expected, intra‐DMN connectivity decreased (t(32) = 7.25; P < 0.0001), while inter‐DMN connectivity increased (t(32) = −6.49; P < 0.0001) from 1‐back to 2‐back. MLR model ΔQ = β ₁ΔS _intra‐DMN + β ₂ΔS _inter‐DMN was statistically significant (F = 3.71; P < 0.05) with a statistically significant increase in the inter‐DMN connectivity effect (β ₂ = −0.0001484; P = 0.021). This result indicates that changes in modularity may emerge as a result of increased connectivity strength between the DMN and other brain systems.

DISCUSSION

The aim of this study was to verify the previous findings showing an increased whole‐brain network integration under increased cognitive demands at the n‐back task [Kitzbichler et al, 2011; Stanley et al., 2014; Vatansever et al., 2015a] and to provide a comprehensive description of subnetwork changes that may be involved in the formation of the global workspace, using hub detection methods and NBS. We found that global network modularity decreased when cognitive demands increased. Moreover, we found that a load‐dependent change of modularity was associated with a change of behavioral performance measured as pRT. We also showed that the number of connector hubs within the DMN and the ventral attention network increased from the 1‐back condition to the 2‐back condition, whereas the number of provincial hubs decreased only within the DMN. Moreover, change in participation coefficient of the DMN nodes was correlated with changes in the whole‐brain modularity and changes in behavioral outcomes. The NBS analysis revealed a cluster of connections whose connectivity increased with increasing cognitive demands (mainly comprised of connections between the DMN and other networks), as well as a cluster of weakened connections comprised of many intra‐DMN connections.

These results provide a valuable replication of the previous findings on load‐dependent network reorganization during the n‐back task and give strong support to GWT by showing that higher cognitive demands break network modularity in a way beneficial for behavioral performance. Moreover, our findings fill in the existing gap in the knowledge of mechanisms responsible for the emergence of the global workspace, by showing a critical role of the DMN in the processes of integration of distinct modules.

Network Modularity Decreases With Increasing Cognitive Demands

Modularity, as a feature of complex networks, facilitates a high level of network adaptation to changing environments [Kashtan and Alon, 2005; Meunier et al., 2010]. In terms of cognitive psychology, “modules” are defined as encapsulated, domain‐specific processors dedicated to automatic, unconscious cognitive processes [Baars, 1988; Fodor, 1983], which have to share the information during effortful, conscious cognition by forming an integrated “global workspace” [Baars, 1988; Dehaene et al, 1998].

By combining the concepts of modularity from cognitive psychology and network science, we showed that the whole‐brain network modularity decreased when the demands of a working memory n‐back task increased. In the 1‐back condition, network nodes were highly functionally connected within modules; in the 2‐back condition, more network nodes were involved in information transfer between modules, which resulted in a decrease of the whole‐brain modularity. A decrease of modularity implies a less segregated and more integrated network connectivity pattern.

An n‐back task requires that participants engage multiple cognitive processes such as: encoding (interpreting each letter), storage (retaining the letter in memory), rehearsal (keeping the content of storage active), matching (comparing the presented letter with the letter presented n trials previously), temporal ordering (keeping the order of the letters), inhibition (suppressing the trace of the oldest letter in memory), and executing an accurate response [Jonides et al., 1997]. Increasing the number of n (as here, from 1‐back to 2‐back) results in a greater demand on storage, rehearsal, temporal ordering and inhibition. The low demand 1‐back task, predominantly requires recognition of previously shown stimuli, and to a large extent can be done automatically and effortlessly. Therefore, this task can be easily performed within functionally dedicated brain subsystems, with no need for information transfer between them. This is highly beneficial from the economical perspective; in segregated processing, the use of mainly short‐distance intra‐modular connections reduces the wiring cost of a network [Bullmore and Sporns, 2012; Meunier et al., 2010]. The segregated information processing pattern is no longer sufficient when cognitive demands increase—as in the 2‐back task. To perform this more effortful task, it is necessary to expend the cost of integrating multiple modules through long‐distance connections. By providing compelling evidence of brain network adaptation into a more efficient—albeit more costly—workspace configuration in response to increasing cognitive demands, our results add to existing support for GWT.

This effort‐dependent modularity shift, which is in line with GWT, was found in the previous studies using an n‐back task. In an MEG study, Kitzbichler et al. [2011] found that whole‐brain network modularity decreased when the load on working memory increased. Consistently with this result, a recent fMRI study by Vatansever et al. [2015a] showed a decrease in modularity from 0‐back to 3‐back (also using 264 Power ROIs for node definition). Conversely, Stanley et al. [2014] found that only regional modularity decreased for the DMN and working memory network as opposed to the whole‐brain modularity, which remained unchanged between 1‐back to 2‐back. However, this study examined functional networks on the voxel level, which was possibly limited to the detection of modular reorganization only at the local level of network description.

It is worth noting that an effort‐dependent modularity breakdown was also reported for tasks other than n‐back, which suggests that this phenomenon is not specific to the working memory domain. For example, by comparing network reorganization during processing of forward and backward masked visual stimuli, Godwin et al. [2015] showed that awareness of the visual target caused a decrease of the network modularity. Modularity decreases were also found in an EEG study by Bola and Sabel [2015] during the performance of a visual discrimination (oddball) task and in an fMRI study by Elton and Gao [2015] during a selective attention task. Moreover, Shine et al. [2015] by comparing different tasks (motor, emotion, relational, gambling, language, social and n‐back) found that, whereas integration and segregation states were common for all the tasks, the effect of global integration was dependent on task demands—the highest level of integration was found in an n‐back task: the lowest level of integration, in a motor task. These results suggest that network integration is not specific to the n‐back task but—in agreement with GWT—arises in highly demanding tasks. We may hypothesize that when the task is too demanding, interference effects in the highly integrated networks will lead to many errors.

Network Modularity Change Predicts Behavioral Outcomes

Although the transition of functional network organization during increasing demands of cognitive tasks supports efficient integration of information, it is more expensive. Is such a costly network reorganization beneficial to behavioral outcomes? Here, we found that effort‐dependent decrease in modularity was associated with smaller decreases in behavioral performance (pRT). The participants whose modularity of functional brain networks strongly decreased tended to retain high performance scores when switching from 1‐back to 2‐back. These results provide evidence that greater network integration extends access to cognitive resources encapsulated within distinct brain modules that are necessary to maintain high levels of behavioral performance when the task difficulty increases. This finding is in line with the aforementioned work by Stanley et al. [2014], who also found that a greater decrease in global modularity was associated with a smaller decline in behavioral performance from 1‐back to 2‐back. Vatansever et al. [2015a] also found a positive correlation between the change in reaction times for correct responses and change of modularity from 0‐back to 3‐back, which is consistent with our finding. These findings taken together present strong evidence for the relevance of effort‐dependent network reorganization to human behavior.

The DMN Plays a Crucial Role in the Global Workspace Formation

The term DMN originally stood for a set of brain regions (including medial prefrontal, posterior cingulate and lateral parietal cortices), the activity of which decreases during certain goal‐oriented tasks [Mazoyer et al., 2001; Raichle et al, 2001; Shulman et al., 1997] and increases during spontaneous, internally directed cognitive processes [Buckner et al., 2008]. In previous literature, the DMN was referred to as a task‐negative network, because of its strong negative correlation with the dorsal attention regions (task‐positive network), routinely active during goal‐directed cognition [Fox et al., 2005; Fransson, 2005]. Some studies suggest that this anticorrelation may reflect competition for limited processing resources between these subnetworks [Fox et al., 2005; Kelly et al., 2008; Weissman et al., 2006].

Our results provide evidence that weakened connectivity strength between the DMN components in performing tasks which require effort may not necessarily mean that the network disengages during the task or competes with a task‐positive network, but actually rearranges its connections to support communication between regions from other subnetworks during goal‐directed behavior. We found that only the DMN and the ventral attention network displayed an increased number of connector hubs, while the number of provincial hubs decreased only within the DMN. These results are complementary to our findings of modularity decrease with increasing cognitive demands; to obtain a high level of integration between modular subsystems during the performance of effortful cognitive tasks, connector hubs—regions with the ability to interconnect distant modules—have to be engaged in forming the global workspace. Connector hubs reduce the shortest path length between remote brain regions, thus increasing the network's efficient communication through long‐distance network connections [Bullmore and Sporns, 2012]. Moreover, by utilizing the NBS approach [Zalesky et al., 2010], we found significant shifts in connectivity strength forming spatial patterns closely related to the division into well‐known large brain systems, including the DMN. The weakened network consisted of many intra‐DMN connections, which decreased their strengths with increasing working memory load. We also found a strengthened network of connections between the DMN and other systems, whose coupling increased with increased cognitive demands. This suggests the DMN plays an essential role in the integration of information between remote brain systems in performing demanding tasks.

Given the fact that both the strengthened and weakened networks are comprised of a similar number of connections, it is tempting to hypothesize that both effects reflect trade‐offs between intra‐ and inter‐module communication. These effects may arise as a consequence of competition for limited brain resources under the requirements of a cognitively challenging task. Moreover, increased inter‐module connectivity in 2‐back, which is supported mainly by long‐distance inter‐hemispheric connections of the strengthened network, is in line with the main idea of GWT, where communication between brain systems is enhanced during more controlled, high‐demand processing [Baars, 1988]. In addition, as stronger inter‐module coupling proved to be related to decreased modularity, the DMN involvement in functional network reorganization provides a potential mechanism underlying the effect of decreased modularity with increasing working memory load. Taken together, these results suggest that network integration is achieved through a change of the connectivity profile of the DMN regions. These highly connected regions suppress their intra‐modular communication and form functional connections to regions in other subsystems, thus changing their function and becoming connector hubs.

Originally, long‐range FPN connections were suggested to play a crucial role in the global workspace formation [Dehaene and Changeux, 2011; Dehaene and Naccache, 2001]. This assumption was initially based on neuroimaging studies showing activations of prefrontal, parietal and anterior cingulate regions during effortful task performance [Duncan, 2010; Dux et al., 2006; Klein et al., 2007; Landmann et al., 2007]. However, a recent study by Gratton et al., [2016] showed that activated regions and connector hubs provide distinct contributions to changes in functional connectivity during task performance, suggesting that they are associated with different network modulation processes. In our study, we exclusively focused on network reorganization processes, not on regional activation processes, where we could expect to discover activity of the FPN. The network perspective fundamentally differs from the activation‐oriented studies in terms of the processes they describe, which may explain why we did not find task‐positive network regions exhibiting a crucial role in the formation of the global workspace. Using dynamic network analysis, Shine et al. [2015] found that a shift toward network integration during an n‐back task was largest not only for the frontoparietal but also the default mode and subcortical regions. Similarly, Stanley et al. [2014] found that the number of connector hubs within the frontoparietal network as well as the DMN network increased from 1‐back to 2‐back. Moreover, by tracking dynamic changes of functional connectivity patterns, Braun et al. [2015] showed that performance in an effortful working memory n‐back task was related to the reconfiguration of highly flexible nodes of the frontal systems, consisting of the nodes commonly associated both with the DMN and with a task‐positive network. These findings suggest that the network perspective offers a view in which dynamic processes related to the DMN and a task‐positive network may be essential to understand the whole network reorganization during the performance of working memory tasks. However, the aforementioned studies did not offer a clear explanation of the network integration processes in terms of the exact dynamics between the DMN and a task positive network in the light of GWT. Our results suggest that the brain system responsible for the global workspace relies on the DMN, which increases the coupling between other large‐scale brain networks such as cingulo‐opercular, fronto‐parietal, somatomotor, salience and visual.

Network integration and formation of the global workspace may be achieved through a rearrangement of the DMN functional connections. Active engagement of the DMN during goal‐directed cognitive processes receives strong support from studies focused on task‐related regional deactivation, which suggests that the magnitude of the deactivation of the DMN regions may reflect a reallocation of processing resources to facilitate task performance [Daselaar et al., 2004; Mayer et al., 2010; Persson et al., 2007]. The engagement of the DMN in network integration processes was also suggested by the recent functional connectivity studies [Fornito et al., 2012; Vatansever et al., 2015a]. For example, Fornito et al. [2012] found that some DMN regions formed a transitional module which enhanced integration with the frontoparietal system during a memory recollection task. Vatansever et al. [2015a] showed that flexible DMN regions actively contribute to working memory by dynamically reorganizing their interactions with other functional subnetworks and claimed that the DMN may be engaged in the global workspace formation. A central location of the DMN regions in the brain and their good communication with other networks make this assumption very plausible [Hagmann et al., 2008; van den Heuvel and Sporns, 2011]. Our NBS results may explain the mechanism of the workspace formation and the DMN engagement in the integration process by showing a rearrangement of connections from the DMN network to other subnetworks. Moreover, the relationship between the DMN changes and global modularity decrease shows that these subnetwork changes may significantly affect integration of the whole‐brain network.

Is the DMN engagement in integration processes specific to working memory tasks? Working memory requires an interplay of multiple cognitive components such as perception, rehearsal, recall, and selecting an appropriate motor response; therefore, it requires an integration of many brain subnetworks [Baars and Franklin, 2003; Dehaene and Naccache, 2001]. Some previous studies linked the DMN to working memory [Anticevic et al., 2010; Hampson et al., 2006; Stanley et al., 2014; Vatansever et al., 2015a]. For example, Hampson et al. [2006] found a positive correlation between the strength of the DMN connectivity and working memory performance and suggested that the DMN may play a role in the facilitation and monitoring of cognitive performance. Anticevic et al. [2010] showed that the temporoparietal junction and the DMN deactivations during encoding predicted working memory performance, which suggests the DMN's role in working memory trace formation. However, several studies report the DMN participation in network integration during tasks engaging other cognitive functions, such as recollection tasks [Fornito et al., 2012], auditory oddball [Arbabshirani et al., 2013], and finger opposition task [Vatansever et al., 2015b]. We hypothesize that the DMN integration may be characteristic of effortful tasks and is not specific to working memory. Future studies should investigate to what extent the DMN is engaged in other tasks and how this engagement is changed by increasing cognitive demands.

Limitations

The present study has several limitations. First, we examined static task‐based connectivity by averaging multiple 1‐back and 2‐back blocks. To examine transitional patterns of network reorganization, future studies should use approaches of dynamic functional connectivity by dividing the task data into short time windows. Moreover, we used a network partitioning into main large‐scale networks provided by previous studies [Cole et al., 2014; Power et al., 2011]. This provided consistency with previous studies, but future analyses should also use data‐driven network division. Finally, the n‐back paradigm which we used involved only two load conditions (1‐back and 2‐back). Therefore, from these findings one cannot infer whether network organization will change proportionally with increasing working memory load. Hence, future studies should examine changes of that character, including conditions such as 0‐back and 3‐back.

CONCLUSIONS

Our findings demonstrate that during increasing cognitive demands the whole‐brain network breaks its highly modular architecture to promote more integrated information processing, which strongly corroborates the main assumptions of GWT. Moreover, the observed transition in the whole‐brain network organization is beneficial for behavioral performance. We also suggest that the long‐range and highly flexible connections of DMN may play an essential role in the formation of an integrated workspace under increasing demands of a goal‐directed n‐back task.

Supporting information

Supporting Information