Abstract
Neuroimaging research involves analyses of huge amounts of biological data that might or might not be related with cognition. This relationship is usually approached using univariate methods, and, therefore, correction methods are mandatory for reducing false positives. Nevertheless, the probability of false negatives is also increased. Multivariate frameworks have been proposed for helping to alleviate this balance. Here we apply multivariate distance matrix regression for the simultaneous analysis of biological and cognitive data, namely, structural connections among 82 brain regions and several latent factors estimating cognitive performance. We tested whether cognitive differences predict distances among individuals regarding their connectivity pattern. Beginning with 3,321 connections among regions, the 36 edges better predicted by the individuals' cognitive scores were selected. Cognitive scores were related to connectivity distances in both the full (3,321) and reduced (36) connectivity patterns. The selected edges connect regions distributed across the entire brain and the network defined by these edges supports high‐order cognitive processes such as (a) (fluid) executive control, (b) (crystallized) recognition, learning, and language processing, and (c) visuospatial processing. This multivariate study suggests that one widespread, but limited number, of regions in the human brain, supports high‐level cognitive ability differences. Hum Brain Mapp 38:803–816, 2017. © 2016 Wiley Periodicals, Inc.
Keywords: multivariate distance matrix regression, cognitive differences, structural connectivity
INTRODUCTION
Finding the brain correlates of individual differences in cognitive ability using neuroimaging approaches and univariate general lineal models raises several issues of interest, due to the fact that (1) correction for multiple comparisons is mandatory, (2) the number of simultaneous statistical tests to correct for is regularly high, and (3) sample sizes are relatively small [Bennet and Miller, 2010; Button et al., 2013; Vul et al., 2009; Yarkoni, 2009; Yarkoni et al., 2010]. The statistical test computed to discern if the variability in a given brain property and a specific cognitive ability are associated might lead to incorrect decisions. In this context, a false positive (Type I error) decision is made when these two variables are in fact not related and we decide they are. On the contrary, a false negative (Type II error) decision happens when these two variables are related and the decision is they are not. The presence of false positives and false negatives in neuroimaging findings is increased because the number of statistical tests computed is usually huge. False discovery rate (FDR), family wise error (FWE), or permutation tests are procedures for controlling Type I errors [Chumbley and Friston, 2009; Nichols, 2012]. However, the probability of false negatives also increases. For reducing both the probability of false positives and false negatives, alternative, and perhaps more efficient, approaches have been proposed [Stelzer et al., 2014].
In this regard, and relying on multivariate frameworks [Margulies et al., 2010; Shehzad et al. 2014] have applied multivariate distance matrix regression (MDMR) [McArdle and Anderson, 2001] to several functional neuroimaging datasets. This approach allows the study of associations between behavioral measures and brain measurement profiles, while reducing the number of assessments and the multiple comparisons challenge. MDMR includes three basic steps: (1) computing the distance between all pairs of individuals (N) with respect to a given set of dependent variables (e.g., brain connectivity pattern) for obtaining a N × N distance matrix, (2) calculating a PseudoF statistic to test the hypothesis that one or more regressor variables (such as cognitive factors) have no relationship to variations in the distance or dissimilarity among individuals, and (3) testing the significance of the PseudoF statistic using simulation‐based tests, such as permutation tests.
As noted by Shehzad et al. [2014] this procedure provides some advantages: (a) several predictors can be analyzed simultaneously, (b) the number of brain variables (e.g., number of brain connections) can be much larger than the number of individuals in the sample, (c) variables of a different nature (categorical, continuous) can be considered in the same model, (d) there are few a‐priori assumptions (e.g., regarding the data distribution) or decisions to make (such as the number of dimensions to extract from the profile‐similarities multidimensional space), and (e) the approach shows good statistical power.
Shehzad et al. [2014] suggested that the application of this approach to structural connectivity would be worthwhile. The current study applies MDMR for testing whether highly similar individuals in their diffusion‐based whole‐brain structural connectivity networks have also similar performance in a set of cognitive latent factors (including fluid ability, crystallized ability, spatial ability, working memory capacity, attention control, and processing speed). Also, we investigated which specific links among pairs of cortical and subcortical regions maximize the predictive power of the cognitive domains included in the MDMR model. Importantly, crossvalidation analyses were also conducted for testing the stability of the observed findings excluding any possible over‐adjustment or circularity [Kriegeskorte et al., 2009].
In general, we expected that participants with similar cognitive performance should show similar connectivity patterns [low distance in the full set of connections], while participants with different cognitive performance should reveal different connectivity patterns. Also, the similarity in a reduced set of links connecting cortical and subcortical regions previously related with cognitive performance should maximize the predictive power of the cognitive domains considered in the study.
METHOD
Participants
Ninety‐four young healthy right‐handed individuals participated in the present study (53 women and 41 men; mean age = 20 years, SD = 1.7). All were university undergraduate paid volunteers. Participants completed a brief questionnaire including questions regarding medical or psychiatric disorders, as well as substance intake, and none was excluded. Written informed consent was obtained in accordance with regulations of Hospital Ruber Internacional (Madrid). The local ethical committee approved the study.
MRI Data Acquisition
Participants were scanned on a General Electric Signa 3T magnetic resonance (MR) scanner, using a whole‐body radiofrequency coil for signal excitation, and a quadrature 8‐channel coil for reception. 3D T1‐weighted anatomical brain MRI scans were acquired with a spoiled gradient echo (SPGR) sequence with the following parameters: TR/TE/PrepTime = 6.8/3.1/750 ms; flip angle 12°; 1 mm slice thickness, a 288 × 288 acquisition matrix and a 24 cm FOV. Diffusion weighted images (DWI) were acquired with single‐shot echo planar sequence with these parameters: 24 cm FOV, TE/TR 78.2/11,000 ms, 96 × 96 acquisition matrix, 2.4 mm slice thickness, 1 image with no diffusion sensitization (i.e., T2‐weighted b 0 image) and 15 DWI (b = 1,000 s/mm2) with gradient directions uniformly distributed on the unit hemisphere, for unbiased angular sampling of diffusion.
Structural Connectivity
We used Freesurfer (version 5.1.0) to segment each subject's cortex in 68 anatomical cortical regions and 14 subcortical regions [Fischl et al., 2004] (see Supporting Information Table I for a description of these 82 regions). DWI images were pre‐processed using FMRIB's diffusion Toolbox (FDT) (Fig. 1). Correction for motion and geometrical distortion due to Eddy currents was performed with the eddycorrect tool in FDT, taking as reference image the average of the two b 0 volumes. Nonbrain tissue from the average b 0 image was removed using the FMRIB's Brain Extraction Toolbox, BET [Smith, 2002].
Figure 1.
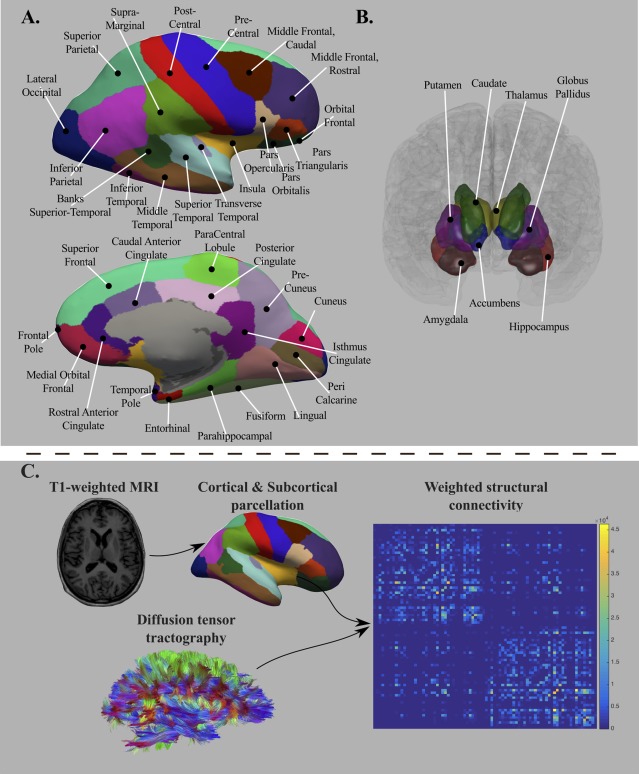
Brain structures defining the ROIs of interest (top panel, A = cortical regions and B = subcortical regions). The bottom panel (C) depicts the analytic sequence for computing the connectivity matrices. The T1‐weighted MRI images were used for cortical and subcortical parcellation, whereas diffusion MRI images were processed for computing diffusion tensor tractography. [Color figure can be viewed at http://wileyonlinelibrary.com]
The obtained brain mask was applied to the remaining DWI images. Diffusion Toolkit (DTK—http://www.trackvis.org) was used to fit the diffusion tensor model using a least squares approach. We employed TensorLine Tractography (Lazar et al., 2003) to estimate the fiber streamlines between the 82 regions. We generated ten streamlines per voxel at random subvoxel locations, using as stopping criteria a maximum curvature angle of 35° between consecutive steps and a lower threshold of fractional anisotropy of 0.1 [Johansen‐Berg et al., 2004]. Only tracts with a length larger than 15 mm were retained.
Regional gray matter masks were dilated to add white matter coverage. The dilation was performed using a spherical morphological operator of one voxel radius, and inter‐regional overlapping was avoided. Structural connectivity networks were represented as symmetric matrices including normalized weights connecting each pair of nodes in the parcellation scheme (82 nodes). Normalized weights in the individual matrices were computed as the number of streamlines connecting each pair of regions divided by the total number of streamlines in the subject's matrix.
For avoiding false positives streamlines, we decided to analyze highly consistent connections, acknowledging both the limitations of the deterministic tractrography approach used here and the limited number of directions of our DWI data. In addition, for connections only present in less than 50% of the subjects, even showing strong intersubject variability, zeros for the remaining subjects will introduce strong bias in MDMR analyses. To keep only the more consistent connections (those present in a large percentage of the sample) in the individual connectivity matrices, we applied one‐tailed (right) one‐sample t tests to each edge in the matrix across subjects. The null hypothesis tested was: the relative number of streamlines connecting each pair of ROIS is equal to zero [(number of streamlines linking any two ROIs/total number of streamlines in the connectivity matrix) = 0]. We used the Bonferroni method to correct for multiple comparisons. Thus, we divided the selected threshold for significance (0.05) by 3,321 pairwise connections [82 ROIs × (82 ROIs − 1)/2]. Connections with a corrected P value lower than 0.05 were set to zero for all subjects. Using this approach, a connection (edge) must be present in approx. more than 50 subjects to be retained in the individual connectivity matrices. Additionally, the 95% of the retained connections were present in a least 75% of the subjects. So, even at the cost of removing intersubject variability, MDMR analyses were run on these corrected matrices.
Psychological Factors
Participants completed a set of cognitive ability tests and computerized tasks. These tests and tasks tapped three ability factors, namely, fluid reasoning (Gf), crystallized ability (Gc), and spatial ability (Gv), along with working memory capacity (WMC), attention control (ATT), and processing speed (PS). Gf assesses the ability for solving novel problems, whereas Gc involves the ability for solving academic types of declarative and procedural problems [Cattell, 1971]. The construction, short‐term retention, and manipulation of mental images define Gv [Lohman, 2000]. WMC involves the simultaneous and online storage and processing of varied amounts of information [Martínez et al., 2011]. Attention allows the allocation of available mental resources [Baddeley, 2002] and the present study considers the control of automatic responses. Finally, reaction time tasks allow the measurement of PS [Sheppard and Vernon, 2008]; participants completed simple verification tasks. All these cognitive factors were estimated by three or more different measures each in order to obtain representative scores at the latent‐variable level. Supporting Information Material provides a detailed description of the measures tapping these cognitive factors, along with the computed confirmatory factor analysis from which the latent scores were obtained.
Multivariate Distance Matrix Regression (MDMR)
This section provides a description of the steps followed for multivariate distance matrix regression (MDMR) computations. The function dissmfac of the library TraMineR will be applied to obtain the MDMR results [Gabadinho & Studer, 2011].
Figure 2 summarizes the required analytic steps: (Step 1) Building individual whole‐brain and reduced structural connectivity profiles, (Step 2) calculation of the distance matrix among individuals in the whole‐brain and reduced structural connectivity profiles, and (Step 3) MDMR analysis setting as dependent variable the computed distance matrices (whole‐brain and reduced) and as independent variables brain volume, age, and the six cognitive domains [fluid reasoning (Gf), crystallized ability (Gc), and spatial ability (Gv), along with working memory capacity (WMC), attention control (ATT), and processing speed (PS)].
Figure 2.
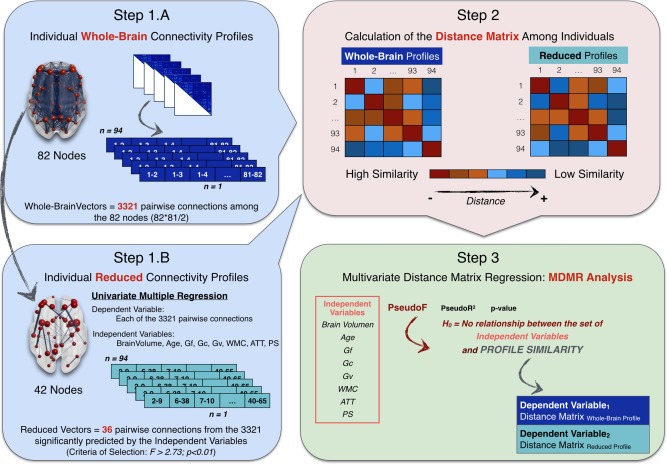
Summary of the analytic steps followed for the MDMR analyses. Step 1: Building individual whole‐brain (1A) and reduced (1B) structural connectivity profiles. Step 2: Calculation of the distance matrix among individuals in the whole‐brain and reduced structural connectivity profiles. Step 3: Multivariate distance matrix regression (MDMR) analysis setting as dependent variable the computed distance matrices (whole‐brain and reduced) and as independent variables brain volume, age, and the six cognitive domains [fluid reasoning (Gf), crystallized ability (Gc), and spatial ability (Gv), along with working memory capacity (WMC), attention control (ATT), and processing speed (PS)]. [Color figure can be viewed at http://wileyonlinelibrary.com]
(Step 1) Building individual whole‐brain and reduced edge‐based structural connectivity profiles. We started the analyses with N = 94 individuals assessed in a set of M = 8 predictor variables (6 latent scores in the considered cognitive domains and two additional variables: age and brain volume = gray matter volume + white matter volume) and a set of P = 3,321 brain measures (all the pairwise connections among brain regions in the parcellation scheme; i.e., from node 1 to node 2, until node 81 to node 82). Therefore, an NxP matrix can be built, where each row contains the individual vector of whole brain structural pairwise connections. Hereafter, each of these vectors will be referred as ‘individual whole‐brain connectivity profiles'.
Furthermore, we selected a subset of linkages or edges presumably relevant for cognitive performance. Univariate multiple regression was applied to select the specific pairwise connections related to our set of predictors, as implemented by Zapala and Schork [2006] for selecting group of genes associated to the predictor variables of interest. Using their approach, each of the 3,321 structural connections among pair of regions was regressed on our predictor variables for retaining the edges where the F statistic was significant (F > 2.73, with 8 and 85 degrees of freedom, alpha = 0.01). A total of S = 36 node pairs (edges) fulfilled this requirement (see Supporting Information Table III). Then, a N × S (94 × 36) matrix was obtained, where each row represented the individual vector of brain structural connections among the selected subset of pairwise connections. Hereafter, each of these vectors will be referred as ‘individual reduced connectivity profiles’.
(Step 2) Calculation of the distance matrix among individuals in the whole‐brain and reduced structural connectivity profiles. The distance between each pair of individual connectivity profiles was obtained using the Euclidean distance metric, resulting in a nonnegative value that reveals how similar/different each pair of profiles is. When both profiles are identical, the Euclidean distance is zero. When they are not, the distance measure increases as their dissimilarity does. For instance, two individuals with an about zero distance in their whole‐brain connectivity profiles have about the same relative number of fibers (over the total number of streamlines computed per subject) connecting the 82 nodes, and, therefore, share a similar connectivity pattern (or, more loosely, a similar brain structure).
Two types of distance matrix (D), based on the whole‐brain (N × P) and reduced (N × S) profiles respectively, were built. The first reflects the dissimilarity (Dij) between each pair of individuals, i and j, in the vector representing their whole‐brain connectivity profiles. For instance, 4th row or column represents the dissimilarity between the 4th participant and the remaining N − 1 (93) participants. The second includes the intersubject dissimilarity on the subset of linkages among brain regions that were significantly related to the predictor variables. These two (D Euclidean − whole brain and D Euclidean − reduced) N × N (94 × 94) distance matrices were submitted to MDMR analysis.
(Step 3) MDMR analysis. MDMR was implemented for assessing whether both, the individual whole‐brain connectivity profiles and reduced connectivity profiles, tended to be more similar in individuals with similar cognitive performance.
Firstly, a PseudoF statistic was computed for testing the hypothesis that the M cognitive factors have no relationship to variation in the distance or dissimilarity of the N individuals observed in the N × N distance/dissimilarity matrices built previously. This statistic is a generalization of the F statistic calculated in multivariate multiple linear regression analyses for testing the null hypothesis β = 0. A brief description of the MDMR methodology can be found in the Supporting Information Material.
The MDMR analysis will provide which predictors (X) are statistically significant along with their proportions of explained variance (PseudoR 2). So, for example, should X1 be a significant predictor and its PseudoR 2 = k; the conclusion would be that X1 explains about a k × 100% of the variation in the similarity of the individual connectivity profiles. The statistical significance of each predictor was calculated using permutation methods (1,000 permutations were run to built the null distribution).
PseudoR 2 values rest on the way they are computed. When computing PseudoR 2 for each independent variable (IV), two strategies can be followed [Shaw and Mitchell‐Olds, 1993] for calculating the sums of squares (SS). The type I SS is incremental: IVs are successively added to the model and the contribution of each one is measured by the SS increase that results when it is introduced. With this method, the measured impact of each IV depends on the order in which they are introduced. With the type II method, the contribution of each IV is measured by the reduction of SS that occurs when we drop it out from the full model. Thus, the order in which the independent variables are introduced in the model does not matter in the type II SS. Therefore we decided to apply this latter strategy.
As summarized by Figure 2 (Step 3), the two 94 × 94 Euclidean‐based distance matrices, D Euclidean − whole‐brain and D Euclidean − reduced, were submitted separately to MDMR analysis as dependent variables. These were the eight predictor variables (M) in the first model tested: fluid ability (Gf), crystallized ability (Gc), spatial ability (Gv), working memory capacity (WMC), attention control (AT), and processing speed (PS) along with age and brain volume (gray plus white matter volume). Also, we tested a second model, including the predictors revealed as significant in Model 1. We did this following the recommendation by Studer et al. [2011].
Validation of findings
-
Replicability of findings using Pearson's correlation as distance metric:
Different distance measures may change the pattern of results when conducting MDMR analyses [Zapala and Schork, 2006, 2012]. For instance, when comparing the profiles of two individuals, the normalized number of fibers can be zero for some pairs of nodes, what does not affect the Euclidean distance metric, but the Pearson correlation observed between the two profiles. Therefore, we used Pearson correlation to check if the observed findings were robust beyond the distance metric used. Pearson correlations among each pair of individual profiles (whole‐brain and reduced) were converted to a distance matrix through formula [5] in Zapala and Schork [2006]. Then, the same MDMR analyses performed for the Euclidean‐based whole‐brain distances matrices were repeated.
-
Replicability of findings using node‐based structural connectivity profiles:
For assessing whether the way of computing the individual brain connectivity profiles affected the results, a vector of 82 values per subject (instead of the original edge‐based approach considering the pairwise connections (3,321) was computed. These values represented each node's strength obtained as the mean of the normalized weights connecting each node with the remaining nodes in the parcellation scheme. Note that this latter node‐based approach for computing whole brain connectivity profiles is closer to the strategy applied by Shehzad et al. [2014]. Next, the Euclidean‐based distance matrix (D Euclidean − nodes) among individuals was computed and the same MDMR analyses run for the original two Euclidean‐based distance matrices (D Euclidean − whole‐brain and D Euclidean − reduced) were repeated.
-
Crossvalidation:
Because of the approach followed in the current study, we finally wondered if the consideration of the same dataset for the successive analytic steps might distort the main findings [Kriegeskorte et al., 2009]. Specifically, the subset of links included in the reduced connectivity profiles (36 edges, see Supporting Information Table III) was selected using univariate multiple regressions in the same sample where latter the MDMR model was applied.
For addressing this crucial issue, we conducted two crossvalidation studies to check whether our results are replicated when different datasets are considered, excluding any possible overadjustment or circularity. The key question to answer is: are the linkages nominated in the reduced profile peculiar to the analyzed group of individuals, and, therefore, largely unstable? As noted by Kriegeskorte et al. [2009] distortion would be absent when selection is “determined only by true effects in the data”.
Study 1
This study involved partitioning the original sample of data into complementary subsets, performing the analysis on one subset, and validating the analysis on the other subset. Then, several rounds of cross‐validation were performed using 500 partitions. Specifically, the subjects in the original sample (N = 94) were randomly assigned to subsamples S1 and S2 (N = 47 each). Next, the procedure used for obtaining the original individual reduced connectivity profiles (3,321 multiple regressions, setting as independent variables the M = 8 predictors and as dependent variables the normalized weight of each connection) was implemented. Two reduced connectivity profiles were obtained [N S1 × L S1 (N S1 = 47 × L S1 = subset of significant linkages after regressions in S1) and N S2 × L S2 (N S2 = 47 × L S2 = subset of significant linkages after regressions in S2]. Finally, two different strategies were followed in the 500 partitions of the original sample:
Condition 1. The distance matrices built using the linkages nominated as reduced connectivity profile for S1 were set as dependent variable in the MDMR analysis for S2 and vice versa. Because we were using the edges selected from one subset of data for validating the findings in the other, if there is no overadjustment or circularity, we expected to find a high proportion (>0.05) of significant P values for the predictors originally related to the reduced connectivity profiles. Also, we verified if the specific linkages nominated as relevant for cognition in the original sample (36 edges) were the same for the random subsamples. In absence of circularity, the 36 edges initially selected would be frequently included in the 1,000 reduced profiles (proportion > 0.05).
Condition 2. The distance matrices built using the linkages nominated as reduced connectivity profile for S1 were set as dependent variable in the MDMR analysis and the values for the scores in the eight predictors corresponding to the subjects in S2 were included as independent variables, and vice versa. Because we were using random assignments for the independent variables, if there is no overadjustment or circularity, we expected to find a low proportion (0.05) of significant P values for the cognitive predictors originally related to the reduced connectivity profiles.
Study 2
The complete group (N = 94) was considered for selecting 1,000 samples and building the reduced connectivity profiles following the same strategy employed originally. Then, MDMR analyses were computed on each sample after randomly permuting the predictors. Because there was no a correspondence between the reduced connectivity profiles and the predictors, we expected to find low values in the PseudoF distribution for the cognitive predictors originally related to the reduced connectivity profiles compared to those obtained in the original sample.
RESULTS
Connectivity: Descriptive
More prominent nodes according to their strength (mean of the normalized weights connecting each node with the remaining nodes in the network) included bilateral precuneus, superior frontal, superior parietal, insula, rostral middle frontal, lateral orbitofrontal, and putamen. These results were in coherence with previous studies nominating the main brain hubs of the brain structural network [van den Heuvel and Sporns, 2011, 2013]. There was a notable convergence in the nodes also having more inter subject variability in connection strength, such as bilateral superior parietal, precuneus, rostral middle frontal, and lateral orbitofrontal.
Brain Structural Connectivity Profiles and Cognitive Factors: MDMR Approach
Table 1 (Left, Model 1) shows that fluid, crystallized, and spatial ability were statistically significant for predicting the similarity among individuals in the whole‐brain connectivity profiles. The percentage of variance explained for each significant predictor, and for the total model was modest (2.7% for fluid, 3.2% for crystallized, 2.2% for spatial, and 9.8% for the total). A similar pattern emerged when the analysis was computed using only the significant predictors in Model 1 (i.e., Gf, Gc, and Gv). Note that in this model, the P value for spatial ability was nonsignificant (P = 0.108), but the total effect turned statistically significant (P = 0.033).
Table 1.
MDMR results (PseudoF, PseudoR 2, and P value) for the full set of independent variables [Model 1. Eight predictors: brain volume, age, fluid reasoning (Gf), crystallized ability (Gc), and spatial ability (Gv), working memory capacity (WMC), attention control (ATT), and processing speed (PS)] and only for the significant predictors in Model 1 [Model 2. Three significant predictors (Gf, Gc, and Gv) when the whole‐brain connectivity profiles were set as dependent variable; and five predictors (brain volume, age, Gf, Gc, and Gv) when the reduced connectivity profiles were set as dependent variable]
| Predictor | Whole‐brain profile | Reduced profile | ||||
|---|---|---|---|---|---|---|
| PseudoF | PseudoR 2 | P value | PseudoF | PseudoR 2 | P value | |
| Model 1 | ||||||
| Brain volume | 1.5958 | 0.0169 | 0.092 | 7.1730 | 0.0652 | 0.001b |
| Age | 1.0712 | 0.0113 | 0.316 | 2.0409 | 0.0185 | 0.040a |
| Gf | 2.5394 | 0.0269 | 0.014a | 7.5708 | 0.0689 | 0.001b |
| Gc | 3.0281 | 0.0321 | 0.005b | 7.6015 | 0.0691 | 0.001b |
| Gv | 2.0812 | 0.0220 | 0.025a | 5.4767 | 0.0498 | 0.001b |
| WMC | 0.6423 | 0.0068 | 0.869 | 1.2468 | 0.0113 | 0.271 |
| ATT | 0.5480 | 0.0058 | 0.962 | 1.5776 | 0.01434 | 0.130 |
| PS | 0.7000 | 0.0074 | 0.774 | 1.8798 | 0.0170 | 0.073 |
| Total | 1.1605 | 0.0984 | 0.169 | 3.1190 | 0.2269 | 0.001b |
| Model 2 | ||||||
| Brain volume | 5.9894 | 0.0560 | 0.001b | |||
| Age | 2.0533 | 0.0192 | 0.041a | |||
| Gf | 2.7894 | 0.0295 | 0.004b | 8.3472 | 0.0781 | 0.001b |
| Gc | 2.6296 | 0.0278 | 0.010a | 6.1217 | 0.0573 | 0.001b |
| Gv | 1.4267 | 0.0150 | 0.108 | 4.0102 | 0.0375 | 0.001b |
| Total | 1.5144 | 0.0480 | 0.033a | 3.7551 | 0.1758 | 0.001b |
PseudoR 2 was computed using a type II sum of squares strategy. The statistical significance of each predictor (P value) was calculated using permutation methods (1,000 permutations were run to built the null distribution). They represent the proportion of times the simulated PseudoFs (computed on random datasets) exceed the empirical PseudoF.
Significant at alpha = 0.05.
Significant at alpha = 0.01.
The same independent variables were still significant when predicting the distances among the reduced connectivity profiles (Table 1—Right, Model 1), plus brain volume and age. Compared to Model 1 for the whole‐brain connectivity profiles, the percentage of variance explained by fluid, crystallized, and spatial ability, as well as by the total model, increased (6.9, 6.9, 5.0, and 22.7% respectively). The analysis conducted on the significant predictors confirmed these results (see Model 2 in Table 1—Right) suggesting remarkably stronger effects when the distance among reduced connectivity profiles (36 connections, see Supporting Information Table III) was predicted.
Validation of findings
-
Replication across distance metrics
When Pearson correlation was used as distance metric (Table 2—left), the outputs from MDMR analyses hardly differ from those shown in Table 1. The differences between the PseudoFs obtained with both metrics for the same predictor were around 0 (the highest difference was 0.05).
-
Replication in the node‐based structural connectivity profiles
After applying MDMR to the 94 × 82 (participants by nodes) node‐based whole brain connectivity distance matrices, all significant factors found for the edge‐based approach were replicated (see Table 1). As observed in Table 2 (right), significant predictors found for edge‐based and node‐based whole brain connectivity profiles were quite similar, except for ‘Total’ in Model 2 (which was marginally significant). In short, the conclusions achieved after analyzing the 3,321edge‐based similarities are substantially those found when the 82 nodes‐based analyses were considered.
-
Crossvalidation
The results obtained for the reduced connectivity profiles (Table 1—right) were similar to those obtained when over‐adjustment was no longer present. Figure 3 displays the findings from the two crossvalidation studies conducted. As observed in Figure 3a, the proportion of models where brain volume, age, Gf, Gc and Gv resulted significant was higher than 0.05. Note that this value (0.05) was not included in their respective confidence intervals, excepting age. Additionally, the frequency of inclusion for the specific linkages included in the original reduced connectivity profile [light blue in Fig. 3b; mean frequency = 176 (min = 80; max = 422); proportion = 176/1,000 = 0.176] was significantly higher than for the remaining linkages [dark blue in Fig. 3b; mean frequency = 16 (min = 1; max = 212); proportion = 16/1,000 = 0.016] in the brain network [Welch two sample t test = 11.418; P = 2.236e−13; H 0 = true difference in means is equal to 0]. Therefore, when the edges selected from one subset of data were used for validating the findings in the other, a high proportion (>0.05) of significant P values was found for the predictors originally related to the reduced connectivity profiles (see Table 1—right, Model 1). This denoted that similarity in the reduced connectivity profiles was predicted by the same cognitive factors (Gf, Gc, and Gv) when over‐adjustment is clearly absent. Also, we demonstrated that the selection of the specific connections nominated as relevant for cognition (reduced connectivity profile, see Supporting Information Table III) did not depend on the original sample tested, since they significantly emerged as significant in the 1,000 datasets tested. However, it should be realized that the frequencies for some connections are low (below 10%, frequency < 100) and then their replicability may be low.
Table 2.
Replication of findings using Pearson's correlation as distance metric (left) and the node‐based approach for obtaining the connectivity profiles (right)
| Predictor | Pearson correlation as distance metric | Node‐based connectivity profiles | ||||
|---|---|---|---|---|---|---|
| PseudoF | PseudoR 2 | P value | PseudoF | PseudoR 2 | P value | |
| Model 1 | ||||||
| Brain volume | 1.6053 | 0.0170 | 0.087 | 1.8044 | 0.0190 | 0.073 |
| Age | 1.0195 | 0.0108 | 0.371 | 1.1559 | 0.0122 | 0.263 |
| Gf | 2.5522 | 0.0271 | 0.914a | 2.7873 | 0.0294 | 0.015a |
| Gc | 3.0124 | 0.0320 | 0.004b | 3.4172 | 0.0361 | 0.007b |
| Gv | 2.0844 | 0.0221 | 0.022a | 2.5251 | 0.0266 | 0.023a |
| WMC | 0.6711 | 0.0071 | 0.847 | 0.5909 | 0.0062 | 0.772 |
| ATT | 0.5689 | 0.0060 | 0.949 | 0.5348 | 0.0056 | 0.845 |
| PS | 0.7012 | 0.0983 | 0.779 | 0.7208 | 0.0076 | 0.645 |
| Total | 1.1582 | 0.0983 | 0.162 | 1.2218 | 0.1031 | 0.139 |
| Model 2 | ||||||
| Gf | 2.7637 | 0.0292 | 0.003b | 3.1572 | 0.0333 | 0.017a |
| Gc | 2.5836 | 0.0273 | 0.010a | 2.7396 | 0.0289 | 0.024a |
| Gv | 1.4226 | 0.0151 | 0.107 | 1.6215 | 0.0171 | 0.138 |
| Total | 1.5022 | 0.0477 | 0.034a | 1.6092 | 0.0509 | 0.068 |
MDMR results are shown (PseudoF, PseudoR 2, and P value) for the full set of independent variables [Model 1. Eight predictors: brain volume, age, fluid reasoning (Gf), crystallized ability (Gc), and spatial ability (Gv), working memory capacity (WMC), attention control (ATT), and processing speed (PS)] and only for the significant predictors in Model 1 [Model 2. Three significant predictors (Gf, Gc, and Gv)]. PseudoR 2 was computed using a type II sum of squares strategy. The statistical significance of each predictor (P value) was calculated using permutation methods (1,000 permutations were run to built the null distribution). They represent the proportion of times the simulated PseudoFs (computed on random datasets) exceed the empirical PseudoF.
Significant at alpha = 0.05.
Significant at alpha = 0.01.
Figure 3.
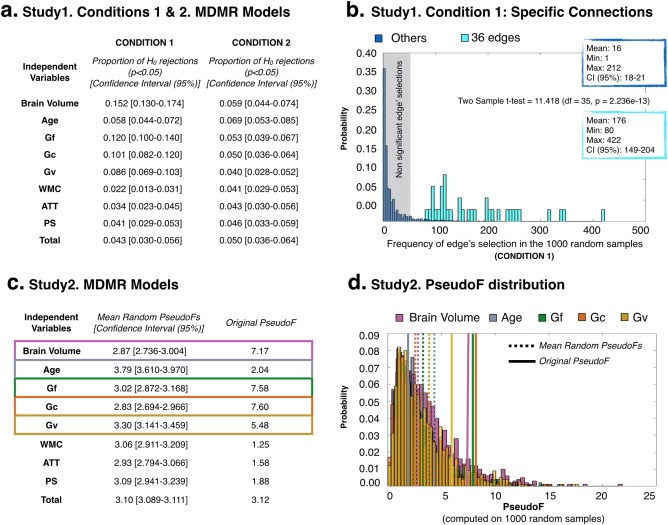
Main findings from the cross‐validation studies: (a) Study1. Conditions 1 and 2. MDMR Models shows the proportion of significant P values (proportion of H 0 rejections, P < 0.05) per independent variable included in the MDMR models computed in 1,000 subsets (N = 47) of the original data. The confidence interval (95%) of these proportions for each predictor is also reported. (b) Study1. Condition 1: Specific Connections displays the frequency of edge's selection in the 1,000 subsets (N = 47) of the original data (Condition 1) for the specific linkages included in the original reduced connectivity profile (light blue) and for the remaining linkages (dark blue) in the brain network. (c) Study 2. MDMR Models show the mean of the distribution and confidence interval (95%) for the PseudoFs computed per predictor in 1,000 randomly permuted datasets (Study 2, N = 94 each). It is also provided the PseudoF computed in the original sample. (d) Study2. PseudoF distribution represents the distribution of the PseudoFs from Study 2 only for the significant predictors in the original model (brain volume, Age, Gf, Gc, and Gv). The lines in the distribution are signaling the mean of the distribution (dashed lines) and the original PseudoFs (solid lines). [Color figure can be viewed at http://wileyonlinelibrary.com]
Finally, we observed that when the MDMR models were computed in random datasets (Study 1, Condition 2, and Study 2), the original significant predictors were no longer significant. Specifically, in Study 1, Condition 2 (see Fig. 3a), we found a low proportion (<0.05) of models were brain volume, Gf, Gc and Gv resulted significant. Also, as demonstrated by Study 2, when there was no relationship between the reduced connectivity profile and the independent variables (since the data for the predictors was randomly permuted), the PseudoF values for the predictors originally related to the reduced connectivity profiles are significantly higher than those obtained in random samples (see Fig. 3c,d), except for age.
Therefore, the crossvalidation studies support the stability of the reported findings regarding the three cognitive factors (Gf, Gc, and Gv) predicting the similarity among subjects in their reduced connectivity profiles.
DISCUSION
Using a methodological approach aimed at alleviating the multiple comparisons issue, namely, multivariate distance matrix regression (MDMR), here we have shown that individuals with similar brain connectivity profiles are also closer in their cognitive level as estimated by fluid, crystallized, and spatial ability latent factors. Furthermore, we identified a subset of 36 linkages connecting distributed brain regions that increased more than twice the predictive power of cognitive performance on brain profiles. Working memory capacity, attention, and processing speed were not significantly related with similarities among individuals in their brain connectivity profiles, suggesting that the observed joint covariation between biological and psychological data cannot be simply generalized across cognitive domains. Finally, our findings were replicated using (a) Pearson's correlation as distance metric, (b) a node‐based approach instead of the original edge‐based approach, and (3) different crossvalidation strategies for avoiding over adjustment or circularity.
Figure 4 depicts one schematic representation of the core network (excluding isolated connections) identified in the present study (the last round in https://dl.dropboxusercontent.com/u/10862393/Video%201_MDMR.mp4 shows this core network). The regions involved in this network have been related with high‐level cognition [Aminoff et al., 2013] including executive control processes [Bedny et al., 2012; Boisgueheneuc et al., 2012; Brabec et al., 2003; Burgess et al., 2007; Elliot et al., 2000, Haupt et al., 2009; Singh‐Curry and Husain, 2009], language related process [Ardila et al. 2014; Margulies and Petrides, 2013], memory/recognition processes [Grill‐Spektor et al., 2001; Zald et al., 2014], and visuospatial processing [Bird and Burgess, 2008; Cavanna and Trimble, 2006, Zhang and Li, 2012]. The three cognitive abilities revealed as significantly associated with brain connectivity profiles crucially require cognitive control (fluid ability, Gf), language processing (crystallized ability, Gc), and visuospatial processing (spatial ability, Gv).
Figure 4.
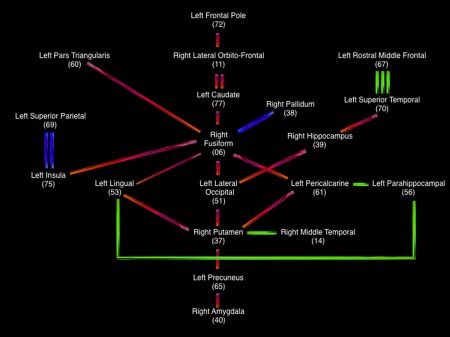
Schematic representation of the nodes connected within the main network identified in the present study. Red lines = right–left connections; Green lines = anterior–posterior connections; blue lines = top/bottom connections. The number of lines represents mean pairwise connection's strength (1 = low, 2 = medium, 3 = large). [Color figure can be viewed at http://wileyonlinelibrary.com]
To what extent are the nodes/regions connected within our network also relevant in previous research? Here we followed one strict inductive (bottom‐up) approach that led to 36 connections implicating several regions distributed across the brain, including neocortical and subcortical structures. These connections were both intrahemispheric (seven on the left and eight in the right) and interhemispheric (twenty‐one).
Some regions connected within the identified network are highlighted in the parieto‐frontal integration theory of intelligence (P‐FIT) [Jung and Haier, 2007]. These regions, thought to support individual differences in cognitive ability, fit the four processing stages considered by this theory: (stage 1) the fusiform gyrus and the inferior parietal for stage one, devoted to the processing of sensory information; (stage 2) the precuneus for information integration and abstraction in stage 2; (stage 3) the rostral middle frontal gyrus and superior frontal gyrus for evaluation cognitive processes in stage 3; and (stage 4) the caudate anterior cingulate for response selection in stage four [Pineda‐Pardo et al., 2016]. Further P‐FIT regions, namely, the superior parietal, pars orbitalis, and pars triangularis, were also identified in our reduced structural network. Therefore, most of the regions comprised by this integrative theory were found in the present study. Figure 5 depicts the set of regions connected within the identified network (https://dl.dropboxusercontent.com/u/10862393/Video%201_MDMR.mp4): green, yellow, orange, and red nodes meet the four processing stages highlighted by the P‐FIT model that were also identified in the present study, whereas gray nodes do not overlap P‐FIT regions.
Figure 5.
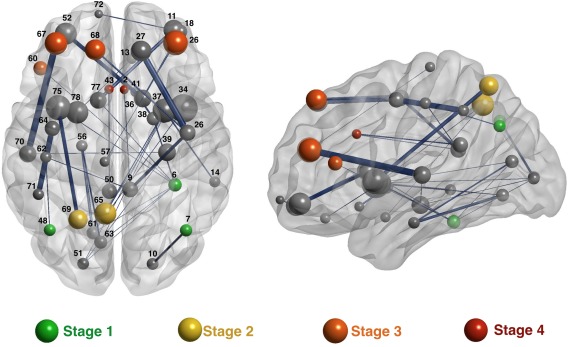
The 36 connections maximizing the association with the cognitive variables. The brain regions (nodes) connected by these 36 links are represented as spheres proportional in size to node's strength computed on the averaged brain network. The width of the links is proportional to the mean weight of the connection. Green, yellow, orange, and red nodes represent brain nodes highlighted by the P‐FIT model also identified in the present study. These colors denote the processing stages proposed by this model, namely, processing of sensory information (stage 1), integration (stage 3), evaluation (stage 3), and response selection (stage 4). The nodes are identified in Supporting Information Table III. [Color figure can be viewed at http://wileyonlinelibrary.com]
MDMR analyses conducted by Shehzad et al. [2014] after their resting state fMRI data showed correlations with intelligence differences (IQ) at the prefrontal cortex, the anterior and posterior cingulate, the lingual gyrus, and the supplemental motor area. Consistent with their results, our findings comprise those cingulate regions and the lingual gyrus as relevant nodes in the structural network. Shehzad et al.'s resting state fMRI findings were generally consistent with the P‐FIT framework [Jung and Haier, 2007] and this is also the case for our structural connectivity results. Nevertheless, discrepancies across studies must be expected due to a host of issues such as the considered analytic approaches, samples’ characteristics, measurement of the phenotypes of interest, and so forth [Colom and Thompson, 2011; Martínez et al., 2015]. In this regard, one recent meta‐analysis failed to found any overlap between brain structural and functional correlates of observed behavioral intelligence differences [Basten et al., 2015]. This result suggests that structural and functional correlates might not be located in the same brain regions. As underscored by Haier et al. [2009] standardization is strongly required for increasing comparability across studies.
On the other hand, the putamen, hippocampus, and superior parietal regions, along with the superior frontal and precuneus have defined the so‐called Rich Club [van den Heuvel and Sporns, 2011, 2013]. In the present study, the putamen was a node especially involved in the reduced connectivity profile serving as way station. In this regard, the results found by Burgaleta et al. [2014] highlighted this subcortical structure for fluid and spatial ability. Specifically, the relative enlargement of the putamen was positively related with these high‐order cognitive abilities. These researchers thought that the finding is substantiated by the acknowledged connection of this structure with the prefrontal cortex. We failed to detect direct connections between the putamen and this latter region in the brain, probably due to the nature of tracking methods and the strategy used for avoiding false positive connections. However, the putamen was connected with the frontal lobes indirectly through brain structures such as the lateral occipital, fusiform gyrus, caudate, hippocampus, superior temporal, lingual gyrus, or insula.
CONCLUSION
In conclusion, the findings reported in the present multivariate study suggest that one widespread, but limited number of regions in the human brain support cognitive ability differences. Specifically, individual differences in three key latent cognitive factors estimating fluid, crystallized, and spatial ability, predicted similarities among individuals regarding a structural network defined by 36 connections among a set of brain regions. Working memory capacity, attention control, and processing speed were cognitive factors unrelated with the identified network. The applied multivariate approach was useful for simplifying a complex dataset defined by a huge number of candidate connections among 82 brain regions.
Although the reported crossvalidation studies reinforce the reported results and, therefore, the main conclusion we provide, acknowledging one replication requirement is mandatory. The stability of the reported results is an important concern. We found that individual differences in three high‐order cognitive factors are related to individual connectivity patterns (1) when the whole‐brain and reduced profiles are considered, (2) using a edge‐based or a node‐based approach for building the connectivity profiles, (3) after the consideration of different distance measures (Euclidean or Pearson's correlation), and (4) when all or just the significant predictors are included in the MDMR equation and in both the original and cross‐validation studies. Despite this, reservations must be noted. Will the observed results remain after considering different cognitive and/or nodes measurements, samples with other characteristics (such as, for instance, elderly), or alternative MDMR strategies? All these germane questions require substantive answers.
Supporting information
Supporting Information
Video 1. The animation depicts progressively the 36 connections maximizing the association with the cognitive variables. Green, yellow, orange, and red nodes represent brain regions highlighted by the P‐FIT model and gray nodes are regions not included in this model. Colors denote processing stages: (1) processing of sensory information (green), (2) integration (yellow), (3) evaluation (orange), and (4) response selection (red). The final round in the animation depicts the schematic representation shown in Figure 4. The nodes are identified in Supporting Information Table III.
Disclosure: The authors do not have any conflict of interest to declare.
REFERENCES
- Aminoff EM, Kveraga K, Bar M (2013): The role of the parahippocampal cortex in cognition. Trends Cogn Sci 17:379–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ardila A, Bernal B, Rosselli M (2014): Participation of the insula in language revisited: A meta‐analytic connectivity study. J Neurolinguistics 29:31–41. [Google Scholar]
- Baddeley A (2002): Is working memory still working? Eur Psychol 7:85–97. [Google Scholar]
- Basten U, Hilger K, Fiebach CJ (2015): Where smart brains are different: A quantitative meta‐analysis of functional and structural brain imaging studies on intelligence. Intelligence 51:10–27. [Google Scholar]
- Bedny M, Pascual‐Leone A, Dravida S, Saxe R (2012): A sensitive period for language in the visual cortex: Distinct patterns of plasticity in congenitally versus late blind adults. Brain Lang 122:162–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennet CM, Miller MB (2010): How reliable are the results from functional magnetic resonance imaging? Ann NY Acad Sci 1191:133–155. [DOI] [PubMed] [Google Scholar]
- Bird CM, Burgess N (2008): The hippocampus and memory: Insights from spatial processing. Nat Rev Neurosci 9:182–194. [DOI] [PubMed] [Google Scholar]
- Boisgueheneuc F, Levy R, Volle E, Seassau M, Duffau H, Kinkingnehun S, Samson Y, Zhang S, Dubois B (2012): Functions of the left superior frontal gyrus in humans: A lesion study. Brain 129:3315–3328. [DOI] [PubMed] [Google Scholar]
- Brabec J, Kraseny J, Petrovicky P (2003): Volumetry of striatum and pallindum in man‐anatomy, cytoarchitecture, connections, MRI and aging. Sb Lek 104:13–65. [PubMed] [Google Scholar]
- Burgaleta M, MacDonald PA, Martínez K, Román FJ, Álvarez‐Linera J, Ramos‐González A, Karama S, Colom R (2014): Subcortical regional morphology correlates with fluid and spatial intelligence. Hum Brain Mapp 35:1957–1968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burgess PW, Simons JS, Dumotheil I, Gilbert SJ (2007): The gateway hypothesis of rostral prefrontal cortex (area 10) function In: Duncan J, Phillips L, McLeod P, editors. Measuring the Mind: Speed, Control, and Age. Oxford: Oxford University Press; pp 217–248. [Google Scholar]
- Button KS, Ioannidis JPA, Mokryisz C, Nosek BA, Flint J, Robinson ESJ, Munafo MR (2013): Power failure: Why small sample size undermines the reliability of neuroscience. Nat Rev 14:365–376. [DOI] [PubMed] [Google Scholar]
- Cattell, RB ( 1971): Abilities: Their Structure, Growth, and Action. Boston: Houghton‐Mifflin. [Google Scholar]
- Cavanna AE, Trimble MR (2006): The precuneus: A review of its functional anatomy and behavioral correlates. Brain 129:564–583. [DOI] [PubMed] [Google Scholar]
- Colom R, Thompson PM (2011): Understanding human intelligence by imaging the brain In: Chamorro‐Premuzic T, von Stumm S, Furnham A, editors. Handbook of Individual Differences. London: Wiley‐Blackwell. [Google Scholar]
- Chumbley JR, Friston KJ (2009): False discovery rate revisited: FDR and topological inference using Gaussian random fields. NeuroImage 44:62–70. [DOI] [PubMed] [Google Scholar]
- Elliot R, Dolan RJ, Frith CD (2000): Dissociable functions in the medial and lateral orbitofrontal cortex: Evidence from human neuroimaging studies. Cereb Cortex 10:308–317. [DOI] [PubMed] [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C, Halgren E, Ségonne F, Salat DH, Busa E, Seidman LJ, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale AM (2004): Automatically parcellating the human cerebral cortex. Cereb Cortex 14:11–22. [DOI] [PubMed] [Google Scholar]
- Gabadinho A, G, NS, Studer MM (2011): Analyzing and visualizing state sequences in R with TraMineR. J Stat Softw 40:1–37. [Google Scholar]
- Grill‐Spektor K, Kourzi Z, Kanwisher N (2001): The lateral occipital complex and its role in object recognition. Vis Res 41:1409–1422. [DOI] [PubMed] [Google Scholar]
- Haier RJ, Colom R, Schroeder D, Condon C, Tang C, Eaves E, Head K (2009): Gray matter and intelligence factors: Is there a neuro‐g? Intelligence 37:136–144. [Google Scholar]
- Haupt S, Axmacher N, Cohen MX, Elger CE, Fell J (2009): Activation of the caudal anterior cingulate cortex due to task‐related interference in an auditory Stroop paradigm. Hum Brain Mapp 30:3043–3056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansen‐Berg H, Behrens TEJ, Robson MD, Drobnjak I, Rushworth MFS, Brady JM, Smith SM, Higham DJ, Matthews PM (2004): Changes in connectivity profiles define functionally distinct regions in human medial frontal cortex. Proc Natl Acad Sci USA 101:13335–13340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung RE, Haier RJ (2007): The parieto‐frontal integration theory (P‐FIT) of intelligence: Converging neuroimaging evidence. Behav Brain Sci 30:135–187. [DOI] [PubMed] [Google Scholar]
- Kriegeskorte N, Simmons WK, Bellgowan PSF, Baker CI (2009): Circular analysis in systems neuroscience: The dangers of double dipping. Nat Neurosci 12:535–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazar M, Weinstein DM, Tsuruda JS, Hasan KM, Arfanakis K, Meyerand ME, Badie B, Rowley H. a, Haughton V, Field A, Alexander AL (2003): White matter tractography using diffusion tensor deflection. Hum Brain Mapp 18:306–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohman DF (2000): Complex information processing and intelligence In: Sternberg RJ, editor. Handbook of Human Intelligence. Cambridge: Cambridge University Press. [Google Scholar]
- Margulies DS, Petrides M (2013): Distinct parietal and temporal connectivity profiles of ventrolateral frontal areas involved in language production. J Neurosci 33:16846–16852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies DS, Böttger J, Long X, Lv Y, Kelly C, Schäfer A, Goldhahn D, Abbushi A, Milham MP, Lohmann G, Villringer A (2010): Resting developments: A review of fMRI post‐processing methodologies for spontaneous brain activity. 23:289–307. [DOI] [PubMed] [Google Scholar]
- Martínez K, Burgaleta M, Román FJ, Escorial S, Shih PC, Quiroga MA, Colom R (2011): Can fluid intelligence be reduced to ‘simple’ short‐term storage? Intelligence 39:473–480. [Google Scholar]
- Martínez K, Madsen S, Joshi AA, Shantanu J, Román FJ, Villalón‐Reina J, Burgaleta M, Karama S, Janssen J, Marinetto E, Desco M, Thompson PM, Colom R (2015): Reproducibility of brain‐cognition relationships using three cortical surface based protocols: An exhaustive analysis based on cortical thickness. Hum Brain Mapp 36:3227–3245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McArdle BH, Anderson MJ (2001): Fitting multivariate models to community data: A comment on distance‐based redundancy analysis. Ecology 82:290–297. [Google Scholar]
- Nichols TE (2012): Multiple testing corrections, nonparametric methods, and random field theory. Neuroimage 62:811–815. [DOI] [PubMed] [Google Scholar]
- Pineda‐Pardo JA, Martínez K, Román FJ, Colom R (2016): Structural efficiency within a parieto‐frontal network and cognitive differences. Intelligence 54:105–116. [Google Scholar]
- Shaw RG, Mitchell‐Olds T (1993): ANOVA for unbalanced data: An overview. Ecology 74:1638. [Google Scholar]
- Shehzad Z, Kelly C, Reiss PT, Craddock RC, Emerson JW, McMahon K, Copland DA, Castellanos FX, Milham MP (2014): A multivariate distance‐based analytic framework for connectome‐wide association studies. Neuroimage 93:74–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheppard LD, Vernon PA (2008): Intelligence and speed of information‐processing: A review of 50 years of research. Pers Individ Differ 44:535–551. [Google Scholar]
- Singh‐Curry V, Husain M (2009): The functional role of the inferior parietal lobe in the dorsal and ventral stream dichotomy. Neuropsychologia 47:1434–1448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM (2002): Fast robust automated brain extraction. Hum. Brain Mapp 17:143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelzer J, Lohmann G, Mueller K, Buschman T, Turner R (2014): Deficient approaches to human neuroimaging. Front Hum Neurosci 8:462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Studer M, Ritschard G, Gabadinho A, Müller NS (2011): Discrepancy analysis of state sequences. Sociol Methods Res 40:471–510. [Google Scholar]
- van den Heuvel MP, Sporns O (2011): Rich Club organization of the human connectome. J Neurosci 31:15755–15786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel MP, Sporns O (2013): Network hubs in the human brain. Trends Cogn Sci 17:683–696. [DOI] [PubMed] [Google Scholar]
- Vul E, Harris C, Winkielman P, Pashler H (2009): Puzzlingly high correlations in fMRI studies of emotion, personality, and social cognition. Perspect Psychol Sci 4:274–290. [DOI] [PubMed] [Google Scholar]
- Yarkoni T (2009): Big correlations in little studies. Inflated fMRI correlations reflect low statistical power. Perspect Psychol Sci 4:294–298. [DOI] [PubMed] [Google Scholar]
- Yarkoni T, Poldrack RA, Van Essen DC, Wager TD (2010): Cognitive neuroscience 2.0: Building a cumulative science of human brain function. Trends Cogn Sci 14:489–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zald DH, McHugo M, Ray KL, Glahn DC, Eickhoff SB, Laird AR (2014): Meta‐analytic connectivity modeling reveals differential functional connectivity of the medial and lateral orbitofrontal cortex. Cereb Cortex 24:232–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zapala MA, Schork NJ (2006): Multivariate regression analysis of distance matrices for testing associations between gene expression patterns and related variables. Proc Natl Acad Sci USA 103:19430–19435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zapala MA, Schork NJ (2012): Statistical properties of multivariate distance matrix regression for high‐dimensional data analysis. Front Genet 3:190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, Li CS (2012): Functional connectivity mapping of the human precuneus by resting fMRI. NeuroImage 15:3548–3562. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information
Video 1. The animation depicts progressively the 36 connections maximizing the association with the cognitive variables. Green, yellow, orange, and red nodes represent brain regions highlighted by the P‐FIT model and gray nodes are regions not included in this model. Colors denote processing stages: (1) processing of sensory information (green), (2) integration (yellow), (3) evaluation (orange), and (4) response selection (red). The final round in the animation depicts the schematic representation shown in Figure 4. The nodes are identified in Supporting Information Table III.


