Cortical connectivity modulation during sleep onset: A study via graph theory on EEG data

Abstract

Sleep onset is characterized by a specific and orchestrated pattern of frequency and topographical EEG changes. Conventional power analyses of electroencephalographic (EEG) and computational assessments of network dynamics have described an earlier synchronization of the centrofrontal areas rhythms and a spread of synchronizing signals from associative prefrontal to posterior areas. Here, we assess how “small world” characteristics of the brain networks, as reflected in the EEG rhythms, are modified in the wakefulness–sleep transition comparing the pre‐ and post‐sleep onset epochs. The results show that sleep onset is characterized by a less ordered brain network (as reflected by the higher value of small world) in the sigma band for the frontal lobes indicating stronger connectivity, and a more ordered brain network in the low frequency delta and theta bands indicating disconnection on the remaining brain areas. Our results depict the timing and topography of the specific mechanisms for the maintenance of functional connectivity of frontal brain regions at the sleep onset, also providing a possible explanation for the prevalence of the frontal‐to‐posterior information flow directionality previously observed after sleep onset. Hum Brain Mapp 38:5456–5464, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Sleep is a complex physiological process, linked with the function of every bodily organ, and its dysregulation has negative impacts for well‐being and health. Despite its importance, after decades of research, much uncertainty remains with respect to brain functional changes occurring when we fall asleep. The known point is that there are remarkable changes between full awake and sleep conditions and that the variety of human states of consciousness and the wakefulness–sleep (W–S) transition are based on the dynamic connectivity of brain regions that continuously interact through complex neural networks with time‐ and task‐varying architecture.

Following this idea, a specific pattern of frequency and topographical electroencephalographic (EEG) changes has been observed at sleep onset [De Gennaro et al., 2001]. In the 5 min interval preceding the appearance of EEG patterns which characterize sleep onset—namely, a sleep spindle or a K‐complex—the slow rhythms are more prominent in power at the more anterior scalp locations (central, frontal, and frontopolar), and at the parietal scalp location when compared with the occipital ones. These findings supported the notion that a spread of synchronizing signals from associative prefrontal to posterior areas has an important role in the wakefulness–sleep transition [De Gennaro et al. 2004;De Gennaro et al. 2005;Marzano et al. 2013]. More recently, Marzano et al. [2013] confirmed that the centrofrontal areas show an earlier synchronization (i.e., they fall asleep first) suggesting the coexistence of wake‐like and sleep‐like electrical brain activity in different cortical areas during the initial sleep stage. In such way, the progressive brain disconnection from the external world as we fall asleep does not necessarily affect primary and higher order cortices at the same time. More in general, these findings strengthen the view of sleep as a local process, with frontal areas crucially involved in sleep homeostasis [Ferrara & De Gennaro, 2011]. According to the local use‐dependent theory, this would derive from a higher sleep need of the frontal cortex, which in turn is due to its higher levels of activity during wakefulness. The fact that different brain regions can simultaneously exhibit different sleep intensities indicates that sleep is not a spatially global and uniform state, as hypothesized in the theory.

Here, the challenge was to understand how the functionally specialized brain areas interact within the frame of dynamic networks during sleep and in particular wakefulness–sleep (W–S) transition. This is particularly interesting when dealing with dynamic interactions among neural assemblies, which change in a time frame in the order of few tens of milliseconds. In fact, the human brain consists of complex inhibitory and excitatory circuits which connect functionally specialized areas with a continuous and time‐varying interplay for processing, integrating and sharing information. The white‐matter (axonal) fibers provide anatomical basis for signal transfer and communication; the whole architecture is not random, but is organized in a so‐called “small‐world” network topology characterized by the combination of a high degree of local clustering (segregation) and of long‐distance connections (integration) [Watts & Strogatz, 1998].

An important technique recently applied to study this small world characteristics and to extract network dynamics from noninvasive measures is based on network analysis drawn from the field of graph theory. Watts and Strogatz [1998] introduced this concept of small‐world networks organization, focusing on an optimal balance between local specialization (segregation) and global integration. This approach is a promising way to characterize brain functional organization [Bassett and Bullmore, 2006] and correlate it with behavior or task‐related performances. For instance, it evaluates whether the functional connectivity patterns among brain areas reproduce the organization of more or less strongly bound networks based on strength the level of synchronization in time‐varying oscillatory neuronal firing of different brain regions as reflected by oscillating EEG rhythms at the recording scalp electrodes overlying them [Vecchio et al. 2014a, 2014b, 2014c; Vecchio et al. 2015a].

Small‐world network architecture might be of paramount importance for cortical dynamics because it represents a balance between local information processing (requiring local connectivity and segregation) and rapid sharing of this information to other regions (requiring longer distance connectivity and integration). Most utilized parameters to describe these graphs are the clustering coefficient (for the segregation) and the path length (for the integration). Previous studies [Ponten et al., 2007; Sporns and Zwi, 2004; Bassett and Bullmore, 2006; Stam, 2004; de Haan et al., 2009] demonstrated that healthy functional and structural brain networks have small‐world properties.

Small‐world parameters during sleep can be, for example, extracted from routine EEG data. Ferri et al. [2007, 2008] preliminarily studied the functional connectivity patterns during wake, NREM and REM sleep showing that the clustering coefficient increased during NREM sleep in frequencies below 15 Hz.

The aim of this study was to determine how small‐world characteristics of the brain networks, as reflected in the EEG rhythms, are modified in the wakefulness–sleep transition comparing the pre and postsleep onset epochs.

SUBJECTS AND METHODS

Participants

A dataset of 40 right‐handed healthy subjects (20 males and 20 females; age range = 18–29, mean age = 23.8 ± 2.88 years) was analyzed. For more procedural details, see Marzano et al. [2013]. All subjects were right‐handed at Handedness Questionnaire [Salmaso and Longoni, 1985] and gave an informed consent after approval of the study protocol by the local Ethical Committee. Experimental procedures were conformed to the Declaration of Helsinski and national guidelines.

Procedure

Sleep recordings have been carried out in a sound‐proof, temperature‐controlled room. The subjects' sleep was undisturbed, started at midnight, and ended after 7.5 hours of accumulated sleep (as visually checked online by expert sleep researchers).

EEG signals were recorded from 19 unipolar derivations of the 10–20 system from scalp electrodes with averaged mastoid reference and were analogically filtered [high‐pass filter at 0.50 Hz and antialiasing low‐pass at 30 Hz (−30 dB/octave) Esaote Biomedica VEGA 24 polygraph].

For sleep scoring, the submental EMG was recorded with a time constant of 0.03 s while bipolar horizontal eye movements (EOG) were acquired from electrodes placed about 1 cm from the medial and lateral canthi of the dominant eye with a time constant of 1 s. Impedance of these electrodes was kept below 5 kΩ.

Data Preprocessing

Central EEG derivation (Cz), EMG, and EOG were used to visually score sleep stages in 12 s epochs, according to the standard criteria [Rechtschaffen, 1968]. The polygraphic signals (19 EEG channels, EOG, and EMG) were A/D converted online with a sampling rate of 128 Hz and stored on the disk of a personal computer. Ocular and muscle artifacts were excluded offline by visual inspection.

Data were then analyzed by Matlab R2011b software (MathWorks), using scripts based on EEGLAB 11.0.5.4b toolbox (http://www.sccn.ucsd.edu/eeglab). Recordings were band‐pass filtered (0.5–30 Hz). EEG data were then fragmented in 2 s epochs, cleaning artifacts (i.e., eye movements, EKG activity, and muscle contraction) using an independent component analysis (ICA) procedure performed in EEGLAB Infomax ICA algorithm [Bell and Sejnowski, 1995; Iriarte et al., 2003; Jung et al., 2000].

Functional Connectivity Analysis

EEG functional connectivity analysis has been performed using the eLORETA exact low resolution electromagnetic tomography [Vecchio et al., 2014a, 2014b, 2014c] software (freely available at http://www.uzh.ch/keyinst/NewLORETA/LORETA01.htm). The eLORETA algorithm is a linear inverse solution for EEG signals that has no localization error to point sources under ideal (noise‐free) conditions [Pascual‐Marqui, 2002].

Based on the scalp‐recorded electric potential distribution, the exact low‐resolution brain electromagnetic tomography (eLORETA) software was used to compute the cortical three‐dimensional distribution of current density. The description of the method and the proof of its exact zero‐error localization property are described in Pascual‐Marqui [2009].

In the current implementation of eLORETA, computations were made in a realistic head model [Fuchs et al., 2002] using the MNI152 template [Mazziotta et al., 2001], with the three‐dimensional solution space restricted to cortical gray matter, as determined by the probabilistic Talairach atlas [Lancaster et al., 2000]. The standard electrode positions on the MNI152 scalp were taken from Jurcak et al. [2007]. The intracerebral volume is partitioned in 6,239 voxels at a 5 mm spatial resolution. Thus, eLORETA images represent the electric activity at each voxel in the neuroanatomic Montreal Neurological Institute (MNI) space as the exact magnitude of the estimated current density. Anatomical labels as Brodmann areas are also reported using MNI space, with correction to Talairach space [Brett et al., 2002].

To obtain a topographic view of the whole brain, brain connectivity was computed with sLORETA/eLORETA software in 84 regions positioning the center in the available 42 Brodmann Areas (BAs: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 17, 18, 19, 20, 21, 22, 23, 24, 25, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47) in left and right hemispheres.

Regions of interest (ROIs) are needed for the estimation of electric neuronal activity that is used to analyze brain functional connectivity. The signal at each cortical ROI consisted of the average electric EEG activities of all voxels belonging to that ROI, as computed with eLORETA.

Among the eLORETA current density time series of the 84 ROIs, intracortical Lagged Linear Coherence, extracted using an all nearest voxel procedure [Pascual‐Marqui, 2007b], was computed between all possible pairs of the ROIs for each of the five independent EEG frequency bands of delta (0.5–4.5 Hz), theta (5–7.5 Hz), alpha (8–11.5 Hz), sigma (12–15.5Hz), and beta (16–24.5 Hz) for each subject.

Starting with the definition of the complex valued coherence between time series x and y in the frequency band ω—which is based on the cross‐spectrum given by the covariance and variances of the signals—the lagged linear coherence in the frequency band ω is reported in acordance with the following equation [Pascual‐Marqui, 2007b]:

$$\mathrm{L}\mathrm{a}\mathrm{g}{R}_{xyw}^2=\frac{{\left[\mathrm{I}\mathrm{m}\mathrm{C}\mathrm{o}\mathrm{v}\left(x,y\right)\right]}^2}{\mathrm{V}\mathrm{a}\mathrm{r}\left(x\right)\times \mathrm{V}\mathrm{a}\mathrm{r}\left(y\right)-{\left[\mathrm{R}\mathrm{e}\mathrm{C}\mathrm{o}\mathrm{v}\left(x,y\right)\right]}^2}$$

where Var is the variance of the signals, and Cov is the complex valued of covariance, with real and imaginary parts denoted as Re(Cov) and Im(Cov) (Pascual‐Marqui 2007a).

This lagged linear coherence was developed as a measure of the true physiological connectivity not affected by volume conduction and low spatial resolution [Pascual‐Marqui, 2007b]. The values of lagged linear connectivity computing between all pairs of ROIs for each frequency band were used as weights of the networks built in the graph analysis.

Graph Analysis

A network is a mathematical representation of a complex system. It is defined by a collection of nodes (vertices) and links (edges) between pairs of nodes. In brain networks, nodes usually represent neuronal assemblies in discrete brain regions, while links represent anatomical, functional or effective connections [Friston, 1994], depending on the dataset. Anatomical connections typically correspond to white matter fiber tracts between pairs of grey matter brain regions (cortical areas or subcortical relays). Functional connections correspond to magnitudes of temporal correlations in activity and may occur between pairs of anatomically unconnected (but functionally cooperating via indirect connections) regions.

In this study, weighted (no thresholded) and undirected networks were built. The vertices of the network are the estimated cortical sources in the BAs, and the edges are weighted by the Lagged Linear value within each pair of vertices. The software instrument used here for the graph analysis was the Brain Connectivity Toolbox (BCT, http://www.brain-connectivity-toolbox.net/), adapted with our own Matlab scripts.

The small world index S ^w that describes the balance between local connectedness and global integration of a network was evaluated on the functional weighted brain networks considering that when S ^w > 1, a network had small‐world properties. Small‐world organization is intermediate between that of random networks, the short overall path length of which is associated with a low level of local clustering, and that of regular networks or lattices, and the high level of clustering of which is accompanied by a long path length [Vecchio et al., 2014b]. This means that nodes are linked through relatively few intermediate steps, and most nodes maintain few direct connections [Miraglia et al., 2016]. Small‐worldness (S ^w) parameter is defined as the ratio between normalized weighted clustering coefficient (C ^w) and normalized weighted characteristic path length (L ^w) with respect to the frequency bands. To obtain individual normalized relative measures, the values of characteristic path length and of clustering coefficient were divided by the mean values obtained by the average of themselves in all bands of each subjects.

The clustering (C) is the ratio of all existing connections between the “neighbors” of a node (nodes that are one step away) and the maximum possible number of edges between the neighbors. C around a vertex i is quantified by the number of triangles in which vertex i participates, normalized by the maximum possible number of such triangles [Onnela et al., 2005; Rubinov and Sporns, 2010].

As triangles are one type of subgraph, the definition of C may be used to yield the weighted clustering coefficient C ^w by replacing the number of triangles with the sum of triangle intensities as follows [Onnela et al., 2005; Rubinov and Sporns, 2010]:

$${ C}^{\mathrm{W}}= \frac{1}{n}\sum _{i\in N}\frac{{2t_i}^W}{k_i(k_i- 1)}$$

where

$$t_i^w= \frac{1}{2}\sum _{j,h\in N}{\left(w_{ij}{w}_{ih}{w}_{jh}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}$$

is the geometric mean of triangles around i, while w_ij are connection weights associated to links (i,j), assuming that weights are normalized such that 0 ≤ w_ij ≤ 1 for all i and j. Of note, in this study the weights come from the lagged linear analysis. Finally, the mean clustering coefficient is computed for all nodes of the graph and then averaged. It is a measure for the tendency of network elements to form local clusters [de Haan et al., 2009].

L ^w is defined as follows [Onnela et al., 2005; Rubinov and Sporns, 2010]:

$$L^W= \frac{1}{n}\sum _{i\in N}\frac{\sum _{j\in N,j\ne i}{d}_{ij}^W}{n-1}$$

with

$$d_{ij}^w=\sum a_{uv}\in g_{i⟷j}^{w}f\left(w_{uv}\right)$$

that represents the shortest weighted path length between i and j. f is a map (e.g., an inverse) from weight to length and $g_{\mathrm{i}}^{\mathrm{w}}$↔j is the shortest weighted path between i and j. To obtain individual normalized relative measures, the values of characteristic path length and of clustering coefficient were divided by the mean values obtained by the average of themselves in all bands of each subjects.

Small‐worldness (S ^w) parameter—obtained as the ratio between normalized C^w and L ^w —was evaluated in all subjects in pre‐ and postsleep onset condition.

Statistical Evaluation

eLORETA statistical evaluation was made on a graph analysis pattern extracted with sLORETA/eLORETA from the brain network (including 84 ROI, 42 ROIs of the left and 42 ROIs of the right hemisphere). The normality of the data was tested using the Kolmogorov–Smirnov test, and the hypothesis of Gaussianity could not be rejected. In line with the aim of the study, an ANOVA design (Statistica 8.0) was carried out for the small world with the factors time (pre‐ and postsleep onset) and band (delta, theta, alpha, sigma, beta).

Lagged linear connectivity comparisons were evaluated using the statistical nonparametric mapping (SnPM) methodology supplied by the LORETA software which is based on the Fisher's permutation test. The empirical probability distribution of the maximum F statistic was estimated via randomization, under the null hypothesis of equality between pre‐ and postsleep onset Lagged linear connectivity values, for each discrete EEG frequency band within the groups. A total of 5000 permutations were used for each randomization test. Owing to the nonparametric nature of the method, its validity does not need to rely on any assumption of Gaussianity [Nichols and Holmes, 2002].

RESULTS

ANOVA (Fig. 1) showed a statistically significant interaction (F(4,156) = 16.232, P < 0.000001) between the factors Time (Pre, Post sleep onset) and Band [delta (0.5–4.5 Hz), theta (5–7.5 Hz), alpha (8–11.5 Hz), sigma (12–15.5 Hz), and beta (16–24.5 Hz)]. Duncan planned post‐hoc comparisons showed that the small world index was Pre > Post in the delta (P < 0.006959) and theta (P < 0.000352) frequency bands and the opposite was found, Pre < Post, in the sigma band (P < 0.000005).

Figure 1.

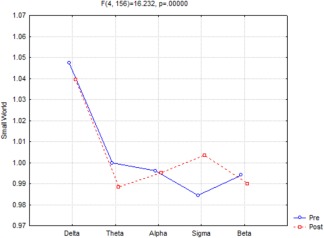
ANOVA significant interaction (F(4,156) = 16.232, P < 0.000001) of the small‐world index among the factors Time (pre‐ and postsleep onset) and Band [delta (0.5–4.5 Hz), theta (5–7.5 Hz), alpha (8–11.5 Hz), sigma (12–15.5 Hz), and beta (16–24.5 Hz)]. Duncan planned post‐hoc testing showed that the pattern pre > post was fitted in the delta (P < 0.006959) and theta (P < 0.000352) band, while the opposite trend pre < post was found in sigma band (P < 0.000005). [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 2 shows the eLORETA Lagged Linear Connectivity significant differences maps of the EEG cortical sources for the W–S transition in the sigma band at 12.5 Hz frequency (i.e., the 0.5 Hz bin centered at 12.5 Hz). The red lines represent the statistically significant differences between pre‐ and post‐ sleep onset. After sleep onset, subjects show an increase of brain connectivity—higher number of connections—in the frontal regions respect to the interval before sleep onset. The same analyses have been carried out for the all bins of the sigma frequency range, without substantial differences.

Figure 2.

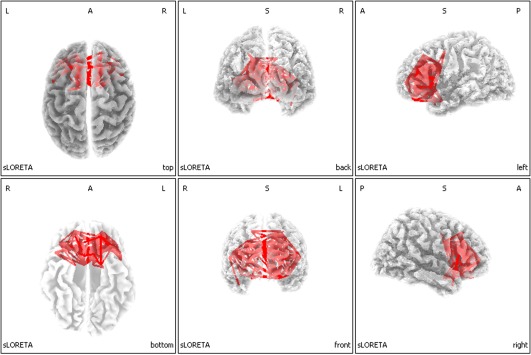
Results of the eLORETA comparison of EEG‐lagged linear connectivity between pre and postsleep onset condition in the sigma band at 12.5 Hz frequency. Red lines indicate connections, which presented increase of coherence after (POST) compared to before (PRE) sleep onset. [Color figure can be viewed at http://wileyonlinelibrary.com]

Just with an illustrative and control aim, Figure 3 reports a square image representation of each band in both pre and post phases. The figure shows the adjacency matrices representing connectivity values between each couple of node (namely each possible couple of Brodmann areas). The only observable finding is represented by slightly higher values of connectivity within hemisphere (light color) respect to between hemispheres. Furthermore, Figure 4 reports the functional coupling distribution as revealed by the lagged linear coherence in the bands showing significant differences.

Figure 3.

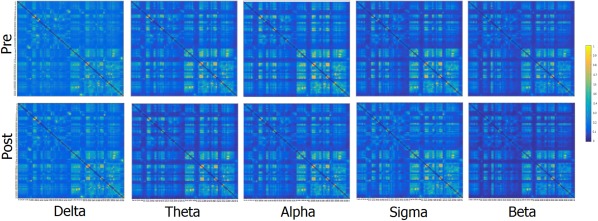
Square image representation of each band in both pre and post. In the axes, there are reported the single nodes of the network: BA 1F, 2P, 3F, 4F, 5P, 6F, 7P, 8F, 9F, 10F, 11F, 13F, 17O, 18O, 19O, 20T, 21T, 22T, 23P, 24F, 25F, 27T, 28T, 29T, 30T, 31P, 32F, 33F, 34T, 35T, 36T, 37T, 38T, 39P, 40P, 41T, 42T, 43P, 44F, 45F, 46F, and 47F first in the left and then in the right hemisphere, where F, T, O, and P represent frontal, temporal, occipital, and parietal, respectively. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 4.

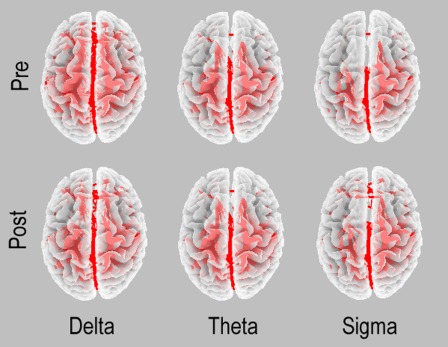
Functional coupling in the two conditions in the EEG frequency bands showing significant differences in the main analysis: delta, theta, and sigma. Arbitrary thresholds were used to illustrate these patterns.

Control Analyses

To be sure that the present results were not influenced by the choice of more nodes than the starting 19 scalp electrodes, we performed a control analysis with only 18 nodes, namely we selected the BAs just under the electrodes (in both left and right hemisphere BA1,2,3, BA5, BA8, BA10, BA18, BA39, BA21,42, BA37, BA45, 47). The analysis (F(4, 156) = 9.7354, P < 0.000001) showed that SW had the same trend as the main analysis but SW significances were obtained only in theta (P < 0.000365) and sigma (P < 0.000013) bands, probably due to a lower spatial resolution of the analysis. Regarding the delta band (P = 0.373440), the analysis shows similar changes (decrease in the post condition) compared to the main analysis, but without reaching statistically significant levels.

As a further control analysis, in order to understand which parameter between C ^w and L ^w was responsible for the SW modulation, we performed statistical evaluation of C ^w and L ^w separately. The analysis showed that, while SW differences were observed in the delta, theta and sigma bands, C ^w(F(4, 156) = 20.659, P < 0.000001), L ^w (F(4, 156) = 19.198, P < 0.000001) presented significant increase only in the sigma band (P < 0.000005 and P < 0.000004, respectively). The final increase of the SW depends on the fact that the increase of C ^w was a little higher (27.1%) than that of L ^w (24.5%).

Finally, to understand whether the spectral power in the different bands might explain the results of connectivity, we performed a changing covariate analysis including the power spectrum of each band (delta, theta, sigma, alpha, beta) as covariate. Hence, we carried out a Time × Band ANCOVA on the values of SW. This new approach fully confirmed the Time × Band interaction of the main principal analysis (F(4,152) = 9.55, P < 0.019), and the post‐hoc analyses replicated previous findings in delta (P < 0.0024), theta (P < 0.00005), and sigma (P < 0.0000045) bands. The effect of the covariate was not significant (F(4,152) = 1,56; P < 0.1900).

DISCUSSION

In this study, we modeled the EEG functional connectivity in the brain networks during the wake‐to‐sleep transition by graph theory application for the evaluation of small‐world characteristics.

The present results show changes in the functional connectivity and small‐world characteristics across the W–S transition. The results suggest that the W–S transition is characterized by a coordinated functional coupling of cortical rhythms generated by a specific organization of the brain network. In particular, results of this study suggested that, in line with previous evidence [Miraglia et al., 2016], processes of cerebral integration and segregation are in continuous modulation across different brain states. Small‐world (SW) properties of the network had different patterns with different trends in the EEG frequency bands. Delta and theta low‐frequency bands presented lower levels of SW after sleep onset compared to the previous interval, while the opposite was found in the sigma bands. Previous studies suggested that lower values of SW, which represent a more ordered structure, are related to a functional disconnection. For example, a correlation has been reported between gamma Small World reduction and memory decline, as revealed by specific memory tests [Vecchio et al., 2015b]. Moreover, significant small worldness difference distinguish normal elderly subjects from AD patients, and a reduction in the hippocampal volume leads to less Small World variability in different EEG frequency bands including a reduction in delta band [Vecchio et al., 2016]. Accordingly, it might be speculated that in delta and theta bands this increased ordered organization indexed by a decrease of small‐world organization, represents a sort of functional disconnection in the functional brain states characterized by the build‐up of the slow‐wave activity associated to the homeostatic sleep pressure. According to this interpretation, the increasingly ordered architecture found in the delta/theta bands in the current study should be further heightened with increased sleep pressure, such as following sleep deprivation.

Few studies have carried out functional coupling analysis in an early phase of the W–S transition. Previous analyses of changes in delta and theta frequencies pointed to a decreased coherence parallel to the increase in power [Morikawa et al., 1993], reaching a maximum in delta/theta coherence in stage 1 followed by a subsequent decline after stage 2 onset [Morikawa et al., 1997]. Similarly, stage 2 onset yielded lower delta/theta coherence values than the sleep stage 1 [Tanaka et al., 2000]. Moreover, the asynchronous onset of sleep in different cortical sites found in a previous study [De Gennaro et al., 2001] yields a decreased delta/theta band coherence parallel to the increased power in the W–S transition [De Gennaro et al., 2004, 2005].

The transition from wakefulness to sleep is characterized by specific spatial and temporal EEG changes evolving over the first minutes subsequent to sleep onset [Marzano et al., 2013]. The frontalization of slow‐wave activity (SWA) is associated with a faster buildup of homeostatic sleep pressure, as expressed by the rising rate of SWA during sleep onset. The theta activity mostly shares a similar temporal and spatial pattern with SWA [Marzano et al., 2013]. Therefore, the whole pattern of covarying changes of slow‐frequency EEG activity at sleep onset of frontal areas points to (A) a higher and earlier EEG synchronization [Marzano et al., 2013], (B) an inversion of directionality from an occipital‐to‐frontal information flow during the presleep period toward a frontal‐to‐parieto‐occipital information flow after sleep onset [De Gennaro et al., 2004, 2005]; (C) a decreased slow‐frequency EEG coherence [De Gennaro et al., 2004, 2005], and (D) a more ordered structure as expressed by the current lower values of small world in slow‐frequency bands.

With respect to the sigma activity, we previously described that functional coupling between anterior and posterior midline cortical areas during the sleep onset was characterized by a significant prevalence of the frontal‐to‐parieto/occipital direction after sleep onset [De Gennaro et al., 2004, 2005]. In this sleep period, spindle frequency is higher and slow wave activity (SWA) is lower than in subsequent intervals [Andrillon et al., 2011]. The maxima of sigma frequency and sigma oscillations are, in fact, detected around the 13–Hz frequency [Marzano et al., 2013]. Here, we show higher functional coupling in frontal regions after sleep onset compared to the waking state; such an increased coupling could justify the prevalence of the frontal‐to‐posterior information flow directionality after sleep onset. This prevalence is maximal at 12.5 Hz (Fig. 2), although it is widespread across the whole frequency band.

More in general, our results resemble the breakdown in cortical effective connectivity both across the central sulcus and the corpus callosum previously showed by using transcranial magnetic stimulation (TMS) together with high density EEG (hdEEG) during NREM sleep of the early part of the night [Massimini et al., 2005]. In that study, the authors measured how the activation of the premotor area is transmitted to the rest of the brain. Keeping in mind that in that study during NREM sleep, the EEG response was stronger but did not propagate beyond the stimulation site [Massimini et al., 2005], it might be speculated that the increased sigma frontal coupling reflect increased local interconnectedness leading both to reinforcement of frontal lobes linkage at the expense of their isolation from the rest of the brain.

As sleep deprivation most strongly affects the functional connectivity of prefrontal cortical areas and the restorative effect of sleep is especially relevant for the maintenance of functional connectivity of prefrontal brain regions [Verweij et al., 2014], our results depict the timing and topography of such specific mechanism at sleep onset. It will be very interesting to compare sleep after a normal 16 h of diurnal wakefulness versus after 40 h of extended wakefulness (i.e., comparing baseline vs postdeprivation sleep onset).

CONCLUSIONS

The present results show that sleep onset is characterized by a less ordered brain network (as reflected by the higher value of small world) in the sigma band for the frontal lobes indicating stronger connectivity, and a more ordered brain network in the low‐frequency delta and theta bands indicating disconnection on the remaining brain areas. This study opens interesting avenues for future researches investigating eventual modifications of brain connectivity and network organization in the evolution of sleep stages