The anatomical scaffold underlying the functional centrality of known cortical hubs

Abstract

Cortical hubs play a fundamental role in the functional architecture of brain connectivity at rest. However, the anatomical scaffold underlying their centrality is still under debate. Certainly, the brain function and anatomy are significantly entwined through synaptogenesis and pruning mechanisms that continuously reshape structural and functional connections. Thus, if hubs are expected to exhibit a large number of direct anatomical connections with the rest of the brain, such a dense wiring is extremely inefficient in energetic terms. In this work, we investigate these aspects on fMRI and DTI data from a set of know resting‐state networks, starting from the hypothesis that to promote integration, functional, and anatomical connections link different areas at different scales or hierarchies. Thus, we focused on the role of functional hubs in this hierarchical organization of functional and anatomical architectures. We found that these regions, from a structural point of view, are first linked to each other and successively to the rest of the brain. Thus, functionally central nodes seem to show few strong anatomical connections. These findings suggest an efficient strategy of the investigated cortical hubs in exploiting few direct anatomical connections to link functional hubs among each other that eventually reach the rest of the considered nodes through local indirect tracts. Hum Brain Mapp 38:5141–5160, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

Spontaneous brain activity at rest observed with functional magnetic resonance imaging (fMRI) is spatially and temporally structured in cortical networks (so‐called resting‐state networks, RSN) closely resembling sets of regions that are collectively activated during tasks [Biswal et al., 1997]. The topology and temporal dynamics revealed by different imaging modalities, for example, fMRI, EEG, and MEG, suggested that these systems are not segregated but interact to allow an efficient integration at rest. Specifically, the topology of functional interaction in the brain shows that some RSN areas, namely cortical hubs, are highly connected and play a central role in the coordination of the communication across the brain by serving as way stations for network traffic [Hagmann et al., 2008; Shirer et al., 2012]. Several structural and functional hub locations have been reported [Bullmore and Sporns, 2012; Hagmann et al., 2008; Power et al., 2013] typically located in medial posterior cingulate cortex (pCC) and lateral (angular gyrus) parietal regions of the default mode network (DMN), and in anterior cingulate and anterior insula, part of the cingulo‐opercular, and lateral frontal and parietal cortex, part of the fronto‐parietal control networks [Buckner et al., 2009; Cole et al., 2010; de Pasquale et al., 2012, 2013; Tomasi and Volkow, 2011). In line with these results, other imaging modalities such as MEG identified a set of regions belonging to the DMN as highly central followed by nodes from the dorsal attention (DAN) and somato‐sensory (SMN) networks [de Pasquale et al., 2012, 2016].

Therefore, anatomical, functional, and electrophysiological data indicate that while some networks play a central role in cross‐network interaction others remain more segregated over time [Betti et al., 2013; Buckner et al., 2009; de Pasquale et al., 2010, 2012, 2013; Marzetti et al., 2013]. This has suggested a number of different hypotheses regarding spatio‐temporal architectures affording network interactions including small‐world models [Achard and Bullmore, 2007], network cores [Bassett et al., 2013; Shanahan, 2012], and dynamic core network [de Pasquale et al., 2016]. Among these models, [van den Heuvel and Sporns, 2013a] proposed a structural architecture where a “rich club” organization among brain hubs is observed. This is characterized by a tendency for high‐degree nodes to be more densely connected among themselves than nodes of a lower degree. In particular, bilateral frontoparietal regions, including the precuneus and superior frontal and parietal cortex, and important subcortical regions including the hippocampus, thalamus, and putamen were found to be densely interconnected, together forming this rich club.

However, the anatomical scaffold of the complex functional architecture is still under debate. On the one hand, the structural connectivity (SC) relates to the biological infrastructure for neuronal signaling [van den Heuvel and Sporns, 2013b], and thus any functional connection is expected to be realized through signal traffic spreading on structural paths. This is supported by a large set of studies, see for example [Skudlarski et al., 2008] where a linear relationship is reported between SC and functional connectivity (FC). On the other hand, caution must be taken since these two measures are intrinsically different. FC, especially when estimated via cross‐correlation, reflects a statistically undirected association which is prone to transitivity (it can be realized through direct and indirect anatomical connections) leading to a propensity for “over‐connection” and high clustering [Zalesky et al., 2012]. Instead, SC mainly reflects direct anatomical connections (even when estimated via probabilistic fiber tracking approaches) and in the presence of complex fiber branching and splitting it penalizes small fibers or complex geometries [Nucifora et al., 2007]. This discrepancy between FC and SC is supported by some studies where, although some predictive value of SC on FC has been reported [Hagmann et al., 2008], the amount of FC variance accounted for by SC appears limited [Messe et al., 2014]. This suggests a complex relationship between these two measures [Honey et al., 2009; Ton et al., 2014; van den Heuvel and Sporns, 2013b]. Furthermore, such relationship is certainly not static, that is, SC has been shown to be continuously shaped over time (see, e.g., Olesen et al. [2003] and in Liston et al. [2006]). As a matter of fact, the developing human brain undergoes a sequence of events involving, at the macroscopic level, both the cortical thickness and gray matter density leading to a continuous network rewiring [Khundrakpam et al., 2016].

In this work, we investigated this complex relationship between FC and SC in a selected set of functional nodes related to nine RSNs consistently reported in the literature. Our hypothesis is that this set of RSNs behaves as an integrated system, extending [Tononi et al., 1998], where functional and anatomical connections link different areas at different scales. We adopted a multiscale community detection and hierarchical clustering (both driven by functional and anatomical DTI data). Then, we compared the patterns of growth of functional and anatomical clusters obtained at the different scales and hierarchies. Eventually, we related these results to the functional centrality, estimated in terms of betweenness centrality, of the investigated nodes. We found that these regions, from a structural point of view, are first linked to each other and successively to the rest of the brain. Furthermore, we obtained that the functional centrality of the investigated nodes, although is observed on a limited set of regions, is inversely related to the number of strong anatomical connections. This seems to suggest that the functional centrality of the considered nodes is realized through few specific structural connections.

MATERIALS AND METHODS

Experimental Setup

Twenty healthy subjects (9 women and 11 men; mean age ± standard deviation: 30 ± 10 years; same sample as in de Pasquale et al. [2013] provided informed written consent and participated in this study, which was approved by the local ethics committee. The study comprised four consecutive resting state sessions. Subjects were told to stay still and relaxed and no particular instructions were given to attend or fixate. The fMRI data were acquired on a 3 T Allegra scanner (Siemens Medical Solutions, Erlangen, Germany) with a maximum gradient strength of 40 mT/m, using a standard quadrature birdcage head coil for both RF transmission and reception. The adopted sequence was a gradient echo‐EPI, with 38 axial slices with a voxel size of 3 × 3 × 3.75 mm³ (matrix size 64 × 64; FOV 192 × 192 mm²; TR = 2470 ms) in ascending order. Each resting‐state session consisted of 200 volumes.

Diffusion‐weighted volumes were acquired using spin‐echo echo‐planar imaging (echo time/repetition time = 89/8500 ms, bandwidth = 2126 Hz/voxel; matrix size 128 × 128; 80 axial slices, voxel size 1.8 × 1.8 × 1.8 mm³) with 30 isotropically distributed orientations for the diffusion‐sensitizing gradients at a b value of 1000 s mm² and six b = 0 images. Two consecutive DTI runs were acquired for each subject.

Additionally, whole‐brain T1‐weighted images were acquired in the sagittal plane using a modified driven equilibrium Fourier transform sequence [Deichmann et al., 2004] (echo time/repetition time = 2.4/7.92 ms, flip angle 15°, voxel size 1 × 1 × 1 mm³).

fMRI Preprocessing

Our preprocessing pipeline consists of several steps performed using a combination of tools from the FMRIB's Software Library (FSL; http://www.fmrib.ox.ac.uk/fsl) and the physiologic estimation by temporal independent component analysis (PESTICA) software [Beall, 2010]. The data are initially motion corrected using the FSL–MCFLIRT tool [Jenkinson et al., 2002] and physiological respiration and cardiac artifacts were removed by means of PESTICA (see de Pasquale et al. [2013] for a detailed description). Eventually, a mean‐based intensity normalization of all volumes; high‐pass temporal filtering; Gaussian low‐pass temporal filtering (FWHM sigma = 2.8); coregistration to the MNI152 standard space (FSL–FNIRT tool) was performed.

Estimation of Functional Connectivity

The analysis on the functional architecture was based on 60 × 60 functional connectivity matrices obtained from a set of nodes previously reported (see Figure 1A; Baldassarre et al. [2012], de Pasquale et al. [2013], Dosenbach et al. [2007], Hacker et al. [2013], He et al. [2007] for complete list of abbreviations and labels for the considered nodes). We restricted our approach on a specific set of nodes since our aim here is to investigate the anatomical architecture of functional nodes belonging to nine RSNs: the dorsal and ventral attention network (DAN and VAN), the default mode network (DMN), the visual network (VIS), the language network (LAN), the somatosensory network (SMN), the auditory network (AUD), the executive control network (CON) and fronto‐parietal network (FPN) (see Baldassarre et al. [2012], de Pasquale et al. [2013], Dosenbach et al. [2007], Hacker et al. [2013], He et al. [2007] for the MNI coordinates of involved areas). This choice allows us to compare these results with previously published wok on the same sample of subjects [de Pasquale et al., 2013] and by using electrophysiological techniques on a subset of the same nodes [de Pasquale et al., 2012, 2016].

Figure 1.

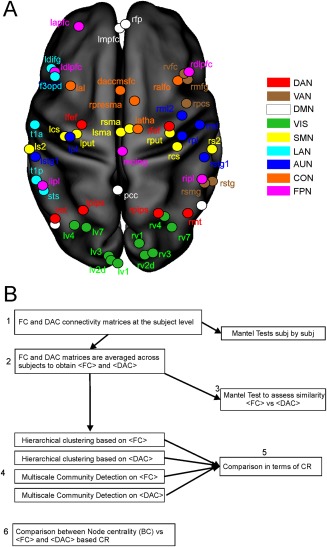
Analysis pipelines. (A) The location of the adopted 60 nodes covering 9 typical resting‐state networks: dorsal (DAN red) and ventral (VAN brown) attention, default mode (DMN white), visual (VIS green), somatosensory (SMN yellow), language (LAN pale blue), auditory (AUD blue), control (CON orange), and fronto‐parietal (FPN pink) networks. (B) A scheme of the analysis pipeline is described in detail in Materials and Methods. [Color figure can be viewed at http://wileyonlinelibrary.com]

Of note, although these regions were assumed to form the above RSNs in our subjects, this assumption was then confirmed during the clustering procedure where these systems emerged without any prior information on the node labeling. We note that, albeit the number of considered nodes is limited, these provide a good coverage of the cortex. Moreover, the limited set considered reduces the computational burden of the DTI probabilistic fiber tracking.

The final connectivity matrices were obtained from single‐run cross‐correlation matrices after Fisher‐transformation as described in de Pasquale et al. [2013]. To identify significant connections and account for the multiple corrections, we adopted a false discovery rate (FDR) approach with alpha = 0.05. Then, the 60 × 60 matrices were extracted at the subject level and averaged across runs. Finally, we averaged the obtained matrices across subjects to obtain a single functional matrix (FC) reflecting the significant connections more reproducible at the group level.

Correlation‐based approaches were demonstrated to provide reliable estimates of functional connectivity [Smith et al., 2011]. However, as the “full” Pearson correlation is unable to discriminate direct versus undirect connections, the partial correlation has been proposed in the literature [Smith et al., 2011]. This measure is the linear correlation between every pair of ROIs when all the contributions from the remaining pairs have been regressed out [Marrelec et al., 2006]. To compare the “full” versus the “partial” correlation, we report in Supporting Information, Figure S1 the average connectivity matrix unthresholded obtained with these two measures. As it can be noted in Supporting Information, Figure S1A, where the two matrices are compared at the same scale, in our case the partial correlation seems to remove too much structure in the connectivity architecture and no significant connections “survive.” We lose both internal and across network connections shown by the “full” correlation measure. To rule out the hypothesis that these connections are not removed but only characterized by a lower intensity, in Supporting Information, Figure S1B, we report the partial correlation results at a lower scale. Only few internal connections within the default mode and the visual networks are obtained. This is probably due to the fact that the number of connections involved with the regression is too large to warrant reliability of the results, see Verma [2013]. This occurs when the number of comparisons is fairly larger than the number of points used to estimate the partial correlation, even in case regularization strategies are applied. In our case, we have 1770 comparisons estimated from 200 points probably yielding unreliable results. This has been observed previously (see for example, Liang et al. [2016] and Ryali et al. [2012]). Please note that when the directionality of the functional connectivity needs to be addressed other possible measures of directed interaction are the Granger causality and transfer entropy [Seth et al., 2015].

Eventually, to evaluate the centrality of the considered nodes we adopted the weighted betweenness centrality (BC) estimated at the group level. This measure reports the fraction of all shortest paths in the network passing through a given node. Thus, nodes with high values of BC participate in a large number of shortest paths [Brandes, 2001].

Estimation of Anatomical Connectivity

To compare DTI and fMRI, we estimated probabilistic tracts from the same set of nodes from the 9 RSNs described above. In particular, for the DTI analysis, we adopted as regions of interest 10 mm spheres [Stanley et al., 2013] centered in the MNI coordinates reported in previous works [Baldassarre et al., 2012; de Pasquale et al., 2012, 2016, 2013; Dosenbach et al., 2007; Hacker et al., 2013; He et al., 2007].

Diffusion‐weighted images were analyzed by the FMRIB Software Library: FMRIB's Diffusion Toolbox [Behrens et al., 2007, 2003]. The acquired data were corrected for the effects of eddy‐current‐induced distortion and subject motion. To register RSN nodes to native diffusion space, we adopted the FDT registration to transform the MNI space into the subject DTI space by means of T1 images as an intermediate step. Probabilistic tractography was carried out by using bedpostX/probtrackX [Behrens et al., 2007]. Bedpostx uses Monte Carlo Markov chain sampling to estimate the diffusion parameters at each voxel. Probabilistic diffusion tractography was carried out by adopting 10,000 streamline samples in each seed voxel to create a connectivity distribution to each of RSN nodes (other probtrackX2 parameters: defaults settings). We chose to increase the default number of streamline samples, typically 5,000, to increase the density of our final matrices. The connectivity between nodes was defined as the number of streamlines (averaged across all voxels within the above spherical ROIs) reaching one ROI when another one was seeded and vice‐versa. Thus, a set of 60 × 60 connectivity matrices were obtained for each subject and each diffusion run (2 runs per subjects). Finally, to use the connectivity matrix as input for the subsequent community detection and clustering procedure, this was symmetrized by computing the average between the original matrix and its transpose.

A final remark must be made on the meaning of the adopted measures. When we consider the probability of anatomical connections estimated via a probabilistic fiber tracking, it must be stressed that this measure—due to the nature of DTI and tracking algorithms involved, given two brain nodes—will reflect the probability of a direct connection between them, typically represented by a large fiber. This will penalize small fibers or complex indirect connections when these will be located close to a large direct fiber. Thus, in what follows we will adopt the notation of direct anatomical connectivity (DAC) to stress that we are showing a subset of possible anatomical connections consisting of direct tracts likely due to large fibers.

Comparison of Functional Versus Anatomical Connectivity

To test the hypothesis that different regions in the investigated RSNs are connected (both functionally and anatomically) at different level of integration, we proceeded as follows. We characterized the progression of the architectures resulting at different scales, that is, intensity of connectivity by means of hierarchical clustering or multiscale community detection. This progression is particularly important for the brain hubs to understand how their centrality is realized to ensure an efficient communication across all brain components. If our hypothesis is correct, we expect to see a progression of the functional clusters from a complete segregation at the node level to the emergence of the typical topography of RSNs to finally observe some across network integration. On the other hand, if this hypothesis is not valid, that is, this interaction is not occurring in a multiscale fashion, then in our clustering we will only observe the network topographies occurring at one single fixed scale with no other interesting structures emerging at any other (coarser or finer) scale.

To this aim, we developed the analysis pipeline schematized in Figure 1B. First, we analyzed the similarity between FC and DAC at the subject level (Fig. 1B, step 1). Then, we averaged the FC and DAC matrices across subjects (Fig. 1B, step 2). At this stage, the DTI data were thresholded to maintain in the average <DAC> the same density observed at the subject level (average density across subjects = 0.42). Eventually, we assessed the similarity of <DAC> and <FC> at the group level (Fig. 1B, step 3). Both steps 1 and 3 employed the Mantel Test which is a statistical procedure developed to assess the significance of correlation between two distance matrices [Sokal and Rohlf, 1995]. To study the architecture of <DAC> and <FC> we collated the progression of the obtained communities and clusters by means of a multiscale community detection algorithm [Blondel et al., 2008] and an hierarchical clustering procedure (Fig. 1B, step 4). The multiscale community detection is based on an algorithm which provides the optimal subdivision of the network into nonoverlapping groups of nodes by maximizing the number of within‐group edges, and minimizing the number of between‐group edges. It is a multi‐iterative generalization of the Louvain community detection algorithm (see Blondel et al. [2008] and Ronhovde and Nussinov [2009] for details). The detection depends only on one parameter, namely γ, which controls the size of the communities, that is, the larger is γ the smaller is the size of the expected clusters. The value γ = 0 corresponds to one cluster while the value γ = 1 provides the classical Louvain Modularity detection. In our approach, we explored the multiscale communities with γ = 0, 0.01, …, 2. In the results, we will show only the values of γ leading to significant changes in the obtained communities.

As far as it regards the hierarchical clustering, we adopted the shortest distance linkage criterion [Anderberg, 1973]. The functional distance was defined as the inverse of the absolute value of FC described above. For the anatomical distance, we adopted the inverse of the probability defined as the fraction of estimated tracts connecting each pair of nodes.

Now, to investigate the role played by the different nodes in this multilevel interaction and in particular to differentiate nodes that during the hierarchical clustering remain largely segregated from those which are soon assigned to a cluster, we introduced the measure of Clustering Rate (CR) (Fig. 1B, step 5). For every node, this is defined as the size of the clusters where a node is assigned during the clustering steps divided by the number of hierarchical thresholds considered (or γ values). The idea behind this measure is to capture the tendency of each node to be grouped to the other considered nodes, that is, if a node is assigned soon in the hierarchical tree to a cluster then its CR will be high. On the other hand, if a node remains segregated during the clustering and only grouped at the end, the CR will be very low. To clarify, let us consider a toy example. If a node n ₁ is assigned to a cluster (size s) at the first scale (or hierarchy), its cluster size will be s at the beginning. Then, based on how the clustering works the node will stay in the first cluster whose size can only increase. Let us suppose that the cluster remains of size s until the end of clustering. Then, the CR of n ₁ will be s. Now, let us consider a second node n ₂ which remains isolated until the last nth step where it is grouped to a cluster of size s. In this case its CR will be n‐times lower than before, namely s/n, thus reflecting a lower tendency to be grouped. Now, to better elucidate the significance of this measure, we performed a simulation to test CR on different scenarios of interaction. This simulation is reported in the Supporting Information, Figures S1 and S2. Based on the proposed scenarios, CR seems to capture well the properties of peripheral and connector hubs. However, it must be acknowledged that the reported scenarios represent only a few examples of the possible architecture of interactions and additional simulations where communication delays, nonlinear interactions, or increasing amounts of non‐Gaussian noise should be considered to deeply investigate the role of CR. These properties are typically modeled in theoretical works on dynamical systems, for example, Kuramoto models, see for example, Schmidt et al. [2015].

Eventually, we investigated the relationship between the nodal centrality, quantified by means of the Betweenness Centrality (BC, see Sporns [2011]) and the CR obtained from the functional and anatomical dendrograms/multiscale communities (Fig. 1, step 6). This step is based on the correlation between these measures.

RESULTS

To compare the direct anatomical connectivity (DAC, see Materials and Methods) and FC over the selected RSN nodes, in Figure 2A, we report their similarity subject by subject [Sokal and Rohlf, 1995). We find a generally weak correlation between these measures across subjects ranging in the interval [0.03 0.15] (average correlation of 0.09 (dashed red line)) and the Mantel test revealed that 100% of subjects showed a statistically significant (all P <0.05) dissimilarity between FC and DAC (solid black bars). It must be stressed that these values relate to the specific set of nodes considered in this study. Thus, a comparison with other reported values on such similarity must be made with caution. If such a low agreement is obtained when averaged across the considered RSNs, a different scenario is obtained when these RSNs are investigated separately (Fig. 2B). First, it can be noted that each RSN shows a quite similar pattern of similarity FC–DAC across subjects, thus suggesting a consistent behavior in the sample. Second, the Mantel test revealed that networks such as LAN and VAN are characterized by a statistically higher FC–DAC similarity across subjects (Fig. 2B asterisk marks, P < 0.05). As matter of fact, this similarity in the language network (LAN) resulted significant in 100% of subjects followed by the ventral attention network (VAN) with 75%, compared to the somatosensory network (SMN) with 25% and dorsal attention network (DAN) with 15% of subjects. Thus, when averaged across subjects, we observed a large gap between LAN and VAN and the other networks (black bars in Fig. 2B). Interestingly, these networks are typically reported as segregated networks acting as local systems, see for example de Pasquale et al. [2010, 2012, 2016, 2013] while the default mode network (DMN), fronto‐parietal (FPN), executive control CON, and SMN have been reported as acting as a functional core of integration in the brain, see for example, Spreng et al. [2013]. Thus, these results suggest that central RSNs exhibit higher dissimilarity between functional and structural architecture than local RSNs. To validate these results, in Supporting Information, Figure S4A, we report the same analyses applied on a second DTI and resting‐state session. It can be noted that both the Mantel test at the subject level and the average similarity network by network produced very similar results to those of Figure 2. To validate these results, we also computed reliability estimates based on a test–retest approach between the connectomes computed from the two acquired DTI and resting state sessions. To this aim, we adopted the intraclass correlation coefficient (ICC) as in Braun et al. [2011]. For the DTI connectomes, we obtained ICC = 0.93 with [0.925 0.938] as confidence intervals. As far as it regards the functional connectomes, we obtained ICC = 0.869 with [0.8609 0.8769] as confidence intervals. These results are encouraging showing an excellent reliability across sessions in the final connectivity matrices. This is important because these matrices represent the starting point of the subsequent analyses.

Figure 2.

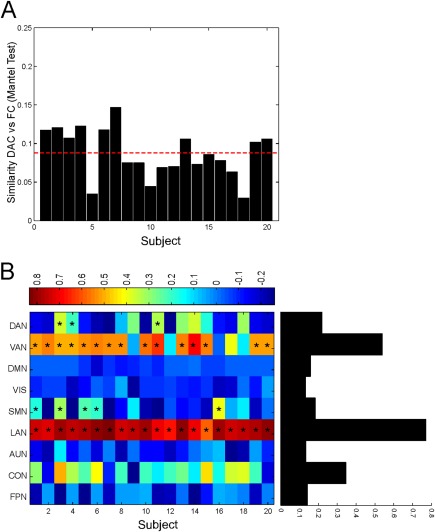
Similarity between functional and anatomical connectivity. (A) The comparison between the overall direct anatomical connectivity (DAC) and functional connectivity (FC) patterns computed subject by subject by means of the Mantel test revealed a poor agreement between them. (B) Comparison DAC versus FC network by network. Each RSN shows a consistent pattern of similarity FC–DAC across subjects (asterisks correspond to P < 0.05 with Mantel test). When averaged across subjects, the similarity FC–DAC is network specific (black bars): central networks such as DMN, FPN, and SMN show a lower resemblance between DAC and FC. [Color figure can be viewed at http://wileyonlinelibrary.com]

To further investigate the relationship between DAC and FC we studied the hierarchical progression of the structural and functional interactions. First, we applied a multiscale community detection on <FC> (Materials and Methods) [Ronhovde and Nussinov, 2009). The results are reported in Figure 3A where we show the first five communities obtained at different scales, namely from γ = 0.88 (the first two communities obtained after γ = 0) with γ varying of 0.01 (please note that in Fig. 3A only values of γ leading to significant changes in the communities are reported). The progression shows that from an initial scenario in which the functional nodes are all separated (γ = 1.18) we observe the emergence of the typical well known RSNs (γ = 1.07): the DMN (white), the SMN (cyan), and VIS (red) and parts of the DAN (gold) and CON (yellow) [Hacker et al., 2013]. As a reference, the typical topography of the considered networks is reported in Figure 1A. Of note, although these regions were a priori assumed to form the selected RSNs in our subjects [Hacker et al., 2013], these systems emerged automatically, without any prior information on the node labeling. This validates our grouping procedures. At subsequent scales, we observe a progressive integration of the DMN with the other systems (red clusters at γ = 1.03; 0.99) until the final result (γ = 0.88) where DMN and SMN are grouped together (cyan). At the next scale, all nodes are grouped in one single community (not reported). Now, to validate this progression and to observe how the different nodes tend to be clustered together, we applied the hierarchical clustering on the same data. The obtained dendrogram is reported in Figure 3B where only clusters obtained at hierarchies leading to significant differences in the progression are shown. It can be noted a clear trend in the hierarchical clustering in line with the previous results. In particular, as in Figure 3A, we started with initial nonstructured clustering at the lowest level, that is, nodes from RSNs are separated (Fig. 3C). Then we observe the emergence of larger subnetworks (Fig. 3D) consisting of parts of VIS (red), bilateral components of SMN (cyan) (including the supplementary motor area (SMA), L/R central sulcus (CS)), and parts of the DMN (L/R mPFC andL/R angular gyrus (AG), white). At the higher hierarchy (Fig. 3E), we observe the emergence of the typical topographies of the considered networks: DMN(white), SMN (cyan), VIS (red), LAN (yellow) parts of the DAN (gold), and VAN (green). Then, we note a progression towards the integration where DMN (white), SMN (cyan) and VIS (red) are still identifiable (Fig. 3F). Finally, we observe the integration between DMN and SMN (Fig. 3G) now grouped in the same cluster (cyan). Notably, this integration observed at step ** (dashed box in Fig. 3) nicely links to two main large interacting systems reported in de Pasquale et al. [2013].

Figure 3.

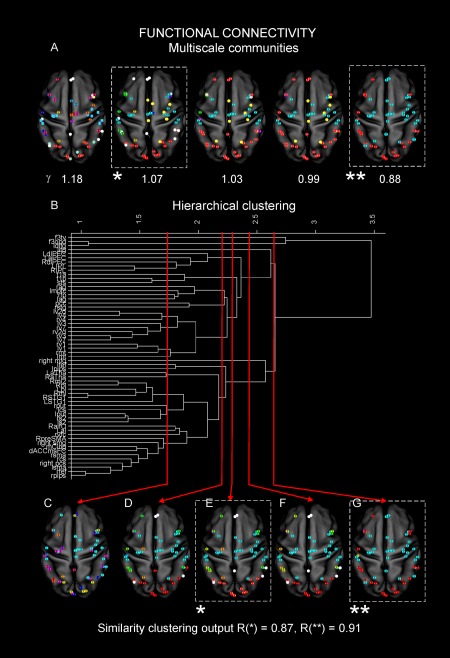
Multiscale functional architecture. (A) We report the first five communities obtained by the community detection from γ = 0.88 (the first two communities obtained after γ = 0) with γ varying of 0.01 (only values of γ leading to a significant changes in the communities are reported). From an initial scenario in which the functional nodes are separated (γ = 1.18), we observe the emergence of the typical well known RSNs at a lower γ: the DMN (white), the SMN (cyan), and VIS (red) and parts of the DAN (gold) and CON (yellow) (Fig. 1A). At subsequent scales, we observe a progressive integration of the DMN with the other systems (red clusters at γ = 1.03; 0.99) until the final result (γ = 0.88) where DMN and SMN are grouped together (cyan). At the next scale, all nodes are grouped in one single community (not reported). (B) Dendrogram from the hierarchical clustering. It can be noted a clear trend in the hierarchical clustering in line with the previous results. (C) An initial nonstructured clustering at the lowest level is observed, that is, nodes from RSNs are isolated (only clusters obtained at hierarchies leading to significant differences in the progression are reported). (D) The emergence of larger subnetworks consisting of parts of VIS (red), bilateral components of SMN (cyan) (including the supplementary motor area (SMA), L/R central sulcus (CS)) and parts of the DMN (L/R mPFC andL/R angular gyrus (AG), white) is shown. (E) At the higher hierarchy, we report the emergence of the typical topographies of the considered networks: DMN (white), SMN (cyan), VIS (red), LAN (yellow) parts of the DAN (gold) and VAN (green). (F) It can be noted a progression toward the integration where DMN (white), SMN (cyan) and VIS (red) are still identifiable. (G) The integration between DMN and SMN now grouped in the same cluster (cyan) is evident. The Rand index is reported when the networks emerged (dashed box, case *, γ = 1.07 and step E, Rand = 0.87) and when the integration among DMN and SMN is observed (dashed box, case **, γ = 0.88 step G, Rand = 0.91). [Color figure can be viewed at http://wileyonlinelibrary.com]

To quantify the agreement between the multiscale community detection and hierarchical clusters, we computed the Rand index at every step of the procedures [Rand, 1971]. We report the values obtained when the networks emerged (dashed box, case *, γ = 1.07 and step E, Rand = 0.87) and when the integration among DMN and SMN is observed (dashed box, case **, γ = 0.88 step G, Rand = 0.91). As these two steps are the most interesting in our interpretation, we report these values in Figure 3. As far as it regards the other steps, when paired as shown in Figure 3, the minimum agreement obtained between the two clustering approaches was Rand = 0.73. This shows that for the cases * and ** the agreement is very high and in general the two procedures produced consistent results in all steps. This is encouraging as the two procedures are independent.

Now, we describe clustering progressions obtained from the anatomical data. In Figure 4A, we report the anatomical multiscale communities obtained by <DAC>. As in Figure 3, we sampled γ every 0.01 starting from 0 (not reported). In this case, the progression of the communities indicates that from a scenario where the nodes are mixed across the considered networks (γ = 0.61), we soon observe (γ = 0.54) a strong backbone of interaction between nodes from the DMN (pCC), SMN (SMA), FPN (mCing), and CON (RpreSMA and dACCmsFC) (red). At subsequent scales (γ = 0.1, 0.08), this backbone loses the FPN node mCing but the strong link among the other nodes is maintained (red) even when only three communities are identified in the brain. Interestingly, these nodes remain more isolated from the rest of the brain until the final scale (γ = 0.05) when they are grouped into a larger community (red). This behavior is also evident from the hierarchical dendrogram displayed in Figure 4B where the previous nodes are soon clustered together (red). As before, at an initial hierarchical level no complete RSNs could be retrieved, but only subnetworks (Fig. 4C). By increasing the threshold, we observe a clustering in which nodes anatomically close to each are linked together in the right and left hemispheres, likely by direct connections (Fig. 4D). At this hierarchy, consistently to what observed with the multiscale community detection, a cluster comprising the same nodes as above from DMN, SMN, FPN, and CON emerges (red). These nodes remain strongly connected and separated from the rest of the brain in the subsequent hierarchies (Fig. 4E,F). In particular, in Figure 4F, additional nodes from DMN (L/R mPFC) join this anatomical backbone (red). Notably, at this level many other nodes even anatomically farther apart than these nodes are linked together. Eventually, these nodes are linked to a larger community (red; Fig. 4G). This is in line with the results in Figure 4A and it shows that these nodes that belong to important central networks are first anatomically linked to each other and only at the highest threshold are finally clustered together with the rest of the brain.

Figure 4.

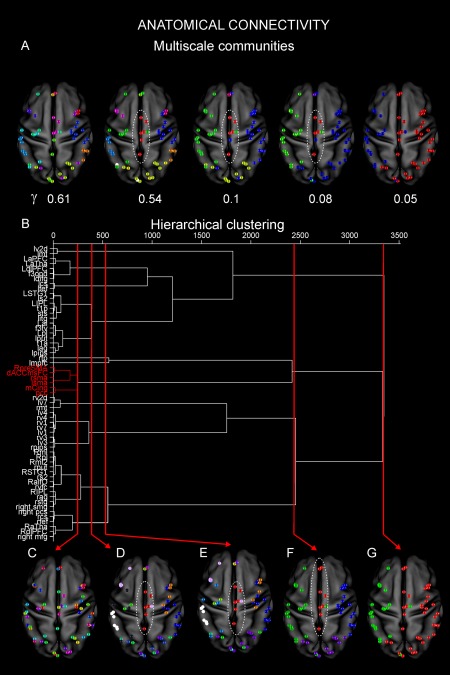
Multiscale anatomical architecture. (A) The multiscale communities obtained by <DAC>. As in Figure 3, we sampled γ every 0.01 starting from 0 (not reported). In this case the progression of the communities indicates that from a scenario where the nodes are mixed across the considered networks (γ = 0.61), we soon observe (γ = 0.54) a strong backbone of interaction between pCC (DMN), SMA (SMN), mCing (FPN), dACCmsFC, and RpreSMA (CON) (red). At subsequent scales (γ = 0.1, 0.08), this backbone loses the node from the FPN but it is maintained (red) even when only three communities are identified in the brain. Interestingly these nodes remain more isolated from the rest of the brain until the final scale (γ = 0.05) when they are grouped into a larger community (red). (B) Hierarchical dendrogram. Functional hubs such as pCC and SMA are soon linked together (red) through other nodes from central networks such as FPN and CON. (C) At an initial hierarchical level, no complete RSNs could be retrieved, but only subnetworks. (D) By increasing the threshold, we observe a clustering in which nodes anatomically close to each are linked together. At this hierarchy, consistently to what observed before, a cluster comprising the same nodes as above from DMN, SMN, FPN, and CON emerges (red). (E) These nodes remain strongly connected and separated from the rest of the brain at the subsequent hierarchies. (F) An additional node from the DMN, namely, L/R mPFC joins this anatomical backbone (red). Notably, at this level, many other nodes even anatomically farther apart than these nodes are linked together. (G) Eventually, these nodes are linked to a larger community (red). Nodes belonging to important central networks are first anatomically linked to each other and only at the highest threshold are finally clustered together with the rest of the brain. [Color figure can be viewed at http://wileyonlinelibrary.com]

Notably, while the multiscale community detection is a complete automatic approach which depends only on the parameter γ, the hierarchical clustering is typically less robust as it depends on several parameters among which the linkage criterion. Therefore, it is important to show that the results obtained with this technique are robust with respect to the choice of the linkage criterion. To this aim, we report in Supporting Information, Figure S5, the results found with different linkage criteria. It can be noted that in all the considered cases we obtained that the same set of nodes are always linked together at the first dendrogram leaf. Furthermore, we also checked the stability of the hierarchical clustering on the second DTI session acquired. The obtained dendrogram is reported in Supporting Information, Figure S4B. It can be noted that the structure of the dendrograms reported in Figure 4 and Supporting Information, Figure S4 is extremely similar.

To summarize, these results show that FC and DAC lead to different hierarchical architectures over the considered nodes: the FC hierarchical tree is dense, that is, all nodes are quickly connected with similar branching distances while the DAC hierarchical tree is more sparse; that is, many leaves are connected quickly and few leaves showed much higher branching distances. Now, to characterize more accurately such hierarchical architecture, we computed the clustering rate (CR) of very node (see Materials and Methods for details). In Figure 5, we report the scatterplot of the functional versus the anatomical CR for the considered nodes (DMN‐red; DAN‐green, VAN‐pink, SMN‐black, VIS‐blue, LAN‐orange, AUD‐cyan, CON‐brown, and FPN‐grey) along with their centroids (circles). To quantitatively identify nodes with anatomical CR statistically lower than the rest of the sample, we first computed the 5^th percentile of the distribution for the obtained CR values (Fig. 5 ‐ black dashed line). Values below this percentile are statistically smaller than the rest of the sample at a significance level = 0.05. Then, to rule out the hypothesis that the obtained values might be influenced by the limited sample size, we also performed a bootstrap procedure. This provided us the 5^th percentile based on 1000 samples (Fig. 5 ‐ red dashed line). In Figure 5A,B, we report the results obtained with the multiscale community detection and hierarchical clustering, respectively. Interestingly, the common nodes that both approaches revealed as significantly different from the rest of the sample (lower than the 5% percentile) are pCC, LmPFC, and SMA. While in both approaches these nodes show a low anatomical CR, the multiscale detection shows that pCC and LmPFC have high functional CR compared to the rest of the sample. This is in agreement with their reported centrality; see the simulation reported in Supporting Information, Figures S2C and S3A. Thus, these nodes are strongly functionally connected but such functional coupling is likely realized through a small number of direct anatomical connections. Other nodes show a high functional CR, see for example the visual nodes in Figure 5A without a corresponding low anatomical CR. This is an important control that suggests that for local networks, the supposed inverse relationship between functional and anatomical connections is not observed.

Figure 5.

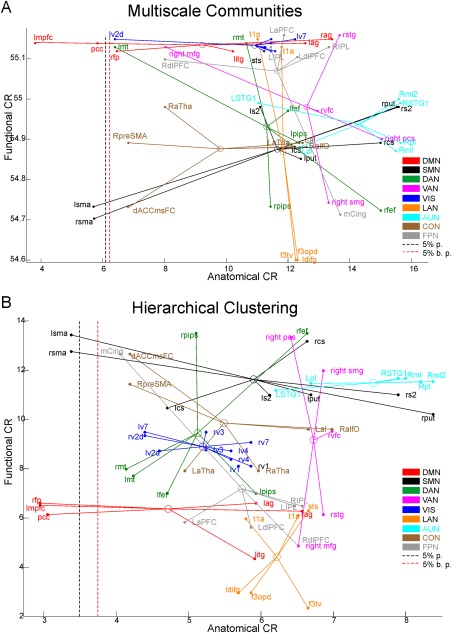
The anatomical versus functional rate of clustering (CR). Scatterplot of the functional versus anatomical CR obtained with multiscale community detection (A) and hierarchical (B) clustering for all nodes of the considered RSNs (DMN‐red; DAN‐green, VAN‐pink, SMN‐black, VIS‐blue, LAN‐orange, auditory‐cyan, control‐brown, and fronto‐parietal‐grey) along with their centroids (circles). The 5% percentile of the CR distribution (black dashed lined) and the bootstrapped 5% percentile (red dashed line) for the CR values are reported. Interestingly, both approaches revealed that only pCC, LmPFC, and SMA show statistically lower anatomical CR from the rest of the sample. [Color figure can be viewed at http://wileyonlinelibrary.com]

We note that the functional CR obtained with the two clustering procedures have some differences, for example, the multiscale community detection highlights high values for the DMN while the hierarchical clustering finds high values for the SMN. These differences might be due to the high density of functional connections that might lead during the clustering to slight different clusters. However, the Rand index (the minimum obtained is 0.71) when all steps are considered, shows that the two procedures are quite consistent.

The results in Figures 4 and 5 suggest that the centrality of pCC and SMA, typically reported as functional hubs [de Pasquale et al., 2012, 2016, 2013] is realized through a specific anatomical backbone connecting these nodes which is shown in Figure 6, where we report the estimated fiber tracts, averaged across subjects, starting from pCC (in red) and SMA (green) overlaid on the T1 MNI template. The emerging anatomical architecture consists of two main anatomical tracts: one mainly anterior–posterior in the direction pCC–mPFC with some lateral branches and one ventro‐dorsal linking SMA to the internal capsule and the cortical–spinal tract. This tract has been widely reported in the literature, see for example Greicius et al. [2009] and van den Heuvel et al. [2008]. Based on these observations, the centrality of these two nodes seems to be inversely related to the magnitude of their direct anatomical tracts. To investigate if these observations generalize to the other functional nodes considered in this study, we computed the correlation between the functional and anatomical CRs and the node functional centrality quantified through the weighted betweenness centrality (BC) of the considered nodes (see Materials and Methods for details; de Pasquale et al. [2016] and Sporns [2011]). In Figure 7A, we report the ranked BC where it can be noted that mCing scores the highest centrality followed by pCC and SMA. Interestingly, these nodes were involved in the anatomical backbone observed in Figure 4. This extends what we found in de Pasquale et al. [2013]: not only pCC and SMA show a high number of links (high degree) with the rest of the brain but also most these links act as bridges (high BC) in the communication with the rest of the brain.

Figure 6.

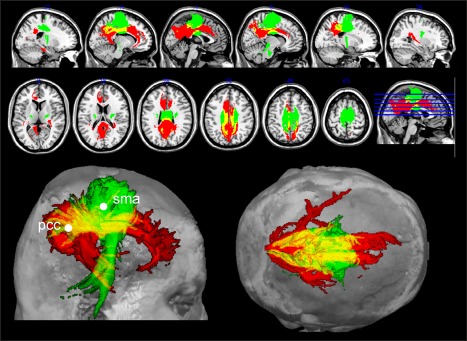
The anatomical backbone pCC‐SMA. Estimated fiber tracts starting from pCC (in red) and SMA (green) and their overlap (yellow). The anatomical architecture emerging from these results is that of two main anatomical tracts: one mainly anterior–posterior in the direction pCC–mPFC with some lateral branches and one ventral–dorsal linking SMA to the internal capsule and the cortical–spinal tract. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 7.

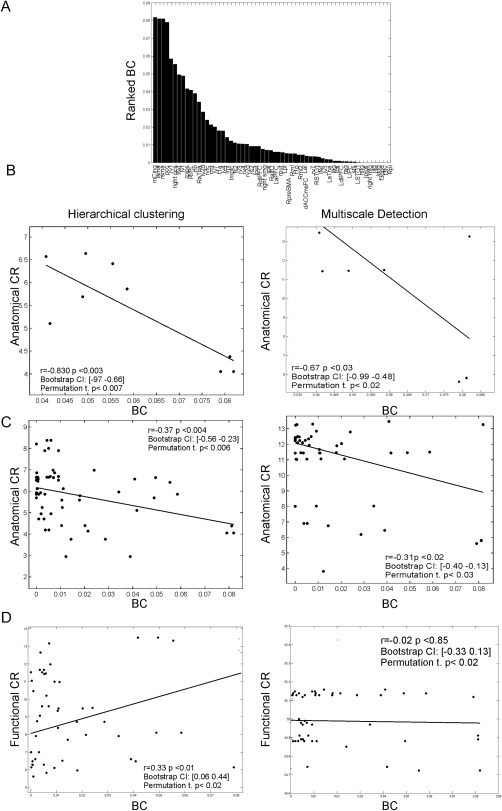
Functional centrality and anatomical CR are inversely related. (A) Ranked betweenness centrality of the considered nodes. pCC and SMA, after mCing (FPN), are the two most central hubs. In the next analyses, to address the statistical significance of the results, we reported in the plots the correlation values and their P values, the obtained bootstrap confidence intervals and the results from the permutation tests. (B) BC and anatomical CR for the first 10 most central nodes are strongly anticorrelated (r = −0.83) with hierarchical clustering (left) and (r = −0.67) with the multiscale community detection (right)). (C) The same analysis extended on the whole sample of nodes still shows an inverse relationship, although with a lower strength (r = −0.37) with hierarchical clustering (left) and (r = −0.31) with multiscale detection (right)). (D) No significant linear relationship between BC and the functional CR was obtained, see the bootstrap confidence intervals with hierarchical clustering (left) and with multiscale detection (right)). On the whole sample, BC and functional CR are not linearly related.

Now, to investigate the relationship between the anatomical CR and BC, we computed the correlation between these two variables for the first ten most central nodes (Fig.7B). The significance of the obtained results is addressed by computing the P value of the correlation coefficient by using the Fisher transformation and thus the asymptotic normality assumption. As the sample size is limited, for each estimated correlation value we also addressed its statistical significance by estimating bootstrap confidence intervals (1000 samples) and permutation tests. These results are shown in Figure 7. We considered as significant only correlation values passing all the three considered criteria (see the reported values in Fig. 7B–D). We obtained that these two measures are strongly anticorrelated both with hierarchical clustering (r = −0.83) and multiscale detection (r = −0.67). Thus, strong functional hubs seem to be characterized by a low anatomical CR. When the same analysis is extended on the whole sample of nodes (Fig. 7C), we obtained that this relationship is still statistically valid although at a lower strength (r = −0.37, with hierarchical clustering and r = −0.31 with multiscale detection). This is reasonable taking into account that in this analysis we also included nodes scoring a very low BC. Eventually, as a control we tested the relationship between BC and the Functional CR (Fig. 7D). Interestingly, no significant correlation between these measures was obtained in this case. In particular, while the multi scale detection shows a nonsignificant correlation between these two measures, the hierarchical clustering reports a positive correlation between these measures (r = 0.33). However, as the bootstrap confidence interval for this value identified a very small correlation value as still significant (r = 0.06 as 5% percentile), we cannot consider this estimate as significant. On the whole, sample BC and functional CR are not linearly related. These results suggest that what we observed for pCC and SMA seems to generalize to the other considered nodes: the higher the functional centrality of a node, the lower is the number of its direct anatomical connections. In general, the considered functional hubs tend to connect toward the end of both the anatomical hierarchical tree and multiscale detection.

DISCUSSION

Summary

In this work, we assumed a set of well‐known RSNs to behave as an integrated network [Tononi et al., 1998], where functional and anatomical connections link different regions hierarchically. We explored and compared such functional and anatomical hierarchical architectures in a specific set of nodes previously reported as belonging to nine main RSNs. Three main findings are presented in this work. First, we show, in general a consistent low similarity between anatomical and functional connectivity across subjects. The degree of similarity between anatomical and functional connectivity differed among the considered networks. In particular, we observed that networks typically reported as highly central, that is, networks more involved with the across‐network integration, such as the DMN, FPN, and SMN [de Pasquale et al., 2012, 2016, 2013], show an agreement between functional and anatomical connectivity lower than more segregated networks such as VAN and LAN. Second, the hierarchical architectures driven by the functional and anatomical data are very different. The functional architecture shows all nodes soon clustered together with hubs in DMN, FPN and SMN being involved from the early stages. Conversely, the anatomical clustering shows that these hubs, at the highest stage, are first connected to each other and then to the rest of the brain. Third, the centrality of the considered nodes is anticorrelated with the anatomical CR, that is, the more central is a node the slower it will cluster with other nodes through direct anatomical connections. This suggests different levels of anatomical integration of cortical hubs. They first exploit few strong and direct anatomical connections, often involving other central areas (see DMN and FPN regions). Then, with a lower strength they are anatomically linked with the other regions in the brain. This seems to represent an efficient strategy of integration where long‐range connections are first ensured through few direct tracts and then by many local links.

The Anatomical Backbone of Functional Hubs

In general, anatomical connections represent the biological infrastructure for neuronal communication [van den Heuvel and Sporns, 2013b]. This might suggest a simple relationship between anatomical and functional connections, see for example Skudlarski et al. [2008], reporting on a linear relationship between them and [Hagmann et al., 2008], showing evidence of a predictive value of the anatomy on the function. However, to compare these quantities, one must be aware of their different intrinsic nature and the methodological limitations involved with their estimation. Functional connectivity in fact, especially when estimated via cross‐correlation, reflects a statistically undirected association between node pairs showing a strong coupling in their BOLD time series. Such association is prone to transitivity and it can be realized through direct and indirect anatomical connections. This might lead to a propensity for “overconnection” and high clustering, see for example, van den Heuvel and Sporns [2013b]. On the other hand, structural connectivity obtained through probabilistic fiber tracking, provides the probability of two nodes being connected based on the number of tracts between them. Tracts passing through regions characterized by many small fibers branching and splitting might result, although to lesser extent than with deterministic approaches, penalized [Nucifora et al., 2007]. For this reason, a direct comparison between these two measures must be cautious. As matter of fact, the functional connectivity implies the anatomical connectivity, but the former cannot distinguish between direct (potentially monosynaptic) and indirect (potentially multisynaptic) tracts [Greicius et al., 2009]. Thus, indirect connections and interregional distance might account for some of the variance in functional connectivity that cannot be explained by structural connectivity [Honey et al., 2009]. In this complex scenario, it has been shown that the enhanced intrinsic excitability and synaptic efficacy might lead to increased FC even when the structural connectivity is diminished as it can be seen in pathological conditions such as epilepsy [Bai et al., 2011].

Our results show a low agreement between these two measures (Fig. 2) that is supported by the literature. As a matter of fact, it has been reported that the DAC alone accounts for only 15% of FC variance and that indirect connections play a strong role in shaping FC and the topographic organization of brain RSNs [Messe et al., 2014]. This supports the notion that network configurations often diverge from the underlying anatomical substrate [Honey et al., 2009; Misic et al., 2016; Ton et al., 2014; van den Heuvel and Sporns, 2013b]. When we investigated these aspects network by network, we obtained that VAN and LAN which are local systems [de Pasquale et al., 2010, 2012, 2016, 2013] with a peripheral FC likely realized by direct anatomical tracts exhibit a good agreement between FC and DAC. Conversely, for DMN, FPN, and SMN that play a central role in the RSN integration, we obtained a lower agreement between these measures (Fig. 2B). This supports the notion of a strong synchronization within regions belonging to highly central systems: one specialized for offline internal mentation (DMN), one for online sensory‐motor functions (SMN), and one acting as a flexible hub of cognitive control (FPN), see for example [Zanto and Gazzaley, 2013]. The integration between these systems is fundamental in the brain due to the role played by the involved networks. On one hand, the DMN has been shown to be preferentially active when individuals are engaged in offline, internally focused tasks, such as episodic memory retrieval, imagination of future events, and perspective taking [Buckner et al., 2008; Sestieri et al., 2011]. On the other hand, the mixed motor‐sensory network showing connectivity with the SMA appears to serve opposite functions, allowing the online exchange of information with the environment, both in terms of processing multiple sensory stimuli and programming/executing behavioral responses. Finally, the FPN has been reported as a control‐type network characterized by the ability to adapt to a wide variety of tasks by initiating and modulating cognitive control abilities [Zanto and Gazzaley, 2013]. Evidence of a continuous interaction between hubs comes also from electrophysiological in terms of a dynamic cortical core of interaction in the brain [de Pasquale et al., 2016]. In this study, a dynamic interchange of cortical hubs ensuring an overall communication in the brain was reported.

We believe that the discrepancy that we found in this work between the sparse‐anatomical and dense‐functional structure (see below) might support this functional efficiency. In fact, the integration is a complex mechanism composed of several levels of interactions occurring at distinct coupling strengths (see for example, de Pasquale et al. [2013]). Thus, to unravel this progression, we applied a multiscale community detection and hierarchical clustering on FC and DAC. We observed again important differences between the anatomical and functional results. Both the functional clustering and multiscale detection revealed a progression in which nodes are first clustered in the known RSNs and then converge to two macrosystems comprising DMN and SMN (Fig. 3). In this progression, functional hubs such as pCC and SMA are grouped to other nodes quickly, that is, at a low hierarchy (or scale). The progression obtained with the anatomical clustering seems opposite, that is, the functional hubs are linked late in the hierarchy to the rest of the brain. When this occurs, they are first linked together through nodes from FPN and CON, and then to the remaining nodes (Fig. 4). To quantify this observation, we computed the measure of rate of clustering (CR, described in Materials and Methods) which revealed that these functional hubs show a high functional CR and low anatomical CR, which is statistically lower than in the rest of the sample (Fig. 5). This suggests that their strong functional centrality is realized by few direct anatomical connections and possibly multiple indirect anatomical connections. There is no direct mapping of functional connections into anatomy but instead few specific connections allowing an efficient functional coupling. In particular, the axis consisting of the anterior posterior fasciculate represents a strong anatomical backbone between pCC and SMA (Fig. 6). This result is in line with previous studies where tracts between the PCC and the medial prefrontal have been demonstrated [Parvizi et al., 2006]. This axis pCC–SMA is also in agreement with what reported in van Oort et al. [2014] and Greicius et al. [2009], where they demonstrated that pCC/RSC (retrospenial cortex) exhibits direct projections with both mPFC and the medial temporal lobe corresponding to different entry points in the rostral and caudal part of pCC. Interestingly, in line with our results, in this work the authors were not able to find projections of pCC to L/R AG and only 17% of the subjects showed fibers connecting MTL to L/R AG. Thus, as in our study, within DMN, pCC remained apparently disconnected from L/R AG. Naturally, pCC is not really disconnected from L/R AG and we argue that this might be due to the difficulty of resolving crossing fibers in tractography analyses [Mori and Zhang, 2006]. As a matter of fact, such laterally running fibers might be extremely difficult to trace through the larger perpendicularly oriented fibers such as the anterior–posterior longitudinal fasciculus and the superior–inferior oriented corona radiata. This is further confirmed by additional DTI studies that identified the tract pCC–mPFC but failed to identify the lateral projections pCC–L/R AG [van den Heuvel et al., 2008, 2009).

These observations on pCC and SMA seem to extend to other nodes in our sample, that is, when we compared the functional centrality of all considered nodes and their anatomical CR. We obtained that in the first 10 most central functional hubs, identified by the betweenness centrality, these two measures are significantly anticorrelated with both multiscale detection and hierarchical clustering methods (r = −0.75 on average, see Fig. 7B) and this trend remains, at a lower strength (r = −0.34 on average, see Fig. 7C), also when considering all the nodes. This confirms that the more central is a node, the lower is the number of direct anatomical connections is involved with. As a control, no significant linear relationship was obtained between the centrality and the functional CR (Fig. 7D). This can be due to the fact that the functional centrality of a node is probably obtained indistinctly through both many and few specific connections.

These observations can be related to the rich club model reported in van den Heuvel and Sporns [2013a]. In the rich club model, it is observed that nodes showing a high degree (k) tends to be directly linked to each other. Thus, “rich” members join a “rich” club. Our findings share some common aspects with this model although with some important differences. First, the nodes involved with the rich club overlap nicely with the nodes that we find, for example, the DMN regions among which pCC. Furthermore, the idea that these hubs are strongly linked is in line with what we found. Nevertheless, a fundamental difference is highlighted with our approach. In van den Heuvel and Sporns [2013a], the rich club property is found for a given k. This corresponds in our approach to consider a given threshold of interaction and then to include only nodes showing at least k connections. In this way, we would lose the information on the progression of the interaction occurring at different scales. Such progression shows that the considered functional hubs link to each other at a relatively low k, that is, when they show few anatomical connections. At that scale, they are not particularly “rich” in anatomical connections. Then, when we consider higher scales in the progression, toward the end of the dendrogram in Figure 4, we observe their final integration with the rest of the brain. At this stage, they become finally very “rich” in anatomical connections. Thus, we seem to disentangle, across different scales, the interaction among hubs, and their property of being central. This is the main difference with the work of van den Heuvel and Sporns [2013a] where these two characteristics are observed “simultaneously,” that is, when they have many connections are directly linked to each other. Here, instead by looking at the progression of interactions we separated the link across hubs, occurring when these have very few and strong connections (low k) with the final integration with the rest of the brain characterized by many weaker connections (high k).

We speculate that the observed strong anticorrelation between functional centrality and anatomical CR suggests that the functional connectivity somehow shapes the anatomy by selecting, among all the available ones, few specific anatomical highways. This pruning of anatomical connections likely favors those ones linking functional cores such as pCC and SMA (Figs. 4 and 6). In general, this might represent an efficient strategy to reach all nodes in the brain: few direct anatomical links connect functional cores which then distribute locally the information by means of small and intricate tracts. This interpretation is supported by the fact that connections are energetically expensive to both maintain and use [Attwell and Laughlin, 2001; Bassett et al., 2010; Chen et al., 2006], thus favoring short and sparse over long and dense links. However, few long connections might be allowed to transmit information between distant regions more efficiently, as is needed during task performance [Hermundstad et al., 2013]. This architecture might represent the anatomical substrate of a distributed neural system as a basis for a “global workspace,” a core system in which segregated functional communities interact [Dehaene et al., 1998; Dehaene and Naccache, 2001]. This efficient anatomical architecture might be explained by known and reported mechanisms observed in the course of development and evolution where the modulation of synaptic activity induces long‐term structural modifications to neural morphology [Sporns et al., 2000].

We hypothesize that in this complex scenario, an important role is played by the dynamics of functional connectivity recently observed in fMRI and other electrophysiological techniques [de Pasquale et al., 2012; Hutchison et al., 2013]. As matter of fact, the nonstationarity of FC might impact Hebbian fire‐wire mechanisms [Caporale and Dan, 2008; Lowel and Singer, 1992]. Functional hubs are continuously exchanging information to ensure an efficient communication within the brain. On the other hand, connections with local (noncentral) nodes are more nonstationary, that is, hubs continuously connect and disconnect from peripheral nodes. For this reason, being the within‐hubs connections more used over time than the rest, it is conceivable that this continuous recruitment might lead to shaping strong direct fibers between these regions of the brain. On the other hand, for the more fluctuating connections the instability does not allow to build such strong anatomical connections. Such instability may allow the brain to be versatile and to quickly reorganize to the environment demands. These observations could be interpreted in the light of the recent results of Gu et al. [2015] reporting that functional hubs provide a structural substrate for the movement of the brain between cognitive processes. Their results show that hub nodes in the brain tend to have high average controllability, indicating that they are critical for moving the brain into many easily reachable states, thereby facilitating a great diversity of functional dynamics. We acknowledge that in this work, the nonstationarity of functional connections was not investigated directly and thus these considerations are speculative. However, to address the impact of the dynamics on the connectivity will represent a future development of this work. We elaborate more on this aspect in the next section.

LIMITATIONS OF THE PROPOSED APPROACH

In this work, we assumed some prior information about the formation of 9 RSNs and the centrality of functional nodes such as the pCC and SMA. The adopted parcellation, although coarser than other reported schemes, still covers the same networks typically reported in the resting‐state literature and thus our results can be compared with previous work. These assumptions are based on a previous work, where in the same sample of subjects, we identified two main functional cores centered on pCC and SMA which linked to two main large systems: one consistent with the default mode network (DMN) gradually connecting to visual regions and the other centered on motor regions gradually connecting to more sensory‐specific portions of cortex [de Pasquale et al., 2013]. In this work, the centrality of these nodes, which in de Pasquale et al. [2013] was obtained in terms of amount of links (degree based measure), was confirmed in terms of betweenness centrality (Fig. 7A). As matter of fact pCC and SMA scored the second and third positions in ranked BC suggesting that these nodes are not only characterized by a high number of functional links (high degree), but these links behave as functional bridges between distinct functional modules. This aspect is particularly important as it has been reported that degree based measures of centrality may be prone to an inflation effect due to the an increased community size, see Power et al. [2011, 2013]. Only a local integration role was assigned to the DMN and SMN in these works. However, as our definition of centrality is based on BC, this measure is less sensitive to such inflation effects and thus our results are in line with the several structural and functional hub locations reported, see Bullmore and Sporns [2012] and Hagmann et al. [2008] typically located in medial (pCC) and lateral (angular gyrus) parietal regions of the default mode network, and in anterior cingulate and anterior insula, part of the cingulo‐opercular (CO), and lateral frontal and parietal cortex, part of the fronto‐parietal control networks [Buckner et al., 2009; de Pasquale et al., 2012, 2013; Cole et al., 2010; Tomasi and Volkow, 2011].

However, it must be acknowledged that the adopted number of nodes limits the generalizability of our results. We stress that, based on the limited number of nodes considered, we cannot draw general conclusions on the whole brain but we limit to state our findings on the selected set of functional nodes and networks. We acknowledge that the number of nodes is still far from hundreds, as for example in Power et al. [2011], but the aim of the work is to investigate these aspects on networks more consistently reported in the fMRI literature. It is not unusual in the literature, when considering the functional labeling of nodes, to include few tens of centroids of the obtained networks, see for example, Yeo et al. [2011], where a stability analyses on the clustering of thousands of nodes provides 7 (or 17 at finer scale) functional systems. Our selection highly relates to these systems and many other centroids published consistently in the literature from different imaging modalities works [Baldassarre et al., 2012; de Pasquale et al., 2012, 2016, 2013; Dosenbach et al., 2007; Hacker et al., 2013; He et al., 2007). Furthermore, please note that dense parcellation schemes will include many neighboring voxels that we expect certainly to inflate degree‐based measures of centrality but not the betweenness centrality that we adopted in this work.

A further limitation of our approach regards the comparison of anatomical and functional connectivity without the adoption of intermediate generative models. As a matter of fact the adoption of a generative model and dynamics could be used to investigate these aspects, such as Messe et al. [2014] and Sporns et al. [2000]. However, to reduce the complexity of the dynamic systems involved, strong assumptions on the adopted parameters are required and this might oversimplify the mechanism investigated. For this reason, some literature (see for example, Betzel et al. [2014], Greicius et al. [2009], Hermundstad et al. [2013], Horn et al. [2014], Khalsa et al. [2014], van den Heuvel et al. [2008, 2009], van Oort et al. [2014], Wang et al. [2013], and Xue et al. [2015]) address these issues without the adoption of a generative model.

Furthermore, the temporal dynamics of brain activity might strongly influence the relationship between functional and anatomical connectivity. It must be noted though that fMRI signals—due to the inevitable hemodynamic filtering—cannot be related to the dynamics of brain activity that occurs a time scale much higher than the final fMRI frequency content. In fact, when these aspects are investigated with electrophysiological techniques, as in our prior MEG work, the evidence is that at a fast scale these fluctuations arise in the order of hundreds of milliseconds [Baker et al., 2014] and at low temporal scales (MEG–BLP for example) these occur in the order of few seconds [Brookes et al., 2014; de Pasquale et al., 2012]. Interestingly, functional hubs observed when the temporal dynamics is taken into account, such as PCC nicely agree with the ones observed in electrophysiological works and in a new fMRI approach to reveal transient functional modes [Smith et al., 2012]. In this last work, it has been shown how the centrality of PCC observed using stationary approaches can be interpreted as the results of the average of different fast dynamic transitions. Similarly, in this paper we focused on the stationary connectivity observed with fMRI, interpreting our findings as the average result of fast dynamic fluctuations more robustly occurring over time.

Eventually, an emerging literature proposes unified approaches for characterizing multiscale brain networks where functional, anatomical and in general multimodal data can be integrated, see for example [Betzel and Bassett, 2016] for a recent review. Our proposed approach and the obtained findings could be, as a future development, included in this unified framework of analyses.

In terms of validating previous assumptions on the centrality of the adopted nodes, the results reported in Figure 3 show that some of the assumed hubs could be actually obtained from the different hierarchical scales. In fact, although no prior information was input to the clustering, Figure 3 shows that the progression of the obtained clusters, in both the hierarchical clustering and multiscale detection (Fig. 3A,E), shows at an intermediate stage the formation of some of the initially assumed RSNs. Moreover, at the higher threshold, corresponding to a high level of integration, these RSNs collapse in one network involving DMN and SMN. Such topography—together with the hubness patterns—validates the evidence of two macrosystems linked through pCC and SMA reported in de Pasquale et al. [2013]. This model is in agreement with a vast fMRI literature where these cortical functional hubs serve as way stations for network integration, although different approaches for the analysis of the fMRI spontaneous activity were applied. Interestingly, the same nodes were found to be hubs also by methods analyzing the rhythmical ongoing activity [Bullmore and Sporns, 2012; Buckner et al., 2009; Cole et al., 2010; de Pasquale et al., 2012, 2016, 2013; Hagmann et al., 2008; Shirer et al., 2012; Tomasi and Volkow, 2011; Zalesky et al., 2014].

Supporting information

Supporting Information Figure 1.

Supporting Information Figure 2.

Supporting Information Figure 3.

Supporting Information Figure 4.

Supporting Information Figure 5.

Supporting Information