Depth‐dependence of visual signals in the human superior colliculus at 9.4 T

Abstract

The superior colliculus (SC) is a layered structure located in the midbrain. We exploited the improved spatial resolution and BOLD signal strength available at 9.4 T to investigate the depth profile of visual BOLD responses in the human SC based on distortion‐corrected EPI data with a 1 mm isotropic resolution. We used high resolution (350 µm in‐plane) anatomical images to determine regions‐of‐interest of the SC and applied a semi‐automated method to segment it into superficial, intermediate, and deep zones. A greater than linear increase in sensitivity of the functional signal at 9.4 T allowed us to detect a statistically significant depth pattern in a group analysis with a 20 min stimulation paradigm. Descriptive data showed consistent depth profiles also in single individuals. The highest signals were localized to the superficial layers of the right and left SC during contralateral stimulation, which was in good agreement with its functional architecture known from non‐human primates. This study thus demonstrates the potential of 9.4 T MRI for functional neuroimaging even in deeply located, particularly challenging brain structures such as the SC. Hum Brain Mapp 38:574–587, 2017. © 2016 Wiley Periodicals, Inc.

Abbreviations

FA

Flip angle

fMRI

Functional magnetic resonance imaging

HRF

Hemodynamic response function

PSF

Point‐spread function

SC

Superior colliculus

SNR

Signal‐to‐noise ratio

TA

Acquisition time

TE

Echo time

INTRODUCTION

A large number of electrophysiological and lesion studies in non‐human primates demonstrated the involvement of the superior colliculus (SC) in saccadic eye movements, fixations, and attentional shifts [May, 2006; Sparks, 2002]. The SC is composed of 7 layers with the superficial layers mainly processing visual information conveyed by afferents from the retina, visual cortex, and the frontal eye fields. The intermediate layers contain neurons mostly involved in oculomotor control, and the deep layers contain multisensory and visuomotor neurons. Neural activation in these layers is associated with eye and head movements.

Although we can expect a similar neural architecture of the macaque and the human SC, many functional features that are currently known from the macaque SC have never been examined in humans. Differences in the anatomy, afferents, and efferents between other mammalian species question a complete congruence of macaque and human SC [May, 2006]. Functional magnetic resonance imaging (fMRI) studies at 3 T demonstrated reliable blood‐oxygen‐level dependent (BOLD) activation in the human SC after visual stimulation [Katyal et al., 2010; Linzenbold et al., 2011; Schneider and Kastner, 2009; Sylvester et al., 2007; Wall et al., 2009; Zhang et al., 2015] and oculomotor control [Krebs et al., 2010a,2010b; Linzenbold et al., 2011]. Specific functional properties of the SC investigated with fMRI include a preference for temporal versus nasal stimulation [Sylvester et al., 2007], shifts and allocation of attention [Katyal and Ress, 2014; Katyal et al., 2010; Schneider and Kastner, 2009], and execution of upper limb movements [Himmelbach et al., 2013; Linzenbold and Himmelbach, 2012]. However, only few of these studies provided a sufficient spatial resolution of functional data acquisition and analysis to investigate the functional depth anatomy of the SC [Katyal et al., 2010; Katyal and Ress, 2014; Linzenbold and Himmelbach, 2012; Zhang et al., 2015]. Particularly these studies were burdened with rather long fMRI data acquisition times of at least 50 minutes for rather simple designs. In some cases, even longer data acquisition times required multiple measurement days and most of these studies therefore examined only small groups of ≤ 5 participants. Apparently, the available techniques at conventional field strengths of 1.5 to 3 T are falling short of spatial resolution and sensitivity that would be necessary to examine human brainstem systems with their small nuclei and subregions with high structural accuracy and functional detail in representative groups of human participants with acceptable data acquisition durations.

These limitations can be addressed by the use of higher field strengths. Up to date, several studies investigated the signal‐to‐noise ratio (SNR) gain at 7 T compared to lower field strengths. Vaughan and colleagues reported the SNR to be at least 1.6 times higher in 7 T relative to 4 T MRI [Vaughan et al., 2001]. Novak et al. [2001] reported early anatomical scans of the human brainstem at 8T with a slice thickness of 2 mm and a then unprecedented in‐plane resolution of up to 195 μm in an in‐vivo measurement. Plantinga et al. [2014] provided an overview of anatomical studies at field strengths ≥ 7 T focusing at the basal ganglia. Consistently across multiple studies they reported considerable increases in sensitivity, SNR, and CNR. Triantafyllou et al. [2005] confirmed the benefit of using 7 T and above field strengths in high resolution experiments, showing a more than linear SNR increase from 1.5 to 7 T for time‐course data. Functional MRI at 7 T systems reported significantly higher functional sensitivity in terms of percent signal change, mean t‐values, number of suprathreshold voxels and contrast to noise ratio [Beisteiner et al., 2011; Zwaag et al., 2009]. More recently, Pohmann et al. [2016] compared for the first time SNR differences in 3, 7 and 9.4 T and reported a supralinear increase of the SNR with the magnetic field strength B₀ (SNR ∼ ${\mathrm{B}}_0^{1.65}$), emphasizing the advantages of using 7 T and above fields for studying small regions in the brain. This gain in sensitivity beyond a linear increase is due to changes in the effective transverse relaxivity [Duyn, 2012] resulting in a boost of BOLD signal change by a factor of about 7 at 9.4 T compared to 3 T. Enhanced SNR at 9.4 T can be traded for an increase in image resolution (e.g. resolution of up to 0.8 × 0.8 × 1 mm³ for functional scans and of 0.2 × 0.2 × 0.5 mm³ for anatomical scans have been demonstrated [Budde et al., 2014; Budde et al., 2014; Ehses et al., 2015]) and/or for a decrease of the number of blocks/events required for the detection of activations. Obviously, functional studies of small anatomical structures and subunits like cortical layers or thalamus and brainstem nuclei could benefit from the use of higher field strengths than 3 T.

However, the increase of the BOLD signal amplitude is associated with specific challenges at ≥ 7 T imaging. A major concern in fMRI at high fields are geometric distortions which increase linearly with field strength (and echo spacing), but also signal voids and blurring associated with EPI acquisitions. These inherent problems of high‐field imaging could turn out to be particularly detrimental for brainstem imaging. To address these problems, different methods have been proposed for conventional field strengths used for clinical applications: the use of B₀ field maps [Jezzard and Balaban, 1995; Reber et al., 1998] or multi‐reference scan methods which correct the distortions arising from different off‐resonance factors [Chen and Wyrwicz, 2001; Wan et al., 1997]. More recent approaches to deal with distortions at high‐field include the point‐spread function (PSF) mapping method [Chung et al., 2011; In and Speck, 2012; In et al., 2015a,b]. The PSF represents the deviation of an image function to the true image function which can be employed for EPI distortion correction [Zeng and Constable, 2002]. In this case a geometrical correction is performed which minimizes the point spread function of the images and will therefore compensate for the EPI distortions correcting the images to their real anatomy. However, there are still some limitations associated with the PSF mapping method, which is applied in 2D and does not specifically account for susceptibility gradients across the imaging plane. In order to accurately determine the shift maps, it is critical to include all relevant voxels, i.e. those voxels that shall be corrected and later be included in the analysis, in the tissue mask used for estimation of the required PSF corrections. In future studies, further improvements could also be achieved from PSF‐corrections based on bi‐polar phase‐encoding schemes [In et al., 2015b]. The PSF correction method has been further optimized particularly for high‐field studies [Zaitsev et al., 2004]. It can improve fMRI data analysis since smaller geometrical differences of the EPI and the anatomical image will result in better co‐registration between the two images. Another major concern at higher fields would be the depth of penetration of the RF which is a particular concern for subcortical structures. However, as described in [Pohmann et al., 2016] the coil used in our study is optimized for the circularly polarized (CP) mode, which will best penetrate the brainstem, eliminating this concern.

As stated above, recent reports of functional signal detection in the primary motor cortex [Budde, Shajan and Zaitsev et al., 2014; Ehses et al., 2015] demonstrated that fMRI at 9.4 T is feasible in humans and has the potential to reach unprecedented temporal and spatial resolutions [Ehses et al., 2015]. In the current study, we aimed to extend these findings with respect to three issues: (1) to demonstrate the feasibility of high‐resolution fMRI in a challenging anatomical structure at 9.4 T; (2) to investigate the effect of a PSF correction on the co‐registration of functional and anatomical data at 9.4 T; and (3) to provide evidence for a functional mapping of visual responses in the human SC in a group of participants that is spatially consistent with the functional maps in macaques. To this end, we implemented a paradigm that was used at 3 T to map visual signals of the SC [Linzenbold et al., 2011].

MATERIALS AND METHODS

Participants

Twelve healthy volunteers with normal or corrected‐to‐normal visual acuity and a mean age of 27 years (range 21 ‐ 34 years; 3 females) participated in this study. In accordance with local research ethics policies and procedures, the volunteers underwent a physical and psychological check‐up by a local physician and provided written informed consent. All investigations were conducted in agreement with the Declaration of Helsinki in its most recent version [World Medical Association, 2013]. Two male participants were excluded because they fell asleep during the measurements, evident from the behavioral results and confirmed upon inquiry after scanning. One female participant moved more than 5 mm during the measurement and was also excluded from the analysis. Thus, data obtained from nine participants (mean age: 28, range: 21–34 years; two females) were used in the final analysis.

Data Acquisition and Imaging Protocol

All measurements were conducted on a 9.4 T whole‐body MRI scanner (Siemens, Erlangen, Germany), using an in‐house‐built head‐coil with a 16‐element dual row transmit array and a 31‐element receive array [Shajan et al., 2014]. As a reference, whole‐brain anatomical images were acquired for each subject using an MP2RAGE [Marques et al., 2010] and a 2D multi‐slice FLASH with the following sequence parameters: MP2RAGE: 0.8 mm isotropic resolution, matrix = 256 × 256 × 192, repetition time (TR) = 6 ms, flip angle (FA) 1 = 4°, FA2 = 6°, inversion TR = 9 s, TI1= 850 ms, TI2 = 3500 ms, acquisition time (TA) = 9 min 11 s, echo time (TE) = 2.3 ms; FLASH: 0.35 × 0.35 × 1 mm³ resolution, matrix = 512 × 512, 15 slices, TE = 21 ms, TR = 500 ms, TA = 1 min 35 s. The functional data were acquired with a 1 mm³ isotropic resolution using a 2D gradient echo EPI: matrix = 256 × 256, with 0.25 mm gap between slices (the excitation pulse covered 1 mm and a gap between slices of 0.25 mm was employed to avoid cross‐talk between slices); TE = 21 ms; TR = 1 s; nominal FA = 53°; bandwidth = 1254 Hz with PSF correction [In and Speck, 2012], a GRAPPA [Griswold et al., 2002] acceleration factor of 4, and partial Fourier of 6/8. Each functional acquisition comprised between 9 and 12 slices (individually adjusted due to specific absorption rate limitations at high‐field). The functional data were acquired with the same inclination and with the same slice center as the 2D FLASH sequence, i.e., perpendicular to the crown of the SC (Fig. 1A). Two functional runs, each consisting of 600 volumes and lasting 10 min were obtained for each subject. For each run, data acquisitions were reconstructed twice resulting in two datasets: one without PSF based distortion correction and a second one with PSF correction.

Figure 1.

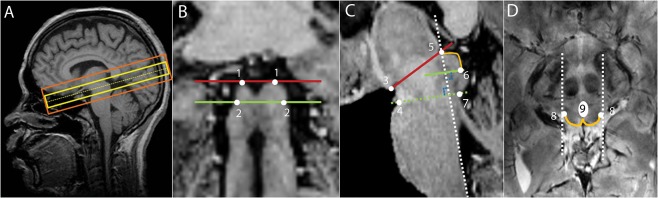
(A) Slice positions of the functional EPI sequence (yellow) and of the anatomical high resolution 2D FLASH sequence (orange) projected on the MP2RAGE image acquired from the same subject; (B) Coronal view of the MP2RAGE sequence, identification of the inferior (green) and superior (red) borders of the SC. (1) most superior edges of the SC; (2) edges that define the boundary between the inferior colliculus and the SC; (C) Sagittal view of the MP2RAGE sequence on which the superior SC border is identified by the line that connects the mammillary body (3) to the superior edge of the quadrigeminal plate (5), the anterior border by the neuroaxis (dashed white line), the inferior border by a line that starts at the inferior edge of the SC (6) and is parallel to the line that connects the superior pontine notch (4) to the inferior edge of the quadrigeminal (7), and the posterior border being defined by the CSF (orange line); (D) Transversal view where (8) refers to the lateral edges of the SC. The posterior boundary is delineated by the orange line and the anterior boundary is delineated by drawing a horizontal line that crosses the posterior bottom part of the periaqueductal gray, taking into account the periaqueductal gray boundaries (9). Finally, the posterior boundaries of both colliculi are delineated by connecting the commissure of the SC to the horizontal line. [Color figure can be viewed at http://wileyonlinelibrary.com.]

Effect of the PSF Correction on the fMRI Data

To directly examine the influence of the PSF correction in the 9.4 T EPI images and its advantages for the analysis, we replicated the acquisition protocol in a phantom comprised of water in an acrylic plastic container with different test grids (Fig. 2). The phantom was placed vertically in the same head coil used for the fMRI measurements, and sagittal slices of the same EPI sequence (with and without PSF correction) were acquired (sequence as described in the Data Acquisition and Imaging Protocol section). In Figure 2A,B sagittal images of the phantom without and with PSF correction, respectively, are shown. In Figure 2C,D, zooms on a 1 mm spaced grid are shown, and in Figure 2E,F the corresponding intensity profiles across this grid are shown. After PSF correction, the distortions are substantially reduced, and the structures inside the acrylic glass phantom are better matched in the EPI images. Furthermore, the intensity variations across the grids are considerably improved due to diminished blurring, enabling us to distinguish details that would not be recognizable otherwise. We also compared the uncorrected and corrected EPI images with the high resolution anatomical images and explored the quality of the coregistration (Fig. 3). As illustrated in Figure 3, PSF correction removed blurring from the EPI images recovering anatomical detail and thereby improving the correspondence between the EPI and the anatomical images. In order to quantify and understand this improvement, we evaluated the shift maps obtained online from the PSF prescan, that quantify the effective voxel dislocation along the phase encode direction. The average and standard deviation of the shift values were evaluated in a SC region‐of‐interest (defined as described below: Region of Interest Analysis). The average shift across subjects was 2.054 mm with a standard deviation of 0.062 mm. These values are in accordance with the visually observed misalignment of the non‐corrected EPI images in comparison with the PSF corrected images. In Figure 3B,E,H this misalignment is highlighted by the blue crosshairs, which show that the edge of the SC in the 2D FLASH corresponds to the edge of the SC in the PSF corrected scans but not in the non‐PSF corrected scans. It is interesting to note that PSF (being an in‐plane correction method) also improves the images in through‐plane direction (Fig. 3C,F,I). These comparisons of the data with and without PSF correction strongly argue for PSF‐correction of EPI images acquired at 9.4 T. Consequently, PSF‐corrected images were used in all following analyses.

Figure 2.

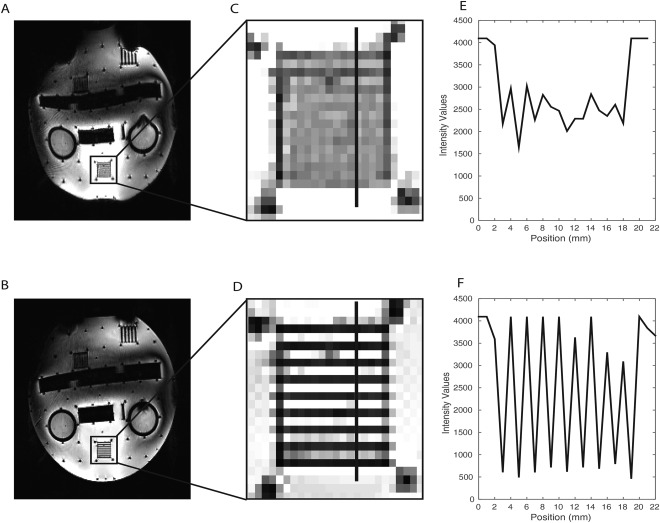
Comparison of the PSF uncorrected and corrected EPI images of a test phantom. A, B: full slice of the uncorrected (A) and PSF corrected (B) EPI image of the phantom respectively; C, D: zooms in the 1 mm spaced grid of the phantom in the uncorrected and PSF corrected images respectively; E, F: Intensity profiles of the 1 mm spaced grid for the uncorrected and PSF corrected images respectively (the position of the profiles are indicated in C and D as a black line perpendicular to the grid orientation).

Figure 3.

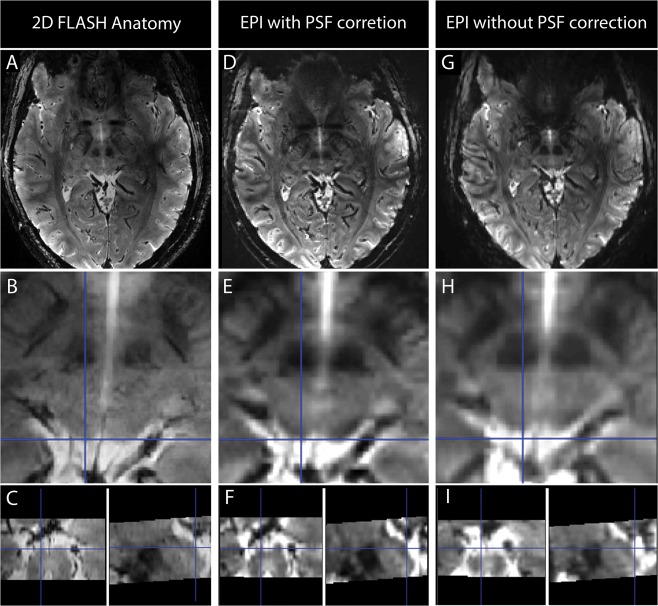
Comparison of the 2D FLASH high resolution anatomical images (A–C) with the EPI scans with PSF correction (D–F) and with the EPI scans without PSF correction (G–I). Both sets of EPI datasets were co‐registered to the 2D FLASH image. In the first row of images spatially congruent slices from the FLASH and EPI acquisition are presented; in the second row a zoomed image of the same slice for the three different datasets is presented and in the third row the sagittal and coronal views of the zoomed images for each dataset are presented. The blue cross‐hair is positioned at the edge of the left superior colliculus and it is concordant in the PSF corrected images and in the 2D FLASH image but not in the images without PSF correction (in which the same point corresponds to CSF). [Color figure can be viewed at http://wileyonlinelibrary.com.]

Stimuli and Design

Visual stimuli were projected on a screen mounted behind the subject. The participants viewed the screen through a mirror placed inside the head coil. A semicircular checkerboard pattern was presented with its medial edge on the fixation position in the central visual field. It extended 7.5° visual angle into either the right or the left hemispace. The checkerboards reversed their contrasts with a frequency of 8 Hz and right and left checkerboards were shown alternating in a block design, interleaved with fixation baseline periods. The duration of each experimental block (either stimulation or baseline periods) was 15 s. The subjects were asked to fixate a red cross in the middle of the screen. To verify the compliance of the participants with the fixation instruction, the red cross randomly changed its color to blue (not more than 5 times per run with a minimum interval of 1 min), and the participants were instructed to press a button every time a color change to blue occurred. The presentation of visual stimuli and the recording of button presses were implemented in Presentation Software (17.0, NeurobehavioralSystems 2014). The percentages of hits and misses were calculated offline for each subject to verify that their fixation was stable and that they were awake and alert throughout the measurement.

GLM Analysis

Image analysis on the single subject level was performed using SPM8 (Wellcome Trust Center for Neuroimaging, London, UK). Preprocessing included motion correction and coregistration of the PSF‐corrected EPI images with the high‐resolution anatomical images. No smoothing was applied to the functional data. For the subject‐level GLM analysis the hemodynamic response function (HRF) implemented in SPM8 was modified using a delay of the response peak relative to the signal onset of 4 s in agreement with a report of shorter HRF peak delays for the human SC [Wall et al., 2009]. Low‐frequency drifts were removed using a high‐pass filter with a cutoff period of 128 s and temporal autocorrelation was accounted for by a first‐order autoregressive plus white noise process as implemented in SPM8. For each subject we created a design matrix comprising two experimental regressors, namely checkerboard left and checkerboard right. Linear contrasts were applied to the beta estimates of the experimental regressors to specify experimental effects of checkerboard stimulation left, checkerboard stimulation right, and of both conditions combined across two sessions. Single subject contrast images were then used for the region of interest group analysis as described below.

Region of Interest Analysis

To detect depth‐dependent signal changes, we delineated depth regions of interest within the SC of each participant. Based on the high resolution FLASH anatomical images, ROIs of the entire SC were drawn manually for each subject in ITKsnap [Yushkevich et al., 2006]. The ROIs were drawn consistently across subjects considering specific anatomical landmarks [Nigro et al., 2014; Oba et al., 2005]. The superior border of the SC was identified by the line that connects the mammillary body to the superior edge of the quadrigeminal. The anterior border was marked by the neuroaxis while taking into account the boundaries of the periaqueductal gray. The inferior border of the SC was defined by a line that starts at the inferior edge of the SC and is parallel to the line that connects the superior pontine notch to the inferior edge of the quadrigeminal. The posterior boundary was defined by the CSF. SC boundaries are shown on coronal, sagittal, and transversal planes of the MP2RAGE contrast image, which had been co‐registered to the high‐resolution 2D FLASH image, in Figure 1B–D. Please note that the ROIs were determined based on anatomical landmarks, independently from the results of the functional analysis.

After manual delineation of the full SC mask (Fig. 4B), we shifted the individual SC ROIs perpendicular to the SC surface, along the orientation of the anatomical and functional scan prescription (cf. Fig. 1A) to generate masks for different depths relative to the surface of the SC. We shifted the masks by 1 and 2 mm in the anterior‐ventral direction to define superficial and intermediate zones, SZ and IZ, and 5 mm in the posterior‐dorsal direction to generate a CSF mask. We then generated depth ROIS by subtracting consecutive, shifted masks from each other (e.g., the SZ zone was generated by subtracting the mask shifted 1 mm in anterior‐ventral direction from the original full SC mask). These depth ROIs were subsequently used for the fMRI analyses, dividing the SC into three zones stretching from the surface to the interior of the structure (Fig. 4C): the superficial zone (SZ, 0‐1 mm from the posterior surface of the SC), the intermediate zone (IZ, 1‐2 mm from the posterior surface of the SC), and the deep zone (DZ). The first two 1 mm zones (SZ and IZ) were created first and the DZ was then defined by subtraction of the SZ and IZ ROIs from the full SC ROI. Thus, the DZ represented the remaining part of the SC that was neither part of the SZ nor the IZ as shown in Figure 4C. These three ROIs were created to correspond to the anatomical layers of the SC [Naidich et al., 2009] (superficial layer, intermediate layer and deep layer). Additionally to the three depth zones in the SC, we also included a ROI that resulted from the subtraction of the original SC ROI from a mask created by shifting the original ROI in the posterior direction along image orientation by 5 mm, thus including CSF, vascular and connective tissue.

Figure 4.

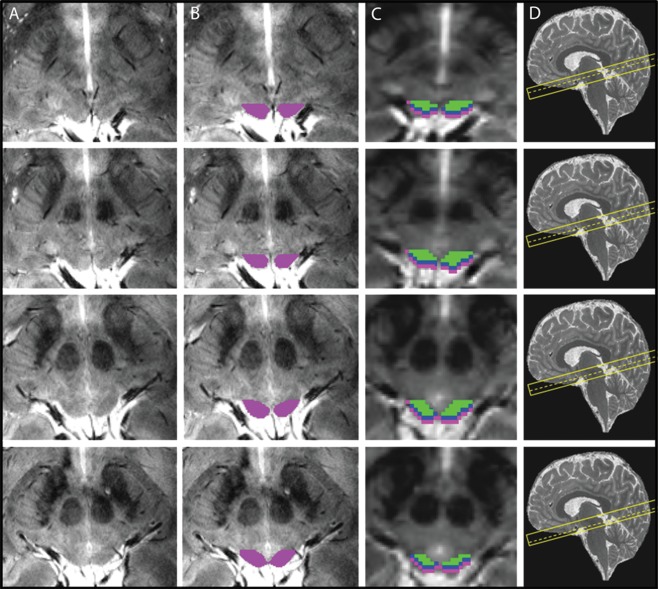
Region‐of‐interest definitions in one participant across five slices. (A) Plain slices of the high resolution 2D FLASH sequence through the SC. (B) ROIs based on the boundaries described in Figure 1 and drawn on each slice overlaid on the high resolution anatomical scans. (C) zones of the SC overlaid on the functional EPI scan, after downsampling the ROIs to match the EPI voxel size. cyan: superficial zone, blue: intermediate zone, green: deep zone. D: slice localization of each image (dashed line) shown on a sagittal MP2RAGE image from the same subject. [Color figure can be viewed at http://wileyonlinelibrary.com.]

Following the definition of depth ROIs we calculated the mean of the beta estimates, calculated in the single subject GLM analysis, across all voxels for each ROI of a participant. These individual mean values were then analyzed in a 2 × 2 × 4 repeated‐measures ANOVA with hemisphere (left vs. right SC), stimulation side of the checkerboard (left vs. right stimulation), and activation depth zone (CSF, SZ, IZ, and DZ) as within‐subject factors, using IBM® SPSS® Statistics 23.0. Significant main effects and interactions were followed up with additional repeated measures ANOVAs and paired t‐tests depending on the results of the preceding analyses. The significance level was set to P < 0.05 (Greenhouse‐Geisser corrected in case of non‐sphericity) for each statistical analysis and Bonferroni‐corrected for multiple comparisons if necessary.

RESULTS

Behavioral Results

We analyzed the button presses for the detection task at the central fixation position to check whether the participants executed their tasks correctly and held their gaze stable at the fixation cross. As already mentioned above, two male participants did not stay alert and pressed the button correctly for only 55.6% and 60.4% of the color changes across the two measurements, respectively. Upon inquiry after the measurement, they reported that they had fallen asleep. Another participant was excluded because motion correction algorithms showed that she moved more than 5 mm during the measurement. Eight of the remaining participants responded to 97% of the color changes and one participant responded to 87% of the trials across both measurement runs. These behavioral data indicate that the subjects successfully fixated the central position and that they were awake and attentive throughout the measurements.

Signal Detection in the SC in Individual Subjects

Figure 5 shows the activation maps of each subject using two different contrasts: checkerboard left versus baseline (red), and checkerboard right versus baseline (yellow). In single subject fixed‐effects analyses we found significant activations in the SC in eight of nine subjects with a small volume corrected P < 0.05 at the voxel‐level. For subject 2 there were no suprathreshold signals even at an uncorrected threshold of P < 0.001. This result was probably due to the fact that there was an incomplete coverage of the SC in this participant that we discovered post‐hoc. The scan prescription did not cover the most rostral part of the SC.

Figure 5.

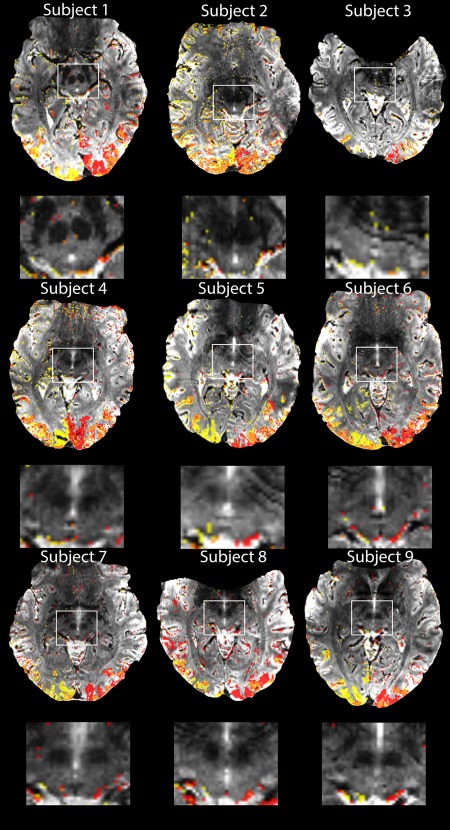
Activation maps obtained in each subject for 20 min functional measurement of hemifield activation, thresholded at p < 0.001 (uncorrected) for illustrative purposes and the corresponding zoomed images of the SC for each subject. Two different contrasts are shown: yellow is the contrast for right hemifield stimulation versus baseline and red for left hemifield stimulation versus baseline. The orange color shows areas with overlapping left‐right activations. [Color figure can be viewed at http://wileyonlinelibrary.com.]

Depth Profiles of BOLD Parameter Estimates

We examined the depth pattern of the right and left SC BOLD signals to contralateral visual stimulation within the predefined ROIs, using the beta maps generated in the single subject GLM analysis. In accordance with our expectations, the signal peak averaged across subjects was found in the SZ (Fig. 6A,B). The detectable signal in the IZ drastically decreased relative to the SZ. We found this pattern in nine out of nine individual datasets for the left SC and in eight out of nine datasets for the right SC upon contralateral stimulation (Fig. 6C,D). Signal changes during ipsilateral hemifield stimulation were generally smaller, but revealed a very similar depth pattern of responses in the SC with strongest activations in the SZ (Fig. 6A,B).

Figure 6.

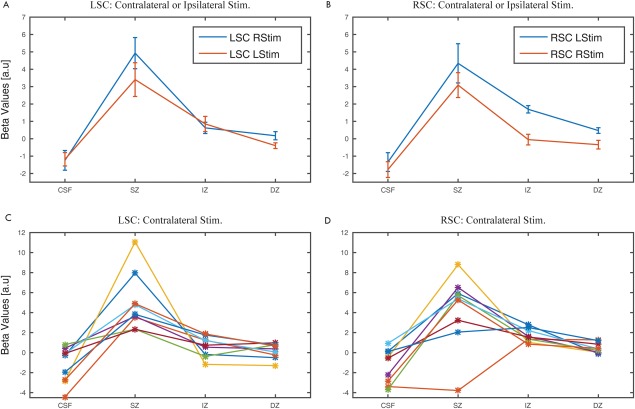
GLM parameter estimates (beta values) obtained for all voxels in each layer. In A and B the average beta values pooled across both stimulation hemifields in the left and right SC, respectively, are shown together with the standard error of the mean. In C and D, the beta values obtained for the left and right SC, respectively for each participant for contralateral stimulation are shown. [Color figure can be viewed at http://wileyonlinelibrary.com.]

To statistically verify these observations, we conducted a 2 × 2 × 4 ANOVA including all experimental factors, namely hemisphere, stimulation side, and depth. Based on the existing knowledge about afferents to the primate SC and its functional topography [May, 2006], we expected lateralized BOLD responses with higher signals in the SC contralateral to visual stimulation, i.e., a significant two‐way interaction of the factors hemisphere and stimulation side. We also expected some ipsilateral visual responses. Previous literature showed the existence of ipsilateral retinotectal projections [May, 2006]. Moreover, our stimulation was not optimized for a retinotopic mapping, reached the vertical midline of the visual field, and likely produced some cross‐over effects between visual hemifields reducing the hemifield specificity. With respect to the depth profile, stronger contralateral signals in general let us expect a depth profile with larger signal differences between individual zones for the SC contralateral to the visual stimulation. Moreover, the distribution of contra‐ and ipsilateral retinotectal projections varies across the visual layers of the SC in various species [May, 2006]. Such dependencies of the signal differences between depth zones should be detectable as a three‐way interaction of the factors hemisphere, stimulation side, and depth zone. However, please note that despite of such specific variations we foremost expected a main effect of the factor zones across all analyses.

Indeed, the full three‐factorial ANOVA revealed a significant interaction of the factors SC hemisphere and stimulation side [F (1, 8) = 11.511, P = 0.004] and a significant three‐way interaction of hemisphere, stimulation side and zones [F (2.447, 19.576) = 9.749, P = 0.001]. Additionally, we found the expected main effect for the factor zones [F (1.836, 14.689) = 15.482, P < 0.001].

The main effect of zones was further investigated by one‐sided post‐hoc t‐tests comparing the mean signal across hemispheres and stimulation sides between the depth zones to see whether beta values determined for each of the four zones were consistent with SC physiology expected from animal models. For a visual stimulation the most superficial layer should have the highest mean beta value and the values should decrease from the superficial zone to the deeper zones and to the CSF. Therefore, we had a priori hypotheses for a pre‐planned set of directional comparisons, namely CSF < SZ, SZ > IZ, and IZ > DZ, with a threshold of P < 0.05/3 = 0.0167. These tests revealed a significant effect for the first pair (CSF < SZ) [P = 0.001; T(8) = −5.251] as well as for the second pair (SZ > IZ) [P = 0.007; T(8) = 3.630]. For the last pair no significant effect was found after correction for multiple comparisons (IZ > DZ) [P = 0.116; T(8) = 1.760].

No significant main effects were found for the factors hemisphere [F (1, 8) = 0.577, P = 0.469] and stimulation side [F (1, 8) = 0.191, P = 0.673] nor was there any significant interaction of the factors hemisphere and zones [F (1.551, 12.411) = 0.200, P = 0.767] and stimulation side and zones [F (1.726, 13.808) = 0.091, P = 0.889].

Following up on the significant three‐way interaction, we further examined the lateralization of signal amplitudes in the different depth zones with two separate repeated measures 2 × 4 ANOVAs for the right and left SC. After Bonferroni correction, the threshold for a significant result was set to P = 0.05/2 = 0.025. According to our explanations above we expected significant main effects of zones and stimulation side and a significant interaction of stimulation side and zones.

For the right SC, we found a significant main effect of the factor zones [F (1.724, 13.794) = 10.370, P = 0.002]. The factor stimulation side was not significant after correction [F (1, 8) = 4.931, P = 0.057] as well as the interaction between zones and stimulation side [F (1.634, 13.075) = 1.548, P = 0.247]. Post‐hoc t‐tests following up on the main effect of zones revealed a significant difference for the first pair (CSF < SZ) [P = 0.002; T(8) = −4.354] as well as for the second pair (SZ > IZ) [P = 0.025; T(8) = 2.764]. For the last pair no significant effect was found (IZ > DZ) [P = 0.240; T(8) = 1.269].

For the left SC, we observed a significant main effect for the factor zones [F (2.222, 17.777) = 16.596, P < 0.001]. We did not find a significant effect for the factor stimulation side [F (1, 8) = 3.976, P = 0.081] and for the interaction between zones and stimulation side [F (1.854, 14.8353) = 1.897, P = 0.186] was not significant after correction for multiple comparisons. We investigated whether differences between each of the four zones of the left SC across stimulation side were consistent with the aforementioned pre‐planned set of directional hypotheses. Again, the first two pairs were significant, but not the last pair (P < 0.05/3 = 0.0167): CSF < SZ: P < 0.001, T(8) = −5.922; SZ > IZ: P = 0.005, T(8) = 3.811; IZ > DZ: P = 0.325, T(8) = 1.048.

In summary, we found the expected depth dependency of visual responses in the right and the left SC. This depth dependency apparently varied with the factor stimulation side and hemisphere as suggested by the significant three‐way interaction. However, the following two‐way ANOVAs did not reveal significant two‐way interactions after corrections for multiple comparisons, but confirmed a main effect of zones for the left as well as the right SC.

Despite of the outcome of the individual pairwise comparisons between superficial, intermediate, and deep zones in the abovementioned analyses, one might object that the significant results in the ANOVAs were mainly driven by the difference between SZ and CSF. Therefore, we conducted a complementary analysis without data from CSF. In these analyses, our previous observation of a main effect of depth zones was confirmed.

Several electrophysiological studies in animals demonstrated an eccentricity‐dependent magnification of the retinotopic representation in the superficial layer of the SC in macaques. Among these, Cynader and Berman [1972] reported that a visual stimulation covering about 10^° of the visual field causes signal increases in about 40% of the superficial layer of a macaque's SC. Ottes et al. [1986] summarized these studies in a quantitative model connecting retinal input with SC visual maps. Using their mapping function on our stimuli, assuming perfect fixation of our participants, we would expect about 34% of the SC visual map to be activated in our measurements. However, electrophysiological data on the one hand and the results of a GLM fit of BOLD signal changes on the other hand, cannot be directly compared, i.e. it is unclear which beta estimate from the GLM in our single subject analyses would correspond to the thresholds chosen by Cynader and Berman [1972] to distinguish between activated and non‐activated neurons based on spike‐rates. Nevertheless, inspecting the distributions of beta estimates of all voxels in the entire ROIs provided some conclusive information. We calculated the probabilities of beta values with a bin width of 1 for all voxels of a ROI for each participant and calculated the group's mean probabilities per bin (Fig. 7). We marked the 66th percentile of the SZ distribution corresponding to the expectation that 34% of the surface betas should be truly activated. Figure 7 shows that indeed beta values above this threshold were extremely unlikely to occur in the deep zone and rather unlikely to occur in the intermediate zone, which otherwise mostly overlapped with each other.

Figure 7.

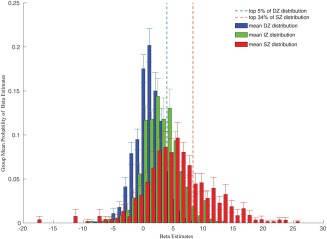
Histograms of the group's mean beta value probabilities in the delineated depth ROIs. Error bars indicate standard deviations across participants. The dashed red line indicates the 66th percentile of the superficial probability density functions, i.e., 34% of the beta values were above this threshold. This threshold was chosen because of animal data and quantitative models that let us expect 34% of the superficial zone to be activated by the visual stimulation. The dashed line indicates the 95th percentile of the deep probability density function. [Color figure can be viewed at http://wileyonlinelibrary.com.]

Neurophysiological mapping of the non‐human primate SCs visual responses also showed that a stimulus presentation in the central 7.5° of the visual field should result in activation of the colliculus with a rostral bias [Cynader and Berman 1972]. Due to our scan orientation (please rf. to Fig. 1), from a group of about 5 slices that covered the whole SC, the 2 top scans covered a rostral portion of the SC, the 2 bottom scans from this group covered a caudal part of the SC. Thus, we calculated the mean beta estimate for the SZ in each participant across rostral and caudal slices. A paired t‐test comparing rostral with caudal means revealed a significant difference with a higher mean beta estimate for the rostral portion of the ROI (mean difference rostral‐caudal: 2.85 (SD 3.06); T(7) = 2.63, P = 0.017 one‐tailed). Please note that subject 2 was excluded from this analysis because the SC was not fully covered in its rostro‐caudal extent for data acquisition.

DISCUSSION

We successfully demonstrated the potential of 9.4 T fMRI for high resolution imaging of the human midbrain in a group of unselected healthy volunteers. The short measurement duration (20 min) makes the approach applicable for studies in larger cohorts. PSF correction enabled us to minimize spatial inconsistencies between functional and anatomical images caused by geometric distortions which increase with B0 field strength and are thus a particular problem at 9.4 T. This correction resulted in a substantially better coregistration between the functional and the anatomical images and thereby allowed the direct projection of anatomical masks created on the basis of FLASH images on the functional data.

The neuroanatomy of the primate SC, its physiology and functional responses in animal models and few fMRI case studies in humans [Katyal et al., 2010; Katyal and Ress, 2014; Zhang et al., 2015] provided us with precise a priori hypotheses for the expected signal pattern. Using lateralized visual hemifield stimulation we expected to detect a depth profile in the respective colliculus contralateral to the visual stimulation. Here, the BOLD responses should be strongest and therefore the chances to detect signal differences at a particularly small spatial scale should be maximized. However, the lateralization of visual responses in the primate colliculus is not perfectly exclusive. The existence of ipsilateral projections [May, 2006] let us expect also some visual responses in the SC ipsilateral to the stimulated hemifield. Finally, due to the lack of a 9.4 T compatible eye tracker we had to rely on a secondary behavioral task to ensure that the participants fixated reliably. Although they obviously did so throughout most of the measurement, frequent or even constant small deviations from the fixation position could not have been detected, as much as rare larger deviations from the fixation position. This was probably one main reason that the interaction of the factors stimulation side and zones was not significant. Please note that these possible inaccuracies worked against our primary objective to detect a depth profile in the first place.

At 3 T, voxel sizes ranging from 4.5 (1.5 × 1.5 × 2) mm³ to 27 (3³) mm³ are typically employed for functional imaging. At 9.4 T, we used 1 mm³ corresponding to a reduction of the SNR far greater than the increase in magnetic field strength in comparison to standard fMRI at 3 T with comparable experimental designs and GLM analyses. Katyal and Ress [2014] recently reported high‐resolution functional measurements of the human SC that represent the current standard of functional midbrain imaging at 3 T. They acquired 68 minutes of data with a voxel volume of 1.7 mm³ for a successful depth mapping of collicular signals. The results reported here provide smaller voxels by 1/1.7 = 57% with a sampling of only 20 min, i.e. only about 30% of the sampling duration in the study of Katyal and Ress [2014]. Using our parameters at 3T we would therefore expect an SNR reduction by a factor of 0.57 * sqrt(0.30) = 0.31, rendering a successful depth mapping with our parameters at 3 T very unlikely. Using these experimental parameters at 9.4 T we found a depth profile with significant differences between depth zones with only 1 mm extent in depth at the group level; the descriptive data showed a consistent depth pattern in all participants in the left SC and 8 of 9 individuals in the right SC for contralateral stimulation (Fig. 6). These findings evidence the promising potential of high‐field imaging yielding a substantial gain in resolution and localization capability combined with the advantage of a short stimulation time even in challenging structures, such as the brainstem.

One major concern for 9.4 T imaging is the noise that deep brain structures (as the SC) are subjected to. With modern phased array coils that consist of many small receiver elements, SNR is much lower in the center of the brain than in the periphery since the sensitivity of each individual element is highest in its vicinity. Furthermore, physiological noise is increased in the deep brain as well. Brooks et al. [2013] described the sources of physiological noise in the brainstem and the consequences for fMRI. While physiological noise increases with the square of the main field strength, thermal noise only increases linearly with the field [Triantafyllou et al., 2005]. Physiological noise is therefore a topic that should be acknowledged in future imaging studies of the brainstem at 9.4 T. However, data obtained at 7 T revealed that the effect of physiological noise (and possible gains in sensitivity by appropriate correction) depends on the spatial resolution of the acquired images [Hutton et al., 2011]. While physiological noise models based on cardio‐respiratory information greatly improved the temporal SNR (tSNR) at conventional voxel volumes of 8–27 mm³, no significant improvements were found for fMRI data acquired with a voxel volume of 2.2 mm³ (in‐plane resolution of 1.1 × 1.1 mm² and 1.8 mm of slice thickness). As our data were acquired with an even higher spatial resolution, we expect only minor effects on the sensitivity to detect activation within the SC. However, this topic needs further investigation and thus future studies should explicitly address whether correction for physiological noise components can even further improve imaging of brain stem structures at 9.4 T.

For investigations of layer specific signals, ROI definition is critical. Here we used a semi‐automatic approach, based on previous work in 2D space and macroanatomical landmarks of the upper brainstem [Nigro et al., 2014; Oba et al., 2005]. Other groups used surface based 3D mapping of the superior colliculi to derive depth definitions and information [Katyal and Ress, 2014]. Both approaches use indirect anatomical information about the typical human layer structure and orientation instead of the actual laminar anatomy of the individual SC. Obviously, a direct anatomical definition of intracollicular regions or layers based on the microstructure of the superior colliculi [Naidich et al., 2009] would be desirable. We believe that high‐field magnetic resonance imaging and quantitative MRI approaches [Deistung et al 2013; Lorio et al., 2016; Zitella et al., 2015] represent important tools to reach this goal.

The venous structure surrounding the tectum has recently been studied by susceptibility weighed imaging (SWI) methods [Cai et al., 2015]. We expect that BOLD‐related signal changes in the main venous vessels (such as the ventral diencephalic segment of the basal vein, and the lateral mesencephalic vein) can be identified in our data. Indeed, signal changes in solitary localized voxels in correspondence with the venous structure surrounding the vertices of the SC can be identified in some subjects depicted in Figure 6. Please note, however, that these signal changes contributed to the results in the CSF mask of our depth ROI analysis, not to the SZ mask.

For functional studies, the great benefit of high magnetic field strengths is the increase in the BOLD effect which depends in large part on the enhanced effects of the local magnetic susceptibility [Duyn, 2012]. As a result of this increase in sensitivity and contrast and increase in resolution, new structural and functional information may be unveiled, opening doors for exploring new applications and to allow the detection of features within the dimensions of the cortical ribbon and, as shown in the present study, within layers of small structures like the SC. Our experiment thus prepares the ground for exploring the full potential of 9.4 T for anatomical definitions of fine‐scaled structures and studies of their functional specialization even in a challenging area as the brainstem. For a true layer‐specific mapping of brain activity in the midbrain, we envisage that further improvements in terms of anatomical definition will enable more detailed subdivisions of the different layers within the SC and improved localization of the functional signals. A success of this endeavor would help to close the gap between neurophysiology in animal models and brain activity measurements in humans and open the field for new medical applications related to the midbrain.