The corticospinal tract profile in amyotrophic lateral sclerosis

Abstract

This work evaluates the potential in diagnostic application of a new advanced neuroimaging method, which delineates the profile of tissue properties along the corticospinal tract (CST) in amyotrophic lateral sclerosis (ALS), by means of diffusion tensor imaging (DTI). Twenty‐four ALS patients and twenty‐four demographically matched healthy subjects were enrolled in this study. The Automated Fiber Quantification (AFQ), a tool for the automatic reconstruction of white matter tract profiles, based on a deterministic tractography algorithm to automatically identify the CST and quantify its diffusion properties, was used. At a group level, the highest non‐overlapping DTI‐related differences were detected in the cerebral peduncle, posterior limb of the internal capsule, and primary motor cortex. Fractional anisotropy (FA) decrease and mean diffusivity (MD) and radial diffusivity (RD) increases were detected when comparing ALS patients to controls. The machine learning approach used to assess the clinical utility of this DTI tool revealed that, by combining all DTI metrics measured along tract between the cerebral peduncle and the corona radiata, a mean 5‐fold cross validation accuracy of 80% was reached in discriminating ALS from controls. Our study provides a useful new neuroimaging tool to characterize ALS‐related neurodegenerative processes by means of CST profile. We demonstrated that specific microstructural changes in the upper part of the brainstem might be considered as a valid biomarker. With further validations this method has the potential to be considered a promising step toward the diagnostic utility of DTI measures in ALS. Hum Brain Mapp 38:727–739, 2017. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Amyotrophic lateral sclerosis (ALS) is a fatal neurodegenerative disease with a diagnosis based on the abnormalities in upper and lower motor neurons, which lead to a progressive atrophy and weakness of the limbs and respiratory muscles.

Neuroimaging studies have strongly contributed to our understanding of neurobiological mechanisms underlying ALS, and, in particular, diffusion tensor imaging (DTI) has proven to be the most reliable magnetic resonance imaging (MRI) technique for assessing microstructural pathological abnormalities in ALS patients [Agosta et al., 2010; Chiò et al., 2014; Turner et al., 2012]. A recent meta‐analysis pooling the results of 77 DTI studies demonstrated that the main structural abnormalities characterizing ALS patients were localized in the corticospinal tract (CST) extending to the frontal white matter as well as in a small region in the posterior limb of the internal capsule [Li et al., 2012]. The degeneration of the CST in ALS is consistent with pathologic findings [Hirano, 1991; Smith, 1960] and metabolic MRI studies [Sudharshan et al., 2011; Wang et al., 2006] and its neurodegeneration is mainly expressed by the presence of reduced values of fractional anisotropy (FA) [Ciccarelli et al., 2006, 2009; Cosottini et al., 2005; Ellis et al., 1999; Karlsborg et al., 2004; Sage et al., 2007, 2009; Sarica et al., 2014; Toosy et al., 2003; Van der Graaff et al., 2011]. Other studies have also found increased mean diffusivity (MD) values, in particular, along the internal capsule and the pons [Karlsborg et al., 2004] and the cerebral peduncle [Hong et al., 2004].

Despite the high number of DTI studies on ALS, the development of reliable diagnostic markers at an individual level remains an open question. The vast majority of ALS imaging studies, using either voxel‐based or regions of interest (ROI)‐based methods, have only reported differences between patients and controls at a group level [Bede and Hardiman, 2014; Chiò et al., 2014; Li et al., 2012]. These studies have yielded consistent neuroanatomical patterns of pathological changes in ALS patients but with overlapping MRI‐related values, not readily transferable to the clinical practice. Moreover, these neuroimaging approaches have specific shortcomings that might have increased the inconsistencies of data in the literature [Abe et al., 2010; Smith et al., 2006; Toga, 2015]. In the ROI‐based methods, the user interaction is required to specify the ROI, and the variability of ROI size, shape, number, and location could influence the significance of the group analysis [Kanaan et al., 2006]. Instead, the main drawback of the voxel‐based approach is the subjects’ registration phase in which a common coordinate system is applied and each voxel is compared. This critical phase could lead to alignment errors and make associating differences between groups to a specific tract difficult [Toga, 2015]. To overcome these limitations, the neuroimaging community has developed a new frontier of tract‐oriented methods, which quantify diffusion parameters along each fiber tract, creating a “tract profile” of diffusion parameters [Yeatman et al., 2012]. The tract‐oriented approaches provide profiles of diffusion parameters for each tract, preserving spatial information that are otherwise lost in ROI‐methods, and maintaining anatomical correspondence unlike in the voxel‐based. Thus, tract‐oriented methods provide a more detailed anatomical picture of disease progression [Yeatman et al., 2012].

The aim of this work was to evaluate the potential of a new advanced imaging method to serve as a biomarker in ALS. For this purpose, we applied, for the first time, the tract profile approach [Yeatman et al., 2012], to better define neurodegenerative processes underlying ALS. Moreover, to validate the group‐based evidence extracted from this technique in a clinically applicable diagnostic usage, we used a machine learning technique that, unlike univariate statistical methods, is able to predict the diagnosis with an estimated accuracy. Machine learning algorithms in clinical neuroimaging has been the most important computational development in the last years to satisfy the primary need of clinicians [Orrù et al., 2012]. Although several studies have assessed the diagnostic value of these techniques applied on Parkinson's disease [Cerasa, 2016] and Alzheimer's disease realms [Cuingnet et al., 2011; Salvatore et al., 2016], achieving over 90% accuracy for disease state classification, machine learning has sparsely been employed for the diagnosis of ALS. With the aim of exploring the latter, we adopted the Random Forest classifier, which has been successfully applied for reducing high dimensional dataset in many scientific realms, by providing a feature important measure [Breiman, 2001]. In the field of neuroscience, Random Forest has been used to assess the relative importance of several measures acquired with neuronal ensemble recording methods [Loh and Shih, 1997] and resulted in significantly higher accuracy compared with other classifiers in the prediction of Alzheimer's [Lebedev et al., 2014].

MATERIALS AND METHODS

Subjects and Clinical Parameters

ALS patients were enrolled from the Neurology unit of the University “Magna Graecia” of Catanzaro. An expert neurologist (P.V.), blind to the aim of this study, with 20 years of experience in motor neuron disorders performed a complete clinical examination. All patients with ALS met the revised El Escorial criteria for probable, probable laboratory supported or definite ALS [Brooks et al., 2000]. All ALS patients were right‐handed and riluzole treatment‐naïve. Motor skills were assessed according to the ALS functional rating scaled revised (ALSFRS‐R) [Cedarbaum et al., 1999]. Moreover, to define and quantify the presence of bulbar involvement, we used the score on the three bulbar items of the ALSFRS‐R (speech, sialorrhoea, and swallowing, a score of four per item representing normal function). We considered as exclusion criteria: the presence of: (a) multifocal motor neuropathy and paraneoplastic neuropathy, according to nerve conduction examinations; (b) forms of dementia, according to the structured clinical interview of the DSM‐IV [Diagnostic and Statistical Manual of Mental Disorders, 4th Edition, American Psychiatric Association, 1994]; (c) history of cerebrovascular disease, head trauma, hypertension or diabetes. Only two patients with a co‐morbid diagnosis of frontotemporal dementia according to the Neary Criteria [Neary et al., 1998] were excluded because of the confounding effects of imaging changes associated with this phenotype. Finally, 24 ALS patients were enrolled and underwent neuroimaging exam. All clinical details are reported in Table 1.

Table 1.

Patient's clinical characteristics

Patients	Sex	Age	Onset‐symptoms	Disease duration (months)	ALSFRS‐R	Bulbar score
# 1	F	54	Limb	10	33	12
# 2	M	69	Limb	36	18	8
# 3	F	55	Limb	23	27	9
# 4	M	52	Limb	15	32	12
# 5	F	58	Bulbar	6	19	4
# 6	F	67	Limb	48	33	8
# 7	M	43	Bulbar	5	21	5
# 8	M	67	Bulbar	3	38	8
# 9	M	65	Limb	15	29	9
# 10	F	72	Limb	1	25	9
# 11	M	43	Limb	24	33	9
# 12	M	60	Limb	24	30	9
# 13	F	71	Bulbar	6	21	9
# 14	F	53	Bulbar	9	20	5
# 15	M	62	Limb	12	18	10
# 16	M	58	Limb	6	37	12
# 17	F	48	Limb	24	33	10
# 18	F	59	Limb	9	29	12
# 19	F	76	Limb	63	15	7
# 20	M	67	Bulbar	6	24	8
# 21	F	63	Limb	36	25	9
# 22	F	72	Bulbar	6	34	7
# 23	F	66	Limb	68	34	9
# 24	M	55	Limb	5	35	12
Mean ± SD	54% Female	60.62 ± 9.06	29% Bulbar	19.16 ± 18.68	27.62 ± 6.81	8.83 ± 2.24

ALSFRS‐R, amyotrophic lateral sclerosis functional rating scaled revised.

Twenty‐four age‐ and sex‐matched, right‐handed, non‐demented, healthy controls [mean age ± SD 61 ± 8.3 (t‐test P‐level= 0.79); 62.5% female, (χ ², P‐level= 0.558)] with no previous history of neurological or psychiatric diseases and with normal MRI of the brain were matched for demographical variables with patients. All participants gave written informed consent, which was approved by the Ethical Committee of the University “Magna Graecia” of Catanzaro, according to the Helsinki Declaration.

Data Acquisition

Brain MRI was performed according to our routine protocol [Sarica et al., 2014] by a 3 T scanner with an 8‐channel head coil (Discovery MR‐750, General Electric, Milwaukee, WI). The protocol included: (a) whole‐brain T1‐weighted scan MRI scanning (SPGR; TE/TR = 3.7/9.2 ms, flip angle 12°, voxel‐ size 1 × 1 × 1 mm³); (b) diffusion‐weighted volumes, acquired by using spin‐echo echo‐planar imaging (TE/TR = 87/10,000 ms, bandwidth 250 kHz, matrix size 128 × 128, 80 axial slices, voxel size 2.0 × 2.0 × 2.0 mm³) with 27 equally distributed orientations for the diffusion‐sensitizing gradients at a b‐value of 1,000 s/mm². Particular care was taken to restrain the subject's movements with cushions and adhesive medical tape. Moreover, before further processing, we visually check the images to exclude all scans with artifacts, largely caused by subject motion.

Data Pre‐Processing

Diffusion images were first converted from DICOM to NifTI format by using the script dcm2nii from the MRIcron1 tool. The FMRIB's v5.0 (Oxford Centre for Functional MRI of the Brain2) Diffusion Toolbox (FDT) was used for correcting eddy current and motion distortion. The non‐diffusion‐weighted images, that is, the first volume image used as reference in DTI data, were skull stripped using the FMRIB's brain extraction tool (BET)3 and used to mask all diffusion‐weighted images [Smith, 2002]. A diffusion‐tensor model was fitted at each voxel using Diffusion Toolkit, generating besides fractional anisotropy (FA), mean diffusivity (MD), axial diffusivity (AD) and radial diffusivity (RD) maps, a raw T2 image with no diffusion weighting (S0). The script dtiMakeDt6FromFSL from the Mr Diffusion toolkit4 was used for aligning the T1 image—the anatomical reference—to the S0 image, obtaining a dt6 MATLAB format file for further analysis, described in the next section.

Automated Fiber Quantification

The Automated Fiber Quantification (AFQ, version 1.2 on MATLAB R2014b) tool [Yeatman et al., 2012] was used for reconstructing the CST and for evaluating diffusion metrics along the tract length. AFQ reconstructs the main white matter tracts, for both hemispheres, and measures FA, MD, AD, and RD along their trajectories. AFQ has been validated against manual tracings in healthy controls [Yeatman et al., 2012] and applied in several clinical realms, such as children born preterm [Yeatman et al., 2012], elderly individuals [Yeatman et al., 2014], autism disorders [Libero et al., 2015] and major depression [Sacchet et al., 2014].

In particular, AFQ uses a three‐step procedure to identify 24 major fiber tracts in an individual's brain. The procedure is based on a combination of the methods described by Hua et al. [2008] and Zhang et al. [2008]: (1) whole‐brain fiber tractography, (2) waypoint ROI‐based fiber tract segmentation, and (3) cleaning and refinement of fiber tracts based on a probabilistic fiber tract atlas. An example of CST reconstruction has been showed in Figure 1. For the first step, the whole‐brain fiber tractography, AFQ uses a deterministic streamline‐tracing algorithm (STT) [Mori et al., 1999] with a fourth‐order Runge–Kutta path integration method with 1‐mm step size. Voxels with FA greater than 0.3 are selected for generating a white matter mask used as a seed. Streamlines are traced bidirectionally along the principal diffusion axis, until the stopping criteria are reached (FA < 0.2 or angle between steps > 30°) [Yeatman et al., 2012]. The output of this first step is a whole‐brain tractography that is used in the next step for segmenting the fiber tracts, using a waypoint ROI‐based method [Wakana et al., 2007]. The pairs of waypoint ROIs define the fibers that pass through stereotypical locations and they are drawn on a group‐average DTI dataset in MNI space, which are then non‐linearly warped to each participant's brain [Friston and Ashburner, 2004]. In the case of the CST, the first ROI defines the entire cerebral peduncle in an axial plane at the level of the decussation of the superior cerebellar peduncle, while the second ROI is placed in the central sulcus, right after the bifurcation to the motor and sensory cortex [Wakana et al., 2007].

Figure 1.

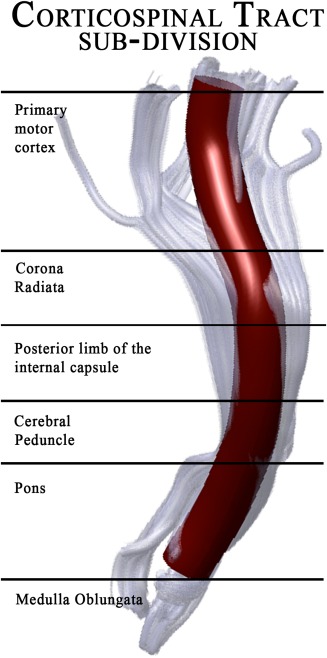
Anatomical sub‐division of the corticospinal tract as reconstructed by AFQ.

In the third step, involving the refinement of segmented fiber tracts, each candidate fiber is compared with a fiber tract probability map created by Hua et al. [2008]. This fiber tract probability map specifies the probability that a voxel is associated with a given fiber tract. Thus, estimated fibers are discarded if their probability of belonging to a fiber is low. Since the tractography process is noise prone, fiber tracts are further cleaned by iteratively discarding outlier fibers that are more than four standard deviations above the mean fiber length or that deviate more than five standard deviations from the core of the fiber tract. The Mahalanobis distance is calculated to estimate the single fiber's contribution to the core, and it corresponds to the probability that a given point belongs to the distribution. Diffusion properties are assessed at each node of each fiber, on an individual subject basis, using spline interpolation of the diffusion properties: FA, MD, AD, and RD.

Statistical and Machine Learning Analysis

To compare the diffusion properties between ALS and controls, mean values and standard deviations (±SD) were plotted [Yeatman et al., 2012] and visually analyzed and then t‐tests were conducted point‐wise along the CST for 100 voxels. A permutation‐based multiple‐comparison correction was applied to determine a statistically significant threshold for P‐values (P < 0.05) [Nichols and Holmes, 2002].

For exploring the relationship between diffusion properties in ALS patients and clinical parameters, a Pearson's correlation analysis was performed point‐wise between voxel diffusion values and ALSFRS‐R/bulbar scores and between voxel diffusion values and disease duration, with the aim of quantifying the degree of this relationship.

Although statistical separability is useful, it gives only a general evaluation of the differences between groups, and it is not able to help predict the diagnosis as well as the machine learning approach [Libero et al., 2015]. Furthermore, machine learning techniques offer the possibility to assess the clinical utility of diffusion parameters. One of the emerging methods to evaluate the prediction power of variables (i.e., how well a variable could discriminate between classes) is Random Forests [Breiman, 2001]. Random Forests is a collection or ensemble of Classification and Regression Trees (CART) [Breiman et al., 1984] trained on datasets of the same size as training set, called bootstraps, created from random resampling of the original training set. Once a tree is constructed, a set of bootstrap datasets, which does not include any particular record from the original dataset (out‐of‐bag examples), is used as test set. The error rate of the classification on test sets is the out‐of‐bag (OOB) estimate of the generalization error. Breiman [1996] showed by empirical evidence that, for the bagged classifiers, the OOB error is accurate as using a test set of the same size as the training set. To classify new input data, as depicted in Figure 2, each individual CART tree votes for one class and the forest predicts the class that has the plurality of votes.

Figure 2.

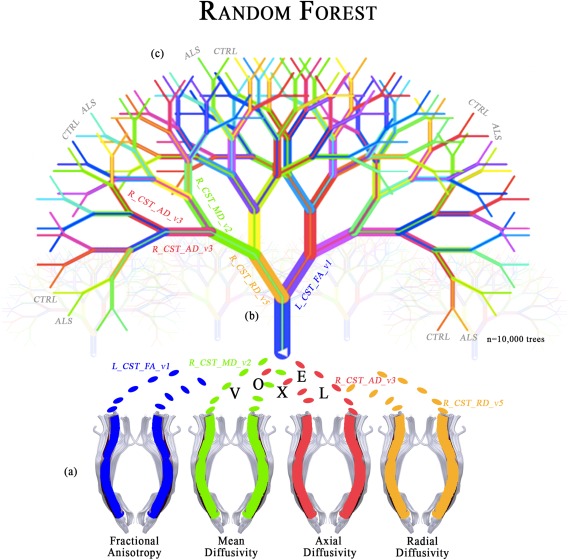
Illustration of the multivariate analysis applied in this study. (a) The dataset composed by all the corticospinal (CST) DTI voxel values of each subject, labeled by diagnosis, is used for training a forest of binary decision trees. Each voxel is labeled by side [left (L) or right (R)], followed by the related diffusion metric (FA, MD, AD, and RD) and its number (from 1 to 100). (b) Each tree is trained on a random subsample of the dataset (bootstrap). At each node a random voxel is chosen as a “splitter variable,” which attempts to separate ALS patients from healthy controls (CTRL). The more often a voxel is chosen as a splitter variable, the higher its “variable importance,” that is, the lower its Gini index. (c) Each tree of the forest gets a vote to predict new subjects. In particular, each new subject traverses each tree until it reaches a terminal node, where the class is predicted as ALS or CTRL.

Random Forest follows specific rules for tree growing, tree combination, self‐testing and post‐processing, it is robust to overfitting and it is considered more stable in the presence of outliers and in very high dimensional parameter spaces than other machine learning algorithms [Caruana and Niculescu‐Mizil, 2006; Menze et al., 2009]. The concept of variable importance is an implicit feature selection performed by Random Forest with a random subspace methodology, and it is assessed by the Gini impurity criterion index [Ceriani and Verme, 2012]. The Gini index is a measure of prediction power of variables in regression or classification, based on the principle of impurity reduction [Strobl et al., 2007]; it is non‐parametric and, therefore, does not rely on data belonging to a particular type of distribution. The Gini index is calculated as follows:

$$Gini\left(D\right)=1-\sum _{j=1}^n{\left(p_j\right)}^2$$ (1)

where D is a dataset with n classes and p_j is the relative frequency of class j in D. If a dataset D, with size N and n classes, is split into two subsets D₁ and D₂ with sizes N₁ and N₂, the Gini index is defined as:

$${Gini}_{split}\left(D\right)=\frac{N_1}{N}Gini\left(D_1\right)+\frac{N_2}{N}Gini\left(D_2\right)$$ (2)

For splitting a node, the attribute value that provides the smallest Gini_split(D) is chosen. A low Gini (i.e., a greater decrease in Gini) means that a particular predictor variable plays a greater role in partitioning the data into the defined classes.

In this study, the analyses were conducted by using R language (version 3.1.2) and the Random Forest package [Liaw and Wiener, 2002]. The dataset contained the CST voxel values of each subject, for each diffusion metric (FA, MD, AD, and RD). The left and right CST were kept separated in order to investigate any asymmetry and neither age nor sex were added as features owing to the almost perfect match of the three groups. In particular, this dataset has 48 rows (subjects), one diagnosis column—ALS or CTRL (healthy control)—and 800 numerical columns, that is, values of 200 voxels for each metric, 100 for each hemisphere. After a data cleaning—for removing columns with missing values (19)—the dimension of the feature space was 781. A binary classifier was then trained by Random Forest on this set, with 10,000 trees in the forest (ntree) and a recommended value for the number of variables considered at each split of $mtry=\sqrt{number of features}$ [Diàz‐Uriarte & Alvarez, 2006], where number of features = 781 (after the data cleaning) and mtry = 27. Voxels were then ranked according to their Mean Decrease Gini and all voxels with a mean decrease gini ≥ 0.1 were selected and extracted for creating a new training set with the most important voxels only. This cutoff was selected so to construct a new classifier with the lowest OOB error. The accuracy of the new classifier was evaluated by the 5‐fold cross validation approach, which estimates the performance by randomly dividing for five times the set into five folds, where four folds are used for training and the remaining one for testing.

RESULTS

Univariate Tract‐Profile Analysis

Figure 3 showed comparisons of diffusion parameters between ALS patients and controls for the CST profile. We found significant differences, surviving corrections for multiple comparisons, in the FA, MD, and RD metrics. The highest differences were detected using FA and RD metrics where DTI values in some parts of CST were not overlapping between groups (Fig. 3a,d). Indeed, ALS patients showed significant bilateral FA reduction and RD increase in the cerebral peduncle, posterior limb of internal capsule, corona radiata, and the primary motor cortex with respect to controls. Otherwise, MD and AD measurements showed small regions of differences (Fig. 3b,c). Considering the former, we depicted significant differences only in the right cerebral peduncle, whereas analysis of AD revealed a very restricted—but not statistically significant—pattern of difference in the right primary motor cortex.

Figure 3.

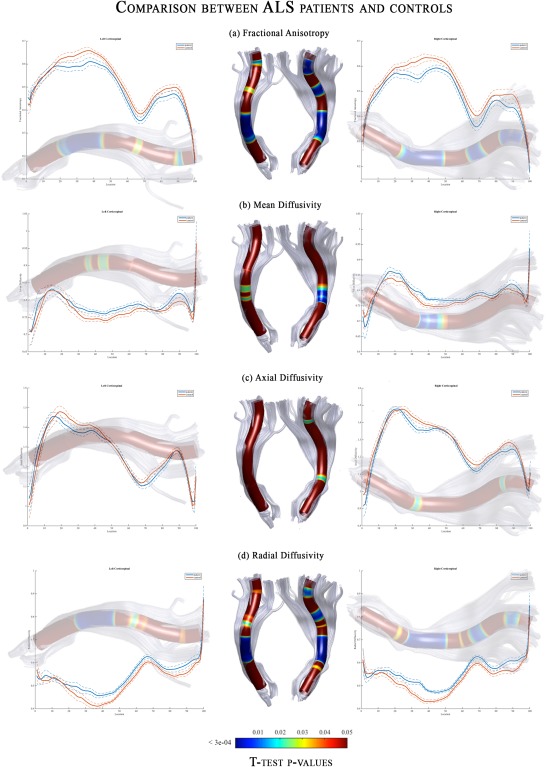
DTI‐related profiles of the CST in ALS patients compared to controls. Plots of mean values are reported voxel by voxels for each group (patients in blue and controls in orange). Dotted lines ±1 SD represent the left and right CST. The x‐axis represents the voxel location (from 1 to 100) and the y‐axis reports the subjects’ group mean values of (a) Fractional Anisotropy, (b) Mean Diffusivity, (c) Axial Diffusivity and (d) Radial Diffusivity. T‐test statistics are plotted using a 3D rendering derived from the AFQ software. The results were thresholded by a conventional criterion for correction for multiple comparisons, which implied an appropriate threshold of significance at p‐level P < 3e‐04. The 3D representation (glass effect) of the tract is added to the plot background so that each location reported on the x‐axis corresponds to the same location in the 3D view. In the middle part of the figure, the same 3D representation is reported for the left and right tract where the P‐values are associated to colors of a heat map (statistically significant differences are displayed in blue). Abbreviations: L, left; R, right; CST, corticospinal; FA, fractional anisotropy; MD, mean diffusivity; AD, axial diffusivity; RD, radial diffusivity.

Correlation Analysis

We performed correlation analyses between DTI metrics and disease severity/duration scales to evaluate the clinical relevance of the detected microstructural changes in the CST (Fig. 4). We found non‐uniform and weak relationships. Indeed, none of the correlation coefficients reached the statistically significant threshold for multiple comparisons, expect for bulbar scores. Indeed, increasing of disease severity correlated with a reduction of microstructural integrity (as measured by AD values) within the right cerebral peduncle (Fig. 4).

Figure 4.

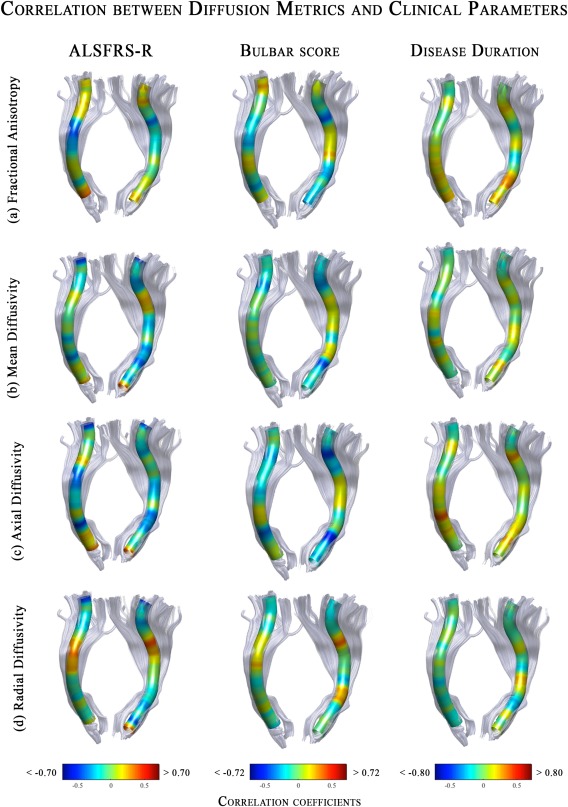
The 3D representations of correlation coefficients between DTI metrics along the CST and ALSFRS‐R scores (left side), bulbar scores (middle) and disease duration (right side) in ALS patients. The color maps report the adjusted thresholds (P < 0.05) for multiple comparisons. Significant negative correlations are colored in blue, whereas positive correlations are in red. Overall, the only significant relationship was detected between bulbar scores and Axial diffusivity values within the cerebral peduncle. Abbreviations: L, left; R, right; CST, corticospinal.

Machine Learning Applied on Tract Profile

Random Forest classifier, trained on all the features, showed an OOB error of 25% and the confusion matrix of the classification of the training set is reported in Table 2.

Table 2.

Performance of Random Forest classifiers, trained on all voxels (without feature selection) and on the most important voxels (with feature selection, mean decrease gini ≥ 0.1)

RF classifier	OOB error	Confusion matrix [Training set]
Without feature selection	25%	Reference
		Prediction	ALS	CTRL	Class error
		ALS	19	5	0.208
		CTRL	7	17	0.291
With feature selection	16.67%	Reference
		Prediction	ALS	CTRL	Class error
		ALS	22	2	0.083
		CTRL	6	18	0.25

Abbreviations: RF, random forest; OOB, out‐of‐bag.

After the feature selection, the classifier trained on the most important voxels (mean decrease gini ≥ 0.1), showed an OOB error of 16.67% (Table 2). The 5‐fold cross validation revealed a mean accuracy of 80%, with a range between 75% and 87.5%.

The analysis of the variable importance, as extracted from the classifier trained on all voxels, showed that voxels influencing the classification of ALS with respect to CTRL were localized mainly in tracts along the cerebral peduncle until the corona radiata in the FA and RD metrics (Fig. 5). The MD‐related measurements of the internal capsule in the right tract presented one significant voxel contributing to ALS classification. Furthermore, no AD voxels resulted to have a significant role in the class prediction, as it could be seen in the plot of the first fifty voxels on the left of Figure 5.

Figure 5.

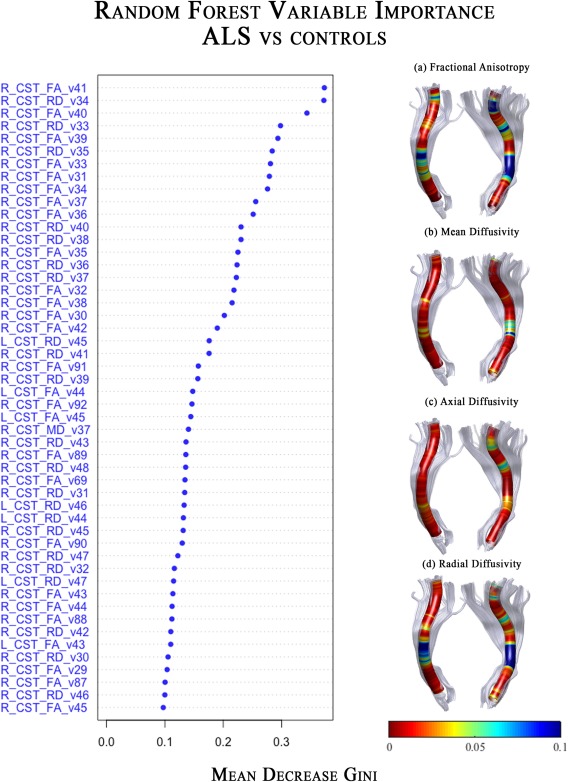
Multivariate Classification results for ALS versus controls. Random Forest classifier, trained on the most important (mean decrease gini ≥ 0.1) voxel DTI metrics of the CST, showed a good performance (mean accuracy: 80%) in discriminating ALS from controls. On the left side, we reported the variable importance plot, which presented the first 50 DTI‐related features (voxels) on the y‐axis, and their relevance for class detection on the x‐axis, ordered top‐to‐bottom as most to least important. On the right side, we plotted the same importance values, but for all voxels of each diffusion metrics, on a representative 3D map. In blue those voxels that have a mean decrease gini ≥ 0.1 on which the classifier was trained. Abbreviations: L, left; R, right; CST, corticospinal; FA, fractional anisotropy; MD, mean diffusivity; AD, axial diffusivity; RD, radial diffusivity. The number of feature corresponds to the location of the voxel along the tract.

DISCUSSION

In this work, we investigated, for the first time, the entire profile of the CST to better define the neurodegenerative processes underlying ALS. We used a double approach moving from univariate to multivariate statistical analyses. At a group level, the most relevant findings were the bilateral FA reduction and RD increase mostly localized in the cerebral peduncle, posterior limb of the internal capsule, and primary motor cortex. Taking into account all DTI measures within the CST, a machine learning algorithm (Random Forest) was able to perform an individual classification of ALS from controls with a mean accuracy of 80% (min 75%, max 87.5%), identifying as biomarkers of this optimal discrimination DTI measures extracted from the cerebral peduncle to the corona radiata.

The CST is recognized as the main pathological site of ALS in the central nervous system. In vivo evaluation of this neural sign has consistently been reported by means of DTI measures [Li et al., 2012]. Indeed, the same bilateral tendency of FA to decrease was found at the internal capsule, cerebral peduncle, pons and pyramids by Toosy et al. [2003]; from the internal capsule to the pyramids by Cosottini et al. [2005]; and in the whole tract by Ciccarelli et al. [2006], Van der Graaff et al. [2011], Wong et al. [2007], and Grapperon et al. [2014]. Our results about the tendency for MD to increase in the right cerebral peduncle matched those observed by Metwalli et al. [2010]. Again, Cirillo et al. [2012] and Grapperon et al. [2014] also consistently reported the lack of significant AD‐related pathological changes in the white matter of ALS patients. Finally, the tract profile approach proposed in this study highlighted the involvement of an additional DTI metric, which generally receives lesser consideration in neuroimaging studies: Radial Diffusivity. Overall, AD and RD are direct measures that represent, respectively, the diffusion in parallel and perpendicular directions to the tract, providing more specific neurobiological information with respect to FA or MD. A decrease in AD has been reported in both rodents and humans with axonal damage associated with axonal swelling and fragmentation [Harsan et al., 2006; Sun et al, 2006], whereas the degree of myelination as well as the changes in the axonal diameters or density are inversely correlated with RD [Alexander et al., 2007]. In our study the absence of differences between groups with AD together with the increase of RD could be explained by the so‐called pseudo‐normalization of AD that happens in acute stages when the axon and myelin debris are removed [Mac Donald et al., 2007], which is when a Wallerian degeneration is present [Pierpaoli et al., 2001]. This explanation is coherent with the clinical characteristics of our ALS cohort (high disease duration and modest motor impairment). Thus, in this scenario, a specific abnormal RD increase could represent a myelin injury with axonal loss, as proposed by Fischer et al. [2004].

Moving from a pathophysiological investigation to an individual characterization, our machine learning algorithm reached an optimal accuracy level for disease state classification. Classification analysis applied on neuroimaging data have been sparsely employed in the ALS realm. Welsh et al. [2013] reached modest results (accuracy of 71.5%) using resting‐state time‐series data for training a Support Vector Machine classifier. Otherwise, a high level of accuracy in classifying ALS patients from controls was only reached by combining DTI with other MRI metrics. Indeed, Filippini et al. [2010] and Foerster et al. [2013] obtained good results by adding whole‐brain voxel‐based volumetric analysis (accuracy 90%) or spectroscopy quantification in the motor cortex (area under the curve, AUC 75%). Taking into account this latter evidence, it should bear in mind that we reached optimal performance only by using DTI information within one specific white matter pathway.

Before drawing conclusions, some important limitations need to be discussed. First, clinically‐related parameters are not strictly connected with microstructural changes along the CST. As already discussed by Bede and Hardiman [2014] and Verstraete et al. [2015], correlation between imaging parameters (mainly DTI) and clinical metrics has far been inconsistent across studies in ALS population [Cosottini et al., 2005; Ellis et al., 1999; Graham et al., 2004; Hong et al., 2004; Metwalli et al., 2010; Sage et al., 2007; Toosy et al., 2003]. As concerns ALSFRS‐R score, one proposed explanation is that this evaluation is heavily dependent on lower motor neuron degeneration, which is not captured by the current imaging techniques. To overcome this limitation, in this study we tried to evaluate the different impact of clinical severity restricted to bulbar impairment (bulbar score from ALSFR‐R scale), reporting a slight relationship between bulbar scores and some DTI measures (i.e., AD) within the cerebral peduncle. Second, longitudinal studies need to be performed to monitor the spread of pathology along the CST in ALS patients [Van der Graaff et al., 2011]. Finally, AFQ provides a framework for combining quantitative imaging data from multiple modalities [Yeatman et al., 2012]. While diffusion imaging is quantitative, diffusion properties are not biologically specific. Future work using quantitative T1 and Proton Density (PD) in combination with DWI‐tractography based fiber tract segmentation will elucidate the precise biological underpinnings of neural injuries in ALS patients.

CONCLUSIONS

We are interested in evaluating the potential of a new advanced imaging method to serve as a biomarker in ALS. The tract profile technique described in this study allows us to both better describe pathophysiological abnormalities characterizing ALS patients and evaluate the robustness of a machine learning algorithm applied on these specific sets of data. We retain that the neuroimaging approach described in this study may open new possibilities for developing multivariate neuroimaging outcomes readily transferable to the clinical practice of ALS. Indeed, there is an urgent need to identify biomarkers, which may be used for helping and improving early diagnosis but that it is hoped will improve and create therapeutic options for ALS patients and ultimately help in the treatment of these patients. Moreover, since previous univariate neuroimaging methods have partially failed in providing definitive and clinically useful biomarkers, machine learning approaches must be employed also for improving individual differential diagnosis of ALS phenotypes with respect to other motor neuron disease disorders (i.e., PMA, PLS), as well as, ALS‐mimicking syndromes (i.e., FTD).

Supporting information

Supporting Information