Adaptive smoothing based on Gaussian processes regression increases the sensitivity and specificity of fMRI data

Abstract

Temporal and spatial filtering of fMRI data is often used to improve statistical power. However, conventional methods, such as smoothing with fixed‐width Gaussian filters, remove fine‐scale structure in the data, necessitating a tradeoff between sensitivity and specificity. Specifically, smoothing may increase sensitivity (reduce noise and increase statistical power) but at the cost loss of specificity in that fine‐scale structure in neural activity patterns is lost. Here, we propose an alternative smoothing method based on Gaussian processes (GP) regression for single subjects fMRI experiments. This method adapts the level of smoothing on a voxel by voxel basis according to the characteristics of the local neural activity patterns. GP‐based fMRI analysis has been heretofore impractical owing to computational demands. Here, we demonstrate a new implementation of GP that makes it possible to handle the massive data dimensionality of the typical fMRI experiment. We demonstrate how GP can be used as a drop‐in replacement to conventional preprocessing steps for temporal and spatial smoothing in a standard fMRI pipeline. We present simulated and experimental results that show the increased sensitivity and specificity compared to conventional smoothing strategies. Hum Brain Mapp 38:1438–1459, 2017. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

The high spatial resolution of functional magnetic resonance imaging (fMRI) allows studying activity patterns on a millimeter scale. However, fMRI data is corrupted by structured and unstructured noise from multiple sources, which degrades the sensitivity of statistical tests. Accordingly, fMRI preprocessing commonly includes spatial smoothing to improve the signal‐to‐noise ratio (SNR) of the data. Spatial smoothing involves applying a low‐pass spatial filter to remove high spatial frequency components. This approach is based on the assumption, formalized in the matched filter theorem, that neural responses are intrinsically smooth [Calhoun et al., 2001; Malonek et al., 1997]. Under this assumption, spatial smoothing allows for optimal detection of neural signals embedded in white noise [Hartvig, 2000]. Moreover, because of imperfect spatial registration, spatial filtering may increase the SNR in studies that combine data across individuals. Spatial smoothing also is a crucial step in using Gaussian random field theory to assess the statistical significance of observed responses [Worsley et al., 1992]. However, a major disadvantage of spatial smoothing is unavoidable inexact correspondence between the filter specification and the activation extent, with consequent loss of spatial resolution. This approach inherently carries tradeoff between sensitivity versus spatial specificity [Bernal‐Rusiel et al., 2010; Friston et al., 1996; Kamitani and Sawahata, 2010; Kruggel et al., 1999; Op de Beeck, 2010; Worsley et al., 1996]. In the context of fMRI, sensitivity is defined as the ability to detect neural responses across different experimental conditions. Specificity is the ability to accurately identify the response locus, that is, to exclude inactive regions. Under‐smoothing retains fine response details (high specificity) but retains noise (low sensitivity). Over‐smoothing reduces noise (high sensitivity) but blurs the fine response details (low specificity). It is important to recognize that sensitivity and specificity are distinct metrics; hence it is theoretically, possible to simultaneously optimize both.

Conventional smoothing is implemented by computing, at each voxel, a locally weighted average, where the weights decrease with distance. The weight‐distance function commonly is modeled as a fixed Gaussian kernel, typically having a full width at half maximum (FWHM) of 3–10 mm [Lazar, 2008; Penny and Trujillo‐Barreto, 2007]. Gaussian kernel smoothing is simple and computational efficient. However, the disadvantage of fixed‐width spatial smoothing is inability to accommodate variable granularity of activation profiles (i.e., changes in the smoothness of the neural signal) or level of voxel noise. Thus, fixed‐width spatial smoothing necessarily involves a tradeoff between increased sensitivity and spatial specificity [Brezger et al., 2007; Smith and Fahrmeir, 2007; Tabelow et al., 2006; Yue et al., 2010].

Several methods have been suggested to improve the sensitivity/specificity tradeoff using more complex adaptive smoothing methods [Lindquist and Wager, 2008; Lindquist et al., 2006; Poline and Mazoyer, 1994; Shafie et al., 2003, Van De Ville et al., 2006, Worsley et al., 1996]. All these methods adaptively select an informative input (informative neighbors) to improve accuracy. Some methods adopt a statistical approach, adapting the local smoothing level according to the degree of uncertainty in the data, thereby accounting for spatially varying noise. Other methods extend the general linear model (GLM) by the addition of smoothness priors on the regression parameters [Bowman et al., 2008; Gössl et al., 2001; Harrison et al., 2007; Penny and Trujillo‐Barreto, 2007; Penny et al., 2005; Yue et al., 2010]. These strategies represent an advance over traditional fixed‐width smoothing but are not drop‐in preprocessing solutions as they necessitate task‐specific knowledge. Furthermore, these methods often depend on difficult modeling choices such as knowing the functional shape of a canonical neural response or the structure and priors of a Bayesian model. Another drawback of these statistical methods is that they often result in complicated posterior distributions that require approximation techniques such as Markov‐Chain Monte‐Carlo (MCMC), variational Bayes inference, and so forth.

Here, we propose to use of Gaussian process (GP) regression‐based methods for a drop‐in replacement to conventional preprocessing spatial smoothing and temporal filtering methods. GP regression is a nonparametric Bayesian method that has received much attention in the machine learning literature [Rasmussen and Williams, 2006]. The GP method is straightforward and theoretically well grounded. In the fMRI context, GP adaptively smooths fMRI data by the mutual learning of the local spatiotemporal characteristics of neural responses and the noise level on a per voxel basis. GP uses this information to vary the degree of smoothing at each voxel.

Although, conceptually attractive, GP use in fMRI data analysis heretofore has been limited by burdensome scaling properties. Naively solving GP inference is limited to datasets with only a few thousand data points [Rasmussen and Williams, 2006]. In a standard fMRI experiment, the number of data points (voxels × volumes) can easily reach hundreds of thousands, if not millions, rendering GP analysis impractical. Recent advances in GP methodology have enabled a substantial acceleration of GP computations in application to data possessing a grid data structure [Gilboa, 2013]. This condition applies very naturally to fMRI data, which lie on a four dimensional grid (three spatial dimensions × time). Recent extensions include the ability to process incomplete grid data, to account for heteroscedastic noise [Gilboa et al., 2015], and to utilize expressive kernels [Wilson et al., 2014]. These developments make GP, for the first time, an attractive spatiotemporal model for single subject fMRI data analysis. Here, we demonstrate the efficiency of GP regression using simulated as well as real data. We compare adaptive GP smoothing to conventional volume‐based smoothing using two performance metrics, sensitivity and specificity, in conditions of low and high noise. Finally, we present a comparison between GP smoothing, volume and surface‐based smoothing on real retinotopic data. We demonstrate that GP analysis increases the extent over which polar angle and field sign maps are reliable. We also show that GP smoothing preserves more information in fMRI responses, thereby improving the identification of distinct stimuli.

MATERIALS AND METHODS

In this section, we provide a short introduction to GP regression and its use in fMRI denoising. We first present the naive GP implementation followed by our extensions that enable application to fMRI data.

GP Regression

In GP regression, a prior distribution over continuous functions is modeled as a GP [Rasmussen and Williams, 2006]. In the context of fMRI, the continuous functions represent the spatiotemporal BOLD response with an input space X = ℝ⁵ = (x,y,z,t,r), where x,y,z are the spatial coordinates and t is the temporal index and r is the run index, and a scalar output $f$(X) = ℝ which in fMRI corresponds to the BOLD response.

The assumption that the data come from a GP distribution means that, for any finite set of voxels, $x_{1,}\dots ,x_N\in X$, their associated BOLD response outputs will be distributed according to a multivariate Gaussian density $p(f_1(x_1),\dots ,f_N(x_N))=N(m_N,K_N)$, where $m_N=m(x_1,\dots ,x_N)$ is a mean vector and $K_N=k{(x_i,x_j;\theta )}_{i,j}$ is the associated covariance matrix. Since it is always possible to zero‐center a dataset, the common practice in GP is to remove the sample mean and, without loss of generality, set the mean function $m_N=m(x_1,\dots ,x_N)$= 0. Hence, the multivariate distribution can be entirely represented using the covariance function $K_N=k{(x_i,x_j;\theta )}_{i,j}$. The covariance function defines the nearness or similarity between data points [Rasmussen and Williams, 2006]. Similarity is often function of distance, which decreases as the distance increases. Intuitively, this means that nearby voxels are more likely to be correlated, both in space and time. The choice of covariance function determines the smoothness degree and structure of GP inference. Not every function is a valid covariance function: A valid covariance function must meet strict conditions. In particular, for every sample of data points, it must produce a semipositive definite covariance matrix.

The literature offers several possibilities corresponding to different prior assumptions about the data [see Rasmussen and Williams, 2006 for complete details]. By far, the most commonly used families of covariance functions are the squared exponential family, Matérn family, rational quadratic family, and so forth. The main choice when using GP is which family of covariance functions $k{(x_i,x_j;\theta )}_{i,j}$ to use. This choice is important since each family of covariance functions allows for different smoothness properties and, consequently, a different posterior distribution. Once the family of covariance functions $k{(x_i,x_j;\theta )}_{i,j}$ is chosen, an optimization method is used to fit its free parameters θ to the fMRI data. Solving this problem with naive GP is straight‐forward. The following section illustrates this principle with fMRI data.

Naive GP

Assume we have N voxels $x_{1,}\dots ,x_N\in X$, where each voxel is a vector of the 3D spatial location, aggregated over time and runs $x_i=(x,y,z,t,r)$. Assuming we chose to use the $k{(x_i,x_j;\theta )}_{i,j}$ covariance function. Then, for any pair of voxels, the $x_i,x_j$ the value of the covariance function $k{(x_i,x_j;\theta )}_{i,j}$ will be a function of θ. By aggregating all the covariance function values to a matrix, where the index i corresponds to row, and the index j corresponds to column, we can construct the covariance matrix $K_N=k{(x_i,x_j;\theta )}_{i,j}$ which is of size N × N. Since the underlying assumption of GP is that the data come from a multivariate Gaussian distribution, we can use the simple form of the conditional multivariate Gaussian distribution to compute the inference. Namely, given a multivariate Gaussian distribution (using standard notation in GP literature)

$$\left[\begin{array}{c}{\mathrm{f}}_1\\ {\mathrm{f}}_2\end{array}\right]\sim N\left(\left[\begin{array}{c}{\mu }_1\\ {\mu }_2\end{array}\right],\left[\begin{array}{cc}{\displaystyle {\sum }_{11}}& {\displaystyle {\sum }_{12}}\\ {\displaystyle {\sum }_{21}}& {\displaystyle {\sum }_{22}}\end{array}\right]\right)$$ (1)

If the values of $f_2$ in Eq. (1) represent the observed noisy BOLD response and $f_1$ are the unknown smooth response, for statistical inference, we need to compute the conditional distribution of $\left(f_1|f_2\right)N(\overline{\mu ,}\overline{\sum })$, where

$$\overline{\mu }={\mu }_1+{\displaystyle {\sum }_{12}{\displaystyle {\sum }_{22}^{-1}\left({\mathrm{f}}_2-{\mu }_2\right)}}$$ (2)

$$\overline{{\displaystyle \sum }}={\displaystyle {\sum }_{11}-}{\displaystyle {\sum }_{12}{\displaystyle {\sum }_{22}^{-1}{\displaystyle {\sum }_{21}}}}$$ (3)

Equation (2) represents the inference of values on $f_2$ given the values of $f_1$, while Eq. (3) represents the inference uncertainty [Rasmussen and Williams, 2006]. Hence, using the GP notations introduced above, to find the smoothed value of a single point

$$m_i=\overline{\mu }\left(x_i\right)=K_{iN}{\left(K_N+D_N\right)}^{-1}f,$$ (4)

where the observed neural response vector $f=\left(f\left(x_1\right),f\left(x_2\right),\dots ,f\left(x_N\right)\right)$, and the vector $K_{iN}=\left(k\left(x_{i,},x_1;\theta \right),k\left(x_i,x_2;\theta \right),\dots ,k\left(x_i,x_N;\theta \right)\right)$. The covariance matrix is defined as $K_N=k{(x_i,x_j;\theta )}_{i,j}$, and $D_N$ is a diagonal noise matrix with the variance of the observation noise s2nj for each voxel x_j, which is assumed to be Gaussian.

Note that if the covariance function parameters θ and the voxel noise levels $D_N$ are known, solving Eq. (4) involves straightforward linear algebra operations. To solve the model selection problem, which corresponds to finding the optimal values for the θ parameters of the covariance matrix (commonly referred to as the hyperparameters) it is common to optimize the log marginal likelihood Z(θ) with respect to θ [see Rasmussen and Williams, 2006 for thorough citations]:

$${\theta }^{*}=\arg {\max }_{\theta }\log Z\left(\theta \right)$$

$$=\arg {\max }_{\theta }\left(0.5\left({\mathrm{f}}^T{\left(K_N+D_N\right)}^{-1}\mathrm{f}+\log |K_N+D_N|+N\log \left(2\pi \right)\right)\right)$$ (5)

Equation (5) is composed of two main components. The ${\mathrm{f}}^T{\left(K_N+D_N\right)}^{-1}\mathrm{f}$ term is a data‐fit component, which increases in value as as the GP model better fits the data. The $\log |K_N+D_N|$ term is a complexity penalty which increases in value as the GP model becomes simpler. Equation (5) represents a tradeoff between underfitting and overfitting the model.

The voxel noise level often is unknown; hence, the $s_{nj}^2$ values must also be optimized in Eq. (5). Although, GP is a powerful and straightforward inference method, application to fMRI formerly was impractical because of runtime and memory demands. Naively solving GP requires operations such as ${\left(K_N+D_N\right)}^{-1}$ and $\log |K_N+D_N|$ which necessitate O $\left(N^3\right)$ runtime operations and O $\left(N^2\right)$ storage. This means that naive GP is restricted to problems of only a few thousand data points. Additional complications with naive GP include that the choice of appropriate covariance matrix is difficult, the noise level of each voxel is unknown, and stationarity must be assumed. Next, we describe our novel approach for utilizing GP for smoothing fMRI data, which overcomes the naive GP complexities and requires less restrictive assumptions.

GP Methods for fMRI Data

Our GP‐based method for fMRI analysis is composed of two independent procedures that can serve as drop‐in replacements for temporal and spatial smoothing in a standard fMRI pipeline. These procedures are drift removal and adaptive smoothing (Fig. 1).

Figure 1.

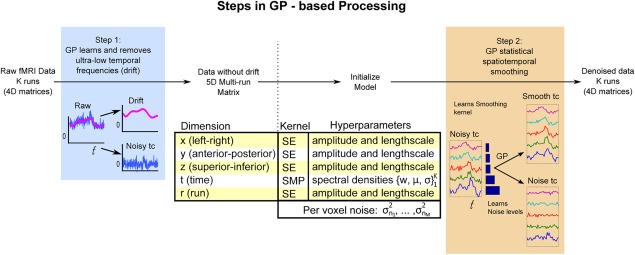
Methodological sketch of GP‐based adaptive smoothing. GP‐based processing is composed of two steps: drift removal and statistical smoothing. Unlike classical preprocessing methods, the GP smoother uses a model‐based statistical approach that jointly learns the smoothing filter and adapts the smoothing level with respect to the local voxel noise. After denoising, the fMRI data can be input to further statistical modeling (such as a GLM) or used directly for testing (e.g., with multivariate analysis). [Color figure can be viewed at http://wileyonlinelibrary.com]

In GP‐based Temporal Drift Removal, GP is applied to model the temporal drift over each run (Fig. 1, Step 1: drift removal). Temporal drift is modeled over the entire brain independently at each voxel and run. The raw fMRI data then can be decomposed into the noisy time course, which contains the neural response (noisy tc), and the temporal drift time course which can be discarded. After removal of the modeled temporal drift, the multiple runs are reassembled into a single 5D data structure, indexed by dimensions: spatial (x, y, z), temporal, and run. Figure 3 presents temporal drifts captured with GP on real fMRI data, showing a $1/f$ characteristic.

Figure 3.

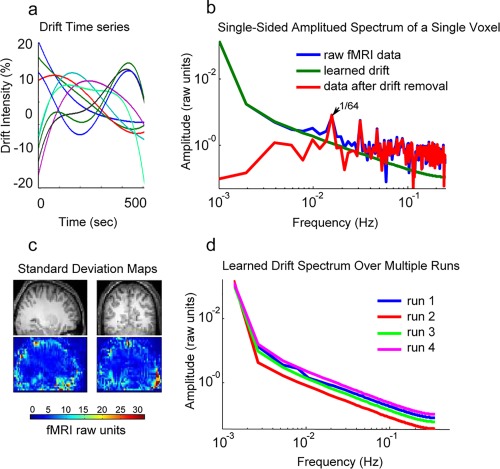
This figure illustrates ultra‐low temporal frequency noise (drift). (a) Shows the GP learned drifts (after mean removal) from nine neighboring voxels. (b) Illustrates the spectral contents of a single voxel's raw data, learned drift, and the data after drift removal. (c) Shows the standard deviation of the drift in each voxel across a slice of brain. (d) Shows the spectral components of the learned drift for the same voxel over four different runs. [Color figure can be viewed at http://wileyonlinelibrary.com]

The next step is the GP‐based adaptive smoothing, where a locally stationary GP is used to adaptively smooth the drift‐removed fMRI data (Fig. 1, Step 2: adaptive smoothing). The GP procedure models the data using a multidimensional kernel composed of one‐dimensional kernels for each dimension (see Model Selection for further details). The method jointly learns the kernels parameters (hyperparameters) and the per voxel noise levels. Figure 1, Step 2, shows the adaptive nature of the method, where the same GP smoother was used to denoise the five noisy time courses. For each time course, the level of smoothing depends on the estimated noise level. The results of GP smoothing are shown as the smooth tc box; the noise components are shown at the bottom.

The input is multiple runs of 5D fMRI data following slice timing correction and compensation for head motion. Jointly analyzing over the 5D data structure confers three benefits. First, GP learns the neural response and noise characteristics simultaneously across space, time and run. Second, it avoids edge effects in the temporal dimension that would result if the runs were concatenated. Finally, in cases where all the runs use the same task paradigm, GP can capture responses that manifest similarly across runs. We emphasize that the GP method is flexible; the user can specifically avoid smoothing over a particular dimension, for example, run, as appropriate (see Discussion for further details).

However, to use GP with fMRI data, it is necessary to deal with the following limitation of naive GP:

Tractability

To utilize GP methodology with fMRI data, the first step is to reduce the O(N3) computational complexity. We achieve this by using a recent advance which take advantage of the inherit Kronecker product structure of covariance matrices that result when the input data lie on a multidimensional grid. Gilboa et al. [2015] shows how the Kronecker product structure can reduce the runtime and memory demands to O $\left(N^3\right)$ and further extend the method to include the ability to process incomplete grid data, to account for heteroscedastic noise. As mentioned previously, the condition for grid input data fits well with fMRI data, where each voxel can be indexed by its three spatial dimensions × time × run.

Model selection

Next, we reduce model selection complexity by defining a separable covariance function in each dimension to be learned from the data. In the three spatial dimensions, we model the correlation function as squared exponential (SE) [Rasmussen and Williams, 2006], which is a standard and commonly used correlation function and closely relates to the commonly used Gaussian convolution kernel. The SE function is an unnormalized Gaussian has two free parameters (hyperparameters): the length scale (which corresponds to the fixed‐width length of the Gaussian convolution kernel) determines the distance of the local interactions, and the output variance, which determines the strength of these local interactions.

To model temporal correlation, we use the spectral mixture product (SMP) kernel. The spectral mixture (SM) kernel was first introduced in Wilson et al. [2014] as

$$k_{\text{SM}}\left(\tau =x-x\text{'}\right)={\displaystyle \sum _{a=1}^A{w}_a^2\exp \{-2{\pi }^2{\tau }^2{\sigma }_a^2\}}\cos \left(2\pi \tau {\mu }_a\right)$$ (6)

where ${\{{\mu }_a,{\sigma }_a^2,w_a^2\}}_{a=1}^A$ are the hyperparameters spectral mixture kernel. This was later extended to multidimensional input in Wilson et al. [2014], where a product is calculated over the individual SM kernels of each dimension

$$k_{\text{SMP}}\left(\tau |\theta \right)={\displaystyle \prod _{p=1}^P{k}_{\text{SM}}\left({\tau }_p|{\theta }_p\right)}.$$ (7)

Equation (7) represents a product of kernels, introduced in Rasmussen and Williams [2006]. It simply means is that we multiply the dimensions of the multidimensional kernel together. This is common practice for extending a one‐dimensional kernel to higher dimensions.

The expressivity of the SMP kernel allows it to learn from the data the complex temporal processes that depend on the experimental design and vary across the brain. To model the correlation between runs, we again use the SE kernel. The SE kernel was chosen again for its simplicity, since there is prior reason to assume a complicated correlation structure between runs. The noise at each voxel is modeled as Gaussian white noise [Wink and Roerdink, 2006].

Local stationarity

Another problem with the commonly used covariance function is the implicit assumption of spatial stationarity. Although, it is possible to assume stationarity and use our GP method over the entire brain, a better assumption is of local stationarity, meaning that local fMRI responses have common characteristics, which is what distinguishes them from uncorrelated noise. To take advantage of this assumption, we parcellate the fMRI data in each run to 5 × 5 equally sized nonoverlapping spatial blocks (the temporal and run dimensions are not parcellated) and 4 × 4 blocks in the cross sections of the first blocks. This results in spatially overlapping parcellated spatial blocks of data where we perform GP analysis and denoising separately. The strength of this parcellation technique is simplicity and the avoidance of strong assumptions. With GP, there are no artifacts near the borders of each block, which commonly appear with other filtering methods. Prior to additional analyses (such as GLM), the denoised blocks are joined together, averaging overlapping areas. Additional details are given in the methodological details section. Averaging of voxels from overlapping blocks is a common unbiased method for combining estimated quantities.

GP on Simulated and Real Data

Simulated data

We use simulated signals to demonstrate the adaptive ability of GP regression with respect to both the response pattern and the local noise level. Although, improvement in simulated data does not guarantee improvements in a real complex neural signal, it does allow for a methodological way to compare the results of the smoothers with respects to the two dominant properties of the data: the local noise level and signal pattern complexity. It is easy to show that, even under these simple conditions, the GP smoother achieves both high SNR and high fidelity as compared to conventional smoothers.

For simplicity, we consider a single spatial dimension corresponding to 30 neighboring voxels. To generate the simulated patterns we randomly sampled time courses with different frequency components. The complexity of the rugged time courses that results from multiple high frequency signals makes it much harder for the smoothing filters to separate signal from noise. To model additive noise, we generated white Gaussian noise using low variance σ ² = 1/20 and high variance σ ² = 1/4 in proportion to the maximum signal value. The simulations were run 20 times. Two performance metrics were evaluated. Sensitivity was computed as the signal to signal‐plus‐noise ratio (SSNR).

$$\text{SSNR} =\frac{f^2}{f^2+s_n^2}$$ (8)

where f represents the uncorrupted signal, (which is known, since it is simulated) and s represents the noise energy used to corrupt the signal. SSNR is equivalent to the more commonly used SNR (ratio between the uncorrupted signal variance and the noise variance). Because it is normalized, SSNR allows for easier comparison between the different activity patterns. SSNR is simply a measure of signal to noise ratio normalized to lie between 0 and 1. This is beneficial when comparing between graphs since all the figures use the same axis limits. There is a one‐ to‐one and onto relationship between SSNR and SNR, meaning that they convey the same information. The relationship is SNR = SSNR/(1‐SSNR) or SSNR = SNR/(SNR + 1).

SSNR was calculated by running the smoother on the signal and noise separately and then calculating the ratio. Specificity was evaluated using the fidelity metric, computed as the Pearson correlation between the true response profile (prior to the addition of noise) and the result after smoothing. An ideal smoother would reduce the noise without corrupting the signal. Thus, an ideal smoother would yield SSNR = 1 and fidelity = 1.

Real data: Stimuli and experimental setup

The presently analyzed fMRI data were acquired during the course of an experiment primarily designed to measure the effect of gaze direction on retinotopic responses and are fully stated in [Strappini et al., 2015]. Data were acquired in six healthy adults with normal or corrected‐to‐normal visual acuity (mean age 27 years, range 26–31, 1 female), and with no past history of psychiatric or neurological disease. All subjects had extensive experience in psychophysical and fMRI experiments and were paid for their participation. We mapped responses to polar angle (measured from the contralateral horizontal meridian around the center of gaze) and eccentricity (distance from the center‐of‐gaze) using standard phase encoded retinotopic stimuli [Sereno et al., 1995]. The stimuli were presented using a wide‐field display [Pitzalis et al., 2006] and consisted of high contrast light/dark colored checks flickering in counter phase at 8 Hz in either a counter‐clockwise rotating wedge or a ring configuration (polar angle and eccentricity mapping, respectively) extending up to 100 degrees of visual angle. The eccentricity ring expanded linearly with a uniform velocity of 1 degree/s. The average luminance of the stimuli was 105 cd/m2. The duration of one complete polar angle or eccentricity cycle was 64 s; 8 cycles were presented during each fMRI run. During retinotopic mapping, subjects were required to maintain fixation on a central cross. Each stimulus 240 type was repeated over multiple (typically 4) fMRI runs.

Imaging Parameters

The fMRI experiments were conducted at the Santa Lucia Foundation (Rome, Italy) using a 3T Allegra scanner (Siemens Medical Systems, Erlangen, Germany). Single shot echo‐planar imaging (EPI) images were acquired with interleaved slice ordering using a standard transmit‐receive birdcage head coil. For the wide‐field retinotopic mapping, 30 slices (2.5 mm thick, no gap, in‐plane resolution 3 × 3 mm) were acquired perpendicular to the calcarine sulcus. Each participant underwent four consecutive scans (two polar angle and two eccentricity). To increase the signal to noise ratio, data were averaged over two scans for each stimulus type (eccentricity and polar angle). These wide‐field retinotopic data were used for the field sign mapping results displayed in Figure 7.

Figure 7.

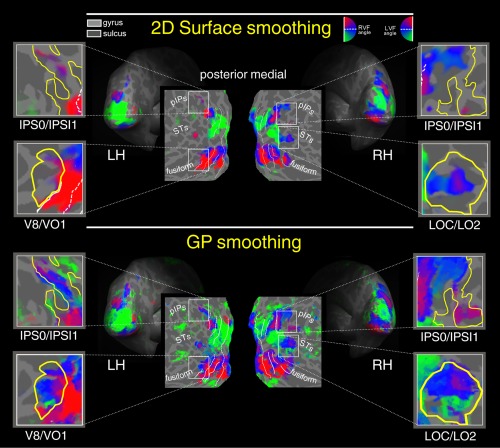
Surface smoothing versus GP smoothing. Retinotopy of polar angle representation on flattened, and inflated reconstructions of the left (LH) and right (RH) hemisphere of one participant. Polar angle retinototopic maps were obtained with two preprocessing variations: iterative surface smoothing 3.20 mm FWHM (first raw) and GP processing (second raw). Color hue indicates the response phase, which is proportional to the polar angle of the local field representation. Red, blue, and green areas represent preference for upper, middle, and lower parts of the contralateral visual field, respectively. On the flat maps, white lines indicate borders betwee the reinotopic visual areas (i.e., vertical and horizontal meridians). The same significance threshold was used for all maps. RVF, Right visual field; LVF, Left visual field. [Color figure can be viewed at http://wileyonlinelibrary.com]

Additionally, 4 fMRI runs of polar angle data were acquired with thicker slices (3.5 mm) oriented approximately parallel to the anterior–posterior commissural plane. These data were used for multivoxel pattern analysis (MVPA) and also for polar angle analysis (results shown in Fig. 6). All runs included 256 single‐shot EPI volumes [repetition time (TR), 2,000 ms; echo time (TE) 30 ms, flip angle 70°, 64 × 64 matrix; bandwidth 2,298 Hz/pixel; FOV 192 × 192 mm]. Overall, 8 fMRI runs were obtained in each of the six subjects (4 runs of retinotopy plus 4 runs polar angle) over two separate days.

Figure 6.

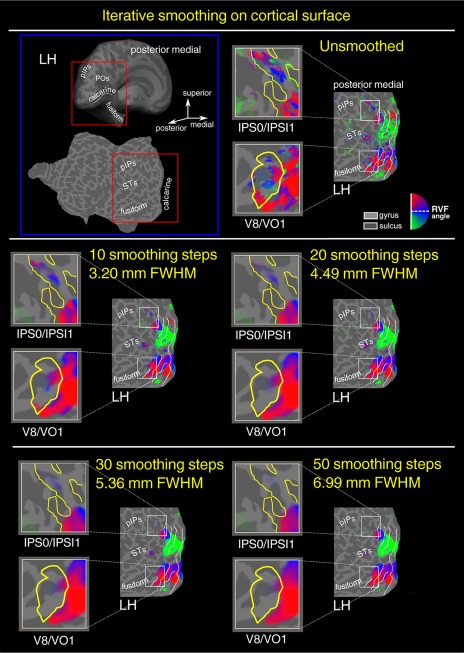
Iterative surface smoothing of polar angle data. In the first raw left panel, an inflated and flattened representation of the left hemisphere (LH) of a representative subject indicating the position of the posterior end of the intraparietal sulcus (pIPs,), the posterior occipital sulcus (POs), the calcarine sulcus, the fusiform gyrus, and the superior temporal sulcus (STSs). The red box superimposed to the inflated and flattened brain shows which portion of the surface was shown in the other panels and in Figures 7–9. Polar angle retinotopic maps were obtained with five different levels of iterative surface smoothing [Hagler et al., 2006], that is, unsmoothed with trend removal only (first raw right panel), 10 smoothing steps (second raw left panel), 20 smoothing steps (second raw right panel), 30 smoothing steps (third raw left panel), 50 smooothing steps (third raw right panel). Color hue indicates the response phase, which is proportional to the polar angle of the local field representation. Red, blue, and green areas represent preference for upper, middle, and lower parts of the contralateral visual field, respectively. On the flat maps, white lines indicate borders betwee the reinotopic visual areas (i.e., vertical and horizontal meridians). The same significance threshold was used for all maps. RVF, Right visual field; LVF, Left visual field. [Color figure can be viewed at http://wileyonlinelibrary.com]

The cortical surface of each subject was reconstructed from three structural scans consisting in sagittally acquired T1‐weighted (MPRAGE, Magnetization Prepared Rapid Gradient Echo) sequence, TI = 910 ms, TE = 4.38 ms, flip angle = 8°, 256 × 256 × 176 matrix, 1 mm cubic voxels, bandwidth = 130 Hz/pixel). Three long MPRAGE scans were used for the reconstruction of the surface and one short MPRAGE scan was used for the registration of the functional data. At the end of each session, an MPRAGE alignment scan was acquired parallel to the plane of the functional scans. The alignment scan was used to establish an initial registration of the functional data with the brain surface. Additional affine transformations that included a small amount of shear were then applied to the functional scans using blink comparison with the structural images to achieve an exact overlay of the functional data onto each cortical surface.

Data Analyses

Anatomical image processing

FreeSurfer was used to reconstruct the cortical surface [Dale et al., 1999; Fischl, 2012] for purposes of visualization only. (No surface analysis was done with GP.) Briefly, the three high‐resolution structural images obtained from each subject were manually registered and averaged. The skull was stripped off by expanding a stiff deformable template out to the dura, the gray/white matter boundary was estimated with a region‐growing method, and the result was tessellated to generate a surface that was refined against the MRI data with a deformable template algorithm. By choosing a surface near the gray/white matter border (rather than near the pial surface, where the macrovascular artifact is maximal), we were able to assign activations more accurately to the correct bank of a sulcus. The surface was then unfolded by reducing curvature while minimizing distortion in all other local metric properties. Each hemisphere was then completely flattened using five relaxation cuts: one cut along the calcarine fissure, three equally spaced radial cuts on the medial surface, and one sagittal cut around the temporal lobe.

GP processing

First, GP regression was used to preprocess the phase‐encoded BOLD fMRI retinotopy dataset as described in details below. Then, we analyzed these processed data using both a MVPA and a standard fast fourier transform (FFT) analysis typically used with retinotopic mapping. Data were also smoothed in the volume and in the surface for comparison with GP regression.

First step: Drift removal

Unlike simulated data, real fMRI data is corrupted by low temporal frequency artifact (drift) that can account for a significant fraction of observed signal variance, depending on locus. Hence, removal of this artifact is a crucial first step. However, accurate modeling of the drift is challenging owing to its complex behavior and heterogeneity. Parametric methods, such as the GLM, cannot reliably separate drift from signal because of uncertain model specification. As a nonparametric Bayesian regression framework, GP allows for great flexibility in modeling the drift. GP modeling learns the drift structure from the fMRI data at each voxel.

Second step: GP adaptive smoothing

Following drift removal, GP is used again to learn the structures of the signal and the noise at each voxel. To make GP regression feasible in the context of fMRI, it is necessary to divide the analysis into spatially overlapping blocks (see Methods section).

Volume and surface‐based smoothing

For the volume‐based smoothing, we applied to polar angle and eccentricity data, before Fourier analysis, a 3D Gaussian kernel of 3 mm FWHM using an in‐house code.

For the surface‐based smoothing we applied to polar angle and field sign data, after Fourier analysis, a various amount of smoothing, (from 3.20 up to 5.90 mm FWHM), by averaging the values of adjacent vertices, with an iterative algorithm implemented in UCSD/UCL FreeSurfer [Hagler et al., 2006]. It has been shown, that this method is computationally more simple and efficient than the iterative smoothing based on diffusion model [Hagler et al., 2006].

Fourier analysis of retinotopic signals

To further assess the power of the GP regression, retinotopic responses were also analyzed using UCSD/UCL FreeSurfer [Dale et al., 1999] based on standard procedures described in detail in many previous publications [e.g., Pitzalis et al., 2006, 2010, 2013; Strappini et al., 2015]. The first (premagnetization steady‐state) 4 volumes were discarded. Motion correction and cross‐scan alignment were performed using AFNI (Analysis of Functional NeuroImages) 3dvolreg (3T data). Phase‐encoded retinotopic data were analyzed by voxelwise Fourier transforming the fMRI time series (after removing constant and linear terms).

Statistical significance of BOLD signal modulations at the stimulus frequency (eight cycles per scan) was computed as the squared Fourier amplitude divided by the summed mean squared amplitude (power) at all other frequencies, which includes noise. Since this analysis does not take into account fMRI time series autocorrelation [Zarahn et al., 1997], these P‐values are properly regarded as descriptive. The second harmonic of the stimulus frequency and very low frequencies (1 and 2 cycles per scan, residual motion artifacts) were ignored. Response phase at the stimulus frequency was used to map retinotopic coordinates (polar angle or eccentricity). In these maps, hue represents phase and saturation represents a sigmoid function of the response amplitude. The sigmoid function was arranged so that visibly saturated colors begin to emerge from the gray background at a threshold of P < 10⁻². Computed significance at the most activated cortical surface loci ranged from P < 10⁻⁵ to 10⁻¹⁰. Boundaries of retinotopic cortical areas were defined on the cortical surface for each individual on the basis of phase‐encoded wide field retinotopy [DeYoe et al., 1994, 1996; Engel et al., 1997; Sereno et al., 1995] and subsequent calculation of visual field sign, which provides an objective means of drawing borders between areas based on the angle between the gradients (directions of fastest rate of change) in the polar angle and eccentricity with respect to the cortical surface [Sereno et al., 1994, 1995]. Each field sign map used here was based on at least four scans (two scans for polar angle and two scans for eccentricity). Details concerning procedures used to define retinotopic regions of interest are given in [Strappini et al., 2015]

Multivoxel pattern analysis

We trained a linear discriminant analysis (LDA) classifier to discriminate between two wedge stimuli presented at two different polar angles within the right upper quadrant (illustrated at the bottom of Fig. 5a). Each wedge was represented as the activity profile captured at the peak of its response. The classification was performed with both a searchlight and regions‐of‐interest (ROIs) approach [Kriegeskorte et al., 2006]. For the searchlight analysis a sphere, 12 mm of diameter centered on each voxel, performed the local classification that yielded an accuracy value for each voxel. Classifier performance was evaluated using data processed with drift removal (“drift removal only”), after GP processing, and data smoothed using a fixed 3D 3 mm FWHM Gaussian kernel. For the ROIs analysis we used multivoxel datasets extracted from retinotopically organized parts of visual cortex, as defined by the visual field map (see section above). The classification was performed on all the voxels contained in the region and yielded one accuracy value for each region. Classifier performance was evaluated using data processed with drift removal (“drift removal only”) and after GP processing. The LDA experiment was organized as a leave‐one‐out cross‐validation design with 11 fMRI runs used for training and one run used for testing. GP processing was applied independently to each fMRI run.

Figure 5.

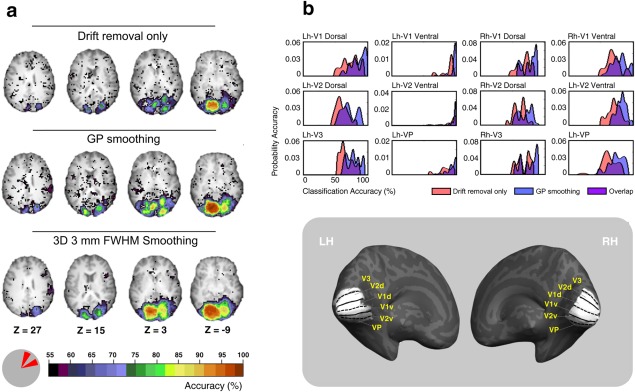
Comparison of searchlight results for smoothed and unsmoothed data. (a) Shows classification accuracy results of four axial brain slices. The classification was performed between two wedge stimuli presented at two different polar angles within the right upper quadrant shown in the bottom left. The top row results are for data after drift removal only (no smoothing), the middle and bottom rows show results for GP and 3 mm FWHM (3 × 3 × 3 mm Gaussian smoother in volume space) smoothed data, respectively. (b) shows the accuracy distributions for 12 retinotopic dorsal and ventral early visual areas. Pink and blue labels refer to data after drift removal only (no smoothing) and post GP smoothing, respectively. Purple label refers to the overlap zone between the two conditions. The corresponding anatomical locations of these visual areas on an inflated reconstruction of the left (LH) and right (RH) hemisphere of one participant are shown in the bottom right. The cortical surface was defined at the gray–white matter border and was inflated to reveal regions within the sulci (concavities, dark gray) as well as on the gyri (convexities, light gray). [Color figure can be viewed at http://wileyonlinelibrary.com]

RESULTS

GP on Simulated Data

Figure 2 shows a comparison, using simulated data, of adaptive smoothing using GP versus fixed‐width Gaussian smoothing. The critical parameters are the smoothness of the underlying response pattern and the noise level. Relatively smooth versus finely structured (“rugged”) response profiles (i.e., the true simulated signal labeled “True”) are modeled, respectively, on the left and right of the figure (blue traces at the top of Fig. 2). Simulations with low versus high additive noise are shown in the lower portion of the figure. The black circles correspond to the observed data (True signal corrupted by noise).

Figure 2.

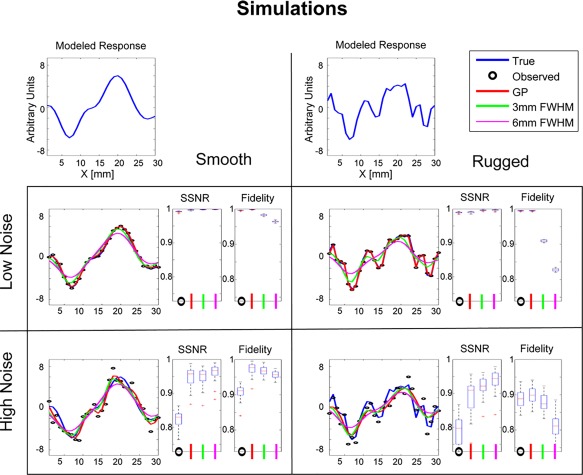
Smoothing comparison of simulated data. The figure shows results for combinations of two conditions—original smoothness level of the true data (first row) and the amount of added white noise (second and third row). For each of the two true patterns, we simulated multiple noisy observations. We compared the GP smoothing results to 3 mm and 6 mm FWHM Gaussian smoothers, and to the unsmoothed data (Observed). On the right of each of the plots, we added summary statistics for each smoother. The metrics used are signal to signal plus noise (SSNR) and fidelity (see text for further details). [Color figure can be viewed at http://wileyonlinelibrary.com]

Inspection of the SSNR box plots of the simulated results in the low noise condition (both for the smooth and ragged patterns) shows that all the smoothing methods improve the SSNR, meaning that the smoothed pattern is closer to the true pattern. Comparison of the 3 mm fixed‐width smoother to the 6 mm provides a good representation of the tradeoff between using a tight smoothing kernel, which allows for better representation of the fine details, and a wide smoothing kernel, which further reduces the effect of the high frequency noise.

This tradeoff can be observed by inspection of the results of the 6 mm fixed‐width smoother, where improvement in the SSNR metric results in corruption of signal fidelity. Another major disadvantage of fixed‐width smoothers is their inability to adapt to the noise levels. In contrast, when the noise level is low, GP uses a weak smoother to avoid corrupting the signal. If the noise level is high, GP uses a strong smoother to reduce the noise. If the response pattern is smooth, GP increases the width of the local smoothing kernel. If the response pattern is finely structured, GP decreases the width of the local smoothing kernel. In summary, the simulated data demonstrate the efficiency of GP regression in terms of its adaptation to the original response pattern and the local noise level. Hence, GP is able to achieve both high SNR and high fidelity.

GP on Real fMRI Data

Here, we assessed the power of GP smoothing to preserve information in fMRI responses reflecting the identity of distinct stimuli. The goal of the following sections is to show that, by performing adaptive GP smoothing on phase‐encoded BOLD fMRI retinotopic data (described in Methods section), it is possible to improve the results of both common multivariate and FFT analyses.

First step: drift removal

Figure 3a illustrates GP learned drifts (after mean signal removal) at nine neighboring voxels from one representative rotating wedge fMRI run. Inspection of these results reveals the high‐intensity, nonlinear nature of the drift components. The effect of drift can best be observed in the temporal frequency domain. Figure 3b shows the spectra at a single voxel of the raw data, learned drift, and the data after drift removal. High amplitudes of low frequencies in the raw fMRI data (blue) correspond to the drift components. GP models and remove the drift (green) while preserving high frequency components (red), for example, the 1/64 Hz component corresponding to the period of the rotating wedge. The raw data spectrum shows no clear separation between the drift artifact and the neural response frequency component. The drift learned by GP had spectral components extending well into the signal frequency band. Thus, a fixed high pass filter would not remove all of the drift as presently modeled.

Drift artifact is notable for its spatial heterogeneity. Figure 3c shows a map of the standard deviation of the drift component. Voxels showing the greatest quantity of drift appear mostly at the edge of the brain, suggesting that this artifact arises either in the CSF or in meningeal blood vessels. The spectral content of learned drift appears to be stable across fMRI runs. Spectra representing a single voxel over four runs are shown in Figure 3d.

Second step: GP adaptive smoothing

Learned correlations for each of the data dimensions are shown in Figure 4a. Three interesting observations follow. First, the learned spatial correlations (in the x, y, and z directions) were characterized by a FWHM of 5–9 mm. This range is consistent with previous estimations (3–10 mm FWHM) of fMRI response point‐spread functions [Lazar, 2008]. Second, the expressive SMP kernel learned meaningful correlation functions that varied throughout the brain. This result is consistent with the understanding that different regions have a different response to the stimuli. Finally, GP modeled practically no smoothing over the run dimension. The lack of smoothing across runs suggests that the fMRI response meaningfully varied over time. Potential neural or physiological factors that account for this result include fatigue and habituation [Arieli et al., 1996].

Figure 4.

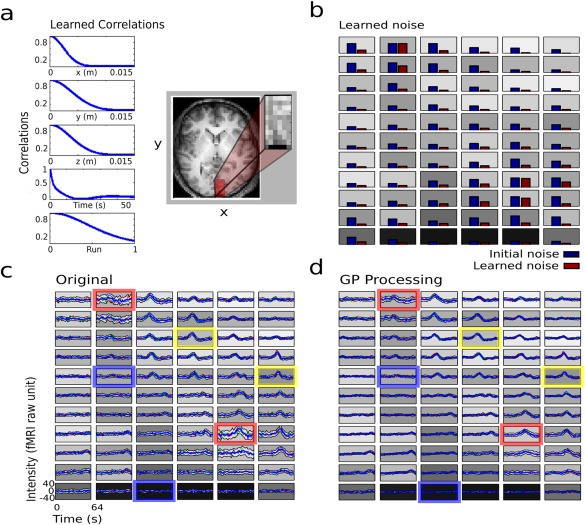
Results of the GP statistical smoother for real fMRI data. (a) Shows the learned correlations for the five dimensions. The figure also shows a 2D representation of the block of image data that was used in the analysis (the block is actually 3D). (b) Shows the learned noise for each voxel in the block. The gray shaded background of each plot corresponds to the anatomical T1‐weighted gray scale from a. (c) Shows the per‐trial representation of each voxel. The trial mean is shown in bold blue and the gray envelope shows the trial‐to‐trial variance. Fig. 4) shows for the same data as in (c) after GP smoothing. The colored outlines represent three cases: voxels with high signal and low noise (yellow), voxels with low signal and low noise (blue), and voxels with high noise (red).). [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 4 illustrates the main idea underlying local noise‐dependent spatial smoothing. Stated simply: leave alone voxels with low noise and strongly smooth voxels with high noise. The learned noise at each voxel is shown in Figure 4b for a subset of voxels (subset indicated by the inset in panel a). The initial noise estimate at each voxel was computed as the variance of the residuals after removing the mean response (sample mean over all the data inside the region). As can be seen in Figure 4b, the learned noise frequently was lower than the initial estimate. This important result reflects the fact that the initial estimate fails to take into account spatial dependencies of the response, leading to overestimation of the noise. Figure 4c,d, illustrate the time courses corresponding to the voxels shown in Figure 4b, before (after drift removal only) and after applying GP. Each plot represents the mean response averaged across eight stimulus cycles. Time courses corresponding to four runs are superimposed and color‐coded in red, green, blue, and cyan. The mean across the four runs is shown as a thicker blue line. The gray envelope about the mean shows the standard deviation across the 32 cycles (8 cycle/run × 4 runs). As is evident in panels c and d, the effect of GP smoothing varied significantly across voxels. Voxels with low signal and low noise (blue outline) as well as voxels with high signal and low noise (yellow outline) were minimally changed by GP smoothing. Conversely, voxels with high noise (red outline) were substantially changed by GP smoothing.

Multivoxel‐Pattern Analysis

We start by examining the results of the searchlight method [Kriegeskorte et al., 2006], which assesses the ability of local multivoxel regions to discriminate between stimuli (see Methods section). Figure 5a illustrates the classification accuracies observed in four axial slices. Comparison of the of the searchlight results obtained with the unsmoothed data to the results obtained using GP processing shows that GP processing improved classification accuracy while preserving the topography of regions with high classification accuracy. These regions correspond to the several distinct, multiple representation of the upper visual field [Sereno et al., 1995]. In comparison, smoothing using a 3D 3 mm FWHM Gaussian kernel blurred the topography of high‐accuracy regions (third row of Fig. 5a). Such loss of spatial specificity is a recognized feature of standard smoothing methods [Fransson et al., 2002; Kamitani and Sawahata, 2010; Lazar, 2008].

For a more detailed comparison, we show, in Figure 5b, the accuracy probability distribution of the voxels in several retinotopically organized regions. Specifically, we considered in the left and right hemisphere three ventral areas representing the upper visual field (V1 ventral, V2 ventral and VP) and three dorsal areas representing the lower visual field (V1 dorsal, V2 dorsal and V3). The anatomical position of these 12 regions is shown in the bottom inset of Figure 5b. The ventral regions located in the left contralateral hemisphere are expected to best differentiate between the two right upper wedges. For each region, we plotted the accuracy distribution (over voxels) for the searchlight using the drift removal only (red), and the GP smoothed data (blue). Note that, as expected, we found the highest (around 100%) searchlight accuracies of both drift removal only and GP smoothed data in the ventral areas of the left hemisphere (second column). Moreover, comparing pre‐ and post‐GP data in the other areas, Figure 5b shows that, while searchlight accuracies of drift removal only data were proximal to 50% (chance level), the GP smoothed data were shifted toward higher values, indicating enhanced preservation of information reflecting the identity of the stimuli.

Retinotopic Mapping

Retinotopic mapping is commonly used to define the boundaries of early visual areas (e.g., V1, V2, V3, V3A, VP, V4v) [McKeefry et al.,1997; Sereno et al., 1995; Tootell and Hadjikhani, 2001; Tootell et al., 1995, 1997; Watson et al., 1993]. Although, surface‐based smoothing of retinotopic data is usually applied to retinotopic maps for a better visualization and intersubject registration, volume‐based smoothing is avoided to preserve specificity of fMRI responses, on which retinotopic mapping critically depends. In fact, it has been shown that surface smoothing is a powerful tool to increase the SNR of BOLD signal while preserving the topological distribution of the activation [Andrade et al., 2001; Hagler et al., 2006]. This property depends on the spatial correlation structure that is based on geodesic rather than Euclidean distances [Chung et al., 2005]. Here, we show that GP smoothing, in combination with surface smoothing, enhances the signal to noise ratio of retinotopic maps while preserving response specificity.

To examine whether increasing the amount of surface smoothing might improve retinotopic results, we first varied the level of iterative smoothing on the surface (Fig. 6). This procedure was aimed to choosing the best 2D surface smoothing value to apply to additional maps. In the left panel (blue box) of Figure 6, an inflated and flattened representation of the left hemisphere (LH) of a representative subject indicates the position of the posterior end of the intraparietal sulcus (pIPs,), the posterior occipital sulcus (POs), the calcarine sulcus, the fusiform gyrus, and the superior temporal sulcus (STSs). The red box, superimposed on the inflated and flattened brain, shows which portion of the surface is shown in the other panels and in Figures 7, 8, 9. Each map shows a color plot of the response of one participant to the rotating wedge stimulus (polar angle), displayed on flat close‐ups. Color hue indicates response phase, which is proportional to the polar angle of the local visual field representation. Only voxels with a response significance exceeding a threshold of P < 0.001 are color‐coded. Polar angle retinotopic maps were obtained with five different levels of iterative surface smoothing [Hagler et al., 2006] that is, no smoothing (first raw, right panel), 10 steps 3.20 mm FWHM surface smoothing (second raw, left panel), 20 steps 4.49 mm FWHM surface smoothing (second raw, right panel), 30 steps 5.36 mm FWHM surface smoothing (third raw, left panel), 50 steps 6.99 mm FWHM surface smoothing (third raw, right panel). In particular, we focused our observations on two regions shown in the close‐ups (white boxes), that is, left intraparietal sulcus (IPS0/IPS1, in correspondence of area V7) and left V8/VO1 (located on the collateral sulcus). Since both regions represent the entire contralateral hemifield (upper‐horizontal meridian‐lower), the phase transition across neighboring voxels is more subtle and susceptible to distortion. Thus, these two regions are suitable for testing smoothing‐related reduction and/or distortion in map specificity. We observed a substantial decrease in the extent of the maps, in both V7 (IPS0/IPS1) and V8/VO1, with increasing levels of spatial smoothing. Previous fMRI studies found several retinotopic maps of the contralateral visual hemifield along the intraparietal sulcus (IPS) starting from V7 (also called IPS0), to IPS1, IPS2, IPS3, and IPS4 [Schluppeck et al., 2005; Sereno et al., 2001; Silver; Swisher et al., 2007]. Note that only the unsmoothed condition and the first level of tested smoothing (10 steps) show evidence of retinotopy in the IPS0/IPS1 close‐up. These retinotopic signals are not robust enough to show the multiple phase reversals cited in previous studies [Schluppeck et al., 2005; Sereno et al., 2001; Silver et al., 2005; Swisher et al., 2007]. Overall, a visual inspection of maps reveals that about 3 mm ≅ 10 steps of iterative surface smoothing represents a good tradeoff between sensitivity and specificity. This value corresponds to the default surface smoothing value implemented in FreeSurfer [e.g., Hagler et al., 2006]. Consequently, we applied this amount of surface smoothing to all the maps shown in the following figures.

Figure 8.

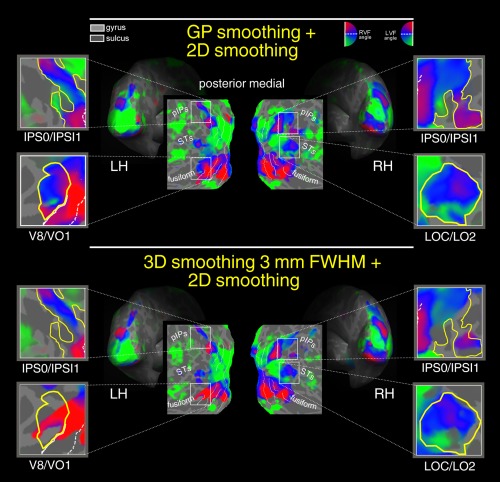
GP smoothing + 2D smoothing versus 3D smoothing + 2D smoothing. Retinotopy of polar angle representation on flattened, and inflated reconstructions of the left (LH) and right (RH) hemisphere of one participant. Polar angle retinototopic maps were obtained with two preprocessing variations: GP processing combined with iterative surface smoothing 3.20 mm FWHM (first raw) and 3D smoothing 3 mm FWHM combined with iterative surface smoothing 3.20 mm FWHM (second raw). Color hue indicates the response phase, which is proportional to the polar angle of the local field representation. Red, blue, and green areas represent preference for upper, middle, and lower parts of the contralateral visual field, respectively. On the flat maps, white lines indicate borders between the reinotopic visual areas (i.e., vertical and horizontal meridians). The same significance threshold was used for all maps. RVF, Right visual field; LVF, Left visual field. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 9.

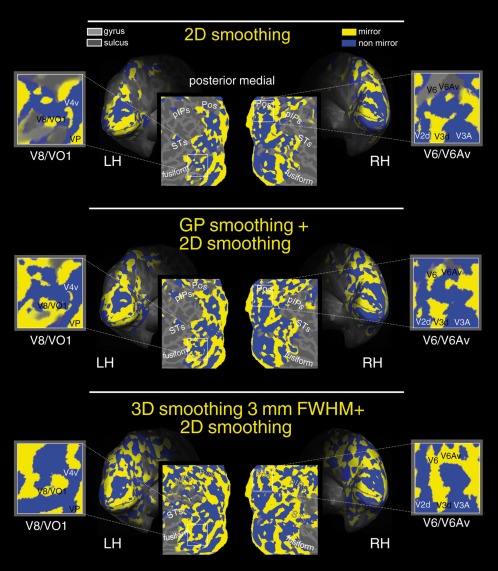
Maps of retinotopic field sign in occipital areas. Analysis of retinotopic data (polar angle and eccentricity) by visual field sign (mirror‐image versus nonmirror‐image visual field representation) [Sereno et al., 1995]. Mirror‐image areas (yellow; e.g., V1), and nonmirror‐image areas (blue; e.g., V2) are shown in the left (LH) and (RH) inflated and flattened hemispheres of one participant. This figure shows field sign maps obtained using different smoothing: 2D surface smoothing only (top), 2D surface smoothing combined with GP smoothing (middle), 2D surface smoothing combined with the traditional volumetric 3D smoothing (bottom). The same significance threshold was used for all maps. Other labels as in Figure 6. [Color figure can be viewed at http://wileyonlinelibrary.com]

Next, we compared polar angle maps obtained by 2D surface smoothing (at the best‐selected smoothing value) and GP smoothing. Figure 7 shows the retinotopic maps obtained with 3.20 mm FWHM (10 steps) 2D kernel surface smoothing (first row) and GP smoothing (second row). Retinotopy of polar angle representation are rendered on flattened, and inflated reconstructions of the left (LH) and right (RH) hemisphere of one participant. Only voxels with a response significance exceeding a threshold of P < 0.001 are color‐coded. As in Figures 5 and 7 illustrates that GP smoothing improved the extent of voxels exhibiting significant retinotopy. The improvement of the GP smoothing is particularly evident in those regions shown in the four close‐ups, that is, left and right IPS0/IPS1 (located on the posterior intraparietal sulcus), left V8/VO1 (located on the collateral sulcus), right LOC/LO2 (located on the lateral occipital region). GP‐smoothing yielded more complete retinotopic maps as compared to surface smoothing. Indeed, in all these four regions, the retinotopic maps were more robust and more extended, revealing also the presence of additional visual field representations. Note that polar angle data shown in Figures 6, 7, 8 were acquired using a wide‐field setup (able to stimulate the entire visual field up to 110 degrees in total visual extent) a methodological refinement to reveal retinotopic maps in higher order visual areas with large receptive fields [e.g., Pitzalis et al., 2006, see also Discussion]. In the first panel (surface smoothing), the fMRI signal in some higher order areas (indicated by the close‐ups) is absent or weak. It is impressive how the GP smoothing (second panel) reveals retinotopic maps signal in these regions. For example, visual area V7, located in the pIPS, is known to contain a complete representation of the contralateral hemifield [e.g., Press et al., 2001] which is revealed only by GP processing (second panel), while the first panel (drift removal only 2D Surface smoothing) shows an incomplete retinotopic map in this region, specifically, only the representation of the upper (red) visual field (as already shown in Fig. 6). Note how in the IPS0/IPS1 close‐up (GP smoothing, bottom row) it is now visible the phase transition of the phase‐encoded signal indicating the presence of multiple maps anterior to V7/IPS0 as found in previous studies [Schluppeck et al., 2005; Sereno et al., 2001; Silver et al., 2005; Swisher et al., 2007].

A similarly impressive result was found in area V8/VO1 [e.g., Brewer et al., 2005; Hadjikhani et al., 1998] located in the fusiform close‐up. This ventral area represents the entire contralateral hemifield with the typical dorsally located lower visual field representation [green; Hadjikhani et al., 1998] visible only in the GP panel. Note how the green (lower) and the blue (horizontal meridian) phases in the left hemisphere are completely canceled out using the surface smoothing only shown on the top row (and in Fig. 6).

Next, we compared two possible combined smoothing solutions. Specifically, we combined the 2D surface smoothing (at the best selected value, step 10) with either the traditional volumetric smoothing or the proposed GP smoothing. The rationale of this approach was to compare a well‐established method in brain mapping studies using surface‐based statistics (i.e., surface smoothing combined with volumetric smoothing) with an alternative method (i.e., surface smoothing combined with an adaptive smoothing method based on GPs regression). Figure 8 shows the polar angle maps obtained combining the surface smoothing with GP smoothing (first row), and standard 3 mm FWHM Gaussian smoothing performed in the volume space (second row). GP‐smoothing yielded more complete retinotopic maps as compared to the 3 mm FWHM smoother. Moreover, the two methods produced quite different topological distribution of response phase. For example, in V8/VO1 with 3 mm FWHM smoothing, the upper representation of the visual field spread over the area that represents the middle and lower portions of the visual field. For ease of comparison, we traced a yellow border around the polar angle maps obtained combing the surface smoothing with GP (Fig. 8, top row) and replicated these yellow contours on the polar angle maps shown in the other figures (6, 7, 8). Results provided evidence in favor of the best preservation of the BOLD signal topography provided by the GP method combined with surface smoothing. Moreover, these results show that the proposed GP smoothing method, in combination with the 2D surface smoothing, might represent a viable preprocessing strategy for single subjects fMRI experiments.

Figure 9 shows visual field sign maps (yellow, mirror image of visual field; blue, non mirror image of visual field) calculated from the maps of polar angle and eccentricity from the same subject shown in Figs. 6, 7, 8 [Sereno et al., 1995]. Cortical surface representations are as in Fig. 6. Improved field sign mapping afforded by GP smoothing is particularly evident in two close‐ups, that is, in left V8/VO1 and in right V6 and V6Av, two medial retinotopic dorsal areas located on the parietooccipital sulcus (Pos) recently revealed by Pitzalis et al. [2006, 2013]. GP processing expanded the extent of the field sign maps. This expansion is evident comparing the field sign maps obtained by 2D surface smoothing only (top) vs. two possible combined smoothing solutions, that is 2D surface smoothing with either the proposed GP smoothing (middle) or the traditional volumetric 3D smoothing (bottom). Particularly impressive are the field sign maps in the higher order visual areas V6 and V6Av (Figure 9, right hemisphere). Note, in the first row, absent field sign assignments (yellow/blue tiles). Note also, in the bottom row, inaccurate field sign assignments, where both V6 and V6Av are yellow. Only the combined 2D surface smoothing with GP smoothing (middle) revealed the correct field signs in V6 and V6Av, as determined by Pitzalis et al. [2006, 2013]. As well, only the GP smoothing maps (combined with 2D smoothing) revealed the typical ‘blue bridge’ that separates V6 from the V3, as documented in Pitzalis et al. [2006, 2013]. At the same time, the field sign maps obtained using the GP smoothing (combined with surface smoothing) generally agree, suggesting that GP processing did not distort the retinotopic information. In contrast, the field sign maps obtained using the 3mm FWHM smoothing (in combination with 2D surface smoothing, lower panel) led to the computation of distorted results.

DISCUSSION

In all scientific fields, observed data are subject to contamination by artifacts. In fMRI, structured and unstructured noise from multiple sources may decrease the sensitivity of statistical tests. In the context of task‐fMRI, intrinsic neural activity may be greatest source of correlated noise [Purdon and Weisskoff, 1998]. Techniques for suppression of correlated noise include GLM denoise [Kay et al., 2013], and selective removal of artifactual spatial independent components [Jenkinson et al., 2012; Mckeown et al., 2003; Robinson and Schöpf, 2013]. See Power et al. [2014, methods section] for a comprehensive review of resting state noise sources. However, it must be mentioned that sensitivity and specificity, as well as geometric distortion, have been improved also through recent developments in MR systems, pulse sequences, reconstruction methods to minimize geometric distortion and the use of prior anatomical knowledge to specify models for fMRI time series [Ben‐Eliezer et al., 2012; Kiebel et al., 2000; Polimeni et al., 2010; Todd et al., 2016; Zeng and Constable, 2002; Zaitsev et al., 2004].

Uncorrelated (thermal) noise is generated primarily by scanner electronics and is present inversely in proportion to acquisition voxel volume [Triantafyllou et al., 2005]. Historically, the principal strategy for suppression of uncorrelated noise has been spatial smoothing. The characteristic spatial scale of BOLD neural responses typically is broader than fMRI voxels. Therefore, spatial smoothing improves the signal to noise ratio (SNR) of fMRI according the matched filter principle. Conventional smoothing is implemented by computing, at each voxel, a locally weighted average, where the weights decrease with distance. The weight‐distance function commonly is modeled as a fixed 3D Gaussian kernel, typically having a full width at half maximum (FWHM) of 3–10 mm [Lazar, 2008; Penny and Trujillo‐Barreto, 2007]. However, fMRI responses characteristically extend over the cortical surface on a cm scale while remaining largely confined to the uppermost layers [Harel et al., 2006]. This response geometry is not well matched to 3D smoothing. It has been shown that improved S/N can be obtained by geodesic smoothing (i.e., smoothing tangential to the cortical surface) [Andrade et al., 2001; Anticevic et al., 2008; Chung et al., 2005]. However, even geodesic smoothing, which provides better specificity than volume‐based smoothing [Hagler et al., 2006; Jo et al., 2007], if it is of fixed width, does not optimally accommodate arbitrary response topographies or take into account wide variability in extent of fMRI responses over the cortical surface. Hence, fixed‐width spatial smoothing (either 3D or geodesic) cannot achieve locally optimal filter matching everywhere. Therefore, the tradeoff between noise suppression and spatial specificity can be optimized only globally [Brezger et al., 2007; Smith and Fahrmeir, 2007; Tabelow et al., 2006; Yue et al., 2010].

Adaptive smoothing strategies overcome this limitation by adjusting the blurring kernel according to the estimated local S/N ratio [Lindquist and Wager, 2008; Lindquist et al., 2006; Poline and Tabelow, 1994; Shafie et al., 2003; Van De Ville et al., 2006; Worsley et al., 1996]. Here, we demonstrate a particular strategy for adaptive smoothing based on GP regression. The core idea behind GP is estimating the magnitude of local uncorrelated noise and then adapting the level of smoothing on a per voxel basis.

The GP method is highly data‐driven, which reduces vulnerability to prior, sometimes arbitrary, assumptions [Lazar, 2008]. For example, it does not requires specification of the experimental design (e.g., a design matrix) or complex model design that is common in other methods that account for the whole inference process [Bowman et al., 2008; Harrison et al., 2007; Penny and Trujillo‐Barreto, 2007; Yue et al., 2010].

These simplifications represent advantages for the practitioner. Our methods may be used as a black‐box drop‐in replacement for conventional preprocessing steps.

Our method is composed of two preprocessing steps. First, infra‐slow signal drifts are removed, followed by locally adaptive spatial smoothing. Here, we demonstrate the advantages of our GP‐based method using both simulations (Fig. 2) and experimental results (Figs. 4, 5, 6, 7, 8, 9). The drift removal stage often is more dominant since the noise energy is at a much higher scale and appears to be a highly effective means of eliminating punctuate sources of artifact, possibly generated by pulsating blood vessels (Fig. 3). Improvements at each step should be compared separately to conventional denoising methods. This is a subject of future research.

GP and Retinotopic Maps

Here, we applied the GP‐based smoothing also on real data. Retinotopic phase‐encoded data are not “standard” event‐related or block‐design. The main difference is in the meaning and the importance of the spatial specificity in retinotopy. Briefly, “retinotopic mapping” is a procedure for mapping the visual world onto the surface of the human brain [e.g., DeYoe et al., 1996; McKeefry and Zeki, 1997; Sereno and Tootell, 2005; Sereno et al., 1995; Tootell and Hadjikhani, 2001; Tootell et al., 1997; Watson et al., 1993]. Phase‐encoded retinotopy involves moving a patterned stimulus slowly through the field of view of the subject. Because different parts of the visual field are stimulated at different times, the timing of the response recorded at a given locus in the gray matter indicates the field location represented by neurons in that region. We apply a FFT at the single voxel level to extract the phase and the amplitude at the stimulus frequency. The phase indicates which part of the visual field is represented at each voxel. We expect to find a systematically progression of the phase (latency) as we move from one voxel to the next. Using this method, we know that location is mapped onto the cortex in an orderly manner, with characteristic reversals at boundaries between visual areas. This technique allows the visual cortex to be mapped with a precision unmatched elsewhere in the human brain, comparable to that achievable in animals using invasive techniques. Thus, retinotopy critically depends on the specificity of fMRI responses. In contrast, in block design paradigms, the expectation is to find a large group of activated voxel with the same phase and, hence, less dependence on spatial specificity. This is why spatial smoothing of retinotopy data generally is avoided and why standard, fixed‐width spatial smoothing is a poor preprocessing choice. Here, we show that GP, being a “Smart” Smoother, preserves high the spatial specificity of retinotopic fMRI signals, unlike conventional smoothing.

The GP method is able also to increase the signal specificity in higher visual areas, such as parietal regions located along the dorso‐lateral intraparietal sulcus (IPs) and the medial parieto‐occipital sulcus (POs). GP revealed some retinotopic areas that were totally missed with other data analysis techniques (e.g., V6 and V6A, [Pitzalis et al., 2006, 2013, 2015; Tosoni et al., 2014, see results section]. Retinotopic mapping in higher order visual areas (i.e., parietal, temporal, and frontal) has historically been challenging. Indeed, the precision of the retinotopic mapping falls rapidly beyond the third and fourth visual complexes [e.g., for review, see Sereno, 1998; Sereno and Tootell, 2005], partly because of deterioration of the orderliness of the representation of space and partly because neurons become increasingly less responsive to simple patterns. For these reasons, standard retinotopic mapping stimuli, which requires no peripheral attention, have proved less useful in higher visual areas. However, Sereno and coworkers further showed how topography can be demonstrated beyond the conventional occipital areas by manipulating the subjects' attention and the visual stimuli features [Hagler and Sereno, 2006; Saygin and Sereno, 2008; Sereno and Huang, 2006]. Notwithstanding the use of such methodological refinements, retinotopic mapping of higher areas is still a hard task, requires expert subjects and repeated acquisition scans. A notably implication of the GP method is its capacity to increase the signal specificity in the retinotopic maps of higher visual areas, such as the parietal regions located along the dorso‐lateral intraparietal sulcus and medial parieto‐occipital sulcus. In this respect, the GP can be considered another methodological refinement that, routinely combined with the other aforementioned methods, like surface‐based smoothing, could increase the resolution power of the retinotopic mapping in higher order visual areas.

Finally, this method presents high localization accuracy in single subject activation maps. This development has important implications. GP regression could represent an important pre‐processing step for “decoding” fMRI approaches, that is, those approaches attempting to determine “how much can be learned about the world … by observing activity” [Naselaris et al., 2011]. Moreover, the single subject approach is important not only to take into account the individual differences (extremely important in vision mapping given that visual areas are like finger prints, different from one subject to the next) but also in clinical diagnosis or in presurgical functional evaluation where no multi‐session or multisubject data exist.

CONCLUSIONS

GP smoothing offers a powerful, yet easy‐to‐use, adaptive smoothing tool. GP regression represent a theoretically rigorous framework in which the smoothing filter structure is learned from the data. GP smoothing allows jointly modeling over space and time, thereby better utilizing spatiotemporal dependence. We show that GP smoothing preserves more information in fMRI responses concerning the identity of stimuli and expands the extent of voxels showing significant retinotopy while conserving spatial specificity. Improving the signal to noise ratio of fMRI data theoretically permits shorter scanning times, more comprehensive experimental designs, less need for expert knowledge and manual adjustment of parameters, and acquisitions with higher spatial and temporal resolution. Finally, our GP methods can be used as a black‐box drop‐in preprocessing tool for single subject fMRI experiments: it is compatible with and can be combined with other denoising techniques and surface‐smoothing. Although, it is beyond the scope of this work, future considerations include comparing our approach with other multiresolution approaches such as the SPM toolboxes [Penny and Trujillo‐Barreto, 2007; Penny et al., 2005], ICA [Hu et al., 2005], and other resampling techniques such as Bullmore et al., [2001]. The GP code is available at https://github.com/ejg20/fmri_gp.

Authors Contributions

The project began when E.G. and F.S. decided to apply GP regression to fMRI data. E.G. developed the algorithm, applied it to the fMRI data, run the simulations and wrote the first version of the draft. F.S. collected the data and performed Fourier and multivoxel pattern analyses. M.M. developed the algorithm for the multivoxel pattern analyses. All the authors contributed to the conception, design, and interpretations of the data; and they all participated in writing the article and revisiting it.