Multiple‐region directed functional connectivity based on phase delays

Abstract

Network analysis is increasingly advancing the field of neuroimaging. Neural networks are generally constructed from pairwise interactions with an assumption of linear relations between them. Here, a high‐order statistical framework to calculate directed functional connectivity among multiple regions, using wavelet analysis and spectral coherence has been presented. The mathematical expression for 4 regions was derived and used to characterize a quartet of regions as a linear, combined (nonlinear), or disconnected network. Phase delays between regions were used to obtain network's temporal hierarchy and directionality. The validity of the mathematical derivation along with the effects of coupling strength and noise on its outcomes were studied by computer simulations of the Kuramoto model. The simulations demonstrated correct directionality for a large range of coupling strength and low sensitivity to Gaussian noise compared with pairwise coherences. The analysis was applied to resting‐state fMRI data of 40 healthy young subjects to characterize the ventral visual system, motor system and default mode network (DMN). It was shown that the ventral visual system was predominantly composed of linear networks while the motor system and the DMN were composed of combined (nonlinear) networks. The ventral visual system exhibits its known temporal hierarchy, the motor system exhibits center ↔ out hierarchy and the DMN has dorsal ↔ ventral and anterior ↔ posterior organizations. The analysis can be applied in different disciplines such as seismology, or economy and in a variety of brain data including stimulus‐driven fMRI, electrophysiology, EEG, and MEG, thus open new horizons in brain research. Hum Brain Mapp 38:1374–1386, 2016. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Networks and connectivity have been proven essential to understand brain organization and function [Park and Friston, 2013]. MRI data is used to construct structural (anatomical links), functional and effective connectivity [Friston, 2011]. The characterization of network connectivity is usually addressed in terms of the distinction between functional and effective connectivity. Functional connectivity refers to statistical dependencies amongst measured time‐series, while effective connectivity rests on an explicit model of how those dependencies were caused (e.g., dynamic causal modeling [Friston et al., 2003] and structural equation modeling [McIntosh and Gonzalez‐Lima, 1994]). Within the functional connectivity, there is a key distinction between directed and undirected functional connectivity. Simple measures such as correlation and coherence return undirected measures of statistical coupling, while procedures that appeal to temporal precedence afford inferences about directed functional connectivity [Friston et al., 2013]. These include Granger causality [Granger, 1969], transfer entropy, and the procedure introduced here that is based upon significant phase delays. Our approach is directed by virtue of characterizing statistical dependencies over time in terms of wavelet decompositions and systematic differences in phase relationships. Furthermore, we transcend the normal (linear) characterization of dependencies to consider high order moments. This allows us to construct measures of functional connectivity among more than two nodes and assign an ordinal or hierarchical ranking to the implicit functional connectivity architecture.

Since BOLD fMRI time‐series are generally ergodic (in a weak sense), time frequency analyses and spectral coherence are appropriate ways to summarize functional connectivity in a compact and efficient fashion. A pair of time‐series is considered coherent if they have a constant relative phase for a given time and frequency windows. Here we show that by using wavelet analysis and calculating connectivity according to spectral coherences, we can construct networks of multiple time‐series (each corresponds to a different region) and provide their directed functional information. For a given frequency window, the network's coherence is defined by phase‐relations of all time‐series in the network, namely, a combined coherence. This is in contrast to networks defined by all possible pairwise coherences among network time‐series, namely, a linear coherence. Clearly, given the endogenous variability in the hemodynamic response function (above and beyond neuronal latencies) the assumption that the hemodynamic lag faithfully reproduces temporal precedence at the neuronal level is tenuous. However, we will make this simplifying assumption to demonstrate the potential usefulness of our measures. Crucially, the analysis described below can be applied to electrophysiological and other imaging modalities that are not confounded by variable hemodynamic delays. Consequently, assuming that time‐lags of BOLD signals correspond to latencies of information flow, BOLD signal phases are used to infer the temporal hierarchy with no need for other assumptions. Directed hierarchy (corresponding to directed functional connectivity) is obtained here by assuming a simple relation (e.g., region A, out of the four, precedes region B), with no need for further statistical models. The mathematical formalism for 4‐region coherence is described and verified by computer simulations including its dependency on coupling strength and noise level. The method's validity is demonstrated on resting‐state functional MRI data of 40 young healthy subjects to characterize the ventral visual system, motor system and default mode network (DMN). We aimed to test whether these systems are composed of linear or combined networks, and whether their temporal hierarchy is well‐defined. The ventral visual system was selected as a test system since its hierarchy is well known, the motor system was selected to test how recurrent connectivity (i.e., the coexistence of bottom‐up and top‐down connections) affects the hierarchical architecture, and the DMN was selected as its hierarchy is not known.

MATHEMATICAL DESCRIPTION

The mathematical description below refers to resting‐state functional MRI but it can be modified to fit other coupled time‐series data in varies disciplines such as seismology, or economy. In neuroscience, it can be used with stimulus‐driven fMRI, electrophysiology, magnetoencephalography (MEG), or electroencephalogram (EEG).

The BOLD Signal

Resting‐state fMRI BOLD signal $S\left(\tau \right),$ can be written as a linear combination of weighted wavelet functions whose time‐frequency (time‐scale) span the relevant frequency range that is defined by the repetition time (TR), number of time points (N), and filter used:

$$S\left(\tau \right)=\sum _{\omega }\sum _t〈S,{\psi }_{\omega ,t}〉·{\psi }_{\omega ,t}\left(\tau \right)=\sum _{\omega }\sum _t{W}_{\omega ,t}·{\psi }_{\omega ,t}\left(\tau \right)$$ (1)

where < > is the inner product and $W_{\omega ,\mathrm{t}}$ is the wavelet coefficient of ${\psi }_{\omega ,\mathrm{t}}$‐the wavelet orthonormal basis:

$${\psi }_{\omega ,t}\left(\tau \right)= a^{-\frac{\omega }{2}}\psi (a^{-\omega }\tau -tb)$$ (2)

where a > 1, b > 0, $\omega$ denotes the frequency (with $\frac{1}{TR·N}$ the lowest frequency and the highest frequency defined by the band‐pass filter) and t the time (shift).

The complex wavelet coefficients can be written in terms of their amplitude and phase:

$$W_{\omega ,t}=\mathrm{A}\mathrm{M}\mathrm{P}(\omega ,t)·\mathrm{e}\mathrm{x}\mathrm{p}\left(i\vartheta \left(\omega ,t\right)\right)$$ (3)

where “i” is the imaginary unit.

Figure 1A and 1B show time‐frequency maps (spectrograms) of $\mathrm{A}\mathrm{M}\mathrm{P}\left(\omega ,t\right)$ for the BOLD signals of two cortical regions for a single subject, while their phases (not shown) fluctuate sharply along time.

Figure 1.

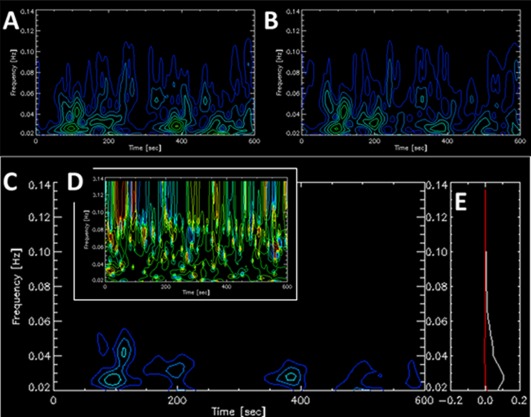
Wavelet time‐frequency contour plots of two cortical regions and the functional connectivity (FC) between them for a single subject. (A) Amplitude wavelet presentation of left precentral gyrus. (B) Amplitude wavelet presentation of right precentral gyrus. (C) Time‐frequency plot of the amplitude values of FC [Eq. (4)] describing the coherence between A and B. (D) Time‐frequency plot of the phase values of the FC in C. (E) Real (in white) and imaginary (in red) components of the FC averged over time with the y‐axis indicating the intensity [Eq. (5)]. The complex FC value averged over time and frequency was (0.93,0.0) and the Pearson's correlation coefficient was 0.90. [Color figure can be viewed at http://wileyonlinelibrary.com]

Pairwise Functional Connectivity

Functional connectivity (FC) between regions “j ₁” and “j ₂” can be defined by their coherence. Figure 1C presents the FC between two cortical regions whose coherences are at the lowest frequency band, as opposed to coherences between two subcortical regions which are at higher frequencies (Supporting Information Figure 1).

Mathematically, pairwise FC equals:

$$\mathrm{F}{\mathrm{C}}_{j_1,j_2}\left(\omega ,t\right)=(W_{\omega ,t}^{j_1})·(W_{\omega ,t}^{j_2}{ )}^{\mathbf{*}}=\mathrm{A}\mathrm{M}{\mathrm{P}}^{j_1}(\omega ,t)\mathrm{A}\mathrm{M}{\mathrm{P}}^{j_2}(\omega ,t)·\mathrm{e}\mathrm{x}\mathrm{p}[i {(\vartheta }^{j_1}\left(\omega ,t\right)-{\vartheta }^{j_2}\left(\omega ,t\right))]\equiv A_{\omega ,t}^{j_1,j_2} ·\exp \left(i{\phi }_{\omega ,t}^{j_1,j_2}\right)$$ (4)

where * denotes complex conjugate and $\mathrm{A}\mathrm{M}{\mathrm{P}}^j(\omega ,t)$ and ${\vartheta }^j\left(\omega ,t\right)$ are the amplitudes and phases, respectively, of the BOLD signal wavelet coefficients in Eq. (3). Note that Eq. (4) is similar to the previously defined cross‐wavelet transform [Chang and Glover, 2010] and to the wavelet transform coherence [Torrence and Webster, 1999]. Using Fourier basis‐set and assuming stationary signals, FC was earlier defined by us in a similar way [Goelman et al., Submitted].

Since resting‐state data is not time‐locked to any particular event, averaging over time is usually performed at the last stage resulting with FC that is frequency dependent:

$$\mathrm{F}{\mathrm{C}}_{j_1,j_2}(\omega )=\sum _t \left\{\frac{({\mathit{W}}_{\mathit{\omega },\mathit{t}}^{j_1})·({\mathit{W}}_{\mathit{\omega },\mathit{t}}^{j_2}{ )}^{\mathbf{*}}}{\sum _{\mathit{\omega }}\sum _{\mathit{t}}\left|{\mathit{W}}_{\mathit{\omega },\mathit{t}}^{j_1}\right|·{|\mathit{W}}_{\mathit{\omega },\mathit{t}}^{j_2}|}\right\}\equiv A_{\omega }^{j_1,j_2} ·\exp \left(i{\phi }_{\omega }^{j_1,j_2}\right)$$ (5)

To obtain a single (complex) FC value, averaging over frequency can also be done, yielding a FC value which is similar to our previous definition using Fourier space analysis [Goelman et al., Submitted], and whose real part corresponds to the Pearson's correlation coefficient:

$$\mathrm{F}{\mathrm{C}}_{j_1,j_2}=\sum _{\omega }\sum _t\left\{\frac{({\mathit{W}}_{\omega ,\mathit{t}}^{j_1})·({\mathit{W}}_{\omega ,\mathit{t}}^{j_2}{ )}^{*}}{\sum _{\omega }\sum _{\mathit{t}}\left|{\mathit{W}}_{\omega ,\mathit{t}}^{j_1}\right|·{|\mathit{W}}_{\omega ,\mathit{t}}^{j_2}|}\right\}\equiv A^{j_1,j_2} ·\exp \left(i{\phi }^{j_1,j_2}\right)$$ (6)

Note that no assumptions of stationary of the BOLD signals or linearity were used to obtain Eqs. (4)–(6). To ensure the numeric of the wavelet decomposition render the real part in Eq. (6) the homologue of Pearson's correlation coefficient, we calculated the FC values of Eq. (6) and Pearson's correlation coefficients for all pairs of Automated Anatomical Labeling (AAL) [Tzourio‐Mazoyer et al., 2002] cerebral regions, for all 40 subjects $\left(\frac{116·115}{2}·40 \mathrm{p}\mathrm{a}\mathrm{i}\mathrm{r}\mathrm{s}\right)$. The correlation between the real part of the FC values and Pearson's correlation coefficients across all pairs was 0.9577 (P value practically zero). On average, the values obtained by Eq. (6) were higher than Pearson's correlation coefficients by 27%.

4‐Region Functional Connectivity

Since Eq. (3) for the BOLD signal and Eq. (4) for pairwise FC have the same form, $W_{\omega ,t}^{j_1}$ in Eq. (4) can be replaced by the FC of two regions [e.g., $(W_{\omega ,t}^{j_1})·{(W_{\omega ,t}^{j_2})}^{*}]$ and $W_{\omega ,t}^{j_2}$ in Eq. (4) by the FC of two other regions [e.g., $(W_{\omega ,t}^{j_3})·{(W_{\omega ,t}^{j_4})}^{*}]$ and thus to obtain FC of 4 regions (hereafter “4‐region‐FC”). There are three independent ways to do these insertions:

$${FC}_{j1,j2,j3,j4}^1(\omega ,t)=\left(W_{\omega ,t}^{j1}\right)·(W_{\omega ,t}^{j2}{ )}^{\ast }·\left(W_{\omega ,t}^{j3}\right)·(W_{\omega ,t}^{j4}{ )}^{\ast }=\prod _{j=1}^4{AMP}_{\omega ,t}^j·\left\{\exp \left[i \left({\vartheta }_{\omega ,t}^{j1}-{\vartheta }_{\omega ,t}^{j2}+{\vartheta }_{\omega ,t}^{j3}-{\vartheta }_{\omega ,t}^{j4}\right)\right]\right\}=\prod _{j=1}^4{AMP}_{\omega ,t}^j{·e}^{i{\phi }^a}$$

$${FC}_{j1,j2,j3,j4}^2(\omega ,t)=\left(W_{\omega ,t}^{j1}\right)·\left(W_{\omega ,t}^{j2}\right)·(W_{\omega ,t}^{j3}{ )}^{\ast }·(W_{\omega ,t}^{j4}{ )}^{\ast }=\prod _{j=1}^4{AMP}_{\omega ,t}^j·\left\{\exp \left[i \left({\vartheta }_{\omega ,t}^{j1}+{\vartheta }_{\omega ,t}^{j2}-{\vartheta }_{\omega ,t}^{j3}-{\vartheta }_{\omega ,t}^{j4}\right)\right]\right\}=\prod _{j=1}^4{AMP}_{\omega ,t}^j{·e}^{i{\phi }^b}$$

$${FC}_{j1,j2,j3,j4}^3(\omega ,t)=\left(W_{\omega ,t}^{j1}\right)·(W_{\omega ,t}^{j2}{ )}^{\ast }·(W_{\omega ,t}^{j3}{ )}^{\ast }·\left(W_{\omega ,t}^{j4}\right)=\prod _{j=1}^4{AMP}_{\omega ,t}^j·\left\{\mathrm{e}\mathrm{x}\mathrm{p}[i ({\vartheta }_{\omega ,t}^{j1}-{\vartheta }_{\omega ,t}^{j2}-{\vartheta }_{\omega ,t}^{j3}+{\vartheta }_{\omega ,t}^{j4}\left)\right]\right\}=\prod _{j=1}^4{AMP}_{\omega ,t}^j{·e}^{i{\phi }^c}$$ (7)

The complete expression for 4‐region‐FC is obtained by their multiplication:

$$F{C}_{j1,j2,j3,j4}\left(\omega ,t\right)={FC}_{j1,j2,j3,j4}^1(\omega ,t)·{FC}_{j1,j2,j3,j4}^2(\omega ,t)·{FC}_{j1,j2,j3,j4}^3(\omega ,t)=\prod _{j=1}^4{AMP}_{\omega ,t}^j·\mathrm{e}\mathrm{x}\mathrm{p}\left(i{\phi }_{\omega ,t}^a\right)·\mathrm{e}\mathrm{x}\mathrm{p}\left(i{\phi }_{\omega ,t}^b\right)·\mathrm{e}\mathrm{x}\mathrm{p}\left(i{\phi }_{\omega ,t}^c\right)= \frac{\left|{\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}1}\right|·\left|{\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}2}\right|·\left|{\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}3}\right|·\left|{\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}14}\right|}{\sum _{\omega }\sum _{\mathit{t}}\left|{\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}1}\right|·{|\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}2}|·{|\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}3}|·{|\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}4}|}·\mathrm{e}\mathrm{x}\mathrm{p}\left(i{\phi }_{\omega ,t}^a\right)·\mathrm{e}\mathrm{x}\mathrm{p}\left(i{\phi }_{\omega ,t}^b\right)·\mathrm{e}\mathrm{x}\mathrm{p}\left(i{\phi }_{\omega ,t}^c\right)$$ (8)

with

$$AM{P}_{\omega ,t}^j=\frac{\left|\right({\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}}\left)\right|}{\sum _{\omega }\sum _{\mathit{t}}\left|{\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}1}\right|·{|\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}2}|·{|\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}3}|·{|\mathit{W}}_{\omega ,\mathit{t}}^{\mathit{j}4}|}$$ (9)

with “j” stands for j1‐j4 and

$$\begin{array}{c}\phi (\omega ,t{ )}^a=\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\{\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{y}[(W_{\omega ,t}^{j_1})·(W_{\omega ,t}^{j_2}{ )}^{*}·\left(W_{\omega ,t}^{j_3}\right)·(W_{\omega ,t}^{j_4}{ )}^{*}],real[((W_{\omega ,t}^{j_1})·(W_{\omega ,t}^{j_2}{ )}^{*}·\left(W_{\omega ,t}^{j_3}\right)·(W_{\omega ,t}^{j_4}{ )}^{*}]\}\phi (\omega ,t{ )}^b=\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\{\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{y}[(W_{\omega ,t}^{j_1})·(W_{\omega ,t}^{j_2})·(W_{\omega ,t}^{j_3}{ )}^{*}·(W_{\omega ,t}^{j_4}{ )}^{*}],real[((W_{\omega ,t}^{j_1})·(W_{\omega ,t}^{j_2})·(W_{\omega ,t}^{j_3}{ )}^{*}·(W_{\omega ,t}^{j_4}{ )}^{*}]\}\\ \phi (\omega ,t{ )}^c=\mathrm{t}\mathrm{a}{\mathrm{n}}^{-1}\{\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{g}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{y}[(W_{\omega ,t}^{j_1})·(W_{\omega ,t}^{j_2}{ )}^{*}·(W_{\omega ,t}^{j_3}{ )}^{*}·(W_{\omega ,t}^{j_4})],real[((W_{\omega ,t}^{j_1})·(W_{\omega ,t}^{j_2}{ )}^{*}·(W_{\omega ,t}^{j_3}{ )}^{*}·(W_{\omega ,t}^{j_4})]\}\end{array}$$ (10)

Supporting Information Figure 2 shows an example of 4‐region‐FC for four subcortical regions that exhibit FC at an intermediate frequency range.

Analytical expressions for FC between more than 4 regions along these lines are in principle possible for networks of 2ⁿ regions (n > 2). Note that averaging across time and frequency can simplify the 4‐region‐FC as was done for pairwise FC [Eqs. (5) and (6)].

Using the Phase to Obtain Directionality

The phase differences between coupled time‐series functions correspond to the time‐latency between them. For pairwise FC, we expect to obtain the same FC value regardless of the order of BOLD signals (which region is defined as “j ₁” and “j ₂”) in Eq. (4). However, interchanging the order results with the complex conjugate of Eq. (4):

$$\mathrm{F}{\mathrm{C}}_{j_1,j_2}\left(\omega ,t\right)=\mathrm{F}{\mathrm{C}}_{j_2,j_1}(\omega ,t{ )}^{*}$$

or,

$${\phi }_{\omega ,t}^{j_1,j_2}=-{\phi }_{\omega ,t}^{j_2,j_1}$$

which indicates that the phase in pairwise FC calculation cannot be used to infer temporal hierarchy and that both the FC and its complex conjugate have to be included in the phase calculations. For the 4‐region‐FC calculation of Eqs. (7,8), the three independent phase expressions of Eq. 10 enable to obtain the phases of three BOLD signals (any three) as a function of the forth:

$$\begin{array}{c}{\vartheta }^{j_2}\left(\omega ,t\right)={\vartheta }^{j_1}\left(\omega ,t\right)\mp \frac{\phi (\omega ,t{ )}^a+\phi (\omega ,t{ )}^c}{2}\\ {\vartheta }^{j_3}\left(\omega ,t\right)={\vartheta }^{j_1}\left(\omega ,t\right)\mp \frac{\phi (\omega ,t{ )}^b+\phi (\omega ,t{ )}^c}{2}\\ {\vartheta }^{j_4}\left(\omega ,t\right)={\vartheta }^{j_1}\left(\omega ,t\right)\mp \frac{\phi (\omega ,t{ )}^a+\phi (\omega ,t{ )}^b}{2}\end{array}$$ (11)

where the minus sign [ $\mp$ in Eq. (11)] results from the derivation of Eqs. (7,8) while the plus sign results from the derivation of the complex conjugate of Eqs. (7,8). Note that $\phi (\omega ,t){}^a$, $\phi {(\omega ,t)}^b$, and $\phi {(\omega ,t)}^c$ are defined in Eqs. (7,8) by the regions' phases ( ${\vartheta }^{j_1}\left(\omega ,t\right),{\vartheta }^{j_2}\left(\omega ,t\right),{\vartheta }^{j_3}\left(\omega ,t\right))$ and, in Eq. (10) by the wavelet coefficients. Crucially, Eq. (11) can be used to obtain the temporal hierarchy of the network. To obtain the directed hierarchy (i.e., whether information flows from j ₁ → j ₂ → j ₃ → j ₄ or j ₁ ← j ₂ ← j ₃ ← j ₄), an assumption is required. It is sufficient to assume a single relation such as ${\vartheta }^{j_1}<{\vartheta }^{j_2}$ to obtain the unique phase expressions for the entire network and thus its directed hierarchy, i.e., directed functional connectivity.

Linear, Combined, and Disconnected Networks

A network composed of four regions can be constructed by Eq. 8 (“4‐region‐FC”) or by using the six possible pairwise coherences calculated in Eq. (4) (“joint‐pairwise‐coherences”). The phases for a 4‐region‐FC network are given by Eq. (11). The phases for a network calculated from six pairwise coherences are:

$$\begin{array}{c}{\vartheta }^2(\omega ,t_1)\approx {\vartheta }^1(\omega ,t_1)\pm \sigma (\omega , t_1{ )}_a\\ { \vartheta }^3\left(\omega ,t_2\right)\approx {\vartheta }^1\left(\omega ,t_2\right)\pm \sigma (\omega , t_2{ )}_b\\ { \vartheta }^4(\omega ,t_3)\approx {\vartheta }^1(\omega ,t_3)\pm \sigma (\omega , t_3{ )}_c\\ { \vartheta }^2(\omega ,t_4)\approx {\vartheta }^3(\omega ,t_4)\pm \sigma (\omega , t_4{ )}_d\\ { \vartheta }^2(\omega ,t_5)\approx {\vartheta }^4(\omega ,t_5)\pm \sigma (\omega , t_5{ )}_e\\ { \vartheta }^3(\omega ,t_6)\approx {\vartheta }^4(\omega ,t_6)\pm \sigma (\omega , t_6{ )}_f\end{array}$$ (12)

where $t_n$ is a time period for which the phase difference between the pairs of BOLD signals is constant for a given frequency and $\sigma (\omega , t_n$) is the phase difference during that time. If both analyses (4‐region‐FC and joint‐pairwise‐coherences) result with a significant FC, it implies that Eqs. (11) and (12) are equal. This means that $t_1=t_2=t_3=t_4=t_5=t_6$ and for example $\sigma {(\omega , t_1)}_a=\frac{\phi {(\omega ,t)}^a+\phi {(\omega ,t)}^c}{2},$ or equivalently that Eq. (12) holds for all times, that is, a dynamically stable network. Such a network is referred hereafter as a linear network. If only the FC obtained by the 4‐region‐FC calculation is significant, the phase‐relations given in Eqs. (7,8) must hold but Eq. (12) is not satisfied. This type of a network is referred hereafter as a combined network. If only the joint‐pairwise‐coherences result with a significant FC [Eq. (12)], it implies that significant coherences between different pairs of regions occur at different times, suggesting that the entire network does not work together or that the regions are functionally connected through higher coherences between a higher (>4) number of regions. Such network is referred hereafter as a disconnected network. Note that this definition differs from the definition used in graph theory for fragmentation.

COMPUTER SIMULATIONS

Computer simulations were used to test the validity of the 4‐region‐FC mathematical expression and to test its dependency on coupling strength and noise. The Kuramoto model was used to simulate a coupled oscillator system with varying coupling strength and noise. This model was chosen since it is well studied and has been extensively used including in the field of neuroscience and specifically in resting‐state FC MRI [Cabral et al., 2011]. Denoting by ${\theta }_n\left(t\right)$ the phase of time‐series n at time t, the coupled oscillators obey the following dynamical equation:

$$\frac{d{\theta }_n}{dt}={\omega }_n+k\sum _{j=1}^{4}sin({\theta }_j\left(t\right)-{\theta }_n(t-{\tau }_{nj})+{\epsilon }_n\left(t\right))$$ (13)

where k is the global coupling strength; ${\omega }_n$ is the nth oscillator frequency, ${\epsilon }_n\left(t\right)$ is the noise and ${\tau }_{nj}$ is a delay matrix. The delay matrix defines the phases of the time‐series functions which can be interpreted as distances [Cabral et al., 2011] or conduction delays. Four coupled time‐series functions expressed as $\sin \left({\theta }_n\right),$ were derived using the Kuramoto model. These functions were used to generate 4‐region‐FC networks by Eqs. (7,8) and then to calculate their phases using Eq. (11). We tested whether these calculated phases equal the predefined phases ( ${\tau }_{nj}$) as a function of the global coupling strength and the noise level.

EXPERIMENTAL METHODS

Computer Simulations

The fourth‐order Runge–Kutta method was used to simulate Eq. (13). The symmetric delay matrix had the following prechosen phase relations: ${\vartheta }^{j_2}-{\vartheta }^{j_1}=0.3 \mathrm{r}\mathrm{a}\mathrm{d}$; ${\vartheta }^{j_3}-{\vartheta }^{j_1}=0.8 \mathrm{r}\mathrm{a}\mathrm{d};$ and ${\vartheta }^{j_4}-{\vartheta }^{j_1}=1.05 \mathrm{r}\mathrm{a}\mathrm{d}$. These phases were chosen arbitrarily with the exception that they are similar to the delays found in resting‐state MRI data. The frequencies $\left({\omega }_n\right)$ were derived from a Gaussian distribution centered at 0.02 Hz with a width of 0.01 Hz. This center frequency was chosen because it is in the range of the dominant frequencies in resting‐state functional MRI data. The global coupling strength was varied from 0.5 to 14. The lower range is the critical coupling strength [Balmforth and Sassi, 2000], while the upper corresponds to the value where the analysis fails. Noise was added for each time step, as a random variable with zero mean and a normal distribution of ${\beta }^2/\Delta t$ with $\Delta t$ the time steps [Tesche and Clake, 1977]. The noise range was 0 $\le \sqrt{\frac{{\beta }^2}{\Delta t}}\le 0.22$, sufficiently wide considering the basis frequency of 0.02 Hz. The initial phases were randomized around the unit circle. 6,000 time‐steps were used with a time‐increment of 0.1 seconds. For each value of the coupling strength and the noise, the simulations were repeated 100 times. Each simulation resulted with four coupled time‐series functions. Wavelet analysis of these functions was carried out, the 4‐region‐FC networks were obtained [Eqs. (7,8)] and their phases were calculated [Eq. (11)]. The means and standard errors of the phases were calculated and presented in the figures. In addition, wavelet analysis of these functions was used to calculate the phase‐differences between pairwise coherences ( ${\vartheta }^{j_2}-{\vartheta }^{j_1}; {\vartheta }^{j_3}-{\vartheta }^{j_1}; {\vartheta }^{j_4}-{\vartheta }^{j_1})$ using Eq. (4), to compare to the results of the 4‐region‐FC analysis. To minimize transient effects, averaging in wavelet space was performed only on points 2,000–4,000 (20–40 seconds) and all wavelet frequencies were averaged together. The simulations were performed using custom‐developed IDL software. The Runge–Kutta algorithm was translated to IDL from FORTRAN using the code given in Daniels thesis [Daniels, 2005].

Subjects

We investigated 42 healthy control young subjects (20 women, age: 24.14 ± 2.67 years). Subjects were recruited among students at the Hebrew University of Jerusalem. Before inclusion, all subjects were clinically interviewed using the Structured Clinical Interview for DSM‐V (SCID‐5) to exclude past or present psychiatric or neurological disorders. One male subject was excluded due to family history of schizophrenia and another male subject was excluded due to anxiety during the MRI scan, which yielded a final sample of 40 subjects (20 women, age: 24.15 ± 2.74 years). The study was approved by the Hadassah Hebrew University Medical Center Ethics Committee. All participants provided written informed consent prior to inclusion in the study in compliance with the Declaration of Helsinki.

MRI Data Acquisition

Magnetic resonance images were acquired with a 3T Siemens MR scanner at the Neuroimaging Unit of the Edmond and Lily Safra Center for Brain Sciences of the Hebrew University with a 20‐channel head coil. Each participant underwent 10‐minute resting‐state functional MRI during which they were instructed to fixate on a visual crosshair, remain still and awake. Immediately after the scan, each participant confirmed not falling asleep. Functional images were acquired using T₂*‐weighted gradient‐echo echo‐planar imaging (GE‐EPI) sequence with TR = 2 sec, TE = 30 ms, image matrix = 64 × 64, field of view = 192 × 192 mm, flip angle = 90°, resolution = 3 × 3 × 3 mm, interslice gap = 0.45 mm. Each brain volume comprised 30 axial slices, and each functional run contained 300 image volumes. High resolution anatomical images were acquired using a sagittal T1‐weighted magnetization‐prepared rapid acquisition gradient echo (MP‐RAGE) sequence with TR = 2,300 ms, TE = 2.98 ms, inversion time = 900 ms, flip angle = 9°, resolution = 1 × 1 × 1 mm. The T1‐weighted images were acquired for coregistration and normalization of the functional images.

Functional MRI Data Preprocessing and Functional Connectivity Analysis

Standard initial preprocessing of functional MRI data was done using Statistical Parametric Mapping (SPM8, Wellcome Trust Centre for Neuroimaging, London, United Kingdom, http://www.fil.ion.ucl.ac.uk/spm/software/spm8 ). First, functional images were spatially realigned using a least squares approach and a six parameter (rigid body) spatial transformation. Subsequently, functional images were coregistered to high resolution T1 anatomical images, normalized to Montreal Neurological Institute (MNI) space and resampled at an isotropic voxel size of 2 mm. The normalized images were smoothed with an isotropic 8 mm full‐width‐at‐half‐maximum Gaussian kernel. Motion parameter estimates were carefully checked for each individual separately. Subjects were excluded if head motion reached voxel size in any direction. Average maximal displacement for subjects was less than 1 mm. Further preprocessed was done using CONN toolbox [Whitfield‐Gabrieli and Nieto‐Castanon, 2012]. Confounds were removed by regression, including motion parameters and the first principal component of CSF and white matter signals. Regression‐out of confounds was done to minimize effects of potential physiological and non‐neuronal signals such as cardiac and respiratory signals, without the risk of artificially introducing anticorrelations into the functional connectivity estimates [Bianciardi et al., 2011; Chai et al., 2011; Fox et al., 2009; Murphy et al., 2009; Weissenbacher et al., 2009]. In the next steps, linear detrending, despiking, and band‐pass filtering (0.01–0.2 Hz) were applied. A wider frequency filter than commonly used was intentionally chosen to test the contribution of higher frequency bands.

Connectivity Analysis

All further calculations were performed with IDL version 8.2.0 (Exelis Visual Information Solutions, Inc.) using custom‐developed software. The complex Morlet wavelet functions were chosen for wavelet analysis since they have been shown to provide a good trade‐off between time and frequency localization [Muller et al., 2004]. We used 3 for the smallest scale, 2 for the time resolution and 25 scales to cover our entire frequency window. Wavelet software was provided by C. Torrence and G. Compo available at: http://paos.colorado.edu/research/wavelets [Torrence and Compo, 1998]. The 25 frequency scales were further averaged into 5 frequency scales: 0.02–0.03 Hz; 0.03–0.044 Hz; 0.047–0.067 Hz; 0.074–0.1 Hz; and 0.1–0.16 Hz.

Selection of Brain Regions

Seed analysis was carried out using the AAL regions. For Brodmann areas analysis, masks of Brodmann areas obtained from the Talairach Daemon atlas were used [Lancaster et al., 2000]. To compare our 4‐region‐FC analysis to the effective connectivity study of Wu et al. [2014], spherical regions of interest (ROIs) centered at the coordinates given by Wu et al. were created using the WFU PickAtlas toolbox [Maldjian et al., 2003, 2004].

Statistics

The statistical analysis was done on the amplitude of the wavelet values [amplitude of Eq. (8‐9)]. On these values, one sample t‐tests were used with a statistical significance threshold of uncorrected voxel‐level P < 0.01 and a cluster‐level threshold of 200 voxels. The cluster size was chosen to set the threshold at P < 0.05, FDR corrected for multiple comparisons. Phases were presented by their group average values on voxels with significant amplitudes.

RESULTS

Computer Simulations

Coupled oscillators produced by the Kuramoto model were used to calculate 4‐region‐FC networks, their phases and the phase‐differences between their pairwise coherences. The means (over 100 simulation runs) and the standard error (SE) of ${\vartheta }^{j_2}-{\vartheta }^{j_1}$ and ${\vartheta }^{j_3}-{\vartheta }^{j_1}$ as a function of the coupling strength and the noise level are shown in Supporting Information Figure 3 (A and B for the 4‐region‐FC and C and D for the pairwise coherences). Results for ${\vartheta }^{j_4}-{\vartheta }^{j_1}$ were similar (not shown). Correct phases were obtained for the 4‐region‐FC calculations for coupling strengths $0.5\le k\le 9.5$ for the model without noise and for coupling strengths $0.5\le k\le 8$ when noise was added to the model. The main effect of noise in the 4‐region‐FC calculations was to reduce the phases by about a fixed value across these coupling strengths. Correct phases were obtained for the pairwise calculations for coupling strengths $0.5\le k\le 8$ for the Kuramoto model with and without noise. The comparison of phase fluctuations between 4‐region‐FC and pairwise calculations for coupling strengths between 0.5 and 8, shows that the 4‐region‐FC analysis is less sensitive to Gaussian noise for the higher noise levels (Supporting Information Figure 4).

Functional Connectivity

Results are presented for the first two wavelet scales (scale 1: 0.02–0.03 Hz and scale 2: 0.03–0.044 Hz) since results for the higher scales were mostly insignificant. The ventral visual system, motor system and default mode network (DMN) were studied. Each system was tested whether it is composed of linear, combined or disconnected quadratic networks and its temporal hierarchy was determined. Using Eq. (7,8), 4‐region‐FC networks were calculated by means of 3‐seed‐Statistical Parametric Maps (hereafter “3‐seed‐SPM”). 3‐seed‐SPMs are seed‐like SPMs but instead of using a single seed, three seeds are used and 4‐region‐FC networks are calculated to construct the 3‐seed‐SPM. For the 4‐region‐FCs calculations, we used the three time‐series functions of the three seeds and a time‐series function of a voxel, for all voxels in the brain. In this way, N 4‐region‐FC networks were used to construct a 3‐seed‐SPM with N the number of voxels. Note that significant clusters in the 3‐seed‐SPMs were defined by the amplitudes (see methods) while means to define significance for the phases will be developed in the future. In addition to the 3‐seed‐SPMs, Eq. (5) was used to calculate for each of these seeds seed‐SPMs that correspond to the amplitude values of the pairwise coherences between the time‐series of the seed and each voxel in the brain. Joint‐seed‐SPM was calculated by taking the mean t‐value for each voxel across the seed‐SPMs of the three seeds. To determine if a system is made of linear, combined, or disconnected quadratic networks, the 3‐seed‐SPM was compared with the joint‐seed‐SPM. For simplicity, comparison was made by counting the shared and unshared significant voxels between the two SPMs. Phases were obtained by Eq. (11) for each subject and their group mean is presented on significant voxels defined in the amplitude 3‐seed‐SPMs.

The ventral visual system

The ventral visual system is used here as a test system to examine the temporal hierarchy obtained by the new 4‐region‐FC analysis, since its hierarchy is relatively well established. The organization of the primate ventral visual system is known to have a sequential order of the visual cortical areas from the visual sensory periphery (the primary visual area or calcarine sulcus) to “higher‐level” areas involved in abstract aspects of vision [Felleman and Van Essen, 1991]. To examine the temporal hierarchy of the ventral visual system, we constructed 4‐region‐FC networks for each subject using the following Brodmann areas (BA): BA17 (primary visual cortex), BA18 (secondary visual cortex), BA37 (fusiform gyrus), and BA21 (middle temporal gyrus). Neural information is expected to flow sequentially from BA17 to BA21 through BA18 and BA37 [Felleman and Van Essen, 1991]. Assuming that time‐lags of the BOLD signals correspond to the latencies of information flow, we expected the phases to be ordered as: ${\vartheta }^{BA17}<{\vartheta }^{BA18}<{\vartheta }^{BA37}<{\vartheta }^{BA21}$. Calculations are presented for wavelet scale 1, with similar results obtained for scale 2. Using Eq. (11), the following phases were obtained (mean ± SE): ${\phi }^a=-0.23 \pm$ 0.16 radians; ${\phi }^b=-0.50 \pm 0.28$ radians; ${\phi }^c=+0.17 \pm 0.14$ radians. Assuming that all phases are smaller than 2π, Eq. (11) gives: ${\vartheta }^{BA18}={\vartheta }^{BA17}+0.03 (\pm 0.11)$ radians; ${\vartheta }^{BA37}={\vartheta }^{BA17}+0.16 (\pm 0.16)$ radians, and ${\vartheta }^{BA21}={\vartheta }^{BA17}+0.37 (\pm 0.16)$ radians which correspond to time latencies of 0.19 seconds from BA17 to BA18, 0.83 seconds from BA18 to BA37, and 1.33 seconds from BA37 to BA21. These results fit the known temporal organization of the ventral visual system [Felleman and Van Essen, 1991].

Second, 3‐seed‐SPMs, seed‐SPMs, and joint‐seed‐SPMs were calculated to identify functional networks of the ventral visual system in the entire brain and to test its linearity and temporal hierarchy. The following seeds were used: left calcarine sulcus, left cuneus and left fusiform gyrus. Supporting Information Figure 5 shows seed‐SPMs for scales 1 and 2 for these three seeds. Substantial overlap is shown between connectivity volumes in these seed‐SPMs. Figure 2 shows the amplitude 3‐seeds‐SPM and joint‐seed‐SPM for wavelet scale 1 with similar results shown for scale 2 (Supporting Information Figure 6). The amplitude 3‐seed‐SPM and the joint‐seed‐SPM are similar to each other with larger connectivity volumes found in the 3‐seed‐SPMs particularly in the occipital and cerebellar regions. For scale 1, the 3‐seed‐SPM resulted with 26,482 significant voxels and the joint‐seed‐SPM with 18,930 significant voxels, 98% of them common to both analyses. For scale 2, the 3‐seed‐SPM resulted with 24,607 significant voxels and the joint‐seed‐SPM with 14,978 significant voxels, 97% of them common to both analyses. These numbers and the visual inspection of the SPMs suggest that the majority of the quadratic networks of the ventral visual system are linear. Note that both analyses identified the sensorimotor cortex to be functionally connected to the ventral visual system.

Figure 2.

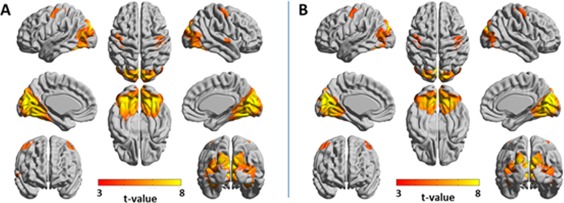
Amplitude 3‐seed‐SPM versus joint‐seed‐SPM of the ventral visual system for wavelet scale 1 (0.02–0.03 Hz). SPMs were constructed from the following seeds: left calcarine sulcus, left cuneus, and left fusiform gyrus. T‐values with P < 0.05, FDR cluster corrected are projected on 3D surface brain templates in MNI space and indicated by the color bar. (A) Amplitude 3‐seed‐SPM, (B) joint‐seed‐SPM. Note the high similarity between the amplitude 3‐seed‐SPM and the joint‐seed‐SPM. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 3 presents the phase 3‐seed‐SPM for wavelet scale 1 and Supporting Information Figure 7 for wavelet scale 2, using the phase of the calcarine sulcus as a reference. Mean group phases are shown for clusters with significant amplitudes. Under the assumption of ${\vartheta }^{\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{e}}<{\vartheta }^{\mathrm{c}\mathrm{u}\mathrm{n}\mathrm{e}\mathrm{u}\mathrm{s}}$ and that the time‐lags of the BOLD signals correspond to the latencies of information flow, the directed hierarchy was obtained for all significant clusters in the brain. As seen, the ventral visual system exhibits a temporal hierarchy generally in line with its known organization.

Figure 3.

Phase 3‐seed‐SPM of the ventral visual system for wavelet scale 1 (0.02–0.03 Hz). SPMs were constructed from the following seeds: left calcarine sulcus, left cuneus and left fusiform gyrus. The phases were calculated with respect to the phase of the left calcarine sulcus and are shown for clusters with significant amplitude (Fig. 2A). (A) The phases in radians are projected on 3D surface brain templates in MNI space and indicated by the color bar. (B) Zoom into nine axial MRI slices covering most of the ventral visual system. MNI z coordinate is indicated for each slice. [Color figure can be viewed at http://wileyonlinelibrary.com]

The motor system

Functional networks of the motor system were identified by using the following seeds: the left precentral gyrus, left supplementary motor area (SMA) and left thalamus. Supporting Information Figure 8 presents seed‐SPMs for these seeds for wavelet scales 1 and 2. Figure 4 presents the amplitude 3‐seed‐SPM and the joint‐seed‐SPM for wavelet scale 1, and Supporting Information Figure 9 shows the amplitude 3‐seed‐SPMs and joint‐seed‐SPM for scale 2. In all scales, the 3‐seed‐SPMs and the joint‐seed‐SPMs were markedly different: in scale 1, the 3‐seed‐SPM resulted with 7,080 significant voxels while the joint‐seed‐SPM resulted with 321 significant voxels, 31% of them common to both analyses. In scale 2, the 3‐seed‐SPM resulted with 3,909 significant voxels while the joint‐seed‐SPM resulted with 3,563 significant voxels, only 14% of them common to both analyses. The 3‐seed‐SPMs included large portions of the precentral gyrus, postcentral gyrus, SMA, thalamus, posterior putamen (in scale 2) and dorsal/posterior insula (scale 2) in both hemispheres. The joint‐seed‐SPMs included smaller parts of the precentral gyrus, postcentral gyrus, thalamus and insula (scale 1) and pre‐ and post‐central regions in both hemispheres in scale 2. The low number of voxels that were significant in both the 3‐seed‐SPM and the joint‐seed‐SPM, suggests that only few networks in the motor system are linear. This can be anticipated also by the inspection of the seed‐SPMs that show minimum overlap between cortical and thalamic seeds, suggesting that coherences between subcortical and cortical regions were only possible through nonlinear phase‐relations. Consequently, we suggest that the motor system, as defined by our seeds, is mainly composed of combined quadratic networks. Of additional interest are regions such as the right somatosensory cortex that were significant only by the joint‐seed‐SPM. Such regions are categorized as belonging to disconnected networks, and could be interpreted as regions connected with the seeds but by higher (>4) order coherences. For example, they could belong to a multiple region network that includes: left thalamus ↔ left SMA ↔ left M1 ↔ right M1 ↔ right S1.

Figure 4.

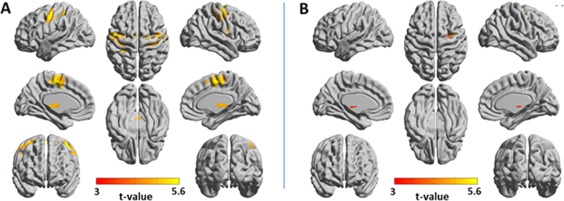
Amplitude 3‐seed‐SPM versus joint‐seed‐SPM of the motor system for wavelet scale 1 (0.02–0.03 Hz). SPMs were constructed from the following seeds: left precentral gyrus, left supplementary motor area and left thalamus. T‐values with P < 0.05, FDR cluster corrected are projected on 3D surface brain templates in MNI space and indicated by the color bar. (A) Amplitude 3‐seed‐SPM, (B) joint‐seed‐SPM. Note the marked differences between the amplitude 3‐seed‐SPM and the joint‐seed‐SPM. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 5 and Supporting Information Figure 10 show the phase 3‐seed‐SPMs for wavelet scales 1 and 2 with the phase of the thalamus as a reference. Figure 5B demonstrates the sensitivity of the analysis: by zooming into the thalamus and presenting the phases with finer color bar, we show that the analysis discriminates between different thalamic nuclei, each with a different phase, as expected by the anatomy [Wu et al., 2014]. Since both bottom‐up and top‐down connections are expected in the motor system, a phase relation for all 4‐region‐FC networks in the motor system cannot be assumed and the system's directed hierarchy cannot be obtained. However, the undirected hierarchy can easily be observed and is of center ↔ out (i.e., sub‐cortex↔cortex) organization: thalamus–SMA–primary motor cortex–sensory motor cortex.

Figure 5.

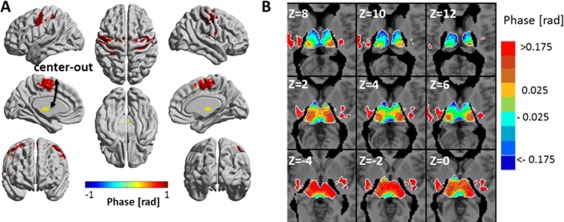
Phase 3‐seed‐SPM of the motor system for wavelet scale 1 (0.02–0.03 Hz). SPMs were constructed from: left precentral gyrus, left supplementary motor area and left thalamus seeds. Phases were calculated with respect to the phase of the left thalamus and are shown for clusters with significant amplitude. (A) The phases in radians are projected on 3D surface brain templates in MNI space and indicated by the color bar. The arrows indicate the suggested center‐out temporal organization. (B) Zoom into nine axial MRI slices at the level of the thalamus with finer color scale for the phase. MNI z coordinate is indicated for each slice. [Color figure can be viewed at http://wileyonlinelibrary.com]

In order to test if the phases are related to the physical distances between brain regions, Supporting Information Table 1 presents the phases (relative to the left thalamus) and the Euclidean distances (calculated between the thalamus and regions' centers) for several AAL regions of the motor system. Each region was the 4th region in a 4‐region‐FC network that included the left thalamus, left SMA and left precentral gyrus. Pearson's correlation (r) between Euclidean distances and phases was 0.79 (P < 0.003), with r = 0.77 for the left hemisphere and r = 0.88 for the right hemisphere. The table (and Fig. 5 and Supporting Information Figure 10) show that the phases are positively related to distances, which strengthen the interpretation of the phases as a measure of the time of information flow.

The default mode network (DMN)

Functional networks of the DMN in the entire brain were identified by using the following seeds: the left medial orbitofrontal cortex, left angular gyrus and left posterior cingulate gyrus. Figure 6 presents amplitude 3‐seed‐SPM and joint‐seed‐SPM for wavelet scale 1 and Supporting Information Figure 11 presents them for scale 2. Supporting Information Figure 12 shows seed‐SPMs of these seeds. The seed‐SPMs show minimum overlap suggesting substantial differences between the 3‐seed‐SPMs and joint‐seed‐SPMs. Indeed, for scale 1, the number of significant voxels in the 3‐seed‐SPM was 23,306 while it was 3,509 in the joint‐seed‐SPM, all of them common to both analyses. In scale 2, the 3‐seed‐SPM resulted with 18,812 significant voxels while the joint‐seed‐SPM resulted with 1,123 significant voxels, all of them common to both analyses. This implies that the majority of the quadratic networks of the DMN are combined networks.

Figure 6.

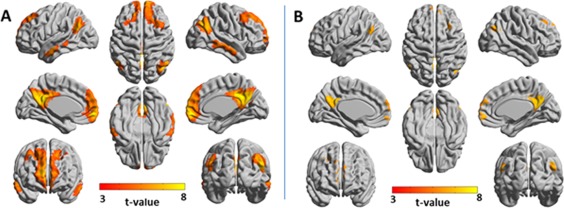
Amplitude 3‐seed‐SPM versus amplitude joint‐seed‐SPM of the default mode network for wavelet scale 1 (0.02–0.03 Hz). SPMs were constructed from the following seeds: left medial orbitofrontal cortex, left angular gyrus and left posterior cingulate gyrus. T‐values with P < 0.05, FDR cluster corrected are projected on 3D surface brain templates in MNI space and indicated by the color bar. (A) Amplitude 3‐seed‐SPM, (B) joint‐seed‐SPM. Note the marked differences between the amplitude 3‐seed‐SPM and the joint‐seed‐SPM. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 7 shows phase 3‐seed‐SPMs for scale 1 with the phase of the left medial orbitofrontal cortex as a reference and Supporting Information Figure 13 shows it for scale 2 for two different choices of a reference. The temporal hierarchy, shown in Figure 7 and Supporting Information Figure 13, suggests an organization along the dorsal ↔ ventral and the anterior ↔ posterior axes (with the latter separated for frontal and posterior cortices). This may propose two or three parallel paths of information flow.

Figure 7.

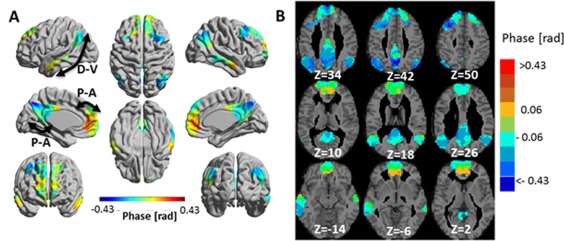
Phase 3‐seed‐SPM of the default mode network (DMN) for wavelet scale 1 (0.02–0.03 Hz). SPMs were constructed from: left medial orbitofrontal cortex, left angular gyrus and left posterior cingulate gyrus seeds. Phases were calculated with respect to the phase of the left medial orbitofrontal cortex and are shown for clusters with significant amplitude. (A) The phases in radians are projected on 3D brain templates in MNI space and indicated by the color bar. The arrows indicate the suggested temporal organizations, with D‐V: dorsal‐ventral and P‐A: posterior‐anterior. (B) Zoom into nine axial MRI slices covering most of the DMN. MNI z coordinate is indicated for each slice. [Color figure can be viewed at http://wileyonlinelibrary.com]

The temporal hierarchy of the DMN was validated by comparing it to the results of a recent study which has used effective connectivity calculated by Bayesian network analysis [Wu et al., 2014]. In this study, Bayesian network analysis for the DMN was conducted on resting‐state data of 14 subjects and effective connectivity was calculated between ROIs selected by independent component analysis (ICA). Here, we conducted 4‐region‐FC calculations for the same ROIs (of the left hemisphere) as in the referred study: posterior cingulate cortex (PCC), medial prefrontal cortex (MPFC), hippocampus (HC), inferior parietal cortex (IPC) and inferior temporal cortex (ITC). Each of these ROIs was the 4th region in a 4‐region‐FC network were the other three regions were the left medial orbitofrontal cortex, left angular gyrus and left posterior cingulate gyrus. The phase of the PCC was used as a reference, along with the assumption of ${\vartheta }^{\mathrm{P}\mathrm{C}\mathrm{C}}>{\vartheta }^{\mathrm{M}\mathrm{P}\mathrm{F}\mathrm{C}}$ based on the finding of the referred study. We obtained the following phase differences (mean ± SE): ${ \vartheta }^{\mathrm{M}\mathrm{P}\mathrm{F}\mathrm{C}}={\vartheta }^{\mathrm{P}\mathrm{C}\mathrm{C}}-0.24 (\pm 0.08)$; ${\vartheta }^{\mathrm{I}\mathrm{P}\mathrm{C}}={\vartheta }^{\mathrm{P}\mathrm{C}\mathrm{C}}+0.02 (\pm 0.08)$; ${\vartheta }^{\mathrm{I}\mathrm{T}\mathrm{C}}={\vartheta }^{\mathrm{P}\mathrm{C}\mathrm{C}}-0.30 (\pm 0.12)$; ${\vartheta }^{\mathrm{H}\mathrm{C}}={\vartheta }^{\mathrm{P}\mathrm{C}\mathrm{C}}-0.18 (\pm 0.2)$. All functional connections between ROIs, defined by their amplitude, were highly significant (t > 10). The phase relations suggest the following temporal hierarchy: ITC → MPFC → HC → PCC → IPC which fits the findings for five (out of six) effective connections found by the Bayesian network analysis [Wu et al., 2014].

DISCUSSION

Analyzing the brain as a set of large‐scale complex networks emerges as a promising strategy to understand brain function in health and disease. However, networks are commonly constructed from undirected pairwise statistical inferences, which limit their interpretation. In contrast, the 4‐region‐FC analysis developed here provides the directed functional connectivity between four time‐series by means of their nonlinear coherences. This analysis is partially related to the field of four‐wave interaction, trispectrum, and/or tricoherence. In these definitions, higher‐order spectra are obtained by Fourier transforms of higher‐order cumulants such that the trispectrum is the Fourier transforms of the fourth cumulants and tricoherence is a measure of the degree of cubic phase coupling. Our analysis is different in that it uses wavelet space and particularly since it uses an inherent symmetry of the wavelet representation which enables to obtain the exact expression for the interaction between four time‐series. Specifically, the same mathematical expression of a single time‐series and of a pairwise coherence enables to obtain an analytical expression for the coherence of four time‐series. In virtue of using the products of four wavelet coefficients, we are implicitly modeling the fourth order statistics of functional connectivity or statistical dependency between four time‐series functions. This sort of characterization enables us to break the symmetries inherent in linear systems analyses (e.g., coherence) and takes us into the realm of nonlinear coupling.

The 4‐region‐FC analysis enables to categorize each quartet of regions as a linear, combined, or disconnected network. This further allows to classify a whole system (e.g., visual or motor) in terms of the congruence or incongruence of explicit three‐way measures of functional connectivity (i.e., 3‐seed‐SPM) and the conjunction of three one‐way measures (i.e., joint‐seed‐SPM). Clearly, this comparison is somewhat anecdotal (based on visual inspection and simple comparison). In principle, it should be possible to test for significant departures from a linear architecture by testing for significant differences between 3‐seed‐SPM measures and joint‐seed‐SPM measures formerly. We will pursue this in future work.

Previous computer simulation studies have suggested that the phase‐lag of pairwise coherences can predict directionality only for a limited range of the coupling strength between the time‐series functions [Hillebrand et al., 2016; Stam and van Straaten, 2012]. To examine how our new analysis depends on the coupling strength and noise, computer simulations were performed using the Kuramoto model. We first demonstrated that the phases of a 4‐region‐FC network infer directionality correctly for global coupling strength comparable to the range found in pairwise coherence simulations. It is hard to relate the value of the coupling strength to any biophysical parameter, thus it remains unclear whether the range of the global coupling strength (in 4‐region‐FC and pairwise coherences analyses) is biological reasonable. However, our experimental results suggest that the coupling between BOLD brain signals, in healthy young subjects, is within the range that gives phases that are related to neuronal information flow. Specifically: (i) the agreement between the temporal hierarchy found by the 4‐region‐FC analysis and the ventral visual system's known organization; (ii) the high correlation between the phases and Euclidean distances in the motor system and (iii) the similar directionality found by the 4‐region‐FC analysis and a previous study applying Bayesian network analysis in the DMN. Second, we note that the phase fluctuations for phases obtained by the 4‐region‐FC analysis were lower than the fluctuations of pairwise coherences. Since 4‐region‐FC analysis is a high order statistic which is less sensitive to Gaussian noise, lower fluctuations are expected. It suggests that the fluctuations observed for example in the visual system (section “The ventral visual system”), are mainly due to individual differences. Consequently, this suggests the possibility of using the new analysis in a single subject.

It must be noted that the categorization of systems (e.g., visual or motor) as mainly composed of linear or combined networks depend on the choice of seeds. To categorize a system fully, a more systematic study of the effect of the choice of seeds is needed and will be done in future work. In here, we only aimed to demonstrate the strength, validity, and capabilities of the new analysis and thus seeds were chosen arbitrarily within a studied system.

In summary, we introduced a new directed functional connectivity method: the 4‐region‐FC analysis method that uses high order statistics to obtain nonlinear interactions between 4 time‐series functions. The full analytical expression for coherences between 4 time‐series was derived, verified by computer simulations and applied to resting‐state fMRI data to obtain directed hierarchy of the ventral visual system, the motor system and the DMN. The analysis can be applied to a variety of different data in brain research and in other disciplines. The new 4‐region‐FC analysis enables to: (i) define functional networks of four time‐series functions; (ii) categorize the architecture of each network as linear, combined, or disconnected; (iii) obtain the network's directed temporal hierarchy and (iv) estimate network information‐transfer efficiency by comparing phases between groups. With the growing interest in describing the brain by global networks using for example graph theory, this new analysis calls for a major revolution in this field by replacing the pairwise interactions with interactions between 4 time‐series functions. This will increase the complexity but will give a more reliable description due to the addition of nonlinearity. In addition, with higher magnetic fields, fMRI data of higher spatial resolution is available and can be used to obtain detailed anatomical paths of information flow and greater understanding of complex processes. All these open new horizons in neuroimaging research.

AUTHOR CONTRIBUTIONS

Gadi Goelman ‐ Conception and design of study, development of the theory, analysis and writing of the article.

Rotem Dan ‐ Data acquisition and preprocessing, assistance in writing of the article.

CONFLICT OF INTEREST

No conflict of interest for all authors.

Supporting information

Supporting Information