Integrated multimodal network approach to PET and MRI based on multidimensional persistent homology

Abstract

Finding underlying relationships among multiple imaging modalities in a coherent fashion is one of the challenging problems in multimodal analysis. In this study, we propose a novel approach based on multidimensional persistence. In the extension of the previous threshold‐free method of persistent homology, we visualize and discriminate the topological change of integrated brain networks by varying not only threshold but also mixing ratio between two different imaging modalities. The multidimensional persistence is implemented by a new bimodal integration method called 1D projection. When the mixing ratio is predefined, it constructs an integrated edge weight matrix by projecting two different connectivity information onto the one dimensional shared space. We applied the proposed methods to PET and MRI data from 23 attention deficit hyperactivity disorder (ADHD) children, 21 autism spectrum disorder (ASD), and 10 pediatric control subjects. From the results, we found that the brain networks of ASD, ADHD children and controls differ, with ASD and ADHD showing asymmetrical changes of connected structures between metabolic and morphological connectivities. The difference of connected structure between ASD and the controls was mainly observed in the metabolic connectivity. However, ADHD showed the maximum difference when two connectivity information were integrated with the ratio 0.6. These results provide a multidimensional homological understanding of disease‐related PET and MRI networks that disclose the network association with ASD and ADHD. Hum Brain Mapp 38:1387–1402, 2017. © 2016 Wiley Periodicals, Inc.

Abbreviations

ADHD

Attention deficit hyperactivity disorder

ADOS

Autism Diagnostic Observation Schedule

ASD

Autism spectrum disorder

AUC

Area under curve

DD

Distance–distance

DTI

Diffusion tensor imaging

FDG

Fluorodeoxyglucose

GH

Gromov‐Hausdorff

MRI

Magnetic resonance imaging

PET

Positron emission tomography

ROI

Regions of interest

SLM

Single linkage matrix

INTRODUCTION

Noninvasive brain imaging techniques such as fluorodeoxyglucose (FDG) positron emission tomography (PET) and T1‐weighted magnetic resonance imaging (MRI) disclose different characteristics of the human brain. PET reveals regional brain metabolism and MRI the brain morphology [Bassett et al., 2008; Gong et al., 2009; He et al., 2007; Phelps et al., 1998]. The inter‐subject and inter‐regional correlation of brain metabolic uptake between brain regions on FDG PET or brain morphology on MRI gives ways to model the brain metabolic or morphologic networks, respectively [Bernhardt et al., 2011; Chen et al., 2008; Chung et al., 2013; He et al., 2007; Hosseini et al., 2012; Huang et al., 2010; Lee et al., 2008; Toussaint et al., 2012]. We refer to these correlation networks based on FDG PET as metabolic networks and those based on T1 MRI as morphological networks, both of which differ from the functional network on functional MRI or structural network on diffusion tensor imaging (DTI). The remaining challenge is to find a way to integrate the networks acquired from the two different imaging modalities of PET and MRI.

The simplest way to integrate two different weighted networks is to find common significant connections by performing a parallel statistical analysis of each modality [Honey et al., 2009; van den Heuvel et al., 2009]. This approach works when one compares each modality within a group or between groups; however, it is difficult to find discordant connections caused by common hidden brain states. Another approach is to construct integrated networks using multimodal imaging data by weighting anatomical connectivity to a functional one [Bowman et al., 2012; Hosseini and Kesler, 2013]. These methods are disadvantageous because it is necessary to determine the proper threshold a priori for each network as well as to choose the mixing ratio of the two in an appropriate way. Bowman et al. (2012) tried to minimize the proposed objective function related with clustering performance, whereas Hosseini et al. (2013) showed the changes of topological measures of the integrated networks at all network densities [Bowman et al., 2012; Hosseini and Kesler, 2013].

In this paper, we propose a new analytical framework based on multidimensional persistent homology that combines networks of two different imaging modalities. We first observed all the changes of topological structure of multimodal integrated networks with various mixing ratios of two modalities without fixing thresholds. Then, we looked for the integrated network having a mixing ratio with the most significant discrimination between the disease group and the controls after performing a 1D projection. The proposed method is a multimodal approach that extends the concept of graph filtration to multiple dimensions [Lee et al., 2012].

We previously proposed the concept of graph filtration based on persistent homology to solve the thresholding problem of unimodal network analysis [Lee et al., 2012]. The multidimensional persistent homology allows two or more thresholds for multimodalities, whereas we vary a single threshold in one dimensional persistent homological analysis [Carlsson and Zomorodian, 2009]. The multifiltration method based on bidimensional persistent homology allowed integration of two different weighted networks into the bisequence of binary networks as the thresholds are varied simultaneously. Here we estimated the number of connected components, called the zeroth Betti number ${\beta }_0.$ It is a fundamental topological quantity in determining the shape of network and distinguishing networks in Algebraic Topology. We also visualized their changes during multifiltration on the β ₀‐plot.

In the bisequence of binary networks, we could extract the sequence of binary networks along a projection line with specific mixing ratio between metabolic and morphological networks. This procedure is a 1D projection of multifiltration. Along the projection line of the sequences of networks, we reorder the edges, reestimate their weights, and construct a new integrated multimodal network. The change in the connected structure of the integrated network could then be represented in an algebraic form, known as a single linkage matrix (SLM). A group comparison of the β ₀‐plot was performed by using a symmetry index and Kolmogorov‐Smirnov‐like (KS‐like) test and deriving a one dimensionally projected SLM using Gromov‐Hausdorff (GH) distance, both of which were based on permutation methods [Chung et al., 2013; Lee et al., 2012].

Our main contributions over the previous publications including our own work [Lee et al., 2012] are as follows:

1. We devise a multivariate extension of univariate persistent homology and its application to multimodal brain network analyses of PET and MRI;

2. We develop a new visualization tool, the β ₀‐plot, for showing the changes of the integrated connected structures of metabolic to morphological correlation networks with various mixing ratios; and

3. We extract the integrated network of metabolic and morphological networks at a certain mixing ratio, discriminating the disease group from the controls by using a 1D projection and its representation as a SLM.

In experiments, we demonstrated the performance of β ₀‐plot and effectiveness of 1D projection using a simulated study with the ground truth. We applied the proposed method, multifiltration, to real datasets consisting of FDG PET and T1 MRI images of 23 attention deficit hyperactivity disorder (ADHD), 21 autism spectrum disorder (ASD) children and 10 pediatric control subjects. The multifiltration is expected to provide a new finding to differentiate between ADHD and ASD, which are brain disorders sharing with similar symptoms.

MATERIALS AND METHODS

Subjects and Image Preprocessing

We used FDG PET and MRI data sets: 23 ADHD children (mean age = 8.1 ±1.6 years), 21 ASD children (mean age = 6.0 ±1.6 years) and 10 control subjects (mean age = 9.5 ±2.6 years). Both ADHD and ASD are neurodevelopmental disorders in children and adolescents. They have numerous overlapping impairments in developmental and cognitive domains. The ADHD children were diagnosed by DSM‐IV diagnostic criteria, Korean version of ADHD rating scale IV (K‐ARS) and Korean version of Kiddie‐Schedule for Affective Disorders and Schizophrenia‐Present and Lifetime version (K‐SADS‐PL). The ASD children were diagnosed by the Korean version of the Autism Diagnostic Interview‐Revised (K‐ADI‐R) and the Korean version of the Autism Diagnostic Observation Schedule (ADOS). The control data was obtained from 10 children who failed to meet the criteria of psychiatric disorder or visited for IQ evaluation. This study was approved by the Institutional Review Board of Seoul National University College of Medicine. PET images were obtained by ECAT EXACT 47 PET scanner (Siemens‐CTI, Knoxville, TN). They were preprocessed using the statistical parametric mapping toolbox (SPM) [Friston et al., 1995]. The MRI data was segmented by customized pediatric templates in Template‐O‐Matic toolbox [Wilke et al., 2008]. All gray matter MRIs were transformed and smoothed and the Jacobian determinant maps were computed based on VBM8 toolbox for SPM.

Network Construction

The brain was parcellated into 93 regions of interest (ROIs) based on AAL [Tzourio‐Mazoyer et al., 2002]. The AAL originally consists of 90 cortical and subcortical regions and 26 cerebellar regions. We used 90 cortical and subcortical regions as nodes and merged 26 cerebellar regions into right and left hemispheres and vermis using the creating ROI option in Marsbar toolbox (http://marsbar.sourceforge.net). The mean FDG uptake within 93 ROIs was extracted as a measurement of PET. The mean Jacobian value within 93 ROIs was extracted as a measurement of MRI using the MarsBar toolbox. The 93 ROIs serve as nodes, $V=\left\{v_1,\dots ,v_p\right\}$ (p = 93).

PET and MRI data have the identical node set V in the same template space. On each node $v_i,$ we have two different imaging measurements ${\mathit{u}}_i^P\in {ℝ}^{n\times 1}$ and ${\mathit{u}}_i^M\in {ℝ}^{n\times 1}$ obtained from PET and MRI, respectively. The distance between two nodes v_i and v_j in the metabolic and morphological networks is estimated by one minus correlation, $x_{ij}=1-\text{corr}({\mathit{u}}_i^P,{\mathit{u}}_j^P)$ and $y_{ij}=1-\text{corr}({\mathit{u}}_i^M,{\mathit{u}}_j^M),$ respectively. We denote the weighted networks for PET and MRI as $\mathcal{P}(V,\mathit{X})$ and $\mathcal{M}(V,\mathit{Y})$, where $\mathit{X}={[x_{ij}]}_{i,j=1,\dots ,p}\in {ℝ}^{p\times p}$ and $\mathit{Y}={[y_{ij}]}_{i,j=1,\dots ,p}\in {ℝ}^{p\times p}$ are the distance matrices of the PET and MRI networks, respectively.

Multidimensional Persistence

The persistent homology has been introduced to solve the thresholding problem of unimodal brain network analysis [Lee et al., 2012]. Given one weighted network $\mathcal{P}(V,\mathit{X})$ and threshold ε a binary network $B_{\mathcal{P}}(\epsilon )$ is obtained by filtering the weighted network $\mathcal{P}(V,\mathit{X})$ by the threshold ε. If the weighted network is repeatedly filtered for the ordered thresholds $\left\{{\epsilon }_{\min }={\epsilon }_1<{\epsilon }_2<\dots <{\epsilon }_q={\epsilon }_{\max }\right\},$ it is decomposed into the sequence of binary networks which satisfy the nested property:

$$B_{\mathcal{P}}({\epsilon }_1)\subseteq B_{\mathcal{P}}({\epsilon }_2)\subseteq \cdots \subseteq B_{\mathcal{P}}({\epsilon }_q).$$

This procedure is called a graph filtration [Giusti et al., 2015; Lee et al., 2011, 2012].

Here we extend this filtration method to the multidimensional version by introducing multidimensional persistence [Carlsson and Zomorodian, 2009]. Suppose that two weighted networks $\mathcal{P}(V,\mathit{X})$ and $\mathcal{M}(V,\mathit{Y})$ are given. They share a common node set, but have different distance matrices between nodes. Two weighted networks are simultaneously bifiltered at two thresholds ω and υ via

$$B_{\mathcal{P},\mathcal{M}}(\omega ,\upsilon )=B_{\mathcal{P}}(\omega )\cap B_{\mathcal{M}}(\upsilon ).$$ (1)

The bifiltered binary network $B_{\mathcal{P},\mathcal{M}}(\omega ,\upsilon )$ is obtained by connecting edges that satisfy $x\le \omega$ and $y\le \upsilon$ in $B_{\mathcal{P}}(\omega )$ and $B_{\mathcal{M}}(\upsilon ),$ respectively. If the threshold values are given by ${\omega }_1<{\omega }_2<\dots <{\omega }_q$ and ${\upsilon }_1<{\upsilon }_2<\dots <{\upsilon }_q,$ the multifiltration can be written as

$$\begin{array}{ccccc}{B}_{\mathcal{P},\mathcal{M}}({\omega }_1,{\upsilon }_1)& \to & \dots & \to & B_{\mathcal{P},\mathcal{M}}({\omega }_q,{\upsilon }_1)\\ \downarrow & & & & \downarrow \\ ⋮& & \ddots & & ⋮\\ \downarrow & & & & \downarrow \\ B_{\mathcal{P},\mathcal{M}}({\omega }_1,{\upsilon }_q)& \to & \dots & \to & B_{\mathcal{P},\mathcal{M}}({\omega }_q,{\upsilon }_q).\end{array}$$

The bifiltration also satisfies the nested property:

$$B_{\mathcal{P},\mathcal{M}}({\omega }_i,{\upsilon }_l)\subseteq B_{\mathcal{P},\mathcal{M}}({\omega }_j,{\upsilon }_m) \text{for} {\omega }_i\le {\omega }_j \text{and} {\upsilon }_l\le {\upsilon }_m.$$ (2)

In Algebraic Topology, the Betti number is used to determine the shape of topological spaces including networks and to distinguish topological spaces [Adler et al., 2010; Carlsson et al., 2005; Edelsbrunner and Harer, 2008; Ghrist, 2008]. The zeroth Betti number β ₀ is the number of CCs which are subsets of the network, where any nodes are connected through edges. In this study, we choose β ₀ as the topological measure and estimate them from the obtained bisequence of binary networks during the bifiltration. The change of β ₀ during filtration is usually visualized by the barcode [Carlsson and Zomorodian, 2009]. However, since the barcode visualizes the change of CCs using bars when varying a threshold, it is not proper to represent the change of β ₀ with respect to two different thresholds ω and υ. Thus, we use β ₀‐plot which visualizes the change of number of CCs with respect to two thresholds ω and υ.

The example of bifiltration is shown in Figure 1. Two networks $\mathcal{P}(V,\mathit{X})$ and $\mathcal{M}(V,\mathit{Y})$ share nodes, but have different distance measures in (a) and (b). Each edge is encoded into a distance pair $(x_{ij},y_{ij})$ and plotted on the distance–distance (DD) domain in (c). When two networks are simultaneously bifiltered at the threshold pair (ω, υ) only edges in the region $x\le \omega$ & $y\le \upsilon$ are connected as shown in (d). The bisequence of binary networks is obtained by bifiltration at $({\omega }_1,{\upsilon }_1),\dots ,({\omega }_4,{\upsilon }_4)$ in (e). Its β ₀‐plot is illustrated in (f). The β ₀ is a decreasing function of (ω, υ) with the range from 1 to P.

Figure 1.

(a, b) Two networks $\mathcal{P}(V,\mathit{X})$ and $\mathcal{M}(V,\mathit{Y})$ are given with a node set V and distance matrices $\mathit{X}=[x_{ij}]$ and $\mathit{Y}=[y_{ij}].$ (c) The distance pair $(x_{ij},y_{ij})$ of the edge connecting nodes i and j is plotted on the x (horizontal) axis and y (vertical) axis of the x–y plane. The color of dot indicates which edge comes from (a) and (b). (d) The bifiltered binary network $B_{\mathcal{P},\mathcal{M}}(\omega ,\upsilon )$ is constructed by connecting edges that satisfy both $x\le \omega$ and $y\le \upsilon .$ In this bifiltered network, the number of CCs β ₀ at (ω, υ) is 2. (e) Bisequence of binary networks is obtained by bifiltration of $\mathcal{P}(V,\mathit{X})$ and $\mathcal{M}(V,\mathit{Y}).$ (f) The number of CCs β ₀ of (e) is plotted on the distance(x)‐distance(y) plane. This is called β ₀‐plot. [Color figure can be viewed at http://wileyonlinelibrary.com]

1D Projection

The filtration is a procedure to add edges in increasing order of edge weights. When two different kinds of distance (or edge weight) measures are defined in the network, the order of adding edges depends upon how to prioritize two measures. Here we change the priority of two measures by controlling a mixing ratio γ between them and increase a pair of thresholds (ω, υ) along the line with mixing ratio

$$y=ax+b,\hspace{1em}\left(a=\frac{\gamma }{1-\gamma }, b=\frac{1-2\gamma }{1-\gamma }c\right)$$ (3)

where γ is in [0, 1] and c is a large enough positive constant satisfying $x,y\in [0,c].$ If we choose γ = 0, two thresholds (ω, υ) are varied along the line y = c and the order of edges is affected only by ω because υ =c and $\left\{(x,y)|x\le \omega \& y\le c\right\}=\left\{(x,y)|x\le \omega \right\}.$ If we choose γ = 1, the order of edges is affected only by υ. The reason why the equation of the line (3) is somewhat complicated is to include such uni‐filtered cases. If 0 < γ < 0.5, the procedure to add edges is more influenced by the change of ω under the condition of $\upsilon \ge b.$ If 0.5 < γ < 1, it is more influenced by the change of υ under the condition of $\omega \ge -b/a.$ If γ = 0.5, it is affected equally by ω and υ.

Suppose that two sequences of thresholds $0\le {\omega }_1\le \dots \le {\omega }_q\le c$ and $0\le {\upsilon }_1\le \dots \le {\upsilon }_q\le c$ are given, and ω_i and ${\upsilon }_i$ satisfy the Eq. (3) with the given γ. The filtration along the line generates a sequence of binary networks as follows:

$$B_{\mathcal{P},\mathcal{M}}({\omega }_0,{\upsilon }_0)\to B_{\mathcal{P},\mathcal{M}}({\omega }_1,{\upsilon }_1)\to \cdots \to B_{\mathcal{P},\mathcal{M}}({\omega }_q,{\upsilon }_q).$$

This procedure is called 1D projection and the projected sequence of bifiltered networks satisfies the persistence property in Eq. (2). We integrate two different kinds of measures of edge weight by 1D projection and control the integration ratio by γ. The example of 1D projection is shown in Figure 2 when γ = 0, < 0.5, = 0.5, > 0.5, and = 1

Figure 2.

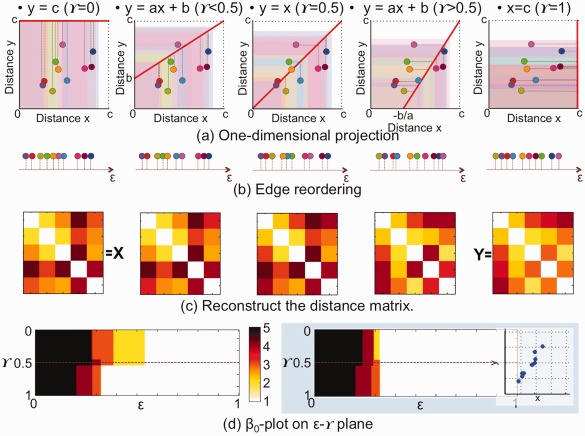
1D projection of the example in Figure 1. (a) The edges are projected onto the line y = ax + b in Eq. (3) when γ = 0, 0.4, 0.5, 0.6, and 1 from left to right. (b) Reordered edges along the projected line. The edge weight (distance) ε is recalculated on the projected line. (c) According to the new edge weights, an edge weight matrix is reconstructed at each γ The reconstructed matrices at γ = 0 and 1 are exactly the same to X and Y in Figure 1 (b). (d) The β ₀‐plot on the x–y plane in Figure 1 (f) is transformed onto the ε − γ plane. As shown in the right blue box, if two kinds of edge weights are similar, β ₀‐plot on the ε − γ plane tends to be symmetric with respect to γ = 0.5. [Color figure can be viewed at http://wileyonlinelibrary.com]

1D projection can be thought as a function π that project the edge onto the line (3) as follows:

$$\pi :(x_{ij},y_{ij})\to (x_{ij}^{\prime },y_{ij}^{\prime })=\{\begin{array}{cc}\left(\frac{y_{ij}-b}{a},y_{ij}\right)\hfill & \text{if} y_{ij}>a{x}_{ij}+b,\hfill \\ \left(x_{ij},a{x}_{ij}+b\right)\hfill & \text{otherwise}.\hfill \end{array}$$

A new edge weight z_ij on the projected line is the normalized Euclidean distance between x‐intercept when γ > 0.5 or y‐intercept when $\gamma \le 0.5$ and $(x_{ij}^{\prime },y_{ij}^{\prime }),$ that is,

$$z_{\gamma ,ij}=\{\begin{array}{cc}\frac{\sqrt{x_{ij}^{\prime 2}+{(y_{ij}^{\prime }-b)}^2}}{\sqrt{c^2+{(c-b)}^2}}\hfill & \text{if} \gamma <0.5,\hfill \\ \frac{\sqrt{{(x{\prime }_{ij}+\frac{b}{a})}^2+y_{ij}^{\prime 2}}}{\sqrt{{(c+\frac{b}{a})}^2+c^2}}\hfill & \text{otherwise}.\hfill \end{array}$$ (4)

The denominator of Eq. (4) is a normalization term to set the maximum threshold value as 1. In this way, an integrated network with a new edge weight matrix ${\mathit{Z}}_{\gamma }=[z_{\gamma ,ij}]$ is obtained at each γ by reweighing and reordering edges on the projected line. We can apply the filtration to the new integrated network and estimate the change of β ₀ by varying a new threshold ε. The proposed method of multifiltration contains all possible edge‐sorting procedures with various mixing ratios γ between two kinds of edge weights.

Figure 2 shows a procedure of 1D projection of the example in Figure 1. In (a), the edges are projected onto the lines with γ = 0, 0.4, 0.5, 0.6 and 1 from left to right. The reordered edges on the projected line are shown in (b) and new integrated edge weight matrices estimated at various γs are shown in (c). After the filtration of each edge weight matrix, the number of CCs ${\beta }_0(\epsilon ,\gamma )$ is plotted on the $\epsilon -\gamma$ plane in the left part of (d). The figure in (d) has the same information of β ₀ as Figure 1(f), but the former is plotted on the $\epsilon -\gamma$ plane and the latter is on the x – y plane. The right part in the blue box of (d) shows another example of DD plot of 10 edges. In this example, two different edge weight measures are highly correlated. In this case, the β ₀‐plot is more symmetric with respect to γ = 0.5 than one in the left part of (d).

β ₀‐Plot Comparison

Chung et al. (2013) proposed Kolmogorov‐Smirnov‐like (KS‐like) test statistic, $T=\underset{\epsilon }{\sup }|{\beta }_0^1(\epsilon )-{\beta }_0^2(\epsilon )|$ for testing the difference between two barcodes ${\beta }_0^1$ and ${\beta }_0^2$ obtained from two different groups [Chung et al., 2013]. KS‐like test statistic can also be applied to multidimensional β ₀‐plot comparison. In our case, β ₀ is a function of two thresholds $(\epsilon ,\gamma )$ instead of one threshold ε:

$$T=\underset{\epsilon ,\gamma }{\sup }|{\beta }_0^1(\epsilon ,\gamma )-{\beta }_0^2(\epsilon ,\gamma )|.$$

The KS‐like test statistic for testing the null hypothesis that two β ₀‐plots were not different is the maximum of absolute value of ${\beta }_0^1(\omega ,\upsilon )-{\beta }_0^2(\omega ,\upsilon ).$ Since we are maximizing over all possible thresholds ε and γ, the multiple comparisons issues are automatically taken care of. The null distribution is estimated by the permutation method.

We also check the symmetry index of β ₀‐plot on the $\epsilon -\gamma$ plane with respect to γ = 0.5. The symmetry index δ is estimated by

$$\delta =\frac{1}{0.5}{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{0.5}|}}{\beta }_0(\epsilon ,\gamma )-{\beta }_0(\epsilon ,1-\gamma )|d\gamma d\epsilon .$$

The more symmetrical the β ₀‐plot is, the closer δ is to 0. If two edge weight matrix are exactly the same, their β ₀‐plot is symmetric and its δ is equal to 0. Although the reverse is not true, we can compare global connected patterns between two edge weight matrices using the symmetry index of their β ₀‐plot. Here, we used the symmetry index of β ₀‐plot in two ways. First, we integrated two different modalities, PET and MRI, using β ₀‐plot and compared global connected patterns between PET and MRI in each group. Second, we applied the β ₀‐plot method to the integrated edge weight matrices of each pair of groups and compared global connected patterns between ADHD and ASD, ADHD and CON, and ASD and CON at various mixing ratio γ.

Single Linkage Matrix and Gromov‐Hausdorff Distance

The single linkage matrix (SLM) D shows the local change of CCs [Carlsson and Mémoli, 2008, 2010; Lee et al., 2012]. The element of SLM $\mathit{D}={[d_{ij}]}_{i,j=1,\dots ,p}$ is the minimum threshold value when two nodes v_i and v_j are connected directly or indirectly by merging into the same CC. The mathematical definition is given by

$$\mathit{D}=[d_{ij}]=[\underset{{}_{P_{ij}}}{\min }\underset{{}_l}{\max }{x}_{p_l,p_{l+1}}],$$

where $P_{ij}=\{v_i=p_0,\cdots ,p_k=v_j\}$ is a path between two nodes v_i and v_j [Gower and Ross, 1969]. The minimum is taken over every possible path P_ij between v_i and v_j. The quantity d_ij is called a single linkage distance (SLD).

The Gromov‐Hausdoff (GH) distance was used for estimating the difference between two matrices such as edge weight matrices and SLMs [Carlsson and Mémoli, 2008, 2010; Lee et al., 2012]. The GH distance can be viewed as a special case of general framework of type‐I‐error estimation under multiple comparisons [Chung, 2013]. Given two SLMs ${\mathit{D}}^1=[d_{ij}^1]$ and ${\mathit{D}}^2=[d_{ij}^2]$ with the same node set V, their difference is found by the hypothesis test by setting up a null hypothesis of no difference between two distances $d_{ij}^1$ and $d_{ij}^2$, and an alternative hypothesis:

$$H_0^B:d_{ij}^1=d_{ij}^2\hspace{0.17em}\hspace{0.17em}\mathrm{v}.\mathrm{s}.\hspace{0.17em}\hspace{0.17em}{H}_1^B:d_{ij}^1\ne d_{ij}^2.$$ (5)

This hypothesis is for local difference of the connectivity $d_{ij}^1$ and $d_{ij}^2$ in two different networks. For the comparison of global difference between two different networks, the hypotheses are given by

$$H_0:d_{ij}^1=d_{ij}^2 \text{for} \text{all} i,j\hspace{0.17em}\mathrm{v}.\mathrm{s}.\hspace{0.17em}{H}_1:d_{ij}^1\ne d_{ij}^2 \text{for} \text{some} i,j.$$ (6)

The null hypothesis H ₀ is the intersection of collection of hypotheses [Chung, 2013]

$$H_0={\displaystyle \underset{\forall i,j}{\cap }{H}_0^B}(i,j).$$

Then, the type‐I error α for testing two sided test under the multiple comparisons is given by

$$\begin{array}{c}\alpha =P\left({\displaystyle \underset{\forall i,j}{\cup }\left\{Z(i,j)>h\right\}}\right)=1-P\left({\displaystyle \underset{\forall i,j}{\cap }\left\{Z(i,j)\le h\right\}}\right)\\ =1-P\left(\underset{\forall i,j}{\sup }Z(i,j)\le h\right)=P\left(\underset{\forall i,j}{\sup }Z(i,j)>h\right),\end{array}$$ (7)

where Z(i, j) is actually $|d_{ij}^1-d_{ij}^2|$, i.e., the difference between SLDs.

The GH distance between two SLMs is defined as

$$d_{GH}({\mathit{D}}^1,{\mathit{D}}^2)=\underset{\forall i,j}{\sup }|d_{ij}^1-d_{ij}^2|$$

[Carlsson and Mémoli, 2008; Lee et al., 2011, 2012; Mémoli, 2011]. d_GH can substitute $\underset{\forall i,j}{\sup }Z(i,j)$ in Eq. (7). Now, we can write the type‐I error of group differences through GH distance as

$$\alpha =P\left(d_{GH}({\mathit{D}}^1,{\mathit{D}}^2)>h\right).$$

The permutation method is performed to test Eq. (6). Two bimodal datasets of PET and MRI for group 1 and group 2 with sample size n ₁ and n ₂ are given. The group labels are shuffled randomly and two distance matrices ${\mathit{X}}^i$ and ${\mathit{Y}}^i$ of PET and MRI networks are estimated for the ith group $(i=1,2).$ By applying 1D projection with γ = 0, …, 1_, we obtain the sequence of edge weight matrices $\frac{1}{2}{\mathit{X}}^i={\mathit{Z}}_0^i,\dots ,{\mathit{Z}}_1^i=\frac{1}{2}{\mathit{Y}}^i$ by the Eq. (4) and one of SLMs ${\mathit{D}}_0^i,\dots ,{\mathit{D}}_1^i.$ This procedure is repeated 5,000 times. Then, we estimate the null distribution of $d_{GH}({\mathit{D}}_{\gamma }^1,{\mathit{D}}_{\gamma }^2)$ at γ = 0, …, 1. Using two original datasets, we estimate $d_{GH}({\mathit{D}}_{true,\gamma }^1,{\mathit{D}}_{true,\gamma }^2)$. Then, the type‐I error α with the hypothesis Eq. (6) for global difference is calculated by the percentile of $d_{GH}({\mathit{D}}_{true,\gamma }^1,{\mathit{D}}_{true,\gamma }^2)$ in the null distribution of $d_{GH}({\mathit{D}}_{\gamma }^1,{\mathit{D}}_{\gamma }^2).$

RESULTS

Simulation

This section describes the performance of β ₀‐plot and the effectiveness of 1D projection using a simulated study with the ground truth. The simulation was used to test whether the symmetry index and KS‐like test statistic were related to the known “ground truth” common connections shared by the bimodal networks. In addition, we showed that the integrated network obtained by the 1D projection represented the group difference better than each unimodal network when the simulated bimodal networks had shared connections.

Data simulation

We simulated two bimodal networks of two groups. A group A had bimodal networks with no shared connections, and the other group B had bimodal networks with shared connections. The percentage of shared connections of group B was varied at 10, …, 100%. Each data of two groups consisted of 20 subjects and 100 nodes [Yoo et al., 2017]. We sampled the data for the first subject from a normal distribution of zero mean and 0.3 standard deviation (s.d.). The data of the remaining 19 subjects was constructed by adding the Gaussian noise with zero mean and 0.1 s.d. to the first sampled data. We then estimated an edge weight matrix based on one minus correlation of the sampled data. This procedure was repeated twice and we assigned the group A to the obtained two edge weight matrices of bimodal networks that shared no common edge. The bimodal networks of group B were constructed by adding the Gaussian noise with zero mean and 0.1 s.d. to two edge weight matrices of group A. To make common connections in the bimodal networks of group B, we selected 10% of edges in one of two edge weight matrices and replaced them with edge weights in the other matrix. During the replacement, we added the Gaussian noise with zero mean and 0.1 s.d. to the replaced edge weights. We then estimated β ₀‐plots of the bimodal networks of groups A and B, their symmetry indexes, and KS‐like tests statistic between them. The simulations were performed 1000 times by increasing the percentage of common connections of the group B by 10% up to 100%.

Simulation results of β₀‐plot

Figure 3a,b illustrate the symmetry index and KS‐like test statistic with respect to the percentage of shared connections. The box plots summarise the results of 1000 simulations. The symmetry index at 0% in (a) was estimated from the β ₀‐plot of group A. The symmetry index at 10%,…, 100% was estimated from the group B. The KS‐like test statistic estimated the difference between β ₀‐plots of groups A and B. From the results, we found that when the percentage of shared connections increased, the symmetry index decreased and KS‐like test statistic increased (P < 0.0001, linear regression analysis). In this way, the symmetry index and KS‐like test statistic are related to the percentage of shared connections in bimodal networks and, therefore, we can use the symmetry index and KS‐like test statistic for estimating the difference between two bimodal networks based on their shared connected structures.

Figure 3.

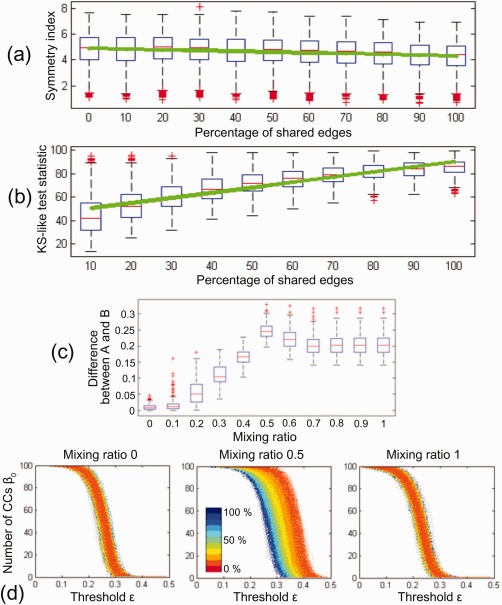
Results of simulated data. (a) Symmetry index of β ₀‐plot and (b) KS‐like test statistic between β ₀‐plots with respect to the percentage of shared edges. The box plots summarize the results of 1,000 simulations. The green line was obtained by the linear regression analysis. When the percentage of shared edges increases, the symmetry index decreases and KS‐like test statistic increases (P < 0.0001 linear regression analysis). (c) Difference between integrated networks of groups A and B at the mixing ratio 0, 0.1,…, 1. The difference between networks were obtained by GH distance between their SLMs. The group difference was maximized at the mixing ratio 0.5 (P < 0.0001, two‐sample t‐test). (d) β ₀‐plots of integrated networks at the mixing ratio 0, 0.5, and 1. The line color represents the percentage of shared connections in the bimodal networks at 0%,…, 100%. The integrated networks at the mixing ratio 0.5 (middle) was affected by the percentage of shared connections (P < 0.0001 linear regression analysis of AUC of β ₀). [Color figure can be viewed at http://wileyonlinelibrary.com]

Simulation results of 1D projection

To demonstrate the effectiveness of 1D projection, we obtained the sequence of integrated networks from the bimodal networks of each group. The sequence of integrated network was estimated at the mixing ratio γ = 0, 0.1,…, 1. The difference between integrated networks of groups A and B was estimated by GH distance of SLMs of integrated network at each mixing ratio. Figure 3c illustrates the difference between groups with respect to the mixing ratio when the group B had the bimodal networks that shared 100% common edges. When γ is 0 or 1, it is the same as the unimodal case. As mentioned in “Data simulation” section, we generated two simulated bimodal networks in groups A and B, one of bimodal networks was similar between the two groups and the other was different. Thus, it is natural that the difference at γ = 0 was smaller than one at γ = 1 in (c). However, the largest difference between groups was found in the integrated networks at γ = 0.5 (P < 0.0001, two‐sample t‐test).

To find the reason why the maximum difference was found at the mixing ratio 0.5, we observed the connected structure of the integrated network at γ = 0.5 by changing the percentage of common edges from 10% to 100%. Figure 3d shows the change of β ₀ over the threshold of the integrated network at γ = 0, 0.5, 1. The line color represents the percentage of common connections. Unlike the unimodal networks at γ = 0 (left) and 1 (right), the integrated network at γ = 0.5 (middle) was affected by the percentage of common edges. When the number of common connections increased, the integrated network at 0.5 was tightly integrated. To quantify the integration pattern, we estimated the area under curve (AUC) of ${\beta }_0.$ The larger the AUC is, the more loosely integrated the network is. We performed the linear regression analysis between AUC and the percentage of shared connections and found the significant relationship between AUC of β ₀ and the percentage of shared connections (P < 0.0001). During the 1D projection, the order of edges is more affected by the larger one of the two edge weights since the multifiltration is done by AND operation in Eq. (1). If the connection information is inconsistent in the bimodal networks, the integrated edge weights tend to follow larger one. Thus, if the bimodal networks do not have any relationship, the integrated network will be loosely integrated. This makes the largest difference in the integrated network at the mixing ratio 0.5 in Figure 3c.

Application

Distance–distance plot

The DD plots of ADHD, ASD and CON are shown in Figure 4a–c. In each plot, the horizontal and vertical axes represent the edge weights of PET and MRI, respectively. Each dot represents an edge and different edges have different colors as shown in (d). The cross‐correlations between distances of PET and MRI in ADHD, ASD and CON were 0.354, 0.205, and 0.194, respectively. They were not statistically significant when compared to the cross‐correlation of random networks obtained by the permutation method. We estimated the distance from dots to the black line y = x and plotted the histogram of distance above the DD plot. The percentage of edges that have larger distance in metabolic connections than in morphological connections was 50.4%, 54.5%, and 68.0% for ADHD, ASD and CON, respectively. The edges of CON (68.0%) were significantly large with the level 0.001 as compared to 5,000 randomly permuted data.

Figure 4.

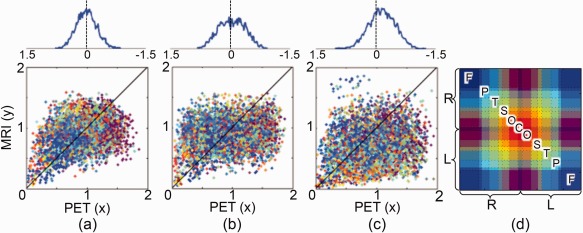
The DD plot of (a) ADHD, (b) ASD and (c) CON. The horizontal and vertical axes represent the distances (1‐corr) of edges on the networks of PET and MRI, respectively. Each dot is an edge and the color of edge is shown in (d). The abbreviations F, P, T, S, O, and C represent frontal, parietal, temporal, subcortical, occipital, and cerebellar regions. R and L represent right and left hemispheres. The black line represents y = x _. The distance from dots to y = x is estimated and its histogram is plotted above each DD plot. [Color figure can be viewed at http://wileyonlinelibrary.com]

β₀‐plot between PET and MRI

We applied the multifiltration method to two distance matrices of PET and MRI of each group. The β ₀‐plots of ADHD, ASD and CON are illustrated in Figure 5a–c, respectively. The horizontal and vertical axes represent the threshold ε and the mixing ratio γ between PET and MRI, respectively. The color of β ₀‐plot is varied depending on the number of CCs β ₀ at (ε, γ)_.

Figure 5.

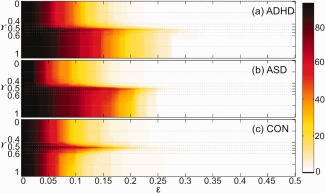
β ₀‐plots between PET and MRI of (a) ADHD, (b) ASD, and (c) CON on the ∈ − γ plane. The vertical axis represents a mixing ratio γ and the horizontal axis represents a new threshold ∈ on the projection line with mixing ratio γ The color in β ₀‐plot in (a,b) is varied according to the zeroth Betti number β ₀ between 1 and the number of nodes P = 93_. When β ₀ becomes larger, the color changes from white to dark red as shown in the right colorbar. [Color figure can be viewed at http://wileyonlinelibrary.com]

We did KS‐like test to show the difference of β ₀‐plot between ADHD and ASD, ADHD and CON, and ASD and CON using the permutation method. The type‐I errors for testing the difference between β ₀‐plots were α = 0.280 (ADHD vs. ASD), 0.022 (ADHD vs. CON), and 0.006 (ASD vs. CON). Thus, in the view of multifiltration, ADHD and CON, and ASD and CON were significantly different with the level 0.05 but ADHD and ASD were not significantly different. The symmetry index with respect to γ = 0.5 on the ε − γ plane was 5.278, 6.393, and 0.500 for ADHD, ASD and CON. When we tested the symmetry index of ADHD, ASD and CON with 5000 randomly permuted data, CON was statistically symmetric with the level 0.005 but ADHD and ASD were not symmetric. Especially, ASD was more asymmetric than ADHD.

β₀‐plot between groups

We estimated the sequence of integrated edge weight matrices of ADHD, ASD and CON at γ = 0, 0.01, 0.02, …, 0.99 and 1. To test the difference between groups, we applied the β ₀‐plot method to the integrated edge weight matrices of pairs of groups at each γ and estimated the symmetry index of β ₀‐plot between ADHD and ASD, ADHD and CON, and ASD and CON at each γ. The results are shown in Figures 6 and 7. In each figure, the first and third rows are the sequence of integrated edge weight matrices obtained by 1D projection. Three β ₀‐plots between ADHD and CON or ASD and CON at γ = 0, 0.5 and 1 are shown in the second row. The symmetry index of β ₀‐plots (in the second row) is displayed in the blue line at the bottom of the figure. In the panel, the vertical and horizontal axes represent the symmetry index and the mixing ratio γ of PET and MRI, respectively. The box plots summarize the results of 5000 randomly permuted data. The red dotted lines indicate the significance level 0.05 of symmetry index. If the symmetry index value is larger than the red dotted line on the top, two groups are different in the view of symmetry of β ₀‐plot.

Figure 6.

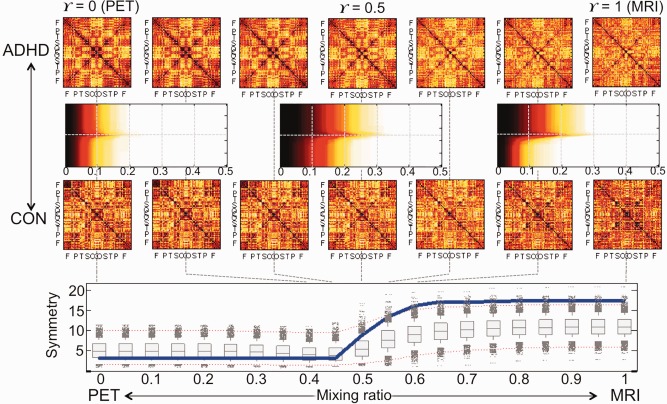
ADHD vs. CON. The first and third rows show the sequence of integrated edge weight matrices of ADHD at γ = 0, 0.4, 0.45, 0.5, 0.55, 0.6, 1 The second row represents the β ₀‐plot between ADHD and CON at γ = 0, 0.5, 1 The blue solid line in the last row shows the symmetry index of β ₀‐plot in the second row. The box plots summarize the results of 5,000 random permutations and two dotted red lines represent the significance level 0.05 (Bonferonni corrected over seven mixing ratios). In the view of symmetry index of β ₀‐plot, the whole brain regions of ADHD network were less integrated than the ones of CON network in the intervals of γ = [0.6, 1] with the level 0.05 (Bonferonni corrected over seven mixing ratios). The AUC of symmetry index at the bottom tended to be large when compared to 5,000 random permutations (P = 0.096). The larger AUC of symmetry index is, the more difference ADHD and CON networks have. [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 7.

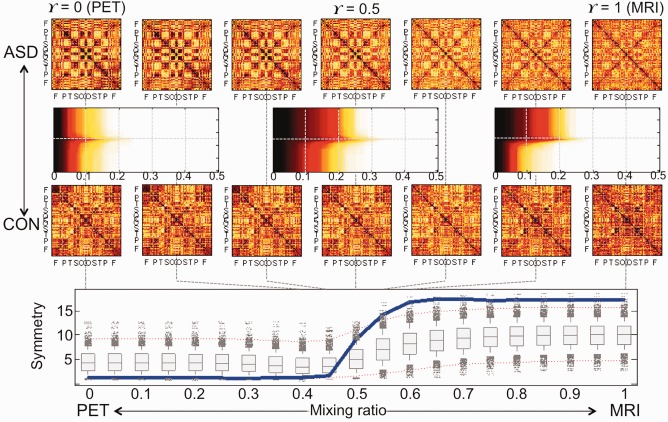
ASD vs. CON. In the view of symmetry index of β ₀‐plot, the brain regions of ASD network were less integrated than the ones of CON network in γ = [0.55, 1] with the level 0.05 (Bonferonni corrected over seven mixing ratios). The AUC of symmetry index at the bottom tended to be large when compared to 5000 random permutations (P = 0.101). The larger AUC of symmetry index is, the more difference ASD and CON networks have. [Color figure can be viewed at http://wileyonlinelibrary.com]

When we compared ADHD and ASD using the symmetry index, we could not find any significant difference between them. The difference between ADHD and CON was found in the intervals of γ = [0.6, 1] and the difference between ASD and CON was found in the intervals of γ = [0.55, 1] (P < 0.05). The integrated edge weight matrix in the intervals of γ > 0.5 was mainly affected by the MRI information. Although the pattern of global integration of ASD and CON was quiet similar in γ = [0, 0.5], the metabolic network of ASD was more tightly integrated than one of CON. On the other hand, the ASD network had looser integration pattern than the CON network when the morphological connectivity mainly affected the integrated edge weight matrix (P < 0.05).

For the multiple comparisons, we calculated the AUC of symmetry index over the mixing ratio. The larger AUC of symmetry index is, the more difference two groups have. The AUCs of symmetry index showed the tendency with the P‐value 0.096 for the test of the difference between ADHD and CON and 0.101 for the difference between ASD and CON. The reason for this insignificant difference is because both ADHD and ASD did not have much difference with the controls at γ = [0, 0.4] (when the metabolic connectivity based on PET mainly dominated in the network integration).

1D projection

We estimated the sequence of edge weight matrices and SLMs at γ = 0, 0.01, 0.02, …, 0.99_, and 1. The sequences of integrated edge weight matrices at γ = 0, 0.4, 0.45, 0.5, 0.55, 0.6_, 1 are plotted in the first and third rows of Figures 6 and 7. The sequence of corresponding SLMs are plotted in Figure 8. We tested the difference of integrated edge weight matrices between ADHD and ASD, ADHD and CON, and ASD and CON based on GH distance and permutation method. ADHD and ASD were significantly different in the intervals of γ = [0, 0.46] and ADHD and CON were significantly different in γ = 0.73, 1 and ASD and CON were significantly different in γ = 0, 0.19 and [0.44, 0.48] with the level 0.05 (Bonferonni corrected over seven mixing ratios). When we tested the difference of SLMs between groups, ADHD and CON were significantly different in γ = [0.54, 0.68] and ASD and CON were significantly different in γ = [0, 0.40] with the level 0.05 (Bonferonni corrected over seven mixing ratios).

Figure 8.

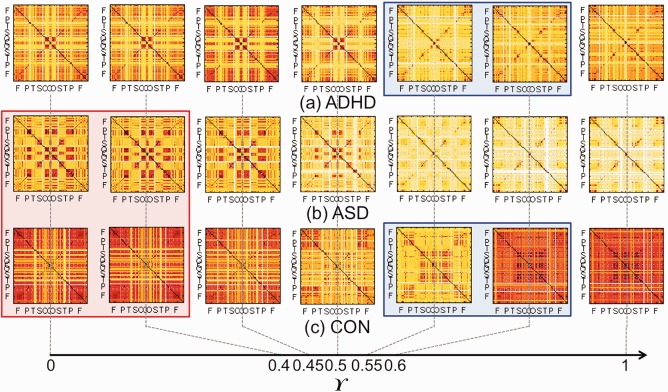
The sequence of integrated single linkage matrices of (a) ADHD, (b) ASD, and (c) CON. The mixing ratio γ is 0 (PET), 0.4, 0.45, 0.5, 0.55, 0.6_, and 1 (MRI). The SLMs of ADHD and CON were significantly different with the level 0.05 in γ = [0.54, 0.68] in the blue box (Bonferonni corrected over the seven mixing ratios). The matrices of ASD and CON were significantly different in γ = [0, 0.40] in the red box (Bonferonni corrected over the seven mixing ratios). [Color figure can be viewed at http://wileyonlinelibrary.com]

Comparison with conventional parametric analysis

When we compared the edge weight matrices between ADHD, ASD and CON based on the conventional parametric analysis, i.e., Fisher's r to z transform and z test, the number of significantly different connections were shown in Table I (P < 0.05, Bonferonni corrected). The difference between ADHD and CON in the metabolic connectivity was found in two connections: (a) between the orbital part of right inferior frontal gyrus and left caudate nucleus, and (b) between right temporal pole and right putamen. ADHD had smaller distance (larger correlation) than CON in both (a) and (b) connections. The difference between ASD and CON in the metabolic connectivity was found in 10 connections. ASD had significantly smaller distances (a) between the orbital part of right inferior/middle frontal gyrus and caudate nucleus, (b) between superior frontal gyrus and left fusiform gyrus, (c) between right lingual gyrus and the dorsolateral part of left superior frontal gyrus, and (d) between left inferior occipital gyrus and left supramarginal gyrus. ASD had significantly larger distances (a) between right paracentral lobule and left middle temporal gyrus, (b) between left amygdala and left postcentral gyrus, and (c) between right olfactory cortex and the triangular part of left inferior frontal gyrus.

Table I.

Number of significantly different connections between groups in the unimodal edge weight matrix of PET and MRI (P < 0.05 Fisher's r to z transform, z test, and Bonferonni correction)

	ADHD	ASD	CON
ADHD		0 (PET)	2 (PET)
ASD	1 (MRI)		10 (PET)
CON	7 (MRI)	0 (MRI)

The difference between ASD and CON was mainly found in the metabolic connectivity in the upper triangular part, while the difference between ADHD and CON was mainly found in the morphological connectivity in the lower triangular part.

In the morphological connectivity, ADHD had smaller distance than ASD only in between left lingual gyrus and left middle temporal gyrus. ADHD had 7 larger morphological distances than CON (a) between left amygdala and left globus pallidum, (b) between right paracentral lobule and hippocampus and left fusiform gyrus, (c) between left inferior temporal gyrus and left inferior parietal gyrus, (d) between right thalamus and left cuneus, (e) between right paracentral lobule and left hippocampus, and (f) between right inferior temporal gyrus and left middle temporal gyrus. There was no significant difference between ASD and CON in the morphological connectivity. The difference between ASD and CON was mainly found in the metabolic connectivity, while the difference between ADHD and CON was mainly found in the morphological connectivity.

DISCUSSION

Edge Weights in Respective Metabolic and Morphological Connectivity Networks

Although the relationship between functional connectivity based on functional MRI and structural connectivity on DTI has been reported in the literature [Bowman et al., 2012; Greicius et al., 2009; Skudlarski et al., 2008; van den Heuvel et al., 2009], the relationship between metabolic and morphological connectivity based on FDG PET and T1 weighted MRI has been rarely documented. Previous studies comparing functional and structural brain connectivity disclosed that the brain regions might be functionally connected through direct or indirect anatomical connections [Bowman et al., 2012]. If metabolic connectivity is related closely to functional connectivity and morphological connectivity to structural connectivity, metabolic connections will tend to have larger distance than morphological connections. In experiments, the metabolic connectivity in CON showed larger edge weights than the morphological connectivity (P = 0.001). However, such a result was not found in ADHD and ASD.

Comparison With Conventional Parametric Analysis

In the results of conventional parametric analysis, the difference between ASD and CON was mainly found in the metabolic connectivity, while the difference between ADHD and CON was mainly found in the morphological connectivity. These results were similar to the results of 1D projection at the mixing ratio 0 and 1 in “1D projection” section. When we tested the group difference of integrated edge weight matrices between ADHD and CON and between ASD and CON based on GH distance and permutation method, ADHD and CON were significantly different in γ = [0.73, 1] where the morphological connectivity mainly affected the integration and ASD and CON were significantly different in γ = 0, 0.19 and [0.44, 0.48 where the metabolic connectivity mainly affected the integration (P < 0.05).

When we compared the groups using SLM, the difference between ADHD and controls was found in the interval γ = [0.54, 0.68] in Figure 8 (P < 0.05). It means that the difference of local connected structure between ADHD and controls might be hidden both in the metabolic and morphological networks and it could be extracted by integrating two different network information. We also compared the difference between modalities based on the symmetry of β ₀‐plot. From the results, the asymmetric change between the metabolic and morphological connectivity was found both in ADHD and ASD, but not found in the controls. In this way, our approach provides complementary information of bimodal brain networks. The standard statistical parametric approach can't incorporate the integration of bimodal network analysis. However, the proposed method could show the integration procedure from one modality to the other and find the maximum difference between groups during the integration.

Asymmetric Change of ASD in the Multidimensional β ₀‐Plot

In Figure 5c, the changes of β ₀‐plot during filtration were almost symmetric between PET and MRI in control subjects. However, the changes looked asymmetric in ASD between PET and MRI in Figure 5b as β ₀ decreased quickly during the filtration in the metabolic connectivity of FDG PET but slowly in the morphological connectivity of T1 MRI. Neurodevelopmental disorders such as ASD involve abnormal functional and structural organizations rather than neuronal cell death or tissue loss as demonstrated by histo‐pathological examinations in ASD which showed that neuronal elimination decreased and myelination increased without neuronal population loss [Aylward et al., 2002; Courchesne et al., 2001]. This dysmaturation could have affected morphological connectivity, which we revealed in this investigation, and would have resulted in the loose integration of morphological connections between brain areas in Figure 7. We interpreted this fact as an indication that the inter‐regional connections were weaker. In ASD, the metabolic connectivity showed the contrary finding of the tighter integration of metabolic connections between brain areas, which would represent a compensatory effort of brain areas to overcome morphological loose connectivity. In brief, the dysmaturation differentially affected the morphological association of gray matter in brain regions and the functional association of cerebral metabolic activity.

Connectivities of Difference Between ADHD and Controls in Local Connected Components

When the global connected structures were compared by the symmetry index of β ₀‐plot between groups in Figure 6, it was shown that the information of MRI was more useful to discriminate ADHD and controls than one of PET. It seems to be related to the brain maturation delay in children with ADHD [Shaw et al., 2007; Vaidya, 2012]. SLMs obtained from the integrated edge weight matrices between ADHD and controls were different in the interval of γ = [0.54, 0.68] with the level 0.05. Using the integrated multimodal network at γ = 0.6 the different single linkage connections were found (a) between right precentral gyrus and other brain regions, (b) basal ganglia and paracentral lobule, temporal pole, amygdala, hippocampus, and occipital and cerebellar regions, and (c) right supramarginal gyrus in the parietal region and some frontal areas such as olfactory cortex, gyrus rectus, inferior frontal and superior frontal regions, (d) left Rolandic operculum in the frontal lobe and other brain regions, and (e) left Heschl gyrus in the temporal lobe and other brain regions (P < 0.05 uncorrected). The regions (a‐c) in ADHD were connected at larger (single linkage) distances than in CON and regions (d,e) are opposite (Fig. 2 in the Supporting Information). The previous structural MRI studies showed that the children with ADHD have structural abnormalities in basal ganglia structures and cerebellar lobules [Shaw et al., 2007; Vaidya, 2012]. The resting‐state functional connectivity studies have also shown that the frontal‐striatal‐cerebellar networks are weaker in children with ADHD [Cao et al., 2006].

Connectivities of Difference Between ASD and Controls in Local Connected Components

In the β ₀‐plot, the ASD network had a little tight integration in the metabolic connectivity, but loose integration in the morphological connectivity. Our experiments had a tendency that the reduced local connections in ASD were mainly observed in the metabolic connectivity, but the increased local connections were in the metabolic connectivity. For example, the reduced connectivity in PET was found (a) between the occipital region and frontal and parietal regions, (b) in the visual cortex, (c) between left angular gyrus in the parietal regions and other brain regions, (d) between thalamus, amygdala, and hippocampus, (e) between thalamus and cerebellum, and (f) between left temporal pole and some frontal areas (gyrus rectus, middle frontal and superior frontal gyrus) and anterior cingulate cortex (P < 0.05 uncorrected). On the contrary, the increased connectivity in MRI was mainly found (a) between some fronto‐parietal regions, (b) basal ganglia and middle and inferior temporal gyrus, and (c) left inferior frontal gyrus and other brain regions (P < 0.05 uncorrected). These results are shown in the Figure 3 in the Supporting Information. The abnormality of the left perisylvian network for language could influence on language impairment and be the cause of the socio‐communication deficit of ASD [De Fossé et al., 2004; Just et al., 2004; Knaus et al., 2010; Palau‐Baduell et al., 2005]. The abnormal global processing along the dorsal visual pathway was reported in autism as being related to “weak central coherence,” which complied with “reduced connectivity in the visual cortex” [Pellicano et al., 2005]. The abnormalities of cerebello‐thalamic circuitry and fronto‐parietal connections were also reported in autism [Minshew and Keller, 2010; Takarae et al., 2007].

Limitations

When the 93 ROIs was defined based on AAL, we merged cerebellar regions into three larger regions in spite of the loss of the spatial specificity. We found that brain PET coverage was less complete in the inferior part of cerebellum. In that case, we needed to approximate them by averaging. The other reason is the research interests [Collin et al., 2011]. Since we wanted to concentrate more on the connectivity of cerebral regions, we merged the cerebellar regions in each hemisphere and vermis using the creating ROI option in Marsbar toolbox.

The KS‐like test statistic for testing the difference of β ₀‐plot and the GH distance for testing the difference of connectivity matrices are maximizing over all possible thresholds ε and mixing ratios γ and over connections, respectively. Thus there is no need for multiple comparisons in the first place. However, when we compared each symmetry index and each SLM in Figures 6, 7, 8, the P‐value should have been corrected for the multiple comparisons over the number of mixing ratio. Since the mixing ratio is a continuous variable, the corrected P‐value is varied depending on how many the mixing ratios are chosen. To solve this problem, we applied the AUC‐based method which estimates the area under the symmetry index curve in Figures 6 and 7 and the obtained results showed only trends of the group differences between ADHD and CON and between ASD and CON in “β₀‐plot between groups” Section. This may be due to the small sample size, especially 10 pediatric controls data using PET. To improve the statistical power, we need to confirm the method in large sample data in the future.

The number of connected components β ₀ that we mainly considered here is the most fundamental topological measure defined in Algebraic Topology. The β ₀‐curve shows how disconnected sub‐networks are integrated into the fully connected network when the threshold increases, but it does not consider how the sub‐networks are densely or sparsely connected. The number of holes in the network is the next topological measure we can use. It is the first Betti number β ₁ in Algebraic Topology. The holes are generated in a connected component and the sparser network tends to have more holes. Therefore, if we extend the proposed method to include the zeroth and first Betti number in the future, we can measure the integration of the whole brain regions as well as the sparsity of connected regions. We can also extend the linear relationship between two modalities to the nonlinear relationship by choosing a monotonically increasing nonlinear function between two modalities.

CONCLUSIONS

By extending the previous filtration method to a multimodal analysis, we can observe the change of topological shape of multimodal brain connectivity by varying two different thresholds simultaneously. We can take a quick look at the relationship between multiple imaging modalities using the multidimensional β ₀‐plot and find the group difference in it. Whereas the controls showed relatively symmetric changes of connected structures between PET and MRI in the β ₀‐plot during multidimensional filtration, ASD showed the more rapid changes of number of CCs at smaller threshold in metabolic connectivity, but the slower changes over a long range of the thresholds during filtration in morphological connectivity. Although we used the number of connected networks as a topological measure here, we suggest that the β ₀‐plot can be applied to the other graph theoretic measures such as small‐worldness and betweenness centrality when the goal is to see their change when two different modalities are integrated. By using a 1D projection, we can integrate multimodal networks of PET and MRI at various mixing ratios and observe the change in topology of the integrated network in which PET and MRI information is mixed. From the integrated network, we found that ADHD had increased morphological connectivity, and ASD also had increased morphological connectivity, but decreased metabolic connectivity. These results provide a multidimensional and multiscale homological understanding of disease‐related metabolic and morphological networks.

Supporting information

Supporting Information