Functional correlates of likelihood and prior representations in a virtual distance task

Abstract

Spatial navigation is an imperative cognitive function, in which individuals must interact with their environment in order to accurately reach a destination. Previous research has demonstrated that, when traveling a predetermined distance, humans must balance between noise in the measurement process and the prior history of traveled distances. This tradeoff has recently been formally described using Bayesian estimation; however, the neural correlates of Bayesian estimation during distance reproduction have yet to be investigated. Here, human subjects performed a virtual reality distance reproduction task during functional Magnetic Resonance Imaging (fMRI), in which they were required to reproduce various traveled distances in the absence of overt navigational cues. As previously demonstrated, subjects exhibited a central tendency effect, wherein reproduced distances gravitated to the mean of the stimulus set. fMRI activity during this task revealed distance‐sensitive activity in a network of regions, including prefrontal and hippocampal regions. Using a computational index of central tendency, we found that activity in the retrosplenial cortex, a region highly implicated in spatial navigation, negatively covaried between subjects with the degree of central tendency observed; conversely, we found that activity in the anterior hippocampus/amygdala complex was positively correlated with the central tendency effect of gravitating to the average reproduced distance. These findings suggest dissociable roles for the retrosplenial cortex and hippocampal complex during distance reproduction, with both regions coordinating with the prefrontal cortex the influence of prior history of the environment with present experience. Hum Brain Mapp 37:3172–3187, 2016. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Distance reproduction represents a fundamental aspect of spatial navigation [Chrastil and Warren, 2014; Etienne and Jeffrey, 2004; Fujita et al., 1993], in which individuals must continuously integrate idiothetic information in order to plan the direction and extent of movement within an environment. Successful distance reproduction requires that individuals coordinate between the perceived estimate of distance within their environment and their memory for previous distances traversed within that environment. Furthermore, distance reproduction is a fundamental component of path integration, or “dead reckoning,” the ability to localize position and heading without overt environmental cues (i.e., landmarks), such as when navigating in low light conditions or without nearby reference points.

Previous studies in humans and animals have suggested a network of regions that are utilized for successful distance reproduction and path integration. Animal research has demonstrated that hippocampal place‐cells track the current location of an animal, usually in reference to a goal or starting location [McNaughton et al., 2006; O'Keefe and Dostrovsky, 1971; Rich et al., 2014]. In humans, hippocampal activation has similarly been associated with longer perceived distances, including relational distances between landmarks [Morgan et al 2011]. However, hippocampal lesions in humans do not result in path integration deficits [Kim et al., 2015; Shrager et al., 2008], suggesting that other regions mediate path integration abilities. Indeed, recent research demonstrates that the hippocampus acts in concert with numerous other cortical and subcortical regions during spatial navigation [Boccia et al., 2014; Chrastil, 2013; Hartley et al., 2003; Iaria et al., 2007; Ito et al., 2015; Kuhn and Gallinat, 2014; Viard et al., 2011; Wolbers et al., 2007, 2005].

Distance reproduction tasks generally require subjects to walk a particular (unknown) distance, and then reproduce that distance [Bremmer and Lappe, 1999; Durgin et al., 2009; Mossioet al., 2008; Petzschner and Glasauer, 2011; Redlick et al., 2001]. To complete this task, subjects may attempt to replicate the sequence of events or visual dynamics presented during the initial encoding phase. More generally, distance reproduction tasks of this type can fall under the larger order of magnitude estimation tasks, where subjects may be asked to estimate, produce or judge a number of other categories, such as length, time, numerosity or size [Lambrechts et al., 2013; Petzschner et al., 2015; Shi et al., 2013]. Neuroscientific investigations of the previous two decades have explored whether magnitude representations rely on separate neural systems for each domain, or on a unified system that abstracts across different subtypes [Bueti and Walsh, 2009]. Recent explorations have identified the right inferior parietal and prefrontal cortex as two sites involved in magnitude processing across a variety of different dimensions. However, understanding the precise roles of these structures is hindered by different results, with some indicating the prefrontal cortex as coding for categorical boundaries [Hayashi et al., 2013], and others suggesting the prefrontal cortex encodes relative magnitude [Genovesio et al., 2011]. Further work from magnitude estimation suggests that the prefrontal cortex is specifically engaged in magnitude estimation during goal formation [Genovesio et al., 2012], specifically during reproduction, but not encoding phase [Jones et al., 2004].

Magnitude estimation, as with any perceptual inference, entails a tradeoff between estimation uncertainty and expectation. Recently, this tradeoff has been formally described using Bayesian modeling [Petzschner and Glasauer, 2011; Petzschner et al., 2015]. Applied to the perception of distance, subjects integrate noisy measurements of perceived distance or direction with a prior memory distribution of experience in the environment. This tradeoff allows for a concomitant reduction in variability, yet leads to systematic biases that come with reliance on the mean of the prior distribution [Jazayeri and Shadlen, 2010]. As such, subject estimates exhibit central tendency, a ubiquitous finding across many behavioral paradigms [Hollingworth, 1910; Kwon and Knill, 2013], in which responses gravitate to the mean of the stimulus set. Under this framework, magnitude representations can be divided into separate representations of prior and likelihood, and tied to potentially distinct neural substrates [O'Reilly et al., 2013; Vilares et al., 2012]. The application of Bayes Theorem in this case can be generally applied to the estimation of any magnitude [Petzschner et al., 2015]. However, although the application of Bayes Theorem is agnostic to the magnitude dimension being estimated, the neural computations that approximate not be; that is, the brain may compute prior and likelihood representations differently, depending on the type of magnitude being estimated [Meyniel et al., 2015; Vilares et al., 2012].

Where might the neural computations underlying the Bayesian tradeoff in distance reproduction occur? Recent investigations have implicated coordination between the hippocampus and retrosplenial cortex (RSC) during successful spatial navigation and path integration [Epstein, 2008; Miller et al., 2014; Sherrill et al., 2013; Vann et al., 2009; Wolbers and Buchel, 2005]. In animals, RSC lesions disrupt spatial learning and alters hippocampal place‐cell selectivity [Cooper and Mizumori, 2001]. In humans, RSC lesions disrupt path integration and route‐planning [Epstein, 2008; Takahashi et al., 1997], and RSC activity is associated with translations between allocentric and egocentric representations in spatial navigation [Sherrill et al., 2013]. Additional work has demonstrated that RSC activity may code for local spatial reference, by determining the current point within an environment [Marchette et al., 2014] relative to spatial landmarks [Augur et al., 2012]. Anatomically, the RSC is strongly connected to numerous other regions implicated in spatial navigation [Miller et al., 2014; Vann et al., 2009; Vass and Epstein, 2013], including prefrontal, parietal, and parahippocampal regions, suggesting that the RSC is ideally situated for integrating a variety of informational and mnemonic cues. In contrast, the hippocampus has been highly implicated in the construction of topographical representations of the environment [Rich et al., 2014], and additionally has been related to the updating of this information over time [Wolbers and Buchel 2005; Wolbers et al., 2007]. Further evidence also suggests that the hippocampus is increasingly activated when subjects approach a goal location [Howard et al., 2011; Sherrill et al., 2013; Spiers and Barry, 2015; Viard et al., 2011]. These findings suggest that hippocampal and RSC activity separately coordinate navigation within an environment, with the hippocampus generating a mental representation of the environment and remembered locations, and the RSC integrating information from the environment into a common reference frame.

Presently, whether the RSC or hippocampus (or both) mediates Bayesian estimation for distance reproduction is unknown. If both likelihood and prior distribution representations were tied to distinct neural regions, then activity between these regions should covary with the amount of reliance on the prior versus the likelihood in estimating distance [O'Reilly et al., 2013; Vilares et al., 2012]. Moreover, they should be invoked at different times during path integration [Hanks et al., 2011]. Recent work by Hanks et al. [2011] has demonstrated that, during perceptual decision making, the weighting influence of prior probability increases throughout the duration of a trial. In the case of distance estimation, where uncertainty linearly grows with the distance, in accordance with Weber's Law, reliance on the prior should scale as the distance grows. Consistently, distance estimates, and magnitude estimates generally, exhibit so‐called “range effects,” wherein the size of the central tendency effect scales with the range of stimuli presented [Petzschner et al., 2015]. At the outset of a planned movement, subjects should indicate where they are likely to travel to [Viard et al., 2011], at which point the likelihood function should be preferably engaged. As subjects approach the target, increased noise in the estimate should necessitate that subjects will increasingly rely on the mean of the prior (see below). To address this, we replicated a virtual reality distance reproduction task [Petzschner and Glasauer, 2011], in which subjects must perform dead reckoning by reproducing a target distance from an egocentric viewpoint. In this way, we could measure the reliance of subject estimates on the prior, by examining central tendency effects. Furthermore, the distance reproduction paradigm allowed us to dissociate activity with different phases of the task, between activation during the initial production and subsequent reproduction phase, when subjects must move with the intention to reproduce the same distance; Also, by varying the distance to reproduce, we could estimate effects associated with parametric changes in distance, as well as activity at the outset of the trial with activity at the end of the trial, when subjects indicated the selected distance.

MATERIALS AND METHODS

Participants

A total of 24, right‐handed subjects (10 females, mean age 22.7 ± SD 2.7 years) with normal or corrected‐to‐normal vision participated in the experiment. Subjects were recruited from the population at George Mason University and had no history or psychiatric or neurological disease. Written consent was obtained from all subjects and the local Institutional Review Board approved the procedures.

Task Design

Stimuli for the experiment were presented in a virtual‐reality (VR) environment created using Vizard 4.0 software (Worldviz). Both the design of the VR environment and the distance estimation task were modeled after the task created by Petzschner and Glasauer [2011]. The VR environment resembled a desert with a textured ground, 20 scattered rocks in the distance, and a clear, sunny sky (Fig. 1). The sky was a simulated 3D dome included in Vizard software, a black and white noise image was used to create the ground texture, and a single rock was modified and imported from SketchUp 3D (Trimble Navigation) and replicated within the VR script. The construction of the VR world was such that environmental distance cues were either absent or unreliable: the initial location of the viewpoint and the position and orientation of each of the rocks was randomized at the start of every trial, and the 3D sky was such that the horizon always appeared to be a constant distance away. Participants controlled the movement of the viewpoint with a continuous button press, and the eye height of the VR viewpoint was set to the approximate eye height of the participant.

Figure 1.

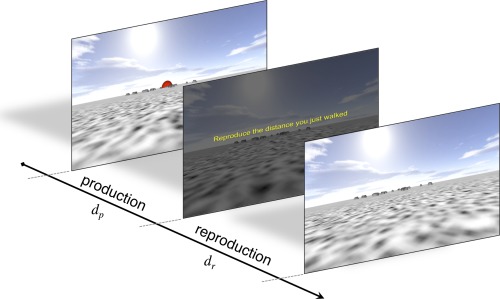
Distance reproduction task. Subjects were initially presented at a random location within a field environment with a random placement of objects. In the production phase, subjects were required to walk toward the red sphere on the horizon. After a predetermined distance (d _p), unknown to the subject, subjects were stopped and told to reproduce the distance they had just walked. In the reproduction phase, subjects walked until they believed they had matched d _p, marking the reproduced distance (d _r) with a button press. Subjects were not aware of the range of distances presented, and did not receive feedback on their performance. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Experimental Procedure

Participants performed a distance estimation task, with each trial consisting of a production and reproduction phase. At the beginning of each trial a red sphere appeared on the horizon of the VR, and participants were instructed to simulate walking forward in the direction of the sphere. After the specified production distance (d _p), movement of the viewpoint was stopped automatically and the environmental lighting was dimmed. The words “reproduce the distance you just walked” were displayed in the center of the screen. After a variable delay of 4–8 s, the words disappeared, and the normal lighting resumed. Participants were allowed to simulate walking forward again and pushed a button until they had reproduced the same distance as during the production phase (d _r). Crucially, the simulated walking speed was randomly altered between the production and reproduction phases so that the participant could not use the time spent simulating walking as a measure of the distance traveled. For each trial, the production phase simulated walking speed was randomly drawn from a uniform distribution (mean speed across trials: 3.23 m/s ± 0.71), and the reproduction phase simulated walking speed was modified such that it was noticeably faster or slower than the production phase speed (maximum ±60% production speed, drawn from a normal distribution; mean speed across trials: 3.37 m/s ± 1.83). Ten production distances were used (d _p = [5, 6, 7, 8, 9, 10, 11, 12, 13, 14] m) with a total of 120 trials (12 trials per sample distance). Although participants were told that the simulated walking speed would change, they were not given any information about the range of production distances used nor were they given feedback on the accuracy of their distance reproductions. Following reproduction, subjects viewed a fixation point for a variable inter‐trial‐interval drawn from an exponential distribution [Dale, 1999] with a minimum duration of 3 s (mean trial duration: 12.68 s ± 4.39). Participants were informed that each trial would begin at a new location within the virtual environment, but the location would remain the same between production and reproduction phases. Prior to the scanning session, participants performed a practice task with 20 trials on a laptop computer. The practice task was identical to the experimental task, with the exception that at the start of the reproduction phase, a yellow barrier marking the correct reproduced distance appeared and remained visible until subjects collided with it, ending the trial.

MRI Acquisition

Subject scans were conducted at the Krasnow Institute for Advanced Study at George Mason University. All scanning was performed on a Siemens Allegra 3T scanner. Visual stimuli were presented on a rear‐projection screen viewed by subjects on a coil‐mounted angled mirror that covered the field of vision for each subject. All subjects initially received a high resolution, T1‐weighted 3‐D magnetization prepared rapid gradient echo scan (TR = 2,300 ms, TE = 3.37 ms, TI = 1,100 ms, matrix size 256 × 256, 0.94 mm isotropic voxels). Gradient‐echo, echoplanar images (EPI) were individually acquired (40 coronal slices, 3 mm slice thickness, TR = 2,000 ms, TE = 25 ms, matrix size 64 × 65, voxel size 3 × 3 × 3.4 mm). EPI volumes were acquired in six separate runs, with each run lasting a variable duration (∼8 min). In each run, participants performed 20 trials, with each distance in the stimulus set presented twice. The variable length of each run was determined by the amount of time necessary for each subject to complete all 20 trials, which differed depending on the randomly determined simulated walking speed. The first three volumes of each run were additionally discarded to allow for steady‐state magnetization.

Data Analysis

For behavioral data, we calculated the reproduced distance as the displacement between the starting point and the location where subjects pressed the response button. The mean reproduced distance was calculated for each of the ten, presented distances in our stimulus set, along with the coefficient of variation (SD/mean). Reproduced distances were then fit with a logarithmic curve (d _r = m • ln(d _p) + b) in which d _r represents the distance reproduced and d _p the distance presented to subjects in the preceding production phase, from which the slope (m) and intercept (b) values were obtained.

Under the Bayesian‐estimation framework, on any given trial, subjects must weigh noisy perceptual information against the uncertainty associated with a given judgment. The optimal solution to this problem can be formulated as:

$$\left(\mu \text{Posterior}\right)\propto \left(\mu \text{Likelihood}\right) • \left(\mu \text{Prior}\right)$$ (1)

In the context of our distance estimation task, the likelihood distribution can be represented by the distance to be reproduced on a given trial, whereas the prior distribution represents the distribution of distances previously experienced [Petzschner and Glasauer, 2011]. Both distributions may be modeled with Gaussian noise. Additionally, a subject must assign a weighting factor to each distribution when multiplying them; as such, a subject may differentially weigh the prior or likelihood when making a response. These weighting factors reflect how much the likelihood or the prior estimate is factored when estimating the posterior. Indeed, substantial individual differences exist between likelihood and prior weightings on tasks involving Bayesian estimation [Cicchini et al., 2012]. By regressing the reproduced distances against the distances in the stimulus set, we can obtain a measure of this weighting [Vilares et al., 2012]. Accordingly, if subjects relied entirely on the likelihood distribution and ignored the prior, then responses will be proportional to the appropriate distance (Fig. 2A), resulting in a slope of one. If, however, subjects rely entirely on the prior distribution, then responses will be approximately equal across all distances, corresponding to the mean of the stimulus set (9.5), and a slope of zero [O'Reilly et al., 2013; Vilares et al., 2012]. A Bayesian observer, in order to reduce variance, will combine likelihood and prior distributions, and thus exhibit a slope value between zero and one. In reproduction tasks, this effect manifests as central tendency, wherein subjects overestimate the smallest magnitude in the stimulus set and underestimate the largest magnitude [Kwon and Knill, 2013; Petzschner et al., 2015; Shi et al., 2013]. However, in contrast to previous reports, we note that subjects may also exhibit substantial, non‐optimal biases in their responses. These effects may manifest as a gross overestimation or underestimation of stimulus set values. Application of a Bayesian model, without factoring in these subject‐specific biases may provide inaccurate estimates. Petzschner and Glasauer, in their formulation of a Bayesian observer, included shift parameter term (Δx) [Eq. (8)], that could account for behavioral differences in distance estimates. A second possibility is that these biases may be construed as “anti‐Bayesian,” in which responses gravitate away from the prior as a result of noise in the encoding process [Wei and Stocker, 2015]. However, Wei and Stocker [2015] note that these shifts occur in the case of an asymmetric prior distribution, which we did not use in our study, and so we think this explanation is unlikely to explain shifts in our data. Nevertheless, these subjects may still be responding optimally, as responses may still gravitate to the mean of previously reproduced intervals, rather than the mean of the stimulus set (Fig. 2B). As such, the intercept of the logarithmic curve mentioned above may be used to quantify this bias. However, we note one problem with this approach; as slope and intercept values are naturally correlated, any change in slope will naturally alter the intercept and so will skew a measurement of bias. In our sample, we thus sought two measures to independently index reliance on the prior (R _prior) and non‐optimal bias (BIAS). We defined BIAS as

$$BIAS=\left|d_{\mathrm{r}}-d_{\mathrm{p}}\right|$$ (2)

which indicates absolute deviations of subject responses from the distances in the stimulus set; this value will be positively correlated with the intercept of the logarithmic curve of subject responses to presented distances, as larger values indicate a deviation from the stimulus set, and so a higher (or lower) intercept (Fig. 2C). We next defined R _prior as

$$R_{prior}=\left|d_{\mathrm{r}}-{\mu }_{\text{prior}}\right|$$ (3)

Figure 2.

Human performance on the distance reproduction task exhibits central tendency and bias. (A) Example reproduction data from a representative subject. Open green circles represent individual trials, with blue circles indicating average reproduction distance for a given sample distance and blue lines indicating the best fitting logarithmic curve. If subjects performed the task ideally, without any reliance on the prior, then reproduced distances should lie along the identity line, indicated by (μ Likelihood). Conversely, if subjects rely entirely on the mean of the prior distribution, then responses should lie entirely along the mean of the stimulus set, indicated by (μ Prior). The optimal tradeoff between measurement noise and prior experience results in human responses lying between these two, with an overestimation of the shortest distance and underestimation of the longest distance. Additionally, subjects may also exhibit non‐optimal bias, as the prior distribution for a given subject (μ Subj Prior) may not be veridical to the actual stimulus set. In this example, subject performance matches the actual stimulus set quite well. (B) A second representative subject, who exhibits a large bias in performance. If performance were measured entirely against the stimulus set, then the subject would appear to overestimate every distance. However, this subject may still be exhibiting central tendency, when measured against their own, individual prior distribution (μ Subj Prior). Here, μ Subj Prior is calculated as the mean of the stimulus set, offset by the average reproduced distance; μ Subj Likelihood is calculated as the sample distance, offset by the average reproduced distance. (C) Dependence and independence of performance indices. Mean R _prior correlates well with the slope of the logarithmic curve (m), whereas BIAS correlates with the intercept (b). Crucially, both indices do not correlate with one another, indicating independence. Displayed r values represent Pearson correlation coefficients. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

In which μ _prior is the mean of the subject prior, defined as the average reproduced distance across the entire session. Here, R _prior represents absolute deviation of subject responses from their mean reproduced distances; this value will be positively correlated with the slope of the logarithmic curve fit to subject responses for presented distances, as large deviations indicate a larger difference between extreme values and the mean, indicating a steeper slope (Fig. 2C). Crucially, both measures are independent of one another, and so changes in one do not associate with changes in the other (Fig. 2C). This step was necessary for planned analyses (see below), where independence between factors was a necessary requirement for multiple regression, in order to avoid confounds resulting from correlated covariates [Andrade et al., 1999].

We additionally note that our above measures of distance share commonalities with another model of distance estimation, one that does not rely on estimates of prior or likelihood. Lappe et al. [2007] developed a leaky integrator model to explain patterns of over or underestimation in a task similar to ours. In their model framework, estimates of virtual distance are influenced by a gain factor (k) that increments during movement, and a leak factor (α) that reduces the integrated estimate. Depending on the context, values of k and α can produce patterns of central tendency when the gain factor is low and the leak factor is high.1

Functional image preprocessing and subsequent data analysis was carried out with SPM8 (http://www.fil.ion.ucl.ac.uk/spm/) [Friston et al., 1995] and Matlab (Mathworks). Slice‐timing acquisition and realignment was applied for all volumes, which were realigned to the first volume of the first run, then normalized into standard stereotaxic (Montreal Neurological Institute) space. All volumes were then smoothed with an 8 mm full‐width at half‐maximum Gaussian kernel.

At the first level, event‐related responses were measured by first convolving events with a canonical hemodynamic response function [Friston et al., 1998]. In the present study, we sought to measure activation related to distance processing at different times in the behavioral sequence. Specifically, we wanted to separately measure activity at the outset and during virtual movement, as well as when subjects reached their estimated distance. This was necessary to test hypothetical differences in when likelihood and prior representations would be most active. We, therefore, designed two general‐linear models (GLMs) for each subject, one corresponding to onset‐locked activation and the other to response‐locked activity. For onset‐related activity, events were time‐locked to the onset of the production and reproduction phases, respectively. In both cases, the BOLD responses were parametrically modeled as boxcars with different lengths depending on the duration of the production (mean 4.3s ± 3.84) or reproduction phases (mean 3.84s ± 2.7), to better account for duration‐related activity [Grinband et al., 2008]. We included an additional, parametric regressor for each phase that was height‐modulated by the length of the traveled distance. For offset‐related activity, events were time‐locked to the offset of each phase. Two, additional parametric regressors, modeled as height‐modulated stick functions, were included for production and reproduction phases, one for duration and one for distance, entered into the GLM in that order. Although duration was not a reliable cue for performing the task, subjects may have been biased by the time taken to reach the production phase distance; the duration regressor was included to assess this possibility. Furthermore, the distance regressor was orthogonalized by the duration regressor, which allowed for the assessment of distance adjusted for duration [Mumford et al., 2015]. For each GLM, a high‐pass filter (128s) was applied to remove non‐specific noise. Six, additional motion‐parameter regressors were included in each GLM to account for head movement‐related signals. The onset‐related analysis interrogated activity developing during simulated walking, whereas the offset‐related analysis examined activity following when subjects finished their movement and made a decision on if they were at the appropriate distance [Cui et al., 2009]. For onset‐related activity, contrast maps were generated examining the difference between reproduction and production phases [REPRO – PRO] and between parametric modulations of distance for each phase [REPRO_dist – PRO_dist]. For offset‐related activity, the same two contrast maps were generated, as well as a third between parametric modulations of duration for each phase [REPRO_time – PRO_time]. At the second‐level, contrast maps were entered into a random‐effects analysis and tested as one‐sample t‐tests. Statistical significance was assessed at a height threshold of P < 0.001 and a cluster threshold of P < 0.05, Family‐Wise Error (FWE) corrected (minimum cluster extent k = 10). Anatomical labels of activation clusters were provided by the AAL atlas [Tzourio‐Mazoyer et al., 2002]. Additional localization of cluster peaks was confirmed with the SPM Anatomy toolbox [Eickhoff et al., 2005].

Lastly, in order to measure individual differences in reliance on the prior, we conducted an additional, second‐level multiple‐regression analysis, with our BIAS and R _prior indices included as separate covariates. In this way, we could independently evaluate neural regions associated with one index while separately controlling for the confounding effects of the other. A third, additional regressor was also included in this analysis: we noted that, although our design attempts to reduce the utility of a time‐based strategy, some subjects may nevertheless have guided their distance reproduction estimates by matching the duration of the production phase distance [Mossio et al., 2008], even though distance estimates are generally more precise than timing estimates [Durgin et al., 2009]. In order to account for this potential influence, we assessed the independent influence of time and distance on reproduction estimates by running a non‐parametric Spearman partial correlation, for each subject, between the change in velocity between production and reproduction phases and the reproduced distance while controlling for the distance presented during the production phase (see Hayashi et al., 2013 for a similar approach in magnitude reproduction). The resulting correlation coefficients were included as a third regressor, to ensure that the measurements of BIAS and R _prior were not driven by a time‐based strategy; we additionally confirmed that this regressor was not correlated with either BIAS (r = 0.047) or R _prior (r = −0.059) regressors; both correlations were additionally confirmed with a permutation test (10,000 permutations, α = 0.95), indicating that neither was higher than chance. Separate, one‐sample t‐tests were run for each index. In order to assess our a priori hypothesis regarding regions of interest in the RSC and hippocampus, we utilized anatomical masks for activation in these regions. The hippocampus was defined using anatomical constraints provided by the WFU PickAtlas [Maldjian et al., 2003]. For the RSC, as no available atlas definitions are currently available for this region, we used a 12 mm spherical volume of interest, centered at the coordinates of previous RSC activation during path integration (MNI: −4, −62, 24) [Wolbers and Buchel, 2005; Wolbers et al., 2007]. Activation in these regions was assessed using the same significance thresholds as described above, but constrained to the smaller volume. We additionally explored whole‐brain activity in each of these contrasts and report these results below.

RESULTS

Behavioral Results

As expected, participant reproductions demonstrated central tendency, with overestimations of the shortest distance in the stimulus set and underestimations of the longest distance [Mean R _prior = 1.57 ± SD 0.414; one‐sample t(23) = 18.596, P < 0.001] [Petzschner and Glasauer, 2011]. Additionally, we found a range of biases across subjects, with some subjects reproducing distances centered on the mean of the stimulus set, and others reproducing distances offset from the stimulus set [Mean BIAS = 3.05 ± SD 2.44; one‐sample t(23) = 6.114, P < 0.001]. Furthermore, we observed one subject who, although they claimed to have understood the task, performed exceptionally poorly, demonstrating a negative slope (m = −2.22), greater than two SDs from the mean. As such, we excluded this subject from our functional Magnetic Resonance Imaging (fMRI) analysis of the effects of R _prior and BIAS. The results of our nonparametric partial correlation also revealed that subjects did show an influence of duration on distance, as rho values were significantly above zero [t(22) = 2.689, P = 0.013]; however, this value was quite low (mean rho 0.1006 ± 0.1918), suggesting that timing only had a marginal influence on estimated distances. Post‐task interviews with subjects indicated a range of strategies for completing the task, with subjects noting that the horizon and distant rocks were not a useful strategy for determining distance traveled.

fMRI Results

For onset‐locked data, we found activation in a network of regions (Fig. 3; Table 1). For the [REPRO – PRO] contrast, this network included activity in the prefrontal cortex, with local maxima in the inferior frontal gyrus (IFG) and anterior cingulate cortex. Additional parietal activation in the inferior parietal cortex and superior temporal gyrus was also detected. Subcortical peaks in the motor‐related areas, including the cerebellum and basal ganglia, were also detected. Lastly, we detected activity in hippocampal and parahippocampal regions. The activations in this contrast indicate regions where activity in the reproduction phase, where subjects were required to estimate the appropriate distance, exceeded activity in the production phase, where subjects were required to encode the presented distance. No significant effects at our threshold were found for the examination of the parametric distance regressor.

Figure 3.

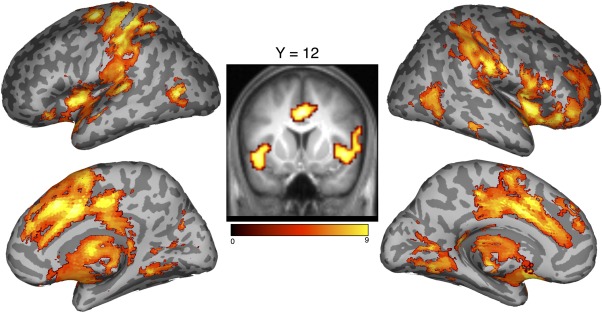
Brain regions activated exclusively while subjects are reproducing target intervals, contrasted against when producing them. A network of prefrontal and parietal regions are exhibited, including medial prefrontal cortex and inferior parietal cortex. Activation is displayed at P < 0.001 peak level, corrected for multiple comparisons at the cluster level (P < 0.05, FWE corrected). The middle panel displays activation overlayed on an averaged scan of subjects’ anatomical data. Color scale indicates t‐score value. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 1.

Reproduction versus productiona

Location	Hemisphere	x	y	z	t‐score	Cluster size
Inferior Frontal Gyrus	L	−42	15	−12	9.72	147
Insula	L	−39	3	0	8.35
	L	−36	0	15	6.86
Cingulate Gyrus	R	0	9	39	9.55	583
	R	0	−6	42	9.07
Anterior Cingulate	R	3	24	30	8.15
Insula	R	45	15	−9	9.39	284
Superior Temporal Pole	R	57	15	−3	7.8
Rolandic Operculum	R	39	3	15	7.46
Precentral	L	−30	−18	60	9.13	276
Inferior Parietal	L	−45	−24	45	8.13
	L	−36	−42	54	7.99
Superior Temporal Gyrus	L	−63	−27	15	8.66	47
Supramarginal Gyrus	R	60	−15	27	8.23	85
	R	63	−21	21	8.15
Lingual Gyrus	L	−27	−63	3	8	78
Cerebellum (Lobule IV)	L	−15	−54	−12	7.61
Middle Occipital	L	−48	−72	9	7.83	12
Pallidus	R	15	0	0	7.78	99
Caudate	R	6	0	9	7.06
Cingulate Gyrus	L	−12	−24	39	7.73	25
Cerebellum (Lobule IV)	R	15	−57	−12	7.59	62
Cerebellum (Lobule IV)	R	15	−54	−30	7.46	29
Parahippocampal Gyrus	R	24	−42	−3	7.29	12
Hippocampus	R	24	−42	6	6.35
Lingual Gyrus	R	36	−57	0	7.13	18
Middle Temporal Gyrus	R	42	−66	6	6.36
Cerebellum (Lobule VIIb)	L	−36	−60	−45	7.13	11
Red Nucleus	L	−3	−21	−6	6.84	12
Thalamus	R	0	−27	3	6.12
Pallidus	L	−24	−9	−6	6.77	13
	L	−18	−3	−3	6.35
Supramarginal Gyrus	R	54	−30	48	6.5	25
	R	54	−30	39	6.19
Inferior Frontal Gyrus	R	48	39	−9	6.41	10

^aMNI coordinates from cluster peaks and local submaxima. Statistical threshold of P < 0.001 height, P < 0.05 cluster (FWE) minimum cluster extent 10 voxels. Bolded regions represent cluster peaks, with submaxima listed below.

For the response‐locked analysis, the [REPRO – PRO] contrast demonstrated activity in white matter near the hippocampus and in the cerebellum (Table 2). This contrast indicated activity following the moment subjects indicated, via button‐press, when they believed they were at the appropriate location. Additionally, for the [REPRO_dist – PRO _dist] contrast examining the parametric effect of produced distance in the reproduction phase, while controlling for walked distance in the production phase, we observed a significant cluster in the right prefrontal cortex, within the IFG and extending into the middle frontal gyrus (Table 3). Crucially, we note that this activity occurs after the response has been made, consistent with previous research demonstrating parametric post‐response activity [Cui et al., 2009]. Additional regions of activation in the medial frontal cortex, superior parietal and middle occipital gyrus were detected but did not exceed our cluster significance threshold. No significant effects were found for the examination of the parametric duration regressor. This finding indicates that the effect of distance in IFG is independent of changes in duration, which may also induce activity in this region [Wiener et al., 2010].

Table 2.

Reproduction versus production, post response‐locked

Location	Hemisphere	x	y	z	t‐score	Cluster size
White Matter	R	33	−18	−9	9	20
Cerebellum (Lobule IV)	R	21	−45	−18	8.97	89
Cerebellum (Loubule VI)	R	15	−63	−18	6.47
Cerebellum (Lobule IV)	L	−15	−48	−12	7.84	46
Cerebellum (Loubule VI)	L	−12	−60	−12	6.94
Cerebellum (Lobule VIII)	L	−33	−60	−51	7.42	15
Vermis	R	6	−57	−6	6.7	10

Table 3.

Parametric effect of distance during reproduction versus production

Location	Hemisphere	x	y	z	t‐score	Cluster size
Inferior Frontal Gyrus *	R	51	21	24	5.89	113
		45	24	12	5.24
		45	18	6	4.59
Superior Medial Frontal Cortex	R	0	27	45	5.14	20
Superior Parietal	L	−21	−54	39	5.06	35
Middle Occipital Gyrus	L	−30	−57	36	4.2

* Survives cluster‐wise FWE correction P < 0.05.

Additionally, we examined activity for the opposite contrast [PRO – REPRO]. For the onset‐locked analysis, we found significant bilateral activation in the occipital cortex, centered on the lingual gyrus (Supporting Information Figure S1; Supporting Information Table S1). For the response‐locked analysis, activity was again found in the bilateral lingual gyri, but an additional significant cluster was found in the left precentral gyrus, extending into the inferior and middle frontal gyri (Supporting Information Figure S1; Supporting Information Table S1). We note that activity in the precentral gyrus was also found in the onset‐locked analysis in roughly the same region, but did not survive cluster correction. No significant effects were found for the parametric effects at in either onset or response‐locked analyses.

For the investigation of our behavioral indices against neural data, we found a significant positive effect of mean R _prior against onset‐locked activity in the [REPRO – PRO] contrast. This effect occurred in the RSC region (MNI: −9, −63, 24, peak t = 5.76, k = 53; Table 4), wherein greater activity was associated with a larger R _prior (Fig. 4; top). For the response‐locked analysis, we detected a significant negative effect of mean R _prior against a cluster of activity in the anterior hippocampus, extending into the parahippocampus and amygdala (MNI: 21, −3, −21, peak t = 4.92, k = 43; Table 4), wherein lower activity was associated with a larger R _prior (Fig. 4; middle). We note that the valence of the relationship here is important, as larger values of R _prior are associated with a reduced central tendency, and so less reliance on the prior. As such, RSC activity was associated with responses that aligned with the mean of the subject likelihood function, whereas the hippocampal cluster activity was associated with responses that aligned with the mean of the subject's prior. No significant effect of the BIAS index or nonparametric rho index on fMRI activation was detected, for either onset or response‐locked data. However, in the onset‐locked [PRO – REPRO] contrast, we detected a significant positive effect of the BIAS index against a cluster of activation in the basal ganglia, centered on the right putamen (MNI: 21, 12, −9; Table 5), wherein greater activity was associated with a larger BIAS value, associated with a greater shift away from presented distances (Fig. 4; bottom).

Table 4.

Regression analysis results for [REPRO – PRO]

Location	Hemisphere	x	y	z	t‐score	Cluster size
Onset‐Locked
Retrosplenial Cortex *	L	−9	−63	24	5.76	53
Precentral Gyrus (BA 6)	R	45	−3	27	4.16	11
		54	−3	27	3.58
Response‐Locked
Hippocampus *	R	21	−3	−21	4.92	43
Putamen		33	3	−9	4.51
		24	0	−6	4.48
Middle Temporal Gyrus	R	51	−42	6	4.66	34
		60	−45	6	3.99
Middle Frontal Gyrus (BA 9)	R	24	33	30	4.54	35
Cingulate Cortex (BA 32)		21	21	30	3.9
Temporal Lobe (BA 37)	L	−45	−42	−3	4.28	13
Parahippocampal Gyrus (BA 36)		−42	−33	−9	3.78

*Survives cluster‐wise FWE correction P < 0.05.

Figure 4.

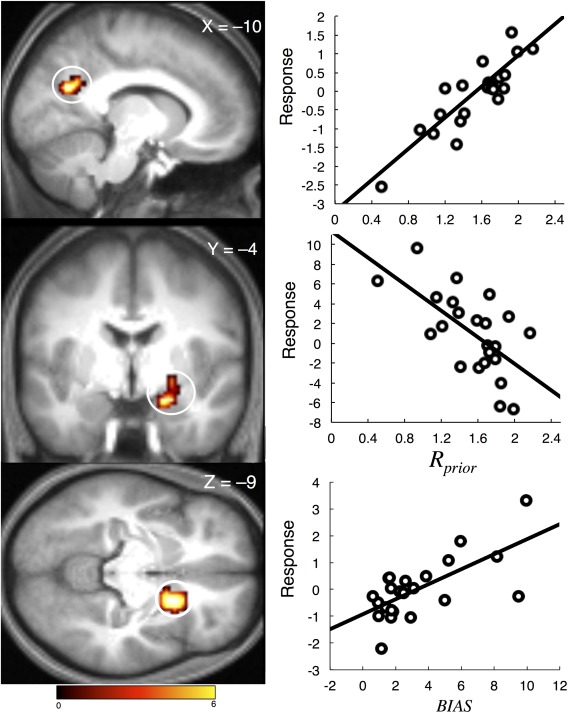
Results of the multiple regression analysis. Activity (beta values, in arbitrary units) in the RSC (top) and hippocampal/amygdala complex (middle) while reproducing distance covaries with our index of the reliance of individual subjects on the prior distribution of reproduced distances (R _prior), independent of the individual mean BIAS values. Conversely, activity in the right putamen (bottom) while encoding distance covaries with our index of general offset from the presented distances (BIAS). At right, the correlation from the peak voxel for each structure is presented, for illustrative purposes only—no additional statistical analyses have been run. Activation is displayed at P < 0.001 peak level, P < 0.05 corrected cluster level. Color scale indicates t‐score value. Activation is displayed on an averaged anatomical scan. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 5.

Regression analysis results for [PRO – REPRO]

Location	Hemisphere	x	y	z	t‐score	Cluster size
Onset‐Locked
Putamen *	R	21	12	−9	6.08	97
Putamen	L	−15	6	−9	4.55	60
	L	−30	6	−12	4.07
	L	−21	6	0	4.01

*Survives cluster‐wise FWE correction P < 0.05.

DISCUSSION

In the present study, we sought to elucidate the neural regions responsible for central tendency in distance reproduction, a task that is relevant for real world path integration. We used a VR task implementing a first‐person perspective in which subjects were required to walk a specified distance, and then reproduce that distance in the absence of overt environmental cues. To characterize human performance and bias, which may take the form of both optimal reliance on a prior distribution and non‐optimal bias away from the mean of the stimulus set, we utilized indices of each pattern that were independent from one another. Our results revealed a number of main findings. First, performance during the reproduction phase specifically recruits a network of subcortical and cortical structures comprising the cerebellum, basal ganglia, and hippocampus, in addition to the prefrontal and parietal cortices. Second, the right IFG is preferentially activated when subjects reach their planned destination, and is specifically modulated by the distance traveled. Third, RSC and anterior hippocampal/amygdala activity during reproduction covaries between subjects with the degree to which subjects rely on the prior distribution of reproduced distances, but in different ways and at different times. Finally, activity in the basal ganglia during the production phase covaries with the degree of non‐optimal bias away from presented distances in the stimulus set.

Our findings are consistent with a wide literature on spatial navigation, demonstrating activation in hippocampal, RSC, and prefrontal regions [Boccia et al., 2014; Chrastil, 2013; Hartley et al., 2003; Iaria et al., 2007; Kuhn and Gallinat, 2014; Park and Chun, 2009; Sherrill et al., 2015; Vass and Epstein, 2013; Viard et al., 2011 ]. Additionally, studies of path integration have found activation in RSC and hippocampal regions, similar to our own [Sherrill et al., 2013; Wolbers and Buchel, 2005]. However, we note that our paradigm is intended to functional dissociate between route encoding and reproduction mechanisms [Chrastil and Warren, 2014]. In the production phase of our task, subjects must walk to a predetermined distance, but have no foreknowledge of which distance in the stimulus set will be presented. In the reproduction phase, subjects have a discrete goal distance in mind. The distance to be produced will thus depend on the accuracy of encoding mechanisms during the initial production phase, as well as comparator mechanisms during the reproduction phase, both of which may be influenced by idiothetic cues and action perception and planning mechanisms [Witt and Riley, 2014]. As such, by contrasting activation in the reproduction phase with the production phase (and vice versa), our analysis controls for such non‐specific effects as visual stimulation and movement production, leaving only activity putatively related to distance encoding or reproduction mechanisms. Furthermore, for parametric regressions, our design allows us to control for the distance and duration traveled in the production phase when examining differential effects of these factors on reproduction activity.

In the production phase, we observed bilateral activity in the occipital cortex, centered on the lingual gyrus that was greater than in the reproduction phase. Additional activation in the left precentral gyrus was also observed during both phases, but only survived cluster correction for the response‐locked analysis (Supporting Information). Several points are worth noting about this activation; first, far less activity was observed during the production than reproduction phase. This finding is in accordance with work from the experimental psychology domain suggesting that, once subjects learn the range of stimuli to be presented, processing during the encoding phase proceeds automatically [Hasher and Zacks, 1984; Nachmias, 2006; Schneider and Shiffrin, 1977]. Indeed, subjects are able to learn the range of a stimulus set relatively quickly [Berniker et al., 2010]. Second, activity in the lingual gyrus has been associated previously with the encoding of general visual memories [Cohen et al., 1997; Courtney et al., 1997; Simons et al., 2006] and spatial encoding [Aguirre et al., 1998; Sulpizio et al., 2013]. Third, activity in the left precentral gyrus may have been related to use of the right‐hand for holding the button press, although it is difficult to say why this region would be more active in the production phase, when the button‐pressing requirement was equivalent.

Additionally, during the production phase, we observed a correlation between basal ganglia activity, centered on the right putamen, and the degree of non‐optimal bias across subjects. The BIAS index we used in our study indicated the degree to which subjects generally over or underestimated the distances in the stimulus set. As such, a high value of BIAS would result if subjects were consistently overestimating the presented distances (Fig. 1A). Given that activation covaried with BIAS in the basal ganglia, one possibility is that habitual tendencies influenced subject performance. Recent work suggests the basal ganglia as a center for regulating habitual behaviors [Yin and Knowlton, 2006], and in the context of spatial navigation the basal ganglia have been associated with egocentric, over‐learned route sequences [Hartley et al., 2003]. The between‐subject difference in basal ganglia activation may thus reflect the degree to which subjects could inhibit (or were susceptible to) inherent biases or errors in the distances they were encoding. Recent research has indicated that the volume of the human putamen correlates with turning bias in a virtual Morris Water Maze task [Yuan et al., 2014]. These biases would likely be corrected in the presence of feedback, which was not provided in the present study, in accordance with the replication of Petzschner and Glasauer's [2011] work.

In the present study, we also observed significant activity in the right IFG after subjects reached their goal distance. Moreover, the distance traveled on a given trial modulated this activity. Although some studies have indicated parametric effects of distance in hippocampal activity, prefrontal activation has been consistently noted in studies of spatial navigation [Boccia et al., 2014; Kuhn and Gallinat, 2014]. Additionally, numerous studies demonstrate activation in this region that is modulated by the processing of stimulus magnitude, across a number of domains [reviewed by Bueti and Walsh, 2009]. Indeed, prefrontal neurons have been found to parametrically encode spatial distances [Genovesio et al., 2011; Merchant et al., 2011]. Moreover, this activity may regionally be tied to task goal representations [Genovesio et al., 2012]. Notably, stimulation of the right prefrontal cortex in a task design similar to ours but investigating a different magnitude dimension, that of time, selectively disrupts performance when applied during stimulus reproduction, not production phases [Jones et al., 2004].

Consistent with Bayesian models of behavior, subjects in our study exhibited central tendency when estimating distances in our stimulus set. This effect manifests as an overestimation of the shorter distances in the stimulus set and an underestimation of the longer distances and is also known as Vierordt's Law. Bayesian models suggest that, in facing estimation uncertainty, subjects gravitate to the mean of the prior distribution, formed from previously experienced trials [Jazayeri and Shadlen, 2010; Kwon and Knill, 2013; Petzschner et al., 2015; Petzschner and Glasauer, 2011 ]. Determining the neural regions responsible for likelihood and prior representations is a current challenge for neuroscience investigations. In recent studies, likelihood representations have been localized to sensorimotor regions, whereas prior representations have been localized to integrative zones where disparate processing streams are combined [Hampton et al., 2006; O'Reilly et al., 2013; Vilares et al., 2012]. In our study, we found that both RSC and hippocampal region activation covaried between subjects with how much a subject relied on the prior when estimating distance. However, each covaried in different ways and at different times. In subjects who showed a strong effect of central tendency, RSC activation was lower at the onset of the reproduction phase and hippocampal/amygdala activity was larger at the offset, when a decision was made. Conversely, greater onset‐locked RSC activity and lower response‐locked hippocampal area activity was found in subjects who showed less of a central tendency effect, and so reproduced more veridical distances. This activity occurred while subjects were reproducing distance, and was not affected by bias. The further implication of these data is that the RSC mediates the ability of a subject to accurately reproduce a just‐previously‐experienced distance, whereas the hippocampus samples the average representation of distances experienced in the environment.

The regions of the RSC and hippocampus observed in the present study are important to distinguish. The hippocampal cluster that we associated with greater reliance on the prior distribution was located in the anterior hippocampus, with some overlap between the amygdala and parahippocampus. This finding is noteworthy, as anterior hippocampal activation has been associated with increasing proximity to goal locations [Viard et al., 2011] and episodic retrieval [Kuhn and Gallinat, 2014]. However, the peak and majority of voxels in this cluster were in the hippocampus (hippocampus: 48%, amygdala: 30%, parahippocampus: 24%). Relatedly, a recent meta‐analysis of 66 fMRI experiments of spatial navigation also found a cluster encompassing these regions, although without speculation on possible underlying function [Boccia et al., 2014]. Recent work has shown that the hippocampus and amygdala are co‐activated while learning object‐location associations [Manelis et al., 2012] and during the retrieval of larger memory loads [Schon et al., 2009]. In contrast, the location of the RSC in our study was found in a region of the occipital parietal cortex. We identified this region as the RSC on the basis of our a priori ROI, chosen from a study involving a similar design [Wolbers and Buchel, 2005]. However, we note that several additional ROIs centered on coordinates from other studies also encompassed this cluster [Dilks et al., 2011; Marchette et al., 2014; Park and Chun, 2009; Sherill et al., 2015], including the RSC location reported by the meta‐analysis of Boccia et al. [2014]. Nevertheless, we do note that the RSC location in our study is not immediately adjacent to the splenium.

The RSC has long been implicated in spatial navigation and path integration (for reviews see Epstein, 2008; Vann et al., 2009]; however, its precise role has remained elusive. Additionally, the RSC is ideally situated to integrate information from a variety of regions, including the hippocampus, prefrontal and parietal cortices [Alexander and Nitz, 2015; Vann et al., 2009]. Evidence suggests that the RSC responds to both ego and allocentric representations of the environment and goal locations [Miller et al., 2014; Sherrill et al., 2013], and combines idiothetic and spatial cues during movement [Wolbers and Buchel, 2005]. RSC lesions in animals performing spatial navigation tasks induce specific deficits when changes to the environment occur or when animals must rely heavily on their internal estimates [Cooper and Mizumori, 2001; Pothuizen et al., 2008]. Additionally, recordings of RSC neurons during navigation demonstrate context specific activation to environmental reward cues, suggesting the RSC encodes goal‐directed spatial information [Alexander and Nitz, 2015; Smith et al., 2012]. Similarly, research in rodent models has suggested that hippocampal place‐cell activation relates to map‐level representations of the environment that may be utilized for reaching a desired goal [McNaughton et al., 2006; Rich et al., 2014].

Given the potential involvement of the RSC in goal‐directed spatial information, one possibility is that greater RSC activation at the onset is related to the ability to accurately situate oneself in the environment. By doing so, the individual will have a better idea of how far they must travel in order to reproduce the correct distance. Indeed, studies of temporal reproduction, another magnitude reproduction task very similar to the one used here, have shown that the accuracy of a to‐be‐reproduced interval is driven most by activity at the beginning of the reproduction phase [Bartolo and Merchant, 2015; Kononowicz and van Rijn, 2015]. In our study, although we asked subjects to plan their movement to the target location, the reproduction of distance was influenced in our task by simulated walking speed [Mossio et al., 2008; Redlick et al., 2001]; however, previous work has demonstrated that subjects can accurately identify traveled distance in a task similar to ours using only ground features [Frenz and Lappe, 2005], and so can identify the distance they must travel.

The relation of the hippocampal/amygdala cluster in our task with central tendency suggests that this region is associated with a sampling of the average reproduced distance. Furthermore, the involvement of this structure at reproduction offset suggests that it mediates the proximity of the subject to the mean of the prior. Accordingly, if a subject is less certain of the distance they must reproduce, they will draw from their memory distribution of traveled distances, which likely relies on the hippocampus, given the involvement of this structure in the generation of topographic spatial representations. Previous research has demonstrated that the hippocampus is more active in poor performers on a spatial navigation task similar in some respects to ours [Baumann et al., 2010].

The findings of the present study suggest that the RSC and hippocampal/amygdala complex mediate the balance between reliance on the prior and likelihood distributions during distance reproduction. More specifically, it suggests that the RSC samples the likelihood function, whereas the hippocampus samples the prior distribution. Notably, in a previous study of Bayesian estimation, Vilares et al. [2012] found that the superior prefrontal cortex mediated the balance between the prior and likelihood for individual subjects. However, this study required subjects to make a probabilistic judgment about the location of a hidden object—a very different task from the one in the present study. In relation to magnitude estimation, the Bayesian model that inspired our design and set of analyses is a general theory that provides an explanation for central tendency. As such, the choice of which magnitude to estimate is arbitrary. Indeed, a current question is whether Bayesian priors are implemented globally or locally in the brain [Petzschner et al., 2015]. In the present study. The findings in the present study raises the interesting possibility that adjudication between the prior and likelihood does not occur in a single, supramodal brain region, but rather occurs in regions that are most suitable to the current task. Indeed, recent work by O'Reilly et al. [2013] using a target interception task (i.e., space invaders) revealed a possible locus for combining predictions based on current and past trajectories in the angular gyrus, another region that may have been ideally suited for integrating information in the task. We thus suggest that RSC and hippocampal complex activation covarying with reliance on the prior in the present study is due to their preferential involvement in spatial navigation. Further, the application of our design to other magnitude dimensions (e.g., time, number, size) would be more likely to reveal regions associated with these tasks with representations of prior and likelihood, rather than the regions found in the present study.

Our application of the Bayesian model to distance reproduction follows from a recent application by Petzschner and Glasauer [2011]. These authors found that central tendency effects could be explained by a Bayesian optimal observer model that used an adaptive prior that learned the distribution of distances over time. Notably, this model has been applied to a number of other magnitude dimensions [Petzschner et al., 2015], suggesting that the present findings may be applicable to a wide range of stimuli. However, the Bayesian model is not the only one that can explain central tendency. Indeed, recent studies have suggested that central tendency effects can also be explained by nonstationary effects in memory [Thurley, 2016; Wiener et al., 2010]. Further, Lappe et al. [2007] proposed a leaky integrator model of distance estimation that relies on parameters that affect the gain and integration of traveled space in memory. This model was designed to explain overestimation and underestimation effects in behavioral tasks similar, but not identical, to our own. However, we note that this model can also accommodate central tendency effects by invoking a low gain and high leak rate. In this case, the model provides an alternative account for central tendency to the Bayesian one that highlights a specific mechanism. We conducted an additional analysis of our data, in which the Lappe model was fit to individual subject data, and parameter estimates were applied in our multiple regression analysis. However, no areas of co‐activation were found that passed our significance threshold. This does not necessarily preclude the possibility that gain and leak parameters (or some combination) are calculated in the neural regions observed in our study, but could suggest that our particular analysis or experimental design are not best suited to the Lappe model. Future studies should be conducted that more closely replicate the tasks used by Lappe et al. [2007] with their model to elucidate the neural correlates of these parameters [Harris and Wolbers, 2012; Lappe and Frenz, 2009; Lappe et al., 2011 ].

CONCLUSIONS

The present study reports, for the first time, an investigation of the neural regions involved in central tendency effects during distance reproduction. These findings suggest that hippocampal and prefrontal regions are utilized for the encoding and estimation of distance, where human subjects are known to produce systematic errors. Activation in the RSC and hippocampal amygdala complex covaried with individual reliance on the prior distribution of reproduced distances, suggesting that these regions mediate the optimal Bayesian tradeoff between uncertainty and expectation during distance reproduction in a virtual reality environment.

Supporting information

Supporting Information

Supporting Information