From evoked potentials to cortical currents: Resolving V1 and V2 components using retinotopy constrained source estimation without fMRI

Abstract

Despite evoked potentials' (EP) ubiquity in research and clinical medicine, insights are limited to gross brain dynamics as it remains challenging to map surface potentials to their sources in specific cortical regions. Multiple sources cancellation due to cortical folding and cross‐talk obscures close sources, e.g. between visual areas V1 and V2. Recently retinotopic functional magnetic resonance imaging (fMRI) responses were used to constrain source locations to assist separating close sources and to determine cortical current generators. However, an fMRI is largely infeasible for routine EP investigation. We developed a novel method that replaces the fMRI derived retinotopic layout (RL) by an approach where the retinotopy and current estimates are generated from EEG or MEG signals and a standard clinical T1‐weighted anatomical MRI. Using the EEG‐RL, sources were localized to within 2 mm of the fMRI‐RL constrained localized sources. The EEG‐RL also produced V1 and V2 current waveforms that closely matched the fMRI‐RL's (n = 2) r _(1,198) = 0.99, P < 0.0001. Applying the method to subjects without fMRI (n = 4) demonstrates it generates waveforms that agree closely with the literature. Our advance allows investigators with their current EEG or MEG systems to create a library of brain models tuned to individual subjects' cortical folding in retinotopic maps, and should be applicable to auditory and somatosensory maps. The novel method developed expands EP's ability to study specific brain areas, revitalizing this well‐worn technique. Hum Brain Mapp 37:1696–1709, 2016. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Evoked potentials (EPs) recorded at the scalp are employed in a wide range of research and clinical applications. However, insights from EPs are limited to general brain dynamics due to the difficulty of localizing current sources in the cortical volume that generate the recorded voltage activity: the inverse problem. The activity recorded on the two‐dimensional (2D) scalp can appear to originate from multiple areas in the three‐dimensional (3D) cortical volume, unless substantial additional constraints are placed on the location of the current sources within the 3D cortex.

Overall, the ability to separate sources depends on factors such as Signal‐to‐Noise ratio (SNR), forward model fidelity, and the source's orientation [Ales et al., 2010; Baillet et al., 2001; Ferree et al., 2001; Hagler et al., 2009; Lütkenhöner, 1998]. Solving the inverse problem requires limiting the number of dipoles, constraining the possible dipole source positions, or additional information. This can be achieved, for example, by restricting to a limited number of point sources [Scherg, 1992; Zhang et al., 1994], or by fixing the sources on the cortical surface using MRI [Dale et al., 2000; Hämäläinen and Ilmoniemi, 1994; Phillips et al., 2002]. These methods allow the separation of sources in different regions, however, they are still confounded by sources located close together if they are close to parallel or anti‐parallel [Dale et al., 1999].

Retinotopy constrained source estimation (RCSE) utilizing an individual's fMRI retinotopic‐layout (fMRI‐RL) has recently shown good success as an additional constraint to solve the close source problem [Ales et al., 2010; Cottereau et al., 2012; Hagler et al., 2009; Hagler and Dale, 2013; Hagler, 2014]. A RL is a collection of retinotopic maps organized anatomically into adjacent strips corresponding to visual areas, e.g. V2 dorsal, V1, and then V2 ventral (Fig. 1E).

Figure 1.

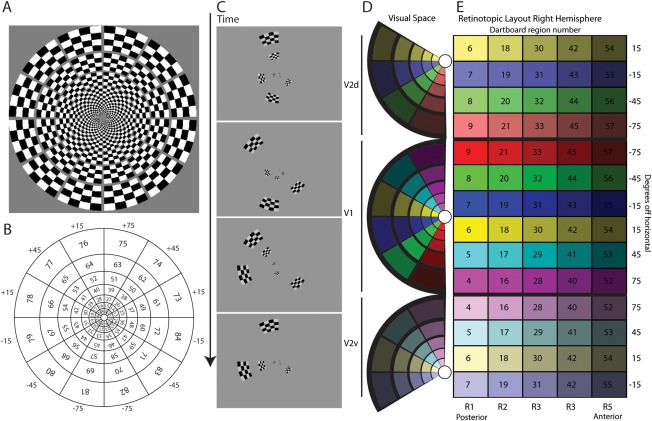
A, Dartboard stimulus with 84 regions. The inner 60 regions were selected after data acqusition for source analysis. Each region is a 4 × 4 checkerboard wedge consisting of 100 cd/m² and <1 cd/m² checks against a 50 cd/m² luminant background. B, Region number and polar angle for each stimulus. C, Example pattern‐pulse sequence. Each frame appears for 10 ms and active regions are on for 3 frames. D. and E, Mapping stimulus presentation in left visual field to cortical retinotopy on the right hemisphere. D, Dartboard regions in visual space (as displayed to subject) mapped to V2 dorsal, V1, and V2 ventral areas. E, Retinotopic layout (HSV color map) of cortical subareas with colors corresponding to regions in visual space. Dipole source HSV color map of right hemisphere. Hue corresponds to sector, saturation area V1 or V2, and Value corresponds to ring, i.e. rows are sectors, and columns are rings with layout V2 dorsal, V1, V2 ventral. Numbers correspond to the dartboard (B) left visual field. Regions 6 to 54 and 7 to 55 are represented in V2 dorsal and ventral to account for their potential to span the horizontal meridian.

However, the fMRI‐RL requires significant equipment and time investment. The fMRI‐RL can also be partially incomplete, and require manual adjustment before being used as a constraint [Goh, 2008].

To improve EEG source localization without fMRI maps, researchers have used magnetoencephalography (MEG) independently and in conjunction with EEG [Brookes et al., 2010; Cicmil et al., 2014; Perry et al., 2011; Sharon et al., 2007; Yoshioka et al., 2008]. Sharon et al. [2007] combined MEG and EEG signals and constrained localization to the gray/white matter boundary segmented from a structural MRI and achieved localization to within 10 mm of an fMRI‐RL based localization. Cicmil et al. [2014] compared localization sources of MEG signals using an anatomical MRI and Minimum Norm Estimation (MNE) [Dale et al., 2000; Gramfort et al., 2014; Hämäläinen and Ilmoniemi, 1994] to Beamformer [Litvak et al., 2011; Woolrich et al., 2011]. Localization accuracy in mm was not reported, however, the minimum source spacing was 4mm. None of these studies decomposed the MEG or EEG signal into V1 or V2 waveform components.

We developed a novel method to replace the fMRI‐RL with an EEG‐RL through user and computer driven optimization utilizing the multifocal VEP (MFVEP) and a structural MRI. The MFVEP activates separate regions in V1 and V2 retinotopically by stimulating separate regions of visual space over time [James, 2003]. Our method produces an RL and simultaneously decomposes the signals into V1 and V2 component waveforms. To distinguish sources between areas V1 and V2, the RL is positioned with V1 in the calcarine sulcus and V2 positioned dorsally and ventrally. Because the calcarine sulcus is a large and obvious cortical landmark, an initial RL can be placed manually. The rough RL is refined in morphology and position with computational optimization. Therefore we can eliminate the fMRI, saving time, cost, and reliability issues while retaining the benefits of an RL in separating close sources.

MATERIALS AND METHODS

Experimental Design

Subjects

Experiment 1: Validation against fMRI

EEG, MRI, and fMRI data were collected from one female and one male, aged 26 and 46 years old, respectively (s001 and s002).

Experiment 2: Application of the method without fMRI

EEG data were collected from five subjects (two females and three males) aged 26 to 42, (M = 32, SD = 6, s136, s151, s152, s153, and s154). One subject in the second group, s151, was excluded because an error in digitizing electrode locations prevented co‐registration with the MRI. All subjects in experiment 1 and 2 (except for s136) had EEG, MRI, and fMRI acquired at the Advanced Magnetic Imaging Centre, Helsinki University of Technology (2008). s136's EEG was recorded at the Australian National University and MRI at the Canberra Hospital [Goh, 2008; Inverso, 2010; Vanni et al., 2005]. The study was approved by the ethical committees of the Hospital District of Helsinki and Uusimaa, and The Australian National University. All subjects were healthy and gave informed consent.

Multifocal stimuli

The multifocal (MF) stimulus was presented in both EEG and fMRI paradigms. The stimuli consisted of dartboard layouts (Fig. 1) scaled inversely by human cortical magnification factor based on published materials to generate responses from patches on the cortical sheet with approximately equal area [Daniel and Whitteridge, 1961; Dow et al., 1985; Horton and Hoyt, 1991; Hubel and Wiesel, 1977; LeVay et al., 1985; Schein and de Monasterio, 1987; Schira et al., 2007; Van Essen et al., 1984]. Area magnification was modeled as:

$$M=\frac{k}{{\left(E+1.0\right)}^2}$$ (1)

M is the areal magnification factor in square mm per square degree of visual field, k is a scaling factor in mm² of cortex (300 mm² in this study), E is the visual field eccentricity in degrees, and the offset 1.0 is the eccentricity in degrees at which the model predicts a drop to 1/4 of the maximal areal magnification. The value is taken within the range of estimates from the cited reports. (Table 1).

Table 1.

Eccentricities of the different rings

Ring	Eccentricity low (°)	Eccentricity high (°)	Eccentricity center (°)
1	1.0	2.2	1.6
2	2.3	3.7	3.0
3	3.8	5.7	4.8
4	5.9	8.3	7.1
5	8.6	11.8	10.2

The scaled dartboard for VEP recordings had 84 regions, in seven rings, each having 12 sectors of 30° polar angle. The waveforms estimated for the inner five rings were used in this study, as they precisely corresponded to the 60 regions used in the multifocal fMRI analysis extending to 12° eccentricity. These five rings were at distinct eccentricities (midpoints at 1.6°, 3.0°, 4.8°, 7.1°, 10.2°). Gaps of 2° polar angle separated sectors and gaps of equivalent width scaled with eccentricity separated successive rings (Fig. 1B). The intention of increasing region size with eccentricity is to stimulate similar sized areas of V1 and thus produce a similar signal magnitude across eccentricities. In addition, fMRI responses for two subjects (s001 and s002) were used, using the multifocal design of Vanni et al. [2005]. This consists of a sequence of 68 blocks of 7.3 s each. Within 67 of the blocks half of the 60 regions are active, with a 4 × 4 checkerboard at mean luminance 22 cd/m², 82% Michelson contrast, contrast reversing at 8.3 reversals per second, while the other half are inactive at uniform luminance of 22 cd/m². The selection of active regions for a block follows a balanced, orthogonal design. EEG stimuli had identical spatial layout, however, with pulsed presentations of 4 × 4 checkerboard wedges, pulsed with 100% Michelson contrast on a 50 cd/m² gray background.

Stimulus presentation

For the EEG, dartboard regions were pulsed on for 33 ms (two frames of the 60 Hz monitor) for s136, and 30 ms (three frames of the 100 Hz monitor) for all other subjects. The screen areas without a region showing remained at the 50 cd/m² mean luminance gray background. Therefore, with each frame one or more regions were present, and the inactive region areas were at background luminance (Fig. 1C and Supporting Information Movie 1). During the ∼4 min EEG recording, each region appeared on average two times per second, giving a total of 484 pulses per region, arranged pseudorandomly in time, according to a quadratic residue binary sequence that positions the pulses at half of the points on a regular train of 0.25‐s steps. This pattern‐pulse stimulus presentation has an increased Signal‐to‐Noise ratio (SNR) at a presentation rate around two to four pulses per second per region [James et al., 2005] compared with the traditionally used contrast‐reversing stimuli [Baseler and Sutter, 1997; Baseler et al., 1994; Slotnick et al., 1999, 2001]. Each of the regions is pulsed with the same sequence, however, the sequence is cyclically shifted to create the pattern, with shifts approximately evenly distributed over the full time length of the run. An EEG recording run contains four segments of 60.9 s mean duration each.

Display

In fMRI, the stimuli were projected with a 3‐micromirror Christie X3™ (Christie Digital Systems, Kitchener, Ontario, CA) data projector to a semitransparent screen, which the subject viewed via a mirror at 35 cm viewing distance. In EEG, s136 viewed the stimulus through a stereoscopic display (two screens viewed via mirrors at 45°; lenses gave an effective infinity viewing distance, refresh rate 60 Hz). Vergence was corrected by the subject adjusting overlapping test images. RGB values were selected individually for each check and the background using a photometer (OptiCal, Cambridge Research Systems Ltd, Rochester, England). Experiments were conducted in a darkened environment with only light from the stimulus and operator displays. All other EEG subjects saw the stimulus on a 19‐inch CRT monitor (Nokia). The monitor's refresh rate was 100 Hz, and was gamma corrected using a photometer (OptiCal, Cambridge Research Systems Ltd, Rochester, England) giving a correction exponent of 1.9. Subjects viewed the monitor at a distance of 30 cm while sitting in a room with minimal background illumination. Stimuli were controlled by Presentation (Neurobehaviorial Systems Inc., CA) for all subjects.

EEG Acquisition and Analysis

A schematic workflow from data acquisition to dipole modeling and V1/V2 waveform decomposition is in the Supporting Information Figure 1.

EEG recording

All EEG recordings were acquired at 256 Hz with a BIOSEMI ActiveTwo (Amsterdam, The Netherlands) system. s136 was recorded with a standard 64‐channel layout. All other subjects were recorded with a modified International 10‐10 system of 74 electrode locations for a denser recording over the occipital cortex. Common mode sense (CMS) and driven right leg (DRL) electrodes were placed at Fz and Fpz, respectively for all recordings. Between two and nine repeats were run per subject.

MFVEP data analysis

Each EEG experimental run of approximately four minutes was processed using in‐house developed MATLAB software (Mathworks, Natick, MA). Data runs and segments were extracted using stimulus markers recorded on the BIOSEMI status channel via a parallel port cable from the stimulus computer. Signals' linear trends were removed then low‐pass filtered at 40 Hz as the waveform of interests' frequency is much less than 40 Hz and to reduce artifacts from 50 Hz power line noise. Signals were then resampled to yield an integral number of samples per stimulus frame (two or four data samples per frame). Resampling frequency was 200 Hz for monitors at 100 Hz and 240 Hz for monitors at 60 Hz. Noisy channels were removed by visual inspection. The signals were then high pass filtered at 1 Hz, and an independent component analysis (ICA) was used to extract eye blinks, using the EEGLAB Package [Delorme and Makeig, 2004]. Because of the magnitude of eye‐blink artifacts, the ICA invariably concentrated eye blink artifacts into one or two components, and the resulting ICA weights were used to subtract the corresponding component of response across all channels, allowing the remaining signal to be used without any rejected segment, similar to Li et al. [2006]. This subtraction, and all subsequent processing used the signals without high‐pass filtering, hence with bandwidth 0 to 40 Hz, to minimize distortion of the waveforms. Finally, channels with outlier artifacts in the signal were removed from the data sets before average referencing.

Fitting MFVEPs with basis functions

The recorded response signals were fitted with a bilinear model, which assumes the response to each stimulus pulse is a linear combination of three empirically estimated basis functions, with separate coefficients for each response channel and for each stimulus field region, producing 3 × 64 × 84 coefficients. Filtering was done to prewhiten response and stimulus signals, assuming a 10th order autoregressive error model for the noise in the recording [Goh, 2008]. The basis functions are initialized as a gamma function and two of its derivatives, while the noise model's filter coefficients' are initialized by an auto‐regression of the signal after removing its trend components. The estimation algorithm iterates between two stages. The first stage fixes the basis functions and pre‐whitening coefficients, and uses weighted least squares (WLS) to estimate the coefficients. The second stage fixes the coefficients and updates the basis functions and pre‐whitening coefficients. This update performs a Gauss‐Newton regression step projecting onto the tangent space giving a local linear approximation to a curved model surface. Channels are pooled with weighting inverse to the estimated channel noise variances. The algorithm stops when the change in cost function meets the tolerance level (an absolute change of less than 10⁻³ for any point in the retinotopic‐layout). For each region and electrode location the response waveform was fit over 300 ms.

Structural MRI Acquisition and Analysis

Structural MRI

Whole head structural MRI was acquired for all subjects using a T1 weighted sequence. s136's was acquired with 1.5 T, acquisition matrix 512 × 512, voxel size in mm, x = 0.5, y = 0.5, z = 1.0. All other subjects' MRIs were acquired with 3 T, acquisition matrix 256 × 256, x = 0.86 to 1.02, y = 0.86 to 1.02, z = 1.0 to 1.5.

Anatomical surface reconstruction from MRI

Experiment 1

3D cortical surfaces were reconstructed with BrainSuite 2.01, with corresponding surface coordinates creating a flatmap [Dogdas et al., 2005; Shattuck and Leahy, 2001, 2002; Shattuck et al., 2001].

Experiment 2

Subjects' 3D cortical surfaces were reconstructed with FreeSurfer 4.5.0 [Dale et al., 1999; Fischl et al., 2001, 1999, 2004; Ségonne et al., 2004]. Flat maps were cut from a 3D inflated surface such that the occipital pole and the calcarine sulcus were at the center.

Coordinate Frame Alignment

Digitized 3D coordinates of the corresponding electrode locations were obtained using a Polhemus FASTRAK digitizer (Colchester, VT) for each subject, together with their fiducial points: Nasion (NAS), Right Pre‐auricular Point (RPA), Left Pre‐auricular Point (LPA) to co‐register with the MRI and fMRI.

fMRI Acquisition and Analysis

Functional MRI data were acquired for two subjects (s001 and s002) using a 3 T MR scanner (Signa VH/i, General Electric Inc.) equipped with a head coil (standard GE quadrature receiver/transmitter) for signal detection. The single shot gradient‐echo echo‐planar imaging sequence had parameters TR = 1,819 ms, TE = 40 ms, acquisition and reconstruction matrices = 64 × 64, FOV = 160 × 160 mm, slice thickness 2.5 mm with no gap and flip angle = 90°. The 24 slices were acquired in interleaved order. The 60‐mm thick stack was oriented at about 90° to the parieto‐occipital sulcus, to acquire data from the occipital and parietal cortices. From each session altogether 272 functional volumes were included in the data analysis. Four sessions were acquired for each subject providing robustness against noise and artifacts. Functional data was converted to Analyze format and processed in SPM5 as described in Vanni et al. [2005]. Briefly, standard motion correction and slice correction were applied. Misalignment between the EPI and anatomical scans caused by magnetic field distortions were corrected using data from specific spin‐echo magnetic field mapping measurement and FSL 3.1 toolbox (Oxford Centre for Functional Magnetic Resonance Imaging of the Brain, Oxford, England). Sixty regression components of the fMRI data were fitted, 1 per stimulus region, with a difference of two gamma functions Hemodynamic Response Function (HRF) model. Constant and linear trend were fitted for each run. The GLM fit of the data produced a volume of beta coefficients and a volume of t‐values for each of the 60 stimulus regions, representing the strength and significance of activation on a 2.5 × 2.5 × 2.5 mm array of voxels. SPM was also used to co‐register the T1 MRI with the fMRI data [Goh, 2008; Vanni et al., 2005].

Source Modeling Method

Forward model

Experiment 1

Forward models for two subjects were created with BrainStorm 2008 [Baillet et al., 2001; Tadel et al., 2011] using a 3 mm discrete source space and conductivities (Sm⁻¹) brain 0.33, skull 0.0042, and scalp 0.33. The head model was the Berg and Scherg's [1994] three sphere model, with spheres distorted to ellipsoids to best fit the 3D electrode locations.

Experiment 2

Forward models were generated with MNE Toolbox 2.7 [Fischl et al., 2004; Hämäläinen and Sarvas, 1989; Jovicich et al., 2006; Mosher et al., 1999; Ségonne et al., 2004] on a 3mm discrete source space and conductivities (Sm⁻¹): brain 0.30, skull 0.006, and scalp 0.30. The head model used the boundery element method, with tessellations from the high resolution MRI for inner skull, outer skull, and scalp [Cuffin, 1995; Cuffin et al., 2001; Ermer et al., 2001; Kybic et al., 2005, 2006; Schlitt et al., 1995].

Integrated modeling

Current waveforms and cortical locations of activations were simultaneously estimated using a nonlinear optimization technique [Goh, 2008]. The retinotopic layout of patches for the 60 visual field regions stimulated and for cortical areas V1 and V2 is parameterized by the 2D surface coordinates of the patch corners. It is assumed that each hemisphere is activated by contralateral visual field, with the five rings of six 30° sectors activating a contiguous 5 × 6 array of patches in area V1, located in the calcarine sulcus (Fig. 1E). Dorsal and ventral sections of area V2 are represented above and below the V1 array, with corresponding eccentricities along the vertical meridian mapped adjacently along the V1/V2 border. Dorsal area V2 maps mainly the lower quadrant of the contralateral visual field, however, to allow the split between dorsal and ventral visual fields to vary around the horizon, four rows of patches are allowed for each section, rather than three, with the optimization partitioning the relative contributions for visual field adjacent to the horizon (Fig. 1E).

Each cortical patch is represented by an equivalent dipole after integration over the corresponding area of surface. The intention is to fit common activation waveforms across multiple patches, in terms of density of current dipole strength per unit area of cortical surface, but allowing for each patch to have a different area and different degree of cortical folding, which reduces the effective dipole strength due to cancellation of electric fields.

Each patch is thus represented by an equivalent normal vector, determined by the mean orthogonal direction to the cortical surface integrated over a given cortical patch. The equivalent normal vector's length is in mm², representing the effective patch area accounting for any cancellations from cortical folding. The normal vector length can be thought of as the area of a flat plane patch that would have the equivalent dipole effect. The equivalent dipole for each patch is rapidly estimated by summation over a fine grid within each square patch. We modeled the activation strength of a patch of cortex in response to presentation of a stimulus pattern on the corresponding visual field region by a waveform of current dipole density, in units of nAm/mm². When multiplied by the equivalent normal vector it gives the dipole strength in nAm, as a vector in 3D space. The equivalent dipole is combined in a dual‐paring operation with the gain covectors for that brain location estimated by the forward model to predict the scalp potentials that would be expected at the array of recording electrodes. See Supporting Information S1 for further details on the modeling method.

V1 and V2 waveforms

The multifocal evoked potential waveforms for each stimulus location and recording channel are all fitted by linear combinations of the three temporal basis functions (see Fitting MFVEPS section). Current dipole waveforms can thus be fitted by linear combinations of the same three temporal basis functions, and hence require just three coefficients to be estimated. In this study we fit one common waveform to all V1 patches, and another common to all V2 patches, hence requiring just six coefficients. While there is a small variation in time‐to‐peak at different eccentricities, the goal is to fit a single pooled waveform to all regions, thus the number of free parameters may be kept small, following the principle of bias‐variance tradeoff [Goh, 2008]. If we denote the region of visual field for source $s$ as $r\left(s\right)$, and wave‐type $\mathrm{w}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}\left(s\right)=1 \mathrm{o}\mathrm{r} 2$, then the predicted response in channel $j$ for stimulation of region $r$, at lag $k$ is the sum of components:

$$\widehat{g}\left(k,r,j\right)=\sum _{s\in S\left(r\right)}{G}_s\left(s,j\right)\times W(k,\mathrm{w}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}\left(s\right))$$ (2)

Here $S\left(r\right)$ is the set of sources responding to visual field region r, generally one V1 source and one V2 source, but two V2 sources, dorsal and ventral, for regions adjacent to the horizontal meridian. The array $W(k,\mathrm{w}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}(s\left)\right)$ models the two current dipole density waveforms over time lag $k$, with $\mathrm{w}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}\left(s\right)$ being the wave‐type for source $s$ (1 or 2 in this model). It represents dipole strength per unit area of cortical sheet, in units nAm/mm².

By representing the currents in this way, calculating the model is relatively fast compared with the summation over all time points, and the statistical efficiency of the estimates is optimized by using a weight matrix calculated as the inverse of the variance matrix of the coefficients fitting VEP waveforms.

The coefficients are estimated with weighted least squares regression for a set of dipole positions and equivalent normal vectors. The linear combination of basis functions and coefficients yield the waveforms over time, and waveform standard errors are created from the regression parameters' estimated variance matrices. The forward matrix is defined on a 3‐mm grid, with tricubic interpolation to find the gain values within grid cells, see Supporting Information Methods S1.1.

Optimization Method and Analysis

Source decomposition and semiautomatic retinotopy

The custom MATLAB software interface (Supporting Information Figs. 2 and 3) assisted in positioning the 2D retinotopic‐layout (RL) on the cortical flat map, separately for each hemisphere. The initial RL is placed at the center of the hemisphere's searchable area by the software. With the aid of the colored structural annotations and the 3D cortical surface, the user then moves the RL into an area that approximately matches typical retinotopy (i.e. V1 within the calcarine sulcus extending up the dorsal and ventral banks, V2 on the cuneus and lingual gyri, and the entire RL wrapping around the occipital pole).

Once the RL is positioned approximately, an optimization step is run to jointly optimize the surface coordinates of patch corners and the coefficients for V1 and V2 current waveforms. While the RL moved across the 2D flat map it simultaneously displayed moving on the 3D cortical surface aiding in its positioning, with display of the fitted V1 and V2 waveforms and the fitness cost (described below). This optimization step uses unconstrained minimization (fminunc) from the MATLAB Optimization toolbox.

User intervention is minimal in placing the RL as the anatomical reconstruction software annotates the calcarine sulcus, cuneus, and lingual gyri. Utilizing the annotations and a knowledge about the average location of retinotopic coordinates in the calcarine sulcus, the initial rough RL placement can be done in 15 to 30 min per subject by the user. The automatic optimization to finely place the RL takes ∼10 to 15 min per subject with an Intel i7 3 GHz processor.

Fitness cost function

The fminunc's cost function accounts for the error in fitting the V1 and V2 waveforms, combined with a term representing deviation of the RL's patch areas from expected human retinotopy area [Schira et al., 2007]. The cost function is proportional to the negative posterior log‐likelihood of the parameter estimates given the observed data. Using the posterior log‐likelihood allows the waveform fit error to be stabilized by a term representing the likelihood of fitted patch area on the cortical surface; in terms of prior expected value and variance. The fit cost is quantified by the sum of squares of residuals between V1 and V2 waveforms forward modeled from RL dipoles and measured multifocal waveforms over regions and channels. This fit‐cost sum of squares ( $S_{\mathrm{f}\mathrm{i}\mathrm{t}}$) is summed with weighting by estimates of the inverse variance of the waveform values. The sum of squares is thus a dimensionless quantity, having a χ ² distribution under the model's assumptions, with degrees of freedom equal to the degrees of freedom of the residuals from the fitting procedure. The inverse‐variance weighting also has the effect of normalizing for variation in noise level in the data between recordings, and thus produces similar cost values across subjects.

The cost term for patch area corresponds to the prior distribution for patch area, and is the sum of squares:

$$S_{\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}}=\sum _{s=1}^{\mathrm{n}\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}\frac{{\left(A_s-{\mu }_s\right)}^2}{{\sigma }_s^2}$$ (3)

This equation models the cortical patch areas ${(A}_s)$ as having independent Gaussian distributions with assumed values for expected value ${\mu }_s$ and variance ${\sigma }_s^2$, for each source, indexed by s, and in this form will also have a χ ² distribution with nsource degrees of freedom.

The denominator ${\sigma }_s^2$ weights the area of the RL's patches such that deviations in area for rows V2 ventral and dorsal ±15 degrees are down‐weighted to 1/20th the area cost of other patches. It is necessary to de‐weight these rows because they both can map portions of the horizontal meridian as it can be entirely in V2 ventral, V2 dorsal, or a mixture of both. Thus rows representing the horizontal meridian will often be different from ${\mu }_s$, and reducing their weight allows the optimization to converge using the more stable patches.

Analysis of the optimization method's retinotopic layout positioning on the flat map

The fMRI retinotopic‐layouts (RL) were randomly moved across the cortical flat map to determine how accurately the RL has to be drawn by the user before optimization. The 360 control points of the fMRI‐RL (180 in each hemisphere) were randomly moved in 1 mm steps on the cortex, and in random directions chosen uniformly for each point in degrees: 0 inclusive to 360 exclusive. The random moves were performed either by holding one hemisphere fixed and moving the opposite or moving both hemispheres at once, yielding three conditions: left only, right only, and left & right. Points were moved from 0.25 to 2 mm in 0.25 mm increments, and 2 to 20 mm in 1 mm increments, giving 26 positions. Thus the area around the true control point is explored at finer detail. Once a random direction was chosen the point moved in that direction for all increment positions as it moved across the cortical flat map. One hundred random directions were chosen for each position, in all, 2,600 RLs were produced per subject per condition (26 mm increments, 100 directions). Each randomly moved RL was optimized with the unconstrained minimization method described in Supporting Information 1.1.3.1. Each optimization required ∼1 min, resulting in 2.2 h of computation per subject.

Analysis of waveforms, dipoles positions, and moments in comparison of EEG‐RL and fMRI‐RL based decompositions

To determine the similarity between the V1 and V2 waveforms decomposed with the EEG‐RL versus fMRI‐RL constraint conditions; the decomposed V1 and V2 from the same MFVEP source through both constraint conditions were correlated by amplitude at each time point for all repeats of subject s001 and s002 separately.

For internal validation of the EEG‐RL constraint method, responses from each hemi‐ring were independently decomposed for each subject. Comparison of responses between hemispheres and rings from independent stimuli provide a cross‐validation for internal consistency.

RESULTS

Decomposed V1 And V2 Waveforms Closely Match Between the fMRI and “Hand‐Drawn” Retinotopic‐Layout Constraint

In this study, we developed a semiautomatic method to generate a retinotopic‐layout (RL) describing visual areas V1 and V2 using EEG without an fMRI scan. This EEG‐RL was used as a constraint to decompose surface VEPs into contributions from their V1 and V2 cortical sources: the Visual Evoked Currents (VECs), measured in terms of current dipole density, in nAm/mm² evoked by pulse presentation of a stimulus pattern over the corresponding visual field region. Comparing their standard errors, the V1 and V2 waveforms derived with EEG‐RL were equivalent to the waveforms derived with an fMRI‐based retinotopic layout (fMRI‐RL) produced for the same subject, r _(1,198) = 0.99, P < 0.0001 (Fig. 2).

Figure 2.

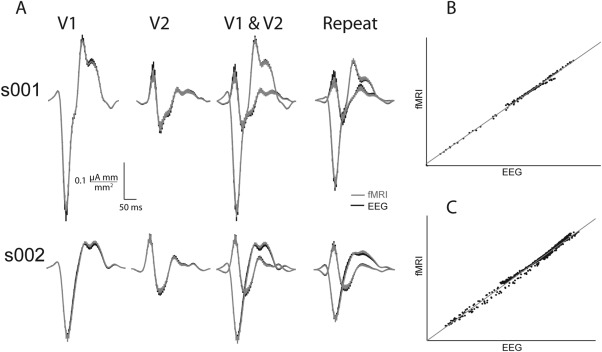
Visual evoked currents (VEC) decomposed with EEG or fMRI retinotopy constrained source estimation (RCSE). A, V1 and V2 waveforms produced with EEG (black) RCSE are similar and within the error of fMRI‐constrained estimation (gray). Repeat depicts waveforms generated using RCSE and the second EEG experimental repeat. B, s001 fMRI versus EEG waveforms using two repeats, r ₍₂₃₈₎ = 0.9998, P < 0.0001. C, s002 fMRI versus EEG waveforms using eight repeats r ₍₅₉₈₎ = 0.996, P < 0.0001.

The EEG‐RL regression produced an R ² = 0.36 for s001 and R ² = 0.41 for s002. The fraction of variance contributed to V1 and V2 are similar: s001: R ² = V1 0.21, V2 0.15. s002 R ² = V1 0.18, V2 0.23. The fMRI‐RL regression produced similar R ² values to the EEG‐RL constraint (s001 R ² = 0.32, s002 R ² = 0.41 for s002, and similar V1 and V2 fractions of variance). Given the complex source configuration with even the simplest visual stimuli, less‐than‐perfect R ² values are anticipated when only V1 and V2 are modeled. In addition, noise, and the residual variance from the cortex patch‐to‐source model transformation, most likely contributed to the unexplained variance.

Using an EEG‐RL requires the layout to be positioned on a cortical‐flat map. This step requires 15 to 30 min of user time, and then an automated optimization process finalizes its position while simultaneously decomposing the VEP waveforms into their V1 and V2 cortical sources. This process creates a subject specific dipole model that can be reused for other experiments. To ensure the forward model is a general model of cortical currents and not over fit to the specific sensor data used, repeated runs of the VEP experiment were decomposed with the forward model to verify the models ability to generalize. The V1 and V2 waveforms from experimental repeats were also within standard error of their corresponding waveforms produced with fMRI‐RLs (Fig. 2).

Consistency in V1 and V2 Waveforms Between Hemispheres

For internal validation, responses to each hemi‐ring were independently decomposed. The left and right hemisphere V1 and V2 responses are expected to be similar within each subject [Ales et al., 2010; Dandekar et al., 2007]. Figure 3 shows that even though the VEP responses are analyzed independently, there is still consistency in waveforms between hemispheres and rings, similar to Ales et al. [2010]. Small deviations are expected due to lower signal‐to‐noise in the limited number of regions, 6 versus 60.

Figure 3.

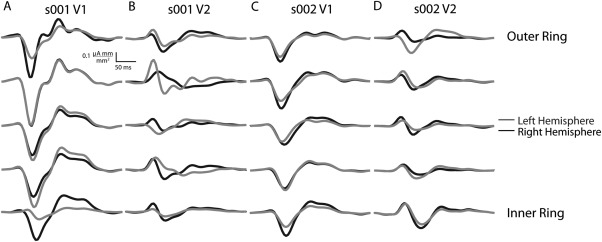
Independently estimated V1 and V2 responses to the five hemi‐ring stimuli from inner ring to outer ring. Each hemi‐ring consists of six regions, one for each sector in the hemi‐field's dartboard. The evoked EEG signal for each hemi‐ring are independent, composed of six regions per hemi‐ring. Even though the data is independent, there is still consistency between hemispheres and rings similar to Ales et al. (2010), deviations are expected due to lower signal‐to‐noise in the limited number of regions, 6 versus 60.

Optimization Finely Places the Retinotopic Map

As the semiautomatic process of generating an EEG‐RL requires the user to position the RL on the cortical sheet before optimization; it is import to measure how the user's chosen RL's position affects the optimization. If the initial RL is too far from the correct location, the optimization will not generate reliable V1 and V2 waveforms. To determine the reliable distance the RL could be placed from the true position, the fMRI‐RL was moved across the cortical flat map in random directions from its initial position. Figure 4 shows how the waveforms decreased in amplitude as the flat map moved across the cortical sheet, starting from the fMRI‐RL's origination position. The optimization reproduced equivalent V1 and V2 waveforms with RL up to 2mm from the original fMRI position with 95% confidence (Fig. 5B), as the RL moves further from optimal the waveforms decrease in amplitude (Fig. 4). The 2 mm distance is a worst‐case as it represents the distance of fully randomized points in the RL; this includes overlapping and folded patches. In real‐world usage the optimization may be tolerant to larger incorrect placements, as indicated by the nearly correct phase and decreased amplitude at 12.75 mm (Fig. 4). Therefore, the user does not have to perfectly place the initial RL to achieve dependable V1 and V2 waveforms as the optimization step will finely place it.

Figure 4.

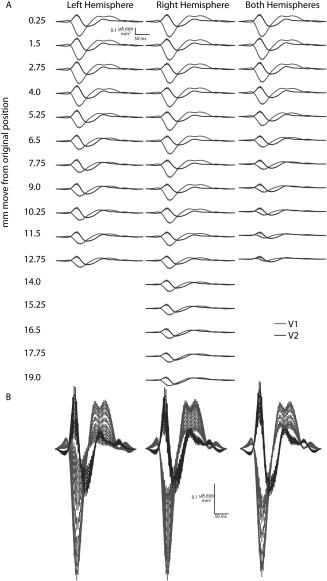
Waveforms from s002 randomly moved across the cortical flat map to determine how accurately the retinotopic‐layout (RL) must be drawn by the user. Either one hemisphere's cortical flat map was fixed and the opposite was moved, or both hemispheres moved at once, yielding three conditions: Left only, right only, and both (left and right). Points were moved randomly from 0.25 to 2 mm in 0.25 mm increments, and 2 to 20 mm in 1 mm increments, giving 26 positions (a subset of points are shown for clarity). The optimization reproduces equivalent V1 and V2 waveforms with RL up to 2 mm from the original fMRI position with 95% confidence. While waveforms after 2 mm appear reasonable, they deviate from the original fMRI waveform by greater than 95% of their points including standard error. This indicates with realistically less than full randomization in the point placement the optimization may be tolerant to larger incorrect placements. A, Left, right, and both hemispheres at a subset of positions in mm from original flat map position. Missing waveforms indicate no valid waveform was found when fitting the model at that position. B, Same as A. overlapping all shown waveforms, and at a different scale.

Figure 5.

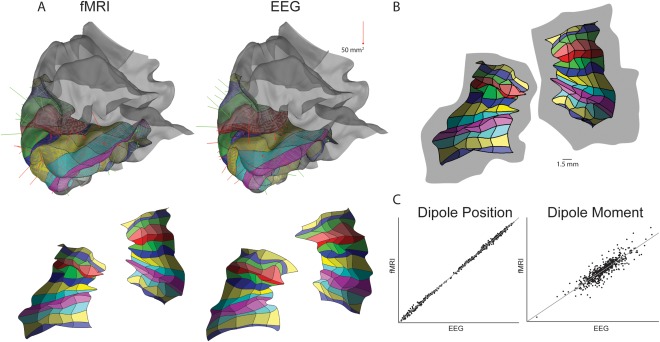
Retinotopic layout (RL) and final dipole comparison between EEG and fMRI Retinotopy Constrained Source Estimation (RCSE). A, Top, RL in fMRI versus EEG‐only on 3D cortical volume of s002 left hemisphere. Both methods place the V1 within the calcarine sulcus and wrap the RL similarly around the occipital pole. Bottom, RL spread on 2D flatmap of cortex. B, Users can place the RL's random control points approximately 2 mm away from their optimal position (gray area) and the optimization will still be successful. C, Dipole positions and moments of EEG versus fMRI RCSE correlate well with each other: Position r ₍₅₉₈₎ = 0.99,P < 0.0001, mean 2mm SD(1.4), Moment (M), r ₍₅₉₈₎ = 0.89,P < 0.0001).

Dipole Angles are Consistent Between EEG‐RL and fMRI‐RL Methods

The forward model is composed of dipole vectors orthogonal to the cortical sheet. The current dipoles create volume currents that propagate and sum through the brain, skull, and scalp to produce the recorded potentials. After independent optimization, both EEG‐RL and fMRI‐RL produced similar waveforms. The resulting dipole vectors had similar positions on the surface, r ₍₅₉₈₎ = 0.99, P < 0.0001, and moment, r ₍₅₉₈₎ = 0.89, P < 0.0001. The 3D vector difference (“angle error”) between EEG‐RL and fMRI‐RL dipoles was on average 8 (SD = 5) degrees (Fig. 5C, Supporting Information Fig. 4). Supporting Information Tables I to IV show the vector differences for all patches.

Extensible to Subjects Using Only the EEG‐RL

Because the aim of our work was to simplify the decomposition of V1 and V2 signal sources without requiring fMRI, we created forward models for four subjects without fMRI, using EEG‐RL data alone. The resulting waveforms were similar to the subjects with fMRI‐RL based decompositions (Fig. 6). The intrasubject differences in amplitude and waveform were attributed to the differences in conductance assumed in BrainStorm versus MNE toolbox and the more accurate BEM head model used for these subjects. There is an agreement in peak time and amplitude between these four subjects, including repeats. s136's repeat differs more than the other subjects because the signal quality was diminished in the second measurement.

Figure 6.

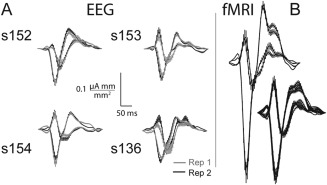
V1 and V2 visual evoked currents decomposed with retinotopy constrained source estimation (RSCE). A, Four subjects' visual evoked currents (VECs) with EEG‐RCSE. Rep 1. is the EEG from the visual evoked potential (VEP) repeat used to create the retinotopic layout (RL). Rep 2. Depicts source currents from the second repeat of the VEP experiment, based on the model created with Rep 1. The VECs produced are similar in amplitude and timing. s136 is an example of a deviant waveform due to noisy EEG. B, Depiction of repeat variation using fMRI‐RCSE: two repeats for left VEC, eight repeats for right VEC.

DISCUSSION

We have demonstrated that constraining dipole decomposition with an EEG retinotopic‐layout (RL) can distinguish close sources without an fMRI‐RL. Beyond the EEG or MEG setup, our method only requires an anatomical MRI. Both EEG and structural MRI are routine examinations in clinical neurosciences, and available in most hospitals without additional investments. Thus, this semi‐automatic method and optimization can be performed in a fraction of time and cost compared with creating an RL from an fMRI. The V1 and V2 waveforms produced with the EEG‐RL also match well with the fMRI‐RL decomposed waveforms of Ales et al. [2010], Hagler et al. [2009], and Hagler and Dale [2013] who were using fMRI‐RLs. This is encouraging because they used different MFVEP stimuli—192 and 96 stimuli with contrast reversing for Ales and sets of 36, 16, 12, and 4 stimuli in Hagler.

The RLs and dipoles on the 3D cortical surfaces and integrated dipoles are also encouragingly similar between the EEG‐RL and fMRI‐RL constraint conditions (Fig. 5). Optimization was able to place the EEG‐RL correctly in the calcarine sulcus and around its ventral dorsal banks to achieve similar dipole orientation and moments to the fMRI‐RL. In addition, the EEG‐RL condition is internally consistent between hemispheres when the fitting is done independently for the two hemispheres (Fig. 3).

While our method was demonstrated with EEG, it is potentially also applicable to MEG. Although MEG cannot detect radial sources, radial sources to the skull form less than 5% of cortical area (defined as 0–15° with radius) [Hillebrand and Barnes, 2002], therefore only a small proportion of sources cannot be detected by MEG. In most cases a patch of active cortex provides some signal from the tangential component of the activation, which is detectable by MEG. In addition, we stimulated 1.0° to 12° eccentricity of the visual field, and outside the foveal presentation in the occipital pole, most of our stimuli are represented in the calcarine sulci and mesial surfaces of the cortex, providing mainly tangential component and thus strong MEG signal. In addition, the skull is transparent to MEG signals, thus avoiding strong smoothing effect contaminating EEG source localization.

The accuracy of algorithms to determine the source signals of surface potentials is limited by simplifications and technical necessities made by the designers. In the method described, the number of visual areas was limited to two (V1 and V2), therefore it is possible signals have contribution from extrastriate areas ignored in the current model, such as V3. This is probably small because multifocal layouts inhibit contribution from neighboring areas; with lateral suppression apparently increasing from V1 towards higher order areas [Pihlaja et al., 2008; Vanni et al., 2005]. Extrastriate areas do, however, produce multifocal responses when the dartboard layout is less dense [Henriksson et al., 2012].

We assumed a single waveform for all V1 patches, and another waveform for all V2 patches. This approach ignores possible differences in the upper and lower visual field locations, and between individual patches. Future work could open up the difference between patches, e.g. by parameterizing the difference with additional independent variables in the model. Our approach is comparable to the approach of Hagler et al. [2009], who assumed a single dipole for each stimulus location and visual area.

The rough user positioning of the initial RL is straightforward given the prior information readily available: annotations from anatomical surface reconstruction software—coloring of the calcarine sulcus, cuneus, and lingual gyri—and knowledge about the average location of the retinotopic coordinates in the calcarine sulcus. Therefore, the method described can be used by a minimally knowledgeable user (‘blind’) without strong prior expectations of the retinotopic layout and source reconstruction. It is possible user bias may affect the resulting decomposition, however, the optimization step done after the user positions the RL minimizes this bias.

Further technical issues limiting the accuracy include the choice of head model, the 3 concentric spheres versus a closer anatomical representation such as Finite Element Model (FEM) [Gencer and Acar, 2004; Hagler et al., 2009; Ollikainen et al., 1999; Wolters et al., 2006], and the accuracy of EEG co‐registration with fMRI and MRI. Hagler provides a thorough treatment of these limiting factors (2009).

The choice of 60 stimuli in the 4 minute EEG stimulation was based on pilots and previous experiments [e.g., Bair et al., 2003; Vanni et al., 2005]. It is likely that a reduced number of stimulus locations could be used to produce a reliable EEG‐RL. For example, Hagler et al. [2009] achieved similar results with 16, and Hagler and Dale [2013] with 36 patches.

Finally, while we endeavored to remove eye artifacts through the automated and manual methods described, it is possible some artifacts from eye movement, where the subject did not fixate consistently, or closed eyes, were present in the final data as this is a possibility in all VEP presentation paradigms. However, we believe the number of repeats for each region and subject reduces the contribution of these artifacts to our findings.

Retinotopy constrained source estimation (RCSE) with user generated EEG‐retinotopic layout method produces waveforms and dipoles comparable to fMRI constrained source analysis. The method described is generally applicable to all cortical areas that have an orderly topographic mapping and a stimulus‐response detectable by EEG or MEG. For example, the somatosensory [Mauguière, 2005] and auditory cortex [Musiek and Baran, 2007] both have mappings and respond to stimuli with evoked potentials.

While the current work decomposed areas V1 and V2, the retinotopic layout can be extended to higher visual areas such as V3 and V4, with an increase in patches on the layout at the expense of a longer optimization time. This might require reduction in the number of visual field regions, given that neighboring regions typically suppress each other [Vanni et al., 2005]. This suppression increases at the higher‐level visual cortices, precluding multifocal mapping at the high‐end object areas; although they are retinotopically organized [Henriksson et al., 2012; Pihlaja et al., 2008].

Future work can make the technique require less user interaction. The optimization step occasionally folds the retinotopic‐layout (RL) over itself at the edges requiring the experimenter to move the corners and unfold it. The weight on the area cost can be increased to avoid folding, however, this is generally undesirable as it will bias towards a population average RL and not the subject's individual layout. In addition, it essentially de‐weights the waveform error cost, which is more representative of the individual being fitted as it derives from the individual's sensor recording. Another approach is to add a bending cost to the patch borders. An interesting prospect emerges from the possibility to parametrize the V1 and V2 kernels, thus creating a statistical distribution of normal population parameters. This would enable statistical testing on single individuals in line with standard clinical laboratory testing, where extreme parameter values could be classified as pathological. In particular, extending this to evaluate posterior brain damage, such a method would enable discerning low‐ and high‐level visual cortex damage, and perhaps provide additional windows for rehabilitation of developmental disorders, such as amblyopia.

It is possible that an EEG‐RL can be created without digitized sensor locations because the retinotopic map is a strong individualized constraint. If an electrode cap is positioned with care to the nasion and inion in the 10 to 20 electrode system, it may be possible to align a standard layout of electrode locations to the MRI‐derived scalp surface with a projection to the surface. This might allow data from old experiments to be source estimated as well.

The major contribution of our method is that it removes the laborious process of creating an fMRI retinotopy to resolve close signal sources in visual areas V1 and V2, allowing many researchers to use their existing EEG or MEG equipment and expertise to investigate intracortical source dynamics. In addition, individual subject differences in cortical folding that confound traditional signal source decomposition are an asset in this approach as experiments are designed to utilize the subjects' folding to place stimuli in optimal visual field locations. The time and cost savings allow more experiments to be performed and more subjects to be studied than is currently possible for many labs without the resources required for an fMRI. This advance hopefully revitalizes the evoked potential, amplifies its versatility, and opens new research possibilities in neural cortical dynamics.

Supporting information

Supporting Information

Supporting Information Movie 1

Supporting Information Table 1

Supporting Information Table 2

Supporting Information Table 3

Supporting Information Table 4