Fact learning in complex arithmetic—the role of the angular gyrus revisited

Abstract

In recent theoretical considerations as well as in neuroimaging findings the left angular gyrus (AG) has been associated with the retrieval of arithmetic facts. This interpretation was corroborated by higher AG activity when processing trained as compared with untrained multiplication problems. However, so far neural correlates of processing trained versus untrained problems were only compared after training. We employed an established learning paradigm (i.e., extensive training of multiplication problems) but measured brain activation before and afte training to evaluate neural correlates of arithmetic fact acquisition more specifically. When comparing activation patterns for trained and untrained problems of the post‐training session, higher AG activation for trained problems was replicated. However, when activation for trained problems was compared to activation for the same problems in the pre‐training session, no signal change in the AG was observed. Instead, our results point toward a central role of hippocampal, para‐hippocampal, and retrosplenial structures in arithmetic fact retrieval. We suggest that the AG might not be associated with the actual retrieval of arithmetic facts, and outline an attentional account of the role of the AG in arithmetic fact retrieval that is compatible with recent attention to memory hypotheses. Hum Brain Mapp 37:3061–3079, 2016. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Mental arithmetic is a particularly well suited domain for investigating learning processes because it requires the integration of declarative (e.g., arithmetic facts), procedural (e.g., algorithms), and conceptual knowledge (e.g., arithmetic principles). In recent years interest regarding the neural mechanisms underlying the acquisition of core arithmetical abilities increased [Delazer et al., 2003, 2005; Grabner et al., 2009a, 2009b; Ischebeck et al., 2006, 2007]. Brain imaging studies deepen our understanding of the mechanisms underlying the acquisition of arithmetic competence. They not only allow for the identification of brain structures involved in learning arithmetic facts and procedures but also for investigating changes in brain activation as a consequence of numerical learning. The majority of studies on numerical learning so far pursued the acquisition of arithmetic facts by means of drill trainings of arithmetic problems ‐ primarily employing difficult multiplication problems [e.g., 43 × 9 =___; Delazer et al., 2003, 2005; Grabner et al., 2009a; Ischebeck et al., 2006]. All of these training studies compared brain activation patterns associated with the processing of either trained or untrained multiplication problems in one fMRI session following up on multiple sessions of drill training [for a different approach see Ischebeck et al., 2007].

A consistent finding of these training studies was stronger activation of the fronto‐parietal network of number processing—such as the left inferior frontal gyrus and the intraparietal sulcus (IPS)—for untrained as compared with trained multiplication problems. In contrast, these studies reported stronger activation1 in ventral parietal cortex—precisely in the left angular gyrus (AG) for trained problems [e.g., Delazer et al., 2003, 2005; Ischebeck et al., 2006]. The authors interpreted this change of brain activation patterns after drill training to reflect a shift from quantity‐based and working memory demanding computations to automatic retrieval of arithmetic facts from long‐term memory [Delazer et al., 2003; Ischebeck et al., 2006]. It was argued that the left AG constitutes the key area for these retrieval processes [e.g., Dehaene et al., 2003]. In particular researchers assumed the left AG to be recruited specifically whenever an arithmetic problem can be solved by retrieval of arithmetic facts from verbal long‐term memory (e.g., multiplication tables such as 2 × 3). A direct comparison of different learning methods (drill vs. strategies) for solving complex multiplication problems seemed to further corroborate the crucial role of the AG in arithmetic fact retrieval [Delazer et al., 2005]. Multiplication problems trained by drill led to stronger involvement of the AG than problems trained by strategies.

Previous work, however, has only focused on comparing brain activation patterns associated with the processing of trained vs. untrained problems after training [Delazer et al., 2003, 2005; Grabner et al., 2009b; Ischebeck et al., 2006]. This means that changes in brain activation due to the actual acquisition of arithmetic facts may not have been evaluated sufficiently because there was no fMRI scan before the training. The exact role of the AG for the acquisition of arithmetic facts is therefore less clear than suggested by published studies. In line with this argument, Grabner et al. [2009b] observed a task‐independent increase of AG activation after extensive drill training not only for multiplication problems but also for a figural‐spatial (non‐verbal) task. This is in line with the view that the AG might be involved in more general processes of learning such as processes of symbol‐referent mapping which are not domain‐specific [Ansari, 2008; Grabner et al., 2013]. These findings challenge the idea that the involvement of the AG in mental arithmetic can be reduced to retrieval processes from verbal long‐term memory.

Moreover, although increased AG activation after training was generally interpreted as an indicator of fact retrieval from long‐term memory, none of the studies cited above investigating the acquisition of arithmetic facts actually evaluated the role of other cortical structures classically associated with long‐term memory such as the hippocampus, parahippocampus, or retrosplenial cortex [Baddeley, 1996; Montaldi and Mayes, 2010]. Only recently, researchers began to elucidate the role of these traditional memory‐related cortex areas in numerical learning [Qin et al., 2014; Rosenberg‐Lee et al., 2014] and arithmetic fact retrieval [Klein et al., 2013, 2016].

In the present study, we employed a learning paradigm identical to the one used in previous studies investigating arithmetic fact learning (i.e., drill training of difficult multiplication problems), but measured brain activation during multiplication problem solving by fMRI scans before and after the training (pre‐ and post‐training fMRI session). This allowed us to evaluate changes in brain activation patterns associated with the actual acquisition of arithmetic facts more specifically than the post‐training comparison of activation patterns elicited by trained vs. untrained problems. In particular, we were interested in the direct comparison of AG activation observed for the same set of items before and after the training. Additionally, attention was paid to the involvement of cortex areas commonly associated with semantic long‐term memory (i.e., hippocampus, parahippocampus, and retrosplenial cortex).

Our specific hypotheses were as follows:

1. Because all previous studies on arithmetic fact learning by drill reported stronger AG activation for trained vs. untrained problems, we expected stronger AG activation for both comparisons—the contrast trained versus untrained multiplication problems of the post‐training session but also the contrast trained problems of the post‐training session vs. the same problems before the training.

2. Taking into account recent observations regarding the involvement of the hippocampus in numerical learning and arithmetic fact retrieval [Qin et al., 2014; Klein et al., 2013, in 2016], we also expected to observe hippocampus activation in the same contrasts (i.e., trained vs. untrained problems of the post‐training session and trained problems of the post‐training session vs. untrained problems of the pre‐training session).

METHODS

Participants

Thirty‐two right‐handed volunteers (24 women, mean age = 22 years; SD = 2) participated in the study after having given their written informed consent in accordance with the protocol of the local Ethics Committee of the Medical Faculty of the University of Tuebingen. All participants had normal or corrected to normal vision and reported neither a previous history of neurological or psychiatric disorders nor weakness in arithmetic.

Stimuli and Design

Three different item sets were used: to avoid simple repetition effects, two sets comprising stimuli that were not trained were generated. The order of these two sets was counterbalanced across participants. In the following, untrained‐1 (UT1) refers to the untrained stimuli of the pre‐training session, whereas untrained‐2 (UT2) refers to the untrained stimuli of the post‐training session. The third set comprised the to‐be‐trained stimuli. This latter set is termed to‐be‐trained (TBT) for the pre‐training session and trained (T) for the post‐training session, to distinguish between pre‐ and post‐training sessions and to emphasize that stimuli are unknown in the pre‐training session.

Each of the three item sets comprised 34 different two‐digit (range 12–98) × one‐digit (range 3–9) multiplication problems (e.g., “36 × 8”). All three sets were matched for the following stimulus properties: problem‐size of factor one (M = 47.91), problem‐size of factor two (M = 5.76) as well as for the problem‐size of the product (M = 263.91). Within the item sets the first factor was odd in 15 and the second factor in 16 of the 34 multiplication problems. To provide challenging multiplication problems the second factor was always larger than two. Consequently, the majority (29 out of 34) of results was a three‐digit number.

Procedure

Imaging data

The experiment was a combined event‐related fMRI and reaction time (RT) study. Participants were scanned twice at the same time of day, with one week in between, both before (pre‐training session) and after (post‐training session) completing five sessions of intensive multiplication training. The TBT item set used in the pre‐test fMRI session, was then trained in five training sessions outside the scanner. Two additional untrained items sets, one in the pre‐training (UT1) and the other in the post‐training (UT2) fMRI sessions were used. In other words, during the pre‐training fMRI session items of the to‐be‐trained set (yet unknown to participants, TBT) and of the untrained sets (UT1) were presented. In the post‐training fMRI session, the items of the second untrained set (UT2, matched for item properties) were presented together with the meanwhile trained problems of the to‐be‐trained set (T).

During pre‐ and post‐training sessions each trial started with the presentation of a fixation cross (500 ms). Subsequently, a multiplication problem together with the correct result and a distractor was presented. Participants then had 7 seconds to respond by pressing one of two MRI compatible response buttons with either their right or left thumb. In case participants responded earlier within this 7 second period, a mask was shown (##× #) to keep item duration fixed and to hold visual input comparable. Each trial was followed by a jittered inter‐trial‐interval of 2.5 seconds on average (ranging from 2,000 to 3,000 ms sec). Each fMRI session comprised 10 practice and 68 experimental trials. Additionally, 20% null‐events of 7.5 seconds duration each were randomly interspersed over each fMRI session. All stimuli were projected on a screen above the head of the participant. Participants viewed the stimuli through a mirror mounted on the head coil of the scanner. Foam pads were used to minimize head movements within the head coil during fMRI acquisition. Multiplication problems were presented centered on the screen. Operands were presented horizontally aligned separated by a centered multiplication sign. All stimuli were presented in white Arial 42 font against a black background. The experiment was performed using Presentation® software (http://www.neurobs.com).

Participants were instructed to indicate as fast and as accurately as possible, which of two solution probes was the correct result. Incorrect solution probes (distractors) always differed from the correct result by 10 to prevent parity‐based solution strategies. To familiarize participants with task requirements and the input devices, they had to solve 10 multiplication problems within the scanner prior to the critical trials. None of these practice items was contained in the critical item sets.

Training procedure

In the training sessions no solution probes were provided and participants had to enter the correct result using the number pad of a standard QWERTZ keyboard.

The multiplication training comprised five training sessions spread over five consecutive days following the pre‐training fMRI session. Participants were trained on the 34 multiplication problems of the to‐be‐trained set (TBT). Overall, each multiplication problem was presented six times. In total, this resulted in 204 trials per training session. Each session was subdivided into three blocks. Order of problem presentation was randomized and the same problem was never presented on two consecutive trials. Each multiplication problem remained visible until the correct result was entered via the number pad. Feedback was provided after each attempt to solve a problem. Participants were instructed to solve the problems as fast and accurately as possible. Training duration decreased on average from approximately 60 min in the first session to about 40 min in the last session.

The paradigm of the present study closely resembled former studies investigating fact learning in complex arithmetic [Delazer et al., 2003; Grabner et al., 2009a, 2009b; Ischebeck et al., 2006]. Nonetheless, the implementation of a two‐alternative forced choice paradigm during fMRI sessions cannot rule out completely that recognition processes might have occurred during task execution. However, we are confident that the free‐production paradigm during the five training sessions in which the result of a multiplication problem had to be reconstructed from scratch did not foster a problem solving strategy predominantly based on recognition processes. Besides, in the discussion section we outline a theory on the retrieval of arithmetic facts from long‐term memory (LTM) which emphasizes the importance of recognition processes for successful retrieval of arithmetic facts.

MRI/fMRI acquisition

A high‐resolution T1‐weighted anatomical scan was acquired with a 3T Siemens Magnetom TrioTim MRI system (Siemens AG; Erlangen, Germany) equipped with a 12‐channel head matrix coil (TR = 2,300 s, matrix = 256 × 256 mm², 176 slices, voxel size = 1.0 × 1.0 × 1.0 mm³; FOV = 256 mm, TE = 2.92 ms; flip angle = 8°). The anatomical scan was performed at the end of the experimental sessions.

Functional T2*‐weighted images were obtained using gradient‐echo Echo planar imaging (EPI; TR = 2,400 ms; TE = 30 ms; flip angle = 80°; FOV = 220 mm, 88 × 88 matrix; 42 slices, voxel size = 2.5 × 2.5 × 3.0 mm³, gap = 10%). Total scanning time was approximately 20 minutes. A baseline (rest) condition was accomplished by including about 20% null events in the paradigm.

Analysis

Behavioral results comprised both response times (RT) and error rates (ER). Analyses of RT were based on trials followed by a correct response only. A subsequent trimming procedure eliminated all trials for which RT fell outside the interval ±3 SD around a participant's mean RT. Elimination of incorrect trials and trimming procedure resulted in a loss of 20% trials. We used linear mixed effects models (LME) to analyze RT data and generalized linear mixed effects models (GLME) with a binomial error distribution and the logit as link function to analyze ER data (see the Supporting Information for results using conventional repeated measures ANOVAs).

Fixed effects in both analyses were item set (trained vs. untrained), session (pre‐training session vs. post‐training session) and the interaction between item set and session. Predictor variables were effect‐coded prior to analyses. In the LME for RT data we used the maximum random effect structure as suggested by Barr et al. [2013]. Thus, we included a random intercept for participants as well as items in the model. Additionally, we included random slopes for item set, session and their interaction in the model. In the analysis of ER data, we included a random intercept for participants as well as items. (G)LME were run using R [R Development Core Team, 2015], and the R package lme4 for linear mixed model analyses [Bates et al., 2014]. P‐values for fixed effects of RT data were derived using the Satterthwaite approximation for degrees of freedom available in the R package lmerTest [Kuznetsova et al., 2015]. To obtain P‐values for fixed effects of ER data, we ran likelihood ratio tests using the R package afex [Singmann et al., 2015]. fMRI data analyses were performed using SPM12 (http://www.fil.ion.ucl.ac.uk/spm). Images were motion corrected and realigned to each participant's mean image. Imaging data was then normalized into standard stereotaxic MNI space (Montreal Neurological Institute, McGill University, Montreal, Canada). Images were resampled every 2.5 mm using fourth degree spline interpolation and smoothed with a 5 mm FWHM Gaussian kernel to accommodate inter‐subject variation in brain anatomy and to increase signal‐to‐noise ratio in the images. The data were high‐pass filtered (128 s) to remove low‐frequency noise components and corrected for autocorrelation assuming an AR(1) process. Brain activity was convolved over all experimental trials with the canonical hemodynamic response function (HRF) and its first time derivative.

Pre‐ and post‐training fMRI sessions were combined on the subject level in a generalized linear model (GLM), using SPM12. For each participant, we added two separate sessions. Consequently, the GLM on the subject level contained a constant for each session. As outlined above, the combination of the two factors item‐set [(to‐be‐)trained vs. untrained] and session (pre‐ vs. post‐training) resulted in four experimental conditions (UT1, TBT, UT2, T). Importantly, to capture the influence of problem difficulty and to control for known effects of problem‐size on AG activation [e.g., Grabner et al., 2007], we included the covariate problem‐size2 (i.e., the size of the result of the multiplication problem) as a parametric regressor in the first level analysis, because it is an established indicator of item difficulty [Campbell and Epp, 2005 for a review].

On the group level, we analyzed the estimated beta weights for each experimental condition of each participant running an ANCOVA with the covariate problem size, using the flexible factorial design option within SPM12. In this model the variance between subjects is assumed to be different but equal for the different conditions and sessions within a subject. An additional test with “unequal” variance between subjects for the different sessions and conditions did not reveal substantial differences.

The SPM Anatomy Toolbox [Eickhoff et al., 2005], available for all published cytoarchitectonic maps from http://www.fz-juelich.de/ime/spm_anatomy_toolbox, was used for anatomical localization of effects where applicable. In areas not yet implemented, the anatomical automatic labeling tool (AAL) in SPM12 (http://www.cyceron.fr/web/aal anatomical_automatic_labeling.html) was used. Activations were thresholded at an uncorrected P‐value of <0.001 at the voxel level with a cluster size of k = 10 voxels and were reported when they remained significant following family‐wise error correction (FWE) at the cluster‐level with P_{cluster‐corr} <0.05.

In line with our hypothesis, we created two anatomical regions of interest (ROIs) for the region of interest analysis using the SPM Anatomy toolbox v2.0 [Eickhoff et al., 2005, 2006, 2007]: an anatomical ROI covering (1) the left AG (areas PGa and PGp) and (2) the hippocampus bilaterally (CA1‐3, DG, EC, and subiculum). since previous work emphasized the role of these areas in arithmetic fact retrieval [Fig. 1; Cho et al., 2012; Dehaene et al., 2003; Delazer et al., 2003; Ischebeck et al., 2006; Klein et al., 2016; Qin et al., 2014]. All ROIs were created using the SPM toolbox MarsBar (http://marsbar.sourceforge.net). Additionally, we ran a multivariate pattern analysis (MVPA) in which we trained a support vector machine for classifying trained vs. untrained items (see the Supporting Information).

Figure 1.

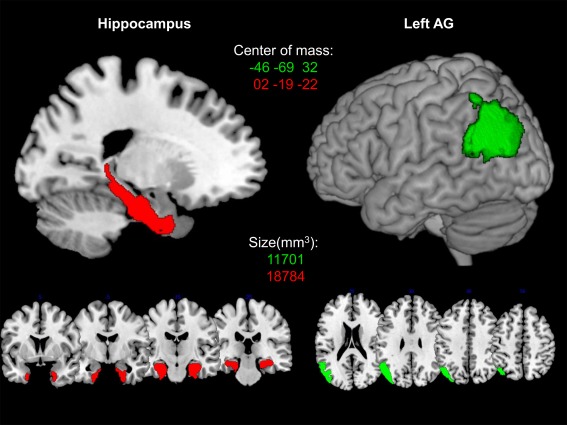
The red color indicates the bilateral hippocampus ROI, comprising areas CA1, CA2, CA3, subiculum, and entorhinal cortex. The green color shows the left AG ROI, comprising the areas PGa and PGp. ROIs are presented on a 3D rendered surface and coronal slices for bilateral hippocampus and axial slices for left AG, respectively. MNI coordinates of the center of mass and size of every ROI in mm³ is denoted in the corresponding color.

RESULTS

Behavioral Results

Pre‐ versus post‐training comparison of RT and ER data

The LME revealed a significant interaction of item set and session [F(1,72.63) = 108.56, P < 0.001] indicating that training effects differed between trained and untrained items. Post‐hoc tests revealed that estimated RT for (to‐be‐)trained and untrained items differed in the post‐training session (estimated mean difference of untrained vs. trained items = 732 ms, P < 0.001) but not in the pre‐training session (estimated mean difference of untrained vs. trained items = −34 ms, P = 0.791). Moreover, mean RT decreased significantly for both untrained and trained items from pre‐ to post‐training session (estimated mean difference for untrained items = 518 ms, P < 0.001; estimated mean difference for trained items = 1,283 ms, P < 0.001) (Fig. 2).

Figure 2.

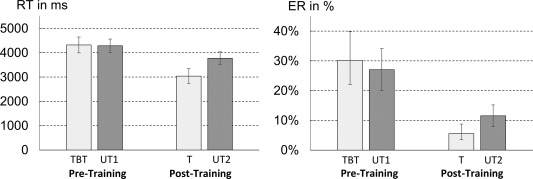
Estimated mean reaction times of the pre‐training (TBT: to‐be‐trained items; UT1: untrained‐1 items) and post‐training (T: trained items; UT2: untrained‐2 items) fMRI session. Error bars indicate 95% confidence intervals of parameters.

Furthermore, the LME revealed a significant main effect of the factor item set [F(1, 102.36) = 7.91, P = 0.006]: participants needed more time to solve untrained (estimated M = 4,028 ms) than (to‐be‐)trained multiplication items (estimated M = 3,679 ms). Additionally, a significant main effect of the factor session was observed [F(1,32.84) = 190.89, P < 0.001]. Participants were significantly faster in selecting the correct answer to a multiplication problem in the post‐training (estimated M = 3,404 ms) than in the pre‐training session (estimate M = 4,304 ms).

A GLME on ER paralleled the results of the RT analysis. We observed a significant interaction of item‐set and session [χ²(1) = 28.68, P < 0.001], corroborating the findings of the RT analysis. Post‐hoc comparisons showed that (to‐be‐)trained items were solved less error‐prone than untrained items in the post‐training session [estimated difference in log odds = 0.80, in%: 6% z = 4.19, P < 0.001] but not in the pre‐training session [estimated difference in log odds = −0.15, in %: −3%, z = −0.99, P = 0.513]. Moreover, similar to RT data, participants’ error rates decreased from pre‐ to post‐training session for both untrained and trained items (estimated difference in log odds for untrained items = 1.04, in%: 16%, z = 9.09, P < 0.001; estimated difference in log odds for trained items = 1.99, in%: 25%, z = 14.95, P < 0.001).

Furthermore, both main effects of item set and session were significant. Participants committed more errors when solving untrained than (to‐be‐)trained items [log odds = −1.51 vs. log odds = −1.84, in %: 18% vs. 14%; χ²(1) = 4.56, P = 0.033]. Moreover, a highly significant main effect of session was observed [χ²(1) = 322.72, P < 0.001] indicating that participants made significantly fewer errors after five sessions of multiplication training (log odds = −2.43 vs. log odds = −0.92, in %: 8% vs. 29%).

In sum, converging results from RT and ER data provide robust evidence that multiplication problem‐solving skill improved significantly after five sessions of extensive multiplication training.

Imaging Results

Comparing trained and untrained items of the post‐training session

Trained items (T) versus untrained items (UT2)

In line with recent results, contrasting trained and untrained multiplication items of the post‐training session revealed reliable activation in left‐hemispheric language areas, the AG, and the basal ganglia. In particular, we observed activation in bilateral AG (PGa) (Fig. 3, Table 1; T–UT2). Furthermore, we found activation in the right supramarginal gyrus (SMG, PFm/PFcm/PFop), bilateral retrosplenial cortex, bilateral middle temporal gyrus, bilateral putamen, and left caudate nucleus. Importantly, we also found activation difference in bilateral hippocampal and parahippocampal areas (Fig. 4A). Further clusters with significant activation were observed bilaterally in the frontal gyrus.

Figure 3.

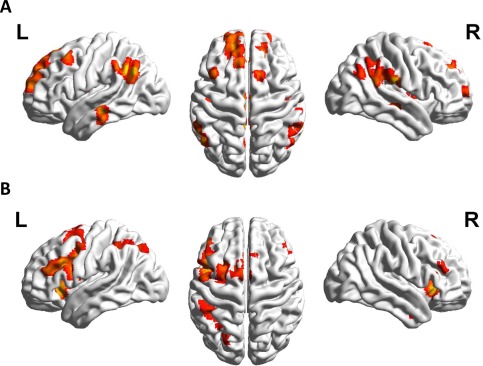
Panel A depicts the comparison of trained and untrained items of the post‐training session (T–UT2). In line with previous research, larger signal change in left angular gyrus as well as further left‐hemispheric language areas was replicated. Panel B reflects the comparison of untrained and trained items of the post‐training session (UT2–T). The activation in the whole fronto‐parietal network of magnitude processing (including IPS activation, see Table 1) reported in previous studies was replicated as well (allz at P_{cluster‐corr} < 0.05, cluster size of k = 10 voxels).

Table 1.

Complex contrasts of cortical regions more strongly involved in the post‐training session either in trained items (T) or in untrained items (UT2)

Contrast	Brain region	MNI (x, y, z)			Cluster size	z
T–UT2	LH angular gyrus (PGa)	−56	−60	35	202	6.35
	RH angular gyrus (PGa)	55	−57	33	35	4.59
	RH supramarginal gyrus (PFcm)	55	−42	25	196	5.31
	RH supramarginal gyrus (PFm)	57	−47	45	24	4.52
	RH supramarginal gyrus (PFop)	60	−22	23	27	6.06
	LH retrosplenial cortex	−6	−45	33	184	5.91
	RH retrosplenial cortex	15	−52	35	301	6.11
	LH ventromedial prefrontal cortex (Fp2)	−8	56	15	739	5.89
	LH middle temporal gyrus	−63	−27	−13	46	5.69
	RH middle temporal gyrus	52	−22	−8	36	4.89
	LH putamen	−31	−10	5	51	4.90
	RH putamen	30	−15	3	176	6.26
	LH caudate nucleus	−21	−27	28	59	4.51
	LH hippocampus (CA1)	−36	−37	−5	14	4.60
	RH hippocampus (DG/CA1)	30	−37	−5	31	4.12
	LH parahippocampal gyrus	−28	−30	−15	60	5.52
	RH parahippocampal gyrus	25	−42	−10	15	4.94
	RH insula	42	3	8	19	4.71
	LH rolandic operculum	−41	−2	18	47	4.67
	LH middle frontal gyrus	−41	18	53	25	5.14
	RH superior frontal gyrus	15	41	38	37	5.55
	LH precentral gyrus	−26	−20	58	25	5.12
	LH middle cingulate cortex	−3	−17	38	85	5.70
UT2–T	LH intraparietal sulcus (hIP2)	−38	−42	40	116	4.08
	LH intraparietal sulcus (hIP3)	−26	−67	48	62	3.99
	LH inferior frontal gyrus (44. IFGoper)	−46	6	28	617	5.97
	LH inferior frontal gyrus (45. IFGtri)	−48	21	30		5.50
	RH inferior frontal gyrus (IFGorb)	32	26	−3	118	6.51
	RH inferior frontal gyrus (IFGtri)	50	33	20	16	3.80
	LH insula	−31	23	−3	98	6.05
	LH supplementary motor area (BA6)	−6	8	58	543	7.09
	RH supplementary motor area (BA6)	12	11	55		5.53
	LH middle frontal gyrus	−26	11	58	109	4.72
	RH middle frontal gyrus	55	33	28	15	4.20
	RH thalamus (prefrontal)	7	−15	3	140	4.43
	LH thalamus (prefrontal)	−6	−17	3	138	5.43
	LH putamen	−16	8	0	13	4.32

P _{cluster‐corr} < 0.05 (k = 10 voxels); MNI, Montreal Neurological Institute coordinates; T, trained items of the post training session; UT2, untrained items of the post‐training session.

Figure 4.

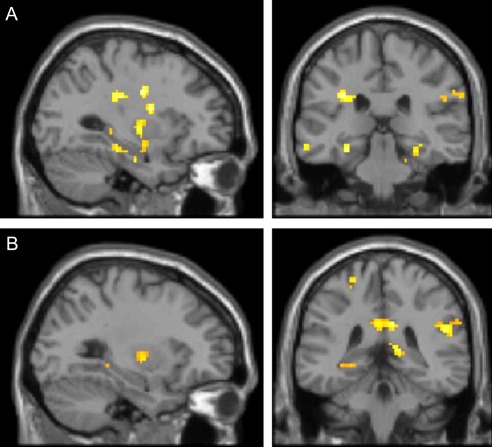
Panel A depicts the comparison of trained and untrained multiplication problems of the post‐training session (T–UT2), showing bilateral hippocampal and parahippocampal activation. Panel B depicts the contrast between trained multiplication problems of the post‐training session and to‐be‐trained (yet unknown) problems of the pre‐training session (T–TBT), showing comparable hippocampal and parahippocampal activation (all at P_{cluster‐corr} < 0.05, cluster size of k = 10 voxels).

Moreover, we conducted region of interest (ROI) analyses to further evaluate the observed activation difference in the left AG and in hippocampal areas. Therefore, we determined left AG and bilateral hippocampus as ROIs (see “Methods” section for details; Fig. 1) using the SPM Anatomy Toolbox v2.0 [Eickhoff et al., 2005, 2006, 2007]. The mean percent signal changes (PSC) relative to fixation within each ROI were extracted for each participant and condition using the MarsBar toolbox (http://marsbar.sourceforge.net). PSC values for the respective conditions were then compared using Bonferroni–Holm corrected paired t‐tests [Holm, 1979]. The analysis revealed that the significant activation difference in the AG and the hippocampus after training (revealed by the whole brain analysis) reflected a relative change in deactivation rather than activation (Fig. 5A). Compared with baseline (rest) stronger deactivation was observed for untrained than trained multiplication problems in the left AG t(31) = 2.70, P = 0.022 and the hippocampus (t(31) = 2.62; P = 0.03; Fig. 5B).

Figure 5.

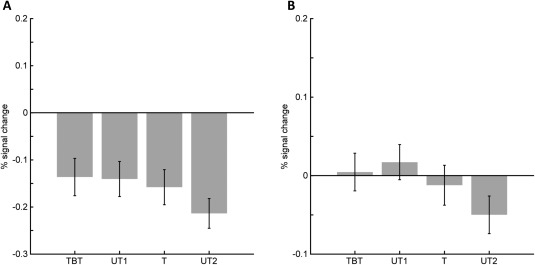
Percent signal change (PSC) for to‐be‐trained (TBT), trained (T), and untrained (UT1, UT2) multiplication problems in pre‐ and post‐training fMRI session. Subjects had to select the correct result to a presented multiplication problem. Panel A depicts results from the left AG (PGa, PGp), reflecting in all conditions a relative change in deactivation rather than activation. Panel B shows the respective pattern in the bilateral hippocampi. While signal change was about 0 before the training, a significant stronger deactivation of the hippocampi is shown after the training for untrained items compared with trained items, revealing that the hippocampus significantly less used when untrained items had to be solved compared with trained items.

Untrained items post‐training (UT2) versus trained items (T)

The reverse comparison between untrained and trained multiplication problems after the training revealed—also in line with previous studies—left hemispheric activation in the intraparietal sulcus (hIP2, hIP3). Further left hemispheric activation was observed for clusters in the insula and putamen, while bilateral activation was found in inferior frontal areas (BA 44 and 45), middle frontal gyrus, supplementary motor area (BA6), and thalamus (Fig. 3, Table 1; UT2–T).

Comparing trained problems with to‐be‐trained problems of the pre‐training session

Trained items (T) versus to‐be‐trained items pre‐training (TBT)

The contrast between trained multiplication problems versus to‐be‐trained multiplication problems before the training revealed no supra‐threshold activation in the (left) AG. Instead, bilateral activation in retrosplenial cortex, supramarginal gyrus, insula, and putamen were observed (Fig. 6A, Table 2; T–TBT). Furthermore, left hemispheric activation was found in the hippocampus and parahippocampus, while right hemispheric activation included inferior frontal gyrus (IFGtri), superior temporal gyrus, thalamus, supplementary motor area (BA6), middle cingulate cortex, and occipital clusters. Both, the ROI analysis with left AG (t(31) = −0.60, P = 0.55) and with bilateral hippocampus (t(31) = −0.66, P = 0.517) as region of interest revealed no activation or deactivation difference for trained problems of the post‐training session and to‐be‐trained problems of the pre‐training session.

Figure 6.

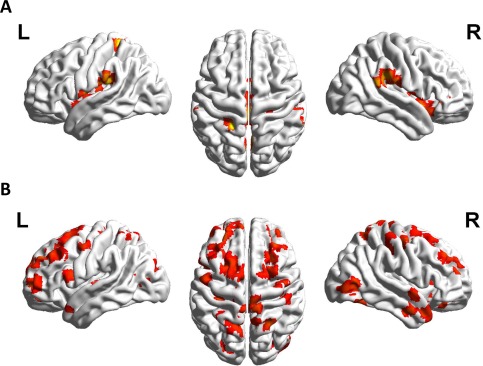
Panel A shows no significant angular gyrus signal change for the contrast between trained multiplication problems of the post‐training session and to‐be‐trained multiplication problems (yet unknown) of the pre‐training session (T–TBT). However, the perisylvian language areas are activated. Panel B depicts the contrast between to‐be‐trained multiplication problems of the pre‐training session and trained problems of the post‐training session (TBT–T). A widely distributed network of brain regions is revealed including clusters in the superior parietal cortex, many frontal clusters as well as temporal activation (all at P _{cluster‐corr} < 0.05, cluster size of k = 10 voxels).

Table 2.

Complex contrasts of cortical regions of either (to‐be‐)trained items (TBT, T) or untrained items before (UT1) and after training (UT2)

Contrast	Brain region	MNI (x, y, z)			Cluster size	z
T–TBT	LH supramarginal gyrus (PFop)	−51	−27	23	111	6.03
	RH supramarginal gyrus (PF)	62	−32	28	186	5.19
	RH insula	50	3	0	20	4.68
	LH insula	−41	3	−8	13	3.76
	RH inferior frontal gyrus (p. Tri)	40	36	0	12	4.56
	RH superior temporal gyrus	65	−47	20	13	5.17
	RH retrosplenial cortex	7	−60	30	153	5.04
	LH retrosplenial cortex	−11	−70	40	53	4.25
	LH retrosplenial cortex	−6	−45	18	37	4.76
	LH hippocampus (CA1)	−38	−20	−23	11	4.46
	LH hippocampus (DG)	−26	−37	−5	40	4.51
	LH parahippocampal gyrus	−33	−42	−8	23	4.28
	RH putamen	32	−10	−3	62	4.90
	LH putamen	−31	−10	3	129	4.63
	RH thalamus	10	−25	10	61	4.95
	RH supplementary motor area (BA6)	2	−10	50	10	3.91
	RH middle cingulate cortex	7	6	43	15	4.41
	LH postcentral gyrus	−23	−37	65	36	3.98
	RH calcarine sulcus (V1)	7	−97	−3	15	4.26
TBT–T	LH putamen	−16	13	0	1045	7.65
	LH caudate nucleusa	−11	11	18		6.72
	RH caudate nucleus	17	18	8	1086	7.62
	RH putamena	20	16	−5		7.62
	LH inferior frontal gyrus (Area 44)	−53	16	15	24	4.29
	RH middle frontal gyrus	27	6	53	60	4.66
	LH middle frontal gyrus	−38	56	10	51	4.00
	LH superior frontal gyrus	−18	16	68	240	4.47
	RH superior frontal gyrus	32	8	68	18	4.11
	LH superior frontal gyrus (Fp1)	−23	56	5	29	5.20
	RH superior parietal lobule (Area 7PC)	27	−55	63	39	5.00
	LH precuneus	−6	−62	60	93	4.52
	RH medial temporal pole	45	11	−30	93	5.05
	LH temporal pole	−41	13	−23	33	4.95
	RH inferior temporal gyrus	52	−67	8	84	4.66
	RH parahippocampal gyrus	32	−15	−23	55	5.73
	LH parahippocampal gyrus	−31	−47	−3	27	4.96
	LH hippocampus	−13	−42	15	13	4.17
	RH fusiform gyrus (Area FG2)	42	−62	−18	22	4.61
	RH postcentral gyrus	45	−25	45	29	4.18
	LH precentral gyrus	−33	−22	60	52	5.19
UT2–UT1	LH intraparietal sulcus (hIP3)	−38	−55	55	97	4.89
	RH insula	35	21	−5	119	5.22
	LH insula	−33	23	0	49	4.32
	LH inferior frontal gyrus (Area 45)	−43	21	28	27	4.30
	LH inferior frontal gyrus (Area 44)	−51	8	23	10	3.57
	RH thalamus	10	−15	0	25	5.70
	LH thalamus	−11	−7	3	16	4.78
	LH precentral gyrus	−43	8	38	30	4.31

^aSecondary peak; P _{cluster‐corr} < 0.05 (k = 10 voxels); MNI, Montreal Neurological Institute coordinates; T, trained items of the post training session; TBT, to‐be trained items of the pre training session; UT2, untrained items of the post training session; UT1, untrained items of the pre‐training session.

We conducted a Bayesian analysis to further examine the potential null effect in AG activation for the contrast trained versus to‐be‐trained (T–TBT) multiplication problems. The Bayes factor (BF) offers a possibility of evaluating evidence in favor of a null hypothesis. The alternative hypothesis is compared with the null hypothesis by means of the BF B which indicates how much more likely the observed data are under the alternative than under the null hypothesis [Dienes, 2014]. We calculated a BF of B = 0.269 in favor of the alternative hypothesis (difference in AG activation). Thus, the evidence in favor of the null hypothesis (no difference in AG activation) was 3.71 (1/0.269) as large as in favor of the alternative hypothesis. This value is above 3, which is considered to indicate substantial evidence in favor of the null hypothesis [Dienes, 2011, 2014].

To‐be‐trained items pre‐training (TBT) versus trained items (T)

Contrasting activation associated with to‐be‐trained multiplication problems before to activation for trained problems after the training revealed activation of a widely distributed network of brain regions with clusters in the basal ganglia, left‐hemispheric language areas as well as bilateral temporal and frontal areas (Fig. 6B, Table 2; TBT–T). In particular, we observed signal change in the bilateral putamen, caudate nucleus, left inferior frontal gyrus (BA44), bilateral middle and superior frontal gyrus (frontal eye fields) as well as in the right superior parietal lobule (Area 7PC). Moreover, right inferior temporal gyrus and bilateral temporal poles as well as bilateral parahippocampal gyrus, left hippocampus, and right fusiform gyrus showed reliable activation.

Comparing untrained problems before and after the training

Untrained items post‐training (UT2) versus untrained items pre‐training (UT1)

Comparing untrained items after to untrained items before the training revealed activation in the left intraparietal sulcus (hIP3), bilateral insula, left hemispheric language areas (BA44/45) and bilateral thalamus (Fig. 7A, Table 2; UT2–UT1). The reverse contrast (untrained multiplication problems before vs. after training; UT1–UT2) did not reveal any supra‐threshold clusters.

Figure 7.

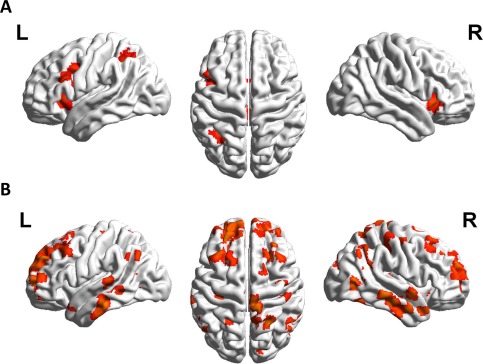
Panel A shows the comparison of untrained items of the pre‐training session with untrained items of the post‐training session (UT2–UT1), revealing activation in left IPS as well as left middle and inferior frontal areas. Panel B depicts the comparison of to‐be‐trained items of the pre‐training session to untrained items of the post‐training session (TBT–UT2), revealing a large fronto‐parietal network of supra‐threshold clusters including the angular gyrus and the intraparietal sulcus.

To‐be‐trained items pre‐training (TBT) versus untrained items post‐training (UT2)

Comparing to‐be‐trained items before to untrained items after the training revealed a large fronto‐parietal network of supra‐threshold clusters including the AG and the intraparietal sulcus (Fig. 7B, Table 2; TBT–UT2). Therefore, although both untrained item sets were matched for item properties brain activation after training differed substantially from brain activation before training.

DISCUSSION

Recent results of multiplication training studies indicated the left AG to be associated specifically with the retrieval of arithmetic facts from long‐term memory [Delazer et al., 2003, 2005; Ischebeck et al., 2006]. However, all these studies evaluated the difference in brain activation patterns for trained and untrained multiplication problems in a single post‐training fMRI session. Consequently, the dynamics of changes in brain activation due to arithmetic fact acquisition remained unsolved, because no study directly compared activation patterns for to‐be‐trained problems before to activation patterns for trained problems after training by means of fMRI. Therefore, we employed a comparable multiplication training in the present study and ran two fMRI sessions—one before and one after the training. This allowed for a full pre‐post training comparison of brain activation patterns.

Importantly, we replicated previous results when we contrasted untrained and trained multiplication problems after the training. For the processing of untrained problems fMRI data indicated stronger relative signal change in bilateral inferior parietal lobules along the IPS, bilateral inferior frontal gyrus as well as in bilateral SMA (Fig. 3B). This fronto‐parietal network of numerical cognition is associated with the manipulation of number magnitude and was observed repeatedly for complex arithmetic tasks [see Arsalidou and Taylor, 2011 for meta‐analysis]. Moreover, for trained problems we observed significant signal change in the left AG (PGa), accompanied by reduced frontal activation (Fig. 3A). So far, this frontal‐to‐AG shift was interpreted to reflect a change in solving the respective multiplication problems from effortful manipulation of magnitudes to the retrieval of arithmetic facts from long‐term memory [Dehaene et al., 2003; Delazer et al., 2003; Grabner et al., 2009a; Ischebeck et al., 2006]. The idea that the AG seems to be critical for the retrieval of multiplication facts from long‐term memory was further supported by our MVPA analysis (see Supporting Information). Average classification accuracy was significantly above chance level and depended on the size of the training effect: It was better for participants with larger training effects. Furthermore, this interpretation seemed to be corroborated by the behavioral data revealing that the decrease in RT and the increase in ER from the pre‐ to the post‐training session were more pronounced for the trained problems.

However, when we contrasted brain activity for trained multiplication problems in the post‐training session with brain activity observed for the very same problems in the pre‐training session, no significant signal change in the left AG was present, even when lowering the threshold to P < 0.01 uncorrected. This result of the pre‐post training comparison was unexpected because we again contrasted brain activation patterns for trained and untrained multiplication problems—with the only difference that the untrained items had to be solved before the training. This observed null effect in left AG activation difference was substantiated by Bayesian analyses indicating it to be reliable. Importantly, apart from the missing left AG signal change, the overall activation pattern was almost identical when contrasting trained and untrained items either between pre‐ and post‐training fMRI sessions or within the post‐training session only. In particular, we found reliable stronger activation in areas associated with retrieval from long‐term memory such as hippocampus and parahippocampal areas as well as signal change in SMG in both contrasts. Thus, the pre‐post‐training comparison does not corroborate the dominant assumption that the left AG is the key area for arithmetic fact retrieval. Instead, our results point toward a central role of brain structures commonly associated with long‐term memory functioning in arithmetic fact retrieval. Activation of the bilateral hippocampus as well as parahippocampal and retrosplenial cortex areas were the most stable pattern of results, when contrasting trained and untrained multiplication problems across pre‐ and post‐training sessions as well as within the post‐training session. This was further supported by the MVPA analysis revealing that classification accuracy did not differ between the hippocampus and the AG. Additionally, classification accuracy for the hippocampus depended on the size of the training effect with increasing classification accuracy for participants with larger training effects (see Figure A of the Supporting Information). Therefore, our results corroborate recent neuro‐imaging findings regarding the importance of areas associated with long‐term memory in arithmetic fact learning [Supekar et al., 2013] and retrieval [Cho et al., 2012; Klein et al., 2013, 2016].

To sum up, in the present study we found AG activation only when comparing trained and untrained items of the post‐training fMRI session (T–UT2) but not for the inter‐session comparison of to‐be‐trained and trained items (T–TBT), a finding which challenges the central role of the AG during the actual retrieval of arithmetic facts. Consequently, two questions arise: (1) when the (left) AG itself may not be involved in the actual retrieval of arithmetic facts, which structures may then subserve this process? And (2) if the (left) AG itself is not involved in actually retrieving arithmetic facts, what is its actual role in retrieval situations?

Regions Subserving Fact Retrieval

For both the intra‐session comparison of trained and untrained multiplication problems (T–UT2), as well as for the inter‐session comparison of trained and to‐be‐trained problems (T–TBT), we observed activation in brain structures typically associated with long‐term memory, such as hippocampus and parahippocampus [Montaldi and Mayes, 2010] and the recognition of familiarity, such as the retrosplenial cortex [see Vann et al., 2009 for a review]. The role of these cortical regions for arithmetic fact retrieval and mathematical learning processes were specified only recently [Cho et al., 2012; Klein et al., 2016; Qin et al. 2014; Supekar et al., 2013].

Based on structural connectivity data, Klein et al. [2016] outline a putative theory on the role of the hippocampus, parahippocampus, and the retrosplenial cortex in arithmetic fact retrieval. Fiber tracking data indicate that AG and hippocampus are not connected directly but via the retrosplenial cortex only. The main connections of the retrosplenial cortex include both ventral and dorsal connections with the hippocampal formation: ventral connections with the parahippocampal region and the entorhinal cortex as well as dorsal connections with the parietal cortex [Klein et al., 2016]. Thereby, the rich connectivity of the retrosplenial cortex with both archicortical structures associated with long‐term memory and neocortical parietal structures associated with the processing of numbers suggests a central role of the retrosplenial cortex in the retrieval of arithmetic facts.

In particular, Klein et al. [2016] argue that familiarity information is extracted in the retrosplenial cortex during a first stage of the retrieval process, reflecting the domain unspecific role of this area in assessing the familiarity of stimuli [e.g., Shah et al., 2001; Sugiura et al., 2005]. Familiarity information is then propagated via two separate bundles to the hippocampus, one via the parahippocampus and one directly to the hippocampus and is available to support retrieval.

The hippocampus itself is thought to integrate familiarity (e.g., from parahippocampal areas, retrosplenial cortex) with recollection information (e.g., from entorhinal cortex) to finally retrieve (arithmetic) fact information, as argued by Montaldi and Mayes [2010]. Interestingly, the network supporting fact retrieval seems to extend to the ventromedial prefrontal cortex (VMPFC) as well [see Atique et al., 2011; Baetens et al., 2013; Spunt et al., 2011].

This putative retrieval model is supported by the findings of the present training study, since, both, the hippocampus as well as the retrosplenial cortex and prefrontal areas were specifically activated during the retrieval of arithmetic facts. Most importantly, this holds true for the intra‐session comparison of trained and untrained multiplication problems (T–UT2) but also for the inter‐session comparison (T–TBT).

In line with this reasoning, Qin et al. [2014] recently provided a comprehensive overview of the involvement of the hippocampus during arithmetic learning and arithmetic fact retrieval. For example, hippocampus activation was observed to be largest while children acquired retrieval‐based and not calculation based solutions. Moreover, by means of multivoxel pattern analysis Qin et al. [2014] demonstrated that adolescents and adults showed less hippocampal activation than children during arithmetic fact retrieval. In contrast, however, the stability of multivoxel activation patterns in the hippocampus and prefrontal cortex across solved problems increased with refinement of retrieval‐based arithmetic problem solving. This was interpreted to reflect the acquisition of more stable representations of arithmetic fact knowledge. Taken together, this seems to suggest that the hippocampus is not only engaged in retrieval from long‐term memory but is also important for arithmetic fact learning in close functional connection with frontal areas [Qin et al. 2014]. This is in line with other recent evidence. Cho et al. [2012] showed that children with better fluency in arithmetic fact retrieval showed more pronounced hippocampal activation. In this vein, Supekar et al. [2013] were able to show that larger hippocampal volume predicted learning improvements in a math tutoring program.

In summary, in the present study we observed the hippocampus, parahippocampus, and retrosplenial cortex to be activated specifically whenever trained problems had to be processed. In this triad the retrosplenial cortex might be most possibly involved in monitoring familiarity information and recognition [Shah et al., 2001; Vann et al., 2009], while the actual retrieval of arithmetic facts may then reflect an integration of familiarity and recollection processes in the hippocampus [Montaldi and Mayes, 2010]. This has important implications for the representation of arithmetic facts. So far, it was supposed that arithmetic fact retrieval is associated with inferior parietal areas such as the AG [Dehaene et al., 2003]. Extending this view, the present data indicate that arithmetic fact retrieval seems to recruit a larger network incorporating the hippocampus with its close connections to frontal, retrosplenial, and parietal areas. In this network, the hippocampus is associated with retrieval processes from long‐term memory, frontal areas may subserve domain‐general cognitive functioning [Qin et al., 2014; Supekar et al., 2013], the retrosplenial cortex may be associated with familiarity recognition [Sugiura et al. 2005], and parietal areas subserve number processing [Klein et al., 2016].

The Role of the AG Revisited?

The missing signal change in the left AG for the pre‐post training session comparison of trained and untrained multiplication problems is also hard to reconcile with another hypothesis on the role of the AG in arithmetic fact retrieval. Following the argument of Ansari [2008, see also Grabner et al., 2013] stronger activation of the left AG after training may reflect processes of automatic mapping between multiplication problems and their associated solutions and thus processes of recognition instead of arithmetic fact retrieval itself. However, mapping and associated recognition processes should be equally strong for both contrasts: in the inter‐session (T–TBT) as well as in the intra‐session (T–UT2) comparison of trained and untrained multiplication problems half of the items were known to participants and should thus trigger these mapping processes. In summary, these results challenge both the fact‐retrieval and the symbol‐referent mapping hypothesis about the role of the left AG in arithmetic fact learning.

A possible explanation for the current findings may be an interindividually varying mixture of multiplication problem solving strategies of the participants in the pre‐training session. It is reasonable to assume that prior to any training participants relied on a combination of fact retrieval (e.g., of interim results) and effortful magnitude manipulations. This account was supported by the rather undifferentiated activation of the two distinct networks responsible for magnitude processing and arithmetic fact retrieval before the training. In this vein, both networks were “ramped up” when participants solved complex multiplication problems without any prior training. One might speculate that only after the training participants were able to solve multiplication problems efficiently and more consistently by either fact retrieval (for trained problems) or magnitude manipulations (for untrained problems). That means trained problems may then be solved primarily by fact retrieval whereas untrained problems still need to be solved by calculation‐based strategies. However, because participants were trained to solve multiplication problems in five sessions of extensive training the required procedures for magnitude manipulation should have been trained as well, as indicated by the decrease in RT for untrained problems in the post‐training session. This means that solving untrained problems relies primarily on magnitude manipulation—before and after training. Nevertheless, as computational procedures (for magnitude manipulation) were incidentally trained during the training phase, the processing of untrained multiplication problems may have changed quantitatively in the sense that the same procedures of magnitude manipulation are used more efficiently. In contrast, for trained problems the change in processing seemed to be qualitative reflecting a transition from effortful magnitude manipulation to direct fact retrieval from long‐term memory.

Following this argument, functional segregation of the magnitude manipulation and the fact retrieval system would have been the ultimate result of extensive training. This might explain why we replicated the commonly reported frontal‐to‐AG shift of activation, when we contrasted brain activation for trained and untrained problems after the training, whereas no AG activation was observed when comparing activation for trained items in the post‐training session with activation for the same problems before the training. Therefore, we suggest that the reported activation of the left AG in arithmetic fact retrieval in previous studies may not have reflected the retrieval of facts from verbal LTM.

Instead, we argue that the known engagement of the left AG in domain‐unspecific processes such as attention regulation [Cabeza et al., 2012; Cabeza, 2008; Humphreys and Lambon Ralph, 2015] might account for the observation of (left) AG activation in studies evaluating arithmetic fact training. In the following we outline an attentional account on the role of the AG in arithmetic fact retrieval.

An Attentional Account on the Role of the AG in Arithmetic Fact Retrieval

Recently a structural and functional subdivision of parietal cortex into dorsal stream areas (in or above the IPS, superior parietal lobule, precuneus, i.e., Brodmann Area 7) and ventral stream areas (AG, SMG, i.e., Brodman Areas 40 and 39) was put forward, based on the specific contribution of these areas for top‐down or bottom‐up driven allocation of attention in memory retrieval [Cabeza et al., 2008, 2012; Cabeza, 2008; Humphreys and Lambon Ralph, 2015]. It was argued that the dorsal part (DPC) of the parietal lobe is part of a domain general fronto‐parietal executive control system that is involved in non‐automatic goal directed memory processes with high executive demands (i.e., top‐down regulated attention). The ventral part (VPC) in contrast was supposed to be involved in more automatic and stimulus‐driven processing with lower executive demands. Interestingly, the latter bottom‐up driven attentional system is not only triggered by external events (e.g., a flashing light), “but also by highly salient internal events, such when a remembered item [e.g., a solution to a trained multiplication problem] ‘pops’ into awareness” [Humphreys and Lambon Ralph, 2015].

Applied to the present case of multiplication fact learning, the typically used contrast of brain activation patterns for trained versus untrained arithmetic problems after the training basically reflects a comparison of tasks with low and high executive as well as distinct attentional demands. In line with the above argument, processing untrained and trained arithmetic problems should differ with respect to top‐down versus bottom‐up driven processing. While the result of a known multiplication problem is activated automatically in a bottom‐up manner by the mere presentation of the respective operands [e.g., Galfano et al., 2003, 2009; Rusconi et al., 2006], this is not assumed for untrained complex arithmetic problems [e.g., Dehaene and Cohen, 1995]. So far, stronger activation of the VPC (i.e., the AG) for trained as compared with untrained multiplication problems after the training was interpreted to reflect direct fact retrieval from verbal long‐term memory [e.g., Delazer et al., 2003, 2005; Ischebeck et al., 2006]. However, in this interpretation it was widely neglected that task execution for trained and untrained problems differs largely with respect to the need for top‐down versus bottom‐up attention [but see Grabner et al., 2013 for an automatic symbol‐referent mapping approach]. Following the above rationale on the dorsal‐ventral subdivision of parietal cortex, one might speculate that stronger activation in the VPC for trained as compared with untrained multiplication problems after the training simply reflects the difference between bottom‐up as compared with top‐down processing.

This account is also compatible with the missing AG activation when contrasting brain activation for trained items with activation for the very same problems prior to any training. In particular, one might speculate that the intermixed and alternating presentation of trained and untrained problems in the post‐training fMRI sessions led to repeated shifts between top‐down (i.e., magnitude manipulations) and bottom‐up (i.e., fact retrieval) driven solution processes, which in turn should be reflected by the activation of VPC areas (including the AG) associated with such shifting demands. In contrast, these shifts between top‐down magnitude manipulations and bottom‐up fact retrieval should be less pronounced for the contrast of brain activation for trained items after and activation for to‐be‐trained problems prior to the training. In particular, prior to the training both the network for magnitude manipulation as well as the network for arithmetic fact retrieval are ramped up and thus require constant monitoring and adaptation (as reflected by VPC, including AG activation). In turn, this led to no observable differences in AG activation for to‐be‐trained problems prior to the training (TBT) and trained problems (T).

The role of the AG in arithmetic fact retrieval might thus reflect its general, domain‐unspecific role of attention allocation in human cognition as described above. In line with this view, the attention to memory (AtoM) model [Cabeza et al., 2008, 2012] posits that VPC activity during memory retrieval reflects attentional adjustment based on incoming information from working memory (WM) and classical memory structures in the medial temporal lobe and not the actual retrieval of information from long‐term memory itself [Cabeza et al., 2008, 2012; Cabeza, 2008]. To be more specific, Cabeza et al. [2008, 2012] argue that analogous to its role in attention allocation “the VPC mediates the bottom up capture of attention by salient memory contents” [Cabeza et al., 2012; p. 342]. Within this framework, the VPC—including the AG—is neither regarded as an accumulator, nor as a buffer for information from WM and medial temporal lobe (MTL; including the hippocampus and parahippocampal areas). Rather, the AG is assumed to serve as a circuit breaker that signals the need for change in the locus of internal attention.

Based on our findings and theoretical consideration of the AtoM model, we hypothesize that the left AG might serve as an interface that adjusts and adapts attentional demands and thereby indirectly allocates cognitive resources during number processing. When a solution of a trained multiplication problem from long‐term memory enters working memory it captures bottom‐up attention, which is then reflected by VPC (AG) activity.

In case a multiplication problem cannot be solved by direct fact retrieval from long‐term memory, activation of the DPC and the fronto‐parietal network of magnitude processing might be ramped up to provide the required top‐down attention and therefore further cognitive resources. As a result, a shift from bottom‐up to top‐down driven processing to solve the multiplication problem at hand occurs. Consequently, we propose that the AG might serve as a circuit‐breaker that adapts and adjusts the relative activation of the magnitude processing and fact retrieval networks. Based on its functional and structural connectivity [e.g., Caspers et al., 2011; Seghier, 2013; Uddin et al., 2010] it is reasonable to assume that this putative interfacing mechanism relies on information from working memory areas in prefrontal cortex as well as areas in the MTL, commonly associated with long term memory including hippocampus and parahippocampal areas. Importantly, in the current study, these areas were consistently activated for both, the comparison of trained versus untrained problems of the post‐training session as well as the comparison of trained problems of the post‐training session with to‐be‐trained problems of the pre‐training session.

Compared with baseline, the left AG was deactivated in all stimulus conditions. This corroborates the findings of previous studies involving mental calculation [e.g., Grabner et al., 2007, 2013; Grabner et al., 2009a, 2009b; Ischebeck et al., 2006; Stanescu‐Cosson et al., 2000]. Comparable deactivations of the left AG during cognitive tasks are not restricted to numerical paradigms but were also observed in various other domains [for a review see Humphreys and Lambon Ralph, 2015; Raichle, 2015]. The AG is a key parietal node of the default mode network. Besides the parietal node, this network is comprised of medial prefrontal and medial as well as lateral temporal cortices [DMN; Raichle, 2015; Raichle et al., 2001]. Compared with a resting period or passive baseline, the DMN is consistently deactivated during cognitive, goal‐directed tasks [for review see Andrews‐Hanna et al., 2014; Buckner et al., 2008; Raichle, 2015]. Furthermore, this network is more strongly deactivated for demanding than easy cognitive tasks [e.g., Mckiernan et al., 2003]. It has therefore been argued that different levels of deactivation in the AG during mental arithmetic simply reflect domain‐general alterations in the DMN resulting from differences in task difficulty [e.g., Wu et al., 2009]. However, this view has been questioned by a recent study of Grabner et al. [2013] showing that a more difficult numerical task led to less deactivation in the left AG. This challenges exclusively DMN‐related explanations of differential activation in the left AG during numerical cognition. In line with this, the fact that we did not find any difference in left AG activation when we compared trained items of the post‐training sessions with to‐be‐trained items of the pre‐training session (T–TBT) is not compatible with mere modulation of the DMN due to changing task difficulty.

Transfer Effects in Difficult Multiplication Learning

Apart from these unexpected results regarding the role of the left AG in arithmetic fact retrieval there was another interesting finding. The pre‐ versus post‐training comparison of behavioral results indicated a transfer effect of the multiplication fact training to untrained problems after training, which were responded to significantly faster than before the training. Importantly, this is in contrast to the previous either magnitude manipulation or fact retrieval distinction assumed for the processing of multiplication problems, which does not consider such transfer effects for drill training [Delazer et al., 2003; Grabner et al., 2009b; Zaunmüller et al., 2009]. Instead, this finding suggests that similar to what was argued for addition and subtraction problems unspecific procedures needed to solve complex multiplications are fostered by extensive training. This finding is in line with a recent argument by Klein et al. [2016]: the authors propose a flexible interplay between fact retrieval and magnitude manipulation in complex arithmetic instead of an either‐or distinction. Already in 1995, Dehaene and Cohen suggested that during complex arithmetic, bilateral intraparietal areas would be recruited whenever direct fact retrieval fails, resulting in semantic re‐coding of the problem by manipulations of the respective magnitudes. However, in previous studies on arithmetic fact learning this could not be investigated because both behavioral data as well as imaging data was only recorded after the training.

Taken together, our findings support the view that training difficult multiplication problems not only improves declarative knowledge (i.e., arithmetic facts) but also provides transfer effects to procedural (e.g., algorithms) and conceptual knowledge (e.g., arithmetic principles), because verbally mediated fact retrieval and magnitude manipulation interact closely.

This interactive nature of magnitude manipulation and arithmetic fact retrieval, reflected in our fMRI data, may be due to the way arithmetic facts are acquired. During training, the results of multiplication problems have to be calculated by effortful magnitude manipulation at a first stage, before they are finally stored in long‐term memory as arithmetic facts after repeated calculation. One may speculate that this dynamic process of learning also occurs during natural learning of basic multiplication facts in childhood [e.g., Campbell and Graham, 1985; Siegler, 1988; see also Domahs and Delazer, 2005]. In this sense, our results support a multiple stages account of learning arithmetic [e.g., Crawford, 2004; Garnett, 1992; Garnett and Fleischner, 1983; Steel and Funnell, 2001; Siegler, 1988]. According to this, the effective acquisition of arithmetic facts during childhood proceeds through at least three stages: In a first stage children need to acquire procedural knowledge of figuring out facts. That means concepts like multiplication and the procedures for magnitude manipulation need to be learned and practiced. In a second, intermediate, stage strategies for remembering facts are developed. For example, one problem is linked to a related problem to solve a task [e.g., for 5 × 6, thinking “5 × 5 = 25, so 5 × 6 = 25 + 5 = 30,” see also Siegler, 1988]. Consequently, during this stage both fact retrieval and magnitude manipulation take place. Finally, in a third stage problems can be recalled directly from LTM as overlearned arithmetic facts. Therefore, the present findings stress the importance of a curriculum that follows these stages of successful arithmetic fact learning [e.g., Stein et al., 1997]. For example, it is crucial that children develop a sound understanding of the concept of multiplication and practice procedures for magnitude manipulation before memorizing multiplication facts.

CONCLUSIONS AND PERSPECTIVES

Taken together, in line with previous findings our results point toward a functional role of the left AG in mental arithmetic. However, by contrasting brain activation for to‐be‐trained multiplication problems prior and trained problems after the training we found evidence indicating that the left AG may not subserve arithmetic fact retrieval per se. Rather, our findings point toward an engagement of the left AG in arithmetic fact retrieval that reflect its domain‐unspecific role for attention allocation during memory retrieval in general [e.g., Cabeza et al., 2012]. We propose that based on the attentional demands of the problem at hand the AG might serve as a circuit breaker that adjusts and adapts relative activation in the neural networks associated with fact retrieval and magnitude manipulation.

Thereby, our data suggest that it may be more appropriate to investigate the influence of numerical learning on the activation of brain networks rather than considering specific brain areas in isolation. Particularly the role of the AG in arithmetic fact retrieval cannot be specified comprehensibly when evaluated in isolation. This role needs to be investigated considering the influence of other brain regions with which the AG is connected in networks subserving long‐term memory functioning such as the hippocampus, parahippocampal areas and retrosplenial cortex [e.g., Klein et al., 2016] but also attention regulation [e.g., Cabeza et al., 2012]. Future studies evaluating changes in functional connectivity of the AG during arithmetic fact learning are needed to substantiate this argument. In fact, it is rather surprising that the AG is still considered the key area for arithmetic fact retrieval even though the exact role of posterior parietal cortex sites in more general long‐term memory functioning is still a matter of controversial debate [see Cabeza et al., 2008, 2012 for review].