Characterizing structural neural networks in de novo Parkinson disease patients using diffusion tensor imaging

Abstract

Parkinson disease (PD) can be considered as a brain multisystemic disease arising from dysfunction in several neural networks. The principal aim of this study was to assess whether large‐scale structural topological network changes are detectable in PD patients who have not been exposed yet to dopaminergic therapy (de novo patients). Twenty‐one drug‐naïve PD patients and thirty healthy controls underwent a 3T structural MRI. Next, Diffusion Tensor Imaging (DTI) and graph theoretic analyses to compute individual structural white‐matter (WM) networks were combined. Centrality (degree, eigenvector centrality), segregation (clustering coefficient), and integration measures (efficiency, path length) were assessed in subject‐specific structural networks. Moreover, Network‐based statistic (NBS) was used to identify whether and which subnetworks were significantly different between PD and control participants. De novo PD patients showed decreased clustering coefficient and strength in specific brain regions such as putamen, pallidum, amygdala, and olfactory cortex compared with healthy controls. Moreover, NBS analyses demonstrated that two specific subnetworks of reduced connectivity characterized the WM structural organization of PD patients. In particular, several key pathways in the limbic system, basal ganglia, and sensorimotor circuits showed reduced patterns of communications when comparing PD patients to controls. This study shows that PD is characterized by a disruption in the structural connectivity of several motor and non‐motor regions. These findings provide support to the presence of disconnectivity mechanisms in motor (basal ganglia) as well as in non‐motor (e.g., limbic, olfactory) circuits at an early disease stage of PD. Hum Brain Mapp 37:4500–4510, 2016. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Parkinson's disease (PD) is the second most common neurodegenerative disorder with a prevalence of 1% among those older than 60 years in industrialized country [de Lau and Breteler, 2006]. Clinically, it is characterized by a specific set of motor symptoms including rigidity, slowness of movement, tremor at rest, and postural instability [Jankovic, 2008]. However, many non‐motor symptoms, such as impaired olfaction, emotional problems, and cognitive impairment, are also present [Chaudhuri et al., 2006] highlighting how PD can be considered a brain multisystemic disease arising from dysfunction in several neural networks [Brooks and Pavese, 2011; Luo et al., 2014; Ziegler et al., 2014]. Evidence of abnormal connectivity between basal ganglia and motor regions [Helmich et al., 2010; Kwak et al., 2010] as well as disrupted functional integration in corticostriatal loops were found at early and advanced stages of PD [Hacker et al., 2012; Helmich et al., 2010; Luo et al., 2014; Seibert et al., 2012]. Moreover, diffusion tensor imaging (DTI) revealed reduced integrity (e.g., reduced fractional anisotropy and increased mean diffusivity) in several white matter tracts in PD patients compared with healthy controls [Gattellaro et al., 2009; Ibarretxe‐Bilbao et al., 2010; Karagulle Kendi et al., 2008; Korgaonkar et al., 2014; Rolheiser et al., 2011; Scherfler, 2005; Ziegler et al., 2014]. There is also evidence from pathological studies that alpha‐synuclein PD can be associated with alterations in white matter in the form of Lewy neurite, which accumulate in brainstem axons and cerebral white matter [Braak et al., 2003].

In recent years, thanks to advances in neuroimaging techniques and graph theory, several studies have started to conceptualize the whole brain as an interconnected network exploring the organization of brain circuits in healthy controls and different populations of patients with neurological and psychiatric diseases [Bernhardt et al., 2015; Bullmore and Sporns, 2009; Filippi et al., 2013; Fornito and Bullmore, 2015; Griffa et al., 2013; Korgaonkar et al., 2014; Nigro et al., 2014; Phillips et al., 2015; Sporns, 2013b; Verstraete et al., 2011; Vértes and Bullmore, 2015; Xie and He, 2012; Zalesky et al., 2010].

Several graph theoretic studies revealed an abnormal topological organization of functional brain networks in PD patients compared with healthy controls. Specifically, Skidmore et al. have combined fMRI and graph analysis and found a smaller global efficiency of brain networks in advanced PD patients when compared with control subjects [Skidmore et al., 2011]. Wei et al. found also that PD had significantly decreased efficiency in the cortico‐basal ganglia motor pathway, with the most pronounced changes in right rostral supplementary motor area, left caudal supplementary motor area, and bilateral primary motor area, primary somatosensory cortex, thalamus, pallidum, and putamen [Wei et al., 2014]. In addition, Dubbelink et al., using magnetoencephalography and graph theory, reported that impaired local efficiency and network decentralization are very early features of PD that continue to progress over time, together with reductions in global efficiency [Olde Dubbelink et al., 2014].

In very recent years few studies have also investigated the presence of altered structural connectivity patterns in PD patients using DTI‐based graph analyses [Aarabi et al., 2015; Batista et al., 2015; Li et al., 2016; Pereira et al., 2015]. For example, Aarabi and colleagues combined DTI and network‐based statistics (NBS) to reveal reduced connectivity in PD in networks comprising motor and non‐motor regions such as cingulum, temporal and frontal regions, parahippocampus, olfactory lobe, and occipital lobe [Aarabi et al., 2015]. A similar study by Batista et al. suggested that cognitive and motor decline in early stages of PD is associated with microstructural changes of white‐matter that extended to the frontal, parietal and temporal regions [Batista et al., 2015]. These findings were confirmed by a recent study conducted by Li et al. in which a widespread pattern of decreased efficiency was found in PD patients relative to healthy controls [Li et al., 2016].

However, these studies investigated specific network components using NBS or included patients who had been previously exposed to medication. Assessing for large‐scale brain network changes in PD patients at early stages and who had not been exposed yet to therapy remains therefore an important issue to address.

In the current study, we therefore used the both graph theory and NBS to investigate the structural topological changes of WM networks in a group of drug‐naïve PD patients compared with healthy controls (21 PD patients, 30 healthy controls). The main aim of the current study was to investigate the primary pathophysiologic changes of PD avoiding the influence of potential confounding factors such as the effects of long‐term medication or secondary factors related to course of illness.

Graph theory provided a powerful and general framework to characterize brain connectivity at global and local levels and offered a collection of metrics that could quantify the segregation and integration of information within the elements (i.e., “nodes” or brain regions) of structural networks in de novo PD patients and healthy controls. NBS allowed to characterize specific large within‐network components using permutation testing, to identify whether and which subnetworks were significantly different between de novo PD and control participants [Zalesky et al., 2010].

Considered the diffusion properties alterations observed in WM tracts of PD together with damages reported in pathological studies, we expected alterations in motor as well as non‐motor circuits including limbic and olfactory circuits which have been implicated at early disease stages [Braak et al., 2003]. To test the hypothesis that these networks showed abnormal “communication” patterns in PD patients, we employed the following graph metrics: (i) centrality measure (i.e., degree and eigenvector centrality), (ii) segregation measures (i.e., clustering coefficient), and (iii) integration measures (i.e., efficiency and path length). Finally, given the alterations in network's hubs organization of PD patients found in Dubbelink et al. [Olde Dubbelink et al., 2014], we identified the hubs nodes (i.e., important brain regions that often interact with many other regions, facilitate functional integration, and play a key role in network resilience to insult) in both groups to test if a re‐organization in the network's hubs was detected also in WM networks of PD patients.

MATERIALS AND METHODS

Participants

We recruited 21 drug naïve patients with PD. The patients were diagnosed according to Gelb criteria for the diagnosis of PD [Gelb et al., 1999]. To support the clinical diagnosis, dopamine transporter single photon emission computerized tomography (DAT‐SPECT) has been also used [Gayed et al., 2015]. Then, normal appearance of the nigrostriatal pathway on DAT‐SPECT was used as exclusion criterion. Disease severity was evaluated using the Unified Idiopathic Parkinson's Disease Rating Scale (UPDRS) [Pearce, 1986] and the Hoehn and Yahr staging [Hoehn and Yahr, 1967]. Moreover, 30 healthy controls with no present or past neurological disease were recruited.

All participants were screened for cognitive impairment, depression and anxiety via Mini‐Mental State Examination (MMSE) [Folstein et al., 1975], Beck Depression Inventory (BDI‐II) and Hamilton Anxiety Rating Scale (HAM‐A) [Hamilton, 1959], respectively. Written informed consent was obtained from all participants. The study was approved by the ethical Committee of the “Magna Graecia” University of Catanzaro, Italy, according to Helsinki Declaration.

Image Acquisition

Neuroimaging data were acquired on a 3 Tesla Unit and using an 8‐channels head coil (Discovery MR‐750, General Electric, Milwaukee, WI). Head movements were minimized using foam pads around participants' heads. The protocol included: (1) a whole‐brain T1‐weighted scan [SPGR; Echo Time (ET) 3.7 ms, Repetition Time (TR) 9.2 ms, flip angle 12°, voxel‐size 1.0 × 1.0 × 1.0 mm³]; (2) a diffusion‐weighted scan that was acquired using a spin‐echo echo‐planar imaging sequence (ET 81 ms, TR 10,050 ms, band‐width 250 kHz, matrix size 128 × 128; 80 axial slices, voxel size 2.0 × 2.0 × 2.0 mm³) with 27 isotropically distributed orientations for the diffusion‐sensitizing gradients at a b‐value of 1.000 s/mm2, and (3) a fast Fluid‐Attenuated Inversion‐Recovery (FLAIR) axial sequence (ET 100 ms, TR 9,500 ms, Inversion Time 2,250 ms, 36 axial slices, Refocus flip angle 90°, voxel size 0.5 × 0.5 × 4.0 mm³).

Data Pre‐Processing and Network Definition

The MATLAB toolbox “Pipeline for Analyzing braiN Diffusion imAges” (PANDA) was used for data preprocessing [Cui et al., 2013]. DTI images were first corrected for eddy current distortions and motion artifacts by applying an affine alignment of the diffusion‐weighted images to the b0 images using the FMRIB's Diffusion Toolbox (FDT, version 5.0; http://www.fmrib.ox.ac.uk/fsl) [Andersson and Skare, 2002]. Next, voxel‐wise FA values were computed using the DTIFIT tool [Pierpaoli and Basser, 1996; Song et al., 2002]. The brain nodes were defined using the Automated Anatomical Labeling (AAL) atlas that includes a total of 90 cortical and sub‐cortical regions (45 for each hemisphere) [Tzourio‐Mazoyer et al., 2002]. Using an affine transformation, individual FA maps were co‐registered to the corresponding T1‐weighted structural images which, in turn, were non‐linearly registered to the MNI‐ICBM152_2mm template. The results of this two‐steps registration were next used to calculate the combined inverse warp that allowed the co‐registration of the AAL atlas to subject‐specific FA maps. To compute the number of fibers connecting each couple of brain nodes, we employed a deterministic tractographic method that used the fiber assignment by continuous tracking (FACT) algorithm [Mori et al., 1999; Xue et al., 1999]. The reconstruction of each fiber was interrupted when the angle of the principal diffusion direction between two adjacent voxels was greater than 35°or when a voxel with a FA value less than 0.1 was reached. In order to reduce the within subjects probability of false positive edge's reconstruction two brain nodes were considered connected when at least three fibers linking them were reconstructed [Shu et al., 2009]. This thresholding procedure has been used in previous studies and had been shown to reduce the risk of false‐positive connections [Shu et al., 2009, 2011]. The overall pattern of white‐matter connections between each couple of brain nodes was computed using a weighted matrix. In the weighted matrix, each entry (edge) represents the product of the number of fibers and mean FA of the connecting fiber that link a couple of brain nodes.

Graph Theory Analyses

The Brain Connectivity Toolbox (http://www.brain-connectivity-toolbox.net/) was employed to compute the local and global network metrics [Rubinov and Sporns, 2010]. Details about these analyses are provided in Supplementary Materials. The BrainNet viewer (http://www.nitrc.org/projects/bnv/) was used to visualize the local significant difference in specific brain regions [Xia et al., 2013].

Local metrics

In order to test whether there were differences between the two groups in specific nodes of the networks, several regional graph measures were considered here, as follows: (i) strength, (ii) betweenness centrality, (iii) eigenvector centrality, (iv) clustering coefficient, (v) local path length, and (vi) local efficiency [Boccaletti et al., 2006; Rubinov and Sporns, 2010; Watts and Strogatz, 1998].

Nodal strength, betweenness and eigenvector centrality are three measures of centrality able to quantify the relative importance of a node within a network [Zuo et al., 2012]. If a node has a high level of centrality, it facilitates information routing in the network, indicating that it has a key role in the overall communication efficiency of a network. On the other hand, if a node displays a reduced centrality, this could indicate an impaired communication between this node itself and the rest of the brain.

Node's strength is the simplest measure of centrality and is defined as the sum of all of the edge weights between this node and all of the other nodes in the network. Regions with a high nodal strength indicate high interconnectivity with other regions. Eigenvector centrality shares with the nodal strength the idea that nodes that have more connections with many other nodes are more central. However, in contrast to nodal strength it favors nodes that are connected to nodes that are themselves central within the network taking into account the entire pattern of connections of the network. So, as a self‐referential measure of centrality, it reflects the capacity of a node with high centrality to connect with other nodes with high eigenvector centrality. The calculation of this metrics is based on the spectral decomposition of the adjacency matrix; more specifically, it is the first eigenvector of the adjacency matrix, which corresponds to the largest eigenvalue. Betweenness centrality of a node is defined as the fraction of all shortest paths in the network that contain a given node. Nodes with high values of betweenness centrality participate in a large number of shortest paths and have an important role in the information transfer within a network.

Together with centrality measures, the nodes of a network could display variable level of segregation and integration of information [Sporns, 2013a]. In order to quantify the segregation ability, the clustering coefficient is the most used metric. It represents the fraction of triangles around an individual node and it is equivalent to the fraction of the node's neighbors that are also neighbors of each other (Watts and Strogatz, 1998). Clustering coefficient represents the ability of a node to communicate with other nodes with which share direct connection.

The ability of an efficient information transfer among distributed nodes (that could not be directly connected) can be measured via local path length and local efficiency. More specifically, local path length is the minimum number of edge that must be traversed to go from one node to another. Local efficiency is calculated as the global efficiency of the subgraph formed by the node's neighbors. It measures the ability of parallel information transfer at local level.

Global metrics

In order to investigate whether there were differences between the two groups in the overall organization of the networks we computed the mean strength, the global efficiency, the global clustering coefficient and the global path length [Boccaletti et al., 2006; Rubinov and Sporns, 2010; Watts and Strogatz, 1998]. The mean strength, the mean clustering coefficient and the global efficiency are the average of the regional strength, clustering coefficient and the regional efficiency of all nodes, respectively. The global path length is the average of the minimum number of connections that link any two nodes in the network. Moreover, to explore the networks' global organization and architecture of WM we calculated also the small‐worldness properties of subject‐specific networks [Bassett and Bullmore, 2006, 2009]. A brain circuit is considered a “small‐world” network when the following criteria are met [Sporns et al., 2004; Watts and Strogatz, 1998]: (i) the global clustering coefficient, C, is significantly greater than the clustering coefficient, C _r, derived from averaging 1,000 randomly connected networks that contain the same numbers of nodes and links (i.e., γ = C/C _r ≫ 1) [Gong et al., 2009]; (ii) the global path length of a network (L) is comparable to the path length coefficient (L _r) derived from averaging 1,000 randomly connected networks that contains the same numbers of nodes and links (λ = L/L _r ∼ 1) [Gong et al., 2009].

Hubs Identification

Hubs are defined as important brain regions that often interact with many other regions, facilitate functional integration, and play a key role in network resilience to insult [van den Heuvel and Sporns, 2013; Hwang et al., 2013; Sporns et al., 2007]. Overall, hubs are nodes that are more central than other nodes within a network. However, no single measure was essential and sufficient for identifying hubs. The integration of more than one graph measures provides a more robust method for hubs' detection. Hence, we employed the four graph metrics described above (i.e., nodal strengths, betweenness centrality, eigenvector centrality and local efficiency) to identify hubs regions. First, we calculated a group‐specific connectivity matrix (one for each group) in which the weight of an edge was the mean of the weights across subjects. Next, we calculated the four metrics and sorted them in descending order (from highest to lowest). The hubs of averaged WM‐network were identified by determining whether a node belonged to: (1) the top 20% nodes with the highest level of strength; (2) the top 20% nodes with the highest level of betweenness centrality; (3) the top 20% nodes with the highest level of eigenvector centrality; and (4) the top 20% nodes with highest level of local efficiency. If a node belonged to one of the above four cases, we added 1 score for this node. Each node was assigned a score ranged from 0 to 4, determined by the above four criterion fulfilled. If a region exhibited a hub score of 2 or higher, it was marked as a hub node [van den Heuvel et al., 2010].

Network‐Based Statistic

To further localize specific pairs of brain regions in which the structural connectivity of WM was altered in de novo PD patients, we used a NBS approach. A detailed description of the NBS methodology is given by Zalesky et al. [2010]. Briefly, a primary cluster‐defining threshold was first used to identify suprathreshold connections, within which the size (i.e., number of edges) of any connected components was then determined. Then, a corrected p value was calculated for each component using the null distribution of maximal connected component size, which was derived empirically using a nonparametric permutation approach.

Statistical Analyses

Two‐tailed t‐tests were used to asses for statistically significant differences in either demographic, neuroimaging and neuropsychological variables (i.e., age, total intracranial volume, total grey matter volume, total white matter volume, cognitive performance) or graph measures between de novo PD patients and controls. Group differences in sex distribution were analyzed using a ${\chi }^2$ test.

An FDR procedure was employed to correct for multiple comparisons in the global and local network analyses. The critical statistical threshold was set to q = 0.05. To check the statistical power for the between‐group comparisons in graph metrics, we also estimated the effect size (Cohen's d) according to Cohen's definition [Cohen, 1992].

Next, to determine the significance levels of altered connectivity networks in NBS analysis, we first performed a two‐sample t test at each edge independently to test for significant differences in the value of connectivity between the two groups. A primary component‐forming threshold (P = 0.05, T = 2.01, two tailed t‐test) was then applied to form a set of suprathreshold edges among which any connected components and their size (number of edges) could then be determined. Next, the statistical significance of the size of each observed component was then evaluated with respect to an empirical null distribution of maximal component sizes obtained under the null hypothesis of random group membership (20,000 permutations). Subnetworks that were significant at a corrected level of P = 0.05 were reported. However, we tested different thresholds to define suprathreshold edges and then to determine any connected components. The results of these analyses are reported in Supporting Information Table S2.

In order to test whether symptoms severity (measured via UPDRS and H&Y) was associated with alterations in graph metrics, we computed Pearson correlation coefficient between global and local metrics and clinical scores. The correlations were considered statistically significant if the relative P were less than 0.05 after false discovery rate correction.

RESULTS

Participants

Table 1 summarizes the demographic, clinical and neuropsychological data of the sample of de novo PD and healthy controls included in this study. No significant differences were observed in age and sex between the two groups, and there were no significant differences in total brain, GM and WM volumes. In addition, PD patients and healthy controls were comparable for cognitive performance, depression, and anxiety.

Table 1.

Demographic, clinical, and neuroimaging data of sample

	HC (n = 30)	De novo PD (n = 21)	t/ ${\mathit{\chi }}^2$ value	P value
Demographic and clinical data
Age at exam (years ± SD)	60.57 ± 8.75	57.90 ± 12.23	t (49) = 0.91	0.37
Gender (% female)	33	28	${\chi }^2$ = 0.13	0.72
Disease duration (months ± SD)	–	19.28 ± 16.32	–	–
UPDRS‐ME (mean ± SD)	–	15.95 ± 6.77	–	–
Hoehn and Yahr (mean ± SD	–	1.5 ± 0.61	–	–
MMSE score	28.54 ± 1.33	28.37 ± 1.81	t (49) = 0.49	0.62
BDI	7.04 ± 5.03	6.00 ± 3.45	t (49) = 0.71	0.48
HAM‐A	8.76 ± 4.56	9.66 ± 4.18	t (49) = −0.71	0.47
Neuroimaging data
Total gray matter volume (ml)	596.43 ± 48.77	603.75 ± 50.51	t (49) = −0.51	0.61
Total white matter volume (ml)	524.44 ± 55.69	548.96 ± 56.10	t (49) = −1.54	0.13
Intracranial volume (ml)	1376.26 ± 119.76	1410.13 ± 101.44	t (49) = −1.05	0.29

All data are expressed as mean ± standard deviation. Chi‐square test was used to test differences in gender distribution; two sample t‐tests were used for other variables. UPDRS‐ME, Unified Idiopathic Parkinson's Disease Rating Scale; MMSE, Mini‐Mental State Examination; BDI, Beck Depression Inventory; HAM‐A, Hamilton Anxiety Rating Scale; HC, healthy controls; de novo PD, De novo PD patients; SD, standard deviation.

Graph Theory Analyses

No main effect of group was found for small world measures (P > 0.1, FDR corrected). This result is consistent with previous finding showing that de novo PD and healthy controls display a similar small world organization of structural and functional networks [Olde Dubbelink et al., 2014; Skidmore et al., 2011]. Moreover, there was no significant main effect of group in the characteristic path length (P > 0.05, FDR corrected). In contrast, a decrease of the global strength, global efficiency, and global clustering coefficient was found in the patients’ group relative to healthy controls (P ≤ 0.02, FDR corrected) (Table 2).

Table 2.

Main effect of group in the global network metrics

	HC	De novo PD	t value	P value (FDR‐corrected)	Cohen's d
Global clustering	0.04 (0.005)	0.03 (0.004)	t (49) = 2.96	0.023	0.84
Global efficiency	0.06 (0.01)	0.05 (0.01)	t (49) = 2.55	0.026	0.73
global strength	1.13 (0.15)	1.03 (0.12)	t (49) = 2.51	0.026	0.72
Characteristic path length	24.49 (4.27)	26.87 (3.77)	t (49) = −2.05	0.09	0.59
Density	0.14 (0.01)	0.14 (0.01)	t (49) = 1.75	0.10	0.5

De novo PD patients displayed a reduced global clustering, global efficiency and global strength in comparison to healthy controls. Data are expressed as mean (SD). No main effect of group was found in the characteristic path length and density. HC, Healthy controls; de novo PD, De novo PD patients; SD, standard deviation.

At a local level de novo PD patients displayed a reduced strength in the bilateral putamen, the right amygdala and in the right lingual gyrus (P < 0.02, FDR corrected) (Fig. 1, Table 3).

Figure 1.

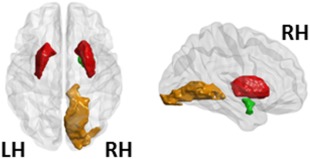
Local network results (strength). Regions that showed a decreased strength as a function of the main effect of group (P < 0.025, FDR corrected). In particular, de novo PD patients showed, relative to HC, a decreased strength in bilateral putamen, right amygdala and right lingual gyrus. The bilateral putamen, the right amygdala and the right lingual gyrus are represented in red, green, and orange, respectively. LH, left hemisphere; RH, right hemisphere. [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 3.

Main effect of group in the local strength

Regions	HC	De novo PD	t value	P value (FDR‐corrected)	Cohen's d
Right putamen	1.12 (0.21)	0.89 (0.21)	t (49) = 3.76	0.022	1.07
Left putamen	1.22 (0.26)	0.97 (0.22)	t (49) = 3.56	0.022	1.02
Right lingual	1.15 (0.28)	0.89 (0.22)	t (49) = 3.58	0.022	1.02
Right amygdala	0.28 (0.07)	0.21 (0.06)	t (49) = 3.51	0.022	1.00

De novo PD patients displayed a reduced strength in the bilateral putamen, in the right lingual gyrus and in the right amygdala. Data are expressed as mean (SD). T‐values were obtained from 2‐sample t‐test. Subscripted numbers in parentheses represent the degree of freedom. A FDR's procedure was applied to correct for multiple comparisons. HC, healthy controls; De novo PD, de novo PD patients; SD, standard deviation.

Moreover, we observed also a reduced clustering in left inferior occipital gyrus in de novo PD patients compared with controls (P < 0.02, FDR corrected) (Fig. 2A, Table 4A). Reduced ability in integration (measured via local efficiency) and segregation (measured via local clustering coefficient) were found in the left pallidum in de novo PD patients when compared with controls (P < 0.02, FDR corrected) (Fig. 2, Table 4).

Figure 2.

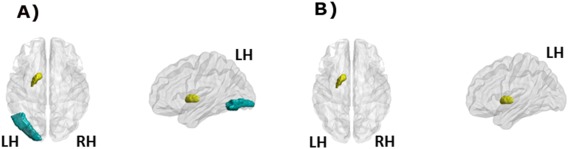
(A) Local network results (clustering). Regions that showed a decreased clustering coefficient in the de novo PD patients relative to HCs (P< 0.026, FDR corrected); (B) Local network results (efficiency). The left globus pallidum showed a decreased efficiency in the de novo PD patients relative to HCs (P < 0.02, FDR corrected). The left pallidum and the inferior occipital gyrus are represented in yellow and blue, respectively. LH, left hemisphere; RH, right hemisphere. [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 4.

Main effect of group in the local clustering and efficiency

Regions	HC	De novo PD	t value	P value (FDR‐corrected)	Cohen's d
A. Local clustering
Left pallidum	0.03 (0.01)	0.02 (0.01)	t (49) = 3.91	0.025	1.12
Left inferior occipital gyrus	0.05 (0.02)	0.04 (0.01)	t (49) = 3.67	0.026	1.04
B. Local efficiency
Left pallidum	0.04 (0.01)	0.03 (0.01)	t (49) = 4.04	0.017	1.15

De novo PD patients displayed a reduced clustering coefficient (A) in the left Pallidum and reduced local efficiency (B) in the left Pallidum. Data are expressed as mean (SD). T‐values were obtained from 2‐sample t‐test. Subscripted numbers in parentheses represent the degree of freedom. A FDR's procedure was applied to correct for multiple comparisons. HC, healthy controls; De novo PD, de novo PD patients; SD, standard deviation.

Finally, we observed an interestingly decrease in regional eigenvector centrality of right olfactory cortex centrality of de novo PD patients when compared with controls (P < 0.05 uncorrected) (Fig. 3, Table 5).

Figure 3.

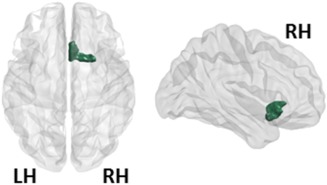
Local network results (eigenvector centrality). The only region that showed a reduced eigenvector centrality in the de novo PD patients relative to HCs was the right olfactory area. The right olfactory area is represented in green. LH, left hemisphere; RH, right hemisphere. [Color figure can be viewed at http://wileyonlinelibrary.com]

Table 5.

Main effect of group in the eigenvector centrality

Regions	HC	De novo PD	t value	P value (uncorrected)	Cohen's d
Right olfactory	0.005 (0.003)	0.004 (0.002)	t (49) = 2.29	0.025	0.65

The Olfactory area was found to be less central in the de novo PD patients relative to HCs. Data are expressed as mean (SD). T‐values were obtained from 2‐sample t‐test. Subscripted numbers in parentheses represent the degree of freedom. HC, healthy controls; De novo PD, de novo PD patients; SD, standard deviation.

No significant main effect of group was found for the betweenness centrality and local path length (P > 0.12, FDR corrected).

Hubs Analysis

As shown in Supporting Information, white matter brain networks in de novo PD patients and controls showed a similar hubs organization (Supporting Information Fig. S1). In particular, fourteen of the hub regions were the same in both groups. These areas included bilateral precentral, bilateral postcentral, bilateral inferior parietal, bilateral superior frontal gyrus, right middle cingulum, right superior parietal, right precuneus, left middle temporal gyrus, right inferior temporal gyrus, and right supramarginal (Supporting Information Fig. S1). Four brain regions (i.e., right middle frontal gyrus and middle temporal gyrus, left insula, and inferior temporal gyrus), were identified as a hub in de novo PD group but not in the HC group. Four brain regions, (i.e., right calcarine, right insula, left middle occipital, and right paracentral lobule) were identified as hubs in the HC group but not in the de novo PD group.

These results were approximately consistent with those obtained from previous studies exploring the hubs organization of brain circuits in healthy controls and different populations of patients with neurological diseases [Gong et al., 2009; van den Heuvel and Sporns, 2011, 2013; Pereira et al., 2015].

NBS Analyses

The NBS identified two subnetworks of reduced connectivity in de novo PD patients (P < 0.05, corrected for multiple comparison) (Fig. 4, Supporting Information Table S1). The largest of the two significant circuits consisted of sixteen edges connecting sixteen different regions (corrected P = 0.009). These connections primarily involved key components of the limbic system, basal ganglia and sensorimotor areas. The second network consisted of six edges linking six nodes (corrected P = 0.018). These edges connected the left thalamus to both left caudate and the left pallidum, the left pallidum to the left putamen, the left putamen to both the left insula and the left middle frontal gyrus (orbital part), and the left insula to the left middle frontal gyrus (orbital part). None of the connections showed increased connectivity in patients relative to controls.

Figure 4.

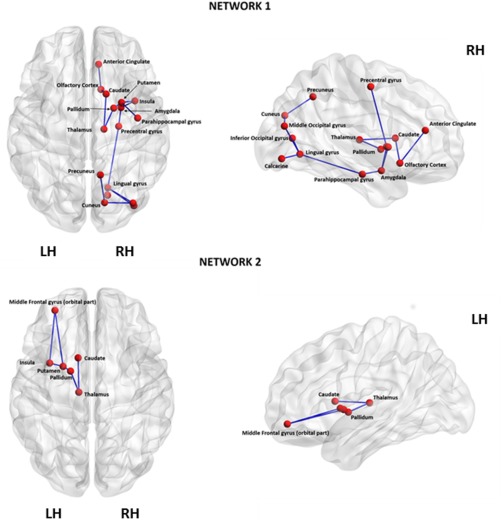
Networks identified to be significantly different between the de novo PD and control groups using Network‐Based Statistical Analysis. Netwotk1 consisted of 16 edges connecting 16 different regions (corrected P = 0.009). These connections primarily involved key components of the limbic system, basal ganglia and sensorimotor areas confirming the involvement of this regions in the pathophysiology of PD. Network2 consisted of six edges linking six nodes (corrected P = 0.018). These edges connected the left thalamus to both left caudate and the left pallidum, the left pallidum to the left putamen, the left putamen to both the left insula and the left middle frontal gyrus (orbital part), and the left insula to the left middle frontal gyrus (orbital part). LH, left hemisphere; RH, right hemisphere. [Color figure can be viewed at http://wileyonlinelibrary.com]

Correlation Between Connectivity Metrics and Clinical Data

No correlations were found in de novo PD patients UPDRS‐ME, Hoehn and Yahr, HAM‐A and BECK scores with global network metrics or regional network metrics (P > 0.05, FDR corrected).

DISCUSSION

In the present study, we studied the whole‐brain structural network's organization in a group of de novo PD patients when compared with a sample of healthy controls. Of note, the two groups were comparable for a series of demographic and neuropsychological variables such as age, sex, cognitive impairment (assessed via the MMSE), and depression and anxiety levels (assessed via DBI‐II and HAMA questionnaires, respectively).

We found altered graph metrics either at a global and local level. More specifically, when compared with healthy controls, PD patients showed a reduced global clustering coefficient, global efficiency and a decreased mean strength of connections. Moreover, at a local level, PD patients, when compared with HCs, displayed decreased clustering coefficient and strength in specific brain regions such as putamen, pallidum, amygdala, and olfactory cortex.

In addition, NBS analyses demonstrated that two specific subnetworks of reduced connectivity characterized the WM structural deficits seen in de novo PD patients. In particular, several key pathways in the limbic system, basal ganglia and sensorimotor circuits showed reduced patterns of communications when comparing PD to HCs.

All together, these findings provide new evidence that disconnection mechanisms within key WM networks play an important pathophysiological role even at early stages of the disease. Although DTI measures are indirect measures of white‐matter integrity, we speculate that the typical PD‐related neurodegenerative mechanisms (e.g., alpha‐synuclein‐driven damage to the presynaptic terminals) may impair axonal transport and consequently produce axonal degeneration and abnormal patterns of communications in the whole‐brain [Braak et al., 2003; Saito et al., 2003]. Interestingly, our data also suggest that PD‐related degenerative mechanisms affecting the white‐matter tracts may be broader than originally thought [Planetta et al., 2014].

In particular, the reduced ability in segregation and integration found in key regions of basal ganglia network (putamen and pallidum) confirms a strong involvement of this motor network in PD pathophysiology. Specifically, the decreased ability for specialized processing (reduced clustering in left pallidum and reduced strength in bilateral putamen) together with decreased ability in combine specialized information from distributed brain regions (reduced efficiency in pallidum) may confirm an unbalanced functioning of direct and indirect dopaminergic pathways in PD patients at the early stages of disease.

Relative to healthy controls, PD patients also showed a reduced centrality in the olfactory cortex, a region strongly involved in the first stage of neuropathological course of PD, suggesting a reduced ability of this region in promoting communication. This finding could suggest a damage of WM tracts connecting olfactory cortex to the other brain regions as reported in previous pathological [Braak et al., 2003] and DTI [Ibarretxe‐Bilbao et al., 2010; Rolheiser et al., 2011; Scherfler, 2005] studies. In addition, the reduced properties observed in this area may confirm the olfactory dysfunction present in approximately 90% of early‐stage PD [Doty, 2012].

Intriguing results were also obtained in the mesolimbic–striatal circuits. Specifically, the NBS analyses showed a reduced connectivity between several regions of striatal and limbic networks such as caudate, putamen, amygdala, and parahippocampal suggesting a decreased ability in information routing among these regions. These findings may confirm recent fMRI data that observed as a reduced function connectivity in mesolimbic–striatal network may be associated with underlying pathology of early non‐motor manifestations in de novo PD patients [Luo et al., 2014].

The current study has several strengths including the use of DAT‐SPECT, to confirm a dopaminergic deficit in all PD cases, and the fact that all patients were drug naïve. Moreover, our study further demonstrates how studying human brain as an interconnected network could be fundamental for understanding large‐scale neuronal organization in the brain obtaining new insights about pathophysiology of brain diseases.

However, some limitations should also be recognized. First, we examined a relatively small number of patients. Hence, our results have to be considered as preliminary to future studies on larger sample of patients. Second, to exclude any global cognitive impairment or dementia we assessed both PD patients and healthy controls via the MMSE. However, we acknowledge that MMSE may have poor sensitivity to detect dementia at early stages compared with other tests (e.g., MoCA), so a more precise characterization of the impact of cognitive symptoms on graph‐measures of connectivity in PD is warranted in future studies. Third, we employed deterministic tractography to define the whole brain white matter networks. Although this method was commonly used in previous DTI studies assessing pathophysiological mechanisms underlying neurodegenerative diseases, this procedure cannot resolve fiber crossing at a voxel level [Mori and van Zijl, 2002]. To overcome this issue, others have employed probabilistic tractography [Korgaonkar et al., 2014], although this technique presents its own disadvantages [Descoteaux et al., 2009]. So, further studies using deterministic and probabilistic tractography are warranted to replicate current results. Fourth, longitudinal studies are required to assess (i) whether these abnormalities in structural brain network are predictive of the clinical–pathological evolution and (ii) how these alterations are associated with the antiparkinson medication. Lastly, it remains to be determined whether the alterations of graph metrics that we identified in specific brain regions of de novo PD patients may represent a useful marker in distinguish idiopathic PD from atypical Parkinsonism.

CONCLUSIONS

In the present work, we combined DTI and graph analysis to explore whether and which alterations in the WM networks organization characterized drug‐free PD patients relative to HCs. We found alterations in the structural connectivity of several motor and non‐motor regions. Our findings confirmed the presence of disconnectivity mechanisms in motor (basal ganglia) as well as in non‐motor (e.g., limbic and olfactory) circuits already at an early stage of disease.

FINANCIAL DISCLOSURES

None of the authors has conflicted of interests.

Supporting information

Supporting Information