MarsAtlas: A cortical parcellation atlas for functional mapping

Abstract

An open question in neuroimaging is how to develop anatomical brain atlases for the analysis of functional data. Here, we present a cortical parcellation model based on macroanatomical information and test its validity on visuomotor‐related cortical functional networks. The parcellation model is based on a recently developed cortical parameterization method (Auzias et al., [2013]: IEEE Trans Med Imaging 32:873–887), called HIP‐HOP. This method exploits a set of primary and secondary sulci to create an orthogonal coordinate system on the cortical surface. A natural parcellation scheme arises from the axes of the HIP‐HOP model running along the fundus of selected sulci. The resulting parcellation scheme, called MarsAtlas, complies with dorsoventral/rostrocaudal direction fields and allows inter‐subject matching. To test it for functional mapping, we analyzed a MEG dataset collected from human participants performing an arbitrary visuomotor mapping task. Single‐trial high‐gamma activity, HGA (60–120 Hz), was estimated using spectral analysis and beamforming techniques at cortical areas arising from a Talairach atlas (i.e., Brodmann areas) and MarsAtlas. Using both atlases, we confirmed that visuomotor associations involve an increase in HGA over the sensorimotor and fronto‐parietal network, in addition to medial prefrontal areas. However, MarsAtlas provided: (1) crucial functional information along both the dorsolateral and rostrocaudal direction; (2) an increase in statistical significance. To conclude, our results suggest that the MarsAtlas is a valid anatomical atlas for functional mapping, and represents a potential anatomical framework for integration of functional data arising from multiple techniques such as MEG, intracranial EEG and fMRI. Hum Brain Mapp 37:1573‐1592, 2016. © 2016 Wiley Periodicals, Inc.

Abbreviations

MEG

magnetoencephalography

MRI

magnetic resonance imaging

INTRODUCTION

Describing the macroanatomy of the human cerebral cortex is a complex task. The geometry of the cortex is variable across individuals and features such as sulci or gyri are difficult to identify, other than at a coarse scale. In particular, it is currently debated how to optimally divide the cortical surface into subregions, which are functionally homogeneous and reproducible across subjects, so to provide a brain atlas for functional mapping or connectivity analysis [De Reus and van den Heuvel, 2013; Tzourio‐Mazoyer et al., 2002]. The goal of our study was to develop an automatic cortical parcellation model for the analysis and interpretation of functional data, and in particular MEG high‐gamma activity (HGA).

The construction of brain atlases relies on the identification of functionally homogeneous cortical regions. Homogeneous cortical units are classically defined by their microstructure, as described by cytoarchitectony or myeloarchitectony [Amunts et al., 2007]. Unfortunately, this type of information is not provided by noninvasive techniques, such as MRI. The challenge is, therefore, to identify regions using macroanatomical features. The link between architectony and macro‐anatomical features, such as sulci, is still debated [Fischl et al., 2008; Weiner et al., 2013], and cortical parcellation schemes based on macroscopic anatomical features have limited capacity in functional segregation [Van Essen et al., 2012]. Beyond the coarse notion of lobes, the level of parcellation corresponding to gyri has been extensively used. Several MRI data processing software use standard anatomical T1‐weighted images to provide cortical parcellation schemes, which can be used for anatomical labeling of functional results [Desikan et al., 2006; Lancaster et al., 2000; Tzourio‐Mazoyer et al., 2002], functional connectivity (FC) inference (Harvard‐Oxford cortical atlas, http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FSL) [Desikan et al., 2006] and structural connectivity analysis [Hagmann et al., 2008]. A category of such methods uses one or several parcellated volumetric atlases to define a parcellation of individual volumes by registration to the atlas(es) [Tzourio‐Mazoyer et al., 2002]. In the case of multiple atlases, a label‐fusion strategy can be used [Klein and Tourville, 2012; Rousseau et al., 2011], as well as a probabilistic approach (Harvard‐Oxford cortical atlas). The main limitation of such approaches is inherent to their volumetric nature: due to the large geometric variability of the cortical surface, 3D registration can only achieve a limited level of cortical intersubject matching [Van Essen et al., 2000]. As a consequence, the match between an individual cortical surface and the volumetric atlas(es) is imprecise and the boundaries between cortical areas are not located where they should. Surface‐based methods are, therefore, preferable: matching is done in a common surface‐based domain, such as a sphere [Fischl et al., 1999] or a plane [Auzias et al., 2013; Van Essen and Drury, 1997], and surface‐to‐surface intersubject matching is more efficient than volume‐to‐volume registration [Anticevic et al., 2008; Van Essen et al., 2000]. Using the Freesurfer software (http://freesurfer.net), a probabilistic surface‐based atlas can be built from a number of manually labeled subjects and used as prior for labeling process adapting the parcellation scheme to single‐subject cortical geometry [Destrieux et al., 2010; Fischl et al., 2004]. Boundaries between cortical areas are then forced to be located as close as possible to the fundus of sulci. Indeed, even though their exact borders are often ill‐defined, gyri are generally bounded by two sets of parallel folds. This notion has been used in [Cachia et al., 2003] to define a subject‐specific gyral parcellation scheme. However, even with this approach, not all gyri can be defined precisely. For example, the dorsal and ventral boundaries of the precentral gyrus, located between the precentral and central sulci, are difficult to determine. Similarly, the posterior boundary of the middle temporal gyrus displays a high variability in the folding pattern across individuals [Shi et al., 2007; Van Essen and Dierker, 2007]. Identifying these boundaries, or searching for a finer level of parcellation, requires tertiary sulci, which are even more variable and cannot be used as landmarks for defining regions and intersubject matching.

To build subgyral parcellation schemes, existing solutions use either functional resting‐state data [Thirion et al., 2014; Yeo et al., 2011] or random anatomical parcellations [Hagmann et al., 2008; Khundrakpam et al., 2015; Messé et al., 2015]. Functional parcellation models usually provide a finer level of subdivision of the cortex and an intrinsically stronger relationship with functional organization. Nevertheless, they require large functional dataset of resting‐state activity and they can be only inferred at the group level (e.g., 500 subjects in [Yeo et al., 2011]). Since coregistration between single subjects and group template is performed using macroanatomy, fitting accuracy is limited. In our work, we put forward a complementary parcellation scheme, named MarsAtlas, based on the spatial organization of key cortical sulci. Such subgyral surface‐based parcellation introduces the notion of alignment and relative orientation of these sulci on the cortical surface. Our results suggest that the parcellation arising from these axes represents a natural tradeoff between spatial resolution and functionally relevant parcellation.

ANATOMICAL MODEL: THE MARSATLAS PARCELLATION ATLAS

When observing cortical macroanatomy, two main orthogonal directions of gyri organization are noticeable along a rostrocaudal and dorsoventral axes. For instance, the pre‐ and postcentral gyri follow the dorsoventral axis and the superior and inferior frontal gyri, the superior and middle temporal, and the cingular gyri follow the rostrocaudal axis. The two extremities in the dorsoventral direction, or poles, are the cingulate gyrus on the medial surface and the insular core laterally, respectively. These two trends of organization define a form of continuity between gyri. For example, in the dorsoventral direction, there is a clear continuity between the precentral insular gyrus, the precentral gyrus, the gyrus of the paracentral lobulus, and the paracentral annectent gyrus. Such organization along two orthogonal directions has been described in [Régis et al., 2005; Toro and Burnod, 2003] and it defines a spherical “meridian/parallel” system between the two above–mentioned poles [Auzias et al., 2013; Clouchoux et al., 2010].

Interestingly, [Sanides, 1969] and [Pandya and Yeterian, 1985] described two preferential trends of cytoarchitectonic organization in monkey, according to two rostrocaudal and dorsoventral axes. These two axes fit with those described in [Régis et al., 2005; Toro and Burnod, 2003] for sulci and gyri. This suggests that a cortical meridian/parallel model may be relevant at the functional level. Indeed, in the central region, the dorsoventral axis corresponds to the somatotopic level of organization and the rostrocaudal axis in the central region corresponds to a gradient of modality. These observations also echo the hierarchical functional organization of the frontal cortex [Amodio and Frith, 2006; Badre and D'Esposito, 2008; Koechlin et al., 2003].

The two orthogonal axes of gyral organization are especially visible at the fetal stage [Régis et al., 2005]. At the adult stage, however, additional variability appears and folding is more complex, and one axis is usually dominant over the other, which might be buried in the depth of folds, also referred to as annectant gyri. A typical example of annectant gyri is the pli‐de‐passage fronto‐parietal moyen [Broca, 1888; Cunnigham and Horsley, 1892; Cykowski et al., 2008]. This gyrus is buried in the depth of the central sulcus, and links the frontal and parietal lobes, orthogonally to the dominant dorsoventral direction along the precentral and postcentral gyri. Many annectant gyri can be observed on the cortical surface [see for instance Ochiai et al., 2004]. They subdivide cortical sulci and define a finer level of description, as well as a hidden continuity of gyri [Régis et al., 2005]. Annectant gyri, however, are variable across subjects, often difficult to detect, and cannot be used consistently. As a result, parcellation schemes based on macroanatomical features often lack subdivisions in the nondominant orientation. For instance, in the Desikan et al. [2006] or Destrieux et al. [2010] parcellation schemes, the pre‐ or postcentral gyri are defined as single regions without finer subdivision reflecting a segregation of the somatotopic gradient. Similarly, the superior temporal gyrus is defined as a single region. The same applies to the parcellation scheme in [Cachia et al., 2003], where the superior, intermediate, middle, and inferior frontal gyri are defined using local sulcal anatomy along the rostrocaudal directions, without any subdivisions in the dorsoventral directions.

In a recent article [Auzias et al., 2013], a novel fully automatic cortical parameterization method, called HIP‐HOP, that implements the meridian model [Régis et al., 2005] has been presented. The HIP‐HOP method is based on a set of primary and secondary sulci that comply to (are aligned with) the model shown in Figure 1. An orthogonal coordinate system is defined, which provides the two main directions of the model at any point of the cortical surface, and implicitly provides an inter‐subject correspondence. Since the process makes use of long‐range alignment of sulci (e.g., the superior temporal sulcus and the inferior frontal sulcus), the underlying orthogonal grid is inferred everywhere on the cortical sheet, even when it is not anchored to local sulcal features. Therefore, a natural parcellation scheme can be defined using the principal axes of the HIP‐HOP parameterization process running along the fundus of selected sulci (Fig. 2). This results in an orthogonal parcellation scheme that complies with dorsoventral/rostrocaudal direction fields consisting of 61 regions per hemisphere (60 regions for the neocortex and the insula).

Figure 1.

The HIP‐HOP parameterization model. A detailed description of all sulci involved can be found at the following link, with the same color code: http://brainvisa.info/doc/documents-4.4/nomenclature/BV_nomenclature.pdf.

Figure 2.

From HIP‐HOP to the MarsAtlas parcellation model (top) and view on an inflated cortical surface (bottom). The atlas is represented on the HipHop138 average template (available at: http://www.meca-brain.org/softwares/hiphop138-cortical-surface-group-template/).

Even though the HIP‐HOP parcellation scheme provides a framework for the creation of anatomical brain atlases, its application for functional mapping using high‐gamma MEG activity is not straightforward. First, it is recognized that tomographic maps based on standard frequency‐domain beamforming can only be computed with a limited spatial resolution (usually several millimeters) [Hansen et al., 2010]. This poses a lower bound on region size under which functional mapping becomes unrealistic. For example, areas such as those around the cingular and insular poles are smaller than the rest of brain regions. As a first approximation, standard beamforming techniques discretize the brain volume into a grid with a 10 mm resolution, where the lead field matrix is calculated. To place at least one source per region, that would require a volume of at least 1000 mm³. If we were to constrain each source to a sphere of 5 mm in radius, that would require a volume of ∼524 mm³. Secondly, large heterogeneities in size across regions may bias functional mapping, privileging larger areas with stronger signal‐to‐noise ratios across participants (and thus more significance results). For example, the elongated form of occipital and temporal regions may be biased in this sense with respect to smaller regions in sensorimotor and premotor cortices. Given that the relative sizes are dictated by the choice of primary and secondary sulci in the anatomical model, larger areas cannot be further subdivided unless additional axes are included into the model. If additional axes were added, smaller regions would appear, thus precluding functional mapping. A solution to both limitations is to merge small regions. This leads to larger regions (i.e., solve issue 1) and improve size homogeneity within the same participant (i.e., the mean size is similar across regions) and stability across participants (i.e., the variance in size of each region across participants is low). The goal of this study was to put forward a grouping scheme (i.e., a parcellation atlas) which responds to these constraints and, at the same time, conforms to the knowledge from literature regarding cortical anatomy and parcellation. Grouping was dictated by a search of a compromise between optimal size, homogeneity across regions and by knowledge from literature.

Concerning the size of the HIP‐HOP regions, a study on two different datasets was conducted and led to the merge of several regions in order to avoid subjects with regions smaller than the minimal spatial resolution required for functional mapping. Details are given in section “MarsAtlas parcellation atlas.” Information about parcellation region size was complemented with additional anatomical notions to create the final MarsAtlas model. Below is a detailed description of how we grouped HIP‐HOP regions for each lobe.

Grouping in the frontal lobe (dorsomedial, dorsolateral, and orbital portions) was performed along the dorsoventral direction. The superior and inferior frontal sulci in the rostrocaudal direction were privileged as main axes, because the intermediate frontal sulcus is more variable across individuals and often appears with several disconnected pieces with variable orientations. This produced the dorsomedial (dm), dorsolateral (dl), and ventral (v) portions of the motor, premotor, and caudal prefrontal areas, (Mdm, Mdl, Mv, PMdm, PMdl, PFcdm, PFcdl, respectively). Only one region was created along the anteroposterior axis, named rostroventral premotor region (PMrv), because it was found to cover primarily BAs 44 and 45 rather than the ventral portion of BA 6. More anteriorly, only the ventromedial prefrontal cortex (PFCvm) was defined as the grouping of two thin and elongated regions running along the antero‐posterior direction. All other HIP‐HOP regions were kept unchanged.

In the cingulate cortex, we used a well‐accepted anatomical parcellation model proposed by Vogt et al. [2009] based on multimodal observations (i.e., structural, circuitry, functional imaging, and receptor architecture), which subdivides the cingulate cortex into four regions, encompassing the anterior cingulate, midcingulate, posterior cingulate, and retrosplenial cortices (ACC, MCC, PCC, and RSC, respectively). Although a direct relation between such subdivision and sulci information cannot be performed, we used the same nomenclature proposed for the ACC, MCC, and PCC and merged HIP‐HOP regions to resemble such model as close as possible. However, we named the most posterior portion the isthmus of cingulate cortex (ICC) to refer to the narrowest portion, which should mainly include BAs 29 and 30. The same nomenclature is used by the Desikan‐Killiany atlas [Desikan et al., 2006]. Such grouping of HIP‐HOP regions in cingulate cortex was also dictated by the requirement that the ACC and MCC had to be part of the frontal lobe, whereas the PCC should be in the parietal lobe. The insular cortex, due to the lack of salient fold, was considered as a single area, even though a further subdivision into anterior and posterior insular cortex may have been reasonable.

In the parietal lobe, the sensorimotor regions confined by the central and post‐central sulci were grouped so to reflect the same grouping over motor and premotor areas. This leads to dorsomedial, dorsolateral, and ventral sensorimotor regions (Sdm, Sdl, Sv, respectively). The medial and dorsal posterior parietal regions are delimited by the post‐central sulcus and the occipito‐parietal fissure in the anteroposterior direction. In the dorsolateral direction, bounds are defined by local folds, such as the ascending branches of temporal sulci, and by longer‐range alignments with the collateral fissure and the posterior occipito‐temporal lateral sulcus. This produced the posterior parietal regions (PCm, SPCm, SPC, IPCd). For the most ventral portion of the parietal cortex, we grouped two HIP‐HOP regions in the ventral portion of the Inferior Parietal Cortex (IPCv). In the occipital lobe, we merged two HIP‐HOP regions corresponding to the Cuneus (Cu) and two areas composing the superior Visual Cortex (VCs). Finally, in the temporal lobe, given their size, the only grouping was performed to create the medial inferior temporal cortex region (ITCm). All other regions were kept unchanged.

The resulting parcellation model, referred to as MarsAtlas (a short name for “Marseille Atlas”), contains 41 cortical regions per hemisphere, as shown in Figure 2 and Table 1. Parcellation labels are grouped in larger regions, which are occipital lobe (5 labels), temporal lobe (6 labels) parietal lobe (8 labels), cingular cortex (4 labels), frontal lobe (13 labels), orbito‐frontal cortex (4 labels), and the insula. Note that, as explained earlier and contrary to previous models, some subdivisions are present in regions with no local macroanatomical features to infer these subdivisions. For instance, the precentral and postcentral gyri are both divided in three distinct dorsomedial, dorsolateral, and ventral regions; the lateral prefrontal regions are divided in rostral and caudal parts; the superior and middle temporal gyri are also divided in rostral and caudal parts; and the cingulate cortex is subdivided in four different parts along the rostrocaudal gradient.

Table 1.

List of MarsAtlas parcellation labels

Label	Lobe/Région	Full name	Brodman Area
VCcm	Occipital	Caudal Medial Visual Cortex	17/18
VCl	Occipital	Lateral Visual Cortex	37/19/18
VCs	Occipital	Superior Visual Cortex	19/39
Cu	Occipital	Cuneus	18/19
VCrm	Occipital	Rostral Medial Visual Cortex	18/19
ITCm	Temporal	Medial Inferior Temporal Cortex	36/37/20
ITCr	Temporal	Rostral Inferior Temporal Cortex	20
MTCc	Temporal	Caudal Middle Temporal Cortex	21/22/39
STCc	Temporal	Caudal Superior Temporal Cortex	22/41/42
STCr	Temporal	Rostral Superior Temporal Cortex	21/22/38
MTCr	Temporal	Rostral Middle Temporal Cortex	20/21/38
IPCv	Parietal	Ventral Inferior Parietal Cortex	40
IPCd	Parietal	Dorsal Inferior Parietal Cortex	39/40/7
SPC	Parietal	Superior Parietal Cortex	7
SPCm	Parietal	Medial Superior Parietal Cortex	7
PCm	Parietal	Medial Parietal Cortex	31
Sv	Parietal	Ventral Somatosensory Cortex	1/2/3
Sdl	Parietal	Dorsolateral Somatosensory Cortex	1/2/3
Sdm	Parietal	Dorsomedial Somatosensory Cortex	1/2/3/5/31
ICC	Cingular	Isthmus Cingulate Cortex	30
PCC	Cingular	Posterior Cingulate Cortex	23
MCC	Cingular	Mid Cingulate Cortex	24
ACC	Cingular	Anterior Cingulate Cortex	24/32
Mv	Frontal	Ventral Motor Cortex	4/6
Mdl	Frontal	Dorsolateral Motor Cortex	4
Mdm	Frontal	Dorsomedial Motor Cortex	4
PMrv	Frontal	Rostral Ventral Premotor Cortex	44/45
PMdl	Frontal	Dorsolateral Premotor Cortex	6/8
PMdm	Frontal	Dorsomedial Premotor Cortex	6
PFcdl	Frontal	Caudal Dorsolateral Prefrontal Cortex	45/46/9
PFcdm	Frontal	Caudal Dorsomedial Prefrontal Cortex	6/8
PFrvl	Frontal	Rostral Ventrolateral Prefrontal Cortex	47/45
Pfrdli	Frontal	Rostral Dorsolateral Inferior Prefrontal Cortex	10/46
Pfrdls	Frontal	Rostral Dorsolateral Superior Prefrontal Cortex	10/9
PFrd	Frontal	Rostral Dorsal Prefrontal Cortex	10/9/8
PFrm	Frontal	Rostral Medial Prefrontal Cortex	9/8
OFCvl	Orbito‐Frontal	Ventrolateral Orbito Frontal Cortex	11/47
OFCv	Orbito‐Frontal	Ventral Orbito Frontal Cortex	11/47
OFCvm	Orbito‐Frontal	Ventromedial Orbito Frontal Cortex	10/11
PFCvm	Orbito‐Frontal	Ventromedial Prefrontal Cortex	32/10/11
Insula	Insula	Insular Cortex	13

MATERIAL AND METHODS

MEG and Anatomical MRI Dataset

We combined MarsAtlas with functional data composed of MEG recordings collected from human participants (n = 11) performing an arbitrary visuomotor mapping task, a canonical instance of visuomotor behavior, in addition to anatomical MRI. The goal was to quantify the statistical validity of MarsAtlas in functional mapping using high‐gamma MEG activity with respect to a recent approach based on MNI‐normalized (Montreal Neurological Institute) Talairach atlas [Brovelli et al., 2015].

Experimental conditions and behavioral tasks

The experimental procedure and data acquisition has been detailed in a previous study [Brovelli et al., 2015]. Here is a brief description of the experimental set‐up and acquisitions. Eleven healthy participants accepted to take part in our study (all were right handed and the average age was ∼23 years old, 4 were females and 7 males), gave written informed consent according to established institutional guidelines and local ethics committee, and received monetary compensation (€50). Participants were asked to perform an associative visuomotor mapping task where finger movements are associated to digit numbers: digit “1” instructed the execution of the thumb, “2” for the index finger, “3” for the middle finger and so on (Fig. 3a). Maximal reaction time was 1 s. After a fixed delay of 1 s following the disappearance of the digit number, an outcome image was presented for 1 s and informed the subject whether the response was correct, incorrect, or too late (if the reaction time exceeded 1 s). Incorrect and late trials were excluded from the analysis, because they were either absent or very rare (i.e., maximum 2 late trials per session). The next trial started after a variable delay ranging from 2 to 3 s (randomly drawn from a uniform distribution) with the presentation of another visual stimulus (Fig. 3b). Each participant performed two sessions of 60 trials each (total of 120 trials). Each session included three digits randomly presented in blocks of three trials.

Figure 3.

Arbitrary visuomotor mapping task. The relation between visual stimulus and motor response is deterministic and highly acquainted. Stimuli were digits from 1 to 5 and appeared at the center of the screen for 1 s. Participants were required to move the finger associated to the digit: “1” instructed thumb movement, “2” the index, etc. The maximum reaction time was 1 s (i.e., stimulus duration). After a fixed delay of 1 s, the feedback image instructed whether the executed motor response was correct, incorrect or late.

Anatomical, functional, and behavioral data acquisition

Anatomical MRI images were acquired for each participant using a 3‐T whole‐body imager equipped with a circular polarized head coil. High‐resolution structural T1‐weighted anatomical image (inversion‐recovery sequence, 1 × 0.75 × 1.22 mm) parallel to the anterior commissure‐posterior commissure plane, covering the whole brain, were acquired. Magnetoencephalographic (MEG) recordings were performed using a 248 magnetometers system (4D Neuroimaging magnes 3600). Visual stimuli were projected using a video projection (DUKANE Image Pro, frame refresh rate: 60 Hz) and motor responses were acquired using a LUMItouch^® optical response keypad with five keys. Presentation^® software was used for stimulus delivery and experimental control during MEG acquisition. Reaction times were computed as the time difference between stimulus onset and motor response. Sampling rate was 2034.5 Hz. Location of the participant's head with respect to the MEG sensors was recorded both at the beginning and end of each run to potentially exclude sessions with large head movements.

Anatomical MRI Dataset

To assess the generalization of MarsAtlas cortical parcellation scheme to a larger population, we analyzed an anatomical MRI dataset from 137 subjects. Particular attention was drawn to gather high‐quality anatomical MRI data from a well‐controlled population of healthy individuals. All participants were right‐handed subjects (69M/68F), and they were selected from the Open Access Series of Imaging Studies (OASIS) database (http://www.oasis-brains.org). For each subject, three to four individual T1‐weighted MP‐RAGE scans were acquired on a 1.5T Vision system (Siemens, Erlangen,Germany) with the following protocol: in‐plane resolution 256 × 256 (1 × 1 mm²), slicethickness = 1.25 mm, TR = 9.7 ms, TE = 4 ms, flip angle = 10°, TI = 20 ms, TD = 200 ms. Images were motion corrected and averaged to create a single image with a high contrast‐to‐noise ratio [Marcus et al., 2007].

MarsAtlas Cortical Parcellation Pipeline

The MarsAtlas pipeline was performed on anatomical MRI data from both datasets as detailed hereafter. After denoising using a nonlocal means approach [Coupé et al., 2008], T1‐weighted MR‐images were segmented using the FreeSurfer “recon‐all” pipeline (http://freesurfer.net). Gray and white matter segmentations of each hemisphere were imported into the BrainVisa software and processed using the Morphologist pipeline procedure (http://brainvisa.info ). White matter and pial surfaces were reconstructed and triangulated, and all sulci were detected and labeled automatically [Mangin et al., 2004; Perrot et al., 2011]. Labeled sulci and white matter meshes were then processed using the HIP‐HOP parameterization method also available in the Cortical Surface BrainVisa toolbox [Auzias et al., 2013; Coulon et al., 2013]. This consisted in mapping the cortical surface to a rectangle using a conformal (angle‐preserving) mapping, and then aligning the main sulci that are part of our model to the axis of the canonical orthogonal parameterization of the rectangular domain. Using inverse‐mapping back to the original surface, we produced a complete parameterization of the cortical surfaces whose axes are aligned with the main sulci that are parts of the Hip‐Hop model (see Fig. 1). These axes were then used to define cortical regions as described in the previous section (see Fig. 2, Table 1). The resulting cortical surface parcellation was then propagated to the volume‐based gray matter segmentation, using a front propagation from the surface through the volumetric cortex segmentation [Cachia et al., 2003], hence producing a volume‐based parcellation of the entire cortex (see Fig. 4). All these processing steps can be performed using the Cortical Surface toolbox in BrainVisa 4.5.

Figure 4.

MarsAtlas parcellation of the white matter surface (left) and of the cortical volume (right) for a representative participant.

Single‐Trial HGA at Cortical Parcellation Labels

Preprocessing and spectral analysis of MEG signals

MEG signals were down‐sampled to 1 kHz, low‐pass filtered to 250 Hz and segmented into epochs aligned on finger movement (i.e., button press). Epoch segmentation was also performed on stimulus onset and the data from −0.5 and −0.1 s prior to stimulus presentation was taken as baseline activity for the calculation of the single‐trial HGA. Artefact rejection was performed semiautomatically. For each movement‐aligned epoch and channel, the MEG signal variance and z‐value were computed over time and taken as relevant metrics for the identification of artefact epochs. All trials with a variance greater than 1.5*10‐24 across channels were excluded from further analyses. Additional metrics such as the z‐score, absolute z‐score, range between the minimum and maximum values were also inspected to detect artefact. Two MEG sensors were excluded from the analysis for all subjects. Spectral density estimation was performed using multitaper method based on discrete prolate spheroidal (slepian) sequences [Mitra and Pesaran, 1999; Percival and Walden, 1993]. To extract HGA from 60 to 120, MEG time series were multiplied by k orthogonal tapers (k = 8; 0.15 s in duration and 60 Hz of frequency resolution, each stepped every 0.005 s), centered at 90 Hz and Fourier‐transformed. Complex‐valued estimates of spectral measures, including cross‐spectral density matrices, were computed at the sensor level for each trial n, time t, and taper k.

Source analysis and calculation of HGA

Source analysis requires a physical forward model or leadfield, which describes the electromagnetic relation between sources and MEG sensors. The leadfield combines the geometrical relation of sources (dipoles) and sensors with a model of the conductive medium (i.e., the headmodel). For each participant, we generated a headmodel using a single‐shell model constructed from the segmentation of the cortical tissue obtained from individual MRI scans as described in section “Anatomical MRI dataset” [Nolte, 2003]. Leadfields were not normalized. At the source level, we compared two atlases, referred to as MNI‐Talairach and MarsAtlas. The goal of functional analyses was to compare the significance and spatial distribution of modulations in HGA based on MarsAtlas with those obtained in a recent study using an MNI‐Talairach atlas, as described in details in [Brovelli et al., 2015]. Briefly, to image MEG sources in the MNI‐Talairach atlas, a 3D grid with regular spacing between the dipole locations of 10 mm was generated for each participant. Individual MRI scans were then warped to the template MRI in MNI152 space, and the normalization parameters were applied to the dipole grid. Such procedure assured that individual subjects’ grid points were located in equivalent brain areas across all subjects according to MNI space. The anatomical position of each source was labelled according to Brodmann area (BA) using the binary representation of the Talairach‐Tournoux atlas [Talairach and Tournoux, 1988] digitized for the Talairach Daemon [Lancaster et al., 2000]. The MNI‐Talairach atlas is currently implemented in the Fieldtrip software [Oostenveld et al., 2011].

In MarsAtlas, anatomical MRI normalization was not required and sources were placed in the single‐subject volumetric parcellation regions. For each parcellation label P, we computed the number of sources nS _P as the ratio of the parcellation label volume and the volume of a sphere of radius equal to 5 mm. This allowed us to have source distances of ∼10 mm. The K‐means algorithm [Tou and Gonzalez, 1974] was used to partition the 3D coordinates of the voxels within a given volumetric parcellation label into nS clusters. The headmodel, source locations and the information about MEG sensor position for both models were combined to derive single‐participant leadfields.

Power at the source level was estimated for both atlases using adaptive linear spatial filtering [Veen et al., 1997]. In particular, we employed the Dynamical Imaging of Coherent Sources (DICS) method, a beamforming algorithm for the tomographic mapping in the frequency domain [Gross et al., 2001], which is a well suited for the study of neural oscillatory responses based on single‐trial source estimates of band‐limited MEG signals [for a series of review see, Hansen et al., 2010]. At each source location, DICS employs a spatial filter that passes activity from this location with unit gain while maximally suppressing any other activity. The spatial filters were computed on all trials for each time point and session, and then applied to single‐trial MEG data. Single‐trial power estimates aligned on movement and stimulus onset were log‐transformed to make the data approximate Gaussian and low‐pass filtered at 50 Hz to reduce noise. Single‐trial mean power and standard deviation in a time window from −0.5 and −0.1 s prior to stimulus onset was computed for each source and trial, and used to z‐transform single‐trial movement‐aligned power time courses. The same normalization procedure was performed for single‐trial stimulus‐related power time courses, so to produce HGAs for the pre‐stimulus period from −1.6 to −0.1 s with respect to stimulation. Finally, single‐trial HGA at each BA (for the MNI‐Talairach) and single‐subject cortical parcellation label (MarsAtlas) was defined as the mean z‐transformed power values averaged across all sources within the same region. The preprocessing steps, artefact rejection, spectral analyses, and source analysis were performed using the FieldTrip toolbox [Oostenveld et al., 2011].

Statistical Analysis

Statistical inference of single‐trial HGAs was performed using a linear mixed‐effect (LME) model approach. LME models are particularly suited for the analysis of data collected from multiple subjects, where it is important to take into account the variability across participants. These models formalize the relation between a response variable and independent variables using both fixed and random effects. Fixed effects model the response variable in terms of explanatory variables as nonrandom quantities. For example, experimental conditions related to population mean may be considered as fixed effects. Random effects are associated with individual experimental units drawn at random from a population, which may correspond to different participants in the study. In other words, whereas fixed effects are constant, random effects are drawn from a prior known distribution. A LME model is generally expressed in matrix formulation as,

$$y=X\beta +Zb+e$$ (1)

where $y$ is the n‐by‐1 response vector and n is the number of observations. $X$ is an n‐by‐p fixed‐effects design matrix and β is the fixed‐effect vector of p‐by‐1, where p is the number of fixed effects. $Z$ is an n‐by‐q random‐effects design matrix and b is a q‐by‐1 random‐effects vector, where q is the number of random effects; e is the n‐by‐1 observation error. The random‐effects vector, b, and the error vector, e, were assumed to be drawn from independent normal distributions. Parameter estimation was performed using maximum likelihood method, using the fitlme.m function in the Statistical Toolbox of Matlab (The MathWorks).

To test for significant modulations in single‐trial HGA and connectivity measures around finger movement with respect to the baseline period, we used a random‐intercept and random‐slope LME model, which is described by,

$$y\left(t\right)={\beta }_0\left(t\right)+{\beta }_1\left(t\right)x_j+b_{0j}\left(t\right)+b_{1j}\left(t\right)z_j+{ϵ}_j\left(t\right)$$ (2)

Where $y\left(t\right)=\left[y_{bl}\left(1\right),y_{bl}\left(2\right),\dots ,y_{bl}\left(np\right),y_{mv}\left(1,t\right),y_{mv}\left(2,t\right),\dots ,y_{mv}\left(np,t\right)\right]$. $y_{bl}\left(j\right)$ is a vector containing the baseline neural activity for all trials and sessions (i.e., data from both sessions were concatenated) for subject $j=\mathrm{1,2},\dots ,np$, where np is the number of participants, at time instant t. Note that t does not refer to trials, but time within each trial. $y_{mv}\left(j,t\right)$ is a vector including the neural data across all trials and two sessions for subject $j$ at time t with respect to movement onset. The design matrices contain two columns. The first column is a vector of ones to model the intercept, and thus it was eliminated from Eq. (2). The second column contains negative ones for baseline trials and ones for event‐related trials, therefore modeling the change with respect to baseline, or slope, and it is referred as $x_j$ and $z_j$ in Eq. (2). Thus, the first and third terms in the right‐hand‐side of Eq. (2) model the intercepts, which correspond to the mean values between baseline and movement‐related activity. The second and fourth terms model the slopes, which are the differences between baseline and movement‐related activity. The ${\beta }_1\left(t\right)$ values are fixed across subjects, whereas the $b_{1j}\left(t\right)$ values model the random variations across subjects. In other words, the parameter ${\beta }_1\left(t\right)$ models the change in neural activity (i.e., HGA power or FC measures) with respect to baseline at each time point t at the group level; the parameter $b_{1j}\left(t\right)$ models the change in neural activity with respect to baseline for each participant j and therefore explains the across‐subjects variability. The across‐subject variability was considered of no interest for the scope of the current analyses. We thus analyzed fixed‐effects representative of the entire population. Given the structure of the fixed‐effect design matrix, significant differences in movement‐related neural activity with respect to baseline can thus be inferred by testing whether β₁ coefficients are significantly >0. More formally, the significance of movement‐related modulations was inferred using a t‐test by testing the null hypothesis H₀: β₁ ≤ 0. Statistical inference was performed for each time point t and each BA for the analysis of HGAs. To account for the multiple comparisons problem at the single time‐point level, we controlled the false discovery rate (FDR) [Benjamini and Yosef, 1995]. The threshold for significance at each time point level was set to q < 0.001. This threshold sets the significance level at each time point. However, it does not provide information about consecutive significant points that may form “temporal clusters.” Thus, to further assess the validity of our results at the “temporal cluster” level, in addition to single time points, we quantified the minimum number of consecutive significant time points required to reject a null hypothesis of absence of a cluster given a chance probability p₀ = 0.5 (two possible outcomes, significant or nonsignificant), and kept only those clusters whose duration exceeded a significance level of 0.001. The exact mathematical formulation is given in the appendix of [Smith et al., 2004].

RESULTS

MarsAtlas Parcellation Atlas

MarsAtlas was created by grouping cortical regions generated using the HIP‐HOP scheme. Grouping was dictated by a compromise between optimal size, homogeneity across regions and knowledge from literature, as detailed in section “Anatomical model: the MarsAtlas parcellation atlas”. The mean volume across MarsAtlas regions was 1.22 +/− 0.54 (mean +/− standard deviation, in percentage values with respect to total cortical volume). Compared with the HIP‐HOP parcellation scheme (0.82 +/− 0.58), MarsAtlas regions have a clear increase in mean volume and a reduction in standard deviation. In particular, the average across subjects of the volume of the smallest region increases from 178 mm³ in HIP‐HOP to 883 mm³ in MarsAtlas. Supporting Information Figure S3 shows the distribution of volume across subjects in each region for both MarsAtlas and HIP‐HOP parcellation schemes, for the two datasets.

The surface‐based and volume‐based MarsAtlas parcellations are illustrated for one participant on Figure 4. Figure 5 shows the results of the cortical parcellation on the white matter surface of five participants. All the regions are present in every subject, with stable spatial relationships between the different parcellation labels. Despite the large folding variability across subjects, we observe a good reproducibility of the parcellation scheme and a good fit with the local cortical anatomy. This fit is particularly good in the lateral frontal lobe even although folding is very complex and variable in this area. It is less so in the temporal lobe where we observe size variations across subjects for a few parcellation labels such (STCr, MTCr). Major sulci that are part of the HIP‐HOP model act as separators between parcellation labels, for instance the central sulcus, the superior temporal sulcus or the cingular sulcus. It is also interesting to see that some separations are not following any sulci and are the results of long distance alignments as specified by the HIP‐HOP model. This concerns the parcellation labels within the precentral gyrus or the cingular gyrus, which are shown to be very stable across subjects (see results below).

Figure 5.

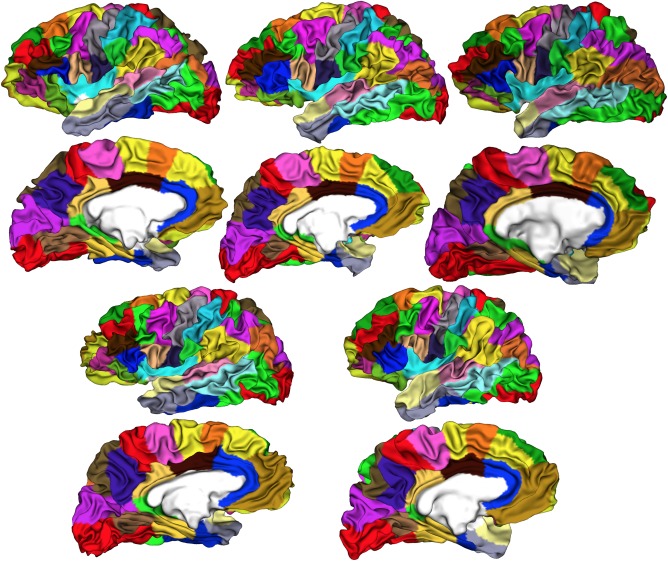
Cortical parcellation on the white matter surface of five participants.

We then performed quantitative analyses across subjects to assess the quality and reliability of our parcellation scheme. The relative volume of each parcellation label was computed at the individual level as the percentage of the gray matter volume with respect to the total gray matter volume. The mean and standard deviation across subjects of the relative volume were then computed (Fig. 6). Note that if parcellation labels were of equal size, their relative volume would have been 1.22%. The largest parcellation labels are in the occipital lobe (average mean: left = 1.87%, right = 1.92%) temporal lobe (MTCc, STCc, MTCr, average mean: left = 1.37%, right = 1.32%), and well as at the parieto‐temporal junction and superior parietal cortex (IPCd, IPCv, SPc, SPCm, average mean: left = 1.63%, right = 1.78%). These parcellation labels display the largest variability, that is, the largest relative volume variations across subjects: occipital lobe (average standard deviation: left = 0.27, right = 0.33), temporal lobe (average standard deviation: left = 0.41, right = 0.39) and parieto‐temporal junction and superior parietal cortex (average standard deviation: left = 0.31, right = 0.35). The smallest regions are in the frontal lobe (average mean: left = 1.12%, right = 1.10%), cingular cortex (average mean: left = 0.39%, right = 0.44%), somatosensory cortex (Sv, Sdl, Sdm, average mean: left = 1.03%, right = 0.91), and orbito‐frontal cortex (OFCvl, OFCv, OFCvm, average mean, left = 1.06%, right = 1.07%) except for label PFCvm. These areas also have the lowest intersubject variability with low average standard deviation: frontal lobe left = 0.18, right = 0.19; cingular cortex left = 0.12, right = 0.13; somatosensory cortex left = 0.14, right = 0.17; orbito‐frontal cortex left = 0.16, right = 0.20). Overall, the entire frontal lobe, the cingular cortex, and somatosensory cortex, show a more regular distribution of sizes between regions, and a better intersubject consistency, than the parietal, temporal, and occipital lobes. These results are very consistent across hemisphere, showing no particular hemispheric bias in our model.

Figure 6.

Volume of each MarsAtlas region relative to the total gray matter volume for the left and right hemispheres for the first dataset (11 subjects). For each region, the average relative volume across subjects is shown, with standard deviation.

The same analysis was also applied to the second dataset comprising anatomical MRI from 137 subjects. As shown on Supporting Information Figure S1 (to be compared with Fig. 6), the distributions of gray‐matter volume across individuals in each cortical region are very similar to those from the MEG dataset. The group‐level reproducibility and consistency of MarsAtlas parcellation is further confirmed by the high and significant correlation (r ² = 0.85, p < 1e‐5) between the two datasets of the average volume per region (Supporting Information Fig. S2).

Single‐Trial and Single‐Region High‐Gamma MEG Activity

Tomographic mapping was performed for HGA (60–120 Hz) by combining multitaper spectral analysis [Percival and Walden, 1993] and frequency‐domain beamforming algorithm [Gross et al., 2001]. Single‐trial and single‐region HGA was quantified as the log‐power values z‐transformed with respect to baseline activity and averaged across sources within the same cortical region. Figure 7 shows exemplar single‐trial HGA aligned on finger movement for the ventral, dorsolateral and dorsomedial motor areas of MarsAtlas (Fig. 7a–c) and for the primary motor cortex according to Brodmann atlas, BA4 (Fig. 7e). In this exemplar participant, HGA modulations >3 standard deviations (z‐score) are visible on a single‐trial basis. The lack of subdivision in the nondominant orientation in BA4 (i.e., the dominant orientation is given by the central sulcus; Fig. 7f) does not allow a functional dissociation between ventral and dorsal portions of motor areas. The cortical parcellation of MarsAtlas, however, includes subdivisions along the dorsoventral direction (Fig. 7d) and, thus can be exploited to map functional data.

Figure 7.

Single‐trial and single‐subject HGA. HGA for MarsAtlas regions shown in (d) for dorsomedial (a), dorsolateral (b), and ventral (c) motor cortex. HGA for BA 4L (e) depicted in (f).

To assess statistical significance at the group level, we used a LME approach. The results of the statistical analysis showed that such functional dissociation along the dorsoventral axis is also present at the group level. Figure 8a shows the time course of HGA for MarsAtlas motor regions and BA4, in the left hemisphere. The activity in the ventral motor cortex (Mv) is lower than in the dorsolateral and dorsomedial motor areas. Most importantly, the significance level of HGA modulations in Mdl and Mdm is comparable to the t‐values observed when the BA4 is analyzed (black curve in Fig. 8a). A similar effect and dissociation between ventral and dorsal portions is observed also in the premotor areas of MarsAtlas and BA6 (Fig. 8b). Overall, these results show that MarsAtlas provides a better functional segregation and localization without any loss of statistical power, in the motor, premotor cortex, and medial prefrontal areas.

Figure 8.

The time course of activation of group‐level t‐values for motor (a) and premotor (b) areas. Black lines correspond to the time course at BAs, whereas colored lines correspond to MarsAtlas regions from ventral to dorsomedial.

Visuomotor‐Related Functional Network

We then analyzed the whole set of cortical regions from MarsAtlas. A functional cortical network is here defined as a set of cortical regions whose HGA displays significant increases in visuomotor‐related HGA with respect to the baseline HGA (averaged from −0.5 to −0.1 s prior to stimulus onset). Figure 9 is a statistical map displaying the time‐course of t‐values for each cortical region grouped in lobes for both hemispheres. The performance of arbitrary visuomotor mappings was associated with a significant increase in HGA over a distributed cortical network covering most of the parietal and frontal areas. The largest increase in HGA was observed over the left parietal lobe, primarily over the dorsal (dorsal intraparietal IPCm and superior parietal cortices SPC) and medial (medial superior and medial parietal cortices) parietal regions, and dorsal somatosensory areas (Sdl and Sdm). The posterior cingulate cortex (PCC) was also found to display a significant increase in HGA. The ventral regions, such as (IPCv and Sv) displayed a smaller modulation in HGA in the left hemisphere and were not significant in the right hemisphere. Over the motor, premotor, and prefrontal cortices, the strongest activation was present over the dorsolateral and dorsomedial regions (PFcdl, PFcdm, PMdl, PMdm, Mdl, and Mdm). In addition, the MCC showed significant increase in activity bilaterally. The ventral and ventromedial prefrontal and orbitofrontal cortices did not display a strong increase in HGA, nor anterior temporal regions.

Figure 9.

Statistical map displaying the cortical regions in MarsAtlas associated with a significant increase in HGA (time‐point and cluster‐level threshold were set to q < 0.001 FDR‐corrected).

To compare the significance of the results between the MarsAtlas and Talairach approach, we computed the percentage of regions displaying a significant increase in HGA over time, where the level of significance at the level of time‐points was q < 0.001 (FDR‐corrected) and P < 0.001 at the level of temporal clusters. Figure 10 shows the percentage of significant areas over time and it shows larger effects for the MarsAtlas approach with respect to the Talairach‐based analysis.

Figure 10.

Percentage of significant time points at the group level over all BAs (bleu) and MarsAtlas cortical regions (green). The time‐point and cluster‐level threshold were set to q < 0.001 FDR‐corrected.

DISCUSSION

MarsAtlas Parcellation Atlas

The goal of this study was to put forward a brain atlas for functional mapping based on macroanatomical information. From the anatomical point of view, we presented a cortical parcellation model that can be defined both on the surface of the white matter and in the segmented volume of the cortical ribbon. This parcellation model is based on a model‐driven parameterization of the cortical surface, relying on long‐distance alignment and relative orientations of sulci, according to the HIP‐HOP model [Auzias et al., 2013]. A major advantage of the HIP‐HOP model is the ability to retrieve the two main trends of organization, rostrocaudal, and dorsoventral [Pandya and Yeterian, 1985; Régis et al., 2005; Sanides, 1969; Toro and Burnod, 2003] even where macroanatomical features show only one of these two directions. Indeed, current results show that such organization is suitable. For example, the cingular cortex is consistently divided in four regions with very little variations across subjects (Fig. 6), although it is defined between the callosal sulcus and the cingulate sulcus (rostrocaudal axis) and no local feature defines the orthogonal direction (dorsoventral). Similarly, even though the lateral frontal lobe shows a large dominance of the rostrocaudal directions, the MarsAtlas parcellation defines subdivision in the dorsoventral direction with little variations across subjects (Fig. 6). The pre‐ and postcentral gyri, for example, that are defined in the dorsoventral directions between the precentral sulcus, the central sulcus, and the postcentral sulcus, are subdivided with good reproducibility, without the help of local anatomical features. In particular, results show that within the precentral gyrus this subdivision is functionally relevant (Figs. 7 and 8).

Performances were assessed by comparing functional results using MarsAtlas with those based on the MNI‐Talairach atlas [from Brovelli et al., 2015]. However, the same comparison could have been performed with other parcellation models such as Desikan et al. [2006] or Cachia et al. [2003]. These parcellation models can be estimated at the single‐subject level, and their parcellation scheme follow primary gyri. Nevertheless, like the Brodmann parcellation in the MNI‐Talairach space, they do not subdivide these gyri because they have access only to the local dominant macroanatomical folding direction (and in particular the central and precentral sulci to define the precentral gyrus). Therefore, they offer similar level of anatomical subdivision and probably functional segregation than the Brodmann parcellation available in MNI‐Talairach. As previously mentioned, the main difference resides in the absence of secondary and orthogonal axes for a full characterization of both rostrocaudal and dorsoventral gradients. The comparison of MarsAtlas with the Brodmann parcellation is therefore a typical illustration of the difference between our parcellation scheme and those mentioned above.

The MarsAtlas parcellation scheme also presents spatially heterogeneous performances. The temporal lobe, for example, does not contain macroanatomical features, either local or long range, along the rostrocaudal direction (Fig. 1). In addition, Figure 2 also shows that our anatomical model has fewer landmarks in the longitude direction in regions posterior to the post‐central sulcus. These limitations are due to the anatomical model used in the HIP‐HOP parameterization process [Auzias et al., 2013], and reflect a lack of stable anatomical landmarks. The lack of stable landmarks in the temporal lobe has several causes. First, there are few folds in the dorsoventral orientation in this area. Secondly, the large variability of fold (in terms of patterns and location) makes their automatic identification complex. Indeed, the variability of the folding patterns around the junctions of the temporal, parietal, and occipital lobes is known to be high [Caspers et al., 2006; Shi et al., 2007; Van Essen and Dierker, 2007]. Results from the literature [Desikan et al., 2006; Fischl et al., 2004] similarly show low reproducibility across subjects within these cortical areas. Despite these limitations, our results show a very good reproducibility of the volume of cortical regions from MarsAtlas across two completely different datasets (Supporting Information Fig. S2).

Interestingly, the cortical model behind MarsAtlas and HIP‐HOP [Auzias et al., 2013] can be further improved by adding non‐sulcus features. In particular, the model presented in [Régis et al., 2005] hypothesizes that sulcal roots, the deepest point in sulci, are the anchors of the orthogonal system MarsAtlas is based on. Algorithmically, these points are known as sulcal pits. Recent work has been published to provide a robust extraction process and study their spatial organization [Auzias et al., 2015; Im et al., 2010; Lohmann et al., 2008]. Specific sulcal pits within some sulci could then be added to the model to constrain and stabilize the position of some axis. In addition to sulcal pits, annectant gyri, or pli‐de‐passage [Cunningham and Horsley, 1892], could be exploited to constrain the model. Annectant gyri are small gyri, often buried in the depth of sulci, and they subdivide sulci while defining a hidden continuity of gyri across the cortical surface [Régis et al., 2005]. The annectant gyri of the superior temporal sulcus, in particular, have been described [Ochiai et al., 2004] and could be used to subdivide the sulcus in a fixed number of parts. Future work will focus on their detection and inclusion in the model.

MarsAtlas‐Based HGA Functional Mapping

From the point of view functional mapping, the first advantage of MarsAtlas is intrinsic in the choice of the HIP‐HOP parametrization model, based on rostrocaudal and dorsoventral gradients, which allows the characterization of neural activity over both the dorsoventral and the rostrocaudal axes. Previous analysis of the same MEG dataset using a Brodmann atlas showed a significant increase in HGA over the sensorimotor and fronto‐parietal network [Brovelli et al., 2015]. The largest increase was observed over the left parietal lobe, both the dorsal (BA 5L and 7L) and lateral areas (BA 39L and 40L), and over sensorimotor (BA 1‐2‐3 and 4) and premotor regions (BA 6). However, information about a potential functional gradient along the dorsoventral axis in sensorimotor, motor and premotor areas was lacking. In the current study, the use of MarsAtlas allowed us to provide evidence of a functional dissociation along such direction and we showed that arbitrary visuomotor mapping primarily relies on the neural activity of the dorsal fronto‐parietal network, rather than the ventrolateral circuits (Fig. 9). These results confirm that gamma activity in human motor and premotor cortices is observed in behaviors requiring motor control [e.g., Cheyne et al., 2008; Crone et al., 1998; Muthukumaraswamy, 2010] and visuomotor coordination [Kennedy et al., 2011], and the known functional organization of motor cortex given the required motor responses (i.e., finger movements). In addition, it confirms the involvement of the dorsal fronto‐parietal network, rather than the ventral circuit, in the transformation of visual information into motor plans [Corbetta and Shulman, 2002; Culham and Valyear, 2006; Wise and Murray, 2000; Wise et al., 1996]. In medial prefrontal cortex, our previous study found the strongest activation in the ventral and dorsal portions of cingulate area (BA 24 and 32, respectively). However, the Brodmann atlas did not allowed us to understand whether such effect was strongest over mid‐ or anterior cingulate regions. Here, we provided evidence that the most significant activation arose from the MCC, rather that the ACC (Fig. 9).This region may correspond to the rostral cingulate zone (RCZ) within the medial frontal areas, which has been described as a crucial node of the human motor system most probably corresponding to the cingulate motor area described in nonhuman primates [Amiez and Petrides, 2014; Picard and Strick, 1996]. We suggest that the increase in HGA in the MCC corresponds to the activation of visuomotor‐related neural populations of the RCZ, and provides support to the notion that portions of the medial prefrontal cortex are required for arbitrary visuomotor mappings [Murray et al., 2000]. Finally, our results confirm significant increase in the left caudal dorsolateral and dorsomedial prefrontal cortex (PFcdl and PFcdm), similar to activations found in BA9 [Brovelli et al., 2015].

Overall, our results suggest that the combination of HGA‐based source imaging approaches and the MarsAtlas parcellation scheme provides crucial information about the spatio‐temporal distribution of cognitive networks. The presence of a dorsoventral gradient allows testing hypotheses, such as those concerning dorsomedial and ventrolateral dissociations in fronto‐parietal networks and their role in visuomotor behaviors [Davare et al., 2011; Fattori et al., 2009]. Furthermore, the rostrocaudal gradient may be crucial for functional mapping of executive functions in the frontal lobe, which is known to display a hierarchical functional organization along the rostrocaudal gradient [Badre and D'Esposito, 2008; Koechlin et al., 2003].

Future Directions

In this study, we focused on HGA, because it represents a proxy of local cortical processing. In particular, HGA can be used for functional mapping of cognitive processes using intracranial EGG [Brovelli et al., 2005; Cheyne and Ferrari, 2013; Crone et al., 2006; Jerbi et al., 2009; Ko et al., 2013; Lachaux et al., 2012], noninvasive [Ball et al., 2008; Darvas et al., 2010; Vidal et al., 2006] and multimodal neurophysiological [Dalal et al., 2009] techniques. In addition, modulations in HGA correlates with BOLD responses in animals [Goense and Logothetis, 2008; Logothetis et al., 2001; Niessing et al., 2005] and humans [Hermes et al., 2012; Lachaux et al., 2007; Nir et al., 2007; Ojemann et al., 2013; Scheeringa et al., 2011]. Therefore, we suggest that the use of HGA in combination with the MarsAtlas could provide an appropriate framework for combining information from multiple functional modalities such as MEG, SEEG and fMRI. Finally, our parcellation scheme may be exploited for anatomical connectivity analysis based on diffusion imaging data [see for example, Hagmann et al., 2008] and provide single‐subject connectivity matrices for the analysis and modeling of FC using fMRI [e.g., Achard and Bullmore 2007].

The study of FC between cortical areas based on single‐trial estimates of HGA has been shown in previous work using Talairach atlas [Brovelli et al., 2015]. Generalization to MarsAtlas is straightforward. FC measures between cortico‐cortical power modulations may reveal connectivity patterns that are complementary (or similar) to those observed using phase‐coherence as a candidate mechanisms for the creation of communication links between brain regions (e.g., the “communication‐through‐coherence” hypothesis) [Fries, 2005]. Finally, given recent evidence of FC patterns undergoing temporal dynamics [Bassett et al., 2011; Hansen et al., 2015; Zalesky et al., 2014], our study provides novel perspectives towards the study of functional connectivity dynamics (FCD) among brain regions and to identify spatio‐temporal patterns associated with behavioral and cognitive processes.

CONCLUSIONS

We presented a cortical parcellation model based on macro‐anatomical information obtained from MRI, called MarsAtlas. We tested its validity in functional mapping using a canonical instance of visuomotor behaviors known as arbitrary visuomotor mapping. We confirmed that visuomotor associations involve an increase in HGA over the sensorimotor and fronto‐parietal network, in addition to medial prefrontal areas. In addition, we showed that MarsAtlas provided crucial functional information along both the dorsolateral and rostrocaudal direction and an increase in statistical significance with respect to a Talairach‐based cortical parcellation, indicating a better functional segregation. We moreover assessed the generalizability of the MarsAtlas parcellation using a second dataset of 137 subjects. Overall, our results suggest that the MarsAtlas represents a good tradeoff between spatial resolution and functionally relevant parcellation, and represents a potential anatomical framework for integration of multimodal functional data. MarsAtlas and the HIPHOP parcellations schemes without the merging of regions (61 regions per hemisphere) will be freely available in the next release of the BrainVisa software (version 4.5, http://brainvisa.info).

Supporting information

Supporting Information

Supporting Information

Supporting Information