A Comparison of the neural correlates that underlie rule‐based and information‐integration category learning

Abstract

The influential competition between verbal and implicit systems (COVIS) model proposes that category learning is driven by two competing neural systems—an explicit, verbal, system, and a procedural‐based, implicit, system. In the current fMRI study, participants learned either a conjunctive, rule‐based (RB), category structure that is believed to engage the explicit system, or an information‐integration category structure that is thought to preferentially recruit the implicit system. The RB and information‐integration category structures were matched for participant error rate, the number of relevant stimulus dimensions, and category separation. Under these conditions, considerable overlap in brain activation, including the prefrontal cortex, basal ganglia, and the hippocampus, was found between the RB and information‐integration category structures. Contrary to the predictions of COVIS, the medial temporal lobes and in particular the hippocampus, key regions for explicit memory, were found to be more active in the information‐integration condition than in the RB condition. No regions were more activated in RB than information‐integration category learning. The implications of these results for theories of category learning are discussed. Hum Brain Mapp 37:3557–3574, 2016. © 2016 Wiley Periodicals, Inc.

INTRODUCTION

Category learning is an essential cognitive process necessary for daily functioning. Without the ability to categorize an object as a threat, for instance, our survival chances would be severely impeded. But how do we learn novel categories? For example, how does a student driver learn to categorize the symbols on the road? Poldrack and Foerde [2008] regard the concept of multiple memory systems as one of the most important contributions to neuroscience in the past quarter century, and one increasingly prominent line of research within this broader field is the idea that there are multiple systems of category learning [Ashby and Maddox, 2011]. Perhaps the most influential multiple systems account is the dual‐process, neurobiologically inspired, competition between verbal and implicit systems (COVIS) model of category learning [Ashby et al., 1998] which is the focus of the current study.

COVIS hypothesizes that there are two neurally and functionally dissociable category learning systems [Ashby et al., 1998]. The explicit system requires considerable use of working memory and executive functioning to test the effectiveness of rules that are generated. This learning system, consequently, works best at learning rule‐based (RB) category structures where the decision boundary separating the categories can be easily verbalized. The most common examples in the literature are unidimensional rules such as “short lines belong in Category A; long lines belong in Category B” (see Fig. 1a), or conjunctive rules such as “short, upright, lines belong in Category A; anything else belongs in Category B” (see Fig. 1b). Conversely, in the implicit, procedural‐based, system, learning occurs by combining information from two or more unrelated stimulus dimensions predecisionally through reliance on immediate feedback to create stimulus‐response associations [Ashby et al., 1998]. The implicit system is usually tested using information‐integration (II) categories (see Fig. 1c) where the optimal decision boundary is typically considered difficult or impossible to verbalize.

Figure 1.

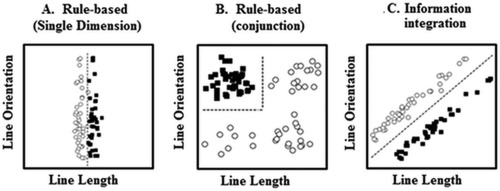
Examples of unidimensional, conjunction, and information‐integration category structures. Each open circle represents one member of Category A; each filled square represents one member of Category B. Figure adapted from Wills et al. [2013] and Zeithamova and Maddox [2006].

One notable aspect of COVIS that distinguishes it from other multiple system accounts of category learning (e.g., ATRIUM) [Erickson and Kruschke, 1998] (RULEX) [Nosofsky et al., 1994] is the detailed neurobiological predictions that it makes regarding the brain regions that underlie the different learning systems. In the explicit system, rule generation and hypothesis testing requires working memory and executive functioning which takes place predominately in the prefrontal cortex [Ashby and Valentin, 2005]. The particular rule to use is selected via the anterior cingulate [Maddox and Ashby, 2004], while the head of the caudate nucleus is responsible for mediating the switch to a different rule. Successful rules are stored in the medial temporal lobes (MTL) for future use [Ashby and Valentin, 2005]. The MTL is also hypothesized to store representations of the decision boundaries used to separate the stimuli into categories [Nomura and Reber, 2008].

In contrast, the implicit system procedurally acquires the stimulus‐response associations necessary for learning II categories [Ashby et al., 1998]. The body and tail of the caudate nucleus receive representations of the visual stimulus perceived [Ashby and Valentin, 2005] and these cells project to the supplementary motor area via the globus pallidus and the thalamus [Maddox and Ashby, 2004]. When feedback indicates a correct response has been made, the substantia nigra releases dopamine which strengthens the association of the stimulus to the correct response [Ashby and Valentin, 2005]. The putamen has also recently been proposed by Waldschmidt and Ashby [2011] to play a key role in the implicit system, as it is assumed to provide information to the motor regions [but see Ell et al., 2011] (who found that focal putamen lesions impaired RB but not II learning).

These neurobiological underpinnings of COVIS have motivated a large number of predictions about how RB and II learning will be differentially affected by behavioral manipulations [for reviews see Ashby and Maddox, 2011; Maddox and Ashby, 2004]. The numerous behavioral dissociations arising out of this work have contributed a great deal to the influence of COVIS. For example, RB learning is impaired by the imposition of a concurrent working memory load while II learning is not, supporting the idea that working memory is more critical for RB than II learning [Waldron and Ashby, 2001; Zeithamova and Maddox, 2006]. Similarly, II learning is disrupted by changing the appropriate response buttons while RB learning is not, in line with the prediction that II learning relies on stimulus‐response procedural associations [Ashby et al., 2003]. Furthermore, delaying feedback for a few seconds [Maddox and Ing, 2005; Maddox et al., 2003], deferring feedback to the end of a block of six trials [Smith et al., 2014], providing the category label prior to making the response [Ashby et al., 2002], and using stimuli which contain both auditory and visual information [Maddox et al., 2006] have all been claimed to impair II but not RB learning. Similarly, some studies have suggested that increasing the number of categories [Maddox et al., 2004c] or reducing the time available to process the feedback [Maddox et al., 2004a] disrupts RB but not II learning.

However, in recent years there have been a growing number of studies that cast doubt on COVIS's interpretation of these behavioral dissociations and posit that the results can be explained by a single, explicit, system [e.g., Newell et al., 2010, 2011, 2013; Nosofsky and Kruschke, 2002; Stanton and Nosofsky, 2007, 2013]. One such example is a study conducted by Lewandowsky et al. [2012] who reconsidered the finding noted above that RB learning relies on working memory to a greater extent than II learning. Specifically, Lewandowsky et al. directly measured the working memory capacity of participants using a battery of both verbal and spatial tasks and used structural equation modeling to reveal a strong relationship between working memory capacity and both RB and II learning, consistent with their proposal that both tasks require the use of working memory. The behavioral evidence as it currently stands, therefore, provides equivocal support for COVIS. An alternative approach to resolving this dispute is to focus directly on the neurobiological predictions of COVIS where it has been argued that single‐system accounts cannot explain the evidence that separable neural systems are engaged during different types of category learning [Worthy et al., 2013].

This neurobiological evidence is currently surprisingly limited, however, as there has been a paucity of studies directly comparing the brain systems involved in RB and II category learning. Perhaps the most prominent study to examine this, although, was by Nomura et al. [2007]. Participants completed either an RB or an II category learning task inside an MRI scanner. The RB category structure was an easy to verbalize unidimensional rule (e.g., Fig. 1a), while the II structure was based on that shown in Figure 1c. Nomura et al. considered their results to be in line with COVIS—dissociable neural activation was found, with the MTL more activated in RB compared with II learning, and the caudate body more activated in II than RB learning. Further evidence of separable systems was found in a reanalysis of Nomura et al.'s data which modeled participants' decision strategies [Nomura and Reber, 2008]. Participants using RB learning strategies showed greater right PFC activity than those using II strategies, and those utilizing II strategies had greater right occipital activation.

More recently, Soto et al. [2013; see also Helie et al., 2010; Waldschmidt and Ashby, 2011] directly contrasted RB and II learning in a multivoxel pattern analysis. While the study had multiple training sessions, the first scanning session (Training Session 1 for the RB task and Training Session 2, following 600 training trials in Session 1, for the II task), prior to the development of automaticity, is most pertinent for the current issue. While there was common activation between RB and II learning (e.g., in the globus pallidus and the extrastriate visual cortex), there were some differences in activation. For instance, consistent with Nomura et al. [2007], the head of the caudate was activated more in RB learning, while activation in the caudate body/tail also differed between the RB and II tasks. However, it is difficult to know whether these neural differences were due to the engagement of separate systems in RB and II learning or whether they are due to participants in the II condition having already received 600 training trials previous to the scanning session while participants in the RB condition had no prior training (brain activation alters over a relatively limited number of trials) [e.g., Koenig et al., 2005; Milton and Pothos, 2011]. While this issue was not the sole focus of Soto et al.'s study it does, nevertheless, compromise any direct comparisons in brain activation between II and RB learning prior to automaticity developing.

Milton and Pothos [2011] found a different pattern of results to Nomura et al. [2007], observing extensive overlap in activation between a Unidimensional RB structure and a complex category structure assumed to have many of the properties of II categories (e.g., optimal decision bounds that were difficult to verbalize). In contrast to Nomura et al., neural differences between the II and RB conditions were minimal and restricted to greater activation in a small region of the left superior frontal lobe in the complex condition relative to the RB condition. While intriguing, one should not draw too strong an inference about these findings with regard to COVIS due to the differences in the stimuli that Milton and Pothos used compared to those traditionally administered in COVIS research. For instance, there were only 18 unique stimuli, with dimensions that were commensurable (rectangle height and ellipse width) and a decision bound that was arguably easier to verbalize than the II structures typically employed (e.g., Fig. 1c). Nevertheless, these findings indicate that further direct comparison of the neural correlates of RB and II category learning is needed.

The aim of the present study, therefore, is to re‐examine Nomura et al.'s [2007] conclusion that there is a differential pattern of brain activation for RB and II categories in line with the predictions of COVIS. The critical difference between the RB and II category structures is often assumed to be that the RB structure is easily verbalizable but the II structure is not. While the RB and II category structures used by Nomura et al. (see Fig. 1a,c) differ convincingly in this factor, there are also nonessential differences between them that may potentially be driving the differences in activation. For instance, the RB structure has only one relevant dimension while the II structure has two relevant dimensions which means that selective attention is required for the RB condition but not for the II condition [Nosofsky and Kruschke, 2002]. This is a concern that has been acknowledged by some COVIS theorists [e.g., Nomura and Reber, 2008; Xie et al., 2015; Zeithamova and Maddox, 2006]. On a different note, multidimensional categorizations are typically more complex and require greater cognitive resources than one‐dimensional categorizations [e.g., Milton et al., 2008; Wills et al., 2015]. This could potentially be driving the more pronounced caudate body activation in the II than the RB condition, particularly given that the involvement of the basal ganglia is thought to be greater for more complex structures [e.g., Ell et al., 2010; Filoteo et al., 2005a, 2005b]. As the II structure is often more difficult to learn than the RB structure [e.g., Ashby et al., 2002, Maddox et al., 2003], Nomura et al. reduced the category separation (i.e., the mean distance between category items as plotted in stimulus space divided by the within‐category variance along the direction of the comparison) in the RB condition relative to the II condition to minimize any performance differences between conditions [see also Lewandowsky et al., 2012 for a discussion of this issue]. While this successfully matched learning rates, it effectively replaces one confound with another because the optimal decision bound is more difficult to perceptually discriminate in the RB than the II condition [Stanton and Nosofsky, 2007]. This confound is potentially critical given that COVIS assumes that the MTL is responsible for storing the precise placement of the decision bound [Nomura and Reber, 2008]. The greater activation in the MTL for the RB condition compared to the II condition could, therefore, be due to this difference in category separation.

To draw strong comparisons about brain activation in RB and II category learning, it is therefore necessary to control for these nonessential differences between the category structures. This has been achieved in previous COVIS related research [e.g., Filoteo et al., 2010; Zeithamova and Maddox, 2006]—but in no previous imaging study—by comparing the II category structure to a conjunctive, RB category structure (see Fig. 1b). The II and the conjunctive category structures both possess two relevant dimensions, have a similar error rate [Filoteo et al., 2010] and are closely matched for category separation.

A study by Edmunds et al. [2015] underscores the importance of controlling for these extraneous variables when comparing RB and II category learning. Edmunds et al. re‐examined Ashby et al.'s [2002] finding that trial‐by‐trial feedback training leads to better categorization performance than observational training for an II structure but not for a unidimensional RB structure. Edmunds et al. argued that Ashby et al.'s dissociation could have been driven by one of the nonessential differences between these category structures highlighted above. In particular, Edmunds et al. posited that the increased difficulty of learning a multidimensional (II) classification compared to a unidimensional classification could have been causing the effect—feedback training may be of greater benefit than observational training more generally but this advantage increases as the problem difficulty rises. To investigate this, Edmunds et al. compared learning of conjunctive and II category structures under both observational and feedback training. Edmunds et al. confirmed that participants are better able to verbalize the conjunctive, RB, structure than the II structure. However, the dissociation predicted by COVIS failed to emerge. Instead, feedback learning was superior to observational learning for both category structures.

The importance of controlling important extraneous variables has also been highlighted in a recent fMRI study conducted by Nosofsky et al. [2012] who reconsidered the classic finding of Reber et al. [1998] that old‐new recognition of dot patterns evokes a different pattern of brain activation to categorization of dot patterns. Nosofsky et al. used the same stimuli across conditions (whereas in Reber et al. the stimuli differed) and more closely equated the task goals of recognition and categorization (normally recognition requires an exact match with the studied item while stimuli can be endorsed as a category member if they are merely similar to previous exemplars) by asking them to adopt a lax criterion for the recognition judgment—participants were told it was important not to miss any old items. Under these conditions, there was little evidence for dissociable systems and the results from both tasks could be accommodated by a single exemplar‐based process.

Another notable aspect of Nomura et al.'s [2007] study is their use of incorrect trials as the baseline comparison to correct responses. While this is a convenient baseline to use and has been employed in other categorization research [e.g., Milton and Pothos, 2011] it may not be the most effective due to difficulties in interpreting what is driving the incorrect response. First, participants may have been using the correct general strategy but had not identified the relevant dimension/precise category structure; for example, participants used a RB strategy but categorized by orientation rather than line length. Second, participants might have used the appropriate dimension but placed the decision bound in the incorrect place. Third, and less commonly, participants may have classified correctly but pressed the wrong button. Fourth, participants may have been guessing or not fully engaged on the trial and fifth, participants could have used a completely different strategy to what was appropriate. It is likely that the errors are a combination of these (and potentially other) mistakes but it is not possible at the individual trial level to determine the source of the error. The first three of these error types appear particularly problematic as they would result in similar activation to correct trials meaning that this is unlikely to be a sensitive baseline. Furthermore, comparing correct and incorrect trials is likely to be confounded with degree of learning as there will be more incorrect trials early in training than later in training. This is particularly an issue when wishing to make inferences across the whole of training as is typically the case. While we present the key analyses with this “incorrect” baseline to aid comparison of our results with Nomura et al.'s, an “odd‐or‐even” task will be our principal baseline. This type of control is increasingly being used in imaging studies of categorization [e.g., Davis et al., 2012a, 2012b, 2014] and while it may superficially seem similar to a RB task (albeit one that is highly automated and engages limited neural resources) [Stark and Squire, 2001] its main advantage is that it is well‐established that it does not recruit the MTL or indeed the frontal lobes [Stark and Squire, 2001], the pivotal regions of COVIS's RB system. Equally, activation in the striatum, the key site of COVIS's implicit system, is also readily identified with an odd‐or‐even baseline task [Zink et al., 2006]. This baseline should, therefore, provide a clear measure of the regions engaged in both RB and II categorization without the involvement of key regions being obscured by their activation in the baseline task as well.

According to how COVIS is often conceptualized [e.g., Nomura et al., 2007], one might predict greater activation in the caudate head, the anterior cingulate, prefrontal cortex, and the MTL (and in particular the hippocampus) for learning a conjunctive RB structure compared to learning an II structure [Ashby and Valentin, 2005]. In contrast, greater activation should be found in the body/tail of the caudate, the putamen and the substantia nigra for the II condition compared to the RB condition [Ashby and Valentin, 2005]. Conversely, if Nomura et al.'s [2007] results were driven by one of the nonessential differences between the RB and II structures outlined above then, when these variables have been better controlled, one might expect that these neural differences would disappear leaving an extensive overlap of activation. Further, given that the II structure is harder to verbalize than the RB structure and yet categorization accuracy is the same [Filoteo et al., 2010], greater activation might be expected in the prefrontal cortex for the II compared to the RB condition to reflect the greater processing demands of finding and applying a less easy to verbalize rule. Alternatively, or perhaps additionally, there may be greater activation in the MTL in the II condition than the RB condition if the lower levels of verbalizability lead to an increase in memory demands to store exceptions in decision space to the rule that is utilized [Davis et al., 2012a].

METHOD

Participants and Design

Forty five‐right‐handed University of Exeter students (26 female, 19 male) with normal or corrected vision completed the experiment for £5 remuneration. Participants were randomly allocated to one of two between‐subject conditions (RB and II). One participant from the RB condition was excluded for failing to reach 50% (chance) accuracy in the final run (although the inclusion of this participant does not alter any of the conclusions of this study), leaving 22 participants in each condition. Participants gave informed consent according to procedures approved by the University of Exeter's School of Psychology Ethics Committee.

Stimuli

The stimuli (see Fig. 2) were a subset of the two‐dimensional II stimuli and conjunctive stimuli (where short, upright lines belong in Category A, and the rest in Category B) employed by Filoteo et al. [2010]. In the original dataset there were 600 stimuli in both conditions; in the present imaging study, 320 of these stimuli were randomly selected (160 stimuli in each category) for each category structure. This number of stimuli was the same as used by Nomura et al. [2007]. Each stimulus was a black line varying on two dimensions: length and orientation. As in Filoteo et al. [2010], there was 5% overlap between the categories so that the maximum accuracy attainable was 95%.

Figure 2.

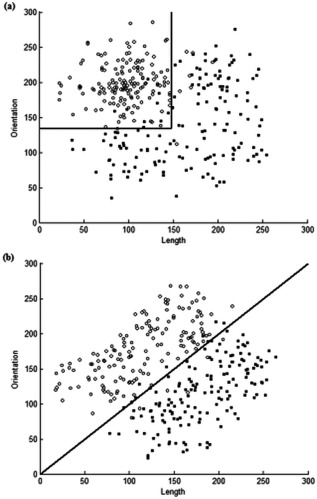
The category structures used for the present study (a) The conjunctive RB condition; (b) The II condition. Solid lines indicate the decision boundary separating Category A (unfilled circles) and Category B (filled squares).

fMRI Imaging

A 1.5‐T Phillips Gyroscan magnet, equipped with a Sense coil, was used to collect images from each participant in one scanning Session. A T2*‐weighted echo planar sequence (TR = 3,000 ms, TE = 45 ms, flip angle = 90°, 36 transverse slices, 3.5 × 2.5 × 2.5 mm) was used. On entering the scanner, the participant's head was secured in place with foam pillows inside the coil to prevent excessive head movement. Participants completed four runs, each containing 205 scans. Five “dummy scans” were completed before every run prior to presentation of the first trial. After the functional scans, standard volumetric anatomical MRI was completed using a 3‐D T1‐weighted pulse sequence (TR = 25 ms, TE = 4.1 ms, flip angle = 30°, 160 axial slices, 1.6 × 0.9 × 0.9 mm).

Procedure

In each scanning run, participants performed two interleaved tasks—the category learning task and an “odd‐or‐even” baseline task. Each run began with 15 odd‐or‐even trials, followed by two blocks of 40 categorization trials. Each run then concluded with another block of 15 odd‐or‐even trials. After each block there was a blank screen of 8,000 ms during which time participants were asked to rest. In total, there were 320 category learning trials, presented in a random order, and 120 odd‐or‐even trials. The stimuli were presented on a back‐projection screen positioned at the foot end of the MRI scanner and viewed via a mirror mounted on a head coil. Responses were measured using a fiber‐optic button box held in the participants' left and right hands. E‐Prime [Psychological Software Tools, 2002] was used for the presentation and timing of stimuli and collection of response data.

In the category learning task, participants were informed that they had to learn into which of two categories a series of stimuli belonged. The trial‐by‐trial procedure for the RB and II conditions was identical. Each trial began with a blank screen lasting a variable interval between 500 ms and 4,000 ms, followed immediately by a black fixation cross presented in the center of the screen for 250 ms. A stimulus then appeared in the middle of the screen for 2,000 ms during which time participants were required to respond by pressing the far right button on the button box with their right hand if they thought the item belonged to Category A or the far left button with their left hand if they thought the item was a member of Category B. Feedback (“correct” or “incorrect”) was then displayed for 500 ms. If participants did not respond in time the message “Time out!!!” appeared on the screen for 500 ms instead. The next trial then immediately began.

The odd‐or‐even task was closely modeled on that used by Stark and Squire [2001; see also Davis et al., 2012a] and had a similar trial‐by‐trial structure to the category learning task. Each trial began with a blank screen lasting between 500 ms and 4,000 ms, followed by a black fixation cross for 250 ms. A randomly generated number from one to nine then appeared in the middle of the screen for 2,000 ms during which time participants had to press the left‐most button if the number was even or the right‐most button if it was odd. Following this, feedback (“correct” or “incorrect”) was presented for 500 ms or if participants did not respond in time a message saying “Time out!!” appeared during this interval.

fMRI Data Analysis

Data analysis was performed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm). Functional images were corrected for acquisition order, realigned to the mean image, and resliced to correct for motion artifacts. The realigned images were coregistered with the structural T1 volume and the structural volumes were spatially normalized. The spatial transformation was applied to the T2* volumes which were spatially smoothed using a Gaussian Kernel of 8 mm full‐width half maximum. Data were high‐pass filtered (128 s) to account for low frequency drifts.

Random effects whole‐brain analyses were completed using the general linear model with a combined statistical threshold of P < 0.001 (uncorrected) and a voxel threshold of 27 contiguous voxels, which together produce an overall corrected threshold of P < 0.05, according to AlphaSim, as implemented in the REST toolbox (Version 1.8) [Song et al., 2011]. Correct trials, incorrect trials, and timeouts were all included as separate regressors in the model. A canonical hemodynamic response function (HRF) together with temporal and dispersion derivatives was used to model the blood oxygen level‐dependent response and the six head movement parameters were included as covariates. Our analyses focused on comparing correct categorization trials (for the RB and II groups separately) to the odd‐or‐even baseline task (although for the principal analyses we also compare correct categorization trials to incorrect trials). In addition, to measure common activation between the RB—baseline contrast and the II—baseline contrast, a conjunction analysis was performed. The contrasts were combined using a logical “and” function through the minimum statistic to the conjunction null hypothesis (MS/CN) [Nichols et al., 2005] technique implemented in SPM8. Both these contrasts were again conducted with a combined threshold of P < 0.001 (uncorrected) and a cluster threshold of 27; note that this approach is highly conservative because it reveals only those regions significantly activated for both the RB (P < 0.05, corrected) and the II (P < 0.05, corrected) conditions. Normalized MNI space coordinates were transformed to Talairach space (http://imaging.mrccbu.cam.ac.uk/imaging/MniTalairach) to establish activation sites as per the atlas of Talairach and Tournoux [1988].

RESULTS

Behavioral Analysis

The mean categorization accuracy across all runs for both the RB and II conditions is displayed in Figure 3. A 4 × 2 mixed‐design analysis of variance (ANOVA) was conducted; the within‐subjects factor was Run (4 levels) and the between‐subjects factor was Categorization task (RB/II). There was a highly significant effect of Run, F(3,126)=12.47, P < 0.001, = 0.229, indicating that performance improved with practice. There was, however, no significant difference between the II and RB conditions in accuracy F(1,42) = 0.14, P = 0.708, = 0.003, BF = 1.04, and no significant interaction between run and categorization task (II or RB), F(3,126) = 1.71, P = 0.169, .= 0.039, BF = 2.00.1

Figure 3.

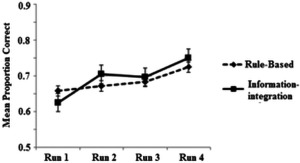
Mean performance across runs in the RB and II conditions. Error bars show standard error.

Imaging Analysis—“Odd or Even?” Baseline Measure

All blocks analysis

Whole‐brain activation across all runs of the category learning task was first analysed for participants in the RB and II conditions separately. Correct RB categorizations led to an extensive pattern of activation (Fig. 4a) including diverse areas of the frontal cortex (including BA's 6, 8, 10, 45, 46, 47), the anterior cingulate, posterior cingulate, the MTL, the bilateral caudate head/body, the putamen, the bilateral inferior and superior parietal lobes, the right superior temporal gyrus, bilateral inferior temporal gyrus, and the bilateral occipital lobes. II category learning also activated these same brain regions (Fig. 4b).

Figure 4.

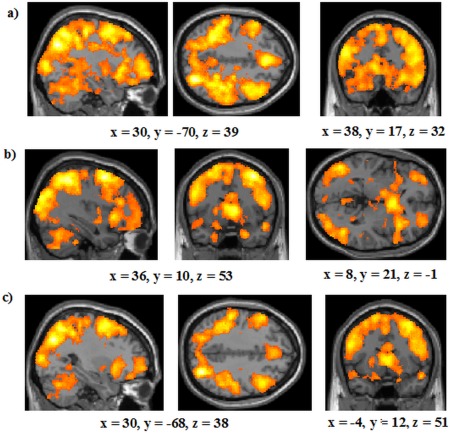
Whole brain analyses on all runs of the study for: (a) areas of activation in the RB condition; (b) areas of activation in the II condition; (c) a conjunction analysis showing areas commonly activated in the RB and II conditions. All analyses are thresholded at P < 0.001 and 27 contiguous voxels. The coordinates indicate the origin for the image displayed. Lighter colors indicate higher z‐scores. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

We also examined whether there were any changes in activation across time for both RB and II learning. To assess this, we directly compared activation in the first half of the experiment (Runs 1 and 2) to in the second half (Runs 3 and 4) for the RB and II conditions separately. No brain regions were more activated in the first half of training compared with the second half of training in either condition. No brain areas were activated more in the second half of training than the first half in the RB condition either. However, in the II condition several regions including the right parahippocampal gyrus (BA 30; see Table 1) were activated more in Runs 3 and 4 than in Runs 1 and 2.

Table 1.

Brain regions activated more in the last runs of the study (Runs 3 and 4) than the first runs of the study (Runs 1 and 2) in the II condition

			Talairach coordinates
Region	Cluster size	BA	x	y	z	z‐score
Right Precentral Gyrus	30	4	26	−25	53	3.84
Right Posterior Parahippocampal Gyrus	36	30	16	−43	4	3.80
Right Thalamus	52	—	18	−21	−1	3.78
Right Substantia Nigra		—	16	−18	−8	3.71
Left Paracentral Lobule	36	3	−18	−38	55	3.56
Left Postcentral Gyrus		5	−20	−41	65	3.48

Note that indented rows indicate voxels in the same cluster as the nonindented row above.

The striking overlap in activation between the tasks was confirmed in a conjunction analysis, looking at common activation across the correct RB—odd‐or‐even contrast and the correct II—odd‐or‐even contrast (both with thresholds of P < 0.001 and 27 contiguous voxels; Fig. 4c). Areas activated included key regions of both COVIS's explicit and implicit systems. Regions linked to the explicit system that were recruited were the MTL, the bilateral caudate head, diverse bilateral areas of the prefrontal cortex (including BA's 6, 8, 10, 46, and 47) and the bilateral anterior cingulate (right BA 25, left BA 33). Areas implicated in the implicit system that were engaged included the bilateral caudate body and the bilateral putamen. When contrasting incorrect trials to the odd‐or‐even task, a similar, if somewhat less extensive, pattern of activation was found including the right caudate body, right putamen, and bilateral caudate head (Supporting Information Fig. 1).

Next, we directly contrasted activation in the RB and II conditions to examine whether there was evidence for the neural dissociations observed by Nomura et al. [2007]. No regions were more active in the RB condition than the II condition (calculated by subtracting correct RB trials—the odd‐or‐even trials from correct II trials—the odd‐or‐even trials). However, diverse regions were more active in the II condition than the RB condition (calculated by subtracting correct II trials—the odd‐or‐even trials from correct RB trials—the odd‐or‐even trials; see Table 2, Fig. 5a). Critically, this included extensive activation in the left MTL (hippocampus/posterior parahippocampal gyrus; 131 voxels; see Fig. 5b for areas of the MTL engaged, with non‐MTL regions masked). The results of these analyses are contrary to the predictions of COVIS, where the MTL is thought to be more critical for RB rather than II learning [e.g., Ashby and Valentin, 2005; Nomura et al., 2007].

Table 2.

Brain regions activated more in the II condition than the RB condition in all runs

			Talairach coordinates
Region	Cluster size	BA	x	y	z	z‐score
Left Hippocampus	212	—	−22	−39	−1	4.02
Left Parahippocampal Gyrus		36	−26	−39	−5	3.78
Left Posterior Cingulate		29	−14	−46	10	3.30
Left Superior Temporal Gyrus	41	21	−52	−6	−11	3.61
Left Precuneus	80	31	−18	−47	32	3.91
Left Cingulate Gyrus		31	−16	−43	34	3.70
Left Thalamus	56	—	−14	−28	16	3.57

Note that indented rows indicate voxels in the same cluster as the nonindented row above.

Figure 5.

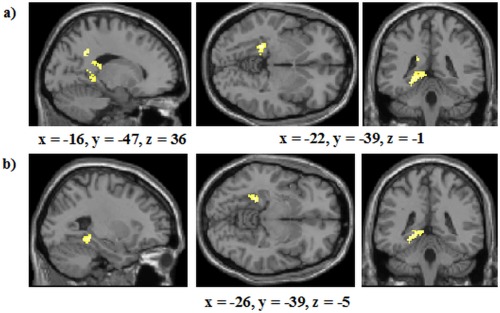
Analyses of areas activated in all runs of the study (a) Whole‐brain analysis of areas more active in the II condition compared with the RB condition; (b) Regions of the MTL more active in the II condition compared with the RB condition; non‐MTL regions were masked in this analysis but the thresholds remained P < 0.001 and 27 contiguous voxels. The coordinates indicate the origin for the image displayed. Lighter colors indicate higher z‐scores. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

However, in spite of the generally greater activation in the II condition than the RB condition, no regions associated with COVIS's implicit system were identified in this analysis. Of course, it is possible that, even though we had almost double the number of participants that Nomura et al. [2007] used (they had 13 in their II condition and 12 in their RB condition), this activation might have been present but below our a priori statistical thresholds. To provide greater sensitivity we, therefore, conducted a region of interest (ROI) analysis using the WFU Pickatlas [Maldjian et al., 2003] comprising the caudate body, the putamen, and the substantia nigra with the more liberal thresholds of P < 0.005 and 10 contiguous voxels (the same thresholds we have used in previous ROI analyses we have conducted) [c.f., Milton et al., 2011, 2012]. We again found no evidence for greater activation in the II condition than the RB condition in these regions. To further confirm this conclusion we examined the relative percent signal change of correct RB and II responding in the caudate body based on the peak right (x = 17, y = −11, z = 28) and left (x = −20, y = −14, z = 29) caudate body activations reported by Nomura et al. [2007]. These percent signal change values were obtained using the Anatomy toolbox [Eickhoff et al., 2007] (Version 2.2). Using independent samples t‐tests, we found no difference between conditions for either the right caudate body, t(42)=1.05, P = 0.300, d= 0.32, BF = 0.84, or for the left caudate body, t(42)=1.00, P = 0.323, d = 0.3, BF = 0.91.2

Analysis of Runs 3 and 4 only

COVIS can potentially explain this pattern of findings by assuming that for the II condition as well as the RB condition the verbal system dominates initially and participants in the II group only switch to the implicit system once there has been sufficient time for the RB system to be proven ineffective [e.g., Filoteo et al., 2010]. Including the initial trials in the analysis could therefore be obscuring the neural differences that emerge later in learning. To investigate this possibility, we analyzed Runs 3 and 4 alone which, according to the results of previous studies [e.g., Filoteo et al., 2010], should provide a sufficient number of trials for participants to switch to the implicit system in the II condition.

A conjunction analysis, using the same thresholds as before, again revealed extensive activation overlap between the RB and II conditions. This included the bilateral putamen, the bilateral caudate body as well as the bilateral caudate head, the prefrontal cortex and the right MTL (Supporting Information Fig. 2). No regions were again more activated in the RB condition than the II condition. However, as before, a number of regions were more activated in the II condition than the RB condition (Supporting Information Table I; Fig. 6a); most prominent amongst these was activation in the bilateral hippocampus/posterior parahippocampal gyrus (left: 207 voxels; right: 44 voxels, Fig. 6b). However, as before, in spite of this generally elevated activation in the II condition compared to the RB condition, there was no evidence for activation of regions linked to COVIS's implicit system. We again conducted a follow‐up ROI analysis comprising the caudate body, the putamen, and the substantia nigra with a threshold of P < 0.005 and a voxel threshold of 10 but no regions were activated in this analysis.

Figure 6.

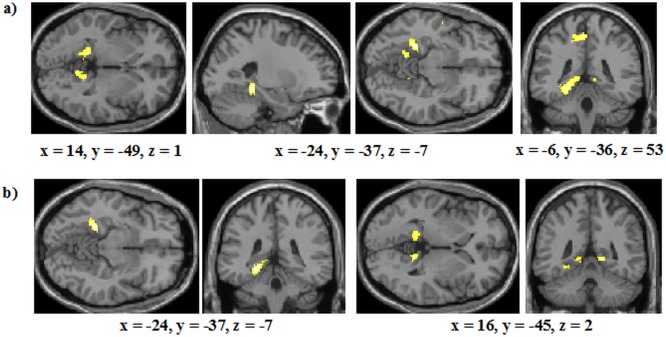
Analysis of Blocks 3 and 4 for: (a) Areas more activated in the II condition than the RB condition. (b) Regions of the MTL more active in the II condition compared with the RB condition; non‐MTL regions were masked in this analysis but the thresholds remained at P < 0.001 and 27 contiguous voxels. The coordinates indicate the origin for the image displayed. Lighter colors indicate higher z‐scores. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Model‐based analysis

The predictions made by COVIS are, of course, dependent on the assumption that more participants in the RB condition are using the explicit system than are participants in the II condition and that a greater number of participants in the II condition are using the implicit system than are participants in the RB condition. If participants in the II condition persist with the verbal system throughout (or alternatively if participants in the RB condition as well as the II condition use the implicit system) then this might explain why our results appear inconsistent with the predictions of COVIS. It is harder, although, from a COVIS perspective to explain why participants in the II condition engaged the MTL, a critical region of the explicit system [Ashby and Valentin, 2005; Nomura and Reber, 2008], more than participants in the RB condition unless one assumes that the II category structure was more effective than the RB structure at engaging the explicit system. While this may seem unlikely, it can be tested using model‐based analysis based on general recognition theory (GRT) [Ashby and Gott, 1988] as is commonly carried out in COVIS related studies [e.g., Ashby et al., 2002; Filoteo et al., 2010; Nomura and Reber, 2008].

For each participant, the GRT analysis determines the decision boundary (from a set of pre‐defined alternatives) that provides the best account of that participant's responses. Each participant is then assigned a strategy type (e.g., “conjunctive”) on the basis of the best‐fitting model.

The unidimensional models assume that the participant determines a criterion along either the orientation or length dimension. As an example, for length, this corresponds to a rule such as: “Assign to Category A if the stimulus is long, or Category B if short.” The unidimensional models have two parameters: the value of the criterion and the variance of internal (criterial and perceptual) noise.

The conjunctive model assumes that the participants make two judgments, one for each stimulus dimension, and then combine these to make a judgment about category membership. The conjunctive rule in the current analysis was: “Assign the stimulus to Category A if it is short and upright, otherwise assign to Category B.” The conjunctive model has three parameters: the two criterion values and internal noise.

The general linear classifier (GLC) model assumes that the decision boundary can be described by a straight line that can vary in gradient and intercept. The unidimensional models are therefore special cases of the GLC model. The GLC model has three parameters: the intercept and slope of the decision bound, plus internal noise.

The random model assumes that participants are responding randomly; it has no parameters.

For each participant, the best fit of each of these models was calculated, and the best‐fitting model selected using Akaike's information criterion [Akaike, 1974]. The results from this analysis, which was performed using the GRT package in the R environment [Matsuki, 2014], are reported in Table 3. Within the COVIS framework, the unidimensional and conjunctive models are considered to represent explicit, RB strategies, while the GLC represents an implicit, information‐integration strategy.

Table 3.

Proportion of participants using the information‐integration (II), conjunctive (CJ), unidimensional (UD), or random (RND) strategies in the RB and II conditions

	II	CJ	UD	RND
Rule‐based	0.22	0.55	0.18	0.05
Information‐Integration	0.59	0.18	0.23	0.00

The results, displayed in Table 3, are generally consistent with previous work indicating that more participants used a conjunctive strategy in the RB condition than in the II condition and that more participants in the II condition used a GLC strategy than in the RB condition. This is the pattern expected and obtained in previous COVIS studies [e.g., Ashby et al., 2002]; therefore, the modeling analyses seem to rule out the possibility (at least within the COVIS framework) that our results were driven by participants not using the intended strategy for their condition. However, the GRT modeling results, as usual, indicate that not all participants are adopting the expected strategy, so we took those participants in the RB condition whose responses were best fit by a conjunctive strategy (12 participants) and compared their brain activation to those participants in the II condition whose responses were best fit by the optimal GLC model (13 participants). Note, the selection of a subset of participants on the basis of their GRT modeling results has seldom previously been carried out in COVIS related studies, perhaps because there are limits to the accuracy of these modeling results [see Donkin et al., 2015; Edmunds et al., 2015, for a discussion] so this analysis should be taken with some caution. Nevertheless, given the nature of our results, these supplementary analyses appear valuable.

A conjunction analysis, using, as before, thresholds of P < 0.001 and 27 contiguous voxels, again revealed an extensive overlap of activation between the RB and II conditions in similar regions to those found in the whole‐group analyses (Fig. 7a). Regions activated included the left MTL, bilateral caudate head, as well as the bilateral caudate body and right putamen. As in the all‐participant analyses, no areas were more active in the RB than in the II condition. No regions were activated more in the II than the RB condition either and, in particular, the prominent MTL activation in the all‐participant analyses did not emerge. One potential reason for this is simply that the smaller number of participants in this model‐based analysis reduced our ability to detect this activation. We therefore conducted a post hoc ROI analysis of the MTL (using the WFU Pickatlas) [Maldjian et al., 2003] with a threshold of P < 0.05 (uncorrected) and a cluster threshold of 79 (which combined produce a corrected threshold of P < 0.05 according to AlphaSim). This revealed activation in the same left hippocampus/parahippocampal gyrus region (cluster size: 115; Fig. 7b) as previously identified.

Figure 7.

Analysis of participants who were shown by the modeling analysis to use the optimal learning strategy overall for all runs of the study: (a) Areas commonly activated in the RB condition and the II condition (with thresholds of P < 0.001 and 27 contiguous voxels); (b) A ROI analysis of areas of the MTL more activated in the II condition compared with the RB condition (with thresholds of P < 0.05 and 79 contiguous voxels). The right most image represents the brain from the bottom. The coordinates indicate the origin for the image displayed. Lighter colors indicate higher z‐scores. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

We again found no activation in regions linked to COVIS's implicit system in the II—RB analysis. We therefore conducted another post hoc ROI analysis comprising the caudate body, substantia nigra, and the putamen in the same manner as for the MTL ROI analysis with cluster thresholds of P < 0.05 (uncorrected) and 41 contiguous voxels (which corresponded to P < 0.05, corrected according to AlphaSim). This also did not produce any significant activation. An additional ROI analysis with these regions using alternative thresholds of P < 0.005 and 10 voxels also yielded no activation. Finally, we repeated these modeling analyses with Runs 3 and 4 alone. These produced the same pattern of results as the all‐run analyses—there was considerable common activation (see Supporting Information Table II) with no regions more activated in the RB compared with the II condition (RB – II). There was, although, as in the corresponding all‐participants analysis, evidence of left MTL activation in a post hoc ROI analysis of the II—RB contrast with thresholds of P < 0.05 and 79 contiguous voxels (cluster size: 157, peak voxel: x = −12, y = −41, z = 4), and no evidence for COVIS's implicit system in either the whole‐brain or ROI analyses.

Correct–Incorrect Trials

To complement the analyses just described we also ran the principal ones using incorrect trials as the baseline. For the all‐blocks analysis, consistent with previous work [e.g., Cincotta and Seger, 2007; Filoteo et al., 2005a, 2005b], we found that the left caudate head was more active on correct trials than incorrect trials (with thresholds of P < 0.001 and 27 contiguous voxels) for both the RB (peak voxel: x = −16, y = 20, z = 5) and II (peak voxel: x = −8, y = 13, z = −6) groups. We again identified, using the same conjunction analysis approach as before, large overlap of activation between the II and RB conditions including bilateral putamen, left caudate body, right MTL, and frontal lobe (including BA 8, 9, 10, and 11; Table 4). We did not, however, detect any differences between II and RB learning. A similar pattern emerged when considering all blocks in the modeling analysis with activation overlap in the conjunction analysis, but no differences detected between II and RB learning.

Table 4.

Brain regions commonly activated in the RB and II conditions in all runs when using incorrect trials as the baseline

			Talairach coordinate
Region	Clustersize	BA	x	y	z	z‐score
Left Medial Frontal Gyrus	693	11	−6	50	−9	5.54
Right Medial Frontal Gyrus		10	10	50	−8	4.81
Left Anterior Cingulate		32	−16	37	−2	3.61
Left Middle Temporal Gyrus	677	39	−52	−65	22	4.36
Left Angular Gyrus		39	−42	−74	31	4.29
Left Inferior Parietal Lobule		39	−46	−68	38	3.79
Right Putamen	70	—	18	9	−9	4.29
Left Superior Parietal Lobule	363	7	−20	−52	58	4.26
Left Postcentral Gyrus		3	−20	−23	47	4.13
Left Precentral Gyurs		4	−14	−24	64	3.92
Right Parahippocampal Gyrus	132	28	16	−5	−13	4.25
Left Putamen	74	—	−14	9	−9	4.20
Right Cuneus	67	18	26	−77	17	4.15
Right Middle Occipital Gyrus		19	24	−85	12	3.29
Right Precuneus	361	7	18	−44	56	4.13
Right Sub‐Gyral		40	24	−38	55	3.97
Right Precentral Gyrus		4	18	−19	58	3.78
Right Middle Temporal Gyrus	193	37	54	−66	5	4.10
Right Superior Temporal Gyrus	263	42	63	−21	12	4.10
Right Postcentral Gyrus		40	65	−20	21	3.69
Left Superior Frontal Gyrus	288	8	−16	39	42	4.02
Left Medial Frontal Gyrus		9	−20	33	30	3.95
Left Middle Frontal Gyrus		8	−28	27	39	3.76
Left Caudate Body	43	—	−20	11	22	3.96
Right Middle Frontal Gyrus	163	11	24	28	−15	3.94
Left Cingulate Gyrus	186	31	−12	−41	33	3.90
Right Cingulate Gyrus		31	8	−41	33	3.80
Left Precuneus	52	31	−14	−57	25	3.87
Left Posterior Cingulate		23	−8	−54	16	3.27
Left Inferior Frontal Gyrus	47	47	−24	33	−10	3.76
Left Middle Occipital Gyrus	112	19	−32	−81	8	3.71
Left Middle Temporal Gyrus	62	21	−54	−47	−3	3.53

Note that indented rows indicate voxels in the same cluster as the nonindented row above.

Looking at Blocks 3 and 4 alone, there was again common activation in the frontal, parietal and temporal lobes (Supporting Information Table III) and no differences between RB and II learning in whole‐brain analyses. However, in a similar ROI MTL analysis to before (thresholds P = 0.05 and 79 contiguous voxels, corresponding to P < 0.05, corrected), we observed greater activation in the II condition than the RB condition in two right hippocampus/parahippocampal gyrus regions (cluster size 215, peak coordinate: x = 24, y = −7, z = −13; cluster size 180, peak coordinate: x = 34, y = −34, z = −12; Supporting Information Fig. 3), with the posterior cluster being in the same area as observed in the corresponding odd‐or‐even comparison. There was, although, again no evidence for activation in regions associated with COVIS's implicit system even when the analogous ROI analyses to those previously conducted were performed. This same pattern emerged when considering Blocks 3 and 4 alone in the modeling analysis.

DISCUSSION

Previous work has found that there is differential brain activity in the learning of RB and II categories with the MTL preferentially recruited for RB compared to II learning while the caudate body is engaged more for II than RB learning [Nomura et al., 2007]. However, we found no evidence for this pattern of dissociable neural activation. In particular, our most noteworthy finding was that the hippocampus/posterior parahippocampal gyrus was significantly more activated in the II condition than the RB condition. In addition, there was a striking overlap of activation between RB and II category learning emphasizing the extensive common neural processes that are engaged in learning both category structures. Common activation included regions thought to be engaged both in the explicit system such as the prefrontal cortex (including BA's 8, 10, 46, and 47), the anterior cingulate, the caudate head, and the MTL, and regions implicated in the implicit system including the posterior caudate, the putamen, and the substantia nigra. This pattern persisted, and indeed became more pronounced, when the second half of training was analyzed alone. We also observed the same basic findings when including only those participants who had used the intended strategy as indicated by GRT modeling analyses.

The striking overlap in activation between RB and II learning is consistent with the idea that RB and II category learning require similar neural processes. Of course, some of this activation is likely to be related to processes not specific to the act of categorization itself but common functions shared by the tasks such as stimulus processing, response selection, feedback monitoring, uncertainty, and attentional demands to name a few possibilities.

A somewhat related way of looking at this common activation is that the behavioral dissociations in past work [e.g., Ashby and Maddox, 2011, but see also Newell et al., 2011] may reflect true differences in the learning system engaged in RB and II categorization but that the functions of these systems share similar neural pathways. For example, Duncan [2010] proposed that there is a multiple‐demand brain network, comprising regions of the prefrontal and parietal cortex, that is responsible for integrating and coordinating the processing of task specific brain areas through dividing the task goal into subtasks, generating the rules to achieve each subgoal and transferring information from one task to another. If such a system organized the specific separable processes needed for learning in the RB or II condition then neural activation overlap (such as in the frontal lobes) between these tasks would be apparent as seen in the present study.

Nevertheless, what is particularly striking about our results and a challenge to COVIS, as it is currently formalized, is that we found extensive regions of the hippocampus/posterior parahippocampal gyrus were activated more in the II condition than the RB condition when COVIS appears to make the reverse prediction that there should be less activation in the II condition than the RB condition in this region.

One important question, therefore, is why we observed a markedly different pattern of results from Nomura et al. [2007]? It appears unlikely that this is due primarily to our choice of the odd‐or‐even task as our primary baseline measure because the same basic pattern of results was observed when we used incorrect trials as the baseline (albeit less pronounced, perhaps for the reasons outlined in the introduction). It, therefore, appears more likely that it is the choice of the RB category structure employed with which to compare the II structure that is driving the qualitatively different pattern of results between studies. Nomura et al. used a unidimensional category structure while we used a conjunctive structure.

Although both conjunctive and unidimensional structures effectively manipulate the relative verbalizability of the optimal decision bound [Edmunds et al., 2015], the advantage of using the conjunctive structure is that it controls for extraneous differences that are present between the unidimensional and the II structure that have been shown in previous work to have an important impact on categorization [e.g., Edmunds et al., 2015; Stanton and Nosofsky, 2007; Wills et al., 2013]. Specifically, the unidimensional structure has only one relevant dimension but the II structure has two relevant dimensions. This means that selective attention is necessary in the RB condition but would be detrimental in the II condition [Nosofsky and Kruschke, 2002]. In addition, multidimensional categorizations are typically more complex and require greater levels of cognitive resources than unidimensional categorizations [Milton et al., 2008; Pothos and Close, 2008; Wills et al., 2013, 2015]. This is likely to lead to greater activation more generally in the II condition than the RB condition and perhaps particularly in the basal ganglia which has been argued to be involved in the learning of more complex category structures [e.g., Ell et al., 2010; Filoteo et al., 2005a].

Related to this, because unidimensional classifications are generally easier to learn than multidimensional classifications [e.g., Ashby et al., 2002; Maddox et al., 2003], Nomura et al. reduced the category separation of the unidimensional structure compared to the II structure. While this enabled error rates to be successfully matched between conditions, this manipulation effectively replaced one confound with another [Stanton and Nosofsky, 2007]. The MTL is assumed to be critical for storing the precise location of the decision bound [Nomura and Reber, 2008] and it seems plausible that this would be more demanding in Nomura et al.'s unidimensional structure, where the decision boundary is more difficult to perceptually discriminate than the II structure which could have been driving the differential activation in this region.

While it may be possible to question our interpretation of these differences, our general point—that controlling between category structures for extraneous factors that have been shown to have a strong influence on categorization allows stronger inferences to be drawn—appears relatively uncontroversial. One might, of course, respond to this by arguing that behavioral dissociations predicted by COVIS have also emerged when using the same category structures as we employed in the present study [e.g., Filoteo et al., 2010; Zeithamova and Maddox, 2006]. However, these behavioral dissociations have already come under detailed critique [e.g., Newell et al., 2010, 2013]; in this regard, our results extend these concerns to previous imaging data. While COVIS has undeniably had a positive impact on the field of categorization by motivating new lines of research and is groundbreaking in terms of the precise neurobiological predictions it makes, our results indicate that it may be in need of revision to accommodate the greater level of MTL activation in II categorization compared to RB categorization that we observed.

Another notable feature of our results is the extensive MTL activation found in the RB and, in particular, the II condition. The precise role that the MTL plays in category learning has been contentious. Some research implicates this region in RB or explicit learning alone [e.g., Nomura et al., 2007; Poldrack et al., 2001], other research shows that the MTL can also be found during II‐like learning [Cincotta and Seger, 2007; Milton and Pothos, 2011], yet further research shows the hippocampus decreases in activation after initial category learning [Seger and Cincotta, 2006], while other studies found no activation at all [e.g., Lopez‐Paniagua and Seger, 2011; Milton et al., 2009; Seger and Cincotta, 2002; Tracy et al., 2003]. While these discrepancies may, of course, relate to the very different categorization tasks used, another possible reason is the choice of the baseline task. It is well established that a resting baseline (such as viewing a fixation cross or a blank screen) leads to activation of the default network which is known to engage the MTL [Buckner et al., 2008]. It is, therefore, possible that the frequent choice of a resting baseline in categorization studies [e.g., Milton et al., 2009; Seger and Cincotta, 2002, 2005; Tracy et al., 2003] may have led to an underestimation of the involvement of the MTL in some past category learning studies.

Having said this, several theories have been proposed with regards the function of the MTL in category learning. For example, Seger et al. [2011] suggested that the anterior hippocampus is necessary for encoding the relationship between a stimulus and a particular response [see also Chua et al., 2007] while the posterior hippocampus is required for the retrieval of the context in which a stimulus has previously been encountered (e.g., retrieving the stimulus‐response mapping). Similar to this, Love and Gureckis [2007] emphasized that the MTL (and specifically the hippocampus) is particularly important for forming abstract codes (known as clusters) which represent stimulus configurations [Davis et al., 2012a, Staresina and Davachi, 2009]. New stimuli that are similar to previously seen configurations will be “captured” by a pre‐existing cluster, but if a stimulus is sufficiently novel, the MTL creates a new cluster for it [Love and Gureckis, 2007]. Inspired by this account, Davis et al. [2012a] [for a related study see also Davis et al., 2012b] conducted an experiment in which the stimuli (schematic beetles) could typically be classified by a single‐property rule but in which there were a few stimuli that were exceptions to that rule. Davis et al. [2012a] found that the MTL was more activated for these exception stimuli than the rule consistent items, and hypothesised that this was due to it being involved in the creation of new clusters to represent the exceptions. Our results seem entirely consistent with these views. Specifically, the MTL activation observed in both the II and RB conditions may reflect that both category structures require the formation of clusters and perhaps in particular the need to encode and retrieve the category label with which a stimulus was associated. The greater MTL activation we observed in the II condition than the RB condition may reflect that the II structure is likely to evoke a greater number of exceptions to the applied rule, requiring the creation of additional clusters. The greater posterior parahippocampal gyrus activation in the second half of training compared to in the first half of training would also be consistent with the idea that the number of clusters increases as exceptions to any rule employed increase.

Our results are consistent with the growing body of evidence that the basal ganglia plays an important role in category learning [for a review see Seger, 2008]. Previous work has found that the caudate head is important for the processing of positive feedback [Cincotta and Seger, 2007; Filoteo et al., 2005a, 2005b; Seger and Cincotta, 2002]. Our finding of activation in the head of the caudate for both RB and II category learning during correct categorization trials compared with incorrect trials further underscores the important role this region has in the processing of positive feedback [Cincotta and Seger, 2007; Filoteo et al., 2005b; Seger and Cincotta, 2002]. The body and tail of the caudate, as well as being linked to COVIS's implicit system, have been shown to activate more for good learners than poor learners in a rule learning task [Seger and Cincotta, 2006]. Additionally, Lopez‐Paniagua and Seger [2011] linked the body and tail of the caudate to stimulus‐response processing. Similarly, the activation in the putamen we observed for RB and II learning may reflect motor planning demands [Cincotta and Seger, 2007]. While there are clearly differences in the procedures used in these studies and ours, it is plausible that these regions serve the same role in RB and II learning. If this is the case then our results would also be consistent with Nosofsky and Stanton's [2005] claim that RB categorization as well as II categorization has a procedural component.

We also found greater activation in the medial prefrontal cortex for correct compared to incorrect responses in both the RB and II conditions. This finding is analogous to the results of Schnyer et al. [2009] who found that patients with ventromedial prefrontal cortex (VMPFC) lesions had impaired learning for both RB and II tasks compared to controls. Schnyer et al. suggested that the VMPFC is responsible for feedback processing in both RB and II learning and is involved in the selection and maintenance of the optimal learning strategies. Our imaging results therefore provide converging support for this previous neuropsychological evidence.

While fMRI provides excellent spatial resolution, it is well known to have limited temporal resolution. One consequence of this is that our study, like Nomura et al.'s [2007], and virtually all extant imaging studies of categorization cannot determine whether the activation identified is driven during the response or feedback processing stages. While the greater activation in the MTL for the II than the RB condition appears unexpected from COVIS's perspective regardless of when it occurs in the category learning process it would, nonetheless, be valuable in follow‐up studies to understand at what stage in the process this difference is occurring. One possibility might be to have a subset of trials where no feedback is provided to examine the relative activation of feedback versus no feedback trials. Another option would be to include an extra variable ITI after the response has been made to identify activation differences between the response and feedback stages [see Lopez‐Paniagua and Seger, 2011, for an example of where this has been done). Both approaches have challenges—for instance, in no feedback trials participants may self‐generate internal feedback, particularly when they have acquired a strong understanding of the category structure. Equally, one consequence of adding an extra ITI is that it would increase the delay between making a response and receiving feedback which has been suggested to disrupt learning in COVIS's implicit system [Maddox and Ing, 2005; Maddox et al., 2003]. Nevertheless, exploring this issue appears a fruitful area for future research.

Another limitation of fMRI is that it is not possible to establish whether all of the diverse areas activated are necessary for the learning of the II and RB structures. For example, it is possible that the activation in the MTL was not essential for the category learning that occurred. While this is plausible, it is still difficult although to explain from this perspective why the MTL activates more for the II condition than the RB condition; in contrast, this difference is readily compatible with the idea that II learning requires greater memory demands to compensate for the absence of an easily verbalizable rule. Nevertheless, to test our explanation for this result, it would be valuable in future to investigate patients with MTL lesions to see if they, as we would predict from our theory, perform worse in acquiring II categories than RB categories. A further prediction derivable from our hypothesis is that people should have enhanced memory for instances after II category learning than after RB learning. As far as we are aware, the former hypothesis has not yet been investigated; however, the latter hypothesis is the subject of ongoing behavioral work in our laboratory.

Finally, there is a temptation to consider our data in the context of whether it is more supportive of single‐system or dual‐system accounts. For instance, the extensive overlap of activation between the RB and II conditions is consistent with the idea that these category structures are learned by the same neural system. According to this view, the greater activation in the II condition relative to the RB condition may just reflect that participants in the II condition, who were learning a more difficult to verbalize decision boundary, had to recruit greater neural resources to reach the same level of performance. Of course, an alternative way of explaining our results is in terms of a dual‐process model such as ATRIUM [Erickson and Kruschke, 1998]. In ATRIUM, one system is RB and is conceptually similar to COVIS's verbal system. The other system is also assumed to be explicit but is exemplar‐based and is responsible for learning when rules are not easily applicable. One possibility, therefore, is that participants were utilizing a suboptimal rule but were supplementing this with an exemplar‐based process for the items in a region of decision space which did not fit into the rules that they were utilizing. The results of Davis et al. [2012a], who found that the MTL was more engaged for exception items than those stimuli which followed a simple rule, would be consistent with this explanation. While our results could, therefore, be conceptualized in either of these ways, we would generally concur with the view of Davis et al. [2012a] who note that given that the criteria for establishing truly qualitatively separable systems are often underspecified, a more profitable way of viewing category learning may be to link brain function to particular processes required. For instance, the prefrontal cortex may be involved in hypothesis generation and rule selection, the caudate head in feedback processing, the caudate body and tail for stimulus‐response associations, and the MTL in storing decision bounds and/or memory for particular exemplars. In this latter example, as discussed previously, the MTL may be an important region for category learning in general but its role could have a greater emphasis in II learning where there are less verbalizable rules than in RB learning which may encourage more specific storage of exemplars [Nosofsky et al., 2012] to supplement any rules that are applied.

CONCLUSION

The present study aimed to build on the limited amount of research that has directly compared the neural regions involved in RB and II category learning. We found that when we controlled for category separation, number of relevant dimensions, and error rates, extensive neural overlap in the learning of RB and II categories emerged and there was no evidence for the pattern of results predicted by COVIS. In particular, we found increased activation in the MTL, long considered critical for explicit memory [e.g., Scoville and Milner, 1957; Squire et al., 2004], for the II condition, which is assumed by COVIS to preferentially recruit the implicit system, compared to the RB condition. Our findings, therefore, extend our understanding of the neural processes that underlie RB and II learning and pose a challenge for COVIS as it is currently instantiated.

Supporting information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information

Supporting Information