Abstract
Dynamic functional brain connectivity analysis is a fast expanding field in computational neuroscience research with the promise of elucidating brain network interactions. Sliding temporal window based approaches are commonly used in order to explore dynamic behavior of brain networks in task‐free functional magnetic resonance imaging (fMRI) data. However, the low effective temporal resolution of sliding window methods fail to capture the full dynamics of brain activity at each time point. These also require subjective decisions regarding window size and window overlap. In this study, we introduce dynamic regional phase synchrony (DRePS), a novel analysis approach that measures mean local instantaneous phase coherence within adjacent fMRI voxels. We evaluate the DRePS framework on simulated data showing that the proposed measure is able to estimate synchrony at higher temporal resolution than sliding windows of local connectivity. We applied DRePS analysis to task‐free fMRI data of 20 control subjects, revealing ultra‐slow dynamics of local connectivity in different brain areas. Spatial clustering based on the DRePS feature time series reveals biologically congruent local phase synchrony networks (LPSNs). Taken together, our results demonstrate three main findings. Firstly, DRePS has increased temporal sensitivity compared to sliding window correlation analysis in capturing locally synchronous events. Secondly, DRePS of task‐free fMRI reveals ultra‐slow fluctuations of ∼0.002–0.02 Hz. Lastly, LPSNs provide plausible spatial information about time‐varying brain local phase synchrony. With the DRePS method, we introduce a framework for interrogating brain local connectivity, which can potentially provide biomarkers of human brain function in health and disease. Hum Brain Mapp 37:1970–1985, 2016. © 2016 Wiley Periodicals, Inc.
Keywords: functional neuroimaging, brain connectivity, brain dynamics, phase synchrony, local connectivity, clustering
Abbreviations
- AAL
Automated anatomical labeling
- BIC
Bayes Information Criterion
- BOLD
Blood oxygenation level dependent
- Cohe‐Reho
Coherence‐based regional homogeneity
- DRePS
Dynamic regional phase synchrony
- fMRI
functional magnetic resonance imaging
- GMM
Gaussian mixture modeling
- KCC‐ReHo
Kendal's coefficient of concordance
- LPSN
Local phase synchrony network
- PCA
Principal component analysis
- PSD
Power spectral density
- ReHo
Regional homogeneity
- RMS
Root mean squared
- ROI
Regions of interest
- RSN
Resting state network
- SW‐ReHo
Sliding window regional homogeneity
Introduction
The human brain can be modeled as a collection of complex functional networks containing interconnected “nodes” that are dynamically interacting with each other on local and global scales [Bullmore and Sporns, 2009; Rubinov and Sporns, 2010; Sporns, 2011]. Non‐invasive neuroimaging methods including functional magnetic resonance imaging (fMRI) have been used to understand such brain network interactions. In this context, task‐free fMRI is a functional brain imaging technique with high spatial resolution, measuring blood oxygenation level dependent (BOLD) changes in response to spontaneous neural activity [Biswal et al., 1995]. The temporal resolution of fMRI data is determined by its repetition time ( ) parameter associated with the time interval between successive excitation pulse sequences applied to the same brain slice. This is the optimal time accuracy which one can reach to investigate the dynamics of brain functionality through BOLD changes.
Improving our knowledge of local network behaviour at a macroscopic level is important for conceptualizing the human brain as a complex dynamic system. The organization of brain networks are both modular and hierarchical [Park and Friston, 2013]. This hierarchical/modular configuration constitutes a potential ground for integrating local neuronal functions at the global level. From this perspective, brain functionality may be viewed as “global integration of local integrators” where short‐range connections are the fundament of specialized functional processing, whilst long‐range connections are generally responsible for higher level cognition [Park and Friston, 2013; Sepulcre et al., 2010]. Brain interactions are also known to be of dynamic nature [Bullmore and Sporns, 2009; Rubinov and Sporns, 2010; Sporns, 2011]. Therefore, it is fair to speculate time‐varying spatial distributions of local functional units for brain networks. Similarity assessment of adjacent brain regions during transient spontaneous brain activity at the spatial resolution of fMRI data may aid our understanding of these functional dynamics [Jiang and Zuo, 2015].
Local network properties of task‐free fMRI can be examined through different methodologies. Integrated local correlation [Deshpande et al., 2009] is a voxel‐wise measure of local coherence in fMRI time series which is applied over the entire length of data. Local functional connectivity density mapping [Tomasi et al., 2014] is another time‐constant voxel‐wise methodology which searches for the Pearson correlation‐based functional connections of a given fMRI voxel until the connectivity edges become lower than a certain threshold. The cross‐correlation coefficients of spontaneous low frequency fluctuations index [Li et al., 2002] is a local measure of fMRI connectivity which computes the average cross‐correlation between spontaneous low‐frequency components of fMRI time series within a region of interest over the scanning time period. Regional homogeneity (ReHo) is based on the Kendall's coefficient of concordance (KCC‐ReHo) [Zang et al., 2004], and evaluates the mean correlation between the fMRI time series at a given voxel and its neighboring voxels. The coherence‐based version of KCC‐ReHo (cohe‐ReHo) [Liu et al., 2010] has also been developed which considers the coherence values of the time series in the frequency domain instead of their temporal correlation (see [Zuo et al., 2013] for more details).
Among the aforementioned methods, KCC‐ReHo has found wide acceptance in brain functional connectivity research, as it is a non‐parametric data‐driven measure with no requirement for Gaussianity of fMRI data, it is computationally fast with minimal parameter settings and is robust to noise [Zuo et al., 2013]. The main limitation of ReHo is the assumption that the dynamics within the brain's functional networks remains stationary over time. However, there is increasing evidence that dynamics of brain functional connectivity during a task‐free situation is nonstationary [Damaraju et al., 2014; Handwerker et al., 2012; Liu and Duyn, 2013; Tailby et al., 2015; Waites et al., 2005; Yu et al., 2015; Zalesky et al., 2014]. In order to mitigate this limitation for KCC‐ReHo, a sliding window version (SW‐ReHo) has been utilized, requiring the assumption of stationarity in the BOLD signal over only short time periods [Hudetz et al., 2015]. In this approach, the KCC‐ReHo measure is successively computed on the segmented BOLD signal, or on the segmented time courses of spatial independent components. This methodology, however, is subject to the Uncertainty Principle, where high temporal resolution can be achieved only at the cost of poor spectral resolution and vice versa [Boashash, 2016].
In this article, we introduce a time‐varying measure of local fMRI connectivity, which alleviates some inherent limitations of using short‐time sliding segments. The proposed method requires minimal parameter tuning with the benefit of not having to define a window length. Dynamic Regional Phase Synchrony (DRePS) maps are obtained as the (spatial) mean of the instantaneous phase coherence within a local neighborhood of fMRI voxels (e.g., within a spatial extent akin to that used in the ReHo method). We show, through simulation, that DRePS achieves higher temporal resolution than the SW‐ReHo approach and investigate its properties within different frequency bands. We also apply DRePS to task‐free fMRI data from 20 healthy controls, and test the hypothesis that dynamic local functional connectivity is associated with local phase synchrony networks (LPSNs), within spatially distributed brain areas.
Materials and Methods
We begin with a description of the existing SW‐ReHo method, as the approach we subsequently describe shares some features, and we will be comparing results of our framework to those of SW‐ReHo.
Exploring Dynamic Local Connectivity in Task‐Free fMRI Data Using SW‐ReHo
Regional characteristics of task‐free fMRI data have been successfully investigated using the ReHo measure [Liu et al., 2008; Tang et al., 2014; Wang et al., 2012; Zang et al., 2004; Zuo et al., 2013]. ReHo computes average Kendall's coefficient of concordance between the fMRI time series at each voxel and its adjacent voxels within a surrounding 3D cube [Zang et al., 2004]. It returns values from 0 to 1 with higher values implying stronger local connectivity. ReHo can be extended to a nonstationary version using a sliding window approach, SW‐ReHo. Sliding window analysis is a widely used way of characterizing variations of spatio‐temporal connectivity in BOLD data, as it is easy to implement and interpret [Hutchison et al., 2013]. SW‐ReHo is based on shifting a set number of data points in time with a pre‐defined overlap while extracting ReHo from each segment. This leads to a series of time‐varying features over time. Accuracy of SW‐ReHo strongly depends on the choices of window size, window shape and overlapping length. Short‐length rectangular windows (i.e., low number of time points) may increase temporal resolution of the feature time series, but it can negatively affect the reliability of ReHo, and reduce the spectral resolution within that window [Zuo et al., 2013]. Overlapping between successive windows can multiply the number of feature points, but the overlapping length nevertheless introduces temporal smoothing to the feature time series. Therefore, development of a time‐varying local connectivity measure for task‐free fMRI data at ‐resolution can improve the temporal precision of brain functionality studies. In the following section, we outline an alternative framework to SW‐ReHo based on the concept of instantaneous phase, which evaluates nonstationary local connectivity of BOLD signal changes at ‐level with no need for window parameter settings.
Instantaneous Phase of fMRI Time Series
We propose that instantaneous mean phase coherence between time series of neighboring fMRI voxels can be used as a time‐varying measure of brain local connectivity. To this end, we employed the concept of analytic associates based on the Hilbert transform [Sun and Small, 2009] to extract the phase information of fMRI time series. Despite the important role of band‐pass filtering in phase synchrony analysis of task‐free fMRI data, its theoretical aspects have not yet been systematically investigated in the fMRI literature. The frequency band of 0.03–0.07 Hz has been used in two previous studies of task‐free fMRI instantaneous phase synchrony analysis, but its justification has been mainly based on practical considerations of minimizing artifact and noise in the data [Glerean et al., 2012; Ponce‐Alvarez et al., 2015]. We take this concept further and discuss the requirements needed for extracting meaningful phase information from nonstationary signals.
A real‐valued signal can be defined without ambiguity based on its instantaneous amplitude and instantaneous phase as follows [Picinbono, 1997]:
| (1) |
where and denote the instantaneous amplitude and phase of , respectively. In order to obtain the phase information , we have to convert the real‐valued presentation of Eq. (1) into a complex form. This can be done by estimating , i.e., the complex analytic associate of using the Hilbert transform [Picinbono, 1997; Sun and Small, 2009]:
| (2a) |
| (2b) |
where and means the Hilbert transform. The complex nature of in the time domain arises from its asymmetric power spectral density (PSD) function having no negative frequency components [Picinbono, 1997]. Extraction of the instantaneous phase signal from is straightforward by re‐writing Eq. (2a) into the following quadrature form:
| (3a) |
| (3b) |
This is, however, only possible if the following relationship is satisfied:
| (4) |
This condition can be examined by using the Bedrosian theorem [Bedrosian, 1963], which deals with the Hilbert transform of the product of two real‐valued signals in the time domain. The Bedrosian's requirement states that if two functions and have non‐overlapping frequency spectra, and the support of the spectrum of is lower than that of , then:
| (5) |
In other words, the low‐frequency envelope of the product can be extracted from its Hilbert transform, but only if and meet the Bedrosian's requirement. Eq. (5) is also known as Bedrosian identity [Venouziou and Zhang, 2008].
As a direct application of the Bedrosian theorem, the left side of Eq. (4) can be split into a pair of slow and fast terms, if the amplitude envelope is low‐pass, the phase signal is high‐pass, and their frequency spectra are distinct [Picinbono, 1997]:
| (6) |
On the other hand, we know from the Hilbert transform properties that is equal to over an infinite time interval [Picinbono, 1997]. However, Eq. (6) is not necessarily equivalent with the following equation [Picinbono, 1997] for real‐world signals due to their finite‐length:
| (7) |
Consequently, we still cannot infer the quadrature form of Eq. (3a) from Eq. (2a) for practical signals, even if they satisfy the Bedrosian's requirement. This implies that for a rigorous evaluation of the credibility of the extracted phase information, one must check both Bedrosian theorem as well as Eq. (7) for the underlying signal. To this end, we computed an error signal based on Eq. (7) as an accuracy indicator of instantaneous phase [Picinbono, 1997]:
| (8) |
In an ideal case of perfect analytic associates, the error signal will be equal to 1.
Dynamic Regional Phase Synchrony (DRePS) of Task‐Free fMRI
Let and be the instantaneous phases of signals and , respectively. The two signals are phase‐locked of order 1:1 if [Mormann et al., 2000]:
| (9) |
Phase synchronization between and can then be quantified using the mean phase coherence given by [Lachaux et al., 1999; Mormann et al., 2000]:
| (10) |
where represents the mean operator. is restricted to the interval [0,1] where reflects no random phase difference between and , whilst approaches zero when the instantaneous phase difference between the two signals increases.
Now, assume and are the instantaneous phase functions of a band‐pass filtered fMRI time series with Bedrosian identity consisting of time‐points ( ) at a given voxel and its neighboring voxels ( ) where is the entire number of non‐zero voxels within a 3D cube centered at x. The DRePS measure associated with the voxel is then computed as:
| (11) |
The function quantifies the instantaneous mean phase coherence between and all of its adjacent neighbors within its associated 3D space. In this study, we considered two sizes of 6 and 26 immediate neighboring voxels with respect to the central voxel, in analogy to the ReHo method [Zang et al., 2004]. This calculation was repeated for every gray‐matter voxel after exclusion of all zero‐value voxels from the neighboring cube. Figure 1 illustrates the schematic procedure of DRePS extraction from a typical 3D cube of size 27.
Figure 1.
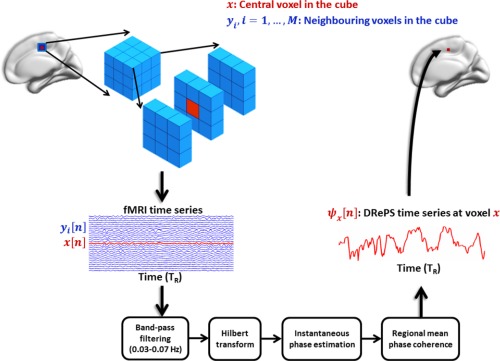
A schematic example of extracting the DRePS measure from a typical moving 3 × 3 × 3 cube of fMRI voxels including a central voxel (red voxel) and its neighboring voxels , (blue voxels). The DRePS time series is obtained by taking the mean of instantaneous phase coherence between the central voxel and its adjacent non‐zero neighbors at different time points. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
The DRePS function extracted from a 4D task‐free fMRI data will be another 4D map with the same single‐ temporal resolution. The DRePS time series at each voxel represents its simultaneous relationship with the nearest neighbors. With a gray matter mask containing 51603 voxels and a fMRI data including 200 volumes, our MATLAB implementation of DRePS takes approximately 40 seconds using a GNU/Linux‐based PC of 2.66 GHz Intel Quad Core i7 CPU and 8 GB of RAM.
Analysis of DRePS: Two Scenarios
We developed two separate scenarios for inspecting the DRePS maps:
Scenario A: In the first scenario (Fig. 2A), we aimed to assess how particular brain regions, segmented a priori, were locally “engaged” (highly synchronous) or “disengaged” (weakly synchronous) over time. The DRePS time series were directly analyzed using a time‐dependent thresholding approach. For each time point, the associated 3D DRePS map was thresholded at the percentile (here, ) of its histogram over all voxels (very high regional synchrony). This provided a binary 3D map of voxels surviving the high local connectivity threshold. The 3D binary map was parcellated using an automated anatomical labeling (AAL) atlas [Tzourio‐Mazoyer et al., 2002] with 90 regions of interest (ROIs) excluding cerebellum. The percentage of suprathreshold voxels within each ROI (i.e., ratio of ones over the ROI size) was then calculated. A spatio‐temporal DRePS percentage plot was obtained for each subject, where the x‐axis was associated with the fMRI volume timing (in ) and the y‐axis represented the ROI indices (Fig. 2A). Each row in reflects the time‐varying quota of a given ROI with high DRePS values.
Figure 2.
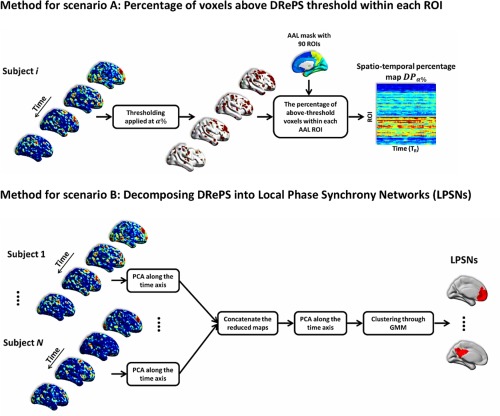
Two scenarios for analysis of DRePS maps: (A) voxels with the most significant DRePS values within each 3D ROI were counted leading to a spatio‐temporal DRePS percentage map, (B) reduced DRePS feature vectors were spatially clustered using Gaussian Mixture Modeling (GMM) resulting in communities of local oscillators in fMRI data called local phase synchrony networks (LPSNs). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
The significance testing for the maps was done through the surrogate data method by generating 1000 random realizations of the null hypothesis based on the original DRePS time series. To this end, all time series inside the gray matter mask of each subject‐specific 4D DRePS map were re‐arranged into a 2D matrix, so that each row was associated with a DRePS time series at a certain voxel. The voxels were then parcellated using the AAL atlas. Each ROI was spatially concatenated over subjects. The concatenated ROIs underwent a permutation testing procedure. At each run, voxels of each concatenated ROI were shuffled and the first set of random voxels with the same size of the underlying ROI was taken. It led to a permuted DRePS map in which the voxels of each ROI and their associated DRePS time series were randomly selected from the group of subjects. This was done to preserve the inherent characteristics of the brain by keeping the same anatomical mask at each permutation, while randomizing the dynamic local network properties over the entire group. The shuffled 4D DRePS maps were subjected to the process of obtaining the maps where each element in the time‐space domain was associated with a null distribution of 1000 values. A 2D spatio‐temporal map with the same size of was obtained via significance thresholding at the 95th percentile of these distributions. The resulting surrogate map was finally used to threshold the subject‐specific percentage maps.
Scenario B: In the second scenario (Fig. 2B), we hypothesized that communities of locally synchronous oscillators within the brain are linked to functional brain activity. Therefore, dimensions of maximal variance in the DRePS data may convey meaningful information about local dynamics of task‐free fMRI data, and one could use this information to segment the brain a posteriori into functionally related regions. From this perspective, each DRePS time series (one per voxel) was treated as a feature vector. A two‐step dimension reduction using principal component analysis (PCA) was conducted. The first step was done at the subject level where the DRePS temporal dimension was reduced from 200 (number of volumes for each subject) to 30. After dimensionality reduction of each individual's 4D DRePS map, they were temporally concatenated over the group of subjects and fed into another PCA with a further reduction to 30 dimensions. The number of principal components was chosen by checking the cumulative sum of eigenvalues. In order to determine the intrinsic grouping in the reduced ‘DRePS feature vectors’, a clustering procedure was applied to the data using Gaussian mixture modeling (GMM) [McLachlan and Peel, 2000]. With GMM, we assume that the data points are generated from a mixture of multi‐dimensional Gaussian distributions whose unknown parameters could be estimated using the iterative Expectation‐Maximization algorithm [McLachlan and Peel, 2000]. GMM was performed over a range of model orders (i.e., number of Gaussians) for which the goodness‐of‐fit was evaluated using Bayes Information Criterion (BIC). The optimum order was then selected as the model order with minimal BIC. The GMM procedure resulted in spatial clusters of voxels with similar DRePS characteristics called local phase synchrony networks (LPSNs).
In order to evaluate spatial overlap between LPSNs and commonly reported resting state networks (RSNs) in fMRI data of healthy subjects, we compared the LPSNs (25, as determined by BIC) obtained from within the frequency band of 0.03–0.07 Hz and cube size of 27 with 21 RSNs provided by another independent study in the same space (i.e., MNI1) [Smith et al., 2012]. Since selecting the RSNs through independent component analysis of our own cohort would be a fairly subjective procedure, we chose to use a set of publicly available and reliable RSNs in our study for the sake of objective and reproducible comparison. The RSNs were acquired from 42 10‐minute fMRI datasets of 5 subjects in 7 sessions2. Each RSN was binarized by thresholding values above two standard deviations of its voxel values. Pair‐wise Jaccard indices were then computed between the LPSNs and binarized RSNs to quantify the similarity and diversity of spatial patterns among them.
Simulation
We created a 3D simulated data representing random phase relationships between synthetic voxels as well as random patterns of phase synchrony with time‐varying attributes in order to:
Evaluate the capability of DRePS for tracking local phase synchrony changes at sample‐rate resolution,
Compare the temporal resolution of instantaneous features generated by DRePS, and window‐based dynamic features obtained by SW‐ReHo for representation of sudden changes in local phase synchrony,
Investigate the effects of the number of adjacent voxels and band pass filtering used in the DRePS calculation.
To this end, we generated a 4D array of size including an inner compartment of size where the first three dimensions represent a spatial volume (Fig. 3A) and the fourth dimension is time (in , here 3 s). The time series at each voxel outside of the inner cube was made of pure background activity . Each voxel in the inner cube was associated with a time series consisting of two components: background activity and synchronous activity masked by (Fig. 3B) and elevated by the factor of 2 to resemble amplitude changes. The signals , and are defined as follows:
| (12) |
where is additive uniform noise between 0 and 1, is a normally distributed random frequency within the range of 0 to , is time‐varying random phase with maximum variation over the unit circle and is a voxel‐independent central frequency locked to . Intuitively, voxels inside the inner cube follow a synchronous pattern governed by , while the phase entrainment between voxels outside of the inner cube is purely random. Figure 3C illustrates an example of four representative time series extracted from the inner cube. In the figure, the phase synchrony mask represents a block of five equidistance single‐ events distributing over to , an individual event starting at and a single‐ event at .
Figure 3.
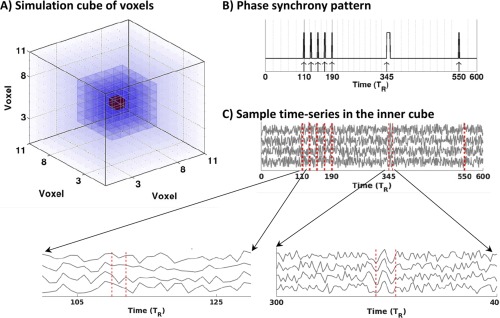
Simulated data: (A) 3D arrangement of voxels in the simulated data. The inner compartment of time series with phase synchrony pattern has been highlighted with greater opacity. The central voxel has been shown in red, (B) phase synchrony pattern , C) four representative time‐series extracted from the inner cube. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
The simulated data was examined by DRePS and SW‐ReHo methods within a wide frequency band of 0.01–0.09 Hz and a narrow frequency band of 0.03–0.07 Hz as well as two moving cubes of 6 and 26 neighboring voxels. The generated data may not necessarily represent the same natural signatures of real fMRI data, but it intends to show the basic idea behind the DRePS analysis procedure.
Subjects and fMRI Scanning Procedure
fMRI data of 20 healthy controls (mean age: 32.4 ± 10 y, 6 female) were used in this study. All subjects were scanned with Siemens (Erlangen, Germany) 3T Trio/Skyra scanners while not performing any specific mental task with eyes closed, and were asked to remain awake. Functional data were acquired using an EPI sequence with 44 interleaved 3 mm slices, = 3 s, = 30 ms, flip angle = 85°, voxel size of 3 × 3 × 3 mm3 and an acquisition matrix of 72 × 72. weighted images were also acquired following the functional scans. A total of 200 volumes of task‐free fMRI data were used for all subjects. The study was approved by the Austin Health Human Research Ethics Committee and all subjects gave written informed consent to participate in the study.
fMRI Data Preprocessing
In the preprocessing pipeline we used SPM8 (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/) and DPARSF [Chao‐Gan and Yu‐Feng, 2010] in MATLAB R2013b (MathWorks Inc., Natick, Massachusetts, United States). Steps included slice timing correction, re‐alignment, coregistration to subject's own weighted images followed by spatial normalization to the standard MNI space (152‐brain average template). The linear trend was removed and white matter and cerebrospinal fluid signals were regressed out from the data. To compensate for head movement inside the MRI scanner, 24 motion re‐alignment parameters were linearly regressed out of the data [Friston et al., 1996]. All volumes with head movement above 0.5 mm were omitted and replaced by time points derived using cubic spline temporal interpolation in order to ensure continuous temporal data for all subjects.
Task‐free BOLD data of each subject were band‐pass filtered within four ranges of 0.01–0.09 Hz, 0.03–0.07 Hz, 0.05–0.09 Hz and 0.03–0.11 Hz. All bands were used for analysis of instantaneous phase (see “Assessing Phase Synchrony Analysis Requirements”) and spectral analysis of DRePS (see “Scenario A: Direct Analysis of DRePS Applied to Real‐World fMRI Data”). However, the frequency interval of 0.03–0.07 Hz was chosen for extracting LPSNs when evaluating DRePS as a nonstationary feature of the brain's dynamic local connectivity (see “Scenario B: DRePS as a Nonstationary Feature of the Brain's Dynamic Local Connectivity”). These frequency bands were chosen to cover different bandwidths (0.04 Hz and 0.08 Hz) and central frequencies (0.05 Hz and 0.07 Hz) relevant to the task‐free fMRI spectral content.
Results
Assessing Phase Synchrony Analysis Requirements
Prior to the DRePS analysis, we examined the Bedrosian's requirement and error signal for the filtered fMRI time series by assessing the low‐band and high‐band components of their analytic associates (i.e., and in Eq. (1), respectively where means the Fourier transform and is the magnitude operator). Also, we computed voxel‐wise temporal average of the root mean squared (RMS) of the deviations of around 1 and its distribution over all voxels for each band‐pass filtered fMRI dataset as a quality indicator of the instantaneous phase signals. Figure 4A illustrates the bandwidths of the z‐scored low‐pass and high‐pass components of analytic associates averaged over voxels for each subject. The grand mean spectra are also overlaid on the subject‐specific curves. Although the narrower bands (i.e., 0.03–0.07 Hz and 0.05–0.09 Hz) represent larger separation of the low‐pass/high‐pass components, a fairly clear distinction can also be observed for wider bands of 0.01–0.09 Hz and 0.03–0.11 Hz. In other words, the Bedrosian's requirement is still relatively retained after applying a wider filtering to the task‐free fMRI data in the DRePS framework. This observation is again verified by estimating the error signals of four band‐pass filters illustrated in Fig. 4B, where is roughly fluctuating around 1 for the bands 0.01–0.09 Hz and 0.03–0.11 Hz with RMS error percentages below 20%. The relevance of these frequency bands for DRePS analysis of task‐free fMRI data, considering the majority of BOLD information within 0.01–0.1 Hz [Biswal et al., 1995], is also shown in “Scenario A: Direct Analysis of DRePS Applied to Real‐World fMRI Data”.
Figure 4.
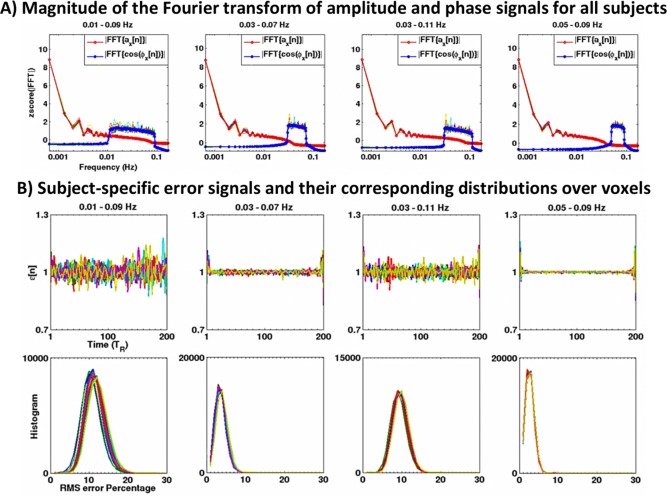
(A) Bandwidths of the low‐pass and high‐pass components of analytic associates [see Eq. (1)] averaged over voxels of each subject. Each subject‐specific curve is illustrated with a single color and the grand mean spectra are shown in bold. The y‐label zscore(|FFT|) means the magnitude of the Fourier transform converted into the z‐score over frequency bins (zero mean and unit variance). Whilst the wider bands exhibit a smaller separation between the low‐pass and high‐pass components compared to the narrower bands, Bedrosian's requirement still remains satisfied. (B) Subject‐specific averages of the error signal over all voxels for the analytic associates of fMRI data within four frequency bands (top row) and their corresponding distributions of the RMS of their deviation from one (bottom row). In all panels, each subject‐specific curve is illustrated with a unique color. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Simulation Results
Figure 5 illustrates the spatio‐temporal local connectivity maps of time series of the inner cube within the simulated data obtained by DRePS (Fig. 5A) and SW‐ReHo approach using a rectangular sliding window of length 's (Fig. 5B). For both methods, a moving cube of neighboring voxels (i.e., 27 voxels in total) and band‐pass filtering of 0.03–0.07 Hz were used. In both maps, the y‐axis has been sorted based on the Euclidian distance between non‐central voxels within the inner cube and the central voxel (red voxel in Fig. 3A) where 0 represents the central voxel and symmetric positive/negative values are associated with equidistant voxels to the center. The rectangular patterns in the SW‐ReHo time series of Fig. 5B reflect the impact of windowing on the short‐time local connectivity estimates: all events shorter than a window length are treated as if they have the same temporal attribute (e.g., last two single events in the map). Also, adjacent events cannot be differentiated temporally if they are close to each other, as seen for the block of events in Fig. 5B. Furthermore, the sliding window approach fails to provide dynamic connectivity information for half the window width each at the beginning and end of the entire time span due to the window length. In contrast, the spatio‐temporal DRePS map of Fig. 5A demonstrates ‐resolution accuracy in tracking phase synchrony changes among voxels. The salt‐and‐pepper noise over the connectivity map obtained by the SW‐ReHo approach is more noticeable than DRePS due to its inherent temporal averaging. For both SW‐ReHo and DRePS, a fading pattern is observed in the vertical profile (along the y‐axis projection) from the central voxel towards the inner cube boundaries. This is expected because of the decrease in the number of synchronous time series within the moving cube of adjacent voxels in both methods when shifting towards the boundaries, resulting in a reduction in the local connectivity estimates.
Figure 5.
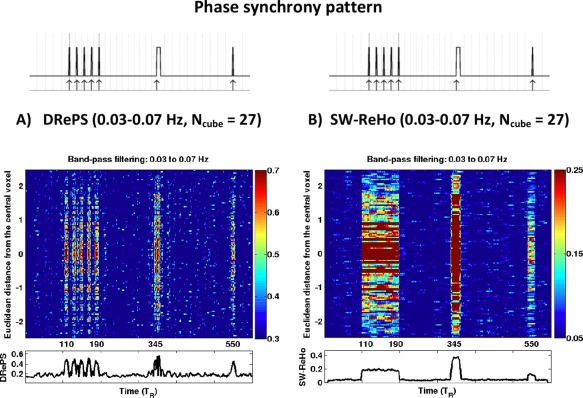
Simulation results: spatio‐temporal local connectivity maps associated with the voxels inside the inner cube of simulated data (Fig. 3A) obtained from the DRePS method (A) and the SW‐ReHo method (B) using the band‐pass filtering of 0.03–0.07 Hz and neighboring size of 26. For each map, the horizontal profile (i.e., averaging over voxels) is presented at the bottom. DRePS provides far superior temporal resolution than SW‐ReHo. The phase synchrony mask (see Fig. 3) is given on top of each map for comparison purposes. See also Supporting Information Fig. S1 for simulation results with other choices of band‐pass filtering and neighboring size. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
The effect of band‐pass filtering and internal smoothing (governed by the number of neighboring voxels in the moving cube) on DRePS/SW‐ReHo was also investigated through simulations. As Supporting Information Fig. S1 demonstrates, the neighboring size of 6 introduces widespread noise over the whole time‐space domain in both DRePS and SW‐ReHo maps. Also, switching between narrowband filtering of 0.03–0.07 Hz and wideband filtering of 0.01–0.09 Hz does not impose a significant change on the spatio‐temporal maps of the simulated data. Due to the mitigating effect of internal smoothing on the noise level of DRePS spatio‐temporal maps, we chose the neighboring size of 26 for task‐free fMRI analysis in the following sections.
Scenario A: Direct Analysis of DRePS Applied to Real‐World fMRI Data
We evaluated the first analysis pipeline delineated in Fig. 2A by applying it to the DRePS 4D maps of 20 healthy control subjects. Figure 6A,B illustrate the plots of a typical subject within two frequency bands of 0.03–07 Hz and 0.01–0.09 Hz after statistical testing, where the insignificant data‐points have been blacked out. All subjects' thresholded percentage plots can be found in the Supporting Information as a .mat file. The spatio‐temporal maps suggest that the highest values in the map are associated with precuneus, occipital and parietal areas (see the horizontal ribbon of high values in Fig. 6A,B).
Figure 6.
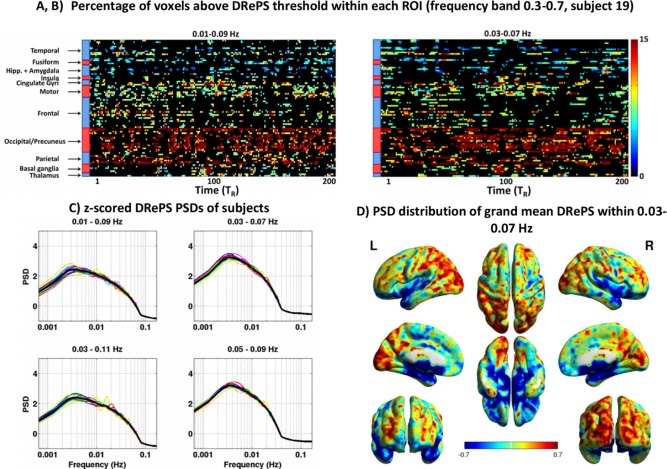
(A,B) Analysis of DRePS time series over the control group: Spatio‐temporal DRePS percentage plot associated with the voxels above the 95th percentile ( ) obtained from band‐pass filtering of A) 0.03–0.07 Hz and (B) 0.01–0.09 Hz, after permutation testing, shown for a typical subject. The insignificant values have been blacked out. (C) Mean PSD of DRePS time series across all voxels for each subject (colored traces), and grand mean over all subjects (black bold line). The PSD values were normalized to z‐scores at the individual level for easier comparison between subjects, (D) Mean power of DRePS time series (band‐pass filtering of 0.03–0.07 Hz, neighboring size of 26) across the entire frequency, up to the Nyquist rate of 0.16 Hz for each voxel, then z‐scored and averaged across all subjects. See also Supporting Information Fig. S2 for the grand mean PSD spatial maps with other choices of band‐pass filtering. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 6D demonstrates the grand mean spatio‐spectral distribution of DRePS time series obtained by averaging subject‐specific PSDs over the entire frequency interval Hz where . The individual PSDs (thin curves in Fig. 6C) were normalized to z‐scores over the frequency bins for easier comparison between subjects. In Fig. 6C, thin curves represent whole‐brain mean spatial frequency for each subject. Spatial patterns consistent with the maps (Fig. 6A,B) are also observed in the spatio‐spectral distribution of DRePS with higher frequency fluctuations in the visual and parietal areas and lower frequency fluctuations in sub‐cortical brain regions (Fig. 6D). There is a consistent peak of ultra‐slow DRePS activity within 0.002–0.02 Hz for all subjects as shown in Fig. 6C which is clearly distinct from the frequency band of the filtered BOLD data (i.e., 0.03–0.07 Hz). This ultra‐slow signature can be observed for all of the four pass‐bands, though its power decreases by widening the band‐pass filter in the DRePS framework (the left column of Fig. 6C vs. the right column). The closely similar spectral properties of DRePS time series within different frequency bands (Fig. 6C) can also be verified by checking the grand mean PSD spatial map of 0.03–0.07 Hz in Fig. 6C and the other corresponding maps in Supporting Information Fig. S2.
Scenario B: DRePS as a Nonstationary Feature of the Brain's Dynamic Local Connectivity
The results of the GMM clustering analysis for DRePS maps obtained through the band‐pass filtering of 0.03–0.07 Hz and cube size of 27 are summarized in Fig. 7. Components associated with the minimum of normalized BIC curves suggested a range of 7.1 ± 3.4 clusters at the individual level (Fig. 7A), while this number varied within the range of 20–30 for the group level (Fig. 7B). In order to improve the statistical power of the spatial DRePS clusters, GMM was only applied to the group data. According to the BIC curve of Fig. 7B, after roughly 25 Gaussian components for the group GMM clustering, BIC changes became relatively stable as denoted by a plateau. Therefore, 25 spatial clusters of brain voxels with normally distributed DRePS characteristics were extracted. In Fig. 7C, eight exemplary clusters out of 25 are shown, all with biologically meaningful brain regions. The clusters can be considered as spatial networks of adjacent/remote brain locations with similar local phase synchrony properties. We call these synchronous networks as LPSNs. The selected components also overlap with commonly reported “long‐range” RSNs [Hoff et al., 2013]. These include a wide range of networks important in task‐free states (precuneus), task‐positive states, salient task‐switching, visual areas and cortical motor behavior. It may establish a link between networks in which amplitude modulation is typically associated with an active task, and locally synchronous fluctuations of the task‐free fMRI data. The full set of 25 LPSNs can be found in Supporting Information as a 4D NIfTI‐1 data format file.
Figure 7.
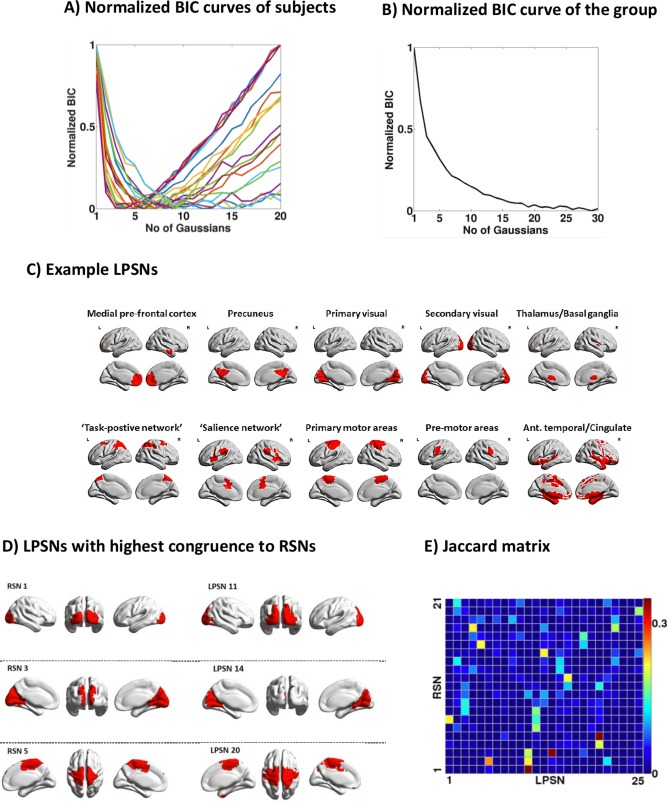
Analysis results of DRePS maps treated as dynamic feature vectors of the brain's local functional connectivity, (A) BIC curves at the individual level obtained after running GMM for different number of Gaussian clusters, (B) the BIC curve at the group level after running GMM for a range of Gaussian clusters, (C) eight exemplary LPSNs obtained from this study, (D) the most similar spatial patterns between RSNs and LPSNs based on the Jaccard similarity matrix, (E) The Jaccard similarity matrix between the RSNs provided by [Smith et al., 2012] and the LPSNs obtained as the outcome of GMM at the group level. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 7E demonstrates the pair‐wise Jaccard indices between the LPSNs and binarized RSNs [Smith et al., 2012] to quantify the similarity and diversity of spatial patterns in two brain network families. As the similarity matrix suggests, RSNs and LPSNs may overlap across different areas. However, the highest overlap is associated with the primary visual area (RSN1 vs. LPSN11), posterior cingulate cortex (RSN3 vs. LPSN14) and motor areas (RSN5 vs. LPSN20) illustrated in Fig. 7D.
Discussion
Brain functional connectivity is intrinsically nonstationary [Chang and Glover, 2010; Damaraju et al., 2014; Handwerker et al., 2012; Liu and Duyn, 2013; Yu et al., 2015; Zalesky et al., 2014], and this property is revealed locally at high temporal resolution by DRePS. This important aspect of brain dynamics may be partly ignored if stationary signal processing tools are employed in fMRI connectivity studies. A common way of addressing nonstationarity in fMRI connectivity analysis is to temporally segment it using a fixed‐length sliding window. A window has to be short enough to satisfy the assumption of stationarity, but narrow segments fail to provide acceptable localization in the frequency domain. In addition, the window shape can have a non‐trivial influence on the spectral signature of functional connectivity results. For example, a rectangular window can introduce a spectral leak to the frequency content of the segmented BOLD changes and indirectly affect fMRI connectivity metrics. These issues, along with the issue of overlapping length between successive windows, have led to a semi‐arbitrary parameter selection paradigm for the sliding window approach in the literature (e.g., see [Allen et al., 2012; Li et al., 2014; Shirer et al., 2011; Yu et al., 2015; Zalesky et al., 2014]). Furthermore, the sliding window approach fails to provide dynamic connectivity information for half the window width each at the beginning and end of the entire time span due to the window length. In contrast to the sliding window approach, the proposed DRePS analysis framework in this article characterizes instantaneous dynamic properties of time‐varying local fMRI connectivity at each time point. Based on the simulation results in Fig. 5, temporal resolution of DRePS time series in capturing the number of synchronous events and their time intervals is higher than time‐varying ReHo estimates obtained by the sliding window approach. It is noteworthy that brain dynamic connectivity may also be examined by other approaches such as adaptive window length methods or wavelet analysis at wide frequency and temporal scales. These techniques may bring different insight into brain function in contrast to the narrow spectral view of DRePS within short frequency bands. Comparison between the DRePS approach and wide‐band dynamic local connectivity methods on the same task‐free fMRI data may be an informative avenue of future research. Also, incorporating a non‐uniform sampling approach such as point process analysis [Tagliazucchi et al., 2012] to the DRePS framework may act as a data reduction step to further facilitate analysis of time‐varying changes of local connectivity in fMRI data.
There is evidence that local neuronal activity and long‐range functional connectivity in the human brain are related to each other [Park and Friston, 2013; Riedl et al., 2014]. This finding suggests that brain function may be supported by dynamically organizing “local neighborhoods” that transiently share synchronized BOLD activity, and are also synchronized with other distant communities to form large‐scale networks [Zang et al., 2004]. This view on local brain connectivity was a motivation for developing DRePS, which quantifies instantaneous regional phase synchronization of BOLD data in a data‐driven and model‐free way. We hypothesize that dynamic information extracted from DRePS time series may reflect spatial clusters of local oscillators in the brain (Fig. 7C). It remains for further research to examine biological relationships between local neighborhoods and large communities in BOLD changes observed in DRePS maps.
Local cortical connectivity of DRePS was most prominent in primary visual cortex and default mode network areas. This observation may be explained due to the high metabolic demands of these brain regions in the healthy brain [Spetsieris et al., 2015]. Low values of dynamic local functional connectivity were mainly observed within deep sub‐cortical brain regions, including the hippocampus and amygdala (Fig. 6A). Indeed, this suggests that neuronal activity in these regions may not fluctuate synchronously within the frequency band to which DRePS analysis was performed. Song et al. (2014) hypothesized that complex and diverse neural activity occurs even within small volumes, particularly in subcortical areas, and this cannot be captured by local connectivity methods such as ReHo (and possibly, the DRePS method presented here). This is in stark contrast to cortical local connectivity of primary visual cortex and “default‐mode” brain nodes. Whether these differences in local connectivity across cortical and subcortical brain regions are an effect of frequencies studied for functional connectivity analysis, or a “neurobiological trait,” requires further attention. This may also originate from a limitation of the DRePS method where the cortical curvatures are ignored by averaging phase difference values over a moving cube of ∼1 cm3. However the DRePS approach is not inherently restricted to cube‐shaped volumes. For example, following additional validation, it might potentially be applied to regions with anatomical constraints derived from structural imaging measures. Further task‐free fMRI connectivity studies are needed for explaining the precise biological underpinnings of temporal local synchrony features.
We believe that LPSNs and RSNs (see Fig. 7D) represent distinct neural processes, in part due to their propensity to detect ‘local’ and ‘global’ connectivity, respectively. Whilst RSNs are associated with large‐scale functional brain networks, we interpret each LPSN as a population of local oscillators in task‐free fMRI data. This may be explained based on the difference between GMM clustering used for generating LPSNs and independent component analysis used for extracting RSNs [Smith et al., 2012]. In contrast to group independent component analysis as a method of extracting “temporally independent sources” of functional connectivity in fMRI data, GMM‐based clustering of DRePS resembles a functional parcellation of the brain using voxel‐wise DRePS feature vectors. It estimates the similarity (i.e., dependence to the same Gaussian distribution) between reduced DRePS feature vectors, and then all voxels with similar distribution form a cluster.
Ultra‐slow fluctuations are an important property of dynamic local connectivity in the normal brain. A recent study has shown nonstationary evolution of global synchronization patterns between the BOLD activities of different brain areas oscillating on an ultra‐slow (<0.01 Hz) time scale [Ponce‐Alvarez et al., 2015]. Our study, in contrast, considers spatial distributions of local phase synchrony with statistically similar dynamics. Nevertheless, the dominant frequency content of the DRePS time series over all subjects remains proximate to that which has been reported previously using global functional connectivity (0.002–0.02 Hz, see Fig. 6C). Emergence and dissolution of high DRePS values (for example, across parts of the default mode network, visual and parietal areas as shown in Fig. 6A) at very slow time scale may be linked to the concept of ultra‐slow connectivity states as discussed in the previous brain connectivity studies [Allen et al., 2012; Cribben et al., 2012; Shirer et al., 2011; Yu et al., 2015]. It means that the DRePS variations are hardly random, but represent structured clusters of connectivity over time.
An important assessment step prior to any Hilbert transform based instantaneous phase analysis study (including DRePS) would be to evaluate Bedrosian identity and error signal (see “Instantaneous Phase of fMRI Time Series”) for the underlying data. Another factor to consider here would be possible dependence between phase information and amplitude changes in finite‐length signals such as fMRI time series. This is reflected in similar patterns of phase synchrony obtained by DRePS and SW‐ReHo (as a solely dependent method to signal amplitude) in Fig. 5 and Supporting Information Fig. S1. However, the main advantage of DRePS over amplitude‐based methods such as SW‐ReHo stems from its higher temporal resolution, as shown in the simulation results. Note that the impact of amplitude changes on phase information is not only relevant to DRePS, but also applies to all other phase synchrony analysis techniques dealing with finite‐length signals. The amplitude variations in task‐free fMRI data may originate from genuine “local phase synchrony” and/or confounding factors such as physiological artifacts, movement etc. In this study, we tried to alleviate these problematic confounds through multiple preprocessing steps as much as possible. Also, internal spatial smoothing of the DRePS framework, inherited from ReHo [Zuo et al., 2013], may enhance signal‐to‐noise ratio, as reflected in the difference between the simulation results of 27 (strong smoothing) and 7 (weaker smoothing) cube sizes in Supporting Information Fig. S1. However, there is still a chance that different physiological variations such as pseudo‐cyclic respiratory and cardiac changes are aliased into the narrow low frequency band of 0.03–0.07 Hz given the of 3 seconds in our study. This aliasing may result in an overlap between non‐neural fluctuations and real dynamic functional connectivity within the applied frequency band. Thus effective minimization of physiological confounds in data acquisition and preprocessing is important in DRePS just as it is important in other fMRI connectivity approaches.
We have shown in Fig. 6 and Supporting Information Fig. S2 that wide‐band filtering may have negligible impact on the analysis outcome of the proposed DRePS methodology. However, excessive expansion of the band‐pass filter can potentially cause considerable standard deviations in the error signal fluctuations. For example, one can see in Fig. 4 that the subject‐specific error signal averages and their corresponding RMS distributions within 0.03–0.07 Hz and 0.05–0.09 Hz are larger than 0.01–0.09 Hz and 0.03–0.11 Hz. This limitation may hamper extension to wider band filtering that may be of interest given recent evidence of BOLD contribution above 0.1 Hz [Chen and Glover, 2015]. A possible solution may be to decompose the BOLD dynamics into frequency bands of interest in order to make the band‐pass filter as restricted as possible [Bajaj et al., 2013; Xue et al., 2014; Zuo et al., 2010].
Non‐stationarity characteristics of task‐free functional connectivity may not be efficiently captured using low temporal resolution fMRI datasets. Indeed, recent fast EPI imaging techniques with sub‐second whole‐brain scanning time hold promise for deeper investigation of non‐linear and nonstationary patterns of brain dynamics [Paton et al., 2013]. From this perspective, the maximal capacity of the DRePS analysis framework is most likely to be exploited when studying brain functional connectivity in fast EPI images.
Conclusion
The current study introduces the instantaneous measure of Dynamic Regional Phase Synchrony (DRePS), based on time‐varying mean phase coherence among neighboring voxels in fMRI data. In contrast to sliding window approaches, DRePS provides single‐TR resolution with no loss of time points and no temporal smoothing. We observed that time‐varying DRePS changes are associated with spatially clustered brain areas, called local phase synchrony networks (LPSNs). Although evaluation of phase synchrony is not the only approach available to interrogate dynamic behavior of brain interactions, we propose that in the emerging field of dynamic functional connectivity, DRePS has the ability to provide new insights into normal and abnormal brain function.
Supporting information
Supporting Information
Supporting Information
Supporting Information
Supporting Information
Footnotes
Montreal Neurological Institute
Publicly available at: http://www.fmrib.ox.ac.uk/analysis/TFMs/sICA22_RSN21.nii.gz. Data were made available by the WU‐Minn Human Connectome Project (1U54MH091657), funded by the 16 NIH Institutes and Centers that Support the NIH Blueprint for Neuroscience Research.
References
- Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD (2012): Tracking whole‐brain connectivity dynamics in the resting state. Cereb Cortex bhs352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bajaj S, Adhikari BM, Dhamala M (2013): Higher frequency network activity flow predicts lower frequency node activity in intrinsic low‐frequency BOLD fluctuations. PLoS One 8:e64466 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bedrosian E (1963): A product theorem for Hilbert transforms. Proc IEEE 51:868–869. [Google Scholar]
- Biswal B, Zerrin Yetkin F, Haughton VM, Hyde JS (1995): Functional connectivity in the motor cortex of resting human brain using echo‐planar mri. Magn Reson Med 34:537–541. [DOI] [PubMed] [Google Scholar]
- Boashash B (2016): Time‐Frequency Signal Analysis and Processing, 2nd Edition: A Comprehensive Reference. The United Kingdom: Academic Press. 1056 p. [Google Scholar]
- Bullmore E, Sporns O (2009): Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:186–198. [DOI] [PubMed] [Google Scholar]
- Chang C, Glover GH (2010): Time‐frequency dynamics of resting‐state brain connectivity measured with fMRI. NeuroImage 50:81–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chao‐Gan Y, Yu‐Feng Z (2010): DPARSF: A MATLAB toolbox for “Pipeline” data analysis of resting‐state fMRI. Front Syst Neurosci 4:13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen JE, Glover GH (2015): BOLD fractional contribution to resting‐state functional connectivity above 0.1 Hz. NeuroImage 107:207–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cribben I, Haraldsdottir R, Atlas LY, Wager TD, Lindquist MA (2012): Dynamic connectivity regression: Determining state‐related changes in brain connectivity. NeuroImage 61:907–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damaraju E, Allen EA, Belger A, Ford JM, McEwen S, Mathalon DH, Mueller BA, Pearlson GD, Potkin SG, Preda A, Turner JA, Vaidya JG, van Erp TG, Calhoun VD (2014): Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia. NeuroImage Clin 5:298–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande G, LaConte S, Peltier S, Hu X (2009): Integrated local correlation: A new measure of local coherence in fMRI data. Hum Brain Mapp 30:13–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Williams S, Howard R, Frackowiak RSJ, Turner R (1996): Movement‐Related effects in fMRI time series. Magn Reson Med 35:346–355. [DOI] [PubMed] [Google Scholar]
- Glerean E, Salmi J, Lahnakoski JM, Jääskeläinen IP, Sams M (2012): Functional magnetic resonance imaging phase synchronization as a measure of dynamic functional connectivity. Brain Connect 2:91–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Handwerker DA, Roopchansingh V, Gonzalez‐Castillo J, Bandettini PA (2012): Periodic changes in fMRI connectivity. NeuroImage 63:1712–1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoff GEA‐J, Van Den Heuvel M, Benders MJNL, Kersbergen KJ, de Vries LS (2013): On development of functional brain connectivity in the young brain. Front Hum Neurosci 7:650 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudetz AG, Liu X, Pillay S (2015): Dynamic repertoire of intrinsic brain States is reduced in propofol‐induced unconsciousness. Brain Connect 5:10–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, Penna SD, Duyn JH, Glover GH, Gonzalez‐Castillo J, Handwerker DA, Keilholz S, Kiviniemi V, Leopold DA, de Pasquale F, Sporns O, Walter M, Chang C (2013): Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage 80:360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang L, Zuo XN (2015): Regional homogeneity: A multimodal, multiscale neuroimaging marker of the human connectome. The Neuroscientist, doi: 10.1177/1073858415595004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lachaux JP, Rodriguez E, Martinerie J, Varela FJ (1999): Measuring phase synchrony in brain signals. Hum Brain Mapp 8:194–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S‐J, Li Z, Wu G, Zhang M‐J, Franczak M, Antuono PG (2002): Alzheimer disease: Evaluation of a functional MR imaging index as a marker. Radiology 225:253–259. [DOI] [PubMed] [Google Scholar]
- Liu D, Yan C, Ren J, Yao L, Kiviniemi VJ, Zang Y (2010): Using coherence to measure regional homogeneity of resting‐state fMRI signal. Front Syst Neurosci 4 Available at: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2893000/. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Duyn JH (2013): Time‐varying functional network information extracted from brief instances of spontaneous brain activity. Proc Natl Acad Sci U S A 110:4392–4397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Wang K, YU C, He Y, Zhou Y, Liang M, Wang L, Jiang T (2008): Regional homogeneity, functional connectivity and imaging markers of Alzheimer's disease: A review of resting‐state fMRI studies. Neuropsychologia 46:1648–1656. [DOI] [PubMed] [Google Scholar]
- Li X, Zhu D, Jiang X, Jin C, Zhang X, Guo L, Zhang J, Hu X, Li L, Liu T (2014): Dynamic functional connectomics signatures for characterization and differentiation of PTSD patients. Hum Brain Mapp 35:1761–1778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLachlan G, Peel D (2000): Wiley Series in Probability and Statistics In: Finite Mixture Models. John Wiley & Sons, Inc; pp 420–427. Available at: http://onlinelibrary.wiley.com.ezp.lib.unimelb.edu.au/doi/10.1002/0471721182.scard/summary. [Google Scholar]
- Mormann F, Lehnertz K, David P, Elger EC (2000): Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients. Phys Nonlinear Phenom 144:358–369. [Google Scholar]
- Park H‐J, Friston K (2013): Structural and functional brain networks: From connections to cognition. Science 342:1238411 [DOI] [PubMed] [Google Scholar]
- Paton B, Raniga P, Egan G (2013): Non‐linear and nonstationary resting state functional connectivity examined using fast (sub‐second) functional MRI. Front Hum Neurosci 7 Available at: http://www.frontiersin.org/Community/AbstractDetails.aspx?ABS_DOI=10.3389/conf.fnhum.2013.212.00056. 23372547 [Google Scholar]
- Picinbono B (1997): On instantaneous amplitude and phase of signals. IEEE Trans Signal Process 45:552–560. [Google Scholar]
- Ponce‐Alvarez A, Deco G, Hagmann P, Romani GL, Mantini D, Corbetta M (2015): Resting‐state temporal synchronization networks emerge from connectivity topology and heterogeneity. PLoS Comput Biol 11:e1004100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riedl V, Bienkowska K, Strobel C, Tahmasian M, Grimmer T, Förster S, Friston KJ, Sorg C, Drzezga A (2014): Local activity determines functional connectivity in the resting human brain: A simultaneous FDG‐PET/fMRI study. J Neurosci off J Soc Neurosci 34:6260–6266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O (2010): Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 52:1059–1069. [DOI] [PubMed] [Google Scholar]
- Sepulcre J, Liu H, Talukdar T, Martincorena I, Yeo BTT, Buckner RL (2010): The organization of local and distant functional connectivity in the human brain. PLoS Comput Biol 6:e1000808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirer WR, Ryali S, Rykhlevskaia E, Menon V, Greicius MD (2011): Decoding subject‐driven cognitive states with whole‐brain connectivity patterns. Cereb Cortex bhr099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Moeller S, Xu J, Auerbach EJ, Woolrich MW, Beckmann CF, Jenkinson M, Andersson J, Glasser MF, Essen DCV, Feinberg DA, Yacoub ES, Ugurbil K (2012): Temporally‐independent functional modes of spontaneous brain activity. Proc Natl Acad Sci 109:3131–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- X Song, Y Zhang, Y Liu (2014): Frequency Specificity of Regional Homogeneity in the Resting‐State Human Brain. PLoS ONE 9:e86818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spetsieris PG, Ko JH, Tang CC, Nazem A, Sako W, Peng S, Ma Y, Dhawan V, Eidelberg D (2015): Metabolic resting‐state brain networks in health and disease. Proc Natl Acad Sci U S A 112:2563–2568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O (2011): The human connectome: A complex network. Ann N Y Acad Sci 1224:109–125. [DOI] [PubMed] [Google Scholar]
- Sun J, Small M (2009): Unified framework for detecting phase synchronization in coupled time series. Phys Rev E Stat Nonlin Soft Matter Phys 80:046219 [DOI] [PubMed] [Google Scholar]
- Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo DR (2012): Criticality in large‐scale brain FMRI dynamics unveiled by a novel point process analysis. Front Physiol 3:15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tailby C, Masterton RAJ, Huang JY, Jackson GD, Abbott DF (2015): Resting state functional connectivity changes induced by prior brain state are not network specific. NeuroImage 106:428–440. [DOI] [PubMed] [Google Scholar]
- Tang Y‐L, Ji G‐J, Yu Y, Wang J, Wang Z‐J, Zang Y‐F, Liao W, Ding M‐P (2014): Altered Regional Homogeneity in Rolandic Epilepsy: A Resting‐State fMRI Study. BioMed Res Int 2014:e960395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasi D, Wang R, Wang G‐J, Volkow ND (2014): Functional connectivity and brain activation: A synergistic approach. Cereb Cortex N Y N 1991 24:2619–2629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzourio‐Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M (2002): Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single‐subject brain. NeuroImage 15:273–289. [DOI] [PubMed] [Google Scholar]
- Venouziou M, Zhang H (2008): Characterizing the Hilbert transform by the Bedrosian theorem. J Math Anal Appl 338:1477–1481. [Google Scholar]
- Waites AB, Stanislavsky A, Abbott DF, Jackson GD (2005): Effect of prior cognitive state on resting state networks measured with functional connectivity. Hum Brain Mapp 24:59–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Saalmann YB, Pinsk MA, Arcaro MJ, Kastner S (2012): Electrophysiological low‐frequency coherence and cross‐frequency coupling contribute to BOLD connectivity. Neuron 76:1010–1020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue S‐W, Li D, Weng X‐C, Northoff G, Li D‐W (2014): Different neural manifestations of two slow frequency bands in resting functional magnetic resonance imaging: A systemic survey at regional, interregional, and network levels. Brain Connect 4:242–255. [DOI] [PubMed] [Google Scholar]
- Yu Q, Erhardt EB, Sui J, Du Y, He H, Hjelm D, Cetin MS, Rachakonda S, Miller RL, Pearlson G, Calhoun VD (2015): Assessing dynamic brain graphs of time‐varying connectivity in fMRI data: Application to healthy controls and patients with schizophrenia. NeuroImage 107:345–355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A, Fornito A, Cocchi L, Gollo LL, Breakspear M (2014): Time‐resolved resting‐state brain networks. Proc Natl Acad Sci 111:10341–10346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zang Y, Jiang T, Lu Y, He Y, Tian L (2004): Regional homogeneity approach to fMRI data analysis. NeuroImage 22:394–400. [DOI] [PubMed] [Google Scholar]
- Zuo X‐N, Di Martino A, Kelly C, Shehzad ZE, Gee DG, Klein DF, Castellanos FX, Biswal BB, Milham MP (2010): The oscillating brain: Complex and reliable. NeuroImage 49:1432–1445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo X‐N, Xu T, Jiang L, Yang Z, Cao X‐Y, He Y, Zang Y‐F, Castellanos FX, Milham MP (2013): Toward reliable characterization of functional homogeneity in the human brain: Preprocessing, scan duration, imaging resolution and computational space. NeuroImage 65:374–386. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information
Supporting Information
Supporting Information
Supporting Information


