Abstract
Spontaneous fluctuations of blood‐oxygenation level‐dependent functional magnetic resonance imaging (BOLD fMRI) signals are highly synchronous between brain regions that serve similar functions. This provides a means to investigate functional networks; however, most analysis techniques assume functional connections are constant over time. This may be problematic in the case of neurological disease, where functional connections may be highly variable. Recently, several methods have been proposed to determine moment‐to‐moment changes in the strength of functional connections over an imaging session (so called dynamic connectivity). Here a novel analysis framework based on a hierarchical observation modeling approach was proposed, to permit statistical inference of the presence of dynamic connectivity. A two‐level linear model composed of overlapping sliding windows of fMRI signals, incorporating the fact that overlapping windows are not independent was described. To test this approach, datasets were synthesized whereby functional connectivity was either constant (significant or insignificant) or modulated by an external input. The method successfully determines the statistical significance of a functional connection in phase with the modulation, and it exhibits greater sensitivity and specificity in detecting regions with variable connectivity, when compared with sliding‐window correlation analysis. For real data, this technique possesses greater reproducibility and provides a more discriminative estimate of dynamic connectivity than sliding‐window correlation analysis. Hum Brain Mapp 37:4566–4580, 2016. © 2016 Wiley Periodicals, Inc.
Keywords: fMRI, dynamic functional connectivity, hierarchical observation modeling, Bayesian inference, functional connection variability, coefficient of determination
INTRODUCTION
Since its inception, resting‐state functional magnetic resonance imaging (rs‐fMRI) has become a valuable tool for the identification of functional networks in the human brain. Resting‐state fMRI works on the assumption that the degree of synchrony between time‐varying blood‐oxygenation level‐dependent (BOLD) signals from spatially distinct brain regions indicates the strength of a functional connection (termed functional connectivity) [Beckmann et al., 2005; Fox and Raichle, 2007]. Most current approaches to the analysis of rs‐fMRI data assume that functional connectivity is constant over the duration of an imaging session. This assumption has the potential to overlook inherent variation in functional connectivity or variability in healthy brain or as a result of neurological disease [Hutchison et al., 2013]. Thus, recent analysis approaches have begun to investigate this potential dynamic behavior of functional connectivity.
One common technique used for dynamic connectivity analysis is sliding‐window cross‐correlation, which determines the temporal cross‐correlation between windowed segments of BOLD fMRI signals over time [Allen et al., 2014; Chang and Glover, 2010; Hutchison et al., 2013; Shen et al., 2015]. Using this technique, it has been shown that regions involved in higher level cognitive functions exhibit highly variable functional connectivity with the posterior cingulate cortex (PCC) of the default mode network (DMN) [Chang and Glover, 2010]. This approach has also demonstrated that functional connectivity networks change over time [Allen et al., 2014], and regions with reciprocal structural connections exhibit lower variability in functional connectivity [Shen et al., 2015]. Sliding‐window correlation analysis also shows that networks exhibit better stability at higher frequencies (0.5–0.8 Hz) [Lee et al., 2013].
The sliding‐window approach has also been used to investigate the consequences of non‐stationary fluctuations on the topological organization of functional brain networks [Zalesky et al., 2014]. It was shown that connections that link spatially distributed sub‐systems across the cortex exhibit the most dynamic behavior, transitioning in and out of correlation. It was suggested that spontaneous reconfiguration of resting‐state functional brain networks to high‐efficiency states represents a balance between optimizing information processing and minimizing metabolic expenditure. Gonzalez‐Castillo et al. [2014] evaluated pairwise connections between non‐overlapping ROIs of a parcellated brain and grouped them into three categories of connections, namely stable positive connections, variable positive connections, and negative connections. Similar to the Zalesky et al. [2014] findings, they found that within‐network connections are mostly static and variable connections correspond to between‐network connections, particularly those associated with higher‐order cognitive functions. They also compared the consistency of static and flexible connections between subjects and found that stable connections are mostly consistent between subjects, but the set of variable positive connections is different from subject to subject. This suggests that variability in functional connections is dependent on the cognitive state of the subject. Indeed, a recent study demonstrated that frontal cortex brain systems change their network configuration during task performance, which may explain the adaptive nature of frontal cortex relevant for cognitive functioning [Braun et al., 2015].
Other techniques have been explored to investigate the dynamic nature of functional connectivity. Using a point‐process based method, it has been demonstrated that brief instances of co‐activation of brain regions can be used to generate maps of the functional networks of the brain [Liu and Duyn, 2013]. That is, the dynamic nature of functional connections can actually be used to determine the presence of the connections themselves.
Despite these observations, previous approaches to analysis do not provide a model of the probabilistic behavior of estimated dynamic connectivity, and thus cannot permit statistical inference of functional connectivity at each point in time. This greatly limits data interpretation. In addition, in the presence of random noise, functional connectivity estimated by sliding‐window cross‐correlation analysis can vary greatly, even when regions are in fact stationary connected (or non‐connected) [Hutchison et al., 2013]. Therefore, sliding‐window correlation analysis is limited to determining if the range of variability of functional connectivity is significantly different between participant groups instead of providing insight into whether or not functional connectivity at a single time point is significant.
Friston et al. [2003] formulates the procedure used in conventional data analysis in terms of hierarchical linear models, and explains how parameters and hyperparameters of the model can be estimated jointly given the observations. Parameters are the effects of interest that determine what to expect in the observations. Hyperparameters correspond to the probabilistic behavior of parameters. Friston et al. [2002b] provides the example of a single‐sample t‐test to clarify this. The parameter in a single‐sample t‐test is the effect of interest that determines if the observations are different from zero. The hyperparameter corresponds to the variance of error between observed data and the parameters of interest. It is important to note that the parameters can be estimated without estimating the hyperparameters. In the example of a single‐sample t‐test, the parameter is estimated by the sample mean. However, in order to make a statistical inference on the estimated parameter (effect of interest), it is necessary to estimate the hyperparameters, say the residual sum of squares. It is valid to say that, in sliding‐window correlation analysis, the parameters are the dynamic connectivity coefficients as a function of time. It is impossible to make an inference on the parameters though, since the probabilistic behavior of the parameters, the hyperparameters, are not estimated by this technique.
In this article we formulate a new form of sliding‐window functional connectivity analysis based on a hierarchical observation model. This model has two levels. The first level parameters are the dynamic connectivity coefficients as a function of time. In the second level, the time‐average connectivity is modeled as our model parameter. First‐ and second‐level hyperparameters in our model correspond to the covariance of parameters. Bayesian estimation is used to jointly obtain model parameters and hyperparameters using an iterative expectation maximization (EM) algorithm. The EM algorithm iteratively updates the estimation of parameters and hyperparameters through expectation (E) and maximization (M) steps. In each (E) step, the conditional estimation of parameters given the data is updated while the hyperparameters are fixed. In the (M) steps, the maximum likelihood estimation of hyperparameters with fixed parameters is updated. This is a Parametric Empirical Bayes (PEB) since the hyperparameters are estimated from the observations. To test and validate our technique, we simulate data using a network topology with both stationary and non‐stationary functional connections based on a dynamic causal modeling forward model with realistic noise/variability components both at the neural and BOLD levels. Finally, we use our technique to analyze human fMRI data and compare its performance to sliding‐window cross‐correlation analysis.
MATERIALS AND METHODS
Theory
The theoretical background of Bayesian inference and its applications in neuroimaging have been presented previously [Friston et al., 2002a, 2002b]. There is an existing natural hierarchy in time‐varying functional connectivity that can be modeled with a two‐level hierarchical modeling approach, which we depict graphically in Figure 1. Our approach can be summarized as follows. In order to estimate dynamic connectivity between an observed signal and a predictor time series, the observed signal is modeled as a linear combination of time‐shifted windowed segments of the predictor signal at the first level. The fact that adjacent windows in the first level of our model overlap forces connectivity to change relatively smoothly over time. To incorporate this knowledge into our linear model, we augment the first level of our model with a second level, which can be thought of as providing prior constraints on the expectation and covariance of the first‐level dynamic connectivity parameters. Using a Bayesian approach, the problem reduces to finding the conditional mean and covariance of the model parameters given the BOLD fMRI time series at functional nodes [Friston et al., 2002b]. This can be done using an iterative expectation maximization algorithm. In this algorithm the parameters and hyperparameters of the hierarchical model are estimated jointly given the observations. Having the posterior density of the parameters, statistical inferences can be made about the estimated connectivity parameters at any specific time. Normalizing the conditional mean by its conditional error gives a t‐statistic for dynamic functional connectivity at any specific time point. The details of our approach follow.
Figure 1.
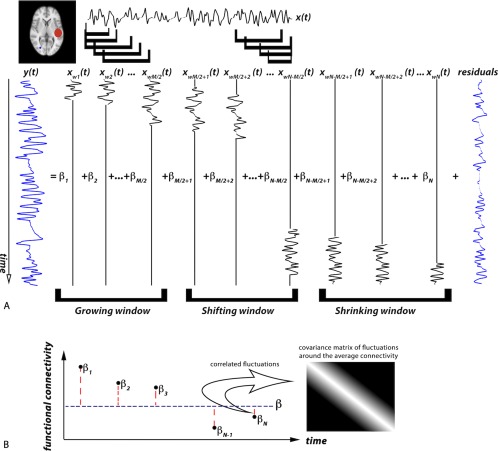
Schematic of sliding‐window hierarchical observation modeling for dynamic connectivity analysis. (A) The time series, , of an ROI (in red) is windowed into time‐shifted overlapping segments and entered into columns of the first‐level design matrix to estimate connectivity parameters, , that best fit a voxel time‐series, . The correspondence between dynamic connectivity time points and BOLD signal is obtained by shortening the window width toward the beginning and end of the BOLD signal in our proposed technique. The model starts with a window width equal to M/2 and grows in width until it reaches its maximum of M time points. From there the centered windows are shifted. The last M/2 windows are shrinking windows. (B) The second level models as distributed about an average, with correlated fluctuations. The covariance matrix of the fluctuations is shown in matrix format in grayscale. [Color figure can be viewed at http://wileyonlinelibrary.com]
Two‐level hierarchical model
We are proposing a voxel‐based approach to model the dynamic connectivity between each voxel's BOLD time series and a model regressor from a given region of interest (ROI). Without loss of generality, let represent the normalized BOLD time series of a random voxel in the brain, and let represent the normalized average time series of a seed ROI (see Fig. 1A). Classical general linear model (GLM) analysis estimates a single parameter that scales the entirety of to best fit the entirety of We model as a linear combination of time‐shifted windowed segments of , namely for the window centered at ith location. To accomplish this, we must estimate a set of parameters over time, , to form the linear combination of Each parameter thus provides a measure of the synchrony (i.e., connectivity) between and within the windowed segment . The complete set of over time thus provides a measure of dynamic connectivity. Because adjacent windows overlap, the estimates of connectivity should not fluctuate rapidly over time (i.e., within a typical imaging repetition time, TR, of 2–3 sec). That is, parameters for windows that overlap should exhibit some degree of correlation, which will dissipate as the overlap decreases. To incorporate this correlation behavior, we introduce a second level into our model, where dynamic functional connectivity is modeled as correlated fluctuations about an average connectivity (see Fig. 1B).
The first level of our technique can thus be expressed as:
| (1) |
where is a N × 1 vector of the normalized observed N‐point time series and is a square (N × N) design matrix constructed from the shifted windowed segments of the normalized model regressor (i.e., ROI signal), . is a N × 1 vector containing the first‐level scaling parameters for each segment of the ROI signal and represents connectivity as a function of time. In Eq. (1), models the first‐level error term. More specifically, the design matrix coefficient at the ith row and jth column, X(i,j), can be written as:
| (2) |
where is the width of each windowed segment, and is a weighting factor equal to the window width at the ith window position. Given the structure of our design matrix, the dynamic connectivity at the ith time point represents the similarity of windowed segments of the observed signal and the model regressor when the window is centered at the ith time‐point. This is an improvement over sliding‐window correlation where a lag is introduced between the observed signal and dynamic connectivity model, and thus dynamic connectivity is shorter than the observed signal. The way our design matrix is constructed allows us to calculate the dynamic connectivity with the same number of time points as the observed signal. However, if windows centered at the first M/2 time points had a width equal to M, they would extend back beyond the first observed data point. This is also true for the last M/2 window positions where the window would extend past the last acquired data point. Therefore, we need to crop the window width for M/2 start and end window positions. Hence, we start with a window width equal to M/2 and grow our window width until we reach our maximum window width, M. From there we start shifting our windows. The last M/2 windows are shrinking windows. As mentioned earlier, is a weighting factor equal to the window width at the ith position.
The first‐level error term, is assumed to be normally distributed, with zero mean and a covariance matrix, . To model the temporal correlations in the first‐level error, we assume a white‐noise distribution and an autoregressive (AR) random process. For conventional fMRI studies, a first‐level AR model is sufficient to capture the temporal correlations, where the temporal correlations decrease as samples become more separated in time (i.e., as overlap decreases) [Friston et al., 2002a]. However, for fast fMRI datasets with TR less than a second, it is suggested to use higher‐order AR models to account for the strong autocorrelation resulting from the higher temporal resolution [Jacobs et al., 2014].
Therefore, can be written as:
| (3) |
where is the variance of the first‐level error at each point, is the identity matrix, and is a weighting factor for the AR(1) random process modeled by The matrix coefficient at the ith row and jth column of , , can be written as:
| (4) |
for a given . The variance and weighting factor at this level are treated as unknown hyperparameters that will be optimized during the estimation step.
First‐level parameters can then be modeled as fluctuations about the average connectivity:
| (5) |
where is an unknown parameter with flat priors and models the average connectivity, and models the fluctuations in connectivity about . Substituting Eq. (5) into Eq. (1) gives:
| (6) |
Further, the weighting factor in Eq. (2) guarantees that , such that:
| (7) |
As we can see from Eq. (7), the first and last terms are identical to conventional GLM analysis, and the middle term models the dynamic connectivity.
In our model we assume that fluctuations in functional connectivity about the average connectivity are normally distributed with zero mean and a covariance matrix, . As discussed earlier, the fact that adjacent windows overlap forces connectivity to be temporally correlated. This correlation decreases as the number of overlapping time points decreases linearly with increasing separation of windows. Thus, the correlation of estimates of dynamic connectivity can be modeled as:
| (8) |
where is the variance of the second‐level fluctuations and models the linearly decreasing correlation between functional connections. The matrix coefficient at the ith row and jth column, , can be written as:
| (9) |
where M is the window width. The negative slope of the correlation factor ( ) defines the decay rate of the correlation between neighboring windows, which is dependent on both the distance between the two windows and the window width. It is important to note that for narrower windows (smaller M) the correlation factor drops more rapidly and allows higher fluctuation in the connectivity parameters, as expected.
This is a two‐level hierarchical observation model, and the parameters and hyperparameters can be estimated using a PEB approach, which has been described for neuroimaging previously [Friston et al., 2002a, 2002b]. In summary, the second‐level design matrix puts constraints on the priors of the first‐level parameters. The average connectivity at the second level is treated as an unknown parameter with flat priors, making our analysis an empirical Bayes approach. Having the prior distribution of parameters, Bayesian estimation is then performed to find the posterior (conditional) probability of the parameters given the data. Under the assumption of a Gaussian distribution of the first‐ and second‐level error terms of our hierarchical model, and that the posterior density of the parameters is also Gaussian, the problem therefore reduces to finding the conditional mean and covariance of the parameters given the observations.
Estimating the posterior density of the first‐level parameters (i.e., dynamic connectivity), we are enabled to perform a statistical inference on the dynamics of functional connectivity. In order to examine the strength of connectivity at a specific time point or over a period of time, a binary contrast vector is set. The contrast of the first‐level conditional mean can then be normalized by its estimated error to give a statistic that indicates the number of standard deviations that the mean is away from zero:
| (10) |
where and are the posterior (conditional) mean and covariance of the dynamic connectivity (level one parameters), respectively, given the data, estimated by an iterative expectation maximization algorithm, and is the binarized contrast vector set to investigate a specified portion of dynamic connectivity. T statistic is thus a test statistic that indicates the number of standard deviations by which the mean of the conditional distribution of the contrast deviates from zero.
Coefficient of determination
Here we propose a measure to quantify the degree of non‐stationarity of a functional connection. The degree of variability of a functional connection can be defined based on a comparison of the sums of squares of the residuals obtained from our dynamic connectivity analysis technique and from a minimal stationary model of connectivity. For the hierarchical model proposed in the previous section, the sum of squares of the first‐level residuals is defined as:
| (11) |
where the first‐level residual, , is defined to be:
| (12) |
After estimating the conventional static connectivity for a minimal GLM model, is defined as the sum of squares of the residuals of that model. This is defined for the minimal static connection model and therefore is the largest possible value for the sum of squares of the model residuals. The improvement in going from this worst possible model to a two‐level dynamic hierarchical model with no assumption on the stationarity of the connections can thus be written as:
| (13) |
In linear regression terminology, is called the coefficient of determination [Dobson and Barnett, 2008]. In cases where a functional connection is stationary in time, the static model is sufficient because the dynamic model converges to the static model. That is, the sum of squares of the residuals is nearly the same for the two models, and tends to zero. However, when a functional connection fluctuates over time, the static model does not provide a good fit, and portions of the variability in the observed signal due to non‐stationarity remain in the error term. On the other hand, the dynamic model provides a better fit, and so tends away from zero. In the case where the dynamic model provides a perfect fit, would reach zero, and the coefficient of determination would reach its maximum value of one. Thus, is bounded between zero and one, with zero indicating a stationary connection and one indicating a highly variable functional connection over time. thus provides a robust estimate of the variability of a functional connection.
Simulation Dataset
A simulation dataset consisting of a set of functional nodes was generated based on dynamic causal modeling (DCM). The length of the simulated time series was 10 minutes. This dataset was simulated in two levels, a neural level and a BOLD level. In the neural level, an external input is fed to each functional node to model the direct neural signal input to the node. The external input is modeled with a random binary (on/off) process to model each neuron in a firing state and at rest, independent from other neurons. The transition probabilities of this process are set such that the mean duration of rest (10 sec) is longer than mean duration of firing (2.5 sec) to model longer average rest than firing. A random process with a strength equal to 1/20 of the state difference of the binary process is then added to model the noise/variability in the neural level. This external input applied in the neural level is therefore sampled at a high sampling rate (every 5 ms). The rate of change in neural signal at each node is then modeled to be a linear combination of the external inputs feeding that node and the effect received from the rest of the network through functional connections connecting the nodes of the network using the DCM:
| (14) |
where is the neural time series, is its rate of change, A is the network matrix governing the network connections between nodes, is the external input to each node and is the weight controlling the effect of external inputs to the network. Connectivity between any pair of nodes can be stationary (connected or non‐connected) or non‐stationary (i.e., fluctuating) over time. A binary random process is applied to non‐stationary functional connections of the network to modulate the state of connectivity over time. Once the node time series are modeled in the neural level, they are converted into a hemodynamic response (or BOLD signal) using the nonlinear balloon model of neurovascular coupling, as described elsewhere [Buxton et al., 1998; Friston et al., 2003] and used previously in similar studies [Smith et al., 2011]. Finally, thermal white noise was added to model noise/variability at the BOLD level. BOLD time‐series are then sampled with the required TR. The simple network topology used to validate our dynamic connectivity analysis technique is shown in Figure 2A. This topology consists of functional nodes with stationary connections, nodes that are not connected, and nodes with connections modulated over time. All of the functional connections are direct connections originating from the hub functional node (node A) to avoid propagation of non‐stationarities to neighboring (adjacent) connections. This enables a stationary connection between nodes A and B while modulating the connectivity between functional nodes A and other nodes. Node B is functionally connected to node A with connection strength set randomly to a mean value of 0.7 and a standard deviation of 0.1 (range limited to 0.5–0.9). These values are adjusted to ensure a functional connection between nodes, but at the same time enable variability from one dataset to another (numbers are close to those used by Smith et al. [2011]). Node C is a functional node not connected to node A, but having an external input to model signals feeding into this node from other functional networks or noise at the neural level. Node D is an isolated node without any external input to model measurement noise. Node E is functionally connected to node A, but is modulated over time between connected and unconnected according to a random external bistable process in order to model a non‐stationary connection. The transition probabilities of this process are set such that the mean duration of connection and interrupted connection are equal and approximately 200 sec. The number of transitions is not limited and depends solely on the bistable random process. There is also an external input feeding to node E in order to model inputs from other functional networks. Knowing the transitions, we can also calculate the proportion of time that Node E is connected to Node A (i.e., from 0 to 1). All other simulation parameters are set accordingly based on previous work [Smith et al., 2011].
Figure 2.
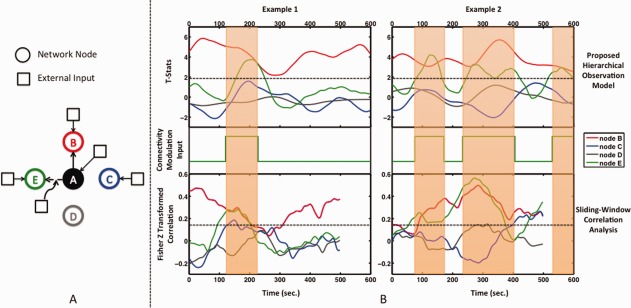
(A) Simulation dataset network topology based on [Smith et al., 2011]. Functional Node A is modeled to have a stationary connection with functional Node B and no connection to nodes C and D, where node C is receiving neural inputs to model a functional node, and node D only receives noise inputs to model a non‐functional node. The connection between node A and functional node E is modeled as a dynamic connection as determined by an external modulation input. (B) Examples of dynamic functional connectivity as determined by our hierarchical observation model (top) and sliding‐window correlation analysis (bottom) (window width = 90 sec), with the corresponding external input modulating the connection strength between node A and node E at the neural level (middle). The state transition of this input modulates the functional connectivity between the nodes at the neural level. Connection variability with a standard deviation of 1/20 of the state difference is applied. This is propagated through the network based on DCM modeling and then translated to a BOLD signal through the balloon model of the hemodynamic response function. The resulting BOLD signal is sampled every 3 sec. The stationary connection of node B is determined to be statistically significant (t > 1.96) at all time points using our approach, while sliding‐window correlation coefficients vary to near zero values. The connection of node E is determined to be statistically significant and in phase with the external modulation input. Note that dynamic connectivity estimated by sliding‐window correlation analysis has fewer time points than the actual BOLD signal due to windowing effect. However, the correspondence between dynamic connectivity time points and BOLD signal is obtained by shortening the window width toward the beginning and end of the BOLD signal in our proposed technique. [Color figure can be viewed at http://wileyonlinelibrary.com]
To investigate the effect of TR and noise level on the performance of our dynamic connectivity analysis technique, different simulation datasets were generated with TRs equal to 2 and 3 sec and noise levels equal to 0.5, 1, and 2 standard deviations of the BOLD signal. For each pair of TR and noise level, 50 realizations of the simulation dataset were generated with a different set of external inputs, connectivity modulation and functional connection strength. In the processing step, node A was considered to be the ROI node and the dynamic connectivity of all other nodes with this node was extracted using two different techniques: our proposed hierarchical observation modeling technique and sliding‐window correlation analysis. To investigate the effect of window width, we ran the analysis on the simulation datasets for different window widths (30, 60, 90, 150, and 300 sec worth of data). To calculate the variability of functional connections obtained by the hierarchical observation modeling technique, we used the coefficient of determination as defined in the previous section; it is a measure of improvement in goodness of fit compared with a static connectivity model. A coefficient of determination cannot be defined for sliding‐window correlation analysis since by its nature it does not provide a model of the residuals. However, various measures have been used previously to assess variability of sliding window correlations. Chang and Glover [2010] used the standard deviation of the Fisher Z‐transformed correlation coefficients as the measure of variability in functional connectivity. The coefficient of variation used by Gonzalez‐Castillo et al. [2014] to assess variability in connections basically divides the standard deviation of the Fisher Z‐transformed correlation coefficients by their average. Therefore, the coefficient of variation places emphasis on regions with high average connectivity and tries to divide them into stable positive connections and variable positive connections. However, it is not clear that a low coefficient of variation corresponds to a low average stable connection or a non‐stable positive connection. Zalesky et al. [2014] developed a statistic based on the height and duration of deviations from the median connectivity to test sliding‐window connectivity for evidence of non‐stationary temporal dynamics. Allen et al. [2014] introduced the amplitude of oscillations and Gonzalez‐Castillo et al. [2014] suggested the coefficient of variation for this purpose. For the sliding‐window correlation analysis, we chose the standard deviation of the Fisher Z‐transformed correlation coefficients as the measure of variability in functional connectivity. This is conceptually closer to the coefficient of determination we used for our proposed technique, as both measures summarize the deviation from an average model considering all time points.
Our aim was thus to compare the performance of the two methods in detecting the node with a modulated functional connection (node E) to the ROI node (node A), among the nodes with stationary functional connections (node B, C, and D) to node A. To perform our detection analysis, a threshold coefficient of determination was set, and nodes above the threshold were classified as highly variable connections, and nodes below the threshold were classified as stationary connections. The threshold was set to give a 5% false positive (FP) rate in detecting stationary connections (nodes B, C, and D to node A) as highly variable. The fraction of true positives (TP) in detecting non‐stationary connections (node E to node A) as highly variable was then calculated. This was, therefore, a measure of success in separating TP estimated from FP estimated variable connections. The FP‐based threshold was estimated from three stationary connections in network topology among all 50 simulated networks. Receiver operating characteristic (ROC) curves of the detection of non‐stationary functional connections among all the connections was compared between sliding‐window correlation analysis and our hierarchical observation modeling technique. From this ROC analysis, we also compared the sensitivity of our technique to that sliding‐window correlation analysis, as a function of the proportion of time that Node E was connected to Node A. This analysis allowed us to determine if our technique was more sensitive at detecting weak (or strong) but variable connections (i.e., when the proportion of time connected was near 0 or near 1).
Real Dataset
In order to compare the accuracy of any two techniques, ground truth is required. Unfortunately, the true state of connectivity between two regions of the brain at a given time is not at hand. Therefore, it is not possible to compare the accuracy of hierarchical observation modeling and sliding‐window correlation analysis using real datasets. It is possible, however, to compare the reproducibility of methods if we have repeated measurements of BOLD signal fluctuations acquired under the same conditions. Obviously, it is impossible to repeat a resting‐state fMRI experiment and expect dynamic connectivity to undergo the same fluctuations as the previous experiment. However, we can approximate repeated measurements of BOLD signals by down‐sampling a fast (low TR) fMRI dataset. Taking the first time point and every nth time point thereafter generates a down‐sampled BOLD signal time course. Another time course can be generated by starting with the second time point and every nth time point thereafter, and so on. As long as the effective TR of the down‐sampled datasets (i.e., original TR × n) is on the order of that of a typical resting‐state fMRI experiment (i.e., 2–3 sec), this procedure will generate n repeated measurements of real data under realistic noise conditions. From these repeated measurements, we can compute dynamic connectivity with a given ROI, expecting its dynamic behavior to be the same across the n data sets. Thus, we have a means to compare the reproducibility of our proposed method to that of sliding‐window correlation analysis. Real data methodology and data analysis are described in detail in the following sections.
Real data methodology
Resting‐state fMRI data from three healthy right‐handed volunteers with no known neurological disorders was provided by the fMRI Lab at the Rotman Research Institute, Toronto, ON, Canada. All images were collected using a Siemens TIM Trio 3 Tesla System (Siemens, Erlangen, Germany) equipped with a 32‐channel phased‐array head coil. Slice‐accelerated single shot gradient‐echo echo planar images (GE‐EPI) (“short TR”) were acquired with the following parameters: TR/TE = 380/30 ms; flip angle = 40°; FOV = 22 × 22 cm; 64 × 64 matrix; 1,880 volumes; fifteen 6.25‐mm thick slices. During image acquisition, subjects were asked to close their eyes and relax. T1‐weighted anatomical images were collected for anatomical registration of the fMRI data (MPRAGE: TR/TE = 2,400/2.43 ms, FOV = 256 × 256 mm, 192 × 256 × 256 matrix, voxel size 1 × 1 × 1 mm).
Image analysis
Preprocessing of resting‐state fMRI data was performed using the FMRIB Software Library (FSL, http://www.fmrib.ox.ac.uk/fsl) and consisted of: brain extraction using the Brain Extraction Tool (BET) [Smith, 2002], motion correction using MCFLIRT [Jenkinson et al., 2002], spatial smoothing (10‐mm FWHM), and temporal high‐pass filtering (using 0.01 Hz as the cutoff frequency). Images were further processed by entering them into a GLM with white matter and CSF signals as well as six translation/rotation head motion parameters as nuisance regressors. This produced a set of zero‐mean residual images for connectivity analysis. The resulting 4D resting‐state fMRI images were then down‐sampled by a factor of 8, generating eight distinct datasets with an effective TR of 3,040 ms.
An ROI was placed within the PCC (a 5 mm radius sphere, centered at Talairach coordinates x = −6, y = −58, z = 28) [Chang and Glover, 2010] to act as a primary node of the default mode network (DMN) of the brain. The average BOLD signal of the voxels within the ROI was then extracted for each of the eight datasets. Dynamic connectivity was estimated between the time series of the PCC ROI and that of every other voxel in the brain independently for each of the eight down‐sampled datasets using sliding‐window correlation analysis and our proposed hierarchical observation model. Maps of mean connectivity and variability for each subject were then generated by computing the temporal average and standard deviation of dynamic connectivity across the eight down‐sample datasets (in the form of t‐statistics for our technique and Fisher Z‐transformed correlation coefficients for sliding‐window correlation analysis). To compare the maps, a threshold was selected so that the total number of voxels in the final maps was equivalent between the two techniques (10% of the total number of brain voxels for mean connectivity and 5% of the total number of brain voxels for variability).
For each subject, the reproducibility of dynamic connectivity was assessed for our technique and sliding‐window correlation by computing Kendall's coefficient of concordance (KCC) for each voxel. KCC is a non‐parametric statistic that assesses the agreement among multiple raters, and has been used previously in fMRI studies [Zang et al., 2004] to evaluate the similarity of a time series of a given voxel with that of its nearest neighbors. Here we are interested in assessing the similarity of n estimated dynamic connectivity time series of a given ROI as a measure of reproducibility of our modeling technique. We then compared the reproducibility of our proposed technique with that of sliding‐window cross‐correlation analysis.
RESULTS
Simulation Dataset
Examples of results obtained from our sliding‐window hierarchical observation model approach and sliding‐window correlation analysis are shown in Figure 2B. For the hierarchical observation model approach, stationary connected Node B remains significantly connected (i.e., t > 1.96) at all time points, whereas for sliding‐window correlation analysis, Fisher‐transformed correlation coefficients vary over a wide range, to near zero in some cases. Non‐connected nodes C and D are deemed insignificant at all time points using our approach; sliding‐window correlation coefficients are also low. The statistical significance of Node E is detected by our model approach, in phase with the modulation input that generated the dynamic connection. Sliding‐window correlation coefficients also show an increase in phase with the modulation input, relative to other time points; however, no statistical significance can be assigned.
Figure 3 shows the percentage of true positives in detecting functional nodes with significantly variable functional connectivity for our analysis technique and sliding window correlation analysis, with different TRs and noise levels at varying window widths. Our proposed technique exhibits a higher percentage of true positives in detecting non‐stationary connections compared with sliding‐window correlation analysis for all TRs, noise levels and window widths.
Figure 3.
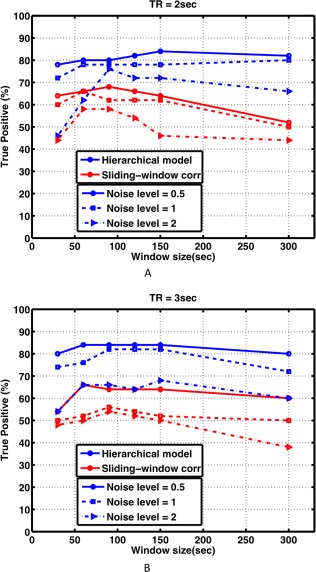
The percentage of true positives (TP) in detecting functional nodes with a non‐stationary (dynamic) connection to node A, for our hierarchical observation modeling technique and sliding‐window correlation analysis, at different noise levels equal to 0.5, 1, and 2 standard deviations of the BOLD signal, with (A) TR = 2 sec and (B) TR = 3 sec. The hierarchical model provides a greater true positive percentage across all conditions and window widths. [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 4 shows ROC curves for the detection of non‐stationary functional connectivity for sliding‐window correlation analysis and our hierarchical observation model technique, for a window width of 90 sec (45 time‐points for TR = 2 sec and 30 time‐points of TR = 3 sec). The hierarchical observation model clearly outperforms sliding‐window correlation analysis for both TRs. Similar results were obtained for other window widths (not shown).
Figure 4.
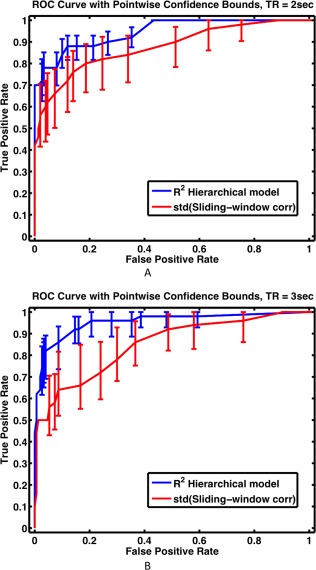
Receiver operating characteristic (ROC) curves for the detection of nodes with non‐stationary functional connections using our hierarchical observation modeling technique and sliding‐window correlation analysis, with (A) TR = 2 sec and (B) TR = 3 sec. The optimal window width of 90 sec was selected based on Figure 3. For our proposed hierarchical observation modeling technique, the coefficient of determination (R 2) was used as the measure of connection variability. For sliding‐window correlation analysis technique, the standard deviation (std) of the Fisher Z‐transformed correlation was used as the measure of connection variability. The hierarchical model possesses greater sensitivity and specificity across all conditions. [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 5A shows static functional connectivity (computed as Fisher Z‐transformed correlation coefficients) between node A and node E as a function of the proportion of time the nodes are connected. Shown below the x‐axis are examples of how the functional connection would be modulated to arrive at the specified proportions. As expected, there is a linear relationship between static estimates of functional connectivity and the proportion of time connected. Thus, low proportions are synonymous with very weak connections, and high proportions are synonymous with very strong connections. Figure 5B shows our measure of variability (the coefficient of determination) of the functional connection between node E and node A as a function of the proportion of time the nodes are connected. The same plot is shown in Figure 5C for the standard deviation of the Fisher Z‐transformed sliding‐window correlation coefficients. The 5% false positive (FP) rate threshold in detecting stationary connections (nodes B, C, and D to node A) as highly variable is depicted by the solid black line. The blue dots indicate the cases where variability was above the 5% false positive rate threshold, meaning they were correctly determined as variable connections (i.e., true positives). The red dots indicate the false negatives. Out of 50 realizations of the simulated variable connections, our hierarchical observation model exhibited only 8 (16%) false negatives, whereas sliding‐window correlation analysis exhibited 18 (36%) false negatives. Note that false negatives arise for very low and very high proportions, that is, for very weak or very strong connections. The false negatives for our model are more contained near proportions of 0 and 1 than sliding‐window correlation analysis, and in fact, some true positives for our model are present near 0 and 0.9. Overall, this demonstrates our technique is more sensitive and accurate at detecting very weak and very strong, but variable connections.
Figure 5.
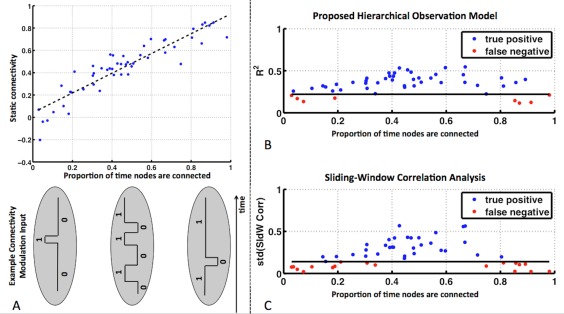
(A) Static functional connectivity between nodes A and E (computed as Fisher Z‐transformed correlation coefficient) as a function of the proportion of the time nodes A and E were connected. Below the x‐axis are examples of external input modulations that give rise to the specified proportions. (B) Coefficient of determination for the functional connection of node E to node A and (C) the standard deviation of the Fisher Z‐transformed sliding‐window correlation coefficients, as a function of the proportion of the time the nodes were connected. The solid black line indicates the 5% false positive (FP) rate threshold in detecting stationary connections (nodes B, C, and D to node A) as highly variable. [Color figure can be viewed at http://wileyonlinelibrary.com]
Real Dataset
Figure 6A shows maps of mean and standard deviation of dynamic connectivity across the eight down‐sampled datasets for one example subject. Regions with significantly high mean connectivity with the ROI are shown in red and include the entire posterior cingulate cortex and lateral parietal cortex. Regions with significantly variable functional connections with the ROI are shown in green. These regions include the inferior and middle frontal cortex (in the z = 22 mm slice), and the inferior and superior parietal lobe (in the z = 42, 52 mm slices). Upon visual inspection, the maps generated by our technique and sliding‐window correlation appear similar.
Figure 6.

(A) Map of temporal average (red) and connection variability (green) of dynamic functional connectivity with PCC for both techniques. Results are thresholded to produce the same number of voxels (10% of the total number of brain voxels for average connectivity and 5% of the total number of brain voxels for connection variability). (B) Functional connectivity time courses are shown for single voxels with high average functional connectivity (red), low average functional connectivity (gray), and highly variable connectivity (green). Although highly variable connections exhibit low average connectivity, functional connectivity is significantly high at some time‐points (i.e., passes the threshold). [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 6B shows time courses of connectivity for three selected voxels: one from the mean connectivity map (i.e., a voxel from the red area), one within gray matter but not within the maps (i.e., an insignificant voxel), and one from the variability map (i.e., a voxel from the green area). At first look, fluctuations in dynamic connectivity extracted using both techniques appear to provide similar information. Both of the red curves show significantly high dynamic connectivity throughout the scan, gray curves are basically below the threshold lines, and green curves show high variability and at some point pass the threshold. However, the proposed hierarchical observation modeling technique provides better discrimination between these voxels in the form of statistical significance of the connection as a function of time. That is, sliding‐window correlation analysis merely captures variation without statistic inference.
Although for real data we did not possess the truth regarding the times when connections and disconnections occur, we could, however, determine the strength of the connections that our technique classified as variable but sliding‐window correlation analysis did not. The average static connectivity (computed as the Pearson cross‐correlation coefficient) for voxels identified as variably connected by both techniques was 0.16 ± 0.04, whereas voxels determined to be variably connected by our technique but not by sliding‐window correlation analysis, exhibited an average static connectivity of 0.11 ± 0.04.
Figure 7 shows maps of reproducibility (expressed as KCC, thresholded at 0.8) for three subjects, for our proposed hierarchical observation modeling technique and sliding‐window correlation analysis. The hierarchical observation modeling technique exhibits greater and more widespread reproducibility within the grey matter compared with sliding‐window correlation analysis, as confirmed by the map of average KCC across the three subjects. Reproducibility is high throughout gray matter for our technique, regardless if it is connected to the PCC or not. This is expected, since a robust technique should generate reproducible results for both high and low functional connections.
Figure 7.
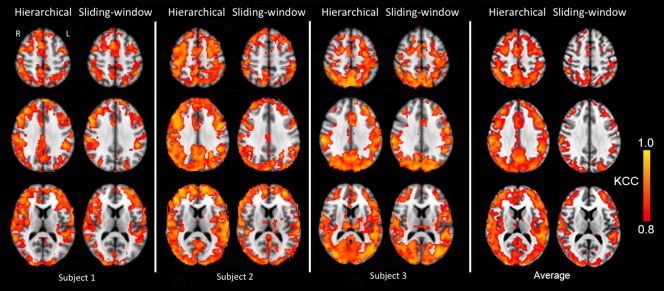
Maps of reproducibility of dynamic connectivity for three subjects for our proposed hierarchical observation modeling technique and sliding‐window correlation analysis, expressed as KCC (thresholded at KCC = 0.8). The hierarchical observation modeling technique exhibits greater and more widespread reproducibility within the gray matter compared with sliding‐window correlation analysis. This is confirmed by the average over all three subjects, at the right. [Color figure can be viewed at http://wileyonlinelibrary.com]
DISCUSSION
We have proposed a two‐level hierarchical observation model for dynamic functional connectivity analysis and solved it with Bayesian estimation. Using simulation datasets we demonstrated that a two‐level hierarchical observation model successfully permits statistical inference of the variability of functional connections. Using real data, we demonstrated that a two‐level hierarchical observation model exhibits better discrimination ability and reproducibility than sliding‐window correlation analysis. Our findings also demonstrate some key technical points, which we discuss below.
Connectivity Fluctuations of Non‐Interest
One main concern about sliding‐window correlation analysis is that white noise, physiological signals and even signals originating from completely disconnected brain regions can give rise to high amplitude fluctuations of functional connectivity [Hutchison et al., 2013]. This was confirmed by our results as well (Fig. 2B). The fluctuations we observed in the sliding‐window correlation of nodes B, C, and D with node A are due to noise properties, and not a real modulation of functional connectivity. In fact, the amplitudes of these fluctuations were on the order of those observed for node E, which did exhibit real modulation. Thus, it is difficult to set a threshold and test the statistical significance of functional connection strength at each time point using sliding‐window correlation analysis. By modeling the residuals in our hierarchical observation model technique, we are enabled to provide statistical inference of the significance of functional connectivity at each time point. So, while there is some modulation of connectivity in the presence of fluctuations of non‐interest using our model, it remains statistically insignificant, whereas real modulations are detected with a high true positive rate (Fig. 3) and high sensitivity and specificity (Fig. 4).
Effect of Window Width
The choice of window width is another concern with sliding‐window correlation analysis. Short duration windows do not capture coherency in the low‐frequency components of resting‐state BOLD signals, and long duration windows fail to detect transitions in functional connectivity states. Gonzalez‐Castillo et al. [2014] did not investigate window widths less than 60 sec in order to maintain sufficient data points to calculate meaningful correlations. Even with fast fMRI datasets with a high number of data points per unit time, window widths less than 100 sec have been shown to generate connectivity maps with high spatial and temporal variability [Lee et al., 2013]. Our results (Fig. 3) support this and clearly demonstrate that the detection power of sliding‐window correlation analysis is highly dependent to the choice of window width. This issue is somewhat resolved by our hierarchical observation model technique. Although windowed segments of the model signal are used as separate regressors in our design matrix, incorporating all segments into a single model reduces the sensitivity to the choice of window width. It is also important to note that detection power is nearly constant when the window width increases above 60 sec.
Our current model states that the correlation between dynamic connectivity extracted from neighboring windows decreases linearly as the windows separate in time. In addition, this decay in correlation is inversely related to window width (i.e., for narrower windows, correlation decreases more rapidly). This permits connectivity to fluctuate more for narrower windows since the window overlap is smaller. However, this assumes that the data have sufficiently high signal‐to‐noise ratio such that the first level parameters do not fluctuate wildly due to noise. Noise effects will dominate if the windows have a narrow width. This can be seen in Fig. 3; for the case when the noise level was equal to twice the standard deviation of the simulated signal, analyzing dynamic connectivity with window widths narrower than 90 sec gave a low true positive rate (<70%). Extending a linear decay model of correlation between dynamic connectivity extracted from neighboring windows to non‐linear models is a possible topic for future work. In addition, our proposed hierarchical model can also be investigated with non‐overlapping windows, by modifying the first‐level design matrix and second level covariance model.
The Effect of TR
Our results show that as the noise level increases, the detection power of highly variable connections decreases. This was the case for both the TR = 2 and TR = 3 sec datasets (Fig. 3). However, it is important to note that the decrease in detection power for TR = 2 sec was smaller than the decrease in detection power for TR = 3 sec (see also Fig. 4). This suggests that detection power is more related to temporal signal‐to‐noise ratio (tSNR) rather than image SNR. In other words, with the same SNR, it is important to collect as many image volumes per unit time as possible to obtain a better estimate of dynamic functional connectivity. Therefore, imaging techniques that permit sub‐second TR, such as MR‐encephalography [Lee et al., 2013], and multiplexed EPI [Feinberg et al., 2010] may further improve dynamic functional connectivity analysis.
Multiple Comparisons in Bayesian Inference
Our two‐level hierarchical observation model extracts the dynamic connectivity between an observed signal and a predictor time series. In order to apply this model to a multivoxel dataset, we have treated each voxel independently. Bayesian inference provides the posterior probability of the effect given the observations for each voxel. In our case, it provides the probability that a single voxel signal and the predictor time series are synchronous at a specific time point given the observations. This differs from classical inference, where the P‐value indicates the probability of obtaining the same (or larger) observation in the absence of connectivity at a specific time point, and the null hypothesis is rejected for extremely low P‐values. A distinct advantage of having the posterior probability is that one can reject the alternative hypothesis, and conclude that two signals are not synchronous at a given time point. This is not possible with classical inference, where one can only reject the null hypothesis. It follows that although the significance of a connection at each time point is being examined, there is no need to adjust for multiple comparisons. This is an important aspect for the examination of dynamic connectivity, since the probability that a connection is significant at a given time point should not be dependent on the length of the dataset.
Spatial information contained within the entire brain volume could also be used to improve our model, by using a spatiotemporal Bayesian model, in which voxel‐specific effects are constrained by responses of other voxels. The application of a spatiotemporal model with empirical Bayes has been explained in detail by Friston et al. [2002b].
The Effect of the Proportion of Time That Nodes are Connected
As expected, static functional connectivity increased linearly with the proportion of time that two nodes were functionally connected (Fig. 5A). Both the coefficient of determination and the standard deviation of sliding‐window dynamic connectivity reached their maximum value when the proportion of the time that nodes were connected was about 0.5 (Fig. 5B,C). In these cases, functional connections are highly variable, and static functional connectivity is unable to model this variable relationship between the nodes. However, the coefficient of determination is higher (more discriminative) for proportions near 0 and 1 and fewer connections are missed (i.e., fewer red dots). Proportions near 0 and 1 represent nodes that are non‐connected or connected for the vast majority of the time, respectively. In other words, both techniques perform equally well for highly variable connections, but our technique is more sensitive at detecting variable connections for weak connections that become momentarily strong and for strong connections that become momentarily weak.
For our real datasets, the examination of the variability maps revealed that the additional voxels identified as variable by our technique exhibited low static functional connectivity. Given the results presented in Figure 5B,C, this finding supports a conclusion that our hierarchical observation modeling technique is more sensitive at classifying briefly variable connections that are weak on average.
Discrimination Power and Reproducibility for Real Datasets
When the maps of mean connectivity and variable connectivity are visually inspected (Fig. 6A), little difference is observed between hierarchical observation modeling and sliding‐window correlation analysis when the number of voxels are equalized. This demonstrates that the two methods possess similar sensitivity for detecting connected and variably connected regions. However, when we observe the time course of connectivity of a single voxel, it is clear that hierarchical observation modeling provides the ability to determine the significance of a connection at any point in time and with better discrimination power than sliding‐window correlation analysis (i.e., the separation between significant and insignificant time courses is much greater for hierarchical observation modeling). As discussed above for simulation datasets, noise and artifacts give rise to high‐amplitude fluctuations in connectivity when using sliding‐window correlation analysis, making it difficult to set a threshold and to test the statistical significance of a functional connection at any given point in time. However, undesired components of the fMRI signal are isolated in the first‐level residual term in our hierarchical observation model, permitting statistical testing at any point in time.
Although method accuracies cannot be compared since the ground truth about the fluctuations in functional connectivity is not known, we were able to compare method reproducibility. As was shown in Figure 7, our hierarchical observation modeling technique gives a more reproducible estimation of the dynamic behavior of functional connectivity within the gray matter for both high and low functional connections. It is important to note that a low functional connection in gray matter is also reproducible with our technique. Results for sliding‐window correlation analysis of real datasets, however, are less reproducible, in agreement with our simulation data, which demonstrated that sliding‐window correlation analysis has a higher rate of false positives for the same detection power.
In summary, a two‐level hierarchical observation model permits statistical inference of dynamic functional connectivity, which is lacking from current analysis approaches. A two‐level hierarchical observation model should have important implications for studies aimed at determining the fluctuating resting states of the human brain and studies investigating the variability of functional connections as a result of neurological and neurovascular disease. These types of studies are increasingly prominent in the current literature, and the modeling framework presented here will provide the means to make statistical inferences of the dynamic nature of functional connections.
ACKNOWLEDGMENTS
The authors would like to thank Dr. Stephen M. Smith and Dr. Mark Woolrich from Oxford University's FMRIB centre for providing the computer code for generating the functional node simulation dataset, which was modified for the purposes of this study. The authors would also like to thank Dr. Jean Chen and Dr. Ali‐Mohammad Golestani from the fMRI Lab of the Rotman Research Institute for providing the short‐TR resting‐state fMRI data.
Contributor Information
Alireza Sojoudi, Email: asojoudi@ucalgary.ca.
Bradley G. Goodyear, Email: goodyear@ucalgary.ca.
REFERENCES
- Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD (2014): Tracking whole‐brain connectivity dynamics in the resting state. Cereb Cortex 24:663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, DeLuca M, Devlin JT, Smith SM (2005): Investigations into resting‐state connectivity using independent component analysis. Philos Trans R Soc Lond Ser B, Biol Sci 360:1001–1013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braun U, Schafer A, Walter H, Erk S, Romanczuk‐Seiferth N, Haddad L, Schweiger JI, Grimm O, Heinz A, Tost H, Meyer‐Lindenberg A, Bassett DS (2015): Dynamic reconfiguration of frontal brain networks during executive cognition in humans. Proc Natl Acad Sci U S A 112:11678–11683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton RB, Wong EC, Frank LR (1998): Dynamics of blood flow and oxygenation changes during brain activation: The balloon model. Magn Reson Med 39:855–864. [DOI] [PubMed] [Google Scholar]
- Chang C, Glover GH (2010): Time‐frequency dynamics of resting‐state brain connectivity measured with fMRI. Neuroimage 50:81–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobson AJ, Barnett AG (2008): An Introduction to Generalized Linear Models, 3rd ed Boca Raton: Chapman and Hall/CRC Press. [Google Scholar]
- Feinberg DA, Moeller S, Smith SM, Auerbach E, Ramanna S, Gunther M, Glasser MF, Miller KL, Ugurbil K, Yacoub E (2010): Multiplexed echo planar imaging for sub‐second whole brain FMRI and fast diffusion imaging. PloS One 5:e15710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Raichle ME (2007): Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev Neurosci 8:700–711. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Glaser DE, Henson RN, Kiebel S, Phillips C, Ashburner J (2002a): Classical and Bayesian inference in neuroimaging: Applications. Neuroimage 16:484–512. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Penny W, Phillips C, Kiebel S, Hinton G, Ashburner J (2002b): Classical and Bayesian inference in neuroimaging: Theory. Neuroimage 16:465–483. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Penny W (2003): Dynamic causal modelling. Neuroimage 19:1273–1302. [DOI] [PubMed] [Google Scholar]
- Gonzalez‐Castillo J, Handwerker DA, Robinson ME, Hoy CW, Buchanan LC, Saad ZS, Bandettini PA (2014): The spatial structure of resting state connectivity stability on the scale of minutes. Front Neurosci 8:138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, Della Penna S, Duyn JH, Glover GH, Gonzalez‐Castillo J, Handwerker DA, Keilholz S, Kiviniemi V, Leopold DA, de Pasquale F, Sporns O, Walter M, Chang C (2013): Dynamic functional connectivity: Promise, issues, and interpretations. Neuroimage 80:360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs J, Stich J, Zahneisen B, Asslander J, Ramantani G, Schulze‐Bonhage A, Korinthenberg R, Hennig J, LeVan P (2014): Fast fMRI provides high statistical power in the analysis of epileptic networks. Neuroimage 88:282–294. [DOI] [PubMed] [Google Scholar]
- Jenkinson M, Bannister P, Brady M, Smith S (2002): Improved optimization for the robust and accurate linear registration and motion correction of brain images. Neuroimage 17:825–841. [DOI] [PubMed] [Google Scholar]
- Lee HL, Zahneisen B, Hugger T, LeVan P, Hennig J (2013): Tracking dynamic resting‐state networks at higher frequencies using MR‐encephalography. Neuroimage 65:216–222. [DOI] [PubMed] [Google Scholar]
- Liu X, Duyn JH (2013): Time‐varying functional network information extracted from brief instances of spontaneous brain activity. Proc Natl Acad Sci U S A 110:4392–4397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen K, Hutchison RM, Bezgin G, Everling S, McIntosh AR (2015): Network structure shapes spontaneous functional connectivity dynamics. J Neurosci 35:5579–5588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM (2002): Fast robust automated brain extraction. Hum Brain Mapp 17:143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Salimi‐Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW (2011): Network modelling methods for FMRI. Neuroimage 54:875–891. [DOI] [PubMed] [Google Scholar]
- Zalesky A, Fornito A, Cocchi L, Gollo LL, Breakspear M (2014): Time‐resolved resting‐state brain networks. Proc Natl Acad Sci U S A 111:10341–10346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zang Y, Jiang T, Lu Y, He Y, Tian L (2004): Regional homogeneity approach to fMRI data analysis. Neuroimage 22:394–400. [DOI] [PubMed] [Google Scholar]


