Non-inferiority Testing for Risk Ratio, Odds Ratio and Number Needed to Treat in Three-arm Trial

Abstract

Three-arm non-inferiority (NI) trial including the experimental treatment, an active reference treatment, and a placebo where the outcome of interest is binary are considered. While the risk difference (RD) is the most common and well explored functional form for testing efficacy (or effectiveness), however, recent FDA guideline suggested measures such as relative risk (RR), odds ratio (OR), number needed to treat (NNT) among others, on the basis of which NI can be claimed for binary outcome. Albeit, developing test based on these different functions of binary outcome are challenging. This is because the construction and interpretation of NI margin for such functions are non-trivial extensions of RD based approach. A Frequentist test based on traditional fraction margin approach for RR, OR and NNT are proposed first. Furthermore a conditional testing approach is developed by incorporating assay sensitivity (AS) condition directly into NI testing. A detailed discussion of sample size/power calculation are also put forward which could be readily used while designing such trials in practice. A clinical trial data is reanalyzed to demonstrate the presented approach.

1. Introduction

With the steady improvements in health care technologies, standard of care, and clinical outcomes, the incremental benefits of newly developed interventions may be only marginal over existing treatments. However, in the presence of established treatments/therapies, placebo-controlled Randomized Control Trials (RCTs) are neither ethical nor clinically justified. Active-controlled NI trial is an attractive alternative in such situations, particularly when a slightly less efficacious treatment may be preferable to a group of patients in view of lower toxicity, less intensive side effects, ease of delivery and other less incapacitating factors. NI trials are intended to show if the new intervention retains a substantial portion of the active control effect, dictated by a pre-specified margin, often termed as NI margin (δ). Such margin must be prospectively defined and should be so chosen to reflect maximum acceptable extent of clinical non-inferiority of an experimental treatment. Further detailed discussion on the construction and desirable properties of NI margin can be found in the regulatory guidelines(FDA (2016), ICHE9 (2009), ICHE10 (2009)) and references (e.g. Althunian et al. (2017), Schumi and Wittes (2011), Brown et al. (2006), Hung and Wang (2004)). NI trials may or may not include a placebo arm due to ethical reasons. Two-arm placebo-free NI trials make two important assumptions regarding Assay Sensitivity (ICHE9 (2009), ICHE10 (2009)) and Constancy and depends heavily on external validations (D’Agostino et al. (2003) and FDA (2016)) and several other limiting factors as specified in Kieser and Stucke (2016). To alleviate some of these issues and if ethically acceptable and practically feasible, it is recommended by EMA (2005) to include a placebo arm in the current trial, resulting in a three-arm “gold-standard” design that has greater confidence concerning AS and lesser concern related to external validity.

For three-arm trial in the Frequentist setup, Pigeot et al. (2003) first proposed the fraction margin approach, where NI margin is adaptively formulated as the pre-specified negative fraction of the unknown effect size of the reference treatment over placebo in the current three-arm trial. Kieser and Friede (2007) extended this approach for the binary outcome for risk difference (RD). While RD is the simplest functional form for binary outcomes, as mentioned in the recent FDA guidance (FDA (2016), Page 24) there are other functionals (e.g., risk ratio (RR), odds ratio (OR), number needed to treat (NNT), risk reduction etc.) which could also be used to test the treatment effect (Hashemi et al., 1997) and claim NI. Under the NI setup, there exists published work for odds ratio using Frequentist’s approach for two-arm trial, see for example Hilton (2010) and Rousson and Seifert (2008), but no work exists for three-arm trial. Also, to the best of our knowledge for RR and NNT (Keefe et al., 2013) type functional form, no work on NI testing exists for either two or three-arm trial. This motivates us to introduce such methods and develop NI test procedure under Frequentist approach in this article. Apart from extending popular tests based on fraction margin approach for such functionals, in this paper we also propose a new approach based on conditional principle which directly employs the AS condition under Frequentist setup. This approach shows additional gain in sample size to achieve a desired level of power under certain situations. Extensive tables are calculated for sample size for all three types of functionals.

The rest of the article is organized as follows. In Section 2, we give the NI hypothesis and the details of NI margin. We show the non-uniqueness of the NI margin for different functionals. In Section 3, we discuss the existing method and propose a conditional Frequentist’s method for testing NI. In Section 4, we discuss the power and sample size calculation for the three functionals. Finally in Section 5, we apply our proposed methods on a published clinical trial data set. We conclude the article with discussions in Section 6. All proofs are provided in supplementary file for brevity purpose.

2. Non-inferiority Hypothesis Testing Setup

For a three-arm trial, fraction margin approach (Pigeot et al. (2003), Kieser and Friede (2007)) is popularly used for testing NI hypothesis and finding the corresponding decision rule. We begin our illustration borrowing the notations from Kieser and Friede (2007). Denote the primary end-points from the Placebo (P), Reference (R) and the Experimental (E) treatment in the current trial by X_P, X_R and X_E respectively, each following Bin (n_l, π_l), where π_l is the probability of success and n_l is the sample size for the l^th arm, l ∈ {P, R, E}. Without loss of generality, we assume that higher response probabilities indicate greater treatment benefits. Gamalo et al. (2011) used the two-arm fixed margin approach for NI testing considering the RD as the function of interest. Kieser and Friede (2007) formulated the three-arm NI hypothesis for binary outcome under fraction margin approach, where NI hypothesis for RD in terms of NI margin δ is given by

$$H_0:{\pi }_E-{\pi }_R\le \delta \text{vs}.H_1:{\pi }_E-{\pi }_R>\delta .$$ (2.1)

In the fraction margin approach, the construction of δ(< 0) can be mathematically expressed as δ = f (π_R − π_P ), where f is a negative fraction f ∈ [−1, 0] assuming the condition of assay sensitivity, that is, π_R − π_P > 0 holds. Figure 1(a) shows the NI region in the difference scale, which is directed to the right of π_R + δ.

Figure 1:

Three-arm NI Trial for (a) RD Margin with δ, (b) RR Margin 1 with δ₁ and (c) ϵ −substantial non-inferiority for NNT

Before discussing the NI testing for a three-arm NI trial in terms of (1) RR, (2) OR and (3) NNT, we first reformulate the NI hypothesis using a general functional form as

$$H_0:\psi \left({\pi }_E,{\pi }_R\right)\le g(\delta )\text{vs}.H_1:\psi \left({\pi }_E,{\pi }_R\right)>g(\delta ),$$ (2.2)

where the decision boundary g (δ) is some function of δ, such that |δ| ∈ [0, 1], which denotes an appropriate portion of the unknown effect size of the active-control over placebo. RD hypothesis expressed in equation (2.1) can be also seen as a special case of above. For example, consider ψ(π_E, π_R) = π_E − π_R, then the boundary is g(δ) = δ, which also happens to be the same as the NI margin itself. In the RR (or OR) scale, one can choose g (δ) = 1+δ, implying the NI margin is δ(< 0), which we term as Margin 1. Choosing a too restrictive δ, that is close to zero, would require large number of subjects to claim NI, whereas a too loose choice of δ may potentially approve a substantially inferior drug. In the RR (or OR) scale we construct δ = δ₁ = f(1 − ψ(π_P, π_R)(< 0), where f ∈ [−1, 0] as in the RD case. Using this expression for δ₁, we can write the hypothesis in (2.2) as

$$H_0^1:\psi \left({\pi }_E,{\pi }_R\right)\le 1+f\left(1-\psi \left({\pi }_P,{\pi }_R\right)\right)\text{vs}.H_1^1:\psi \left({\pi }_E,{\pi }_R\right)>1+f\left(1-\psi \left({\pi }_P,{\pi }_R\right)\right).$$ (2.3)

In practice, clinical considerations should drive the choice of f and some of the reasonable values are $-\frac{1}{2},-\frac{1}{3},-\frac{1}{5}$. For all testing (e.g. RD, RR, OR etc.) choosing f = 0 implies NI margin is zero, hence the hypothesis in (2.1) and (2.3) becomes the superiority test of π_E over π_R. While for f = −1 the active control loses its practical significance over placebo, hence the test reduces to the simple superiority test of π_E over π_P. This can be easily checked for all functional forms considered in this paper. Note that, construction of a margin must satisfy these two boundary conditions. However, there may be other possible mathematical form which can adhere to these, thus implying such a margin may not be unique. To elucidate this fact one can also formulate the NI hypothesis by taking g(δ) = δ and constructing δ = δ₂ = (ψ(π_P, π_R))^−f(> 0) where f ∈ [−1, 0] (see Wangge et al. (2013)). In this case the NI margin is 1 − g(δ) = 1 − δ₂, which we term as Margin 2. Thus the NI hypothesis under Margin 2 becomes

$$H_0^2:\psi \left({\pi }_E,{\pi }_R\right)\le {\left(\psi \left({\pi }_P,{\pi }_R\right)\right)}^{-f}\text{vs}.H_1^2:\psi \left({\pi }_E,{\pi }_R\right)>{\left(\psi \left({\pi }_P,{\pi }_R\right)\right)}^{-f}.$$ (2.4)

The two NI margins satisfy both the boundary conditions for f = 0 and −1, however, lead to two slightly different NI testing. Next, we discuss the specific cases for RR, OR and NNT.

2.1. Risk Ratio

Margin 1 : For RR the function $\psi \left({\pi }_E,{\pi }_R\right)=\frac{{\pi }_E}{{\pi }_R}$ and $\psi \left({\pi }_P,{\pi }_R\right)=\frac{{\pi }_P}{{\pi }_R}$. Thus under Margin 1, the NI hypothesis testing in (2.3) becomes:

$$H_0^1:\frac{{\pi }_E}{{\pi }_R}\le 1+f(1-\frac{{\pi }_P}{{\pi }_R})\text{vs}{H}_1^1:\frac{{\pi }_E}{{\pi }_R}>1+f(1-\frac{{\pi }_P}{{\pi }_R}).$$ (2.5)

Margin 1, i.e. δ = δ₁ is constructed as the fraction of the difference between the unity and ratio of placebo to active control (reference) treatment effect, in the current three-arm trial.

As can be seen from Figure 1 (b), the NI region is directed to the right side of the point (1+δ₁). Clearly from (2.5) we see that for f = 0 and f = −1, the test satisfies two boundary conditions. Now putting θ = 1 + f and after simplification the hypothesis in equation (2.5) can be written as

$$H_0^1:{\pi }_E-\theta {\pi }_R-(1-\theta ){\pi }_P\le 0\text{vs}{H}_1^1:{\pi }_E-\theta {\pi }_R-(1-\theta ){\pi }_P>0,$$ (2.6)

where θ is the pre-specified fraction of the effect of the reference drug relative to the placebo. The test drug would be non-inferior if its efficacy relative to placebo achieves at least θ×100% of the efficacy of the reference drug compared to placebo. Although different values of θ (θ ∈ [0, 1]) are chosen for different purposes, specifically for the NI testing of the new drug, θ is restricted in [0.5,1), thus making sure that the new drug retains at least 50% effect of the active control.

Margin 2 : For $\psi \left({\pi }_E,{\pi }_R\right)=\frac{{\pi }_E}{{\pi }_R}$ and $\psi \left({\pi }_P,{\pi }_R\right)=\frac{{\pi }_P}{{\pi }_R}$, the NI hypothesis testing in (2.4) under RR Margin 2 can be written by taking logarithm as

$$\begin{gathered} H_0^2:\log \left({\pi }_E\right)-\log \left({\pi }_R\right)\le -f\left[\log \left({\pi }_P\right)-\log \left({\pi }_R\right)\right]\text{vs}. \\ {H}_1^2:\log \left({\pi }_E\right)-\log \left({\pi }_R\right)>-f\left[\log \left({\pi }_P\right)-\log \left({\pi }_R\right)\right]. \end{gathered}$$ (2.7)

Taking θ = 1+f as before, the following hypothesis can be written after some simplification

$$H_0^2:\log \left({\pi }_E\right)-\theta \log \left({\pi }_R\right)-(1-\theta )\log \left({\pi }_P\right)\le 0\text{vs}.H_1^2:\log \left({\pi }_E\right)-\theta \log \left({\pi }_R\right)-(1-\theta )\log \left({\pi }_P\right)>0.$$ (2.8)

Compared to the Margin 1 hypothesis in (2.6), Margin 2 hypothesis above represents the testing in the logarithm of each proportion (i.e. π_l, l ∈ {P, R, E}). The interpretation of θ in terms of effect retention in the log scale is little more involved compared to Margin 1. Albeit, since all the Frequentist tests are asymptotic normal approximation, the log transformed version of Margin 2 is expected to perform better.

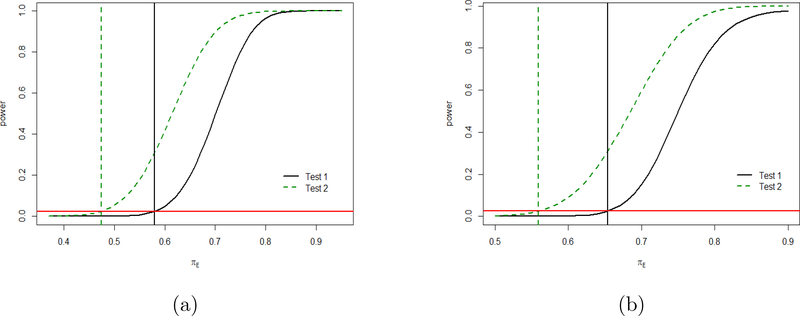
To compare the NI regions we plot the boundary g(δ) as function of θ ∈ [0, 1] for test 1 and test 2 respectively in Figure 2 (a) and observe that both are increasing functions of θ. The area above the two curves are the respective NI regions, which happen to be bounded within the unit square. The vertical line corresponds to θ = 0.5 and the region to its right corresponds to the values of θ chosen for NI testing. However, for all values of θ, the NI region for NI hypothesis testing 2 (2.8) is bigger than that for NI testing 1 (2.6), implying that the NI testing 2 is more powerful as compared to the NI testing 1. This is also depicted in Figure 3 (a) where we plot the power curves for θ = 0.8 and total sample size of N = 300 under equal allocation, keeping π_R and π_P fixed at 0.7 and 0.1 respectively. Details of the derivation for the power curves are given later in Section 3. The vertical lines represent the respective values of π_E under the null hypothesis for the respective margins.

Figure 2:

Comparison of NI regions for RR tests in (a) and OR tests in (b).

Figure 3:

Comparison of power curves for two margins of RR in (a) and OR in (b).

Remark 1: Since Margin 2 is formulated in the logarithm scale, same value of θ will have different impact in terms of margin width, thus further affecting resulting NI test. One can show that under the same preservation level θ (or loss-of-effect f) of E and for fixed control effect in the RR scale $(\frac{{\pi }_R}{{\pi }_P})$, the ratio $\frac{{\pi }_E}{{\pi }_P}$ has to exceed a smaller quantity under Margin 2 as compared to Margin 1 for E to be non-inferior. This implies that the NI test based on Margin 2 gives a little more relaxed margin as compared to the test based on Margin 1, without compromising θ. This is equivalent to saying that if we fix the NI margin or equivalently the quantity that $\frac{{\pi }_E}{{\pi }_P}$ needs to exceed for E to be non-inferior, then θ under Margin 2 has to be larger than that under Margin 1 to achieve this. Denoting θ by θ₁ under Margin 1 and by θ₂ under Margin 2, we can express θ₁ as a function of θ₂ as ${\theta }_1=\frac{{(\frac{{\pi }_R}{{\pi }_P})}^{{\theta }_2}-1}{\frac{{\pi }_R}{{\pi }_P}-1}$. Although in this paper we calculate the power and sample size under Margin 2 across different θ for all functionals, the same will be true under Margin 1 for a slightly smaller θ which can be readily obtained from the above relation between θ₁ and θ₂. For example, when π_R = 0.7 and π_P = 0.5 giving $\frac{{\pi }_R}{{\pi }_P}=1.4$, and taking θ₂ = 0.8, we obtain the value of θ₁ as 0.772.

Remark 2: Note that when the function of interest is Risk reduction, the function ψ(π_E, π_R) takes the form $1-\frac{{\pi }_E}{{\pi }_R}$. From (2.5) we have $H_0^1:1-\frac{{\pi }_E}{{\pi }_R}\ge -f(1-\frac{{\pi }_P}{{\pi }_R})\text{vs}.H_1^1:1-\frac{{\pi }_E}{{\pi }_R}<-f(1-\frac{{\pi }_P}{{\pi }_R})$. Hence the NI hypothesis and test procedures developed for risk ratio is exactly identical for risk reduction, and thus the latter does not need any separate derivation. Risk Reduction is another possible functional form mentioned in the FDA guidance (FDA, 2016).

2.2. Odds Ratio

Margin 1 : For OR the function $\psi \left({\pi }_E,{\pi }_R\right)=\frac{\frac{{\pi }_E}{\left(1-{\pi }_E\right)}}{\frac{{\pi }_R}{\left(1-{\pi }_R\right)}}$, and similarly one can define ψ(π_P, π_R). Thus, under Margin 1, the NI testing in (2.3) becomes the following:

$$H_0^1:\frac{\frac{{\pi }_E}{\left(1-{\pi }_E\right)}}{\frac{{\pi }_R}{\left(1-{\pi }_R\right)}}\le 1+f(1-\frac{\frac{{\pi }_P}{\left(1-{\pi }_P\right)}}{\frac{{\pi }_R}{\left(1-{\pi }_R\right)}})\text{vs}.H_1^1:\frac{\frac{{\pi }_E}{\left(1-{\pi }_E\right)}}{\frac{{\pi }_R}{\left(1-{\pi }_R\right)}}>1+f(1-\frac{\frac{{\pi }_P}{\left(1-{\pi }_P\right)}}{\frac{{\pi }_R}{\left(1-{\pi }_R\right)}})$$ (2.9)

Clearly from (2.9) we see that for f = 0, the margin δ₁ becomes 0 and hence the above test will be a superiority test of the experimental treatment (E) over the control (R) in the current trial since $\frac{{\pi }_E}{\left(1-{\pi }_E\right)}\le \frac{{\pi }_R}{\left(1-{\pi }_R\right)}\Rightarrow {\pi }_E\le {\pi }_R$. Again for f = −1, we see that the test (2.9) becomes the simple superiority test of π_E over π_P. Now putting θ = 1 + f and after some simplification the above test becomes

$$H_0^1:\frac{{\pi }_E}{\left(1-{\pi }_E\right)}-\theta \frac{{\pi }_R}{\left(1-{\pi }_R\right)}-(1-\theta )\frac{{\pi }_P}{\left(1-{\pi }_P\right)}\le 0\text{vs}.H_1^1:\frac{{\pi }_E}{\left(1-{\pi }_E\right)}-\theta \frac{{\pi }_R}{\left(1-{\pi }_R\right)}-(1-\theta )\frac{{\pi }_P}{\left(1-{\pi }_R\right)},$$ (2.10)

where θ holds the similar interpretation as described in the context of RR before.

Margin 2 : The NI hypothesis testing in (2.4), under Margin 2, can be written by taking logarithm as

$$\begin{gathered} H_0^2:\log (\frac{{\pi }_E}{(1-{\pi }_E)})-\log (\frac{{\pi }_R}{(1-{\pi }_R)})\le -f(\log (\frac{{\pi }_P}{(1-{\pi }_P)})-\log (\frac{{\pi }_R}{(1-{\pi }_R)}))\text{vs}. \\ {H}_1^2:\log (\frac{{\pi }_E}{(1-{\pi }_E)})-\log (\frac{{\pi }_R}{(1-{\pi }_R)})>-f(\log (\frac{{\pi }_P}{(1-{\pi }_P)})-\log (\frac{{\pi }_R}{(1-{\pi }_R)})). \end{gathered}$$ (2.11)

Taking θ = 1 + f the following test can be obtained from (2.7) after some simplification

$$\begin{gathered} H_0^2:\log (\frac{{\pi }_E}{(1-{\pi }_E)})-\theta \log (\frac{{\pi }_R}{(1-{\pi }_R)})-(1-\theta )\log (\frac{{\pi }_P}{(1-{\pi }_P)})\le 0\text{vs}. \\ {H}_1^2:\log (\frac{{\pi }_E}{(1-{\pi }_E)})-\theta \log (\frac{{\pi }_R}{(1-{\pi }_R)})-(1-\theta )\log (\frac{{\pi }_P}{(1-{\pi }_P)})>0. \end{gathered}$$ (2.12)

Similar to RR, we plot NI regions and the power curves for OR under the two tests resulted from the respective NI margins in Figure 2 (b) and Figure 3 (b) respectively. We again observe that test 2 is more powerful compared to test 1 for OR since the former gives a more relaxed margin compared to the latter under fixed θ and fixed control effect in the OR scale. The relation between the two preservation levels under the respective margins in the OR scale becomes ${\theta }_1=\frac{{\left(\frac{{\pi }_R/(1-{\pi }_R)}{{\pi }_R/(1-{\pi }_P)}\right)}^{{\theta }_2}-1}{\frac{{\pi }_R/(1-{\pi }_R)}{{\pi }_P/(1-{\pi }_P)}-1}$. Note that as in RR case the logarithm transformations make the data conform more closely to the Normal distribution giving better asymptotic performance.

2.3. NNT

As discussed for RD the NI hypothesis in (2.1) and (2.2) will be of the following form:

$$H_0:{\pi }_E-({\pi }_R+\delta )\le 0\text{vs}.H_1:{\pi }_E-({\pi }_R+\delta )>0,$$ (2.13)

where the boundary g(δ) = δ, which is constructed as the negative fraction of the unknown difference between the control and placebo in the current trial (Kieser and Friede, 2007). Since NNT is the inverse of RD, one would want the value of NNT to be as small as possible. The higher the value of NNT, less effective is the treatment (Keefe et al., 2013). The ideal case would be when all patients in the treatment arm show improvement while none in the control arm has improved leading to the value of NNT to be 1. For treatments like pain killer for acute pain, an effective treatment is expected to have an NNT between 2–5. In other situations like using aspirin after heart attack, a quite higher NNT (40 +) would indicate an effective therapy, while NNT can be as low as 1 for treating a sensitive bacterial infection with antibiotics (Cook and Sackett, 1995). In the context of NI testing for RD, experimental intervention E is declared to be non-inferior over R if the treatment effect π_E exceeds π_R +δ, (δ < 0) (in Figure 1 (a)). Hence the NI hypothesis for NNT can be formulated from (2.13) by taking the reciprocal of both sides. However, to avoid taking the reciprocal of 0, one can formulate NI hypothesis, where E will be declared ϵ-substantially non-inferior over R if π_E exceeds π_R + δ + ϵ, where ϵ > 0 is a pre-chosen small integer. We write the ϵ-substantial NI hypothesis below:

$$H_0:{\pi }_E-({\pi }_R+\delta )\le ϵ\text{vs}.H_1:{\pi }_E-({\pi }_R+\delta )>ϵ.$$ (2.14)

Figure 1 (c) shows the ϵ-substantial non-inferiority region which is to the right of the point π_R + δ + ϵ. Now we formulate the NI hypothesis for NNT from (2.14) in the following with the condition that π_E > π_R + δ

$$H_0:\frac{1}{{\pi }_E-({\pi }_R+\delta )}\ge 1/ϵ=D\text{vs}.H_1:\frac{1}{{\pi }_E-({\pi }_R+\delta )}<1/ϵ=D,$$ (2.15)

where D is a positive integer denoting the additional number of patients required to declare NI of E over R (Cook and Sackett, 1995). Note that in case π_E < (π_R + δ), NI testing of E over R does not have any practical meaning. After some simplification and putting θ = 1 + f, f ∈ [−1, 0] and δ = f (π_R − π_P ), the NI hypothesis for NNT in (2.15) takes the form:

$$H_0:{\pi }_E-\theta {\pi }_R-(1-\theta ){\pi }_P\le ϵ\text{vs}{H}_1:{\pi }_E-\theta {\pi }_R-(1-\theta ){\pi }_P>ϵ.$$ (2.16)

This is exactly same as the hypothesis for RD when ϵ → 0. The interpretation of θ and f remain same as for the RD case.

3. Proposed Approach for NI Testing

For testing NI hypothesis we follow the general guideline developed by Pigeot et al. (2003) and Kieser and Friede (2007). The MLE of the Binomial proportion π_l is ${\widehat{\pi }}_l=\frac{X_l}{n_l}$ and its variance is given by $\frac{{\pi }_l(1-{\pi }_l)}{n_l}$, l ∈ {E, R, P}. In the Frequentist’s approach the test statistics are based on the maximum likelihood estimator (MLE) of the parametric function ψ (π_E, π_R) and ψ (π_P, π_R) and under asymptotic normality, the statistic $\frac{\psi ({\widehat{\pi }}_E,{\widehat{\pi }}_R)-g(\widehat{\delta })}{\sqrt{Var(\psi ({\widehat{\pi }}_E,{\widehat{\pi }}_R))}}$ is assumed to follow N (0, 1) under H₀ in (2.2), where $g(\widehat{\delta })$ is some function of $\psi ({\widehat{\pi }}_P,{\widehat{\pi }}_R)$. Instead of MLE one may also consider the restricted maximum likelihood estimator (RMLE) of π_l subject to the constraint ψ (π_E, π_R) = g (δ). More specifically for risk difference the test statistic for three-arm NI testing is $\frac{T}{\sqrt{{\sigma }_T^2}}$, where, $T={\widehat{\pi }}_E-\theta {\widehat{\pi }}_R-(1-\theta ){\widehat{\pi }}_P$ and ${\sigma }_T^2=\frac{{\pi }_E(1-{\pi }_E)}{n_E}+{\theta }^2\frac{{\pi }_R(1-{\pi }_R)}{n_R}+{(1-\theta )}^2\frac{{\pi }_P(1-{\pi }_P)}{n_P}$. Though Pigeot et al. (2003) explicitly mentioned that superiority of the reference over placebo (i.e the AS condition) must be tested before one employs fraction-margin approach for testing NI hypothesis. However, in practice this key first step is often ignored. This may lead to somewhat over estimation of the sample size. Moreover the AS condition (either tested or assumed) is not used further in NI testing itself. In this article we first develop traditional Frequentist’s approach of NI testing for RR, OR and NNT closely following the marginal approach developed earlier for RD. It turns out as a common rule that the pretest of AS over NI is subordinated in the complete test procedure. As mentioned in Mielke and Munk (2009) the power of simply testing NI nearly coincides with the power of complete (or joint) test procedure for commonly used alternatives. Thus, the focus of testing non-inferiority is almost always on NI hypothesis itself, albeit AS condition must be verified first in all practical examples. We note that, for all the examples in the current manuscript we always ensured first that the AS condition is met. However, since the two test statistics used for AS and NI, respectively, are correlated, we put forward the fact that the hypothesis for NI testing must be tested conditionally based on the fact that the AS null hypothesis is rejected already. Next, we propose the conditional approach of NI testing, thus incorporating the AS condition π_R − π_P > 0 in the Frequentist’s statistic itself.

In the following two subsections we give the Frequentist’s approach of NI testing based on the marginal and conditional approach. We discuss NI testing for both Margin 1 and Margin 2. Note that all Frequentist’s tests are asymptotic approximate and the performance of such tests depend upon the accuracy of transformation for all the functions. We note that one can also perform score test or likelihood ratio test (Mielke, 2010; Tang et al., 2014) to conduct the NI testing. However, in our experience the performance of such tests are very close to that of normal approximation. This is not completely surprising given the large sample size, which, often is a general characteristic of many NI trials. Specifically, some additional results of score test in that direction are included in supplementary material. Albeit, as suggested by one reviewer these are all plausible alternatives and may enhance performance of the test in certain situations.

3.1. Test Procedure and Sample Size: Marginal Approach

Rather than developing separate tests for RR, OR and NNT, we first write the the NI hypotheses in (2.6), (2.8), (2.10) and (2.12) and (2.15) in a general form as

$$H_0:g({\pi }_E)-\theta g({\pi }_R)-(1-\theta )g({\pi }_P)\le ϵ\text{vs}.H_1:g({\pi }_E)-\theta g({\pi }_R)-(1-\theta )g({\pi }_P)>ϵ,$$ (3.1)

where ϵ ≥ 0. For RR and OR, ϵ = 0 while for NNT, ϵ > 0. For RR test 1: g(π_l) = π_l, for RR test 2: g(π_l) = log(π_l). For OR test 1: g(π_l) = π_l/(1 − π_l) and for OR test 2: g(π_l) = log(π_l/(1 − π_l)), and for NNT, g(π_l) = π_l, l ∈ {E, R, P}. Now consider the test statistic $T=g({\widehat{\pi }}_E)-\theta g({\widehat{\pi }}_R)-(1-\theta )g({\widehat{\pi }}_P)-ϵ$ for testing the NI hypothesis in (3.1), ${\widehat{\pi }}_l$ being the MLE of π_l, l ∈ {E, R, P}. The variance of T will be ${\sigma }_T^2=Var(g({\widehat{\pi }}_E))+{\theta }^{2}Var(g({\widehat{\pi }}_R))+{(1-\theta )}^{2}Var(g({\widehat{\pi }}_P))$, where $Var(g({\widehat{\pi }}_l))\simeq Var({\widehat{\pi }}_l){(g^{\prime }({\widehat{\pi }}_l))}^2$ at ${\widehat{\pi }}_l={\pi }_l$, for l ∈ {E, R, P}. For g(π_l) = π_l, ${\sigma }_l^2=\frac{{\pi }_l(1-{\pi }_l)}{n_l}$ (RR test 1 and NNT); for g(π_l) = log(π_l) _{${\sigma }_l^2=\frac{(1-{\pi }_l)}{n_l{\pi }_l}$}; for g(π_l) = π_l/(1 − π_l), ${\sigma }_l^2=\frac{{\pi }_l}{n_l{(1-{\pi }_l)}^3}$; and for g(π_l) = log(π_l/(1 − π_l)), ${\sigma }_l^2=\frac{1}{n_l{\pi }_l(1-{\pi }_l)}$. Now under asymptotic normality we assume $Z=T/\sqrt{{\sigma }_T^2}~N(0,1)$ under H₀, since μ_T = E(T) = g(π_E) − θg(π_R) – (1 − θ)g(π_P) − ϵ = 0 under H₀. So the rejection criteria will be Z > z_1−α, where z_1−α is the 100(1−α)% of the standard Normal distribution. The value of α is usually chosen to be 0.025.

3.1.1. Sample Size

For the sample size determination we first derive the power function of the above test procedure. We use the notation π_l,1 to denote the proportion in the l^th arm under the alternative hypothesis, and π_l,0 to denote the same under H₀. Borrowing notations from Kieser and Friede (2007), let ψ = g(π_E) − θg(π_R) – (1 − θ)g(π_P) − ϵ and let ψ₁ = g(π_E,1) − θg(π_R,1) − (1 − θ)g(π_P,1) − ϵ for the alternative to be detected. The variance of the MLE $\widehat{\psi }$ under H₁ will be $Va{r}^{H_1}(\widehat{\psi })={\sigma }_{E,1}^2+{\theta }^2{\sigma }_{R,1}^2+{(1-\theta )}^2{\sigma }_{P,1}^2$, where ${\sigma }_{l,1}^2$ is ${\sigma }_l^2$ with π_l replaced by π_l,1 and the expression of ${\sigma }_l^2$ for NNT and different RR and OR tests are described above. Now, for simplicity, we express the sample size in the reference (n_R) and the experimental (n_E) arms as the ratio r₁ and r₂ respectively of the sample size n_P = n, say, in the placebo arm such that n_P : n_R : n_E = 1 : n_R/n_P : n_E/n_P = 1 : r₁ : r₂. Here r₁ and r₂ are known positive quantities that determine the allocation ratio of the sample sizes in the arms R and E respectively, relative to the arm P. The total sample size, thus, would be N = n(1 + r₁ + r₂). Since $Va{r}^{H_1}(\widehat{\psi })$ involves n_P, n_R and n_E we replace the latter two in terms of the ratios of n_P and denote ${\tau }_1^2=n_{P}Va{r}^{H_1}(\widehat{\psi })$ under H₁. Analogously, ψ₀ and τ₀ denote the same expressions as ψ₁ and τ₁, replacing π_l,1 by π_l,0 under H₀, satisfying the restriction g(π_E,0) − θg(π_R,0) – (1 − θ)g(π_P,0) = ϵ and this implies ψ₀ = 0. Under asymptotic normality $Z_0=\sqrt{n_P}\widehat{\psi }/{\tau }_0$ and $Z_1=\sqrt{n_P}(\widehat{\psi }-{\psi }_1)/{\tau }_1$ are assumed to follow N(0, 1) under H₀ and H₁ in (3.1) respectively. Hence, the asymptotic expression of power is given by

$$P_{H_1}(Z_0\ge z_{1-\alpha })=P_{H_1}(Z_1>z_{1-\alpha }\frac{{\tau }_0}{{\tau }_1}-\sqrt{n_P}\frac{{\psi }_1}{{\tau }_1})=1-\mathrm{\Phi }(z_{1-\alpha }\frac{{\tau }_0}{{\tau }_1}-\sqrt{n_P}\frac{{\psi }_1}{{\tau }_1}),$$ (3.2)

where Φ(·) denotes the cumulative distribution function of N(0, 1). For achieving a power of (1 − β) % the sample size n_P can be obtained explicitly as

$$n_P={(z_{1-\alpha }{\tau }_0+z_{1-\beta }{\tau }_1)}^2\frac{1}{{({\psi }_1)}^2}.$$ (3.3)

3.2. Test Procedure and Sample Size: Conditional Approach

We introduce our conditional approach for NI hypothesis testing given in (3.1) by incorporating the AS condition (i.e. π_R > π_P ). For finding the MLE we truncate the parameter space of (π_E, π_R, π_P ) such that it belongs to {π_E, π_R, π_P : π_E ∈ [0, 1], π_R ∈ [0, 1], π_P ∈ [0, 1], π_R > π_P }. One may develop an LR-test based on the statistic

$$T=g({\widehat{\pi }}_E)-\theta g({\widehat{\pi }}_R)-(1-\theta )g({\widehat{\pi }}_P)-ϵ$$ (3.4)

under null hypothesis subject to the imposed condition (π_R > π_P ) via Wald-type test. Following Mutze et al. (2015) one can improve the convergence via the restricted maximum likelihood (RML) which requires solving under H₀

$$({\widehat{\pi }}_{E,RML},{\widehat{\pi }}_{R,RML},{\widehat{\pi }}_{P,RML})=\underset{g({\pi }_E)-\theta g({\pi }_R)-(1-\theta )g({\pi }_P)-ϵ\le 0,{\pi }_R>{\pi }_P}{\arg \max }\log l({\pi }_E,{\pi }_R,{\pi }_P),$$ (3.5)

where logl(π_E, π_R, π_P ) denotes the log-likelihood. This optimization problem can be solved numerically but no closed form expression is possible. One practical strategy to reduce computational burden, that is often recommended in practice, is to work with unrestricted MLE which is $T_{ML}=g({\widehat{\pi }}_{E,ML})-\theta g({\widehat{\pi }}_{R,ML})-(1-\theta )g({\widehat{\pi }}_{P,ML})-ϵ$, however only considering the part restricted by ${\widehat{\pi }}_{R,ML}>{\widehat{\pi }}_{P,ML}$, which is $T_{RML}\simeq T_{ML}\ast I\left[{\widehat{\pi }}_{R,ML}-{\widehat{\pi }}_{P,ML}>0\right]$. This strategy (see Huang et al. (2011) and Kulldorff (1997)) is proved to be quite useful in many practical applications. Since working with product of random variables is little cumbersome, one can further show that $f(T_{RML})\simeq f(T_{ML}|{\widehat{\pi }}_{R,ML}-{\widehat{\pi }}_{P,ML}>0)\times Pr\left[{\widehat{\pi }}_{R,ML}-{\widehat{\pi }}_{P,ML}>0\right]$. Since $0\le {\widehat{\pi }}_{R,ML},{\widehat{\pi }}_{P,ML}\le 1$, are i.i.d. random variables, it is easy to prove $Pr\left[{\widehat{\pi }}_{R,ML}-{\widehat{\pi }}_{P,ML}>0\right]=\frac{1}{2}$ which can be absorbed as a constant. Hence for all practical purpose one can consider the distribution of the test statistic, $(T_{ML}|{\widehat{\pi }}_{R,ML}>{\widehat{\pi }}_{P,ML})\equiv (g({\widehat{\pi }}_{E,ML})-\theta g({\widehat{\pi }}_{R,ML})-(1-\theta )g({\widehat{\pi }}_{P,ML})-ϵ|{\widehat{\pi }}_{R,ML}>{\widehat{\pi }}_{P,ML})$. For notational simplicity from now onwards we denote the ML estimate ${\widehat{\pi }}_{l,ML}$ by ${\widehat{\pi }}_l$, l ∈ {E, R, P}. Note that for the specific forms of g(π_l) defined above for RR, OR and NNT, g(π_l) is monotone in π_l, l ∈ {E, R, P}. Hence imposing the restriction π_R > π_P is equivalent to g(π_R) > g(π_P ). This leads to the modified test statistic for NI testing: $(W=g({\widehat{\pi }}_E)-\theta g({\widehat{\pi }}_R)-(1-\theta )g({\widehat{\pi }}_P)-ϵ|g({\widehat{\pi }}_R)>g({\widehat{\pi }}_P))$. We write W as (U – ψV – ψ|V > 0), where $U=g({\widehat{\pi }}_E)-g({\widehat{\pi }}_P)$ and $V=g({\widehat{\pi }}_R)-g({\widehat{\pi }}_P)$ are two correlated random variables. Under the asymptotic normality of W we have $\frac{W-{\mu }_w}{{\sigma }_w}~AN(0,1)$, where E[W] = μ_w and $V[W]={\sigma }_w^2$.

Lemma 3.2.1 Under conditional normal approximation, the mean μ_w and variance ${\sigma }_w^2$ of $W=g({\widehat{\pi }}_E)-\theta g({\widehat{\pi }}_R)-(1-\theta )g({\widehat{\pi }}_P)-ϵ|g({\widehat{\pi }}_R)-g({\widehat{\pi }}_P)>0$, for ϵ ≥ 0 are given by

$$\begin{gathered} {\mu }_w={\mu }_U+{\sigma }_U\frac{\rho }{c}\varphi (d)-\theta \left({\mu }_V+{\sigma }_V\frac{1}{c}\varphi (d)\right)-ϵ \\ {\sigma }_w^2={\sigma }_U^2\left[1+\frac{{\rho }^2}{c}d\varphi (d)-{\left(\frac{\rho }{c}\varphi (d)\right)}^2\right]+{\sigma }_V^2\left[1-\frac{\varphi (d)}{c}\left(\frac{\varphi (d)}{c}-d\right)\right] \\ -2\theta [{\sigma }_U{\sigma }_V\frac{\rho }{c}(c+d\varphi (d))+{\sigma }_U{\mu }_V\frac{\rho }{c}\varphi (d)+{\sigma }_V{\mu }_U\frac{1}{c}\varphi (d)+{\mu }_U{\mu }_V \\ -\left({\mu }_U+{\sigma }_U\frac{\rho }{c}\varphi (d)\right)\left({\mu }_V+{\sigma }_V\frac{1}{c}\varphi (d)\right)]. \end{gathered}$$ (3.6)

More specific values can be obtained for different tests as below,

$$\begin{gathered} {\mu }_U={\pi }_E-{\pi }_P,{\mu }_V={\pi }_R-{\pi }_P,,{\sigma }_l^2=\frac{{\pi }_l(1-{\pi }_l)}{n_l},l\in \{E,R,P\}:RRtest1, \\ {\mu }_U=\log ({\pi }_E)-\log ({\pi }_P),{\mu }_V=\log ({\pi }_R)-\log ({\pi }_P),,{\sigma }_l^2=\frac{(1-{\pi }_l)}{n_l{\pi }_l},l\in \{E,R,P\}:RRtest2, \\ {\mu }_U=\frac{{\pi }_E}{1-{\pi }_E}-\frac{{\pi }_P}{1-{\pi }_P},{\mu }_V=\frac{{\pi }_R}{1-{\pi }_P}-\frac{{\pi }_P}{1-{\pi }_P},{\sigma }_l^2=\frac{{\pi }_l}{n_l{(1-{\pi }_l)}^3},l\in \{E,R,P\}:ORtest1, \\ {\mu }_U=\log (\frac{{\pi }_E}{1-{\pi }_E})-\log (\frac{{\pi }_P}{1-{\pi }_P}),{\mu }_V=\log (\frac{{\pi }_R}{1-{\pi }_P})-\log (\frac{{\pi }_P}{1-{\pi }_P}),{\sigma }_l^2=\frac{1}{n_l{\pi }_l(1-{\pi }_l)}:ORtest2, \\ {\sigma }_U^2={\sigma }_E^2+{\sigma }_P^2,{\sigma }_V^2={\sigma }_R^2+{\sigma }_P^2,\rho =\frac{Var({\widehat{\pi }}_P)}{\sqrt{Var(U)Var(V)}}=\frac{{\sigma }_P^2}{\sqrt{{\sigma }_U^2{\sigma }_V^2}},d=-\frac{{\mu }_V}{{\sigma }_V},c=1-\mathrm{\Phi }(d). \end{gathered}$$

Proof: See A.1 in the file of supplementary material.

As before, we denote under H₀, π_E by ${\pi }_E^{null}$ and under H₁, π_E by ${\pi }_E^{alt}$ as point alternative. Under H₀, the expression of ${\pi }_E^{null}$ can be obtained by solving $g({\pi }_E^{null})=g({\pi }_P)+\theta (g({\pi }_R)-g({\pi }_P))+ϵ$. Under H₁, ${\pi }_E^{alt}$ satisfies $g({\pi }_E^{alt})-\theta g({\pi }_R)-(1-\theta )g({\pi }_P)>ϵ\Rightarrow (g({\pi }_E^{alt})-g({\pi }_P))>\theta (g({\pi }_R)-g({\pi }_P))+ϵ$. Note π_E is involved in the expression of the mean and variance of W. Hence under asymptotic normality, we have the following

$$\frac{W-{\mu }_w^{null}}{{\sigma }_w^{null}}~AN(0,1)\text{under}{H}_{0,}\text{and}\frac{W-{\mu }_w^{alt}}{{\sigma }_w^{alt}}~AN(0,1)\text{under}{H}_1.$$

The critical region of the test is given by W > k^∗, where k^∗ is obtained by assuming a test of size $\alpha :P_{H_0}(W>k^{*})=\alpha$, implying $k^{*}={\mu }_w^{null}+z_{1-\alpha }{\sigma }_w^{null}$, where z_1−α is the 100(1 − α)% percentile point of the N (0, 1) distribution.

3.2.1. Sample Size

Using our proposed approach we can calculate sample size for the assessment of NI to attain a desired power. We give the expression of the power of the test for a point alternative ${\pi }_E={\pi }_E^{alt}:P_{H_1}(W>k^{*})=1-\mathrm{\Phi }\left(\frac{k^{*}-{\mu }_w^{alt}}{{\sigma }_w^{alt}}\right)$. Now to obtain the power function of the test we fix π_R, π_P and θ and vary ${\pi }_E^{alt}$. The sample size n_P = n (of the arm P) is calculated from the following equation so that the power achieved is at least 100(1 − β)%:

$$P_{H_1}(W>k^{*})\ge 1-\beta \Rightarrow \mathrm{\Phi }\left(\frac{k^{*}-{\mu }_w^{alt}}{{\sigma }_w^{alt}}\right)\le \beta .$$ (3.7)

For example, setting β at 20%, or the power at 80%, n is determined from equation (3.7). In our sample size calculation we fix π_R and π_P and vary ${\pi }_E={\pi }_E^{alt}$ under H₁ satisfying $H_1:g({\pi }_E^{alt})-\theta g({\pi }_R)-(1-\theta )g({\pi }_P)>ϵ$. Under H₀, ${\pi }_E={\pi }_E^{null}$ is obtained from $g({\pi }_E^{null})-\theta g({\pi }_R)-(1-\theta )g({\pi }_P)=ϵ$. We obtain the power function by varying ${\pi }_E^{alt}$. Thus, we obtain n_P from (3.3) for each ${\pi }_E^{alt}$ and obtain the sample size in the other arms and hence the total sample size as a function of the allocation ratios.

4. Sample Size Tables for the Non-Inferiority Testing

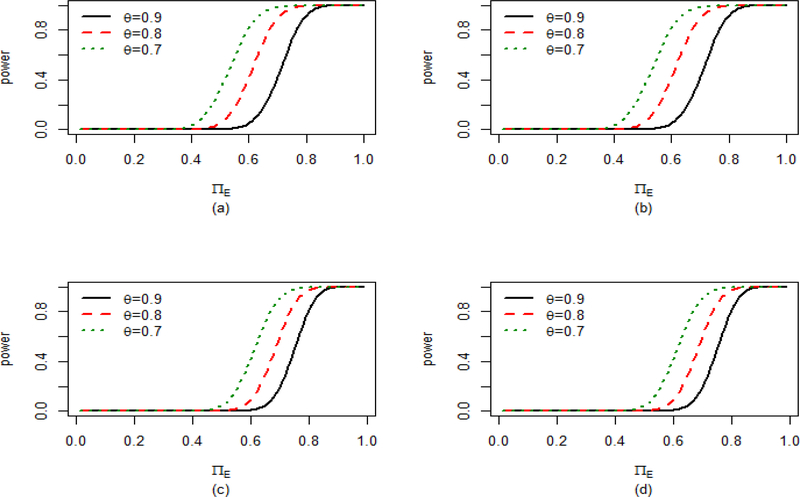
Before going to the sample size calculation we generate the power curves under both the conditional and marginal approaches to get an idea about the operating characteristics of the proposed methods. In Figure 4, we plot the power curves corresponding to three different values of θ : 0.9, 0.8 and 0.7 for RR and OR. The power curves for NNT can be similarly obtained but not shown. The three values of θ correspond to f = −0.1, −0.2 and −0.3 respectively, which correspond to the three choices of the NI margin. This implies that the experimental drug, in comparison to placebo, must achieve at least 90%, 80% and 70% respectively of the effect of the active control with respect to the placebo in order to be noninferior. From Figure 4, we observe that as θ decreases, the power curve becomes steeper which means for smaller θ the proposed test is more powerful than that for higher θ. This makes sense as for smaller θ (or larger f) it is easier to declare NI of the experimental drug over the reference, since in that case the new drug has to preserve smaller proportion of the control drug in the current trial in order to be non-inferior.

Figure 4:

Power curves for different θ under (a) RR Conditional, (b) RR marginal, (c) OR Conditional and (d) OR Marginal approaches keeping π_R = 0.7 and π_P = 0.1

Next we refer to the Sections 3.1.1 and 3.2.1 for the sample size determination under our proposed marginal and the conditional approach respectively. As discussed earlier, sample sizes in the placebo, reference and the experimental arms are denoted by n, r₁n and r₂n respectively, with r₁, r₂ ≥ 1. To compute (n_E, n_R, n_P ), we consider three possible allocations for (P, R, E): (1 : 1 : 1), (1 : 2 : 2) and (1 : 2 : 3) of the total sample size N. Hence, for the allocation (1 : 1 : 1), r₁ = r₂ = 1, for (1 : 2 : 2), r₁ = r₂ = 2 and for (1 : 2 : 3) the values are r₁ = 2 and r₂ = 3. The power expression of the proposed conditional approach does not give an explicit solution for n_P and hence an iterative process is needed. We determine the sample size under the two approaches for θ = 0.8 and 0.7 for (π_R = 0.7, π_P = 0.1) and (π_R = 0.6, π_P = 0.55). For NNT since we are considering ϵ −substantial non-inferiority, we choose ϵ = 0.05 which is equivalent to treating an additional 20 patients in order to see the benefit of the experimental drug; that is, to declare NI of E over R. We present the sample size for RR in Table 1, for OR in Table 2 and for NNT in Table 3.

Table 1:

Sample Size for RR to Achieve a Power of 80 % for θ = 0.8 and θ = 0.7, α = 0.025 and π_E ϵ [0.65, 0.9] under Three Different Allocations. The simulated power (SimP) is also reported to show that calculated sample size is adequate to guarantee 80% power except for minor numerical fluctuation.

Allocation					πR = 0.7, πP = 0.1						πR = 0.6, πP = 0.55
					Conditional			Marginal			Conditional			Marginal
P	R	E	θ	πE	nP	N	SimP	nP	N	SimP	nP	N	SimP	nP	N	SimP
1	1	1	0.8	0.9	27	81	0.874	27	81	0.876	40	120	0.977	43	129	0.909
				0.85	33	99	0.874	33	99	0.883	55	165	0.958	58	174	0.873
				0.8	42	126	0.877	42	126	0.870	82	246	0.944	86	258	0.857
				0.75	56	168	0.879	56	168	0.869	136	408	0.927	141	423	0.836
				0.7	79	237	0.878	79	237	0.857	278	834	0.899	286	858	0.812
				0.65	124	372	0.882	124	372	0.846	909	2727	0.877	915	2745	0.808
			0.7	0.9	24	72	0.865	24	72	0.887	38	114	0.969	39	117	0.904
				0.85	28	84	0.854	28	84	0.898	52	156	0.949	53	159	0.870
				0.8	33	99	0.857	33	99	0.894	76	228	0.934	77	231	0.848
				0.75	40	120	0.862	40	120	0.888	124	372	0.912	125	375	0.838
				0.7	51	153	0.873	51	153	0.884	245	735	0.894	247	741	0.813
				0.65	68	204	0.875	68	204	0.872	734	2202	0.871	737	2211	0.813
1	2	2	0.8	0.9	17	85	0.807	17	85	0.788	22	110	0.977	22	110	0.906
				0.85	21	105	0.830	21	105	0.827	30	150	0.961	30	150	0.874
				0.8	27	135	0.854	27	135	0.863	44	220	0.935	44	220	0.852
				0.75	35	175	0.859	35	175	0.879	73	365	0.923	73	365	0.841
				0.7	49	245	0.871	49	245	0.873	147	735	0.906	148	740	0.833
				0.65	76	380	0.884	76	380	0.862	470	2350	0.876	471	2355	0.818
			0.7	0.9	17	85	0.809	17	85	0.813	21	105	0.957	21	105	0.905
				0.85	19	95	0.805	19	95	0.835	29	145	0.943	29	145	0.886
				0.8	23	115	0.835	23	115	0.868	42	210	0.922	42	210	0.864
				0.75	28	140	0.825	28	140	0.889	68	340	0.906	68	340	0.839
				0.7	35	175	0.845	35	175	0.898	133	665	0.888	133	665	0.824
				0.65	47	235	0.866	47	235	0.898	395	1975	0.877	395	1975	0.814
1	2	3	0.8	0.9	15	90	0.787	15	90	0.771	18	108	0.983	19	114	0.934
				0.85	18	108	0.822	18	108	0.807	25	150	0.974	25	150	0.890
				0.8	23	138	0.849	23	138	0.848	36	216	0.959	37	222	0.872
				0.75	30	180	0.854	30	180	0.867	60	360	0.952	60	360	0.839
				0.7	42	252	0.874	42	252	0.884	120	720	0.937	121	726	0.832
				0.65	64	384	0.894	64	384	0.875	381	2286	0.914	382	2292	0.817
			0.7	0.9	14	84	0.767	14	84	0.760	18	108	0.976	18	108	0.929
				0.85	17	102	0.813	17	102	0.818	24	144	0.963	24	144	0.894
				0.8	20	120	0.820	20	120	0.852	34	204	0.941	34	204	0.872
				0.75	24	144	0.807	24	144	0.878	55	330	0.928	55	330	0.851
				0.7	31	186	0.829	31	186	0.899	108	648	0.913	108	648	0.830
				0.65	41	246	0.868	41	246	0.914	318	1908	0.897	318	1908	0.817

Table 2:

Sample Size for OR to Achieve a Power of 80 % for θ = 0.8 and θ = 0.7, α = 0.025 and π_E ϵ [0.65, 0.9] under Three Different Allocations. The simulated power (SimP) is also reported to show that calculated sample size is adequate to guarantee 80% power except for minor numerical fluctuation.

Allocation					πR = 0.7, πP = 0.1						πR = 0.6, πP = 0.55
					Conditional			Marginal			Conditional			Marginal
P	R	E	θ	πE	nP	N	SimP	nP	N	SimP	nP	N	SimP	nP	N	SimP
1	1	1	0.8	0.9	20	60	0.801	20	60	0.801	20	60	0.862	21	63	0.819
				0.85	31	93	0.794	31	93	0.794	32	96	0.838	34	102	0.793
				0.8	49	147	0.796	49	147	0.796	54	162	0.824	57	171	0.782
				0.75	85	255	0.804	85	255	0.804	102	306	0.824	107	321	0.783
				0.7	165	495	0.809	165	495	0.809	232	696	0.819	241	723	0.788
				0.65	415	1245	0.8054	415	1245	0.805	844	2532	0.809	853	2559	0.798
			0.7	0.9	15	45	0.800	15	45	0.800	19	57	0.858	20	60	0.831
				0.85	21	63	0.791	21	63	0.791	30	90	0.836	31	93	0.805
				0.8	30	90	0.807	30	90	0.808	51	153	0.828	52	156	0.795
				0.75	45	135	0.800	45	135	0.801	93	279	0.819	95	285	0.790
				0.7	72	216	0.806	72	216	0.806	205	615	0.816	209	627	0.792
				0.65	125	375	0.805	125	375	0.805	681	2043	0.806	686	2058	0.796
1	2	2	0.8	0.9	11	55	0.808	11	55	0.808	11	55	0.849	11	55	0.829
				0.85	16	80	0.808	16	80	0.808	17	85	0.834	18	90	0.809
				0.8	26	130	0.804	26	130	0.804	29	145	0.826	30	150	0.796
				0.75	45	225	0.801	45	225	0.801	54	270	0.823	55	275	0.798
				0.7	87	435	0.803	87	435	0.803	122	610	0.815	124	620	0.792
				0.65	220	1100	0.806	220	1100	0.806	434	2170	0.801	437	2185	0.790
			0.7	0.9	8	40	0.801	8	40	0.799	10	50	0.830	10	50	0.827
				0.85	12	60	0.818	12	60	0.818	17	85	0.829	17	85	0.825
				0.8	17	85	0.809	17	85	0.809	28	140	0.822	28	140	0.817
				0.75	26	130	0.789	26	130	0.789	50	250	0.807	50	250	0.801
				0.7	41	205	0.817	41	205	0.817	110	550	0.803	110	550	0.797
				0.65	71	355	0.810	71	355	0.810	362	1810	0.799	362	1810	0.796
1	2	3	0.8	0.9	9	54	0.809	9	54	0.809	9	54	0.859	9	54	0.837
				0.85	13	78	0.831	13	78	0.831	14	84	0.831	14	84	0.803
				0.8	22	132	0.809	22	132	0.809	23	138	0.822	24	144	0.795
				0.75	37	222	0.792	37	222	0.792	43	258	0.816	44	264	0.789
				0.7	72	432	0.806	72	432	0.806	98	588	0.819	99	594	0.793
				0.65	182	1092	0.804	182	1092	0.804	349	2094	0.808	352	2112	0.796
			0.7	0.9	7	42	0.811	7	42	0.811	8	48	0.804	8	48	0.806
				0.85	10	60	0.797	10	60	0.797	13	78	0.804	13	78	0.803
				0.8	14	84	0.803	14	84	0.803	22	132	0.806	22	132	0.799
				0.75	22	132	0.807	22	132	0.807	40	240	0.809	40	240	0.804
				0.7	34	204	0.807	34	204	0.807	88	528	0.809	88	528	0.804
				0.65	60	360	0.827	60	360	0.827	289	1734	0.801	289	1734	0.796

Table 3:

Sample Size for NNT to Achieve a Power of 80 % for θ = 0.8 and θ = 0.7, ϵ = 0.05, α = 0.025 and π_E ϵ [0.65, 0.9] under Three Different Allocations. The simulated power (SimP) is also reported to show that calculated sample size is adequate to guarantee 80% power except for minor numerical fluctuation.

Allocation					πR = 0.7, πP = 0.1						πR = 0.6, πP = 0.55
					Conditional			Marginal			Conditional			Marginal
P	R	E	θ	πE	nP	N	SimP	nP	N	SimP	nP	N	SimP	nP	N	SimP
1	1	1	0.8	0.9	35	105	0.809	35	105	0.809	38	114	0.858	41	123	0.829
				0.85	55	165	0.820	55	165	0.820	61	183	0.844	65	195	0.820
				0.8	95	285	0.812	95	285	0.812	109	327	0.833	115	345	0.804
				0.75	195	585	0.812	195	585	0.812	238	714	0.823	247	741	0.807
				0.7	584	1752	0.802	584	1752	0.802	837	2511	0.807	846	2538	0.800
				0.65	7248	> 104	0.804	7248	> 104	0.804	> 104	> 104	-	> 104	> 104	-
			0.7	0.9	22	66	0.800	22	66	0.800	36	108	0.870	37	111	0.832
				0.85	32	96	0.793	32	96	0.793	56	168	0.843	58	174	0.818
				0.8	49	147	0.799	49	147	0.799	99	297	0.831	101	303	0.804
				0.75	82	246	0.813	82	246	0.813	209	627	0.820	213	639	0.812
				0.7	161	483	0.806	161	483	0.806	674	2022	0.805	679	2037	0.798
				0.65	431	1293	0.799	431	1293	0.799	> 104	> 104	-	> 104	> 104	-
1	2	2	0.8	0.9	18	90	0.813	18	90	0.813	21	105	0.866	21	105	0.825
				0.85	28	140	0.800	28	140	0.800	33	165	0.852	34	170	0.832
				0.8	48	240	0.808	48	240	0.808	58	290	0.831	59	295	0.811
				0.75	99	495	0.813	99	495	0.813	126	630	0.823	127	635	0.807
				0.7	295	1475	0.813	295	1475	0.813	432	2160	0.806	434	2170	0.795
				0.65	3660	> 104	0.799	3660	> 104	0.799	> 104	> 104	-	> 104	> 104	-
			0.7	0.9	12	60	0.791	12	60	0.791	20	100	0.856	20	100	0.834
				0.85	17	85	0.798	17	85	0.798	31	155	0.832	31	155	0.822
				0.8	26	130	0.797	26	130	0.797	54	270	0.824	54	270	0.815
				0.75	42	210	0.801	42	210	0.801	113	565	0.811	113	565	0.806
				0.7	83	415	0.8173	83	415	0.817	360	1800	0.807	360	1800	0.803
				0.65	221	1105	0.805	221	1105	0.805	6848	> 104	0.799	6848	> 104	0.799
1	2	3	0.8	0.9	15	90	0.803	15	90	0.803	17	102	0.860	18	108	0.841
				0.85	23	138	0.806	23	138	0.806	27	162	0.856	28	168	0.833
				0.8	39	234	0.823	39	234	0.823	48	288	0.849	48	288	0.818
				0.75	79	474	0.821	79	474	0.821	102	612	0.815	104	624	0.807
				0.7	235	1410	0.809	235	1410	0.809	350	2100	0.811	352	2112	0.805
				0.65	2903	> 104	0.794	2903	> 104	0.794	12809	> 104	0.801	12809	> 104	0.801
			0.7	0.9	9	54	0.803	9	54	0.803	16	96	0.844	17	102	0.852
				0.85	13	78	0.812	13	78	0.812	26	156	0.849	26	156	0.833
				0.8	20	120	0.820	20	120	0.820	44	264	0.821	44	264	0.812
				0.75	33	198	0.806	33	198	0.806	92	552	0.819	92	552	0.811
				0.7	64	384	0.808	64	384	0.808	290	1740	0.800	291	1746	0.805
				0.65	172	1032	0.801	172	1032	0.801	5508	> 104	0.794	5508	> 104	0.795

We present the sample sizes for the placebo arm only in the tables, however those for the arms R and E can be obtained by multiplying it with the allocation ratios. The total sample size for the allocation (1 : 1 : 1) is $3n_P^{(1)}$; that for (1 : 2 : 2) is $5n_P^{(2)}$; while for (1 : 2 : 3) it is $6n_P^{(3)}$, where $n_P^{(1)}$, $n_P^{(2)}$ and $n_P^{(3)}$ are the respective sample size for the placebo arm under the three different allocations. From all three tables we observe that the sample size under the conditional approach is smaller or at most equal to that calculated under the marginal approach to achieve a power of 80%. It is clear from Tables 1, 2 and 3 that the two approaches behave nearly identically when π_R >> π_P. However, when their difference is smaller, conditional approach tends to improve power for fixed sample size. Also we observe that the sample size requirement decreases with decrease in θ for a fixed power, which is consistent to the power curve plots. For NNT we observe that the sample size requirement is bigger as compared to those for RR and OR since we test for ϵ-substantial non-inferiority (ϵ > 0) and hence for fixed θ, the margin allowance for NNT is smaller than that for RR and OR.

Although appealing at first glance, one may not want to use a balanced study design in the NI context from two aspects: (i) due to ethical reasons in case an effective treatment exists, the number of patients receiving the placebo should be kept as small as possible, and (ii) as pointed out by Koch and Tangen (1999), the difference between E and R should be expected to be much smaller than the difference of both of them relative to placebo so that the latter ones are easier to detect. As observed by Pigeot et al. (2003) for continuous outcome, the necessary sample size required for the unbalanced allocations is remarkably smaller compared to the balanced one. We observe similar results for the sample size under NNT from Table 3. From Table 2 for OR we notice that the necessary sample size is remarkably smaller for the unbalanced allocation (1 : 2 : 2) as compared to a balanced design (1 : 1 : 1) and a minor reduction is again obtained for the unbalanced allocation (1 : 2 : 3) as compared to (1 : 2 : 2). However, for RR the sample sizes do not follow the same pattern, particularly when the difference between π_R and π_P is large, with respect to the allocation, as can be seen from Table 1. Apart from the difference in the functional form, this might also be due to the fact that even after logarithmic transformation of RR it still yields a somewhat skewed distribution that do not conform to the normal approximation quite well as compared to OR or NNT.

5. Application

We illustrate our proposed Frequentist methods for RR, OR and NNT with a published dataset from a three-arm comparative study on major depressive disorder. This dataset is described in Higuchi et al. (2009). Hida and Tango (2011) as well as Ghosh et al. (2016) also considered this specific dataset in their paper. Hida and Tango (2013) proposed a Frequentist’s version of the problem for binary outcomes and Ghosh et al. (2018) considered the Bayesian version of the same for risk difference. The objective of the depression trial was to compare the efficacy and safety of duloxetine (E) with those of paroxetine (R) and placebo (P). This study was a double-blinded, randomized, parallel-group active-controlled study of a six-week treatment with the following number of patients in each arm: duloxetine (n_E = 147), paroxetine (n_R = 148) and placebo (n_P = 145). The primary endpoint was continuous type which is the change in HAMD-17 total score from baseline at the end of sixth week. Hida and Tango (2011) considered two binary outcomes for their Frequentist approach namely, Response and Remission. Response is the primary outcome defined as the reduction of more than 50% total. Remission is the secondary outcome which is defined as maintaining HAMD-17 score of ≤ 17 at the end of 6 weeks. We present the data in Table 2, in terms of Response and Remission. We analyze both the Response and Remission outcomes separately using our proposed approach. To make a meaningful interpretation of the effect of the experimental drug, a clinically acceptable margin reflecting the largest loss of effect is chosen to determine non-inferiority of the experimental drug over the control. Here, we vary θ in the range [0.5, 0.8] to explore different possibilities. For the marginal approach the p−value of the test for NNT and for Margin 2 of both RR and OR is calculated as

$$p-\text{value}=P_{H_0}(T>T_{\text{obs}})=1-\mathrm{\Phi }(\frac{\sqrt{n_P}T{T}_{\text{obs}}}{\sqrt{{\tau }_0^2}}),$$ (5.1)

where $T_{\text{obs}}=g({\widehat{\pi }}_E)-\theta g({\widehat{\pi }}_R)-(1-\theta )g({\widehat{\pi }}_P)-ϵ$ is the Frequentist’s statistic under the existing approach and ${\tau }_0^2=n_{P}Var(T)$ under null hypothesis. The quantity ϵ is chosen to be 0.05 for the analysis under NNT, while ϵ = 0 for RR and OR. For the conditional Frequentist approach we calculate the p−value as

$$p-\text{value}=P_{H_0}(W>W_{\text{obs}})=1-\mathrm{\Phi }(\frac{W_{\text{obs}}-{\mu }_w^{null}}{{\sigma }_w^{null}}),$$ (5.2)

where $W_{\text{obs}}=g({\widehat{\pi }}_E)-\theta g({\widehat{\pi }}_R)-(1-\theta )g({\widehat{\pi }}_P)-ϵ|g({\widehat{\pi }}_R)-g({\widehat{\pi }}_P)>0$ is the Frequentist’s test statistic for the conditional testing and ${\mu }_w^{null}$ and ${\sigma }_w^{2null}$ are the mean and variance of W under null hypothesis as given in Section 3. The Frequentist p−values are reported in Table 5 and Table 6 for RR, OR and NNT for the Response and the Remission data respectively.

Table 5:

Frequentist p-values for the Response Data

	RR		OR		NNT (ϵ = 0.05)
θ	Conditional	Marginal	Conditional	Marginal	Conditional	Marginal
0.5	0.047	0.047	0.041	0.041	0.227	0.227
0.55	0.059	0.059	0.054	0.055	0.272	0.272
0.6	0.075	0.075	0.072	0.073	0.320	0.321
0.65	0.094	0.094	0.094	0.095	0.372	0.374
0.7	0.119	0.119	0.122	0.123	0.426	0.428
0.75	0.149	0.150	0.155	0.157	0.479	0.482
0.8	0.186	0.187	0.193	0.195	0.532	0.535

Table 6:

Frequentist p-values for the Remission Data

	RR		OR		NNT (ϵ = 0.05)
θ	Conditional	Marginal	Conditional	Marginal	Conditional	Marginal
0.5	0.085	0.085	0.080	0.080	0.379	0.38
0.55	0.101	0.101	0.099	0.099	0.424	0.426
0.6	0.121	0.121	0.121	0.121	0.470	0.473
0.65	0.146	0.146	0.147	0.148	0.516	0.519
0.7	0.174	0.175	0.177	0.179	0.559	0.564
0.75	0.207	0.209	0.212	0.215	0.601	0.606
0.8	0.245	0.248	0.245	0.254	0.640	0.645

The respective p−values are compared with α = 0.025 to deduce the final decision. From both Table 5 and Table 6, we observe that p−values decrease as θ decreases implying greater chance of declaring NI for smaller values of θ, since p − value < α implies rejection of NI. Also we observe that the p−values under the conditional approach is smaller or at most equal to that under the marginal approach which is consistent to the sample size calculation under all three functionals. However, since none of the p−values is smaller that α = 0.025 NI null hypothesis can not be rejected and hence NI can not be claimed for any of the tests across any θ for all the functionals.

6. Discussion

In this paper we have presented fraction margin based Frequentist test procedures for the “gold standard” three-arm NI trial which includes a placebo arm for binary endpoints with RR, OR and NNT type functionals. This is an important methodological contribution in view of the recent FDA guideline. We also introduced a conditional test of NI. For both RR and OR, we showed the non-uniqueness of the NI margin and constructed two examples of that. We made a comparison among them to identify the one yielding better operating characteristic. Additional guidance is required from regulators if one plans to choose a unique NI margin for all situation. We also note that NI testing for NNT can be regarded as the -substantial NI testing under the risk difference case. We tabulated the sample size under three different types of allocation for RR, OR and NNT, which should provide a good starting point for accessing sample size when designing such trials. We also note that the tests based on asymptotic approximation perform favorably since usually in NI testing the number of patients in each treatment arm is moderately large. In case of small sample size exact method of NI testing can be developed using Fisher’s exact test following Wellek (2005), Hasselblad and Lokhnygina (2007) and Zaslavsky (2013). However, all of these articles presented the exact approach for two-arm NI testing and most of them considered NI testing for rate difference as the function of interest only. To the best of our knowledge there exists no published work on exact testing approach for three-arm NI trial and hence this should be considered as an important future work. Also as suggested by one reviewer, likelihood ratio test or score test are potential alternatives to the asymptotic tests.

Historical information plays substantial role in the design and analysis of NI trial. Hence NI trial has to be reflected in several substantive aspects, for e.g. the choice of δ, the question of whether a placebo can be included as an additional arm of the study, assay sensitivity, etc. From the sample size tables we have observed that the proposed conditional test yields identical power and hence sample size as that of the marginal test when the active control is substantially superior to placebo. However, when the control is marginally superior to placebo, the proposed conditional approach yields smaller sample size as compared to the marginal approach for a fixed power. Also analysis of our clinical trial data suggest that both the methods perform comparably in all situations, however, the p−values under the conditional approach are always found to be smaller or at most equal to that obtained under the marginal one. This essentially supports the observation we made in the difference of sample size quantification between the two methods. Also we note that although in this article we considered sample size allocation motivated by Pigeot et al. (2003) and Koch and Tangen (1999), one may also consider optimal allocation to treatment arms following the line of Singer (2001) and Pigeot et al. (2003) for continuous outcome. However, when the outcome is binary, derivation of optimal allocation formula for various functional forms still remains an open problem.

We note that under the fraction margin approach the fraction “f” is pre-specified, while the NI margin δ is unknown. Hence the value of δ can vary greatly depending on the estimated effect size of the reference treatment, i.e. as a function of $(g({\widehat{\pi }}_R),g({\widehat{\pi }}_P))$. As evident, the information gained from the historical trial/s may play a significant role in NI trial design and hierarchical Bayesian approach may provide an attractive framework to achieve this. In this article we restricted ourselves to the Frequentist approach only, but that is definitely an avenue worth exploring in future. On the other hand in the fixed margin approach (see Hida and Tango (2013) and Ghosh et al. (2018)), with three-arms, the joint testing of NI and AS may be performed which needs additional care since it may produce conservative test with restrictive type-I error (Chuang-Stein et al., 2007; Dmitrienko et al., 2009) under intersection-union test. Albeit development of such procedure for RR, OR and NNT under alternative definition of type-I error (e.g. average testing error of Chuang-Stein et al. (2007)) is another interesting open problem.

Table 4:

Remission and Response as Outcome in the Depression Trial of Higuchi et al. (2009)

Outcome	Duloxetine	Paroxetine	Placebo
Remission	50	49	32
Response	80	78	56
Total	nE = 147	nR = 148	nP = 145