Acoustic radiation force optical coherence elastography for elasticity assessment of soft tissues

Abstract

Biomechanical properties of soft tissues are important indicators of tissue functions which can be used for clinical diagnosis and disease monitoring. Elastography, incorporating the principles of elasticity measurements into imaging modalities, provides quantitative assessment of elastic properties of biological tissues. Benefiting from high-resolution, noninvasive and three-dimensional optical coherence tomography (OCT), optical coherence elastography (OCE) is an emerging optical imaging modality to characterize and map biomechanical properties of soft tissues. Recently, acoustic radiation force (ARF) OCE has been developed for elasticity measurements of ocular tissues, detection of vascular lesions and monitoring of blood coagulation based on remote and noninvasive ARF excitation to both internal and superficial tissues. Here, we describe the advantages of the ARF-OCE technique, the measurement methods in ARF-OCE, the applications in biomedical detection, current challenges and advances. ARF-OCE technology has the potential to become a powerful tool for in vivo elasticity assessment of biological samples in a non-contact, non-invasive and high-resolution nature.

Introduction

Biomechanical properties are important for the assessment of tissue functions and status which provides unique information to diagnose clinical diseases and monitor disease progression. The differences of biomechanical properties due to changes in structures and interactions at the molecular, cellular and tissue levels have been assessed in conventional clinical practices. Palpation is a classic method for assessment of changes in biomechanical properties and has been commonly used for the discovery of breast cancers, functional assessment of abdominal organs, and diagnosis of skin diseases. The main idea of whether the tissue is hard or soft could provide important information about disease diagnosis and progression. However, palpation only provides a qualitative assessment of tissue stiffness, relies on personal experiences and lacks clinical standards. More accurate methods without manual intervention are necessary for correct and repeatable diagnosis.

Over the past two decades, different imaging modalities have been developed for mapping biomechanical properties of soft tissues benefiting from the rapid progression of different biomedical imaging platforms, which are collectively called elastography. A typical elastography usually includes three main steps: induction of deformation or vibration within the tissues, detection of the deformation, vibration or vibration propagation, and elasticity estimation of tissues. Different noninvasive imaging techniques incorporating the principles of elasticity measurements have been developed in biomedical research and clinical applications, such as ultrasound elastography (1–9), magnetic resonance elastography (10–15), optical coherence elastography (OCE) (16–23), elastography based on Brillouin microscopy (24), atomic force microscopy (25), multiphoton microscopy (26), and laser speckle imaging (27). Each technique has its unique field of view, penetration depth, imaging speed and spatial resolution and, thus, can be used in different applications. Magnetic resonance elastography has deep penetration and wide field of view with a limited spatial resolution of 1-3 mm, and the mechanical properties of brain tissue (14,28,29), heart (30), liver (31), and breast (32) have been assessed. In order to increase the spatial resolution, ultrasound elastography has been developed for the detection of lesions in breasts (33,34), livers (35,36) and corneas (37). However, ultrasound elastography has a spatial resolution of over 100 μm, which cannot detect smaller lesions in clinical applications. Brillouin microscopy has shown particular promise for medical applications with high resolutions of 1.5 and 0.3 μm in the axial and lateral directions (38) and a penetration depth of 0.1-3.0 mm (16). The elastography based on Brillouin microscopy has been used to detect elastic properties of ocular tissues, such as the cornea (39,40) and crystalline lens (41), and measure cell mechanics (42). However, because the measured relationship was not constant between the longitudinal modulus measured by Brillouin microscopy and the Young’s modulus commonly used to assess elasticity in current biomedical applications, the use of Brillouin microscopy was limited. A better understanding of the correlation between the longitudinal modulus measured by Brillouin microscopy and the Young’s modulus measured by conventional elastography is essential to translate the Brillouin technology for biomedical applications (16). Optical coherence elastography incorporating elasticity measurement principles with optical coherence tomography (OCT) has provided an opportunity for the elasticity imaging of tissues with a spatial resolution of ~10 μm. OCT is a noninvasive and three-dimensional (3D) imaging technique with penetration of several millimeters and field of view of ~1 cm, which performs high-resolution imaging within the optical scattering media using broadband light sources with short coherence length (43,44). OCT has the ability to detect displacement responses within a sub-micrometer. Benefiting from the OCT technique, OCE has a higher spatial resolution and higher sensitivity for elasticity measurement, compared with magnetic resonance elastography and ultrasound elastography.

For a typical OCE measurement, external force is applied to the samples to induce deformation, vibration or vibration propagation which is detected by an OCT system. Many techniques have been developed to apply external force, such as acoustic radiation force (ARF) (45–51), air-puff pulse (52–55), laser pulse (56,57), needle probe (58,59) and PZT actuator (60–66). The force loading mechanisms can be separate into two categories: quasi-static compression and dynamic excitation. The needle probe and PZT actuator can induce deformation based on quasi-static compressive loading at low rates (58,65). The resulting local strain is measured in the tissue and the detection depth could cover the OCT imaging range. Invasive insertion of the needle probe enables OCE to detect deeper tissues. However, it’s not easy for compressive loading methods with needles to quantify the elastic moduli in vivo and compare measured values from different systems. The ARF, air-puff pulse, laser pulse and PZT actuator dynamically excite samples to induce vibration or vibration propagation, which is used to assess elastic properties. The air-puff pulse, laser pulse and PZT actuator only excite the surfaces of samples, which results in limited depth of elasticity detection, and may be only suitable for detection of samples located on the body surface, such as corneas and skin. However, ARF can remotely excite both the surface and the interior of samples and, thus, has the ability to detect the elasticity of both internal tissues, such as retinas and crystalline lens, and superficial tissues, such as corneas, vascular walls and skin. Due to the non-contact and non-invasive nature, ARF-OCE has provided a powerful tool for in vivo elasticity measurements with high resolution. This review will focus on the OCE systems based on ARF excitation. The technologies described in this review can also be extended to other excitation methods.

In an ARF-OCE system, the ARF from an ultrasound transducer remotely induces vibrations. The ARF is an interaction of an acoustic wave with an obstacle in the wave propagation path. The ARF magnitude |F| [kg/(cm²·s²)] at a given spatial location can be evaluated by the following equation (67):

$$|F|=\frac{2\times \alpha \times I}{c}$$ (1)

where α [Np/cm] is the frequency-dependent attenuation coefficient in the tissue, I [W/cm²] is the temporal average intensity of the acoustic beam at the location and c [cm/s] is the ultrasound speed. The spatial distribution of I is determined by design of an ultrasound transducer. For most soft tissues, the ultrasound attenuation is approximately comprised in a range of 0.5-1.0 dB/(cm·MHz) (68). The attenuation increases with the increase of the frequency and propagation path length (68). When the ultrasound transducer with a frequency of 3.0 MHz is used to induce vibration in a tissue with the attenuation of 1.0 dB/(cm·MHz), the attenuation coefficient α is 3.0 dB/cm (i.e. 0.35 Np/cm). Then the penetration depth is 1.0 cm with an intensity loss of 3.0 dB in the tissue.

In order to qualitatively and quantitatively determine elastic properties, different elasticity estimation principles can be incorporated. First, we’ll describe and compare the elasticity estimation methods used in ARF-OCE. Then, current biomedical applications of ARF-OCE will be introduced. Finally, the challenges and advances to meet these challenges will be discussed.

Elasticity measurement methods

Tissue elasticity is used to describe tissue resistance to being deformed non-permanently when a stress is applied. The elastic modulus of a tissue is calculated by the slope of the stress–strain curve during the elastic deformation process, including three primary parameters, that is, Young’s modulus, shear modulus and bulk modulus. In biomedical applications, Young’s modulus and shear modulus are usually measured to assesses the elastic properties of soft tissues with simplification of tissue biomechanical properties, where the tissues are regarded as mechanically homogeneous and incompressible materials in a small region. The ratio of load stress and small deformation strain remains constant in a small homogeneous region of the incompressible elastic tissue, which is direction-independent in an isotropic tissue and is direction-dependent in an anisotropic tissue (7,17,20).

From the vibration measurement by OCT to the estimation of elastic properties, three methods have been used in current research, including the comparison of vibration amplitudes (45), determination of resonant frequencies (46) and calculation of elastic wave velocities (49). Vibration amplitudes can be compared directly to qualitatively assess the elastic properties when the same pressure is applied to different samples. A softer tissue will present smaller vibration amplitudes. Resonant frequency can be determined with the sweeping of ARF modulation frequencies because resonant frequency is in a linear relationship with the square root of the Young’s modulus. Elastic wave propagation can also be visualized to calculate the elastic modulus based on the quantified relationship between a wave velocity and a elastic modulus.

Comparison of vibration amplitude

In order to compare elastic properties by measurements of vibration amplitudes using ARF-OCE, the applied force usually excites the samples parallel to or oblique to the OCT beam, and the vibrations are detected by a phase-resolved Doppler OCT method.

Young’s modulus E, as an important parameter for characterization of the elastic properties in biomedical applications, is the ratio of the stress σ to the strain ε, which can be described as:

$$E=\frac{\sigma }{\epsilon }=\frac{F/S}{\Delta z/z_0}$$ (2)

where F is the applied force, S is the area of force application, Δz is the length of the object changes, z₀ is the original length of the object. When the ARF is uniform in a range much larger than the OCT beam, approximately the same tensile stress is applied to the sample in the OCT imaging area. As the ARF induces small object displacements so that the strain is small enough (less than 0.1), ε can be used as the first-order approximation to assess the relative Young’s modulus (45).

For calculation of the strain ε, the OCT methods can be used to measure the displacement of an object within an time interval: that is, the vibration velocity V(t). Then the vibration amplitude Δz parallel to the OCT beam from time t₁ to t₂ can be determined by the following equation:

$$\Delta z={\int }_{t_1}^{t_2}V(t)dt$$ (3).

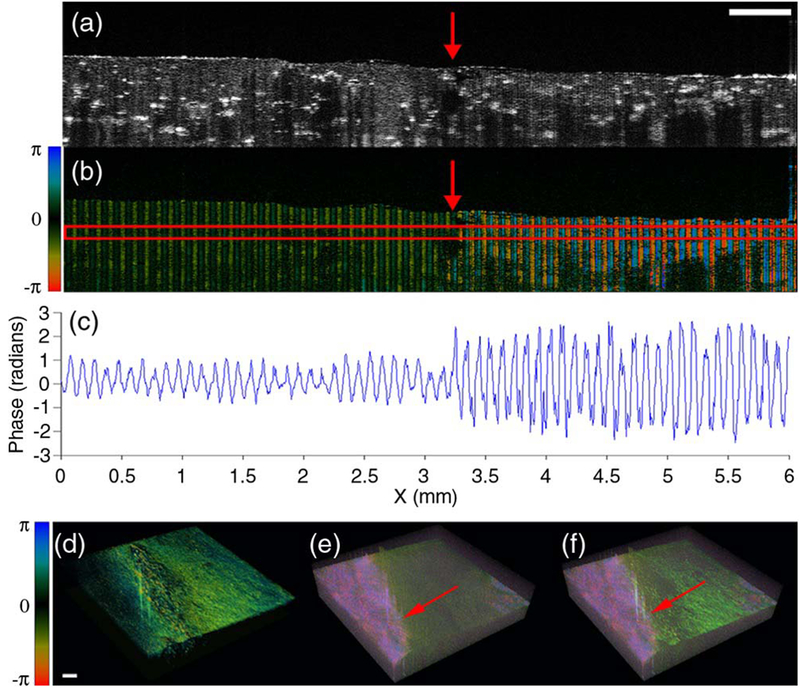
If the original sample thickness z₀ along the vibration direction is the same, the comparison of the vibration amplitude Δz will enable assessment of relative Young’s moduli when the same experimental setup is used (45,47). Figure 1 shows OCT and OCE measurements in a side-by-side agar phantom. The right part is softer than the left part. Doppler phase shift image in Figure 1(b), phase amplitudes in Figure 1(c) and 3D OCE image in Figure 1(e) show differences between the parts with different stiffness (45). It should be noticed that the excitation frequency should be selected far away from the resonant frequency of the samples when the vibration amplitudes are compared by direction.

Figure 1.

Vibration amplitude measurements for elasticity mapping using ARF–OCE in a side-by-side agar phantom. (a) OCT intensity image. The right part is softer than the left part. (b) Doppler phase shift image with ARF excitation. (c) Phase amplitudes. (d) 3D OCT, (e) 3D OCE, and (f) fused OCT and OCE images. Scale bars: 500 μm. The figure has been reprinted with permission from Qi et al., 2012. Copyright © (2012) SPIE (45).

Resonant frequency detection

Soft tissue as an elastic material can be modeled by an elastic spring when the viscosity is neglected and the deformation is relatively small (less than 0.1%) (46). The applied force F can be calculated by Δz × k, where Δz is the displacement from the original position and k is the elastic constant. Based on the definition of the Young’s modulus from Equation 2, the Young’s modulus can also be described by the following equation (46):

$$E=\frac{F/S}{\Delta z/z_0}=\frac{k\times z_0}{S}$$ (4).

To the extent that the elastic sample obeys Hooke’s law, the harmonic vibration frequency f is determined by the mass M of an object and the elastic constant k:

$$f=\frac{1}{2\pi }\times \sqrt{\frac{k}{M}}$$ (5).

With the same mass, the harmonic vibration frequency f is only related to elastic constant k, which can be considered as a characteristic frequency of a sample. Substituting elastic constant k determined from Equation 5 into Equation 4 yields the following equation:

$$E=\frac{4{\pi }^2\times M\times z_0}{S}\times f^2$$ (6).

Therefore, the characteristic frequency of the sample is in a linear relationship with the square root of the modulus and can be used to quantify the Young’s modulus.

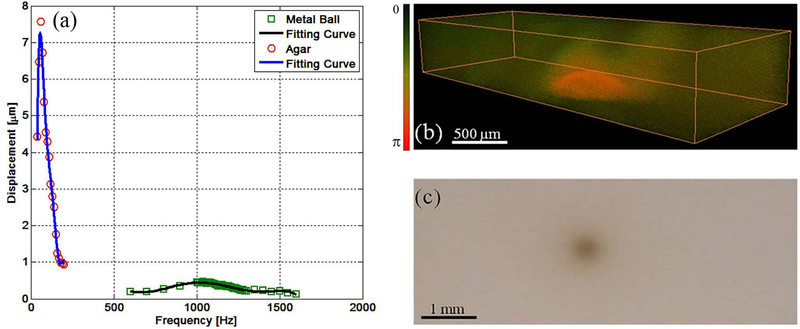
In order to match the intrinsic frequency of a sample, different ARF modulation frequencies are swept and the vibration amplitudes are measured by Doppler OCT. The resonant frequency can be detected with the maximum vibration amplitude, which is regarded as the intrinsic frequency of a sample. So the mechanical resonant frequency can characterize and identify tissues with different elastic properties. In Figure 2, the ARF modulation frequency is swept within a range of 50 Hz to 1600 Hz, and the resonant frequency of the agar and metal ball is 60 Hz and 1080 Hz, respectively (46). Under a modulation frequency of 1080 Hz, the metal ball produced higher vibration amplitudes compared to the surrounding agar.

Figure 2.

Resonant frequency measurements for elasticity mapping using ARF–OCE. (a) Frequency response of the agar and metal ball. (b) 3D OCE image under a modulation frequency of 1080 Hz. (c) 2D sample image. The figure has been reprinted with permission from Qi et al., 2013. Copyright © (2013) AIP (46).

Elastic wave velocity calculation

When ARF dynamically excites a sample at one location, elastic waves can be generated to propagate from the excitation location to the surround medium in the interior or near the surface of the sample. By tracking the wave propagation using OCT and measuring the wave velocity, elastic properties can be quantified and mapped. During elastic wave propagation, the elastic properties can be assessed in a larger range as long as the wave propagation can be visualized. The elastic waves propagating in the interior of a thick sample are called body waves, including the compressional wave and shear wave, and the elastic wave traveling close to the surface with a penetration depth of about one wavelength is a Rayleigh wave.

The shear wave is most commonly detected for elasticity measurements. The shear wave is a transverse wave with the propagation direction perpendicular to the applied force direction and vibration direction. After ARF excitation, the shear wave is present in the lateral region of the force away from the sample surface. The shear modulus μ is usually quantified by the measurement of the shear wave velocity V_s using the following equation (7):

$$\mu =\rho \times V_S^2$$ (7)

where ρ is the density of the sample. Based on an approximate relation between the shear modulus μ and the Young’s modulus E, that is, E = 2μ × (1 + ν), the Young’s modulus of a homogeneous isotropic sample can be determined by the following equation (7):

$$E=2\rho \times \left(1+\nu \right)\times V_S^2$$ (8)

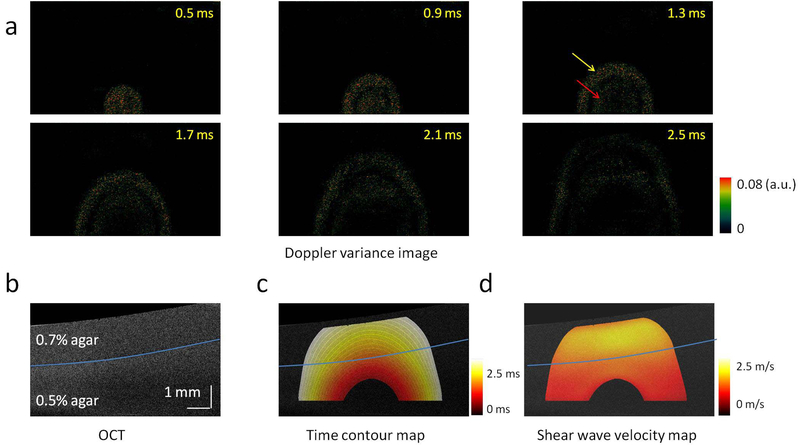
where ν is the Poisson’s ratio of the sample. The Poisson’s ratio is approximately 0.5 for biological tissues, because they can be considered as imcompressionable materials under small strains. Young’s modulus E can be determined by $3\rho \times V_S^2$. Figure 3 shows shear wave propagation in a two-layer phantom with 0.7% agar in the top layer and 0.5% agar in the bottom layer (49). The shear wave velocity speeds up after the wave travels from the soft layer to the stiff layer.

Figure 3.

2D visualization of shear wave propagation and mapping of shear wave velocities in a two-layer phantom. (a) Doppler variance images during shear wave propagation. (b) OCT image of the two-layer phantom. (c) Time contour map of the shear wave propagation. (d) 2D map of the shear wave velocity. The figure has been reprinted with permission from Zhu et al., 2016. Copyright © (2016) Springer Nature (49).

The compressional wave is a longitudinal wave propagating along the force direction and vibration direction in a compressible medium. The velocity of a compressional wave in a homogeneous isotropic sample is related to the bulk modulus K (modulus of incompressibility), the shear modulus μ (modulus of rigidity) and the density ρ of the sample, which can be determined by the following equation (35):

$$V_C=\sqrt{\frac{K+4\mu /3}{\rho }}$$ (9).

When the bulk modulus is 2.2 GPa, the shear modulus is 1 kPa and the density is 1000 kg/m³ for a soft sample with a high percentage of water, the theoretical velocity of the compressional wave will be ~1.5 km/s. Due to high speed propagation of a compressional wave and relatively low A-line rates of current OCT systems, the velocity of the compressional wave cannot be quantified.

The Rayleigh wave, a type of surface wave, travels near the surface of a sample. The Rayleigh wave has an evanescent component inside the sample which can be detected in a depth of about one wavelength. When the ARF excitation location is close to the sample surface and the induced wave wavelength is equivalent to OCT imaging depth, the detected elastic wave should be considered as a Rayleigh wave. For a homogeneous isotropic sample, the Young’s modulus E can be calculated based on the Rayleigh wave velocity V_R as follows (56,69):

$$E=\frac{2\rho \times {(1+\nu )}^3}{{(0.87+1.12\nu )}^2}\times V_R^2$$ (10)

where ν is the Poisson’s ratio and ρ is the density of the sample. Comparing Equations 10 and 8 shows that the Rayleigh wave propagates at a similar speed as the shear wave: V_R = 0.95V_S, when the Poisson’s ratio of the sample is 0.5 (5).

If the sample is thin in comparison with the wavelength of the induced elastic wave, such as a cornea, the elastic wave propagation is partly guided by the top and bottom boundaries of the thin sample with consecutive reflections, known as a Lamb wave (37). The Lamb wave has highly dispersive behaviors. In a vacuum, the frequency-dependent Lamb wave velocity V_L has been approximated by the following equation at a low frequency (37,70):

$$V_L=\sqrt{\frac{2\pi \times f\times h\times V_S}{\sqrt{3}}}$$ (11)

where f is the frequency and h is the sample thickness. If the thin sample is surrounded by liquids or soft solids, such as in vivo cornea, the Lamb wave velocity can be corrected by a factor of $1/\sqrt{2}$ due to a total leakage of the compressional wave and total reflection of the shear wave at both boundaries, which can be modeled by the following equation (37,71):

$$V_L=\sqrt{\frac{\pi \times f\times h\times V_S}{\sqrt{3}}}$$ (12).

Incorporating the relationship between the Young’s modulus E and the shear wave velocity V_S, that is, $E=3\rho \times V_S^2$, the Young’s modulus can be calculated by the Lamb wave velocity via the following equation:

$$E=\frac{9\rho \times V_L^4}{{(\pi \times f\times h)}^2}$$ (13)

where V_L is the Lamb wave velocity at the frequency of f.

For an ARF-OCE application, an appropriate model of elastic wave propagation should be selected based on the sample geometry and the region of elasticity measurements.

OCT detection methods

Although each elasticity measurement method has its unique principle, vibrations are commonly measured by OCT systems. In methods of vibration amplitude comparison and resonant frequency detection, vibration amplitudes will be quantified and compared. Meanwhile, in the method of wave velocity calculation, the vibration propagation will be visualized without the need of amplitude quantification. In order to sensitively quantify the vibration amplitude along the OCT beam, a phase-resolved Doppler OCT method has been developed (72). For the visualization of vibration propagation, both the phase-resolved Doppler OCT method and Doppler variance OCT method have been applied (73).

Combining Doppler principle with OCT, phase-resoved Doppler OCT extracts the phase information from the OCT complex data and calculates the phase shifts Δφ_i,j(t) at the position of the j_th A-line and the i_th depth between the time t and t + τ, where τ is the time interval between A-lines. The vibration velocity V_i,j(t) along the OCT beam direction can be determined by the following equation (74–78):

$$V_{i,j}(t)=\frac{{\lambda }_0\times \Delta {\phi }_{i,j}(t)}{4\pi \times n\times \tau }$$ (14)

where λ₀ is the vacuum center wavelength of the OCT light source and n is the refractive index of the sample. The phase shift is measured based on a cross-correlation algorithm (76,79):

$$\Delta {\phi }_{i,j}(t)={\mathit{tan}}^{-1}\left[\frac{\mathit{Im}(F_{j,i}\cdot F^{\ast }{}_{j+1,i})}{\mathit{Re}(F_{j,i}\cdot F^{\ast }{}_{j+1,i})}\right]$$ (15)

where F_j,i is the OCT complex signal at j_th A-line, i_th depth and time t, and F_j+1,i is the OCT complex signal at j + 1_th A-line, i_th depth and time t + τ. Substituting V_i,j(t) from Equation 14 into Equation 3, the vibration amplitude at the j_th A-line and the i_th depth can be determined by the following equation:

$$\Delta z_{i,j}={\int }_{t_1}^{t_2}\frac{{\lambda }_0\times \Delta {\phi }_{i,j}(t)}{4\pi \times n\times \tau }dt$$ (16).

Phase shift measurement is sensitive to the displacement parallel to the OCT beam and cannot detect a displacement perpendicular to the OCT beam.

In the case of orthogonal ARF excitation, the vibrations are perpendicular to the OCT beam. Therefore, we recently developed OCT Doppler variance method for the sensitive detection of transverse vibrations. The Doppler variance ${\sigma }_{j,i}^2$ at the position of the j_th A-line and the i_th depth can be determined by the OCT data with the following equation (73,76,77,79,80):

$${\sigma }_{j,i}^2(t)=\frac{1}{{(2\pi \cdot \tau )}^2}\cdot \left(1-\frac{2\cdot |F_{j,i}\cdot F^{\ast }{}_{j+1,i}|}{|F_{j,i}{|}^2+|F_{j+1,i}{|}^2}\right)$$ (17)

where F_j,i and F_j+1,i are the OCT signals at the time t and t + τ, respectively. The Doppler variance method is sensitive to the transverse vibration, and will not be distorted by bulk motion and phase wrapping, so the data processing will be simpler and quicker (81).

Depending on the applications, parallel, orthogonal and oblique ARF excitation can be applied, and thus, the positions between the ARF excitation device and OCT imaging lens are flexibly selected. For parallel and oblique ARF excitation, phase-resolved Doppler OCT can quantify the vibration amplitudes along the OCT beam. In applications for orthogonal and oblique ARF excitation, Doppler variance OCT can detect the vibrations perpendicular to the OCT beam. The elasticity measurement methods are compared in Table 1.

Table 1.

A comparison among elasticity measurement methods using ARF-OCE.

	Imaging region	Measurement parameter	Excitation mode	Elasticity assessment	Measurement time	detection method
Comparison of vibration amplitude	Shallow and deep region of sample with complex geometry	Vibration amplitude	Oblique and parallel excitation	Qualitative	short	Phase-resolved Doppler OCT
Resonant frequency detection	Shallow and deep region of sample with complex geometry	Resonant frequency	Oblique or parallel excitation	Quantitative	long	Phase-resolved Doppler OCT
Shear wave measurement	Deep region of thick sample	Wave velocity	Oblique, parallel and orthogonal excitation	Quantitative	long	Phase-resolved Doppler OCT and Doppler variances
Rayleigh wave measurement	Shallow region of thick sample	Wave velocity	Oblique, parallel and orthogonal excitation	Quantitative	long	Phase-resolved Doppler OCT and Doppler variances
Lamb wave measurement	Thin sample	Wave velocity	Oblique, parallel and orthogonal excitation	Quantitative	long	Phase-resolved Doppler OCT and Doppler variances

Biomedical applications of ARF-OCE

As a noninvasive, high resolution cross-sectional imaging modality, OCT has been used in the structural and functional imaging of the ocular tissues (82), brain (76,83,84), oral tissue (85), larynx (86), airway (87,88), skin (89), artery (90,91), digestive tract (92), etc. Incorporating ARF excitation to both superficial tissues and deep tissues with the noninvasive nature, ARF-OCE can be applied for a broader range of biomedical applications. Here we describe a few examples in the elasticity measurements of ocular tissues, detection of vascular lesions and monitoring of blood coagulation.

Elasticity measurements of ocular tissues

As ARF can excite the ocular tissues located on the body surface, such as the cornea, and in the interior, such the crystalline lens, choroid and retina, ARF-OCE has been a unique tool for elasticity measurements of ocular tissues based on comparison of vibration amplitudes and detection of elastic waves.

The cornea is an important tissue for light refraction, composed of cross-linked collagen fibers. When the collagen fiber network is disrupted, the refractive function of the cornea will change, and thus, the vision will be impaired, such as in the case of Keratoconus (93). The disruption of the collagen fiber network accompanies the changes in the elastic properties of the cornea. Therefore, the measurement of elastic properties is essential to diagnose Keratoconus and monitor its treatment. Qu et al. reported on a real-time ARF-OCT system for the mapping of the relative elasticity of corneal tissues (94). ARF from a focused ring transducer excited the cornea of a fresh ex vivo rabbit eyeball with a uniform stress field in a lateral region of 400 μm by 400 μm and an axial field of 5 mm. The OCT beam passed through the central aperture of the ring transducer, which was parallel to the ARF direction. The phase-resolved Doppler method detected the vibration amplitude in 3D. Compared to the healthy cornea, the vibration amplitude became much lower after a formalin soaking for 12 hrs, indicating that the tissue was much stiffer. After injection of the formalin solution inside the healthy cornea to induce local cross-linking, the distribution of vibration amplitudes was measured, and the relative elasticity of corneal tissue was mapped in Figure 4 (94). This study showed ARF-OCE has the capabilities to demonstrate corneal cross-linking.

Figure 4.

Imaging of ex vivo rabbit cornea with injection of formalin solution. (a) OCT image of cornea. (b) Displacement magnitude image. (c) Displacement quantification along the lateral positions. The figure has been reprinted with permission from Qu et al., 2016. Copyright © (2016) IEEE (94).

Mechanical waves have also been visualized in the cornea by an ARF-OCE system. Nguyen et al. reported the visualization of elastic wave propagation in an ex vivo porcine cornea using ARF-OCE (95). A single-element transducer generated ultrasound, which was coupled by a plastic cone to the cornea. The transducer was placed on the same side as the OCT imaging beam, and the ARF obliquely excited the cornea to avoid blocking the OCT imaging beam. Phase-resoved OCT visualized the elastic wave propagation in the cornea. Recently, Ambroziński et al. employed focused, air-coupled ultrasound to induce mechanical vibrations at the interface between the cornea and the air through reflection-based ARF (96). The ARF obliquely excited the cornea with ~45 degrees to avoid blocking the OCT beam. The vibrations were detected by phase-resolved OCT so that the mechanical wave propagation was visualized. The system generated a quantitative elastogram by measurements of mechanical waves in ex vivo porcine cornea. The influence of intraocular pressures on the corneal elasticity was also studied by comparison of vibration amplitudes. The average group wave velocity at 40 mmHg was more than twice as that at 10 mmHg intraocular pressure. The vibration displacement induced by the ARF excitation decreased when the intraocular pressure increased.

Elasticity measurement of the crystalline lens is important for the monitoring of presbyopia because presbyopia is generally caused by the loss of elasticity of the lens. As the lens is located posterior to the cornea and iris, it is a challenge to excite the lens for elastography. Wu et al. used an ARF-OCE system to assess age-related changes in the elasticity of an ex vivo rabbit lens (97). The ARF focused on the surface of the crystalline lens obliquely and remotely through the cornea and the aqueous humor. Due to the transparent property of the lens, OCT can only image the surface of the lens. After ARF excitation, displacement profiles along the OCT beam were recorded on the surface of the lens by phase-resolved Doppler OCT. Comparison of the maximum displacements between young rabbit lenses and mature lenses indicated an increase of lens stiffness with age.

In order to assess the elastic properties of retinal layers, Qu et al. developed an ARF-OCE system for in vivo elasticity mapping of rabbit retinal layers (98). By measuring the tissue deformation after ARF excitation, elasticity of different retinal layers was compared before and after retinal inflammation disease formation caused by blue light exposure. The stiffness of five layers was measured to increase gradually from the ganglion side to the photoreceptor sides of the retina in both healthy and diseased rabbit models, which is shown in Figure 5. The top 4 layers generally were softer and the bottom layer was stiffer for the healthy tissue. Song et al. assessed the elastic properties in ex vivo porcine retinal and choroidal tissues based on shear wave measurements (99). A linear phased array ultrasound transducer was used to induce shear waves and an OCT beam was set on the opposite side of the sample to image wave propagation. The shear waves visualized by phase-resolved Doppler methods were used to calculate the Young’s modulus. The Young’s modulus of the choroidal tissue was 34.4 kPa, which was much higher than that of the retinal tissue of 6.2 kPa.

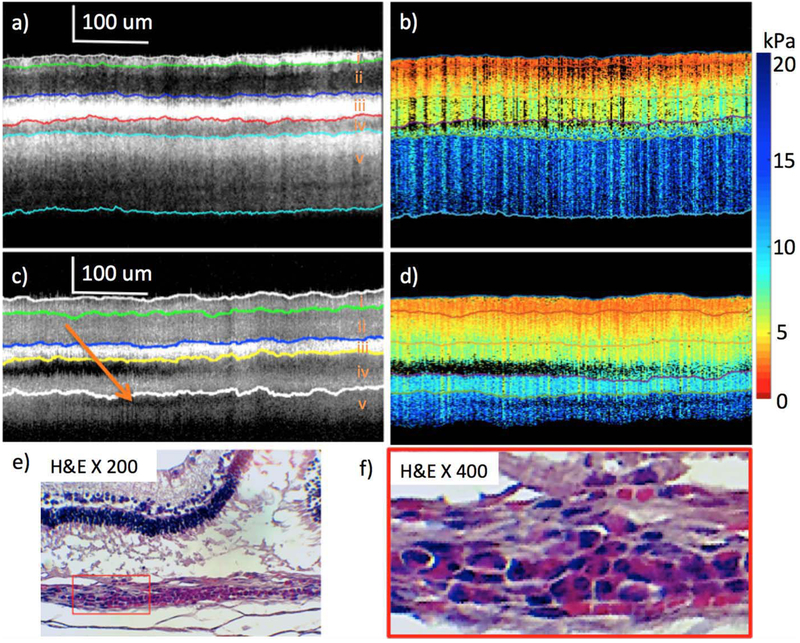
Figure 5.

Comparison of healthy and diseased rabbit retinal layers. (a) and (b) are OCT and elastogram of healthy retina at week 4. (c) and (d) are OCT and elastogram of abnormal portion of retina at week 8. (e) and (f) are H&E staining images with 200 and 400 magnification after euthanization at week 8. The figure has been reprinted with permission from Qu et al., 2018 which is an open access article distributed under the terms of the Creative Commons CC BY license, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. (98).

Detection of vascular lesions

Coronary heart disease is the most common type of heart disease, and the major underlying cause is atherosclerosis. Atherosclerosis develops slowly beginning in childhood and takes decades to advance. In atherosclerosis, mechanical properties change in the walls of the artery. Biomechanical properties of the arterial wall correlate with the stability of the plaques. Due to the tube structures of the arteries, it’s not easy to visualize the elastic wave propagation, and thus, vibration amplitudes are commonly quantified for elasticity assessment.

In 2012, Qi et al. demonstrated the potential of ARF-OCE for the elasticity mapping of an ex vivo atherosclerotic human cadaver coronary artery (45). During ARF excitation, phase-resolved Doppler OCT detected a strong contrast of vibration amplitudes in the artery. The plaque region, comprising of stiffer tissues, presented less vibrations while the normal softer tissue presented larger vibrations. Based on the comparisons of vibration amplitudes, the region of atherosclerotic lesions could be identified. As the ultrasound transducer and OCT scan lens were located on opposite sides of the sample, the system was not convenient for clinical applications.

In 2014, Qi et al. improved the ARF-OCE system by use of a focused ring ultrasonic transducer (47). The ultrasonic transducer was placed on the same side of the OCT lens, and the OCT beam passed through the central aperture of the ring transducer which was more suitable for the applications. Because the ARF induced the displacement parallel to the OCT beam, the phase-resolved Doppler shift measurements could sensitively detect the vibration amplitudes. Significant differences in vibration displacements were recorded between the softer fibrous cap and the stiffer necrotic core from the elastogram. However, because of the large size of the ultrasound transducer and OCT lens, the system was not used for in vivo applications.

Recently, Qu et al. designed a miniature probe for mapping elastic properties of vascular lesions (100). An OCT lens with a diameter of 0.7 mm was inserted into the middle aperture of a ring ultrasound transducer with an outer diameter of 3.5 mm and an inner diameter of 0.8 mm. The ultrasound beam and OCT beam were uniaxial and located on the same side. Vibration amplitudes of an ex vivo human cadaver coronary artery were measured by the phase-resolved OCT method. Atherosclerotic plaque, intimal thickening and atheroma, and relatively healthy tissues were differentiated based on the differences of vibration amplitudes, which is shown in Figure 6. The design of a miniature probe makes it applicable for in vivo elastography.

Figure 6.

Elastography and histology of an ex vivo human cadaver coronary artery. (a) OCT image. (b) Elastogram. (c) H&E staining under 4£ magnification. The black arrow indicates the smooth muscle layers in the media of the artery, the blue arrow indicates the intimal thickening and atheroma. The left region with lower displacement indicates a thicker atherosclerotic plaque. The figure has been reprinted with permission from Qu et al., 2017. Copyright © (2017) Springer Nature (100).

Although the comparison of vibration amplitudes can assess the relative elasticity of arterial lesions, it’s not easy to quantify the elastic properties, and the results from different systems cannot be compared directly. Measurement of the resonant frequency was developed to quantify the elastic properties by Qi et al. (46) without requirement of ARF calibration. Resonant ARF-OCE measurements were performed on a section of ex vivo human coronary artery with atherosclerotic plaques. The thin loose region of the fibrous cap showed a higher vibration amplitude at 500 Hz; meanwhile, a thicker denser portion of the fibrous cap showed higher vibrations at 800 Hz, which indicated that different fibrous caps have different resonant frequencies and different elasticities. Measurements of resonant frequencies have the potential to quantify the elasticity of arterial tissues in vivo.

Monitoring of blood coagulation

Blood coagulation is the process in which blood changes from a liquid to a gel and forms a clot. Disorders of coagulation are disease states that can result in life-threatening bleeding or thrombotic disorders. Coagulation tests are required for the diagnosis of blood diseases, such as thrombophilia and hemophilia, treatment monitoring for people who take medications, such as aspirin and warfarin, and are sometimes recommended before surgery (101–104). Xu et al. reported on the use of ARF-OCE for ex vivo assessment of coagulation properties of whole blood based on shear wave measurements (105). During blood coagulation, changes in the elastic property of the blood sample increased the shear modulus of the sample and altered the propagating velocity of the shear wave in the sample. In the ARF-OCE system, ARF excited porcine whole blood in a container with a thin-film window for the ultrasound pass. The OCT beam orthogonal to the ARF direction detected the transverse vibration with the Doppler variance method. The shear wave propagation could not be visualized directly in a wide range because of the shallow OCT penetration in blood. Therefore, the ratio of the time delay of the shear wave arriving at the same point to the changing step of the ARF focus was calculated for the determination of shear wave velocities and shear modulus. Dynamic blood coagulation status can be quantitatively monitored by relating the shear modulus with clinically relevant coagulation metrics. Because of its rapid and quantitative nature, this system has the potential to be used for rapid point-of-care testing in the applications of diagnosis of coagulation disorders and monitoring of therapies.

Challenges for clinical translation

ARF-OCE incorporates the ability of remote and noncontact ARF excitation to both superficial and deep tissues with high-resolution, noninvasive, 3D OCT imaging. It has been used for elasticity measurements of ocular tissues, detection of atherosclerotic lesions and assessment of blood coagulation function based on the measurement of vibration amplitudes, determination of resonant frequencies, and the calculation of elastic wave velocities. However, its application in clinical diagnosis and researches still presents several challenges, including detection range, imaging speed and clinical adoption.

Extension of detection range

The detection range of ARF-OCE is determined by the OCT imaging range, the range of elastic wave propagation in wave velocity measurement, and the range of uniform ultrasound force in vibration amplitude related measurement. In wave velocity measurement, the wave propagation can be detected by OCT within only several millimeters near the ARF excitation position due to the rapid attenuation of wave propagation in the sample. The ARF focus should be repositioned at multiple locations for the detection of a larger range which is time consuming and increases the complexity of the system. In order to extend the range of wave propagation, a linear phased array ultrasound transducer can be developed as the programmable wave excitation source to launch the ARF focus at desired locations and, thus, to induce the shear wave in a larger range. This has been demonstrated by Song, et al. (99). After launching the focused ARF at six locations, the shear wave can be tracked in a region of 8 mm by 2.1 mm, which covers the OCT scanning range. In the vibration amplitude related measurement, an ideal ultrasound transducer generates uniform acoustic radiation force in a larger range. However, it will be compromised between the range of the uniform ARF field and the magnitude of the ARF.

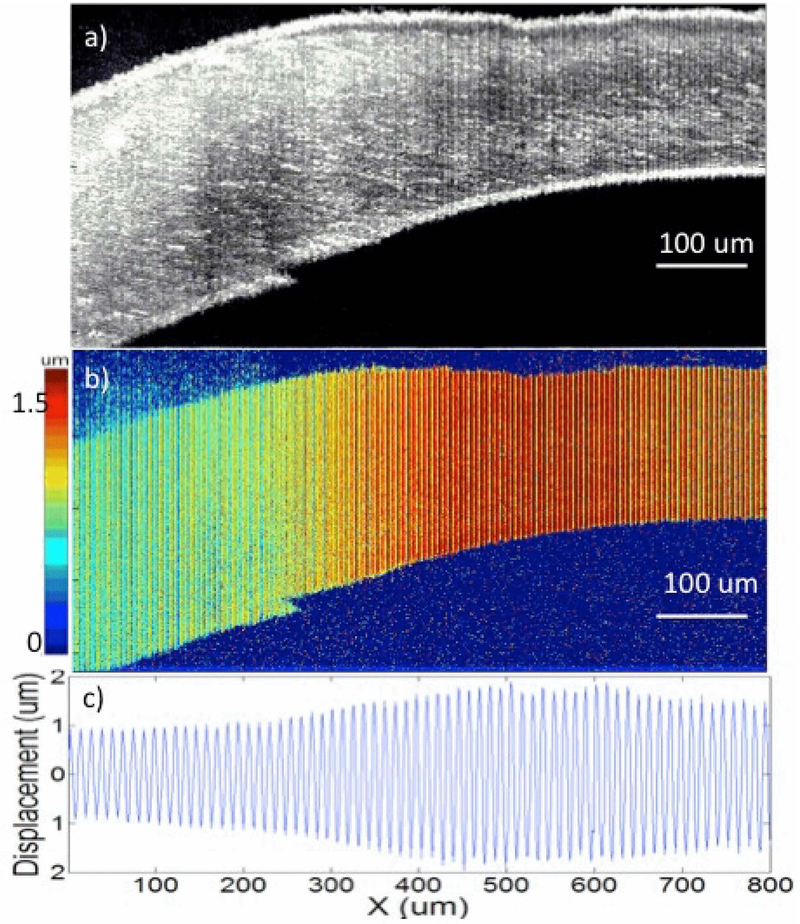
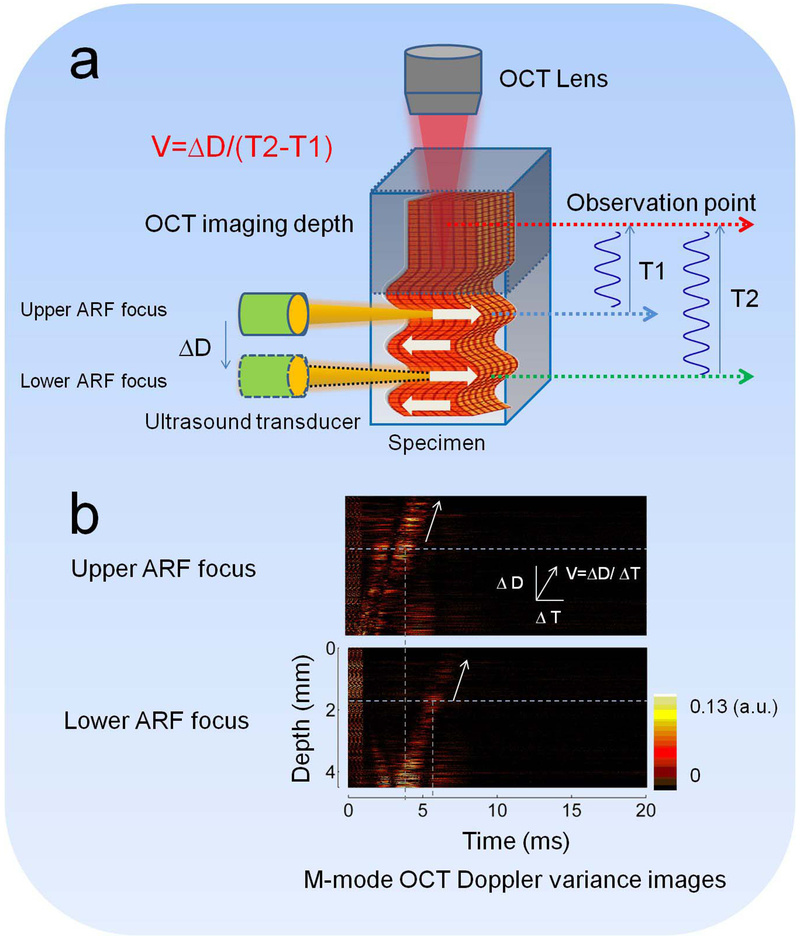
Besides the challenges from the limitation of wave propagation range and uniform force range, the OCT imaging range also limits the ARF-OCE detection range. The OCT lateral scanning range can usually cover ~1 cm by ~1 cm with the use of a galvo mirror. However, the imaging depth can only cover 0.5-3 millimeters, depending on the scattering properties of tissues. Recently, Yi et al. developed an OCT system with a 1.7 μm swept source laser to readily extend the penetration depth into the tissue because of the longer wavelength, compared with typical system with a 1.3 μm swept source laser (91). Based on tests using an intravascular OCT system, the imaging depth in the 1.7 μm system was approximately two times higher than in the 1.3 μm system. Zhu et al. reported on an ARF orthogonal excitation OCE (ARFOE-OCE) technique for quantification of elastic moduli beyond the limitation of the OCT imaging depth (48). In the ARFOE-OCE system, the ARF orthogonal to the OCT beam induced the vibrations inside a sample, which were detected by a Doppler variance method. The shear wave was visualized by the M-scan during propagation from the ARF focus to the sample surface. When the transducer was moved downward with a known step ΔD under the OCT imaging depth, the time delay (T₂ − T₁) was measured for the wave arriving at the same observation point in the OCT imaging depth. The shear wave velocity between the two ARF positions under the OCT imaging depth was calculated to be equal to ΔD/(T₂ − T₁). Therefore, the ARF-OCE detection depth can extend beyond the OCT imaging depth. The schematic of the ARFOE-OCE method is shown in Figure 7.

Figure 7.

Extending detection depth using ARFOE–OCE. (a) Schematic of the ARFOE–OCE system. (b) Mmode OCT Doppler variance images with different ARF focus positions. The time delay was observed for the wave propagation when the ARF focus was moved downward. Figure (a) has been reprinted with permission from Zhu et al., 2016. Copyright © (2016) SPIE (50) and Figure (b) has been reprinted with permission from Zhu et al., 2015. Copyright © (2015) OSA (48).

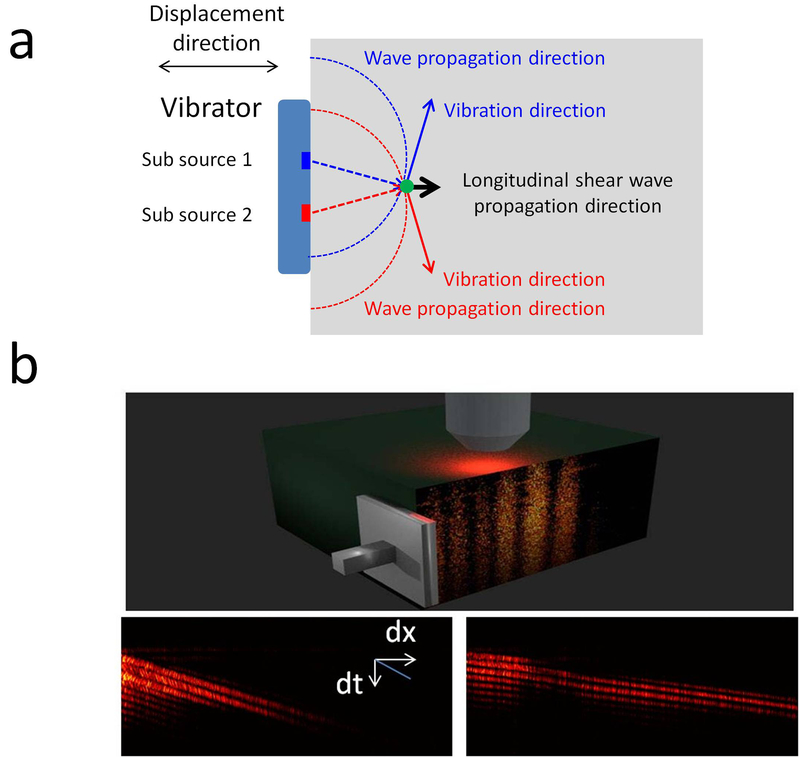
Elastic wave measurements can quantify the elastic properties of tissues. However, current measured elastic waves are transverse waves, where the wave propagation direction is perpendicular to the ARF excitation direction, and thus, only the elastic modulus in the lateral region of the force can be detected. Elastic wave measurements cannot provide the elastic information in the axial region of the force. Meanwhile, the elastic properties are directionally dependent in many biological tissues, such as optical nerves and muscles. For an anisotropic sample, elasticity can only be determined along the wave propagation direction. Therefore, transverse wave measurements allow the determination of the elastic properties perpendicular to the ARF direction and miss the elastic information along the force direction. In order to address these challenges, a longitudinal shear wave imaging was developed to map the elastic properties along the force direction in the axial region of the force (61). The longitudinal shear wave propagated parallel to the force direction due to the sum contribution of vibrations induced by multiple sub-sources, which is shown in Figure 8. Incorporating the principle of longitudinal shear wave generation, ARF-OCE has a great opportunity to map the elastic properties in extended regions, including the lateral region and the axial region of ARF, and measure the directionally dependent moduli in an anisotropic sample.

Figure 8.

Longitudinal shear wave induced by a vibrator source. (a) Generation of a longitudinal shear wave. (b) Spatio–temporal OCT Doppler variance images at a given depth in 0.50% (left) and 0.75% (right) agar phantoms. The figure has been reprinted with permission from Zhu et al., 2017. Copyright © (2017) AIP (61).

Increase of imaging speed

The detection speed of ARF-OCE mainly depends on the OCT imaging speed. Because of limitation of the OCT A-line rate, conventional ARF-OCE employs an M-B scan mode to detect the vibrations and capture wave propagation in a wide range. In the M-B scan mode, each B scan consists of hundreds of M scans at each OCT beam position, and the ARF repeatedly excites the same location for OCE measurements at different OCT beam positions (48,49,51). The M-B scan is time consuming and results in an acquisition time up to several minutes, which is not feasible for in vivo applications. Meanwhile, in a stiffer tissue with higher elastic modulus, the elastic wave velocity will increase and may not be detectable by the conventional frame rate of 50-200 kHz using the M-B scan. An OCT system with a higher A-line rate is required for rapid elasticity mapping in a wide range and for elasticity measurements in a stiffer tissue. Recently, an FDML swept source laser with an A-scan rate of ~1.5 MHz has been applied in the OCT system for elastography (55). Due to the single excitation and rapid B scan acquisition, this system may be useful for applications where measurement time is critical.

Clinical adoption of ARF-OCE

The clinical adoption of the ARF-OCE devices is important for in vivo imaging. First, a miniature endoscopic probe is required in order to detect cardiovascular lesions which incorporates an ultrasound transducer into an OCT imaging lens. The integration of the ultrasound transducer and OCT lens will increase complexity of the design. The reliability of a miniature ultrasound transducer with high power should also be improved. Second, the ultrasound transducer and OCT lens should be placed on the same side of the detected tissue for in vivo applications. In order to avoid blocking the OCT beam, the ARF will excite the tissues at an oblique angle to the OCT beam. The oblique ARF excitation will induce vibrations not parallel to the OCT beam, which decreases the sensitivity for phase-resolved Doppler detection, and will generate complicated elastic wave propagation for subsequent analysis. An alternative solution is the use of a ring transducer for the co-aligned ARF excitation parallel to the OCT beam in which the OCT beam passes through the central aperture of the transducer. Third, the coupling between the ultrasound transducer and tissue is required to guide the ultrasound into the tissues. Ultrasound gel is commonly used to couple the transducer and tissue (51,99), and water can also match the ultrasound into the tissue (48,49,94,105). An air-coupled piezo-ceramic transducer can send ultrasound signals to the tissue through air, which may be useful for the non-contact vibration induction at the interface between the tissue and air, and has been applied to generate elastic waves in ex vivo porcine corneas (96,106). The orthogonal ARF excitation OCE system also provides an opportunity for the probe design in ophthalmic applications, where the ultrasonic signals could reach the target ocular tissues through the eyelid or the outer corner of the eye without affecting the cornea (48).

Conclusions

ARF-OCE has the ability for noninvasive, high-resolution elasticity assessment of soft tissues. Based on different principles of elasticity measurement, including comparison of vibration amplitudes, resonant frequency detection and elastic wave velocity calculation, relative elasticity distribution and quantitative elastic moduli can be characterized and mapped ex vivo and in vivo. Due to remote and noncontact ARF excitation, ARF-OCE has been applied for elasticity measurements of superficial tissues and deep tissues, such as elasticity measurements of ocular tissues, detection of vascular lesions and monitoring of blood coagulation. Although the detection range, detection speed and clinical adoption remain challenging, ARF-OCE has great potential to become a powerful elasticity imaging tool for clinical diagnosis, disease monitoring and point-of-care testing.