Predictability and Uncertainty in the Pleasure of Music: A Reward for Learning?

Abstract

Music ranks among the greatest human pleasures. It consistently engages the reward system, and converging evidence implies it exploits predictions to do so. Both prediction confirmations and errors are essential for understanding one's environment, and music offers many of each as it manipulates interacting patterns across multiple timescales. Learning models suggest that a balance of these outcomes (i.e., intermediate complexity) optimizes the reduction of uncertainty to rewarding and pleasurable effect. Yet evidence of a similar pattern in music is mixed, hampered by arbitrary measures of complexity. In the present studies, we applied a well-validated information-theoretic model of auditory expectation to systematically measure two key aspects of musical complexity: predictability (operationalized as information content [IC]), and uncertainty (entropy). In Study 1, we evaluated how these properties affect musical preferences in 43 male and female participants; in Study 2, we replicated Study 1 in an independent sample of 27 people and assessed the contribution of veridical predictability by presenting the same stimuli seven times. Both studies revealed significant quadratic effects of IC and entropy on liking that outperformed linear effects, indicating reliable preferences for music of intermediate complexity. An interaction between IC and entropy further suggested preferences for more predictability during more uncertain contexts, which would facilitate uncertainty reduction. Repeating stimuli decreased liking ratings but did not disrupt the preference for intermediate complexity. Together, these findings support long-hypothesized optimal zones of predictability and uncertainty in musical pleasure with formal modeling, relating the pleasure of music listening to the intrinsic reward of learning.

SIGNIFICANCE STATEMENT Abstract pleasures, such as music, claim much of our time, energy, and money despite lacking any clear adaptive benefits like food or shelter. Yet as music manipulates patterns of melody, rhythm, and more, it proficiently exploits our expectations. Given the importance of anticipating and adapting to our ever-changing environments, making and evaluating uncertain predictions can have strong emotional effects. Accordingly, we present evidence that listeners consistently prefer music of intermediate predictive complexity, and that preferences shift toward expected musical outcomes in more uncertain contexts. These results are consistent with theories that emphasize the intrinsic reward of learning, both by updating inaccurate predictions and validating accurate ones, which is optimal in environments that present manageable predictive challenges (i.e., reducible uncertainty).

Introduction

Although rewards like food or socializing provide clear adaptive benefits, abstract pleasures with esthetic value, such as music, have long stumped scholars (Darwin, 1871). Music is particularly adept at establishing and manipulating patterns of melody, rhythm, and other features, and is often most pleasurable after sudden and dramatic changes (Sloboda, 1991; Grewe et al., 2007). Activity in the NAc, a central node of the brain's reward system, reflects how much a listener enjoys a musical stimulus overall (Salimpoor et al., 2011, 2013) and increases after pleasurable musical surprises (Shany et al., 2019), suggesting that much of music's power stems from the predictions it engenders and exploits (Meyer, 1956; Huron, 2006).

Yet surprises are often unpleasant. A study based on a naturalistic concert found that listeners responded negatively to the most surprising musical phrases, most of which occurred during a complex and stylistically unfamiliar piece (Egermann et al., 2013). Listeners also tend to dislike surprises during short, experimenter-controlled stimuli, where context is lacking (Koelsch et al., 2008; Brattico et al., 2010), but seem most likely to enjoy them in naturalistic and familiar music (Sloboda, 1991; Grewe et al., 2007). These findings imply that musical events are pleasurable when the surrounding musical context allows for relatively certain predictions, which may be related to evidence of caudate dopamine transmission preceding moments of peak musical pleasure (Salimpoor et al., 2011).

Surprises are generally important feedback signals that guide belief updates and adaptive behavior in ever-changing environments (den Ouden et al., 2010; Friston, 2010). Inevitably, completely predictable events preclude learning because they offer no new information, but unforeseeable, seemingly random surprises are equally unhelpful because they're indecipherable. An intermediate degree of predictability (i.e., a manageable challenge) therefore enhances learning, piquing curiosity and attention in the process (Kang et al., 2009; Abuhamdeh and Csikszentmihalyi, 2012a,b; Gottlieb et al., 2013; Kidd et al., 2014; Baranes et al., 2015; Daddaoua et al., 2016; Oudeyer et al., 2016; Brydevall et al., 2018). Learning engages the dopaminergic reward system, such as other adaptive benefits, often making manageable challenges highly motivational and pleasurable (Bromberg-Martin and Hikosaka, 2009; Kang et al., 2009; Abuhamdeh and Csikszentmihalyi, 2012a,b; Jepma et al., 2012; Ripollés et al., 2014; Brydevall et al., 2018). Could the manageable challenge of foreseeable musical surprises help explain musical pleasure?

Berlyne described the appeal of manageable challenges with an inverted U-shaped “Wundt” effect, named for the scholar who first linked pleasure to intermediate levels of arousal (Wundt, 1874; Berlyne, 1974). Across esthetic domains, Berlyne proposed that intermediate complexity–concerning features such as predictability, surprise, or uncertainty–optimizes curiosity and liking. Yet evidence for musical Wundt effects is mixed: a review of 57 studies found them in only 15 (Chmiel and Schubert, 2017), whereas many others suggested greater preferences for prototypical or familiar music that was subjectively simpler (Zajonc, 1968; Hargreaves et al., 2005). Although these 15 studies provide some support for Wundt effects, the evidence is weak because of their different and arbitrary measures of complexity; a critical test of this effect requires both well-defined independent variables and heterogeneous sampling of them to identify potential curvilinear effects.

We designed the present two studies to address these problems. First, we formally measure the unpredictability and uncertainty of unaltered real-world music to encapsulate these aspects of musical complexity and relate them to pleasure. Using information-theoretic modeling (Pearce, 2005), we express unpredictability as the negative log probability (or information content [IC]) of a musical event given the preceding context and the prior long-term exposure of the model, and the uncertainty of the prediction as the entropy of the corresponding probability distribution. Second, we ensure quantifiably wide ranges of these variables to test the Wundt effect rigorously. In Study 1, we investigate how musical unpredictability and uncertainty affect liking and the musical features that contribute to them. In Study 2, we replicate the key findings of Study 1 and explore the additional influence of veridical familiarity.

Study 1

Materials and Methods

Participants and procedure.

Forty-four healthy volunteers with normal hearing (25 females, mean age ± SD = 21.56 ± 3.31 years) participated in this experiment. Since our model of the information-theoretic properties of the stimuli is based on Western tonal folk and classical music, we excluded 3 additional volunteers who listed atonal or jazz music, which frequently deviate from the structures of folk and classical music, among their five favorite genres in an open-ended screening questionnaire during recruitment.

To learn more about the participants' individual backgrounds and differences, we asked them to complete three questionnaires after providing informed consent. The Goldsmiths Musical Sophistication Index (Gold-MSI) measured their abilities to engage with music, with questions about their musical recognition, discernment, education, and more (Müllensiefen et al., 2014). It has five subscales, distinguishing active engagement, perceptual abilities, musical training, emotions, and singing abilities. The Barcelona Music Reward Questionnaire (BMRQ) scored the degree to which the participants associate music with reward, focusing on music seeking, emotion evocation, mood regulation, sensory-motor, and social reward (Mas-Herrero et al., 2013). Finally, the Big Five Inventory assessed their personality traits for extraversion, neuroticism, openness, agreeableness, and conscientiousness (Caprara et al., 1993), although these results are not reported here.

After the questionnaires, participants listened to each stimulus over professional monitor headphones (Audio-Technica), preset to a comfortable volume, via a computer running Presentation software (Neurobehavioral Systems) while a fixation cross appeared on the screen. Afterward, they rated how much they liked it on a Likert scale from 1 (very little) to 7 (very much), and indicated whether they recognized the stimulus (not necessarily by name, but by the music) so that we could exclude these trials from our analyses to avoid confounding music-syntactic predictability with effects of familiarity. Since 1 participant rated every single trial as familiar, we excluded this participant from all analyses. Another participant withdrew from the study approximately halfway through, for reasons unexplained, but the existing data were maintained. The resulting sample of 43 volunteers recognized the music in 431 (18.44%) of 2337 trials, with a mean ± SD of 10.02 ± 7.81 per participant; these familiar trials were therefore excluded, leaving 1906 trials for analysis. Pairwise correlations showed that stimuli with lower mean duration-weighted IC (mDW-IC; see below) were more likely to be rated as familiar (Pearson's r₍₅₃₎ = −0.28, p = 0.04). There was no significant relationship between exclusions and mean duration-weighted entropy (mDW-Ent) (Pearson's r₍₅₃₎ = −0.11, p = 0.43).

Before the listening task, participants experienced two practice trials using stimuli that did not occur during the experiment for familiarization and to ensure that they understood the instructions. To avoid anchoring effects, we sorted the stimuli into five clusters of mDW-IC (see below) using k-means clustering, and randomly selected one stimulus from each cluster to constitute the first five stimuli of the experiment. This procedure allowed the participants to acclimate to the range of mDW-ICs present in the experiment. After these five stimuli, the remaining 50 occurred in a random and participant-specific order.

To ensure the participants' attention, we included an orthogonal task in which they had to press the “Enter” key as soon as they heard the timbre of a stimulus change. A practice “attention trial” warned the participants about this task and allowed them to practice; afterward, they occurred pseudo-randomly every 6 ± 2 trials during the experiment. The participants responded to every timbre change within the 2 s allotted, with a mean ± SD reaction time of 0.82 ± 0.23 s, indicating that they were attentive throughout the task. Moreover, linear regression models indicated that these reaction times did not significantly vary with musical sophistication (F_(1,41) = 1.01, p = 0.32), musical reward sensitivity scores (F_(1,41) = 0.25, p = 0.62), or any of their subscales (all other p values > 0.40), suggesting that these factors did not affect task attention.

Stimuli.

All 55 stimuli, plus the two for the rating practice trials and the nine for the “attention trials,” were excerpts of real, precomposed music collected from public Musical Instrument Digital Interface databases. Most stimuli came from the following websites: www.osk.3web.ne.jp/∼kasumitu/eng.htm and www.classicalarchives.com/midi.html. We opted for real music instead of custom-built stimuli to more faithfully represent naturalistic listening experiences and the greater range of subjective responses it engenders.

To this same end, the stimuli contained examples of several musical genres from a wide range of time periods, composers, tonalities, and meters (Table 1). We used only monophonic stimuli (i.e., containing only one tone at a time) to avoid the confounding effects of harmony (i.e., chordal relationships) and polyphony (i.e., multiple voices), and we reduced other confounds by normalizing their peak amplitudes to the same level with Audacity (1999–2018 Audacity Team), limiting the stimuli to 30 ± 2 s, and synthesizing the Musical Instrument Digital Interface stimuli into Waveform Audio File (WAV) format. We also standardized the tempo of each stimulus to either 96, 120, or 144 bpm, whichever sounded most musically appropriate, with MuseScore (2018 MuseScore BVPA). These considerations constrained our stimuli to excerpts that were either solo pieces or solo melodic lines from polyphonic pieces.

Table 1.

Stimulus details^a

Piece	Excerpt time (approximate)	Composer	Year	Key	Meter	Studies	mDW-IC	mDW-Ent
Streams of Kilnaspig	0:00–0:30	Irish traditional	Unknown	G major	Compound duple	1, IS	2.34	3.62
Eighteen Studies for the Flute, Op. 41, No. 11	1:30–2:00	Joachim Andersen	1891	F major	Simple duple	1, 2, IS	2.99	2.23
When This Cruel War is Over	1:00–1:30	American traditional	1863	Bb major	Simple duple	1, IS	3.72	3.86
Seven Variations on a Theme from Silvana, J. 128, Op. 33, Var. 7	8:00–8:30	Carl Maria von Weber	1854	Bb major	Compound duple	1, 2 (clar), IS	3.89	2.87
12 Fantasias for Solo Flute, No. 3, Vivace	0:45–1:15	Georg Philipp Telemann	1733	B minor	Simple duple	1, IS	3.93	2.64
Eighteen Studies for the Flute, Op. 41, No. 18	0:50–1:20	Joachim Andersen	1891	F minor	Compound duple	1, IS	4.04	2.6
12 Fantasias for Solo Flute, No. 3, Vivace	0:10–0:40	Georg Philipp Telemann	1733	B minor	Simple duple	1, IS	4.08	2.45
Young Cowherd	0:00–0:30	Chinese traditional	Unknown	G major	Simple duple	1	4.1	3.75
Sakura	0:00–0:30	Japanese traditional	Unknown	D minor	Simple duple	1	4.23	4.39
Orchestral Suite No. 2 in B minor, BWV 1067	2:45–3:15	Johann Sebastian Bach	1739	B minor	Simple duple	1, 2, IS	4.52	3.95
Eighteen Studies for the Flute, Op. 41, No. 1	0:45–1:15	Joachim Andersen	1891	C major	Simple duple	1, 2, IS	4.97	3.6
Five Divertimentos, K. 439b, No. 2, mvmt. 4	0:50–1:20	Wolfgang Amadeus Mozart	1785	C major	Simple triple	1, IS	5	3.12
Gavotte	0:00–0:30	François-Joseph Gossec	Unknown	C major	Simple duple	1, IS	5.04	2.32
Maiden Voyage	2:50–3:20	Herbie Hancock	1965	A minor	Simple duple	1	5.16	3.32
Seven Variations on a Theme from Silvana, J. 128, Op. 33, Theme	0:00–0:30	Carl Maria von Weber	1854	Bb major	Compound duple	1, IS	5.31	3.76
Drei Fantasiestücke, Op. 73, No. 1	0:30–1:00	Robert Schumann	1849	A minor	Simple duple	1, 2 (clar), IS	5.36	4.06
Five Divertimentos, K. 439b, No. 2, mvmt. 4	3:50–4:20	Wolfgang Amadeus Mozart	1785	G major	Simple triple	1, IS	5.47	3.54
35 Exercises for Flute, Op. 33, No. 3	1:00–1:30	Ernesto Koehler	1880s	F major	Simple triple	1, IS	5.54	4.01
Eighteen Studies for the Flute, Op. 41, No. 6	1:00–1:30	Joachim Andersen	1891	B minor	Simple triple	1, IS	5.57	4.09
Carmen Suite No. 1, Aragonaise	0:45–1:15	Georges Bizet	1882	D minor	Simple triple	1, IS	5.61	3.65
Orchestral Suite No. 2 in B minor, BWV 1067	0:00–0:30	Johann Sebastian Bach	1739	B minor	Simple duple	1, IS	5.61	3.52
35 Exercises for Flute, Op. 33, No. 15	0:00–0:30	Ernesto Koehler	1880s	E major	Simple duple	1, IS	5.63	3.62
Drei Fantasiestücke, Op. 73, No. 1	1:15–1:45	Robert Schumann	1849	A minor	Simple duple	1, IS	5.63	3.97
Eighteen Studies for the Flute, Op. 41, No. 10	0:00–0:30	Joachim Andersen	1891	C# minor	Compound duple	1, 2 (prac), IS	5.65	4.13
35 Exercises for Flute, Op. 33, No. 10	0:00–0:30	Ernesto Koehler	1880s	D major	Simple duple	1, IS	5.8	4.16
Study No. 1 in C major, Op. 131	0:00–0:30	Giuseppe Gariboldi	1900	C major	Simple duple	1, IS	5.92	3.81
Flute Concerto No. 2 in G minor, RV439 “La notte”	10:00–10:30	Antonio Vivaldi	1729	C minor	Simple duple	1, IS	5.93	3.63
Dolly Suite Op. 56, No. 1	0:10–0:40	Gabriel Fauré	1893	G major	Simple duple	1, IS	5.98	4.2
Flute Concerto No. 2 in G minor, RV439 “La notte”	9:15–9:45	Antonio Vivaldi	1729	G minor	Simple duple	1, IS	6.06	3.83
Solo de Concours	4:00–4:30	André Messager	1899	Bb major	Simple duple	1 (prac), 2 (clar), IS	6.09	4.22
Student Instrumental Course: Flute Student, Level II book: pg. 12 exercise no. 2	0:10–0:40	Douglas Steensland, Fred Weber	2000	Ab major	Simple duple	1, 2, IS	6.09	4.11
Eighteen Studies for the Flute, Op. 41, No. 6	0:00–0:30	Joachim Andersen	1891	B minor	Simple triple	1 (prac), 2, IS	6.09	4.07
Fantaisie, Op. 79	0:30–1:00	Gabriel Fauré	1898	E minor	Simple triple	1, IS	6.21	4.14
12 Fantasias for Solo Flute, No. 5, Allegro	0:37–1:17	Georg Philipp Telemann	1733	C major	Simple triple	1, IS	6.49	3.70
12 Fantasias for Solo Flute, No. 10, Dolce	1:57–2:27	Georg Philipp Telemann	1733	G minor	Simple duple	1, IS	6.4	3.02
35 Exercises for Flute, Op. 33, No. 2	0:07–0:37	Ernesto Koehler	1880s	G major	Simple duple	1, IS	6.61	3.79
12 Fantasias for Solo Flute, No. 10, Presto	2:45–3:15	Georg Philipp Telemann	1733	F# minor	Simple triple	1, IS	7.09	4.1
Eighteen Studies for the Flute, Op. 41, No. 8	1:30–2:00	Joachim Andersen	1891	F# minor	Simple triple	1, 2, IS	7.27	4.19
Con Alma	1:15–1:45	Dizzy Gillespie	1954	Ab major	Simple duple	1, IS	7.63	4.03
35 Exercises for Flute, Op. 33, No. 11	1:00–1:30	Ernesto Koehler	1880s	A minor	Compound duple	1, IS	7.84	4.64
Syrinx	2:15–2:45	Claude Debussy	1913	Bb minor	Simple triple	1, IS	7.87	3.95
Orchestral Suite No. 2 in B minor, BWV 1067	3:45–4:15	Johann Sebastian Bach	1739	E minor	Simple duple	1, IS	8.05	4.5
Nocturnes, Op. 37, No. 1	0:30–1:00	Frédéric Chopin	1839	C minor	Simple duple	1, IS	8.08	4.41
Seven Early Songs, Die Nachtigall	0:30–1:00	Alban Berg	1907	A major	Simple triple	1, IS	8.19	3.47
Les Folies d'Espagne, Nos. 7 and 8	0:10–0:40	Marin Marais	1701	E minor	Simple triple	1, 2, IS	8.6	2.84
Nocturnes, Op. 37, No. 1	0:00–0:30	Frédéric Chopin	1839	C minor	Simple duple	1, IS	8.66	4.32
Les Folies d'Espagne, No. 5	0:00–0:30	Marin Marais	1701	E minor	Simple triple	1, IS	9.48	3.5
Le Rossignol en Amour	1:45–2:15	François Couperin	1722	G major	Simple triple	1, IS	9.56	3.85
Caravan	0:00–0:30	Duke Ellington, Juan Tizol	1936	C minor	Simple duple	1	10.35	5.3
Citygate/Rumble	1:00–1:30	Chick Corea	1986	Db major	Simple duple	1, IS	10.75	3.78
First Rhapsody	0:30–1:00	Claude Debussy	1910	F# minor, E minor	Simple duple	1, 2, IS	10.9	4.32
Alone Together	0:45–1:15	Arthur Schwartz	1932	D minor	Simple duple	1, 2, IS	10.93	3.85
Seven Early Songs, Traumgekrönt	0:30–1:00	Alban Berg	1908	G minor	Simple duple	1, IS	11.15	4.08
Les Folies d'Espagne, No. 1	0:00–0:30	Marin Marais	1701	E minor	Compound triple	1, 2 (prac), IS	11.28	4.47
Le Jamf	0:45–1:15	Bobby Jaspar	1960	Eb major	Simple duple	1	11.31	3.96
Syrinx	0:00–0:30	Claude Debussy	1913	Bb minor	Simple triple	1, IS	13.21	3.32
Mei	0:37–1:07	Kazuo Fukushima	1962	Atonal	Simple duple	1, 2, IS	16.52	4.62
35 Exercises for Flute, Op. 33, No. 5	0:03–0:33 (piano at 2.5)	Ernesto Koehler	1880s	G major	Simple duple	1 (attn.)	10.71	3.61
Ballet of the Shepherds (from Armide, Wq. 45)	0:05–0:35 (piano at 7.5)	Christoph W. von Gluck	1777	Eb major	Simple duple	1 (attn.)	14.46	3.64
Baldwin's Music, Exercise No. 4	0:00–0:30 (piano at 8.8)	Baldwin's Music	Unknown	F major	Simple duple	1 (attn.)	10.57	3.89
Waltz (from Coppélia)	0:50–1:20 (piano at 12.3)	Léo Delibes	1870	C major	Simple triple	1 (attn.)	8.15	4.02
22 Studies in Expression and Facility, Op. 89, No. 6	0:00–0:30 (piano at 15.0)	Ernesto Koehler	1904	D minor	Simple duple	1 (attn.)	4.95	4.14
Fuku Ju So	0:02–0:32 (piano at 18.8)	Japanese traditional	Unknown	A minor	Simple duple	1 (attn.)	6.4	4.47
Scheherazade, Op. 35, mvmt. 3 (The Young Prince and The Young Princess)	0:00–30:00 (piano at 21.7)	Nikolay Rimsky-Korsakov	1888	B minor	Simple triple	1 (attn.)	4.42	3.90
Sicilienne, Op.78	0:00–0:30 (piano at 24.4)	Gabriel Fauré	1893	G minor	Compound duple	1 (attn.)	6.17	4.04
Baldwin's Music, Exercise No. 1	0:00–0:30 (piano at 25.7)	Baldwin's Music	Unknown	G major	Simple duple	1 (attn.)	6.47	4.36

^aStimulus details for all 55 experimental stimuli and 9 “attention trial” stimuli. IS = rated for unexpectedness by an independent sample, clar = presented in a clarinet timbre during Study 2, prac = presented as a practice stimulus, “(piano at)” = when the stimulus changed from flute to piano timbre (from its start).

We converted these well-controlled stimuli into naturalistic-sounding WAV files with the Kontakt 5 synthesizer (2018 Native Instruments) within the Ableton Live 9 digital audio workstation (2018 Ableton). We generated each excerpt with a flute digital synthesizer (except for the “attention trials” stimuli, which switched from flute to piano timbre during the excerpt), digitally filtered them to resemble the acoustics of a music studio, and randomly shifted the note onsets on the order of milliseconds using Ableton's Groove Pool with 25% randomization for “humanization” (i.e., to prevent the stimuli from sounding mechanistic and unnatural).

Information-theoretic modeling.

We used the Information Dynamics of Music model (IDyOM) (Pearce, 2005, 2018) to characterize both the unpredictability and uncertainty of our stimuli. Across many different experimental paradigms and musical samples, IDyOM has proven to provide reliable computational measures of pitch unpredictability/surprise (as represented by IC) and uncertainty (as represented by entropy) in Western listeners (Pearce, 2005; Pearce and Wiggins, 2006; Pearce et al., 2010; Omigie et al., 2012; Egermann et al., 2013; Hansen and Pearce, 2014; Sauvé et al., 2018), significantly outperforming similar models and explaining up to 83% of the variance in listeners' pitch expectations (Pearce, 2005, 2018; Pearce et al., 2010; Hansen and Pearce, 2014). IDyOM has also successfully predicted several electrophysiological measures of expectancy violation (Carrus et al., 2013; Omigie et al., 2013), and even psychophysiological and subjective emotional responses (Egermann et al., 2013; Sauvé et al., 2018).

Before modeling our stimuli, we trained IDyOM on a large corpus of Western tonal music, including 152 Canadian folk songs (Creighton, 1966), 566 German folk songs from the Essen folk song collection (Schaffrath, 1992), and 185 chorale melodies harmonized by Bach (Riemenschneider, 1941) as in other applications of IDyOM (e.g., Pearce, 2005; Pearce and Wiggins, 2006; Egermann et al., 2013; Hansen and Pearce, 2014). This training set allowed IDyOM to learn the statistical structure of Western tonal music via variable-order Markov modeling (Pearce, 2005), emulating the implicit statistical learning that human listeners are also thought to undertake during long-term enculturation in a musical style (for review, see Pearce, 2018). The trained model therefore represents the musical syntax that listeners learn over years of exposure to Western music (Fig. 1).

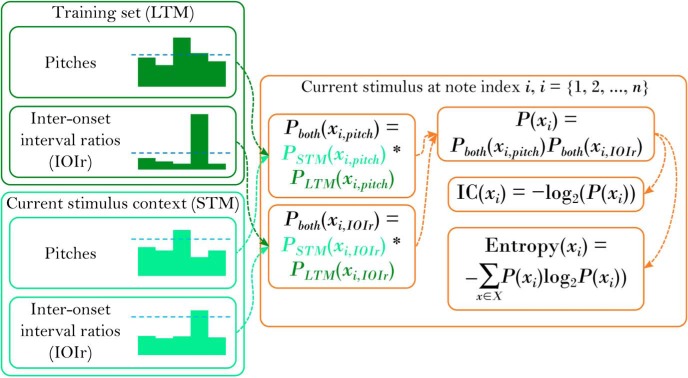
Figure 1.

IDyOM model. We used the IDyOM model (Pearce, 2005, 2018) to systematically measure music unpredictability as IC and entropy. As configured here, IDyOM first builds a long-term model (LTM) of the statistical structure of a large training set of 903 melodies, represented as sequences of pitches and inter-onset interval ratios (IOIr). In a new stimulus melody with n notes, IDyOM then estimates the probability of each possible continuation x from an alphabet X, at each note index i based on the LTM and a short-term model (STM) learned dynamically within the current stimulus (i.e., from note 1 to note i). To combine the probabilities derived from the LTM and STM, IDyOM first computes a geometric mean (signified by '*') of the LTM and STM probabilities for pitch and IOIr separately, weighting each according to its entropy such that predictions based on higher-entropy models are less influential, and then multiplies these resulting pitch and IOIr probabilities. It then computes the note's IC as its negative log probability to the base 2, and its entropy as the expected value of the IC across all possible continuations (X). The result is a reliable computational measure of pitch unpredictability and uncertainty based on long- and short-term musical statistics. In the present studies, we averaged these note-by-note measures across each stimulus to represent each 30 s stimulus as one unit.

Since listeners further learn and update their expectations online while listening to individual pieces of music (Castellano et al., 1984; Kessler et al., 1984; Oram and Cuddy, 1995; Loui et al., 2010), IDyOM also dynamically learns the statistical structure of each stimulus in its test set (for review, see Pearce, 2018). The models we used here were configured to integrate these respective “long-term” and “short-term” probabilities, weighting each according to its entropy such that the higher-entropy model (i.e., that with a flatter probability distribution, reflecting greater predictive uncertainty) is discounted relative to the lower-entropy model. Our models therefore measured the IC of each note (as its negative log probability to the base 2) given prior learning of the structure of the training corpus and the preceding musical context within the piece at hand. IC indicates the unpredictability of a note and therefore reflects the degree to which a stored memory of that event may be compressed by discarding redundancies; compression and redundancy reduction are thought to contribute to psychological processes such as pattern recognition and similarity perception (Chater and Vitányi, 2003). The models similarly measure the entropy of each predictive context (as the expected value of the IC across all possible continuations) based on learning of long- and short-term structure, yielding higher values when there were many equally unlikely continuations (i.e., the context is uncertain/unstable) and lower values when there were only a few very likely continuations.

Note-by-note IC and entropy can be computed using different musical features as input to IDyOM: one could model the probability of the next pitch, registral direction, time, inter-onset interval ratio, etc., and one could model these “viewpoints” independently or simultaneously. Motivated by both music theory and empirical findings that illustrate the role of representing and predicting rhythmic information (e.g., Clarke, 2005; Lumaca et al., 2019) and pitch information such as pitch intervals and scale degrees (Dowling, 1978; Pearce and Müllensiefen, 2017) in perceiving and responding to music, we selected four alternative viewpoints to use with IDyOM: inter-onset interval ratio, chromatic pitch, chromatic pitch interval, and chromatic scale degree.

We then generated seven IDyOM configurations from these viewpoints. Three of these configurations used the sole timing viewpoint (inter-onset interval ratio) to compute the probability of a note's onset while one of the three pitch-based viewpoints (chromatic pitch, chromatic pitch interval, or chromatic scale degree) computed the pitch probability before combining these as the joint probability of the note. Three other configurations computed note probabilities in the same way but predicted both onset time and pitch using a single viewpoint that linked the respective timing and pitch viewpoints. In the seventh implementation, we combined the timing viewpoint with the linked chromatic pitch interval and chromatic scale degree viewpoints, based on the known role of pitch intervals and scale degrees, and their relationship, in music perception (Dowling, 1978; Krumhansl, 1990; Pearce and Müllensiefen, 2017). We also considered versions of these models that weighted the IC of each note by its duration as an indicator of salience, as in Krumhansl (1990).

We selected between these models by comparing the IC output of each to the unexpectedness ratings of an independent sample of 24 participants (17 females and 7 males, mean age ± SD = 22.08 ± 2.70 years, mean musical experience ± SD = 2.89 ± 4.52 years) who did not participate in the present studies. These listeners were all neurologically healthy and with normal hearing, and they rated 52 of the 57 possible stimuli (Table 1) in real time, a few minutes after providing informed consent and hearing them once each (unpublished data). Comparisons used linear mixed-effects models with random slopes and intercepts for each subject to separately fit the fixed effects of either mean (averaged across each stimulus) IC or mDW-IC. We also examined the effects of mean entropy as a control condition to ensure that the chosen model would be able to distinguish between mean IC (i.e., the unpredictability or unexpectedness of a melody; see above) and the related but discernable phenomenon of mean entropy, which is more directly associated with the uncertainty or instability of a melody than its unexpectedness (Pearce, 2005; Hansen and Pearce, 2014).

Comparisons with unexpectedness ratings revealed that the best-fitting IDyOM implementation was that based on an independent combination of inter-onset interval ratio and chromatic pitch, and that the variable that best explained subjective unexpectedness ratings (measured by Akaike information criteria [AIC] and F tests of the model's fixed effect) was mDW-IC (R² = 0.13, p < 0.001) (for more details on the models tested, see Table 2).

Table 2.

Comparing IDyOM configurations^a

Model source viewpoints	Regression predictor	Fixed effect (β)	p	R2	AIC
(ioi-ratio cpitch)	Mean IC	4.93	<0.001	0.10	3854.6
	mDW-IC	6.16	<0.001	0.12	3845.7
	Mean entropy	11.51	0.012	0.06	3866.7
ioi-ratio cpitch*	Mean IC	4.33	<0.001	0.09	3856.4
	mDW-IC*	5.99*	<0.001*	0.13*	3844.0*
	Mean entropy	18.09	0.109	0.05	3869.8
(ioi-ratio cpint)	Mean IC	3.40	0.005	0.07	3864.0
	mDW-IC	5.89	<0.001	0.10	3852.3
	Mean entropy	2.17	0.751	0.04	3873.1
ioi-ratio cpint	Mean IC	3.65	0.001	0.08	3860.7
	mDW-IC	5.28	<0.001	0.10	3851.8
	Mean entropy	7.71	0.613	0.04	3872.5
(ioi-ratio cpintfref)	Mean IC	5.26	<0.001	0.09	3856.8
	mDW-IC	6.76	<0.001	0.11	3848.5
	Mean entropy	12.86	0.065	0.05	3869.1
ioi-ratio cpintfref	Mean IC	4.92	<0.001	0.09	3855.9
	mDW-IC	6.27	<0.001	0.11	3849.2
	Mean entropy	21.01	0.292	0.04	3872.1
ioi-ratio (cpint cpintfref)	Mean IC	3.84	<0.001	0.08	3859.7
	mDW-IC	5.17	<0.001	0.10	3851.2
	Mean entropy	−4.32	0.823	0.04	3873.2

^aThis table shows the seven IDyOM configurations tested. In all cases, IDyOM predicts the chromatic pitch and onset time of a note using one or more source viewpoints (corresponding to musical attributes). Viewpoints may be used in isolation or linked with another viewpoint, indicated with parentheses. For example, (ioi-ratio cpitch) indicates a model that predicts notes based on the tuple of constituent viewpoints, e.g. (1, 60) for a middle C whose inter-onset interval is the same as the previous note's. For each configuration, we used linear mixed-effects models to compare the output mean IC, mDW-IC, and mean entropy of each stimulus, given the corresponding model, to the unexpectedness ratings of an independent sample of 24 participants who did not participate in the present studies. The fixed-effect coefficient (β), p value, coefficient of determination (R²), and AIC of each model are given. This process revealed that the mDW-IC measure based on unlinked ioi-ratio and cpitch was the best correlate of subjective unexpectedness, and so we used this implementation for the present studies.

*Best-fitting model.

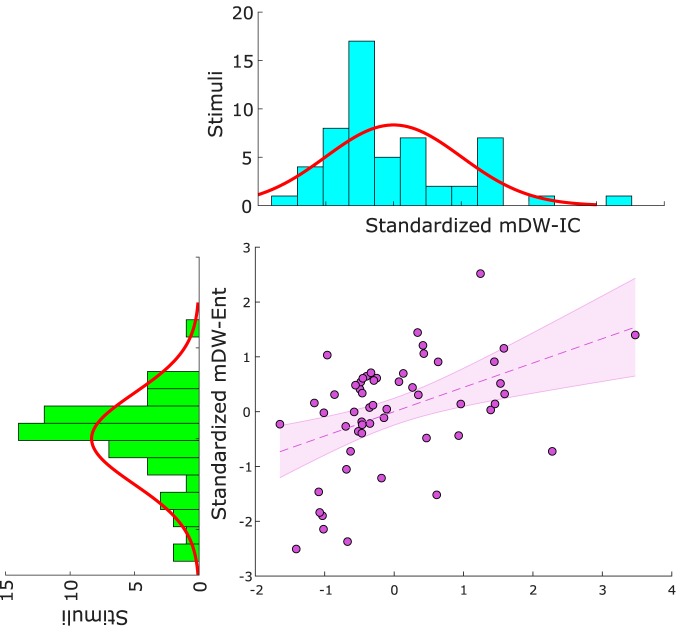
To better understand the mDW-IC variable, we investigated its pitch and timing contributions with partial correlations based on the separate probability distributions for chromatic pitch and onset time that IDyOM generated before combining them for overall note IC. Using Spearman's nonparametric partial correlations to account for non-normal data, we found that mDW-IC was correlated both with mean duration-weighted chromatic-pitch IC after controlling for the effect of mean duration-weighted onset IC (Spearman's ρ_p(52) = 0.72, p_p < 0.001) and with mean duration-weighted onset IC after controlling for the effect of mean duration-weighted chromatic-pitch IC (Spearman's ρ_p(52) = 0.77, p_p < 0.001). These results verify that both pitch and timing features contribute to music predictability, as detected by our measure of mDW-IC. We also found that mDW-IC positively correlated with mDW-Ent (Pearson's r₍₅₃₎ = 0.44, p < 0.001; Fig. 2), even though the model selection procedure had shown that mean entropy was not significantly associated with subjective unexpectedness ratings (p = 0.11; Table 2).

Figure 2.

Stimulus unpredictability and uncertainty distributions. Using formal mathematical modeling of musical unpredictability and uncertainty, we developed 55 stimuli, all excerpts of real, precomposed music, that varied across quantifiably wide ranges of mDW-Ent (i.e., the average entropy of all notes in a stimulus weighted by their durations) and mDW-IC (i.e., the average IC of all notes in a stimulus weighted by their durations). We standardized these measures with z scores to compare them, and so the standardized mDW-Ent and standardized mDW-IC are shown here. These features were positively correlated (Pearson's r = 0.44, p < 0.001).

Experimental design and statistical analysis.

The 43 participants analyzed (24 females and 19 males) listened to the stimuli and rated their familiarity and liking after each one, as described above. Several prior studies of musical preferences have averaged results across participants, even though musical preferences are highly subjective and variable (for review, see Brattico and Jacobsen, 2009). Rather than blending together the ratings of different listeners and potentially blurring over meaningful effects in the process, we opted for linear mixed-effects models, enhancing our power to detect group-level results by accounting for the random effect of subject (Diggle et al., 2002; Zuur et al., 2009). Excluding stimuli rated as familiar (see above), we leveraged the remaining trials for linear mixed-effects models with the fitlme function in MATLAB. Following the procedure recommended by Diggle et al. (2002) and Zuur et al. (2009), we first optimized the random-effects structure of a “beyond-optimal” model (including all relevant fixed effects and interactions) according to the AIC via restricted maximum likelihood estimation, then optimized the fixed-effects structure via likelihood ratio tests of nested models and AIC content of other models using maximum likelihood estimation, and finally evaluated the model with restricted maximum likelihood estimation. Separate mixed-effects models evaluated the main effects of mDW-IC and mDW-Ent, using z-scored values of these variables to allow for comparisons between their linear and quadratic effects.

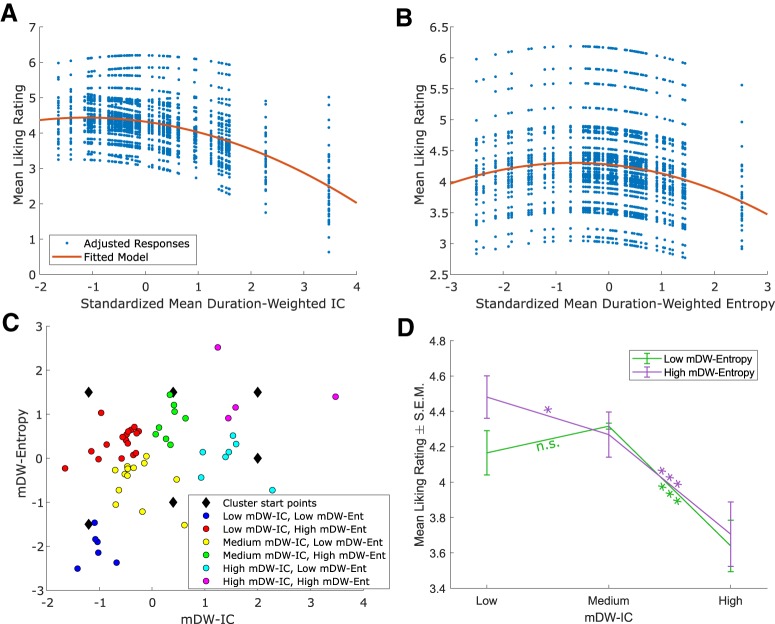
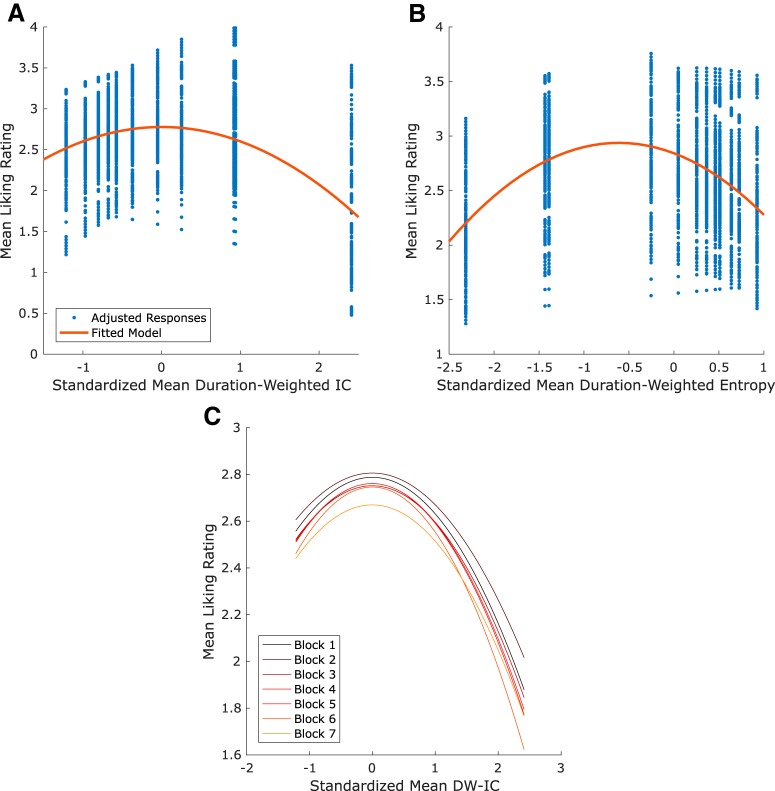
MDW-IC and mDW-Ent represent distinct, albeit related, aspects of complexity, with mDW-IC reflecting the surprise of a piece and mDW-Ent its uncertainty or instability (see above). We therefore explored how musical surprise might interact with the uncertainty/instability of its context to affect liking ratings. To avoid the collinearity of these related variables and to simplify the complex interactions of potentially linear and quadratic effects, we classified each stimulus according to its mDW-Ent and mDW-IC using MATLAB's k-means clustering algorithm to obtain data-driven and well-balanced groups. Starting with six points approximately corresponding to stimuli of low or high mDW-Ent and low, medium, or high mDW-IC (see below), this algorithm identified six stimulus clusters through Euclidean distance minimization without using any information about the participants' liking ratings. The category with low mDW-IC and low mDW-Ent contained six stimuli, while there were 17 stimuli with low mDW-IC and high mDW-Ent, 13 with medium mDW-IC and low mDW-Ent, 8 with medium mDW-IC and high mDW-Ent, 7 with high mDW-IC and low mDW-Ent, and 4 with high mDW-IC and high mDW-Ent (Fig. 3C). Although these groups are not perfectly balanced, they represent an unbiased and robust classification of our stimuli that allows for a repeated-measures ANOVA. We then conducted a repeated-measures ANOVA on the average liking ratings in each of these categories, testing for main effects of mDW-IC and mDW-Ent as well as their interaction. We additionally planned to investigate the nature of any interactions with post hoc Tukey–Kramer Honest Significant Difference tests.

Figure 3.

Behavioral effects of unpredictability and uncertainty. Linear mixed-effects analyses revealed significant Wundt effects in Study 1. A, The optimal model of mDW-IC explained 26.3% of the variance in liking ratings (p < 0.001) with negative linear (β = −0.21, p < 0.001) and quadratic (β = −0.09, p < 0.001) effects. It also had significant random intercepts and slopes across subjects (intercept 95% CI = 0.54, 0.86, slope 95% CI = 0.11, 0.29). Red curve indicates the fitted model. Blue dots represent the mean liking ratings for each stimulus adjusted according to the model's random effects. B, The optimal model of mDW-Ent explained 19.1% of the variance in liking ratings (p = 0.03), with negative linear (β = −0.09, p = 0.009) and quadratic effects (β = −0.06, p = 0.003) and significant subject-varying random intercepts (95% CI = 0.54, 0.86). Red curve indicates the fitted model. Blue dots represent the mean liking ratings for each stimulus adjusted according to the model's random effects. C, We used k-means clustering to categorize our stimuli. Starting with six points (black diamonds) to distinguish low and high mDW-Ent along with low, medium, or high mDW-IC, this procedure yielded the six stimulus categories that we used for repeated-measures ANOVA. D, A repeated-measures ANOVA reaffirmed the main effect of mDW-IC (F_(1.70,69.63) = 34.45, partial η² = 0.51, p < 0.001, using Greenhouse–Geisser correction since Mauchly's test of sphericity was violated) but not mDW-Ent (F_(1,41) = 2.84, p = 0.10), and also suggested an interaction between the two on liking ratings (F_(1.71,70.21) = 3.17, partial η² = 0.07, p = 0.06). Planned comparisons reflected the Wundt effect of mDW-IC when mDW-Ent was low (high mDW-IC < low mDW-IC: p < 0.001; high mDW-IC < medium mDW-IC: p < 0.001; low mDW-IC vs medium mDW-IC: p = 0.35), but not when mDW-Ent was high, when liking ratings for low mDW-IC were significantly greater than those for medium mDW-IC (p = 0.01; high mDW-IC < low mDW-IC: p < 0.001; high mDW-IC < medium DW-IC: p < 0.001). Likewise, there was a significant preference for stimuli with high mDW-Ent over low mDW-Ent when mDW-IC was low (p = 0.001), but not when mDW-IC was medium (p = 0.60) or high (p = 0.85), implying that uncertain contexts amplify the pleasure of predictability. n.s. = not significant, *p < 0.05, ***p < 0.001.

Finally, we tested whether the hypothesized Wundt effect between mDW-IC and liking would vary according to individual differences in music reward sensitivity and music sophistication. In this case, accounting for subject as a random effect would obscure the subjective effects of interest, and so we used simple linear regression models rather than mixed effects. To evaluate the shape of each individual's Wundt effect, we collapsed the curve between mDW-IC and liking into a distribution by weighting the mDW-IC of each stimulus by the participant's rating. This procedure represented greater preferences for stimuli with mDW-IC values as more positively skewed distributions (i.e., with more mass on the lower mDW-IC end and flatter tails on the positive end), and greater preferences for stimuli of higher mDW-ICs as more negatively skewed distributions. Likewise, sharper preferences produced distributions with greater kurtosis, and flatter preferences yielded distributions with less kurtosis. Excluding stimuli the participants rated as familiar, we compared these Wundt-effect parameters to total scores on the Barcelona Music Reward Questionnaire (Mas-Herrero et al., 2013) and the Gold-MSI (Müllensiefen et al., 2014). In the case of a significant relationship, we explored the effects of the relevant questionnaire's subscales with stepwise linear regression using MATLAB's stepwiselm function to identify those that best explained the variance in the Wundt effect's parameters.

Results

There was a significant Wundt effect between liking ratings and mDW-IC (Fig. 3A), indicated by the optimal model of mDW-IC, which contained significant negative linear (β = −0.21, p < 0.001) and quadratic effects (β = −0.09, p < 0.001). The overall model had significant random intercepts and mDW-IC slopes across subjects (intercept 95% CI = 0.54, 0.86, slope 95% CI = 0.11, 0.29), and it explained 26.3% of the variance in liking ratings (p < 0.001). Comparable models with only the linear or quadratic term explained 25.3% and 26.0% of the variance, respectively, and the optimal model (which combined these terms) fit the data significantly better than each of these alternatives (linear-only model likelihood ratio test χ²(1, N = 43) = 22.23, p < 0.001; quadratic-only model likelihood ratio test χ²(1, N = 43) = 17.20, p < 0.001).

There was also a significant Wundt effect between liking ratings and mDW-Ent (Fig. 3B), and the optimal mDW-Ent model also contained significant negative linear (β = −0.09, p = 0.009) and quadratic effects (β = −0.06, p = 0.003). The overall model had significant subject-varying random intercepts (95% CI = 0.54, 0.86), and it explained 19.1% of the variance in liking ratings (p = 0.03). This model fit the data significantly better than alternative models that were identical, except for their exclusion of either the linear or quadratic mDW-Ent term, which explained 19.1% and 19.0% of the variance, respectively (linear-only model likelihood ratio test χ²(1, N = 43) = 8.31, p = 0.004; quadratic-only model likelihood ratio test χ²(1, N = 43) = 6.21, p = 0.01).

We used k-means clustering to categorize the stimuli (Fig. 3C). The repeated-measures ANOVA model reaffirmed the main effect of mDW-IC (F_(1.70,69.63) = 34.45, partial η² = 0.51, p < 0.001, using Greenhouse–Geisser correction since Mauchly's test of sphericity was violated), but not that of mDW-Ent (F_(1,41) = 2.84, p = 0.10). This analysis also suggested an interaction between the two (F_(1.71,70.21) = 3.17, partial η² = 0.07, p = 0.06; Fig. 3D). Planned comparisons of this interaction resembled the Wundt effect of mDW-IC when mDW-Ent was low (high mDW-IC < low mDW-IC: p < 0.001; high mDW-IC < medium mDW-IC: p < 0.001; low mDW-IC vs medium mDW-IC: p = 0.35), but not when mDW-Ent was high, when liking ratings for low mDW-IC were significantly greater than those for medium mDW-IC (p = 0.01, high mDW-IC < low mDW-IC: p < 0.001; high mDW-IC < medium DW-IC: p < 0.001). Likewise, there was a significant preference for stimuli with high mDW-Ent over low mDW-Ent when mDW-IC was low (p = 0.001), but not when mDW-IC was medium (p = 0.60) or high (p = 0.85). This analysis therefore implies that predictability is more desirable in more uncertain contexts.

Despite the strong group-level Wundt effects, linear models fit to individual participants exhibited considerable intersubject variability. These models' R² values ranged from 0.005 to 0.42, with a mean of 0.12 and a SD of 0.09, and had negative quadratic coefficients for 31 of the 43 participants. We also observed substantial differences in the participants' music sophistication (Gold-MSI mean ± SD = 71.65 ± 21.68) and musical reward sensitivity (BMRQ mean ± SD = 80.79 ± 8.97). While this sample was consistent with other reports of musical reward sensitivity scores (Mas-Herrero et al., 2013), and individuals within the sample scored from the second to 91st percentile of normative musical sophistication scores (Müllensiefen et al., 2014), the average musical sophistication score was at approximately the 30th percentile of the norm.

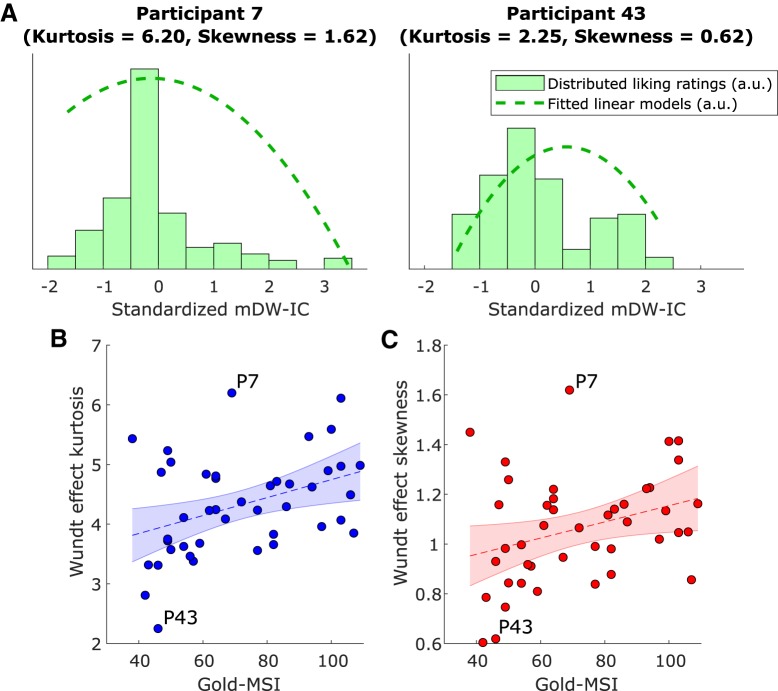
Nonetheless, measuring the kurtosis and skewness of each participant's Wundt effect (Fig. 4A) revealed a significant positive regression between musical sophistication and the Wundt effect's kurtosis (Fig. 4B), such that relatively more sophisticated participants had sharper distributions, that is, more focused preferences (F_(1,41) = 7.43, p = 0.009, β = 0.02, R² = 0.15). A follow-up stepwise regression on the five Gold-MSI subscales selected only “Perceptual Abilities” (F_(1,41) = 6.50, p = 0.01, β = 0.04, R² = 0.14), indicating that music-listening skills drove the overall effect. This subscale includes questions about the respondent's ability to recognize different versions of the same song, detect out-of-tune or out-of-time events, and so on, thus reflecting fine-grained musical perceptual skills that may emerge from musical training and listening but also from incidental exposure, genetics, etc. (Müllensiefen et al., 2014). Kurtosis and skewness were strongly correlated (r₍₄₁₎ = 0.94, p < 0.001), and musical sophistication also positively correlated with the Wundt effect skewness (Fig. 4C), as relatively more sophisticated listeners exhibited more positively skewed ratings, that is, greater preferences for stimuli of lower mDW-IC (F_(1,41) = 4.76, p = 0.03, β = 0.003, R² = 0.10). Once again, a follow-up stepwise regression selected only the “Perceptual Abilities” subscale (F_(1,41) = 5.89, p = 0.02, β = 0.009, R² = 0.13). Parsing the independent contributions of kurtosis and skewness with partial correlations, we found a stronger effect of kurtosis after controlling for skewness (ρ_p(40) = 0.27, p_p = 0.08) than vice-versa (ρ_p(40) = −0.14, p_p = 0.38), although neither partial correlation was significant.

Figure 4.

Individual differences in Wundt effects. Individual differences in the Wundt effects of Study 1 could be explained in part by musical sophistication, as measured by the Gold-MSI (Müllensiefen et al., 2014). A, We represented each participant's Wundt effect as a distribution of mean liking ratings across mDW-ICs by multiplying these measures together, resulting in flatter distributions for those with similar preferences across the mDW-IC spectrum, sharper distributions for those with more particular preferences, and so on. We then measured the kurtosis and skewness of each distribution, reflecting the sharpness and asymmetry of the participant's preferences, respectively. To illustrate this analysis, we show the distribution for Participant 7, on the left, who exhibits the greatest kurtosis and skewness of the sample, and Participant 43, on the right, who has the lowest kurtosis and second-lowest skewness. B, There was a significant positive correlation between Gold-MSI scores and the kurtosis of the Wundt effect, revealing sharper preferences for relatively more sophisticated participants (F_(1,41) = 7.43, p = 0.009, β = 0.02, R² = 0.15). C, There was also a significant positive correlation between Gold-MSI scores and the skewness of the Wundt effect, wherein more sophisticated listeners also had greater relative preferences for stimuli of lower mDW-IC (F_(1,41) = 4.76, p = 0.03, β = 0.003, R² = 0.10). In both cases, the Gold-MSI “Perceptual Abilities” subscale was the only one to survive follow-up stepwise regressions (kurtosis effect: F_(1,41) = 6.50, p = 0.01, β = 0.04, R² = 0.14; skewness effect: F_(1,41) = 5.89, p = 0.02, β = 0.009, R² = 0.13), indicating that music-listening skills drove these results. Kurtosis and skewness were also highly correlated (r = 0.94, p < 0.001), complicating the interpretations of these results. P7 = Participant 7, P43 = Participant 43.

The total BMRQ score was not significantly related to the kurtosis of the Wundt effect (F_(1,41) = 0.25, p = 0.62) or its skewness (F_(1,41) = 0.05, p = 0.83), and a t test did not differentiate between the participants with and without significant Wundt effects on this scale (t₍₄₁₎ = 0.15, p = 0.88). Together, these findings illustrate that systematically measuring predictability and uncertainty yields reliable Wundt effects for both variables, as well as individual differences that might arise from the listeners' musical sophistication. In Study 2, we tested the reliability of these results in another sample with a subset of the stimuli, and examined how the listener's immediate experience with a musical excerpt (i.e., hearing it multiple times in one sitting, might affect these patterns).

Study 2

Materials and Methods

Participants and procedure.

This experiment had 27 healthy participants (14 females, mean age ± SD = 23.96 ± 5.72 years) with normal hearing, none of whom participated in Study 1. They had 8.07 ± 6.40 years of musical training, and 12 of them were still active musicians. After providing informed consent, they listened to each stimulus over speakers set to a comfortable volume via a computer running Presentation software (Neurobehavioral Systems) while a fixation cross appeared on the screen. The procedure was very similar to Study 1's, but with a few key differences: in Study 2, we used only a subset of the stimuli from Study 1 (see below; Table 1). Participants rated continuously how much they liked each stimulus as they listened, using keyboard buttons 1–4, and were instructed to have one of these buttons down whenever a stimulus was playing. Participants also rated how much they liked the stimulus, the overall arousal they felt from it, and their familiarity with it after it ended, again from 1 to 4; the results of these poststimulus ratings are not reported here. The familiarity ratings were simply to ensure that participants were aware of hearing the same stimuli repeated; no trials were excluded for familiarity in this study as the stimuli were presented multiple times each. Each participant was assigned a random stimulus order, and the stimuli were presented in this order seven times in a row. There were no breaks between repetition blocks other than the few seconds that separated each trial. Instead of beginning with stimuli across five clusters of the stimulus subset, we avoided anchoring effects in Study 2 by selecting the two practice stimuli to have moderately low and high mDW-IC (Table 1). Study 2 had no “attention trials” task since providing real-time ratings was already an engaging and active task; and although we do not report the data here, we also recorded psychophysiological responses (skin conductance, heart rate, pulse amplitude, breathing rate, and respiratory amplitude). Finally, based on research suggesting that musical playing and listening experience especially affect music processing (Gold et al., 2013; Hansen and Pearce, 2014; Pearce, 2014), we streamlined Study 2's questionnaires to focus on the participants' years (if any) of playing music and approximate weekly hours of music listening, instead of asking about musical sophistication, music reward sensitivity, or personality.

Stimuli.

The stimuli for this experiment were a subset of those used in Study 1 (Table 1). We chose these 12 stimuli to represent the full range of mDW-IC, yet with fewer stimuli so that we could repeat them several times without dramatically lengthening the task. We processed and modeled the information-theoretic properties of these stimuli exactly as in Study 1. The only difference was that three of the stimuli were presented in the original clarinet timbre rather than flute (Table 1). Wilcoxon rank-sum tests of participants' responses, standardized to the rating scales of the two studies (see above), verified that this timbre difference had no significant effect on overall liking ratings (Seven Variations on a Theme from Silvana median = 0.50 in Study 1 and 0.47 in Study 2, Z = 734.50, p = 0.19; Drei Fantasiestücke median = 0.33 in Study 1 and 0.48 in Study 2, Z = 995.00, p = 0.43; Solo de Concours not analyzed because it was a practice stimulus in Study 1, yielding unreliable ratings).

Experimental design and statistical analysis.

The 27 participants of this study (14 females and 13 males) listened to the stimuli and rated them as described above. As in Study 1, we used linear mixed-effects models to detect generalizable effects while accounting for the subjectivity of the participants. We built mixed-effects models using the same method as in Study 1. Four separate mixed-effects models evaluated how liking ratings changed according to the main effect of mDW-IC, the main effect of mDW-Ent, the main effect of repetition, and the interaction between mDW-IC and repetition. We did not assess interactions between mDW-IC and mDW-Ent in this study due to the limited stimulus set. To allow for comparisons between linear and quadratic effects of mDW-IC, mDW-Ent, and repetition, we standardized these variables as z scores before conducting any analyses.

Results

The best-fitting model of liking and mDW-IC (p < 0.001) explained 41.6% of the variance with a negative quadratic mDW-IC term (β = −0.18, p < 0.001), illustrating a Wundt effect (Fig. 5A). This model had no fixed linear term for mDW-IC, but significant random intercepts for each subject (95% CI = 0.31, 0.58) as well as random slopes for each subject's effects of mDW-IC (95% CI = 0.15, 0.29), mDW-IC² (95% CI = 0.10, 0.19), and Repetition (95% CI = 0.05, 0.09). Comparing AICs showed that this model described the data more parsimoniously than a model with only a linear mDW-IC term (AIC with mDW-IC² = 4657.9, AIC with mDW-IC = 4681.4), but a likelihood ratio test was not possible because the models were not nested. Similarly, adding a linear mDW-IC term to the best-fitting model did not yield a significantly better fit (likelihood ratio test χ²(1, N = 27) = 1.08, p = 0.30).

Figure 5.

Behavioral effects of unpredictability, uncertainty, and repetition. Linear mixed-effects analyses revealed significant Wundt effects in Study 2. A, The optimal model of mDW-IC explained 41.6% of the variance in liking ratings (p < 0.001) with only a negative quadratic effect (β = −0.18, p < 0.001) and significant random intercepts and slopes across subjects (intercept 95% CI = 0.31, 0.58, mDW-IC slope 95% CI = 0.15, 0.29, mDW-IC² slope 95% CI = 0.10, 0.19, repetition slope 95% CI = 0.05, 0.09). Red curve represents the fitted model. Blue dots represent the mean liking ratings for each stimulus adjusted according to the model's random effects. B, The optimal model of mDW-Ent explained 34.9% of the variance in liking ratings (p < 0.001), with negative linear (β = −0.31, p < 0.001) and quadratic effects (β = −0.25, p < 0.001). This model also had significant subject-varying random intercepts (95% CI = 0.30, 0.58), slopes for mDW-Ent (95% CI = 0.26, 0.49), slopes for mDW-Ent² (95% CI = 0.82, 0.97), and slopes for repetition (95% CI = 0.05, 0.09). Red curve represents the fitted model. Blue dots represent the mean liking ratings for each stimulus adjusted according to the model's random effects. C, The best-fitting model of liking and repetition, which included an interaction term between mDW-IC and liking, significantly fit the data (R² = 0.42, p < 0.001), but not better than an alternative model that excluded the fixed effects of repetition (likelihood ratio test χ²(1, N = 27) = 3.42, p = 0.18). Even so, this model indicated that the Wundt effect did not significantly change across repetitions, as the interaction term was not significant (p = 0.38).

We observed a similar Wundt effect between liking and mDW-Ent (Fig. 5B), with the optimal model of these variables explaining 34.9% of the variance with significant negative linear (β = −0.31, p < 0.001) and quadratic effects (β = −0.25, p < 0.001). Like the mDW-IC model above, this model allowed for randomly varying intercepts (95% CI = 0.30, 0.58) and slopes of mDW-Ent (95% CI = 0.26, 0.49), mDW-Ent² (95% CI = 0.82, 0.97), and Repetition (95% CI = 0.05, 0.09) for each subject (p < 0.001). Compared with alternative models with only the linear or quadratic mDW-Ent term, this model fit the data significantly better (linear-only model likelihood ratio test χ²(1, N = 27) = 19.95, p < 0.001; quadratic-only model likelihood ratio test χ²(1, N = 27) = 13.91, p < 0.001).

The best-fitting model of liking and Repetition (R² = 0.81, p < 0.001) also had a negative quadratic effect (β = −0.003, p < 0.001), with liking ratings decreasing from the first to seventh presentation of the stimuli. This model allowed for randomly varying intercepts for each stimulus (95% CI = 0.22, 0.56) as well as randomly varying intercepts (95% CI = 0.56, 0.69) and Repetition slopes (95% CI = 0.08, 0.11) for each combination of stimulus and subject.

The Wundt effect of mDW-IC on liking ratings did not significantly change across repetitions, as the optimal model of liking that included an interaction of mDW-IC and repetition effects showed no significant interaction (p = 0.38; Fig. 5C). Although this overall model was significant (R² = 0.42, p < 0.001), it was not significantly better than a model that was identical, except that it excluded the fixed effects of Repetition (likelihood ratio test χ²(1, N = 27) = 3.42, p = 0.18).

As in Study 1, the strong group-level Wundt effect comprised significant interindividual variability. Individual-participant R² values ranged from 0.001 to 0.54, with a mean of 0.24 and a SD of 0.17, whereas 23 of 27 had negative quadratic terms. Once again, kurtosis and skewness were positively correlated (r₍₂₅₎ = 0.95, p < 0.001), but these parameters did not significantly vary with participants' musical backgrounds (years of music playing kurtosis F_(1,25) = 0.01, p = 0.92; hours of weekly listening kurtosis F_(1,25) = 0.18, p = 0.68; years of music playing skewness F_(1,25) = 0.08, p = 0.78; hours of weekly listening skewness F_(1,25) = 0.22, p = 0.65). Likewise, the participants with and without significant Wundt effects did not meaningfully differ in years of musical training (t₍₂₅₎ = −0.43, p = 0.67) or hours of weekly music listening (t₍₂₅₎ = 0.45, p = 0.66), as measured with independent-samples t tests.

Discussion

The present studies represent a diligent test of the controversial Wundt effect, validating an inverted U-shaped relationship between complexity and liking. Using rigorous definitions of complexity and entropy as independent variables, based on computational modeling of real-world music, we find reliable evidence of the Wundt effects in esthetic musical judgments. Linking esthetic pleasure to information-theoretic measures, we also implicate models of motivation, information seeking, and learning (Abuhamdeh and Csikszentmihalyi, 2012a; Oudeyer et al., 2016) in aspects of music listening, including attention (compare Gottlieb et al., 2013; Baranes et al., 2015; Daddaoua et al., 2016), anticipation (compare Bromberg-Martin and Hikosaka, 2009; Salimpoor et al., 2011), and pleasure (compare Meyer, 1956; Salimpoor et al., 2011).

Our information-theoretic approach provides a systematic model of unpredictability, operationalized as mDW-IC, and uncertainty, as mDW-Ent (compare Pearce, 2005, 2018). We chose model parameters by identifying the best-fitting correlation with a separate sample of unexpectedness ratings (Table 2), yielding a quantified measure of unpredictability that incorporates pitch and timing information.

We leveraged our systematic complexity measures and wide-ranging, natural stimuli to replicate Wundt effects across two separate samples of participants (Figs. 3A,B, 5A,B). This nonlinear pattern explained between 19% and 42% of liking ratings and fit significantly better than purely linear effects. In addition to quadratic terms, three of the four regression models contained significant negative linear components: a relatively common finding, sometimes even occurring without a Wundt effect (Hargreaves et al., 2005; for review, see Chmiel and Schubert, 2017). These results could indicate hierarchical preferences wherein listeners like medium complexity more than simple (i.e., prototypical) music (Hargreaves et al., 2005; Chmiel and Schubert, 2017), and then highly complex music. This interpretation would be better supported, however, if we had included very simple stimuli, such as isochronous repeating tones or musical scales. Like others, the present studies excluded such stimuli in favor of real-world pieces, leaving the simpler end of the complexity distribution relatively undersampled.

In Study 2, repeating stimuli multiple times progressively reduced preferences across the mDW-IC spectrum while leaving the Wundt effect unchanged (Fig. 5C). While other studies have described pleasure increasing with familiarity (Zajonc, 1968), this “mere exposure” effect emerges when stimuli are repeated among distractors, or across several hours/days (Tan et al., 2006; Hunter and Schellenberg, 2011), thereby allowing participants to consolidate what they've heard and forget specific features of it, or at least experience less fatigue, and thus continue to learn (Berlyne, 1971; Chmiel and Schubert, 2017). Since Study 2 illustrated decreased liking across multiple repetitions of the same stimuli over a short time span, resembling novelty preferences (for review, see Oudeyer et al., 2016), this result likely reflects participants' boredom rather than shifting preferences for certain degrees of predictability. Structural and veridical predictability (i.e., familiarity) therefore seem to influence liking differently (for a review of studies that show them to have similar effects, see Chmiel and Schubert, 2017).

Between our two studies, individually fit Wundt-effect models explained between 0.1% and 54% of the liking variance, demonstrating both the low statistical power of within-subject analyses and meaningful individual differences. Musical sophistication, particularly perceptual abilities, explained a significant portion of these differences: participants with significant Wundt effects were generally more sophisticated than those without, and more sophisticated participants had sharper preferences for simpler stimuli (Fig. 4). Yet kurtosis and skewness were strongly correlated, and partial correlations suggested that musical sophistication is more closely related to sharper preferences than to preferences for simpler stimuli. Moreover, the present sample fell in just the 32nd percentile of normative musical sophistication scores; and since more sophisticated listeners exhibit stronger associations between musical IC and unexpectedness ratings (Hansen and Pearce, 2014), a sample with more sophisticated listeners and/or a broader stimulus range, including simpler ones than those used here, might reveal a more nuanced effect. Nonetheless, more sophisticated listeners might indeed be more sensitive to musical predictability, perhaps due to more confident predictions and/or greater attention to music-syntactic violations, that shift their optimal level toward stimuli with lower IC (compare Hansen and Pearce, 2014; but for an alternative hypothesis, see Pearce, 2014).

Although mDW-IC and mDW-Ent were strongly correlated (Fig. 2), an ANOVA with categorized stimuli showed that preferences are more complicated than merely an overall liking for intermediate complexity, as high entropy amplified preferences for predictability to exceed those of greater unpredictability (Fig. 3D). This pattern implies that the Wundt effect arises primarily from the relative stability of low-entropy stimuli, whereas instability shifts preferences toward more-predictable events that can validate listeners' uncertain predictions. Future research should better distinguish these variables to elucidate the generalizability of this finding.

Our results suggest that learning about musical structure may be intrinsically rewarding. Reducing uncertainty (i.e., reducing high mDW-Ent with low mDW-IC) and seeking information (i.e., incorporating medium mDW-IC during low mDW-Ent) are essential elements of learning, and appear to convey reward value (Bromberg-Martin et al., 2010; Oudeyer et al., 2016; Brydevall et al., 2018). People are willing to sacrifice money to reduce uncertainty about future rewards, such as how big they'll be, even when that information has no influence on the rewards themselves (Brydevall et al., 2018), and reducing uncertainty elicits dopamine transmission and reward-system activity (Bromberg-Martin and Hikosaka, 2009; Brydevall et al., 2018). Learning new information about one's environment, like the identities of blurry images, the meanings of pseudowords, or the answers to trivia questions, similarly engages dopamine release and NAc activity (Kang et al., 2009; Jepma et al., 2012; Ripollés et al., 2014, 2018). Intermediate complexity, which maximizes both reducible uncertainty and learnable information, thus optimizes reward-related responses (Oudeyer et al., 2016). Within this framework, it is possible that pleasurable musical surprises and the Wundt effect derive from the same predictive and motivational processes that adapt our beliefs and actions to our environments, such as predictions that descend from the frontal cortex to the auditory cortex and brainstem and prediction errors that ascend in the reverse direction (compare Koelsch et al., 2019). Meanwhile, these pathways and subcortical structures, like the NAc, may mediate the reward of seeking and obtaining information in music as in other domains (Kang et al., 2009; Jepma et al., 2012; Ripollés et al., 2014; Brydevall et al., 2018).

The intrinsic reward of learning might also explain a range of previous music-esthetic findings. The emotional impact of musical surprises (Meyer, 1956; Sloboda, 1991; Huron, 2006; Grewe et al., 2007) could derive from powerful feedback signals facilitating learning, and the distinct dopaminergic activity before and during peak pleasure moments (Salimpoor et al., 2011) from curious anticipation and evaluation. In goal-directed learning, dopamine neurons encode both uncertainty leading up to predicted outcomes and “reward prediction errors” (RPEs) afterward, which signal how much better or worse the outcomes were than predicted (Fiorillo et al., 2003). We recently used fMRI to identify RPE-related activity during music processing in the NAc with a reinforcement-learning paradigm, using musical outcomes that were either unaltered and pleasant or distorted and unpleasant (Gold et al., 2019). This discovery illustrates how music might engage the reward network by manipulating expectations; yet it is unclear how musical events can be “better” or “worse” than expected, and thus why this network might process these events during naturalistic music listening. Based on an intrinsic reward for learning, one possibility is that ostensibly value-neutral musical surprises elicit positive RPEs when they facilitate learning, which would occur when the surrounding context affords the formation of a predictive model and the surprises contribute to this model. Conversely, surprises that detract from one's model might be experienced as penalties, and thus negative RPEs. Sequences of intermediate predictability and uncertainty would be most conducive to this learning process (compare Oudeyer et al., 2016), consistent with the present results and others, which indicate that surprises are pleasant when the context is stable enough for them to be informative and unpleasant otherwise (Sloboda, 1991; Grewe et al., 2005, 2007; Koelsch et al., 2008; e.g., Brattico et al., 2010; Egermann et al., 2013). The reward system's response to musical information-theoretic properties has not yet been studied, but we predict that the NAc would be more engaged by intermediate complexity, based on the present data.

Since music constantly manipulates interweaving structures, all but the most predictable stimuli have some degree of uncertainty (Meyer, 1956; Huron, 2006; Vuust, 2010; Zald and Zatorre, 2011; Gebauer et al., 2012). Music thus enables uncertain predictions about multiple interacting structures, the anticipation of their outcomes, and learning, especially when the music is complex but decipherable. This learning process could enhance predictions for future events, and induce dopaminergic reward-system activity for both uncertain anticipation and learning-related RPEs (compare Fiorillo et al., 2003), potentially accounting for the pleasure these surprises so often elicit (Meyer, 1956; Sloboda, 1991; Huron, 2006; Steinbeis et al., 2006; Grewe et al., 2007). Our findings support this interpretation by rigorously replicating the Wundt effect with formal modeling of musical complexity, implicating prediction-based learning in the enduring mystery of how abstract stimuli, such as music, can be so pleasurable.