Skip to main content
PMC home page
eLife logoLink to eLife
. 2019 Nov 7;8:e51177. doi: 10.7554/eLife.51177

Selection on mutators is not frequency-dependent

Yevgeniy Raynes 1,✉, Daniel Weinreich 1
Editors: Patricia J Wittkopp2, Patricia J Wittkopp3
PMCID: PMC6867826  PMID: 31697233

Abstract

The evolutionary fate of mutator mutations – genetic variants that raise the genome-wide mutation rate – in asexual populations is often described as being frequency (or number) dependent. Mutators can invade a population by hitchhiking with a sweeping beneficial mutation, but motivated by earlier experiments results, it has been repeatedly suggested that mutators must be sufficiently frequent to produce such a driver mutation before non-mutators do. Here, we use stochastic, agent-based simulations to show that neither the strength nor the sign of selection on mutators depend on their initial frequency, and while the overall probability of hitchhiking increases predictably with frequency, the per-capita probability of fixation remains unchanged.

Research organism: None

Introduction

Mutator alleles have been found at considerable frequencies in populations of infectious and commensal bacteria (Matic et al., 1997; LeClerc et al., 1996; Oliver et al., 2000), viruses (Suárez et al., 1992), and pathogenic fungi (Healey et al., 2016; Billmyre et al., 2017; Boyce et al., 2017). Mutators are also believed to be widespread in many cancers (Loeb, 2011; Lengauer et al., 1997), and have been repeatedly observed to overtake microbial populations during laboratory evolution experiments (Sniegowski et al., 1997; Shaver et al., 2002; Barrick et al., 2009; Notley-McRobb et al., 2002; Pal et al., 2007; Mao et al., 1997; Raynes and Sniegowski, 2014; Voordeckers et al., 2015). Yet, unlike directly beneficial mutations that are favored by natural selection because they increase an organism’s reproductive success (i.e., its fitness), mutator mutations generally do not appear to be inherently advantageous (Raynes and Sniegowski, 2014), except potentially in some viruses (Furió et al., 2005; Furió et al., 2007). Instead, mutators experience indirect selection, mediated by persistent statistical associations with fitness-affecting mutations elsewhere in the genome. As a result, mutators may invade an adapting population by hitchhiking (Smith and Haigh, 1974) with linked beneficial mutations even when they have no effect on fitness of their own (Sniegowski et al., 2000).

Whether or not mutators can successfully hitchhike to fixation has often been described as depending on the initial prevalence of mutator alleles in a population - most commonly referred to as frequency or number dependence (Raynes and Sniegowski, 2014; Sniegowski et al., 2000). This view holds that to replace the resident non-mutators, mutators must generate a beneficial mutation that escapes genetic drift and sweeps to fixation before their non-mutator competitors do. Accordingly, it has been proposed that mutators may be expected to invade (i.e., are favored by selection) only when already present in sufficient numbers to produce the successful beneficial mutation first, and lose their advantage (i.e., are disfavored by selection) when too rare to do so (reviewed in Raynes and Sniegowski, 2014; Sniegowski et al., 2000).

This frequency-dependent interpretation of mutator success has been primarily motivated by mutator dynamics observed in experimental studies of laboratory microbial populations. Most famously, in a series of pioneering experiments, Lin Chao and colleagues showed that mutator strains of the bacterium E. coli could supplant otherwise isogenic non-mutator strains by hitchhiking with beneficial mutations when initialized above a critical threshold frequency but would decline when initialized below it (Chao and Cox, 1983: reproduced in Figure 1A; Chao et al., 1983). Since then, a similar pattern has been recapitulated in several other studies in E. coli and S. cerevisiae (Thompson et al., 2006; Gentile et al., 2011; de Visser and Rozen, 2006; Le Chat et al., 2006). Critically, a frequency-dependent framing of indirect selection on mutators implies a change in the sign or the strength of indirect selection with frequency. Here, we use stochastic, agent-based computer simulations to demonstrate that on the contrary, indirect selection on mutators is independent of frequency.

Results and discussion

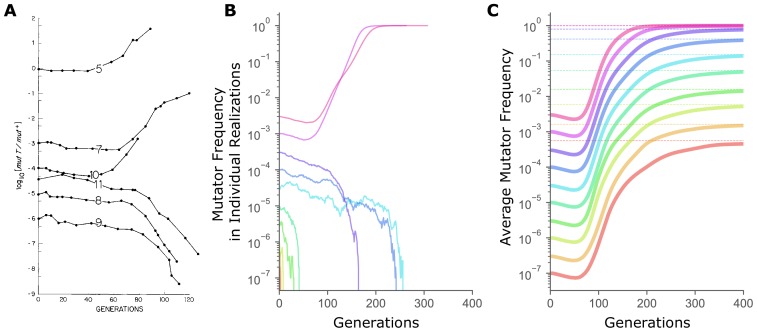
Our computer simulations (Raynes, 2019) model asexual populations that mimic microbial evolution experiments under generally-accepted parameter values (Raynes et al., 2018). Figure 1B shows mutator frequency dynamics in randomly chosen simulations initialized across four log-orders of starting frequency, x0, which recapitulate experimental observations of the critical frequency threshold for hitchhiking reproduced in Figure 1A. As in Figure 1A, single, randomly-chosen realizations (i.e., simulation replicates) started below a threshold frequency end in mutator loss, while randomly-chosen realizations started above end in fixation (Figure 1B).

Figure 1. The sharp transition between fixation and loss in mutator dynamics at different starting frequencies is due to limited sampling.

(A) Changes in the ratio of the mutator and the wild-type alleles of the E. coli mutT locus over time in continuous chemostat cultures. (Figure 1 from Chao and Cox, 1983). (B) In simulations, mutator trajectories in individual realizations initiated at different starting frequencies recapitulate the experimental observation of the frequency-threshold for mutator hitchhiking. Parameter values used are typical of microbial experimental populations (Raynes et al., 2018): N = 107, Udel = 10−4, Uben = 10−6, constant sben = 0.1, constant sdel = -0.1. Mutators mutate 100× faster than non-mutators. (C) Average mutator trajectories across realizations do not show evidence of the frequency-threshold. On average, mutators increase in frequency at all x0, showing that selection favors mutators independent of frequency. Average mutator frequency always eventually reaches the expected Pfixx0 (dashed horizontal lines) calculated in Figure 2. Mutator frequencies averaged across 106 simulation runs at x0= 10−7 and x0= 3×10−7, and across 105 simulation runs for all other starting frequencies. For simulations with exponentially distributed selection coefficients see Figure 1—figure supplement 1.

Figure 1—source data 1. Numerical data represented in Figure 1.
Data set includes mutator frequencies in randomly-chosen individual realizationss and mutator frequencies averaged across all realizations.

© 1983 John Wiley and Sons. All Rights Reserved

Figure 1 reproduced from Chao and Cox, 1983 with permission.

Figure 1.

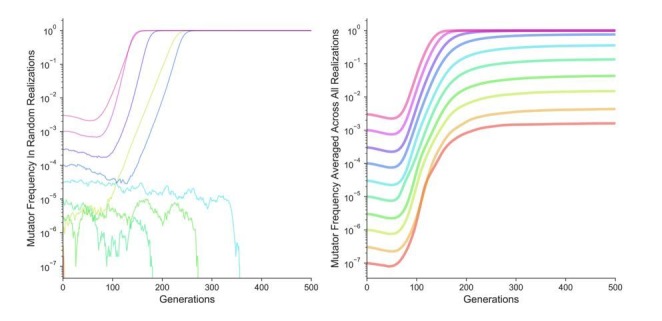
Figure 1—figure supplement 1. Simulations with exponentially distributed selection coefficients confirm that the frequency-dependent threshold in mutator dynamics is due to limited sampling.

Figure 1—figure supplement 1.

(A) Mutator trajectories in individual realizations. (B) Average mutator trajectories across realizations. Mutator frequencies averaged across 105 simulation runs. Parameter values as in Figure 1 except N = 106, and beneficial and deleterious mutations are now randomly drawn from an exponential distribution with the mean sben = 0.1 and sdel = −0.1 respectively.
Figure 1—figure supplement 1—source data 1. Numerical data represented in Figure 1—figure supplement 1.
Data set includes mutator frequencies in randomly-chosen individual realizationss and mutator frequencies averaged across all realizations.
Open in a new tab

Critically, fixation of an allele in a finite population is a probabilistic process influenced both by selection and random genetic drift, and even beneficial mutations will frequently be lost by chance alone. As such, whether an allele is truly favored or disfavored by selection can only be ascertained by evaluating its expected behavior averaged across many replicate, independent realizations. Indeed, if we consider the expected mutator frequency averaged across many replicate simulations, the threshold-frequency effect disappears (Figure 1C). Instead, the average mutator frequency ultimately rises above the starting frequency at all x0, suggesting that mutators are, in fact, favored by selection in these populations regardless of starting frequency. (For more on why mutators are favored in large populations such as these see Raynes et al., 2018). The transient decline in average frequency seen in Figure 1C reflects selection against the deleterious load inherent to mutators (Kimura, 1967), and will be explored in a forthcoming publication].

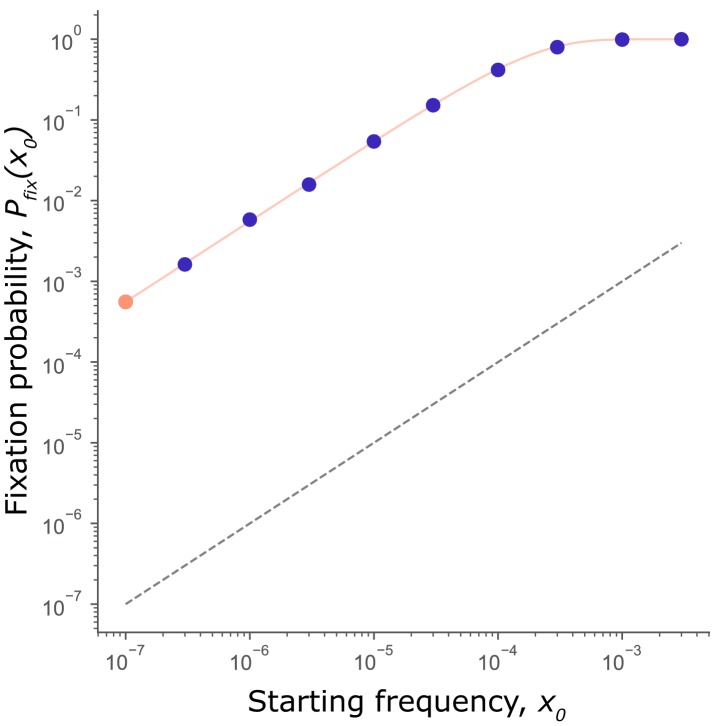
To confirm that selection on mutators is independent of starting frequency, we measured the fixation probability of a mutator allele, Pfix(x0), at each initial frequency, x0 simulated in Figure 1. Given the stochasticity of the fixation process (and following Good and Desai, 2016; Raynes et al., 2018; Wylie et al., 2009), we compare Pfix(x0) to the probability of fixation of a neutral allele, given simply by x0. If a mutator is favored, we expect it to fare better than neutral (i.e., Pfix(x0)>x0), and worse than neutral (i.e., Pfix(x0)<x0) if disfavored. As Figure 2 shows, Pfix(x0) exceeds the fixation probability of a neutral allele for all x0, as anticipated in Figure 1C and confirming that the sign of selection on mutators does not depend on starting frequency.

Figure 2. Mutator fixation probability is not frequency-dependent.

Figure 2.

Open in a new tab

Fixation probability, Pfixx0, of a mutator initiated at frequency x0 (circles: orange for x0=1/N, purple for x0>1/N). Data from simulations in Figure 1. Pfixx0 scales with but never crosses the fixation probability of a neutral mutation (x0; black dashed line). Thus, mutators are favored at all starting frequencies. The expected fixation probability Pfixx0 (solid orange line), calculated from the fixation probability of a single mutator, Pfixx0=1/N = 5.6×10−4 (orange point) using Equation 1 is indistinguishable from the Pfixx0 observed in simulations, demonstrating that the per-capita fixation probability at every frequency is independent of x0 and equal to Pfixx0=1/N.

Figure 2—source data 1. Numerical data represented in Figure 2.
Data set includes fixation probabilities of a mutator allele at each initial frequency shown.

Furthermore, while Pfixx0 of a mutator increases with x0, it does so exactly as expected for a frequency-independent mutation. Under frequency-independent selection Pfixx0 is simply the probability that at least one of the x0N alleles reaches fixation (where N is the population size). By definition of frequency-independent selection, the per-capita fixation probability is a constant, written, Pfixx0=1/N. Correspondingly, Pfixx0 for any x0 can be calculated as

Pfixx0=1-(1-Pfixx0=1/N)x0N (1)

As the orange line in Figure 2 shows, Pfixx0 calculated with Equation 1 is indistinguishable from Pfixx0 observed in simulations, confirming that the per-capita fixation probability is independent of x0 and equal to Pfixx0=1/N at any x0. Thus, while the expected fixation probability of a mutator increases with x0, the per-capita fixation probability remains unchanged, confirming that individual mutators do not become more likely to hitchhike to fixation when present at higher frequencies in a population.

Why then do mutators in experimental populations appear destined to go extinct when initially rare (e.g. Chao and Cox, 1983)? Given that this behavior has been documented across different systems and selective environments (as well as in our stochastic simulations in Figure 1B), it seems unlikely to depend on any shared biological property of the experimental systems. Consider, however, that the per-capita fixation probability of a mutator is relatively low – in our simulations, operating under realistic parameter values, Pfixx0=1/N = 5.6×10−4. Thus even when mutators are favored, most experimental replicates with rare mutators are expected to end in mutator extinction, and only those started at frequencies higher than roughly 1/[NPfixx0=1/N] are expected to end mostly with mutator fixation. Considering only a single or even a few realizations at each starting frequency (as in Figure 1A or B) would, most likely, result in observing only the most expected outcome for each x0. Indeed, all experimental studies that have documented the frequency-based transition included only a few populations at each starting frequency. Such limited sampling across a broad range of starting frequencies in these experiments would explain the sharp transition between fixation at high frequencies and loss at lower ones even when selection is frequency-independent (see also Tanaka et al., 2003). We expect that observing the dynamics in Figure 1C would be possible with more experimental replication, which, however, may not always be experimentally feasible.

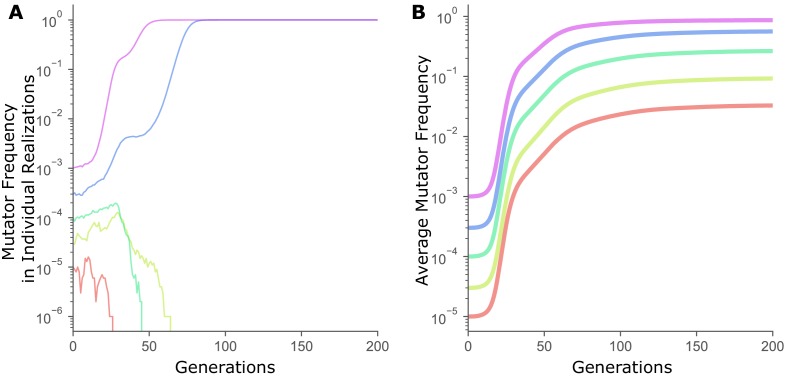
In fact, the critical frequency-dependent transition observed in Figure 1A and 1B is not unique to mutators. Recall that Pfixx0 of any mutation not under frequency-dependent selection, nevertheless, increases with starting frequency, x0 (Equation 1). For example, even for a directly beneficial mutation, the probability of fixation from low frequencies is relatively low (Figure 3A Inset), Accordingly, as Figure 3A illustrates, single realizations of the dynamics of a directly beneficial mutation also exhibit a threshold-like switch from fixation to loss. In contrast, expected frequency dynamics averaged across many independent realizations confirm that beneficial mutations are favored by selection independent of starting frequency (Figure 3B). Indeed, only for mutations under truly frequency-dependent selection do both the individual realizations (Figure 3C) and the expected dynamics averaged across many realizations (Figure 3D) exhibit an actual frequency-dependent transition.

Figure 3. Frequency threshold in dynamics of fitness-affecting mutations.

Figure 3.

Open in a new tab

(A) Individual realizations of a simulation initiated with a directly beneficial mutation of size sben = 0.01 at a starting frequency x0. Population size, N = 107. Inset: Fixation probability of a beneficial mutation of size sben =0.01 at N = 107. Dashed line is given by Pfixbenx0=1-e-2sbenNx01-e-2sbenN (Kimura, 1962), while circles are values of Pfixbenx0 measured in simulations (averaged across 105 runs). (B) Average frequency trajectories of a beneficial mutation of size sben = 0.01 in (A) averaged across all 105 runs of simulation. (C) Individual realizations of a simulation initiated with a mutation under frequency dependent selection, with the selection coefficient s(x) = b + mx, where x is the frequency, b = -0.02, and m = 0.1, at N = 107. (D) Average frequency trajectories of the frequency-dependent mutation in (C) averaged across all 105 runs of simulation. All panels are on a log-log scale for clarity.

Figure 3—source data 1. Numerical data represented in Figure 3.
Data set includes frequencies of a beneficial mutation and a frequncy-dependent mutation in randomly-chosen individual realizations and averaged across all replicate realizations.

In summary, our results demonstrate that neither the strength nor the sign of selection on mutators depend on initial frequency or number. Instead, we show that in populations favoring higher mutation rates, mutators consistently fare better than the neutral expectation (Figure 1 and Figure 2) regardless of starting frequency. Most importantly, the per-capita probability of fixation remains unchanged with frequency. We conclude that the frequency threshold observed in earlier experiments is, therefore, an artifact of limited experimental sampling rather than a frequency-dependent change in selective effect.

Materials and methods

Individual-based, stochastic simulations employed here have been previously described (Raynes et al., 2018). In brief, we consider haploid asexual populations of constant size, N, evolving in discrete, non-overlapping generations according to the Wright-Fisher model (Ewens, 2004). Populations are composed of genetic lineages - subpopulations of individuals with the same genotype. A genotype is modeled as an array of 99 fitness-affecting loci and 1 mutation rate modifier locus, which in a mutator state raises the genomic mutation rate m-fold. For computational efficiency, simulations in Figure 1 assume constant fitness effects: beneficial mutations at the fitness loci increase fitness by a constant effect sben, while deleterious mutations decrease fitness by a constant effect sdel. We assume additive fitness effects and so calculate fitness of a lineage with x beneficial and y deleterious mutations as wxy=1+xsben-ysdel. In simulations in Figure 1—figure supplement 1, beneficial and deleterious fitness effects are randomly drawn from an exponential distribution with the mean sben = 0.1 and sdel = -0.1 respectively. Simulations start with the mutator allele at a frequency of x0 and continue until it either fixes or is lost from a population.

Every generation the size of each lineage i is randomly sampled from a multinomial distribution with expectation N·fi·(wi/w-), where fi is the frequency of the lineage in the previous generation, wi is the lineage’s fitness, and w- is the average fitness of the population (w-=∑fi∙wi). Upon reproduction, each lineage acquires a random number of fitness-affecting mutations M, drawn from a Poisson distribution with mean equal to the product of its size and its total per-individual mutation rate, Uben+Udel, where Uben and Udel are the deleterious and beneficial mutation rates respectively. The number of beneficial and deleterious mutations is then drawn from a binomial distribution with n=M and P = Uben/Uben+Udel and new mutations are assigned to randomly chosen non-mutated fitness loci.

Data availability

All simulated data were generated in Julia 1.0. Simulation code is available under an open source MIT license at https://github.com/yraynes/Mutator-Frequency (Raynes, 2019; https://github.com/elifesciences-publications/Mutator-Frequency).

Acknowledgements

We thank Paul Sniegowski, Lin Chao, and Benjamin Galeota-Sprung for comments on the manuscript. Simulations were performed on the computing cluster of the Computer Science Department at Brown University. The work was supported by National Science Foundation Grant DEB-1556300.

Funding Statement

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Contributor Information

Yevgeniy Raynes, Email: yevgeniy_raynes@brown.edu.

Patricia J Wittkopp, University of Michigan, United States.

Patricia J Wittkopp, University of Michigan, United States.

Funding Information

This paper was supported by the following grant:

  • National Science Foundation DEB-1556300 to Yevgeniy Raynes, Daniel Weinreich.

Additional information

Competing interests

No competing interests declared.

Author contributions

Conceptualization, Software, Investigation, Writing—original draft, Writing—review and editing.

Conceptualization, Supervision, Funding acquisition, Project administration, Writing—review and editing.

Additional files

Transparent reporting form

Data availability

Simulation code is available at https://github.com/yraynes/Mutator-Frequency (copy archived at https://github.com/elifesciences-publications/Mutator-Frequency).

References

  1. Barrick JE, Yu DS, Yoon SH, Jeong H, Oh TK, Schneider D, Lenski RE, Kim JF. Genome evolution and adaptation in a long-term experiment with Escherichia coli. Nature. 2009;461:1243–1247. doi: 10.1038/nature08480. [DOI] [PubMed] [Google Scholar]
  2. Billmyre RB, Clancey SA, Heitman J. Natural mismatch repair mutations mediate phenotypic diversity and drug resistance in Cryptococcus deuterogattii. eLife. 2017;6:e28802. doi: 10.7554/eLife.28802. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Boyce KJ, Wang Y, Verma S, Shakya VPS, Xue C, Idnurm A. Mismatch repair of DNA replication errors contributes to microevolution in the pathogenic fungus Cryptococcus neoformans. mBio. 2017;8:e00595. doi: 10.1128/mBio.00595-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chao L, Vargas C, Spear BB, Cox EC. Transposable elements as mutator genes in evolution. Nature. 1983;303:633–635. doi: 10.1038/303633a0. [DOI] [PubMed] [Google Scholar]
  5. Chao L, Cox EC. Competition between high and low mutating strains of Escherichia coli. Evolution. 1983;37:125–134. doi: 10.1111/j.1558-5646.1983.tb05521.x. [DOI] [PubMed] [Google Scholar]
  6. de Visser JA, Rozen DE. Clonal interference and the periodic selection of new beneficial mutations in Escherichia coli. Genetics. 2006;172:2093–2100. doi: 10.1534/genetics.105.052373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ewens W. Mathematical Population Genetics. New York: Springer; 2004. [Google Scholar]
  8. Furió V, Moya A, Sanjuán R. The cost of replication fidelity in an RNA virus. PNAS. 2005;102:10233–10237. doi: 10.1073/pnas.0501062102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Furió V, Moya A, Sanjuán R. The cost of replication fidelity in human immunodeficiency virus type 1. Proceedings of the Royal Society B: Biological Sciences. 2007;274:225–230. doi: 10.1098/rspb.2006.3732. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gentile CF, Yu SC, Serrano SA, Gerrish PJ, Sniegowski PD. Competition between high- and higher-mutating strains of Escherichia coli. Biology Letters. 2011;7:422–424. doi: 10.1098/rsbl.2010.1036. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Good BH, Desai MM. Evolution of mutation rates in rapidly adapting asexual populations. Genetics. 2016;204:1249–1266. doi: 10.1534/genetics.116.193565. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Healey KR, Zhao Y, Perez WB, Lockhart SR, Sobel JD, Farmakiotis D, Kontoyiannis DP, Sanglard D, Taj-Aldeen SJ, Alexander BD, Jimenez-Ortigosa C, Shor E, Perlin DS. Prevalent mutator genotype identified in fungal pathogen Candida Glabrata promotes multi-drug resistance. Nature Communications. 2016;7:11128. doi: 10.1038/ncomms11128. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kimura M. On the probability of fixation of mutant genes in a population. Genetics. 1962;47:713–719. doi: 10.1093/genetics/47.6.713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Kimura M. On the evolutionary adjustment of spontaneous mutation rates. Genetical Research. 1967;9:23–34. doi: 10.1017/S0016672300010284. [DOI] [Google Scholar]
  15. Le Chat L, Fons M, Taddei F. Escherichia coli mutators: selection criteria and migration effect. Microbiology. 2006;152:67–73. doi: 10.1099/mic.0.28418-0. [DOI] [PubMed] [Google Scholar]
  16. LeClerc JE, Li B, Payne WL, Cebula TA. High mutation frequencies among Escherichia coli and Salmonella pathogens. Science. 1996;274:1208–1211. doi: 10.1126/science.274.5290.1208. [DOI] [PubMed] [Google Scholar]
  17. Lengauer C, Kinzler KW, Vogelstein B. Genetic instability in colorectal cancers. Nature. 1997;386:623–627. doi: 10.1038/386623a0. [DOI] [PubMed] [Google Scholar]
  18. Loeb LA. Human cancers express mutator phenotypes: origin, consequences and targeting. Nature Reviews Cancer. 2011;11:450–457. doi: 10.1038/nrc3063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mao EF, Lane L, Lee J, Miller JH. Proliferation of mutators in A cell population. Journal of Bacteriology. 1997;179:417–422. doi: 10.1128/jb.179.2.417-422.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Matic I, Radman M, Taddei F, Picard B, Doit C, Bingen E, Denamur E, Elion J. Highly variable mutation rates in commensal and pathogenic Escherichia coli. Science. 1997;277:1833–1834. doi: 10.1126/science.277.5333.1833. [DOI] [PubMed] [Google Scholar]
  21. Notley-McRobb L, Seeto S, Ferenci T. Enrichment and elimination of mutY mutators in Escherichia coli populations. Genetics. 2002;162:1055–1062. doi: 10.1093/genetics/162.3.1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Oliver A, Cantón R, Campo P, Baquero F, Blázquez J. High frequency of hypermutable Pseudomonas aeruginosa in cystic fibrosis lung infection. Science. 2000;288:1251–1253. doi: 10.1126/science.288.5469.1251. [DOI] [PubMed] [Google Scholar]
  23. Pal C, Maciá MD, Oliver A, Schachar I, Buckling A. Coevolution with viruses drives the evolution of bacterial mutation rates. Nature. 2007;450:1079–1081. doi: 10.1038/nature06350. [DOI] [PubMed] [Google Scholar]
  24. Raynes Y, Wylie CS, Sniegowski PD, Weinreich DM. Sign of selection on mutation rate modifiers depends on population size. PNAS. 2018;115:3422–3427. doi: 10.1073/pnas.1715996115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Raynes Y. Github; 2019. https://github.com/yraynes/Mutator-Frequency [Google Scholar]
  26. Raynes Y, Sniegowski PD. Experimental evolution and the dynamics of genomic mutation rate modifiers. Heredity. 2014;113:375–380. doi: 10.1038/hdy.2014.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Shaver AC, Dombrowski PG, Sweeney JY, Treis T, Zappala RM, Sniegowski PD. Fitness evolution and the rise of mutator alleles in experimental Escherichia coli populations. Genetics. 2002;162:557–566. doi: 10.1093/genetics/162.2.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Smith JM, Haigh J. The hitch-hiking effect of a favourable gene. Genetical Research. 1974;23:23–35. doi: 10.1017/S0016672300014634. [DOI] [PubMed] [Google Scholar]
  29. Sniegowski PD, Gerrish PJ, Lenski RE. Evolution of high mutation rates in experimental populations of E. coli. Nature. 1997;387:703–705. doi: 10.1038/42701. [DOI] [PubMed] [Google Scholar]
  30. Sniegowski PD, Gerrish PJ, Johnson T, Shaver A. The evolution of mutation rates: separating causes from consequences. BioEssays. 2000;22:1057–1066. doi: 10.1002/1521-1878(200012)22:12&#x0003c;1057::AID-BIES3&#x0003e;3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
  31. Suárez P, Valcárcel J, Ortín J. Heterogeneity of the mutation rates of influenza A viruses: isolation of mutator mutants. Journal of Virology. 1992;66:2491–2494. doi: 10.1128/jvi.66.4.2491-2494.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Tanaka MM, Bergstrom CT, Levin BR. The evolution of mutator genes in bacterial populations: the roles of environmental change and timing. Genetics. 2003;164:843–854. doi: 10.1093/genetics/164.3.843. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Thompson DA, Desai MM, Murray AW. Ploidy controls the success of mutators and nature of mutations during budding yeast evolution. Current Biology. 2006;16:1581–1590. doi: 10.1016/j.cub.2006.06.070. [DOI] [PubMed] [Google Scholar]
  34. Voordeckers K, Kominek J, Das A, Espinosa-Cantú A, De Maeyer D, Arslan A, Van Pee M, van der Zande E, Meert W, Yang Y, Zhu B, Marchal K, DeLuna A, Van Noort V, Jelier R, Verstrepen KJ. Adaptation to high ethanol reveals complex evolutionary pathways. PLOS Genetics. 2015;11:e1005635. doi: 10.1371/journal.pgen.1005635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wylie CS, Ghim CM, Kessler D, Levine H. The fixation probability of rare mutators in finite asexual populations. Genetics. 2009;181:1595–1612. doi: 10.1534/genetics.108.094532. [DOI] [PMC free article] [PubMed] [Google Scholar]

Decision letter

Editor: Patricia J Wittkopp1
Reviewed by: Timothy Cooper

In the interests of transparency, eLife publishes the most substantive revision requests and the accompanying author responses.

Acceptance summary:

Mutator genotypes have elevated mutation rates, introducing more deleterious, neutral, and beneficial mutations into a population each generation than ("wild-type") non-mutator genotypes. Prior work has shown that such mutator genotypes are unlikely to become fixed within a population when they exist at low frequencies. This study challenges that view and advances our understanding of evolutionary processes by showing that the probability of mutator genotypes fixing within a population are not dependent upon their starting frequency in the population. The authors argue and then show via many simulations that the probability of fixation does not change with starting frequency under the parameter space of a typical experimental evolution study.

Decision letter after peer review:

Thank you for submitting your article "Selection on mutators is not frequency-dependent" for consideration by eLife. Your article has been reviewed by three peer reviewers, and the evaluation has been overseen by Patricia Wittkopp as the Senior and Reviewing Editor. The following individual involved in review of your submission has agreed to reveal their identity: Timothy Cooper (Reviewer #3).

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

This study shows that the per-capita probability of fixation of mutator genotypes, including the beneficial, neutral or deleterious mutations they produce, are not dependent on starting frequency. This goes against conventional wisdom because experiments with mutator genotypes of microbes have indicated that mutators fail to invade from low starting frequencies, i.e., below the level of their relative increases in beneficial mutation supply rate. The authors argue and then show via many simulations that the probability of fixation does not change with starting frequency under the parameter space of a typical experimental evolution study. This is a notable finding.

Essential revisions:

1) The primary concern raised (and supported by all three reviewers) is that the paper presents a straw man argument. As the authors note numerous times in the manuscript, the argument that selection for mutators is dependent on frequency is "common intuition". But the reviewers were not convinced that this intuition is widespread. They thought most people would agree that the probability of fixation is related to mutator frequency, but not that the selective coefficient/advantage for a given mutator changes with frequency in a population.

Basic evolutionary theory would suggest that if the selective advantage of a mutator is due to its linkage with a beneficial mutation, then this selective advantage will be related to the probability of causing a beneficial mutation (i.e., the ratio of beneficial and deleterious mutation rates). This should be independent of how many mutators there are in a population. Of course the probability that a mutator genotype will fix increases with the frequency of mutators. This is simply true for neutral and beneficial mutations in finite populations. In the case of a mutator genotype, it is also true because there is an increase of sampling of mutations and the probability that one of the mutators in the population hits on a beneficial mutation to hitchhike with. But the selective advantage of any individual mutator should not change. I guess what I am saying is that results of the paper seem to demonstrate what a careful consideration of mutators would suggest and that this research is not debunking some wide-held view. That being said, it is a clear and thoughtful demonstration of the phenomenon, which apparently has not been published before, and may contribute to the interpretation of experimental results.

2) A similar straw-man-like concern: Regarding relevance – the argument that the authors who have found evidence of frequency-dependence (Chao and Cox, 1983, Thompson et al., 2006, Gentile et al., 2011, de Visser and Rozen, 2006, Le Chat et al., 2006) simply did not sample enough to find evidence of frequency-independence is not satisfying because the pattern has replicated across systems and laboratories. This suggests there's more to the biological story here that your simulations fail to capture. What might this be? Please add a paragraph proposing reasons for this disconnect. For instance, could this be a property of the DFE, where one particular type of highly beneficial mutation trumps all, and the lucky genotype that acquires this mutation becomes destined to fix? Could this be a property of the degree of clonal interference or the effective population size, both of which alter drift?

3) About the methods: It seems as though the way the simulations are set up, all deleterious and all beneficial mutations have the same fitness cost/benefit. Is there a reason why the authors didn't draw from a distribution of fitness effects? I am not sure how much changing this would influence the results, but it does seem more biologically realistic. Perhaps commenting on this approach of simulations and parameters would be helpful.

eLife. 2019 Nov 7;8:e51177. doi: 10.7554/eLife.51177.sa2

Author response

Essential revisions:

1) The primary concern raised (and supported by all three reviewers) is that the paper presents a straw man argument. As the authors note numerous times in the manuscript, the argument that selection for mutators is dependent on frequency is "common intuition". But the reviewers were not convinced that this intuition is widespread. They thought most people would agree that the probability of fixation is related to mutator frequency, but not that the selective coefficient/advantage for a given mutator changes with frequency in a population.

Basic evolutionary theory would suggest that if the selective advantage of a mutator is due to its linkage with a beneficial mutation, then this selective advantage will be related to the probability of causing a beneficial mutation (i.e., the ratio of beneficial and deleterious mutation rates). This should be independent of how many mutators there are in a population. Of course the probability that a mutator genotype will fix increases with the frequency of mutators. This is simply true for neutral and beneficial mutations in finite populations. In the case of a mutator genotype, it is also true because there is an increase of sampling of mutations and the probability that one of the mutators in the population hits on a beneficial mutation to hitchhike with. But the selective advantage of any individual mutator should not change. I guess what I am saying is that results of the paper seem to demonstrate what a careful consideration of mutators would suggest and that this research is not debunking some wide-held view. That being said, it is a clear and thoughtful demonstration of the phenomenon, which apparently has not been published before, and may contribute to the interpretation of experimental results.

We agree that our conclusion that selection on mutators is not frequency-dependent could be arrived at by a “careful consideration” of the evolutionary forces acting on them. However, as we now further emphasize in the paper, mutator dynamics have been repeatedly described as being frequency- or number-dependent in the literature (Introduction, last paragraph). By definition this means that the fitness of an individual mutator allele would depend on its frequency and not only that the probability of fixation increases with frequency (which is true for a frequency-independent allele as well). The goal of our paper is to clarify this feature of selection on mutators by providing a clear demonstration of frequency independence.

We also appreciate the concern that while we present this misconception as a “common intuition,” it may not be as widely held as we may think. In the revision we have attempted to be more careful about not mischaracterizing the extent to which this intuition has dominated the field. We instead reframe our description of this issue in the mutator literature, especially in the experimental literature (Abstract and Introduction, last two paragraphs), where it has been advanced in a number of very influential papers. Thank you for helping us to more accurately focus this point.

2) A similar straw-man-like concern: Regarding relevance – the argument that the authors who have found evidence of frequency-dependence (Chao and Cox, 1983, Thompson et al., 2006, Gentile et al., 2011, de Visser and Rozen, 2006, Le Chat et al., 2006) simply did not sample enough to find evidence of frequency-independence is not satisfying because the pattern has replicated across systems and laboratories. This suggests there's more to the biological story here that your simulations fail to capture. What might this be? Please add a paragraph proposing reasons for this disconnect. For instance, could this be a property of the DFE, where one particular type of highly beneficial mutation trumps all, and the lucky genotype that acquires this mutation becomes destined to fix? Could this be a property of the degree of clonal interference or the effective population size, both of which alter drift?

We thank you and the reviewers for raising this point. We had not previously recognized the opportunity to discuss the difference in experimental organisms and environments in our interpretation of mutator dynamics. You and the reviewers wonder if the explanation for the pattern could be biological. But on the contrary, for us the fact that this pattern has been observed in different systems and environments strengthens our claim of a single, theoretical explanation. Observations from diverse systems appear to preclude the possibility that any system-specific selective property of a mutator or the available DFE could be responsible for the observation, since different alleles were used in different environments. This point is developed in the fifth paragraph of the Results and Discussion. Regarding the suggestion of a dependence in DFE we would also refer to our response to point 3, below.

Likewise, on first principles we could not see how clonal interference or population size effects could explain the apparent frequency-dependent threshold in mutator dynamics observed in individual competitions, as the threshold effect disappears when many replicates of the same competition are considered. To test this question, we conducted additional simulations parameterized exactly as those in Figures 1B and 1C except the mutation rate of the non-mutators was set to 0. This eliminates any interference from the non-mutatators. As Author response image 1 shows (averaged across 5∙104 simulation runs), the pattern in Figure 1B and 1C is recapitulated in the absence of interference – random individual simulation replicates (left panel) still appear to be frequency-dependent, while average dynamics confirm that mutators are favored (i.e., increase in frequency) at all starting frequencies.

Author response image 1.

Author response image 1.

Open in a new tab

We find that the most satisfying (and parsimonious) explanation for previous experimental observations is, therefore, the limited sampling, common to all experiments. Our simulations show that such limited sampling would produce the frequency-dependent switch even when selection is truly not frequency-dependent. In the revision, we now discuss the likelihood of the biological explanation for the dynamics in different systems and the fact that the limited sampling is the most parsimonious explanation for this result in the fifth and sixth paragraphs of the Results and Discussion).

3) About the methods: It seems as though the way the simulations are set up, all deleterious and all beneficial mutations have the same fitness cost/benefit. Is there a reason why the authors didn't draw from a distribution of fitness effects? I am not sure how much changing this would influence the results, but it does seem more biologically realistic. Perhaps commenting on this approach of simulations and parameters would be helpful.

We thank you and the reviewers for this suggestion. Indeed, following our earlier work (Raynes et al., 2018 and 2019) we have assumed constant fitness effects for computational efficiency (as is now described in the first paragraph of the Materials and methods) given the large size of simulated populations. To confirm that drawing fitness effects from a distribution would not impact the conclusions of our study we have conducted additional simulations and include these in the revised manuscript. In these simulations, we allow for both beneficial and deleterious to be drawn from exponential distributions (with means equal to sben and sdel values used Figure 1). Given the added computational requirements, we have reduced the size of simulated populations (now 106 vs. 107 in Figure 1) and the number of starting frequencies. These new simulations (now reported in the Figure 1—figure supplement 1) recapitulate our main observation – individual, randomly-chosen realization show a frequency-dependent breakpoint while average frequency dynamics are consistent with positive selection at all starting frequencies.

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Supplementary Materials

    Figure 1—source data 1. Numerical data represented in Figure 1.

    Data set includes mutator frequencies in randomly-chosen individual realizationss and mutator frequencies averaged across all realizations.

    elife-51177-fig1-data1.csv (60.1KB, csv)
    Figure 1—figure supplement 1—source data 1. Numerical data represented in Figure 1—figure supplement 1.

    Data set includes mutator frequencies in randomly-chosen individual realizationss and mutator frequencies averaged across all realizations.

    elife-51177-fig1-figsupp1-data1.csv (73KB, csv)
    Figure 2—source data 1. Numerical data represented in Figure 2.

    Data set includes fixation probabilities of a mutator allele at each initial frequency shown.

    elife-51177-fig2-data1.csv (219B, csv)
    Figure 3—source data 1. Numerical data represented in Figure 3.

    Data set includes frequencies of a beneficial mutation and a frequncy-dependent mutation in randomly-chosen individual realizations and averaged across all replicate realizations.

    elife-51177-fig3-data1.csv (364.1KB, csv)
    Transparent reporting form
    elife-51177-transrepform.docx (245.2KB, docx)

    Data Availability Statement

    All simulated data were generated in Julia 1.0. Simulation code is available under an open source MIT license at https://github.com/yraynes/Mutator-Frequency (Raynes, 2019; https://github.com/elifesciences-publications/Mutator-Frequency).

    Simulation code is available at https://github.com/yraynes/Mutator-Frequency (copy archived at https://github.com/elifesciences-publications/Mutator-Frequency).

    Articles from eLife are provided here courtesy of eLife Sciences Publications, Ltd

    RESOURCES