A single ChIP-seq dataset is sufficient for comprehensive analysis of motifs co-occurrence with MCOT package

Abstract

Recognition of composite elements consisting of two transcription factor binding sites gets behind the studies of tissue-, stage- and condition-specific transcription. Genome-wide data on transcription factor binding generated with ChIP-seq method facilitate an identification of composite elements, but the existing bioinformatics tools either require ChIP-seq datasets for both partner transcription factors, or omit composite elements with motifs overlapping. Here we present an universal Motifs Co-Occurrence Tool (MCOT) that retrieves maximum information about overrepresented composite elements from a single ChIP-seq dataset. This includes homo- and heterotypic composite elements of four mutual orientations of motifs, separated with a spacer or overlapping, even if recognition of motifs within composite element requires various stringencies. Analysis of 52 ChIP-seq datasets for 18 human transcription factors confirmed that for over 60% of analyzed datasets and transcription factors predicted co-occurrence of motifs implied experimentally proven protein-protein interaction of respecting transcription factors. Analysis of 164 ChIP-seq datasets for 57 mammalian transcription factors showed that abundance of predicted composite elements with an overlap of motifs compared to those with a spacer more than doubled; and they had 1.5-fold increase of asymmetrical pairs of motifs with one more conservative ‘leading’ motif and another one ‘guided’.

INTRODUCTION

Combinatorial binding of multiple transcription factors (TFs) to the regulatory region provides for fine-tuning of the gene expression dynamics in response to distinct internal and external signals (1–4). Investigation of pairwise TF interactions upon binding to DNA is a basis for understanding larger TF complexes formation and functioning (1,5–7). Composite element (CE) is the minimal functional unit that consists of two co-located motifs for pairwise interaction between partner TFs on regulatory DNA (5,8–11). Mutual location and orientation of the TF binding sites within the CE is drastically important for TFs cooperation or competition on the regulatory DNA (5,8). Reflecting this, many known and predicted CEs have a rigid and compact structure with an overlap of the motifs (5,12,13). Chromatin immunoprecipitation (ChIP)-based high throughput techniques (ChIP-chip, ChIP-seq, ChIP-exo) locate TF binding to genomic DNA in vivo (14,15) and facilitate bioinformatics identification of CEs functional in certain condition (16). In order to identify putative CEs one should apply a motif discovery procedure, e.g. (17–20). In particular, two approaches were developed earlier.

As a first approach, one can trace if there are enriched spacings between the genome-wide binding profile of studied TF and predicted profiles for other TFs. SpaMo (21) and iTFs (22) tools efficiently discover CEs with a spacer within a single ChIP-seq dataset, but they omit the big class of CEs with an overlap (Table 1).

Table 1.

Comparison of various tools for prediction of CEs in ChIP-seq data

Tool name	Sufficiency of a single dataset of peaks	Prediction of overlapped motifs	URL	Reference
SpaMo	Yes	No	http://meme-suite.org/tools/spamo	(21)
iTFs	Yes	No	http://veda.cs.uiuc.edu/iTFs/	(22)
GEM	No	Yes	http://groups.csail.mit.edu/cgs/gem/	(13)
TACO	No	Yes	http://bioputer.mimuw.edu.pl/taco/	(12,24)
MCOT	Yes	Yes	https://gitlab.sysbio.cytogen.ru/academiq/mcot-kernel	This work

As a second approach, co-occurrence of TF binding calls from two (or more) ChIP-seq datasets can serve as an estimate of combinatorial TF binding (23). Thus, GEM tool (13) integrates genome-wide read coverage information for two or more TFs, a posterior prediction of motifs discovered potential CEs with a spacer or an overlap of motifs. TACO tool (12,24) also started analysis from a library of ChIP-seq or cell-type specific DNase-seq datasets. Analysis of a single dataset consisted in integration of the rest datasets in a background model. Subsequent enrichment tests for various pairs of motifs allowed prediction of potential CEs with a spacer or an overlap of motifs. Despite these tools are capable of prediction of CEs with an overlap, they have limitations that substantially restrict their application in routine practice (Table 1). Generation of a library of ChIP-seq or DNase-seq experiments is labor, cost consuming and is hardly feasible for non-model organisms.

In this research, we suggest to apply foreground data to generate a background model with a permutation procedure (25). This advance allows prediction of CEs within a single ChIP-seq dataset. We implement this approach in a Motifs Co-Occurrence Tool (MCOT) that identifies overrepresented CEs and describes their structural variants. By an analysis of single, reciprocal and multiple ChIP-seq profiles we prove that MCOT is a reliable prognostic software that will make the experimental analysis of combinatorial TF binding cheaper and more effective.

MATERIALS AND METHODS

Input data and parameters

ChIP-seq peaks

Each ChIP-seq dataset (peaks) were retrieved from GEO according to annotations from GTRD (26), ReMap (27) and Cistrom DB (28). Totally, we extracted 117/47 human/mouse datasets for 57 distinct TFs and ∼75 various cell/tissue/treatment conditions (Supplementary Table S1).

Anchor motif

We defined the anchor motif as the top-scored result in a list of motifs from the de novo search generated for peaks by the HOMER tool (http://homer.ucsd.edu/homer/, (17)). For de novo search, we took peaks as the foreground sequences and shuffled these sequences to generate the background sequences. An anchor motif should have the significant match (Tomtom, http://meme-suite.org/tools/tomtom, (29)) to known matrix of immunoprecipitated TF.

Partner motif(s)

MCOT have two running modes: it searches for the co-occurrence of anchor motif with either sole or multiple partner motifs. For one partner TF and certain tissue/cell/treatment condition, the best approach to estimate the partner motif is to search for ChIP-seq data for partner TF in the same conditions. If such data are absent or even a certain TF cannot be suspected as a partner, we get hundreds potential partner motifs form a public library, e.g. human/mouse matrices from the Hocomoco database (http://hocomoco11.autosome.ru/, (30)). We computed position weight matrices (PWMs) from frequency matrices with log-odds weights (31). For each partner PWM, we computed the P-value of the best hit (Supplementary Table S2). This value allowed decide whether stringent thresholds for PWMs applicable to filter out false positives. Thus, we discarded from analysis motifs with these P-values above 2E–5 (Supplementary Figure S1).

Motifs mapping

Recognition of motifs

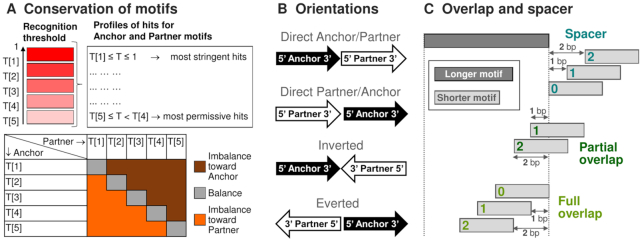
To guarantee the same stringency for PWMs, we generated for each PWM the comprehensive list of thresholds (32). Then, we estimated for all thresholds False Positive Rates (FPRs) as probabilities of hits for respective whole-genome datasets of upstream regions of human/mouse protein coding genes of length 2 kb. Distinct start positions for 19795/19991 human/mouse genes we extracted from Gencode 27/M15 (33). Finally, we took the unified set of five expected FPRs, {5.24E–5, 1.02E–04, 1.9E–4, 3.33E–4, 5E–4} and computed five thresholds {T[k]} for each PWM. The profile of the most stringent hits contained hits T ≥ T[1], the next profiles comprised scores in the ranges T[k] ≤ T < T[k-1], index k = 2, 3, 4, 5 denotes the conservation level of a motif (Figure 1A).

Figure 1.

Classification of structural CEs variants with respect to and conservation of anchor and partner motifs (A), their mutual orientation (B), overlap or spacer (C). Cyan, green and light green colors on the panel B distinguish CEs with a spacer, partial and full overlaps, respectively. The color range from red to pink on the panel A denotes the conservation level of a motif; brown/orange and grey colors mark imbalance in CEs with more conserved anchor/partner motifs and a balance between conservation of motifs.

Permutation procedure

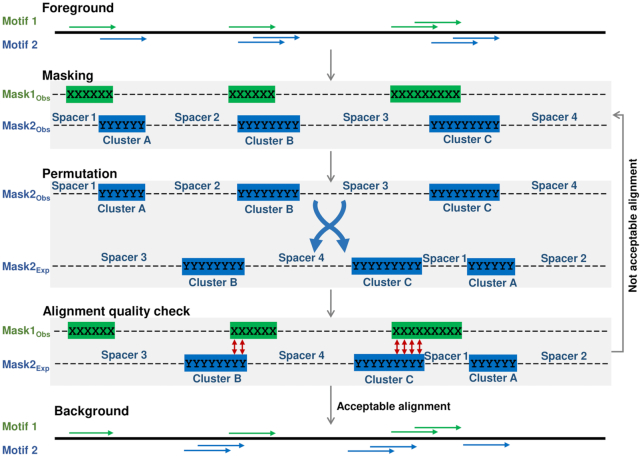
MCOT applied the permutation procedure to estimate the expected co-occurrence for a pair of motifs (see Supplementary Data 1, Text 2). The novelty of this procedure consisted in partitioning of a profile of hits for a certain motif onto clusters of non-overlapping hits (Figure 2, ‘Masking’). Next, MCOT shuffled clusters and spacers between them (‘Permutation’, (25)) and ascertained that shuffled and original versions of a peak were perfectly aligned (‘Alignment quality check’).

Figure 2.

MCOT permutation procedure. ‘Foreground’ shows profiles of hits for two motifs, green and blue colors mark fixed and selected for permutation profiles. ‘Masking’ partitions each profile onto ‘clusters’ of hits and spacers. ‘Permutation’ shows a real (top) and shuffled (bottom) orders of clusters and spacers. ‘Alignment quality check’ illustrates the checkpoint of permutation. ‘Background’ shows the result of permutation.

Classification of CEs

MCOT classify CEs according to the ratio of conservation of two motifs, their mutual orientation and the presence of their overlap or spacer between them (Figure 1).

Conservation of motifs

If anchor and partner motifs refer to profiles of T[k_Anchor] and T[k_Partner] thresholds than criteria k_Anchor < k_Partner, k_Anchor > k_Partner and k_Anchor = k_Partner define CEs with more conserved anchor, partner motifs and equal conservation of motifs (Figure 1A).

Orientation

MCOT defines two direct orientations in CEs according to zero/positive or negative shift between centers of 5′-anchor-3′ and 5′-partner-3′ motifs; two reverse orientations respect to Inverted or Everted CEs (Figure 1B).

Overlap and spacer

MCOT runs five parallel computation flows for five CE types: Any (spacer or overlap), Full (one motif located entirely within another one), Partial (all the rest overlaps); Overlap (full and partial); Spacer (Figure 1C). The minimal and maximal spacer lengths are parameters, their default values are 0 and 29 bp. The maximal spacer length should be less than the sum of the minimal length of a peak, the lengths of anchor and partner motifs.

Similarity of anchor and partner motifs

In the case of overlap, to restrict the false predictions, MCOT estimated the significance of similarity between anchor and partner motifs. A match P-value < 0.05 marked predictions that can be a consequence of motifs similarity. To compute this P-value, according to previous analysis (34), MCOT used two similarity measures for a pair of matrix columns (35,36) (see Supplementary Data 1, Text 1 and Supplementary Figure S2).

Significances for CEs enrichment and their asymmetry

The significance of two-sided Fisher's exact test proves a potential CE as follow. For all 25 combinations of motifs conservation (k_Anchor, k_Partner) we count: (a) real peaks Obs_tot / permuted sequences Exp_tot that contained both motifs and (b) respective numbers Obs_CE+/Exp_CE+ corresponding to occurrence of at least one CE (Figure 3, 2 × 2 table ‘CE enrichment’). Since for each CE we consider 25 combinations of motifs conservation, we used Bonferroni correction for the significance of CE, P-value < 0.05/25 = 0.002.

Figure 3.

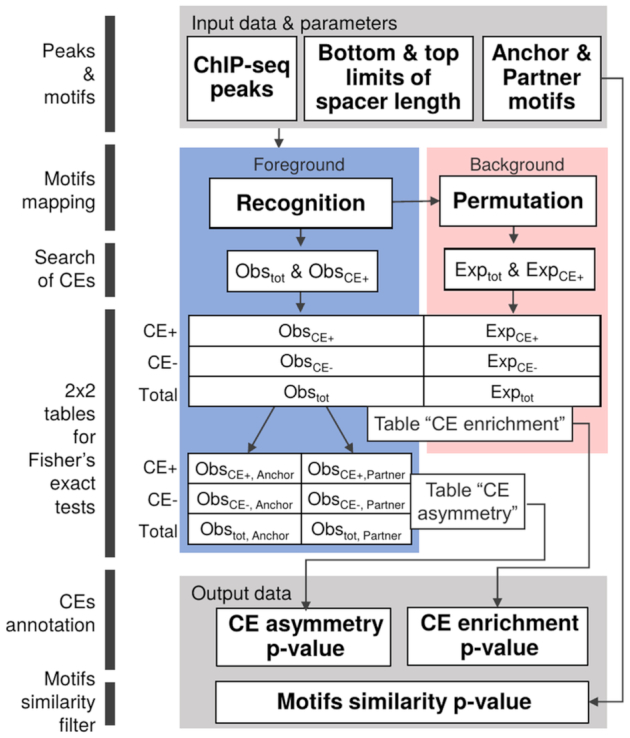
MCOT algorithm scheme. Grey color highlights input and output data. Pink and blue colors imply observed and expected data. Motifs mapping in peaks (Recognition) is performed for five stringencies (see Figure 1A) and it prepares profiles of hits for both motifs. These profiles are used to generate background profiles with mutually independent occurrences of anchor and partner motifs (Permutation). Observed and expected profiles of hits for anchor/partner motifs are further used for CEs search. Fisher's exact tests are applied to estimate CE enrichment and CE asymmetry (P-values) (see Materials and Methods). Output data also incorporate P-value that characterizes the similarity of anchor and partner motifs.

We subdivided predicted CEs on three classes: an anchor motif was more conserved than a partner motif (‘Anchor’, k_Anchor < k_Partner), vice versa (‘Partner’, k_Partner > k_Anchor), a similar conservation of motifs (‘Equal’, k_Anchor = k_Partner) (Figure 1A). As described above, for each class we computed the respective 2 × 2 table {Obs_tot,X / Exp_tot,X versus Obs_CE+,X / Exp_CE+,X}, (X = Anchor, Partner, Equal; index of class; Figure 3, 2 × 2 table ‘CE enrichment’). These calculations implied the integrated counts of sequences for five diagonal cells for ‘Equal’ class, each of the rest classes referred to ten cells in 5 × 5 table (Figure 1A). Finally, we applied the Fisher's exact test to compute the significance of CEs for each class.

Similarly, we estimated the significance of asymmetry ‘Anchor vs. Partner’ in CEs according to the 2 × 2 table of counts {Obs_CE+,Anchor / Obs_tot,Anchor versus Obs_CE+,Partner / Obs_tot,Partner} (Figure 3, 2 × 2 table ‘CE asymmetry’)_. The ratio of these two fractions Fold defines criteria Fold > 1 and Fold < 1 of the asymmetry toward an anchor and partner motifs. The absence of the significance of the asymmetry toward an anchor or partner motif means balanced conservation of two motifs. Otherwise, the significance of this asymmetry denotes their imbalanced conservation. Since MCOT implied five computation flows and distinguished three conservation classes, we applied Bonferroni's correction for the significance of asymmetry, P-value < 0.05/15 ≈ 0.0033.

MCOT performance test for the benchmark dataset of CEs

To estimate MCOT predictive efficiency we applied the benchmark dataset of True Positive (TP) CEs of 29 distinct pairs of TFs (Supplementary Table S3). This list was compiled earlier for TACO tool (24) performance estimation. We excluded from analysis (a) five TF pairs since for the respective ChIP-seq datasets we found dimeric anchor motifs in de novo search (17) and the corresponding motif in the Hocomoco database (30) were also dimeric; (b) two pairs that contained not bHLH motif with not quite clearly assigned respective TF. The juxtaposition of the list of remaining 22 TF pairs and the whole pool of 164 ChIP-seq datasets (see above) brought 80 distinct ChIP-seq datasets (Supplementary Table S3). For TF pairs that respected to an in vitro research we took in analysis all available datasets for both TFs of each pair, for TF pairs that were studied in specific cells/tissues conditions we analyzed only datasets in relatively close conditions.

We estimated the False Positive (FP) rate for each ChIP-seq dataset as the P-value for the ‘Overlap’ or ‘Spacer’ computation flow depending on presumed CE structure (Supplementary Table S3 and (24)). For each TF pair the total estimate of FP rate we computed as the median of FP rates for a respective list of ChIP-seq datasets. The MCOT sensitivity we computed as the True Positive fraction that respected to certain FP rate.

TF-TF interaction data for validation of MCOT predictions

We applied data on physical interactions of proteins from BioGRID (37) and EdgeExpress (38) to test CE predictions for all 117 ChIP-seq datasets of 45 distinct human TFs (Supplementary Table S1). Besides anchor motifs, we employed 396 partner motifs from the Hocomoco database (30, see above). Next, we applied MCOT with the threshold 1E-10 for CE significance for five computation flows. We used the Fisher's exact test to estimate the significance of enrichment of TF-TF interaction for all predicted pairs of anchor-partner TFs. To avoid manipulations with too small counts in Fisher's tests we took in analysis ChIP-seq datasets (a) with anchor TFs possessing at least 25 interactors in a list from the Hocomoco database and (b) with at least 15 predicted CEs in the ‘Any’ computation flow. These criteria retained 52 datasets for 18 TFs.

Implementation

MCOT is implemented in C++ and can run in Linux and Windows platforms. The computation time may vary from several seconds to a few hours depending on the input data size. Supplementary Figure S3 represents the MCOT run time as a function of the total peak number and the mean peak length. We performed these calculations for all 164 ChIP-seq datasets mentioned above.

RESULTS

Basic concepts of MCOT algorithm

CE with an overlap of TF binding sites implies that the motifs satisfy certain sequence constraints. Dealing with these constraints is the main obstacle in identification of CEs with an overlap within a single dataset. The crucial challenge is the construction of a background profile of hits for a one motif to test the hypothesis on the statistical independence of its co-occurrences in DNA with another motif (16). If we fix hits of one motif, than the expected distribution for spacer locations of another motif is uniform and it does not depend on the structure of two motifs (21). Whereas the respective expected distribution for overlap locations of motifs is not uniform and it depends on the structure of two motifs. As far as we know, up to now the modeling of expected distribution of overlaps for two motifs is not considered elsewhere. Hence, we fix a profile for one motif and propose the permutation procedure for a profile of another motif. This procedure preserves the number of hits and their potential to self-overlapping (Figure 2; Materials and Methods, Supplementary Data 1, Text 2). To perform a permutation we partition a profile onto (a) distinct clusters that contain sole or overlapped hits and (b) spacers between the clusters. Besides the hits number, the resulting background profile preserves a clumping pattern of the foreground profile, in particular (a) distributions of the number of hits in clusters and of cluster lengths and (b) the distribution of spacer lengths.

Additionally, we apply the systematic set of five threshold ranges for motifs recognition. Thus, for a potential CE we consider balanced and imbalanced combinations of motifs conservation. This analysis of fine CE structure may facilitate an explanation of mechanism for particular CE action.

With these innovations we developed MCOT, a universal tool for motifs co-occurrence study, that identifies in a single ChIP-seq dataset CEs of various structure—homotypic (anchor-anchor) and heterotypic (anchor-partner); with different ratios of motifs conservation (Figure 1A), Inverted, Everted, or Direct (Figure 1B); with a spacer or with full/partial overlap of motifs (Figure 1C). The term ‘anchor’ refers to the immunoprecipitated TF in a ChIP-seq experiment.

General description of MCOT algorithm

As an input data and parameters, MCOT requires (Figure 3): DNA sequences of a ChIP-seq dataset (peaks); the frequency matrix for an anchor motif; the frequency matrix for a partner motif or assignment of the library with motifs of potential partner TFs; the range of spacer lengths. In this work, we used human/mouse motifs libraries from Hocomoco database (30).

First, MCOT maps anchor and partner motifs in peaks taking into account five threshold ranges for each motif (Figure 1A). Second, MCOT starts five parallel computation flows to identify five types of CEs: Any (spacer or overlap), Spacer (no overlap), Overlap, and Full/Partial (overlaps) (Figure 1C). Third, for each peak, MCOT performs the permutation procedure and generates background hits distributions for both motifs (Figure 2). Finally, for each computation flow and each combination of motifs conservation, MCOT compares observed and expected frequencies of CEs and estimates the significance of their enrichment by the Fisher's exact test (see Materials and Methods, Figure 3, 2 × 2 table ‘CE enrichment’).

As an output data, for each anchor-partner pair of motifs MCOT provides (a) detailed statistics of significances for CEs enrichment and their asymmetry (Figure 3, 2 × 2 tables ‘CE enrichment’ and ‘CE asymmetry’), and (b) profiles that show the fraction of peaks with specific mutual orientation/location of motifs (Figure 4). The most common spacer/overlap length(s) for specific structural variant of CEs may be interpreted as it most overrepresented ‘optimal’ length(s).

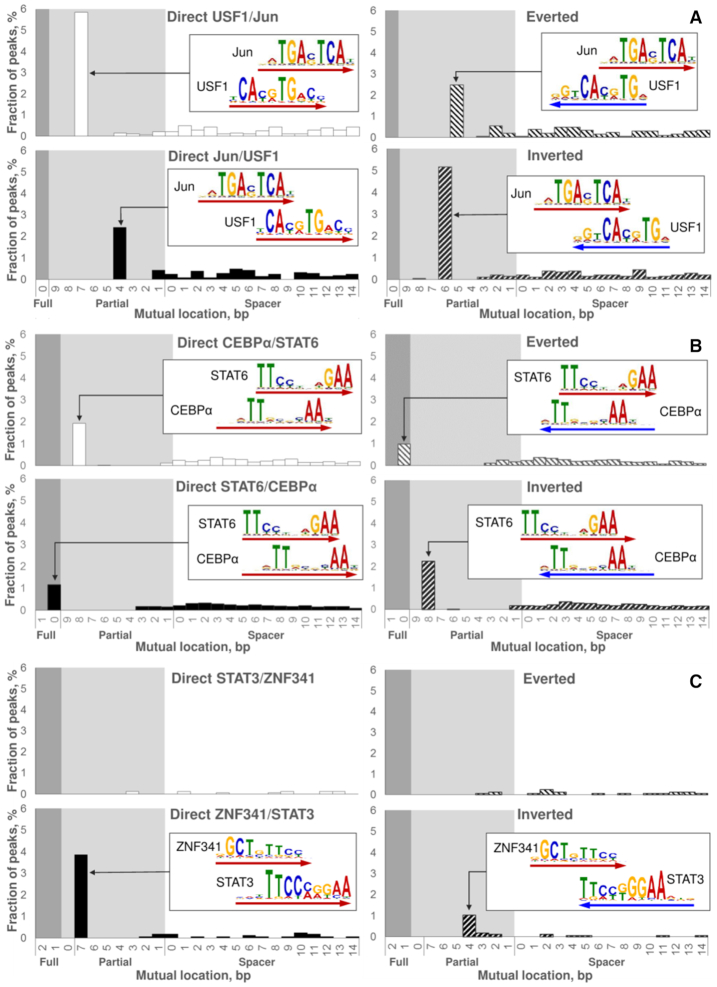
Figure 4.

Examples of predicted CEs. The reciprocal analysis of two ChIP-seq datasets: fine structure of Jun/USF1 CEs (A); novel CEs STAT6/CEBPα (B). Analysis of a single ChIP-seq dataset: novel CEs ZNF341/STAT3 (C). Here we represent the analysis of Jun (A) and STAT6 (B) peaks, the respective reciprocal datasets of USF1 and CEBPα peaks we provided in Supplementary Figures S4 and S8. In reciprocal analyses (A, B) we derived partner motifs from the de novo motif search (17) in a ChIP-seq dataset for the respective TF; analysis of a single ChIP-seq dataset (C) meant extraction of a partner motif from the Hocomoco database (30). In each panel, four charts respect to four mutual orientations of motifs within CEs (Figure 1B), the logo alignment and the arrow point to the most abundant CE variant for each orientation. Axes X denote mutual locations of two motifs (Figure 1C), the ranges of full/partial overlaps and spacers are marked with dark/light grey and white backgrounds. Axes Y denote the fraction of peaks that contains potential CE with a specific mutual location and orientation.

An overlap of significantly similar motifs may imply a false positive prediction. To discriminate respective CEs in output data, MCOT provides a motifs similarity filter that estimates the significance of match between anchor and partner motifs (see Materials and Methods; Supplementary Data 1, Text 1).

Reciprocal analysis of two ChIP-seq datasets

In this section, we verify MCOT capability to predict CEs for known cases of combinatorial TF action. Additionally, we compare MCOT results to the other tools that allow motifs overlaps. To show the robustness, we perform a reciprocal analysis of two ChIP-seq datasets (one for each partner TF), obtained for the same cell/tissue type and conditions. Below are the examples of MCOT application to ChIP-seq pairs, which have already been analyzed for combinatorial binding of the corresponding TFs previously. In this analysis, we retrieved both TF binding motifs by de novo motif search (17) in the corresponding peak dataset. Hence, we applied MCOT with the same pair of motifs to both ChIP-seq datasets.

MCOT comparison to GEM

Previously, a comprehensive pairwise analysis of 214 ENCODE ChIP-seq experiments for 63 human TFs with GEM tool identified 390 potential CEs (13). Among them the Jun/USF1 was the top-ranked for K562 cells. The authors identified one structural CE variant, Direct Jun/USF1 with an overlap of motifs. MCOT analysis of respective ChIP-seq datasets (GSM935411 and GSM803441, replicate 1) confirmed significant Jun/USF1 CEs with an overlap (P-value < 3E–22) in Jun peaks. Moreover, it distinguished four structural CE types instead of one reported earlier (13) (Figure 4A). MCOT found Direct USF1/Jun, Inverted, Everted and Direct Jun/USF1 CEs with overlaps of 7, 6, 5 and 4 bp in 5.8%, 5.2%, 2.5% and 2.4% of peaks, respectively. The reciprocal MCOT analysis with the USF1 anchor confirmed these structural types of CEs (Supplementary Figure S4). Overall, MCOT detected Jun/USF1 CEs in about 15.9% and 23.4% of Jun and USF1 peaks. Another CE example, deduced for human H1 embryonic stem cells by (13) and proven with MCOT is RXRA/USF1 (Supplementary Figure S5). The reciprocal analysis of RXRA and USF1 datasets supported Direct RXRA/USF1 and Inverted USF1/RXRA CE variants.

MCOT comparison to TACO

AR/FoxA1 is a well-known example of a cooperative action of two TFs (12,39–41). De novo motif search in AR peaks (40) from ChIP-seq data for prostate cancer cells LNCaP treated with dehydrotestosterone (DHT) for 1 h identified a bipartite motif AR-FoxA1. Bioinformatics analysis of DNAse I hypersensitivity data for the same cell line with the method beyond TACO tool (24) confirmed the enrichment of AR/FoxA1 CE with 4 bp spacer (12). MCOT analysis of AR peaks (40) confirms CEs with spacers below 30 bp (P-value < 2E–7) and detects the most common Direct AR/FoxA1 CE with 4 bp spacer (2.1% of AR peaks, Supplementary Figure S6A). In addition, MCOT identifies other potential CE variants (e.g. Everted with 7 bp spacer, 1.5%). Reciprocal analysis of FoxA1 ChIP-seq dataset (40) confirmed the significant AR/FoxA1 CEs with spacers (P-value < 4E–3) and overlaps (P-value < 6E–5), the most common was Everted CE with overlap of 3 bp (1.5% of peaks, Supplementary Figure S6B).

Novel CEs predictions with MCOT

Next, we performed CEs search for TF pairs with only proven genomic colocalization. We checked potential CEs formed by STAT6, activated in course of alternative polarization of macrophages with interleukin-4 (IL-4) treatment, and macrophage lineage determining TFs CEBPα, JUNB, IRF8 and SPI1 (42). All ChIP-seq datasets were generated in mouse bone marrow-derived macrophage (BMDM) cells treated with IL-4 for 1 h (43). CEs with spacers formed by STAT6 anchor (GSM2845664) and all four partner motifs were significant (Supplementary Figure S7). CEs with an overlap of motifs were significant for CEBPα, IRF8 and SPI1. Overall, STAT6/SPI1 and STAT6/CEBPα were the most significant. However, SPI1 and STAT6 motifs have shown moderate similarity (P-value ∼ 0.051); therefore, we kept only CEBPα (GSM2845732) for further analysis. There are four most abundant structural variants of STAT6/CEBPα CEs (Figure 4B): Inverted, Direct CEBPα/STAT6, Direct STAT6/CEBPα and Everted variants had overlaps of 8, 8, 10 and 10 bp; they were mapped in 2.2%, 1.9%, 1.2% and 1.0% of STAT6 peaks, respectively. Recognition of STAT6/CEBPα CEs for the anchor CEBPα motif confirmed the enrichment of these four CE variants (Supplementary Figure S8). Overall, MCOT detects STAT6/CEBPα CEs in about 6.3% and 4% of STAT6 and CEBPα peaks (Figures 4B, Supplementary Figure S8). Previously, it was shown that CEBPβ cooperated with STAT6 for induction of the human Iϵ promoter (44), thus CEs STAT6/CEBPα are promising for further analysis. Supplementary Figure S9 shows another example of novel CEs prediction for TFs RELA and IKZF1 with known genomic colocalization; previous analysis (45) have shown the strong enrichment of sequence GGAA that was common for both motifs. Respective two datasets were performed for mouse BMDM cells with lipopolysaccharide (LPS) treatment (45). MCOT analysis proved the significance of Direct RELA/IKZF1 and Everted CEs in Any, Full, Partial and Overlap computation flows in the reciprocal analysis; MCOT reported the highest significance for full overlaps of motifs. In total, about 16.5% and 15.6% of RELA and IKZF1 peaks contained two major structural types of CEs.

A single ChIP-seq dataset analysis

Since MCOT results received with a reciprocal analysis of ChIP-seq datasets for Jun/USF1, RXRA/USF1, AR/FoxA1, STAT6/CEBPα and RELA/IKZF1 are consistent; we consider that a single dataset is sufficient for MCOT to produce relevant predictions of CEs with both overlaps and spacers. Moreover, MCOT analysis confirms and substantially supplements the previous knowledge on the overrepresentation of CEs. It extends information retrieved by TACO and GEM tools, providing higher resolution results wherein it requires a single dataset to run. In this section, we illustrate MCOT application for CEs recognition in a single ChIP-seq dataset, i.e. without requirement of a priori knowledge about potential partners. To perform massive analyses we used the Hocomoco database (30). The lists of human/mouse potential partners comprised 396/353 motifs (see Materials and Methods). For each anchor motif, MCOT tested one homotypic (anchor-anchor) and a multitude of heterotypic CEs (anchor-partner).

Newly studied TF: ZNF341 case study

ZNF341 is a recently characterized regulator of immune homeostasis in human (46,47). The ChIP-seq data on ZNF341 (GSE107719) were performed for Epstein-Barr virus transformed lymphoblastic B cell lines. MCOT identifies 19 CEs with an overlap and two CEs with a spacer (Supplementary Table S4, P-value < 0.05/25/396 ≈ 5E–6). The hierarchical classification of TFs (48) substantially supported interpretation of predicted partner TFs. Among top-scoring partner TFs that respected to CEs with overlaps of motifs we found the known regulator of immune homeostasis STAT3. Recently, ZNF341 has been detected as a transcriptional regulator of STAT3 (46,47). Thus, the prediction of ZNF341/STAT3 CEs is important for further elucidation of STAT3-mediated mechanisms of immune homeostasis. MCOT detected two major structural variants of ZNF341/STAT3 CEs in ∼4.9% of ZNF341 peaks (Figure 4C), P-value < 3E–11 (computation flow ‘Overlap’). Overall, ZNF341 regulation of STAT3 gene (45) with ability to simultaneously form the ZNF341/STAT3 CEs can form a highly interconnected regulatory circuit for these two TFs. Only two CG-rich partner motifs SALL4 and ZIC2 respected to CEs with a spacer. This is in good accordance with previous studies (46,47) where the extended ZNF-like motif contained G-rich flanking sequence.

Well studied TF: RELA case study

TF NF-κB is a key player in inflammation, cancer development and progression, thus being extensively studied (49). In order to investigate still largely unexplored responsiveness to inflammatory signals of the alternatively polarized macrophages at the transcriptional level, ChIP-seq data (GSM2845659) for LPS-activated subunit of NF-κB, RELA (p65), were obtained (43) for mouse BMDM cells, treated with IL-4 and further with LPS. For RELA dataset MCOT identifies 39 CEs with an overlap and 14 CEs with a spacer (Supplementary Table S5, P-value < 5E–6). The first rank among TFs that respect to CEs with an overlap we found for IKZF1 (Ikaros). Recent study (45) confirmed that Ikaros is expressed in macrophages and may cooperate with RELA participating in the complex transcriptional response to pathogen challenge. Among other partner motifs that are involved in CEs with overlaps, we distinguished those for TEF-1 (TEAD1/2/4), HSF (HSF1/2), STAT (STAT3/4/5A/6) and C/EBP (CEBPϵ/δ/α) families. Notably, the top-ranked partner TFs are IL-4-activated STAT6 and lineage-determining macrophage TF CEBPα (P-value < 8E–13 and P-value < 2E–9). Both TFs are known to act in conjunction with NF-κB family members (44,50). Moreover, the genomic colocalization of STAT6 and RELA peaks were detected in the original work (43). RELA/STAT6 CE variants with 5–10 bp overlaps of motifs we found in 12.7% of RELA peaks (Supplementary Figure S10A). 8.2% of RELA peaks contained RELA/CEBPα CEs with 6–9 bp overlaps of motifs. Additionally, ∼6% of RELA peaks contained CEs with either a small overlap (1–2 bp) or short spacer (3 bp or less) (Supplementary Figure S10B). A number of top-ranked partner TFs that respect to CEs with a spacer (Supplementary Table S5) include TFs of above mentioned families C/EBP and STAT and other to which macrophage lineage determining TFs belong: ETS factors SPIB and SPI1, interferon-regulatory factors IRF4/8, and bZIP factors JUN and FOS, which are the subunits of AP-1 (42). AP-1 has been recently distinguished to facilitate RELA chromatin association by their cooperativity in HeLa and MEF cells (51).

Both in case of newly (ZNF341) and well studied (RELA) TFs MCOT is able to retrieve relevant predictions of CEs of any structure. These predictions extend our knowledge on the mechanisms of TFs functioning. Taken together, the potential of MCOT to identify all possible CEs within a single ChIP-seq dataset and without prespecified TF partners makes it a beneficial tool for the routine studies of gene regulatory regions.

Benchmark ChIP-seq data collection

To test MCOT predictions, we collected 117 human and 47 mouse ChIP-seq datasets for 57 distinct TFs (Supplementary Table S1). We retrieved potential partner motifs from the Hocomoco database (30) as described above. The whole lists of potential CEs for 164 mammalian ChIP-seq datasets are available in Supplementary Tables S6–S9. Such elements depending on the composition of binding TFs and their affinity to distinct sites as well as the specificity of TF–TF and TF–DNA interactions may be either cooperative or competitive. The former implies that two TFs bind simultaneously and potentiate each other, while the latter means exclusive binding of two TFs (5). Supplementary Figure S11 compares predicted CEs with overlaps of motifs and those with spacers for subgroup of 37 human ChIP-seq datasets.

MCOT outperforms existing CE prediction methods

To compare MCOT predictive efficiency with previously developed tools we applied the benchmark dataset of 22 TF pairs that were compiled earlier for TACO tool verification (24, see Supplementary Table S3 and Materials and Methods). For these TF pairs we extracted 80 respective ChIP-seq datasets (Supplementary Table S3) from the total pool of ChIP-seq data (Supplementary Table S1, Materials and Methods). Examples of output MCOT profiles that show the percentage of peaks with specific mutual orientation/location of motifs in TF pairs of the benchmark dataset are listed in Supplementary Figure S12. For 21, 20 and 18 out of 22 TF pairs (95%, 91% and 82%) FP rates were below 0.05, 3E–3 and 4E–4 (Supplementary Table S3, Supplementary Figure S13). Earlier, Jankowski et al. (24) proved that for the same benchmark dataset (Supplementary Table S3) TACO predicted ∼80% TF pairs with FP rate ∼0.1, while SpaMo (21) and iTFs (22) performed substantially worse. We may conclude that MCOT revealed the best performance among available CE prediction tools.

Validation of CE predictions by TF–TF interactions

To validate the predicted CEs we checked the hypothesis that they respected to known protein-protein interactions between anchor and partner TFs. We compiled the subset of 52 human ChIP-seq datasets for 18 distinct TFs and performed the Fisher's exact test that checked the enrichment protein-protein interaction between anchor and partner TFs respecting to predicted CEs for five computation flows (see Materials and Methods). Figure 5 illustrates that ∼65% of ChIP-seq datasets and 63% of anchor TFs respect to the significant enrichment (P-value < 0.01) of known protein-protein interactions of anchor and partner TFs respecting to predicted CEs (P-value < 1E–10). Supplementary Table S10 shows significances of the Fisher's exact test for five computation flows and 52 ChIP-seq datasets.

Figure 5.

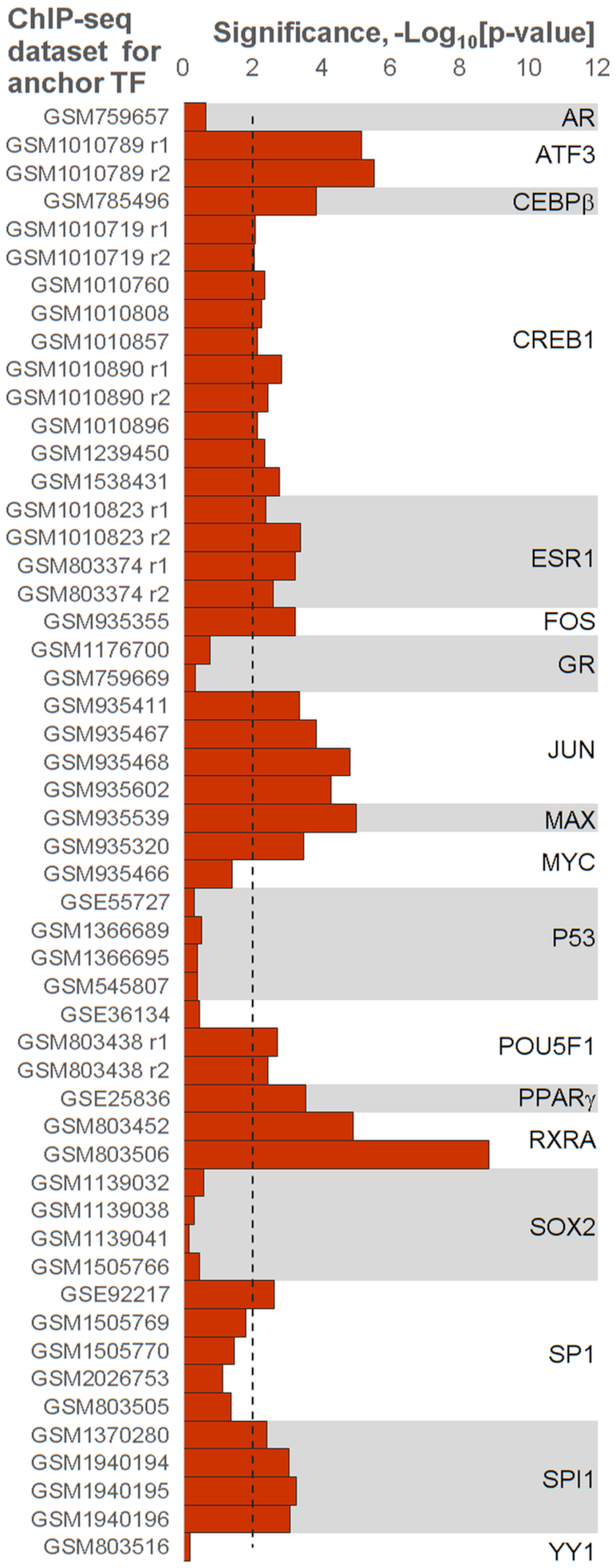
Confirmation of predicted CEs with known protein-protein interactions between anchor and partner TFs. Axis X denotes the significance of the Fisher's exact test that checks the enrichment of known protein-protein interactions among anchor and partner TFs that respect to predicted CEs. Axis Y marks ChIP-seq datasets for anchor TFs. The dashed line denotes the Bonferroni-corrected threshold, P-value < 0.01. This figure provides the experimental support for MCOT predictions.

Massive analysis of abundance and asymmetry of CEs

To annotate the potential CEs with MCOT more thoroughly we demonstrate below how testing of various stringencies for anchor and partner motifs may further clarify the CE structure. MCOT applies five conservation levels for each motif to identify CEs (see Materials and Methods). Consequently, we may estimate the enrichment of CEs (a) with more conservative anchor or partner motifs and (b) with their similar conservation. We composed 5 × 5 tables for all combinations of motifs conservation (Figure 1A) and estimated overall significances for CEs with dominating anchor or partner motifs or for those with similar conservation (see Materials and Methods). Generally, anchor motifs of CEs were more conservative than partner motifs; this imbalance was very substantial for anchor pioneer TFs (52) FoxA1, SPI1 and CEBPα (Supplementary Figure S14).

For a certain anchor-partner pair, the most abundant predicted CEs may respect to a balanced stringency of anchor and partner motifs, or one of the motifs tends to dominate. To test which possibility happens, we applied the Fisher's exact test to check whether asymmetry of motifs conservation in predicted CEs was significant (see Materials and Methods). Mentioned above datasets for TFs RELA and IKZF1 with proven genomic colocalization (45) illustrate the robustness of prediction of asymmetry within CEs. Figure 6 shows the 5 × 5 tables for RELA/IKZF1 CEs with the anchors RELA and IKZF1 for ‘Full’ computation flow. For these anchors the asymmetry toward RELA motif is highly significant, P-value < 2E-9 and P-value < 6E–11. The application of the Bonferroni-corrected threshold P-value < 0.0033 (see Materials and Methods) revealed moderate significances of asymmetry toward RELA motif P-value < 3E–3 and P-value < 2E–3 in ‘Any’ and ‘Partial’ computation flows for IKZF1 and RELA anchors, respectively. Thus, irrespective to selection of anchor motif, we revealed a profound asymmetry in conservation of the motifs with substantially more conservative RELA motif.

Figure 6.

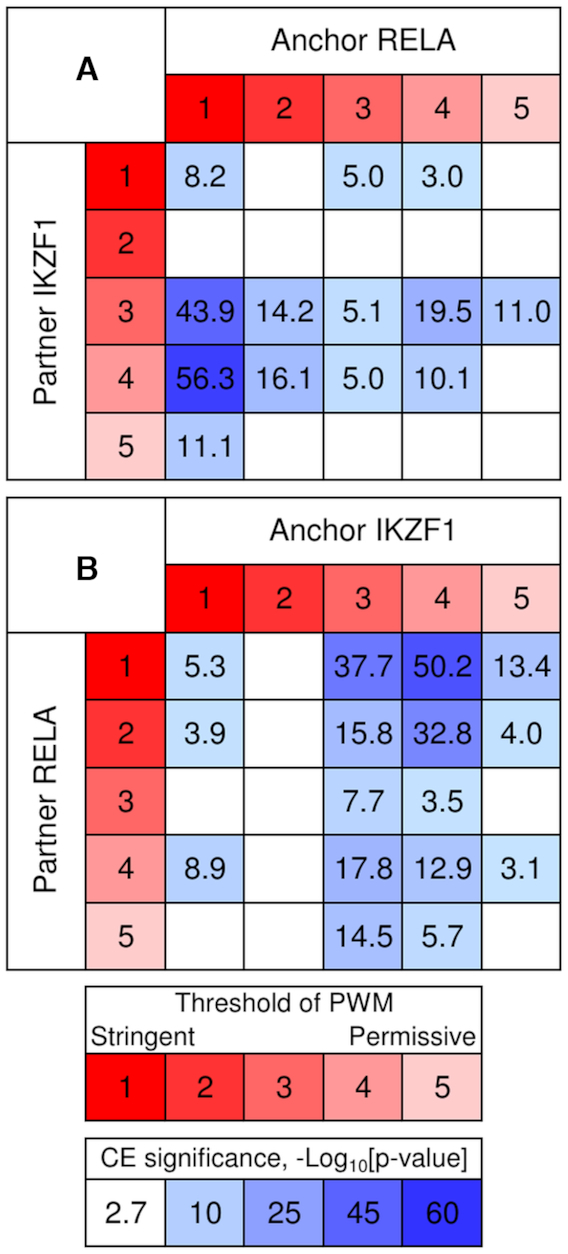
Asymmetry of motifs conservation within predicted CEs RELA/IKZF1. The significance of CEs with an overlap of RELA and IKZF1 motifs with anchor RELA (A) and IKZF1 (B) as a function of motif conservation. Red/rose colors denote variation of stringency from the most conservative (red, 1) to the most permissive (rose, 5). Light/dark blue colors mark the significance of CE (P-value < 0.002) (see Materials and Methods). This figure shows that irrespective to the selection of anchor motif in CEs RELA/IKZF1 the motif RELA is more conserved than IKZF1 motif.

We applied Fisher's exact test to perform the massive analysis of asymmetry between anchor and partner motifs of predicted CEs (see Materials and Methods). We used thresholds P-value < 5E-6 and P-value < 0.0033 for significances of CEs and asymmetry within CEs. The abundance of CEs with overlaps of motifs more than twice exceeds that of CEs with spacers (7292 versus 2956, Figure 7). We found that 41.2% of all predicted CEs with overlaps have one participant significantly more conservative than another (29.5%/11.6% had more conserved anchor/partner motifs); while for CEs with spacers respective fractions are lower 32.2% (22.1%/9.1%) (Figure 7). Since short spacers may imply an overlap of two TF-DNA complexes, we repeated calculations for longer spacers and confirmed that the fraction of asymmetrical CEs fell until 29.4%; on the contrary, compared to all overlaps, full overlaps of motifs increased this fraction up to 46.4%, while partial overlaps decreased it until 37.0% (Supplementary Figure S15). The lists of potential CEs with significant asymmetry of motifs for 164 mammalian ChIP-seq datasets are available in Supplementary Tables S11–S14. Thus, the analysis of motifs conservation asymmetry provides a deeper insight into mechanism of collaborative action of TFs.

Figure 7.

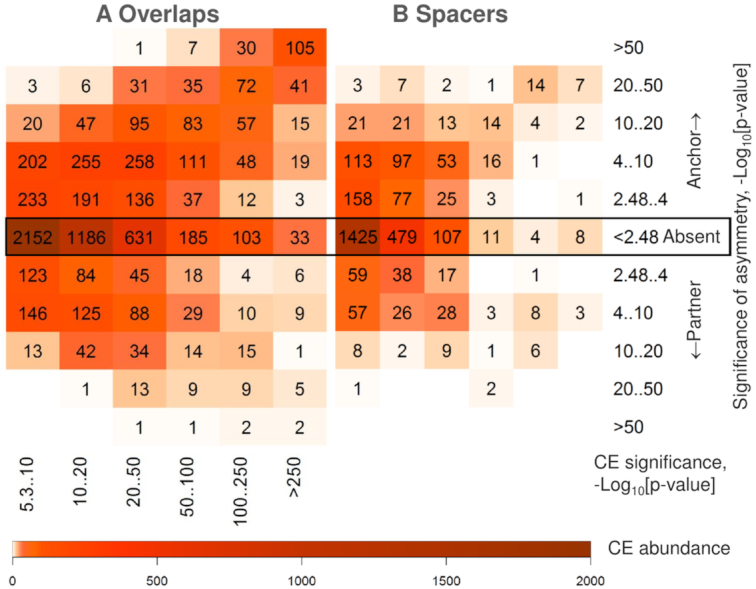
Abundance and asymmetry of predicted CEs with overlaps of motifs and with spacers. Abundance of heterotypic CEs with overlaps of motifs (A) and those with spacers of length below 30 bp (B) as a function of the CE significance (axes X) and the significance of asymmetry in conservation between anchor and partner motifs (axes Y), see Materials and Methods. The color keys show the CE abundance for 117/47 human/mouse ChIP-seq datasets (see Supplementary Table S1). CEs consisted of an anchor motif and either of 396/353 partner motifs from the Hocomoco human/mouse libraries (30), see Materials and Methods. CEs without the significant match of anchor and partner motifs (P-value > 0.05) were kept in analysis. This figure shows that predicted CEs with overlaps compared to those with spacers are more abundant and more often comprise two motifs of various conservation.

DISCUSSION

Due to their structural and functional simplicity, CEs represent a convenient model to study complex mechanisms of gene expression regulation provided by the crosstalk of multiple signaling pathways (5,8–10). Therefore, a comprehensive search and structural characterization of such elements is a tempting idea. However, due to an extremely high regulatory potential of DNA (53) in silico recognition of CEs in complete genome sequences is still a challenging problem in computational biology.

CEs prediction has been greatly simplified by recruiting ChIP-seq datasets. This allows performing CEs search in short genomic regions (100–1000 bp) where TF binding takes place in vivo. Colocalization analyses of TF binding calls derived from distinct ChIP-seq data sets represent a popular group of approaches that give an idea about functional interplay of TFs (16). If the binding events are predicted with a high spatial resolution (e.g. using the motifs mapping), such analyses allow a prediction and a detailed structural characterization of the corresponding СЕs (Table 1) (13). However, in view of a multiplicity of TFs in higher eukaryotes (e.g. over 1600 TFs in human, (54) and considering the molecular machinery significantly rearranges in a cell/tissue/organ/stage-specific manner, checking all the pairs under different conditions requires myriads of ChIP-seq experiments (26). Therefore, a comprehensive in silico screening procedure capable of the maximum information retrieval from a single ChIP-seq data set would be indispensable both to guide co-occurrence studies, and to design SELEX or ChIP-reChIP-seq experiments.

The major challenge for development of such screening procedures is due to the limitations of the accessible null models. For example, the available tools that apply analytical tests based on general null models, e.g. SpaMo (21) and iTFs (22) fail to predict CEs with an overlap of TF binding motifs being thereby insufficiently informative. The use of analytical tests with specifically selected background regions to estimate a null model (e.g. TACO (12,24) allows a comprehensive search of CEs but brings us back to the requirement of multiple well-ordered datasets to be prepared. Thus, a simulation of expected distribution appears a good alternative. To our knowledge, this idea has not been implemented for motifs co-occurrence analyses so far.

To address this issue, we worked out an accurate permutation procedure that (a) provided an independent mutual positioning of the hits for a pair of motifs, wherein (b) considered the sequence constraints required for the motifs overlapping (Figure 2). Moreover, a background profile preserved such important characteristics of the foreground as the number of the motifs hits in each peak and the clustering tendency of hits, thereby providing more realistic significance estimates than a background based on a general permutation procedure would do (16). Using this algorithm to generate a background, we developed the software package MCOT for the comprehensive prediction of CEs in a single ChIP-seq dataset. MCOT provides a universal possibility to search for CEs consisting of both overlapping and non-overlapping motifs in a single ChIP-seq data set, unlike the other published tools (Table 1). Besides, MCOT provides several original capacities (e.g. motifs similarity filter, a convenient classification of CEs structure, flexibility in terms of motifs conservation within a CE and settings for spacer length) that precise the results and simplify their interpretation.

Development of sophisticated background model provides MCOT capacity to substantially complement predictions of spaced motifs of existing tools in a single ChIP-seq dataset, e.g. SpaMo (21). In addition, MCOT successfully predicts the known CEs with an overlap and spacer (e.g. Jun/USF1, AR/FoxA1, Figures 4A, Supplementary Figures S4–S6) that supports relevance of MCOT predictions.

MCOT application to search for new CEs in a single ChIP-seq dataset allowed obtaining intriguing results. For ZNF341 or RELA ChIP-seq datasets MCOT predicts a lot of promising potential CEs (Supplementary Tables S4 and S5), most of them were not revealed yet. We would like to emphasize that MCOT facilitates the studies for poorly studied TFs, because the knowledge about TF’s potential partners proposes the mechanistic insights of its action. MCOT application to the ChIP-seq data for ZNF341, a recently discovered regulator of immune homeostasis (46,47), unveiled a combinatorial interplay of ZNF341 with other immune homeostasis and cell fate TFs. Among them there is an immune rheostat STAT3, which hyperactivation or inactivation results in human disease like immunodeficiency, autoimmunity and cancer (55). STAT3 has been shown being the ZNF341 target (46,47), thus MCOT predicts an existence of feedforward loop, wherein ZNF341 regulates transcription of its partner for cooperative transcriptional regulation of immune defense.

The first ranked partner motif for RELA dataset in the list of overlapping motifs respect to IKZF1 TF (Supplementary Table S4). Recent study (45) demonstrated that RELA and IKZF1 may cooperate in macrophages during response to pathogen challenge, but the co-occurrence of their motifs have been not studied yet.

An interplay between different TFs is crucial for tuning transcriptional regulation during establishment and maintenance of cell phenotypes in metazoans and in response to environment stimuli (1–4). On the genome-wide level, such an interplay is provided by clustering of the corresponding TF binding sites referred to as cis-regulatory modules (CRMs) (56). The results of massive screen for potential CEs within 164 ChIP-seq datasets support the idea of constrained clustering of the regulatory regions with CEs of various structure (11,13). It has been proposed that CEs with an overlap of TF binding motifs are widespread and important from biological point of view (5,8,24).

The massive check of protein-protein interactions (37,38) among participants of predicted CEs have shown that for over 60% of anchor TFs and the same portion of ChIP-seq datasets experimentally proved TF-TF interactions are significantly overrepresented in predicted anchor-partner TF pairs (Figure 5). Hence, the massive analysis of protein-protein interactions between TFs that respect to participants of predicted CEs provides the experimental support for MCOT predictions.

The analysis of motifs conservation within the most significant CEs for two reciprocal ChIP-seq datasets of RELA and IKZF1 have shown that independently of the selection of an anchor motif, RELA motif had more conservative motif than IKZF1 within CE (Figure 6).

MCOT application to 164 ChIP-seq datasets for 57 various TFs have shown that abundance of potential CEs with overlaps of motifs more than twice exceeds that of CEs with spacers (Figures 7). This estimate also is supported by the previous analysis (12). The comparison between asymmetry within CEs with overlaps of motifs and those with spacers allows propose that an overlap more commonly implied a pair of ‘leading’ and ‘guided’ motifs with various conservation (Figure 7). The substantial difference of conservation guarantees the steady mechanics of a step-by-step collaborative regulatory action of multiple TFs on gene expression. The analysis of the most comprehensive collection of 265 manually collected CEs from the TRANSCompel database (57) have shown the significant negative correlation between PWM scores of two motifs within CEs; this significance was absent for a respective permuted data sample (10). Thus, the theoretical analysis of the most comprehensive experimental CE collection supports MCOT massive screen of asymmetry within predicted CEs between anchor and partner motifs. This result confirms that MCOT predictions refer to functional CEs.

CONCLUSIONS

• We have shown that a single ChIP-seq dataset is sufficient for discovering of motifs co-occurrence with a spacer and with an overlap;

• We developed the software package MCOT for the comprehensive prediction of CEs in a single ChIP-seq dataset;

• We validated the MCOT package with experimentally and theoretically proven cases of motifs overlapping derived from the reciprocal analysis of several pairs of two ChIP-seq datasets;

• The massive analysis 52 ChIP-seq datasets for 18 human TFs confirmed that for over 60% of datasets and anchor TFs predicted CEs respected to known protein-protein interactions of anchor and partner TFs;

• The massive analysis of 164 ChIP-seq datasets for 57 mammalian TFs revealed that CEs with overlaps of motifs compared to those with spacers were more than doubled, and had 1.5 fold increase of asymmetric fraction with one motif significantly more conservative than another.

DATA AVAILABILITY

MCOT is implemented in C++ on Linux and Windows platforms and is available in the GitLab repository, https://gitlab.sysbio.cytogen.ru/academiq/mcot-kernel

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Russian Foundation for Basic Research [18-29-13040]; State Budget Project [0324-2019-0040]. Funding for open access charge: Russian Foundation for Basic Research [18-29-13040].

Conflict of interest statement. None declared.