Abstract
Indole-3-carbinol (I3C) is the product of the enzymatic hydrolysis of glucobrassicin in the human body. I3C exhibits diverse bioactivities. It is used as a supplement to enhance the efficiency of some cancer therapies and is available as an over-the-counter dietary supplement described as a potential antioxidant, among other health benefits. Thus, it is important to develop an in-depth understanding of its antioxidant activity. In this study, the hydroxyl radical scavenging of I3C has been investigated in silico under physiologically relevant conditions (aqueous and lipid-mimetic pentyl ethanoate environment) using thermochemical and kinetic calculations. For benchmarking purposes, the results were compared to known experimental data. The overall reaction rate constant of the HO• radical scavenging of I3C in water was found to be 2.30 × 1010 M–1 s–1 and over two times lower in lipid-mimetic pentyl ethanoate solvent at 7.74 × 109 M–1 s–1. The results also highlighted that the HO• radical scavenging follows almost exclusively the radical adduct formation mechanism (>94%) in a lipid mimetic medium, whereas this mechanism contributes about 60% in aqueous environments. I3C is considered a dopamine-like antioxidant, its main function being prevention of oxidative degradation of lipids; our study supports this view.
1. Introduction
Indole-3-carbinol (I3C, Figure 1) is formed by the enzymatic hydrolysis of indole glucosinolates in the human body. I3C is believed to exhibit potentially beneficial biological activities, including regulation of drug metabolizing enzyme systems, anticancer properties with low toxicity, and antioxidant activity.1−7 The latter aspect of the bioactivity of I3C was somewhat neglected against the others. However, oxidative damage is now believed to be a factor in several diseases.8,9 It was shown that ionizing radiation-induced formation of HO• radicals causes the majority (60–70%) of tissue damage in biological systems.10 This radical can react with almost any molecule in its neighborhood by several different mechanisms and at multiple possible positions.11 It is also responsible for most oxidative damage of DNA.12 Thus, the hydroxyl radical scavenging activity of natural products is a crucial aspect of their cancer–preventive activity and hence, it is the emphasis in the evaluation of antioxidant activity.11−17
Figure 1.
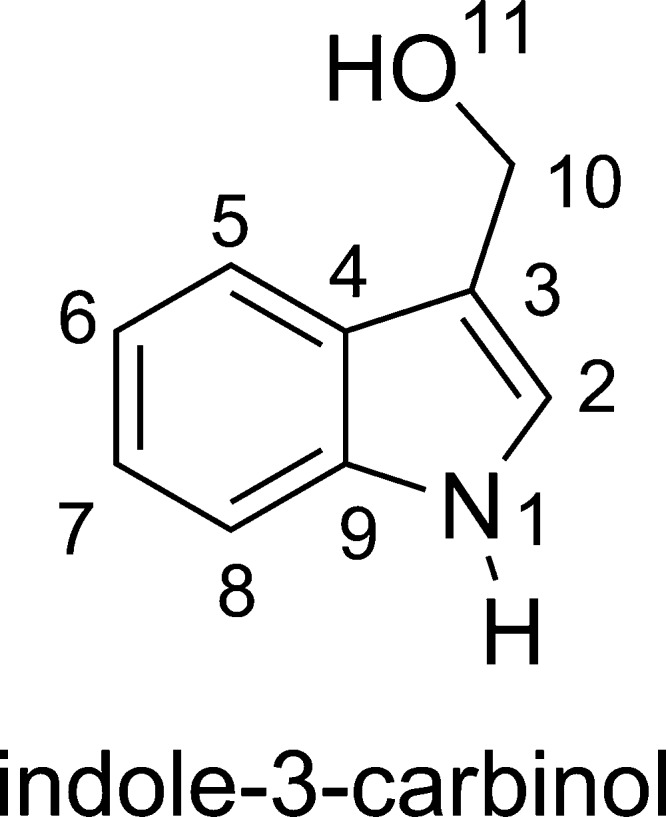
Structure of I3C.
Experimental studies showed that I3C and its derivatives have potential radical scavenging activity with some I3C derivatives exhibiting higher antioxidant activity than vitamin E (i.e., α-tocopherol) in the DPPH model expressed by IC50 values.2 The rate constant for the reaction between I3C and HO• in aqueous solution was experimentally determined to be 1.5 × 1010 M–1 S–1 and attempts were made to reproduce this value in silico.18 The computational works focused on the formation of radical cations and radicals from I3C and thus chose single electron transfer (SET) or/and hydrogen atom transfer (HAT) mechanisms to model the reaction.18,19 However, as the radical adduct formation (RAF) mechanism plays an important role in the HO• scavenging of double C=C bond-containing compounds,13,16,17,20 these studies could not fully explain the experimentally obtained rate constant values. Moreover, the radical scavenging activity of I3C in lipid media has not been investigated.
This study aims to (1) model the HO• scavenging activity of I3C in physiologically relevant environments following three main antioxidant mechanisms (HAT, SET, and RAF) by using thermodynamic calculations; (2) evaluate the kinetics of HO• radical scavenging in comparison with experimental values; and (3) in light of the kinetic data, assess the favored antioxidant mechanism of I3C specific to each chemical environment.
2. Results and Discussions
2.1. Acid–Base Equilibria
Antioxidant activities of neutral and ionized compounds can show substantial differences.13,17 To perform calculations on the dominant form under physiological conditions, the protonation states of the acidic moieties need to be determined first. Proton affinities underpin pKa, and therefore these were calculated. As shown in Table S1 (Supplementary Information), the lowest PA value was observed at the N1–H bond. Thus, the acid–base equilibrium of I3C was calculated for this group.21−23 The pKa was calculated by using the model shown in (1), following the literature.24 The value of pKa is defined by eq 2.22,24,25
| 1 |
| 2 |
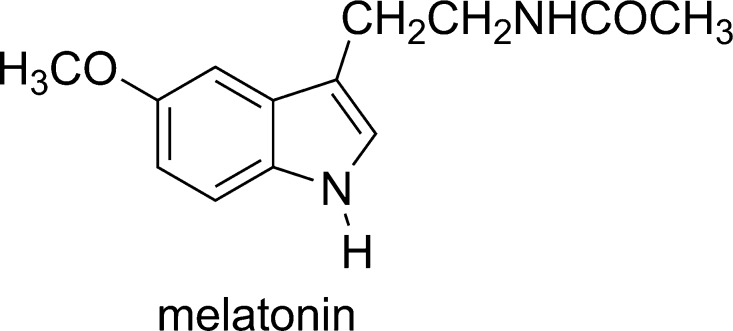
where the HRef is melatonin (Figure 2) with the experimental pKa (N–H) = 12.3.26 The calculated pKa value in this work is 10.73. Consistently, I3C was modeled in its neutral form due to the low ability of deprotonation at physiological pH (7.40), where neutral I3C is the main form (99.95%) of this compound. Thus, the sequential proton loss electron transfer27,28 was not considered in this study.
Figure 2.
The reference molecule (HRef) for calculating pKa.
The path and environment-specific reactivities of I3C toward HO• radicals in polar (water) and nonpolar (pentyl ethanoate) environments via the HAT, SET, and RAF mechanisms were considered according to the following reactions
2.2. Thermochemical Evaluation
Bond dissociation energies (BDEs) and ionization energies (IEs) of I3C were calculated, and the results are shown in Table S1, Supporting Information. It was showed that the lowest BDE value was observed at the C10–H bond with 85.0 and 86.9 kcal/mol in the aqueous and lipid media, respectively. BDE values for N1–H and O11–H are higher at 91.7 and 101.3 kcal/mol, respectively, in water, whereas 93.6 and 103.9 kcal/mol, respectively, in the nonpolar medium. These values for the other C(2–8)–H bonds are considerably higher in the range of 112.8–122.9 kcal/mol. At the same time, the SET occurs more easily in the water than in the pentyl ethanoate solvent (IE = 105.3 and 129.8 kcal/mol, in the polar and nonpolar solvents, respectively, Table S1, Supporting Information). Thus, the radical scavenging of I3C following the HAT mechanism is defined by the C10–H, O11–H, and N1–H bonds.
The Gibbs free energies (ΔG°) of the reaction between I3C and HO• radicals following the SET, HAT, and RAF pathways were computed and are shown in Table 1. It is important to point out that the reactions of I3C and the HO• radical are spontaneous (ΔG° < 0) in most cases, apart from the SET mechanism (ΔG° = 43.0 kcal/mol) in nonpolar solvent, the HAT mechanism in the C2–H bond (ΔG° = 1.3 and 1.9 kcal/mol in polar and non-polar media, respectively), and the RAF mechanism in the C4 and C9 positions in all of the studied media. It was found that for the HO• radical scavenging, the HAT mechanism decides the reaction rate at the X–H (X = C10, O11, N1) bonds in water as well as pentyl ethanoate solvents with low ΔG° values (−13.6 to −35.1 kcal/mol), whereas the RAF mechanism occurs at the C2, C3, C5, and C8 positions with ΔG° values in the range of −11.6 to −19.6 kcal/mol). Reactions with positive ΔG° value (i.e., nonspontaneous reactions) normally have a nonzero but still very little contribution to the overall rate constants;,13 thus in this study, only the spontaneous HO• radical scavenging pathways (negative ΔG° values) were used to compute the overall reaction rate constant (koverall) for the HO• scavenging of I3C.
Table 1. Calculated ΔG° of the Reaction between I3C and the HO• Radical in the Studied Solvents (in kcal/mol).
| |
Solvents |
||
|---|---|---|---|
| mechanism | water | pentyl ethanoate | |
| SET | –0.5 | 46.5 | |
| HAT | N1 | –28.5 | –24.5 |
| O11 | –13.6 | –14.5 | |
| C2 | 1.3 | 1.9 | |
| C5 | –7.9 | –4.9 | |
| C6 | –7.4 | –5.3 | |
| C7 | –7.4 | –5.3 | |
| C8 | –6.4 | –4.7 | |
| C10 | –35.1 | –31.2 | |
| RAF | C2 | –19.6 | –19.5 |
| C3 | –12.4 | –11.7 | |
| C4 | 7.9 | 6.4 | |
| C5 | –12.2 | –12.4 | |
| C6 | –6.0 | –5.1 | |
| C7 | –8.5 | –7.9 | |
| C8 | –11.6 | –11.7 | |
| C9 | 1.2 | 1.1 | |
2.3. Kinetic Study
Thermodynamic spontaneity does not guarantee that a reaction would proceed with an appreciable rate; therefore, activity is assessed based on kinetics.29 The rate constants of the hydroxyl radical scavenging reactions following the three main pathways (SET, HAT, RAF) in the studied environments were calculated, and the results are presented in Table 2. The koverall in water is 2.30 × 1010 M–1 s–1, just under three times higher than in the pentyl ethanoate solvent (7.74 × 109 M–1 s–1). The rate constant calculated for water is in good agreement with the experimental value (kexp = 1.50 × 1010 M–1 s–1).18 Antioxidant activity is dominated in both cases by the RAF mechanism, > 94% in lipidic and about 60% in aqueous environment; in the latter case, the SET mechanism also contributes ∼33% (the nuclear reorganization energy: λ = 5.3 kcal/mol, kD = 8.00 × 109 M–1 s–1, kapp = 7.70 × 109 M–1 s–1) to the overall rate constant. However, the SET mechanism has no contributions in the overall rate constant in the nonpolar environment with the highest ΔG⧧ (112.3 kcal/mol). These results suggest that RAF is the main pathway for the hydroxyl radical scavenging of antioxidant activity of I3C, also considering the activity of indolyl radicals and radical cations.18,30−32 It is worth noticing that the reactions between C6(7,8) with OH radical following the RAF mechanism have considerable contributions (∼30%) in the overall rate constant in the polar solvent, whereas these contributions in the nonpolar environment are minor (∼8%). In contrast, the RAF reaction of C5 + OH in the lipid environment has lower TS energy and ΔG⧧ values (Table 2) compared to these figures for the rest of the carbon atoms of the aromatic ring (C6, C7, and C8), resulting in high rate constants for that reaction (kapp (C5–OH-RAF) = 2.10 × 109 M–1 s–1) with a 27.1% contribution to the overall rate constant. On the other hand, the HAT mechanism only plays a minor role in the hydroxyl radical scavenging of I3C (∼3 and ∼4% contributions in the overall rate constant in the polar and nonpolar media, respectively). The results explain why is I3C a good antioxidant2,33 despite the high BDE (X–H) (X = N, C, O) values (85.0–122.9 kcal/mol, Table 1). Comparing with typical antioxidants such as Trolox (2.78 × 1010 M–1 s–1),13 glutathione (7.68 × 109 M–1 s–1),24 caffeine (2.15 × 109 M–1 s–1),14 edaravone (1.35 × 1010 M–1 s–1),15 and melatonin (1.85 × 1010 M–1 s–1)16 in aqueous media, the reaction is faster than most and only slightly slower than that of Trolox (1.3 times). In a lipid environment, I3C can be considered one of the most active antioxidants, with an activity comparable to dopamine (1.75 × 1010 M–1 s–1).17
Table 2. Gibbs Free Energies of Activation (ΔG⧧, kcal/mol), Tunneling Corrections (κ), Rate Constants (keck and kapp, M–1 s–1), and Branching Ratios (Γ, %) of the I3C-Oxidation by HO• Radicals in the Studied Solvents.
| |
Water |
pentyl ethanoate |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| mechanism | ΔG⧧ | κ | keck | kapp | Γ | ΔG⧧ | κ | keck | kapp | Γ | |
| SET | 2.0 | 5.3a | 2.20 × 1011 | 7.70 × 109 | 33.5 | 112.3 | 6.2a | ∼0.0 | ∼0.0 | ∼0.0 | |
| HAT | O11 | 7.4 | 17.1 | 3.97 × 108 | 3.48 × 108 | 1.5 | 8.3 | 20.0 | 1.10 × 108 | 1.00 × 108 | 1.3 |
| N1 | 7.9 | 16.8 | 1.68 × 108 | 1.58 × 108 | 0.7 | 9.2 | 15.6 | 1.87 × 108 | 1.86 × 107 | 0.2 | |
| C5 | 10.2 | 15.6 | 3.20 × 106 | 3.20 × 106 | ∼0.0 | 13.0 | 11.8 | 2.30 × 104 | 2.30 × 104 | ∼0.0 | |
| C6 | 10.1 | 8.6 | 2.00 × 106 | 2.00 × 106 | ∼0.0 | 11.1 | 7.0 | 3.10 × 105 | 3.10 × 105 | ∼0.0 | |
| C7 | 10.2 | 8.7 | 1.79 × 106 | 1.79 × 106 | ∼0.0 | 11.0 | 6.9 | 3.70 × 105 | 3.70 × 105 | ∼0.0 | |
| C8 | 11.7 | 13.0 | 2.12 × 105 | 2.12 × 105 | ∼0.0 | 12.0 | 8.4 | 7.70 × 104 | 7.70 × 104 | ∼0.0 | |
| C10 | 6.1 | 1.8 | 3.90 × 108 | 3.40 × 108 | 1.5 | 6.7 | 2.9 | 2.30 × 108 | 2.20 × 108 | 2.8 | |
| RAF | C2 | 0.7 | 1.0 | 3.90 × 1012 | 2.70 × 109 | 11.8 | 3.4 | 1.0 | 2.20 × 1010 | 2.40 × 109 | 31.0 |
| C3 | 0.7 | 1.0 | 4.00 × 1012 | 2.70 × 109 | 11.8 | 3.5 | 1.0 | 1.70 × 1010 | 2.30 × 109 | 29.7 | |
| C5 | 3.9 | 1.2 | 2.10 × 1010 | 2.40 × 109 | 10.5 | 3.9 | 1.0 | 9.40 × 109 | 2.10 × 109 | 27.1 | |
| C6 | 4.4 | 1.1 | 8.20 × 109 | 2.00 × 109 | 8.7 | 7.8 | 1.1 | 1.30 × 107 | 1.30 × 107 | 0.2 | |
| C7 | 4.0 | 1.1 | 1.70 × 1010 | 2.30 × 109 | 10.0 | 7.1 | 1.1 | 4.30 × 107 | 4.20 × 107 | 0.5 | |
| C8 | 3.9 | 1.1 | 1.70 × 1010 | 2.30 × 109 | 10.0 | 5.5 | 1.1 | 7.00 × 108 | 5.50 × 108 | 7.1 | |
| koverall | 2.30 × 1010 | 7.74 × 109 | |||||||||
The nuclear reorganization energy (λ).
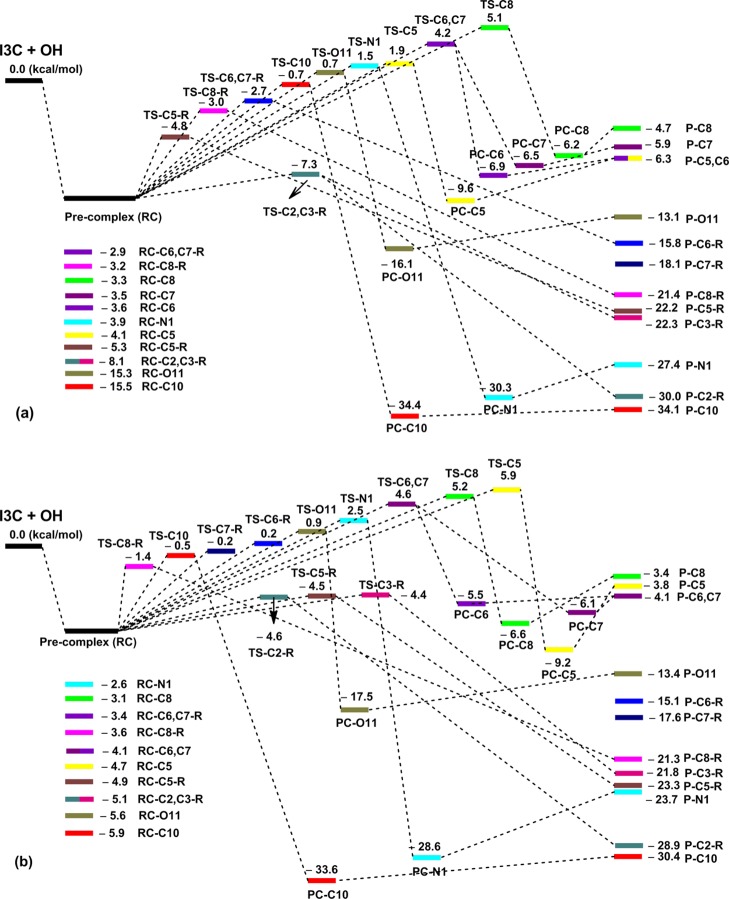
Study of the potential energy surfaces (Figure 3) indicated that there was a correlation between the relative energies (ΔH°) of the transition states and the rate constants. The lowest transition-state TS energies were observed for the formation of TS-C2(C3)–OH-RAF at −7.3 and −4.6 kcal/mol (relative to the separated reactants) in the aqueous and lipid media, respectively. These are the same moieties that yielded the highest values of rate constants for the RAF mechanism (kapp (C2–OH) = 2.70 × 109 and 2.40 × 109 M–1 s–1 in water and pentyl ethanoate, respectively, whereas the diffusion-limited rate constants are kD = 2.7 × 109 M–1 s–1 in the studied environments). The highest TS energies were observed for the formation of TS-C8–OH and TS-C5–OH in polar and nonpolar solvents, respectively. These reactions have the lowest rate constants (kTS-C8–OH = 2.12 × 105 M–1 s–1, kTS-C5–OH = 2.30 × 104 M–1 s–1) and contribute very little in the Γ (∼0%). It was found that the tunneling corrections (κ) contribute significantly in the rate constants of the HAT mechanism (κ = 1.8–20.0, Table 2), whereas those for the RAF mechanism are only 1.0 and 1.2 in all of the studied media.
Figure 3.
The potential energy surfaces of the reaction between I3C and HO• in water (a) and pentyl ethanoate (b) by the HAT and RAF mechanisms (R) [the y-axis units are the relative energies (ΔH°)].
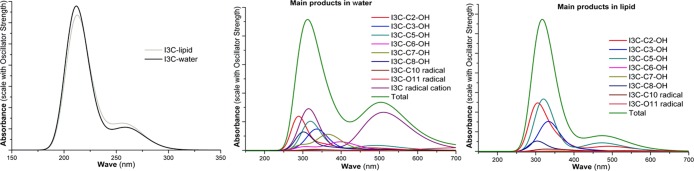
The UV–vis spectra of the starting reactants (I3C), the main products [the products with branching ratios Γ > 1% (Table 2)], and the totals of I3C and HO• radical reactions were computed in aqueous and lipid media and are shown in Figure 4. The totals were achieved by the additivity of the relative abundance and the absorbance of the formed products with their branching ratios. As seen in Figure 4, the starting reagent, I3C has two bands, the stronger at 214 and 217 nm and a weaker one at 263 and 262 nm in aqueous and lipid environments, respectively. These results are in good agreement with the experimental UV–vis spectra of I3C observing bands at 217 and 277 nm.34 This affirms that the UV–vis calculating method is reliable. The observable spectrum, that is, the sum of the spectra of all products (total—Figure 4) has two bands, the stronger at 312 nm and the weaker at 504 nm in aqueous medium. This is also in good agreement with the reported experimental spectra (peaks at 310 and 530 nm) by the reaction of I3C and HO• radicals at pH 7.4 in aqueous solution.18 This agreement confirms that the calculated results are correct and the main products of the hydroxyl radical scavenging of I3C are I3C–C–OH-RAFs of C2–C8 (∼60%) and I3C+• (33.5%). Thus, the RAF mechanism plays a deciding role in the HO• radical scavenging of I3C in water. For the lipid environment, the main products are formed by the RAF mechanism, that is I3C–C(2,3,5,8)–OH (>94%). Thus, the sum of product spectra has two bands at 317 and 473 nm (Figure 4).
Figure 4.
The calculated UV–vis spectra of I3C and the main product of its reaction with HO• radical in water and pentyl ethanoate solvents.
3. Conclusions
The hydroxyl radical scavenging of I3C was studied by thermochemical and kinetic calculations. It was found that the overall reaction rate constant of the HO• radical scavenging in water is 2.30 × 1010 M–1 s–1 and approximately three times lower in pentyl ethanoate solvent (7.74 × 109 M–1 s–1). The rate constant calculated in water is in good agreement with reported experimental values. It was shown that the HO• radical scavenging is defined by the RAF mechanism (>94%) in lipidic environment, whereas in aqueous solution, the RAF is closer to about 60% and the SET contributes 33.5%. According to the calculations, I3C is expected to exhibit antioxidant activity comparable to dopamine, thus it holds the potential for use in preventing oxidative degradation in lipid environments.
4. Computational Methods
M05-2X functionals with the solvation model density (SMD) were used for kinetic calculations in both water and pentyl ethanoate solvents, following the quantum mechanics-based test for the overall free radical scavenging activity (QM-ORSA) protocol.13,20,35−38 The rate constant (k) was calculated by using the conventional transition-state theory and 1 M standard state as39−42
where σ is the reaction symmetry number that represents reaction path degeneracy (which was calculated following the literature43,44), κ accounts for tunneling corrections which were calculated using the Eckart barrier,45kB and h are the Boltzmann and Planck constants, respectively, and ΔG⧧ is Gibbs free energy of activation of the studied reaction. The SET reaction barriers were corrected by using the Marcus Theory,46,47 whereas the Collins–Kimball theory was used to calculate the apparent rate constants (kapp) in solvents.48 The diffusion limit rate constant (kD) for an irreversible bimolecular reaction was calculated according to the literature.13,49 To minimize over-penalizing entropy in solution, the corrections proposed by Okuno50 were performed under the consideration of the free volume theory following the Benson correction.13,51 The overall rate constant (koverall), and branching ratios (Γ) were computed following the QM-ORSA model.13
In this study, the lowest electronic energy conformer for inclusion in the analysis was obtained by hindered internal rotation treatment.52−54 The correction of transition states was confirmed by intrinsic coordinate calculations and the presence of only one single imaginary frequency.
Here, the BDE, IE, and PA of the I3C–H moiety determines the enthalpy of the following processes.
| 3 |
| 4 |
| 5 |
The reaction enthalpies of the individual steps of the radical scavenging mechanism in the studied environments (at 298.15 K and 1 atm) were calculated as follows.55,56
| 6 |
| 7 |
| 8 |
The enthalpy value for the hydrogen atom in the solvent was calculated at the same level of theory, whereas the calculated enthalpies of the proton (H+) and electron (e–) were taken from the literature.56−59 All calculations were performed with the Gaussian 09 suite of programs at the M05-2X/6-311++G(d,p) level.60 Kinetics were calculated by using the Eyringpy program.61,62 The UV–vis absorption spectra were calculated using the time-dependent DFT methodology, at the theoretical level PBEO/6-311++G(d,p).63,64 Solvent effects on the vertical excitation energies were considered by using the SMD model.65
Acknowledgments
The research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2018.308.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.9b02782.
BDE and PA for X–H bonds, Cartesian coordinates, and frequency and energies of all transition states of the reactions in water and pentyl ethanoate (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Arnao M. B.; Sanchez-Bravo J.; Acosta M. Indole-3-carbinol as a scavenger of free radicals. IUBMB Life 1996, 39, 1125–1134. 10.1080/15216549600201302. [DOI] [PubMed] [Google Scholar]
- Benabadji S. H.; Wen R.; Zheng J.-B.; Dong X.-C.; Yuan S.-G. Anticarcinogenic and antioxidant activity of diindolylmethane derivatives. Acta Archaeol. Sin. 2004, 25, 666–671. [PubMed] [Google Scholar]; http://www.chinaphar.com/article/view/8198
- Fahey J. W.; Zalcmann A. T.; Talalay P. The chemical diversity and distribution of glucosinolates and isothiocyanates among plants. Phytochemistry 2001, 56, 5–51. 10.1016/s0031-9422(00)00316-2. [DOI] [PubMed] [Google Scholar]
- Vo Q. V.; Trenerry C.; Rochfort S.; Wadeson J.; Leyton C.; Hughes A. B. Synthesis and anti-inflammatory activity of indole glucosinolates. Bioorg. Med. Chem. 2014, 22, 856–864. 10.1016/j.bmc.2013.12.003. [DOI] [PubMed] [Google Scholar]
- Lee M.-K.; Chun J.-H.; Byeon D. H.; Chung S.-O.; Park S. U.; Park S.; Arasu M. V.; Al-Dhabi N. A.; Lim Y.-P.; Kim S.-J. Variation of glucosinolates in 62 varieties of chinese cabbage (brassica rapa l. Ssp. Pekinensis) and their antioxidant activity. LWT--Food Sci. Technol. 2014, 58, 93–101. 10.1016/j.lwt.2014.03.001. [DOI] [Google Scholar]
- Yu L.; Gao B.; Li Y.; Wang T. T. Y.; Luo Y.; Wang J.; Yu L. Home food preparation techniques impacted the availability of natural antioxidants and bioactivities in kale and broccoli. Food Funct. 2018, 9, 585–593. 10.1039/c7fo00948h. [DOI] [PubMed] [Google Scholar]
- Vo Q. V.; Rochfort S.; Nam P. C.; Nguyen T. L.; Nguyen T. T.; Mechler A. Synthesis of aromatic and indole alpha-glucosinolates. Carbohydr. Res. 2018, 455, 45–53. 10.1016/j.carres.2017.11.004. [DOI] [PubMed] [Google Scholar]
- Cooke M. S.; Evans M. D.; Dizdaroglu M.; Lunec J. Oxidative DNA damage: Mechanisms, mutation, and disease. FASEB J. 2003, 17, 1195–1214. 10.1096/fj.02-0752rev. [DOI] [PubMed] [Google Scholar]
- Nunomura A.; Perry G.; Aliev G.; Hirai K.; Takeda A.; Balraj E. K.; Jones P. K.; Ghanbari H.; Wataya T.; Shimohama S.; Chiba S.; Atwood C. S.; Petersen R. B.; Smith M. A. Oxidative damage is the earliest event in alzheimer disease. J. Neuropathol. Exp. Neurol. 2001, 60, 759–767. 10.1093/jnen/60.8.759. [DOI] [PubMed] [Google Scholar]
- Vijayalaxmi; Tan D.-X.; Herman T. S.; Thomas C. R. Jr. Melatonin as a radioprotective agent: A review. Int. J. Radiat. Oncol., Biol., Phys. 2004, 59, 639–653. 10.1016/j.ijrobp.2004.02.006. [DOI] [PubMed] [Google Scholar]
- Galano A.; Mazzone G.; Alvarez-Diduk R.; Marino T.; Alvarez-Idaboy J. R.; Russo N. Food antioxidants: Chemical insights at the molecular level. Annu. Rev. Food Sci. Technol. 2016, 7, 335–352. 10.1146/annurev-food-041715-033206. [DOI] [PubMed] [Google Scholar]
- Chatgilialoglu C.; D’Angelantonio M.; Guerra M.; Kaloudis P.; Mulazzani Q. G. A reevaluation of the ambident reactivity of the guanine moiety towards hydroxyl radicals. Angew. Chem., Int. Ed. 2009, 48, 2214–2217. 10.1002/anie.200805372. [DOI] [PubMed] [Google Scholar]
- Galano A.; Alvarez-Idaboy J. R. A computational methodology for accurate predictions of rate constants in solution: Application to the assessment of primary antioxidant activity. J. Comput. Chem. 2013, 34, 2430–2445. 10.1002/jcc.23409. [DOI] [PubMed] [Google Scholar]
- León-Carmona J. R.; Galano A. Is caffeine a good scavenger of oxygenated free radicals?. J. Phys. Chem. B 2011, 115, 4538–4546. 10.1021/jp201383y. [DOI] [PubMed] [Google Scholar]
- Pérez-González A.; Galano A. Oh radical scavenging activity of edaravone: Mechanism and kinetics. J. Phys. Chem. B 2010, 115, 1306–1314. 10.1021/jp110400t. [DOI] [PubMed] [Google Scholar]
- Galano A. On the direct scavenging activity of melatonin towards hydroxyl and a series of peroxyl radicals. Phys. Chem. Chem. Phys. 2011, 13, 7178–7188. 10.1039/c0cp02801k. [DOI] [PubMed] [Google Scholar]
- Iuga C.; Alvarez-Idaboy J. R.; Vivier-Bunge A. Ros initiated oxidation of dopamine under oxidative stress conditions in aqueous and lipidic environments. J. Phys. Chem. B 2011, 115, 12234–12246. 10.1021/jp206347u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Błoch-Mechkour A.; Bally T.; Sikora A.; Michalski R.; Marcinek A.; Gebicki J. Radicals and radical ions derived from indole, indole-3-carbinol and diindolylmethane. J. Phys. Chem. A 2010, 114, 6787–6794. 10.1021/jp912121y. [DOI] [PubMed] [Google Scholar]
- Najafi M.; Najafi M.; Najafi H. Dft/b3lyp study of the substituent effects on the reaction enthalpies of the antioxidant mechanisms of indole-3-carbinol derivatives in the gas-phase and water. Comput. Theor. Chem. 2012, 999, 34–42. 10.1016/j.comptc.2012.08.008. [DOI] [Google Scholar]
- Galano A.; Alvarez-Idaboy J. R. Guanosine+ oh radical reaction in aqueous solution: A reinterpretation of the uv– vis data based on thermodynamic and kinetic calculations. Org. Lett. 2009, 11, 5114–5117. 10.1021/ol901862h. [DOI] [PubMed] [Google Scholar]
- Liu M.; Xu M.; Lee J. K. The acidity and proton affinity of the damaged base 1, n 6-ethenoadenine in the gas phase versus in solution: Intrinsic reactivity and biological implications. J. Org. Chem. 2008, 73, 5907–5914. 10.1021/jo800891c. [DOI] [PubMed] [Google Scholar]
- Pliego J. R. Jr. Thermodynamic cycles and the calculation of pka. Chem. Phys. Lett. 2003, 367, 145–149. 10.1016/s0009-2614(02)01686-x. [DOI] [Google Scholar]
- Chen M.; Lee J. K. Computational studies of the gas-phase thermochemical properties of modified nucleobases. J. Org. Chem. 2014, 79, 11295–11300. 10.1021/jo502058w. [DOI] [PubMed] [Google Scholar]
- Rebollar-Zepeda A. M.; Campos-Hernández T.; Ramírez-Silva M. T.; Rojas-Hernández A.; Galano A. Searching for computational strategies to accurately predict pk as of large phenolic derivatives. J. Chem. Theory Comput. 2011, 7, 2528–2538. 10.1021/ct2001864. [DOI] [PubMed] [Google Scholar]
- Bryantsev V. S.; Diallo M. S.; Goddard W. A. Iii. Calculation of solvation free energies of charged solutes using mixed cluster/continuum models. J. Phys. Chem. B 2008, 112, 9709–9719. 10.1021/jp802665d. [DOI] [PubMed] [Google Scholar]
- Mahal H. S.; Sharma H. S.; Mukherjee T. Antioxidant properties of melatonin: A pulse radiolysis study. Free Radical Biol. Med. 1999, 26, 557–565. 10.1016/s0891-5849(98)00226-3. [DOI] [PubMed] [Google Scholar]
- Vo Q. V.; Nam P. C.; Van Bay M.; Thong N. M.; Cuong N. D.; Mechler A. Density functional theory study of the role of benzylic hydrogen atoms in the antioxidant properties of lignans. Sci. Rep. 2018, 8, 12361. 10.1038/s41598-018-30860-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vo Q. V.; Nam P. C.; Thong N. M.; Trung N. T.; Phan C.-T. D.; Mechler A. Antioxidant motifs in flavonoids: O–h versus c–h bond dissociation. ACS Omega 2019, 4, 8935–8942. 10.1021/acsomega.9b00677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galano A.; Raúl Alvarez-Idaboy J. Computational strategies for predicting free radical scavengers’ protection against oxidative stress: Where are we and what might follow?. Int. J. Quantum Chem. 2019, 119, e25665 10.1002/qua.25665. [DOI] [Google Scholar]
- Solar S.; Getoff N.; Surdhar P. S.; Armstrong D. A.; Singh A. Oxidation of tryptophan and n-methylindole by n3. Cntdot., br2.-, and (scn)2.-radicals in light-and heavy-water solutions: A pulse radiolysis study. J. Phys. Chem. 1991, 95, 3639–3643. 10.1021/j100162a038. [DOI] [Google Scholar]
- Shen X.; Lind J.; Merenyi G. One-electron oxidation of indoles and acid-base properties of the indolyl radicals. J. Phys. Chem. 1987, 91, 4403–4406. 10.1021/j100300a039. [DOI] [Google Scholar]
- Jovanovic S. V.; Steenken S. Substituent effects on the spectral, acid-base, and redox properties of indolyl radicals: A pulse radiolysis study. J. Phys. Chem. 1992, 96, 6674–6679. 10.1021/j100195a029. [DOI] [Google Scholar]
- Goyal R. N.; Kumar A.; Gupta P. Oxidation chemistry of indole-3-methanol. J. Chem. Soc., Perkin Trans. 2 2001, 618–623. 10.1039/b006855l. [DOI] [Google Scholar]
- Li Z.; Wei X.; Li L.; Liu Y.; Fang Z.; Yang L.; Zhuang M.; Zhang Y.; Lv H. Development of a simple method for determination of anti-cancer component of indole-3-carbinol in cabbage and broccoli. J. Food Nutr. Res. 2019, 5, 642–648. 10.12691/jfnr-5-9-3. [DOI] [Google Scholar]
- Zhao Y.; Schultz N. E.; Truhlar D. G. Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions. J. Chem. Theory Comput. 2006, 2, 364–382. 10.1021/ct0502763. [DOI] [PubMed] [Google Scholar]
- Vélez E.; Quijano J.; Notario R.; Pabón E.; Murillo J.; Leal J.; Zapata E.; Alarcón G. A computational study of stereospecifity in the thermal elimination reaction of menthyl benzoate in the gas phase. J. Phys. Org. Chem. 2009, 22, 971–977. 10.1002/poc.1547. [DOI] [Google Scholar]
- Black G.; Simmie J. M. Barrier heights for h-atom abstraction by ho2 from n-butanol—a simple yet exacting test for model chemistries?. J. Comput. Chem. 2010, 31, 1236–1248. 10.1002/jcc.21410. [DOI] [PubMed] [Google Scholar]
- Furuncuoğlu T.; Ugur I.; Degirmenci I.; Aviyente V. Role of chain transfer agents in free radical polymerization kinetics. Macromolecules 2010, 43, 1823–1835. 10.1021/ma902803p. [DOI] [Google Scholar]
- Evans M. G.; Polanyi M. Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 1935, 31, 875–894. 10.1039/tf9353100875. [DOI] [Google Scholar]
- Eyring H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107–115. 10.1063/1.1749604. [DOI] [Google Scholar]
- Truhlar D. G.; Hase W. L.; Hynes J. T. Current status of transition-state theory. J. Phys. Chem. 1983, 87, 2664–2682. 10.1021/j100238a003. [DOI] [Google Scholar]
- Vo Q. V.; Van Bay M.; Nam P. C.; Mechler A. Is indolinonic hydroxylamine a promising artificial antioxidant?. J. Phys. Chem. B 2019, 123, 7777–7784. 10.1021/acs.jpcb.9b05160. [DOI] [PubMed] [Google Scholar]
- Pollak E.; Pechukas P. Symmetry numbers, not statistical factors, should be used in absolute rate theory and in broensted relations. J. Am. Chem. Soc. 1978, 100, 2984–2991. 10.1021/ja00478a009. [DOI] [Google Scholar]
- Fernández-Ramos A.; Ellingson B. A.; Meana-Pañeda R.; Marques J. M. C.; Truhlar D. G. Symmetry numbers and chemical reaction rates. Theor. Chem. Acc. 2007, 118, 813–826. 10.1007/s00214-007-0328-0. [DOI] [Google Scholar]
- Eckart C. The penetration of a potential barrier by electrons. Phys. Rev. 1930, 35, 1303. 10.1103/physrev.35.1303. [DOI] [Google Scholar]
- Marcus R. A. Chemical and electrochemical electron-transfer theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. 10.1146/annurev.pc.15.100164.001103. [DOI] [Google Scholar]
- Marcus R. A. Electron transfer reactions in chemistry. Theory and experiment. Rev. Mod. Phys. 1993, 65, 599. 10.1103/revmodphys.65.599. [DOI] [Google Scholar]
- Collins F. C.; Kimball G. E. Diffusion-controlled reaction rates. J. Colloid Sci. 1949, 4, 425–437. 10.1016/0095-8522(49)90023-9. [DOI] [Google Scholar]
- Von Smoluchowski M. Study of mathematical theory of the kinetics of the coagulation of colloidal solutions. Z. Phys. Chem. 1918, 92, 129–168. [Google Scholar]; https://apps.dtic.mil/dtic/tr/fulltext/u2/841609.pdf
- Okuno Y. Theoretical investigation of the mechanism of the baeyer-villiger reaction in nonpolar solvents. Chem.—Eur. J. 1997, 3, 212–218. 10.1002/chem.19970030208. [DOI] [PubMed] [Google Scholar]
- Benson S.The foundations of chemical kinetics; ACS Publication: Malabar, Florida, 1982. [Google Scholar]
- Liu Y.; Yin C.; Smith M. C.; Liu S.; Chen M.; Zhou X.; Xiao C.; Dai D.; Lin J. J.-M.; Takahashi K.; Dong W.; Yang X. Kinetics of the reaction of the simplest criegee intermediate with ammonia: A combination of experiment and theory. Phys. Chem. Chem. Phys. 2018, 20, 29669–29676. 10.1039/c8cp05920a. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Liu F.; Liu S.; Dai D.; Dong W.; Yang X. A kinetic study of the ch2oo criegee intermediate reaction with so2,(h2o)2, ch2i2 and i atoms using oh laser induced fluorescence. Phys. Chem. Chem. Phys. 2017, 19, 20786–20794. 10.1039/c7cp04336h. [DOI] [PubMed] [Google Scholar]
- Le T. H. M.; Tran T. T.; Huynh L. K. Identification of hindered internal rotational mode for complex chemical species: A data mining approach with multivariate logistic regression model. Chemom. Intell. Lab. Syst. 2018, 172, 10–16. 10.1016/j.chemolab.2017.11.006. [DOI] [Google Scholar]
- Thong N. M.; Quang D. T.; Bui N. H. T.; Dao D. Q.; Nam P. C. Antioxidant properties of xanthones extracted from the pericarp of garcinia mangostana (mangosteen): A theoretical study. Chem. Phys. Lett. 2015, 625, 30–35. 10.1016/j.cplett.2015.02.033. [DOI] [Google Scholar]
- Rimarčík J.; Lukeš V.; Klein E.; Ilčin M. Study of the solvent effect on the enthalpies of homolytic and heterolytic n–h bond cleavage in p-phenylenediamine and tetracyano-p-phenylenediamine. J. Mol. Struct.: THEOCHEM 2010, 952, 25–30. 10.1016/j.theochem.2010.04.002. [DOI] [Google Scholar]
- Bartmess J. E. Thermodynamics of the electron and the proton. J. Phys. Chem. 1994, 98, 6420–6424. 10.1021/j100076a029. [DOI] [Google Scholar]
- Urbaniak A.; Szeląg M.; Molski M. Theoretical investigation of stereochemistry and solvent influence on antioxidant activity of ferulic acid. Comput. Theor. Chem. 2013, 1012, 33–40. 10.1016/j.comptc.2013.02.018. [DOI] [Google Scholar]
- Donald W. A.; Demireva M.; Leib R. D.; Aiken M. J.; Williams E. R. Electron hydration and ion– electron pairs in water clusters containing trivalent metal ions. J. Am. Chem. Soc. 2010, 132, 4633–4640. 10.1021/ja9079385. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Scalmani G.; Barone V.; Mennucci B.; Nakatsuji H.; Caricato M.; Li X.; Izmaylov A. F.; Bloino J.; Zheng G.; Sonnenberg J. L.; Ehara M.; Toyota K.; Fukuda R.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Vreven T.; Montgomery J. A. Jr.; Peralta J. E.; Bearpark M. J.; Heyd J.; Brothers E. N.; Staroverov V. N.; Kobayashi R.; Normand J.; Rendell A. P.; Burant J. C.; et al. Gaussian 09; Gaussian, Inc.: Wallingford CT, 2009.
- Dzib E.; Cabellos J. L.; Ortíz-Chi F.; Pan S.; Galano A.; Merino G. Eyringpy: A program for computing rate constants in the gas phase and in solution. Int. J. Quantum Chem. 2019, 119, e25686 10.1002/qua.25686. [DOI] [Google Scholar]
- Dzib E.; Cabellos J. L.; Ortiz-Chi F.; Pan S.; Galano A.; Merino G.. Eyringpy 1.0.2; Cinvestav: Mérida, Yucatán, 2018. [Google Scholar]
- DiLabio G. A. Accurate treatment of van der waals interactions using standard density functional theory methods with effective core-type potentials: Application to carbon-containing dimers. Chem. Phys. Lett. 2008, 455, 348–353. 10.1016/j.cplett.2008.02.110. [DOI] [Google Scholar]
- Charaf-Eddin A.; Planchat A.; Mennucci B.; Adamo C.; Jacquemin D. Choosing a functional for computing absorption and fluorescence band shapes with td-dft. J. Chem. Theory Comput. 2013, 9, 2749–2760. 10.1021/ct4000795. [DOI] [PubMed] [Google Scholar]
- Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.