Abstract
We first report three reliable analytical expressions of the entropy, enthalpy and Gibbs free energy of carbon dioxide (CO2) and perform predictions of these three thermodynamic quantities on the basis of the proposed analytical expressions and in terms of experimental values of five molecular constants for CO2. The average relative deviations of the calculated values from the National Institute of Standards and Technology database over the temperature range from 300 to 6000 K are merely 0.053, 0.95, and 0.070%, respectively, for the entropy, enthalpy, and Gibbs free energy. The present predictive expressions are away from the utilization of plenty of experimental spectroscopy data and are applicable to treat CO2 capture and storage processes.
1. Introduction
Carbon dioxide (CO2) as a greenhouse gas has been regarded a main contributor of global warming. Davis et al.1 suggested that the people would continue to confront increasing global mean temperatures and sea level rise if current greenhouse gas concentrations remain constants in the atmosphere. As CO2 has a key influence to global climate change, CO2 capture and storage (CCS) technologies are becoming more and more important topics for reducing CO2 emission. CO2 capture technologies can be classified as three types: post-combustion, pre-combustion, and oxy-fuel combustion. Adsorbing CO2 is one of post-combustion capture technologies.2 Many efforts have been made to develop efficient approaches of adsorbing CO2.3−35 To optimally design such processes, we require accurate and reliable thermodynamic property data on CO2. For some diatomic substances, the improved versions of some well-known oscillators such as the improved Tietz oscillator have been applied to represent the internal vibration of a diatomic molecule for constructions of universal analytical expressions of thermodynamic properties.36−50 A CCS process simulation needs a combination of an equation of state (EoS) with the Helmholtz free energy or Gibbs free energy.51−55 The accurate three-parameter EoS proposed by Jaubert et al.56 and the EoS developed by Span and Wagner57 on the basis of the Helmholtz free energy are available in CCS process simulators. An analytical expression of the thermodynamic property can combine the simplicity of the analytical expression with the solid theoretical background of the statistical thermodynamic theory. However, it is difficult for chemists and engineers to obtain reliable analytical expressions of the thermodynamic quantities for gaseous substances. Although Span and Wagner57 proposed an empirical polynomial analytical representation for the ideal-gas part of the Helmholtz free energy of CO2, it includes 13 adjustable parameters, which were determined by fitting plenty of experimental data points. To date, one has not reported any analytical expressions governing the entropy, enthalpy, and Gibbs free energy for CO2 from the view of the first principle. Therefore, it is of considerable interest to explore suitable analytical expressions of the thermodynamic properties for CO2.
The aim of this work is to establish suitable analytical expressions of the thermodynamic properties for the triatomic substance CO2. Compared with a diatomic substance, the generation of analytical expressions of the thermodynamic properties shows considerably greater challenges. To verify the effectiveness of the present predictive models, we apply three analytical expressions to predict the variations of the entropy, enthalpy, and Gibbs free energy with respect to temperature for CO2 and compare the predictive results with the available data from the National Institute of Standards and Technology (NIST) database.58 The NIST data are compiled by the utilization of NIST-JANAF Thermochemical Tables, which is constructed by Chase59 in terms of plenty of theoretical or experimental spectroscopic constants.
2. Results and Discussion
To show the accuracy and reliability of the proposed predictive models, we calculate the entropy, enthalpy, and Gibbs free energy values at the pressure of 1 bar and different temperatures. This performance needs experimental data on the O–CO bond energy, O–C equilibrium bond length, and stretching and bending vibrational frequencies in the CO2 molecule. We consult the experimental data given by Itikawa,60 and list the required molecular constant values for the ground electronic state of CO2: De = 5.451 eV, reCO = 1.160 Å, ωes = 1388 cm–1, ωea = 2349 cm–1, and ωeb = 667.4 cm–1. Taking q = – 10 and employing the experimental data of the five molecular constants De, reCO, ωes, ωea, and ωeb, the predictive values of molar entropy, enthalpy, and reduced Gibbs free energy for CO2 are produced in terms of eqs 13–15 from 298 up to 6000 K. The predictive results are depicted in Figure 1, in which the green solid lines represent the theoretically predictive results and the blue solid circles refer to the NIST data.58 From Figure 1, we observe that the predictive values show excellent agreement with the NIST data in the entire temperature range. The average relative deviations of the predictive data from the NIST data in a wide range of temperatures from 300 up to 6000 K for the entropy, enthalpy, and reduced Gibbs free energy are 0.053, 0.95, and 0.070%, respectively. These results indicate that our three predictive models are of very high accuracy to predict the entropy, enthalpy, and Gibbs free energy for CO2. In our calculations, the reduced molar Gibbs free energy, Gr = – (G – H298.15)/T, of CO2 from the NIST database58 is 213.8 J·mol–1·K–1 at 298 K. The molar Gibbs free energy calculated by the aid of eq 20 is −22,901.65 J·mol–1 at 298 K. On the basis of these two values, we obtain the value of 40,810.75 J·mol–1 at 298.15 K for the molar enthalpy. When T = 6000 K and ωe = ωeb, the value of e–Θv/T reaches at the maximum, e–Θv/T = 0.852 < 1; thus, eq 2 is always valid in our calculations.
Figure 1.

Temperature variation of the thermodynamic properties of CO2 for (A) molar entropy, (B) molar enthalpy, and (C) reduced molar Gibbs free energy.
3. Conclusions
In summary, we first present suitable analytical expressions of the molar entropy, enthalpy, and Gibbs free energy for CO2. The average relative deviations between the theoretical predictive values and the NIST data ranging from the temperatures of 300 to 6000 K are 0.053, 0.95, and 0.070%, respectively, for the entropy, enthalpy, and reduced Gibbs free energy of CO2. The present predictive expressions exhibit satisfactorily accuracies and simple and straightforward characteristics and are away from the requirements of plenty of experimental spectroscopy data. The methodology developed in our work opens up a new pathway serving as constructions of accurate and efficient analytical expressions of thermodynamic properties for other triatomic substances such as water and hydrogen sulfide. It is expected that the present predictive models could aid the design and optimization of CCS processes.
4. Computational Methods
Figure 2 shows that CO2 is a centrosymmetric linear molecule and possesses symmetric stretching, antisymmetric stretching, and bending vibration modes. However, as a diatomic molecule is consisted of two atoms, it merely possesses a kind of stretching vibration. Hence, addressing vibrations of the CO2 molecule is much more difficult than treating the vibration of the diatomic molecule such as the nitrogen molecule. Here, we treat the internal symmetric stretching vibration of the CO2 molecule in terms of the improved Tietz oscillator61 and deal with the antisymmetric stretching and bending vibrations with the help of the harmonic oscillator. According to the vibrational partition function given in eq 14 of ref (50) for the improved Tietz oscillator, the partition function corresponding to the symmetric stretching vibration for CO2 is expressed as
 |
1 |
in which De denotes the energy serving
as dissociating CO2 into O–CO, k refers to the Boltzmann constant, T is the temperature,
symbol erfi represents the imaginary
error function, 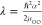 ,
,  ,
,  ,
,  ,
, 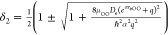 , and
, and  . Here, h is the Planck
constant, μOO refers to the reduced
mass of two oxygen atoms, reOO = 2reCO (reCO represents
the C–O equilibrium length), q denotes a dimensionless
variable, and the symbol ± stands for the plus and minus in the
cases of a positive value and negative value of q, respectively. The parameter α reads as
. Here, h is the Planck
constant, μOO refers to the reduced
mass of two oxygen atoms, reOO = 2reCO (reCO represents
the C–O equilibrium length), q denotes a dimensionless
variable, and the symbol ± stands for the plus and minus in the
cases of a positive value and negative value of q, respectively. The parameter α reads as  , where
, where 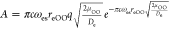 , c is the speed of light,
and ωes represents the symmetric stretching vibration
frequency. The contributions of the excited states to the partition
function are represented by the factor
, c is the speed of light,
and ωes represents the symmetric stretching vibration
frequency. The contributions of the excited states to the partition
function are represented by the factor  . The highest vibrational quantum number, vmax, reads as
. The highest vibrational quantum number, vmax, reads as
 |
where [x] refers to the greatest integer, which is less than x.
Figure 2.

Schematic diagram of the vibration modes of the carbon dioxide molecule.
The vibrational partition function for a harmonic oscillator is given by36
| 2 |
where Θv refers to the vibrational characteristic temperature and is expressed as Θv = hcωe/k. Here, ωe denotes the vibrational frequency.
We consider the canonical ensemble. From the following basic thermodynamic relationships
| 3 |
| 4 |
| 5 |
we obtain the molar vibrational entropy, enthalpy, and Gibbs free energy referring to the symmetric stretching vibration for CO2, respectively
 |
6 |
 |
7 |
 |
8 |
where R is the universal gas constant.
With the help of thermodynamic formulas above (eqs 3–5), we obtain the molar vibrational entropy, enthalpy, and Gibbs free energy serving as contributions of the antisymmetric stretching and bending vibrations for CO2, respectively
| 9 |
| 10 |
| 11 |
in which Θva and Θv are the respective vibrational characteristic temperatures for the antisymmetric stretching mode and bending mode. They are defined as Θva = hcωea/k and Θv = hcωeb/k, where ωea and ωeb are the vibrational frequencies corresponding to the antisymmetric stretching vibration and bending vibration, respectively.
To simplify the mathematical calculation, it is reasonable to assume that the interaction between two molecules is not considered and the CO2 molecule is regarded as a rigid rotor. The molar translational and rotational entropies are given respectively by37
| 12 |
| 13 |
where mCO2 stands for the mass of the CO2 molecule, P represents the gas pressure,
Θr refers
to the rotational characteristic temperature, 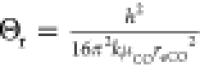 . Here, μCO represents
the reduced mass of carbon and oxygen atoms. The molar translational
and rotational enthalpies can be written as follows,36 respectively
. Here, μCO represents
the reduced mass of carbon and oxygen atoms. The molar translational
and rotational enthalpies can be written as follows,36 respectively
| 14 |
| 15 |
The molar translational and rotational Gibbs free energies are expressed in terms of the following two representations,38 respectively
| 16 |
| 17 |
The total molar entropy, enthalpy, and Gibbs free energy for CO2 can be determined from the following formulas
| 18 |
| 19 |
| 20 |
By inputting the experimental values of De, reCO, ωes, ωea, and ωeb in our predictive models, we can predict the molar entropy, enthalpy, and Gibbs free energy for carbon dioxide. Our prediction approaches rely only on requirements of experimental data of five molecular constants for CO2. It is superior to the conventional computation models, which need a large amount of experimental spectroscopy data.
Acknowledgments
This work was supported by the Key Program of National Natural Science Foundation of China under grant no. 51534006 and the Sichuan Province Foundation of China for Fundamental Research Projects under grant no. 2018JY0468.
The authors declare no competing financial interest.
References
- Davis S. J.; Caldeira K.; Matthews H. D. Future CO2 emissions and climate change from existing energy infrastructure. Science 2010, 329, 1330–1333. 10.1126/science.1188566. [DOI] [PubMed] [Google Scholar]
- Lee S. Y.; Park S. J. A review on solid adsorbents for carbon dioxide capture. J. Ind. Eng. Chem. 2015, 23, 1–11. 10.1016/j.jiec.2014.09.001. [DOI] [Google Scholar]
- Datta S. J.; Khumnoon C.; Lee Z. H.; Moon W. K.; Docao S.; Nguyen T. H.; Hwang I. C.; Moon D.; Oleynikov P.; Terasaki O.; Yoon K. B. CO2 capture from humid flue gases and humid atmosphere using a microporous coppersilicate. Science 2015, 350, 302–306. 10.1126/science.aab1680. [DOI] [PubMed] [Google Scholar]
- Wang B.; Côté A. P.; Furukawa H.; O’Keeffe M.; Yaghi O. M. Colossal cages in zeolitic imidazolate frameworks as selective carbon dioxide reservoirs. Nature 2008, 453, 207–211. 10.1038/nature06900. [DOI] [PubMed] [Google Scholar]
- Nugent P.; Belmabkhout Y.; Burd S. D.; Cairns A. J.; Luebke R.; Forrest K.; Pham T.; Ma S.; Space B.; Wojtas L.; Eddaoudi M.; Zaworotko M. J. Porous materials with optimal adsorption thermodynamics and kinetics for CO2 separation. Nature 2013, 495, 80–84. 10.1038/nature11893. [DOI] [PubMed] [Google Scholar]
- McDonald T. M.; Mason J. A.; Kong X.; Bloch E. D.; Gygi D.; Dani A.; Crocellà V.; Giordanino F.; Odoh S. O.; Drisdell W. S.; Vlaisavljevich B.; Dzubak A. L.; Poloni R.; Schnell S. K.; Planas N.; Lee K.; Pascal T.; Wan L. F.; Prendergast D.; Neaton J. B.; Smit B.; Kortright J. B.; Gagliardi L.; Bordiga S.; Reimer J. A.; Long J. R. Cooperative insertion of CO2 in diamine-appended metal-organic frameworks. Nature 2015, 519, 303–308. 10.1038/nature14327. [DOI] [PubMed] [Google Scholar]
- Trickett C. A.; Helal A.; Al-Maythalony B. A.; Yamani Z. H.; Cordova K. E.; Yaghi O. M. The chemistry of metal–organic frameworks for CO2 capture, regeneration and conversion. Nat. Rev. Mater. 2017, 2, 17045. 10.1038/natrevmats.2017.45. [DOI] [Google Scholar]
- Sherman B. J.; Ciftja A. F.; Rochelle G. T. Thermodynamic and mass transfer modeling of carbon dioxide absorption into aqueous 2-piperidineethanol. Chem. Eng. Sci. 2016, 153, 295–307. 10.1016/j.ces.2016.07.019. [DOI] [Google Scholar]
- Ammendola P.; Raganati F.; Chirone R. CO2 adsorption on a fine activated carbon in a sound assisted fluidized bed: Thermodynamics and kinetics. Chem. Eng. J. 2017, 322, 302–313. 10.1016/j.cej.2017.04.037. [DOI] [Google Scholar]
- Singh V. K.; Kumar E. A.; Saha B. B. Adsorption isotherms, kinetics and thermodynamic simulation of CO2-CSAC pair for cooling application. Energy 2018, 160, 1158–1173. 10.1016/j.energy.2018.07.063. [DOI] [Google Scholar]
- Sherman B. J.; Rochelle G. T. Thermodynamic and mass-transfer modeling of carbon dioxide absorption into aqueous 2-amino-2-methyl-1-propanol. Ind. Eng. Chem. Res. 2017, 56, 319–330. 10.1021/acs.iecr.6b03009. [DOI] [Google Scholar]
- Gargiulo V.; Alfè M.; Ammendola P.; Raganati F.; Chirone R. CO2 sorption on surface-modified carbonaceous support: Probing the influence of the carbon black microporosity and surface polarity. Appl. Surf. Sci. 2016, 360, 329–337. 10.1016/j.apsusc.2015.11.026. [DOI] [Google Scholar]
- Gargiulo V.; Alfè M.; Raganati F.; Lisi L.; Chirone R.; Ammendola P. BTC-based metal-organic frameworks: Correlation between relevant structural features and CO2 adsorption performances. Fuel 2018, 222, 319–326. 10.1016/j.fuel.2018.02.093. [DOI] [Google Scholar]
- Raganati F.; Alfe M.; Gargiulo V.; Chirone R.; Ammendola P. Isotherms and thermodynamics of CO2 adsorption on a novel carbon-magnetite composite sorbent. Chem. Eng. Res. Des. 2018, 134, 540–552. 10.1016/j.cherd.2018.04.037. [DOI] [Google Scholar]
- Raganati F.; Alfe M.; Gargiulo V.; Chirone R.; Ammendola P. Kinetic study and breakthrough analysis of the hybrid physical/chemical CO2 adsorption/desorption behavior of a magnetite-based sorbent. Chem. Eng. J. 2019, 372, 526–535. 10.1016/j.cej.2019.04.165. [DOI] [Google Scholar]
- Ben-Mansour R.; Habib M. A.; Bamidele O. E.; Basha M.; Qasem N. A. A.; Peedikakkal A.; Laoui T.; Ali M. Carbon capture by physical adsorption: Materials, experimental investigations and numerical modeling and simulations – A review. Appl. Energy 2016, 161, 225–255. 10.1016/j.apenergy.2015.10.011. [DOI] [Google Scholar]
- Ben-Mansour R.; Basha M.; Qasem N. A. A. Multicomponent and multi-dimensional modeling and simulation of adsorption-based carbon dioxide separation. Comput. Chem. Eng. 2017, 99, 255–270. 10.1016/j.compchemeng.2017.01.040. [DOI] [Google Scholar]
- Ben-Mansour R.; Qasem N. A. A.; Antar M. A. Carbon dioxide adsorption separation from dry and humid CO2/N2 mixture. Comput. Chem. Eng. 2018, 117, 221–235. 10.1016/j.compchemeng.2018.06.016. [DOI] [Google Scholar]
- Qasem N. A. A.; Ben-Mansour R. Energy and productivity efficient vacuum pressure swing adsorption process to separate CO2 from CO2/N2 mixture using Mg-MOF-74: A CFD simulation. Appl. Energy 2018, 209, 190–202. 10.1016/j.apenergy.2017.10.098. [DOI] [Google Scholar]
- Qasem N. A. A.; Ben-Mansour R. Adsorption breakthrough and cycling stability of carbon dioxide separation from CO2/N2/H2O mixture under ambient conditions using 13X and Mg-MOF-74. Appl. Energy 2018, 230, 1093–1107. 10.1016/j.apenergy.2018.09.069. [DOI] [Google Scholar]
- Ferreira D.; Magalhães R.; Taveira P.; Mendes A. Effective adsorption equilibrium isotherms and breakthroughs of water vapor and carbon dioxide on different adsorbents. Ind. Eng. Chem. Res. 2011, 50, 10201–10210. 10.1021/ie2005302. [DOI] [Google Scholar]
- Lei M.; Vallieres C.; Grevillot G.; Latifi M. A. Thermal swing adsorption process for carbon dioxide capture and recovery: Modeling, simulation, parameters estimability, and identification. Ind. Eng. Chem. Res. 2013, 52, 7526–7533. 10.1021/ie3029152. [DOI] [Google Scholar]
- Ntiamoah A.; Ling J.; Xiao P.; Webley P. A.; Zhai Y. CO2 Capture by Temperature Swing Adsorption: Use of Hot CO2-Rich Gas for Regeneration. Ind. Eng. Chem. Res. 2015, 55, 703–713. 10.1021/acs.iecr.5b01384. [DOI] [Google Scholar]
- Richou M.; Martin C.; Denoyel R.; Llewellyn P.; Roubin P. Microporosity of carbon deposits collected in the Tore Supra tokamak probed by nitrogen and carbon dioxide adsorption. Carbon 2009, 47, 109–116. 10.1016/j.carbon.2008.09.041. [DOI] [Google Scholar]
- Mason J. A.; Sumida K.; Herm Z. R.; Krishna R.; Long J. R. Evaluating metal-organic frameworks for post-combustion carbon dioxide capture via temperature swing adsorption. Energy Environ. Sci. 2011, 4, 3030–3040. 10.1039/c1ee01720a. [DOI] [Google Scholar]
- Wang L.; Liu Z.; Li P.; Yu J.; Rodrigues A. E. Experimental and modeling investigation on post-combustion carbon dioxide capture using zeolite 13X-APG by hybrid VTSA process. Chem. Eng. J. 2012, 197, 151–161. 10.1016/j.cej.2012.05.017. [DOI] [Google Scholar]
- Hedin N.; Andersson L.; Bergström L.; Yan J. Adsorbents for the post-combustion capture of CO2 using rapid temperature swing or vacuum swing adsorption. Appl. Energy 2013, 104, 418–433. 10.1016/j.apenergy.2012.11.034. [DOI] [Google Scholar]
- Zhang Z.; Yao Z. Z.; Xiang S.; Chen B. Perspective of microporous metal–organic frameworks for CO2 capture and separation. Energy Environ. Sci. 2014, 7, 2868–2899. 10.1039/C4EE00143E. [DOI] [Google Scholar]
- Riboldi L.; Bolland O. Evaluating pressure swing adsorption as a CO2 separation technique in coal-fired power plants. Int. J. Greenhouse Gas Control 2015, 39, 1–16. 10.1016/j.ijggc.2015.02.001. [DOI] [Google Scholar]
- Prats H.; Bahamon D.; Alonso G.; Giménez X.; Gamallo P.; Sayós R. Optimal Faujasite structures for post combustion CO2 capture and separation in different swing adsorption processes. J. CO2 Util. 2017, 19, 100–111. 10.1016/j.jcou.2017.03.007. [DOI] [Google Scholar]
- Psarras P.; He J.; Wilcox J. Effect of water on the CO2 adsorption capacity of amine-functionalized carbon sorbents. Ind. Eng. Chem. Res. 2017, 56, 6317–6325. 10.1021/acs.iecr.6b05064. [DOI] [Google Scholar]
- Zhou Z.; Balijepalli S. K.; Nguyen-Sorenson A. H. T.; Anderson C. M.; Park J. L.; Stowers K. J. Steam-stable covalently bonded polyethylenimine modified multiwall carbon nanotubes for carbon dioxide capture. Energy Fuels 2018, 32, 11701–11709. 10.1021/acs.energyfuels.8b02864. [DOI] [Google Scholar]
- Montagnaro F.; Balsamo M. Modelling CO2 adsorption dynamics onto amine-functionalised sorbents: A fractal-like kinetic perspective. Chem. Eng. Sci. 2018, 192, 603–612. 10.1016/j.ces.2018.08.009. [DOI] [Google Scholar]
- Ghosh S.; Ramaprabhu S. Green synthesis of transition metal nanocrystals encapsulated into nitrogen-doped carbon nanotubes for efficient carbon dioxide capture. Carbon 2019, 141, 692–703. 10.1016/j.carbon.2018.09.083. [DOI] [Google Scholar]
- Ma S.; Wang Y.; Liu Z.; Huang M.; Yang H.; Xu Z.-L. Preparation of carbon nanofiber with multilevel gradient porous structure for supercapacitor and CO2 adsorption. Chem. Eng. Sci. 2019, 205, 181–189. 10.1016/j.ces.2019.05.001. [DOI] [Google Scholar]
- Jia C.-S.; Wang C.-W.; Zhang L.-H.; Peng X.-L.; Tang H.-M.; Zeng R. Enthalpy of gaseous phosphorus dimer. Chem. Eng. Sci. 2018, 183, 26–29. 10.1016/j.ces.2018.03.009. [DOI] [Google Scholar]
- Jia C.-S.; Zeng R.; Peng X.-L.; Zhang L.-H.; Zhao Y.-L. Entropy of gaseous phosphorus dimer. Chem. Eng. Sci. 2018, 190, 1–4. 10.1016/j.ces.2018.06.009. [DOI] [Google Scholar]
- Peng X.-L.; Jiang R.; Jia C.-S.; Zhang L.-H.; Zhao Y.-L. Gibbs free energies of gaseous phosphorus dimer. Chem. Eng. Sci. 2018, 190, 122–125. 10.1016/j.ces.2018.06.027. [DOI] [Google Scholar]
- Jia C.-S.; Zhang L.-H.; Wang C.-W. Thermodynamic properties for the lithium dimer. Chem. Phys. Lett. 2017, 667, 211–215. 10.1016/j.cplett.2016.11.059. [DOI] [Google Scholar]
- Song X.-Q.; Wang C.-W.; Jia C.-S. Thermodynamic properties for the sodium dimer. Chem. Phys. Lett. 2017, 673, 50–55. 10.1016/j.cplett.2017.02.010. [DOI] [Google Scholar]
- Buchowiecki M. Ro-vibrational coupling in high temperature thermochemistry of the BBr molecule. Chem. Phys. Lett. 2018, 692, 236. 10.1016/j.cplett.2017.12.051. [DOI] [Google Scholar]
- Khordad R.; Avazpour A.; Ghanbari A. Exact analytical calculations of thermodynamic functions of gaseous substances. Chem. Phys. 2019, 517, 30–35. 10.1016/j.chemphys.2018.09.038. [DOI] [Google Scholar]
- Khordad R.; Ghanbari A. Analytical calculations of thermodynamic functions of lithium dimer using modified Tietz and Badawi-Bessis-Bessis potentials. Comput. Theor. Chem. 2019, 1155, 1–8. 10.1016/j.comptc.2019.03.019. [DOI] [Google Scholar]
- Wang J.-F.; Peng X.-L.; Zhang L.-H.; Wang C.-W.; Jia C.-S. Entropy of gaseous boron monobromide. Chem. Phys. Lett. 2017, 686, 131–133. 10.1016/j.cplett.2017.08.047. [DOI] [Google Scholar]
- Jia C.-S.; Wang C.-W.; Zhang L.-H.; Peng X.-L.; Tang H.-M.; Liu J.-Y.; Xiong Y.; Zeng R. Predictions of entropy for diatomic molecules and gaseous substances. Chem. Phys. Lett. 2018, 692, 57–60. 10.1016/j.cplett.2017.12.013. [DOI] [Google Scholar]
- Jiang R.; Jia C.-S.; Wang Y.-Q.; Peng X.-L.; Zhang L.-H. Prediction of enthalpy for the gases CO, HCl, and BF. Chem. Phys. Lett. 2019, 715, 186–189. 10.1016/j.cplett.2018.11.044. [DOI] [Google Scholar]
- Jia C.-S.; You X.-T.; Liu J.-Y.; Zhang L.-H.; Peng X.-L.; Wang Y.-T.; Wei L.-S. Prediction of enthalpy for the gases Cl2, Br2, and gaseous BBr. Chem. Phys. Lett. 2019, 717, 16–20. 10.1016/j.cplett.2019.01.001. [DOI] [Google Scholar]
- Jiang R.; Jia C.-S.; Wang Y.-Q.; Peng X.-L.; Zhang L.-H. Prediction of Gibbs free energy for the gases Cl2, Br2, and HCl. Chem. Phys. Lett. 2019, 726, 83–86. 10.1016/j.cplett.2019.04.040. [DOI] [Google Scholar]
- Jia C.-S.; Zhang L.-H.; Peng X.-L.; Luo J.-X.; Zhao Y.-L.; Liu J.-Y.; Guo J.-J.; Tang L.-D. Prediction of entropy and Gibbs free energy for nitrogen. Chem. Eng. Sci. 2019, 202, 70–74. 10.1016/j.ces.2019.03.033. [DOI] [Google Scholar]
- Jia C.-S.; Wang C.-W.; Zhang L.-H.; Peng X.-L.; Zeng R.; You X.-T. Partition function of improved Tietz oscillators. Chem. Phys. Lett. 2017, 676, 150–153. 10.1016/j.cplett.2017.03.068. [DOI] [Google Scholar]
- Lasala S.; Chiesa P.; Privat R.; Jaubert J.-N. Modeling the thermodynamics of fluids treated by CO2 capture processes with Peng–Robinson + residual Helmholtz energy-based mixing rules. Ind. Eng. Chem. Res. 2017, 56, 2259–2276. 10.1021/acs.iecr.6b04190. [DOI] [Google Scholar]
- Lasala S.; Chiesa P.; Privat R.; Jaubert J.-N. Measurement and prediction of multi-property data of CO2-N2-O2-CH4 mixtures with the “Peng-Robinson + residual Helmholtz energy-based” model. Fluid Phase Equilib. 2017, 437, 166–180. 10.1016/j.fluid.2017.01.016. [DOI] [Google Scholar]
- Xu X.; Lasala S.; Privat R.; Jaubert J.-N. E-PPR78: A proper cubic EoS for modelling fluids involved in the design and operation of carbon dioxide capture and storage (CCS) processes. Int. J. Greenhouse Gas Control 2017, 56, 126–154. 10.1016/j.ijggc.2016.11.015. [DOI] [Google Scholar]
- Lasala S.; Chiesa P.; Privat R.; Jaubert J.-N. Sizing and operating units for the purification and compression of CO2-based streams: The impact of thermodynamic model accuracy. J. Supercrit. Fluids 2018, 140, 336–347. 10.1016/j.supflu.2018.04.010. [DOI] [Google Scholar]
- Najafi-Marghmaleki A.; Barati-Harooni A.; Mohammadi A. H. Impact of gas impurities on CO2 mole fraction: Application in carbon capture and storage (CCS) processes. Int. J. Greenhouse Gas Control 2017, 57, 173–184. 10.1016/j.ijggc.2016.12.008. [DOI] [Google Scholar]
- Le Guennec Y.; Privat R.; Jaubert J.-N. Development of the translated-consistent tc-PR and tc-RK cubic equations of state for a safe and accurate prediction of volumetric, energetic and saturation properties of pure compounds in the sub- and super-critical domains. Fluid Phase Equilib. 2016, 429, 301–312. 10.1016/j.fluid.2016.09.003. [DOI] [Google Scholar]
- Span R.; Wagner W. A new equation of state for carbon dioxide covering the fluid region from the triple-point temperature to 1100 K at pressures up to 800 MPa. J. Phys. Chem. Ref. Data 1996, 25, 1509–1596. 10.1063/1.555991. [DOI] [Google Scholar]
- National Institute of Standards and Technology (NIST) NIST Chemistry WebBook; National Institute of Standards and Technology, NIST Standard Reference Database Number 69, 2017, http://webbook.nist.gov/chemistry/.
- Chase M. W.NIST-JANAF Thermochemical Tables; Journal of Physical and Chemical Reference Data Monographs No. 9; American Institute of Physics: 1998. [Google Scholar]
- Itikawa Y. Cross sections for electron collisions with carbon dioxide. J. Phys. Chem. Ref. Data 2002, 31, 749–767. 10.1063/1.1481879. [DOI] [Google Scholar]
- Jia C.-S.; Diao Y.-F.; Liu X.-J.; Wang P.-Q.; Liu J.-Y.; Zhang G.-D. Equivalence of the Wei potential model and Tietz potential model for diatomic molecules. J. Chem. Phys. 2012, 137, 014101 10.1063/1.4731340. [DOI] [PubMed] [Google Scholar]



