Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2014 May 21;35(10):5295–5305. doi: 10.1002/hbm.22550

Heritability of structural brain network topology: A DTI study of 156 twins

Marc M Bohlken 1,✉, René CW Mandl 1, Rachel M Brouwer 1, Martijn P van den Heuvel 1, Anna M Hedman 1, René S Kahn 1, Hilleke E Hulshoff Pol 1
PMCID: PMC6868932  PMID: 24845163

Abstract

Individual variation in structural brain network topology has been associated with heritable behavioral phenotypes such as intelligence and schizophrenia, making it a candidate endophenotype. However, little is known about the genetic influences on individual variation in structural brain network topology. Moreover, the extent to which structural brain network topology overlaps with heritability for integrity and volume of white matter remains unknown. In this study, structural network topology was examined using diffusion tensor imaging at 3T. Binary connections between 82 structurally defined brain regions per subject were traced, allowing for estimation of individual topological network properties. Heritability of normalized characteristic path length (λ), normalized clustering coefficient (γ), microstructural integrity (FA), and volume of the white matter were estimated using a twin design, including 156 adult twins from the newly acquired U‐TWIN cohort. Both γ and λ were estimated to be under substantial genetic influence. The heritability of γ was estimated to be 68%, the heritability estimate for λ was estimated to be 57%. Genetic influences on network measures were found to be partly overlapping with volumetric and microstructural properties of white matter, but the largest component of genetic variance was unique to both network traits. Normalized clustering coefficient and normalized characteristic path length are substantially heritable, and influenced by independent genetic factors that are largely unique to network measures, but partly also implicated in white matter directionality and volume. Thus, network measures provide information about genetic influence on brain structure, independent of global white matter characteristics such as volume and microstructural directionality. Hum Brain Mapp 35:5295–5305, 2014. © 2014 Wiley Periodicals, Inc.

Keywords: twin, heritability, network, DTI

INTRODUCTION

Knowledge about the extent to which genes and environment shape human brain structure is of fundamental importance to our understanding of both typical and atypical brain development. During the past decade, important advances have been made in our understanding of the genetic influences on human brain structure as it has been shown that both grey and white matter volume are highly heritable [Baaré et al., 2001; Peper et al., 2007; Thompson et al., 2001; Wright et al., 2002]. Genetic influences on brain structure are not limited to its global morphology. Diffusion tensor imaging (DTI) studies have shown that additive genetic factors account for a significant part for the variation in measures of white matter microstructural properties such as fractional anisotropy (FA) and magnetization transfer ratio (MTR) [Brouwer et al., 2010; Chiang et al., 2009, 2011; Pfefferbaum et al., 2001].

In recent years, the advance of network approaches to brain connectivity has had a major impact for understanding the organization of the human connectome as it is a powerful way to characterize the topology of structural connections between brain regions. Using DTI, the organization of network topology has been studied extensively by the application of graph theoretical approaches where the connectivity of the brain is represented in a matrix [Achard et al., 2006; Bullmore and Sporns, 2009; Micheloyannis et al., 2006; Van den Heuvel et al., 2010]. Individual differences in network topology are associated with heritable phenotypes such as intelligence and schizophrenia [Basset et al., 2008; Fornito et al., 2012; Li et al., 2009; Van den Heuvel et al., 2010]. Such observations make individual network topology a candidate endophenotypic marker for linking genes to behavioral traits (Thompson et al., 2013). For white matter volume, it has already been shown that considerable genetic associations with these phenotypes exist [Hulshoff Pol, 2004, 2012; Posthuma et al., 2002].

Determining the heritability of structural brain network topology is an important step forward in understanding mechanisms through which genetic influences on brain morphology eventually contribute to human behavior in health and disease. However, little is known about the heritability of individual variability in network topology. In this study, the heritability of network topology was assessed using a twin model. To estimate the relative influence of genes and environment on network characteristics, the twin model focuses on the difference in resemblance for a particular trait between monozygotic (MZ) twins who share (nearly always) 100% of their genes relative to dizygotic (DZ) twins who share on average 50% of their segregating genes. As both types of twins are thought to share a similar amount of environmental factors, a trait can be assumed to be heritable if MZ twins resemble each other closer than DZ twin pairs. Twin modeling can also be applied to study genetic correlations between traits by calculating correlations across twins and traits [Bohlken et al., 2014; van Soelen et al., 2012].

Using this type of genetic modeling, the heritability of the normalized characteristic path length and normalized clustering coefficient were estimated. Because genetic influences are known to play a major part in many brain characteristics that may also influence network topology, such as total white matter volume and white matter mean FA the genetic model was expanded to incorporate these features. Thus, genetic correlations between traits could be estimated to test whether the sources of genetic variance are independent.

METHODS

Subjects

In this study 156 twins (60% female) participated, consisting of 45 MZ, and 33 DZ complete twin pairs. Of the DZ twins, five pairs were opposite sex pairs (DOS). These twins were newly recruited in the period between 2009 and 2013 as part of the newly acquired U‐TWIN cohort. All subjects were between the age of 18 and 67 years (mean 31.9, s.d. 13.6 years). The MZ and DZ twin groups did not differ significantly in age, handedness or sex (for details see Table 1). Substance use and mental health were assessed by the Comprehensive Assessment of Symptoms and History (CASH) [Andreasen et al., 1992]. Upon participation, all subjects gave their written informed consent. This study was approved by the Medical Ethical Committee of the UMC Utrecht and the experiments were in accordance with the Declaration of Helsinki.

Table 1.

Sample demographics

Sample demographics
Mean age Handedness r Sex
MZ 33.6(14.0) 89% 58% female
DZ 30.4(13.5) 79% 59% female
Open in a new tab

Scan Acquisition

MRI scans were acquired on a Philips Achieva scanner operating at 3 T, using an eight‐channel SENSE head‐coil. For each participant, a T1‐weighted scan and a set of two DTI scans were collected. The T1‐weighted three‐dimensional fast‐field echo scan was acquired with the following parameters: 2,200.8 mm contiguous slices; echo time (TE) 4.6 ms; repetition time (TR) 10 ms; flip angle 8°; in‐plane voxel size 0.75 × 0.75 mm2.

The diffusion scans consisted of a single shot EPI‐DTI with 30 diffusion weighted scans (b = 1,000 s/mm2) with non‐colinear gradient directions and five diffusion‐unweighted scan (b = 0 s/mm2), TR/TE = 7,035/68 ms, FOV 240 mm, matrix 128/128, 75 slices at 2 mm thickness, no gap, SENSE factor 3, no cardiac gating. The two transversely acquired diffusion‐weighted datasets were acquired using the same parameters but with reverse k‐space readout, allowing for the correction of weighted imaging artifacts and increasing signal to noise ratio [Andersson et al., 2003].

Scan Processing

For each individual dataset, the T1‐weighted image was used for anatomical reference, the selection of nodes in the brain network and the calculation of total white matter volume (wmVOL). Brain regions were selected automatically using the FreeSurfer segmentation pipeline (V5.1; http://surfer.nmr.mgh.harvard.edu) [Fischl et al., 2004]. By automatically segmenting subcortical structures, and parcellation of the cortex, the brain was divided into 82 distinct anatomical regions. These regions represented the nodes in the network analysis. Subsequently, an individual mask was created containing all 82, segmented anatomical regions for each subject. This mask was registered to the DTI data set using a six‐parameter rigid body transformation with nearest neighbor interpolation. The registration fit was visually checked for all individual datasets, to ensure that no gross misalignments occurred.

Preprocessing of the diffusion weighted scans was performed with the diffusion toolbox of Andersson et al. [Andersson and Skare, 2002; Andersson et al., 2003] and in‐house developed software [Mandl et al., 2010]. First, susceptibility artifacts were corrected by calculating a distortion map based on the two b = 0 images acquired with reversed k‐space readout. Subsequently it was applied to the two sets of 30 direction‐weighted images. This resulted in a corrected DTI set consisting of a single b = 0 image and 30 corrected weighted images, thereby avoiding the need for non‐linear registration approaches to the T1‐weighted images [Andersson et al., 2003]. The DTI set was corrected for Eddy‐current distortions and small head movements by realigning all scans to the diffusion‐unweighted image [Andersson and Skare, 2002].

Diffusion Profile Modeling and Fiber Tractography

Modeling of the diffusion profile was performed using a constrained compressed sensing algorithm called Crossing Fiber Angular Resolution of Intra‐Voxel structure (CFARI) [Landman et al., 2012]. CFARI models the diffusion profile in each voxel as a finite mixture of discrete and independent compartments, defining the diffusivity within each compartment separately. This has the advantage that it provides a robust framework for identifying intra‐voxel structure and is able to estimate fiber tracts in areas of high fiber complexity (e.g. crossing fibers) despite the limited number of 30 diffusion orientations in which the DTI data were acquired. CFARI is implemented in the Java Image Science Toolkit (JIST) and is publicly available (http://www.nitrc.org/projects/jist) [Lucas et al., 2010].

Tractography was performed using an approach called INtravoxel Fiber Assegnment by Continuous Tractography (INFACT) [Landman et al., 2012], which is a continuous tracking method based on the FACT algorithm [Mori and van Zijl, 2002]. Conventional tensor fitting was used to calculate the FA value within each voxel in the white matter (JIST). All voxels with FA > 0.3 were used as starting seeds for tractography. Tracing was ended when a voxel with FA < 0.15 was encountered or when the turning angle exceeded 45°. A Runge‐Kutta solver was used for determining tract continuation. After tractography was completed, all fibers shorter then 10 mm were discarded, as they were deemed spurious. Finally, all remaining fibers were linearly extended by 5 mm in the orientation prior to termination to maximize the probability of penetration into the grey matter. The presence of a white matter connection between two grey matter regions was determined by labeling each streamline with the grey matter areas it connects based on the anatomical segmentation mask.

Calculating Mean FA

A value of mean FA in the white matter was calculated per subject. This was achieved by averaging the FA value across all voxels through which a white matter connection was traced using INFACT, within each subject. This way, only voxels that participated in the connectivity analysis, and thus in determining the network parameters, contributed to the value of mean FA. After calculating the wmFA, a total of six scans were excluded from further DTI/network analysis due to statistically deviant values (i.e. more then three standard deviations away from the mean).

Reconstruction of Individual Networks

Individual networks were determined based on the reconstructed fiber tracts combined with the collection of segmented brain regions [Van den Heuvel and Sporns, 2011]. The brain network can mathematically be described as G = (V, E), consisting of a set of nodes (V) and edges (E). In this study V consists of the 82 distinct brain regions per subject. For each pair of brain regions i and j, it was determined whether there was a connection between them, based on the reconstructed fibers. If a connection was found between i and j, it was added to the connectivity matrix. This procedure was repeated for all possible combinations of i and j until the binary connectivity matrix was filled. The matrix was computed by simply adding the value 1 for every connection between node i and j to the connectivity matrix, creating a binary connectivity matrix.

Clustering coefficient (C) and characteristic path length (L) parameters were calculated using the Brain Connectivity Toolbox [Rubinov and Sporns, 2010]. Figure 1 shows a graphical representation of the way C and L were calculated. To correct for topology differences based on the number of edges in the connectivity matrix, a randomization procedure was performed. In each individual connectivity matrix, every edge was reshuffled 10 times, averaged over 250 trials. From these randomized matrices, individual L random and C random were computed by averaging over the trials. The normalized characteristic path length lambda (λ) was calculated as: λ = L/L random. The normalized clustering coefficient gamma (γ) was calculated as: γ = C/C random (Fig. 2).

Figure 1.

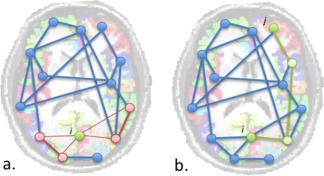
Figure 1

Open in a new tab

Calculation of C and L. a. The clustering coefficient (C) of node i is informative about the local connectedness of the network and is given by the ratio of the number of connections between the direct neighbors of node i and the maximum number of possible connections between the neighbors of node i. b. Characteristic path length (L) of node i gives information about how close it is to all other nodes in the network. It is calculated by averaging the distance d ( i , j ) to all other nodes j in the network. The distance d ( i , j ) between the two nodes is defined as the minimum number of edges that have to be crossed to get from i to j.

Figure 2.

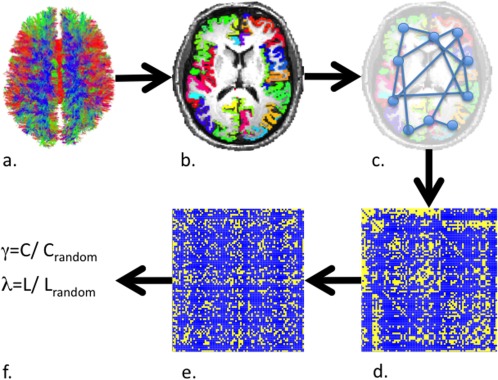
Figure 2

Open in a new tab

Flowchart of the DTI connectivity analysis. a. Tracking of individual fiber tracts was performed using a constrained sensing algorithm (CFARI). b. Individual anatomical labeling was performed for 68 cortical and 14 subcortical regions. c. Using the individual anatomical labeling, it was determined which regions of the brain were interconnected. d. This resulted in an individual connectivity matrix which depicts all edges between nodei , j where i and j are defined as each possible pair of brain regions. From these matrices, individual values for C and L were calculated. e. Each individual connectivity matrix was randomized. From this C random and L random were obtained. f. Subsequently λ and γ could be calculated.

Statistical Analysis

All statistical analyses were carried out using the R statistical software package [version 1.40, R Core Team, 2012]. Because the twin sample included DOS twins, individual connectivity based network parameters (γ and λ), as well TB and wmFA, were corrected for subject's sex and age using a linear regression. All further data analysis was carried out on the unstandardised residuals from these regressions.

Structural Equation Modeling

The twin model was implemented using structural equation modeling (SEM) approaches, in which the contributions of additive genetic effects (A), shared environmental effects (C), and unique environmental effects (E) to trait variation and covariation are estimated by maximum likelihood. SEM was implemented in OpenMx software [Boker et al., 2011] in R [R Core Team, 2012].

To estimate the phenotypic and genetic correlations between network parameters (γ and λ), wmFA and wmVOL, a trivariate model was used. In this model, the covariances between binary network parameters, wmFA and wmVOL were decomposed into genetic and environmental sources. Decomposition of covariance between traits was carried out based on the comparison of cross‐trait/cross‐twin correlations for MZ and DZ twins (i.e., the correlation between a trait (e.g., λ) of twin 1 with another trait (e.g., wmVOL) of twin 2, where twin 1 and twin 2 represent a twin‐pair) [Neale and Cardon, 1992]. If the absolute value of the correlation between λ of twin 1 and wmVOL of twin 2 is larger in MZ twins than in DZ twins, this indicates that genes influencing λ (partly) overlap with genes that influence wmVOL. In other words, there is a genetic correlation between the two traits. If this correlation is less than twice as large in MZ twins as compared to DZ twins, there is a common environmental correlation between the two traits. Finally, it is possible that a unique environmental component drives the association between two traits. In this case, there is a correlation between the two traits, but only within persons (and not between members of a twin pair), for an extensive discussion of the model see [Van Soelen et al., 2012].

Determining the Best Model Fit

The full trivariate model incorporates six genetic paths, six common environmental paths and six unique environmental paths. Assuming that each observed trait should include at least one unique environmental path to incorporate random noise, a full evaluation of all possible trivariate submodels would require 215 = 32,768 model fits. As it is not feasible to reliably assess the fit of this many models, a two‐step fitting procedure was adopted. First, it was assessed whether additive genetic or common environmental factor where of significant influence on each observed trait separately, using univariate modeling. Thus, it was tested whether the full ACE model (family resemblance is attributable to both additive genetic and environmental factors) fitted as well as an AE model (family resemblance is solely attributable to additive genetic effects), a CE model (family resemblance is solely attributable to common environmental factors), or an E model (no family resemblance), favoring the simplest model explaining the data best [Neale, 2004]. Testing contributions of the latent A, C, E factors on specific variables was done comparing the likelihoods of nested models (−2 log likelihood difference is then χ 2 distributed). A χ 2 larger than 3.84 (1 df) indicates a significant difference at α = 0.05, which means that the reduced model provided a significantly worse fit to the data. If a variance component could be dropped based on the univariate model fit, it was not considered in the trivariate model. If a variance component could not be dropped based on the univariate model fit, it was incorporated in the trivariate model. In the case that univariate model selection could not determine whether dropping A or C provided a better fit to the data, both components were added to the trivariate model. Subsequently, it was assessed which combination of paths belonging to each component resulted in the best fit by comparing all possible combinations to the full ACE model. If dropping a model component did not result in a significant drop in fit, it was considered a superior model. If two models contained an equal number of components, a choice was made based on the Akaike Information Criterion (AIC) [Akaike, 1974].

Network Thresholding

Unthresholded matrices are thought to be more susceptible to false positive connections [De Reus et al., 2013]. Therefore, the heritability analysis was repeated several times after the application of a group threshold. This threshold was set to allow only connections that were present in a certain percentage of subjects. This procedure started at a threshold of 0% overlap (no threshold), moving with increments of 10% to a threshold of 90% (connections are only considered valid if found in at least 90% of subjects). After the removal of below threshold connections, the γ‐ and λ‐parameters were recalculated and heritability was assessed using the trivariate model.

RESULTS

Network Parameters and Global Brain Measures

To assure that no a priori group differences between MZ and DZ twins were present, their mean global brain measures and network parameters were compared. Such a priori group differences were not observed on wmVOL (p = 0.22), wmFA (p = 0.89), λ (p = 0.59), or γ (p = 0.67). Furthermore, within‐twin‐within‐trait correlations were calculated to point out face validity of genetic influence (Table 2).

Table 2.

Imaging and network measures

Measure outcomes and twin correlations
γ λ wmFA WM (vol in ml)
Mean (s.d.)
MZ 1.56(0.09) 1.04 (0.01) 0.36(0.01) 511.1 (50.6)
DZ 1.56(0.11) 1.05 (0.01) 0.36 (0.01) 500.2 (51.7)
Correlation (95% C.I.)
MZ 0.64 (0.42 : 0.79) 0.54 (0.28 : 0.73) 0.61 (0.37 : 0.77) 0.94 (0.89 : 0.97)
DZ 0.37 (0.02 : 0.64) 0.12 (−0.24 : 0.45) 0.24 (−0.11 : 0.55) 0.46 (0.13 : 0.69)
Open in a new tab

Model Selection

Univariate model fitting showed that wmVOL, γ and λ were best described by an AE model, as dropping C from the model did not reduce the model fit significantly. For wmFA, although the AIC value of the AE model was slightly lower, dropping A or C did not result in a significantly worse model fit (Supporting Information Table 1). Therefore, a trivariate model containing AE paths for wmVOL, ACE paths for wmFA and AE paths for γ or λ was subsequently assessed. All possible combinations of modeling a2,2, a2,3, c2,2 and c2,3 paths were examined. Based on the AIC value, the model containing only a2,2 and a2,3 was considered the best fit (Supporting Information Table 2). Thus a trivariate model incorporating AE for wmVOL, AE for wmFA and AE for γ or λ was considered the best fit for the data (Figs. 3 and 4).

Figure 3.

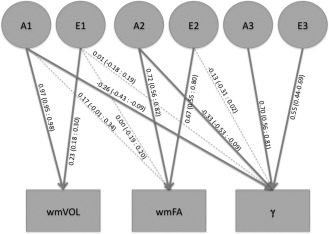
Figure 3

Open in a new tab

Trivariate model output for γ. The variance in the traits shown in the boxes is decomposed into additive genetic (A) and environmental (E) influences denoted with circles. Standardized path coefficients (95% confidence interval) are displayed for each decomposition, fat arrows indicate a significant contribution.

Figure 4.

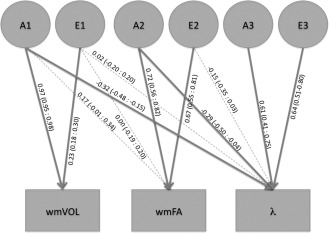
Figure 4

Open in a new tab

Trivariate model output for λ. The variance in the traits shown in the boxes is decomposed into additive genetic (A) and environmental (E) influences denoted with circles. Standardized path coefficients (95% confidence interval) are displayed for each decomposition, fat arrows indicate a significant contribution.

Heritability of Network Parameters and Global Brain Measures

The heritability of γ was estimated at 0.68 and the heritability of λ was estimated at 0.57. The heritability of wmVOL was estimated to be 0.95 and the heritability of wmFA was estimated to be 0.55 (Table 3).

Table 3.

Trivariate model output

AE trivariate model
Measure h2 e2 Rph FA RgFA ReFA Rph WM Rg WM Re WM
WM 0.95 (0.91 : 0.97) 0.05 (0.03 : 0.09) 0.17 (−0.00 : 0.33) 0.23 (−0.01 : 0.46) 0.01 (−0.27 : 0.29) ‐ ‐ ‐
wmFA 0.55 (0.35 : 0.70) 0.45 (0.30 : 0.65) ‐ ‐ ‐ 0.17 (−0.00 : 0.33) 0.23 (−0.01 : 0.46) 0.01 (−0.27 : 0.29)
γ 0.68 (0.48 : 0.80) 0.32 (0.20 : 0.52) −0.38 (−0.51 : −0.22) −0.47 (−0.69 : −0.19) −0.23 (−0.48 : 0.37) −0.26 (−0.41 : −0.08) −0.33 (−0.52 : −0.11) −0.01 (−0.29 : 0.31)
λ 0.57 (0.32 : 0.73) 0.43 (0.27 : 0.68) −0.37 (−0.50 : −0.21) −0.47 (−0.73 : −0.14) −0.22 (−0.47 : 0.05) −0.31 (−0.46 : −0.15) −0.43 (−0.64 : −0.20) 0.04 (−0.28 : 0.34)
Open in a new tab

Columns one and two provide estimates of heritability and environmental factors on WM, wmFA, γ and λ from a trivariate model incorporating WM, wmFA and λ (γ, respectively). Column three shows the phenotypic correlation with wmFA. In column four and five show the genetic and environmental correlations with FA. Column six shows the phenotypic correlation with WM. Columns seven and eight display the genetic and environmental correlations with WM. All estimates are followed by a 95% conficence interval (CI) between brackets.

Genetic Sources Acting on Network Parameters

The standardized path estimates were obtained from the trivariate model to show which factors influence the genetic variability in γ and λ (see Supporting Information Table 2). The path coefficients show that the genetic variance in λ and γ is explained by three separate genetic factors.

The first genetic factor that contributes to γ is shared with wmVOL and explains 16.2% of the genetic variance and for 11.0% of the total variance in γ. The second genetic factor that contributes to γ is shared with wmFA and explains 10.6% of the genetic variance and 7.2% of the total variance in γ (Fig. 3). The genetic factor that contributes only to γ was estimated to explain 73.1% of the genetic variance and 49.5% of the total variance in the trait.

The first genetic factor that contributes to λ is shared with wmVOL and explains 18.6% of the genetic variance and for 10.5% of the total variance in λ. The second genetic factor that contributes to λ is shared with wmFA and explains 14.8% of the genetic variance and 8.4% of the total variance in λ (Fig. 4). The genetic factor that contributes only to λ was estimated to explain 66.6% of the genetic variance and 47.6% of the total variance in the trait.

Genetic and Phenotypic Correlations

In concordance with the genetic factors found to act on γ, significant negative phenotypic and genetic correlations were observed between with wmFA (r ph= −0.38; r g = −0.47) and with wmVOL (r ph = −0.26; r g = −0.33). For λ, significant negative phenotypic and genetic correlations were observed between λ and wmFA (r ph = −0.37; r g = −0.43). Furthermore, significant negative phenotypic and genetic correlations were estimated between λ and wmVOL (r ph = −0.31; r g = −0.43). wmVOL and wmFA showed no significant correlations (see Table 3 for AE model output).

Network thresholding

Putting a group‐mask based threshold on the connectivity matrices resulted in a decrease of estimated genetic variance as the threshold increased (Fig. 5). The heritability estimate for γ remained relatively stable until the threshold exceeded 40%; the heritability of λ remained relatively stable until the group threshold exceeded 50%.

Figure 5.

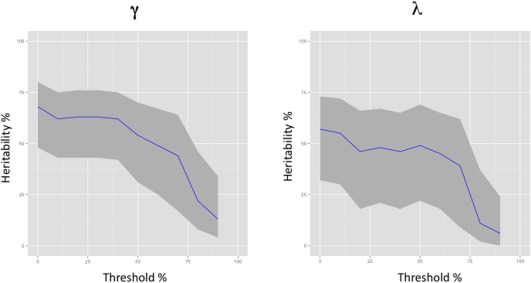
Figure 5

Open in a new tab

Heritability plotted against network group threshold, for both γ and λ. Results were obtained from the trivariate model. The grey area surrounding the plot line is the 95% confidence interval of the heritability estimate.

DISCUSSION

In 156 monozygotic and dizygotic twins, the heritability of individual variation in structural brain network topology was studied. Characteristics of global network connectivity (normalized characteristic path length and normalized clustering coefficient) were estimated using genetic modeling. Both the normalized clustering coefficient and normalized characteristic path length of the structural brain network were found to be under substantial genetic influence. The heritability of the normalized clustering coefficient was estimated to be 68%, whereas the heritability of the normalized clustering coefficient was estimated to be 57%. Genes implicated in white matter volume (h 2 = 96%), and genes implicated in mean FA (h 2 = 55%) each contributed separately and significantly to the heritability of both network topology parameters.

Our finding of genetic influence on the normalized characteristic path length is consistent with a few recent reports on heritability of brain networks, including that of functional and structural connectivity [Fornito et al., 2011; Jahanshad et al., 2012b; Van den Heuvel et al., 2013a]. As a shorter average path length allows more integrated and direct communication between distant brain regions [Van den Heuvel et al., 2013a], these studies including the present thus support the contention that the global efficiency of the structural brain network is under substantial genetic control. To our knowledge, the heritability of the normalized clustering coefficient in structural brain networks has not been studied before. However, our finding of genetic influence on both topological properties is in line with current ideas about genetically determined cost‐efficient wiring of the human brain, as a the structural network architecture of the human brain suggests a trade‐off between local clustering and long distance integration of information [Bullmore and Sporns, 2012].

Extending on previous observations of network heritability, the present study allowed for further discrimination as to the genetic sources acting on network parameters by using trivariate genetic modeling. Genetic sources from white matter volume and mean FA were found to each contribute significantly to network topology. White matter volume was even estimated to be under near complete genetic control (h 2 = 0.95). This is higher compared to previous studies [Baaré et al., 2001; Blokland et al., 2012; Peper et al., 2007]. In contrast to previous research, the current study used 3T MRI T1‐weighted imaging instead of 1.5T MRI to determine white matter volume. Increased signal‐to‐noise ratio of 3T structural imaging might have caused the increase in the genetic component estimated by producing less measurement error. There is generally no common environmental influence estimated on white matter volume [Blokland et al., 2012]. In our study, this was also the case as the DZ correlation was almost exactly 50% of the MZ correlation. Another factor that might have attributed to the high estimate for white matter heritability is the broad age range of the sample (18–67 years). Although a linear correction for age was applied before estimation of heritability, we cannot be entirely sure that all variance due to age was taken out of the data. Therefore, any residual age variance might have been attributed to the genetic component, as it is non‐random. The genetic correlation between white matter volume and both topological network properties was negative. For the normalized characteristic path length, this finding suggests that a partially shared genetic source between these phenotypes benefits global structural brain network efficiency as a larger body of white matter allows for more integrated long distance connections [Van den Heuvel et al., 2013a]. Simultaneously, this influence might cause the normalized clustering coefficient to decrease as the relative emphasis on long distance integration possibly results in a lower degree of clustering in the network.

White matter mean FA was substantially influenced by additive genetic factors. The estimate of 55% in the present study is in line with current estimates in twins [Jahanshad et al., 2013b]. Although the AE model was assessed to be the best fit to the data, the influence of common environmental factors on mean FA cannot be entirely ruled out as the model fit was not significantly reduced when the A component was dropped. Therefore, it could be that the estimated heritability of mean FA is slightly increased due to model selection. The influence on this is probably minor as the monozygotic and dizygotic twin correlations clearly suggest substantial genetic influence.

The genetic correlation between white matter mean FA and both topological network properties was estimated to be ‐.47, explaining < 10% of the total variance in each network parameter. The observation that mean FA is equally negatively correlated to both network parameters suggests a general influence on the structural brain network. Possibly, a higher mean FA allows for more abundant long distance connections, decreasing the normalized characteristic path length. Simultaneously, this influence might cause the network to be less clustered as connections tend to travel further instead of connecting locally.

The largest proportion of genetic variance in both the clustering coefficient and normalized characteristic path length was estimated to be independent of white matter volume and mean FA. This is an important finding as it shows that topological network measures provide new information about genetic influences on human brain structure that is not captured by global aspects of white matter tissue. Therefore, global network properties could be considered an endophenotype, providing new possibilities for linking genetic influence to brain structure. This is in line with the findings of several imaging genetics studies that were able to find associations between genetic variants and structural brain network topology [Dennis et al., 2011, 2012; Marenco et al., 2007]. As individual differences in network topology are associated with heritable diseases such as autism, Alzheimer's and schizophrenia [He et al., 2010; Jahanshad et al., 2013a; Liu et al., 2008; Lo et al., 2010; Micheloyannis et al., 2006; Van den Heuvel et al., 2010, 2013b], our findings thus suggest that mathematical estimates of structural network topology might prove a candidate endophenotypic marker for disease liability. Thus, the genetic influence on global network topology is to a large extent independent of other global brain measures and therefore provides new information about genetic influence on brain structure.

Although the correlation between white matter volume and mean FA was quite sizeable, it did not reach significance. Possibly, this has been the result of insufficient power as the confidence intervals around the correlation were quite substantial. To our knowledge, the genetic association between white matter volume and mean FA has not been studied before. It has been shown that white matter partial volume effects can be of influence on DTI tractography analyses [Vos et al., 2011]. This relationship might have introduced a correlation between both features of white matter. Importantly, our data show that both attributes of white matter are influenced by (partly) independent genetic factors. This shows that although both features might be correlated, they also provide independent information about genetic influence on human brain structure.

The extent to which genetic factors were estimated to influence the normalized characteristic path length was slightly lower in the present study (h 2 = 0.57) compared to earlier work (h 2 = 0.76) [Jahanshad et al., 2012]. This difference might be explained by the differences in network characterization. The previous study adopted a fixed edge approach, where the Euclidian distance between the connected nodes weighted each edge. Because of the specific focus on topology in the present study, the edges of the individual network were kept binary. Hence, the connectivity parameter itself was more dependent on the distribution of edges in the network and less on the distance. This allowed for the partitioning of genetic variance into distinct sources.

The network thresholding procedure showed that the heritability of both normalized clustering coefficient and normalized shortest path length remained fairly stable until the threshold reached a point at which at least 40% to 50% intersubject overlap was required for a connection to be maintained. This is quite close to the 60% threshold at which was estimated to be the ideal trade‐off between finding false‐positive and false‐negative connections [de Reus et al., 2013]. It is not surprising that the heritability goes down with higher thresholds as more variance is selected out with every increase. In fact, network parameters showed the highest heritability estimate when no threshold was applied. This suggests that although “false‐positive” connections may exist, they show a good degree of measurement reliability, as this is supported by a high correlation within monozygotic twins.

Some limitations on the interpretation of genetic models should be taken into consideration when interpreting our results. First, although the interpretation of a genetic correlation (as it is described above) is consistent with a partially overlapping set of genes directly influencing both phenotypes, the genetic model does not take into account other mechanisms. Processes such as linkage‐disequilibrium, phenotypic causality or environmentally mediated effects of one genetically influenced trait may also explain a genetic correlation on another [de Moor et al., 2008; Rijsdijk and Sham, 2002]. However, both mean FA and white matter volume are traits in which additive genetic factors are known be of major influence. Also, the within twin within trait correlations of the normalized path length were consistent with an additive genetic pattern (MZ correlations about two times larger than the DZ correlation) therefore it seems unlikely that the genetic correlation estimated is entirely explained by non‐genetic factors. Second, measurement reliability is a known issue for tractography‐based networks. Estimates for the test‐retest reliability of the average shortest path length and clustering coefficient vary between 0.3 and 0.7, depending partly on the type of scan and tractography algorithm [Basset et al., 2011; Dennis et al., 2012, 2013]. In the current study, it was not possible to directly assess the test‐retest reliability. However, the lower bound of the confidence interval for the heritability of white matter mean FA was estimated at 0.35. This can be considered a proxy for the lower bound of the test‐retest reliability of the DTI scan. Although a reliability of 0.35 is not ideal, significant genetic contributions could be estimated. We can however not exclude the possibility that genetic contributions were underestimated due to measurement error.

In summary, this study provides evidence that individual variation in topological aspects of the structural human brain network is under influence of additive genetic factors. One genetic factor is shared with white matter volume and another is shared with white matter microstructural properties. Importantly, a major proportion of genetic variance in both network parameters can be considered independent of global aspects of white matter. This suggests that mathematical estimates of structural network topology provide novel information about genetic influences on human brain structure. Moreover, our findings suggest that aspects of network topology might be considered as endophenotypic markers for heritable brain disorders such as schizophrenia or autism, as these disorders have been associated with alterations in structural network topology.

Supporting information

Supplementary Information Table I.

Click here for additional data file. (59KB, doc)

Supplementary Information Table II.

Click here for additional data file. (81KB, doc)

Supplementary Information Table III.

Click here for additional data file. (68.5KB, doc)

This article was published online on 21 May 2014. An error was subsequently identified. This notice is included in the online and print versions to indicate that both have been corrected 6 June 2014.

REFERENCES

  1. Achard S, Salvador R, Whitcher B, Suckling J, Bullmore E (2006): A resilient, low‐frequency, small‐world human brain functional network with highly connected association cortical hubs. J Neurosci 26:63–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Achard S, Bullmore E (2007): Efficiency and cost of economical brain functional networks. PLoS Comput Biol 3:e17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Akaike H (1974): A new look at the statistical model identification. Automatic Control IEEE Trans 19.6:716–723. [Google Scholar]
  4. Andersson JLR, Skare S, Ashburner J (2003): How to correct susceptibility distortions in spin‐echo echo‐planar images: application to diffusion tensor imaging. Neuroimage 20:870–88. [DOI] [PubMed] [Google Scholar]
  5. Andersson JLR, Skare S (2002): A model‐based method for retrospective correction of geometric distortions in diffusion‐weighted EPI. Neuroimage 16:177–99. [DOI] [PubMed] [Google Scholar]
  6. Andreasen NC, Flaum M, Arndt S (1992): The Comprehensive Assessment of Symptoms and History (CASH) An instrument for assessing diagnosis and psychopathology. Arch Gen Psychiatry 49:615. [DOI] [PubMed] [Google Scholar]
  7. Baaré WFC, Pol HEH, Kahn RS (2001): Quantitative genetic modeling of variation in human brain morphology. Cereb Cortex 11:816–824. [DOI] [PubMed] [Google Scholar]
  8. Bassett DS, Brown JA, Deshpande V, Carlson JM, Grafton ST (2011): Conserved and variable architecture of human white matter connectivity. Neuroimage 54:1262–1279. [DOI] [PubMed] [Google Scholar]
  9. Bassett DS, Bullmore E, Verchinski B a, Mattay VS, Weinberger DR, Meyer‐Lindenberg A (2008): Hierarchical organization of human cortical networks in health and schizophrenia. J Neurosci 28:9239–9248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Blokland GAM, de Zubicaray GI, McMahon KL, Wright MJ (2012): Genetic and environmental influences on neuroimaging phenotypes: A meta‐analytical perspective on twin imaging studies. Twin Res Hum Genet 15:351–371. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bohlken MM, Brouwer RM, Mandl RCW, van Haren NEM, Brans RGH, van Baal GCM, de Geus EJC, Boomsma DI, Kahn RS, Hulshoff Pol HE (2014): Genes contributing to subcortical volumes and intellectual ability implicate the thalamus. Hum Brain Mapp 35:2632–2642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Boker S (2011): Openmx: An open source extended structural equation MODELING. Psychometrika 76:306–317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Brouwer RM, Mandl RCW, Peper JS, van Baal GCM, Kahn RS, Boomsma DI, Hulshoff Pol HE (2010): Heritability of DTI and MTR in nine‐year‐old children. Neuroimage 53:1085–1092. [DOI] [PubMed] [Google Scholar]
  14. Bullmore E, Sporns O (2009): Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 10:186–198. [DOI] [PubMed] [Google Scholar]
  15. Chiang M‐C, Avedissian C, Barysheva M, Toga AW, McMahon KL, de Zubicaray GI, Wright MJ, Thompson PM (2009): Extending genetic linkage analysis to diffusion tensor images to map single gene effects on brain fiber architecture. Med Image Comput Assist Interv 12:506–513. [DOI] [PubMed] [Google Scholar]
  16. Chiang M‐C, McMahon KL, de Zubicaray GI, Martin NG, Hickie I, Toga AW, Wright MJ, Thompson PM (2011): Genetics of white matter development: a DTI study of 705 twins and their siblings aged 12 to 29. Neuroimage 54:2308–2317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Chiang M‐C, Barysheva M, McMahon KL, de Zubicaray GI, Johnson K, Montgomery GW, Martin NG, Toga AW, Wright MJ, Shapshak P, Thompson PM (2012): Gene network effects on brain microstructure and intellectual performance identified in 472 twins. J Neurosci 32:8732–8745. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Dennis EL, Jahanshad N, Rudie JD, Brown J a, Johnson K, McMahon KL, de Zubicaray GI, Montgomery G, Martin NG, Wright MJ, Bookheimer SY, Dapretto M, Toga AW, Thompson PM (2011): Altered structural brain connectivity in healthy carriers of the autism risk gene, CNTNAP2. Brain Connect 1:447–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dennis EL, Jahanshad N, Toga AW, McMahon KL, de Zubicaray GI, Martin NG, Wright MJ, Thompson PM (2012): Test‐retest reliability of graph theory measures of structural brain connectivity. Med Image Comput Assist Interv 15:305–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Fischl B, Kouwe A, van der Destrieux C, Halgren E, Ségonne F, Salat DH, Busa E, Seidman LJ, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale AM (2004): Automatically parcellating the human cerebral cortex. Cereb Cortex 14:11–22. [DOI] [PubMed] [Google Scholar]
  21. Fornito A, Zalesky A, Bassett DS, Meunier D, Ellison‐Wright I, Yücel M, Wood SJ, Shaw K, O'Connor J, Nertney D, Mowry BJ, Pantelis C, Bullmore ET (2011): Genetic influences on cost‐efficient organization of human cortical functional networks. J Neurosci 31:3261–3270. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Fornito A, Zalesky A, Pantelis C, Bullmore ET (2012): Schizophrenia, neuroimaging and connectomics. Neuroimage 62:2296–2314. [DOI] [PubMed] [Google Scholar]
  23. Van den Heuvel MP, Mandl RCW, Stam CJ, Kahn RS and Hulshoff Pol HE (2010): Aberrant frontal and temporal complex network structure in schizophrenia: A graph theoretical analysis. J Neurosci 30:15915–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Van den Heuvel MP and Sporns O (2011): Rich‐club organization of the human connectome. J Neurosci 31:15775–15786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Van den Heuvel MP, van Soelen ILC, Stam CJ, Kahn RS, Boomsma DI and Hulshoff Pol HE (2013a): Genetic control of functional brain network efficiency in children. Eur Neuropsychopharmacol 23:19–23. [DOI] [PubMed] [Google Scholar]
  26. Van den Heuvel MP, Sporns O, Collin G, Scheewe T, Mandl R, Cahn W, Goni J, Hulshoff Pol H, Kahn R (2013b): Abnormal rich club organization and functional brain dynamics in schizophrenia. JAMA Psychiatry 70:783–792. [DOI] [PubMed] [Google Scholar]
  27. Hilleke E. Hulshoff Pol, Brans RGH, Haren NEM, van Schnack HG, Langen M, Baare WFC, Oel CJ, van Kahn RS (2004): Gray and white matter volume abnormalities in monozygotic and same‐gender dizygotic twins discordant for schizophrenia. Biol Psychiatry 55:126–130. [DOI] [PubMed] [Google Scholar]
  28. Hulshoff Pol HE, van Baal GCM, Schnack HG, Brans RGH, van der Schot AC, Brouwer RM, Kahn RS (2012): Overlapping and segregating structural brain abnormalities in twins with schizophrenia or bipolar disorder. Arch Gen Psychiatry 69:349–359. [DOI] [PubMed] [Google Scholar]
  29. Jahanshad N, Prasad G, Toga AW, Mcmahon KL, Zubicaray GI De, Martin NG, Wright MJ, Thompson PM (2012): Genetics of path lengths in brain connectivity networks : HARDI‐based maps in 457 adults. MBIA 7509:29–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Jahanshada N, Rajagopalana P, Huaa X, Hibar DP, Nira TM, Toga AW, Clifford R. Jack J, Saykinc AJ, Green RC, Weiner MW, Medland SE, Montgomery GW, Hansell NK, McMahon KL, Zubicaray GI, de Martin NG, Wright MJ, Thompson PM (2013a): Genome‐wide scan of healthy human connectome discovers SPON1 gene variant influencing dementia severity. Proc Natl Acad Sci USA 110:4768–4773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Jahanshad N, Kochunov P V, Sprooten E, Mandl RC, Nichols TE, Almasy L, Blangero J, Brouwer RM, Curran JE, de Zubicaray GI, Duggirala R, Fox PT, Hong LE, Landman BA, Martin NG, McMahon KL, Medland SE, Mitchell BD, Olvera RL, Peterson CP, Starr JM, Sussmann JE, Toga AW, Wardlaw JM, Wright MJ, Hulshoff Pol HE, Bastin ME, McIntosh AM, Deary IJ, Thompson PM, Glahn DC (2013b): Multi‐site genetic analysis of diffusion images and voxelwise heritability analysis: A pilot project of the ENIGMA‐DTI working group. Neuroimage 81:455–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Landman B a, Bogovic J a, Wan H, El Zahraa ElShahaby F, Bazin P‐L, Prince JL (2012): Resolution of crossing fibers with constrained compressed sensing using diffusion tensor MRI. Neuroimage 59:2175–2186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Li Y, Liu Y, Li J, Qin W, Li K, Yu C and Jiang T (2009): Brain anatomical network and intelligence. PLoS Comput Biol 5:e1000395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Lucas BC, Bogovic JA, Carass A, Bazin P‐L, Prince JL, Pham D, Landman BA (2010): The Java image science toolkit (JIST) for rapid prototyping and publishing of neuroimaging software. Neuroinformatics 8:5–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Mandl RCW, Schnack HG, Luigjes J, Van den Heuvel MP, Cahn W, Kahn RS, Hulshoff Pol HE (2010): Tract‐based analysis of magnetization transfer ratio and diffusion tensor imaging of the frontal and frontotemporal connections in schizophrenia. Schizophrenia Bull 36:778–787. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Marenco S, Siuta M a, Kippenhan JS, Grodofsky S, Chang W‐L, Kohn P, Mervis CB, Morris C a, Weinberger DR, Meyer‐Lindenberg A, Pierpaoli C, Berman KF (2007): Genetic contributions to white matter architecture revealed by diffusion tensor imaging in Williams syndrome. Proc Natl Acad Sci USA 104:15117–15122. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Micheloyannis S, Pachou E, Stam CJ, Breakspear M, Bitsios P, Vourkas M, Erimaki S, Zervakis M (2006): Small‐world networks and disturbed functional connectivity in schizophrenia. Schizophr Res 87:60–66. [DOI] [PubMed] [Google Scholar]
  38. Mori S, van Zijl PC (2002): Fiber tracking: principles and strategies—A technical review. NMR Biomed 15:468–480. [DOI] [PubMed] [Google Scholar]
  39. Neale MCCL, Cardon LR (1992): Methodology for Genetic Studies of Twins and Families (No. 67). Kluwer Academic, Dordrecht. [Google Scholar]
  40. Peper JS, Brouwer RM, Boomsma DI, Kahn RS, Hulshoff Pol HE (2007): Genetic influences on human brain structure: a review of brain imaging studies in twins. Hum Brain Mapp 28:464–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Pfefferbaum A, Sullivan EV, Carmelli D (2001): Genetic regulation of regional microstructure of the corpus callosum in late life. Neuroreport 12:1677–1681. [DOI] [PubMed] [Google Scholar]
  42. Posthuma D, de Geus EJC, Baare W, Hulshoff Pol HE, Kahn RS, Boomsma DI (2002): The association between brain volume and intelligence is of genetic origin. Nat Neurosci 5:83–84. [DOI] [PubMed] [Google Scholar]
  43. R Core Team (2012): R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. ISBN 3‐900051‐07‐0. Available at: http://www.R-project.org/.
  44. Rubinov M, Sporns O (2010): Complex network measures of brain connectivity: Uses and interpretations. Neuroimage 52:1059–1069. [DOI] [PubMed] [Google Scholar]
  45. Van Soelen ILC, Brouwer RM, van Baal GCM, Schnack HG, Peper JS, Collins DL, Evans a C, Kahn RS, Boomsma DI, Hulshoff Pol HE (2012): Genetic influences on thinning of the cerebral cortex during development. Neuroimage 59:3871–3880. [DOI] [PubMed] [Google Scholar]
  46. Sporns O, Zwi JD (2004): The small world of the cerebral cortex. Neuroinformatics 2:145–162. [DOI] [PubMed] [Google Scholar]
  47. Smit DJ, Stam CJ, Posthuma D, Boomsma DI, De Geus EJC (2008): Heritability of “small‐world” networks in the brain: a graph theoretical analysis of resting‐state EEG functional connectivity. Hum Brain Mapp 29:1368–1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Thompson P, Cannon TD, Narr KL, Erp T, Van Poutanen V, Huttunen M, Lönnqvist J, Kaprio J, Khaledy M, Dail R, Zoumalan CI, Toga AW (2001): Genetic influences on brain structure. Nat Neurosci 4:1–6. [DOI] [PubMed] [Google Scholar]
  49. Thompson PM, Ge T, Glahn DC, Jahanshad N, Nichols TE (2013): Genetics of the connectome. Neuroimage 80:475–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Wright IC, Sham P, Murray RM, Weinberger DR, Bullmore ET (2002): Genetic contributions to regional variability in human brain structure: Methods and preliminary results. Neuroimage 17:256–271. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information Table I.

Click here for additional data file. (59KB, doc)

Supplementary Information Table II.

Click here for additional data file. (81KB, doc)

Supplementary Information Table III.

Click here for additional data file. (68.5KB, doc)

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES