Abstract
Resting‐state functional connectivity (FC) is highly variable across the duration of a scan. Groups of coevolving connections, or reproducible patterns of dynamic FC (dFC), have been revealed in fluctuating FC by applying unsupervised learning techniques. Based on results from k‐means clustering and sliding‐window correlations, it has recently been hypothesized that dFC may cycle through several discrete FC states. Alternatively, it has been proposed to represent dFC as a linear combination of multiple FC patterns using principal component analysis. As it is unclear whether sparse or nonsparse combinations of FC patterns are most appropriate, and as this affects their interpretation and use as markers of cognitive processing, the goal of our study was to evaluate the impact of sparsity by performing an empirical evaluation of simulated, task‐based, and resting‐state dFC. To this aim, we applied matrix factorizations subject to variable constraints in the temporal domain and studied both the reproducibility of ensuing representations of dFC and the expression of FC patterns over time. During subject‐driven tasks, dFC was well described by alternating FC states in accordance with the nature of the data. The estimated FC patterns showed a rich structure with combinations of known functional networks enabling accurate identification of three different tasks. During rest, dFC was better described by multiple FC patterns that overlap. The executive control networks, which are critical for working memory, appeared grouped alternately with externally or internally oriented networks. These results suggest that combinations of FC patterns can provide a meaningful way to disentangle resting‐state dFC. Hum Brain Mapp 35:5984–5995, 2014. © 2014 The Authors. Human Brain Mapping published by Wiley Periodicals, Inc.
Keywords: functional magnetic resonance imaging, dynamic functional connectivity, resting state, matrix factorization
INTRODUCTION
Brain networks reconfigure over years [Dosenbach et al., 2010], days [Bassett et al., 2011], and seconds [Chang and Glover, 2010; Cribben et al., 2012; Ekman et al., 2012; Eryilmaz et al., 2011]. Fast, dynamic reconfigurations may occur in response to a changing external environment or spontaneously while a subject is at rest. In particular, spontaneous fluctuations in the temporal correlation of the BOLD activity of distinct brain regions have first been highlighted in the default mode network [DMN; Chang and Glover, 2010] and since been shown to occur in many other large‐scale networks [Allen et al., 2014; Hutchison et al., 2013a; Liu and Duyn, 2013; Smith et al., 2012]. Using unsupervised learning techniques, recent work has identified reproducible groups of functional connections that evolve in a similar manner, which we here call “functional connectivity (FC) patterns” [Allen et al., 2014; Eavani et al., 2013; Leonardi et al., 2013; Li et al., 2014]. The occurrence of various FC patterns across time challenges the assumption of unique and stable correlations during rest [Allen et al., 2014; Chang and Glover, 2010], and links between FC variability and neural activity have been reported [Allen et al., 2013; Chang et al., 2013]. Early work also suggests that these patterns are altered in several neuropsychological diseases [Jones et al., 2012; Leonardi et al., 2013; Li et al., 2014], highlighting the potential importance of dFC to provide insights that are complementary to traditional, static FC [see, e.g., Hutchison et al., 2013a, for a review].
Sliding‐window correlation analysis has been the most commonly used approach to study dynamic FC (dFC) across time and Allen et al. [2014] combined it with k‐means clustering to separate dFC into several so‐called “FC states”. In related work, Li et al. [2014] also used k‐means clustering as a first step to identify FC patterns. Preliminary results indicate that four different tasks can be successfully distinguished in individual subjects by applying k‐means clustering to sliding‐window correlations [Gonzalez‐Castillo, 2013]. Thus, dFC is sensitive to changes in cognitive states and provides enough information to reveal them. Based on these results it has been suggested that dFC may cycle through multiple discrete states during rest [Hutchison et al., 2013a]. We posit that clustering inevitably models dFC as a succession of states because its aim is to find a simple representation by approximating each windowed FC estimate by a single FC pattern. The simplicity of clustering makes it an attractive, yet also restrictive approach, and to our knowledge there is no study evaluating the importance of the implicit sparsity assumption.
Alternatively, it has been proposed to represent dFC as a linear combination of multiple FC patterns by applying principal component analysis [PCA; Leonardi et al., 2013] and a tensorial extension for task data enabled accurate classification of two cognitive states [Leonardi and Van De Ville, 2013]. PCA is a more flexible approach, but it can be prone to overfitting. Again, we posit that PCA inevitably models dFC as the combination of all (orthogonal) patterns.
Here, we explore whether dFC is better described by a succession of separated FC states or by the joint expression of multiple FC patterns. We want to understand whether sparsity is relevant from a conceptual point of view and how the FC patterns should be interpreted.
We evaluate the impact of sparsity by casting both k‐means clustering and truncated SVD/PCA1 as matrix factorizations, which decompose dFC into components and associated time‐dependent weights. In clustering, each dFC estimate is approximated by a single component with a weight of one, while in PCA each estimate is approximated by a linear combination of all orthogonal components (Fig. 1). Thus, clustering assumes a maximally sparse model, while PCA assumes no sparsity (but orthogonality). Sparse matrix factorizations can be seen as generalizations of both k‐means clustering and truncated SVD, and have previously been shown to well describe BOLD activity and static FC [Eavani et al., 2012; Lee et al., 2011, 2013].
Figure 1.
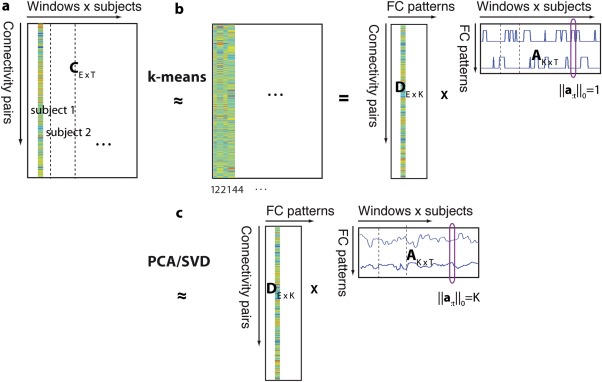
(a) dFC is temporally concatenated across multiple subjects to form matrix C. (b) k‐Means clustering separates the data into K clusters, thereby approximating C by a succession of the cluster centroids, for example, the first dFC estimate is approximated by centroid 1, the second and third by centroid 2,…. This can be seen as decomposing the dFC matrix C into K FC patterns (D) and associated sparse weights (A), where only one FC pattern may have a nonzero weight at each instance in time ( ). (c) PCA or SVD decomposes the dFC matrix into K FC patterns and associated nonsparse, orthogonal weights ( K). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
To explore the importance of temporal sparsity, we performed an empirical study. First, to test the feasibility of the proposed approach, we generated simulated data. Second, we decomposed dFC during three subject‐driven cognitive states, which provide a more naturalistic view of continuous, cognitive processing than traditional task data. Importantly, as we know the cognitive state a subject is in, we can compare the estimated FC patterns and associated weights with the known experimental paradigm. Third, we decomposed dFC during resting state.
METHODS
Participants and Data Acquisition
Twenty‐four healthy, right‐handed subjects (age range 18–30 years, 15 females) participated in this study. The data have previously been used to decode subject‐driven cognitive states [Shirer et al., 2012]. The study was approved by the institutional review board of Stanford University and informed consent was obtained from each subject.
Functional images were acquired on a 3.0T GE scanner (repetition time (TR) = 2 s, echo time (TE) = 30 ms, fiip angle = 80°, 1 interleave, matrix size 64 × 64, field‐of‐view (FOV) = 22 cm). A high‐resolution structural scan was acquired using an axial 3D fast spoiled gradient recalled echo sequence (162 slices, 0.86‐mm2 in‐plane and 1‐mm through‐plane resolution, TR = 5.9 ms, TE = 2 ms, fiip angle = 15°, FOV = 22 cm).
Participants were scanned for 10 min each while resting and completing three subject‐driven tasks: counting backwards from 5000 in steps of three (subtraction task), recalling the events of their day (episodic memory task), and silently singing a song (music task). No stimulus was presented and the investigator only marked the start and end of each 10‐min scan. Subjects were instructed to keep their eyes closed. A debriefing confirmed that all subjects stayed awake and were able to perform the tasks throughout the scan.
Preprocessing
Data were preprocessed and analyzed using FMRIBs Software Library (FSL version 4.1). The first six volumes were discarded to allow the MR signal to equilibrate. Data were corrected for motion, normalized to the MNI template, and smoothed with a 6‐mm Gaussian kernel. Subject's heart rate and respiration rate were monitored during the scan and regressed out from the fMRI data, together with the six motion parameters and their derivatives, cerebrospinal fiuid and white matter signals, and a brain‐averaged signal. Finally, data were high‐pass filtered (>0.01 Hz). The used set of motion regressors has previously shown good performance in connectivity studies of low‐motion subjects [Satterthwaite et al., 2012], and the healthy undergraduates included in this study moved little [0.017 ± 0.008 mm mean framewise displacement, vs. 0.029 ± 0.004 mm for the low‐motion group in Satterthwaite et al.)
BOLD activity was averaged within 78 functional ROIs, which were previously defined from thresholded independent components estimated from 14 of the 24 subjects and one other subject [http://findlab.stanford.edu/functional_ROIs.html, cerebellar ROIs were excluded; Shirer et al., 2012].
Dynamic Functional Connectivity Analysis
DFC estimation
We estimated dFC between all N = 78 ROIs using sliding‐window Pearson correlations [Chang and Glover, 2010]. The 78 × 78 correlation matrices were estimated using a window size of 30 TRs (60 s) and the window shifted by 5 TRs (10 s) for subsequent estimations, resulting in 53 windows for each subject and state. These choices are similar to values reported in the literature [Allen et al., 2014; Handwerker et al., 2012; Hutchison et al., 2013b; Leonardi et al., 2013] and Shirer et al. [2012] reported that different cognitive states were well distinguished with 60 s of data.
Each correlation matrix was Fisher Z‐transformed. We will refer to the vectorized, upper triangular part of each correlation matrix as “windowed FC.” Next, we temporally concatenated the windowed FC of each subject s to construct one resting‐state and one task‐based connections × windows matrix , where and W = 53 and 3 × 53 = 159 for resting‐state and task, respectively. For both the resting‐state and task‐based matrices , we subtracted the mean from each row (connection) before concatenating the centered across subjects to form a connections × (windows × subjects) matrix (Fig. 1a). The row‐wise centering of removed differences in average dFC (a measure of “static” FC) between subjects, evidenced by the fact that FC patterns estimated from phase‐randomized dFC lose all structure only after the centering step [Leonardi et al., 2013]. This step also improved the correct identification of the three subject‐driven tasks with k‐means clustering. The adjusted rand index (ARI), which measures the similarity between two data labelings and is adjusted for chance levels [Hubert and Arabie, 1985; Rand, 1971], was 0.74 with centering and 0.27 without, where a value of 0 indicates a random labeling and a value of 1, a perfect labeling.
DFC matrix factorization
We start from a generic formulation of matrix factorizations: . That is, the dFC matrix is represented as the multiplication of K FC patterns, stored as the columns of the matrix , and their associated time‐dependent weights (i.e., their importance in representing dFC at each window) in , where indexes the first column of matrix . The problem of jointly learning D and A can be formulated as
| (1) |
where arg min indicates that D and A are chosen such as to minimize the approximation error , and is the Frobenius norm, which is defined as the sum of all entries squared (matrix ‐norm). k‐Means clustering and truncated SVD represent two special cases of the more general Eq. (1).
In k‐means clustering, each windowed FC is approximated by one pattern, which corresponds to a strict sparsity constraint on the time‐dependent weights A (Fig. 1b):
| (2) |
The constraint implies that each windowed FC is approximated by a single FC pattern (as the ‐norm counts the number of nonzero entries), and that the associated weights are binary. Equation (2) describes k‐means clustering with a squared Euclidean distance: , where indicates exclusive and exhaustive cluster membership, are all windowed FCs assigned to cluster k, and is the associated cluster center that equals the average of all windowed FCs assigned to that cluster. In other words, k‐means clustering finds the cluster assignments that minimize the within‐cluster distance , where measures the distance between the two vectors. The distance in k‐means clustering is not limited to the Euclidean distance, however, and we here use one minus the correlation, which allows the weights to vary positively and compensate for differences in scaling.
Truncated SVD corresponds to different constraints (Fig. 1c):
| (3) |
where I is the identity matrix, that is, D is orthogonal, and D contains the first few eigenvectors of the connectionwise covariance matrix , and . indicates that each dFC network is approximated as a combination of all FC patterns. This constraint does not need to be imposed, but we include it for the sake of comparison between approaches.
k‐Means clustering and truncated SVD can be generalized by k‐SVD [Aharon et al., 2006]:
| (4) |
where the case generalizes k‐means clustering (i.e., without constraining the values to be binary or positive) and the case generalizes PCA (i.e., without enforcing orthogonality, which, however, still leads to a solution that spans the same subspace as one can be represented as a linear combination of the other). Using this generalization only the sparsity of the weights separates the two approaches. For solving Eq. (4), we used a fast implementation in the optimization toolbox SPArse Modeling Software (SPAMS, http://spams-devel.gforge.inria.fr/; Mairal et al., 2010). The optimization problem is not jointly convex in D and A, but can be solved by alternately updating either matrix while the other one is held fixed. At each iteration, SPAMS sequentially updates the weights A using orthogonal matching pursuit and, given the novel weights, the FC patterns D using a block‐coordinate descent approach.
Simulated and null data
We generated data under a spatiotemporal separability assumption by multiplying K = 3 FC patterns with random time courses that corresponded either to the case of separated or joint expression. The three subject‐specific FC patterns were estimated from average dFC during each of the three subject‐driven, cognitive states subtraction, memory, and music (Supporting Information Fig. 1a). This incorporated a fair amount of intersubject variability as can be expected in real fMRI data. To generate subject‐specific connection‐by‐window simulated data, we multiplied with randomly generated time courses : , where and (Supporting Information Fig. 1b). The subtraction FC pattern negatively correlated with the other two FC patterns (Pearson r < −0.6), and so to avoid ambiguity in expression of the FC patterns, we used positive weights. The subject‐specific FC patterns were estimated from average FC during each of the three subject‐driven cognitive states subtraction, memory, and music (Supporting Information Fig. 1a). This incorporated a large amount of intersubject variability as can be expected in real fMRI data. To simulate the separated expression of FC patterns, we randomly set three entries of per column to zero, that is, (Supporting Information Fig. 1b), to simulate the joint expression of FC patterns, we left as is. Finally, we added zero‐mean Gaussian noise with σ = 0.2 to each subject's data matrix .
To model the case of static FC across time, we generated by multiplying K = 1 subject‐specific FC pattern with a random time course and by adding noise. This null data preserves the overall correlation structure and fluctuations in FC purely reflect varying strength of the same underlying network topology.
Evaluation of matrix factorizations
Recovery of FC patterns
We compared the performance of k‐means clustering, truncated SVD and k‐SVD (with S = 1 and S = K) by assessing how well they recovered the true, underlying FC patterns used in the simulations. Here we set K to the true number of 3, and we study how to estimate K below. Because differed slightly between subjects, we used averaged across all subjects as the “true” FC patterns, we would like to recover. We quantified recovery for each algorithm by matching the true and the estimated FC patterns. We first calculated the Pearson correlations between the true and estimated FC patterns, and then matched the true and estimated FC patterns using the Hungarian algorithm [Kuhn, 1955; Munkres, 1957]. The Hungarian algorithm finds the matching that maximizes the sum of similarity measures (here correlation coefficients) between all corresponding pairs. For PCA, we estimated only FC patterns because the components represent axes in a lower‐dimensional space and the rank of was two. The recovery of the third FC pattern was assessed from the negative correlations (i.e., one estimated FC pattern recovered two true FC patterns, one of which with a flipped sign). k‐SVD drops the orthogonality constraint and its weights vary both positively and negatively. Therefore, we assessed its performance for both K = 3 and K = 2, for the former and latter reason cited before, respectively. For K = 3, we used the absolute values of the correlation coefficients because the sign of the FC patterns is arbitrary.
We report the smallest correlation coefficient between all corresponding pairs (worst recovery) across 100 simulations. Because k‐means clustering performed best overall in recovering the true FC patterns, we retained only k‐means clustering for the following steps (see later).
Number of FC patterns
We chose the number of FC patterns K by evaluating the reproducibility of the FC patterns in split‐half resamplings. The matrices were randomly assigned to one of two (independent) data sets of 12 subjects each. k‐Means clustering was applied separately to each data set, the cross‐correlation between the estimated FC patterns estimated, and the best matching estimated using the Hungarian algorithm. We define the reproducibility as the smallest correlation coefficient between all corresponding pairs (least reproducible FC pattern), and repeated all steps for 24 random splits. The split‐half reproducibility worked well to estimate K in our case, but other measures of intersubject reproducibility have also been proposed in the literature [e.g., Mehrkanoon et al., 2014].
Once K was determined, we applied k‐means clustering one final time to the entire data set. We visualize the K FC patterns after reshaping and symmetrizing them into 78 × 78 matrices.
Separated versus joint expression of FC patterns
k‐Means clustering assigns each windowed FC to a single FC pattern by picking the one it is most similar to. That is, k‐means clustering explores how well each windowed FC is approximated by each FC pattern individually, but then binarizes this information by assigning it to the one with maximal similarity. We calculated the correlation of each windowed FC with all K FC patterns to generate a nonsparse weight matrix A*, and assessed the asymmetry of the histogram of all correlation coefficients by calculating its skewness (Fig. 2). The skewness of symmetrically distributed data is zero, and nonzero skewness indicates asymmetry.
Figure 2.
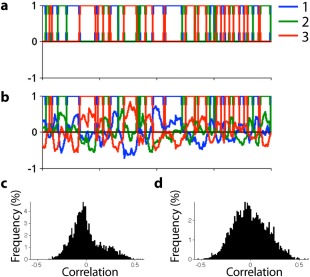
(a) k‐Means clustering assigns each dFC network to one of three clusters. (b) This assignment is guided by the similarity of each dFC network to all three FC patterns. We interpret the similarity of each dFC network to all FC patterns as a nonsparse weight matrix A*. (c) The histogram of A* distinguishes separated (left) and joint (right) expression of FC patterns. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
RESULTS
Simulated dFC
First, we compared how well k‐means clustering, truncated SVD/PCA and k‐SVD ( and ) recovered the true, underlying FC patterns in simulations. For the simulation of separated expression of FC patterns, k‐means clustering clearly outperformed all other algorithms, which is in line with the sparsity constraint of k‐means clustering (correlation coefficient of worst recovered FC pattern for k‐means clustering 0.94 vs. <0.7 for all other algorithms, Bonferroni corrected P values <10−10; Fig. 3a). For the simulation of joint expression, the different algorithms performed comparably (correlation coefficients of worst recovered FC pattern 0.58–0.7; truncated SVD significantly better than k‐SVD with K = 2, S = 1 or K = 2, S = 2, Bonferroni corrected P values 0.004 and 0.04, respectively; Fig. 3a). Because (i) k‐means clustering performed best for the separated expression and comparably for the joint expression, (ii) it avoids the ambiguity of the sign of the FC patterns (in k‐SVD and truncated SVD the sign of the FC patterns is arbitrary), and (iii) it avoids the choice of the parameter S necessary for k‐SVD, we estimated all further FC patterns with k‐means clustering.
Figure 3.
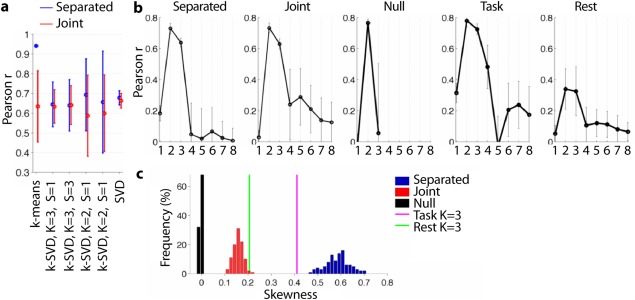
(a) Average correlation coefficient of true FC patterns with those estimated using k‐means clustering (K = 3), sparse matrix factorizations (k‐SVD with K = 3, S = 1; K = 3, S = 3; K = 2, S = 1, and K = 2, S = 2), and PCA (K = 2) for both simulated separated and joint expression of FC patterns. Error bars represent standard deviation across simulations. (b) Split‐half reproducibility for K = 1, 2,…, 8 for simulations (separated, joint, and null), subject‐driven task‐based and resting‐state dFC. Error bars represent standard deviation across splits. (c) Skewness of time‐dependent weights A* for simulations and experimental subject‐driven task‐based and resting‐state dFC. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
The split‐half reproducibility for different numbers K of FC patterns showed a clear drop once K exceeded the number of underlying FC patterns for both the separated and joint expression of FC patterns (i.e., ; Fig. 3b). In the null data, only K = 2 FC patterns were reproducible, corresponding to the trivial cases of above and below average FC (shown in Supporting Information Fig. 2).
The histogram of the weights A* was highly asymmetric for the case of separated expression (large, positive skewness; Figs. 2c and 3c). That is, each windowed FC resembled only one FC pattern strongly at each time point and thus many correlations were close to zero. The histogram of the weights A* was only weakly asymmetric for the simulations of joint expression (small, positive skewness; Figs. 2d and 3c). Because each windowed FC resembled all FC patterns to some extent, correlations were more evenly distributed. The histogram of the weights A* was symmetric for the null data, as each windowed FC correlated equally strongly with both estimated FC patterns (one positive, one negative correlation coefficient). Supporting Information Fig. 3 shows that these observations also hold when (i) simulating joint expression of 2 (instead of 3) FC patterns a time, and (ii) when using K = 4 FC patterns for either type of simulation (where the fourth FC pattern was estimated from average dFC during the resting‐state scan).
The split‐half reproducibility of the FC patterns and the shape of the histogram of the time‐dependent correlations with the FC patterns A* could thus provide information on the underlying type of data generation.
Subject‐Driven Task‐Based dFC
Figure 4a shows windowed FC averaged across windows and subjects for each subject‐driven task (after folding and symmetrizing): the subtraction task was characterized by strong FC in the visuospatial (VS) network, the episodic memory task by strong FC in the vDMN (retrosplenial cortex/medial temporal lobe network), and the music task by strong FC in the language network and the dDMN. These results are in line with those of Shirer et al. [2012].
Figure 4.
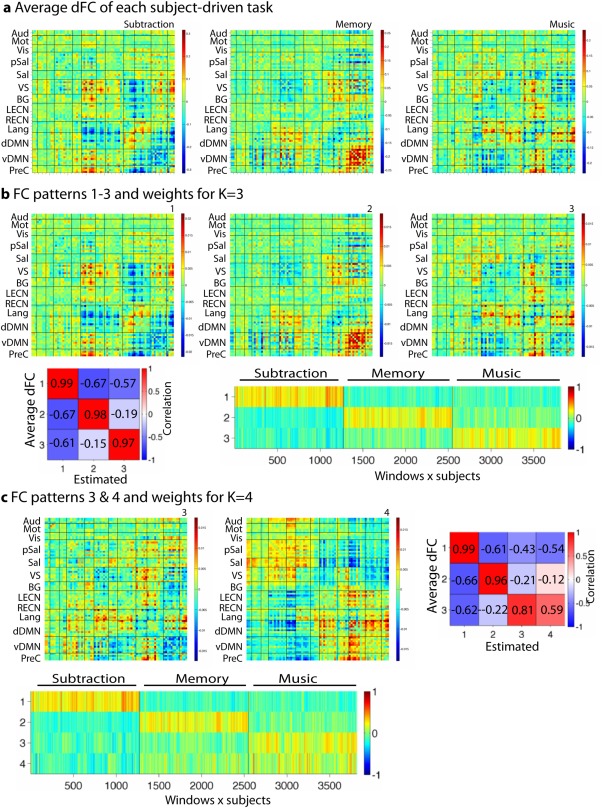
(a) Average dFC of the three subject‐driven tasks: subtraction, memory and music. (b) Estimated FC patterns (K = 3), correlation between average dFC of each task and the estimated FC patterns, and correlation coefficients of windowed FC with all 3 FC patterns across windows and subjects. The x‐axis is arranged by task, rather than by subject. (c) Same as b for K = 4 (only the two music‐related FC patterns are shown as the others do not change). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 5.
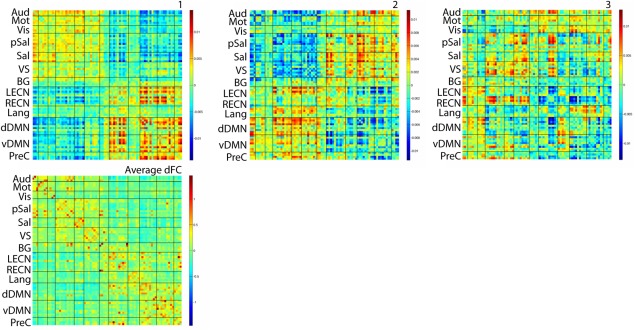
FC patterns estimated during resting‐state (1–3) and dFC averaged across all windows and subjects. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 3b shows the split‐half reproducibility for task‐based dFC, which starts to drop at K = 3, and is small after K = 4. This suggests 3 or 4 FC patterns best describe the data. For K = 3, the asymmetry of the histogram of the weights A* was close to that for the simulated separated expression (Fig. 3c), correctly suggesting that a separated expression of the FC patterns well describes the data. For K = 4, the asymmetry of the histogram of the weights A* lied in between the cases for separated and joint expression (Supporting Information Fig. 3e).
In Figure 4b, we illustrate the FC patterns estimated for K = 3 and their associated time‐dependent weights A*. Each one of the three FC patterns strongly resembled one of the three average networks shown in Figure 4a (Pearson correlation between two vectors, r = 0.99, 0.98, and 0.97, all P values <10−10) and the weights separated the three cognitive states well (ARI of k‐means labeling 0.74).
The fourth FC pattern showed two large groups of coevolving connections: one centered on externally oriented networks (salience, VS, and primary sensory networks) and one centered on internally oriented networks (DMN; Fig. 4c). The fourth FC pattern was specific to the music condition: it correlated with average FC during the music task and its weights indicated that it was predominantly—and consistently across subjects—expressed during this task (see also Supporting Information Fig. 4).
In Supporting Information Figure 5, we compare the FC patterns estimated using k‐means clustering, k‐SVD, and truncated SVD. For both k‐SVD and truncated SVD, we obtained better results for K = 2 FC patterns, where one FC pattern was similar and dissimilar to the subtraction and memory or music average dFC, respectively. k‐SVD estimated FC patterns similar to average dFC (|r| > 0.75). Because of the orthogonality constraint, PCA showed smaller correlation values (r < 0.7 for the recovery of average memory and music dFC).
Resting‐State dFC
For resting‐state dFC, split‐half reproducibility dropped after K = 3 and the asymmetry of the histogram of the weights A* overlapped with the simulated joint expression (Fig. 5). This suggests that three FC patterns that are jointly expressed best describe resting‐state dFC (Fig. 3b, c).
The estimated FC patterns showed distinct, large‐scale network topologies. FC pattern 1 revealed two groups of coevolving connections: a first group composed of the primary sensory (auditory, motor, and visual), salience and VS (or dorsal attention network) networks, and a second group of bilateral executive control networks (ECN) and the DMN. FC pattern 2 showed interactions in the opposite direction to that of FC pattern 1. We note again that each dFC time series was centered, which means that these FC patterns reflect excursions around average FC. Thus, FC pattern 2 does not indicate positive correlation between externally and internally oriented networks, rather it indicates their reduced separation once average FC is added again (and combined with the other FC patterns). FC pattern 3 highlighted a salience–VS–RECN group. A second group of connections in FC pattern 3 showed visual and language ROIs connected to the DMN.
In Supporting Information Figure 6, we compare the FC patterns estimated using k‐means clustering, k‐SVD and truncated SVD. For both k‐SVD and truncated SVD, we again obtained better results for K = 2 FC patterns, because the first two FC patterns estimated using k‐means clustering were anticorrelated (r = −0.62). Overall, all algorithms resulted in similar FC patterns (|r| > 0.75 with the FC patterns obtained with k‐means clustering).
DISCUSSION
We revisited k‐means clustering and PCA, two recently proposed approaches to identify reproducible network configurations from windowed FC, to study the importance of temporal sparsity for the representation of dFC. To compare k‐means clustering to truncated SVD/PCA, we generalized them as a sparse matrix factorization. For data simulated according to both separated and joint expression of FC patterns, k‐means clustering showed the best recovery of the underlying FC patterns overall. We then evaluated split‐half reproducibility to identify the number of FC patterns from the data, and the asymmetry of the histogram of the time‐dependent weights to assess whether the FC patterns occurred exclusively or jointly over time. Our results indicate that separated FC patterns are a good representation of subject‐driven task‐based dFC, while a joint expression of FC patterns is better suited for resting‐state dFC.
Subject‐Driven Task‐Based FC Patterns
We first analyzed dFC during three free‐streaming, subject‐driven cognitive states. Shirer et al. [2012] previously showed that these states could be distinguished with high accuracy using supervised learning (i.e., training a classifier on data with known cognitive states) and Gonzalez‐Castillo et al. [2013] recently reported that four different tasks could be identified from dFC alone by clustering windowed FC estimates of individual subjects. We extend these findings by showing that subject‐driven cognitive states can be successfully identified from dFC of multiple subjects using unsupervised learning. The fact that FC fluctuations can be related to changes in subject‐driven cognitive states is highly encouraging. Further, the correct identification of states from multi‐subject dFC was improved by first centering each subject's dFC time series so that fluctuations reflected deviations from average FC.
We identified the model parameters, such as the number of FC patterns and their temporal expression, in a data‐driven way. This indicated that task‐based dFC was well modeled using three separated FC patterns. However, a fourth FC pattern was also reproducible across independent split‐half datasets and this FC pattern occurred preferentially during the music state. Interestingly, the music state was the most difficult state to classify in the original study by Shirer et al. [2012] (60% vs. >80% accuracy for the other states). The occurrence of this FC pattern with varying strengths over time (Supporting Information Fig. 4) might suggest that subjects did not continuously perform the assigned task. The FC pattern resembled the first resting‐state FC pattern (r = 0.64), with, however, stronger contributions of the DMN and salience networks. As this FC topology resembles the FC pattern that splits the resting‐state networks into two major groups, it could be reminiscent of more intrinsic, resting‐state like, fluctuations of dFC that are intermixed with the task‐based FC patterns, and thus explain why the asymmetry of the weights is less close to the separated case than for K = 3 FC patterns.
Resting‐State FC Patterns
We next analyzed dFC during unconstrained resting state and based on our findings, we suggest that a joint expression of multiple FC patterns is a better adapted and more flexible view of dFC than a succession of k‐means centroids. Even though we identified the FC patterns using k‐means clustering, there was strong evidence that they are in fact jointly expressed. Reassuringly, k‐SVD and truncated SVD resulted in similar FC patterns.
Based on split‐half reproducibility, we estimated three FC patterns that had a rich structure and showed distinct network configurations. For example, a fragmentation between salience and VS connections, on one hand, and default mode (DM) connections, on the other hand (FC pattern 1). FC pattern 2, which encoded the opposite direction of interactions, indicated that the separation between these two groups of networks is less pronounced at other instances in time (average FC was removed before clustering the data so positive correlation in these FC patterns is not the same as in a standard correlation matrix). In FC pattern 3, the DMN was connected to the visual and language networks, but not the RECN, which was here connected to the salience and VS networks, suggesting different modes of internetwork interaction. Both Allen et al. [2014] and Liu and Duyn [2013] also observed correlations and coactivations, respectively, of DMN and visual regions. The ECN is critical for working memory and was grouped alternately with networks that scan the environment (salience and VS in pattern 3) and with networks that ruminate over recent events or episodic memories (DMN in pattern 1). This suggests that flexible interactions between the ECNs and externally and internally oriented networks are critical for monitoring, maintaining, and manipulating recent information. The switching in connectivity was specific to the right ECN, which has previously been linked to visual and spatial working memory [Cabeza and Nyberg, 1997, 2000]. Previous work has also suggested interactions between the ECN and VS [e.g., LaBar et al., 1999] and between the ECN and DMN [e.g., Spreng et al., 2010].
Here we observed only three FC patterns that were reproducible across independent data sets. Different, but generally larger, values have been reported in the literature for related studies. Several factors—apart from the decomposition approach—are likely to play a role: first, the way K is chosen. We used a strict measure of reproducibility, while the choice of K was guided by accuracy (or approximation error) instead in Leonardi et al. [2013] and Allen et al. [2014]. Second, the number of included subjects. For example, Allen et al. [2014] clustered dFC of over 400 subjects into seven states in initial work, and into five states in a follow‐up study with 23 subjects [Allen et al., 2013]. Third, the parameters of the acquisition (such as the TR and scan duration), the choice of ROIs, and the window length, might all play roles. All studies mentioned above used (different) ROIs to reduce the spatial dimensionality of the data. As is the case for studies of static FC, different atlases hamper an easy comparison of results across studies. We hope that future work will help to clarify some of these issues. Lastly, because the correlation structure is averaged across the full window duration, changes in network topology that occur on faster time scales are unlikely to be picked up. In exploratory analyses, we shortened the window length to 44 s, but did not observe a larger number of reproducible FC patterns in resting‐state dFC. We did not decrease the window length further as the identification of the cognitive states for the subject‐driven task data deteriorated for 30 s windows (ARI 0.33 for 30 s, 0.63 for 44 s, and 0.74 for 60 s). Alternative techniques that circumvent sliding‐window estimates might be better able to reveal faster network reorganizations [Eavani et al., 2013; Liu and Duyn, 2013; Smith et al., 2012].
CONCLUSION
DFC is a promising new measure of brain activity that can be extracted from fMRI data and has the potential to provide new insights into brain function. In this work, we investigated whether dynamic functional network configurations were better described as a succession of separated FC states or rather as a combination of multiple FC patterns. We presented a systematic and data‐driven analysis in terms of split‐half reproducibility and distribution of time‐dependent weights for simulated and experimental fMRI data from subject‐driven cognitive states and resting‐state. These results suggested that a superposition FC patterns provided the best decomposition of resting‐state dFC and highlighted the role of ECN in driving fluctuations of dFC.
The meaning of decomposing resting‐state dFC remains to be further validated and is an exploratory technique, as also pointed out by Hutchison et al. [2013a, b]. The fact that different cognitive states can be identified from dFC alone is encouraging, but generative and computational models are needed to understand how dFC emerges and is best analyzed. One promising avenue to improve the interpretation of dFC is to combine approaches as the ones presented here with concurrent EEG or other physiological, behavioral, or clinical measures [Allen et al., 2013; Chang et al., 2013; Preti et al., 2014].
Supporting information
Supplementary Information
ACKNOWLEDGMENTS
The authors thank Jonas Richiardi and Bernard Ng for helpful discussions and advice, and Işık Karahanoğlu for feedback on the manuscript.
Conflict of interest: All authors declare no conflict of interest
Footnotes
Technically, PCA decomposes a matrix only into (principal) components and it is the singular value decomposition (SVD) that decomposes it into components and weights. For centered data, the principal components of PCA are, however, equal to the left singular vectors of SVD. The weights can then be obtained by a projection of the data onto the components.
REFERENCES
- Aharon M, Elad M, Bruckstein A (2006): K‐SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans Sig Proc 54:4311–4322. [Google Scholar]
- Allen EA, Eichele T, Wu L, Calhoun VD (2013): EEG signatures of functional connectivity states. Poster 3120, Organization for Human Brain Mapping (OHBM) Annual Meeting, Seattle, WA. [Google Scholar]
- Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD (2014): Tracking whole‐brain connectivity dynamics in the resting state. Cereb Cortex 24:663–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Wymbs NF, Porter MA, Mucha PJ, Carlson JM, Grafton ST (2011): Dynamic reconfiguration of human brain networks during learning. Proc Natl Acad Sci USA 108:7641–7646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabeza R, Nyberg L (1997): Imaging cognition: An empirical review of PET studies with normal subjects. J Cogn Neurosci 9:1–26. [DOI] [PubMed] [Google Scholar]
- Cabeza R, Nyberg L (2000): Imaging cognition II: An empirical review of 275 PET and fMRI studies. J Cogn Neurosci 12:1–47. [DOI] [PubMed] [Google Scholar]
- Chang C, Glover GH (2010): Time‐frequency dynamics of resting‐state brain connectivity measured with fMRI. NeuroImage 50:81–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Liu Z, Chen MC, Liu X, Duyn JH (2013): EEG correlates of time‐varying BOLD functional connectivity. Neuroimage 72:227–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cribben I, Haraldsdottir R, Atlas LY, Wager TD, Lindquist MA (2012): Dynamic connectivity regression: Determining state‐related changes in brain connectivity. NeuroImage 61:907–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dosenbach NUF, Nardos B, Cohen AL, Fair DA, Power JD, Church JA, Nelson SM, Wig GS, Vogel AC, Lessov‐Schlaggar CN, Barnes KA, Dubis JW, Feczko E, Coalson RS, Pruett JR, Jr , Barch DM, Petersen SE, Schlaggar BL (2010): Prediction of individual brain maturity using fMRI. Science 329:1358–1361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eavani H, Filipovych R, Davatzikos C, Satterthwaite TD, Gur RE, Gur RC (2012). Sparse dictionary learning of resting state fMRI networks. Proceedings on Pattern Recognition in NeuroImaging (PRNI), pp. 73–76, IEEE CS, London, UK. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eavani H, Satterthwaite T, Gur R, Gur R, Davatzikos C (2013). Unsupervised learning of functional network dynamics in resting state fMRI. In: Proceedings on Information Processing in Medical Imaging (IPMI), pp. 426–437, Springer LNCS, Asilomar, CA. [DOI] [PMC free article] [PubMed]
- Ekman M, Derrfuss J, Tittgemeyer M, Fiebach CJ (2012): Predicting errors from reconfiguration patterns in human brain networks. Proc Natl Acad Sci USA 109:16714–16719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eryilmaz H, Van De Ville D, Schwartz S, Vuilleumier P (2011): Impact of transient emotions on functional connectivity during subsequent resting state: A wavelet correlation approach. NeuroImage 54:2481–2491. [DOI] [PubMed] [Google Scholar]
- Gonzalez‐Castillo J, Hoy, C ., Handwerker, D ., Robinson, M ., Bandettini, P . (2013). Detection of consistent cognitive processing at the single subject level using whole‐brain fMRI Connectivity. Presentation at Soc Neurosci, San Diego (CA). [Google Scholar]
- Handwerker DA, Roopchansingh V, Gonzalez‐Castillo J, Bandettini PA (2012): Periodic changes in fMRI connectivity. NeuroImage 63:1712–1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubert L, Arabie P (1985): Comparing partitions. J Classification 2:193–218. [Google Scholar]
- Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, Della Penna S, Duyn JH, Glover GH, Gonzalez‐Castillo J, Handwerker DA, Keilholz S, Kiviniemi V, Leopold DA, de Pasquale F, Sporns O, Walter M, Chang C (2013a): Dynamic functional connectivity: promise, issues, and interpretations. NeuroImage 80:360–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Gati JS, Everling S, Menon RS (2013b): Resting‐state networks show dynamic functional connectivity in awake humans and anesthetized macaques. Hum Brain Mapp 34:2154–2177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones DT, Vemuri P, Murphy MC, Gunter JL, Senjem ML, Machulda MM, Przybelski SA, Gregg BE, Kantarci K, Knopman DS, Boeve BF, Petersen RC, Jack CR, Jr (2012): Non‐stationarity in the “resting brain's” modular architecture. PLoS One 7:e39731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhn HW (1955): The Hungarian method for the assignment problem. Naval Res Logistics Q 2:83–97. [Google Scholar]
- LaBar KS, Gitelman DR, Parrish TB, Mesulam M (1999): Neuroanatomic overlap of working memory and spatial attention networks: A functional MRI comparison within subjects. NeuroImage 10:695–704. [DOI] [PubMed] [Google Scholar]
- Lee K, Tak S, Ye JC (2011): A data‐driven sparse GLM for fMRI analysis using sparse dictionary learning with MDL criterion. IEEE Trans Med Imaging 30:1076–1089. [DOI] [PubMed] [Google Scholar]
- Lee J, Jeong Y, Ye JC (2013). Group sparse dictionary learning and inference for resting‐state fMRI analysis of Alzheimer's disease. In: Proceedings on IEEE International Symposium on Biomedical Imaging (ISBI), pp. 540–543, IEEE, San Francisco, CA.
- Leonardi N, Van De Ville D (2013). Identifying network correlates of brain states using tensor decompositions of whole‐brain dynamic functional connectivity. In: Proceedings on IEEE International Workshop on Pattern Recognition in Neuroimaging (PRNI), pp. 74–77.
- Leonardi N, Richiardi J, Gschwind M, Simioni S, Annoni J‐M, Schluep M, Vuilleumier P, Van De Ville D (2013): Principal components of functional connectivity: A new approach to study dynamic brain connectivity during rest. NeuroImage 83:937–950. [DOI] [PubMed] [Google Scholar]
- Li X, Zhu D, Jiang X, Jin C, Zhang X, Guo L, Zhang J, Hu X, Li L, Liu T (2014): Dynamic functional connectomics signatures for characterization and differentiation of PTSD patients. Hum Brain Mapp 35:1761–1778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Duyn JH (2013): Time‐varying functional network information extracted from brief instances of spontaneous brain activity. Proc Natl Acad Sci USA 110:4392–4397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mairal J, Bach F, Ponce J, Sapiro G (2010): Online learning for matrix factorization and sparse coding. J Mach Learn Res 11:19–60. [Google Scholar]
- Mehrkanoon S, Breakspear M, Boonstra TW (2014): Low‐dimensional dynamics of resting‐state cortical activity. Brain Topogr 27:338–352. [DOI] [PubMed] [Google Scholar]
- Munkres J (1957): Algorithms for the assignment and transportation problems. J Soc Ind Appl Math 5:32–38. [Google Scholar]
- Preti MG, Leonardi N, Karahanoglu FI, Grouiller F, Genetti M, Seeck M, Vulliemoz S, Van De Ville D (2014): Epileptic network activity revealed by dynamic functional connectivity in simultaneous EEG‐fMRI. In: Proceedings of the Eleventh IEEE International Symposium on Biomedical Imaging: From Nano to Macro (ISBI'14), pp. 9–12, IEEE, Beijing, China.
- Rand WM (1971): Objective criteria for the evaluation of clustering methods. J Am Stat Assoc 66:846–850. [Google Scholar]
- Satterthwaite TD, Wolf DH, Loughead J, Ruparel K, Elliott MA, Hakonarson H, Gur RC, Gur RE (2012): Impact of in‐scanner head motion on multiple measures of functional connectivity: Relevance for studies of neurodevelopment in youth. NeuroImage 60:623–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirer WR, Ryali S, Rykhlevskaia E, Menon V, Greicius MD (2012): Decoding subject‐driven cognitive states with whole‐brain connectivity patterns. Cereb Cortex 22:158–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Moeller S, Xu J, Auerbach EJ, Woolrich MW, Beckmann CF, Jenkinson M, Andersson J, Glasser MF, Van Essen DC, Feinberg DA, Yacoub ES, Ugurbil K (2012): Temporally‐independent functional modes of spontaneous brain activity. Proc Natl Acad Sci USA 109:3131–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spreng RN, Stevens WD, Chamberlain JP, Gilmore AW, Schacter DL (2010): Default network activity, coupled with the frontoparietal control network, supports goal‐directed cognition. NeuroImage 53:303–317. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Information


