Logical circularity in voxel‐based analysis: Normalization strategy may induce statistical bias

Abstract

Recent discussions within the neuroimaging community have highlighted the problematic presence of selection bias in experimental design. Although initially centering on the selection of voxels during the course of fMRI studies, we demonstrate how this bias can potentially corrupt voxel‐based analyses. For such studies, template‐based registration plays a critical role in which a representative template serves as the normalized space for group alignment. A standard approach maps each subject's image to a representative template before performing statistical comparisons between different groups. We analytically demonstrate that in these scenarios the popular sum of squared difference (SSD) intensity metric, implicitly surrogating as a quantification of anatomical alignment, instead explicitly maximizes effect size—an experimental design flaw referred to as “circularity bias.” We illustrate how this selection bias varies in strength with the similarity metric used during registration under the hypothesis that while SSD‐related metrics, such as Demons, will manifest similar effects, other metrics which are not formulated based on absolute intensity differences will produce less of an effect. Consequently, given the variability in voxel‐based analysis outcomes with similarity metric choice, we caution researchers specifically in the use of SSD and SSD‐related measures where normalization and statistical analysis involve the same image set. Instead, we advocate a more cautious approach where normalization of the individual subject images to the reference space occurs through corresponding image sets which are independent of statistical testing. Alternatively, one can use similarity terms that are less sensitive to this bias. Hum Brain Mapp 35:745–759, 2014. © 2012 Wiley Periodicals, Inc.

INTRODUCTION

Puzzled by an abundance of papers reporting highly significant correlations in fMRI studies, Vul et al. 2009 eventually discovered a permeating statistical bias characterized by such related terms as “circularity” and “nonindependence.” Although producing much discussion in the fMRI community [Kriegeskorte et al., 2010], subsequent literature has demonstrated the general presence of such bias in neuroscience research [Kriegeskorte et al., 2009]. In this article, we demonstrate how this concept of circularity can potentially extend to a fundamental neuroimaging analysis technique, voxel‐based analysis, using fractional anisotropy (FA) data.

Similarly, we were perplexed by the disparity in statistical results of one of our recent analyses [Stone et al., 2011] using the same diffusion tensor imaging (DTI) data and same voxel‐based analysis technique but different normalization algorithms. Despite distinctively better alignments with one popular method, there was little difference in the statistical results between the two approaches. It was eventually discovered that the incommensurability between alignment quality and effect size in our analysis was also due to a subtle, yet significant circularity bias which we explain below in the context of FA population studies.

The seminal work of Basser et al. [1994a, 1994b] established DTI as a viable investigatory MRI technique. DTI's sensitivity to brain architecture [Assaf and Pasternak, 2008; Basser and Pierpaoli, 1996] enables promising analysis possibilities assessing neuro‐structural differences in cross‐population studies [Arnone et al., 2008; Kantarci et al., 2010; Kubicki et al., 2005; Rametti et al., 2010]. Two popular comprehensive software packages for assessing population differences include the Statistical Parametric Mapping (SPM) Matlab‐based toolkit (http://www.fil.ion.ucl.ac.uk/spm/) for voxel‐based morphometry (VBM) [Ashburner and Friston, 2000] and the tract‐based spatial statistics (TBSS) framework [Smith et al., 2006] (http://www.fmrib.ox.ac.uk/fsl/tbss/index.html). VBM continues to find application to FA studies [Kakeda and Korogi, 2010; Preziosa et al., 2011; Takao et al., 2010] despite concerns about its general validity [Bookstein, 2001; Davatzikos, 2004] and, in particular, with respect to DTI [Chung et al., 2008; Jones et al., 2005]. The TBSS framework was partially developed in response to these concerns in which voxel values are projected onto a template white matter skeleton for increased statistical power.

Although there are substantive differences in normalization between these and other analysis protocols, a core commonality includes direct FA‐to‐FA registration using various similarity metrics. The sum of squared differences (SSD) image similarity metric is perhaps the easiest to interpret (it drives the image intensity difference to zero), is computationally efficient (compute the image difference and gradient), and is therefore widely used. Some of the most popular registration methods (e.g. variants of SPM, Demons [Thirion, 1998], FSL's nonlinear image registration tool (FNIRT), and large deformation diffeomorphic metric mapping (LDDMM) [Beg et al., 2005]) rely on this metric and yield reasonable performance levels [Klein et al., 2009]. However, suppose the SSD metric is used to find a set of M transformations that map a population of M FA images, $\{I_1,\dots ,I_M\}$, to a representative FA template, J, for statistical testing between groups. This results in the optimal transformations, $\{T_1^{*},\dots ,T_M^{*}\}$, which minimize the SSD metric over the population, i.e.,

$$T^{*}=\underset{T_1,\dots ,T_M}{\arg \text{min}}\sum _{m=1}^M\sum _{n=1}^N{(I_m\left(T_m\left(x_n\right)\right)-J\left(x_n\right))}^2,$$ (1)

where the inner summation indexes over all N voxels of the region of interest. Switching the order of the summations and recognizing that a principal criterion for the selection of J is such that it be a good approximation of the mean of the aligned images, it becomes apparent on inspection of the inner summation that the transformation solution,

$$T^{*}=\underset{T_1,\dots ,T_M}{\arg \text{min}}\sum _{n=1}^N\left(\sum _{m=1}^M\underset{\propto \hspace{1em}\text{voxelwise}\hspace{1em}\text{variance}}{{(I_m\left(T_m\left(x_n\right)\right)-J\left(x_n\right))}^2}\right),$$ (2)

is that which minimizes the average voxelwise group variance.1 Reducing the group variance will also directly affect the value of a standard population statistical assessment, the Student's t test.2

Thus, instead of normalization based on anatomical alignment followed by statistical testing, direct normalization using SSD of the images to be statistically compared explicitly conflates attempts at anatomical alignment with optimizing the statistical testing results that one will ultimately use to assess hypotheses. This immediately evokes a sense of circularity in the analysis [Kriegeskorte et al., 2009]. According to Kriegeskrote et al., “An analysis is circular (or nonindependent) if it is based on data that were selected for showing the effect of interest or a related effect.” Direct FA‐to‐FA template registration will produce transformations that align (or select) voxels such that the statistical testing result (or the effect of interest) is increased (assuming one is using Student's t test). Although the SSD metric is able to provide visually attractive (although not necessary anatomically correct) alignments across subjects, the voxel‐level details (that is, which voxels are matched where) are strikingly important in terms of the effect on detection power.

Various processing choices may mitigate the effects of such bias. Gaussian smoothing following normalization, nonparametric testing [Rorden et al., 2007], statistical analysis based on orthogonal projections onto the white matter skeleton [Smith et al., 2006], and the use of more robust similarity metrics may all impact the outcome. However, such choices are often made ad hoc and/or post hoc and, to our knowledge, not with the realization of the potential for circularity bias described by Eq. (2).

Instead of direct FA‐to‐FA template mapping for alignment to the normalized space, we advocate an independent alignment strategy in which the FA images are mapped to the common reference space via intra‐subject FA‐to‐T1 mapping followed by T1‐to‐T1 template alignment thus eliminating all direct FA‐to‐FA registrations. The key point is that the intensity value differences used to assess alignment (i.e., the similarity metric) in FA‐to‐T1 and T1‐to‐T1 normalizations are independent of the intensity value differences used for the postalignment statistical analysis. It should be noted that this discussion is certainly not limited to studies involving FA. Such bias can occur anytime the images used for normalization are nonindependent of the statistical analysis as defined by the similarity metric and statistical testing. For example, following Eq. (2), circularity could theoretically be an issue for VBM if one directly registered individual subject gray matter density (GMD) images to a representative GMD template image using SSD‐related similarity measures (e.g., optimized VBM [Good et al., 2001]).

Fundamentally, these issues are historically rooted in a much deeper context concerning model‐based inferences and the validity of such inferences. As mentioned previously, the contributions of Bookstein et al. 2001, who explored related issues specifically with respect to spatial normalization and VBM, and the work of Vul et al. 2009 are extremely relevant to this work. However, apposite discussion extends earlier and broader to such exemplars as the seminal work of Akaike 1974 and his eponymous goodness‐of‐fit measure for assessment of competing statistical models whereby the number of parameters factors into decisions about model selection. Such considerations, however, are typically excluded in the voxel‐based analysis paradigm where fitting high‐dimensional image data using SSD‐based image metrics results in systematic “overfitting.” This may result in incorrect inferences about the data but is also pernicious due to the inflated nature of these statistical inferences and the susceptibility of the current research environment to claims of statistical significance [Dickersin, 1990].

Two sets of experiments establish that the similarity metric can significantly affect voxel‐based analysis outcomes and that, based on the previous description of circularity bias, the relationship in performance variability and similarity metric is to be expected. Specifically, we show that whereas SSD and Demons substantially overestimate statistical significance, mutual information (MI) and cross‐correlation (CC) are less susceptible although the effect is not negligible. Furthermore, we also show that this effect persists even with the common practice of postnormalization smoothing before mass univariate statistical testing.

Given this general overview, the experimental sets can be briefly characterized as follows:

• Simulated DTI Data: Using a simulated DTI generator, FA images based on male/female populations were generated in situ thus guaranteeing anatomical alignment before processing. The simulated images in each group were then “registered” to the FA image of the defining DTI template using four common similarity metrics (CC, Demons, MI, and SSD). Receiver operating characteristic (ROC) curves based on voxel‐based analysis for each of these scenarios demonstrate that effect size is maximized over anatomical alignment and that this effect size varies with similarity metric. Additional experiments establish that this trend persists even for commonly used smoothing kernels and the TBSS projection step.

• Real Traumatic Brain Injury (TBI) Data: FA data of TBI survivors and controls were normalized to a template using four common similarity metrics (CC, Demons, MI, and SSD). Additional exploration included normalization via the subjects' anatomical T1‐weighted images as well as the default registration for TBSS. Voxelwise statistical testing was also performed with and without smoothing. Even though ground truth is not available for such data, the SSD and Demons metrics showed increased statistical power as evidenced by a general decrease in voxelwise P‐values. This increase in detected effects may not be complemented by increased anatomical registration accuracy.

All major processing steps were performed using publicly available software including the open source Advanced Normalization Tools (ANTs; http://www.picsl.upenn.edu/ANTs) which should facilitate reproducibility for the interested reader.

MATERIALS AND METHODS

After describing the simulated and TBI data sets, which consist of both T1‐weighted and FA images, we briefly sketch how the population‐specific, unbiased T1‐weighted template is made from the set of the subject T1‐weighted images (Anatomical T1‐weighted Image Template Construction section). This methodology was used to construct a T1‐weighted template from the Nathan Kline Institute (NKI)/Rockland data. The described template‐building process was also used to generate a second T1‐weighted template from the TBI data which was used as the normalized space for analysis. All FA images for the corresponding data set are normalized to their respective T1‐weighted template. We detail how this is performed without using any direct FA‐to‐FA image registrations in Simulated DTI Gender Cohort Creation section. Once all the NKI/Rockland FA data are aligned in the space of its T1‐weighted template, a generative DTI model is formulated which is used to produce the simulated DTI gender cohort. This process is described in Simulated DTI Gender Cohort Creation section. Finally, an explanation of the statistical methods used to quantify circularity bias for these data is given in Statistical Methods section.

Imaging Data

NKI/Rockland data for generation of the simulated DTI gender cohort

Data from the first 14 weeks of a prospective data‐sharing initiative sponsored by the 1,000 Functional Connectomes Project (FCP)3 were downloaded on January 15, 2011 and consisted of 74 subjects (average age in years: 32.4 ± 17.8). Due to various issues (e.g., lack of corresponding T1‐weighted image, failed DTI reconstruction, and age matching requirements) only 62 subjects (21 females and 41 males) were used. Each imaging session for each subject produced a 64‐directional DTI scan (parameters: conventional single‐shot spin echo planar pulse sequence, repetition time (TR) = 10,000 ms, echo time (TE) = 91 ms, axial acquisition, and voxel size = 2 × 2 × 2 mm³) and a T1‐weighted anatomical scan (parameters: TR = 2,500 ms, b = 1,000 s/mm² for each direction, 58 contiguous slices of 2.0 mm thickness, inversion time (TI) = 1,200 ms, TE = 3.5 ms, flip angle = 8°, 192 contiguous slices of 1.0 mm thickness, field of view (FOV) = 256 × 256 mm², and voxel size = 1 mm³). Images were anonymized including defacing of the T1‐weighted images. Diffusion tensor data associated with each of the data sets were reconstructed from the diffusion weighted sequences using Camino (http://camino.org.uk/)—an open source toolkit for diffusion MRI processing and analysis [Cook et al., 2006] in combination with ANTs‐based registration for motion correction of the DTI sequence.

Diffuse TBI data

The TBI data used in this study are part of a larger effort investigating the relationship between various neuroimaging indices and cognitive and functional abilities in long‐term survivors of TBI (principal investigator: John Whyte). A total of 17 controls and 16 patients with TBI were used for the analysis presented in this work. Each patient had a history of nonpenetrating TBI of at least moderate severity defined by significant and well‐documented loss or alteration of consciousness following injury in addition to meeting several other exclusionary criteria. The healthy volunteers were matched in terms of age, gender, ethnicity, handedness, and years of education. High‐resolution T1‐weighted anatomic images were obtained using a 3D MP‐RAGE imaging sequence with the following acquisition parameters: TR = 1620 ms, TI = 950 ms, TE = 3 ms, flip angle = 15°, 160 contiguous slices of 1.0 mm thickness, FOV = 192 × 256 mm², matrix = 192 × 256, 1 excitation with a scan time of 6 min, and voxel size = 1 mm³. A total of 30‐directional DTI images were also obtained. Diffusion tensor data were reconstructed using Camino. A more detailed data description can be found in Avants et al. 2008.

Anatomical T1‐Weighted Image Template Construction

For the data processing described in the following sections (both simulated and real TBI data), we normalize images to an unbiased template created from the T1‐weighted images. This unbiased template constitutes our normalized space for warping all FA images of the population for further analysis.

Various approaches exist for determining the normalized space such as selection of a pre‐existing template based on a single subject, e.g., the Talairach atlas [Talairach and Tournoux, 1988], or a publicly available averaged group of subjects, e.g. the MNI [Collins et al., 1994] or ICBM [Mazziotta et al., 1995] templates. One challenge with standard templates is that they may inadvertently bias one's results by enabling better normalization of subjects to which the template is more similar. This issue is exacerbated when dealing with populations that have high variance (e.g., due to disease) and/or when one's normalization method is low‐dimensional (i.e., not flexible enough to capture large shape differences).

Population‐specific templates alleviate some of these issues by deriving a most representative image from the population. Coupling the intrinsic symmetry of SyN pairwise registration [Avants et al., 2008] and an optimized sharpening/averaging of the template appearance, Symmetric Group Normalization is a powerful framework for producing optimal population‐specific templates [Avants et al., 2010]. Given a set of representative images, $\{I_1,\dots ,I_M\}$, optimization involves finding the set of paired diffeomorphic transformations, $\{({\phi }_1^1,{\phi }_2^1),\dots ,({\phi }_1^M,{\phi }_2^M)\}$, the optimal template appearance, J*, and corresponding coordinate system, $\psi \left(\mathbf{x}\right)$, which minimize the cost function

$$\sum _{m=1}^M[D(\psi \left(\mathbf{x}\right),{\phi }_1^m(\mathbf{x},1))+\Pi (I_m\left({\phi }_2^m(\mathbf{x},0.5)\right),J^{*}\left({\phi }_1^m(\mathbf{x},0.5)\right))]$$ (3)

where D is the diffeomorphic shape distance,

$$D(\phi (\mathbf{x},0),\phi (\mathbf{x},1))=\int 0^1\Vert v(\mathbf{x},t)\Vert {}_L\mathrm{dt},$$ (4)

dependent on the choice of linear operator, L, and $v$ is the diffeomorphism‐generating velocity field,

$$v\left(\phi (\mathbf{x},t)\right)=\frac{d\phi (\mathbf{x},t)}{\mathrm{dt}},\hspace{1em}\phi (\mathbf{x},0)=\mathbf{x}.$$ (5)

$\Pi$ is the choice of similarity metric, often neighborhood CC [Avants et al., 2008], calculated in the virtual domain midway between each individual image and the current estimate of the template. We first initialize $\left\{({\phi }_1^M,{\phi }_2^M)\right\}$ and $\psi \left(\mathbf{x}\right)$ to identity and then iterate over the following steps: (1) compute the pairwise transformations given the current template; (2) update the optimal template appearance; (3) update $\psi \left(\mathbf{x}\right)$ (the template shape) to minimize the population deformation.

Simulated DTI Gender Cohort Creation

We establish the potential for circular strategies in voxel‐based analysis to induce bias by simulating a population dataset with known group difference. This simulation creates a signal difference that is patterned on the same underlying anatomical shape, thus minimizing the confound of spatial alignment at the outset of experimental analysis.

To provide realistic ground truth FA data, we implemented the method of Van Hecke et al. 2009, which we have also made available to the public [Tustison et al., 2011]. Given a DTI atlas, a b = 0 image, a scheme file indicating the gradient directions, and a cohort of aligned DTI data to model intersubject intensity/tensor variability, the algorithm generates simulated data sets with user‐specified pathology and noise. Theoretically, the resulting simulated data are created in situ and are thus, by definition, anatomically aligned. Any actual anatomical discrepancies in the aligned cohort are incorporated into the generative model as Gaussian‐based intersubject variability in appearance alone (i.e., we do not directly vary the underlying anatomical shape). Therefore, anatomical accuracy is only relevant in terms of precise modeling of the variance of intersubject variability and not whether such intensity variance exists with aligned anatomy. In other words, even a perfectly aligned cohort will manifest some degree of intensity‐based intersubject discrepancies and the resulting intensity differences between images are what drive the pair‐wise image registration to minimize such variability (not anatomy). As previously mentioned, this artificially inflates statistical testing results.4 It should be noted that there are other possible sources of image intensity differences such as noise and neuropathology which could increase the effects but the use of the diffusion weighted image (DWI) simulator permits limiting the experimental data to a study of only normal subject variability differences where the effects are demonstrated. However, the effects of these potential misalignments are minimized through the use of high‐performance SyN [Klein et al., 2009] driven solely by the high‐resolution T1‐weighted anatomical images and the use of a relatively large cohort.

The aligned DTI data were generated using the following steps to warp each DTI to the standard space defined by a population‐specific T1‐weighted template (cf., Fig. 1):

• An anatomical T1‐weighted template was constructed from 30 randomly selected subjects from the NKI/Rockland data set using the template‐generating method described in Anatomical T1‐weighted Image Template Construction section. The process is represented in the middle of Figure 1, where we show axial slices of 5 of the 30 NKI/Rockland subjects used to create the ANTs T1 template (shown in the middle). The green double‐sided squiggly arrows represent the derived transformations (affine + SyN) used to create the T1 template. The T1‐weighted template was then registered (affine + SyN) to the MNI152 template for purposes of comparison with TBSS which uses the FMRIB58 template (also normalized to the MNI152 template). Axial slices of the FMRIB58 and MNI152 templates are situated on the right of Figure 1.

• Each of the 62 NKI/Rockland T1‐weighted images was registered (affine + SyN) to the T1‐weighted template. Each T1‐weighted image was also segmented using N4 bias correction [Tustison et al., 2010] and Atropos n‐tissue segmentation [Avants et al., 2011] to isolate the white matter region to be used as a registration mask for alignment with its corresponding DTI. A representative individual T1 subject (with superimposed segmentation results) is shown at the lower left of Figure 1, where the transformation to the T1 template is represented by a red double‐sided squiggly arrow.

• Each of the 62 NKI/Rockland DT images was registered to the corresponding subject's T1‐weighted image using a transform composition derived by optimizing an initial rigid transformation followed by an optimized deformable (i.e., SyN) transform (represented by the straight and squiggly vertical arrows, respectively, on the left side of Fig. 1). The rigid transform was found by optimizing the alignment between the average DWI and the masked white matter T1‐weighted image of the same subject. The resulting linear transform was used as an initial transform in performing distortion correction by minimizing the residual nonrigid alignment between the average DWI and the masked T1‐weighted image.

• Finally, for each of the 62 DTI, we composed the previously described transforms which provide a composite mapping from each DTI to the MNI152 template without any direct FA‐to‐FA registrations (represented by the blue arrow at the top of Fig. 1 and standard protocol for TBSS).

Figure 1.

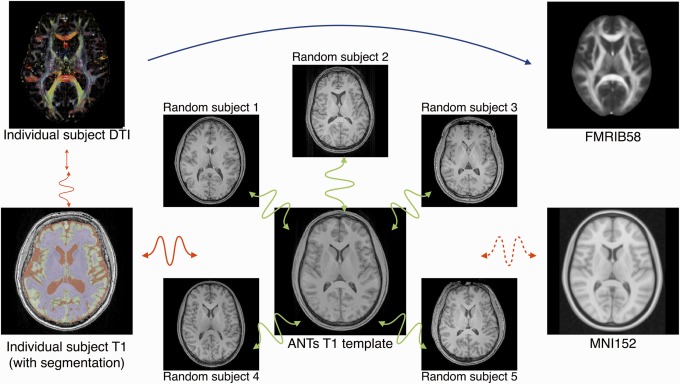
In contrast to approaches which require direct FA‐to‐FA registration (represented with the blue arrow), our proposed modification first constructs an optimal anatomical template as illustrated in the center of the figure. The FA image is then rigidly mapped, with distortion correction, to the individual T1 using the white matter mask as shown on the left. Each individual T1 is then nonrigidly registered to the anatomical template. Optionally, one can register the T1 template to the MNI152 template which resides in the same space as the FMRIB58 template. Thus, the composite transform, carefully constructed without any FA‐to‐FA image registration, can take an individual subject's FA map (or other DTI‐derived measure) to the desired standardized coordinate system. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The transformed DTI were reoriented to the MNI152 template using the preservation of principal direction method [Alexander et al., 2001]. Once all the DTI data are aligned, the next step involves creating the generative DWI model [Van Hecke et al., 2009] by first averaging both the aligned DT and b = 0 images. The 62 aligned DTI were averaged using the log‐Euclidean framework [Arsigny et al., 2006] to create the DTI atlas. Similarly, the 62 aligned b = 0 images were averaged to create the representative b = 0 image for simulated DTI creation. The derived FA image from the DTI atlas and the b = 0 image are shown in Figure 2. An FA mask was created by thresholding the FA image of the DTI atlas at 0.2.

Figure 2.

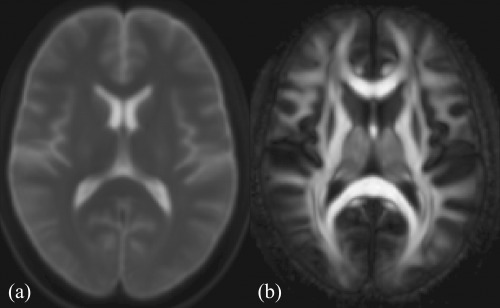
Mid‐axial slice of the (a) average b = 0 image and (b) FA image derived from the DTI atlas used to create the simulated gender data sets.

The 41 aligned male DTI were used to generate 18 “Control” 30‐direction diffusion‐weighted images with neither simulated noise nor pathology. Similarly, the 21 aligned female DTI were used to generate 19 “Experimental” diffusion‐weighted image sets. These simulated DTI were reconstructed using Camino which were then used to produce individual FA images. The number of simulated subjects in each group was chosen based on the median number of control and experimental subjects from the sampling of FA studies described in [Van Hecke et al., 2009].

Statistical Methods

We employ two complementary tools for examining the impact of image registration strategy on statistical outcome: the ROC and the cumulative distribution function (CDF). We provide a brief summary of these tools and their purpose in this study.

ROC analysis

The ROC may be used to look at the performance of a continuous model against a known classification when the threshold on the model is varied. In this study, the ground‐truth is determined by the voxels that—via simulation—we know have a significant difference between groups. We choose P < 0.05 to determine the ground truth. This leads to two classes of voxels: those that are significantly different between groups and those that are not. As we vary the threshold on the statistical map that is generated by a registration algorithm, we can compare the identified voxels against this ground truth and draw the ROC [Fitzpatrick et al., 1998; Wenzel et al., 2010].

CDFs

Empirically constructed CDFs have been used with maps of P‐values, derived from registration, to visually quantify detection power [Brun et al., 2008; Hua et al., 2009]. In this case, one examines the area under the CDF that is to the left of some statistical cutoff, usually P < 0.05. If one assumes that the method is not producing biased results, then the method that has a greater area under the CDF, left of cutoff, has greater detection power.

RESULTS

Simulated Data Set

To demonstrate the significance of circularity bias on voxelwise analysis and to demonstrate its correspondence with different common similarity metrics, we used the simulated DTI images described earlier to quantify such effects in FA. Since each simulated DTI and derived FA map was generated in the MNI152 template space, the cohort is already anatomically aligned. However, as described in the introduction, localized image registration using common similarity metrics drive the alignment towards minimizing local intensity differences (not necessarily anatomical differences) thereby inducing false positives. To test this, we applied ANTs registration using default regularization and transformation parameters with four common similarity metrics: neighborhood CC, Demons, MI, and SSDs. We limited optimization to 10 iterations at the full resolution level.5 As neither noise nor pathology was introduced, only the differences associated with the gender cohort modeling are responsible for driving the registration.

Voxelwise analysis included performing Student's t test within the DTI masked region (FA ≥ 0.2) for both the ground truth (i.e., anatomically aligned) data set and performing the same calculations for each of the four registration scenarios. We used a significance level cutoff of P = 0.05 to determine ground truth significant voxels in the already aligned data set. We then varied the significance level cutoff for each of the registered data sets. In addition, standard practice is to smooth the images following normalization and before statistical testing where the kernel size is typically dependent upon one's estimate of the registration accuracy. We tested the application of common kernel sizes of 4 mm and 8 mm full width at half maximum (FWHM) and juxtaposed those results with no smoothing in Figure 3. ROC curves are given for each of the three cases. We also included P‐value CDFs [Yanovsky et al., 2009]. However, ROC curves incorporate false/true positives and false/true negatives, the P‐value CDFs directly illustrate that certain metrics induce false positives. False elevation of statistical power is caused by a general decrease in P‐values. This decrease in P‐values causes a left‐shift in the CDF which is observed for both the SSD and Demons metrics.

Figure 3.

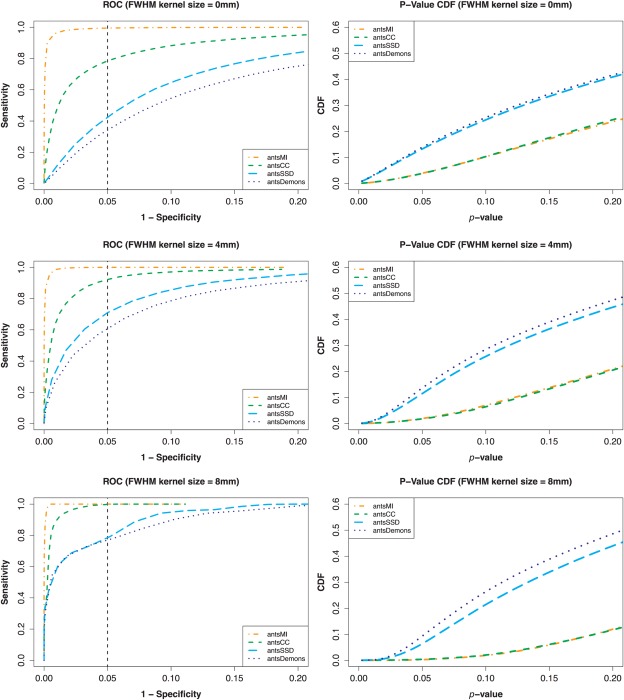
Postnormalization smoothing analysis of the simulated data for FWHM kernel sizes of 0 mm, 4 mm, and 8 mm. The ground truth data is smoothed in the same way as the normalized data. Left column: ROC curves plotting (1 − specificity) vs. sensitivity for the different similarity metrics for voxelwise analysis. Smoothing tends to ameliorate the bias effect but the relative strength continues to correlate with similarity metric. Right column: A relative increase in (false) statistical power induced by SSD and Demons, as described in the text, resulted in more voxels having lower P‐values. This will be manifested as a left‐shifted CDF curve which is apparent in the SSD and Demons metrics for all selected smoothing kernel sizes. In summary, improvements in detection power (if judged by the area under the CDF that is below 0.05) do not imply results that are closer to the truth (which is shown by examining total area under the ROC curve). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Visual comparison of the significant regions associated with the voxelwise analysis for ground truth data and the data using the different similarity metrics for P ≤ 0.05 shown in Figure 4 demonstrates the potential severity metric choice can have on results. Table 1 provides further evidence of inflated statistical significance, where we looked at the percent change from ground truth of the statistically significant regional volumes for each of the four metrics and each of the three smoothing parameters. Significance increases dramatically with amount of smoothing for the SSD and Demons metrics. Additionally, we evaluated the effects of registration regularization on degree of increased statistical significance with findings evincing little to no consequence.

Figure 4.

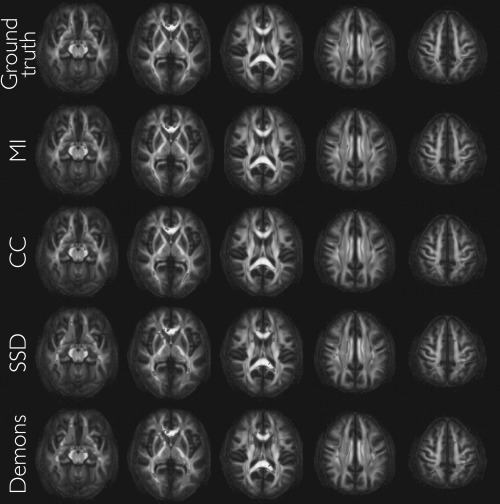
Top row: Axial slices of the DTI atlas‐derived FA map showing the ground truth significant differences (P ≤ 0.05, smoothing = 4 mm FWHM, uncorrected for multiple comparisons) between control (male) and experimental (female) groups. Rows 2–4: Same axial slices showing varying changes in significant regions following ANTs registration using different similarity metrics. The key point is that there is no anatomical misalignment between the groups before the registration algorithm is run. Although detection power “improves”, (particularly with the SSD and Demons metrics) this is not due to improved anatomical alignment but rather due to local effects related to circularity bias induced by the relationship between the test statistic and the similarity metric. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 1.

Percent change in volumes of significant voxels relative to the ground truth after registration of the simulated aligned data (P ≤ 0.05) and following the specified smoothing

	MI	CC	SSD	Demons
0 mm	−0.2%	−1.9%	245%	262%
4 mm	−3.4%	−9.9%	485%	597%
8 mm	−20.3%	23%	1,960%	2,945%

The middle row corresponds to the results shown in Figure 4.

We also performed a similar assessment where instead of performing voxelwise calculations over the entire white matter mask, we analyzed the FA skeleton projection characteristic of TBSS using the relevant portions of the TBSS scripts found in the FMRIB software library (FSL; http://www.fmrib.ox.ac.uk/fsl/). The FA image produced from the DTI atlas was used to produce a common skeleton for all comparisons. The associated ROC curves are given in Figure 5. Although projection does have slightly mitigating effects, the associated bias is still significant across certain metrics.

Figure 5.

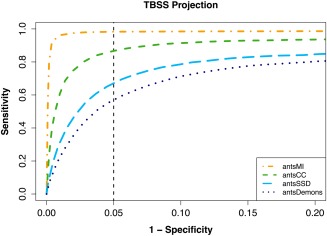
ROC curves plotting (1 − specificity) vs. sensitivity for the different similarity metrics using TBSS projections onto the mean FA skeleton. Degree of locality and correspondence to Eq. (2) resulted in performance disparity between the different metrics. As SSD and the SSD‐like Demon's formulation minimize voxelwise group variance, we see the greatest bias in those two metrics. In contrast, MI and CC are less susceptible to bias with MI performing quite well. Comparing voxelwise (cf., Fig. 3) and projection results, it is apparent that the TBSS projection strategy only slightly improves the effects of bias for the simulated data. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Despite the experimental set‐up ensuring anatomical alignment in the ground truth data, the resulting bias effects accord with our earlier description of the problem with these similarity metrics and direct FA‐to‐FA template normalization. However, MI shows relatively little bias due to its statistical formulation and relative nonlocality in contrast to the SSD and SSD‐like Demons metrics which are formulated such that they explicitly minimize voxelwise group variance and thus cause an elevation in false positives.

TBI Cohort

Even under conditions of no noise, no pathology, Gaussian modeling of intersubject variation and precise anatomical alignment, the simulated data demonstrated the presence of circularity bias that varied with similarity metric. In this section, we use data that was analyzed in [Stone et al., 2011] and show how bias is potentially manifested in real FA analysis. We investigated the following FA‐to‐FA template normalization strategies for each subject, where we used the FMRIB58 template distributed with the FSL toolkit as the FA template:

• antsCC: Direct individual FA‐to‐FMRIB58 template normalization using ANTs with the CC similarity metric,

• antsDemons: Direct individual FA‐to‐FMRIB58 template normalization using ANTs with the Demons similarity metric,

• antsMI: Direct individual FA‐to‐FMRIB58 template normalization using ANTs with the MI similarity metric,

• antsSSD: Direct individual FA‐to‐FMRIB58 template normalization using ANTs with the SSD similarity metric,

• tbss: Direct individual FA‐to‐FMRIB58 template normalization using FNIRT (also available in FSL) with the optimal configuration parameters for the FMRIB58 template encapsulated in the config file, FA_2_FMRIB58_1mm.cnf also distributed with the FSL toolkit, and

• antsT1: Indirect normalization where a subject's FA image is mapped to the individual T1‐weighted image via a composite transform pictorially described in Figure 1. First, a T1‐weighted template was created from the entire T1 cohort. The template generating process (described in Anatomical T1‐weighted Image Template Construction section) resulted in a set of transformations describing the mapping from each T1‐weighted image to the template. Second, the T1‐weighted template was then registered to the MNI152 template by optimizing an affine transform followed by a deformable transform (i.e., SyN) using ANTs. Third, we optimized a rigid transform plus a highly constrained, distortion‐correcting, deformable transform which maps the subject's FA image to the same subject's T1‐weighted image. The final composite mapping which warps each subject's FA image to the MNI152 template (which resides in the space of the FMRIB58 template) consists of the ordered set of transforms from the individual subject's FA image to the corresponding T1‐weighted image, the individual subject's T1‐weighted image to the T1‐weighted template, and, finally, from the T1‐weighted template to the MNI152 template.

For each of these scenarios, the normalized images were smoothed using a kernel size of 3.5 mm (FWHM). Voxelwise analysis was then performed within the region defined by thresholding the rescaled FMRIB58 template (rescaled to [0,1], thresholded at FA ≥ 0.2). Application of Student's t test (one‐tailed, α = 0.95) at each voxel between the smoothed experimental and control group FA images resulted in a set of P‐values for each experiment. As standard practice typically applies multiple comparisons correction to this mass univariate statistical testing, we used false discovery rate (FDR) correction to produce a set of corrected P‐values.

Given the lack of ground truth, we are unable to provide ROC curves for comparison of bias significance. However, as with the simulated data, the CDFs of the corrected P‐values for the different normalization strategies facilitate visualization of the correlated increase in statistical power with choice of normalization strategy. A bias which (falsely) decreases P‐values will yield a left‐shifted CDF. This trend is illustrated in Figure 6.

Figure 6.

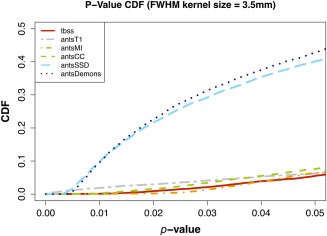
Student's t test results (one‐tailed, α = 0.95) for the smoothed (kernel size = 3.5 mm FWHM) TBI FA data aligned to the FMRIB58 template adjusted for multiple comparisons (FDR). Elevated statistical power is seen in the t‐test with the similarity metrics with the most correspondence to Eq. (1), namely the SSD and Demons metric. Results for the other metrics including TBSS and the T1‐weighted template‐based strategy (“antsT1”) remain fairly stable between the two tests. TBSS and the 4 ANTs metric results were all obtained using direct registration involving subject FA and the FMRIB58 template. The antsT1 results were also obtained in FMRIB58 space with the following transformation composition: subject FA → subject T1‐weighted image → group T1‐weighted template → common T1‐weighted template → MNI152 (FMRIB58) template. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The CDF of the voxelwise FA coefficient of variation (CV) of the aligned images is shown for each case in Figure 7. The CV at each voxel is defined as the variance divided by the mean over the population of FA values. Thus, those metrics which best minimize the voxelwise variance would trend towards greater alignment as quantified by the CV [Van Hecke et al., 2011]. As minimization of the groupwise variance will also minimize the CV, it is expected that the SSD and Demons metrics will produce relatively superior alignments to the other strategies. Despite the fact that no direct FA‐to‐FA registrations were performed, the “antsT1” normalization produced better alignments than “tbss” (which supports previous findings demonstrating improved performance of anatomical alignment using ANTS over FNIRT [Klein et al., 2009]). These can be visually assessed in Figure 8 where we plotted the resulting mean FA images for both sets of normalizations. Although direct FA‐to‐FA registration with common similarity metrics gives “better alignment” such alignment is produced at a cost of significant Type 1 errors and does not guarantee improved anatomical correspondence.

Figure 7.

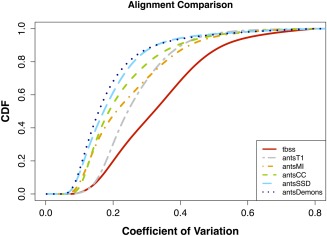
Comparison of the different alignment strategies in normalizing the TBI data to the FMRIB58 template. Assessment is quantitated using the voxelwise CV of the FA. TBSS and the 4 ANTs metric results were all obtained using direct registration involving subject FA and the FMRIB58 template. The curve denoted as “antsT1” was also obtained in FMRIB58 space with the following transformation composition: subject FA → subject T1‐weighted image → group T1‐weighted template → common T1‐weighted → template MNI152 (FMRIB58) template. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 8.

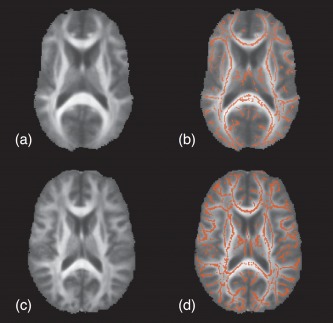
Qualitative comparison of mean FA images used in TBSS taken from the TBI data described in Materials and Methods section. The mean FA image illustrated in (a) is created by mapping the sample FA population to the default FMRIB58 template which is the standard protocol for TBSS. In comparison, the mean template represented in (c) is created from alignment of the population sample to the optimal T1‐weighted template as described in the article. The respective skeleton masks in (b) and (d) are created by thresholding the resulting skeleton values ≥ 0.2. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

All these issues point to fundamental considerations concerning the clinical interpretability of results in which circularity bias is shown to have a significant impact with commonly chosen registration parameters. Given the fundamental nature of normalization for neuroimaging, it is important that proper experimental set‐up be given priority over obtaining statistical significance. As we have shown, in simulated and real data, that statistical power can be artificially inflated based on similarity metric choice, and that these are some of the most commonly used metrics, we encourage investigators to exercise caution in making such normalization choices.

DISCUSSION AND CONCLUSIONS

Prior evaluation work using anatomically labeled data indicates that MI, CC, Demons, and SSD metrics are all capable of producing high quality anatomical alignment [Klein et al., 2009]. All this work, though, compares the quality of alignment at a relatively coarse scale of major gyri, lobes, and regions. At the voxel level, it is nearly impossible to determine the ground truth correspondence [Rohlfing, 2012]. Indeed, there is no reason to believe that subtle differences between a set of alignment strategies (induced, in the experiments of this article, by changing the similarity metrics used in image registration) that all apparently work well should be considered significant. This work, however, highlights a dramatic impact of similarity metric choice on detection power in template‐based FA studies. Our contention is that this dramatic “improvement” in detection power is not due to better anatomical alignment. Rather, it is a result of the circularity/nonindependence of the normalization and statistical estimation strategy. Consequently, we recommend that future work should take greater care when pairing normalization strategy with statistical analysis. Furthermore, we recommend that researchers make efforts to maintain independence between these two critical stages of a population study. That is, the features that drive the minimization of a similarity metric should be independent of the features that will be used in hypothesis testing. In particular, one should avoid combining the SSD and Demons metrics for normalization with Student's t test for assessing image‐derived differences. A final point is that CDFs and other power assessment methods cannot be regarded as meaningful comparison techniques in the presence of normalization/statistical nonindependence.

Perhaps the closest work to ours is by Wenzel et al. [2010]. The authors used ROC curves to examine the impact of registration strategy on the ability to identify effects in PET. They found that their own method, which uses CC, performed better than the SSD‐based SPM2 with respect to simulated data. Our findings suggest that the difference in performance is due, in part, to the choice of similarity metric. However, this cannot be verified without further investigation into methodological specifics. Also, the work of Freire and Mangin 2001 demonstrated that rigid body motion correction algorithms for alignment of fMRI data show a similar trend in that more robust similarity metrics, such as MI, are less susceptible to bias caused by intensity outliers (e.g., activation) than SSD. This could potentially provide additional motivation for favoring more robust similarity metrics in normalization.

Caveats with our analysis include a lack of ground truth in the clinical component of the study. Additionally, we are not addressing the biological plausibility of our results nor do we intend to (in this article) enter into discussion on the mechanisms of TBI, gender difference, and DTI that may lead to the detected results. Rather, we focus on the technical issue of circularity caused by normalizing the image feature of interest with functions that maximize the statistic used in hypothesis testing. We also cannot argue that our analysis invalidates previous studies in which circularity might be an issue. Finally, we do not address the very promising work concerning whole tensor DTI normalization [Zhang et al., 2007], DTI template‐based strategies [Van Hecke et al., 2011], or other related methods [Jbabdi et al., 2010].

Instead, we encourage the community to re‐examine normalization and analysis methods and to consider the potential confounds highlighted in this article and others [Ridgway et al., 2008]. Rank tests provide a more conservative alternative as does the methodology presented here based on DT‐to‐T1‐weighted intrasubject mapping and T1 normalization. To our surprise, we could not find a prior publication that directly addresses this issue. Two reasons may be that the majority of technical work with DTI has focused on more cutting‐edge issues, while the clinical work is hampered by publication bias [Dickersin, 1990] and the seductive siren song of generating statistically significant results. An additional reason may be that only recently have toolkits emerged to enable easy comparison of statistical techniques (via R [R Development Core Team, 2011]), normalization methods (ANTs), and diffusion tensor processing (Camino).