Exploring spatiotemporal network transitions in task functional MRI

Abstract

A critical question for cognitive neuroscience regards how transitions between cognitive states emerge from the dynamic activity of functional brain networks. Here we combine a simple data reorganization with spatial independent component analysis (ICA), enabling a spatiotemporal ICA (stICA) which captures the consistent evolution of networks during the onset and offset of a task. The technique was applied to functional magnetic resonance imaging (MRI) (FMRI) datasets involving alternating between rest and task, and to simple synthetic data. Starting and finishing time‐points of periods of interest (anchors) were defined at task block onsets and offsets. For each subject, the 10 volumes following each anchor were extracted and concatenated spatially, producing a single 3D sample. Samples for all anchors and subjects were concatenated along the fourth dimension. This 4D dataset was decomposed using ICA into spatiotemporal components. One component exhibited the transition with task onset from a default mode network (DMN) becoming less active to a frontoparietal control network becoming more active. We observed other changes with relevance to understanding network dynamics, for example, the DMN showed a changing spatial distribution, shifting to an anterior/superior pattern of deactivation during task from a posterior/inferior pattern during rest. By anchoring analyses to periods associated with the onsets and offsets of task, our approach reveals novel aspects of the dynamics of network activity accompanying these transitions. Importantly, these findings were observed without specifying a priori either the spatial networks or the task time courses. Hum Brain Mapp 36:1348–1364, 2015. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

A critical question for cognitive neuroscience regards how transitions between cognitive states emerge from the shifting balance in activity of functional brain networks. According to the dominant model, cognitively challenging tasks, such as a visually cued working memory task, evoke well‐recognized patterns of activation and deactivation with functional neuroimaging [Fox et al., 2005; Smith et al., 2009]. For example, frontal and parietal regions form the frontoparietal control network (FPCN), which typically activates with sensory and motor systems during many cognitively challenging tasks [Dosenbach et al., 2007; Vincent et al., 2008]. In contrast, activity within posterior cingulate, ventromedial frontal, and lateral parietal cortex, forming the default mode network (DMN), is typically increased at rest, when thought is unfocused or focused internally [Buckner et al., 2008; Raichle et al., 2001], and is typically decreased during externally focused tasks [Chang and Glover, 2010; Fox et al., 2005]. The perceived dichotomy of activity between the DMN and FPCN encourages a caricature of network dynamics where an active DMN represents a basal state of brain activity that is transiently interrupted or “turned off” during task conditions, whilst the FPCN (alongside sensory and motor systems) activates. When the active, task state finishes, the FPCN and sensorimotor systems turn off, leaving the brain to return to its basal state of DMN‐predominant activity.

However, this dichotomous model may be overly simplistic. There is evidence that the dynamics of the interactions between functional brain networks supporting cognitive functions are much more complex. For example, functional connectivity between brain networks, even at rest, has been shown to be nonstationary, fluctuating over time [Chang and Glover, 2010]. Further, there is increasing evidence that cognitive control relies on transient competitive or cooperative interactions between brain networks [Cocchi et al., 2013; Hellyer et al., 2014; Zalesky et al., 2014]. Therefore, in the context of a given cognitive task, there may be multiple different network transitions, and these transitions could involve more complexity than an on–off cycle between the DMN and the FPCN. Further, it has been proposed that the spatial composition of the networks themselves may be nonstationary and may adapt to cognitive demands [Leech et al., 2014]. For example, the spatial pattern of the DMN evoked by even quite similar cognitive tasks can vary substantially [Harrison et al., 2011; Leech et al., 2011, 2014; Seghier and Price, 2012; Utevsky et al., 2014]. This phenomenon, of spatial variation of network organization with cognitive state, has been observed for multiple brain networks across a range of tasks [e.g., Gordon et al., 2014; Mennes et al., 2013]. Further, the spatial organization of the networks varies across individuals and relates to cognitive performance [e.g., Filippini et al., 2012; Mennes et al., 2010; Smith et al., 2014]. Therefore, the configuration of functional brain networks is not static, but context dependent, changing over time when transitioning between cognitive states.

Current methodologies are unable to easily evaluate complex situations where both the temporal aspects of the interactions between networks and the spatial configuration of those networks can vary with cognitive demands. Specifically, traditional analyses using the regression of psychological time courses onto voxelwise functional data are not designed to identify coherent functional connectivity patterns across the brain, nor do they capture the relationships that exist between spatial activation patterns across time. In contrast, data‐driven approaches, including independent component analysis (ICA) and principal component analysis (PCA), do extract functional networks of brain regions, and can be used to examine the interactions between networks across task conditions [e.g., Allen et al., 2014, see also Duff et al., 2012, who use a hybrid approach involving ICA on task regression statistic maps]. However, whilst these data‐driven methods capture the complexity of activity over time in terms of multiple networks, they assume that any individual network is spatially static, varying only in the activity level or magnitude across time. Consequently, they cannot determine whether the spatial properties of networks evolve in a consistent manner across time and cannot differentiate between these competing perspectives. Where existing approaches have been used to study spatial nonstationarity, it has typically been done following an ICA. For example, independent components may be estimated for different datasets and then these are compared, or else a set of independent components are calculated and then back‐projected onto different task datasets, and the resulting spatial maps for different datasets are shown to be different [Duff et al., 2012; Gordon et al, 2012; Leech et al., 2011; Utevsky et al., 2014]. While these approaches reveal changing network structure with task, they do so over long timescales (i.e., minutes), and are unable to show rapid (e.g., <10 s) shifts in network structure that accompany shifts in cognitive state.

Here, we present a novel method for spatiotemporal ICA (stICA) of task Functional MRI (FMRI) data that is designed to assess the spatial evolution of functional brain networks within the context of transitions between cognitive states. This is different from previous ICA approaches that focus on finding independent components in either the spatial or temporal domain [e.g., Beckmann and Smith, 2004], and indeed, from many other stICA approaches which do not allow for both spatial and temporal nonstationarity [e.g., Stone et al., 2002]. To identify components that, for a given temporal window, can vary both in space and time, we propose a simple reorganization of data that is subsequently used with standard spatial ICA. Specifically, we rearrange adjacent FMRI time‐points in space, before performing the ICA (Fig. 1). The key difference between this approach and spatial or temporal ICA [e.g., Beckmann et al., 2005; Smith et al., 2012] or other forms of stICA [e.g., Stone et al., 2002] is that time is remapped into space, such that both the input and the output spatial maps contain multiple time‐points; a voxel at a given spatial coordinate (e.g., in MNI space), has multiple independent representations for different time‐points. Therefore, a component resulting from the ICA procedure contains voxels that can covary across both space (within a brain at a given time‐point) and time (across different time‐points within the component). However, our approach generates components that can evolve spatially over time, thereby providing a simple data‐driven method for observing the dynamics of network activity accompanying the onset and offset of a cognitive task, without having to specify the networks a priori or assume the spatial distribution of networks is fixed over time. This method allows us to capture two phenomena that can be difficult to capture using a spatial ICA: (i) consistent sequences of transitions between different networks that occur under specific cognitive conditions (e.g., when switching between tasks, performing sequential actions, or reacting to a stimuli); (ii) situations in which the spatial configuration of a network changes across time. We explore this approach using both a simple synthetic dataset and empirical FMRI data from a working memory and target detection tasks.

Figure 1.

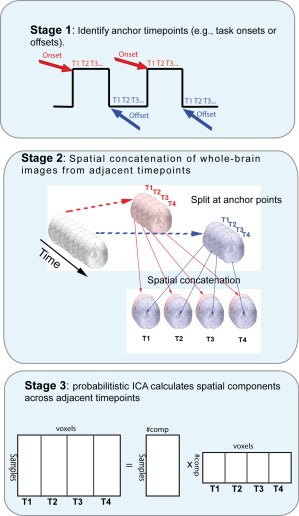
Transition spatiotemporal independent component analysis (transition stICA). Schematic showing high‐level description of the approach. Anchor points of theoretical interest are defined, such as marking the time‐point at the start or end of task blocks. The subsequent N volumes following each anchor point (in this example, four) are then rearranged and spatially concatenated along the lateral/medial dimension (although the choice of spatial dimension is arbitrary). The four‐volume wide spatial map for each anchor point is then concatenated in the fourth dimensions (i.e., what is normally thought of as the temporal dimension), and the data is then entered into an ICA. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

METHODS

Transition stICA

Figure 1 illustrates the data reorganization and analysis involved in the transition stICA. The approach starts by defining anchor points, that are the starting and finishing time‐points of periods that are theoretically interesting (Fig. 1, top). In this work, we investigate the onset and offset of task blocks both in simulated and empirical task FMRI datasets (involving interleaved task‐rest blocks). Therefore, we define our anchor points as the first time‐point and the last time‐point of each task block. Given the slow changes in the hemodynamic response, these time‐points reliably precede any detectable task‐evoked change in the neural signal (i.e., change from rest to task or from task to rest). For each dataset (i.e., each subject or simulated subject), we extracted the whole‐brain simulated or empirical FMRI volume at each anchor time‐point and the following nine time‐points. We then spatially concatenated the 10 volumes extracted for each anchor point (i.e., each task block onset or offset) along the medial–lateral dimension (Fig. 1, middle). (The dimension over which data is spatially concatenated has no effect on the results of the analysis; we chose to use the medial–lateral dimension for practical and illustrative purposes.) For the empirical FMRI data, this involved taking an image of dimension 23 × 28 × 23 voxels, and creating a sample of dimensions 230 × 28 × 23 voxels. Multiple samples (i.e., 10 volume‐wide images) were then temporally concatenated along the fourth dimension (normally referred to as the “temporal dimension” in spatial ICA of FMRI data; Fig. 2, middle). This resulted in an image for the empirical dataset with 230 × 28 × 23 × 1,080 voxels (i.e., one 10 × 3D volume × 1,080 samples). Finally, the resulting 4D dataset was decomposed into independent components (each size 230 × 28 × 23 voxels) by performing a probabilistic ICA, implemented in Melodic 3.13 (Fig. 1, bottom). We provide a Unix shell script in Supporting Information (tardis) that uses tools from FSL to perform the data reorganization, prior to a Melodic ICA (see Supporting Information).

Figure 2.

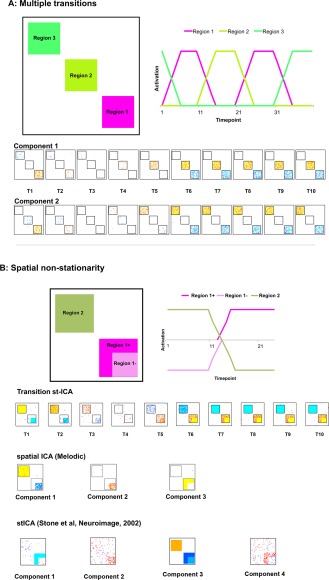
Simulated FMRI data, method and results of spatiotemporal independent component analysis (stICA). Two examples of simple synthetic data illustrating two different examples that the transition stICA approach can detect. (A) Two symmetric transitions where Region 1 precedes either Regions 2 or 3 with equal frequency, or Regions 2 or 3 precede Region 1. Top left is an illustration of the spatial patterns used to generate the synthetic data. Top right is an illustration of the timecourses used, with the spatial patterns, to create transitions. Below are the components found from the stICA. (B) A second simulation, illustrating a case of spatial nonstationarity. Regions 1 and 2 are anticorrelated, but Region 1 is a different size when it is deactivated than when it is activated. At the bottom of 2B we see: first, the transition stICA that captures the spatial nonstationarity; followed by two additional ICA approaches: an example of a standard spatial ICA and an alternative stICA [Stone et al., 2002] both of which fail to capture the spatial nonstationarity and anticorrelated network structure. Voxels are displayed at z‐values where the probability of a voxel being part of the component rather than noise was >0.95. To aid visualization, square black boxes have been placed around the distinct regions in the ICA output. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The ICA algorithm we use (Melodic 3.13 [Beckmann et al., 2005]) finds spatially independent components. However, since we have reorganized volumes of the same brain acquired at different time‐points into the same three dimensions normally used to code for space, the ICA will now find spatiotemporal components: that is, the algorithm is optimizing independence over both space and time. A key assumption is that over the course of the temporal analysis window (i.e., the number of adjacent concatenated volumes), there are patterns that have a temporal dependency (i.e., that extend over multiple adjacent time‐points). However, in the situation where there is no consistent temporal structure but consistent spatial structure (e.g., when variation between adjacent volumes is random but there are voxels that covary consistently with each other), the resulting components will be restricted to single time‐points, and the same voxel (defined in terms of, e.g., MNI coordinates) will appear at multiple time‐points (see Simulation Results section).

We quantitatively assessed the spatial evolution over time of each spatiotemporal component identified. For the empirical FMRI‐derived components (size 230 × 28 × 23 voxels), we subdivided the image along the medial–lateral dimension to produce 10 volumes (23 × 28 × 23 voxels), corresponding to the within‐component time‐points. Spatial correlation and mutual information between all pairs of within‐component volumes were calculated, resulting in two (10 × 10) similarity matrices. The two measures are expected to be broadly complementary but provide different information about the changing spatiotemporal relationship. Mutual information is a more comprehensive statistical measure, tracking the existence of any statistical (spatial) relationship over time, while the correlation provides information about the direction of the relationship (i.e., whether it is positive or negative).

Simulated FMRI Data

We used simulated FMRI data to demonstrate the transition stICA procedure, and how it differs from standard spatial ICA, and to show it is able to detect spatiotemporal components when ground truth is known. Two simple scenarios were simulated in MATLAB (R2014a) involving transitions between regions of activation (described below). All simulations involved the simple representation of brain activity as 3D synthetic data (dimensions 100 × 100 × time). The example datasets have a small number of spatial data points (100 × 100) compared to empirical FMRI data. However, for the simple stylized simulations (where there were only a few, relatively sparse, signals), the degree of sparseness of the data was (as in FMRI data) high relative to the number of voxels suggesting that ICA is still an appropriate tool to use. The synthetic data are similar or larger than that used in other ICA simulations [e.g., Stone et al., 2002], supporting our use of similar sized simulations.

We generated pixel timecourses where activation, deactivation and baseline states were modeled as all pixels within a specified region being set to 1, −1, or 0, respectively. Regions composed of adjacent 20 × 20 pixels (Fig. 3A, B, top right) were defined. To all pixel timecourses (Fig. 2A, B, top right) we added Gaussian noise (mean = 0, s.d. = 0.2). The synthetic data were, as described above, divided up based on predefined anchor points, spatially concatenated and combined across datasets. The resulting dataset was then decomposed into spatiotemporal components.

Figure 3.

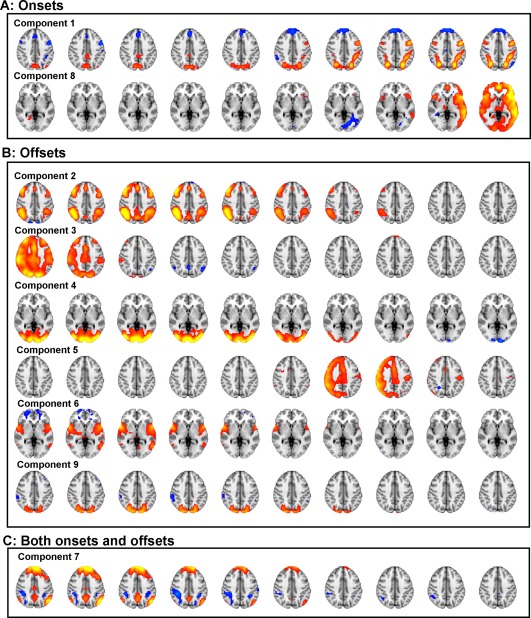
Nine spatiotemporal components extracted from a 30‐component spatiotemporal independent component analysis (stICA). Time is presented from left to right, different columns representing the 10 time‐points following an anchor point. Cool colors represent voxels negatively coupled to the component and warm colors positively coupled. All components were classified according to whether they were significantly (Bonferroni‐corrected for multiple comparisons) more activated for task onset anchor points, (A) or offsets (B), or neither (C). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The first simulation (Fig. 2A) demonstrates a scenario where a given pattern of activation could be followed by two different patterns of activation. It involved three regions and a temporal structure as follows: The activation of Region 1 is followed equally frequently by activity either in Regions 2 or 3, and then the period of activation of Regions 2 and 3 are followed by the activation Region 1. This results in four possible transitions: Region 1 → Region 2 and its symmetric transition Region 2 → Region 1; and Region 1 → Region 3 and its symmetric transition Region 3 → Region 1. When a region was fully activated (on), its timecourse was set to 1, when fully inactive (off) it was set to 0. When a region was turned on, its activity linearly increased over 5 TRs to full activation; similarly, when turned off, its activity linearly decreased over 5 TRs to 0. One hundred datasets were generated with 40 TRs per dataset, resulting in a dataset with dimension 100 × 100 × 400. Given that we implemented slow onset or offsets in the signals (crudely approximating a hemodynamic response function), anchor points were placed at the starts of transitions, which were 10 TRs apart (i.e., TR = 1, 11, 21, 31), capturing the start states and end states of the transitions. We predicted that the transition stICA should find two components, with each component reflecting a separate symmetric pair of transitions (one for Region 1 → Region 2 and its reverse; and a second for Region 1 → Region 3 and its reverse).

The second simulation (Fig. 2B) explores the scenario where there is spatial nonstationarity, and consists of two regions, one of which region shape consistently with a transition. To simulate this scenario, Region 1 had two spatial patterns, either Region 1+ which contains 20 × 20 pixels, or Region 1− which contains a subset of 15 × 15 of the pixels in Region 1+. In this simple simulation, Region 2 is activated, Region 1− is deactivated. In contrast, Region 2 is deactivated and Region 1+ is activated. In this simulation, regions become either fully active (value set to 1) or fully deactivated (value set to −1). For each transition, a region's activity linearly increased or decreased over 5 TRs. One hundred datasets were generated with 30 TRs per dataset, resulting in a 100 × 100 × 300 dataset. Anchor points were again set to the start points of the transitions, at TR = 1, 11, 21. We predicted that the transition stICA should find a single component reflecting the changing spatial pattern of Region 1, with the smaller area corresponding to Region 1− being initially deactivated and Region 2 activated, followed by a spatially larger Region 1+ becoming activated and Region 2 becoming deactivated.

In addition to the transition stICA approach, we also calculated independent components using alternative approaches: (a) Melodic ICA without the reorganization (i.e., standard spatial ICA); and (b) an alternative form of spatiotemporal ICA proposed by Stone et al., [2002]. Stone et al.'s approach does not involve any data reorganization, but instead simultaneously maximizes both spatial and temporal independence. For all approaches (i.e., the transition stICA, spatial ICA and Stone et al.'s stICA), we used default parameters except where stated otherwise.

Empirical FMRI Dataset

Participants

FMRI datasets from 68 healthy control participants (50 female, mean age 30.9 ± 2.76 1s.d.) involving blocks alternating between rest (fixation) and either target detection or 2‐back working memory task conditions (see below) were obtained from the Human Connectome Project [Van Essen et al., 2013]. These were all the FMRI datasets publicly available from this project at the time, in late 2013. Participants provided written informed consent.

FMRI data acquisition and preprocessing

Four hundred and five gradient‐echo echo planar images were collected with whole‐brain coverage using an accelerated multiband acquisition protocol [Feinberg et al., 2010; Moeller et al., 2010; Setsompop et al., 2012] with the following parameters: repetition time = 720 ms; echo time = 33.1 ms; flip angle = 52°; FOV = 208 × 180 mm (RO × PE); Matrix = 104 × 90 (RO × PE); Slice thickness = 2.0 mm; 72 slices with 2.0 mm isotropic voxels; Multiband factor = 8; Echo spacing = 0.58 ms; and bandwidth = 2,290 Hz/Px. For each participant, two runs were acquired, one with phase encoding from right‐to‐left and the other from left‐to‐right.

The data was minimally preprocessed according to the standard Human Connectome Project preprocessing pipeline, described in Fischl [2012], Glasser et al., [2013], and Jenkinson et al., [2002, 2012]. In brief, this included: (i) correction for field inhomogeneities, (ii) motion correcting the data; and (iii) transforming and resampling the data into 2 × 2 × 2 mm³ MNI152 standard space. We down‐sampled the data to 8 × 8 × 8 mm³ voxel resolution to mitigate the computational requirements of the modified probabilistic ICA step (see below). Additionally, the data were temporally filtered using a 30‐s high‐pass filter (although qualitatively similar results were obtained without any temporal filtering).

FMRI stimuli and design

The FMRI tasks are reported in detail on the website of the Human Connectome Project: (http://www.humanconnectome.org/documentation/Q1/task-fMRI-protocol-details.html). Briefly, participants underwent blocks of either target detection (0‐back) or 2‐back trials interspersed with blocks of rest (fixation). Participants were visually presented with blocks of pictures of places, tools, faces or body parts. Stimuli were projected onto a computer screen behind the participant's head via a mirror approximately 8cm from the participant's eyes. During each run, there were four long blocks separated by approximately 15 seconds of rest (fixation). Each of the long blocks (approximately 50 seconds) consisted of two shorter blocks (approximately 25 seconds each) with either target detection or 2‐back stimuli from one of the four categories. At the start of each of the short blocks, the task type (2‐back or target detection) and target (if target detection) was displayed for 2.5 seconds. This was then followed by 10 trials of 2.5 seconds. Each stimulus was presented for 2 seconds with an inter‐trial interval of 500ms. For simplicity, we analyzed only the beginning (placing anchor points at the start of the onset) and end (placing anchor points at the start of the offset) of the long blocks, although future work could explore the transitions between different task states rather than between rest and different tasks as here. Each participant performed two runs of the task. The block presentation order was the same across participants.

FMRI analysis

For the empirical FMRI data, we spatially concatenated the 10 volumes extracted for each anchor point (i.e., each task block onset or offset) along the medial–lateral dimension (Fig. 2, middle), providing a period (10 × 720 ms = 7.2 s) encompassing the peak of the hemodynamic response function, which occurs about 4–6 s following stimulus delivery [Logothetis, 2002]. Here, per subject, we have two runs with four task onset samples and four task offset samples for each run. To remove any subject‐specific mean signal effects, each voxel within the spatially concatenated data was demeaned within a run (in the fourth dimension) before being concatenated across runs and subjects (also in the fourth dimension). This resulted in a single 4D dataset, with 1,088 samples (68 subjects × 2 runs × 8 onsets/offsets).

The 4D dataset was then decomposed into different components using spatial probabilistic ICA (Fig. 2, bottom). The ICA was decomposed into 20‐, 30‐, and 70‐independent components, to investigate if the results were robust to different levels of decomposition, and the consistency of the components calculated at different dimensionality was assessed using spatial correlation. For example, each component derived at 20‐dimensions was spatially correlated with each component at 70‐dimensions, to assess which, if any, components were preserved in both analyses. As a further validation step, a separate analysis was performed after concatenating 15 rather than 10 adjacent time‐points, and then analyzing the data using a 30‐dimensional ICA. For display purposes, components were thresholded following mixture modeling (as part of the Melodic process) using a probability >0.95 that a voxel was more likely component than noise (the thresholds for each component are presented alongside the Supporting Information Figures that present each component in more detail).

Each component consisted of a spatial map and had an associated set of weights (with one value per 1,088 samples). In typical spatial ICA, the weights are considered as the component time course, with a value for each TR, representing how strongly active that component is at that time‐point. Here, we do not have time‐points as with a spatial ICA. Instead, since we input a sample for each time window (e.g., for each 10 time‐points), the transition stICA results in a component weight for each sample, representing how strongly active it is, for that sample. These weights can be used to investigate whether a specific component was involved in specific task conditions. To do this, the weight vector (1,088 data points for each component) were entered as the dependent variable into a mixed effects general linear model (using fitlme in MATLAB R2014a). The model contained fixed effect main effects for both task sequence (i.e., onset/offset) and task type (2‐back or target detection) and the interaction between the two as well as subject (since there were multiple samples per subject), modeled as a random intercept. Overall model F‐statistics were calculated to investigate if the component was modulated by the task (Bonferroni‐corrected for multiple comparisons), and t‐statistics were calculated for the main effects and for the interactions to see if they were significantly different from the null hypothesis (i.e., no difference).

RESULTS

Simulation Results

Simulated transitions between multiple networks

Figure 2A presents the results from the transition stICA performed on the first simulated dataset. The synthetic data contained four symmetrical transitions (Region 1 ↔ Region 2 and Region 1 ↔ Region 3). A transition stICA was calculated with two components. The two components strongly resembled the expected transitions. The first component represented the transition from Region 1 → Region 2. This is shown as (from left to right) a decline in activation in Region 1 to a negatively activated state, while simultaneously there is an increase in activation in Region 2. This captures the pattern of activity starting at the anchor point at TR 11. Because the underlying transition pattern was symmetric between Region 1 → Region 2 and Region 2 → Region 1, this component also captures the reverse transition starting at TR = 21 (i.e., if the component is multiplied by −1, it captures the transition from Region 2 to Region 1). The second component resembles the transition between Region 1 and Region 3, with again, Region 1 deactivating over time (from left to right) and Region 3 activating. This is consistent with the anchor point starting at TR = 31. Again, this component also captures the reverse transition from Region 3 to Region 1 that starts at TR = 1.

We note that the data is demeaned and variance normalized as part of the preprocessing with Melodic; as such the “baseline” inactive state for the different Regions is negative, rather than 0 (as in the inputted timecourse shown in the figure) and the negative “baseline” value is different between Region 1 and Regions 2 and 3, which are active only half as frequently.

We also note that a standard spatial ICA does not capture the transitions in the same form. A spatial ICA on the original data (i.e., performed by running Melodic without the spatial reordering step) revealed three components, corresponding to Regions 1, 2, and 3, but did not directly find the different transitions. We also applied an alternative form of spatiotemporal ICA [Stone et al., 2002] to the simulated dataset. This approach finds components that are maximally independent across both space and time; however, unlike our approach it does not explicitly allow for both spatial and temporal nonstationarity. As with the standard spatial ICA, this alternative form of stICA does not explicitly find the different transitions.

Simulated transitions involving spatial nonstationarity

The second simulation (Fig. 2B) demonstrates the approach when there is spatial nonstationarity (i.e., the regional pattern of activation changes with the transition). A transition stICA was calculated with a single component: theoretically, the minimum necessary to capture the transition. The component displayed spatial nonstationarity: starting (on the left) with a region resembling Region 1− (the reduced size square area) negatively weighted while Region 2 was positively weighted. This then changed over time into Region 1+ (the larger square area) being positively weighted and Region 2 being negatively weighted. Again, we note that the standard Melodic spatial ICA failed to produce a component structure that easily captures the ground truth. Figure 2B, bottom, shows the results of a spatial ICA with three components (a number which might be expected to capture all three states: Region 1−, Region 1+, and Region 2). This analysis splits Region 1 into two separate spatial patterns, rather than replicating the spatial organization of Region 1− and Region 1+. The same difficulty of the standard spatial ICA to capture the underlying spatiotemporal structure (because of the nonstationarity of Region 1) occurs with 1‐, 2‐, 5‐, or 10‐component analyses. Similarly, the alternative stICA (Fig. 2B, bottom) performs similarly to the spatial ICA at the dimensions tested (2, 4, and 10 components: the available code only functioned when even numbers of components were specified) and fails to find components that reflect the underlying transition structure.

Empirical Results

Network transitions with task onset and offset

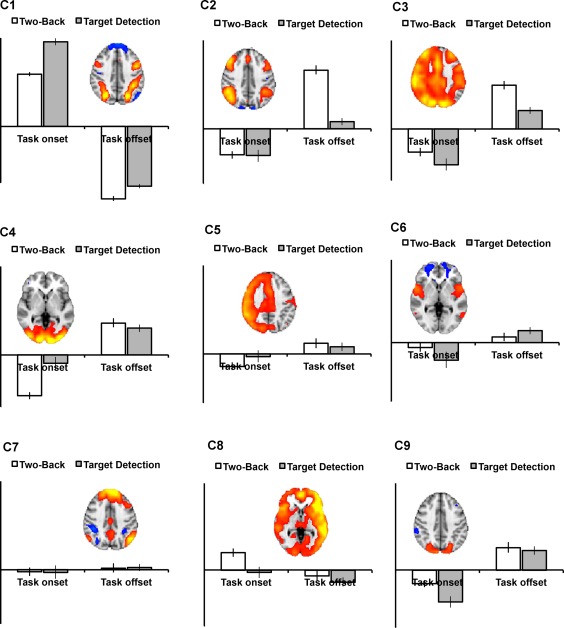
We performed the transition stICA on the empirical task FMRI data, extracting 30 components. Nine components are presented in Figure 3 (more detailed presentations of the components are included in the Supporting Information). A mixed effects general linear model comparing each component's loadings with the task condition (i.e., whether a sample was working memory or target detection and whether it was an onset or offset) showed that eight components were significantly affected by the task (Bonferroni correcting for multiple comparisons). Two components were positively weighted with task onsets and six with task offsets. In addition, we present another component (Component 7) that, although not being modulated by the task (e.g., onset/offset) is reported here because it has a strong resemblance to the canonical DMN. The other 21 components are presented in Supporting Information Figure 9.

Within Component 1, we see over time (i.e., from left to right in Fig. 3), the component changes dramatically, consistent with a shift from being in a resting state to a state performing an externally focused cognitive task. The component weights revealed that it was strongly weighted to the onset anchor points, that is, a transition from rest to task. Figure 4 shows the temporal evolution in the spatial pattern within each component (using spatial correlation and mutual information between time‐points within the component). We see that Component 1 evolves such that the first and last time‐points are highly spatially anticorrelated (although, the anticorrelation is not perfect and, as we see below in Figure 5B, the spatial patterns are nonstationary, changing with the transition).

Figure 4.

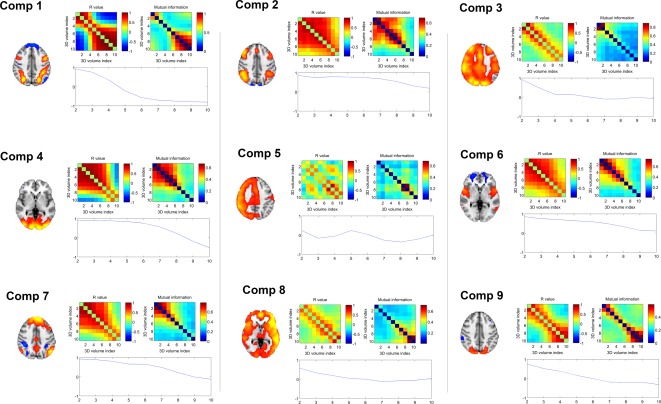
Assessing spatial change over time within spatiotemporal components. For each component, the similarity matrix (calculated using spatial correlation and mutual information) between each time‐point is presented. In addition, the spatial correlation between the first time‐point and each additional time‐point is also presented. Brain images shown are a representative time‐point from within each spatiotemporal component. Full components are shown in Figure 3 and Supporting Information. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 5.

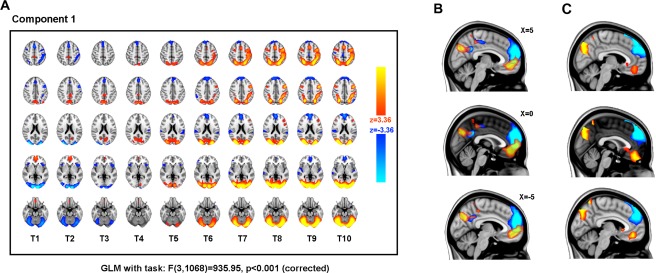
The first non‐noise spatiotemporal component identified by a 30‐component spatiotemporal independent component analysis (transition stICA). (Component 1 in Fig. 4.) The component was strongly weighted to onset anchor points, that is, a transition from rest to task. (A) The component is shown in multiple axial planes (top to bottom, MNI Z co‐ordinate = 50, 40, 20, 0, and −20), with time presented from left to right (T1–T10). Cool colors represent voxels negatively coupled to the component and warm colors positively coupled. (B) The evolving spatial organization of the medial default mode network regions of the component is shown for time‐points T1 and T10, with voxels coupled to the component at the first timepoint T1 (thresholded z > 2) shown in red, and voxels within the final time‐point (T10) in blue (component thresholded z < −2). The three panels show different X‐coordinates in MNI space. (C) The same as in B, but with the difference in z‐statistic between T1 and T10, thresholded at z > 3 (restricted to DMN regions: i.e., positively weighted z‐scores from T1 and negatively weighted z‐scores from T10). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The majority of the offset components showed the reverse temporal evolution from Component 1. Components 2, 4, 6, and 9 displayed a shift over time from typically task‐positive networks of brain regions being active to being inactive (Fig. 3B, Components 2, 4, 6, and 9). As with Component 1, this progression is consistent with the temporal change predicted based on a canonical hemodynamic response model of a task offset. These findings suggest the modified ICA has decomposed the offset periods into multiple different well‐recognized functional networks. Component 2 is composed of bilateral superior parietal, lateral, and medial superior frontal regions, a variant on FPCNs. Components 4 and 9 are visual networks localized to predominantly occipital regions. As with Component 1, Figure 4 shows these components shifting over time to a spatially anticorrelated state. Component 6 is composed of bilateral anterior insula/frontal operculum and medial frontal regions, consistent with another typical network involved in cognitive control [Bonnelle et al., 2012; Menon and Uddin, 2010].

Of the remaining components, Component 7 strongly resembles the canonical DMN and anticorrelated parts of the dorsal attention network, displaying a gradual reduction in activity over time. Surprisingly, this network was not significantly more active in task onsets (where a reduction of DMN might be expected to accompany task engagement) than offsets (P = 0.37, uncorrected for multiple comparisons).

Three components, 3, 5, and 8, partially resembled right‐ or left‐lateralized FPCNs (although all three extended over much of the gray matter in the cortex, possibly reflecting some form of global signal). Component 5 is only transiently present (for three time‐points) which is inconsistent with the expected extended hemodynamic temporal smoothing of the neural signal, and appears in the middle of the time window. It seems likely that this component may be non‐neural in origin (Fig. 3). Further, the spatial correlation and mutual information of the network is not consistent with a smooth transition between states (Fig. 4). Components 3 and 8 are also more transient than predicted based on the typical hemodynamic response (Figs. 3 and 4) as such it is unclear whether they are neural or non‐neural, or possibly a mixture of the two. If these components are non‐neural then the source of the noise is an open question for future work. One possibility is that there may be some degree of subtle task‐locked movement or other physiological signal. This would have a different time course and different effects on the MR images than the blood oxygen level dependent (BOLD) effect, and so be captured as separate components.

Transitions Between Networks and Network Nonstationarity

The spatiotemporal evolution of Component 1 is presented in more detail in Figure 5. At time‐point one (T1, Fig. 5A), there are positively coupled medial frontal and parietal regions (reminiscent of the medial nodes of the DMN), and negatively coupled occipital, superior parietal, presupplementary motor area, and dorsolateral prefrontal regions (regions typically activated by externally focused cognitive tasks). This pattern evolves over time (i.e., within the spatiotemporal component), with the expected frontoparietal system becoming apparent from T5 (approximately 3.5 s from the task onset) and being fully established by T7 (approximately 5 s post onset). This is consistent with the timing of the peak of the canonical hemodynamic response function (about 4–6 s) [Logothetis, 2002].

In general, Component 1 captures the change in spatial pattern expected for a transition between the resting state and an active externally focused cognitive task. However, the component also suggests that, rather than the network resembling the DMN simply changing from a relatively “active” state to a relatively “less active” state, its spatial organization also changes (Fig. 5B). In particular, we see that in the first time‐point (Fig. 5B, red), the DMN extends posteriorly from the posterior cingulate and precuneus and shows activation in areas of ventral anterior cingulate and paracingulate frontal regions. In contrast, by time‐point 10 (Fig. 5B, blue), the network is relatively deactivated and we see that, while there are areas of overlap with the first‐time‐point, the parietal regions extend anteriorly, and the frontal regions extend into superior frontal regions. The same evolution within Component 1 was seen at a range of thresholds for component inclusion, and when comparing other time‐points, for example, T2 with T9. Figure 5C shows the difference in z‐statistic between T1 and T10, suggesting that the nonstationarity, we observe is not merely a function of the threshold chosen, but reflects a shift in the spatial pattern of the DMN with task state.

Network Transitions and Different Task Demands

Up to now, we have only considered how the components are weighted differently for task onset and offset. However, task blocks were composed of two different externally focused cognitive tasks: either a target detection (i.e., 0‐back) or a 2‐back task. Both tasks had a similar composition, with a visually presented picture stimulus cueing a forced choice cognitive decision followed by a motor response (button press). Both tasks had the same intertrial and interstimulus timings. However, the tasks differed in terms of their cognitive demands, with target detection requiring a single target picture to be maintained in memory across the whole block, while the 2‐back required the continuous updating of items in working memory. Consistent with their different cognitive demands, the two tasks showed a difference in terms of behavior, with the target detection being performed more accurately and more rapidly (mean of median accuracy = 0.92, s.d. = 0.09; mean of median reaction time = 807 ms, s.d. = 134) than the 2‐back task (mean of median accuracy = 0.82, s.d. = 0.12; mean of median reaction time = 1,028 ms, s.d. = 137).

Figure 6 shows how different components are loaded for the two tasks, and for the onsets and offsets of the two tasks. Table 1 presents results from 2 × 2 mixed effects general linear models (with a random intercept accounting for subject) performed for each component, with task type (target detection or 2‐back) and task onset (block onset or offset) as main effects and also including a task type by onset interaction. We found that task onset/offset was the most significant predictor, but that for some components there were significant differences between task‐type. Of the components weighted heavily for task onset, Component 1 (the network that transitions from a default‐mode type network to a frontoparietal control type network) was significantly more heavily involved with the onset of the target detection than the onset of the 2‐back task. For the components involved in the offset of tasks, Component 2 (a frontoparietal network) was more involved with the offset of the 2‐back than the target detection task, as was Component 3. Component 8 had a significant overall model F statistic (see Supporting Information Figure 8) but neither of the main effects nor the interaction was significant on its own.

Figure 6.

Assessing spatial change over time within spatiotemporal components. For each component, the similarity matrix (calculated using spatial correlation and mutual information) between each time‐point is presented. In addition, the spatial correlation between the first time‐point and each additional time‐point is also presented. Brain images shown are from an illustrative time‐point from within each spatiotemporal component to help interpretation. Full components are shown in Figure 4 and Supporting Information. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 1.

Results from 2 × 2 mixed effects general linear models performed for each component, with task type (target detection or 2‐back) and task onset (block onset or offset) as main effects and also including a task type by onset interaction

Component	Condition	T	P (one tailed)
C1	2‐Back vs target detection	−3.45	<0.005
	Onset vs offset	39.94	<0.0001
	Interaction	−3.85	<0.005
C2	2‐Back vs target detection	8.27	<0.0001
	Onset vs offset	−5.44	<0.0001
	Interaction	−5.77	<0.0001
C3	2‐Back vs target detection	3.97	<0.005
	Onset vs offset	−8.48	<0.0001
	Interaction	−1.45	Ns
C4	2‐Back vs target detection	0.87	Ns
	Onset vs offset	−5.56	<0.0001
	Interaction	−4.24	<0.001
C5	2‐Back vs target detection	0.49	Ns
	Onset vs offset	−1.44	Ns
	Interaction	−1.35	Ns
C6	2‐Back Vs Target Detection	−0.87	Ns
	Onset vs offset	−4.04	<0.0005
	Interaction	1.83	Ns
C7	2‐Back vs target detection	−0.075	Ns
	Onset vs offset	−0.68	Ns
	Interaction	0.10	Ns
C8	2‐Back vs target detection	0.90	Ns
	Onset vs offset	1.40	Ns
	Interaction	1.36	Ns
C9	2‐Back vs target detection	0.46	Ns
	Onset vs offset	−7.57	<0.0001
	Interaction	1.59	Ns

Robustness of Network Transitions

The number of components extracted with an ICA can substantially affect the findings, and typically involves a trade‐off between specificity of the networks found and interpretability. For example, in a recent analysis, we found that certain important functional networks only became apparent at higher dimensionality [i.e., >50 components extracted, see Geranmayeh et al., 2014]. For this reason, it was important to show that the present results were robust to different dimensionalities, and so we reran the original analysis, extracting 20 and 70 components. The comparisons of the 20‐ and 70‐dimensional analyses with the original 30‐component analysis are presented in Figure 7A. We found a very close correspondence between Component 1 from the original analysis (Fig. 7A, middle row) with the two other analyses (Fig. 7A, top and bottom). When using spatial correlation to quantitatively compare across the components extracted, there were very strong correspondences for the majority of the original nine components of interest (Fig. 7B).

Figure 7.

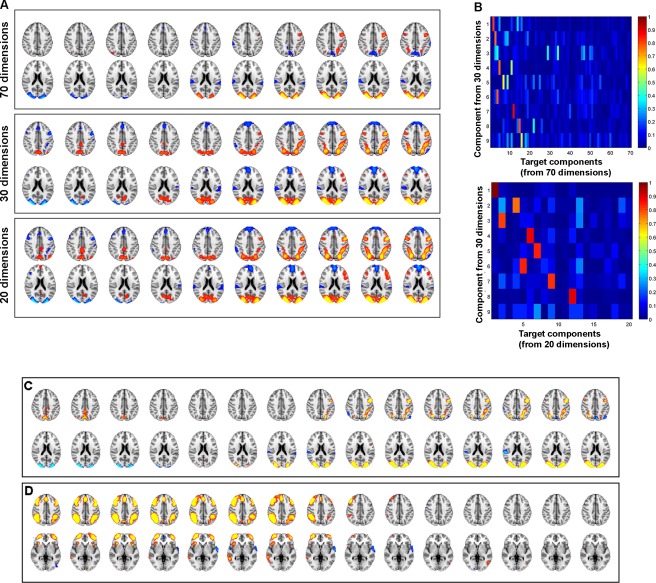
Demonstrating the robustness of the findings with different analyses. (A) The homologue of Component 1 from the 30‐component transition stICA (middle row) in both a 20‐ (bottom) and a 70‐component (top) analysis. (B) Matrix of spatial correlation between each of the nine non‐noise components from the 30‐component transition stICA and components from either the 20‐ (top matrix) or 70‐dimension analyses (bottom) coefficients. Absolute correlation coefficient values are plotted, since the sign of the correlation between components is not important for assessing spatial similarity. This shows strong, unique correlations between most of the nine components and homologues in the 20‐ and 70‐dimension analyses. (C and D) Exploring the results when spatially concatenating 15 rather than 10 time‐points, using a 30‐dimensional transition stICA. Time is from left to right. (C) The homologue of Component 1 (see Fig. 3A for comparison), (D) the homologue of Component 2 (see Fig. 3B). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

To show that the results were tolerant to different numbers of adjacent time‐points being concatenated, Figure 7C, D (in comparison with equivalent components shown in Fig. 3) show the very strong similarity in specific components between analyses conducted with 15 time‐points and the original analysis with 10 time‐points. We note that, within Component 1, the medial DMN structures (i.e., posterior cingulate and ventromedial prefrontal cortex, cold colors) that are present in the original 10‐time‐point analysis do not survive the conservative statistical threshold used in the 15‐time‐point analysis. However, at lower thresholds, these regions are present.

DISCUSSION

Here, we found our simple adaptation to a frequently used data‐driven approach robustly defines transitions in simulated data and empirical FMRI data, involving well‐recognized functional networks that accompany the onset and offset of a cognitive task. The approach explicitly focuses on spatiotemporal transitions rather than either temporal or spatial patterns, and allows for both spatial and temporal nonstationarity as well as making explicit how a spatial pattern can be involved in different transitions. From a cognitive perspective, our approach captures transitions between brain networks, which can allow investigation of the mechanisms underlying cognitive transitions that are fundamental to efficient and flexible behavior. Our results are consistent with the current understanding of a broad dynamical pattern, based on previous studies: a DMN that becomes less active while a set of FPCNs become more active with the onset of task. However, in this first exploration of our novel approach, we have observed a number of more subtle changes with potentially important consequences for understanding network dynamics.

Although this work is primarily a proof of concept study, there are several interesting neurobiological findings that the analysis reveals in addition to the expected transition between DMN and FPCN with task. First, the DMN has sometimes been described as a spatially consistent and stable network; however, increasingly it is seen to be more reactive to task demands [e.g., Harrison et al., 2008; Leech et al., 2011, 2014; Seghier and Price, 2012]. However, here, we see the DMN that is anticorrelated with the FPCN has a changing spatial distribution with cognitive state. The DMN shifts to a more anterior/superior pattern of relative deactivation during task from the more posterior inferior pattern of activation during rest. More work is needed to understand the functional significance of this spatial variation; given that we anchor the analyses to periods when the DMN and FPCNs are expected to be dominant (given the extensive prior literature). Therefore, it remains possible that the transitions we observe are not between networks that are truly linked (e.g., at rest), but instead have been mixed together, because of the neural response to the specific task demands (something that requires future work across multiple tasks). However, one more intriguing possibility is that the DMN and other functional networks are spatially dependent and may be constantly shifting their spatial organization to approximately balance activation and inhibition across space, to maintain a specific neural dynamical regime as we have recently proposed [Leech et al., 2014]. In a similar vein, a second DMN component was identified, consistent with the DMN playing multiple functional roles [Leech and Sharp, 2014; Leech et al., 2012]. Further, this DMN component, which showed initially activated (positive component coupling) DMN regions reducing in activation over time, was equally weighted to task onsets and offsets; that is, there was a “reducing” DMN component following the onset of task (as typically expected) but also following the end of task and into rest. This suggests that the transition to rest from task is not necessarily a completely passive process. Instead, it may be more of an active process, consistent with recent results suggesting a transient increase in DMN activity following task [Mullinger et al., 2013].

Our analysis also suggests an asymmetry between task onset and offset: that is, transitioning to rest is not the same as transitioning into task. There were two components that accompanied the onset of the task: (i) a DMN‐type component that transitioned into frontoparietal and visual networks (that typically activate during these types of task [Bonnelle et al., 2011; Sharp et al., 2011]); (ii) an extensive network covering much of the gray matter but centered on frontal executive systems including bilateral insula and anterior cingulate regions (which, given its late onset and extensive activation pattern, may be noise and may relate to the global signal that is often regressed out in seed based analyses). The offset of task was followed by multiple components showing a “reducing” pattern (i.e., activation reducing over time). Components C4 and C9, which both show initially positive coupling of the visual regions to the component, were significantly associated with task offsets and not task onsets. Within the components there was reducing activation over time and eventual deactivation (negative component coupling) in C4. This is as expected for the end of a visual task moving into rest. One possible explanation for the existence of relatively few onset components compared to multiple different offset components is that transitioning from an unconstrained rest state to a cognitive task involves an initial transition into a highly constrained neural state that is relatively consistent across both tasks. Over time during the task block, more heterogeneous neural processes may become evident, possibly because the relatively homogenous set of neural processes necessary to establish a new cognitive set are no longer necessary, allowing a more unconstrained or metastable state [Hellyer et al., 2014], or because of variability in how task performance is sustained over time [Leech et al., 2014]. Although rest periods appeared to be more variable, this may be because we know less about the rest state, rather than an inherent difference between task and rest. Task periods are relatively easy to interpret (since there is an explicit task, with well‐described demands) while rest periods are less so. There can be multiple different states of “rest” [Hayden et al., 2009], and it is likely that the type of network activity observed during rest depends on general context, the preceding task demands and other factors such as levels of overall arousal.

The transitions evoked by the onsets or offsets of the two different tasks (i.e., target detection or 2‐back) also differed. Although components were generally weighted to being overall task onset or offset, there was also a smaller influence from the type of task, such that Component 1, although involved for both tasks, was more heavily weighted for the target detection task. Similarly, for offsets, Component 2 (a second FPCN) was more heavily weighted for the 2‐back. These findings may reflect shared neural systems supporting similar cognitive operations involved in both tasks. But they also imply that the 2‐back task may involve additional cognitive resources, shown as the engagement during onset (and the disengagement during offset) of additional frontoparietal systems. Differences between onsets and offsets, and between tasks, may also reflect heterogeneity across subjects in how they performed the task. This is something that can be studied in the future by looking at datasets where there is considerable individual variability in task strategy or performance, for example, in patient groups or more executive tasks that elicit a variety of behavioral strategies.

Our transition stICA approach modifies a well‐accepted spatial ICA procedure by rearranging adjacent time‐points in space, before performing the ICA on samples concatenated across subjects. This approach generates components that are not constrained in space or time (except by the size of the rearranging time window), but rather span both dimensions. By anchoring the analyses to data from time periods associated with the onset and offset of a cognitive challenging task, our approach reveals novel aspects of the dynamics of network activity accompanying the transition into and out of task conditions. Importantly, these findings were observed without having to specify a priori either the spatial networks or the specific task time courses (specifying instead only the anchor points) and allowing the spatial distribution of networks to evolve over time.

While our simulations were highly simplified, they enabled us to demonstrate some important aspects of our stICA approach, supporting our application of the approach to empirical FMRI data. The simulations also allowed comparison with standard spatial ICA where ground truth was known. We found stICA was able to directly capture two phenomena defined within the synthetic data: (i) a consistent transition between networks and (ii) nonstationarity of networks over time. We found that standard spatial ICA (implemented in Melodic) in both cases failed to produce components that captured the underlying spatiotemporal structure of the data as clearly. To uncover this structure with spatial ICA, additional analysis steps using the component timecourse would be necessary, and accurately pulling apart the appropriate underlying transition structure would depend on the choice of additional analysis approach.

Our approach differs in important ways from existing approaches to investigating functional brain networks during cognitive tasks. In the traditional mass univariate voxelwise approach, a time‐course known to be associated with the task is regressed with functional data, to find voxels which are active during task and rest. This produces a single map of regions that are associated with the time‐course, but may miss the possibility that regions associated with the task are the result of activity or competition between or within multiple functional networks over time. More recently, data‐driven approaches, such as spatial ICA, have been used to define networks of brain regions, and the time‐course of networks have been compared with a time‐course associated with the task. Comparing the output of our stICA procedure to standard spatial ICA is nontrivial. For instance, the model order of a spatial ICA would need to be far higher to capture the same rich description of spatiotemporal transitions. Increasing the model order comes with problems of multiple comparisons and in interpretation, and this approach still assumes stationarity of spatial pattern of components, which may not be the case.

While we have focused on using ICA to find spatiotemporal components within FMRI data, a similar rearranging approach (rearranging time into space) could also be combined with other functional connectivity approaches, and could be used with other functional data. For example, alternative clustering approaches such as PCA could be used. Indeed, seed‐based approaches could also be used by selecting a voxel from the first time‐point, and maps computed based on voxels that significantly covary with this voxel at the same time‐point and across different time shifts could be calculated. However, such mass univariate approaches would fail to take full advantage of the multivariate nature of the data, and the fact that there are likely to be different temporally evolving components (depending on task), within‐individual and across‐individual differences.

One of the key advantages of our approach is that it is methodologically simple (involving simple spatial rearranging of the data). As such, it has considerable potential, in principle, as an exploratory data analysis tool across a range of FMRI challenges. Currently, we present results for a slow blocked FMRI design, but the approach could also be used for short event‐related designs. However, for event‐related data, there will be complexities to do with the precise alignment between when images are acquired and the onsets/offsets of events. Further, to interpret how the components are weighted onto different tasks would require convolving event onsets and durations with canonical hemodynamic responses (which was not necessary in the current situation). The length of the time window can also be modified depending on the neurobiological question, and there is no in principle minimum or maximum time window that need be used. Finally, the approach could also be applied to resting state data, although this lacks explicit time‐points to anchor the analyses, and so could be too unconstrained. One approach would be to analyze resting state data by performing a two step procedure: (1) a data‐driven classification (e.g., k‐means clustering) to label brain volumes into different well‐recognized states (e.g., canonical resting states, Smith et al., 2009]) and identify transition points between them; (2) using these transition points to define anchors for our approach (data rearrangement followed by ICA), and thereby characterizing the transitions between different states during rest.

Supporting information

Supplementary Information

Supplementary Information Figure 1.

Supplementary Information Figure 2.

Supplementary Information Figure 3.

Supplementary Information Figure 4.

Supplementary Information Figure 5.

Supplementary Information Figure 6.

Supplementary Information Figure 7.

Supplementary Information Figure 8.

Supplementary Information Figure 9.