Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2012 Sep 27;35(2):444–454. doi: 10.1002/hbm.22190

Dissociated neural correlates of quantity processing of quantifiers, numbers, and numerosities

Wei Wei 1, Chuansheng Chen 2, Tao Yang 3, Han Zhang 1, Xinlin Zhou 1,✉
PMCID: PMC6869002  PMID: 23019128

Abstract

Quantities can be represented using either mathematical language (i.e., numbers) or natural language (i.e., quantifiers). Previous studies have shown that numerical processing elicits greater activation in the brain regions around the intraparietal sulcus (IPS) relative to other semantic processes. However, little research has been conducted to investigate whether the IPS is also critical for the semantic processing of quantifiers in natural language. In this study, 20 adults were scanned with functional magnetic resonance imaging while they performed semantic distance judgment involving six types of materials (i.e., frequency adverbs, quantity pronouns and nouns, animal names, Arabic digits, number words, and dot arrays). Conjunction analyses of brain activation showed that numbers and dot arrays elicited greater activation in the right IPS than did words (i.e., animal names) or quantifiers (i.e., frequency adverbs and quantity pronouns and nouns). Quantifiers elicited more activation in left middle temporal gyrus and inferior frontal gyrus than did numbers and dot arrays. No differences were found between quantifiers and animal names. These findings suggest that, although quantity processing for numbers and dot arrays typically relies on the right IPS region, quantity processing for quantifiers typically relies on brain regions for general semantic processing. Thus, the IPS does not appear to be the only brain region for quantity processing. Hum Brain Mapp 35:444–454, 2014. © 2012 Wiley Periodicals, Inc.

Keywords: numerical processing, intraparietal sulcus, numerosity, quantity processing, quantifier

INTRODUCTION

Numbers can be represented in different forms, such as Arabic numbers (e.g., 1, 2, and 3), dots (e.g., •, ••, and •••), number words (e.g., one, two, and three), Roman numerals (I, II, and III), and so on. Many studies have focused on the neural basis of numerical processing and have explored how the human brain processes various number forms [Ansari et al., 2006; Dehaene, 1996; Piazza et al., 2004; Pinel et al., 2001, 1999, 2004].

Several lines of neuropsychological and neuroimaging studies have shown that the intraparietal sulcus (IPS) plays an important role in the representation and manipulation of abstract numerical quantity or magnitude regardless of modality [visual or auditory; Cohen Kadosh et al., 2007; Dehaene et al., 2004, 2003, 1999; Eger et al., 2003; Kadosh et al., 2005; Piazza et al., 2007; Simon et al., 2002, see a review by Cohen Kadosh et al., 2008]. First, the numerical distance effect [Moyer and Landauer, 1967] in numerical comparison tasks (e.g., Which of the numbers 5 and 6 is bigger?) is localized to the IPS [Pinel et al., 2001]. For example, an early PET study found that activation in the IPS was greater for the number pairs with a smaller numerical distance (e.g., 5 vs. 6) than for the number pairs with a larger numerical distance [e.g., 2 vs. 9; Dehaene, 1996].

Second, the IPS shows greater activation during numerical processing relative to non‐number processing. In a functional magnetic resonance imaging (fMRI) study with a target detecting paradigm, numbers produced greater activation than did colors and letters, regardless of the modality of stimuli [i.e., auditory and visual; Eger et al., 2003]. Research has demonstrated that semantic processing of numbers (e.g., Is six larger than five?) elicited greater activation in the IPS compared with processing of ferocity of animals [Thioux et al., 2005].

Third, researchers have found greater activation in the IPS when participants perform arithmetic processing with a greater demand on quantity processing (e.g., approximate calculation) than that with a greater demand on verbal processing [e.g., exact calculation; Dehaene et al., 1999; Lemer et al., 2003; Pica et al., 2004; Stanescu‐Cosson et al., 2000]. Another study found that multiplication, which mainly relies on verbal codes, induced greater activation in the angular gyrus, whereas subtraction, which mainly relies on quantity processing, induced greater activation in the IPS [Lee, 2000].

Fourth, studies also found that the IPS is sensitive to both symbolic and nonsymbolic numerical magnitude [Cantlon et al., 2006; Dehaene et al., 2003; Piazza et al., 2004; Venkatraman et al., 2005]. Participants were shown sets of dots varying in shape and number and their bilateral IPS was found to respond only to changes in number, not those in shape [Piazza et al., 2004]. Similarly, researchers found that the bilateral IPS was activated by changing numbers rather than changing areas of squares [Ansari et al., 2006]. However, not all studies found the same results. For example, there were no significant adaptive activation changes in the parietal lobe when participants were performing a number comparison task [Shuman and Kanwisher, 2004]. Cohen Kadosh et al. 2011 also used the adaptation paradigm of fMRI and found that the format change (e.g., from dots to digits) elicited a greater adaptation effect than did the magnitude change in the same intraparietal region.

Number‐specific processing has been used as evidence for the abstract quantity hypothesis about the IPS. This hypothesis, also known as the notation‐independent hypothesis, posits that quantity processing is housed in the same IPS region regardless of its notations [Dehaene, 1996; Eger et al., 2003; Pinel et al., 2001; Venkatraman et al., 2005]. All previous evidence for this hypothesis has relied on quantity processing of numbers and numerosities. Quantities, however, can also be represented by natural language (i.e., quantifiers). For example, frequency adverbs (e.g., always, occasionally, and seldom) describe the number of times certain events take place. Linguists consider frequency adverbs as representing magnitude information [Bass et al., 1974; Schriesheim and Novelli, 1989; Schriesheim and Schriesheim, 1978]. Words other than adverbs (e.g., adjectives, pronouns, and nouns) also denote quantity. For example, quantifiers such as “some,” “many,” “plenty,” and “countless” pertain to “how many.” In fact, quantifier has been defined as a determiner or pronoun that expresses quantity information [Oxford Dictionary, 2000] and treated as a type of numerical concept without exact number [Cappelletti et al., 2006]. It is thus reasonable to conclude that quantifiers and numbers both contain quantity information, although the quantity expressed by quantifiers is not as exact as that expressed by numbers. We nevertheless rely on both of them to express quantity information in our daily life. Some primitive tribes that have not developed a mature number system (e.g., Arabic digits) can only use quantity words (e.g., some, many, not many, so many, and really many) to convey quantity information [Pica et al., 2004].

According to the notation‐independent hypothesis, semantic processing of quantifiers should also be subserved by the same brain region that processes numbers and numerosities. Several neuropsychological and neuroimaging studies have been conducted to investigate the neural basis of processing quantifiers [Cappelletti et al., 2006; Cipolotti et al., 1991; McMillan et al., 2005, 2006; Morgan et al., 2011; Polk et al., 2001; Troiani et al., 2011, 2009]. Results from these neuropsychological studies have been inconsistent. Several neuropsychological studies showed that quantifier processing and numerical processing shared similar semantic magnitude systems in the brain. To illustrate, one report described a patient with lesions in the left parietal lobe who had impaired abilities to process symbolic numbers and number‐related words (e.g., dozen, half, pair, single, and quarter). Notably, this patient showed normal processing of other semantic knowledge [Polk et al., 2001]. Similarly, a patient with semantic dementia was found to show impaired ability to process nonquantifier words (e.g., the girl with blond hair) but had a normal capacity to understand quantifier words (e.g., several apples, a lot of cars) and numerical knowledge [Cappelletti et al., 2006]. In contrast, corticobasal degeneration patients show impaired understanding of verbal quantifiers [e.g., McMillan et al., 2006; Morgan et al., 2011; Troiani et al., 2011, 2009] and numbers [e.g., Halpern et al., 2004; McMillan et al., 2006], but often have normal language abilities [e.g., Troiani et al., 2011]. Finally, one neuroimaging study of normal adults compared the neural bases of first‐order versus higher order quantifiers. The first‐order quantifiers identify a number state, such as “at least 3,” “at most 5,” “exactly 2,” and “between 4 and 6.” The higher order quantifiers involve comparisons of the relative size of sets, such as “less than half,” “more than half,” and “an even number of” [McMillan et al., 2005, 2006]. Both types of quantifiers activated the right inferior parietal cortex possibly due to its role in number processing, but the higher order quantifiers induced a higher degree of activation in the right dorsolateral prefrontal cortex perhaps due to the involvement of working memory [McMillan et al., 2005].

Other results suggest that quantifier processing could be dissociated from numerical processing, which seems to support the notation‐dependent hypothesis (i.e., quantifiers use notations different from numbers and thus should involve different neural basis). For example, a Gerstmann's syndrome patient with severely impaired number processing could correctly decide which of two measurement terms denoted greater quantity. The terms included weight (e.g., gram, kilo, tonellata, and quintale) and length units [e.g., meter, centimeter, and kilometer; Cipolotti et al., 1991]. Although corticobasal degeneration patients relative to controls could not understand perfectly the cardinal quantifiers (e.g., “The blonde lady is holding more than three flowers”), but their processing of logical quantifiers (e.g., “There are some orange pumpkins in the red truck”) was not impaired [Morgan et al., 2011]. Finally, Troiani et al. 2009 found that numerical quantifiers (e.g., “at least three,” “more than two,” and even vs. odd) activated the parietal lobe more than did logical quantifiers (e.g., some and all), which instead elicited greater activation in the cingulate gyrus.

To determine whether the processing of quantifiers would lead to a category‐specific neural response in the parietal cortex, quantifiers should be directly compared against nonquantity words, which has not been done in previous neuroimaging studies. In this study with a sample of healthy Chinese adults, the brain activation elicited by both quantifiers and nonquantity words were directly compared. As a comparison task, participants also judged the ferocity of animals because a previous study found that greater activation in the IPS was elicited by numbers than by the ferocity of animals [Thioux et al., 2005].

In sum, this study tested two alternative hypotheses: the notation‐independent hypothesis and the notation‐dependent hypothesis. The notation‐independent hypothesis would predict that semantic processing of quantifiers would elicit greater activation in the IPS region than would semantic processing of animal names because the processing of all types of quantity (including that conveyed by quantifiers) should be processed in the IPS. The notation‐dependent hypothesis of quantity processing would predict that semantic processing of quantifiers and animal names would elicit a similarly low level of activation in the parietal region because neither of these two types of stimuli involves numbers. It should be noted that, as mentioned above, there are different types of quantifiers such as numerical, logical, first‐order, higher order, frequency adverbs, and quantity pronouns and nouns [McMillan et al., 2005, 2006; Morgan et al., 2011; Troiani et al., 2009]. When numerical quantifiers are included the stimulus set, the processing of numbers (e.g. “3” in the quantifier “more than 3”) may confound the results because it is difficult to determine whether the brain responds to the whole quantifiers or to the numbers in the quantifiers. Therefore, to provide a clean test of the notation‐dependent versus notation‐independent hypotheses, this study used quantifiers without actual numbers (i.e., frequency adverbs and quantity pronouns and nouns, see Methods section for details).

METHODS

Participants

A total of 20 healthy right‐handed undergraduates (mean age = 20.6 years and range = 18.8–22.5 years) were recruited from Beijing Normal University. Half of them were male. Participants had no history of neurological or psychiatric disorders or head injury. Informed written consent was obtained from each participant after the procedures of the experiment were explained. This study was approved by the Institutional Review Board of the Imaging Center for Brain Research in the Institute of Cognitive Neuroscience and Learning at Beijing Normal University.

Materials, Experimental Design, and Procedure

To investigate brain activation for the semantic processing of quantifiers, animal names and numbers, we used the semantic distance judgment task [Mummery et al., 1998; Zannino et al., 2006]. Six types of materials were used in this study: frequency adverbs (e.g., always, often, and frequently), quantity pronouns/nouns (e.g., many, some, and few), Arabic digits, animal names (e.g., tiger, leopard, and sheep), number words, and dot arrays (see Appendix).

For each trial, one target item was presented in the upper part of the screen, and two optional items were shown in the lower part (one at the left side and the other at the right side). Participants were asked to choose the one that had the smaller semantic distance from the target item. For example, one trial had “some” as the target item and “many” and “myriad” as optional items. Participants should choose “many” as the correct answer, because “some” is semantically closer to “many” than to “myriad.” For the dot arrays, semantic relation was defined as closeness in number of dots, although participants did not know the exact number of dots for each array. There were 27 trials for each type of materials (or condition). To minimize the practice effect across conditions (i.e., Arabic digits, number words, and dot arrays), we did not use the same numerical values for the three conditions.

Scanning was done in three runs with a block design. Each run included six task blocks (36 s per block) separated by six blocks of resting (24 s per block). Each task block included nine trials (4 s per trial) per condition. Each condition occurred only once within a run. The experimental procedure is represented in Figure 1.

Figure 1.

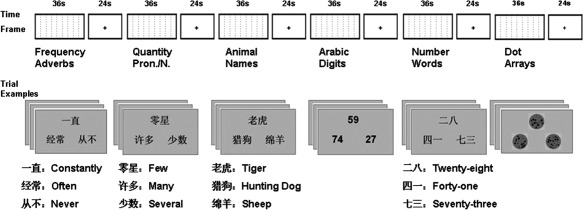
Figure 1

Open in a new tab

The experimental procedure and examples of stimuli in this study. Each participant was scanned in three 6‐min runs. Each run contained six task blocks (one block of nine trials for each type of material) and six fixation blocks. The order of the six blocks was arranged in a balanced Latin square design. pron.: pronoun and n: noun.

The order of trials in each task block was randomized for each participant. The task blocks were arranged according to a balanced Latin‐square design. For the task blocks, participants were asked to press a button to choose the correct answer as quickly and accurately as possible. For the resting blocks, participants were requested to view the fixation sign “+” at the center of the screen. Before the scanning, participants were given practice trials. The entire experiment lasted about half an hour.

Apparatus and Imaging Parameters

Stimulus presentation and behavioral data recording were controlled by a program developed using Microsoft Visual Basic on an IBM ThinkPad laptop. The stimuli were projected onto a translucent screen placed at the back of the magnet bore. Participants viewed the screen, at a distance of about 30 cm from the eyes, through a mirror mounted on the head coil.

Imaging was performed on a Siemens 3T Trio scanner (Munich, Germany) using a standard eight‐channel head coil. After automatic shimming of the magnetic field, a three‐dimensional high‐resolution T1 anatomical image was acquired for coregistration with the functional images. Next, functional volumes were acquired using a multiple slice T2*‐weighted echo planar imaging sequence. The following parameters were used: repetition time = 2000 ms; echo time = 30 ms; flip angle = 90°; matrix dimensions = 64 × 64; field of view = 200 mm; slice thickness = 4 mm. A total of 32 slices covered the entire brain.

Image Processing and Statistical Analysis

Individual fMRI data sets were analyzed using the SPM5 software (Wellcome Department of Imaging Neurosciences, University College London, UK, http://www.fil.ion.ucl.ac.uk/spm). All volumes were realigned to the first volume and spatially normalized to a common value to correct for whole‐brain differences over time. Afterward, images were smoothed using an isotropic Gaussian kernel of 8 mm and a high‐pass filter at a cutoff of 128 s.

We calculated parameter‐estimated images for individual participants across the whole brain. We then conducted group analyses with random effects on the brain activation maps of all participants. There were three steps for the group analyses. We first calculated the brain activation for each condition relative to fixation. The contrasts between the six conditions were then conducted with a lenient threshold, P < 0.01. Finally, to reveal the regions that were significantly activated by different tasks, we conducted conjunction analyses [Friston et al., 1999; Price and Friston, 1997]. The minimum T‐field was computed across different tasks. The voxels that were significant in all tasks were retained. Conjunction analyses on selected contrasts (see Results section for specific contrasts) were conducted to show (1) number‐ and numerosity‐related brain activations, (2) quantity‐related brain activations, and (3) quantifier‐related brain activations.

RESULTS

Behavioral Results

The averaged reaction time and error rates for each condition are shown in Figure 2. Analysis of variance with repeated measures (six conditions) revealed that the condition or material type had no significant effect on either the reaction time [F (1, 19) = 1.24, P = 0.304] or the error rates [F (1, 19) = 0.05, P = 0.831].

Figure 2.

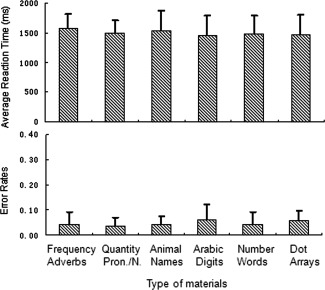
Figure 2

Open in a new tab

Mean reaction time (ms) and error rates by types of materials. pron.: pronoun and n: noun.

Imaging Results

The activation patterns for the six conditions relative to fixation are presented in Table 1 and Figure 3. In the following paragraphs, we summarize the results from the conjunction analyses.

Table 1.

Loci of brain activation for six types of materials

Type of material Brain region t value Volume Coordinates
Frequency adverbs Right middle occipital gyrus 14.59 4976 27 −93 6
13.4 −18 −99 0
12.67 −21 −90 3
Left supplementary motor area 11.14 284 −6 15 51
Left precentral gyrus 10.83 1172 −42 6 33
9.45 −27 −3 48
8.92 −45 21 27
Right middle frontal gyrus 6.11 102 39 3 66
6 30 0 51
5.99 39 −3 48
Quantity pron./n Left inferior parietal gyrus 14.28 902 −27 −54 42
8.81 −45 −39 42
Right middle occipital gyrus 12.96 3833 24 −96 6
12.79 18 −102 12
12.69 −21 −99 9
Left precentral gyrus 11.88 1667 −42 3 30
9.1 −30 24 3
9.07 −33 0 48
Right inferior parietal gyrus 9.63 338 30 −60 48
6.29 42 −42 45
Right precentral gyrus 6.87 157 45 3 30
6.24 33 −3 39
5.85 33 −3 48
Animal names Left superior parietal gyrus 10.72 796 −27 −60 45
9.75 −27 −48 39
4.79 −3 −72 45
Right calcarine gyrus 10.56 2837 24 −96 3
9.18 9 −75 −27
8.81 −24 −93 9
Right superior parietal gyrus 8.87 422 27 −60 45
6.14 21 −72 57
5.9 39 −42 42
Left inferior frontal gyrus 8.71 869 −45 9 30
8.29 −45 21 27
7.92 −27 −3 51
Arabic digits Left superior parietal gyrus 14.17 3948 −27 −63 48
10.28 27 −60 48
9.71 −15 −99 9
Left middle frontal gyrus 9.23 754 −24 −3 51
9.19 −45 6 27
8.15 −9 12 51
Right insula 8.32 124 30 21 3
Left insula 7.18 117 −30 21 3
5.77 −30 27 12
Number words Left superior parietal gyrus 14.71 5818 −27 −63 51
13.53 −27 −54 45
12.75 −33 −48 42
Left inferior frontal gyrus 10.47 474 −45 6 27
7.31 −30 21 6
6.42 −45 21 27
Left supplementary motor area 9.06 143 −6 9 54
6.37 12 12 51
5.94 9 21 48
Left middle frontal gyrus 8.41 231 −27 −3 51
6.95 −39 0 63
Dot arrays Left middle occipital gyrus 17.84 6417 −15 −99 9
17.45 15 −102 12
17.2 18 −99 0
Right inferior frontal gyrus 11.46 229 51 9 27
7.02 60 12 39
Left inferior frontal gyrus 8.45 147 −45 6 27
Right middle frontal gyrus 6.98 136 48 33 24
Left supplementary motor area 6.39 102 −6 15 51
6.04 9 18 51
Right precentral gyrus 6.37 103 36 −3 51
Open in a new tab

Height threshold: t = 4.65, P < 0.00001, and uncorrected. Extent threshold: k = 50 voxels. Voxel size: 3 × 3 × 3 mm3.

Figure 3.

Figure 3

Open in a new tab

Brain activation for the six types of materials relative to fixation. Clusters that survived P < 0.00001 (uncorrected) with spatial extent k > 50 voxels were considered statistically significant. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Number‐ and numerosity‐related brain activations

Based on the conjunction analysis of contrasts “Arabic digits – animal names,” “number words – animal names,” and “dot arrays – animal names,” numbers, and numerosities (i.e., Arabic digits, number words, and dot arrays) showed notation‐independent processing at the right IPS (P < 0.01, voxel = 20, uncorrected, see the top panel of Figure 4).

Figure 4.

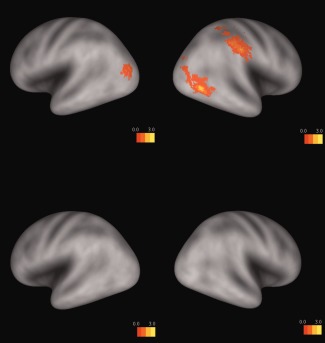
Figure 4

Open in a new tab

Number words, Arabic digits, and dot arrays elicited greater activation than animal names in the right IPS based on the conjunction analysis of contrasts “Arabic digits – animal names,” “number words – animal names,” and “dot arrays – animal names” (P < 0.01, voxel = 20, uncorrected, and the top panel). Quantifiers (frequency adverbs and quantity pronouns/nouns) did not show any notation‐independent processing at the parietal cortex based on the conjunction analysis of contrasts “Arabic digits – animal names,” “number words – animal names” and “dot arrays – animal names,” “frequency adverbs – animal names,” and “quantity pron./n – animal names” (P < 0.01, voxel = 20, uncorrected, and the bottom panel). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Quantity‐related brain activations

The conjunction analysis of contrasts “Arabic digits – animal names,” “number words – animal names” and “dot arrays – animal names,” “frequency adverbs – animal names,” and “quantity pron./n – animal names” showed that no brain regions were significantly activated when quantity is broadly defined to include that of quantifiers as well as that of numbers and numerosities (P < 0.01, voxel = 20, and uncorrected; see the bottom panel of Figure 4). In other words, there were no quantity‐related brain activations shared by quantifiers, numbers, and numerosities.

Quantifier‐related brain activations

Relative to Arabic digits, number words, and dot arrays, quantifiers (i.e., frequency adverbs and quantity pronouns and nouns) elicited more activation in the left middle temporal gyrus and inferior frontal gyrus, based on the conjunction analysis of contrasts “frequency adverbs – Arabic digits,” “frequency adverbs– number words,” “frequency adverbs – dot arrays,” “quantity pron./n – Arabic digits,” “quantity pron./n – number words,” and “quantity pron./n – dot arrays,” (P < 0.01, voxel = 20, and uncorrected; see the top panel of Figure 5). Additionally, numbers and numerosities (i.e., Arabic digits, number words, and dot arrays) elicited more activation in the right IPS than quantifiers (i.e., frequency adverbs and quantity pronouns and nouns), based on the conjunction analysis of contrasts “Arabic digits – frequency adverbs,” “number words – frequency adverbs,” “dot arrays – frequency adverbs,” “Arabic digits – quantity pron./n,” “number words – quantity pron./n,” and “dot arrays – quantity pron./n” (P < 0.01, voxel = 20, and uncorrected; see the bottom panel of Figure 5).

Figure 5.

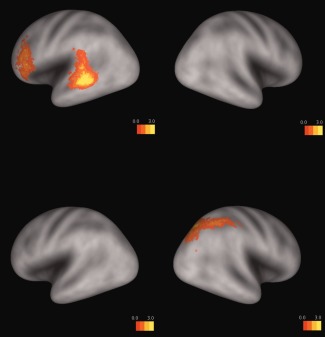
Figure 5

Open in a new tab

Quantifiers elicited more activation in the left middle temporal gyrus and inferior frontal gyrus than numbers and numerosities based on the conjunction analysis of contrasts “frequency adverbs – Arabic digits,” “frequency adverbs– number words,” “frequency adverbs – dot arrays,” “quantity pron./n – Arabic digits,” “quantity pron./n – number words,” and “quantity pron./n – dot arrays” (P < 0.01, voxel = 20, uncorrected, and the top panel). Numerical materials elicited more activation in the right IPS than quantifiers based on the conjunction analysis of contrasts “Arabic digits – frequency adverbs,” “number words – frequency adverbs,” “dot arrays – frequency adverbs,” “Arabic digits – quantity pron./n,” “number words – quantity pron./n,” and “dot arrays – quantity pron./n” (P < 0.01, voxel = 20, uncorrected, and the bottom panel). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

DISCUSSION

The objective of this study was to investigate whether the quantity processing of quantifiers (frequency adverbs and quantity pronouns/nouns), numbers (Arabic digits and number words), and numerosities (dot arrays) shared the same neural correlates in the IPS. Quantifiers did not produce greater activation in the IPS than did the control material of animal names. In contrast, numerical materials (i.e., Arabic digits and number words) and dot arrays consistently induced greater activation in the IPS region than did animal names and quantifiers. These results suggest a clear neural dissociation between the quantity processing of quantifiers and that of numbers and numerosities.

This dissociation between the quantity processing of quantifiers and that of numbers and numerosities is evidence against the abstract quantity hypothesis (or the notation‐independent hypothesis) in the IPS. According to the abstract quantity hypothesis, the activation of quantity processing of quantifiers should be similar to the activation of quantity processing of numbers and dot arrays in the IPS. We compared quantifiers, numbers, and dot arrays with a control semantic task (animal names). This was done because an earlier study found that number comparison tasks differed from the processing of animal names (animals varying in ferocity) in the bilateral IPS [Thioux et al., 2005]. Our results showed greater activations in the IPS for numbers and dot arrays than for both quantifiers and animal names. It appears that the quantity processing of numbers and dot arrays is subserved by the IPS, but the quantity processing of quantifiers is not. In other words, the IPS may be specific to the processing of numbers and dot arrays, rather than quantity processing in general. These results supported the hypothesis of notation‐dependent quantity processing in the brain.

Quantifiers were found to produce greater activation than Arabic numbers, number words and dot arrays only in the left middle posterior temporal gyrus and the left inferior frontal gyrus. These regions are associated with general semantic processing and verbal processing [Booth et al., 2006]. Thus, the quantity processing of quantifiers may share similar neural mechanisms as general semantic and verbal processing.

The dissociation between quantifier and number processing was consistent with some of the previous neuropsychological studies. These studies found that patients who had damages to their parietal cortex showed impairment in number processing but retained the ability for quantifier processing [Cipolotti et al., 1991; Morgan et al., 2011]. For example, Cipolotti et al. 1991 found that the patient with damage to her parietal cortex could not complete the simplest arithmetic problems and multiplication table, but she could judge which of two measure terms had greater quantity information (e.g. gram, kilo, meter, and centimeter). Morgan et al. 2011 found that corticobasal degeneration patients had a selective deficit for cardinal quantifiers (e.g., “The blonde lady is holding more than three flowers”) compared to healthy seniors, but the processing of logical quantifiers (e.g., “There are some orange pumpkins in the red truck”) was normal. These studies showed neural dissociation in quantifier and numerical processing.

Our results, however, appeared to be different from several other neuropsychological studies that found a close association between quantifier processing and number processing [Cappelletti et al., 2006; McMillan et al., 2006; Morgan et al., 2011; Polk et al., 2001; Troiani et al., 2011]. Some of the discrepancies may have been due to the use of materials. For example, the quantifiers used by Polk et al. 2001 included words such as “dozen,” “pair,” “twin,” “half,” “quartet,” and “sextet.” These words appear to contain specific number information (12, 2, etc.), which might have accounted for the similarity between their semantic processing and that of numbers. Similarly, the studies of the corticobasal degeneration patients [e.g., McMillan et al., 2006; Morgan et al., 2011; Troiani et al., 2011] also used quantifiers that contained actual numbers (numerical or cardinal quantifiers such as “more than three”). Similarly, Troiani et al.'s 2009 finding that numerical quantifiers induced greater activation in the parietal lobe than did logical quantifiers can be explained by the number words embedded in their numerical quantifiers (e.g., “at least three” and “more than two”). In sum, previous neuroimaging studies used both numerical and non‐numerical quantifiers, which makes it difficult to distinguish whether the brain is processing the whole phrases as one unit (i.e., the whole quantifiers only) or the components (i.e., both the quantifiers and the specific numbers). In our study, we excluded any quantifiers that include actual numbers to investigate how “pure” quantifiers are processed and to provide a clean test of the notation‐dependent and ‐independent hypotheses. It seems clear from both Troiani et al. study and our study that “pure” quantifiers (or logical quantifiers in Troiani et al.) are not processed in the IPS but are rather processed in the brain's language areas. These results also suggest that it is important to distinguish quantifiers with and without numbers. We should hasten to add that, because we did not include a condition with numerical quantifiers, the above discussion is speculative. Future research should compare directly quantifiers with and without explicit numbers.

Finally, our finding on surface may lead to the question whether non‐numerical quantifiers (including logical quantifiers) would have any quantity information. However, as we argued in Introduction section, quantifiers in natural language contain information of quantity [Hubbard et al., 2008; Rajapakse et al., 2005], denote numerical concepts without explicit specification of an exact number [Cappelletti et al., 2006], and serve as a language‐based counting system for tribal people without a formal number‐based system [Pica et al., 2004].

In summary, this study found neural dissociations for the processing of quantifiers, numbers, and numerosities. Although the quantity processing of numbers and numerosities relies on the IPS, the quantity processing of quantifiers without actual numbers relies on the left inferior frontal gyrus and the left middle temporal gyrus. The results of this study suggest that the IPS is not the only brain region for all types of quantity processing, which is consistent with the growing literature that semantics are supported by distributed networks [Patterson et al., 2007].

MATERIALS FOR SEMANTIC PROCESSING IN THIS STUDY

Conditions Chinese name Pronunciation English Word frequencya
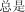
Frequency adverbs graphic file with name HBM-35-444-g006.jpg zng shì always 254.93
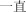
graphic file with name HBM-35-444-g007.jpg yı zhí constantly 731.85
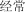
graphic file with name HBM-35-444-g008.jpg jıng cháng often 100.28
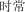
graphic file with name HBM-35-444-g009.jpg shí cháng frequently 4.92
graphic file with name HBM-35-444-g010.jpg yu shí sometimes 77.12
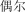
graphic file with name HBM-35-444-g011.jpg u ěr occasionally 20.15
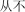
graphic file with name HBM-35-444-g012.jpg cóng bù never 15.59
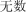
Quantity graphic file with name HBM-35-444-g013.jpg wú shù myriad 19.50
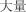
pronouns/nouns graphic file with name HBM-35-444-g014.jpg dà liàng abundance 25.04
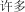
graphic file with name HBM-35-444-g015.jpg x duo many 60.04
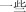
graphic file with name HBM-35-444-g016.jpg yı xie some 510.72
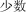
graphic file with name HBM-35-444-g017.jpg sho shù several 7.15
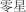
graphic file with name HBM-35-444-g018.jpg líng xıng few 0.51
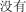
graphic file with name HBM-35-444-g019.jpg méi yu none 3226.48
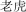
Animal names graphic file with name HBM-35-444-g020.jpg lo h tiger 10.97
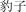
graphic file with name HBM-35-444-g021.jpg bào zi leopard 1.07
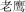
graphic file with name HBM-35-444-g022.jpg lo yıng eagle 7.48
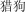
graphic file with name HBM-35-444-g023.jpg liè gu hunting dog 1.82
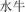
graphic file with name HBM-35-444-g024.jpg shu niú buffalo 3.19
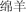
graphic file with name HBM-35-444-g025.jpg mián yáng sheep 2.71
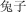
graphic file with name HBM-35-444-g026.jpg tù zi rabbit 23.76
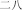
Number words graphic file with name HBM-35-444-g027.jpg èr shi ba twenty‐eight
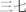
graphic file with name HBM-35-444-g028.jpg san shi qı thirty‐seven
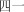
graphic file with name HBM-35-444-g029.jpg sì shi yı forty‐one
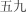
graphic file with name HBM-35-444-g030.jpg w shi ji fifty‐nine
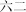
graphic file with name HBM-35-444-g031.jpg liù shi èr sixty‐two
graphic file with name HBM-35-444-g032.jpg qı shi san seventy‐three
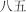
graphic file with name HBM-35-444-g033.jpg ba shi w eighty‐five
Arabic digits 27 èr shi qı twenty‐seven
36 san shi liù thirty‐six
42 sì shi èr forty‐two
59 w shi ji fifty‐nine
65 liù shi w sixty‐five
74 qı shi sì seventy‐four
83 ba shi san eighty‐three
Dot arrays Inline graphic (20)
Inline graphic (25)
Inline graphic (30)
Inline graphic (35)
Inline graphic (40)
Inline graphic (45)
Inline graphic (50)
Open in a new tab
a

The word frequency (per million) for frequency adverbs, quantity pronouns/nouns, and animal names came from the SUBTLEX‐CH (Cai and Brysbaert, 2010).

REFERENCES

  1. Ansari D, Dhital B, Siong S. (2006): Parametric effects of numerical distance on the intraparietal sulcus during passive viewing of rapid numerosity changes. Brain Res 1067:181–188. [DOI] [PubMed] [Google Scholar]
  2. Bass B, Cascio W, O'Connor E. (1974): Magnitude estimations of expressions of frequency and amount. J Appl Psychol 59:313–320. [Google Scholar]
  3. Booth J, Lu D, Burman D, Chou T, Jin Z, Peng D, Zhang L, Ding G, Deng Y, Liu L. (2006): Specialization of phonological and semantic processing in Chinese word reading. Brain Res 1071:197–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cai Q, Brysbaert M. (2010): SUBTLEX‐CH: Chinese word and character frequencies based on film subtitles. PLoS One 5:e10729. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cantlon J, Brannon E, Carter E, Pelphrey K. (2006): Functional imaging of numerical processing in adults and 4‐y‐old children. PLoS Biol 4:844–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Cappelletti M, Butterworth B, Kopelman M. (2006): The understanding of quantifiers in semantic dementia: A single‐case study. Neurocase 12:136–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Cipolotti L, Butterworth B, Denes G. (1991): A specific deficit for numbers in a case of dense acalculia. Brain 114:2619. [DOI] [PubMed] [Google Scholar]
  8. Cohen Kadosh R, Cohen Kadosh K, Kaas A, Henik A, Goebel R. (2007): Notation‐dependent and ‐independent representations of numbers in the parietal lobes. Neuron 53:307–314. [DOI] [PubMed] [Google Scholar]
  9. Cohen Kadosh R, Lammertyn J, Izard V. (2008): Are numbers special? An overview of chronometric, neuroimaging, developmental and comparative studies of magnitude representation. Prog Neurobiol 84:132–147. [DOI] [PubMed] [Google Scholar]
  10. Cohen KR, Bahrami B, Walsh V, Butterworth B, Popescu T, Price C. (2011): Specialization in the human brain: The case of numbers. Front Hum Neurosci 5:62. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Dehaene S. (1996): The organization of brain activations in number comparison: Event‐related potentials and the additive‐factors method. J Cogn Neurosci 8:47–68. [DOI] [PubMed] [Google Scholar]
  12. Dehaene S, Molko N, Cohen L, Wilson A. (2004): Arithmetic and the brain. Curr Opin Neurobiol 14:218–224. [DOI] [PubMed] [Google Scholar]
  13. Dehaene S, Piazza M, Pinel P, Cohen L. (2003): Three parietal circuits for number processing. Cogn Neuropsychol 20:487–506. [DOI] [PubMed] [Google Scholar]
  14. Dehaene S, Spelke E, Pinel P, Stanescu R, Tsivkin S. (1999): Sources of mathematical thinking: Behavioral and brain‐imaging evidence. Science 284:970–974. [DOI] [PubMed] [Google Scholar]
  15. Eger E, Sterzer P, Russ M, Giraud A, Kleinschmidt A. (2003): A supramodal number representation in human intraparietal cortex. Neuron 37:719–726. [DOI] [PubMed] [Google Scholar]
  16. Friston KJ, Holmes AP, Price C, Büchel C, Worsley K. (1999): Multisubject fMRI studies and conjunction analyses. Neuroimage 10:385–396. [DOI] [PubMed] [Google Scholar]
  17. Halpern C, Glosser G, Clark R, Gee J, Moore P, Dennis K, McMillan C, Colcher A, Grossman M. (2004): Dissociation of numbers and objects in corticobasal degeneration and semantic dementia. Neurology 62:1163–1169. [DOI] [PubMed] [Google Scholar]
  18. Hubbard EM, Diester I, Cantlon JF, Ansari D, Van Opstal F, Troiani V. (2008): The evolution of numerical cognition: From number neurons to linguistic quantifiers. J Neurosci 28:11819–11824. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Kadosh R, Henik A, Rubinsten O, Mohr H, Dori H, van de Ven V, Zorzi M, Hendler T, Goebel R, Linden D. (2005): Are numbers special? The comparison systems of the human brain investigated by fMRI. Neuropsychologia 43:1238–1248. [DOI] [PubMed] [Google Scholar]
  20. Lee K. (2000): Cortical areas differentially involved in multiplication and subtraction: A functional magnetic resonance imaging study and correlation with a case of selective acalculia. Ann Neurol 48:657–661. [PubMed] [Google Scholar]
  21. Lemer C, Dehaene S, Spelke E, Cohen L. (2003): Approximate quantities and exact number words: Dissociable systems. Neuropsychologia 41:1942–1958. [DOI] [PubMed] [Google Scholar]
  22. McMillan C, Clark R, Moore P, Devita C, Grossman M. (2005): Neural basis for generalized quantifier comprehension. Neuropsychologia 43:1729–1737. [DOI] [PubMed] [Google Scholar]
  23. McMillan C, Clark R, Moore P, Grossman M. (2006): Quantifier comprehension in corticobasal degeneration. Brain Cogn 62:250–260. [DOI] [PubMed] [Google Scholar]
  24. Morgan B, Gross RG, Clark R, Dreyfuss M, Boller A, Camp E, Liang TW, Avants B, McMillan CT, Grossman M. (2011): Some is not enough: Quantifier comprehension in corticobasal syndrome and behavioral variant frontotemporal dementia. Neuropsychologia 49:3532–3541. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Moyer RS, Landauer TK. (1967): Time required for judgements of numerical inequality. Nature 215:1519–1520. [DOI] [PubMed] [Google Scholar]
  26. Mummery C, Patterson K, Hodges J, Price C. (1998): Functional neuroanatomy of the semantic system: Divisible by what? J Cogn Neurosci 10:766–777. [DOI] [PubMed] [Google Scholar]
  27. Oxford Dictionary (2000). Oxford Advanced Learner's Dictionary. Oxford: Oxford University Press. [Google Scholar]
  28. Patterson K, Nestor PJ, Rogers TT. (2007): Where do you know what you know? The representation of semantic knowledge in the human brain. Nat Rev Neurosci 8:976–987. [DOI] [PubMed] [Google Scholar]
  29. Piazza M, Izard V, Pinel P, Le Bihan D, Dehaene S. (2004): Tuning curves for approximate numerosity in the human intraparietal sulcus. Neuron 44:547–555. [DOI] [PubMed] [Google Scholar]
  30. Piazza M, Pinel P, Le Bihan D, Dehaene S. (2007): A magnitude code common to numerosities and number symbols in human intraparietal cortex. Neuron 53:293–305. [DOI] [PubMed] [Google Scholar]
  31. Pica P, Lemer C, Izard V, Dehaene S. (2004): Exact and approximate arithmetic in an Amazonian indigene group. Science 306:499–503. [DOI] [PubMed] [Google Scholar]
  32. Pinel P, Dehaene S, Riviere D, LeBihan D. (2001): Modulation of parietal activation by semantic distance in a number comparison task. Neuroimage 14:1013–1026. [DOI] [PubMed] [Google Scholar]
  33. Pinel P, Le Clec'H G, van de Moortele P, Naccache L, Le Bihan D, Dehaene S. (1999): Event‐related fMRI analysis of the cerebral circuit for number comparison. Neuroreport 10:1473. [DOI] [PubMed] [Google Scholar]
  34. Pinel P, Piazza M, Le Bihan D, Dehaene S. (2004): Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments. Neuron 41:983–993. [DOI] [PubMed] [Google Scholar]
  35. Polk T, Reed C, Keenan J, Hogarth P, Anderson C. (2001): A dissociation between symbolic number knowledge and analogue magnitude information. Brain Cogn 47:545–563. [DOI] [PubMed] [Google Scholar]
  36. Price CJ, Friston KJ. (1997): Cognitive conjunction: A new approach to brain activation experiments. Neuroimage 5:261–270. [DOI] [PubMed] [Google Scholar]
  37. Rajapakse R, Cangelosi A, Coventry K, Newstead S, Bacon A. (2005): Grounding linguistic quantifiers in perception: Experiments on numerosity judgments In: 2nd Language & Technology Conference: Human Language Technologies as a Challenge for Computer Science and Linguistics, Poznañ, Poland, April 21–23, 2005. [Google Scholar]
  38. Schriesheim C, Novelli L. (1989): A comparative test of the interval‐scale properties of magnitude estimation and case III scaling and recommendations for equal‐interval frequency response anchors. Edu Psychol Meas 49:59. [Google Scholar]
  39. Schriesheim C, Schriesheim J. (1978): The invariance of anchor points obtained by magnitude estimation and pair‐comparison treatment of complete ranks scaling procedures: An empirical comparison and implications for validity of measurement. Educ Psychol Meas 38:977. [Google Scholar]
  40. Shuman M, Kanwisher N. (2004): Numerical magnitude in the human parietal lobe: Tests of representational generality and domain specificity. Neuron 44:557–569. [DOI] [PubMed] [Google Scholar]
  41. Simon O, Mangin J, Cohen L, Le Bihan D, Dehaene S. (2002): Topographical layout of hand, eye, calculation, and language‐related areas in the human parietal lobe. Neuron 33:475–487. [DOI] [PubMed] [Google Scholar]
  42. Stanescu‐Cosson R, Pinel P, Van De Moortele P, Le Bihan D, Cohen L, Dehaene S. (2000): Understanding dissociations in dyscalculia: A brain imaging study of the impact of number size on the cerebral networks for exact and approximate calculation. Brain 123:2240. [DOI] [PubMed] [Google Scholar]
  43. Thioux M, Pesenti M, Costes N, De Volder A, Seron X. (2005): Task‐independent semantic activation for numbers and animals. Cogn Brain Res 24:284–290. [DOI] [PubMed] [Google Scholar]
  44. Troiani V, Clark R, Grossman M. (2011): Impaired verbal comprehension of quantifiers in corticobasal syndrome. Neuropsychology 25:159–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Troiani V, Peelle JE, Clark R, Grossman M. (2009): Is it logical to count on quantifiers? Dissociable neural networks underlying numerical and logical quantifiers. Neuropsychologia 47:104–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Venkatraman V, Ansari D, Chee MWL. (2005): Neural correlates of symbolic and non‐symbolic arithmetic. Neuropsychologia 43:744–753. [DOI] [PubMed] [Google Scholar]
  47. Zannino GD, Perri R, Pasqualetti P, Paola MD, Caltagirone C, Carlesimo GA. (2006): The role of semantic distance in category‐specific impairments for living things: Evidence from a case of semantic dementia. Neuropsychologia 44:1017–1028. [DOI] [PubMed] [Google Scholar]

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES