Age‐related changes in the topological organization of the white matter structural connectome across the human lifespan

Abstract

Lifespan is a dynamic process with remarkable changes in brain structure and function. Previous neuroimaging studies have indicated age‐related microstructural changes in specific white matter tracts during development and aging. However, the age‐related alterations in the topological architecture of the white matter structural connectome across the human lifespan remain largely unknown. Here, a cohort of 113 healthy individuals (ages 9–85) with both diffusion and structural MRI acquisitions were examined. For each participant, the high‐resolution white matter structural networks were constructed by deterministic fiber tractography among 1024 parcellation units and were quantified with graph theoretical analyses. The global network properties, including network strength, cost, topological efficiency, and robustness, followed an inverted U‐shaped trajectory with a peak age around the third decade. The brain areas with the most significantly nonlinear changes were located in the prefrontal and temporal cortices. Different brain regions exhibited heterogeneous trajectories: the posterior cingulate and lateral temporal cortices displayed prolonged maturation/degeneration compared with the prefrontal cortices. Rich‐club organization was evident across the lifespan, whereas hub integration decreased linearly with age, especially accompanied by the loss of frontal hubs and their connections. Additionally, age‐related changes in structural connections were predominantly located within and between the prefrontal and temporal modules. Finally, based on the graph metrics of structural connectome, accurate predictions of individual age were obtained (r = 0.77). Together, the data indicated a dynamic topological organization of the brain structural connectome across human lifespan, which may provide possible structural substrates underlying functional and cognitive changes with age. Hum Brain Mapp 36:3777–3792, 2015. © 2015 Wiley Periodicals, Inc.

INTRODUCTION

Lifespan is a dynamic process with significant changes in brain structures and functions (Craik and Bialystok, 2006; Sowell et al., 2004). Advanced neuroimaging techniques have allowed for the examination of these age‐related changes in vivo (Bartzokis et al., 2012; Fair et al., 2008; Shaw et al., 2008). Longitudinal structural MRI studies have demonstrated increasing white matter (WM) volumes and inverted U‐shaped trajectories of gray matter (GM) volumes in developing children and adolescents (Giedd et al., 1999). After maturation, both cerebral WM and GM exhibit degenerative processes with healthy aging (Madden et al., 2012; Sowell et al., 2003).

With the technique of diffusion tensor imaging (DTI), the microstructural changes of cerebral WM under various conditions can be quantified (Basser et al., 1994). When fitted with age, the integrity of most major WM tracts exhibited inverted U‐shaped trajectories across lifespan, and the peak occurred at ages varying from 20 to 40 years old (Hasan et al., 2009a, 2009b; Kochunov et al., 2012; Lebel et al., 2012; Li et al., 2013; Yeatman et al., 2014). These changes could be attributable to increases in axon diameter, myelination, synaptic pruning, and cell shrinkage (Bartzokis et al., 2012; Morrison and Hof, 1997; Terry et al., 1987). Besides DTI, other imaging techniques have also revealed the inverted U‐shaped curve over lifespan. Specifically, the changes of myelin sheath in several fiber bundles have been found to follow different Poisson trajectories by magnetic susceptibility map (Li et al., 2014). However, most previous studies have focused on the lifespan trajectory of specific WM tracts. Age‐related changes in the interactions between different brain regions, which can be studied at system level by network analysis, remain largely unknown. Describing the brain network and its trajectory across the human lifespan is a fundamental goal of neuroscience, the importance of which was recently underscored by the establishment of the NIH Human Connectome Project (Sporns et al., 2005; Van Essen et al., 2013).

Recent works have suggested that large‐scale WM structural networks can be mapped from diffusion MRI tractography and analyzed with graph‐theoretical approaches, that is, the so‐called structural connectome (Bullmore and Sporns, 2009). Using connectome‐based approaches, many studies have shown that human WM networks exhibit many nontrivial topological properties, such as small‐worldness, modularity, and rich‐club organization (Bullmore and Sporns, 2009; van den Heuvel and Sporns, 2011). Specifically, several recent studies have demonstrated that the topological efficiency of WM networks increases linearly during development (Collin and van den Heuvel, 2013; Hagmann et al., 2010; Huang et al., 2013; Yap et al., 2013) and decreases during normal aging (Gong et al., 2009), providing further insights into the cognitive decline of this process (Wen et al., 2011). In a recent review paper, Collin and van den Heuvel (2013) suggested that the changes of connectome organization throughout the lifespan should follow an inverted U‐shaped pattern. However, seldom studies have validated the hypothesis and little is known about the age‐related alterations of the topological organization of human WM networks across the lifespan.

In this study, we used diffusion MRI deterministic tractography and graph‐theoretical approaches to examine age‐related alterations in the topology of WM structural networks in a cohort of healthy subjects ranging from 9 to 85 years old. At a system level, we aimed to chart the age trajectories of human WM networks from both global and regional perspectives, to provide a complete view of the topological changes of the structural connectome over age. These studies are important for elucidating the path by which optimal healthy development and aging are promoted and distinguishing early brain changes in neuropsychiatric diseases from normal development and aging processes.

MATERIALS AND METHODS

Participants

This study included 113 healthy, right‐handed subjects (age range, 9 to 85 years; mean age, 38.2 ± 21.4 years; 50 females) from the NKI/Rockland Sample (NKI‐RS), which is provided by the Nathan Kline Institute (NKI, NY) and publicly available at the International Neuroimaging Data‐sharing Initiative (INDI) online (http://fcon_1000.projects.nitrc.org/indi/pro/nki.html) (Nooner et al., 2012). The NKI Institutional Review Board approved the research protocol to collect and share the data. A detailed description of the subjects' INDI database identifiers and corresponding demographic information is provided in a previous study (Cao et al., 2014). The gender distributions in the different age groups are presented in Supporting Information Figure S1.

Data Acquisition

All participants were scanned with a Siemens Trio 3.0 Tesla MRI scanner. Among other imaging sequences, depending on the indication, a high‐resolution 3D T1‐weighted image was acquired using a magnetization prepared rapid gradient echo sequence with 1 mm isotropic voxels [repetition time (TR)/echo time (TE) = 2500/3.5 ms, inversion time = 1200 ms, field of view (FOV)  = 256 × 256 mm², 192 slices]. The diffusion MRI scan was acquired with conventional acquisition parameters with 2 mm isotropic voxels and 64 gradient directions (b = 1000 s/mm², 12 nondiffusion b = 0 images, TR/TE = 10,000/91 ms, FOV = 256 × 256 mm², 58 slices). Further details regarding the acquisition protocol of the study images are available on the INDI website.

Data Preprocessing

GM/WM segmentation

GM and WM segmentation was implemented by SPM8 software (http://www.fil.ion.ucl.ac.uk/spm/software/spm8). First, individual T1‐weighted structural images were coregistered to the b = 0 images using a linear transformation. The transformed structural images were then segmented into GM, WM, and cerebrospinal fluid (CSF) by a unified segmentation algorithm (Ashburner and Friston, 2005). The brain size for each participant was obtained by computing the total GM, WM, and CSF volumes.

DTI data preprocessing

The preprocessing included eddy current and head motion correction, estimation of the diffusion tensor and calculation of the fractional anisotropy (FA). Briefly, the eddy current distortions and motion artifacts in the DTI data were corrected by applying an affine alignment of each diffusion‐weighted image to the b = 0 image. Accordingly, the b‐matrix was reoriented based on the transformation matrix (Leemans and Jones, 2009). After that, the diffusion tensor elements were estimated (Basser et al., 1994) and the corresponding FA value of each voxel was calculated (Basser and Pierpaoli, 1996). All preprocessing procedures of the DTI data were performed with the FDT toolbox in FSL (http://www.fmrib.ox.ac.uk/fsl).

Network Construction

Nodes and edges are the two fundamental elements of a network. In this study, we constructed individual WM structural networks using the following procedures.

Network node definition

The Automated Anatomical Labeling (AAL) template (Tzourio‐Mazoyer et al., 2002) was subdivided into 1024 regions with equal size (H‐1024) to define the network nodes (Zalesky et al., 2010). The procedure has been previously described (Bai et al., 2012; Cao et al., 2013; Zalesky et al., 2010) and was performed using SPM8 software (http://www.fil.ion.ucl.ac.uk/spm/software/spm8). Briefly, individual T1‐weighted images were coregistered to the b = 0 images in the DTI space. The transformed T1 images were then nonlinearly transformed into the ICBM152 T1 template in the Montreal Neurological Institute (MNI) space. The inverse transformations were used to warp the H‐1024 template from the MNI space to the DTI native space. Discrete labeling values were preserved using a nearest‐neighbor interpolation method. Using this procedure, we obtained 1024 cortical and subcortical regions, each representing a node of the brain network (Fig. 1).

Figure 1.

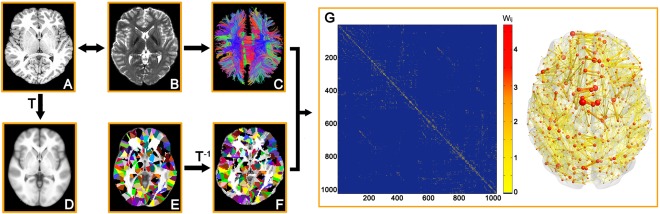
The flowchart of WM network construction by diffusion MRI. (1) The coregistration of a T1‐weighted image (A) to b = 0 image (B) for each subject. (2) The nonlinear registration from the individual T1‐weighted image in DTI space to the ICBM152 T1 template in the MNI space (D), resulting in a nonlinear transformation (T). (3) The application of the inverse transformation (T ⁻¹) to the H‐1024 template in the MNI space (E), resulting in subject‐specific parcellation in the DTI native space (F). All registrations were implemented in the SPM8 package. (4) The reconstruction of the whole‐brain WM fibers (C) was performed using deterministic tractography in DTI‐studio. (5) The weighted networks of each subject (G) were created by computing the number of the streamlines that connected each pair of brain regions. The matrix and 3D representation (axial view) of the WM structural network of a representative healthy subject are shown in the right panel. The nodes are located according to their centroid stereotaxic coordinates, and the edges are coded according to their connection weights. The network was visualized using BrainNet Viewer software (http://www.nitrc.org/projects/bnv/). See the Methods and Materials for further details. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com]

WM tractography

Diffusion tensor tractography was implemented with DTI‐studio software (http://www.dtistudio.org/), using the "fiber assignment by continuous tracking (FACT)" method (Mori et al., 1999). All of the tracts in the dataset were computed by seeding each voxel with an FA that was greater than 0.2. The tractography was terminated if it turned at an angle greater than 45 degrees or reached a voxel with an FA of less than 0.2 (Mori et al., 1999). For each subject, tens of thousands of streamlines were generated to etch out all of the major WM tracts.

Network edge definition

For the network edges, two regions were considered structurally connected if there were at least one fiber streamline with two end‐points that were located in these two regions (Bai et al., 2012; Shu et al., 2011; Zalesky et al., 2011). Specifically, we defined the number of interconnecting streamlines ended in two regions as the weights of the network edges. As a result, we constructed the H‐1024 fiber number (FN)‐weighted WM network for each participant, which was represented by a symmetric 1024 × 1024 matrix (Fig. 1).

Network Analysis

Small‐world properties

To characterize the topological organization of WM structural networks, several following graph metrics were assessed: network strength (S _p), cost, global efficiency (E _glob), local efficiency (E _loc), shortest path length (L _p), clustering coefficient (C _p), small‐world parameters (λ, γ, and σ), and robustness (Achard et al., 2006; Rubinov and Sporns, 2010; Watts and Strogatz, 1998). For regional characteristics, we considered the nodal efficiency (Achard and Bullmore, 2007). See the Supporting Informations for detailed definitions of these network metrics. All network analyses were performed using in‐house GRETNA software (http://www.nitrc.org/projects/gretna/) and visualized using BrainNet Viewer software (http://www.nitrc.org/projects/bnv/) (Xia et al., 2013).

Rich‐club organization

A “rich‐club” in networks is defined as the phenomenon that the high‐degree nodes of a network tend to be more densely connected among themselves than expected by chance (Colizza et al., 2006; McAuley et al., 2007). The brain's rich‐club has been described previously (Collin et al., 2013; van den Heuvel et al., 2012; van den Heuvel and Sporns, 2011). For the weighted networks, the rich‐club coefficient (RC) ${\varphi }^w(k)$ is given by (Opsahl et al., 2008):

$${\varphi }^w(k)=\frac{W_{>k}}{{\displaystyle {\sum }_{l=1}^{E_{>k}}{w}_l^{\text{ranked}}}}$$

with E_{> k} denoting the subset of edges between the hub nodes with a strength > k, W _>k denoting the total sum weights of this subset, and W _ranked denoting the ranked collection of weights in the network, with weights W representing the number of fiber streamlines of the edges. $\varphi (k)$ was normalized relative to the ${\varphi }_{\text{random}}(k)$ of a set of comparable random networks (n = 500) of equal size and degree sequence, giving a normalized RC ${\varphi }_{\text{norm}}(k)=\varphi (k)/{\varphi }_{\text{random}}(k)$ (Colizza et al., 2006; McAuley et al., 2007). Here, the threshold k is defined as the mean plus one standard deviation (mean+std) of nodal strength across regions. On the basis of the categorization of the nodes of the network into hub and non‐hub regions, edges of the network were classified onto rich‐club connections, linking hub nodes to hub nodes; feeder connections, linking hub nodes to non‐hub nodes and local connections linking between non‐hub nodes.

Modularity

The modularity Q(p) for a given partition p of the brain network is defined as (Newman and Girvan, 2004):

$$Q(p)={\displaystyle \sum _{s=1}^{N_{\mathrm{m}}}\left[\frac{l_s}{L}-{\left(\frac{d_s}{2L}\right)}^2\right]}$$

where N _m is the number of modules, L is the number of connections in the network, l_s is the number of connections between nodes in module s, and d_s is the sum of the degrees of the nodes in module s. The modularity index quantifies the difference between the number of intramodule links of actual network and that of random network in which connections are linked at random. The aim of this module identification process is to find a specific partition (p) which yields the largest network modularity, Q(p). Several optimization algorithms are currently available with different advantages, here, we adopted a simulated annealing approach (Newman, 2006).

Statistical Analysis

Age effects

To determine whether age effects on network metrics were linear or nonlinear, both the linear regression model and the Poisson model were fitted separately after regressing out the effects of gender and brain size (Yan et al., 2011). The model for detecting age‐related linear changes was formulated as follows:

$$Y={\beta }_0+{\beta }_1\times \text{age}$$

and the Poisson model for detecting age‐related nonlinear changes was formulated as:

$$Y=w_1\times \text{age}\times e^{-w_2\times \text{age}}+w_3$$

Each fitting parameter of the two models, as well as the fit as a whole, was assessed for significance using F‐tests (Lebel et al., 2012; Yeatman et al., 2014). Then, the Akaike's information criterion (AIC) (Akaike, 1974; Hurvich and Tsai, 1989) was used to determine the best‐fitting model. AIC reflects a trade‐off between the likelihood and complexity (i.e., number of parameters) of a model. The regression model with the lowest AIC value was chosen as the best model to fit the data. Identification of age of peaks (AoPs) or troughs along the developmental trajectory is critical to the study of timing differences in maturation/degeneration across brain regions. The AoP was calculated using the derivative of the Poisson curve as follows, in which $w_2$ is the second parameter from the above Poisson model:

$$\text{AoP}=1/w_2$$

Gender Effects

To explore gender‐related changes, we adopted the general linear model and focused on the positive (female > male) and negative (male > female) contrasts by treating gender as a predictor and age and brain size as covariates. To test for age trajectory differences, separate fits were performed and the fitting parameters were compared between males and females. If the fitting parameters were not significantly different, genders were combined for the final fitting.

Support Vector Regression Analysis

For age prediction, we used support vector regression (SVR) with a linear kernel function and the default settings of C = 1 and epsilon = 0.001 in the LIBSVM Toolbox (http://www.csie.ntu.edu.tw/~cjlin/libsvm/) (Dosenbach et al., 2010; Iuculano et al., 2014). Leave‐one‐out cross‐validation was used to evaluate the SVR model. Each subject was designated the test subject in turns while the remaining ones were used to train the SVR predictor. The decision function derived from the training subjects was then used to make a prediction about the test subject's age. Pearson correlation coefficient between the actual and predicted ages was calculated to assess the prediction accuracy. All global and local network metrics, including the network strength, cost, global and local efficiency, small‐world parameters, RC, modularity, robustness, anatomical distance of the connections, and nodal efficiency were used as features for the SVR predictor. Permutation test was implemented to obtain the significance of prediction accuracy by retraining each prediction model 10,000 times after randomly permuting the age labels. The P‐value was calculated by counting the number of permutations achieving higher Pearson correlation coefficient than the nonpermutated data.

Reproducibility Analysis

Effects of brain parcellation

In addition to the high‐resolution parcellation, we also used the low‐resolution AAL (L‐AAL) template (Tzourio‐Mazoyer et al., 2002) with 90 brain regions to define network nodes. For each participant, the L‐AAL FN‐weighted WM network was constructed and analyzed with the similar procedure that was performed in the H‐1024 network. Statistical analyses were used for both global and regional network properties to investigate the effects of age on the topological organization of L‐AAL WM networks.

Effects of curve fitting approaches

In addition to the Poisson model, we also used a nonparametric local smoothing spline model to estimate the age‐related trajectory of network metrics (Fjell et al., 2010). The estimation of the smoothing spline model was performed in R software (http://www.r-project.org/). The smoothness parameter of cubic smoothing spline functions was optimized by minimizing the generalized cross‐validation criterion (Ziegler et al., 2012).

RESULTS

Age‐Related Changes in Small‐World and Network Efficiency

First, we observed prominent small‐world organization in WM networks across the lifespan: for each subject, the WM network has similar characteristic path length and higher clustering compared with the matched random networks. Regarding the efficiency metrics, both global and local efficiency exhibited an inverted U‐shaped trajectory with age (E _glob: r ² = 0.34, P < 10⁻⁵; E _loc: r ² = 0.24, P < 10⁻⁵) (Table 1 and Fig. 2A). All small‐world properties also exhibited a nonlinear trajectory with age, including the L _p (r ² = 0.34, P < 10⁻⁵), C _p (r ² = 0.17, P = 4 × 10⁻⁵), gamma (r ² = 0.08, P = 0.02), and sigma (r ² = 0.09, P = 0.005) (Table 1 and Fig. 2B). See Table 1 for additional details of other network metrics. Most global network metrics peaked at approximately the third decade, suggesting an important time point of maturation and degeneration of the human brain WM network.

Table 1.

Age‐related trajectories of global network metrics across lifespan

Network metrics	H‐1024				L‐AAL
	Curve shape	R 2	P value	AoP (years)	Curve shape	R 2	P value	AoP (years)
S p	2	0.35	<10−5	33.1	2	0.35	<10−5	32.1
Cost	2	0.36	<10−5	29.7	2	0.35	<10−5	29.1
E glob	2	0.34	<10−5	34.1	2	0.32	<10−5	33.2
E loc	2	0.24	<10−5	32.9	2	0.29	<10−5	33.0
L p	−2	0.34	<10−5	33.4	−2	0.33	<10−5	32.2
C p	−2	0.17	4 x 10−5	26.2	−2	0.27	<10−5	23.2
Lambda	−1	0.01	N.S.	—	−1	0.02	N.S.	—
Gamma	−2	0.08	2 x 10−2	33.7	−2	0.20	<10−5	29.8
Sigma	−2	0.09	5 x 10−3	32.9	−2	0.21	<10−5	30.6
Robustness	2	0.34	<10−5	32.6	2	0.19	<10−5	34.1

Note: −1: linear decrease with age; 2: inverted U‐shaped trajectory; −2: U‐shaped trajectory; N.S.: not significant.

Figure 2.

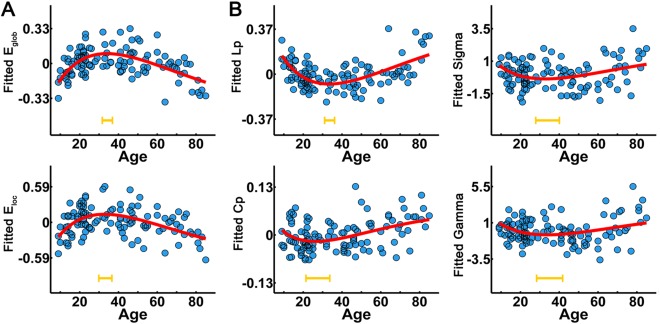
The lifespan trajectories of the global network metrics of the WM network. (A) The lifespan trajectories of global and local network efficiency. (B) The lifespan trajectories of small‐world properties (L _p, C _p, gamma, and sigma). The blue dots represent the adjusted values of each subject after controlling for gender and brain size. The curve‐fitted lines are shown in red. The orange bars at the bottom denote the age of peak and its 95% confidence interval. Significant age‐related nonlinear trajectories were found for these global network metrics (all P < 0.05). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

For nodal efficiency, 212 of 1024 regions exhibited nonlinear changes with age (P < 0.05, Bonferroni correction), and the most prominent alterations were located primarily in the bilateral prefrontal cortices (superior and middle frontal gyri, anterior cingulate cortex, and precentral gyrus), superior and middle temporal gyri, putamen, and caudate nucleus (Fig. 3A). The peak ages for nodal efficiency varied across areas, from 20 years for the superior and middle frontal gyri to 40 years for the bilateral lingual gyrus, posterior cingulate cortex, lateral parietal, and temporal lobe (Fig. 3B). Notably, most of the regions with late age of peaks were within the default‐mode network (DMN) (Raichle et al., 2001), suggesting that the prefrontal cortex reaches maturation/degeneration earlier than the posteromedial cortex and lateral temporal regions of the DMN. Importantly, homotopic regions exhibited similar age‐related trajectories of nodal efficiency, suggesting synchronous changes of homotopic regions across lifespan (for more details, see the Supporting Information and Supporting Information Fig. S2).

Figure 3.

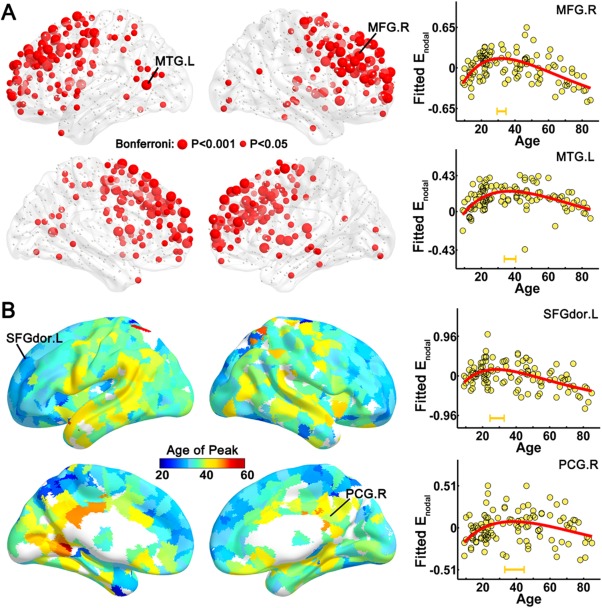
The distribution of regions with significant age‐related alterations and the age of peaks across regions. (A) A 3D representation of brain regions with significant age‐related alterations of nodal efficiency. The red nodes represent regions with inverted U‐shaped trajectories with age (P < 0.05, Bonferroni correction); node size represents the significance of the age‐related alterations. Two representative nodes were selected to depict the age‐related trajectory curves of nodal efficiency, one is located in the right middle frontal gyrus (MFG.R) (upper right panel) and the other is in the left middle temporal gyrus (MTG.L) (lower right panel). (B) A 3D representation of the age of peaks across the regions with nonlinear trajectories (P < 0.05). Different colors of regional surface (from blue to red) represent different age of peaks. To present the early and late age of peaks, two nodes located in the left dorsal superior frontal gyrus (SFGdor.L) and the right posterior cingulate gyrus (PCG.R) were selected to depict the trajectory curves, respectively. The age of peaks (±95% confidence interval) were marked with orange bars. The surface visualization of WM networks was accomplished using the BrainNet Viewer software (http://www.nitrc.org/projects/bnv/).

Age‐Related Changes in the Modular Structure of WM Network

To evaluate the age‐related alterations in modularity and modular structure, we first performed individual module analyses. The modularity values were greater than 0.6 for all subjects, and a significant modular structure of the WM network across lifespan was observed compared with the matched random networks (all Z > 20). The modularity and module number did not exhibit significant trends with age (all P > 0.05), suggesting that major organization remains stable across lifespan. To investigate the group‐based module structure of the WM networks, we calculated the mean network by averaging the connection matrices of all subjects, which was thresholded by the group mean sparsity and followed by a modular analysis. Twelve modules were identified for the group‐averaged network, as shown in Figure 4A. Most of the modules were distributed in a symmetric pattern, including bilateral pre/postcentral gyrus modules, dorsal lateral frontal modules, and temporo‐parietal modules, while some modules were distributed along the cortical middle line, consisting of regions from bilateral hemispheres, such as supplementary motor area module, medial superior frontal module, orbital frontal module, and occipital lobe module. For the subcortical regions, most of regions from the same subcortical structures were assigned to the same modules (Fig. 4A). Then, the connection strengths of both intramodule and intermodules across the 12 modules were calculated for each subject. Significant age‐related nonlinear changes of intramodule and intermodule connections were observed, and were especially located in the bilateral prefrontal and temporal cortices (P < 0.05, Bonferroni correction) (Fig. 4B,C and Supporting Information Table S1).

Figure 4.

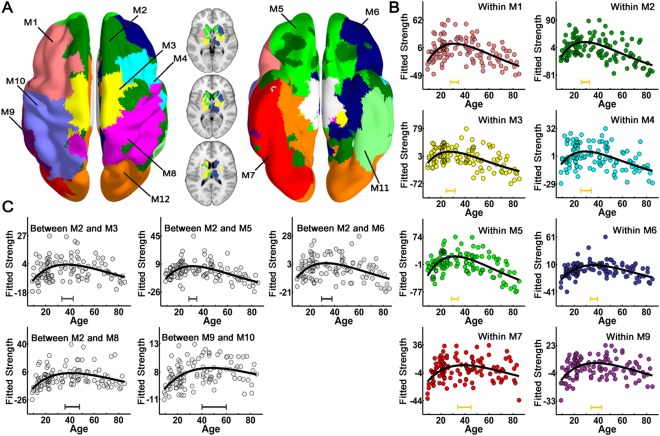
The modular structure of the group‐averaged WM network and lifespan trajectories of the connection strength of intramodule and intermodules. (A) The left panel is a 3D representation of the group‐based modular structure (axial view) from top to bottom, with the bottom to top representation shown in the right panel. The modular structure of the subcortical regions was showed in the middle, with three axial slices overlaid on the volume template. Twelve modules were identified for the mean WM network and represented by different colors. Significant age‐related nonlinear changes of intramodule and intermodule connections were found and were primarily located in the bilateral prefrontal and temporal cortices (P < 0.05, Bonferroni correction). The dots with different colors corresponding to each module represent the intramodule connection strength (B) and the dots in gray represent intermodule connection strength (C) after controlling for gender and brain size. The curve‐fitted lines are shown in black. The bars at the bottom denote the age of peak and its 95% confidence interval. M1: left dorsal frontal cortex; M2: medial superior frontal cortex; M3: supplementary motor area; M4: right dorsal frontal gyrus; M5: orbital frontal cortex; M6: right inferior frontal and parahippocampal cortex; M7: left temporo‐occipital cortex; M8: right pre‐ and postcentral gyrus; M9: left middle temporal cortex; M10: left pre‐ and postcentral gyrus; M11: the right middle and inferior temporal gyrus; M12: the occipital cortex.

Age‐Related Changes in the Rich‐Club Organization of WM Network

To quantify the rich‐club organization, we calculated the RC and normalized RC individually (van den Heuvel and Sporns, 2011). The normalized RC values were greater than one for all participants, suggesting a characteristic rich‐club organization across lifespan. When fitted with age, both the RC and normalized RC decreased linearly with age (RC: P = 0.002; normalized RC: P = 0.0001) (Fig. 5B). As shown in Figure 5A, for the childhood and young adult groups, the hub regions were mainly distributed in the medial frontal, parietal, and occipital cortices. In contrast, reduced frontal regions and their connections in the rich‐club component were observed for the most elderly group (>70 years old) compared with the younger groups. We further investigated the age‐related changes of the strength of the rich‐club (between hub nodes), feeder (between hub and non‐hub nodes), and local (between non‐hub nodes) connections, all of which exhibited a nonlinear inverted U‐shaped trajectory across lifespan (rich‐club: r ² = 0.23, P < 10⁻⁵; feeder: r ² = 0.36, P < 10⁻⁵; local: r ² = 0.24, P < 10⁻⁵) (Fig. 5C).

Figure 5.

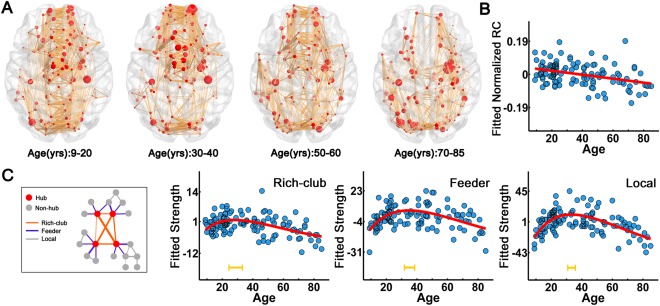
Rich‐club organization and its lifespan trajectories. (A) The rich‐club organization of different age subgroups. The red nodes represent the hub regions with mean Z‐scores of the nodal strength as nodal size. The orange lines represent the WM connections between hub regions identified from the average matrix of different subgroups. (B) Lifespan trajectory of normalized RC with age. (C) Lifespan trajectories of the strength of the rich‐club, feeder and local connections. The blue dots represent the adjusted values after controlling for gender and brain size. The curve‐fitted lines are shown in red. The orange bars at the bottom denote the age of peak and its 95% confidence interval. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Age‐Related Changes in the Distance of Structural Connectivity

The anatomical distance of the edges was defined as the mean physical length of the fiber pathways connecting two regions (Fig. 6A). Figure 6B provides several representative short (<75 mm) and long‐distance (>75 mm) WM connections. The average anatomical distance of the network exhibited an inverted U‐shaped trajectory with age (r ² = 0.32, P < 10⁻⁵) (Fig. 6C). When classified by anatomical distance, the absolute amounts of both short‐distance and long‐distance connections increased during childhood and adolescence and decreased in older age (short: r ² = 0.23, P < 10⁻⁵; long: r ² = 0.39, P < 10⁻⁵) (Fig. 6C). However, the proportion (percent) of short connections exhibited a U‐shaped trajectory with age, whereas long‐distance connections exhibited an inverse trajectory with age (r ² = 0.35, P < 10⁻⁵) (Fig. 6C).

Figure 6.

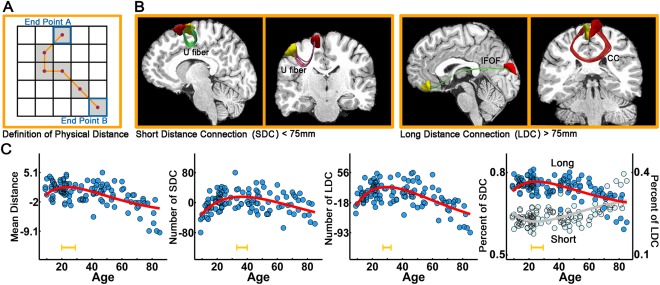
The lifespan trajectories of the structural connectivity distance. (A) The distance of the anatomical connections is defined as the mean physical length along the fiber pathways connecting two regions. (B) Four representative short‐ (<75 mm) and long‐distance fiber connections (>75 mm) are shown in the right panel. IFOF: inferior fronto‐occipital fasciculus; CC: corpus callosum. (C) The lifespan trajectory of the mean network distance and the trajectories of the number and percent of short‐ and long‐distance connections. The blue dots represent the adjusted values after controlling for gender and brain size. The curve‐fitted lines are shown in red. The orange bars at the bottom denote the age of peak and its 95% confidence interval. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Gender Effects

For the global network metrics, no significant gender effect or trajectory differences between genders were observed (all P > 0.2) (Supporting Information Fig. S3). At the regional level, the gender effect did not survive after the multiple comparison correction and the fitting parameters between genders showed no significant difference (all P > 0.05).

Age Prediction

When all of the global and local network metrics were combined as input features for age prediction, a high estimation accuracy was obtained, with a correlation r = 0.77 between the actual versus predicted ages (P < 10⁻⁴) (Fig. 7). Among all of these metrics, nodal efficiency showed the best prediction ability (r = 0.72).

Figure 7.

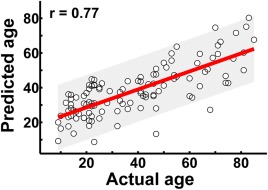
The prediction of individual age based on the graph metrics of structural connectome. The scatter plot depicts actual versus predicted age bounds of 95% confidential interval. Pearson correlation coefficient between the actual and predicted ages was calculated to assess the prediction accuracy. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Reproducibility of Findings

L‐AAL parcellation

The results exhibited similar lifespan trajectories for all global network properties compared with those from H‐1024 parcellation (Table 1 and Supporting Information Fig. S4A). Highly significant correlations between the global network metrics from different parcellations were observed (all r > 0.45, P < 10⁻⁶) (Supporting Information Fig. S4B). For regional alterations with age, comparable spatial distributions, and age of peaks of brain regions with nonlinear trajectories were found (P < 0.05, Bonferroni correction) (Supporting Information Fig. S4C).

Nonparametric fitting

By fitting with a local smoothing spline model, similar lifespan trajectories and age of peaks for most global and regional network properties were estimated (Supporting Information Fig. S5). Only some metrics with less significant age‐related alterations, such as C_p, gamma and sigma, the estimated age of peaks are more sensitive to the fitting approaches.

DISCUSSION

In this study, we investigated the age‐related changes in the structural connectome in a cohort of healthy subjects from 9 to 85 years old. Our main results are summarized as follows. First, the topological efficiency of the WM structural networks exhibited an inverted U‐shaped trajectory across lifespan, with the peak age at approximately the third decade. Second, the brain areas and connections with the most prominent changes were located in the prefrontal and temporal cortices, with heterogeneous trajectories across regions. Third, the hub integration decreased linearly with age, especially accompanied by the loss of frontal hubs and their connections. Finally, based on the graph metrics of structural connectome, accurate predictions of individual age were obtained. Together, our results provide new insight into the age‐related changes in the brain structural connectome over the human lifespan, which are crucial for our understanding of the human connectome and how it may give rise to brain function, including the occurrence of brain disorders across the lifespan.

Age‐Related Alterations in the Global Topology of the WM Network

One of the most important findings was an inverted U‐shaped trajectory of the topological efficiency of the WM network across lifespan, which is consistent with the hypothesis proposed by Collin and van den Heuvel (2013). With the similar diffusion MRI technique, Hagmann et al. (2010) observed a linear increase in network efficiency during late development, and Gong et al. (2009) revealed a reduction in local efficiency during aging. In the present cross‐sectional study, the subject ages ranged from 9 to 85 years old; thus, both the late developmental and aging stages were integrated into one cohort. Interestingly, A negative quadratic trajectory of the global efficiency was also found in structural covariance networks (Wu et al., 2012) and an inverted U‐shaped trajectory of the local efficiency was identified in functional network (Cao et al., 2014). The similar age‐related trajectories between structural and functional connectome across lifespan may support the notion that the structural changes are the underlying substrate of brain function changes. However, the relationship between structural and functional connectivity is not simply one‐to‐one correspondence (Greicius et al., 2009; Hermundstad et al., 2013; Honey et al., 2009; Horn et al., 2014), some functional connections within the default mode network were found precede the maturation of structural connectivity (Supekar et al., 2010; Zielinski et al., 2010). Although increased coupling between structural and functional connectivity during the early development was reported (Hagmann et al., 2010), the relationship between structural and functional connectome across the entire lifespan should be further studied.

The age‐related changes in the WM connectome architecture can be attributed to an adjustment in the strength of the structural connectivity (Collin and van den Heuvel, 2013), which is supported by the similar nonlinear trajectories of the integrity of the major WM tracts across lifespan (Kochunov et al., 2012; Lebel et al., 2012; Mwangi et al., 2013; Yeatman et al., 2014). Increased structural connectivity during development can be ascribed to increases in axonal diameter and myelination, as well as synaptic pruning and modification (Morrison and Hof, 1997; Paus, 2010; Rademacher et al., 1999; Yeatman et al., 2014). Decreased structural connectivity during aging may be due to neuronal shrinkage, loss of small axon fibers and WM degeneration (Bartzokis et al., 2012; Terry et al., 1987; Yeatman et al., 2014). These changes in microstructural properties result in considerable changes in the connectome architecture, including continuing increases in the capacity for information integration and a topology that is increasingly capable of facilitating higher order cognitive functions during development. Importantly, we found that the peak ages for network efficiency in information transfer occurred around the third decade, consistent with previous findings suggesting that the maturation of the WM lasts into the third and fourth decades (Kochunov et al., 2012; Lebel et al., 2012; Westlye et al., 2010; Yeatman et al., 2014). Moreover, we found that several other nontrivial topological properties, such as small‐world parameters and robustness, also showed nonlinear alterations across lifespan with a peak age around the 3rd decade. Notably, the peak ages for network efficiency or small‐world parameters fell within the range reported for peaks of average level of cognitive performance with age in 30s (Salthouse, 2005; Schroeder and Salthouse, 2004). The changes of WM connectome architecture may be the underlying basis of cognitive abilities and the quantified graph metrics of brain connectome may be measurable biomarkers of these variations.

Age‐Related Alterations Across Brain Regions and Connections

The brain regions and connections with the most significant nonlinear age‐related changes were primarily located in the frontal and temporal cortices. These results are compatible with the postmortem findings for the most prominent age‐related changes in neuronal size in the frontal and temporal lobes (Terry et al., 1987). Neuroimaging studies have also reported that the integrity of the WM tracts in the frontal and temporal cortices, such as the genu of the corpus callosum, superior longitudinal fasciculus and uncinate fasciculus, follows an inverted U‐shaped trajectory across lifespan (Hasan et al., 2009a; Kochunov et al., 2012; Lebel et al., 2012). In addition, structural, functional, and metabolic alterations with age also predominantly occur in the prefrontal cortices with a quadratic trajectory (Shaw et al., 1984; Sowell et al., 2003; Wang et al., 2012).

Importantly, we noticed asynchronous maturation/degeneration across regions. The posterior cingulate and lateral temporal cortices displayed prolonged maturation/degeneration compared with the prefrontal cortices. Previous neuroimaging studies also revealed different lifespan trajectories for different WM tracts, with peak ages varying from 20 to 40 years old (Hasan et al., 2009a, 2009b; Kochunov et al., 2012; Lebel et al., 2012; Li et al., 2013; Yeatman et al., 2014). Specifically, WM connectivity peaks later in the posterior cingulate and temporal cortices relative to the frontal WM (Bartzokis et al., 2001; Kochunov et al., 2012; Lebel et al., 2012). The earlier peak ages in prefrontal cortices may indicate the earlier maturation during development or the vulnerability to aging of these regions compared with posterior cortices. Evidence from structural MRI study has shown that the frontal lobe is among the first to become impaired in aging (Raz, 2000). Several DTI studies have also suggested that the anterior WM composed of small, thinly myelinated fibers (Bartzokis et al., 2012; Glasser and Van Essen, 2011) are more susceptible to aging than the posterior WM (e.g., through myelin loss or damage) (Ota et al., 2006; Pfefferbaum et al., 2000; Salat et al., 2005a). Moreover, an anterior‐posterior gradient for GM shrinkage and WM degeneration with aging has been consistently reported (Raz et al., 1997; Salat et al., 2005b). In contrast, regions that were affected last by aging were primarily distributed throughout the DMN. The hierarchical maturation/degeneration across regions suggest possible neural mechanisms for critical time points in the maturation and decline of related cognitive functions.

Age‐Related Alterations in the Modular Structure

Through the modular analysis, significant age‐related nonlinear changes of intramodule and intermodule connections were found primarily located in the bilateral prefrontal and temporal cortices. Prefrontal cortex is involved in some higher level function such as planning, reasoning, decision‐making, and executive functions (Alvarez and Emory, 2006; Craik and Bialystok, 2006), which undergo dramatic changes with age. An age‐related association between frontal volume and executive function across lifespan was found by Zimmerman et al. (2006). Temporal cortex was also found showing prominent age‐related changes in neuronal size (Terry et al., 1987). Interestingly, the peaks for prefrontal and temporal modules were consistent with the range reported for the peaks on various cognitive measures such as inductive reasoning, spatial visualization, episodic memory, and perceptual speed (Salthouse, 2009), suggesting that the age‐related adjustment of module organization may support for alterations of cognitive ability across lifespan.

Age‐Related Alterations in Rich‐Club Organization

The rich‐club organization of the WM networks was evident across lifespan, indicating that the rich‐club structure is a common and basic property of large‐scale brain structural networks, which may support for efficient global information transfer in the brain (Colizza et al., 2006; McAuley et al., 2007; van den Heuvel et al., 2012). Consistent results showed that it is found among the first to develop in the neural circuitry of C. elegans (Towlson et al., 2013) and already present by 30 week gestation of the newborn human brain (Ball et al., 2014; van den Heuvel et al., 2014). Although all of the strength of the rich‐club, feeder, and local connections exhibited inverted U‐shaped trajectories with age, the RC and normalized RC decreased with age. This may due to the preference of enhancing non‐rich club connections compare with rich‐club connections during the development of brain. Rich‐club nodes were essential infrastructure for the integration of different sets of functional domains (van den Heuvel and Sporns, 2013) and were found having high metabolic energy and long maturational trajectories (Collin et al., 2014). In our results, inhomogeneous age‐related changes with heavy loss of frontal hubs and their connections around 70 years were found. This is consistent with our regional efficiency and module findings and is supported by previous researches that frontal connections are more susceptible to aging (Ota et al., 2006; Salat et al., 2005b). The reorganization of rich‐club structure further manifested that frontal hubs contribute much in forming the efficient backbone for whole brain communication during the early and middle age and start to be replaced by other rich‐club members in the late age. However, the biological mechanisms for the reorganization of this core architecture and whether the variations were the substructure of changes of cognitive functions with aging need further study.

Age‐Related Alterations in Distance‐Dependent Structural Connectivity

Although both short and long‐distance connections increased during development and decreased during aging, the relative proportion of the short‐range connectivity decreased with maturation, suggesting the presence of dual changes in functional integration and segregation with wiring distance (Supekar et al., 2009). The long‐range connections decreased their proportion during aging, supporting the idea that long‐range connections are more vulnerable to normal aging (Tomasi and Volkow, 2011). Importantly, our findings parallel this alteration pattern of distance‐dependent functional connectivity with age in the same cohort (Cao et al., 2014).

Methodological Issues

Several methodological issues should be addressed. First, the samples were obtained using a cross‐sectional design. Future studies with longitudinal MRI data are required to validate the findings observed here. Second, the edges of the WM networks were reconstructed by deterministic tractography, which may result in the loss of existing fibers due to the “fiber crossing” problem (Mori and van Zijl, 2002). Nevertheless, our results were cross‐validated by different brain parcellations (H‐1024 and L‐AAL). Future studies should employ more advanced tractography techniques, such as probabilistic tractography to define the network edges (Gong et al., 2009). Third, we utilized DTI tractography to construct the WM networks. The combination of the multimodal MRI techniques (structural and functional MRI) would yield a comprehensive understanding of the relationship between structural and functional changes across lifespan (Betzel et al., 2014; Chan et al., 2014). Finally, to support the nonlinear changes in the structural networks as a neural basis of cognitive changes with age, further studies of cognitive function and brain structure are needed to assess the relationships between brain maturation, aging, and cognitive changes across lifespan.

Supporting information

Supporting Information