Brain systems involved in arithmetic with positive versus negative numbers

Abstract

Positive number arithmetic is based on combining and separating sets of items, with systematic differences in brain activity in specific regions depending on operation. In contrast, arithmetic with negative numbers involves manipulating abstract values worth less than zero, possibly involving different operation–activity relationships in these regions. Use of procedural arithmetic knowledge, including transformative rules like “minus a negative is plus a positive,” may also differ by operand sign. Here, we examined whether the activity evoked in negative number arithmetic was similar to that seen in positive problems, using region of interest analyses (ROIs) to examine a specific set of brain regions. Negative‐operand problems demonstrated a positive‐like effect of operation in the inferior parietal lobule with more activity for subtraction than addition, as well as increased activity across operation. Interestingly, while positive‐operand problems demonstrated the expected addition > subtraction activity difference in the angular gyrus, negative problems showed a reversed effect, with relatively more activity for subtraction than addition. Negative subtraction problems may be understood after translation to addition via rule, thereby invoking more addition‐like activity. Whole‐brain analyses showed increased right caudate activity for negative‐operand problems across operation, indicating a possible overall increase in usage of procedural rules. Arithmetic with negative numbers may thus shows some operation–activity relationships similar to positive numbers, but may also be affected by strategy. This study examines the flexibility of the mental number system by exploring to what degree the processing of an applied usage of a difficult, abstract mathematical concept is similar to that for positive numbers. Hum Brain Mapp 35:539–551, 2014. © 2012 Wiley Periodicals, Inc.

INTRODUCTION

Beyond simply representing quantities, numbers are often used in computations, such as determining how much money one has, how much the temperature has changed, or what the total height of a building is. Sometimes, though, we must compute not just how much there is, but how much there is not, as in engineering or accounting. In these situations, negative numbers must be used to represent below‐zero amounts. The introduction of negative numbers in mathematics is often a difficult point for students, as negatives operate differently than positive numbers and require use of a new set of rules and algorithms. Acquiring these new rules may be particularly important for advanced mathematics. Understanding negative numbers is an important component of algebra performance, itself a predictor of future mathematics achievement [Peled and Carraher, 1993; Peled et al., 1989], due to the possibility of negative problem solutions. Mathematics achievement thus requires not only an understanding of individual negative number values, but also the ability to operate on them in an appropriate manner. Use of individual negative numbers has been demonstrated to draw on basic number systems like with positives [Gullick et al., 2012], but whether arithmetic with negatives also relies on different neural networks than positives has not previously been investigated.

Negative number arithmetic instruction generally begins in the sixth grade after the introduction of negative numbers themselves [Education, 2010]. We focus here on negative addition and subtraction, typically taught first. Multiplication and division with positive versus negative numbers mainly differs in the working memory requirement of keeping track of the number of negative signs and not in the mechanics of the operation, and so these operations are not included here.

Arithmetic With Positive Numbers

Even within positive numbers, all operations may not be performed in the same manner. After formal acquisition of the basic principles of arithmetic (set combinations) and number–sentence construction, addition is most often practiced through speeded drills relying on memorized “fact sentences” (e.g., “three plus four equals seven”), not calculation of sums with each presented instance. Solving addition problems may thus rely more on declarative memory and less on quantity understanding, at least for simple, practiced problems [Ashcraft and Stazyk, 1981; Domahs and Delazer, 2005; Svenson and Sjoberg, 1981/1982]; this strategy can be seen even in early elementary school [Ashcraft and Fierman, 1982; Hamann and Ashcraft, 1985]. In contrast, subtraction is not usually trained or drilled in school to the same extent as addition. Problem solution instead seems to be more dependent on direct calculation, not stored math facts [Barrouillet et al., 2008; Kamii et al., 2001]. While it is certainly possible to memorize “seven minus four equals three,” participants are likelier to calculate or count out differences [Campbell and Xue, 2001]. Indeed, while college students reported high retrieval rates for addition and multiplication problems, the rate was much lower for subtraction [Campbell and Xue, 2001]. Further, unlike with addition, training and experience serves to make subtraction more efficient, but does not encourage retrieval strategies [Ischebeck et al., 2006]. These two operations thus appear to draw most strongly on different strategies.

Addition and subtraction may be separable neurally as well, as demonstrated both by functional neuroimaging and by clinical patient work. Verbal fact retrieval generally appears to draw heavily on the angular gyrus (AG) and connected corticostriatal loops through the basal ganglia. Dehaene, in the Triple Code Model of numeric processing [Dehaene and Cohen, 1997; Dehaene et al., 2003, 2004], proposed the AG to be the site of retrieval and storage of complex memorized verbal information, including highly practiced and rote memorized number fact sentences. In contrast, direct calculation seems to draw on the intraparietal sulcus (IPS), the basic quantity‐representation region. Indeed, the AG does generally show increased activation for addition relative to subtraction [Fehr et al., 2007; Grabner et al., 2008; Ischebeck et al., 2006]. Ischebeck et al. 2006 and Delazer et al. 2003 have also noted that training in addition (and multiplication), potentially promoting better fact retrieval, increases AG and decreases IPS activity. Interestingly, recent work has indicated that these increased AG activations for addition may be in fact relative deactivations, with less deactivation during addition than subtraction [Rosenberg‐Lee et al., 2011]. The authors proposed that as the AG is involved in the default network, this lessened deactivation is still reflective of a relatively increased involvement of the AG in addition.

Subtraction seems to draw more heavily on the IPS than addition to support these calculations in typical adults [Kong et al., 2005]. Though Arsalidou and Taylor 2011 noted that addition also tended to involve the inferior parietal lobule generally, Rosenberg‐Lee et al. 2000 found that no IPS subregions showed significant addition‐related activity, whereas all three subregions of the left IPS demonstrated significant subtraction‐related activity. Subtraction also demonstrates less AG activation [or a greater deactivation, Rosenberg‐Lee et al., 2011] than addition, perhaps because memorized fact sentences are less used [Dehaene and Cohen, 1997; Domahs and Delazer, 2005]. Clinically, Dehaene and Cohen 1997 noted that while inferior parietal lesion patient M.A.R. was slightly impaired on arithmetic in all operations, this deficit was significantly worse for subtraction problems. In contrast, while patient deficits in addition and multiplication often co‐occur, subtraction impairments do not always appear as well [Cohen et al., 2000; Dagenbach and McCloskey, 1992]. As such, subtraction procedures seem to be stored and used differently than those for addition.

Arithmetic With Negative Numbers

These operation‐specific differences, though, are known only for calculations with positive numbers. Arithmetic with negative numbers may be similar to that for positives within each operation, with addition demonstrating increased AG and decreased IPS reliance, and subtraction the reverse. However, there are additional factors that may make brain and behavioral responses for even basic calculation with negatives different from that for positives.

To start, arithmetic with negative numbers may simply be more difficult than with positives, either across operations or differentially within them. While most adults eventually grasp the principles of negative calculation, Kilhamn 2004 found that one‐third of a college‐student sample was unable to perform a simple negative subtraction problem such as “(−3) – (−8),” clearly demonstrating that negative number arithmetic remains problematic for many. Similarly, when faced with double‐signed negative subtraction problems, children may ignore one sign or perform the operation and only then negate the answer [Vlassis, 2004]. Harder positive number problems—previously defined as whether carrying (for addition) or borrowing (for subtraction) is required [Kong et al., 2005]; whether the problems include memorized versus nonmemorized facts [Gruber et al., 2001]; or whether the answer is large (>10) or small [<10; Das et al., 2010; Fehr et al., 2007]—may demonstrate increased prefrontal cortex activity, often including the bilateral medial frontal gyrus or ventrolateral prefrontal cortex, anterior cingulate gyrus, and left inferior frontal gyrus [Fehr et al., 2007; Gruber et al., 2001; Kong et al., 2005; Menon et al., 2000]. If negative‐operand problems are more difficult than positive, they may demonstrate increased prefrontal activity across operations as well.

Difficulty aside, arithmetic with negative numbers is typically not taught in the same manner as with positives. Calculation with negatives is not drilled and practiced; instead, students are often instructed in algorithms for converting problems involving negatives into ones containing positive numbers, like the rule that “minus a negative is plus a positive.” Similar sign‐cancellation techniques also rely on a general‐format rule that requires application to an individual problem. These strategies may rely more on procedural arithmetic instead of declarative or quantitative knowledge. With positive numbers, procedural arithmetic knowledge describes the rules and algorithms implemented to solve certain types of problems [Domahs and Delazer, 2005]. For example, instead of memorizing the 1s multiplication table (1 × 2 = 2, 1 × 3 = 3, etc.), these facts are consolidated into a single generalizable rule: 1 × N = N. Similarly, “anything times zero is zero,” and any number plus (or minus) zero is itself. While these general rules may be stored verbally, they differ from memorized fact tables in that they are by themselves incomplete: they require application to the numbers in the problem presented to be used. Rule‐based problems tend to be solved quickly and accurately [LeFevre et al., 1996], as the recognition of a relevant rule may either allow direct calculation or avoid specific fact recall.

These algorithms seem to be stored separately from other arithmetic facts in the brain. For example, patients may be impaired on typical arithmetic but able to answer 0 × N problems [see Dagenbach and McCloskey, 1992; McCloskey et al., 1991; Pesenti et al., 2000; Semenza et al., 2006; Sokol et al., 1991]. Functional imaging has also supported a neural dissociability of algorithms from fact sentences. Jost et al. [2012, 2004] compared brain activities for zero‐multiplication (i.e., rule application) problems with that for smaller and larger multiplication problems. Zero‐operand problems were responded to fastest, and demonstrated increased left caudate (at the head), right inferior frontal gyrus, bilateral middle temporal gyrus, and bilateral ventral/posterior AG activity; fact‐based problems (both small and large) demonstrated increased anterior AG, IPS, and basal ganglia (thalamus and putamen) activity. The heightened activity in the head of the left caudate was theorized to be specific to rule implementation. (Jost et al. 2004 noted that separate subregions of the AG were likely involved in each problem type, as the peak positions were quite different.) If negative arithmetic problems are particularly reliant on algorithm use, they may thus involve increased activity in this area as well.

Only a few studies have previously examined how we undertake negative number arithmetic, either quantitatively or qualitatively. Mukhophadhyay et al. [2000, 1997; see also Nunes, 1993, p. 65] demonstrated that an informal conceptualization of negative‐operand calculation was sufficient for solution of some, but not all, problems: children could determine whether a protagonist in a story would end up in debt, but could not work with formal equations involving negatives without adequate instruction. Not surprisingly, adults with a stronger understanding of negative number arithmetic were likelier to use negative numbers in equation setup, instead of rearranging the operands to avoid negatives [Prather & Alibali, 2008].

More recently, Das et al. 2010 examined behavioral responses to addition and subtraction with negative numbers, comparing responses to standard positive problems with negative recasted problems. A negative addition problem such as “7 + −3” was considered a recasted version of “7 – 3.” Das et al. 2010 found that while responses for problems involving negatives were generally slower than for positives, this difference was larger for recasted addition than subtraction problems, and concluded that participants translated the problems back to their original positive number operations. Further, the presence of a minus sign was proposed to have primed the operation of subtraction, regardless of the actual operation presented in the problem, thereby aiding subtraction problem processing but interfering with addition.

This study, though, was limited in the facets of negative number arithmetic examined. Only homogenous positive or mixed‐operand (one positive and one negative operand) problems were used, excluding homogenous negative problems. A recasting strategy is inefficient for problems with two negative operands, as “recasting” these problems still results in operations involving at least one negative number and so cannot be a complete explanation. Further, in problem presentation, negative numbers were always surrounded by parentheses, such as “7 + (−4).” This format was presumably chosen to help distinguish the subtraction minus signs from those indicating polarity, but is unusual and possibly distracting.

Aim of the Present Study

This study aimed to extend the current work on positive number arithmetic to determine the brain areas supporting negative number addition and subtraction, and whether the activities found are similar to those expected for positive numbers. Such investigation of applied numeric situations with difficult quantities can inform our understanding of the flexibility of the mental number system beyond simple incorporation of individual values by demonstrating whether manipulation of these abstract numbers is like that for concrete positive quantities. As this study aimed to first examine whether the processing of addition and subtraction was similar in positive‐operand and negative‐operand problems, we focus only on single‐digit problems to maximize the chance of finding operation differences.

Arithmetic tasks tend to use one of three tasks: answer production, answer verification, or answer selection. Functional magnetic resonance imaging (fMRI) paradigms generally use one of the latter two, as recording participant‐generated responses can be methodologically difficult. Answer verification uses a yes or no decision as to whether the presented solution to a problem is correct. While simple, some have argued that verification alone allows participants to simply determine if the presented answer “matches” their stored representation, using only recognition procedures and skipping any individual calculation. Answer selection involves choosing the correct solution to a presented problem, usually between two options. The distance between a distracter incorrect answer and a correct option can influence response times; foil distance must thus be balanced between closer and farther options. Participants may still attempt to avoid calculation by deciding which answer they recognize, but this strategy is unlikely for single‐digit problems. We thus used an answer selection task to discourage response matching and encourage calculation or memorized answer retrieval where possible.

Negative number processing is known to draw more heavily on the IPS and further parietal regions than positive number processing [Chassy and Grodd, in press; Gullick et al., 2012], but has also been noted to demonstrate typical neural comparison effects in this region [Gullick et al., 2012]. Negative‐operand problems may thus demonstrate an overall increase in IPS activity across operation, but whether differences between operations within each operand sign category are the same can still be investigated (e.g., do negative‐operand problems demonstrate a positive‐like pattern of activity in the IPS, with a greater percent signal change for subtraction than addition?). Further, other regions particularly involved in arithmetic may not show this overall sign difference but may demonstrate a different pattern based on operation.

For positive‐operand trials, addition problems were expected to show more AG activity, and subtraction problems to show increased IPS activity. Negative number arithmetic problems, across operations, were expected to show increased IPS activity, consistent with previous comparison work [Gullick et al., 2012] and the increased difficulty of negatives [Kilhamn, 2004], but also increased caudate activity, reflecting rule invocation and use. Additionally, while positive number addition problems tend to be learned by rote, negative addition problems are not; it is possible that negative addition problems will evoke less AG activity than positive addition problems, as there are no memorized facts to apply. Negative subtraction problems are likely to be at least partially translated into addition problems, thus could involve relatively more AG activity than their negative addition counterparts (which may be translated to subtraction problems). In contrast, if any minus signs prime subtraction, as Das et al. 2010 suggested, IPS activity may be raised and AG dampened for all negative number problems relative to positive, with no operation‐based differences within negative‐operand trials.

METHODS

Participants

Participants were 24 (12F) undergraduates, ages 18–23 years (mean = 19; 10 years). All were right handed, as assessed by the Edinburgh Handedness Inventory [Oldfield, 1971], with no history of learning disorder or disability, or neurological disorder or damage. Participants were paid $30 or given class credit. Two additional participants were excluded from analyses, due to low task accuracy (two standard deviations below mean) or scanner error.

Stimuli

A single “problem set” of stimuli was created for use with all participants. Experimental stimuli were two‐operand arithmetic problems, with two answer choices. All participants saw the same set of problems. Equations were created by using paired combinations of the numbers 1–9, excluding doubles (e.g., “1 + 1”), for 44 equations. Each digit was used an equal number of times. Half the problems presented used two positive numbers as operands, and half two negative numbers. Negative‐operand problems used the same digits as positive problems, but with negative signs. No “mixed” problems (one positive and one negative operand) were included. Addition and subtraction problems were used in both signs. Subtraction equations were constructed from the same operands as addition problems; operand order was arranged to create problems where the solution had the same sign as the operands.

Problems were balanced for difficulty and foil parity. Half the problems within each operand presented a “close distance” answer foil, and half a “far” foil. Close distance foil problems were expected to be more difficult, as choosing between the right answer and a close option is harder than between the correct answer and a clearly incorrect alternative. Close distance foils were 1 or 2 above or below the correct answer; far foils were off by 5 or 6. Foil parity was thus also balanced between matching and not matching that of the correct answer. All analyses collapsed across foil distance and parity (see Jasinski & Coch, 2012).

These procedures resulted in 176 unique experimental trials (88 in each sign; 44 addition, 44 subtraction, half with close distance foils and half with far; see Table 1, e.g., stimuli). Participants also answered two further types of arithmetic problems during the experimental session (double‐digit arithmetic problems; subtraction problems where the answer was of a different sign than the operands), but these problems are not analyzed here (see Supplementary Table I). As such, while 12 total conditions were included in the experiment (2 signs × 2 difficulty levels × 3 total operations), only four conditions are here discussed (2 signs × 2 operations, only single‐digit operands, all answers of the same sign as the operands).

Table 1.

Example stimuli

	Operand sign
Operation	Positive		Negative
Foil distance	Close	Far	Close	Far
Addition	3 + 5 = 8 <> 10	3 + 5 = 8 <> 3	−3 + −5 = −8 <> −10	−3 + −5 = −8 <> −3
Subtraction	5 – 3 = 2 <> 1	5 – 3 = 2 <> 8	−5 − −3 = −2 <> −1	−5 – −3 = −2 <> −8
Control	& + ! = @ <> $	& + ! = @ <> %	−& + −! = −@ <> −$	−& + −! = −@ <> −%

About 288 control trials were also included. Control trials presented equation‐formatted ASCII symbol strings, such as “−& + −! = −%,” meant to control for the visual presentation of numbers and equations. Half the control trials used positive symbols, and half negative; half were also subtraction formatted, and half addition. Participants were instructed to randomly choose one of the presented ASCII “answers” to control for decision‐making and button‐pressing processing.

Procedure

After giving informed consent, participants completed a survey testing their knowledge of signed number usage and operations, including placement on a number line, comparisons, basic calculation, equations and inequalities, and word problem solving. Participants were also given the Math Concepts and Applications subtest of the Kaufmann Test of Educational Achievement‐II [Kaufman and Kaufman, 2004].

Participants then began the fMRI session after completing 20 representative practice trials. The session consisted of eight event‐related and four blocked‐design functional runs. In each trial of the fMRI session, participants were shown an arithmetic problem in the top‐center of the screen and were asked to choose the correct solution of two answers presented below to the left and the right. Left and right side responses were counterbalanced. Problems were presented for 2.5 s, followed by a 500‐ms blank screen; participants could respond at any point within the display time, and were encouraged to respond quickly and accurately.

Event‐related runs

Stimuli were divided into eight event‐related experimental runs, with 102 trials per run (66 experimental and 36 controls). Run order was counterbalanced across participants. Each run included five or six trials from each of the four experimental cells here discussed (positive addition single‐digit problems, etc.), as well as trials from other conditions not here analyzed. Trials were presented in pseudorandom order. No more than six consecutive trials of the same operation, four consecutive trials of the same operand sign, or four consecutive trials of the same response side were allowed. Control trials were introduced at least once every six experimental trials, at 1, 2, or 3‐TR repetitions, and were thus used to jitter the presentation of experimental trials to create uncorrelated condition regressors.

Blocked runs

Subsequently, four block‐design functional runs were acquired, which presented the same stimuli in 11‐trial blocks of pseudorandomized arithmetic problems (again presenting no more than six trials of the same operation, or four trials of the same sign, in a row) and six‐trial blocks of control trials. These blocked runs represent an independent dataset and were used to make a functional mask for ROI analyses.

In all cases, stimulus presentation, trial timing, and response recording was achieved using E‐Prime presentation software (Psychological Software Tools, Pittsburgh, PA). Stimuli were presented using a Panasonic DT‐4000U DLP projector, and each functional run was synchronized with the onset of the first trial to ensure accuracy of event timing. Response times and accuracy were measured using fiber optic button press boxes (Cedrus Lumina response pads; San Pedro, CA).

Data Acquisition

Functional images were acquired in a 3T Philips Achieva Intera MRI scanner at the Dartmouth Brain Imaging Center. In each of the 12 functional imaging runs, we acquired 102 whole‐brain T ₂*‐weighted echoplanar images (EPI). Forty‐five‐slice EPI image volumes were acquired using Philips interleaved sequence maximizing the distance between neighboring slices; here, slices were acquired in intervals of 7. The following parameters were used for acquisition: slice thickness = 3 mm, no skip; repetition time (TR) = 3 s; echo time (TE) = 35 ms; flip angle, 90°; matrix, 80 × 80; field of view (FOV), 240 mm; and transverse plane. Two additional volumes were discarded at the beginning of each run to allow for equilibrium effects. In addition, a high resolution, magnetization‐prepared rapid acquisition gradient echo image was acquired at the end of the session (TR, “shortest”; TE, 4.6 ms; FOV, 240 mm; matrix, 256 × 256; sagittal plane; slice thickness, 0.9375 mm; 160 slices).

Analysis

Behavioral analyses

Behavioral data were analyzed to determine response time and accuracy, and any differences by sign category and operation for single‐digit problems using Repeated Measures Analyses of Variance (ANOVAs). The Greenhouse‐Geisser correction was applied when the assumption of model sphericity was violated.

fMRI analyses

All functional data across runs were examined for artifact by creating signal to noise maps in MATLAB (version 7.7.0 R2008b; The MathWorks, Inc., Natick, MA) with a modified script available at http://dbic.dartmouth.edu/wiki/index.php/Noise_Detection. fMRI data were processed using SPM8 (Welcome Department of Cognitive Neurology, London, UK, http://www.fil.ion.ucl.ac.uk/spm). Preprocessing steps for all runs for each subject included the following steps. Reorientation: The center of each functional image was reoriented such that the origin was at the midsagittal anterior commissure. Slice Timing: Differences in image acquisition time between slices were corrected using the first slice as reference using SPM8′s Fourier phase shift interpolation. Realignment: Head motion was realigned to the mean image using the least‐squares approach and a six‐parameter rigid‐body spatial transformation. Estimation was performed at 0.9 quality, 4 mm separation, 6‐mm FWHM (full‐width at half maximum) smoothing kernel, using second‐degree B‐Spline interpolation. Reslicing was performed using fourth‐degree B‐Spline interpolation. The realignment parameters were examined for excessive motion (defined as <1 mm motion in any direction); no participants were excluded based on motion. Smoothing: Images were smoothed using a 6‐mm FWHM Gaussian kernel (e.g., twice the voxel size).

First‐level individual statistics: Event‐related runs

All event‐related runs from each individual were analyzed together using a mass‐univariate approach based on the general linear model. Modeled factors were based off behavioral analyses to allow comparison of similarly difficulty positive‐ and negative‐operand problems. Three factors with 5 total levels were modeled as predictors of interest for the current study (control trials; 2 signs × 2 operations, only single‐digit operands, all answers of the same sign as the operands). Two further factors were modeled as further predictors of no interest for the current analysis (double‐digit arithmetic problems; subtraction problems where the answer was of a different sign than the operands), similar to the behavioral analyses, along with the six realignment parameters from motion correction. A high‐pass filter of 128 s was used to remove slow signal drift. Summary contrast maps were created for each individual to take to second‐level group analysis. Based on the specific planned group level tests, the contrast for each stimulus class within each group, versus control, was created. Only single‐digit noncrossing problems were here analyzed. These contrasts maps were normalized to the SPM8 EPI template using a trilinear interpolation, writing 3 mm³ voxels. Mask images for each individual were examined to ensure full brain coverage.

First‐level individual statistics: Blocked runs

All blocked runs from each individual were analyzed together using a mass‐univariate approach. Two factors were modeled, with two total levels: experimental and control trials. Contrasts of experimental > control trials were created. These contrasts maps were normalized to the SPM8 EPI template using a trilinear interpolation, writing 3 mm³ voxels. Mask images for each individual were again examined to ensure full brain coverage.

Second‐level group statistics: ROIs

The contrast between blocked run experimental > control conditions determining all task‐related brain activity was performed at P <0.05 (uncorrected). This contrast was then imported into MarsBar [Brett et al., 2002]. ROIs were defined as the intersection of these task‐activated voxels and the MarsBar anatomical atlas definition of each area of interest. This method allows selection of only voxels within a specific region that were active during task performance, and further allows separation of neighboring regions, such as the inferior parietal lobule (IPL) from the AG and the superior parietal lobule. As the AG tends to show relative deactivations from baseline, a control > experimental contrast, again performed at P <0.05 (FDR corrected), was instead used to define task‐activated voxels in this region. These regions were then applied to the independent event‐related data to test specific region‐related hypotheses by extracting the percent signal change for each condition, again using MarsBar, and comparing by problem sign and operation within each region.

Second‐level group statistics: Whole‐brain analyses

Besides the planned ROI analyses, random‐effects whole‐brain analyses were also undertaken on the event‐related data to determine the influence of problem sign and operation on neural activity in other brain areas. Contrasts were undertaken at peak P < 0.001 (uncorrected), cluster P < 0.05 (False Discovery Rate corrected), cluster size k >10. Coordinates are MNI (Montreal Neurological Institute) using ICBM152. Anatomical regions were assigned by a combination of xjview [Cui et al., 2011], visual inspection, and Talairach daemon after transformation to Talairach space [Brett, 2006; Lancaster et al., 1997]. The anatomical region listed is for the peak voxel location and, for clusters less than 1, 000 voxels, the locations of the three most significant subpeaks. For clusters greater than 1, 000 voxels, we examined up to 32 subpeak locations (as provided by SPM8) to better characterize the extent of the activation. These subpeak locations are listed by lobe in the tables. In all cases, IPS activity was confirmed by hand if the analyses demonstrated significant activity in the inferior or superior parietal lobules.

RESULTS

Behavioral Results

All participants scored well on both the KTEA‐II: Math Concepts and Applications subtest (mean raw score = 82.9 of 88, SD = 3.98) and the integer knowledge survey test (mean score = 60.13 of 62, SD = 3.45). Given this relatively uniform high performance, no further analyses were conducted using these tests.

Sign × operation

A 2 (sign: positive, negative) × 2 (operation: addition, subtraction) repeated measures ANOVA was first conducted on to examine any differences in response accuracy. Positive‐operand problem responses (mean = 0.958) were significantly more accurate than negative (mean = 0.915, F(1, 23) = 13.21, MSE (Mean Squared Error) = 0.045, P = 0.001, η² = 0.253). There was no significant main effect of operation (F(1, 23) = 2.11, P = 0.16), and no significant interaction (F(1, 23) = 1.76, P = 0.198).

A 2 × 2 repeated measures ANOVA was then conducted to examine any differences in response time. Positive‐operand problem responses (mean = 1,133 ms) were significantly faster than negative (mean = 1,447 ms, F(1, 23) = 215.88, MSE = 2,362,772, P < 0.001, η² = 0.715). Addition problem responses (mean = 1,215 ms) were significantly faster than subtraction (mean = 1,365 ms, F(1, 23) = 91.17, MSE = 544,219, P < 0.001, η² = 0.165). A significant interaction was also seen, F(1, 23) = 7.94, MSE = 37,913, P = 0.010, η² = 0.011. Negative‐operand problems demonstrated a greater response time difference between addition and subtraction problems than did positive‐operand problems; negative subtraction problems garnered the slowest responses overall (see Fig. 1).

Figure 1.

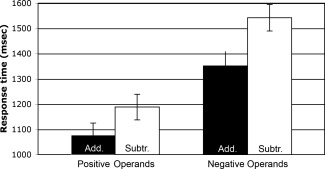
Response time effects. Response times demonstrated significant effects of operand sign and operation. Positive‐operand problems were responded to faster than negative, and addition problems were responded to faster than subtraction. All comparisons were significant at P < 0.001. Error bars indicate one standard error of the mean.

A 2 (sign) × 2 (foil distance: close, far) Repeated Measures ANOVA was then performed to examine any differences in response times between close and far‐distance foils across signs. As previously shown, positive‐operand problems were responded to faster than negative, F(1, 23) = 266.77, MSE = 3,134,136, P < 0.001, η² = 0.893. There was also a significant main effect of foil distance, where far foils (mean = 1,262) were responded to faster than close (mean = 1,282), F(1, 23) = 9,632.63, MSE = 6.545, P = 0.018, η² = 0.003. Importantly, there was no significant interaction between sign and foil distance, indicating that closer foils were consistently slower than farther across operand signs (F < 1).

fMRI Results: ROIs

Sign × operation

fMRI data was first analyzed within the independently defined ROIs to determine whether positive‐ and negative‐operand problems demonstrated similar neural activities within and across operations. Percent signal changes for each experimental condition were extracted from each of the six ROIs (IPL, caudate, and AG, in each hemisphere) using MarsBar [Brett et al., 2002], then compared separately using Repeated Measures ANOVAs. These comparisons were conducted by sign and operation (see Table 2 for percent signal change for each condition in each ROI). Given the large number of comparisons tested, a Bonferroni correction was applied, and so significance was evaluated at α/6, or P = 0.008.

Table 2.

Mean percent signal change for each ROI in each condition, sign × operation

	Positive		Negative
	Addition	Subtraction	Addition	Subtraction
L IPL	0.053	0.11	0.144	0.203
R IPL	0.022	0.051	0.064	0.121
L Caudate	0.042	0.045	0.067	0.059
R Caudate	0.008	0.01	0.02	0.037
L AG	−0.003	−0.117	−0.286	−0.062
R AG	0.114	−0.032	−0.125	0.060

The IPL was hypothesized to demonstrate increased activity to negative‐operand problems, and to subtraction problems. The left IPL ROI was centered at (−40, −48, 46) and included 503 voxels; the right IPL ROI was centered at (40, −46, 48) and included 141 voxels. Within the left IPL, there was a significant main effect of sign, F(1, 23) = 47.72, MSE = 0.205, P <0.001, η² = 0.304, and of operation, F(1, 23) = 14.32, MSE = 0.081, P = 0.001, η² = 0.12, but no significant interaction (F < 1). In the right IPL, there was a trend toward a significant main effect of sign, F(1, 23) = 7.14, MSE = 0.075, P = 0.014, η² = 0.105, but no significant effect of operation when corrected F(1, 23) = 5.28, MSE = 0.045, P = 0.031, η² = 0.063, and no significant interaction (F < 1). Bilaterally, then, negative‐operand problems demonstrated a greater percent signal change than positive‐operand problems; subtraction problems demonstrated a greater percent signal change than addition in the left IPL (see Fig. 2a).

Figure 2.

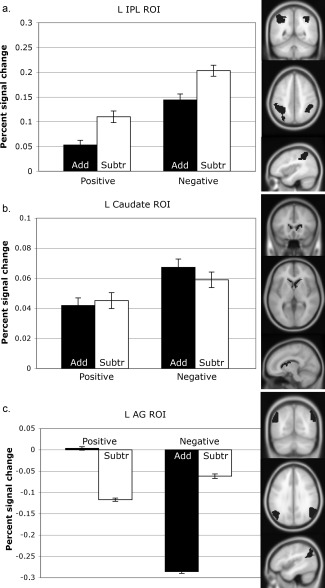
ROI percent signal changes. (a) The inferior parietal lobule demonstrated significant effects of operand sign and operation. Negative‐operand problems demonstrated a greater percent signal change than positive, and subtraction problems demonstrated a greater percent signal change than addition. (b) The caudate trended toward a marginal effect of sign, with negative‐operand problems demonstrating a marginally greater percent signal change than positive. (c) The angular gyrus demonstrated significant effects of operand sign and operation, as well as a significant interaction. Positive‐operand addition problems demonstrated a relative increase in percent signal change than positive subtraction problems. Negative‐operand addition problems, though, demonstrated a greater decrease in percent signal change than negative subtraction problems. L hemisphere ROIs shown. Error bars indicate one standard error of the mean.

The caudate was hypothesized to demonstrate increased activity for negative‐operand problems, given their use of rules and algorithms. The left caudate ROI was centered at (−14, 2, 17) and included 88 voxels; the right caudate ROI was centered at (16, 7, 14) and included 153 voxels. As the percent signal changes extracted from this region were themselves quite small, we examined the between‐subjects intercept to determine whether there was significant activity > control in the caudate. There was significant activity in the left caudate, F(1, 23) = 4.875, MSE = 0.273, P = 0.038, η² = 0.175, but not in the right caudate (F < 1). No comparisons survived correction for multiple comparisons in the remaining left caudate ROI (see Fig. 2b).

While the IPL and caudate tend to demonstrate differences in relative increase in percent signal change from baseline, the AG has been noted to show differences as relative decreases in activity [see Rosenberg‐Lee et al., 2011]. As such, the blocked run mask for the AG was created using the control > experimental contrast, then taking its intersection with the atlas AG definition. This method left a sizeable AG region in each hemisphere. The left AG ROI was centered at (−48, −64, 33) and included 201 voxels; the right AG ROI was centered at (50, −61 35) and included 317 voxels.

The AG was expected to demonstrate relatively more activity for positive‐operand problems than negative, and more activity to addition than subtraction problems. In the left AG, there was a significant main effect of sign, F(1, 23) = 139.23, MSE = 0.328, P < 0.001, η² = 0.233, a trend toward a significant main effect of operation, F(1, 23) = 10.82, MSE = 0.065, P = 0.003, η² = 0.046, and a significant interaction, F(1, 23) = 142.48, MSE = 0.710, P < 0.001, η² = 0.504. In the right AG, there was a significant main effect of sign, F(1, 23) = 458.54, MSE = 0.129, P < 0.001, η² = 0.152, no significant main effect of operation when corrected (F(1, 23) = 5.13, MSE = 0.009, P = 0.033, η² = 0.011) but a significant interaction, F(1, 23) = 267.52, MSE = 0.655, P < 0.001, η² = 0.77. Bilaterally, positive‐operand addition problems demonstrated relatively more activity than positive subtraction; in contrast, negative‐operand addition problems demonstrated relatively less activity than negative subtraction (see Fig. 2c).

To confirm that the patterns of percent signal changes found in each ROI were indeed significantly different (e.g., to demonstrate that negative‐operand problems did not simply demonstrate a greater percent signal change across operations within each ROI), a 2 (sign) × 2 (operation) × 6 (ROI) Repeated Measures ANOVA was then conducted. There was a significant main effect of ROI, F(5, 115) = 4.95, MSE = 2.173, P = 0.021, Greenhouse‐Geisser corrected, ε = 0.305, η² = 0.143, and of operation, F(1, 23) = 13.47, MSE = 0.130, P = 0.001, η² = 0.006, but not of sign (F < 1). There was a significant interaction between ROI and sign, F(5, 115) = 42.891, MSE = 0.297, P < 0.001 Greenhouse‐Geisser corrected, ε = 0.529, η² = 0.034, between ROI and operation, F(5, 115) = 2.499, MSE = 0.032, P = 0.035 Greenhouse‐Geisser corrected, ε = 0.583, η² = 0.003, and between sign and operation, F(1, 23) = 87.01, MSE = 0.501, P < 0.001, η² = 0.023. There was also a significant three‐way interaction, F(5, 115) = 42.91, MSE = 0.358, P < 0.001 Greenhouse‐Geisser corrected, ε = 0.496, η² = 0.039. As such, the different ROIs demonstrated significantly different patterns of activity by operations and operand sign.

fMRI Results: Whole‐Brain Analyses

Event‐related fMRI data was then analyzed on a whole‐brain basis to determine if any further areas were differentially involved in sign and operation processing. Comparisons were undertaken at peak P < 0.001 (uncorrected), cluster P < 0.05 (FDR corrected), cluster k>10.

Comparisons were first conducted by sign. Negative‐operand problems demonstrated more activity across the brain than did positive‐operand problems, including in parietal (bilateral inferior, superior parietal lobule), subcortical (right caudate and thalamus), and frontal (bilateral inferior, middle frontal gyrus, left superior frontal gyrus) regions, as well as in the occipital cortex and cerebellum. Positive‐operand problems demonstrated more activity than negative in the bilateral AG, temporal regions (inferior, middle, and superior temporal gyrus), and frontal areas (bilateral medial superior frontal gyrus, left middle and superior frontal gyrus; see Fig. 3, Table 3). The significant increase in caudate activity for negative‐operand problems is notable, as the ROI analysis was not significant when corrected for multiple comparisons

Figure 3.

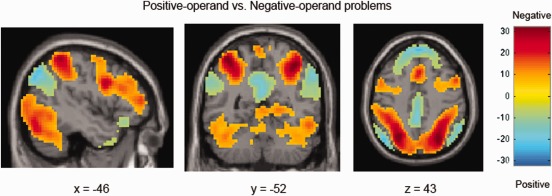
Positive‐operand versus negative‐operand problems. Negative‐operand problems (in warm colors) demonstrated increased activity in the bilateral inferior and superior parietal lobule and the caudate. Positive‐operand problems (in cool colors) demonstrated increased activity in the bilateral angular gyrus. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 3.

Sign: positive vs. negative‐operand problemsa

MNI coordinates			Cluster size	Location of peak voxel	Peak t
Positive > negative‐operand problems
−60	−64	25	539	L superior temporal gyrus, angular gyrus	6.24
−3	62	7	1092	L medial superior frontal gyrus	6.08
			Subclusters	Bilateral medial superior frontal gyrus
−9	−46	37	266	L middle cingulate, R posterior cingulate	5.6
−69	−28	−11	160	L middle, inferior temporal gyrus	5.52
60	−55	43	348	R inferior parietal lobule, angular gyrus, superior temporal gyrus	5.32
69	−28	−14	110	R middle, inferior temporal gyrus	4.32
−30	23	49	34	L middle frontal gyrus	4.08
Negative > positive−operand problems
−27	−64	52	10394	L superior parietal lobule	10.37
			Subclusters	Bilateral inferior, middle, superior occipital lobule, lingual gyrus, L fusiform gyrus; Bilateral inferior, superior parietal lobule; Bilateral cerebellum crus1, crus2, R vermis 6
−45	5	28	901	L inferior frontal gyrus (operculum)	6.97
			Subclusters	L inferior, middle, superior frontal gyrus, precentral gyrus
0	14	52	263	Bilateral supplementary motor area, R middle cingulate	6.85
60	14	37	887	R middle frontal gyrus	6.6
			Subclusters	R middle, inferior frontal gyrus
33	26	−5	104	R inferior frontal gyrus, caudate	5.2
27	−31	10	32	R caudate	4.92
18	−16	19	62	R thalamus	4.7
−30	17	10	55	L insula, inferior frontal gyrus	4.64

Results reported at threshold of peak voxel level P < 0.001 (uncorrected), cluster P < 0.05 (FDR corrected), and cluster size k > 10.

Comparisons were then conducted by operation, between addition and subtraction problems. Addition problems demonstrated more activity than subtraction in only the occipital cortex (bilateral cuneus, left superior occipital gyrus). Subtraction showed more activity than addition in several regions, including in parietal (bilateral inferior, superior parietal lobule) and frontal (bilateral inferior, middle frontal gyrus) areas, as well as occipital and cerebellar regions (see Fig. 4, Table 4).

Figure 4.

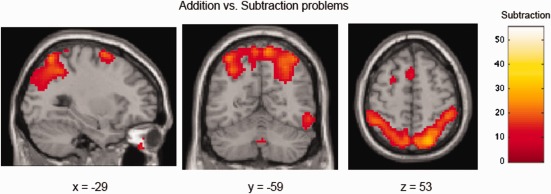
Addition versus subtraction problems. Subtraction demonstrated more activity than addition in the bilateral inferior and superior parietal lobule and frontal lobe. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 4.

Operation: addition vs. subtraction problemsa

MNI coordinates			Cluster size	Location of peak voxel	Peak t
Addition > subtraction problems
12	−100	28	129	Bilateral cuneus, L superior occipital gyrus	4.66
Subtraction > addition problems
−12	−70	58	3051	L superior parietal lobule	8.01
			Subclusters	Bilateral inferior, superior parietal lobule; Bilateral middle occipital gyrus
48	−76	−11	302	R inferior occipital gyrus, inferior temporal gyrus	6.52
−27	5	61	659	L middle frontal gyrus	5.6
			Subclusters	L inferior, middle frontal gyrus, precentral gyrus
33	2	61	100	R middle frontal gyrus	5.17
−3	−64	−38	48	L cerebellum 8	5.03
−57	−67	−8	212	L inferior occipital gyrus, inferior temporal gyrus	4.92
30	32	−2	30	R inferior frontal gyrus	4.35
30	−67	−32	34	R cerebellum crus1	4.2
0	14	55	53	Bilateral supplementary motor area	4.15
−30	−64	−35	41	L cerebellum crus1	4.04
48	11	13	44	R inferior frontal gyrus	4.02

Results reported at threshold of peak voxel level P < 0.001 (uncorrected), cluster P < 0.05 (FDR corrected), and cluster size k > 10.

DISCUSSION

The goal of this study was to determine whether the brain areas typically involved in positive number arithmetic demonstrated the same operation–activity relationships in negative‐operand problems, and to investigate any other brain areas particularly involved in negative number addition and subtraction. This study represents the first neuroimaging investigation of arithmetic with negative numbers, and thus a first step in moving beyond examinations of simple comparisons with abstract numbers to more complex uses of these concepts.

As hypothesized, positive subtraction problems showed more IPS activity than addition trials, supporting the idea that subtraction is particularly reliant on the IPS. Negative‐operand problems also demonstrated this relationship, with greater IPL activity for subtraction than addition. This difference between operations within negative‐operand problems indicates that, while the presence of a minus sign may prime subtraction and thus increase IPS activity, as proposed by Das et al. 2010, it does not overwhelm all operation differences. Alternatively, this parietal activity may reflect task difficulty, as negative‐operand and subtraction problems were each responded to slower and less accurately than positive‐operand and addition problems, respectively, but these effects cannot be disentangled at this level. Under either explanation, though, these results are consistent with the operand‐based effects expected for positive number problems.

Positive addition problems were also hypothesized to demonstrate increased activity about subtraction trials in the AG. As noted by Rosenberg‐Lee et al. 2000, these differences were characterized by relative decreases in activity from baseline: the percent signal change in the AG for positive addition problems was not significantly different from baseline, but was significantly greater than that for positive subtraction problems. However, this relationship was not conserved in negative‐operand problems. Instead, negative subtraction problems showed relatively more activity than negative addition in the AG. A major strategy for solving negative subtraction problems is to translate them into addition, changing “minus a negative” into “plus a positive.” This switch removes the double‐negative sign, which has been noted to be particularly difficult for both children and adults [Kilhamn, 2004; Vlassis, 2004], and leaves a simplified addition problem. Because of this change, negative number subtraction problems may invoke addition‐like as well as subtraction‐related processing, leading to the reversal found. That the whole‐brain contrast of addition versus subtraction did not include the AG is likely because of the reversed effects described within the ROI.

Negative addition problems demonstrated a significant deactivation in the AG, also indicating a deviation from positive addition processing. This difference, though, may not be due to operation conversions, as negative addition problems may not use translations as frequently as negative subtraction. First, negative addition problems do not present two of the same sign in a row, avoiding the double‐sign confusion that may encourage problem transformations. (Negative addition problems also show less IPS activity than subtraction, further indicating that the problem may not be translated.) Second, general differences between operand signs may better explain the decreased AG activity for negative addition problems. Negative number arithmetic problems generally, and negative addition problems specifically, are not as practiced as their positive number counterparts, as they are learned later and are not drilled to the same extent. As (relative) increases in AG activity are taken to reflect use of rote‐memorized positive addition facts, the significant deactivation for negative addition problems may demonstrate that there is no memorized fact to retrieve in this condition. Generally, though, this AG activity demonstrates that, while negative number arithmetic problems showed the expected operation–activity pattern in the IPS, they do not always conform to the positive number relationships across the brain and may involve different strategies.

The relationship between sign and activity across operation was also examined. The IPL (significantly) and caudate (whole‐brain only) demonstrated more activity to negative‐operand problems than to positive. Again, this IPS activity could reflect differences in difficulty between the signs, as negative‐operand problems did show lengthened response times and decreased response accuracies, but may also indicate overall differences in processing. As negative number problems may involve more direct calculation (thus increased IPS activity) than positive problems, they should demonstrate increased IPS activity and slowed response times, as found. Further, the reversed effects found in the AG may indicate use of a different processing strategy, potentially the described transformation of negative subtraction into addition, which would add time in this condition only.

The slight increase in caudate activity found for negative numbers is likely related to the general‐purpose rules learned for negative number arithmetic, especially for subtraction. While the overall activity in the caudate was low, the right caudate demonstrated significant negative > positive‐operand problem activity in the whole‐brain contrast. Though this effect is small, it does match the a priori hypothesis of negative > positive, possibly reflecting a weak but perhaps still informative effect. The caudate has been shown previously to be especially active for problems involving zero as an operand [Jost et al., 2009], another case of general rule invocation. These transformation rules may be specific to arithmetic with negative numbers, as they attempt to translate negatives into more a practiced positive number counterpart, even if they are not strong.

Across the whole brain, negative number problems also demonstrated increased activity in further parietal lobe areas, including the superior parietal lobule, as well as subcortical, frontal, temporal, and occipital regions. These results are consistent with those found by Gullick, Wolford, and Temple 2012 for negative versus positive number comparisons: negative trials demonstrated increased superior occipital gyrus and inferior and superior parietal lobule activity, as well as increased caudate activity. Whether used as simple comparators or in more complex operations, negative numbers may demonstrate increased occipital and parietal activity. Further, the increased prefrontal cortex activity for negative‐operand problems may reflect the increased difficulty of negative number arithmetic, consistent with difficulty effects previously reported [Fehr et al., 2007; Gruber et al., 2001; Kong et al., 2005].

This study represents a first attempt to detail the neural circuitry involved in usage of negative numbers in more complex mathematics situations. The use of ROIs based on the intersection of task‐related activity and anatomy allowed for specific investigations of these effects and interactions within independently defined hypothesized regions. While overall harder than positive‐operand problems, negative number arithmetic effects were not solely driven by difficulty differences, and demonstrated activities based on operation and strategy use. Negative‐operand arithmetic problems showed some operation‐based activities similar to that expected for positive‐operand problems, with more activity in the IPS for subtraction than addition. However, negatives also showed a different pattern of activity in the AG, perhaps due to the translation of negative subtraction problems to addition format. As such, arithmetic with negative numbers is supported by the same neural systems as positives, but operation‐specific activity is also dependent on rules specific to negative processing. The mental number system is thus flexible enough to at least allow some incorporation of negative numbers (demonstrated by the typical operation effects in the IPS), even if other strategies are also used.

Supporting information

Supporting Information Table