Efficiency of weak brain connections support general cognitive functioning

Abstract

Brain network topology provides valuable information on healthy and pathological brain functioning. Novel approaches for brain network analysis have shown an association between topological properties and cognitive functioning. Under the assumption that “stronger is better”, the exploration of brain properties has generally focused on the connectivity patterns of the most strongly correlated regions, whereas the role of weaker brain connections has remained obscure for years. Here, we assessed whether the different strength of connections between brain regions may explain individual differences in intelligence. We analyzed‐functional connectivity at rest in ninety‐eight healthy individuals of different age, and correlated several connectivity measures with full scale, verbal, and performance Intelligent Quotients (IQs). Our results showed that the variance in IQ levels was mostly explained by the distributed communication efficiency of brain networks built using moderately weak, long‐distance connections, with only a smaller contribution of stronger connections. The variability in individual IQs was associated with the global efficiency of a pool of regions in the prefrontal lobes, hippocampus, temporal pole, and postcentral gyrus. These findings challenge the traditional view of a prominent role of strong functional brain connections in brain topology, and highlight the importance of both strong and weak connections in determining the functional architecture responsible for human intelligence variability. Hum Brain Mapp 35:4566–4582, 2014. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

Our brain is a complex system of interconnected regions spontaneously organized into distinct networks [Achard et al., 2006; Hagmann et al., 2008; Sporns et al., 2002]. The integration of information between and within these specialized, spatially distributed but functionally linked brain regions is a continuous process that can be observed even when the brain is in a quiescent state, i.e., not engaged in any particular task [Greicius et al., 2003; Raichle et al., 2001; Stam, 2004]. Our ability to evaluate the surrounding environment and to respond quickly to demanding situations is, at least in part, dependent upon this ongoing integration of information. Recent studies have shown that the functional architecture of the brain follows specific patterns aimed at maximizing system efficiency [Achard and Bullmore, 2007; Eguiluz et al., 2005; Sporns and Zwi, 2004]. Global communication efficiency is supported by long‐distance connections, while high levels of local neighborhood clustering enable efficient local processing [Watts and Strogatz, 1998]. Similar to other biological and nonbiological complex networks, like the macaque cortex, metabolic networks, electronic circuits, and peer‐to‐peer networks [Humphries and Gurney, 2008], this organization allows adequate information transfer at modest wiring costs in terms of physical neuronal connections within brain regions. Accumulating evidence suggests that such intrinsic, spontaneous brain functional architecture is correlated with cognitive functioning and may help explain individual differences in a variety of cognitive and behavioral domains, including personality traits and overall intelligence [Adelstein et al., 2011].

In the last decade, functional connectivity analysis has been recognized as one of the most promising and efficient approach to investigate complex brain networks [Bassett and Bullmore, 2009]. Briefly, this approach is based on the computation of the statistical dependency between pairs of brain regions, that is, the magnitude of temporal coherence between their hemodynamic fluctuations. The interaction between brain regions results in a connectivity matrix, which represents all possible inter‐regional connections by means of nodes, i.e., regions, and edges, i.e., their connections. Using methodological approaches derived from graph theory [Rubinov and Sporns, 2010], it is thus possible to compute several indices representing diverse network properties, such as the ability to integrate information between distant nodes, the presence of functional subnetworks, and local processing. Despite the advantages for network analysis and visualization, a main caveat of graph theory‐based analysis on the whole connectivity matrix is that it captures both strong and weak brain connections, thereby preventing a clear distinction between their contribution to brain functioning, and consequently to cognition. This is a relevant limitation, as recent evidence suggests that information transfer within the human brain is optimized by means of both modular, strong connections and intermodular, weak ones. This organization maximizes the information flow, and tunes up the overall system to its well‐known small‐world configuration [Gallos et al., 2012a, b]. Interestingly, the role of weak ties has been already documented in other complex systems, suggesting that weak connections are primary contributors to the stability of biological functions [Csermely, 2004], protein‐to‐protein interaction [Ma and Gao, 2012], efficiency of mobile communication networks [Onnela et al., 2007], and the spreading of information within social communities [Granovetter, 1983]. Weak connections may also play a role in the symptomatology of schizophrenic patients [Bassett et al., 2012]. This suggests an association between the configuration of strong and weak brain connections and individual phenotypes, and puts forward the need to accurately isolate and characterize the functional properties of connections of different strength in order to understand their role in interindividual variability explanation.

The theoretical definition of intelligence and the explanation of its neurobiological basis is one of the most intriguing, yet controversial issues in modern psychology and neuroscience [Colom et al., 2010; da Rocha, et al., 2011; Deary et al., 2010; Neubauer and Fink, 2009]. Several studies have shown that the volume [Jung and Haier, 2007; Rushton and Ankney, 2009], structural wiring [Chiang et al., 2008], magnitude of local coherence [Wang et al., 2011] and system efficiency [da Rocha et al., 2011; Neubauer and Fink, 2009; van den Heuvel et al., 2009] of the brain may explain a consistent portion of interindividual variability in intellectual performance, as well as genetic‐molecular factors behind its heritability [Friedman et al., 2008; Payton, 2009]. van den Heuvel et al. (2009) demonstrated that intellectual performance, expressed in terms of Intelligence Quotient (IQ), i.e., a weighted sum of crystallized (the experience‐dependent component of intelligence—cG) and fluid intelligence (reflecting the brain efficiency regardless of education and experience—fG), correlated with overall brain global efficiency, measured as—the mean length of all paths. In addition, Cole et al. (2012) have recently provided evidence of a correlation between left dorsolateral prefrontal cortex (DLPFC) “connectedness” (i.e., its weighted degree) and individual fG. These authors also demonstrated different patterns of interaction between connections of different strength within the DLPFC and resting‐state networks like the default mode and the dorsal attention network. These two contributions suggest that overall brain functioning correlates with both crystallized and fluid intelligence (without taking into account connection strength), and that the connectivity strength profile of a specific region within the prefrontal lobe may explain a reasonable amount of variance in intelligence levels, at least for what concern its fluid component.

Here we put forward the idea that the organization of strong and weak connections at the whole‐brain level may differentially contribute to explain inter‐individual cognitive variability. We analyzed functional connectivity at rest in ninety‐eight healthy adult individuals of different age, and correlated brain topology indices with IQ scores. The question of interest was to assess whether these correlations are driven by variability in specific portions of the connectivity‐strength distribution, or rather by the functional topology of the brain regardless of connections strength. To these aim, we (i) collected data from a complete set of regions covering both cortical and subcortical structures, (ii) divided pairwise connections into different connectivity strength classes, (iii) adopted a complete set of graph topology indices which may represent both distributed and local brain functioning, and (iv) correlated such topological information with robust estimation of overall intelligence.

MATERIALS AND METHODS

Sample and Behavioral Measures

We adopted the freely available NKI‐Rockland database (part of the FCP/INDI sharing initiative, http://www.fcon_1000.projects.nitrc.org), which includes a broad phenotypic characterization of 207 healthy subjects (age 4–85), as well as structural (anatomical and DTI) and functional (resting‐state fMRI) neuroimaging data. From the NKI‐Rockland database, a selection of subjects was performed to ensure (i) an equal number of males and females, given the evidence of interactions between biological sex and intellectual abilities [Haier et al., 2005; Payton, 2009], (ii) an equal distribution of age groups, and (iii) that all subjects were right handed. The selection resulted in a final sample of 98 right‐handed subjects (49 males), with mean age of 34 years (range 18–65, SD = 14). Each contributor's respective ethics committee approved submission of deidentified data to be implemented into the ICBM dataset in the 1000 Functional Connectomes Project. The institutional review boards of NYU Langone Medical Center and New Jersey Medical School approved the receipt and dissemination of the data [Song et al., 2012].

Intelligence Scores

Intellectual performance was measured with the Wechsler Abbreviated Scale of Intelligence (WASI) [Weschsler, 1999]. WASI is a shortened version of both the Wechsler Adult Scale of Intelligence (WAIS‐III) [Weschsler, 1997], and the Wechsler Intelligence Scale for Children (WISC‐IV) [Bagby et al.,1994; Wechsler, 2003]. The WASI consists of four subscales: Vocabulary, Similarities, Block Design, and Matrix Reasoning. The four subscales converge into three different overall scores: a standardized, full‐scale intelligence quotient (FSIQ); a verbal IQ score (VIQ) which indexes word knowledge, verbal reasoning, and concept formation; and a performance IQ score (PIQ) representing abstract reasoning skills, visual information processing, visual‐motor coordination, simultaneous processing, and learning abilities. The psychometric properties of the WASI include high concurrent validity, demonstrated by strong correlations with the WAIS‐III FSIQ (r = 0.92; n = 248), as well as good reliability coefficients ranging from 0.92 to 0.98 for the VIQ, 0.94 to 0.97 for the PIQ, 0.96 to 0.98 for the full FSIQ [Ryan et al., 2003]. We applied a clustering procedure in order to extract well‐defined groups of different intelligence levels (i.e., IQ scores) from our sample. The two‐step clustering analysis (clustering criterion = Akaike's Information Criterion, log‐likelihood) was performed using SPSS software (SPSS 19, SPSS, Chicago, IL) and resulted in three clusters; namely, High (n = 37; mean age = 35 ± 15; mean FSIQ = 122 ± 7), Average (n = 35; mean age = 34 ± 14; mean FSIQ = 107 ± 6) and Low IQ (n = 26; mean age = 34 ± 12; mean FSIQ = 88 ± 7) (Table 1; Fig. 1). The three groups did not differ in age (t 0.310, P = 0.587) and gender distribution (χ² = 0.392, P = 0.476). To account for within‐group FSIQ variability, we also collected distances from cluster's center (CCD) for each subject and used it as covariate during the analysis of covariance (ANCOVA).

Table 1.

Intelligence quotient data

(A)				Overall dataset					(B)	High_IQ		Med_IQ		LowIQ		(C)	ANCOVA
	M (98)	SD (98)	viq	piq	bd	voc	sim	mat		M 98	SD98	M98	SD98	M98	SD98		f	sig
fsiq	109	12	0.712a	0.823a	0.875a	0.466a	0.521a	0.878a		122	5	107	4	88	10		175.165	<0.001
viq	108	13		0.834a	0.531a	0.897a	0.856a	0.443a		115	9	106	10	92	10		43.303	<0.001
piq	110	12			0.828a	0.712a	0.797a	0.832a		121	6	107	6	92	7		97.088	<0.001
bd	55	9				0.423a	0.554a	0.753a		63	4	54	4	40	6		148.088	<0.001
voc	55	9					0.533a	0.361a		59	7	53	9	49	10		7.972	<0.001
sim	55	8						0.463a		60	6	54	7	48	6		19.69	<0.001
mat	56	8								63	4	55	5	44	9		57.697	<0.001

^aCorrelation is significant at the 0.01 level (2‐tailed)

Average values for WASI overall IQs, i.e., Full scale (FSIQ), Performance (PIQ), and Verbal (VIQ) and for each subtest, both for the overall sample (panel A) and for each IQ subgroup (panel B). Main effects of between IQ groups ANCOVA are reported (panel C; covariates of age, total brain volume and CCD), post hoc comparisons were all significant (Bonferroni's P < 0.05 corrected). The correlational structure within main IQs and subtests is also provided. Note: BD = block design, VOC = vocabulary, SIM = similarities, MAT = visuo‐spatial abstract reasoning matrices.

Figure 1.

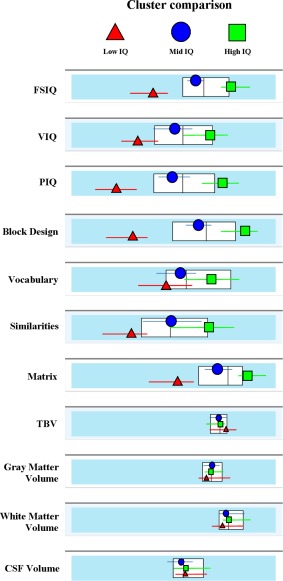
Results of the clustering procedure. Average values of Intelligence scores and brain morphometry for the three IQ groups resulting from the two‐step clustering procedure (Akaike's Information Criterion, log‐likelihood). The results confirmed a good separation between High‐IQ, Average‐IQ, and Low‐IQ subjects for the main IQ scores (FSIQ, PIQ, VIQ) and subtests, whereas no significant difference emerged for total brain, gray matter, white matter, and CSF volumes. White boxes represent the 3th quintile (central line) as well the 2th and 4th ones (left and right edges) of the overall sample distribution. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

fMRI Data Acquisition

Neuroimaging data were acquired on a 3.0‐T Siemens MAGNETOM TrioTim (Siemens, The Netherlands). A three‐dimensional T1‐weighted MPRAGE image was acquired in the axial plane (TR/TE 2500/3.5 ms; 192 slices; slice thickness 1 mm; flip angle 8°; voxel size 1.0 × 1.0 × 1.0 m; acquisition time 10.42 min). Resting‐state fMRI data were acquired using T2‐weighted BOLD images (TR/TE 2500/30 ms; 38 interleaved slices; slice thickness 3 mm; 260 volumes; flip angle 80°; voxel size 3.0 × 3.0 × 3.0 mm; acquisition time 10.55 min). Fieldmaps were available for each participant's fMRI scan.

fMRI Data Preprocessing

Data were preprocessed and analyzed at the Department of Medicine, Surgery and Neuroscience of the University of Siena. Functional images preprocessing was carried out using SPM8 (Wellcome Department of Cognitive Neurology, Institute of Neurology, University College London; http://www.fil.ion.ucl.ac.uk/spm/) within the Matlab computing environment (http://www.mathworks.com, MathWorks, MA). The first five volumes of functional images were discarded for each subject to allow for steady‐state magnetization. EPI images were first corrected for inhomogeneity using fieldmaps regression, then slice‐time adjusted and finally realigned and resliced to the mean volume for head motion correction. Two recent studies suggested that head motion during MRI scanning may induce significant changes in functional connectivity estimation and consequently affect the calculation of local and global topological indices [Power et al., 2012; Van Dijk et al., 2012]. To address this issue, we used two approaches (i) canonical regression of motion vectors (by eliminating subjects whose head motion exceeded 1.0 mm or rotation exceeded 1.0°) and (ii) time series interpolation based on the displacement indices proposed by Power et al. (2012), i.e., framewise displacement (FD) and the RMS variance of the temporal derivative (DVARS). Functional time points showing FD > 0.5 mm and DVARS > 0.5 were interpolated using a cubic spline function. This allowed the comparison of graph properties obtained with each motion correction approach.

Structural images were coregistered to the mean volume of functional images and subsequently segmented using a routine in SPM8. We applied the Hidden Markov Random Field model to remove isolated voxels. To obtain a more accurate spatial normalization, we applied the SPM8 DARTEL (Diffeomorphic Anatomical Registration Through Exponentiated Lie) [Ashburner, 2007] module and created a customized gray matter template from all subjects' segmented images. We then applied a nonlinear normalization procedure with subsequent affine‐only normalization to the Montreal Neurological Institute (MNI) template brain to functional images, and resampled voxels to an isotropic 3 × 3 × 3 mm voxel size. Linear trends were removed to reduce the influence of the rising temperature of the MRI scanner and all functional volumes were band‐pass filtered at 0.01 Hz < f <0.08 Hz to reduce high frequency noise and/or aliasing with physiological noise.

A debate exists as to whether the deconvolution of potential confounding signals (mainly physiological, low‐frequency respiratory and cardiac noise) from the grey matter time courses should be performed prior to the computation of the correlation matrix [Biswal et al., 2010]. In the present investigation, we opted to regress out motion parameters and signals derived from four white matter and CSF regions of interest (ROIs). This approach proved effective in enhancing within‐subject and test–retest reliability (at 45 min and 5–16 months) [Liang et al., 2012; Schwarz and McGonigle, 2011]. Moreover, global signal was not removed, given that the thresholding procedure that we applied to the connectivity matrix (see following section) explicitly relies on correlations distribution, and that global signal removal is known to artificially alter the topological properties of connections in the left tail of the correlation histogram [Murphy et al., 2009; Schwarz and McGonigle, 2011].

Overview of Network Analysis and Thresholding Procedure

Network nodes were defined by parcellating the brain into 90 cortical and subcortical ROIs according to the automatic anatomical labeling atlas (AAL) [Tzourio‐Mazoyer et al., 2002], one of the most commonly employed atlas for network analyses [Achard and Bullmore, 2007; Achard et al., 2006; Liu et al., 2008; Wang et al., 2010]. As recently suggested [Craddock et al., 2013; Zalesky et al., 2010], different anatomical parcellation schemes may impact functional connectivity estimation. To rule out any effect of the a priori selection of a specific atlas on the correlation between intelligence and brain topology, we carried out the main analyses using three additional atlases for functional images parcellation and analysis (one anatomical, two functional). Analogous results were obtained across the four atlases (details about the atlases and results are included in Supporting Information). The computation of topological properties requires the creation of a so‐called adjacency matrix, which graphically represents the overall brain organization in terms of nodes (brain regions) and edges (representing the dependency between the BOLD time series of each pair of brain regions). Here, adjacency matrices were obtained for each subject by computing the pairwise zero‐lag correlation coefficients (“r”) between the mean BOLD time series of all possible voxels within each ROI, leading to a 90 × 90 matrix with 4,005 edges, i.e., connections. These normalized edges represented the whole range of possible functional links between cortical and/or subcortical regions, covering strong (r > 0.7), intermediate (0.2 < r < 0.7), and weak (0 < r < 0.2) connections, as well as negative ones (r ≤ 0) (as described in [Schwarz and McGonigle, 2011]). Several studies have shown that topological properties, including modularity and small‐worldness, may be better identified and reliably quantified by analyzing thresholded version of the full adjacency matrix (composed by a subpopulation of overall connections falling above a certain r value) [Achard and Bullmore, 2007].

Here, we studied whether strong and weak brain connections differentially contribute to individual differences in IQ by applying the thresholding procedure for graph topology computation suggested by Schwarz and McGonigle [2011]. Assuming that sparsity estimates are inversely related to connection strength, this procedure is based on the computation of different sparsity windows retaining connections falling within a lower ( $r_{\mathrm{c}}{}_{\Downarrow }$) and an upper bound ( $r_{\mathrm{c}}{}_{\Downarrow }$). For instance, a sparsity window that retains connections within the 15% and the 20% of the distribution leads to the representation of the 15th to the 20th percentile of the strongest connections in the brain. Briefly, each adjacent matrix, aij, was computed according to the following formula:

$$a_{ij}=\{\frac{1,r_{\mathrm{c}}{}_{\Downarrow }◃r_{ij}◃r_{\mathrm{c}}{}_{\Uparrow }}{0,r_{\mathrm{c}}{}_{\Downarrow }◃r_{ij}◃r_{\mathrm{c}}{}_{\Uparrow }}$$

where r_ij represents the correlation range of interest, $r_{\mathrm{c}}{}_{\Downarrow }$is correlation upper bound, $r_{\mathrm{c}}{}_{\Downarrow }$is the lower one, “0” represents correlation values falling below or above the range of interest and therefore excluded from the matrix, and “1” correlation values falling within that range and therefore preserved in the matrix. This allows a characterization of brain topology within predefined sparsity ranges of interest (e.g., weak, intermediate, and strong brain connections). For a synthetic explanation of analysis workflow (see Fig. 2).

Figure 2.

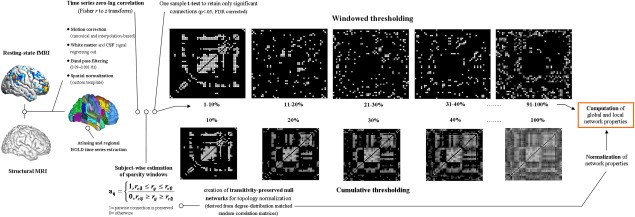
Preprocessing, thresholding, and graph‐topological properties computation workflow. Schematic representation of the major steps for network topology computation, involving images preprocessing, the thresholding procedure based on the connectivity strength and topology indices computation. From left to right, images underwent canonical preprocessing involving two different approaches for motion correction, removal of possible confounding factor related to breathing and cardiac signals, temporal band‐pass filtering, coregistration, and spatial normalization using the DARTEL module for SPM. Four different atlases (2 functional, 2 anatomical) were used for resting‐state parcellation into regions of interest and consequent BOLD signal time series extraction. A one‐sample t test was applied over resulting connectivity matrices to retain only significant connections, which were used to define several matrices based on connectivity strength and representing strong, intermediate, and weak brain connections (windowed thresholding, upper row). A few matrices obtained at identical sparsity values with the windowed and cumulative thresholding approaches are shown to highlight the different representation of brain connectivity resulting from the procedures. To normalize graph topology indices, an Hirschberger‐Qi‐Steuer algorithm was used to create transitivity preserved null networks based on the random correlation matrices matched for degree‐distribution. Considering our focus on connectivity strength distribution, all previous steps including matrix thresholding were performed at the single subject level. Additional details are provided in Methods. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The distribution of correlation coefficients varies across subjects, and its shape determines network organization [Schwarz and McGonigle, 2011]. As the aim of our study was to estimate the correlation between individual IQs and the magnitude of different correlation strengths, we based our analysis on individually thresholded matrices instead of using group‐averaged strength values. In this way, we avoided connection strength misrepresentations that may arise by averaging high and low connection strengths across individuals. Moreover, topological properties were estimated separately for each participant, so that subjects with High or Low IQs independently contributed to the topological profile of their group. We then calculated the network properties for five windows of different connection strength. This resulted in five “quintile” matrices for each participant, representing the strongest (window [1] = 1–20%, hereafter Q1), intermediate (window [2] = 21–40%, Q2, window [3] = 41–60%, Q3, window [4] = 61–80%, Q4) and weakest brain connections (window [5] = 81–100%, Q5). The division of cost windows into quintiles was performed to avoid inconsistent IQ‐network property correlation coefficients between neighboring windows that could arise using finer grained sparsity resolutions (e.g., 1 or 2% sparsity windows) (see [Schwarz and McGonigle, 2011], for a similar approach). In addition, a vast literature supports the conversion of weighted matrices to binary graphs [Bassett and Bullmore, 2009; Dosenbach et al., 2010], in which the information about pairwise connections is downgraded to a simple representation of their presence or absence. Our aim to identify an interaction between connectivity strength and IQ discouraged this approach; we thus computed topological properties starting from weighted matrices [Latora and Marchiori, 2001], obtaining both global (an unique value referred to the overall brain, i.e., brain local efficiency) and local (a values for each brain region) indices.

Finally, we computed a two‐tailed, one‐sample t test for each participant and quintile matrix to ensure that topological features were computed on statistically reliable connections and thus to avoid type I errors [Zalesky et al., 2012a]. Only connections surviving the false discovery rate (FDR, P < 0.05) correction for multiple comparisons were used for subsequent analyses.

Below, we report a brief summary of network properties that entered the statistical analyses, assuming: (N) as the set of all nodes in the network, (n) as the number of nodes, (k) as a specific node, (L) as the set of all links in the network, (l) as the number of links, (i, j) as the link between nodes i and j, (aij) as the connection status between i and j (aij = 1 when link i, j exists; aij = 0 otherwise). Properties were calculated using the Brain Connectivity Toolbox (http://www.sites.google.com/site/bctnet/).

Integration and Brain Distributed Processing

Distributed information processing is a key feature of cognitive functioning [Yeo et al., 2011]. To assess long‐distance, inter‐regional functional connections within the quintile brain networks, two indices were selected, the Global efficiency ‐ E, and the largest connected component ‐ LCC. Network E is usually conceptualized as expression of overall network information processing, and defined as:

$$E=\frac{1}{n}{\displaystyle \sum _{i\in N}{E}_i=}\frac{1}{n}{\displaystyle \sum _{i\in N}\frac{{\displaystyle {\sum }_{j\in N,j\ne i^{d}i{j}^{-1}}}}{n-1}},$$

where d represents the distance matrix, whose ij values represent the shortest path length (or distance) between all pairs of nodes. At the neurophysiological level, a network with high E _Loc is composed of nodes placed at short distance from each other. This configuration allows a fast interaction between nodes and enhances high functional integration. Therefore high E values represent better overall brain information processing, compared to low ones. The E was preferred over the widely‐used average path length (which represents the average number of steps along the shortest paths for all possible pairs of network nodes) because of its lower sensitivity to the presence of disconnected, or very weakly connected, nodes [Zalesky et al., 2012b]. We hypothesized that the correlation between brain organization and connection strength might be reflected in the overall “connectedness”, that is, the number of subnetworks composed by subsets of tightly connected regions (i.e., components). In this context, the size of the largest connected component—LCC, an index usually applied for complex networks resilience estimation [Albert et al., 2000], was defined as the largest number of nodes constituting a component. LCC was computed as:

$$d_{ij}={\displaystyle \sum _{a_{uv}{{\displaystyle \in g}}_{i\underset{}{\leftrightarrow }j}}}{a}_{uv\text{'}}$$

with gi ↔ j representing the shortest path between nodes i and j (disconneted pairs = ∞). Each cell within the resulting matrices represents the minimum number of steps (node‐to‐node connections) required to connect each pair of nodes, so that a (i, j) blank cell indicates the impossibility to directly or indirectly connect nodes i and j.

Segregation and Brain Local Processing

Local processing reflects the synchronization between adjacent neuronal populations, a functional prerequisite for several cognitive functions within the motor, visual, somatosensory, and also memory domains [Ding et al., 2011]. Local and global efficiency are mutually responsible for a network's ability to sustain parallel information transfer [Latora and Marchiori, 2001]. Here, we characterized brain segregation using the Local efficiency index ‐ E _Loc, a measure of the average efficiency within local subgraphs or neighborhoods. E _Loc has been calculated as follows:

$$E_{\text{Loc}\hspace{0.17em}}=\frac{1}{n}{\displaystyle \sum _{i\in N}}{E}_{\text{Loc}}{}_{,i}=\frac{1}{n}{\displaystyle \sum _{i\in N}\frac{{\displaystyle \sum j,h\in N,j\ne ia{i}_j{a}_{ih}{\left[d_{jh}\left(N_i\right)\right]}^{-1}}}{k_i(k_i-1)}}$$

where E _{Loc ,} i is the local efficiency of node i, and dj h(Ni) is the length of the shortest path between j and h, that contains only neighbors of h. High levels of E _Loc represent better information processing at the local, compared to the global, level.

Regional Centrality for Overall Brain Processing

An intrinsic feature of brain networks is regional degree, which reflects the existence of a limited number of regions showing a large number of connections, thus crucially contributing to network information flow and stability [Bullmore and Sporns, 2012]. We hypothesized that the relevance of a node for the overall network dynamics might correlate with individual IQs. We thus estimated nodes' betweeness centrality ‐ b_i, which reflects the number of the shortest node‐to‐node paths that pass through a specific node. B_i for the node i has been defined as:

$$b_i=\frac{1}{(n-1)(n-2)}{\displaystyle \sum _{\begin{array}{c}h,j\in N\\ h\ne j,h\ne i,j\ne i\end{array}}}\frac{{\rho }_{hj}(i)}{{\rho }_{hj\text{'}}}$$

where ρhj is the number of shortest paths between h and j, and ρhj (i) is the number of shortest paths between h and j that pass through i.

Statistical Analysis

Statistical analyses were carried out on E, E _Loc, bi, and LCC values for each quintile matrix. We first conducted a linear regression analysis to assess the relationship between each quintile matrix network property and IQs (FSIQ, VIQ, PIQ, and subtests). Average values for each network property (a single value representing the whole brain property) were entered as independent variables, while IQs scores were dependent variables (resulting into four different regression models for each IQ score). To further substantiate any variation of network properties as a function of intellectual performance, we conducted an analysis of covariance, separately for each network property, with intelligence (three levels, representing the three IQ clusters) as between‐subject factor, and connection strength (five levels, representing the five quintile windows) as within‐subjects factor. Age, CCD, body mass index (BMI), and gender were used as covariates. An alpha = 0.05 was chosen as significance level for all analysis, and post hoc comparisons were computed using Bonferroni's correction.

Multivariate Nodal Characteristics Classification Procedure

To identify the contribution of specific anatomical regions to the observed brain behavior correlations, we performed a multivariate classification procedure between High‐IQ and Low‐IQ groups. A vector of nodal properties (nodes n = 90) for each participant (High‐IQ n = 37, Low‐IQ n = 26) was built, resulting in a 66 × 90 matrix for each graph property. Using the Weka software [Frank et al., 2004], a support vector machine (SVM) algorithm was tested through the leave‐one‐out cross‐validation (folds = 65), resulting in an estimation of the overall correct classification percentage, as well as in a node‐specific discriminative weight, which reflects the contribution of each region to the overall classification process. The classification process included those network properties that resulted in a significant difference between IQ clusters in the ANCOVA. As SVM is biased by group size, for the leave‐one‐out cross validation we equated the size of the two groups by selecting a few random subsamples from the group with the bigger size, and then selected the most reliable pattern of classification across subsamples. The parameter c for penalization of misclassified samples was optimized for each SVM using a grid search algorithm suggested for this machine learning approach. The algorithm increases the c exponentially, refines the grid search around c providing maximum classification accuracy in the leave‐one‐out cross validation, and then selects the c providing the highest cross validation accuracy in the refined grid [Lei and Zhou, 2012].

Moreover, an additional analysis was performed to identify the most discriminative functional connections encompassing the regions resulting from the previous SVM analysis. A vector of pairwise connection values (i.e. correlation coefficients) was created for each participant (High‐IQ n = 37, Low‐IQ n = 26), only for those connections (i) involving the brain regions identified in the SVM analysis, (ii) belonging to the strength window/s that showed a significant difference between High‐G and Low‐G subjects, and (iii) surviving the one sample t test (P < 0.05, FDR corrected). The procedure to correct for different group sizes described above was then applied.

RESULTS

As evident from Figure 2a, the subdivision of brain networks into quintiles resulted in five particular representations of brain topology as a function of the connection strength distribution. Consistent with previous research [Schwarz and McGonigle, 2011], the adjacency matrix obtained by retaining the strongest node‐to‐node connections (Q1, $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.75 ± 0.03 = sparsity 1%; $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.53 ± 0.08 = sparsity 20%) revealed a pattern of strong interhemispheric links between corresponding ipsi and contralateral brain regions. The matrix in the ultralow correlations window (Q5, $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.18 ± 0.12 = sparsity 81%; $r_{\mathrm{c}}{}_{\Downarrow }$ = −0.16 ± 0.11 = sparsity 100%) included Pearson's coefficients around zero, suggesting that topological information in the extreme left tail of the correlation distribution may not be biologically meaningful [Bassett et al., 2012]. The boundaries of the remaining quintile windows were $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.52 ± 0.08 = sparsity 21%, $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.42 ± 0.10 = sparsity 40% for Q2, $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.41 ± 0.10 = sparsity 41%, $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.33 ± 0.11 = sparsity 60% for Q3, and $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.32 ± 0.11 = sparsity 61%, $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.20 ± 0.16 = sparsity 80% for Q4.

As shown in Figure 3b, the linear regression analysis showed that E values referring to Q4 (i.e., 61–80% sparsity values) positively correlated with the FSIQ (t 4.534, β 0.683, P = 0.001, adjusted R ²=0.375), VIQ (t 3.459, β 0.598, P = 0.003), and the PIQ (t 4.295, β 0.454 P = 0.001), as well as with the WASI subtests: Similarities (t 3.343, β 0.356, P = 0.002), Block design (t 3.542, β 0.322, P < 0.001), Vocabulary (t 3.221, β 0.344, P = 0.003), and Matrix (t 3.378, β 0.398, P = 0.003). A positive correlation was also found between Str E values and the FSIQ (t 1.933, β 0.294, P = 0.023, adjusted R ² = 0.117), the VIQ (t 2.134, β 0.314, P = 0.020), and the PIQ (t 1.834, β 0.267, P = 0.043). No other topological information derived from each quintile window reached statistical significance in the regression analysis.

Figure 3.

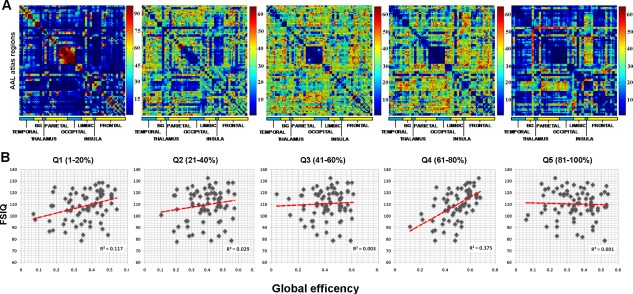
Inter‐regional connectivity distribution and regression analysis results. (a) The five panels show the distribution of pairwise connectivities over the whole sample (n = 98). For illustrative purposes, weighted adjacency matrices referring to each sparsity window were binarized (i − j = 1 if connection is present, 0 otherwise), and summed together across subjects. Thus, each i – j value in the resulting matrices represents the number of participants reporting that connection, leading to a graphical plot of the most representative connections for each sparsity window. Color bar represents the number of connections/edges. For example, the Q1 (sparsity 1–20%) shows an edge distribution ranging from not present (deep blue) to present in all participants (n = 98, dark red). It must be noticed that the original weighted matrices were composed of pairwise connections which survived a one‐sample t test analysis performed at the individual level (P < 0.05 FDR corrected). This test was performed to restrict the subsequent analyses on the most reliable connections. (b) Amount of intellectual functioning variance explained (adjusted R ²) by E values within each connectivity window. Regression equations built using E values led to the explanation of 37.5% of interindividual differences in the FSIQ. Results of the VIQ and the PIQ are not shown as they exhibit the same pattern with the function explaining 32 and 34% of interindividual variance in verbal and performance abilities, respectively. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The results from the linear regression analysis were substantiated by the ANCOVA results (Fig. 4). E values were significantly different across the three clusters only in Q4 (F ₉₇ = 5.64, P = 0.003) and Q1 (F ₉₇ = 3.21, P = 0.029). Bonferroni‐corrected pairwise comparisons for Q4 values indicated that this difference resulted from higher E values for High‐IQ subjects compared to average (P = 0.023) and Low‐IQ ones (P = 0.015), which in turn did not differ from one another (P = 0.456). The same trend was observed for Q1 (High‐IQ vs. Average‐IQ, P = 0.035; High‐IQ vs. Low‐IQ, P = 0.021; Average‐IQ vs. Low‐IQ, P = 0.478).

Figure 4.

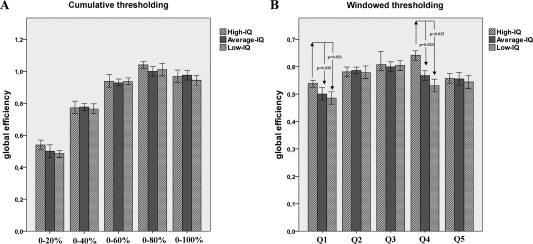
Global efficiency differences within strong and weak brain connections. The figure shows the mean E values of participants included in the High, Average and Low‐IQ groups. For illustrative purposes, panels (a) and (b) report E values computed using the cumulative or windowed thresholding procedure, respectively. A statistically significant difference between High and Average‐Low IQ subjects in the Q4 window is evident (sparsity 61–80%; boundaries: lower $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.18 ± 0.12; upper $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.32 ± 0.11; *P = 0.003). Moreover, a weaker difference is present for E values representing the first 20% of stronger brain connections (Q1; boundaries: lower $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.53 ± 0.08; upper $r_{\mathrm{c}}{}_{\Downarrow }$ = 0.75 ± 0.03). In this case, topological properties are identically captured by the cumulative and windowed solutions.

A Possible Two‐Level Structure Underlying for Intelligence

As shown in Figure 3, Q1 demonstrated an increased concordance across participants in the distribution of strong connections, with a core of pairwise connections representing almost the entire connectivity variability within the sparsity window. The reduced variability within this window may explain the lack of significant correlations between connectivity profiles and intelligence. This suggests that these connections may act as moderately stable backbones for brain functioning [van den Heuvel et al., 2012], whose alterations might be significantly captured in the case of severe pathological conditions affecting cognition [Bassett et al., 2012; Di et al., 2013; Rudie et al., 2012; Santarnecchi et al., 2012; Tijms et al., 2013]. One may hypothesize that a combination of Q1 and Q4 connections accounts for the largest variability in IQ levels. This would support the already validated idea that strong and weak ties contribute differently to the transformation of the brain from a modular, large‐world structure, to an efficient small‐world organization [Gallos et al., 2012a,b]. Here, we tested this additional hypothesis by calculating a multiple regression model which included the topological properties of both Q1 and Q4 as independent variables, and the FSIQ as dependent variable. The resulting model led to an improvement of IQ variability explanation (adjusted R ² = 0.515, t 6.734, β 1.023, P = 0.001).

Anatomical Features of Weak Connections

The identification of a significant relationship between strong and weak brain connections and individual cognitive functioning deserves indepth evaluation of their anatomical representation. Thus, we additionally investigated connection length distributions within weak and strong brain connections by approximating two classes representing short (<50 mm) and long (>50 mm) connections. As previously documented [Bassett et al., 2012; Schwarz and McGonigle, 2011], marked differences are visible in Figure 5, with strong connections (Q1) showing prevalent interhemispheric, equally distributed short and long connections, while weak connections (Q4) are mainly represented by long distance projections between and within hemispheres. This graphical pattern suggests an increased number of inter/intrahemispheric connections between different brain lobes within Q4 compared to Q1, a feature which may account for the higher E–IQ interaction observed for Q4. We reasoned that this structure may be responsible for the differences between IQ groups. We therefore calculated the ratio of interlobes connections (the number of interlobes links with respect to the overall number of possible connections, computed for every possible combination, including frontal, temporal, parietal, occipital, and limbic lobe, for both left and right hemispheres) within the Q4 matrix, separately for each subject. We then tested an ANCOVA model (covariates of age, TBV, CCD, Bonferroni's corrected), including factors of “Ratio values” and “Intelligence level”. No value reached statistical significance.

Figure 5.

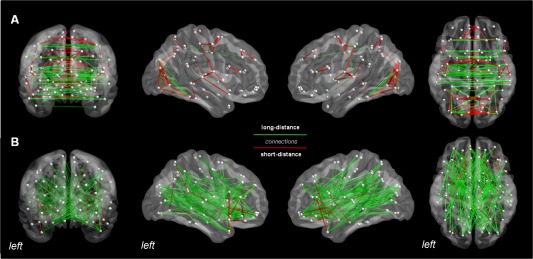
Topological organization of strong and weak connections. Panel (a) reports the most represented pairwise connections (edges >95th percentile) across all subjects (n = 98) for the Q1 (1–20%, upper row) and the Q4 windows (61–80%, lower row), respectively. Shown from left to right are coronal, right and left sagittal, and axial views. Color‐coding corresponds to short (red, <50 mm) and long (green, >50 mm) connections. As evident from the figure, Q1 showed prevalent interhemispheric, short and long connections, while Q4 long distance, inter‐intrahemispheric balanced projections. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Identification of Most Discriminative Brain Regions

Considering the small amount of IQ variance explained by strong connections, multivariate pattern analysis was performed on Q4 data only. SVM classification indicated a pattern of brain regions that discriminated between High‐IQ and Low‐IQ subjects with a correct classification rate of 88.25% (confidence interval [CI]: 0.67–0.91; accuracy = 0.81; sensitivity = 0.74; specificity = 0.92). Features that overcame the 95th percentile were plotted on a three‐dimensional glass brain in order to show brain areas that mostly contributed to IQ differences between clusters. The classifier weights were higher (>95th percentile) in a group of regions located in the bilateral anterior cingulate cortex, bilateral superior frontal gyrus (medial part), left superior frontal gyrus (dorsal part), right hippocampus, right post central gyrus and right temporal pole (Figs. 5 and 6). This result indicated that small changes of E values in these regions determine changes of the decision function to a greater extent compared to other regions with lower classifier weights. Finally, as shown in Figure 7, the pattern of functional connections of these regions was able to discriminate between High‐IQ and Low‐IQ subjects with a correct classification rate of 72.19% (confidence interval [CI]: 0.61–0.79; accuracy = 0.73; sensitivity = 0.71; specificity = 0.82). Network analysis results are plotted onto glass cortical surfaces using BrainNet Viewer (http://www.nitrc.org/projects/bnv/).

Figure 6.

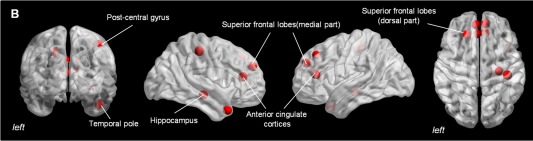
Most discriminative brain regions for IQ groups separation. The figure shows the results of the multivariate pattern classification procedure performed between IQ groups (correct classification rate of 88.25%), using a support vector machine (SVM) algorithm on E values referring to the Q4 sparsity window. Acknowledged the multivariate nature of classification results, this graphic representation shows brain regions that carry most of the discriminative weight between IQ levels (>95th percentile), suggesting that these are the brain areas whose E values mostly contributed to the decision boundary. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 7.

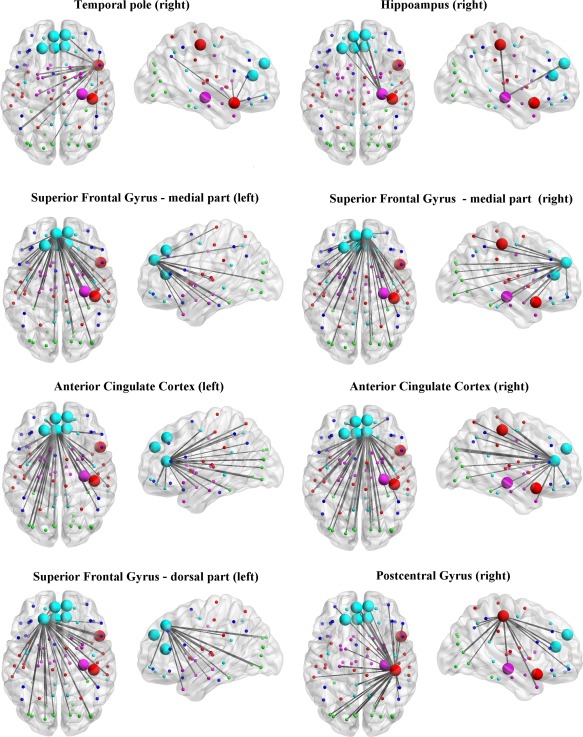
Most discriminative functional connections. The figure shows the results of the multivariate pattern classification procedure performed between IQ groups (correct classification rate of 72.19%), using a support vector machine (SVM) algorithm on correlation coefficient values referring to pairwise connections (i) within the Q4 sparsity window and (ii) encompassing those regions identified in the SVM classification based on regional E values (see Fig. 5). This graphic representation shows functional connections that carry most of the discriminative weight between High‐IQ and Low‐IQ subjects (>95th percentile). In order to ease visualization, connections have been shown separately for each of the eight regions. Legends: nodes' color refer to different brain lobes: Light Blue = frontal component of Default Mode Network; Red = Sensorimotor and Temporal lobe/auditory network; Green = visual network; Purple = basal ganglia network; Dark Blue = dorsal attention network.

On the basis of the nonphysiological meaning of the Q5 window stated above, and in order to ease reading, in the Discussion we will refer to the Q1 and Q4 correlation windows as “strong” and “weak” brain connections, respectively.

DISCUSSION

Topological measures of brain networks have proven to be a reliable instrument for the understanding of healthy and pathological brain functioning [Bullmore and Bassett, 2011; Sporns, 2011]. In the last years, novel approaches for brain network computation and analysis have shown that the topological properties of the brain may vary significantly if the strength of connections is taken into account, and that strong and weak connections may play different roles in overall brain functioning [Bassett et al., 2012; Cole et al., 2012; Gallos et al., 2012b; Schwarz and McGonigle, 2011]. When applied to the investigation of the neurobiological basis of human intelligence, this kind of brain topology analysis demonstrated a positive correlation between global brain communication efficacy and intellectual performance, and more specifically, that shorter functional distances between brain regions corresponded to higher IQ scores [van den Heuvel et al., 2009]. Here, we hypothesized that this correlation between brain topology and intelligence may depend on specific subpatterns of connection strength, and that strong and weak connections play different, or at least mutual, roles in supporting individual intellectual abilities. Consistent with this hypothesis, our results showed that the intelligence scores of healthy subjects are positively correlated with the average communication efficacy of brain networks. Crucially, this occurred for network efficiency estimates computed for weak and strong brain connections separately, with a prominent, yet unexpected involvement of the former.

Little has been said previously about the role of weak brain connections, particularly because of methodological and conceptual issues [Achard and Bullmore, 2007; Bassett and Bullmore, 2009]. Under the general assumption that “stronger is better”, the topological exploration of functional brain architecture has mainly focused on the connectivity patterns of the most strongly correlated regions, for both diagnostic purposes [Bassett et al., 2008; Liu et al., 2008; Zhang et al., 2011] and the understanding of their neurophysiological significance [Achard et al., 2006; Sporns and Zwi, 2004; Stam, 2004]. As a consequence, the role of weak connections has remained obscure for years. This is somehow surprising, given that the relevance of weak connections in complex networks other than the brain had already been stressed many years ago. For instance, Granovetter [1973] and Beck et al., [1996] pointed out the importance of weak relationships (ties) between members in complex social networks, for the maintenance of overall system dynamics, and the spreading of new ideas and information.

Only recently, new evidence has clarified that the optimization of information processing in the human brain relies on both strong and weak connections [Gallos et al., 2012a; Schwarz and McGonigle, 2011], and that weak connections may be a useful marker for specific pathological conditions [Bassett et al., 2012]. The observation that strong correlations may not carry the highest sensitivity for the discrimination of pathological conditions or higher‐cognitive ability profiles may appear counterintuitive at first glance, but a few issues deserve consideration. In the last decade, the vast majority of brain topology investigations suggesting biologically significant network features (like the “small‐world” behavior, modularity, and assortativity) were based on the cumulative thresholding procedures. This approach leads to a blurring of correlation strength distributions by over‐representing stronger connections. Interestingly, as demonstrated by Schwartz and McGonigle [2011, 2012], the topological properties of the brain are instead strongly dependent on the right tail of the correlation distribution. Theoretically, this may be consistent with a conceptualization of stronger connections as a relatively stable framework for the functional architecture of the human brain, hence determining a high degree of stability [Gallos et al., 2012a; van den Heuvel et al., 2012]. Following this reasoning, it is not surprising that, as our data suggested, the largest part of individual variability in normal brain functioning related to high‐order cognition could be rather explained by weak ties. Furthermore, one may hypothesize that this variability may rely on multiple connectivity windows instead of just a specific one, and that the interplay among them determines optimal or suboptimal network configurations, which in turn correspond to behaviorally relevant patterns.

The interaction between intelligence and brain connectivity depicted in our data supports this hypothesis, and demonstrates a two‐level connectivity structure which explains nearly half of the variability of IQ levels. This scenario confirms and goes beyond previous evidence on the correlation between intelligence and brain efficiency obtained by looking at all possible connections [van den Heuvel et al., 2009], and other evidence that focused on specific anatomical regions [Cole et al., 2010]. However, additional considerations on the role of strong and weak connections are needed in order to understand their specific contribution. In the present study, the global efficiency of weak brain connections, which has been shown to reflect long‐distance functional connections in our and previous studies [Bassett et al., 2012; Schwarz and McGonigle, 2011], was higher in individuals with high intellectual performance. This network property is a measure of how close the nodes of a network are globally connected, and can therefore be interpreted as an index of efficient information processing in the brain [Bullmore and Bassett, 2011]. Interestingly, as confirmed by van den Heuvel et al. [2009], only topological indices representing network integration, like average path length and global efficiency, seem to correlate significantly with intelligence levels. Functional neuroimaging studies are generally consistent with the notion that “more intelligent brains”, compared to average ones, allocate less functional resources for successful performance on cognitive tasks. In other words, they distribute information processing in a more efficient way [Bauer et al., 2007]. Consistent with this view, increased information transfer between brain regions connected through long‐distance connections may lead to an overall increase of inter‐hemispheric and, most importantly, internetworks communication, with direct implications for cognitive functioning [Carter et al., 2010; Doron et al., 2012; Modha and Singh 2010].

The crucial role of long‐distance connections in intellectual performance should also be considered in light of their effects on complex network functioning at a system level. Structural data of different biological systems (primate cortex, nematode Caenorhabditis elegans and neurons within frontal ganglia) have shown that long connections affect the efficiency of short paths [Kaiser and Hilgetag, 2006], and evidence of a correlation between long‐association fibers integrity and processing speed has been demonstrated in normal and pathological conditions [Turken et al., 2008; Yu et al., 2008]. The relevance of long‐distance projections is also substantiated by evidence of better wiring costs achieved through a higher amount of long‐distance projections, suggesting that neural systems are not optimized exclusively for minimal global wiring [Chen et al., 2006; Chklovskii et al., 2004]. Of relevance, Gallos et al. [2012a] have recently demonstrated that weak intermodular connections play a crucial role in transforming the brain from its modular structure, mainly supported by strong connections, to its well‐known small‐world regime, a configuration which massively optimizes information processing without impacting network wiring costs. Moreover, it must be considered that the connectivity structure obtained with our thresholding procedure based on connection strength artefactually segregate strong and weak connections without considering the networks they functionally belong to. Thus, this does not allow an exploration of the interaction between intelligence and multilevel dynamics. Further ad hoc analyses assessing the interactions between modularity, small‐worldness, connectivity strength, and IQ are therefore needed.

On a different line of research, electrophysiological studies involving EEG recording have shown a somehow opposite pattern of correlation between brain electrical activity and intelligence. For instance, Thatcher et al. [2008] demonstrated that the duration of phase shift and phase lock at the local level (i.e., between neighbor electrodes) could be predictive of IQ scores in children and adolescents, suggesting that the balancing between these two neurophysiological indices may be responsible for speed and efficiency of information processing. A replication of this evidence using voxel‐wise, high‐resolution local connectivity fMRI analysis could help integrate those findings with the results of the present study.

In our study, verbal, performance and full intelligence quotients significantly correlated with the E of connectivity matrices built using regions covering the 61–80% of overall connections (i.e., representing 21–40th percentile of weakest brain correlations), with E values leading to an 88.25% of correct classification between subjects with high and low‐average intelligence scores. From a neurobiological point of view, analyzing sparsity windows within the left tail of the correlation distribution may raise concerns about the real meaning of the magnitude and sign of these correlations, whose coefficients may be negative and confidence intervals may fall below zero. In this respect, it should be noted that the sparsity windows that gave rise to significant correlations in the current study were not the ones in the extreme left tail. In addition, confidence intervals for “r” were far from zero, which indicates that these correlations likely reflect physiologically meaningful, inter‐regional connections.

Furthermore, even though IQ scores correlated with brain overall global efficiency, the multivariate pattern of classification showed that a number of brain regions including the bilateral prefrontal lobes (mainly superior frontal gyri and anterior cingulate cortices), right hippocampus, temporal, and parietal lobes contributed to the discrimination of intellectual performance. This finding may be interpreted within the framework of the parietofrontal integration theory of intelligence [Jung and Haier, 2007], which received large experimental support using a number of imaging techniques, such as structural MRI [Narr et al., 2007], diffusion weighted MRI [Chiang et al., 2009] and task‐fMRI [Choi et al., 2008; Yuan et al., 2012]. In particular, the anterior cingulate cortex has been associated with intellectual functioning because of the positive correlation between its fractional anisotropy and intelligence [Chiang et al., 2009], and for structurally interconnecting the medial frontal lobes [van den Heuvel et al., 2008]. In this respect, our finding of an involvement of the prefrontal lobes bilaterally may suggest that an increase of information transfer between these regions and the rest of the brain plays a crucial role in higher‐order cognition [Negyessy et al., 2012]. Moreover, consistent with previous research [Gour et al., 2011; Maguire et al., 2000], the involvement of the hippocampus and temporal pole may be expression of their central role in memory, and an increase in their seed‐to‐brain information transfer may represent a preparatory process for evoked activity. The SVM analysis of the connectivity profile of these regions confirmed that their long‐range connections could discriminate between High‐G and Low‐G subjects with the highest accuracy and confidence, with an interesting pattern of connectivity linking the hippocampus to prefrontal regions. Finally, it must be noted that all regions identified for their intelligence‐dependant E modulation, except the postcentral gyrus, are part of the default mode network [Fox et al., 2005]. The interaction between the distribution of connectivity strength and resting‐state intrinsic networks, and the question as to whether their interplay determines the level of cognitive functioning, awaits further investigation [Yuan et al., 2012].

Interestingly, these observations narrow down the functional role that can be assigned to global spontaneous brain functioning, especially in terms of cognitive performance prediction. Our data suggest that 37% of variance in the full scale intelligence quotient can be predicted by taking into account the efficiency of a single portion of brain connectivity (i.e., weak brain connections), without focusing on the role of specific networks or regions. Compared to other studies based on evoked brain activity in specific regions [Cole et al., 2012; Song et al., 2008] or complex models integrating both functional responses and structural information [Choi et al., 2008], our data configure weak brain connections as a key neural substrate of intelligence, even when related to spontaneous hemodynamic fluctuations at rest.

Finally, even though the windowed approach applied here offers an interesting alternative point of view for the understanding of brain connectivity, it should be noted that our results were obtained through an averaging of brain dynamics occurring during the whole experimental acquisition time, and thus our findings are based on the assumption that brain activity is stable in time. In contrast, recent evidence has shown that different temporal and spatial patterns alternate in time, even during the resting state [Allen et al., 2012; Park et al., 2012]. These variations may be expression of cognitive properties like flexibility, vigilance and adaptive processes, making the analysis of such temporal variability within strong and weak connections a key point for future investigations. Furthermore, it should be noted that anatomical variability and traditional indices of brain functioning associated with intelligence such as speed of processing, working memory, and executive functions, may only represent endophenotypes for intelligence. In other words, they may be intermediate physiological markers that contribute to intelligence but that do not directly represent it. Therefore, considering the strong link between genetic factors and brain oscillations [Fornito et al., 2011; Glahn et al., 2010], models taking into account gene–intelligence interactions along the connectivity strength distribution are needed.

In summary, our results confirmed the primary role of distributed information processing as the brain feature that contribute most to the variability of human intellectual functioning. Most importantly, we demonstrated that this property reflects a two‐level connectivity structure composed of strong and weak brain connections, and that weak connections explained the largest portion of interindividual variance in IQ. This finding contributes to reinvigorate the debate about the relevance of weak connections in complex networks.

Supporting information

Supplementary Information Figure 1.