A framework for the design of flexible cross‐talk functions for spatial filtering of EEG/MEG data: DeFleCT

Abstract

Brain activation estimated from EEG and MEG data is the basis for a number of time‐series analyses. In these applications, it is essential to minimize “leakage” or “cross‐talk” of the estimates among brain areas. Here, we present a novel framework that allows the design of flexible cross‐talk functions (DeFleCT), combining three types of constraints: (1) full separation of multiple discrete brain sources, (2) minimization of contributions from other (distributed) brain sources, and (3) minimization of the contribution from measurement noise. Our framework allows the design of novel estimators by combining knowledge about discrete sources with constraints on distributed source activity and knowledge about noise covariance. These estimators will be useful in situations where assumptions about sources of interest need to be combined with uncertain information about additional sources that may contaminate the signal (e.g. distributed sources), and for which existing methods may not yield optimal solutions. We also show how existing estimators, such as maximum‐likelihood dipole estimation, L2 minimum‐norm estimation, and linearly‐constrained minimum variance as well as null‐beamformers, can be derived as special cases from this general formalism. The performance of the resulting estimators is demonstrated for the estimation of discrete sources and regions‐of‐interest in simulations of combined EEG/MEG data. Our framework will be useful for EEG/MEG studies applying time‐series analysis in source space as well as for the evaluation and comparison of linear estimators. Hum Brain Mapp 35:1642–1653, 2014. © 2013 Wiley Periodicals, Inc.

INTRODUCTION

Electro‐ and magnetoencephalography (EEG and MEG) provide neuroscientists with millisecond‐by‐millisecond measures of brain activation, while spatial resolution is inherently limited due to the non‐uniqueness of the inverse problem [Hämäläinen et al., 1984; Sarvas, 1994]. Many previous studies, in particular those using event‐related potentials (ERPs), have therefore mainly focused on timing aspects of perceptual and cognitive processes in signal space. However, separating time courses for distinct brain regions is still highly desirable. For example, in connectivity analysis it is essential to distinguish relationships between time series due to “leakage” or “cross‐talk” from those due to true activation of different sources [e.g. Lachaux et al., 2006; Michalareas et al., in press; Schoffelen and Gross, 2005]. Unless cross‐talk can be ruled out, it is not possible to infer with certainty that two (or more) time series from different regions are independent or correlated. This problem represents the fundamental ill‐posedness of the EEG/MEG inverse problem: there is not enough information in the data to estimate activity independently for more sources than there are degrees of freedom in the measurements [e.g. Bertero et al., 1985].

In a number of applications, spatial filters are applied to the data in order to extract the signal of interest (and conversely, to suppress the signals of no interest). The degree of leakage or cross‐talk between brain regions for spatial filters can be evaluated by means of cross‐talk functions (CTFs) (also previously called averaging kernels or resolution kernels) [Backus and Gilbert, 1968; Grave de Peralta Menendez et al., 1997; Liu et al., 1998; Schoffelen and Gross, 2005]. For a spatial filter designed to extract activity from one target location in the brain, a CTF describes how activity from other locations leaks into the estimate at the target location. In the theoretical part of this paper, we will describe a novel framework for incorporating three different types of constraints into the design of spatial filters:

1. Suppress cross‐talk within a small set of target locations or ROIs

2. Minimize cross‐talk from other locations anywhere in the brain

3. Minimize the effect of noise.

Several authors have already pointed out relationships among existing methods [Grave de Peralta Menendez et al., 1997; Gross and Ioannides, 1993; Hauk, 2011; Imada, 1999; Mosher et al., 2002; Sekihara et al., 2006; Wipf and Nagarajan, 2009]. However, to our knowledge none of these studies has used all three of the constraints presented above simultaneously. The combination of all three constraints opens the door for the design of novel spatial filters not previously described in the literature. These novel estimators may be particularly useful when a priori knowledge needs to be combined with more general constraints, as we will illustrate below.

Spatial resolution of linear estimates from EEG/MEG measurements is already limited by the fact that one cannot separate more sources than there are independent measurements, i.e. at most the number of sensors. In reality, the number of independent sources is far less. For example, the standard settings in the Neuromag Maxfilter software used in the preprocessing pipeline of Elekta Neuromag MEG systems include 64 signal components [Taulu and Simola, 1997].

Despite the limitations of the EEG/MEG inverse problem, we have some degrees of freedom for finding the optimal compromise of competing constraints, e.g. to extract activity from some regions of interest, while suppressing activity from other sources and noise. As an illustration, we may be interested in connectivity between anterior temporal lobe (ATL) and inferior frontal gyrus (IFG). We assume that both are active in our experiment and would therefore like to find a way to separate their activities. We cannot assume that they are the only sources of our signal, so we would also like to minimize the contribution of any other brain sources as much as possible. At the same time, we are sure that posterior temporal and parietal areas are the least likely to contribute to our signal. We may therefore want to improve separability between IFG and ATL at the expense of larger cross‐talk from posterior areas, while at the same time suppressing noise as much as possible.

The most straightforward way to separate activity from different regions of interest is to model activity only for these regions, for example by seeding dipole sources at the locations from where we assume activity to arise. Dipole strengths can then for example be estimated using a maximum‐likelihood approach [Lütkenhöner, 1989]. This means that the model tries to explain all data using only these sources. As long as the number of parameters of the resulting model is lower than the degrees of freedom of the measurements, the model is overdetermined and has a unique solution [Bertero et al., 1985; Scherg, 2009]. Such a model would have ideal properties if it fitted reality, but may fail completely if not—i.e. when it does not account for some sources that significantly contribute to the signal. In the example above, we may seed dipoles into the ATL and IFG, plus possibly other regions that we suspect to contribute to our signal. If, against our expectations, a source in the posterior temporal lobe also contributes to the signal, our estimates may be misleading.

A more general approach is taken by distributed source models [Fuchs et al., 1999; Grave de Peralta Menendez and Gonzalez Andino, 1998; Hämäläinen and Ilmoniemi, 2004; Michel et al., 2010]. In the least constrained case, they assume that sources are equally likely to be active anywhere in the brain, and attempt to find a source distribution that explains the data under further global constraints, such as that overall source strength is minimal according to some norm. For classical L2 minimum norm estimation (MNE) it can be shown that it does not only yield the source distribution with minimal source energy that accurately predicts the data, but also that it provides optimal spatial filters in the sense that the spatial spread of CTFs is minimized under the assumption that all sources are equally likely to be active [Backus and Gilbert, 1968; Grave de Peralta Menendez et al., 1997; Hauk, 2011; Menke, [Link]]. MNE optimizes the spread of CTFs under the assumption that activity could arise from anywhere—not only from a few regions of interest. In the example above, we may apply MNE to our data and then extract the signals from sources in ATL and IFG. We may even look at CTFs for different locations within ATL and IFG, and pick those that we think are maximally independent from each other. However, there is now no guarantee that sources in IFG can be sufficiently suppressed—the best may still not be good enough.

Beamformer‐type methods have become increasingly popular for time‐series analysis of MEG data [Barnes et al., 2006; Brookes et al., 2008; Sekihara et al., 2006; Van Veen et al., 2009]. They are usually introduced as spatial filtering methods that maximally focus on the activity of interest while separating it from other sources and noise. In this general form this is a feature of all linear source estimation procedures. The crucial assumption of the most commonly used linearly‐constrained minimum variance (LCMV) beamformer is that all activity is captured in the data covariance matrix [Van Veen et al., 2009]. Due to this dependency on the data beamformers are sometimes called “adaptive”: while minimum‐norm‐type methods only depend on the source and head model (except for regularization procedures that take into account noise covariance as well), beamformers crucially depend on the covariance matrix of the data to be analyzed. As with the above‐mentioned dipole models, this type of method has ideal properties as long as the underlying assumptions are met. It is not straightforward to test the assumptions about the data covariance matrix; determining the generators of the data covariance matrix is subject to the same inverse problem as determining the generators of the signal. In our ATL/IFG example, the general application strategy would be similar to minimum‐norm‐type methods: spatial filters are computed either for a priori selected locations, or for locations with maximum signal power. These CTFs will depend on the data covariance matrix, and there is no guarantee that they will be optimal for our particular purpose of separating ATL and IFG.

The purpose of this study is not to exhaustively compare and judge these different methods. Rather, we will provide a general framework that will make explicit under which assumptions different estimators are optimal. Moreover, we will provide tools to design novel spatial filters for situations that have so far not been covered by existing methods.

METHODS

Concepts and Terminology

In this section, we introduce the basic concepts needed for the design and interpretation of spatial filters. Bold small letters (w) refer to vectors, and matrices are indicated by capital bold letters (“F”). Superscripted “T” and “−1” (i.e. ^T and ⁻¹) denote vector or matrix transposition and inversion, respectively. In order to minimize the use of vector or matrix transpositions, some vectors will be introduced as column vectors (e.g. with dimension m × 1), and some as row vectors (1 × m).

The generators of EEG and MEG signals are commonly modeled as primary current density [Hämäläinen et al., 1984]. For most numerical implementations of source estimation methods, it is necessary or advantageous to discretize this continuous distribution into a limited number of homogeneously distributed point‐like dipoles (hundreds to thousands), e.g., at vertices of the triangulated cortical surface or in voxels of the brain volume. For each of these point sources, one can compute the signal at the m sensors that this source would produce if it were active with unit strength, resulting in the forward solution vector or lead vector f _i (m × 1, index i of n sources). In the following, we will also refer to this as topography of source i. The signal y (m × 1) produced by a continuous primary current distribution can then be approximated as the weighted sum of all individual lead vectors

$$\mathbf{y}=\sum _{i=1}^n{s}_i{\mathbf{f}}_i$$ (1)

where s _i are the strengths of the i sources. For simplicity, we do not distinguish between fixed and free orientations here: In the case of fixed orientations, n is the number of locations on the cortical surface; for free orientations, the sum may include 2 or 3 forward solutions at each location. Organizing all f _i vectors as columns of the forward solution matrix F (m × n, usually just called “forward solution” or “leadfield matrix”), one can formulate this equation in more compact form

$$\mathbf{y}=\mathbf{\text{Fs}},$$

i.e. y is a linear combination of the columns of F weighted by the elements of s (n × 1).

In EEG/MEG source estimation, we are given the data d (m × 1)1 that consist of activity from the brain as well as measurement noise n (m × 1):

$$\mathbf{d}=\mathbf{y}+\mathbf{n}=\mathbf{\text{Fs}}+\mathbf{n}.$$ (2)

Linear estimators, or linear spatial filters, attempt to produce estimates ${\stackrel{\wedge }{s}}_i$ of the source strengths $s_i$ by multiplying the data d (m × 1) with a vector w _i (1 × m):

$${\stackrel{\wedge }{s}}_i={\mathbf{w}}_i\mathbf{d}$$ (3)

This vector should ideally project only on the lead vector of the target source, and not at all on those of other sources or on noise. This would require w _i to be orthogonal to (n − 1) lead vectors, which is not possible when the number of modeled sources n is larger than the number of sensors (and dimension of ${\mathbf{w}}_i$) m (and in reality the degrees of freedom in the data are smaller than m). This fundamentally limits the spatial resolution of any source estimation technique. A combination of Eqs. (1)–(3) yields

$${\stackrel{\wedge }{s}}_i={\mathbf{w}}_i\mathbf{d}={\mathbf{w}}_i(\mathbf{y}+\mathbf{n})={\mathbf{w}}_i(\mathbf{\text{Fs}}+\mathbf{n})={\mathbf{w}}_i\sum _{j=1}^n{s}_j{\mathbf{f}}_j+{\mathbf{w}}_i\mathbf{n}=\sum _{j=1}^n{s}_j({\mathbf{w}}_i{\mathbf{f}}_j)+{\mathbf{w}}_i\mathbf{n},$$ (4)

meaning that an estimated source strength is the sum of weighted projections of the spatial filter on all lead vectors, and its projection on the noise.

If the spatial filter w _i cannot be orthogonal to all columns of the lead field matrix F, this means that some sources of no interest may “leak” into the estimate of the source of interest. If we can be sure that those sources that could leak into our estimate are not active in our experiment, this is not a problem. However, this information cannot come from the data, but has to be established a priori. If we do not have this information, we would like to find ways to minimize contributions from sources of no interest and noise as much as possible. The effect of all sources on our estimate can be described by the “cross‐talk function” (CTF), i.e. by applying our spatial filter w _i to all vectors in the forward solution matrix F:

$${\mathbf{\text{CTF}}}_i={\mathbf{w}}_i\mathbf{F},$$

where CTF _i (1xn) describes how much sources represented by each lead vector (or column of F) leak into the estimate for source i, i.e., Eq. (4) can be written as

$${\stackrel{\wedge }{s}}_i=\sum _{j=1}^n{s}_j{\mathbf{\text{CTF}}}_{\mathrm{ij}}+{\mathbf{w}}_i\mathbf{n}.$$ (5)

In the noiseless case, the estimate ${\stackrel{\wedge }{s}}_i$ is therefore a weighted sum of the real source strengths s, where the weightings are given by the CTF. For the original case of continuous functions it was therefore called “averaging kernel” [Backus and Gilbert, 1968].

The CTF can also be expressed as

$${\mathbf{\text{CTF}}}_i={\mathbf{w}}_i\mathbf{F}=\sum _{j=1}^m{w}_{\mathrm{ij}}{\mathbf{F}}_{j.},$$ (6)

which shows that the CTF is a weighted sum of the rows of the forward solution F, i.e. the leadfields of individual sensors. This imposes a fundamental constraint on the type of CTFs we can achieve for any linear estimator or spatial filter. It also indicates why adding more sensors, especially from different sensor types, can improve spatial resolution: The more leadfield vectors there are in Eq. (5), and the more mutually independent they are, the more flexibility there is for designing the shape of a CTF. However, adding more sensors that add only little independent information (e.g. more electrodes to an already dense electrode array) may only have very minor effects on resolution.

So far, we have only referred to one spatial filter w _i for one target source. We can of course compute spatial filters for all target sources, i.e. for indices i between 1 and n. These can be arranged as rows of an inverse operator matrix G (n × m), such that the estimates for all sources ${\stackrel{\wedge }{s}}_i$ can be computed as a vector:

$$\stackrel{\wedge }{\mathbf{s}}=\mathbf{\text{Gd}}=\mathbf{G}(\mathbf{y}+\mathbf{n})=\mathbf{\text{GFs}}+\mathbf{\text{Gn}}=\mathbf{\text{Rs}}+\mathbf{\text{Gn}}.$$ (7)

The matrix $\mathbf{R}=\mathbf{\text{GF}}$ (n × n) is the “resolution matrix” which describes the relationship between the real sources s and the estimated sources $\stackrel{\wedge }{\mathbf{s}}$ in the absence of noise [Grave de Peralta Menendez et al., 1997; Hauk, 2011; Liu et al., 1998; Menke, [Link]]. The rows of R are the CTFs. The columns of R are the “point‐spread functions” (PSFs) that describe how the estimate of the activity of a point source with unit strength is spread across all other sources.

An interesting special case is the L2 minimum‐norm estimate

$${\mathbf{G}}_{\text{MNE}}={\mathbf{F}}^T({\mathbf{\text{FF}}}^T+{\lambda }^2\mathbf{C}){}^{-1},$$ (8)

where ${\lambda }^2\mathbf{C}$ is a regularization term that will be explained in more detail later. Its resolution matrix is

$${\mathbf{R}}_{\text{MN}E}={\mathbf{G}}_{\text{MNE}}\mathbf{F}={\mathbf{F}}^T({\mathbf{\text{FF}}}^T+\lambda \mathbf{C}){}^{-1}\mathbf{F}.$$ (9)

This matrix is symmetric (given that C is symmetric), meaning that, for MNE, CTFs and PSFs for a source i are identical.

Noise normalization procedures have been suggested to improve localization accuracy of MNE estimators [Dale et al., 2000; Lin et al., 2002; Pascual‐Marqui, 2008]. Their general principle is to weight the MNE inverse operator matrix with a diagonal matrix that transforms the corresponding solution into signal‐to‐noise ratios, i.e.

$${\mathbf{G}}_{\mathrm{N}}={\mathbf{\text{WG}}}_{\text{MNE}},$$ (10)

where W is an n × n diagonal matrix that contains noise‐based correction factors for each source. This changes the resolution matrix to

$${\mathbf{R}}_{\mathrm{N}}={\mathbf{G}}_{\mathrm{N}}\mathbf{F}={\mathbf{\text{WG}}}_{\text{MNE}}\mathbf{F}={\mathbf{\text{WR}}}_{\text{MNE}}.$$ (11)

Because W is diagonal, each row of ${\mathbf{R}}_{\text{MNE}}$—i.e., each CTF—is just multiplied by one element of the diagonal of W. This only affects the CTFs' overall amplitude, but not their shapes. For PSFs, however, it can affect amplitude as well as shape [Hauk et al., 2010]. This means that noise normalization procedures such as dSPM or sLORETA have the same leakage or cross‐talk as the non‐normalized MNE.

The effect of leadfield weightings (e.g. depth weighting [Lin et al., 2002]) on CTFs is not straightforward to predict. These approaches have so far mainly been evaluated using point‐spread functions, but since the corresponding resolution matrices are not necessarily symmetric, the results may not generalize to CTFs. A detailed comparison of these approaches is beyond the scope of this paper.

Designing Optimal Spatial Filters

Here, we introduce a general framework for the design of optimal CTFs under three different constraints. We are looking for a linear estimator w (1 × m, m = number of sensors; we omit the subscript index i in the following) that fulfills the following constraints:

1. Discrete Source Constraint: We would like to separate activity of the target source from that of a few a priori selected sources. Thus, we would like to make sure that the projection on several topographies is exactly predicted:

   $$\mathbf{\text{wP}}=\mathbf{i},$$ (12)

   where P is a m × p matrix with p horizontally concatenated forward solutions, and i a target vector (1 × p). Choosing i to contain the value 1 in one element (the target) and 0 in all others would correspond to complete separation of the target source from the other sources. The topographies in P can for example be obtained for isolated dipole sources, regions‐of‐interest, or from the measured data.
2. Distributed Source Constraint: Any other brain sources should contribute to the estimate as little as possible. This can be achieved through the following minimization constraint:

   $$\text{min}\Vert \mathbf{\text{wF}}-\mathbf{t}\Vert {}^2=(\mathbf{\text{wF}}-\mathbf{t}){(\mathbf{\text{wF}}-\mathbf{t})}^T$$ (13)

   with F as leadfield matrix (m × n) and t (1×n) as a target vector in source space. This constraint expresses that we wish the CTF to be as close as possible in the least‐squares sense to the desired target t. For example, t may contain the value 1 in a target location and 0 everywhere else.
3. Noise Constraint: Noise should affect our estimate as little as possible. This results in the following minimization constraint:

   $$\text{min}\left({\mathbf{\text{wCw}}}^T\right),$$ (14)

   where C (m × m) is a covariance matrix that should contain all sources that are to be suppressed, for example estimated from pre‐stimulus baseline intervals.

Constraint 1) should be fulfilled exactly. 2) and 3) are both minimization constraints, and can be combined into one constraint by introducing a regularization parameter ${\lambda }^2$:

$$\begin{array}{c}\multicolumn{1}{c}{\text{min}((\mathbf{\text{wF}}-\mathbf{t}){}^2+{\lambda }^2{\mathbf{\text{wCw}}}^T)\Rightarrow \text{min}({\mathbf{\text{wSw}}}^T-2{\mathbf{\text{wFt}}}^T)\text{with}\hspace{1em}\mathbf{S}={\mathbf{\text{FF}}}^T+{\lambda }^2\mathbf{C}}\end{array}$$ (15)

The exact constraint (1) under the minimization constraint [Eq. (14)] can be solved using the method of Lagrange multipliers [see Appendix, and e.g. Menke, [Link]]:

$$\mathbf{w}=({\mathbf{\text{tF}}}^T+(\mathbf{i}-{\mathbf{\text{tF}}}^T{\mathbf{S}}^{-1}\mathbf{P})({\mathbf{P}}^T{\mathbf{S}}^{-1}\mathbf{P}){}^{-1}{\mathbf{P}}^T){\mathbf{S}}^{-1}$$ (16)

with S as above.

In the literature on spatial filtering, it is common to use the term “pass‐band” for signals from sources of interest (i.e. whose signal is supposed to pass the spatial filter), and “stop‐band” for signals that should be suppressed (i.e. they should be stopped by the spatial filter) [e.g. Van Veen et al., 2009]. In our framework, choices of i and t (and in particular where they are zero and non‐zero) reflect which signals are classified as pass‐band or stop‐band. In experimental work, these choices should be justified by sound a priori knowledge about the neuronal generators.

Generalizations

Any weighting that is applied to the data before source estimation also needs to be applied to the projection matrix P, the leadfield matrix F and the covariance matrix C: if the data are transformed by $\tilde{\mathbf{d}}={\mathbf{W}}_d\mathbf{d}$, then P and F should be replaced by $\tilde{\mathbf{F}}={\mathbf{W}}_d\mathbf{F}$ and $\tilde{\mathbf{P}}={\mathbf{W}}_d\mathbf{P}$, respectively. This may be necessary, for example, when combining different sensors types such as gradiometers, magnetometers and EEG using pre‐whitening [Fuchs et al., 1998; Molins et al., 2003].

It is also possible to add a weighting matrix D to Eq. (12), such that $\text{min}\Vert \mathbf{\text{wF}}-\mathbf{t}\Vert {}^2=(\mathbf{\text{wF}}-\mathbf{t})\mathbf{D}{(\mathbf{\text{wF}}-\mathbf{t})}^T$. Contributions from different parts of the source space can then be penalized differently. This changes Eq. (14) to

$$\text{min}({\mathbf{\text{wSw}}}^T-2{\mathbf{\text{wFDt}}}^T)\hspace{1em}\text{with}\hspace{1em}\mathbf{S}={\mathbf{\text{FDF}}}^T+{\lambda }^2\mathbf{C}$$

that can be solved in the same way using Lagrange multipliers. For simplicity, we did not use the weighting matrix D in our simulations.

Special Cases

In this section, we present three special cases derived from Eq. (15): 1) maximum‐likelihood estimates for fixed dipole models, 2) L2 minimum‐norm estimates, and 3) linearly constrained minimum‐variance (LCMV) beamformers.

1. We assume that the only sources that contribute to our signal are captured in Eq. (11) (discrete sources constraint), i.e. their forward solutions are arranged as columns in the matrix P. Therefore, we ignore the source space constraint by setting F and t to zero. i at this point can be arbitrary but non‐zero. In addition, we want to suppress noise, as specified in Eq. (3). Equation (15) then simplifies to

   $$\mathbf{w}=\mathbf{i}{\left({\mathbf{P}}^T{\mathbf{C}}_N^{-1}\mathbf{P}\right)}^{-1}{\mathbf{P}}^T{\mathbf{C}}_N^{-1},$$ (17)

   where ${\mathbf{C}}_{{}^N}$ is the noise covariance matrix. The expression following i is the maximum likelihood estimate for a fixed dipole model. Note that this expression without i provides the matrix for all sources in the model. Multiplying it with i provides a spatial filter for the target source. For example, if we want to fully separate a target source from other sources in P, and therefore define a target vector i that includes only zeros, and the value 1 only for the target source, then w is just one row of the maximum likelihood estimate for all sources ${\left({\mathbf{P}}^T{\mathbf{C}}^{-1}\mathbf{P}\right)}^{-1}{\mathbf{P}}^T{\mathbf{C}}^{-1}$. Furthermore, note that if P only contains one column, e.g. the forward solution of one target source F _.j, then the resulting estimator is

   $$\mathbf{w}=({\mathbf{F}}_{.j}^T{\mathbf{C}}_N^{-1}{\mathbf{F}}_{.j}){}^{-1}{\mathbf{F}}_{.j}^T{\mathbf{C}}_N^{-1}=\frac{{\mathbf{F}}_{.j}^T{\mathbf{C}}_N^{-1}}{{\mathbf{F}}_{.j}^T{\mathbf{C}}_N^{-1}{\mathbf{F}}_{.j}},$$ (18)
2. We assume that all sources are equally likely to contribute to the signal. We do not have a specific discrete source constraint, but for each target source, we would like to minimize the contribution from all other sources as much as possible. In the distributed source constraint [Eq. (12)], let the target be the source that corresponds to the jth column of the forward solution matrix F, i.e. F _.j. Equation (11) can be used as a normalization constraint, for example requiring ${\mathbf{\text{wF}}}_{.j}=1$, i.e. i = 1 and $\mathbf{P}={\mathbf{F}}_{.j}$. The ideal CTF in this case would contain zeroes everywhere except at the location of the target source, i.e. $t_k=0\hspace{1em}\text{for}\hspace{1em}\text{all}\hspace{1em}\mathrm{k}\hspace{1em}\ne \mathrm{j}\mathrm{,}\hspace{1em}{t}_k=1\hspace{1em}\text{for}\hspace{1em}k=j.$ We would also like to minimize the effect of noise on our estimate, as in Eq. (13). Noting that in this case ${\mathbf{\text{tF}}}^T={\mathbf{F}}_{.j}^T$, we find that Eq. (15) simplifies to

   $$\begin{array}{c}\multicolumn{1}{c}{\mathbf{w}=({\mathbf{\text{tF}}}^T+(\mathbf{i}-{\mathbf{\text{tF}}}^T{\mathbf{S}}^{-1}\mathbf{P})({\mathbf{P}}^T{\mathbf{S}}^{-1}\mathbf{P}){}^{-1}{\mathbf{P}}^T){\mathbf{S}}^{-1}=({\mathbf{F}}_{.j}^T+(1-{\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}{\mathbf{F}}_{.j})({\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}{\mathbf{F}}_{.j}){}^{-1}{\mathbf{F}}_{.j}^T){\mathbf{S}}^{-1}={\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}+({\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}{\mathbf{F}}_{.j}){}^{-1}{\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}-({\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}{\mathbf{F}}_{.j})({\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}{\mathbf{F}}_{.j}){}^{-1}{\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}=({\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}{\mathbf{F}}_{.j}){}^{-1}{\mathbf{F}}_{.j}^T{\mathbf{S}}^{-1}=\frac{{\mathbf{F}}_{.j}^T({\mathbf{\text{FF}}}^T+\lambda {\mathbf{C}}_N){}^{-1}}{{\mathbf{F}}_{.j}^T({\mathbf{\text{FF}}}^T+\lambda {\mathbf{C}}_N){}^{-1}{\mathbf{F}}_{.j}}(17)}\end{array}$$ (19)

   The nominator of this solution is the L2 minimum norm estimate for source index j. The denominator is a result of our initial normalization constraint i = 1. Note that this normalization only affects the amplitude, but not the shape of CTFs.

3. Assume that we neither have a specific discrete source nor distributed source constraint, but we assume that all sources contributing to our signal are captured in the data covariance matrix ${\mathbf{C}}_D$. We want a spatial filter that projects on a source of interest, e.g. column j of our lead field matrix F, i.e. F _.j, while at the same time minimizing its projection on the data covariance matrix, which contains contributions from the source of interest, other to‐be‐suppressed brain sources as well as noise. In this case, we can choose i = 1 and $\mathbf{P}={\mathbf{F}}_{.j}$ as before, ignore the distributed source constraint by setting t and F to zero, and use the data covariance matrix ${\mathbf{C}}_D$ as the noise constraint. We then obtain

   $$\begin{array}{c}\multicolumn{1}{c}{\mathbf{w}=(({\mathbf{F}}_{.j}^T{\mathbf{C}}_D^{-1}{\mathbf{F}}_{.j}){}^{-1}{\mathbf{F}}_{.j}^T){\mathbf{C}}_D^{-1}=\frac{{\mathbf{F}}_{.j}^T{\mathbf{C}}_D^{-1}}{{\mathbf{F}}_{.j}^T{\mathbf{C}}_D^{-1}{\mathbf{F}}_{.j}}}\end{array}$$ (20)

   which is the linearly constrained minimum variance beamformer [Van Veen et al., 2009]. The success of this estimator depends on whether the data covariance captures all sources that may be simultaneously active with the source of interest. Note that this expression is formally identical to the maximum likelihood estimator for a single dipole source in Eq. (16b), except that matrix C is the data covariance matrix in one case and the noise covariance matrix in the other.

In a more specific case, we may want to apply the above constraint, while at the same time completely suppress the activity from a separate source. In this case, we can add the topography of the to‐be‐suppressed source as a column to matrix P, and choose vector i = [1, 0]. The resulting spatial filter will have zero projection on the to‐be‐suppressed topography. This is the principle of the “null‐beamformer” [Mohseni et al., 2008] or “multiple constrained minimum‐variance beamformer with coherent source region suppression (LCMV‐CSRS)” [Popescu et al., 1987]. Some authors have used more than one to‐be‐suppressed components, e.g. from a singular‐value decomposition of the leadfield for a region‐of‐interest [Dalal et al., 2006; Popescu et al., 1987]. However, these approaches have not made use of the “distributed source constraint” in our framework.

Regions Versus Locations

In many situations, especially in experiments on higher cognitive functions, we are interested in “regions” of interest (ROIs) rather than “locations” of interest: We expect activity extended over a larger brain area (e.g. anterior temporal lobe), rather than a point source at a specific location with a specific orientation. Our framework allows handling this problem flexibly: One may represent each ROI by one or more topographies in the projection matrix P, e.g., from a singular value analysis of all forward solutions within an ROI. In other words, we can take the sub‐matrix of the leadfield matrix F that contains all forward solutions of an ROI, and reduce it to one or a few of its principal components. A similar approach has been used in Dalal et al. [2006] and Popescu et al. [1987]. Visualization of the corresponding CTFs will inform us to what degree activity from particular ROIs is either extracted or suppressed.

SIMULATIONS

In this section, we illustrate the use and performance of our framework with three simulated examples. We would especially like to demonstrate the flexibility of linear estimation techniques in designing estimators that are tailor‐made for a specific purpose. The examples are built in proof‐of‐concept manner; the aim is to both illustrate the concepts used in the framework and propose novel ways for building inverse estimators.

In our first example, we illustrate the crosstalk of minimum‐norm (MN) estimates between sources in ATL and IFG regions and demonstrate the benefit of adding the stop‐band constraint of our framework. In the second example, we build a more complex spatial filter that focuses on one region while suppressing some crosstalk from multiple other regions. Finally, in the third example, we illustrate a case, in which the desired CTF cannot be obtained due to the inherent ill‐posedness of the inverse problem.

All simulations were carried out using the sample dataset of MNE software (http://www.martinos.org/mne/) that comprises anatomical MR images obtained with an MPRAGE sequence, reconstructed cortical surfaces and boundary surfaces for the skull and scalp, and MEG/EEG data acquired with an Elekta Neuromag Vectorview system (306 MEG sensors and 60 EEG sensors). The forward model F and noise covariance matrix C were built with MNE tools as described in the MNE manual: The source space was defined by tessellating the cortical surface into two meshes with a total of 8192 vertices. The MR set and boundary surfaces were semiautomatically co‐registered with the sensors. The surfaces of skull and scalp were tessellated with 2562 vertices per surface, and a 3‐shell boundary‐element model was built. At each vertex of the source space, a dipole oriented normally with respect to the cortical surface was placed, and for these dipoles, a lead field matrix F for MEG and EEG sensors was constructed. The noise covariance matrix C was assembled from pre‐stimulus data. The cortical source meshes, F, and C were then imported to Matlab, where all further processing was carried out. In all examples, combined EEG + MEG data were used; the combining of different sensor types was done by pre‐whitening the lead fields with the matrix C ^−1/2 [Fuchs et al., 1998].

In all examples, we have used regions‐of‐interest (ROIs) for setting either the target of the filter (pass‐band) or the region from which the crosstalk is to be suppressed (stop‐band). Compared with model optimization using lead‐fields of individual vertices, the ROI approach adds model realism for cases where brain activation must be assumed to be spatially extended. It is important to note that whenever brain activation is averaged (or otherwise combined) across vertices within an ROI, the CTF for this average is the average of the individual CTFs. Analyzing ROIs instead of individual vertices can therefore make the problem of cross‐talk or leakage worse. Our framework can take this into account, as we will explain below.

The ROIs were defined with the help of a graphical user interface: the cortical (source) mesh was visualized, and the vertices in a region were selected using the mouse pointer. After defining the ROI, the lead‐vectors corresponding to the sources in the ROI could, in principle, be directly used for defining the signal‐space constraint matrix P of Eq. (11). Depending on the size and shape of the ROI, the forward solutions for different vertices are correlated with each other to some degree (e.g., forward solution for vertices on opposite walls of a sulcus will have a strong negative correlation). In order to efficiently reduce the number of components in matrix P, while still allowing for variability within the ROI, we applied standard singular‐value‐decomposition (SVD) to P and selected the most dominant singular vectors which explained a large amount of variance for the ROI. Note that this does not affect the interpretation of the estimator—the resulting CTF is all that matters for its application to data.

Combining Discrete and Distributed Source Constraints

This example addresses the case already discussed in the Introduction. We assume that there is activity in both anterior temporal lobe (ATL) and inferior frontal gyrus (IFG), and we would like to separate them from each other. In Figure 1a, the CTF of the MN estimator for a source at vertex i in ATL is shown (indicated by blue dot). Most of the contribution to the estimate comes from the ATL region (indicated by cloud of black dots), as intended. However, there is also considerable leakage from the inferior frontal gyrus (cloud of white dots), which we would like to suppress.

Figure 1.

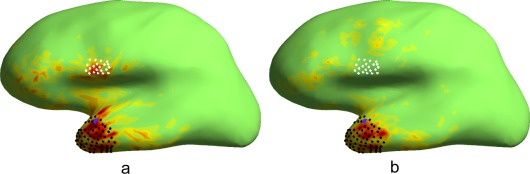
Cross‐talk functions (CTFs) for two different spatial filters aimed at extracting signals from anterior temporal lobe (ATL) while suppressing signals from inferior frontal gyrus (IFG). a) CTF for a classical minimum norm estimator (i.e. using the distributed source constraint) created for a target source (blue dot) in ATL. The CTF has largest amplitudes in ATL as desired. However, it also shows leakage from more distant locations, such as IFG. The area with largest leakage is indicated by a cloud of white dots. b) CTF for a novel estimator, derived by combining the distributed source constraint of a) with a discrete source constraint for IFG. The estimator was designed to optimally project on signals from the target location (blue dot), to suppress leakage from the IFG region (white dots), and to minimize leakage from all other brain areas. This had the intended effect that leakage from inferior frontal areas is reduced. Both images are presented with the same color scale.

In order to suppress the leakage from IFG, we use the discrete source constraint of Eq. (11) by setting the projection of w on the six first SVD components in the IFG region to zero. In addition, we use the distributed‐source and noise constraints as in the derivation of the MN estimator, targeting at vertex i and minimizing the contribution of noise. The CTF of the resulting spatial filter is visualized in Figure 1b. Leakage from IFG is now significantly suppressed. In addition, overall leakage from superior temporal lobe and middle frontal lobe has decreased as well, while leakage from pre‐central cortex has slightly increased.

Spatial Filters for Regions‐of‐Interest

In this example, we illustrate how spatial filters can be focused to a certain region of interest. Assume we are interested in signals from the tip of the occipital lobe (“V1”), independently from higher‐level object vision areas in the left occipital (LO) cortex. Therefore, we would like to focus the estimator on the tip of V1 while suppressing leakage from LO and surrounding areas. In Figure 2a, we present the CTF of the MN estimator for the tip of V1, computed as the sum of CTFs for the vertices in the region. It still contains contributions from surrounding areas, e.g. around the black and white dots, that we would like to suppress. We therefore designed a spatial filter on the target region using the following criteria:

1. Discrete source constraint for the pass‐band: the projection of w on the first SVD component of lead vectors from the target region (marked with blue points) was forced to one, in order to make sure the estimator is focused on our target ROI.

2. Discrete source constraint for the stop‐band: the projection of w on lead vectors of a set of sources with high crosstalk in the MN estimator (sources in the LO marked with white points, other sources with black points) was forced to zero, in order to explicitly suppress signals from sources that we assume may be active, but would confound the result of our estimate.

3. Distributed‐source and noise constraints: the filter response to all sources and noise was minimized according to Eq. (14) with t set to zero, in order to minimize the leakage from all other possibly active sources and noise.

Figure 2.

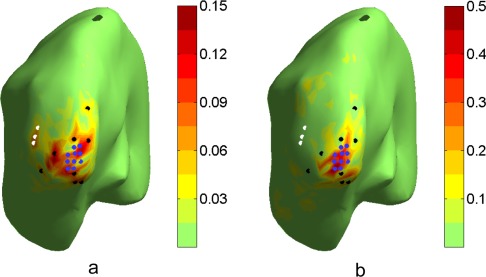
CTFs for two spatial filters aimed at extracting activity from the tip of the occipital lobe (“V1,” blue dots), while suppressing leakage from surrounding higher‐level visual areas. a) CTF for a classical minimum norm estimator (i.e. using the distributed source constraint) created for an ROI (blue dots) around V1. The CTF is centered around V1, but shows leakage from several areas outside the target ROI (e.g. around the black dots, and with a clear peak at some distance highlighted by white dots). b) CTF for a novel estimator, which combined the distributed source constraint with the discrete source constraint. The estimator was designed to optimally project on signals from the ROI around V1 (blue dots), while explicitly suppressing leakage from surrounding areas (black and white dots). The resulting CTF is more focused around V1, as intended.

The CTF of the resulting spatial filter is shown in Figure 2b. The filter is better focused around the V1 tip than the previous estimator (Fig. 2a). Leakage from the LO is clearly suppressed, and leakage from the vertices marked in black is zero. Some new leakage is introduced for example at locations inferior to the ROI, and with lower amplitude at larger distances.

Cross‐Talk Suppression Gone Wrong

The flexible design of cross‐talk functions is obviously only possible within general resolution limits of EEG/MEG measurements. In the last example, we therefore illustrate that our framework cannot circumvent the inherent ill‐posedness of the inverse problem: if there are active sources with highly correlated forward solutions, it may be impossible to satisfyingly distinguish between the activities arising in these regions.

In the previous example, some increased leakage was introduced close to the target region. In Figure 3a, the resulting CTF of the previous example is shown, rotated and zoomed in closer to the tip of V1. Below the target region (marked with blue dots) the CTF shows two peaks (green dots), which ideally we would like to remove, using exactly the same method as in the previous example. In this case, we therefore added two new lead vectors (marked with green dots) to the discrete‐source constraint of the stop‐band. The CTF of the resulting filter is shown in Figure 3b. The estimator is now sensitive to large regions outside the target area, and overall the CTF is very patchy. Clearly, the filter is not focused at the tip of V1 anymore. This highlights the importance of visualizing and evaluating CTFs for specific estimators.

Figure 3.

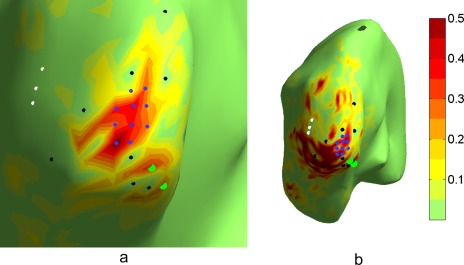
Illustration of a case where leakage suppression has been unsuccessful. a) The CTF optimized for V1 as in Figure 2b, zoomed closer into V1. White and black dots indicate areas for which leakage was supposed to be suppressed; b) novel estimator, which in addition to a) also attempts to suppress leakage from two locations close to V1 (light green dots). Although the imposed constraints are fulfilled (see CTF values in the direct vicinity of white, black and green dots), the CTF is very widespread and patchy, and not focused around V1 as desired.

A likely explanation for the failure to design a satisfying estimator in this case is that the correlation coefficients between the pass‐band vector and the new suppression points are −0.96 and 0.85, while the corresponding (absolute values of) correlations for the original suppression points were between 0.1 and 0.46. This means that topographies in the stop‐band and pass‐band are very similar, and trying to fully separate them leads to a spatial filter with large spatial variation among sensors.

DISCUSSION

We presented a new framework for the design of flexible cross‐talk functions (DeFleCT). In contrast to existing spatial filtering methods, the framework allows the combination of constraints for multiple discrete as well as distributed sources and noise, and comprises several existing spatial filtering methods as special cases (minimum norm estimation, maximum likelihood dipole strength estimation, linearly‐constrained minimum variance beamformer, and null‐beamformer). Importantly, it allows the design of novel spatial filters where specific a priori information needs to be combined with more general constraints. This was demonstrated in simulations using a realistic head model and a combined EEG/MEG measurement configuration.

CTFs describe the effect of all sources in the model (e.g. distributed across the cortical surface) on the output of a spatial filter [Backus and Gilbert, 1968; Grave de Peralta Menendez et al., 1997; Liu et al., 1998; Menke, [Link]]. Spatial resolution of EEG/MEG depends on a number of variables such as source location, depth, and orientation [Fuchs et al., 1999; Grave de Peralta‐Menendez and Gonzalez‐Andino, 1998; Hauk et al., 2010; Molins et al., 2003]. In our view, no matter which method was used to create a spatial filter, evaluating spatial resolution by means of CTFs for individual measurement configurations and specific purposes is the key for avoiding misinterpretation of results. However, inspection of CTFs for existing methods may reveal that they are not suitable for a particular purpose, e.g. that there is leakage among brain areas that are supposed to be separated in the analysis. In this case, we may want to change the properties of our spatial filter based on further a priori knowledge, e.g. minimizing leakage from some areas while allowing more leakage from areas that we consider the least likely to contribute to the signal. Our novel approach enables us to do this, as we illustrated in our simulations.

It is important to note that designing spatial filters with associated CTFs for a specific purpose is not biased or circular. By designing a CTF with specific properties we make our assumptions explicit (e.g. about where we do or do not expect activation), and the CTF tells us objectively which sources may or may not contribute to our result. In contrast, focusing on point‐spread functions (PSFs) and determining that an inverse estimator produces a peak at the correct location when the true source is at this location is not very informative, because it does not tell us whether other sources (or combinations of sources) may be mislocalized to this location [Grave De Peralta Menendez et al., in press].

The concept of CTFs is, in principle, independent from the methods used to derive a spatial filter. A spatial filter may have been designed for the purpose of estimating the strength of one source under the assumption that there are no other active sources (as in maximum likelihood dipole estimation). One can still ask, looking at the CTF, how other sources would project on this estimate if they were active. There is a fundamental difference between the case in which we assume there only is one source, and the case in which we are only interested in one particular source, while other (potentially unknown) sources may still contribute to the signal. If we design a spatial filter for the former case, we should not be surprised if its CTF is not satisfactory for the latter. A priori assumptions do not change the fundamental physical limitations of our measurements—our belief that there is no source in IFG does not change the fact that if there were, it would still project on the estimate for activation in ATL. If we think CTFs are relevant for the interpretation of our spatial filter, then we admit that we are expecting multiple or distributed sources. In such a case, the design of a spatial filter should already take these cases into account. Our novel approach allows a large range of constraints to be implemented.

As has been pointed out previously, normalization procedures that have previously been suggested to improve localization properties of minimum norm estimates (e.g. dSPM [Dale et al., 2000] or sLORETA [Pascual‐Marqui, 2008]) do not affect the shape of CTFs [Hauk et al., 2010]. For example, the correlation between time courses extracted for different dipole sources should be the same for any of these methods (although in practice some differences may occur due to different regularization criteria). These methods are therefore not providing the flexibility with respect to CTFs as the approach introduced here. In our simulation section, we also presented an approach that deals with spatially extended ROIs rather than isolated dipolar sources, similar to previous studies [Dalal et al., 2006; Popescu et al., 1987]. Topographies for sources at different voxels or vertices within an ROI can vary substantially depending on location and orientation. Representing an ROI by means of principal components of the corresponding subsection of the leadfield provides a principled way of dealing with this problem.

There are still physical limits as to what can be achieved with EEG/MEG measurements, which we demonstrated in our final simulation example. CTFs are necessarily linear combinations of the rows of the leadfield matrix [Backus and Gilbert, 1968; Grave de Peralta Menendez et al., 1997; Menke, [Link]]. The row of the leadfield matrix associated with one sensor is its sensitivity profile with respect to sources of unit strength at each source location (vertices or voxels). A CTF that cannot be described as a linear superposition of these distributions cannot be designed with any method. Therefore, the more leadfields (i.e. the more sensors) there are, the better our chances to at least approach the ideal CTF. Furthermore, the more independent the leadfields are, the more likely we are to achieve a wide range of CTF shapes. Therefore, different sensor types (e.g. gradiometers, magnetometers, EEG electrodes) with independent or orthogonal leadfields are advantageous. However, there will still be limits to what can be achieved, no matter how many sensors or sensor types we use.

We did not systematically investigate the influence of noise on spatial filters in the present study. All common linear estimation methods incorporate noise in a similar way: the projection of the spatial filter on the noise covariance matrix is minimized. The trade‐off between noise‐sensitivity and spatial resolution is well‐documented [Backus and Gilbert, 1968], and common to all linear estimators [e.g. Bertero et al., 1988]. As a general rule, we can assume that the more emphasis we put on noise suppression, the more we have to sacrifice with respect to spatial resolution.

In order to allow generalizable conclusions, method comparisons must specify the purpose for which the methods are selected, such as the estimation of a single active source, or a source of interest in the presence of other possibly active sources. Therefore, illustrations of results from real data may not be informative for purposes of method comparisons. The fact that one method works well with one particular data set does not mean that it will work well with other data sets, where source distributions or noise structure may be different. We therefore need a framework that demonstrates whether methods are designed for similar or different purposes. Our framework fulfills this requirement.

The fact that several existing methods fall out of our framework under different starting assumptions shows that one can only find the “best” spatial filter for a clearly specified purpose. The methods should follow the assumptions, not vice versa. For example, if we expect leakage from all brain locations with equal probability, then the MN estimator provides an optimal CTF, with minimal cross‐talk across all sources. If we know that our signal is produced by only a few dominant sources (dipoles or ROIs), then the maximum likelihood estimator provides zero cross‐talk from the specified sources. In our framework, an LCMV beamformer can be interpreted as a spatial filter that attempts filtering out the signal from one source (or ROI), while suppressing all other sources that contribute to the data covariance matrix. From this, it follows the well‐known finding that beamformers perform best for uncorrelated sources. Furthermore, they assume that all sources that contribute to the signal are captured in the data covariance matrix. This assumption may be difficult to justify in the case of evoked responses, where the sources of interest may be short‐lived (e.g. tens of milliseconds), while the covariance matrix is computed for intervals of several hundreds of milliseconds or more. A more detailed comparison of different estimators must be left for future studies.

We hope that our approach will prove useful both for the evaluation and comparison of methods, as well as for EEG/MEG studies applying time‐series analysis in source space.

LAGRANGE MULTIPLIERS

The method of Lagrange multipliers is a standard techniques for solving linear optimization problems [e.g. Aster et al., 2011; Menke, [Link]]. In our framework, the problem is to find the linear estimator w that fulfills

$$\mathbf{\text{wP}}=\mathbf{i}$$ (21)

under the minimization constraint of Eq. (14)

$$\text{min}({\mathbf{\text{wSw}}}^T-2{\mathbf{\text{wFt}}}^T).$$

First, one defines the Lagrange function:

$$\Lambda (\mathbf{w})={\mathbf{\text{wSw}}}^T-2{\mathbf{\text{wFt}}}^T+\alpha ({\mathbf{P}}^T{\mathbf{w}}^T-{\mathbf{i}}^T).$$

The derivative of this function with respect to w is:

$$\frac{d\Lambda (\mathbf{w})}{d\mathbf{w}}=2\mathbf{\text{wS}}-2{\mathbf{\text{tF}}}^T+\alpha {\mathbf{P}}^T.$$

Lagrange's method consists of 1. Determining w that yields $\frac{d\Lambda (\mathbf{w})}{d\mathbf{w}}=0.$ 2. Substituting the result into A1, solving for α. 3. Substituting α into 1, yielding the final solution for w.

This results in

$$\mathbf{w}=({\mathbf{\text{tL}}}^T+(\mathbf{i}-{\mathbf{\text{TF}}}^T{\mathbf{S}}^{-1}\mathbf{P})({\mathbf{P}}^T{\mathbf{S}}^{-1}\mathbf{P}){}^{-1}{\mathbf{P}}^T){\mathbf{S}}^{-1}.$$