Automatic whole brain tract‐based analysis using predefined tracts in a diffusion spectrum imaging template and an accurate registration strategy

Abstract

Automated tract‐based analysis of diffusion MRI is an important tool for investigating tract integrity of the cerebral white matter. Current template‐based automatic analyses still lack a comprehensive list of tract atlas and an accurate registration method. In this study, tract‐based automatic analysis (TBAA) was developed to meet the demands. Seventy‐six major white matter tracts were reconstructed on a high‐quality diffusion spectrum imaging (DSI) template, and an advanced two‐step registration strategy was proposed by incorporating anatomical information of the gray matter from T1‐weighted images in addition to microstructural information of the white matter from diffusion‐weighted images. The automatic analysis was achieved by establishing a transformation between the DSI template and DSI dataset of the subject derived from the registration strategy. The tract coordinates in the template were transformed to native space in the individual's DSI dataset, and the microstructural properties of major tract bundles were sampled stepwise along the tract coordinates of the subject's DSI dataset. In a validation study of eight well‐known tracts, our results showed that TBAA had high geometric agreement with manual tracts in both deep and superficial parts but significantly smaller measurement variability than manual method in functional difference. Additionally, the feasibility of the method was demonstrated by showing tracts with altered microstructural properties in patients with schizophrenia. Fifteen major tract bundles were found to have significant differences after controlling the family‐wise error rate. In conclusion, the proposed TBAA method is potentially useful in brain‐wise investigations of white matter tracts, particularly for a large cohort study. Hum Brain Mapp 36:3441–3458, 2015. © 2015 Wiley Periodicals, Inc.

INTRODUCTION

Diffusion magnetic resonance imaging (MRI) can be used to probe the microstructural properties of the white matter in vivo [Basser and Pajevic, 2003; Conturo et al., 1999; Jones et al., 1999; Lee et al., 2005]. When diffusion MRI is aided with tractography, the microstructural properties along a specific fiber tract bundle can be determined. Such tract‐based analysis is often performed using manual tractography. However, this approach has technical limitations that hamper wide applications to neuroscience research. Manual tractography is highly operator dependent and time‐consuming [Huang et al., 2004; Zhang et al., 2010a]. Furthermore, manual tractography performed on individual subjects is prone to reconstruction errors, owing to poor signal‐to‐noise ratio (SNR), complex fiber geometry and subject's head motion [Wakana et al., 2007].

Several automated methods have been proposed for image‐based population studies [Goodlett et al., 2009; Guevara et al., 2012; Li et al., 2010; O'Donnell and Westin, 2007; Smith et al., 2006; Suarez et al., 2012; Taquet et al., 2014; Wang et al., 2011b; Wassermann et al., 2010; Yendiki et al., 2011; Zhang et al., 2010b]. The automated methods for tract‐specific analysis can be categorized into two approaches. One approach is the template‐based approach in which a template is constructed and all subjects' images are registered to the template [Goodlett et al., 2009; Smith et al., 2006; Taquet et al., 2014; Zhang et al., 2010b]. Fiber tracts or tract skeletons, either reconstructed directly on the template or on individual datasets followed by averaging them on the template, are transformed to diffusion datasets of individual subjects. The index of microstructural property such as fractional anisotropy (FA) or mean diffusivity is sampled within the targeted tracts. Another approach performs local deterministic tractography or global tractography [Guevara et al., 2012; Li et al., 2010; O'Donnell and Westin, 2007; Suarez et al., 2012; Wang et al., 2011b; Wassermann et al., 2010; Yendiki et al., 2011] on the diffusion dataset of each individual subject. Tract‐specific analysis is achieved by sampling microstructural property index within the tracts reconstructed on individual datasets. Both approaches address limitations of the manual approach and are potentially useful for a large cohort study. The template‐based approach has high SNR from the registered datasets. It has the advantage of reconstructing robust fiber pathways that are common to all subjects. This approach, however, depends on the accuracy of the registration techniques, and overlooks the individual variations of fiber pathways. In contrast, the individual‐based approach preserves the individual details of fiber pathways, but may be subjected to variations of reconstruction outcome due to variable image quality on individual datasets. In this article, we aimed to improve the template‐based approach by proposing an advanced registration algorithm and a comprehensive list of fiber pathways reconstructed on a diffusion spectrum imaging (DSI) template.

To date, there is no template that provides a comprehensive list of major tract bundles of the human brain for the whole brain tract‐based analysis. Currently, operators need to reconstruct their targeted tracts on their own diffusion template. They may have difficulties in producing the correct tracts due to limited angular resolution of the diffusion template. Even if a high‐angular resolution diffusion template is available, operators still require sufficient knowledge in neuroanatomy and skills of tractography to reconstruct the targeted tracts. Although an atlas comprising 30 long fibers and 29 short U‐fibers has been provided by Zhang et al. [2010b], as the authors acknowledged, the atlas was reconstructed based on diffusion tensor imaging (DTI) datasets and may miss important connections, leading to inaccurate estimation of fiber orientations.

Besides the lack of a comprehensive list of tracts, accurate registration of diffusion‐weighted (DW) images are crucial in population analyses [Taquet et al., 2014]. Previous works have demonstrated that orientation information derived from full tensor provided superior results for connectional anatomy in intersubject registration [Park et al., 2003; Ruiz‐Alzola et al., 2002; Suarez et al., 2012]. However, other studies suggested that superior registration results could be obtained using structural information derived from T1‐weighted (T1W) images [Smith et al., 2012; Zollei et al., 2010]. Another approach performs two‐step image transformation using b ₀ image and FA map. However, unsatisfactory registration was noted at the superficial part of the white matter tracts due to insufficient information of cortical anatomy in diffusion datasets [Zhang et al., 2010b]. Previous studies already found that accurate alignment of the brain anatomy between diffusion weighted images can be achieved if high‐resolution anatomical images such as T1W images are incorporated in image registration [Greve and Fischl, 2009; Robinson et al., 2014; Studholme, 2008]. This kind of registration strategy can provide more accurate transformation in regions close to cortical regions than the registration based on DW images only. High SNR and high anatomical definition of the T1W images can aid morphological registration of DW images. Such registration strategy, however, has not been applied to the automated template‐based approach yet.

In this study, we proposed a new automatic method, called tract‐based automatic analysis (TBAA), to analyze microstructural properties along most of major fiber tract bundles of the whole brain. The proposed method accomplishes this via two key developments. First, we built a tract atlas comprising 76 major fiber tract bundles on a high‐quality DSI template, NTU‐DSI‐122 (see Supporting Information I) [Hsu et al., 2015]. Second, we developed a novel strategy for registration of DSI datasets by incorporating anatomical information of the T1W images and microstructural information of the DSI datasets. With these two developments, the predefined tract bundles in the DSI template could be transformed to native space in the individual's diffusion datasets accurately, allowing reliable sampling of the microstructural properties along the tracts.

To test the accuracy of the TBAA method and demonstrate its clinical feasibility, the paper was organized into three parts. First, we described the fiber tract bundles reconstructed on the DSI template, two‐step registration strategy, and TBAA procedures. Second, validation studies were performed to test the geometric agreement between the tracts reconstructed on the DSI template and those reconstructed manually. In addition, within‐group variability of the sampled values derived from the TBAA method was compared with those derived from the manual method. Finally, we demonstrated the feasibility of the TBAA method in patients with schizophrenia.

MATERIALS AND METHODS

Reconstruction of 76 Major Tract Bundles on NTU‐DSI‐122 Template

DSI tractography on the NTU‐DSI‐122 template was performed using a streamline‐based algorithm adapted for DSI data, and 76 major tract bundles were reconstructed by a multiple region‐of‐interest (ROI) approach [Huang et al., 2004]. To select ROIs for each targeted tract objectively, we used an automated anatomical labeling (AAL) system [Tzourio‐Mazoyer et al., 2002] from WFU Pickatlas (version 3.0.4) to define 58 cortical and subcortical regions as ROIs on the Montreal Neurobiology Institute (MNI) template and then transformed ROIs to the NTU‐DSI‐122 template. These ROIs were placed by two coauthors (W.Y.I.T. and Y.C.L.) who were familiar with the brain structures and experienced in DSI tractography for more than seven years. Each targeted fiber bundle was constructed by assigning 2 or 3 ROIs, and the streamlines passing through all of the associated ROIs were segmented as the targeted tract. The ROIs associated with each tract were selected based on anatomical knowledge.

The 76 major white matter tract bundles were categorized into association, projection, and commissural tract systems according to anatomical definitions. The details of the tract bundles and associated ROIs for each tract bundle are listed in Table 1. The entire fiber tracking was performed using the DSI Studio software (http://dsi-studio.labsolver.org). The details of tractography procedure are described in the Supporting Information II.

Table 1.

List of 76 white matter tracts

No.	System	Subgroup	Name	Connected ROIs	Connected ROIs
1	Association		L_AF	L_inferior frontal gyrus opercular part	L_superior temporal gyrus
2	Association		R_AF	R_inferior frontal gyrus opercular part	R_superior temporal gyrus
3	Association		L_cingulum of main body component	L_cingulate gyrus (anterior + middle parts)	L_cingulate gyrus posterior part
4	Association		R_cingulum of main body component	R_cingulate gyrus (anterior + middle parts)	R_cingulate gyrus posterior part
5	Association		L_cingulum of hippocampal component	L_cingulate gyrus posterior part	L_hippocampus
6	Association		R_cingulum of hippocampal component	R_cingulate gyrus posterior part	R_hippocampus
7	Association		L_frontal aslant tract	L_SMA	L_inferior frontal gyrus opercular part
8	Association		R_frontal aslant tract	R_SMA	R_inferior frontal gyrus opercular part
9	Association		L_fornix	L_mammillary body	L_hippocampus
10	Association		R_fornix	R_mammillary body	R_hippocampus
11	Association		L_IFOF	L_orbitofrontal gyrus	Occipital lobe
12	Association		R_IFOF	R_orbitofrontal gyrus	Occipital lobe
13	Association		L_ILF	L_temporal pole	Occipital lobe
14	Association		R_ILF	R_temporal pole	Occipital lobe
15	Association		L_perpendicular fasciculus	L_angular gyrus	L_temporal‐parietal gyrus
16	Association		R_perpendicular fasciculus	R_angular gyrus	R_temporal‐parietal gyrus
17	Association		L_SLF I	L_superior frontal gyrus	L_precuneus
18	Association		R_SLF I	R_superior frontal gyrus	R_precuneus
19	Association		L_SLF II	L_inferior frontal gyrus triangular part	L_middle occipital gyrus
20	Association		R_SLF II	R_inferior frontal gyrus triangular part	R_middle occipital gyrus
21	Association		L_SLF III	L_inferior frontal gyrus opercular part	L_angular gyrus
22	Association		R_SLF III	R_inferior frontal gyrus opercular part	R_angular gyrus
23	Association		L_stria terminalis	L_septal nuclei	L_amygdala
24	Association		R_stria terminalis	R_septal nuclei	R_amygdala
25	Association		L_UF	L_orbitofrontal gyrus	L_superior temporal pole
26	Association		R_UF	R_orbitofrontal gyrus	R_superior temporal pole
27	Projection	CST	L_CST of hand	Brain stem	L_primary motor cortex of hand component
28	Projection	CST	R_CST of hand	Brain stem	R_ primary motor cortex of hand component
29	Projection	CST	L_CST of trunk	Brain stem	L_ primary motor cortex of trunk component
30	Projection	CST	R_CST of trunk	Brain stem	R_ primary motor cortex of trunk component
31	Projection	CST	L_CST of mouth	Brain stem	L_ primary motor cortex of mouth component
32	Projection	CST	R_CST of mouth	Brain stem	R_ primary motor cortex of mouth component
33	Projection	CST	L_CST of toe	Brain stem	L_primary motor cortex of toe component
34	Projection	CST	R_CST of toe	Brain stem	R_primary motor cortex of toe component
35	Projection	CST	L_CST of geniculate fibers	Brain stem	L_primary motor cortex of throat component
36	Projection	CST	R_CST of geniculate fibers	Brain stem	R_primary motor cortex of throat component
37	Projection	FS	L_FS of OFC	L_striatum (putamen + caudate)	L_orbitofrontal gyrus
38	Projection	FS	R_FS of OFC	R_striatum (putamen + caudate)	R_obritofrontal gyrus
39	Projection	FS	L_FS of VLPFC	L_striatum (putamen + caudate)	L_inferior frontal gyrus + middle frontal gyrus
40	Projection	FS	R_FS of VLPFC	R_striatum (putamen + caudate)	R_inferior frontal gyrus + middle frontal gyrus
41	Projection	FS	L_FS of DLPFC	L_striatum (putamen + caudate)	L_medial frontal gyrus + superior frontal gyrus
42	Projection	FS	R_FS of DLPFC	R_striatum (putamen + caudate)	R_medial frontal gyrus + superior frontal gyrus
43	Projection	FS	L_FS of precentral gyrus	L_striatum (putamen + caudate)	L_precentral gyrus
44	Projection	FS	R_FS of precentral gyrus	R_striatum (putamen + caudate)	R_precentral gyrus
45	Projection		L_Medial lemniscus	Brain stem	L_thalamus
46	Projection		R_Medial lemniscus	Brain stem	R_thalamus
47	Projection	TR	L_TR of VLPFC	L_thalamus	L_obritofrontal gyrus + middle frontal gyrus + inferior frontal gyrus
48	Projection	TR	R_TR of VLPFC	R_thalamus	R_obritofrontal gyrus + middle frontal gyrus + inferior frontal gyrus
49	Projection	TR	L_TR of DLPFC	L_thalamus	L_medial frontal gyrus + superior frontal gyrus + SMA
50	Projection	TR	R_TR of DLPFC	R_thalamus	R_medial frontal gyrus + superior frontal gyrus + SMA
51	Projection	TR	L_TR of precentral gyrus	L_thalamus	L_precentral gyrus
52	Projection	TR	R_TR of precentral gyrus	R_thalamus	R_precentral gyrus
53	Projection	TR	L_TR of postcentral gyrus	L_thalamus	L_postcentral gyrus
54	Projection	TR	R_TR of postcentral gyrus	R_thalamus	R_postcentral gyrus
55	Projection	TR	L_TR of auditory nerve	L_thalamus	L_Heschl's gyrus
56	Projection	TR	R_TR of auditory nerve	R_thalamus	R_Heschl's gyrus
57	Projection	TR	L_TR of optic radiation	L_thalamus	L_superior occipital gyrus
58	Projection	TR	R_TR of optic radiation	R_thalamus	R_superiro occipital gyrus
59	Commissure		Anterior commissure	Front column of fornix	Bilateral cerebral hemispheres
60	Commissure		Posterior commissure	Dorsal aspect of the upper end of the cerebral aqueduct	Bilateral cerebral hemispheres
61	Commissure	CC	CC of genu	L_orbitofrontal gyrus	R_orbitofrontal gyrus
62	Commissure	CC	CC of DLPFC	L_medial frontal gyrus + superior frontal gyrus	R_medial frontal gyrus + superior frontal gyrus
63	Commissure	CC	CC of VLPFC	L_inferior frontal gyrus + middle frontal gyrus	R_inferior frontal gyrus + middle frontal gyrus
64	Commissure	CC	CC of SMA	L_supplementary motor areas	R_supplementary motor areas
65	Commissure	CC	CC of precentral gyrus	L_precentral gyrus	R_precentral gyrus
66	Commissure	CC	CC of paracentral lobule	L_paracentral lobules	R_paracentral lobules
67	Commissure	CC	CC of inferior parietal lobule	L_inferior parietal lobules	R_inferior parietal lobules
68	Commissure	CC	CC of postcentral gyrus	L_postcentral gyrus	R_postcentral gyrus
69	Commissure	CC	CC of superior parietal lobule	L_superior parietal lobules	R_superior parietal lobules
70	Commissure	CC	CC of superior temporal gyrus	L_superior temporal gyrus	R_superior temporal gyrus
71	Commissure	CC	CC of middle temporal gyrus	L_middle temporal gyrus	R_middle temporal gyrus
72	Commissure	CC	CC of temporal pole	L_temporal poles	R_temporal poles
73	Commissure	CC	CC of hippocampus	L_hippocampus	R_hippocampus
74	Commissure	CC	CC of amygdala	L_amygdala	R_amygdala
75	Commissure	CC	CC of precuneus	L_precuneus	R_precuneus
76	Commissure	CC	CC of splenium	L_occipital lobe	R_occipital lobe

AF: arcuate fasciculus; CC: corpus callosum; CST: corticospinal tract; DLPFC: dorsal lateral prefrontal cortex; FS: frontal‐striatum; IFOF: inferior frontal occipital fasciculus; ILF: inferior longitudinal fasciculus; L: left; OFC: orbitofrontal cortex; R: right; SLF: superior longitudinal fasciculus; SMA: supplementary motor area; TR: thalamic radiation; UF: uncinate fasciculus; VLPFC: ventral lateral prefrontal cortex.

Once constructed, the tract was verified to ensure that the entire trajectory follows the anatomical landmarks based on the knowledge of brain structures [Haines, 2008; Nolte, 2009; Nolte and Angevine, 2013; Schmahmann and Pandya, 2007]. For the tracts that had been constructed on DTI templates, we checked the compatibility of our tracts with those derived from DTI data [Catani and Thiebaut de Schotten, 2008; Makris et al., 2005; Mori et al., 2008; Wakana et al., 2005]. For each tract bundle, the lengths of the reconstructed streamlines were restricted to within a certain range; the difference among streamlines was less than 10 steps (1 step = 1 mm). Each streamline of the tract bundle was subdivided into evenly spaced steps; the number of steps was determined by the mean number of steps of the tract bundle. The step coordinates along the streamlines were saved as the sampling coordinates of the tract bundle.

Registration Strategy

A two‐step registration strategy was used in the TBAA method including anatomical information provided by the T1W volume images and microstructural information provided by DSI datasets [Hsu et al., 2012]. First, a tissue probability map (TPM) is calculated from the T1W images of each subject using the method of unified segmentation provided from SPM12 [Ashburner and Friston, 2005]. During this step, the DSI dataset of each participant, j ( ${\mathrm{D}\mathrm{S}\mathrm{I}}^{\mathrm{j}}$), is registered to its own ${\mathrm{T}\mathrm{P}\mathrm{M}}^{\mathrm{j}}$ by performing rigid body transformations between the b₀ volume of ${\mathrm{D}\mathrm{S}\mathrm{I}}^{\mathrm{j}}$ and ${\mathrm{T}\mathrm{P}\mathrm{M}}^{\mathrm{j}}$. The registration here is performed by minimizing the normalized mutual information between these two imaging modalities. A mean TPM ( ${\mathrm{T}\mathrm{P}\mathrm{M}}^{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$) is estimated from the average of the ${\mathrm{T}\mathrm{P}\mathrm{M}}^{\mathrm{j}},$ and the transformation, ${\mathrm{\phi }}^{\mathrm{j}},$ is obtained between ${\mathrm{T}\mathrm{P}\mathrm{M}}^{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ and ${\mathrm{T}\mathrm{P}\mathrm{M}}^{\mathrm{j}}$ by using the method of geodesic shooting provided from SPM12 [Ashburner, 2009; Ashburner and Friston, 2011; Miller et al., 2006]. The individual ${\mathrm{D}\mathrm{S}\mathrm{I}}^{\mathrm{j}}$ is then transformed into mean TPM space according to ${\mathrm{\phi }}^{\mathrm{j}},$ and the q‐space signals are reoriented using the rotational component of the Jacobian of ${\mathrm{\phi }}^{\mathrm{j}}$ [Hsu et al., 2012], which results in a registered DSI dataset. An intermediate DSI template is constructed by averaging all of the registered DSI datasets.

Second, each registered DSI dataset is normalized to the intermediate DSI template by LDDMM DSI [Hsu et al., 2012], which generates deformation maps, ${\mathrm{\theta }}^{\mathrm{j}}$. A final study specific template (SST) is then constructed by averaging all of the normalized DSI datasets. The combination of these two transformations constitutes the transformation, ${\phi }^{\mathrm{j}}\circ {\theta }^{\mathrm{j}}$, between each individual DSI dataset and SST. By applying the two‐step registration, the major transformations among subjects are estimated and coregistered using high‐resolution information of T1W volume images throughout the first step. Slight alignments of fiber orientations and slight spatial correspondence of white matter structures among subjects are improved throughout the second registration step of LDDMM‐DSI using the full DSI data to allow high‐definition construction of the SST [Hsu et al., 2012].

The registration between SST and NTU‐DSI‐122 template is based on the same rationale of two‐step registration. First, the ${\mathrm{T}\mathrm{P}\mathrm{M}}^{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ is registered to MNI space using unified segmentation, which obtains a transformation, $\varphi$. The SST is transformed into MNI space according to $\varphi$, reorients the q‐space signals with the rotational component of the Jacobian of ϕ. Second, the transformed SST is then registered to the NTU‐DSI‐122 template by LDDMM DSI. This results in a deformation map, $\mathrm{\chi }$. The combination of these two transformations, $\mathrm{\psi }\circ \mathrm{\chi }$, constitutes the transformation between the SST and the NTU‐DSI‐122 template.

TBAA Procedures

The procedures of the TBAA method are displayed in a flow chart in Figure 1 and described below. The proposed registration strategy is used in (1) and (2) of the procedures and the proposed atlas is used in (3) of the procedures.

1. DSI data of a group of subjects are registered using two‐step registration strategy to create a single SST. The SST is used to address the bias from group differences in disease or age which may happen if individual DSI data were registered directly to the DSI template.

2. The SST is registered to the NTU‐DSI‐122 template according to the two‐step registration described above.

3. Sampling coordinates are transformed from the NTU‐DSI‐122 template through the SST to individual DSI data via the composition of the transformation, ${\phi }^{\mathrm{j}}\circ {\theta }^{\mathrm{j}}\circ \mathrm{\psi }\circ \mathrm{\chi }$.

4. Once the sampling coordinates are transformed, the generalized FA (GFA), an index reflecting the microstructural properties of the fiber tract [Fritzsche et al., 2010; Gorczewski et al., 2009], is sampled along the transformed coordinates in native space. The sampled GFA values along each tract bundle form a one‐dimensional series of GFA values or so called GFA profile. The GFA value at each step is the average of the GFA values at the same step of the streamlines. For each subject, the GFA profiles of the tract bundles throughout the entire brain following a systematic categorization form a 2D array comprising 76 rows of information of GFA values, which is referred to as a “connectogram.” The number of GFA values for each row is determined as the steps of each reconstructed tract at the NTU‐DSI‐122 template. This 2D connectogram is a standardized format that contains tract‐specific information along the 76 tract bundles. The directions of the profiles are defined as anterior to posterior for association fibers, right to left for commissural fibers, and inferior to superior for projection fibers. A 3D connectogram is obtained after stacking the 2D connectogram data of all the studied subjects.

Figure 1.

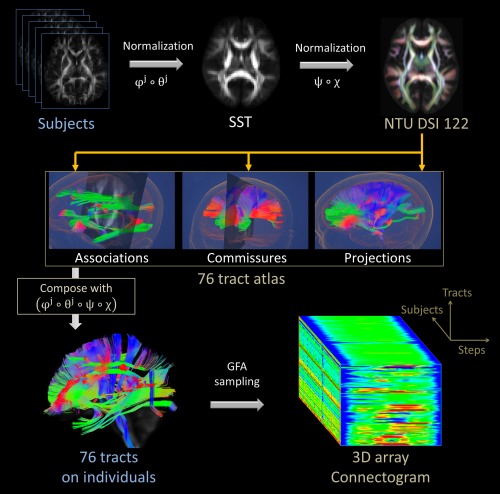
The flow chart of the tract‐based automatic analysis procedures. SST: study‐specific template; GFA: generalized fractional anisotropy. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Validation of TBAA

We tested the accuracy and variability of the TBAA method by comparing it with the manual method. The tracts reconstructed in the NTU‐DSI‐122 template were superimposed with those reconstructed by manual tractography to evaluate the geometric agreement of the two methods. In addition, the within‐group variability of the GFA profiles derived from the TBAA method was compared with those derived from the manual method. The validation was performed in 20 healthy adults (age: 25.3 ± 4.5, range: 19–31, 10 males, 10 females) without a history of psychiatric disorders.

Acquisition of DSI Data

All images were acquired on a 3T MRI system (Trio, Siemens, Erlangen, Germany) with a 32‐channel phase array head coil. T1W imaging was performed using a 3D magnetization‐prepared rapid gradient echo (MPRAGE) sequence: repetition time (TR)/echo time (TE) = 2000 ms/3 ms, flip angle = 9°, field of view (FOV) = 256 × 192 × 208 mm³, acquisition matrix = 256 × 192 × 208, resulting in isotropic spatial resolution of 1 mm³. A single‐shot spin‐echo echo‐planar imaging sequence, embedded with twice‐refocused diffusion‐sensitive gradients for reducing the eddy‐current induced distortions [Reese et al., 2003], was employed for DSI acquisition. The following imaging parameters were used: TR/TE = 9600/130 ms, FOV = 200 mm, slice thickness = 2.5 mm, slice number = 54 and in‐plane spatial resolution = 2.5 mm. The diffusion acquisition scheme composed of 102 diffusion‐encoding directions corresponding to grid points located in a half sphere of diffusion‐encoding space (q‐space) within a radius of 3 units, which corresponds to a b _max of 4000 s mm⁻² [Kuo et al., 2008].

Head motion may occur during DSI acquisition due to a relatively long scanning time. In the presence of strong diffusion‐sensitive gradients, especially those with high b‐values, jerky head motion induces signal loss in the DW images. For the DSI datasets with severe signal loss, the lost signals cannot be completely restored through postprocessing methods and should be discarded. Therefore, all DSI datasets underwent a quality assurance procedure by counting the number of DW images that had significant signal dropout. All of the acquired DSI datasets [54 slices × (101 directions DWI + 1 null image) = 5508 images] were scrutinized by calculating the signals in the central square (20 × 20 pixels) of each image. If the average signal intensity of an image (after correcting for its b value) was lower than two standard deviations from the mean of all images, the image was considered as signal loss. We previously found that the DSI dataset with more than 90 images of signal loss caused significant reduction of GFA values and should be discarded.

Reconstruction of DSI Data

For each voxel of the DSI dataset, the 102 diffusion‐attenuated signals of a half‐sphere were projected to fill the other half of the sphere based on the fact that the data in q‐space are real and symmetrical around the origin [Kuo et al., 2008]. A 3D Fourier transform was performed to obtain a probability density function (PDF). An orientation distribution function (ODF) was obtained by computing the second moment of the PDF along each of the 362 radial directions in a sixfold tessellated icosahedron. To determine the local tract directions within each voxel, an iterative approach was used to decompose the ODF into several constituent Gaussian ODFs [Yeh and Tseng, 2013]. The GFA at each voxel was quantified using the following formula: GFA = (standard deviation of the ODF)/(root mean square of the ODF) [Tuch, 2004].

Geometric Agreement of Tracts between NTU‐DSI‐122 Template and Manual Tractography

In native space of each subject's DSI data, we performed manual tractography using the same approach as that used for tract reconstruction in the NTU‐DSI‐122 template. The bilateral AF, the main body component of bilateral CG, bilateral corticospinal tracts from the trunk of the primary motor cortex (CST of the trunk), genu and splenium of the corpus callosum were reconstructed. Dice coefficients were calculated to assess the geometric agreement of the tracts reconstructed on the template and those reconstructed by manual tractography [Dauguet et al., 2007]. To evaluate the geometric agreement of the tracts close to cortical regions, target tracts were divided into two parts, the deep white matter part and superficial white matter part. The superficial white matter part was defined as the 10% portion of the tract that approaches cortical regions. In this way, the superficial white matter parts was selected as the 10% portions at the two ends of the AF, genu, and splenium, and the 10% portion of the CST close to the motor cortex. The remaining portion of the tracts was assigned as deep white matter part.

Dice coefficient D was defined as

$$\mathrm{D}(\mathrm{a},\mathrm{b})=\frac{2({\mathrm{V}}_{\mathrm{a}}\cap {\mathrm{V}}_{\mathrm{b}})}{({\mathrm{V}}_{\mathrm{a}}+{\mathrm{V}}_{\mathrm{b}})},$$

where V_a and V_b were the voxels traversed by tract bundle a and tract bundle b, respectively. All of the reconstructed tracts, including the template tracts and those made by manual tractography in the individual's native space, were transformed to the SST to compute the Dice coefficient.

Within‐Group Variability of GFA Profiles Derived from TBAA and Manual Methods

Functional difference (FD) between two different tracts were calculated following the methods provided by Gouttard et al. to assess the functional variability of the GFA profiles derived from the TBAA method and those derived from the manual method [Gouttard et al., 2012].

Functional difference (FD) was defined as

$$\mathrm{F}\mathrm{D}=\frac{1}{n}\sum _{i=1}^{\mathrm{n}}\left|{\mathrm{f}}_{\mathrm{a}}\left({\mathrm{t}}_i\right)-{\mathrm{f}}_{\mathrm{b}}\left({\mathrm{t}}_{\mathrm{i}}\right)\right|\times \frac{1}{{\mathrm{f}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}}$$

where ${\mathrm{f}}_{\mathrm{a}}\left({\mathrm{t}}_i\right)$ and ${\mathrm{f}}_{\mathrm{b}}\left({\mathrm{t}}_i\right)$ were the measured GFA values at step t_i for tract bundle a and tract bundle b (i = 1, 2, …, n, where n was the number of steps of the tract bundle), respectively, and the ${\mathrm{f}}_{\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}$ was the GFA value of the same tracts averaged over 20 subjects. The FD indicated the mean absolute difference between 2 GFA profiles, that is, ${\mathrm{f}}_{\mathrm{a}}\left({\mathrm{t}}_i\right)$ and ${\mathrm{f}}_{\mathrm{b}}\left({\mathrm{t}}_i\right)$. The comparison of FD values was performed in native space. GFA profiles were measured in the individual's native space using either the sampling coordinates transformed from the DSI template to native space or the coordinates obtained from the manually reconstructed tracts. For each studied tract bundle in the TBAA method, there were 20 GFA profiles sampled in native space of 20 individuals. Therefore, 190 FD values were derived from all possible pairs of profiles. Similarly, there were 190 FD values that were derived from the GFA profiles using the manual method. A Student t‐test was performed to compare the differences in FD values between these two methods.

To demonstrate that two GFA profiles of the same tract were consistent, Pearson correlation coefficients were analyzed for 190 pairs of GFA profiles that were derived from either the TBAA method or manual method.

Demonstration of TBAA

We tested the feasibility of the TBAA method by showing its capability of detecting aberrant tracts in patients with schizophrenia. A stepwise comparison of the connectograms between the patients with schizophrenia and healthy controls were performed and the familywise error rate (FWER) was controlled to correct probable false positives owing to multiple comparisons. The results were compared with previous results in the literature on schizophrenia.

Fifty‐four patients with schizophrenia and 54 healthy controls matched in age and gender were selected for analysis (patients age: 34.4 ± 8.6, range: 19–52, 29 males, 25 females; controls age: 32.3 ± 9.0, range: 19–49, 28 males, 26 females). Patients who met the criteria listed in the Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition for schizophrenia were recruited by attending psychiatrists at the National Taiwan University Hospital. The diagnosis of schizophrenia was confirmed based on the semistructured Diagnostic Interview for Genetic Study—Chinese Version. Community volunteers without a history of psychiatric disorders were recruited as healthy controls. All participants were Han Chinese, right‐handed and free of neurological abnormalities, physical deformities, substance abuse problems or mental deficits. The institutional review board of the hospital approved the study, and informed consent was obtained from all participants before examination.

Statistical Analysis of TBAA Results in Patients with Schizophrenia

Having obtained the 2D connectogram for each subject, a stepwise comparison was performed between the two groups. The group difference of GFA was standardized for each step of a fiber tract bundle using a t‐statistic, which was weighted using threshold‐free cluster enhancement (TFCE) for further analysis [Smith and Nichols, 2009]. A permutation test (5000 times) based on a TFCE‐weighted statistical image was used for statistical inference. A maximal statistic approach was used to control the FWER [Nichols and Hayasaka, 2003] (see Supporting Information III).

A Specificity Test of the TBAA Method

To test the specificity of the TBAA method, we performed leave‐N‐out analysis to compare the difference between two subgroups of control subjects and the difference between a subgroup of control subjects and a subgroup of patients. For the controls‐vs.‐controls comparison, 27 controls randomly selected from the control group were paired with the rest of 27 controls. For the controls‐vs.‐patients experiment, 27 controls randomly selected from the control group were paired with 27 patients randomly selected from the patient group. A total of 100 combinations of control‐vs.‐control pairs and 100 combinations of control‐vs.‐patient pairs were selected. We performed the TBAA method and the same statistical analysis to calculate the segments with significant difference for each pair. Significant segments cumulated over 100 combinations produced a cumulant map of tract alteration, ranging from 0 to 100.

RESULTS

Reconstruction of 76 Tract Bundles on NTU‐DSI‐122 Template

A total of 76 major fiber tracts were reconstructed on the NTU‐DSI‐122 template (Table 1). Thirteen pairs of association fibers were segmented into the arcuate fasciculus, the cingulum of main body component, cingulum of hippocampal component, frontal aslant tracts, the fornix, the superior longitudinal fasciculus (SLF) I, SLF II, SLF III, the inferior longitudinal fasciculus, the inferior frontal‐occipital fasciculus, the uncinate fasciculus, the stria terminalis, and the perpendicular fasciculus. Thirty‐two projection fibers were classified into 10 portions of the corticospinal tracts, two medial lemniscus, eight frontal‐striatal tracts, and 12 thalamic radiations. The 18 commissural fibers included the anterior commissure, the posterior commissure, and 16 segments of callosal fibers which passed through the corpus callosum (Fig. 2). The reconstructed fiber tracts were rendered in 3D images overlaid with 2D cross sectional images of brain structures (Fig. 2 and please visit http://140.112.137.122/TBAA_tractatlas, for Windows and Mac systems).

Figure 2.

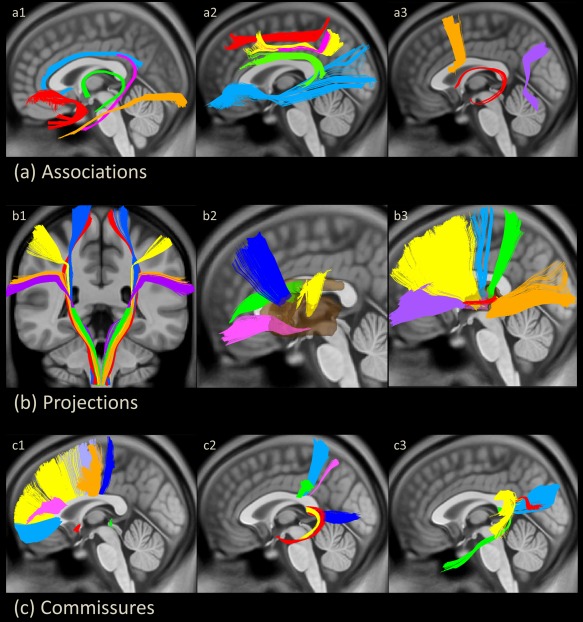
The tract atlas containing 26 association tracts (a), 32 projection tracts (b) and 18 commissural tracts (c). (a1) Uncinate fasciculus in red, cingulum bundle of the main body component in light blue, cingulum bundle of the hippocampal component in pink, fornix in green and inferior longitudinal fasciculus in orange. (a2) Inferior frontal‐occipital fasciculus in light blue, arcuate fasciculus in green, superior longitudinal fasciculus (SLF) I in red, SLF II in pink and SLF III in yellow. (a3) Frontal aslant tract in orange, stria terminalis in red, and perpendicular fasciculus in purple. (b1) Medial lemniscus fiber tracts in green and corticospinal tract from the primary motor cortex of the toe in red, trunk in blue, hand in yellow, mouth in orange and throat (geniculate fibers) in purple. (b2) Frontal striatum of the orbital frontal cortex in pink, ventral lateral prefrontal cortex (VLPFC) in green, dorsal lateral prefrontal cortex (DLPFC) in blue and precentral component in yellow. (b3) Thalamic radiation of VLPFC in purple, DLPFC in yellow, precentral component in light blue, postcentral component in green, auditory nerve in red and optic radiation in orange. (c1) Corpus callosum (CC) of the genu in light blue, DLPFC in yellow, VLPFC in pink, supplementary motor area in light purple, precentral component in orange, paracentral component in blue, anterior commissure in red and posterior commissure in green. (c2) CC of inferior parietal lobule in green, postcentral component in light blue, superior parietal lobule in pink, hippocampus in yellow, amygdala in red and precuneus in blue. (c3) CC of superior temporal cortex in yellow, temporal pole in green, middle temporal cortex in red and splenium in light blue. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Geometric Agreement and within‐Group Variability between Template Tracts and Manual Tractography

Eight fiber tracts, that is, the bilateral AF, bilateral CG of the main body component, bilateral CST of the trunk, genu and splenium, from the template tracts were selected to compare with the same tracts reconstructed by manual tractography. Dice coefficients evaluated in 20 individuals were very high (mean 0.73 ± 0.14) in both the deep white matter part (mean 0.73 ± 0.14) and the superficial white matter part (mean 0.73 ± 0.15) (Table 2).

Table 2.

Dice coefficients of the template and manual tracts in the deep and superficial white matter

	Deep white matter	Superficial white matter
Left arcuate fasciculus	0.70 ± 0.15	0.71 ± 0.13
Right arcuate fasciculus	0.69 ± 0.16	0.70 ± 0.15
Left cingulum	0.75 ± 0.11	None
Right cingulum	0.73 ± 0.11	None
Left corticospinal tract	0.73 ± 0.13	0.77 ± 0.15
Right corticospinal tract	0.74 ± 0.15	0.78 ± 0.16
Genu	0.71 ± 0.12	0.69 ± 0.14
Splenium	0.75 ± 0.14	0.73 ± 0.13

The mean FD of the TBAA method was significantly lower than the mean FD of the manual method in all of the tracts except genu (Table 3).

Table 3.

Comparison of functional differences between TBAA and manual methods

	TBAA method (Mean ± SD)	Manual method (Mean ± SD)	P value
Left arcuate fasciculus	0.125 ± 0.035	0.150 ± 0.042	<0.0001b
Right arcuate fasciculus	0.128 ± 0.037	0.149 ± 0.040	<0.0001b
Left cingulum	0.121 ± 0.040	0.187 ± 0.057	<0.0001b
Right cingulum	0.123 ± 0.038	0.175 ± 0.053	<0.0001b
Left corticospinal tract	0.067 ± 0.021	0.104 ± 0.031	<0.0001b
Right corticospinal tract	0.071 ± 0.026	0.125 ± 0.035	<0.0001b
Genu	0.124 ± 0.044	0.129 ± 0.045	0.379
Splenium	0.122 ± 0.034	0.138 ± 0.051	0.007a

^a P‐value < 0.01.

^b P‐value < 0.0001.

TBAA: tract‐based automatic analysis.

To visualize the above results, Figure 3 shows the GFA profiles of 20 subjects derived from TBAA and those from the manual method. It is clear that the GFA profiles derived from the manual method had larger within‐group variability than those from the TBAA method.

Figure 3.

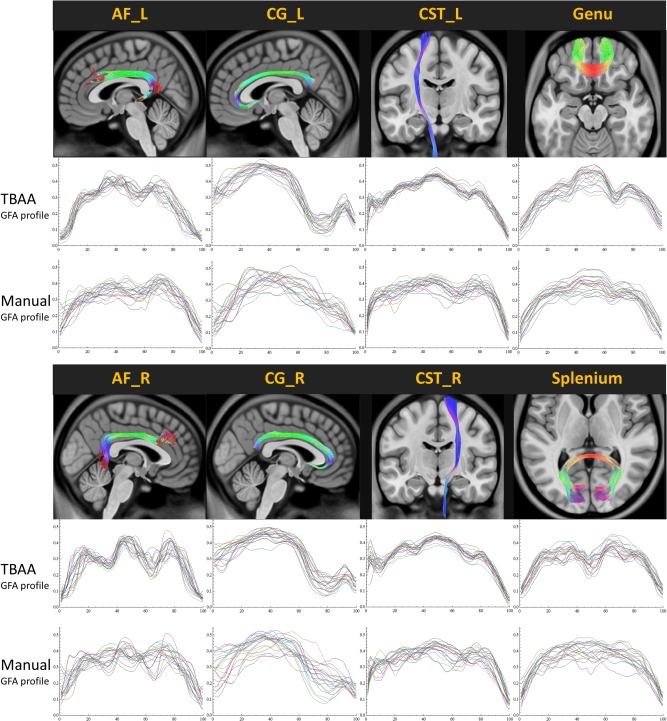
Generalized fractional anisotropy (GFA) profiles of 20 healthy individuals derived from the tract‐based automatic analysis method and those derived from the manual method. The thin curves indicate GFA profiles of individual subjects and thick curves indicate the average GFA profiles over 20 subjects. AF: arcuate fasciculus; CG: cingulum bundle; CST: corticospinal tract; L: left; R: right. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Comparisons of the Pearson correlation coefficients (r) between each pair of GFA profiles showed that the GFA profiles derived from the TBAA method were more consistent (r values from 0.915 to 0.971) than those derived from the manual method (r values from 0.713 to 0.927).

Aberrant Tracts in Patients with Schizophrenia

There was no significant difference in signal dropout counts between patients and controls (21 ± 22 vs. 20 ± 21; P = 0.53). A collection of 2D connectograms was obtained from 108 studied subjects and could be visually presented in a normalized format as a 3D array matrix (Fig. 4).

Figure 4.

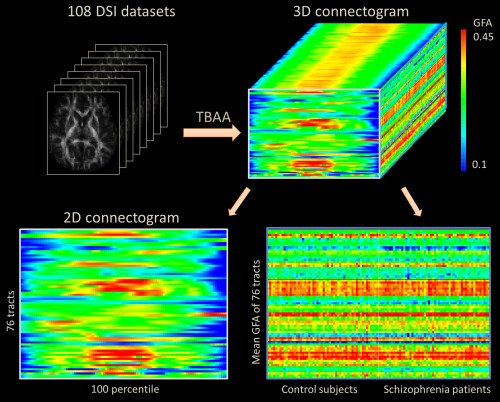
The output of the tract‐based automatic analysis (TBAA), a standardized matrix of 3D array connectogram which contains a stack of 2D connectograms of a group of subjects. GFA: generalized fractional anisotropy. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

This 3D array matrix is a standardized format of data, which can be reduced to two 2D arrays by projecting the data along the subject‐axis or step‐axis, respectively. The 2D array on the left is a 2D connectogram that is averaged across subjects. This array shows the variation in GFA profiles for the two groups. The 2D array on the right is a 76 × 108 matrix presenting the mean GFA values for 76 tracts in each subject. This array presents variations in the mean GFA of tract bundles for each individual subject.

After applying TFCE and controlling the FWER, we found 20 clusters located in 15 fiber tracts that showed significant differences (FWER adjusted P < 0.05) between the schizophrenia and control groups. As shown in Figure 5, 11 tracts contained clusters with GFA values that were significantly higher in the control group than the schizophrenia group (red clusters in the connectogram and red shadows in the GFA profiles), 3 tracts contained clusters with GFA values that were significantly lower in the control group than the schizophrenia group (green clusters in the connectogram and green shadows in the GFA profiles), and 1 tract contained clusters with both significantly higher and lower GFA values.

Figure 5.

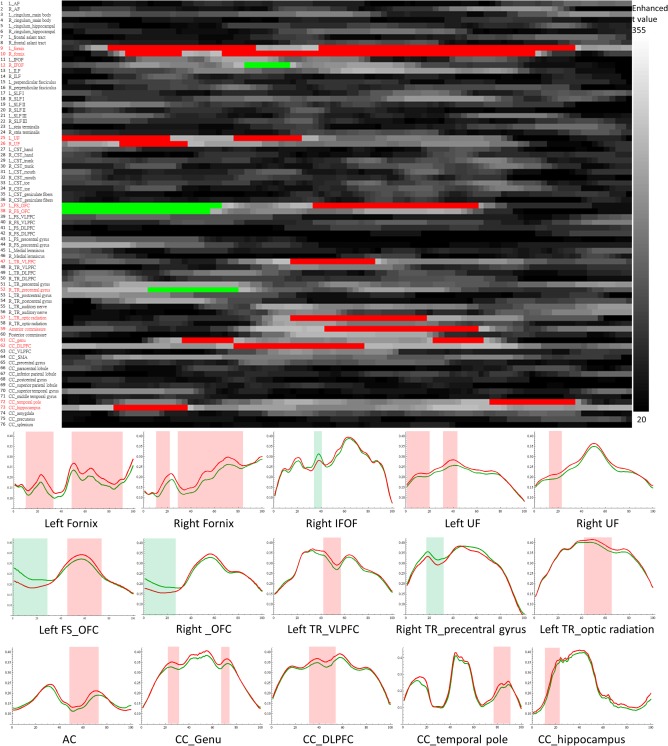
Whole brain tract comparison between patients with schizophrenia and healthy controls using tract‐based automatic analysis. The 2D array in the upper panel shows enhanced t value maps (in gray levels) computed from the threshold free cluster enhancement. Tracts with significant difference among 76 tracts are shown in red in the list on left and the generalized fractional anisotropy (GFA) profiles of these tracts are shown in the lower panel (profiles of controls in red and profiles in patients in green). The red areas show the segments containing significantly higher GFA values in controls than in patients. The green areas show the segments containing significantly lower GFA values in controls than in patients. AC: anterior commissure; CC: corpus callosum; DLPFC: dorsal lateral prefrontal cortex; FS: frontal‐striatum; IFOF: inferior frontal occipital fasciculus; OFC: orbitofrontal cortex; TR: thalamic radiation; UF: uncinate fasciculus. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

In the association fiber tracts, the bilateral fornices, bilateral uncinate fasciculus, and right inferior frontal occipital fasciculus contained significant clusters. In the commissural fiber tracts, clusters were identified in the anterior commissure and four components of the corpus callosum, including the genu, dorsal lateral prefrontal cortex, temporal pole and bilateral hippocampi. In the projection fiber tracts, significant clusters occurred in the bilateral frontal‐striatum tracts of the orbital frontal cortex, left thalamic radiation of the ventral and optical components and right thalamic radiation of the precentral component.

The cumulant map of the control‐vs.‐control comparison showed 19 non‐zero segments, ranging from 1 to 3, in 17 tracts. The maximal cumulant value of 3 was distributed in 3 tracts only (Fig. 6a). In contrast, the cumulant map of the controls‐vs.‐patient comparison revealed 40 non‐zero segments in 38 tracts, ranging from 1 to 97 (Fig. 6b). Furthermore, the pattern of the cumulant map appeared very similar to the map of significant difference between 54 patients and 54 controls in our original results (Fig. 5). The test results indicate that the TBAA method has high specificity.

Figure 6.

The cumulant maps of (a) the control‐vs.‐control comparison and (b) the control‐vs.‐patient comparison. To visualize cumulant values of the segments, the range of the grayscale level in each map was adjusted to an appropriate range. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

DISCUSSION

In this study, we proposed an automatic method, TBAA, to analyze the microstructural properties along fiber tract bundles. The TBAA method accomplishes the task using two developments. First, it uses a comprehensive list of major tract bundles in the human brain which were reconstructed on a DSI template, NTU‐DSI‐122. Second, it uses an accurate registration strategy between individual DSI datasets and the DSI template. Using this registration strategy, TBAA showed high geometric agreement between the manual tracts and template tracts, even at the superficial part of the fiber tract bundles. Moreover, the method showed smaller within‐group variability of GFA measurement as compared to the manual method. In the feasibility test, TBAA yielded satisfactory sensitivity and specificity in differentiating aberrant tracts in patients with schizophrenia. The TBAA method addresses the limitations of the manual approach and provides an enhanced version of automated approach for tract‐based analysis. It enables high throughput and objective analysis of the microstructural properties of the major tract bundles over the whole brain.

In the proposed TBAA method, the trajectories of the tracts were verified to be consistent with the anatomy of known fiber pathways. Once the coordinates of these tracts were transformed to individual DSI data, they were used to automatically sample the tract integrity of each individual subject. Such knowledge‐based information greatly reduces the requirement for operator expertise and ensures highly reproducible results (Table 2). Approximately 30–40 min are required to complete the registration of each set of DSI data on a personal computer (e.g., CPU: i7 3.4GHz with 8 GB RAM). Compared with the manual approach, this is an extremely short period of time to perform a tract‐based analysis of the entire brain. Additionally, virtually no manpower is required because most of the TBAA procedures are automatic.

In the present study, we performed detailed segmentation of the tracts over the whole brain and made a comprehensive list of tract bundles. The success lies in the fact that the tract bundles were reconstructed on the NTU‐DSI‐122 template [Hsu et al., 2015] rather than a DTI template. DTI models water diffusion as a 3D Gaussian, which can be characterized by a symmetric rank two tensor [Basser et al., 1994]. The Gaussian model limits DTI to define only one single tract orientation for each voxel, which makes deterministic tractography extremely difficult in regions of the white matter containing complex fiber crossings. DSI models the diffusion signal as the Fourier pair of the PDF [Wedeen et al., 2005]. Fiber crossings can be resolved by determining the maximal orientation(s) of the PDF in situ. With the high‐quality (high SNR and high angular resolution) DSI template, we successfully reconstructed most of the known major tract bundles compatible with neuroanatomy, and we also identified thin tract bundles that are difficult to be tracked using DTI data. For instance, CG bundles that we identified contain medial and dorsal prefrontal connections as well as temporal and parietal connections via parahippocampal part of CG which is very difficult to reconstruct completely [Metzler‐Baddeley et al., 2012]. We also identified the fornix connecting mammillary bodies and hippocampus. Notably, the columns of the fornix that arch downward behind the anterior commissure and end in the mammillary body were clearly shown in our atlas. Moreover, the frontal aslant tracts connecting supplementary motor area and Broca's area [Catani et al., 2013] were also identified in our atlas. Another thin tract, stria terminalis, which was difficult to be reconstructed in the DTI template [Li et al., 2010], was determined in our atlas showing the connection between septal nuclei and amygdala. For the projection fiber system, the medial lemniscus carried sensory information passing through the brainstem to the thalamus was found in the present study. Furthermore, we separated the corticospinal tracts into five components comprising the toe, trunk, hand, mouth, and geniculate fibers according to different body parts of the cortical homunculus in the primary motor cortex. The white matter tract atlas embedded in the TBAA method is comprehensive and potentially valuable for brain research and clinical applications.

Compared with traditional tractography, the TBAA method showed high geometric agreement between the template tracts and manual tracts in both the deep white matter and superficial white matter parts for all of the eight tested tracts (Table 2). The high agreement of tract positions implies that our registration strategy, which incorporates anatomical information of T1W images into registration, indeed helps. To implement the anatomical information, we created an intermediate template first using high resolution T1W images by nonlinear registration and performed the second registration using DW images by LDDMM DSI [Hsu et al., 2012]. By performing this registration strategy, our results showed high geometric agreement between the template tracts and manual tracts not only at the deep white matter part (Dice coefficient = 0.73 ± 0.14), but also at the superficial white matter part (Dice coefficient = 0.73 ± 0.15). This strategy is compatible with a recent report that the tractography improves the termination of the pathways close to the gray–white matter junction if the white matter TPM derived from high‐resolution T1W images is incorporated [Smith et al., 2012].

Recent studies suggest that variations in FA or GFA values along a tract bundle may be more informative than the average value of the entire tract [Johnson et al., 2013; Maddah et al., 2008; Smith et al., 2006; Taquet et al., 2014]. Compared with the manual method, the TBAA method presented larger variation of the GFA values along the tracts (Fig. 3) and smaller within‐group variability of the GFA values (Table 3). The correlation coefficients of GFA profiles also showed higher functional agreements of the measured GFA values in the TBAA method than the manual method. The small variability and high correlation of GFA values ensure the applicability of the stepwise analysis in the TBAA method.

To test the feasibility of the TBAA method, we performed a stepwise comparison of the tract integrity between schizophrenia patients and healthy subjects. Because this involves multiple comparisons, TFCE was used to weight the t‐statistic and the FWER was controlled. We found significant differences in 20 clusters involving 5 association fibers and 5 callosal fibers. These tracts have been consistently reported in previous studies [Boos et al., 2013; Camchong et al., 2011; Wang et al., 2011a]. Notably, we also detected clusters with significant differences in projection fibers, such as in frontostriatal tracts and thalamic radiation, which are seldom reported in the literature. Our results demonstrate that the TBAA method is a feasible and sensitive method that can be used to differentiate the integrity of aberrant tracts in the brains of a large cohort of patients with schizophrenia.

According to our methodology, TBAA is primarily used for the tract‐based analysis of DSI data. However, it also applies to high angular resolution diffusion imaging (HARDI) and DTI data. Specifically, a DTI dataset can be derived from NTU‐DSI‐122 by sampling the DW volume images with b‐value 1000 s/mm² along 18 noncolinear directions via linear interpolation. The 18 interpolated DW volume images and the b ₀ volume image can be processed using linear fitting to generate the tensor map. Each individual DTI dataset can be registered to the DTI template via linear transformation [Friston et al., 1995], followed by a nonlinear registration algorithm, LDDMM‐DTI [Cao et al., 2006]. The existing tract coordinates can be transformed from the DTI template to native DTI space via a transformation between the template and individual DTI datasets. A similar approach can also be applied to HARDI data.

TBAA improves the template‐based approach by providing a comprehensive list of white matter tract bundles on a DSI template, NTU‐DSI‐122, and an advanced registration algorithm that ensures accurate registration in both image and diffusion domains. The trajectories of the reconstructed tract bundles have been confirmed to follow the anatomical landmarks on the accompanying T1W images of the template. A two‐step registration strategy is used to register a group of DSI datasets to create a SST, and to register the SST to the NTU‐DSI‐122 template. By transforming the sampling coordinates from the template space to the native space, the microstructural property index of the tract bundles is extracted for each individual dataset. One should note that TBAA belongs to the template‐based approach which assumes that the tract bundles reconstructed on the template, once transformed to the individual's native space, can represent individual's tract bundles. Comparing to the individual‐based automated tractography, TBAA overlooks the individual variations of fiber pathways but provides a common trunk of the pathways for comparisons. Comparing to the approach that estimates the structural connectivity [Daducci et al., 2012; Hagmann et al., 2007], TBAA and other tract‐specific analyses focus on measuring microstructural property of each individual tract bundle, whereas the structural connectivity approach emphasizes the network property of the connected brain regions.

The TBAA method has limitations. First, the method is not applicable to subjects with macroscopic brain lesions, such as brain tumors and congenital anomalies, or to subjects that have experienced a stroke. These lesions would cause large errors in the spatial registration of the brain images and provide incorrect localization data of white matter sampling. Second, the NTU‐DSI‐122 template was developed from healthy adults that were 20–40 years old. The registration error between individual DSI data and the DSI template may increase if the age of the studied subjects deviates from this age range. This limitation can be ameliorated by building a series of age‐dependent templates with similar tract coordinates that are transformed for various ages. Third, in the current version of TBAA, only 76 major tract bundles are reconstructed. This may not meet the needs for finer tracts that connect specific brain regions. Nonetheless, one could perform diffusion tractography to reconstruct tracts of interest on the DSI template and apply the tract coordinates using the TBAA method. Finally, this study only uses GFA as an index of microstructural property. Other voxel‐based indices that are more specific to other aspects of microstructural properties are readily applicable to the TBAA method.

In conclusion, we proposed an automatic method, TBAA, for tract‐based analysis over the whole brain. Compared with previous tract‐specific analyses, TBAA provides a comprehensive list of the white matter tracts in the human brain and an accurate registration strategy for spatial normalization. In the validation experiment, TBAA shows high geometric agreement with the tracts reconstructed manually on individual datasets. It also shows small within‐group variability of the measured GFA values. In the feasibility demonstration on patients with schizophrenia, TBAA is capable of detecting aberrant tracts that are consistently reported previously. Therefore, TBAA is potentially valuable for systematic investigation of tract integrity over the whole brain, particularly in a large cohort study.

Supporting information

Supporting Information