Connectivity cluster analysis for discovering discriminative subnetworks in schizophrenia

Abstract

In this manuscript, we present connectivity cluster analysis (CoCA), a novel computational framework that takes advantage of structure of the brain networks to magnify reproducible signals and quash noise. Resting state functional Magnetic Resonance Imaging (fMRI) data that is used in estimating functional brain networks is often noisy, leading to reduced power and inconsistent findings across independent studies. There is a need for techniques that can unearth signals in noisy datasets, while addressing redundancy in the functional connections that are used for testing association. CoCA is a data driven approach that addresses the problems of redundancy and noise by first finding groups of region pairs that behave in a cohesive way across the subjects. These cohesive sets of functional connections are further tested for association with the disease. CoCA is applied in the context of patients with schizophrenia, a disorder characterized as a disconnectivity syndrome. Our results suggest that CoCA can find reproducible sets of functional connections that behave cohesively. Applying this technique, we found that the connectivity clusters joining thalamus to parietal, temporal, and visuoparietal regions are highly discriminative of schizophrenia patients as well as reproducible using retest data and replicable in an independent confirmatory sample. Hum Brain Mapp 36:756–767, 2015. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

Schizophrenia is often characterized as a disease of disconnectivity in the brain [Friston and Frith, 1995, Fornito et al., 2012]. Several studies have been performed to test this hypothesis using resting state fMRI data in the last two decades. Unfortunately, the regions showing disconnectivity in the disorder are inconsistent across studies [Pettersson‐Yeo et al., 2011]. Liang et al. [2006] noticed that functional abnormalities in patients with schizophrenia are distributed across several regions of the brain rather than localized. Bluhm et al. [2007] observed significantly reduced strength of functional connections between posterior cingulate and the lateral parietal, medial prefrontal, and cerebellar regions in disease subjects. Conversely, Zhou et al. [2007] found reduced functional connectivity between bilateral hippocampi and posterior cingulate cortex, extrastriate cortex, medial prefrontal cortex, and parahippocampus gyrus in disease cases. Salvador et al. [2010], noted that hyperconnectivity of medial and orbital frontal structures with caudate, right hippocampus, and amygdala were associated with schizophrenia. Pettersson‐Yeo et al. [2011] summarized the findings from 35 studies in chronic schizophrenia patients, including those mentioned. While connectivity in the frontal lobe is among the most commonly implicated functional connections, there were a number of other strong candidate circuits implicated in psychosis such as frontotemporal connections, connectivity of corpus callosum, and anterior cingulate gyrus to cortical and subcortical regions such as the thalamus

Most of these studies first construct a brain network (using a standard Automated Anatomical Labeling [AAL] atlas [Tzourio‐Mazoyer et al., 2002]) for each subject from the resting state fMRI data where each AAL region is a node and edges connect every pair of regions. The strength of an edge between a pair of nodes is computed as the correlation between the mean time series of voxels from each region. The association between two regions is evaluated using a standard t‐test to compare differences in the connectivity strength (time series correlation) of the regions between subjects with schizophrenia and those without. The issue of multiple comparisons is handled using a common false discovery rate (FDR) approach. All those edges that are statistically significant after FDR correction, according to a user‐chosen threshold, are treated as implicated edges in schizophrenia. A graph with n nodes has $\left(\begin{array}{c}n\\ 2\end{array}\right)$ connections, and even for graphs with small number of nodes the number of connections is often very large, for example, a graph with 90 nodes will have 4,005 connections. The large number of such connections along with low signal‐to‐noise ratio hinders the chance of discovering true associations.

To address this challenge, Zalesky et al. [2010] proposed a network‐based statistic (NBS) approach. NBS first evaluates the significance of association for every edge in a brain network and then constructs a network with only those edges whose t‐statistic is greater than a user‐specified threshold. The largest connected component in this newly constructed network is evaluated for statistical significance using a randomization experiment. The key contribution of this approach is that instead of evaluating individual edges for significance, it evaluates the biggest connections. However, it still relies on the univariate testing of edges to determine the interesting edges to construct the network and so low signal‐to‐noise ratio can adversely affect this step and the outcome of this approach. Another approach in the form of spatial pairwise clustering (SPC) [Zalesky et al., 2012] is proposed to control the FDR by leveraging the spatial proximity of the nodes in the edges whose t‐statistic is greater than a user‐specified threshold. This approach groups two (or more) edges into one where each node in one edge is close to the corresponding nodes in the other edge. The group with greatest number of edges is then evaluated for statistical significance using a randomization experiment that is similar to that of NBS. This approach is also limited due to the use of univariate testing of individual edges and due to the fact that there could be connections that are not in close proximity that are disrupted in schizophrenia.

In this article, we propose an alternative approach, Connectivity Cluster Analysis (CoCA), to discover disrupted subnetworks in schizophrenia while controlling the FDR. Our approach is based on two key observations. First, the functional connections are assumed to be statistically independent of each other (that is, the strength of two functional connections in a subject are not related) in traditional univariate testing, in NBS, and in SPC. However, studies have shown that there are several subnetworks within the brain, suggesting that the connections within the subnetworks and those that are in between two subnetworks behave similarly [Lee et al., 2012, van den Heuvel et al., 2008]. Moreover, individual testing of connections from a subnetwork that are strongly related can penalize the resulting P values during multiple hypothesis correction, thereby leaving only those connections that, perhaps by chance, show the greatest group differences. Second, due to the noise in fMRI data testing connections individually will result in the selection of only a few connections from different underlying subnetworks resulting in spurious findings like diffuse disconnectivity [Liang et al., 2006]. Lack of adherence to these two observations in earlier approaches could be contributing to inconsistent findings.

Empirically, multiple groups of brain regions that are found to exhibit strongly correlated BOLD time series are deemed to work together toward a specific function and are, therefore, referred to as modules [Meunier et al., 2009]. The presence of modules also results in redundant information in terms of functional connections in the brain network. For example, consider a part of a hypothetical brain network shown in Figure 1, where three blue and two green nodes are shown. These blue and green sets of nodes represent two modules where the functional connectivity (correlation) of the nodes within each set is expected to be strong. For each subject, the time series for blue and green nodes are shown. When all blue nodes and the green nodes “emit” their respective time series, then all the six connections between blue and green nodes will show very similar correlation values. Therefore, the presence of modularity results in multiple connections with similar strengths as shown in the example in Figure 1. These connections with similar strengths will potentially inflate the number of hypotheses that are tested when group differences are studied. This problem is further compounded by the fact that the noise inherent in the measured BOLD signal will distort the P values irregularly and so the connections that are significantly associated with the group in question tend to be different in different scenarios. In summary, low signal‐to‐noise ratio and the redundancy in the connections pose a challenging problem for studying the “disconnectivity hypothesis” in schizophrenia.

Figure 1.

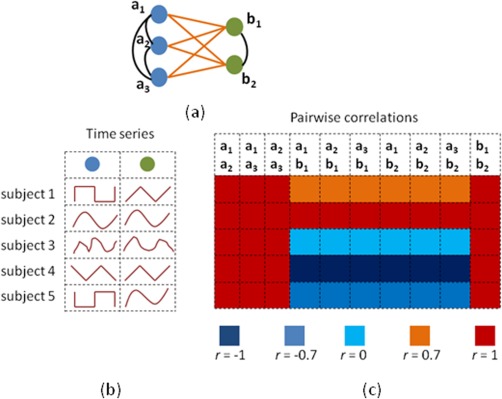
An example to illustrate the presence of duplicate connections. The network with three blue and two green nodes has two types of connections: (i) within group (shown in black), (ii) across group (shown in orange). The within group connections are those that have high correlations in all subjects. The across group connections can be high or low, but they all have the same strength. Instead of studying group differences using each of the within group and across group connections, one can represent them as groups and study the significance of each group in explaining group differences. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The CoCA approach first groups functional connections with similar correlation values over a group of (healthy and disease) subjects into clusters, and represents the cluster with its mean functional connectivity. The connectivity clusters thus discovered can be further used to study their role in disease. In grouping similar functional connections, CoCA reduces the redundancy in the analysis, by representing a cluster with the mean functional connectivity strength of its constituent edges CoCA addresses the low signal‐to‐noise ratio in fMRI data. Moreover, several regions in the brain are known to work synergistically to achieve a specific function (e.g., visual network, frontoparietal control network [Fornito and Harrison, 2012]); the CoCA approach has the potential to reveal, in a data‐driven fashion, the synergistic relationships between different regions of the brain, as well as their role in disease.

A key component of the CoCA approach is choosing the appropriate number of clusters: too few clusters will result in loss of signal and too many clusters will reduce data redundancy suboptimally. We also examine whether an emphasis on reproducibility of the clusters on data collected from same samples also enhances replicability of the results in independent sample sets. Following the terminology established in [Wisner et al., 2013], we refer to the consensus between features or findings from two different sets of fMRI scans obtained from the same sample as reproducibility. We refer to the consensus between findings from two sets of samples as replicability. We repeat our approach on a confirmatory sample to study cross‐sample replicability. Our results indicate that the associated connectivity clusters are not only reproducible in the same sample but also replicable in independent sample sets. We compare our findings with that of NBS to demonstrate the additional value of the CoCA approach.

METHODS

Connectivity Cluster Analysis

Discovering subnetworks

Using the AAL atlas to define 90 brain regions, we summarized the voxel level time series for each region by computing the average time series of the member voxels from each fMRI scan. We then constructed a brain network where the 90 brain regions of interest (ROIs) were nodes and edges connected all pairs of nodes. The correlation between the mean time series from two regions was treated as the weight of the edge connecting the two regions. Using all the brain networks computed from cases and controls, each with 4,005 functional connections (ROI pairs), we performed Ward's method for clustering on the functional connections with a Euclidean distance metric [Tan, 2007]. The ROI pairs constituting each cluster were expected to behave cohesively, due to the Euclidean distance metric used. This allowed us to interpret each cluster as a functional subnetwork that was active or inactive in a given subject.

Determining the number of clusters

Several approaches for choosing the number of clusters have been studied in the statistics and machine learning community. They include ratio of within‐cluster and between cluster distances [Tan, 2007], information‐theoretic criteria [Still and Bialek, 2004] and gap‐statistic [Tibshirani et al., 2001]. In this article, we use the gap‐statistic approach that determines the appropriate choice for number of clusters as one where the gap (difference) between the logarithm of within clusters distances in a given dataset and the expected logarithm of within clusters distances for a dataset with similar range of values is maximal.

Computing features from subnetworks

Functional networks from all subjects can be represented as a data matrix with n subjects (cases + controls) as rows and $\left(\begin{array}{c}90\\ 2\end{array}\right)$ = 4,005 functional connections as columns. To estimate the association of functional connections in schizophrenia a two‐sided t‐test is generally performed on each of the columns individually. Now, to test our hypothesis that the discovered subnetworks (clusters) may be associated with diagnostic status, we need to represent the submatrix of size |subjects| × |ROI pairs| that belong to a cluster as a vector of |subjects| × |cluster|. To do this, we have to summarize the activity of the subnetwork by considering the strength of the functional connections that constitute the cluster. This can be done in several ways including computing the mean of the functional connections that form a cluster, the median or the variance. The mean or median values would indicate the activity of the subnetwork in a given subject, whereas the variance would reflect the cohesiveness of the cluster. Here we are interested in understanding the association between the activity of a subnetwork and the disease, and so we rely on mean of the values to determine the activity of the cluster.

We compared the results of CoCA with that of existing approaches, univariate testing and NBS, to demonstrate advantages of CoCA.

Construction of a Synthetic Dataset and Comparison

We created a synthetic fMRI dataset with 100 subjects (50 cases and 50 controls). For each “synthetic” subject, we created a random set of 90 time series to represent fMRI signal measured from each of the 90 AAL regions. Real fMRI data has natural modules in the data such as visual and auditory regions. To detect this structure, we first computed the median value of a functional connection overall all subjects in T1 data for all functional connections. We then created a brain network of 90 regions by placing an edge when the median functional connectivity was greater than 0.8. The components (connected set of nodes) in this network are treated as natural modules. We imposed this module structure onto the synthetic data using the same time series along with Gaussian noise (mean = 0, sigma = 1) for all the regions within the same component. For example, a, b, and c were brain regions that formed one module. To impose this structure on the synthetic data, we randomly selected one of these brain regions and used its “synthetic” time series for the other two regions after adding a small amount of random noise. This process results in fMRI data that yielded networks with similar properties for all the 100 subjects and so there was no signal to separate hypothetical cases from controls in the data. We then imposed a signal to separate cases from controls by using the same time series (with Gaussian noise) for the regions in the components that had six and eight regions, respectively, in a selected percentage of cases. The selected percentages were 4, 10, 20, 30, 40, 50, and 60%. The resultant dataset should have had (8 × 6=) 48 connections that exhibit different connectivity strength in the selected subjects.

We then used univariate testing, NBS, and CoCA to evaluate the degree to which they recovered the 48 imputed edges. For the univariate testing approach, we selected the top 48 edges with significant P values and computed the number of imputed edges that were recovered. For NBS, we selected the top 2% edges (80 connections) to construct the network and further discovered the biggest connected component. Note that the number of edges chosen for network construction here was higher than that of the imputed number of edges. The fraction of imputed edges that were part of the discovered largest connected component was computed for NBS. For CoCA, we found 50 clusters and the subnetwork with the significant P value was used to determine the fraction of imputed edges that were recovered. Note that in this synthetic evaluation, we did not compare the significance values or perform any FDR correction for univariate testing of CoCA as our goal was to test the relevance of the selected connections to that of the imputed connections.

Samples

A set of 27 chronic schizophrenia patients (23 male and 4 female, age: mean = 34.1, SD = 9.6) and 31 healthy subjects (24 male and 7 female, age: mean = 30, SD = 9.6) were enrolled for the study as per [Camchong et al., 2009]. Written informed consent was provided by all the subjects and they received payment for participation. All subjects recruited in this study were free of neurological problems. Schizophrenia diagnosis was confirmed according to the Structured Clinical Interview for DSM‐IV. fMRI data was obtained from these 58 subjects at two different time points 9 months apart. We refer to the first set of scans as T1 data and the second set of scans as T2 data. We also used a set of scans from 75 schizophrenia subjects (52 male and 23 female, age: mean = 36.4, SD = 11.8) and 105 healthy subjects (69 male and 36 female, age: mean = 37.6, SD = 12.6) as our cross‐validation sample to replicate our findings obtained from T1 and T2 data.

In terms of characterizing the sample at T1, the mean (n = 25) total score for the scale for the assessment of negative symptoms (SANS) was 34.04 (std. = 14.58) and for the scale for the assessment of positive symptoms (SAPS) was 23.64 (std. = 14.26). For the cross‐validation sample, the mean (n = 55) of SANS and SAPS was 32.32 (std. = 15.78) and 27.29 (std. = 17.35), respectively. With regard to medication, among patients at T1 (n = 27), 20 were on one atypical drug and no typical drugs, two were on two atypical drugs and no typical drugs, and five were not on any antipsychotic drugs. At T2, 17 were on one atypical drug and no typical drugs, two were on two atypical drugs and no typical drugs, and eight were not on any antipsychotics. Of the patients in our cross‐validation sample (n = 75), 63 were on one atypical drug and no typical drugs, six were on two atypical drugs and no typical drugs, two were on one atypical and one typical drug, one was on a typical antipsychotic, and three subjects were not on any antipsychotics.

Image Acquisition and Preprocessing

A 6‐min‐resting state fMRI scan was collected from each subject using a Siemens Trio 3T scanner (Erlangen, Germany). Sequence parameters: gradient‐echo EPI 180 volumes, TR = 2 s, TE = 30 ms, 34 contiguous AC‐PC aligned axial slices, voxel size = 3.4 × 3.4 × 4 mm, matrix = 64 × 64 × 34. Participants were instructed to be as still as possible, keep their eyes closed and stay awake. At the end of the scan, all participants were asked to recollect if they fell asleep. A replacement scan was obtained from one participant who reported having fallen asleep. A high‐resolution T1‐weighted anatomical image was acquired using a magnetization prepared rapid gradient echo sequence.

Preprocessing on each scan was performed using FMRI Expert Analysis Tool Version 5.91, part of FMRIB's Software Library [Smith et al., 2004]. Motion correction was carried out using MCFLIRT [Jenkinson et al., 2002]. B0 fieldmap unwarping was performed using acquired field maps and PRELUDE+FUGUE [Jenkinson, 2003, 2004] to correct for geometric distortion. Slice‐timing correction was carried out using Fourier‐space time‐series phase‐shifting. Voxels that are not part of the brain were removed using BET [Smith, 2002]. Spatial smoothing was performed using a Gaussian kernel of FWHM 6 mm. Highpass temporal filtering was performed to remove low‐frequency artifacts mostly due to signal drift in scanner stability (Gaussian‐weighted least‐squares straight line fitting, with sigma = 50.0 s). Functional images were then registered into standard space (Montreal Neurological Institute‐152) using standard procedures.

Measuring Reproducibility of Subnetworks

We first generated 150 clusters from the T1 and T2 datasets of the same subjects independently. The choice of 150 clusters was obtained using the gap‐statistic approach mentioned above. We then estimated the similarity in the cluster configurations by computing Jaccard similarity between the clusters discovered from T1 and T2 datasets. Jaccard similarity for any two clusters is computed as the fraction defined by the number of functional connections that are shared by both the clusters divided by the total number of functional connections present in both the clusters [Tan, 2007]. Note that this is a conservative estimate of the similarity between two clusters, as it penalizes for any functional connections that are not shared. We selected the most reliable clusters, that is, those that had a Jaccard score greater than 0.5, for further evaluation.

RESULTS

Performance Evaluation of CoCA in Simulated Data

We first created synthetic datasets by imposing connections between two selected modules with various signal strengths, that is, fraction of cases in which the imputed signal was relatively higher than normal. We then used univariate testing, NBS, and CoCA to evaluate the degree to which they recovered the 48 imposed edges. These results are shown in Figure 2. When signal strength is extremely low (4%) and when the signal strength is higher than (60%), all three approaches perform similarly, with very low and very high recovery, respectively. As hypothesized, NBS performed better than the univariate testing in most cases. CoCA outperformed both NBS and univariate testing when the signal strength was not too weak or not too strong (10%–40%). The high recovery score of CoCA in contrast to that of NBS and univariate testing was mainly due to its ability to directly group the imposed between‐module connections and thereby handle the low signal‐to‐noise ratio. Therefore, these results shed light on the ability of CoCA to recover the imposed between‐module connections with low‐moderate signal, a circumstance that is likely to characterize many empirical datasets.

Figure 2.

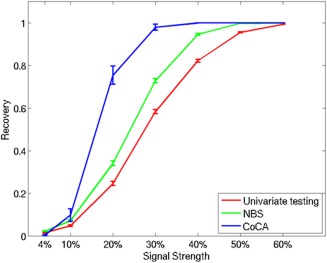
Fraction of imputed edges recovered using univariate testing, NBS, and CoCA at different signal strengths.

Application of CoCA to Empirical Schizophrenia Data

We first studied the effect of the number of clusters on redundancy using gap‐statistic. We chose k = {20, 30, 40, 50, 100, 150, 200, 250, 300, 350, 400, 500}. For every choice of k, we computed the gap‐statistic as shown in Figure 3. Higher gap‐statistics indicate a greater difference in the within‐cluster logarithm of the sum of the distance from that of the null distribution. The gap‐statistic stays above 4 for k = 150, 200, and 250. As our goal was to reduce redundancy among the connections and a smaller number of clusters are effective in achieving this goal we chose k = 150.

Figure 3.

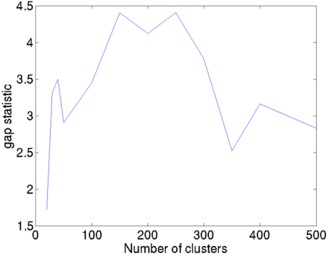
Relationship between the number of clusters and gap‐statistic. The maximum gap is seen at k = 150 and 250.

A test of reproducibility of clusters was performed by comparing how similar the cluster configurations (i.e., the functional connections that are part of a cluster) were when discovered from T1 and T2 data sets independently. Figure 4 shows the overlap in the connections between every pair of clusters where one cluster is from T1 and the other is from T2, as measured by their Jaccard score. The clusters were ordered in decreasing order of the Jaccard scores between two scans. Note that Jaccard is a conservative score that penalizes a pair of clusters when either of them have a connection that is not a part of the other clusters. We chose a threshold of 0.5 for the Jaccard score used to select the most similar clusters. There were 37 clusters that passed this threshold.

Figure 4.

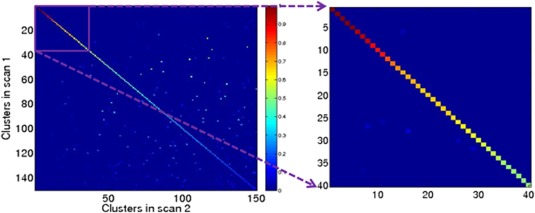
Pairwise Jaccard scores for 150 clusters discovered from T1 and T2 data, independently. Jaccard scores reflect the degree of similarity in connectivity cluster composition. Larger the Jaccard similarity, greater is the confidence that the connectivity cluster is nonrandom. There are 37 clusters with a Jaccard score greater than 0.5.

We then computed the cluster connection strength of each of the 37 selected clusters in each subject as described in the Methods section. We further evaluated the reproducibility of cluster connection strengths (computed as the correlation of 37 cluster connections strengths in each subject at T1 and T2) for each subject and compared it to that of individual connections. The distribution of the correlations for all 58 subjects (27 cases and 31 controls), computed using clusters on T1, T2 data as well as individual functional connections is shown in Figure 5. This figure suggests that the reproducibility of the features obtained from clusters was high (mean r = 0.71, SD r = 0.14) compared to that of individual connections (mean r = 0.61, SD r = 0.12). Thus the reduction in noise from summarizing a set of functional connections resulted in 13% more variance being accounted for across timepoints. This is a marked effect.

Figure 5.

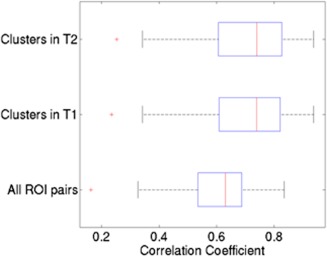
Replicability of the functional connections, measured as the correlation of connectivity strength derived from T1 and T2 data using the clusters. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

In the above comparison, the number of ROI pairs was 4,005 while the number of clusters was only 37. Correlations between cluster means and individual connections were not directly comparable as the number of data points in computing the correlations were very different. To account for this difference, we randomly sampled 37 ROI pairs from each subject and computed the intersession reproducibility. We repeated this for 10,000 random samples of 37 ROI pairs. We then computed the fraction of random samples whose median correlation was greater than the median correlation of cluster mean values to attain a P value of 0.0074.

Characterizing Connectivity Clusters in Patients with Schizophrenia

Using the 37 reliable clusters between T1 and T2 data, we constructed connectivity cluster strength and evaluated them for association with schizophrenia. The cluster strength values of the reliable clusters were tested for association using a t‐test‐based analysis in T1 and T2 data, independently (See Supporting Information Figure 1, for examples of clusters, how their strength is computed and used to study group differences). The P values of these clusters are shown in Figure 6. The Clusters 24, 19, and 8 were the best three clusters in T1 data in the decreasing order of their discriminative power. Similarly, Clusters 8, 24, and 19 were the best three clusters in T2 data. The same set of clusters was found to be highly associated with schizophrenia in both the T1 and T2 datasets, indicating high reproducibility of the findings. All of these clusters had a significance value that was better than P value 0.05 (−log(P value) = 1.3), however, this threshold does not account for multiple comparisons. To avoid inflating experimentwise error, we computed FDR by generating a null distribution of P values by permuting the labels on the subjects and computing the P values for the 37 subnetworks, 1,000 times. The FDR suggested the probability for any subnetwork to P value equal to or higher than the one seen in the true label scenario by random chance. The FDR values of these clusters in T1 data were 0.5%, 0.5%, and 0.2%, respectively, and the FDR values in T2 data were 0%, 0%, and 0%, respectively. These strong significance values and the fact that the same clusters were significant in both datasets are suggestive of their role in schizophrenia. Effect sizes for these clusters are reported in Table 1.

Figure 6.

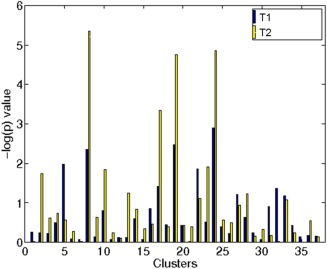
Discriminative power of 37 reliable clusters in T1 and T2 data. Clusters 8, 19, and 24 are top 3 discriminative clusters in T1 and T2 data. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 1.

Statistical significance of the three clusters, 8, 19, and 24, from the T1, T2, and the CV datasets.

Sample	Cluster	−log P value	t‐Statistic	Degrees of freedom	Effect size
Time 1 (T1)	8	4.95	2.97	54.28	1.38
	19	3.82	3.05	55.95	0.79
	24	1.83	3.40	54.57	0.84
Time 2 (T2)	8	4.91	5.09	54.87	1.90
	19	3.39	4.73	51.55	1.10
	24	2.25	4.77	55.08	1.36
Cross‐validation (CV)	8	4.95	4.52	172.51	0.89
	19	3.82	3.87	174.08	0.56
	24	1.83	2.46	167.31	0.35

Note: Cluster configurations from T1 and T2 are used to compute these values in T1 and T2 datasets, respectively. Cluster configurations from T1 are used to compute these values for the CV sample. The values were very similar when cluster configurations from T2 were used.

Figure 7 shows the wireframe diagrams for three clusters, 8, 19, and 24. Note that all the three clusters were bilateral that involved thalamus in the left and right hemispheres. Cluster 8 composed of connections between thalamus and primarily striate visual regions, whereas Cluster 19 composed of connections between thalamus and extrastriate, lateral visual regions. Cluster 24, conversely, composed of connections between thalamus and lateral temporal cortex. All clusters were generally bilateral, although this was not a constraint of the method. Figure 8 shows the mean connection strength of the members of these clusters in T1 and T2 datasets. In all cases, patients showed greater connectivity strength than did healthy controls.

Figure 7.

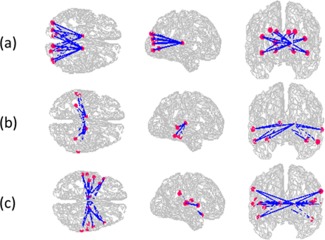
Best three discriminative subnetworks in the brain: (a) thalamus and visual region (Cluster 8), (b) thalamus and parietal region (Cluster 19), and (c) thalamus and temporal regions (Cluster 24), respectively. FDR values for these three clusters are 0.005, 0.005, and 0.002, respectively. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 8.

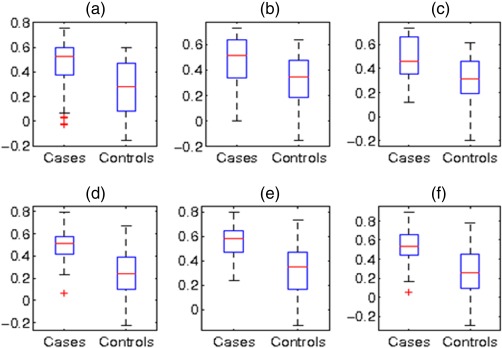
Distribution of mean connection strength for each of the top three discriminative clusters in T1 [(a), (b), and (c)] and T2 data [(d), (e), and (f)]. In all these subnetworks, the connections are stronger in schizophrenia as opposed to healthy subjects. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Cross‐Validation of Connectivity Clusters in Schizophrenia

We also evaluated the significance of association of the three clusters, 8, 19, and 24, discovered from T1 data on an independent cross‐validation sample with 75 schizophrenia subjects and 105 healthy subjects. The −log(P value) for Clusters 8, 19, and 24 were 4.9554, 3.8280, and 1.8335, respectively. Effect sizes and t‐statistics for the cross‐validation sample are reported in Table 1. Our independent sample evaluation confirmed the replicability of these associations in independent datasets.

Comparison of CoCA with alternative approaches

To compare the performance of CoCA with univariate testing and NBS, we computed the P values and FDR for individual connections as well as P values for the largest connected component. The P values and FDR for individual connections are shown in Supporting Information Figure 2. The connection with best P value in T1 has an FDR of 0.29 indicating the adverse impact of redundancy and noise in the data. Conversely in T2 there are 111 connections with P value ≤ 0.05 and FDR < 5%.

NBS is an alternative approach that can discover discriminative subnetworks from functional networks. It first discovers significantly associated functional connections in schizophrenia and then constructs a network using the most significant connections. The largest connected component from this network is then recovered and a P value to quantify its statistical significance is computed by repeating the NBS approach on data obtained by random permutation of class labels. Figures 9a and 9b show the subnetworks discovered using NBS from T1 and T2 data, respectively. Each of these subnetworks had 20 connections of which only two were common. In addition, the two subnetworks were not significantly different between patients and controls. The lack of agreement between the subnetworks in T1 and T2 datasets and poor P values indicate that the noise in the data was preventing from discovering reliable associations in the data, whereas our approach circumvents this problem by first discovering clusters that group similar signals as well as filters for unreliable clusters.

Figure 9.

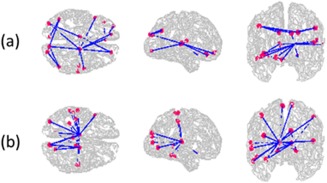
Subnetworks discovered using a competing NBS approach from (a) T1 and (b) T2 data. Twenty edges were selected in each of these networks and only two of them are common. The P values for these networks are 0.07 and 0.32, respectively. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Demographic, Clinical, and Behavioral factors

We evaluated the relationship between the cluster connectivity strength for the Clusters 8, 19, and 24 (found in T1 data) and the demographic, clinical, and behavioral factors. We correlated the age of all the subjects (T1 and the cross‐validation sample) used in this article with the connectivity strength of the three clusters (8, 19, and 24) that were found to be significantly associated with schizophrenia. These results are shown in Supporting Information Figure 3a–c. We found a weak but significant relationship r = 0.13 (P value < 0.02) with cluster 19 and age. The other two clusters did not show a significant relationship with age.

We also evaluated the relationship between gender and the strength of the three clusters. We found no relationship between gender and connectivity strength, as shown in Supporting Information Figure 3d–f.

SANS and SAPS were assessed for 80 schizophrenia subjects (25 from T1 and 55 from the cross‐validation sample) with the structured clinical interview. These results are shown in Supporting Information Figure 4. There was no significant relationship between either of these variables with that of connectivity of the three clusters that were found to be significantly associated with schizophrenia. Antipsychotic dosage information that was collected as part of Camchong et al. [2011] study was used to assess Chlorpromazine dosage equivalents for 18 schizophrenia subjects. For these subjects, the relationship between cluster connectivity strength and Chlorpromazine dosage was assessed. These results are shown in Supporting Information Figure 5. We did not find any significant relationship between medication and connectivity of the three clusters (8, 19, and 24), perhaps due to the noise inherent to this means of measuring medication effects.

DISCUSSION

We studied the hypothesis that redundancy and noise in the edges of brain network can be reduced by grouping similar edges over a group of subjects using a data‐driven approach known as CoCA. Using synthetic data we demonstrated that CoCA is suited to address the redundancy and noise in the connections much more than the competing approaches. We also studied the relevance of these connectivity clusters to schizophrenia. We found that connectivity clusters are in fact an efficient representation of the connectivity data, and we determined that for our dataset the optimal number of clusters was 150. In an analysis of all connectivity clusters with adequate reproducibility, connections from thalamus to parietal, temporal, and visuoparietal regions were most highly associated with schizophrenia. These thalamic clusters were significantly predictive of the disorder in both baseline and retest datasets. They were also found to be significantly associated with schizophrenia in an independent sample. These thalamic clusters showed hyperconnectivity in patients with schizophrenia. We also found that these connectivity clusters could not be discovered using state‐of‐the‐art subgraph association methods.

Established, edge‐based evaluation has several limitations and some subnetwork based evaluation approaches [Fornito et al., 2011, Zalesky et al., 2010] that are perceived to be better for capturing intraregional disruption in the case of schizophrenia also have these limitations. These approaches first evaluate the association of every edge separately and so the problem of noise is not directly addressed. Moreover, the redundancy that exists between connections is ignored. Our results on a synthetic dataset demonstrate that CoCA has the ability to address these problems by grouping redundant and often noisy edges into clusters that dramatically reduce the number of hypothesis tests, thereby improving power. Although in our evaluation, we imposed only one set of between‐module connections, in reality there can be more between module connections that are associated with schizophrenia and CoCA has the ability to directly find them. This is demonstrated in our evaluation of CoCA on real fMRI datasets.

Our results on real datasets demonstrate that not only do these earlier approaches find subnetworks involving different nodes from what our CoCA approach discovered, but also that their findings are inconsistent between T1 and T2 datasets. These observations suggest the utility of the CoCA‐based approach for discovering subnetworks associated with schizophrenia. The key parameter of our approach is the choice of number of clusters. This parameter is unique to our approach because the existing techniques do not deal with grouping features. One could arbitrarily choose a number of clusters, and work with the resultant clusters. However, this will affect the degree to which the redundancy and noise are handled. Furthermore, this also affects the reproducibility of the findings. We provided a systematic analysis to choose this parameter that took into consideration the redundancy of the features. Our results suggested that if too many clusters are chosen the redundancy between the clusters is high and when too few (<150) clusters are chosen the redundancy is still high because of grouping too many nonrelated features together which results in the loss of information.

Improving reproducibility and replicability is a primary motivation for the CoCA technique. Existing resting state fMRI base studies that test every edge in the functional network for association with schizophrenia report findings that do not agree with each other. Lack of replicability could be attributed to various factors including small sample size, noise in the data, difference in the scanners, difference and study population, preprocessing pipelines used, and choice of analysis techniques. However, no efforts have evaluated the replicability of the reported graph theoretic analysis based findings in the context of schizophrenia. In this article, we quantify replicability of the findings using state‐of‐the‐art analysis techniques and compare it to that of the proposed CoCA approach. Our findings suggest that the state‐of‐the‐art analysis techniques result in findings that are less reproducible, whereas the findings of CoCA approach are not only reproducible on data from the same set of subjects but also replicable in independent subjects. Our results indicate that the lower than expected level of reproducibility and replicability with existing studies derives from the triangle of fMRI problems from noise, redundancy, and multiple hypothesis testing [Zalesky et al., 2010] may be overcome by clustering functional connections in an optimal manner.

We discovered that connectivity clusters connecting thalamus to parietal, temporal, and visuoparietal regions are associated with schizophrenia. Multiple graph theoretic analysis studies of resting state fMRI data have reported that frontotemporal disconnection is associated with schizophrenia, in addition to prefrontal cortex disconnectivity with parietal and temporal cortices [Fornito et al., 2011; Liu et al., 2008; Repovs et al., 2011; Zalesky et al., 2010]. These findings suggest that disconnectivity in schizophrenia is diffuse in multiple regions of the brain, that is also observed using NBS approach on our data. However, it is important to note that using T1 and T2 data we observed that diffuse disconnectivity is associated with schizophrenia but the disconnections are not consistent between T1 and T2 data. This lack of consistency could be partly attributed to the noise in the data, that our CoCA approach is capable of handling, due to which our thalamic connectivity clusters are found to be consistent.

Moreover, we found that thalamus exhibits hyperconnectivity in schizophrenia subjects, while existing studies report hypoconnectivity in most of their findings. Consistent with the current result, Skudlarski et al. [2010] and Zhang et al. [2012] also reported that hyperconnectivity in thalamus to be associated with schizophrenia. This suggests that connectivity that is higher than normal could result in functional disruption. Recent work by Driesen et al. [2013] found that N‐methyl‐d‐aspartate glutamate receptor (NMDA‐R) antagonist ketamine, that is known to affect gamma oscillations, when administered to 22 subjects resulted in schizophrenia like symptoms as well as global hyperconnectivity in resting state fMRI data. While this study relates hyperconnectivity with schizophrenia like symptoms, it does not shed light on the reason for hyperconnectivity. Moreover, the inconsistency between studies that report hyperconnectivity and hypoconnectivity in schizophrenia requires further investigation.

Limitations and future work

Although we show the utility of using connectivity clusters that are capable in addressing challenges relevant to fMRI data as well as result in consistent findings, our study has several limitations. First, the proposed CoCA approach discovers connectivity clusters that are common in both the healthy and disease subjects. It is possible that some connectivity clusters exist in only healthy subjects or the disease subjects. CoCA approach will not be able to discover such connectivity clusters. One potential approach to address this limitation is to use CoCA to first discover clusters in each of the groups separately on one dataset and test for group differences on a different dataset. Second, the brain network constructed relies on the AAL map based parcellation and the effect of this on the findings is yet to be studied. Moreover, we use 90 brain region in this map, and the effect of granularity of this map on the choice of number of clusters, reproducibility, and the reported associations needs to be studied. Third, our findings are based on 6‐min‐scan length that is commonly used in the community, although 6 min may be too short for optimally reliable estimates of connectivity. Moreover, the edges in the brain network have been found to be dynamic and we hypothesize that the connections in the brain networks do not change with time. The effect of dynamic brain connections on our analysis needs to be studied. Fourth, information pertaining to the degree of severity of disease, psychopathology scores (SANS/SAPS) and antipsychotic drug dosage is not available on all disease subjects. We restricted our analysis of the effect of disease severity and antipsychotic drug use on the discovered clusters to those samples for which this information was available. Sixth, our study is also limited by the moderate sample size in our T1 and T2 datasets. Sixth, our findings are based on our analysis on resting state fMRI data and their relevance to task‐based fMRI datasets is yet to be studied. In addition, we did not consider the impact of choice of preprocessing steps such as spatial smoothing, motion regression, white matter regression, CSF signal regression, and global signal regression on the outcome. These steps and the respective parameter choices were earlier found to affect the outcome [Triantafyllou et al., 2006, Weissenbacher et al., 2009].

CONCLUSION

Schizophrenia is a disease that is characterized by the disconnectivity in the brain [Fornito and Harrison, 2012, Friston and Frith, 1995]. Disconnectivity hypothesis has mainly been studied with respect to each functional connection individually [Fornito and Harrison, 2012], while it is increasingly found that there exist subnetworks in the brain that accomplish specific functions. We proposed a novel connectivity cluster analysis approach, called CoCA, that can directly find subnetworks in the brain that are associated with schizophrenia. This approach is capable of addressing the noise and redundancy in edge‐based analysis that has been conventionally used in graph theoretic analysis of brain networks in the context of schizophrenia. We found that connectivity clusters connecting thalamus to parietal, temporal, and visuoparietal regions are associated with schizophrenia and they exhibit hyperconnectivity. We demonstrated that these findings are not only consistent between two datasets collected from same set of subjects, but also between those collected from independent samples.

ACKNOWLEDGEMENTS

This work was supported by UMN Doctoral Dissertation Fellowship, NSF Grant IIS‐1355072, and NIMH grants R01MH060662 and R01MH084861. Dr. MacDonald III has consulted for Astellas Pharma.

Supporting information

Supplementary Information Figure 1

Supplementary Information Figure 2

Supplementary Information Figure 3

Supplementary Information Figure 4

Supplementary Information Figure 5