Common and dissociated mechanisms for estimating large and small dot arrays: Value‐specific fMRI adaptation

Abstract

An fMRI pair‐adaptation paradigm was used to identify the brain regions linked to the apprehension of small and large numbers of items. Participants classified stimuli on the basis of their numerosities (fewer or more than five dots). We manipulated the type of repetition within pairs of dot arrays. Overall processing of pairs with small as opposed to large quantities was associated with a decreased BOLD response in the midline structures and inferior parietal cortex. The opposite pattern was observed in middle cingulate cortex. Pairs in which the same numerosity category was repeated, were associated with a decreased signal in the left prefrontal and the left inferior parietal cortices, compared with when numerosities changed. Repetitions of exact numerosities irrespective of sample size were associated with decreased responses in bi‐lateral prefrontal, sensory‐motor regions, posterior occipital and left intraparietal sulcus (IPS). More importantly, we found value‐specific adaptation specific to repeated small quantity in the left lateral occipito‐temporal cortex, irrespective of whether the exact same stimulus pattern repeated. Our results indicate that a large network of regions (including the IPS) support visual quantity processing independent of the number of items present; however assimilation of small quantities is associated with additional support from regions within the left occipito‐temporal cortex. We propose that processing of small quantities is aided by a subitizing‐specific network. This network may account for the increased processing efficiency often reported for numerosities in the subitizing range. Hum Brain Mapp 35:3988–4001, 2014. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

It has long been known that our ability to enumerate visually presented stimuli varies with the number of items presented. The enumeration of a small sample of items (1–4) is near perfect and proceeds rapidly. In contrast, enumerating a large sample of items display is substantially slower and RTs and errors are increased with each extra item that needs to be counted [Mandler and Shebo, 1982; Trick and Pylyshyn, 1993]. This contrast, between efficient enumeration of small numerosities (termed “subitizing”), and less efficient enumeration of larger quantities, has led some researchers to suggest that distinct processes are involved in these two instances: a parallel subitizing process and a serial counting process. This dual route model proposes a special role for subitizing. In contrast to this dual route model, a single process model has also been proposed [Balakrishnan and Ashby, 1991; Gallistel and Gelman, 1992]. This latter model suggests that a common counting process serves for both small and large quantities, but enumerating small numbers of elements is more efficient as it is less taxing in terms of the information units to be processed, and also enables processing with higher resolution over short time periods [Ross, 2003].

The single route model is supported primarily by evidence from fMRI studies. These studies typically contrast counting responses to small versus larger sample sizes. Using this comparison, no specific areas for the enumeration of small arrays (1–4 items) have been identified: instead, all areas active enumerating small arrays are also activated to at least the same degree or more when counting larger arrays [Piazza et al., 2003, 2002; Sathian et al., 1999]. For example, Piazza et al. [2002] report activations in a network comprising of extrastriate middle occipital and intraparietal areas which increased in spatial extent and intensity with increasing numbers over the subitizing range (1–4 dots). Since counting large quantities involves more mental processes than small number of items [e.g., individuating and localizing the items, switching attention and inhibiting “re‐counting”; Tuholski et al., 2001], the greater activation often observed for counting large numerosities is not surprising. No region shows the opposite pattern, i.e. a stronger response when counting a small number of items versus larger arrays. Therefore these studies seem to advocate a single process that mediates counting of all array sizes. The dual route model is supported primarily by the observation that the enumeration of fewer than four items is characterized by a very shallow slope, suggesting the elements may be processed in parallel. Mandler and Shebo [1982] suggested that the efficiency of subitizing may rely on a pattern matching process, as small quantities tend to form similar simple shapes (e.g., line, triangle). [see also Logan and Zbrodoff, 2003]. Neuropsychological studies have demonstrated single dissociations, with patients that cannot count larger numerosities, but can quantify less than four items—whether by serially counting them [e.g., Dehaene and Cohen, 1994; Demeyere and Humphreys, 2007] or by fast efficient subitizing [Demeyere et al., 2010]. A recent MEG study by Vuokko et al. [2013] also supports the dual route model. These authors documented early bilateral posterior temporo‐parietal responses during subitizing, whereas serial counting of larger quantities was linked to a spread of activity from bilateral parietal areas to frontal regions.

The direct comparison between counting and subitizing means that counting will always be more difficult and more time consuming and larger numerosities inherently contain subitizable numerosities. Under conditions of short durations however, larger numerosities can no longer be accurately enumerated, and the observer needs to resort to estimation: the process becomes error‐prone and the size of the errors increases with the set size [e.g., Revkin et al., 2008]. From here it follows, that to address the question whether there is a special role for small set apprehension, different to larger quantities, without the confound of task difficulty differences, the comparison that should be made is with estimation, rather than enumeration.

Subitizing has been proposed to be simply high resolution estimation, with estimation operating in the same way above and below the subitizing range, again proposing a single route process [Cordes et al., 2001; Dehaene and Changeux, 1993]. However, Revkin et al. [2008] found that discrimination difficulty as determined by Weber's law, is similar across numersosities ranging from 1 to 4 as numerosities 10–40, although precision was much higher for the subitizable quantities, demonstrating that the efficiency associated with subitizing processes is specific to small numerosities, supporting a dual route hypothesis.

The dual route model fits with a recent model, proposed by Feigenson et al. [2004], which suggests there are two distinct core systems of numerical representations and quantity estimation. The first system is concerned with approximate representations of large numerical quantities. This first core system is assumed to gives a noisy representation of number and is sensitive to the ratio between numerosities. It can be thought to underlie the process of estimation. The second core system deals with the precise representation numbers, in particular small sets of subitizable quantities.

Recent studies based on neuroimaging methods [Ansari et al., 2007; Cutini et al., 2013; Demeyere et al., 2012] suggest that small numbers are processed using both generic shared mechanism for processing of any size quantity, but crucially can also be supported by additional processes that are unique to small size items. In support of some shared mechanisms for assessing small and large discrete quantities, it has been shown that, in neurological patients, the ability to enumerate small and large dot arrays is correlated, and lesions to the fronto‐parietal network extending to posterior occipital cortex impair the ability to enumerate any size sample size—even in the subitizing range [accuracy data—Demeyere et al., 2012]. However, a closer look at the neuropsychological literature also suggests a dissociation between subitizing and counting, consistent with a dual process account. For example, patients can have preserved subitizing with impaired counting abilities [Dehaene and Cohen, 1994; Demeyere et al., 2010]. Similarly, within the same group of patients who show some evidence for shared mechanism for enumeration processing of small and large sample sizes (see above), there was also evidence supporting double dissociations [Demeyere et al., 2012]. Lesions to the left occipital cortex extending to middle temporal areas, the prefrontal and sensori‐motor regions led to subitizing impairments (e.g., reduced parallel and efficient processing of small set size—based on the reaction times), while lesions to intraparietal sulcus (IPS) caused a larger impairment in serial counting.

Few studies have directly compared estimation with subitizing. Ansari et al. [2007] examined numerical comparison processes of arrays with small (1–4) and large (10–40) numbers of elements. The task was to decide which of a two displays is numerically larger. Similarly to the study with the neuropsychological patients [see above, Demeyere et al., 2012], Ansari and colleagues reported a common mechanism for processing small and large elements in bilateral Inferior parietal lobules extending to the left precuneus. However, in addition, they reported double dissociations between comparisons for small and large dot arrays; with increased activation in right occipital‐parietal cortices when processing large compared with small quantities; and a larger involvement of the right inferior parietal cortex (specifically TPJ) when processing small versus large quantities. Activity in this latter region also correlated with individual differences in the ability to process large arrays, suggesting that the inferior parietal cortex may support enumeration of both small and large arrays. Similarly, selective modulation of the right TPJ during subitizing under dual load conditions was found in an fMRI study by Vetter et al. [2011].

Other evidence, from studies using event‐related potentials, can be used to support the dual route model. Hyde and Spelke [2009], for example, compared the processing of small quantities of dots (1–3) to larger numerical quantities (8–24). They found that an early evoked component (N1) was present when small quantities of dots were enumerated but not when large numerosities were counted. In contrast, a later component, the P2p, was associated with the processing of large discrete elements, but not small numbers. Furthermore, Cutini et al. [2013], using fNIRS, recently observed distinct hemodynamic patterns for estimations of quantities within and outside the subitizing range over bilateral IPS.

One key region that is commonly reported to be involved in enumerating both small and large quantities is the bilateral IPS [e.g., Ansari et al., 2007; Demeyere et al., 2012]. It has been suggested that the IPS is involved in representing exact, discrete quantities that can be counted [Castelli et al., 2006]. It is also suggested that regions within the right posterior occipito‐parietal network support counting processes [e.g., Ansari et al., 2007; Demeyere et al., 2012; Roggeman et al., 2011]; while the left posterior parieto‐occipital cortices and premotor areas specifically support subitizing [Demeyere et al., 2012].

In the current study, we re‐visited the debate around the single versus dual route for small and large quantity processing. Here, we capitalize on a novel paradigm we have developed [Demeyere and Humphreys, 2012], which supports a behavioral dissociation of processing small and large sample arrays and avoids confounding response enumeration times with sample size. Notably, we assess processing differences between small and large numerosities using an identical task while controlling for task difficulty across displays. In this paradigm, participants are presented with 1–11 items and are asked to judge whether the number of items is greater (classified as “Large”) or smaller (classified as “Small”) than 5. We show a “number specific repetition effect” in the subitizing range: judging two sequentially presented identical quantities from the small category range (subitizing range: 1–4) facilitates responses, whereas different quantities from the same small category show no facilitation (e.g., larger repetition effects for exact [3 → 3] than nonexact numerosities [3 → 2 elements]). In contrast, these repetition effects were not number specific for repeated quantities in larger range arrays (>5), (e.g., equal repetition effects for exact [8 → 8] and nonexact numerosities [8 → 11 elements]). This effect provides evidence for the automatic processing of exact numbers of elements in the small category arrays—leading to repetition priming when the exact number is repeated but not when different numerosities from the same response category (small) are repeated. Large numerosities are not exactly represented and so generate equally large repetition effects for identical and nonidentical numerosities in their response category (large). These effects held even when estimation decisions could not be based on factors such as overall brightness, the area covered by patterns or the similarity of the patterns on number repeat trials.

The present study exploited these differential repetition effects in an fMRI pair‐repetition paradigm [Kourtzi and Kanwisher, 2000]. In brief, the rationale of the pair‐repetition paradigm (fMRI‐adaptation) is based on the observation that repeating information is associated with decreased responses is regions that are coding this information [Grill‐Spector et al., 2006; Grill‐Spector and Malach, 2001]. The advantage of this manipulation is that it controls for any confounding processes of the stimuli type (change in luminance, density, increase on WM capacity etc) by focusing only on the repeated aspect of the stimulus (e.g., number of dots). fMRI‐adaptation paradigms have been used successfully before to investigate various processes related to numerosities [Cantlon et al., 2006; Piazza et al., 2004; Roggeman et al., 2011; Shuman and Kanwisher, 2004].

Using an fMRI adaptation paradigm it was shown that bilateral IPS activation decreases for repeated quantities relative to magnitude change of arrays size [Cantlon et al., 2006; Piazza et al., 2004; although see Shuman and Kanwisher, 2004]. Roggeman et al. [2011] show that processing along the occipito‐parietal processing stream is sensitive to quantity repetitions of relative small numerosities (up to 5) [see also Santens et al., 2010]. Although none of the previous studies explicitly test the single versus dual route hypothesis, while controlling for task difficulty and other potential confounding factors.

In the present study we examined the neural representation of small (<5) and large (>5) quantities using a paired‐repetition fMRI paradigm. Importantly, as the task difficulty and demands are identical across both range of display [Demeyere and Humphreys, 2012], any observed difference can only be associated with a dissociation of processing small numerosities and the processing of large numerosities. Participants were asked to judge whether each dot array presented fewer or more than five dots, by mentally categorizing them as “Small” or “Large,” however explicit responses were only required on rare catch trials; to ensure that motor responses or response selection processes did not confound the effects.

We examined differences in the processing of two different magnitudes, small and larger quantities, in the brain by manipulating the repeated aspects in each pair of dots arrays. There were four pair types: (1) different size categories (no‐Rep): the two arrays presented numerosities from the two different magnitude categories smaller and larger than five (e.g., 3 → 8); (2) Magnitude‐Category repetition (rep‐Cat): the two arrays contained a different number of dots, but were both from the same category (e.g., 2 → 3; 8 → 11); (3) Repetition of numerosities but not of form (rep‐Num): here both arrays contained the same number of dots, but they were positioned differently on the screen (re‐randomized positions); and finally (4) exact repetition (rep‐Exact), the array display repeated twice, such that both the number of dots and their positions was identical. Note that all pair‐repetitions (rep‐Cat, rep‐Num and rep‐Exact), include a decision repetition (e.g., large‐large), while in the no repetition condition (no‐Rep), the category decision changes between the two arrays (e.g., large‐small). To avoid confounding the results of quantity repetition with decision repetition the analysis focused on comparisons between conditions where decision repetition was controlled for. Although for completeness we also report comparison that involved category change.

We asked the following questions: (i) Is the magnitude of the sample size categorically divided to small and large arrays, based on initial relative size estimation? This was identified by comparing responses to pairs in which the category (sample size) was repeated compared with when it was changed (rep‐Cat; e.g., small‐small and large‐large vs. no‐Rep pairs: small‐large and large‐small). Note that the results here could be confounded by decision repetition and hence preparation for response selection. However, additional comparisons were not confounded by the repetition of decision/response selection: (ii) Are different processes engaged in estimating small and large magnitudes of sample sizes independent of the exact number of items? For this we compared small versus large pairs; (iii) finally and most importantly we wanted to investigate the source for the specific behavioral priming effect that is observed for the subitizing small range as opposed to the large arrays [Demeyere and Humphreys, 2012]. Here, we examined whether there were brain regions that showed a greater adaptation for number repetition in the small category but not in the large.

METHOD

Participants

Twelve healthy subjects (three males and nine females, mean age: 26 years; range 20–34, 10 right handed), gave written informed consent according to ethical procedures of the Birmingham University Imaging Centre (BUIC). None of the participants had previous neurological or psychiatric symptoms and all had normal or corrected vision.

Stimuli

The numerosities presented in the “Small” category were 2, 3, and 4, while they were 6, 8, and 11 in the “Large” category. These quantities represent “visually discriminable” numbers with a Weber discriminability ratio of between 0.75 and 0.80 [see also Shuman and Kanwisher, 2004]. Each stimulus was presented on a screen situated outside the scanner and projected onto a mirror 30 cm above participants, subtending a visual angle of ≈10°. The displays were presented on a grey background. The dots were randomly positioned around the centre of the screen. A fixation cross was always presented in the centre of the screen. The dots were made by combining binary noise with a circular Gaussian envelope, presented on a grey background. To avoid systematic variation of luminosity with numerosities, the dots were randomly sampled (with replacement) from a list of 10 elements. These 10 elements were measured by a Minolta LS110 light meter, to fall within a range of 1 cd/m² from the average background luminosity. The luminosity of the background measured 12.2 cd/m², the dots in the list were chosen so that there were four items “darker” than the background with luminosity values: 11.2 cd/m², 11.7; two similar to the background: cd/m², 12.2 cd/m², and four with brighter luminosity than the background: 12.7 cd/m², 13.2 cd/m². These values were measured on a high‐resolution CRT monitor in a completely darkened room. By sampling the elements in this way, luminosity was not the same in each display across all numerosities, but there was no consistent relationship in which larger displays always have a larger luminosity than smaller displays (e.g., it is possible that a display numerosity 8 could be “lighter” or “darker” than a display with numerosity 2), and on average the luminosity was the same across the number conditions. For an example, see Figure 1. We did not control for overall surface area of the display. In addition to the strong relation between numerosity and visual cues in daily life, recent evidence has pointed towards the impossibility of controlling all visual cues related to numerosity—for example, when factors such as luminance are controlled, people integrate other visual variables when estimating displays [Gebuis and Reynvoet, 2012]. We also note that the adaptation design focuses on the relation between the displays rather than the displays themselves.

Figure 1.

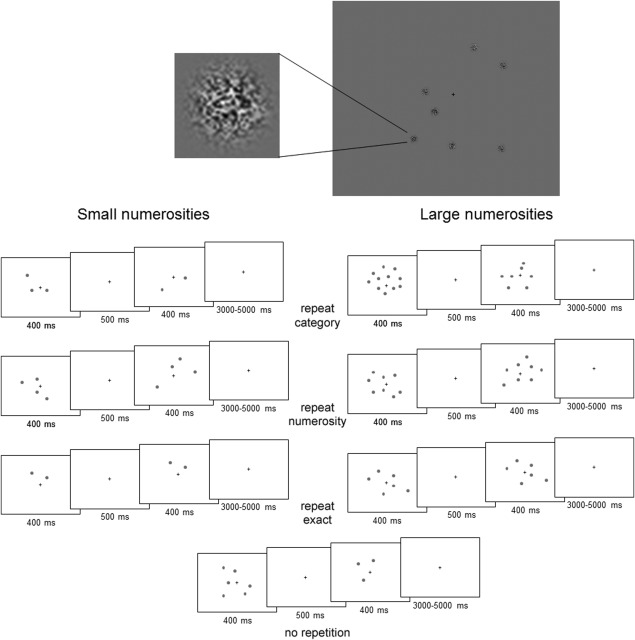
Top: Example display. Below: Schematic illustration of the sequence of events containing examples of the different repetition conditions for small and larger numerosities. The first and second stimulus were modeled together in a pair as an event in the hemodynamic response function.

Design and Procedure

A 2 (numerosities/magnitude category: large, small) by 4 (repetition type: across categories) (no‐Rep); same category (but different sample size; rep‐Cat); within‐category repeat sample size (rep‐Num) and within category identical repetition (rep‐Exact) design was used. In the no repetition condition, consecutive displays were drawn from the different response categories (small then large, or large then small). However, here, apart from a change in number category there was also a potential response change (see below). Critically, in the three repetition conditions the decision processes were identical across trials. On identical repetition trials, exactly the same pattern and same number of elements repeated across trials. On number repetition trials the pattern changed but the same number of dots appeared on consecutive trials. In the category repetition condition, the numbers of dots on consecutive trials were either both small, or both large, but in each case the displays contained different numbers of dots. See Figure 1 for an overview of the design and procedure of the experiment.

We used an event‐related jittered design, in which one event consisted of a paired presentation of two numerosity stimuli [in a similar procedure to Cohen Kadosh et al., 2007]. Each block started with a 20 s fixation period to allow for T1 equilibration. Next, the paired numerosity displays were presented, each for 400 ms with a 500 ms fixation interval. This was followed by a jittered period of fixation for 3,000–5,000 ms. (averaging out at 4,000 ms over the block). The stimuli were presented in eight blocks, each containing 73 paired presentations [6 rep‐Exact, 6 rep‐Num, and 6 rep‐Cat—2 for each numerosity—and 30 no repetition (no‐Rep) trials]. Each block contained seven catch trials.

On ∼10% of the trials (7/73) a response was required. These sparse response trials occurred in pseudo‐random positions throughout the block, after a paired display. In these trials the cue (“1” or “2”) appeared immediately after the presentation of the second array and remained on screen for 1,000 ms and was followed by a fixation period of 2,500 ms. Responses were made with the index and middle finger of the right hand. The key‐presses and reaction times to these trials were recorded. Figure 1b illustrates the sequence of events on a trial.

We asked participants to mentally assign the displays to their respective categories (<5 “Small,” >5 “Large”). However, for the majority of the trials, no explicit response was required; on occasional catch trials subjects were cued (with a red number 1 or 2, after the paired numerals, this number corresponded to the first or second display in the pair) to indicate the relative size (small or larger than 5) of the first or the second display. These catch trials were modeled separately in the analysis, so as not to confound any resulting activation with response selection [see Gobel et al., 2004]. Previous studies have used paradigms with catch trials to insure participants are engaged in the task and to avoid confounding the repetition effects with the response change [e.g., Cantlon et al., 2006; Cohen Kadosh et al., 2007; Piazza et al., 2004]. We note, that while explicit response was not required it is possible that participant did prepare a response for each trial hence our main analyses focus on comparisons across conditions in which decision/potential responses repeated across the pair of arrays.

Image Acquisition

Imaging was performed using a 3 T scanner (Achieva Philips) with an eight channel phase array coil. Structural images were acquired with a T1‐weighted sequence. Functional images were acquired with a gradient echoplanar T2* sequence by using blood oxygenation level‐dependent contrasts. Each functional volume was composed of 29 slices (2.5 mm thickness with a 1.1 mm gap, nominal voxel size 3 × 3 × 3 mm³), positioned to cover most of the brain (with the emphasis on covering the whole of the frontal and parietal lobes). This meant that the most ventral visual areas were not imaged in all participants and hence were excluded from the group analysis. Repetition time (TR) was 2 s, TE was 35 ms, and there was an 80° flip angle. A total of 205 functional volumes were acquired continuously in one scanning session. There were eight functional imaging sessions in total.

Data Analysis

The data were analyzed with SPM5 (Wellcome Department of Imaging Neuroscience, London; http://www.fil.ion.ucl.ac.uk/spm). The first five volumes of images were discarded to allow for T1 equilibration. The remaining 200 (8× sessions) functional image volumes were realigned to the first image [Ashburner and Friston, 2005] and unwarped to account for movement by distortion interactions [Andersson et al., 2001], the images were then normalized to the standard MNI space [Ashburner and Friston, 2005]. Finally, the data were smoothed using 8 × 8 × 8mm³ FWHM Gaussian kernel to account for residual intersubject variability.

The data were analyzed using the general linear framework. Individual events were modeled by a canonical synthetic hemodynamic response function [Friston et al., 1998]. The analysis was based on two‐step summary statistics [Penny et al., 2003a]. At the first level, we used the general linear model to generate parameter estimates for event‐related activity at each voxel for each subject in response to the presentation of each of the paired‐stimulus conditions. Regressors of no interest included the catch‐trials, the six movement parameters to correct for residual signal changes due to head movement, and a set of harmonic repressors to model slow fluctuation (1/128 Hz) in the signal that is typically associated with scanner and biological noise. Consistent effects across subjects were tested in a second level analysis, in which subjects were treated as random variables [Penny et al., 2003b]. The analysis focused on comparing repetition effects within the small and large number categories. We focus on effects that survive multiple comparison thresholds, but for completeness we report clusters larger than 50 voxels at P < 0.001 uncorrected threshold.

RESULTS

Behavioral Results on the Rare Catch Trials

On average, participants gave correct responses on 86.8% of the catch trials (for technical reasons, the accuracy data from one participant were not available for analysis, and the behavioral analysis was conducted on the remaining eleven subjects.). As these response trials were cued sparsely, the high level of performance on the catch trials means that we can be confident that participants paid appropriate attention to the stimuli on nontarget trials. There were no behavioral differences between the responses for small and large number displays [t(10) = 1.495, P = 0.166].

Neuroimaging Results

A random effects analysis of the neuroimaging data was carried out to evaluate the different areas demonstrating adaptation of the BOLD response to the contrasting paired numerosity trials.

Category Repetition Versus No‐Category Repetition

To test the general effects of repeating the stimulus category, we compared the 6 “within category” repetition conditions (rep‐Cat, rep‐Num, rep‐Exact) independent of the relative size, to the no‐repetition (no‐Rep) pairs. Repetition of category was associated with reduced activity most notably in the left superior frontal gyrus, the left middle frontal gyrus and the left superior parietal lobe, including IPS. The full results are given in Table 1. This demonstrates that adaptation occurs when a category is repeated compared with when paired trials belonged to different relative categories. As noted above, while these areas may contribute to the processing of both small and larger quantities we cannot rule out the potential decision‐change confound imbedded in this comparison. Thus it may be that these effects are related to the repetition of internal response decisions or it may reflect the added requirement for response switching when paired items differed in category or of holding in memory more than one response.

Table 1.

Summary of a random effects analysis contrasting repeated category pairs and different category pairs

Location	X	Y	Z	Z (peak vx)	Cluster size
Adaptation to categories
Left superior frontal gyrus	−16	4	54	4.69	82a
Left supplementary motor area	−10	6	60	3.82
Left middle frontal gyrus	−28	12	48	4.21	52
Left inferior parietal lobule	−26	−54	32	4.09	65a

X, Y, and Z refer to the stereotaxic MNI coordinates of the centre of activation. The threshold for significance of the clusters reported here was set at a voxel‐wise uncorrected P < 0.001—whole brain—and a spatial extent of 50 functional voxels.

^aFWE cluster corrected (P < 0.05).

Repetition of Small Category Versus Large Category

To isolate regions that showed reduced activation when the specific category response was repeated (both small vs. both large numbers of items), activity was averaged across all pair types ([rep‐Cat and rep‐Num and rep‐Exact]: small vs. large). There were significant patterns of reduced activation for larger numerosities in the left middle cingulate and for small numerosities in bilateral anterior cingulate, bilateral posterior cingulate, bilateral angular gyri and bilateral superior frontal gyri. We note that the midline and inferior parietal structures associated with reduced response to repeated small numerosities when compared with repeated large numerosities overlap with the “default mode network” typically also associated with the easier processing demands [Schwartz et al., 2005]. We elaborate on the implication of these findings in the discussion. A whole brain image is provided in Figure 2, with the full table of results given in Table 2.

Figure 2.

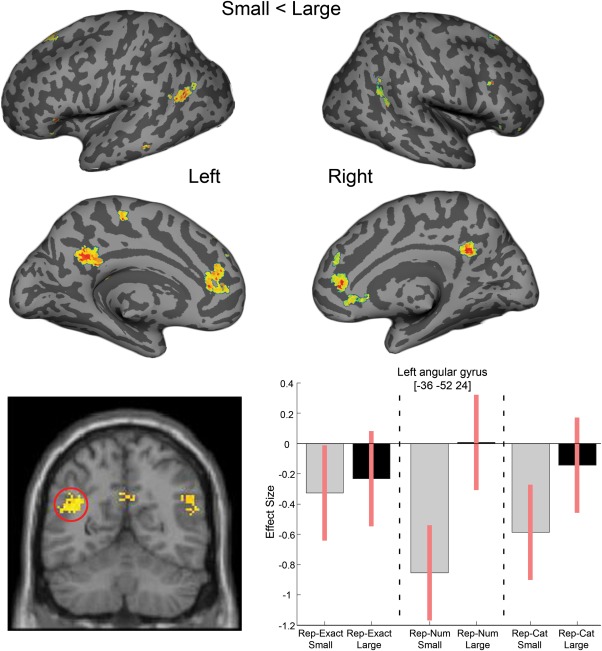
Brain regions showing reduced activation for pairs of small numerosities, compared with pairs of large numerosities. Top: Whole brain SPM contrasts were overlaid on a surface based representation of the MNI canonical brain using the SPM SurfRend Toolbox (written by I. Kahn; http://spmsurfrend.sourceforge.net). Bottom: Contrast estimates and 90% confidence intervals for the simple effects in the peak voxel of the left angular gyrus adaptation.

Table 2.

Summary of a random effects analysis contrasting repeated large number pairs versus repeated small number pairs

Location	X	Y	Z	Z (peak vx)	Cluster size
Large < small
Left middle cingulate	−14	4	30	5.31b	232a
Small < large
Right anterior cingulate	12	38	4	5.26b	110a
Left anterior cingulate	−12	42	20	4	199a
Bilateral posterior cingulate	−14	−40	26	4.66	359a
Left precuneus	−8	−50	32	4.06
Left middle temporal gyrus	−44	−62	24	4.39	242a
Left angular gyrus	−36	−52	24	3.99
Right angular gyrus	54	−56	20	4.04	122a
Right middle temporal gyrus	54	−64	36	3.95
Left superior frontal gyrus	−16	32	50	3.91	59

X, Y, and Z refer to the stereotaxic MNI coordinates of the centre of activation. The threshold for significance of the clusters reported here was set at a voxel‐wise uncorrected P < 0.001—whole brain—and a spatial extent of 50 functional voxels.

^aFWE cluster corrected (P < 0.05).

^bFWE corrected significant at peak voxel level.

Numerosity Specific Repetition

To assess whether there was a numerosity‐specific adaptation effect within the response categories, we compared adaptation when the same numerosity was repeated versus when consecutive trials had different numerosities from the same response category ([rep‐Num and rep‐Exact] vs. rep‐Cat), irrespective of the magnitude (small and large). Relative to pairs of different numbers from the same response category, a network of regions showed reduced response whenever the same number of items appeared twice consecutively. These regions included the bilateral lingual gyrus, bilateral SFG, bilateral anterior cingulate, left superior and inferior parietal lobules, left rolandic operculum, right inferior frontal gyrus, right postcentral gyrus and right precuneus (see Fig. 3). The full table of results is given in Table 3. As can be seen in the charts of Figure 3, similar repetition effects were present for both large and small numerosities independent of exact pattern repetition (Rep‐Cat > Rep‐Exact ≈ Rep‐Num).

Figure 3.

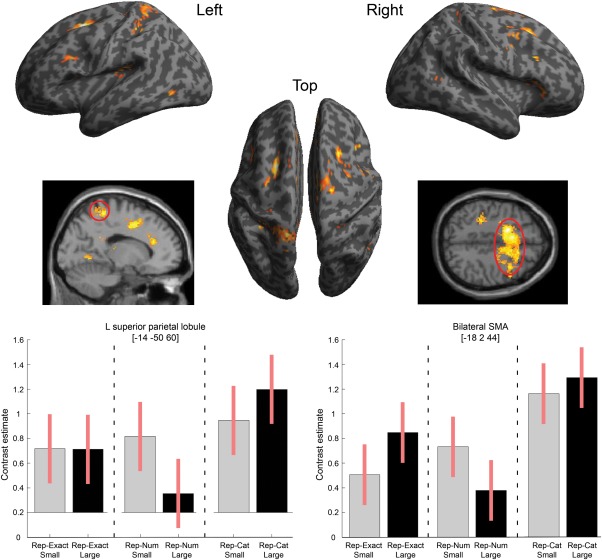
Regions showing reduced activation (adaptation) for repetitions of the same numerosity, compared with different numerosities from the same category for both small and large numbers of items. Top: Results overlaid on SPM inflated surface render. Bottom: Plots of contrast estimates and 90% confidence intervals for the simple effects conditions in the peak voxel of the left superior parietal gyrus (left graph) and the peak voxel of the large bilateral superior frontal gyrus cluster (right graph).

Table 3.

Summary of a random effects analysis contrast of small and large repeated numerosities < repeated response category, different numerosities

Location	X	Y	Z	Z (peak vx)	Cluster size
Contrast: Rep‐Cat > (Rep‐num + Rep‐Exact)
Bilateral supplementary motor area	−18	2	44	6.50b	2198a
Bilateral supplementary frontal gyrus	−8	10	46	6.31b
Right inferior frontal gyrus	44	26	6	4.65	172a
Right postcentral gyrus	16	−40	54	4.13	62a
Left superior parietal lobule	−16	−42	60	5.62b	383a
Left inferior parietal lobule	−34	−38	44	4.82	139a
Left lingual gyrus	−36	−60	−2	5.54b	805a
Right lingual gyrus	30	−62	0	5.14b
Right precuneus	24	−50	28	4.18	57
Left rolandic operculum	−42	−30	18	5.10b	200a
Right putamen	26	−14	16	4.83	118a
Left anterior cingulate	−10	32	24	4.95b	779a
Right anterior cingulate	12	42	18	4.89
Left posterior cingulate	−12	−42	24	4.46	70a

X, Y, and Z refer to the stereotaxic MNI coordinates of the centre of activation. The threshold for significance of the clusters reported here was set at a voxel‐wise uncorrected P < 0.001—whole brain—and a spatial extent of 50 functional voxels.

^aFWE cluster corrected (P < 0.05).

^bFWE corrected significant at peak voxel level.

Interaction of Numerosity Specific Repetition and Category Magnitude

The main interest of the study was whether the contrast between number‐specific adaptation for estimating small quantities in the subitizing range is different from this contrast in the larger numerosity range [see previous behavioral results—Demeyere and Humphreys, 2012]. In these comparisons we used category repetition as our baseline, as it controls for decision/response selection repetition. To test for changes in number repetition for small versus large numbers, we formulated the interaction between response category and repetition types (small: rep‐Num and rep‐Exact < rep‐Cat; large: rep‐Num and rep‐Exact > rep‐Cat). This interaction highlighted areas in the left occipital gyrus (see Tables 4 and 5). We next tested more explicitly whether the interactions were driven by the number‐specific adaptation in the subitizing range by formulating two simple effect contrasts: Small: rep‐Exact < rep‐Cat and Small: rep‐Num < rep‐Cat). We constrained the analysis to include only regions that showed the above interaction (by inclusively masking the results). Here, we again found the same areas as before as well as added regions in bilateral superior frontal gyrus and left posterior cingulate gyrus. Table 5 compares the results for the small exact pattern repetitions versus the small number repetitions. An overlay of the two simple contrasts is also given in Figure 4.

Table 4.

Summary of a random effects analysis of an interaction between response category (small and large) and repetition types (Repeat exact and repeat number versus repeat category—that is, different number in same category)

Location	X	Y	Z	Z (peak vx)	Cluster size
Interaction S/L with Cat/Num/Ex
Left postcentral gyrus	−54	−18	30	4.25	60a
Left lateral occipital complex	−36	−62	4	4.23	79b
Right putamen	24	18	2	4.1	55a

X, Y, and Z refer to the stereotaxic MNI coordinates of the centre of activation. The threshold for significance of the clusters reported here was set at a voxel‐wise uncorrected P < 0.001—whole brain—and a spatial extent of 50 functional voxels.

^aFDR cluster corrected (P < 0.05).

^bFWE cluster corrected (P < 0.05).

^cFWE corrected significant at peak voxel level.

Table 5.

Summary of a random effects analysis of the simple effects of small exact and small number repetitions masked inclusively (at P < 0.05 uncorrected) by the interaction between response category and repetition types (see Table 4)

Location	Contrast Small num < Small cat		Contrast Small exact < Small cat
	MNI (X, Y, Z)	Z (Voxels)	MNI (X, Y, Z)	Z (Voxels)
Lateral occipital gyrus	−38, −60, 0	4.88 (122b)	−36, −60, −2	5.82a (263b)
Left superior frontal gyrus			−12, 10, 46	5.7a (63b)
Right superior frontal gyrus	16, 16, 48	4.51 (71b)	10, 4, 48	5.62a (136b)
Left postcentral gyrus	−54, −18, 30	4.49 (58c)	−60, −14, 24	5.13a (96b)
Left posterior cingulate gyrus			24, −46, 32	5.10a (126b)
Inferior frontal sulcus			38, 24, 24	5.05a (52b)
Right putamen	26, 20, 0	4 (52)

X, Y, and Z refer to the stereotaxic MNI coordinates of the centre of activation. The threshold for significance of the clusters reported here was set at a voxel‐wise uncorrected P < 0.001—whole brain—and a spatial extent of 50 functional voxels.

^aFWE corrected significant at peak voxel level.

^bFWE cluster corrected (P < 0.05).

^cFDR cluster corrected (P < 0.05).

Figure 4.

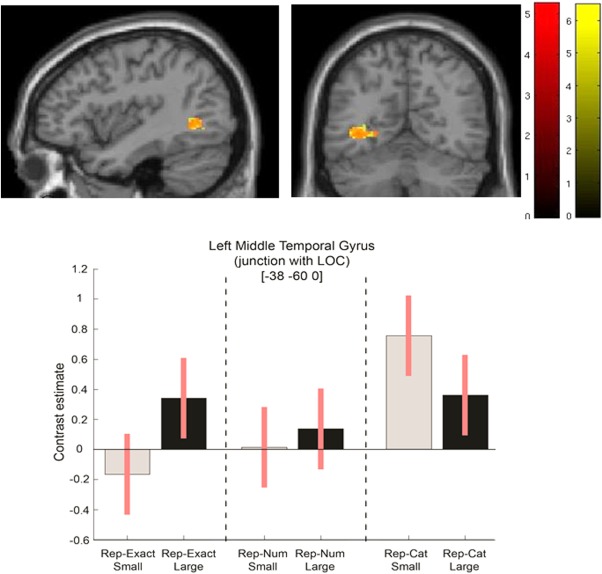
The left lateral occipital sulcus shows small number specific adaptation. Simple effect of small rep‐Exact < rep‐Cat (yellow overlay) and rep‐Num < rep‐Cat (red overlay) masked inclusively by the Interaction (S/L response category × category/number repetition conditions) overlaid on a single‐subject representation of the MNI canonical brain. Contrast estimates and 90% confidence intervals for the masked simple effect in the peak voxel.

DISCUSSION

The aim of this study was to test the predictions made by the single versus the dual routes hypotheses for quantity processing of small (less than five) and large (more than five) dot arrays, using function‐lesion mapping approach. Importantly we observed a unique neural mechanism that involves only in the processing of small numerosities. Thus providing support for the dual route hypothesis. However, the current results revealed also a shared neural mechanism for processing large and small quantities, highlighting the fact that neural mechanisms for processing large quantities were also used for processing small quantities. This later finding provides some support for an existing shared single route for processing any quantity.

The results can be summarized in three sections: (i) the effect of different levels of implicit quantity repetition, irrespective of the magnitude category (i.e., large and small) was evident in the left middle superior frontal gyri and the left superior parietal lobe, including the intra parietal sulcus (IPS). These regions showed reduced response to pairs from the same general number category (both >5 or both <5) compared with mixed‐categories pairs (Table 1). Repetition effects for the same exact number of items (irrespective of the magnitude) were observed in the bilateral lingual gyrus, bilateral SFG, bilateral anterior cingulate, left superior and inferior parietal lobules, left rolandic operculum, right inferior frontal gyrus, right postcentral gyrus and right precuneus (Fig. 3, Table 3). (ii) The difference between smaller and larger quantity estimations, irrespective of repetition type (i.e., identical, number or category pair‐repetition) was found in the left middle cingulate that showed reduced activation to pairs of large numerosities, compared with smaller quantities. The opposite effect, where adaptation was found for repetitions of small numerosities (in contrast with larger quantities >5), was observed in bilateral anterior and posterior midline structures within the cingulate, bilateral angular gyrus and left middle temporal gyrus (Fig. 2, Table 2). Finally, (iii), an interaction between repetition type (ex/num/cat) and number category (small/large) was observed in the left lateral occipital sulcus, postcentral gyrus and the right putamen. These regions show a reliable repetition effect only when the same small numerosities repeat but not for large (Fig. 4, Tables 4 and 5). We term this a value‐specific adaptation effect for small numbers.

Quantity Repetitions

A network of areas including superior, and middle frontal gyri and the inferior parietal lobe showed functional adaptation to repeated presentations of numerosities within the same magnitude category (e.g., small‐small, large‐large) as compared with different categories (e.g., small‐large). The IPS is traditionally associated with the processing of symbolic numbers [e.g., Dehaene et al., 1998, 2003], although more recent reports have also demonstrated bilateral IPS responses to quantities of dots [e.g., Piazza et al., 2007] and the responses may thus be notation independent [although see Cohen Kadosh et al., 2007]. Although as noted before, the comparison between the same and different number magnitudes includes a potential confound of quantity repetition with response repetition and hence any interpretations on the specificity of these regions to quantity estimation should be made with caution.

There was a large network of regions with reduced activations to repeated pairs of the same numerosity. These areas included regions within the frontal and parietal cortices, occipital regions and anterior and posterior midline structures (Table 3, Fig. 2). These results are in line with our previous reported VBM findings [Demeyere et al., 2012], showing that lesions of an extended network, including the posterior occipital cortex as well as frontal and parietal regions, affected the ability to accurately report numerosities of arrays.

Differential Activations for Larger Versus Smaller (Subitizable) Quantities

Irrespective of the different types of repetition, the contrast of activation for pairs of small versus pairs of larger numerosities revealed regions including the bilateral angular gyri, anterior and posterior cingulate and other areas within prefrontal cortex (superior and inferior frontal gyri). This brain activation pattern partially resembles the well documented default mode network. It is often observed that conditions with easier processing demands are associated with higher activation of this network [for a review, see Schwartz et al., 2005]. Thus, it is possible that despite there being no overall behavioral differences for processing small and large arrays, observed in this task [see the Results here, also Demeyere and Humphreys, 2012], the processing of fewer dots was easier than the processing of larger numbers of dots. Nevertheless, involvement of some of these regions, have also been reported before in other studies that examines quantity processing. Specifically, the angular gyrus has been implicated in studies on calculation and the retrieval of arithmetic facts [e.g., Grabner et al., 2009]. In addition, the neuropsychological syndrome associated with problems in more general number understanding and mental calculation, dyscalculia, has also been associated with lesions to the left angular gyrus. For example, damage to the angular gryus is linked to Gerstmann's syndrome, where acquired dyscalculia co‐occurs with finger agnosia, left–right disorientation and agraphia [Gerstmann, 1940]. We also note that the left angular gyrus also showed a numerosity specific adaptation (see Table 3).

The anterior and posterior cingulate and superior frontal gyrus have been shown previously to be involved in counting. It is possible that participants did try to count the arrays here, despite this not being a task requirement and the short presentation durations that were used to prevent this. Piazza et al. [2003] also found a large network of occipital (calcarine, middle occipital), parietal (anterior and posterior IPS), insular, prefrontal and subcortical areas that were more activated for counting than subitizing. It is likely that various operations come into play when large quantities are presented—not just processes involved in estimation but counting processes and greater demands on working memory. The recruitment of frontal and cingulate regions in our study likely reflects these additional processes.

Value‐Specific Adaptation Within Versus Outside the Subitizing Range

Prior studies have reported activation in the right TPJ when estimation decisions are made to small rather than large numbers [Ansari et al., 2007], while other studies have not reported any subitizing‐ specific activation [compared with serial counting: Piazza et al., 2002; Sathian et al., 1999]. Different from these overall contrasts, we conducted a finer grained analysis based on number‐specific adaptation. We observed a small, but highly significant cluster in the lateral occipital sulcus for the interaction between repetition type (ex/num/cat) and number category (small/large). This cluster was specific to repeated same number values in the subitizing range, an effect that was independent of whether the dots appeared at the same location and in the same shape across arrays or at different locations. A similar response pattern was also seen in the left postcentral sulcus and right putamen, although weaker.

Our findings are consistent with there being a distinct subitizing process, separate from the enumeration of larger numbers, which gives rise to an exact representation of small numbers (e.g., “two”). When this process is repeated a neural adaptation effect is apparent. When consecutive small numbers differ, however, contrasting values are computed and there is minimal adaptation. The specific involvement of the lateral occipital sulcus in this value‐specific adaptation effect in the subtizing range, is of particular interest, as it could highlight potential mechanism associated with the increase efficiency of enumerating small arrays of items. The lateral occipital sulcus is hypothesized to extract and represent two‐dimensional shape [Kourtzi and Kanwisher, 2001; Denys et al., 2004]. One account of the efficient enumeration of small number is that participants enumerate small quantities by recognizing their associated, distinct patterns [Logan and Zbrodoff, 2003; Mandler and Shebo, 1982], and the involvement of the lateral occipital sulcus in processing small arrays of items here is consistent with this. Less consistent, however, is the finding of value‐specific rather than pattern‐specific adaptation—adaptation took place between two different patterns with the same value and not just patterns that maintained the same shape. Maintenance of the exact pattern was less critical than maintenance of the exact value. However, even though the exact pattern changed on adaptation trials, it can be argued that the similarity of each pair of small, same‐value patterns (e.g., two triangles or two rectangles) was sufficient to support strong pattern‐based adaptation in the number repeat condition. Roggeman et al. [2011] reported a large cluster in the right inferior occipital gyrus related to repeated patterns (and repeated locations) of nonsymbolic small quantities (up to 5). They propose that the inferior occipital gyrus forms part of an initial stage of number processing in which the spatial locations of elements are “processed and stored” in an object location map. Again, since repetition of the same locations was not critical for the value adaptation effect, the results do not fit this interpretation. Rather than propose either pattern or location‐specific adaptation in this region, an alternative suggestion is that there is an assimilation of exact small number values (two, three, and four items), irrespective of the exact pattern or the locations in which the elements fall. Demeyere and Humphreys [2012] discussed this in terms of the idea that subitization involves applying a limited number of FINSTs [Fingers of Instantiation; Trick and Pylyshyn, 1993] to a display. Repetition of the same FINST operation here, within the lateral occipital sulcus, would lead to value‐specific, neural adaptation.

Our results also fit with the suggestion made by Feigenson et al. [2004], that there are two distinct core systems of numerical representation that are independent of learning or culture. The first system is concerned with approximate representations of large numerical quantities. This core system gives us a noisy representation of number, which, here, leads to generalized adaptation across different numerical values. This system can be thought to underlie the process of estimation. The second core system deals with the precise representation of numbers. This second system can be thought to underlie the immediate parallel processing of smaller numerosities—subitization. This second “exact” system is sensitive to absolute number, as opposed to the first core system which is sensitive to the inter‐relations between numerosities, and it supports the value‐specific adaptation we observed.

CONCLUSION

This study assessed the coding of nonsymbolic numerosities using a novel paired adaptation procedure. Participants carried out an approximate estimation task that did not require participants to distinguish between the actual numerosities presented. Despite this, there was evidence for a neural difference in the lateral occipital sulcus between larger and smaller numerosities specific to when the exact same value was repeated (for small numbers, relative to a different‐quantity, same response baseline). This suggests that participants classified exact numbers within the small numerosity by directly assimilating their value—a process specific to the subitizing range. Our results suggest that subitizing involves immediate apprehension of exact visual number and that this process may be distinct from pattern recognition and from the processes involved in the estimation of larger numbers.