Neural substrates of numerosity estimation in autism

Abstract

Visual skills, including numerosity estimation are reported to be superior in autism spectrum disorders (ASD). This phenomenon is attributed to individuals with ASD processing local features, rather than the Gestalt. We examined the neural correlates of numerosity estimation in adults with and without ASD, to disentangle perceptual atypicalities from numerosity processing. Fourteen adults with ASD and matched typically developed (TD) controls estimated the number of dots (80–150) arranged either randomly (local information) or in meaningful patterns (global information) while brain activity was recorded with magnetoencephalography (MEG). Behavioral results showed no significant group difference in the errors of estimation. However, numerical estimation in ASD was more variable across numerosities than TD and was not affected by the global arrangement of the dots. At 80–120 ms, MEG analyses revealed early significant differences (TD > ASD) in source amplitudes in visual areas, followed from 120 to 400 ms by group differences in temporal, and then parietal regions. After 400 ms, a source was found in the superior frontal gyrus in TD only. Activation in temporal areas was differently sensitive to the global arrangement of dots in TD and ASD. MEG data show that individuals with autism exhibit widespread functional abnormalities. Differences in temporal regions could be linked to atypical global perception. Occipital followed by parietal and frontal differences might be driven by abnormalities in the processing and conversion of visual input into a number‐selective neural code and complex cognitive decisional stages. These results suggest overlapping atypicalities in sensory, perceptual and number‐related processing during numerosity estimation in ASD. Hum Brain Mapp 35:4362–4385, 2014. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

Adults can usually, quickly and accurately estimate the number of people in a room or the number of chocolates remaining in a box. This ability to estimate the number of items in a group, referred to as numerosity estimation, involves basic perceptual but also complex cognitive processes, including verbal counting and symbolic representation that is acquired gradually over childhood. Our skills in manipulating numerical quantities and estimating and comparing them are considered a fundamental ability, which helps us make sense of the external world [Butterworth, 1999; Dehaene, 1997]. Several studies have been interested in numerosity processes and recently its neural correlates and its timing have been investigated.

How Do We Think and Reason About Numbers?

Behavioral studies established that our ability to enumerate visually presented stimuli varies with the number of items present. Several studies implicate one system for representing large, approximate numerical magnitudes, and a second system for the precise representation of small numbers of individual objects [Feigenson et al., 2004]. In other words, estimating and counting are subserved by functionally distinct processes [Demeyere et al., 2012]. When shown arrays of dots, only a minimal difference in response latencies is seen between one, two, three and four items. If five or more items are shown, the response latency increases linearly by about 300 ms per every added item [Trick, 1992]. A similar discontinuity has been noticed in the proportion of errors: from five items onwards, the more numbers or quantities are large, the more their processing becomes approximate and imprecise. This so‐called “numerical size effect” is well‐replicated and can be observed across development and species [Brannon and Terrace, 1998; Feigenson et al., 2004; Huntley‐Fenner and Cannon, 2000; Xu and Spelke, 2000]. Throughout studies of numerical cognition, two other behavioral effects have been reported repeatedly: the “distance effect” (i.e., two quantities are more difficult to discriminate if they are closer to each other [Moyer and Landaeur, 1967]) and the “SNARC effect” (spatial numerical association of response codes) (i.e., small numbers are associated with the left and large numbers with the right side of the brain [Dehaene et al., 1993]). These effects are thought to reveal important characteristics of the semantic organization of numerical magnitudes. In this vein, it has been hypothesized that numbers are spatially organized along a continuum, a “mental number line,” where magnitudes close to each other share more variance in representational signal than those relatively far apart and are therefore harder to discriminate [Ansari et al., 2006; Castronovo and Seron, 2007b]. This hypothesis suggests that the number line is oriented from left to right, with small numbers on the left side and large numbers on the right side [Dehaene et al., 1993; Fias et al., 1996].

Brain Correlates of Numerosity

Humans and non‐human animals both have neural representation of quantity or “number sense” [Chong and Evans, 2011]. From pioneer studies in animals [Nieder and Miller, 2004; Nieder et al., 2002; Sawamura et al., 2002; Thompson et al., 1970] and lesion studies in humans [Gerstmann, 1940; Hécaen, 1961; Henschen, 1919], it is known that the parietal and the frontal cortices contain neurons that code for numerosity. The analysis of these neurons' latencies in animals suggested that the parietal neurons first extract the numerosity information and then project it to the prefrontal cortex neurons which would be involved in the online maintenance of the information [Nieder and Miller, 2003, 2004]. Using various neuroimaging approaches, the activation of the parietal lobes during numerosity processing, together with precentral and prefrontal cortices in humans have been widely confirmed [Burbaud et al., 1999; Chochon et al., 1999; Dehaene et al., 1996; Pesenti et al., 2000; Piazza et al., 2004; Zago et al., 2001] [for a review see Dehaene et al., 2003]. The activation of the parietal cortices is consistently reported in quantity processing of nonsymbolic numerosities, such as dot displays [Castelli et al., 2006; Nieder and Miller, 2004; Nieder et al., 2002; Piazza et al., 2004; Sawamura et al., 2002], as well as in comparisons of continuous quantities such as luminosity, angle sizes and line lengths [Faillenot et al., 1998; Fias et al., 2003; Fulbright et al., 2003; Kadosh et al., 2005; Pinel et al., 2004]. Recent studies revealed that, within the inferior parietal lobule (IPL), the intraparietal sulcus (IPS) is critical for numerical quantity processing [Andres et al., 2005; Cappelletti et al., 2007; Dormal et al., 2008]. Another parietal region, the precuneus is also active in several tasks requiring number manipulations [Dehaene et al., 2003], in numerical comparisons [Heine et al., 2011; Kaufmann et al., 2005; Pinel et al., 2001], approximation [Dehaene et al., 1999] and discrimination [Hayashi et al., 2013]. However, the precuneus is clearly not specific to the number domain. Rather, this region is also relevant in the implementation of a wide range of highly integrated tasks, including visuo‐spatial imagery and episodic memory retrieval [Cavanna and Trimble, 2006], decision making [Albrecht et al., 2013; Gerlach et al., 2000] and self‐processing operations [den Ouden et al., 2005; Lou et al., 2004], processes which are related to numerosity estimation processing. For example, our ability to track multiple objects [Pylyshyn, 1989] and to store items temporally [Luck and Vogel, 1997] are both constrained by the number of objects.

Thus, neuroimaging studies have reported numerosity‐sensitive regions across the brain but the processes leading up to activation of these areas also needs to be considered as a part of the overall numerosity processing. Before the conversion into a number‐selective neural code, sensory perception of visual input is needed and sensitivity of primary occipital areas to numerosity perception has been shown [Fink et al., 2001; Santens et al., 2010], confirming that numerosity is already represented in low‐level visual areas. Following this view, vision has long been considered to be essential in the emergence of the numerical representations and abilities [Simon, 1997, 1999; Trick and Pylyshyn, 1994], notably in its spatial format. Moreover, there is evidence that perceived numerosity is susceptible to adaptation to primary visual features such as color, contrast, size and speed [Burr and Ross, 2008], arguing for perceived numerosity as an independent primary visual property. Taken together these findings suggest that the visual system has the capacity to “see” numerosity, before the emergence of more complex and specialized number processes. However, other theoretical proposals have been made, where the importance of visual processing in the elaboration of numerical representations is not emphasized [Dehaene, 1997b; Gelman and Gallistel, 2004]. Hence, the question “does visual processing play a role in the elaboration of the representation of numerosities?” remains an on‐going debate.

Thus, the literature suggests that the sense of number is not a unitary mechanism but rather a composite of distinct processes occurring in series and involving basic perceptual as well as complex cognitive brain networks.

Electrophysiological studies have mainly used paradigms of numerosity comparison or detection of changes in small quantities, to investigate numerosity processing, focusing on the distance and/or the notation effects. The involvement of parietal regions has been confirmed, showing a distance effect on posterior parietal regions when processing numerical quantity [Dehaene, 1996; Pinel et al., 2001; Turconi et al., 2004]. Electrophysiological data reliably show that stimulus identification and estimation of quantity occur around 200 ms [Hyde and Spelke, 2009; Hyde and Wood, 2011; Libertus et al., 2007; Nan et al., 2006; Pagano and Mazza, 2012]. However, some studies also found an earlier modulation of brain activity (N1 range, 140–200 ms) in response to number‐related tasks [Hyde and Spelke, 2009; Libertus et al., 2007; Nan et al., 2006; Temple and Posner, 1998] which they linked with the perceptual processing of the visual stimuli. For example, when asked to classify stimuli as bigger or smaller than 5, event related potentials indicate that inputs from Arabic digits (1) and from dot patterns (•) evoked significant differences associated with the distance effect between 120 and 230 ms, on the N1 and P2 recorded at the parieto‐occipito‐temporal junction [Temple and Posner, 1998]. However, using the same number comparison task with Arabic (e.g., 1) and verbal stimuli (e.g., one), Dehaene et al. [1996] found a distance effect starting only from N1‐P2 transition (174–198 ms) to P2 (206–230 ms) and including the P3 component (236–360 ms), suggesting that number processes can occur later. During a similar task, Pinel et al. [2001] observed a later distance effect at about 320 ms, mainly in parietal areas distributed bilaterally along the IPS and in the precuneus; activation of these regions decreased as the numerical distance between the target and the stimulus increased. Processing simple problems (for example single‐digit multiplications) appeared to involve left and right inferior parietal sites and to be completed between 300 and 600 ms after the operand presentation, whereas the same parietal activations appeared to be prolonged for complex problems [Kiefer and Dehaene, 1997].

Thus, neuroimaging studies also suggest that the analysis of quantity starts early, within the first perceptual steps (around 140–200 ms in the N1 time window) after stimulus presentation in posterior areas, and continues from 200 ms for up to 400 ms in parietal and frontal regions, involved in numerical processing.

Autism and Numerosity

Autism is a severe developmental disorder characterized by impairments in communication, social interaction and restrictive/repetitive behaviors. Despite these symptoms, specific exceptional abilities are frequently reported [Caron et al., 2004; Grandin, 2009; Mottron et al., 2009; Soulières et al., 2010], and even though they are not part of the diagnostic criteria, these abilities were described in the early observations of Hans Asperger [1944]. It is known that, of these abilities, people with ASD tend to excel in the domain of visuo‐spatial tasks, for example, in visual search performance [Almeida et al., 2010a; Dakin and Frith, 2005; Joseph et al., 2009; Kaldy et al., 2011; O'Riordan and Plaisted, 2001; O'Riordan et al., 2001]. As examples, they have a special propensity to quickly spot a misaligned book in a bookcase or detect the hidden shapes in embedded figures [Russell‐Smith et al., 2012].

The phenomena associated with superior performance on visual tasks have been addressed by two theories, which argue that people with ASD perceive the word differently: the weak central coherence hypothesis (WCC) [Dakin and Frith, 2005; Happé and Frith, 2006] and the enhanced perceptual function hypothesis (EPF) [Dakin and Frith, 2005; Mottron et al., 2006]. The WCC hypothesis highlights the performance of individuals with ASD as showing a processing bias for local information and relative failure to extract meaning or “see the big picture,” whereas typically developing people (TD) present a tendency to process visual information for overall Gestalt at the expense of details [Frith, 1989]. In contrast to WCC, EPF [Mottron and Burack, 2001; Mottron et al., 2006] does not assume that there is a failure of global processing but proposes that in autism enhanced processing of stimulus elements is facilitated. These hypotheses may explain why individuals with ASD tend to display superior performance on visuo‐spatial tasks [Almeida et al., 2010b; Grinter et al., 2009], which necessitates the processing of local features, rather than focusing on the global meaning. Supporting these models are data showing that individuals with ASD experience difficulties in tasks of visual illusions [Happé, 1996] and in processing context‐dependent information [Happé, 1997], which require holistic information processing. It is suggested that people with autism present a preferential use of lower level sensory information leading to excellent and very focused attention to detail, which may also predispose the development of numerosity estimation skills [Baron‐Cohen et al., 2009]. It seems relevant that local processing positively impacts the ability to localize single elements in space and thus our performance for correctly individualizing and estimating their number. According to this view, there are many behavioral, neuropsychological and neuroimaging data, reporting that numbers and space processing are closely connected and probably share some common underlying mechanisms [Fias and Fischer, 2005; Hubbard et al., 2005]. Moreover, as vision is the more important source of spatial information, it seems relevant to assume that the relation between numerical and spatial representations can develop from visual perception cues.

However, among visuo‐spatial investigations in ASD, numerosity estimation has been rarely assessed. There are a few reports of superior and highly specialized capacities. For example, Sacks [1985] described 26‐year‐old twins brothers with ASD (IQs = 60) who spontaneously guessed the number of matches (111) dropped on the floor (i.e., and simultaneously remarking that 111 is 3*37) [Sacks, 1985], and Smith [1983] reported the case of Zacharias Dase, who demonstrated the same ability, but for large quantities of peas (i.e., 79 and 183). How could they count so quickly? Questioned by the authors, these number prodigies indicated, as best they could, that they did not “work it out,” but just “saw” their number, in a flash [Sacks, 1985], suggesting a possible link between numerosity estimation and perceptual processes. In the same vein, Soulières et al. [2010] reported remarkable abilities in estimation for several quantifiable dimensions (rank, numerosity, time, weight, length, surface, distance) in two children with ASD at 9 years of age.

However, several concerns need to be taken into account when looking at these various results. These previous anecdotal reports are observed in not more than 1 or 2 ASD individuals and have not been replicated in a larger group of people with ASD. Furthermore, given prior research showing visual search abilities being linked with ASD symptomatology in children with ASD [Joseph et al., 2009] and with autistic traits in typically developing (TD) adults [Brock et al., 2011; Russell‐Smith et al., 2012], the wide heterogeneity of symptoms in ASD could lead to different results for a numerosity estimation task in a group study.

Thus, numerosity estimation is an enigmatic aspect of autism, which deserves investigation to assess possible superior performances in ASD. Moreover, to date, no study has looked at the brain correlates of numerosity processing in ASD.

The current study investigated behavioral responses to numerosity estimation and its neural substrates in young adults with and without autism. To explain quantity processing in ASD, hypotheses about perceptual processes could be advanced, or skills for numerosity estimation could result from the numerosity process itself. To disentangle numerosity processing from perceptual atypicalities in autism, participants were asked to estimate the number of discrete elements (local information) arranged either randomly or in a meaningful pattern (global information). fMRI studies have reported brain regions that are implicated in numerosity estimation, but provide little indication on when in time the processes occur. ERP studies contribute timing information, but have poor spatial resolution. For the current study, we used MEG which provides excellent temporal resolution of ongoing neuronal activation in the brain and also very good spatial resolution [Hari et al., 2010 for a review]. Although with different aims to our study, two recent reports have used MEG investigations for numerosity processing. Simos et al. investigated estimation and simple addition in TD children (aged 8–14) with or without math difficulties [Simos et al., 2008] whereas Vuokko et al. examined the temporal and spatial pattern of the brain activation during subitizing (2–4 items) and exact counting (five to eight items) in TD adults [Vuokko et al., 2013]. Thus, the current study represents the first assessment of large numerosity in terms of both timing and brain localization in TD and clinical populations using MEG. Furthermore, this work is also the first to determine whether perceptual encoding impacts numerosity processes.

Because there are no prior studies targeting these specific concerns with MEG, one of our aims is purely exploratory, i.e., to ascertain what neurophysiological responses are detected when people with ASD are engaged in numerosity estimation and how the meaningfulness of the dot patterns impacts these responses. Associated with this, and tied mainly to the case studies, we investigated whether individuals with ASD exhibit special behavioral abilities for quantity estimation. Moreover, based on previous functional imaging studies, we expected TD people to evoke activations in number processing‐related brain areas as well as in visual regions within 400ms. Finally, we expected to see differential modulations of behavioral and brain responses according to the meaningfulness of the dot patterns in TD and ASD participants.

METHODS

Subjects

The initial sample included 17 typically developed (TD) and 16 adults with diagnostic of autism spectrum disorders (ASD). Of these subjects, three control and two ASD participants provided too few artefact‐free trials (fewer than 80% of the presented trials) and were removed from the sample. The final sample in both groups consisted of 14 TD and 14 ASD adults. All participants had normal or corrected‐to‐normal vision; they did not have any metallic implants or ferromagnetic dental work and gave informed written consent. The study was approved by the research ethics board at the Hospital for Sick Children in Toronto.

ASD participants (four females; mean = 24.77 years ± 3.96) had been diagnosed by a registered medical professional experienced with autistic spectrum disorders according to DSM‐IV [APA, 1994] criteria. The Autism Diagnostic Observation Schedule (ADOS, module 4) [Lord et al., 2000] was completed by a psychologist before inclusion, and average score was 9.8 ± 3.9. TD participants (four females; mean = 24.92 years ± 3.78) were matched by age and sex with ASD participants and none had a history of behavioral, psychiatric or neurological disorders. For both groups, IQ was assessed by the WASI [Wechsler, 1999] (ASD: 107.8 ± 13.3; TD: 119.8 ± 8.5). The chronological age (U = 92; P = 0.8) and the IQ (U = 63; P = 0.11) were not significantly different between the two groups of participants (Mann–Whitney Test).

Task and Stimuli

The stimuli consisted of 224 pictures (200 × 150 pixels) composed of between 80 and 150 dark grey dots on a light grey background. Dots were circular with a diameter of four pixels. In each picture the dots were distributed randomly within either an animal shape (112 pictures) or a nonanimal shape controlled to have no obvious meaningful form (112 pictures). A total of eight different animal shapes were used (butterfly, camel, chicken, dog, donkey, mouse, panther, seal) and eight different nonanimal shapes (see Fig. 1). Size and shape of the patterns remained constant irrespective of number of dots presented, with four different pictures of each animal and non‐animal shape for each 10 dot range (e.g., 80–90 dots). Randomisation of dot positioning was achieved by plotting points in a regular arrangement of set density and then adding jitter to each dot randomly along both the x and y axes. Magnitude of jitter was distributed randomly between positive and negative values equalling the maximum deviation that did not allow adjacent dots to touch. The range of dots composing each stimulus was constrained by the representation of a meaningful pattern (the minimum number of dots required to represent an animal form without ambiguity) while the size of each overall picture remained constant (150 dots being the maximum allowed where adjacent dots did not touch).

Figure 1.

Examples of stimuli composed of respectively 106, 83, and 102 dots, arranged in a non‐meaningful (stimulus 1, nonanimal) or a meaningful shape (stimulus 2 and 3, animal).

Stimuli were back‐projected onto a screen in front of the subjects by a video projector situated outside the MEG room, using the software Presentation (Neurobehavioral Systems, Albany CA). Stimuli were presented in one single block, centrally for 600 ms, one at a time on a grey background, slightly darker than the stimulus background, positioned 60 cm in front of the subject. The visual presentation was followed 1,000 ms later by a brief single tone sound, signaling that the subject should respond. Between trials, right after the stimulus, a fixation cross was displayed on the screen to maintain subject focus. The interstimulus interval was randomized between 4,500 and 5,500 ms. Subjects were instructed to look at the pictures and wait until the tone had sounded before verbally estimating the number of dots displayed in the pattern. The responses were recorded as audio signals and transcribed after the experiment. The participants were able to pause the run whenever they wanted, to rest for a few minutes. No feedback concerning performance or numbers of dots presented was given to subjects during the study. However, before the experiment, ten pictures were presented as practice trials during which the exact number of dots contained in each picture was displayed on the screen after the subject's answer. This sequence allowed us to ensure that subjects understood the task and gave them an idea of the range in the number of dots.

Behavioral Analyses

The analyses were conducted on the absolute estimation errors (i.e., absolute difference between the estimated number of dots and the actual number of dots) using repeated measures ANOVAs with numerosity and shape as within‐subject factors and group as between‐subject factor [Group (2: ASD/TD) × Shape (2: Animal/Non‐animal) × Numerosity (i.e., number of dots; 7: 80–90/90–100/100–110/110–120/120–130/130–140/140–150)] (Model 1). To investigate the variability of the absolute mean error of estimation, the same ANOVAs were conducted on their standard deviation (STDV) and their coefficient of variation (CoV = STDV/mean).

Then, to determine more precisely the estimation strategy of TD and ASD participants, additional analyses were performed on the error of over‐ and under‐estimation errors according to the number of dots in the pattern (i.e., difference score with respect to the exact answer) in another ANOVA model with numerosity and error direction as within‐subject factors: [Group (2: ASD/TD) × Numerosity (7: 80–90/90–100/100–110/110–120/120–130/130–140/140–150) × Error Direction (2: Under‐/Over‐estimation)] (Model 2).

All results were corrected for multiple comparisons using a Greenhouse‐Geisser (G‐G) test [Greenhouse and Geisser, 1959]. All results were corrected for multiple comparisons using a Greenhouse‐Geisser (G‐G) test [Greenhouse and Geisser, 1959]. The G‐G test adjusts the degrees of freedom in the ANOVA to correct for any potential association between the variables and inconstant variance across condition. Significant interactions were followed by Newman–Keuls post hoc tests. An alpha level of 0.05 was used for all statistical tests, after correction.

MEG Procedure

MEG data were acquired on a 151‐channel whole‐head MEG system with axial gradiometers (CTF/MISL, Coquitlam, B.C.) at the Hospital for Sick Children in Toronto. Participants were first trained on the numerosity estimation on a PC computer just outside the MEG room, with the same procedure used in the MEG. After the short test sequence, subjects lay supine with their head in the dewar of the MEG, inside the dimly lit magnetically shielded room. Prior to data acquisition, three fiducial coils were placed at the nasion and pre‐auricular points to localise the subject's head relative to the MEG sensors. The system allowed head localisation to an accuracy of 1 mm. Head localisations were completed before and after the experimental procedure, to confirm that participants remained still. Results were not contaminated by mouth movement (oral answer) as subjects waited for the tone before answering.

Data were recorded continuously with an on‐line bandpass of 0–100 Hz, and filtered off‐line to 0.1–30 Hz. The order of presentation of blocks was counterbalanced across subjects to cancel any bias of condition order. The MEG study required 15–20 min.

MRI Scan

All subjects also had a structural MRI to facilitate localisation of the sources of the MEG activity. To ensure accurate MEG–MRI coregistration, immediately after completion of the MEG, the fiducial coils were replaced with MRI contrast markers in the same locations and an anatomic MRI was acquired for all subjects on a 3T MAGNETOM Tim Trio (Siemens AG, Erlangen, Germany) MRI scanner in an adjacent suite to the MEG. A set of 192 high‐resolutionT1‐weighted sagittal images were acquired using a 3D MPRAGE sequence.

Anatomical T1 images were acquired from the MRI scanner as dicom files and changed to “.mri” format to allow for fiducial locations to be labeled using a program called MRIViewer. Multisphere headmodels were created based on initial fiducial positions that had been registered on the T1 anatomical image [Lalancette et al., 2011]. Brain anatomical images were normalized to a template using SPM2.

MEG Data Analyses

Preprocessing and GFP

Each dataset was inspected for trials with evident artefacts such as blinks and heartbeats, and removed on a trial‐by‐trial basis. Trials were averaged for three categories (i.e., 1. All = Animal+ Non‐Animal; 2. Animal; 3. Non‐Animal) to generate the event‐related fields (ERFs) for each participant. Grand‐averaged waveforms were calculated for each category. We then calculated the Global Field Power (GFP), which is the root mean squared power across sensors, for our grand‐averaged datasets for the “All” condition, to visualize temporal changes in the overall amplitude of the magnetic field measured by the MEG and to determine latency windows of interest. According to the literature on numerosity processing, we generated a frontal GFP plot, based on 38 sensors over the frontal lobes, and a posterior GFP plot, based on 20 sensors over the occipital and parietal cortices. Based on peak latencies seen in these GFP plots, the data for each participant were parsed into eight epochs from 80 to 500 ms poststimulus (i.e., 80–120 ms; 120–180 ms; 180–220 ms; 220–290 ms; 290–350 ms; 350–400 ms; 400–450 ms; 450–500 ms).

Event‐related beamformer (ERB)

Source analyses were performed on these eight time windows using a vector beamforming algorithm written in‐house [Quraan et al., 2011], an adaptation of the synthetic aperture magnetometry (SAM) algorithm [Vrba and Robinson, 2001]. The vector beamformer technique is effective in calculating source activity at single time points, to image time‐locked activity [Sekihara et al., 2001], as it uses the whole signal across trials to calculate the weights of a spatial filter for each voxel using the SAM minimum variance beamforming algorithm, which are then applied to the epoch‐averaged data.

Source images from the beamformer analyses were calculated for each individual in each time window, normalised into stereotaxic space using SPM2 and averaged across individuals. Images had a spatial resolution of 5 mm. To test for significant within‐group activity (i.e., Animal vs. Non‐Animal), nonparametric paired permutation tests were done on subtracted beamformer images (2048 permutations), generating activation maps of P < 0.01 (corrected). Between group differences (ASD vs. TD) were tested using unpaired permutation tests, P < 0.01 (corrected), on subtracted ERB images (2,048 permutations). Images were examined and the highest 10% of peak activations were noted along with their Talairach coordinates.

To further specify the chronometry of the significant sources, the grand averaged rectified time‐courses of activation were calculated for the coordinates at each peak of interest [Cheyne et al., 2006] using the same statistical analyses as was done on the beamformer images, non‐parametric permutations test (permutations >5,000).

RESULTS

Behavioral Data

Mean absolute error of estimation (ANOVA Model 1)

Across all conditions, the mean absolute error of estimation appeared larger for ASD (M = 25.9; SD = 8.3) than TD (M = 21.1; SD = 3.9) participants but did not reach significance (Fig. 2a).

Figure 2.

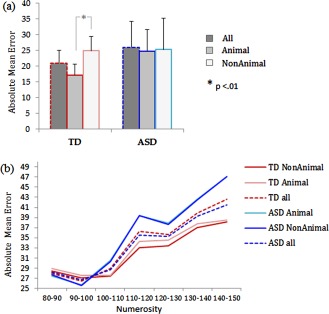
Behavioural results. (a) Absolute mean error, i.e., number of dots difference between estimate and actual presentation. A significant effect due to the meaningfulness of dot patterns was seen only in TD participants; TD participants made larger errors for the dots arranged in animal shapes. These results suggest that TD subject's ability to estimate numerosity is affected by their global perception of dot patterns. (b) Absolute mean error according to the number of dots displayed in the pattern for both group and condition. A significant numerosity × group interaction was observed, revealing that an actual difference existed between ASD and TD when estimating large numerosities only. Furthermore, a numerosity × shape interaction indicated that the main shape effect observed on this variable was also driven by large numerosity patterns. These results suggest that the number of dots impact estimation abilities in a different way in ASD and TD participants.

However, a main effect of numerosity and a numerosity × group interaction was found. The absolute mean error became larger with increasing numbers of dots in the pattern (F(6,156) = 5.7, P = 0.005; η² = 0.18), confirming the previously reported “numerical size effect.” In addition, the numerosity × group interaction indicated that the difference between ASD and TD in the mean error of estimation was driven by large numerosities (Fig. 2b). When the pattern was composed of more than 100 dots, a group effect appeared. More precisely, according to the Newman–Kheuls tests, the mean errors evoked by patterns of 110–120 (P = 0.013), 120–130 (P = 0.015), 130–140 (P = 0.026), and 140–150 (P = 0.034) dots were larger in ASD than TD participants.

Moreover, a main effect of the meaningfulness of the dot patterns (Animal vs. Non‐Animal) (F(1,26) = 13.3; P = 0.001; η ² = 0.33) and an interaction effect between shape and group (TD vs. ASD) (F(1,26) = 11.3; P = 0.002; η ² = 0.30) was found. Post‐hoc comparisons revealed that this interaction was driven by TD participants: no significant within‐group effect was found in ASD subjects between the response evoked by animal (M = 25.2; SD = 9.9) and non‐animal (M = 24.8; SD = 6.8) shapes, whereas TD participants had significantly more difficulty accurately estimating the number of dots arranged in animal shapes (M = 24.9 dots; SD = 4.5) than estimating nonmeaningful (nonanimal) patterns (M = 17.2 dots; SD = 3.4) (P < 0.001) (Fig. 2a,b). Finally another significant interaction was observed between numerosity and shape (F(6,156) = 2.2, P = 0.04; η ² = 0.08), as animal shapes were associated with larger mean absolute errors than nonanimal shapes for patterns composed of 120–130 (P < 0.001) and 130–140 (P = 0.002) dots.

To investigate whether the variability/dispersion of the mean absolute errors changed across numerosity, we also performed the same ANOVA (model 1) on their standard deviation (STDV) and on their coefficient of variation (CoV = STDV/mean). The results showed that the STDV of the absolute errors increased with the size of the pattern—as did the mean—in ASD (F(6,78) = 2.3, P = 0.04; η ² = 0.15) but not in the TD participants (F(6,78) = 0.8, P = 0.51). These additional data indicated that ASD variability in numerical estimation became larger across the number of dots whereas TD participants remained more stable in their estimation. Moreover, the CoV was constant across the number of dots composing the pattern, regardless of participant group, suggesting that when corrected by the mean, the variation of the mean error remained stable across group and conditions.

These results suggested: (1) that TD presented a non‐significant tendency to have lower mean absolute error than ASD (Fig. 2a), (2) that the numerical size effect was greater in ASD than TD, i.e., their estimation was less linear across numerosities (Fig. 3), and (3) that the global meaningfulness of dot arrangements, the animal‐shaped stimuli, significantly affected TD subjects' ability to estimate numerosity whereas ASD subjects did not appear sensitive to this factor (Fig. 2a,b).

Figure 3.

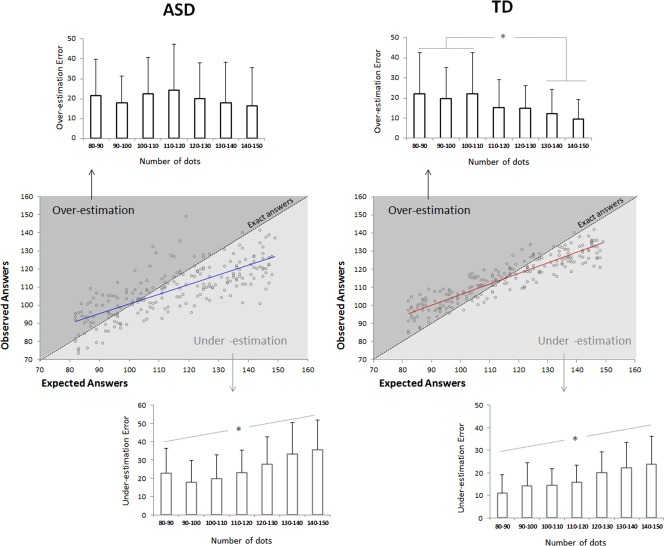
Behavioural results: Strategy used to process numerosity. The middle graphs correspond to the plot of the mean of the observed answers as a function of the expected answers for each stimulus, separately for each group. The dotted black line is the exact answers function whereas the actual answers were represented in the plain blue (for ASD) and red (for TD) lines. According to this, the area above the black line contains all the stimuli that lead to over‐estimation whereas the dots below this line are the stimuli followed by under‐estimation. These plots showed a global numerical size effect on the strategy used to process patterns of dots in both group and revealed that this effect is stronger in ASD participants. The top and bottom graphs specify respectively the magnitude of Over‐ and Under‐estimation errors according to the number of dots. ASD and TD participants tended to make larger underestimation error for large than small numerosities. The reverse result was only observed in the TD group: TD participant tended to make larger overestimation error for small than large numerosity.

Estimation strategy: Direction of error (ANOVA Model 2)

The “numerical size effect” on the ability to estimate number of discrete elements was confirmed by this second analysis, showing that both TD and ASD errors were impacted by the number of dots (F(1,27) = 4.2; P = 0.048; η ² = 0.074). A numerosity × group interaction also validated our previous finding that the numerical size effect was stronger in ASD than TD (F(6,162) = 2.5; P = 0.021; η ² = 0.086).

More importantly, this second analysis revealed a significant interaction between numerosity and the direction of errors (F(6,162) = 18.1; P < 0.001; η ² = 0.40), suggesting that this numerical size effect was more prominent when considering under‐ than over‐estimation errors in both group (Fig. 3). In other words, ASD and TD participants tended to make larger underestimation errors for large than small numerosity (Fig. 3, bottom). In the TD group only, post‐hoc analyses (Newman–Keuls) revealed that the overestimation error was significantly higher when the pattern was composed of 80–90 to 100–110 dots than when it was 130–140 (P = 0.033) and 140–150 (P = 0.002) dots (Fig. 3, top), suggesting that TD participant tended to make more overestimation errors for small than large numbers.

MEG data

MEG results are reported first across conditions (“all”) to investigate the neural correlates of numerosity processing in general, then the effects of global and local processing (i.e., the arrangement of the dots) are reported.

Numerosity Processing

GFP waveforms

Large amplitude differences of prominent MEG peaks between the TD and ASD cohorts occurred at 80–180 ms and 180–400 ms in posterior sites (Fig. 4a) and then until 500 ms after numerosity estimation in frontal areas (Fig. 4b). These differences of GFP waveforms were driven by greater power over all sensors sites in TD than ASD participants. Finer temporal analyses in smaller epochs within these periods (i.e., 80–120 ms; 120–180 ms; 180–220 ms; 220–290 ms; 290–350 ms; 350–400 ms; 400–450 ms; 450–500 ms) allowed us to follow the time‐course of the source activations that appeared in the contrast TD–ASD.

Figure 4.

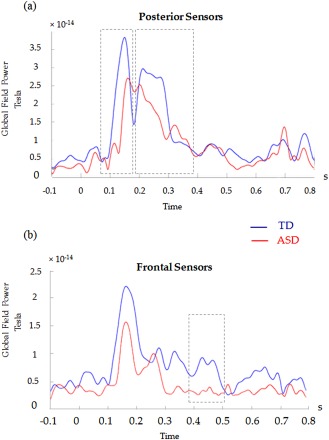
Global field power (GFP) of all stimuli in ASD and TD groups. (a) GFP calculated from the 20 posterior sensors. (b) GFP calculated from the 38 frontal sensors. Dotted rectangular shapes (i.e., 80–180 ms, 180–400 ms, 400–500 ms) indicate the large time windows of interest which were then parsed into finer epochs.

Localization and time‐courses of sources

Source analyses in the contrast TD–ASD revealed significant differences of source amplitudes of activation and/or localisation (P < 0.05 uncorrected) in occipital, temporal, parietal and then frontal areas between the two groups during numerosity estimation (Table 1). In both hemispheres, significant amplitude differences (TD > ASD) were found in visual areas, the lingual gyrus (BA17) and the cuneus (BA18), at early stages of numerosity processing in the 80–120 ms time window. The associated time‐course of the left cuneus showed a large, dispersed peak with amplitude differences at 100 and 120 ms (Fig. 5a).

Table 1.

Locations and time windows of brain areas showing greater activation in TD than ASD subjects during numerosity processing

				Talairach coordinates
Time windows	Regions	BA	Structures	x	y	z	Pseudo‐Z
80–180ms
80–120 ms	Occipital cortex	17	L. /R. Lingual gyrus	±10	−92	0	0.59
		18	L./R. Cuneus	±20	−81	27	0.67
120–180 ms	Posterior Parietal cortex	7	R. Precuneus	26	−72	50	0.65
	Temporal cortex	19	R. Middle Temporal gyrus	50	−63	12	0.57
180–400 ms
180–220 ms	Temporal cortex	37	R. Middle Temporal gyrus	45	−63	8	0.43
	Posterior Parietal cortex	40	R. Inferior Parietal Lobule	50	−51	53	0.19
	Anterior premotor cortex	6	R. Precentral gyrus	59	3	51	0.18
350–400 ms	Posterior Parietal cortex	7	L Superior Parietal Lobule	−35	−56	49	0.36
		40	R. Inferior Parietal Lobule	54	−42	39	0.35
400–500 ms
400–450 ms	Prefrontal Cortex	44	R. Precentral G.	50	10	9	0.39
	Frontal cortex	10	L. Medial Frontal Gyrus	−15	63	−3	0.34
	Somatosensory cortex	2	R. Postcentral Gyrus	59	−18	24	0.12
450–500 ms	Frontal cortex	10	Superior frontal gyrus	±25	53	−3	0.39

Figure 5.

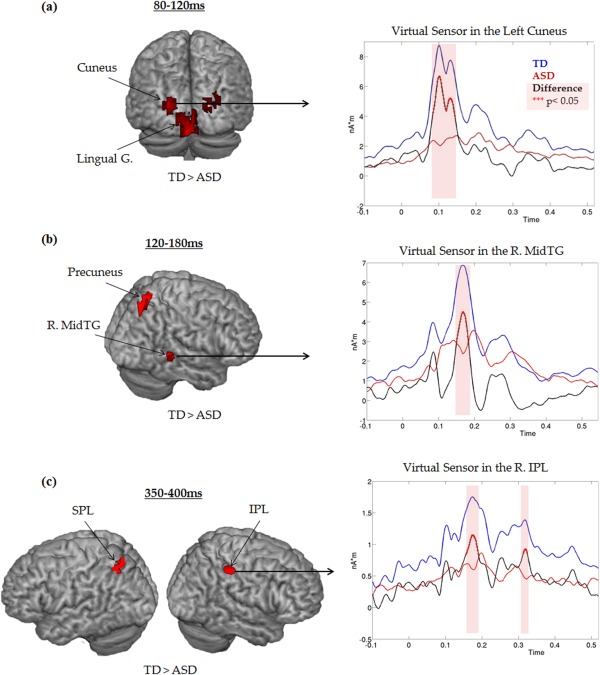
The 3D brain representation of the significant occipital, temporal and parietal source differences (localization and time‐courses) between ASD and TD participants during numerosity estimation. The contrast TD > ASD for source localization was associated with the grand averaged rectified time courses of activation at each Talairach coordinate of interest. (a) At the first step of numerosity processing (80–120 ms), significant group differences were identified in primary and secondary visual areas, i.e., lingual gyrus (BA17) [±10 −92 0] and cuneus (BA18) [±20 −81 27]. Time course activation in the left cuneus also showed group differences in this time window. (b) At 120–180 ms, sources identified are in right middle temporal gyrus (R MidTG) (BA19) [50 −63 12] and right precuneus (BA7) [26 −72 50] appeared more active in TD than ASD participants. Time course of activation in the R. MidTG revealed differences between the two groups in this time window. (c) At later stages of numerosity processing, from 180 to around 400 ms, sources identified were mainly parietal. For example, at 350–400 ms, differences in activation were observed in L. superior parietal lobule (SPL) (BA7) [−35 −56 49] and in R. inferior parietal lobule (IPL) (BA40) [54 −42 39]. At this time point again, time courses showed significant differences in the time course of activation in the R. IPL.

At 120–180 ms, source analyses revealed differences in the right precuneus (BA7) and in the right middle temporal gyrus (MidTG) (BA19). The time course of MidTG showed that difference between the groups (TD > ASD) reached significance at 170 ms (Fig. 5b).

From 180 until 400 ms, a group effect (also TD > ASD) was measured in parietal regions. At 180–220 ms, in addition to differences in activation in the right MidTG (BA37) and precentral gyrus (BA6), a significant source was also found in the inferior parietal lobule (IPL; BA40). At 350–400 ms, group differences in parietal regions were extended, showing significant sources in the left superior parietal lobule (SPL; BA7) and the right IPL (BA40). The time course of the IPL revealed that source analysis differences reported between 180 and 400 ms were driven by differences peaking at 180 and 310 ms (Fig. 5c).

Finally, after 400 ms, source differences were found in prefrontal and frontal areas. At 400–450 ms, activations in the right precentral gyrus (BA44, Broca's area), left medial frontal gyrus (BA10) and right postcentral gyrus (BA2) were greater in TD. At 450–500 ms, a source was found in the superior frontal gyrus (SFG) (BA10) in both hemispheres in TD but not ASD subjects who only showed activation of right premotor cortex (right precentral gyrus activation, BA6) (Fig. 6).

Figure 6.

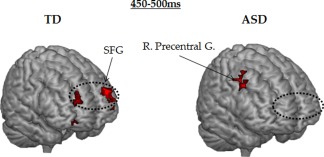
The 3D brain representation of the significant frontal sources differences between ASD and TD participants during numerosity estimation. At 450–500 ms, when frontal activations were observed bilaterally in superior frontal gyrus (SFG) (BA 10) [±25 53 −3] in TD subjects, only a right precentral gyrus activation (BA 6) [35 −8 33] was reported in ASD participants.

In summary, numerosity processing in ASD appeared to involve atypical source amplitudes in occipital, temporal and parietal areas but also a deficit of frontal source activation in the later time windows.

Thus, parietal and frontal activations, which are known to be involved specifically in numerosity processes, appeared to be affected in ASD. The occipital and temporal differences could be explained, in contrast, by differences of sensitivity in global perception. To test this hypothesis, the same analyses of numerosity processing were performed according to the shapes of the dot patterns [i.e., global meaningful (animal) or local not meaningful (random patterns)].

Global vs. Local Processing

GFP waveforms

Differences of GFP waveforms between Animal and Non‐Animal shapes were noticed between 120 and 300 ms in both groups (Fig. 7). In TD participants, a first peak was observed around 180 ms, driven by greater power over posterior sensors sites for non‐meaningful patterns of dots (nonanimal stimuli) compared to meaningful patterns (animal stimuli). This first peak was followed by a reversed GFP difference between 220 and 290 ms, when animal shapes evoked greater power than nonanimal shapes over the same sites. In contrast, for ASD participants, amplitude differences driven by a greater power for nonmeaningful pattern of dots, appeared only later, from 220 to 300 ms.

Figure 7.

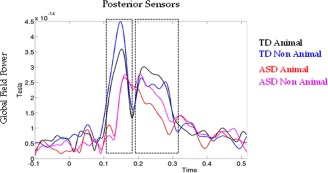
Global field power (GFP) of animal and nonanimal shape stimuli in ASD and TD groups, calculated for posterior sensors. The peak observed in the GFP revealed that differences between the two types of stimuli appear around 120 ms (first rectangular shape, NA>A) and continue until 290 ms (second rectangular shape, A>NA) in TD participants. In ASD participants, GFP differences are observed only in the second rectangular shape (NA>A).

Localization and time‐courses of sources

In the TD group, a global meaning effect was localized in temporal cortices from 120 to 180 ms until 220–290 ms (Animal > Non‐Animal) (Table 2). At 120–180 ms, animal shapes activated more right inferior temporal cortex (BA20), right fusiform gyrus (BA37) and left superior temporal gyrus (BA22) than nonmeaningful patterns of dots. At 180–220 ms, source activation differences (A>NA) were found in right STG (BA22) and left STG (BA39). At 220–290 ms, greater temporal activation continued for animal compared to nonanimal shapes in TD subjects; source analyses for the contrast A>NA revealed significant activations of left MidTG (BA37) and left superior temporal gyrus (STG) (BA 42).

Table 2.

Locations and time windows of brain areas modulated by meaningfulness of the stimuli in TD and ASD subjects during numerosity processing. (A: animal; NA: non‐animal)

						Talairach coordinates
	Contrast	Time windows	Regions	Structures	BA	x	y	z	Pseudo‐Z
TD
	A > NA	120–180 ms	Temporal cortex	R. Inf. temporal gyrus	20	54	−20	−20	0.16
				R. fusiform gyrus	37	45	−59	−10	0.14
				L. superior temporal gyrus	22	−35	−52	21	0.13
		180–220 ms	Temporal cortex	R. superior temporal gyrus	22	45	−53	16	0.29
				L. superior temporal gyrus	39	−40	−57	26	0.19
		220–290 ms	Temporal cortex	L. middle temporal gyrus	37	−50	−49	−2	0.23
				L. superior temporal gyrus	42	−50	−15	1	0.15
ASD
	NA>A	290–350 ms	Temporal cortex	L. middle temporal gyrus	39	−40	−62	17	0.17

In ASD participants, no significant differences of activations were observed between the two shape categories before 290–350 ms, at which point the left MidTG (BA39) appeared more active for Non‐Animal than Animal (contrast NA>A) stimuli (Table 2).

These results suggest that TD participants discriminated the two shape categories earlier than the ASD individuals. Moreover, the TD group showed sensitivity to the global meaning of the stimuli with greater activity, while the ASD group showed effects only later and they responded more to non‐animal than animal shapes.

DISCUSSION

The present study reports new data on spatiotemporal brain dynamics of numerosity estimation in adults with and without ASD, with a focus on the role of local/global perception. Behavioral results did not reveal overall special ability or impairment in ASD participants for numerosity estimation but highlighted that they are not affected by meaningfulness of dot pattern, and showed a stronger numerical size effect compared to the TD group. The underlying cerebral sources were affected in autism, showing a different way of processing cognitive inputs from occipital to temporal, parietal and then frontal areas, ranging from 80 to 500 ms. Moreover, analyses based on the meaningfulness of the dot patterns, demonstrated a global effect of dot arrangement (A>NA) on temporal sources at 120–290 ms in TD participants whereas ASD participants exhibited a delayed (290–350 ms) and opposite effect (NA>A) at the same location.

Behavioral Data

Numerosity estimation in TD people

The results suggest an impact of the numerosity magnitude on estimation abilities. This is also called the “numerical size effect”: responses become less accurate and particularly more under‐estimated (rather than over‐estimated) with increasing numbers of dots in the pattern.

First, this finding indicates a nonlinear pattern of responses across numerosities. This behavioral signature has been described in the psychophysical literature which argued that estimation is based on a numerical representation obeying Weber's law [Brysbaert, 1995; Castronovo and Seron, 2007a,b; Crollen et al., 2011; Dehaene, 1992, 1997; Gallistel and Gelman, 1992, 2000]. Weber's law is characterized by: (1) the linear increase of both (a) means and (b) variability of estimates with increasing numerical magnitude, as well as by, (2) the observation of constant coefficients of variation (CoV), and (3) the development of inaccuracy across numerosity sizes. In this study, even if the TD participants' behavior fit with the 1st (a), 2nd and 3rd points, we did not observe a significant effect of numerosity size on the STDV of the absolute mean errors, suggesting that the classical “Weber” view on numerosity estimation abilities cannot, by itself, account for our results. On the other hand, our data support the more recent proposals made in the literature postulating that the experience humans have with numbers and quantities could have an impact on the way they represent corresponding magnitudes [Booth and Siegler, 2006; Verguts et al., 2005] or access them [Lipton and Spelke, 2005]. Following this idea, if subjects have prior experience in the range of numbers, they could demonstrate specific patterns of performance in numerical estimation where a more precise linear‐rule representation without, or even with less, scalar variability is involved [Booth and Siegler, 2006; Verguts et al., 2005]. Thus, providing participants with some information about the numerosity tested could reduce the amount of variability, and also improve the accuracy of the responses [Krueger, 1984; Lipton and Spelke, 2005]. In our study, despite the fact that no feedback concerning performance or the number of dots presented was given during the experiment, ten pictures were presented as practice trials before entering the MEG room. For each trial, the exact number of dots contained in each picture was displayed on the screen after the subject's answer. Previous studies indicated that even a minimal amount of implicit feedback seemed sufficient to produce an immediate and long lasting “calibration” of the mapping [Izard and Dehaene, 2008; Minturn and Reese, 1951; Whalen et al. 1999]. Thus, it could be suggested that the practice session may have allowed TD participants to “calibrate” their estimates, influencing their experience of the range of the presented numerosities and increasing the stability of their responses.

Furthermore, when looking at the strategy used to process numerosity and especially the direction of the errors made, the data revealed a tendency to under‐estimate rather than over‐estimate the number of dots displayed in the pattern: the larger the numerosities, the stronger the underestimation. This result is concordant with previous findings which showed that this tendency is common in perceptual tasks [Castronovo and Seron, 2007b; Crollen et al., 2011; Kaufman et al., 1949; Krueger, 1972; Mandler and Shebo, 1982]. Even if underestimation responses are observed in most of the cases, some studies also report a tendency to overestimate. Hollingsworth et al. tested a wide range of values and found that participants overestimated the least numerous arrays, and underestimated the most numerous ones [Hollingsworth et al., 1991]. Our data replicate this effect by showing a larger magnitude of over‐estimation errors for patterns with 80–110 dots compared to ones with 130–150 dots in TD participants. To account for this finding, Castronovo and Seron proposed the bidirectional mapping hypothesis [Castronovo and Seron, 2007b]. According to this hypothesis, over‐ and under‐estimation in numerosity tasks are due to the direction of the bi‐directional mapping process that takes place between the nonsymbolic numerical representation (which is assumed to be approximate) and the symbolic numerical representation (which is assumed to be linear and precise) [Fias and Verguts, 2004; Piazza et al., 2007; Verguts and Fias, 2004]. Estimation of the number of dots contained in a pattern involves a nonsymbolic to symbolic numerical mapping in that people have to use approximate information to make a precise decision. This mapping direction has systematically led to under‐estimated numerosities [Castronovo and Seron, 2007a; Crollen et al., 2011; Krueger, 1972; Whalen et al., 1999] which may explain why we found a strong bias toward under‐estimation compared to over‐estimation errors in our study.

Finally, our findings also furnished insights as to whether local/global perception interacts with numerosity estimation processes. TD subjects performed less accurately for animal shape than non‐animal shape patterns. The differences in estimation of animal and random patterns of dots in TD may suggest a neural propensity to search for patterns. Following this idea, organization of dots in an animal shape would be perceived by TD participants and influence their performance by requiring stronger cognitive control to ignore this global perception, which acts as a handicap for numerosity processing.

To conclude, our results fit previous evidence that numerical estimation tasks present regular and predictable behavioral data: the signature of Weber's law, the impact of experience on the variability of estimates and the under‐estimation pattern of performance in perception tasks. Thus, in light of previous insights, the behavioral data observed in TD participants appear reliable and its comparison with the data collected in ASD participants shed new light on our understanding of numerosity processing in this disorder.

Numerosity estimation in ASD people

Although special abilities in various types of computational and visuo‐spatial tasks have been reported in ASD, numerosity estimation has been rarely assessed. Previous anecdotal reports observed in 1 or 2 autistic individuals have been published and showed superior estimation abilities, as reviewed in the introduction [Sacks, 1985; Smith, 1983; Soulières et al., 2010]. However, these findings have not been confirmed in a group of subjects with ASD. Here, we have addressed this gap in the literature and have not observed such special abilities in a group of 14 high functioning adults with ASD. Inconsistent reports of behavioral abnormalities in numerosity processing are not particularly surprising given the wide spectrum of autistic symptoms of ASD. ASD is diagnosed on the basis of a triad of symptoms including difficulties with social interaction and communication, along with narrow interests and repetitive behaviors. These symptoms are not equally expressed along the autistic spectrum; some individuals present more social deficits whereas others are more affected by narrow interests and repetitive behaviors. According to clinical observation, the development of number estimation skills in autism may originate with the 3rd axis of the triad, meaning that ASD individuals who develop this ability could be those who present a restricted interest for number processes. A narrow interest for numbers could promote a preferential use of numerosity information leading to effective strategies for quantity estimation, which could predispose the development of a numerosity estimation “talent.” In the present group of 14 individuals with ASD, this rare characteristic was not found and no special abilities were observed.

In contrast, we found that ASD subjects had poorer skills when estimating the number of dots than TD subjects for large numerosity (>100 dots). The ability to estimate the number of items in a group emerges early in development and involves basic perceptual and complex cognitive processes including verbal counting and symbolic representation that are acquired gradually over childhood [Izard et al., 2008; Nieder and Dehaene, 2009]. ASD is a multifaceted and heterogeneous disorder marked by atypical early brain growth, abnormal patterns of white matter development [Courchesne et al., 2003; Mak‐Fan et al., 2013], and impairment in numerous cognitive domains by age three [APA, 2000], which undoubtedly alter developmental trajectories. Thus, it is not surprising that the atypical brain maturation in ASD may impede the development of mechanisms involved in numerosity estimation, from the development of sensory capacities to more complex functions. This view is consistent with studies focusing on other developmental disorders [e.g., attention‐deficit hyperactivity disorder (ADHD) [Kaufmann and Nuerk, 2008], Williams syndrome [Van Herwegen et al., 2008]) which also report significant deficits of basic number processing skills. Our results also indicate that differences between TD and ASD in numerosity estimation exist and are driven by the number of dots displayed in the pattern (i.e., “size effect”). According to this, the contrast of our results with previous work may also be underlined by the fact that larger numerosities (>80) were presented in this study than those used in earlier studies. Special abilities might be observed in ASD with small numbers (<80) whereas impairment are seen with large numerosities (>100). In other words, ASD people may have abnormal extreme numerosity processing. Further investigations are needed to test this behavioral hypothesis.

The results also revealed that, like the TD, the ASD participants present a tendency to under‐estimate perceived numerosity but that this effect is stronger in ASD. Moreover, analyses of the STDV indicated that the variability of the absolute mean error of ASD subjects increases with increasing numerosity whereas the CoV remains constant, suggesting that the distribution of ASD estimation followed Weber's law previously described in TD population. However, these findings also indicate that ASD participants presented a larger spread of their responses than the TD group (i.e., they are more sensitive to Weber's law) and, we assume that this difference may be due to a differential experience with the presented numerosities [Booth and Siegler, 2006; Lipton and Spelke, 2005; Verguts et al., 2005]. Results of this study in TD participants highlighted a constant variability of estimation with increasing numerosity after a short practice session. In ASD, sensory and perceptual abnormalities may lead to experiencing numerosities in a different way than TD people. ASD subjects' experience with numerosities was less proficient than was seen in the TD subjects, so their adherence to Weber's law for their numerical processing was more pronounced, resulting in more approximate (i.e., less linear) numerical estimation skills.

Finally, this study revealed the role of local/global perception abnormalities reported in ASD on their performances to estimate numerosity. Behavioral results have shown that ASD participants' abilities to estimate numerosity were not affected by the global meaning of dot patterns whereas TD subjects performed less accurately for animal shape than non‐animal shape patterns. These results suggested that the global understanding of visual patterns was not favored in ASD, which is consistent with current theories. The weak central coherence theory (WCC) [Frith, 1989; Happé and Frith, 2006] as well as enhanced perceptual functioning (EPF) [Mottron and Burack, 2001; Mottron et al., 2006] propose an atypical cognitive style during perceptual processing in autism: contrary to TD, those with ASD see “the trees before the forest” [Happé and Booth, 2008; Happé and Frith, 2006]. In other words, while TD subjects search for patterns, ASD may be oriented toward single elements. ASD subjects may not look for the “big” picture and process animal and random organization of dot patterns the same way, element by element, to estimate numerosity. Thus, we assume that the lack of influence of the global shape on ASD performance does not reflect a deficit per se but rather a cognitive strategy biased toward local elements. However, given the absence of direct evidence for the integrity of global shape processing in ASD in the current study, further research is needed to validate this assumption. Another possible explanation possible explanation to this “global blindness” comes from a deficit in rapid saccade planning which may cause problems in visually disengaging from individual objects on display [Karmiloff‐Smith et al., 2012]. This suggestion could also explain why ASD people succeed at small exact number discrimination (as previously reported) but have difficulty estimating large approximate quantities.

Thus, rather than special abilities for number estimation, a stronger numerical size effect (i.e., adherence to Weber's law was more pronounced) and a response impervious to the global meaning of dot patterns were seen in ASD in our study. In other words, differences between ASD and TD subjects in numerosity estimation appeared to be driven by the number of dots and the shape of the presented pattern. The MEG data revealed several atypical cortical activation patterns during this processing which help explain these differences in abilities, as discussed below.

MEG data

The findings of this study demonstrate the spatial‐temporal organization of brain processes implicated in number estimation in adults with and without autism. As reviewed in the introduction, although the parietal lobe has been suggested as a key substrate for the domain‐specific representation of quantities, numerosity processing also engages other brain regions before and after the emergence of the numerosity‐selective representation. Consistent with this view, our MEG results showed source abnormalities in ASD participants during numerosity estimation in parietal regions, but also in occipital, temporal, and frontal areas.

Neural Correlates and Time Course of Numerosity Estimation in TD

As MEG allows the investigation of the time‐course of brain activity, the current work complements the numerosity information available in TD people by distinguishing the separable processes and their cerebral correlates involved in numerosity estimation.

Occipital sources within 80–120 ms

The activity found in these regions is consistent with previous neuroimaging studies which demonstrated that numerosity processing activated an early network of visual areas in the bilateral occipital cortices [Fink et al., 2001; Santens et al., 2010]. Numerosity and visual cues appear highly correlated in real life. For example, when more apples are added to a pile of apples, the size of the pile increases; or when more people enter a room, the density increases. Accounting for this are studies assuming a role of visual information in the elaboration of the semantic representation of small and large numerosities [Gebuis and Reynvoet, 2012; Hollingsworth et al., 1991] and in the emergence of numerical abilities across development [Simon, 1997, 1999]. As an example, in TD people estimations were influenced by the visual properties of the dot arrays, with larger estimates when the dot arrays consisted of dots with a smaller diameter, aggregate surface or density but a larger convex hull [Gebuis and Reynvoet, 2012]. The reliance on visual cues to estimate numerosity suggests that the existence of an approximate number system that can extract numerosity independently of the visual cues is unlikely. Instead, humans may estimate numerosity by weighing the different visual cues present in the stimuli. Going further with this view, visual processing could be considered as a property of numerosity estimation. Furthermore, in numerical cognition, the role of the occipital cerebral regions has been emphasized in the evolution of our numerical representations and skills. Some authors [Newcombe, 2002; Simon, 1997, 1999; Trick and Pylyshyn, 1994] postulate a non‐numerical model, the “object‐file model,” to account for the numerosity discrimination abilities observed with preverbal infants. Recently, researchers have investigated the role of visual experience in the development of numerosity processing by comparing the performance of early blind and sighted individuals in number comparison and parity judgment tasks [Castronovo and Seron, 2007a; Crollen et al., 2013; Szucs and Csepe, 2005]. The most recent study demonstrated that early visual experience drives the development of an external coordinate system for the visuo‐spatial representation of numbers [Crollen et al., 2013]. However, other theoretical proposals have also been made, where the importance of visual processing in the elaboration of numerical representations is not accentuated (i.e., the sense of number that allows manipulating and understanding numerosity exists whatever the modality of presentation) [Dehaene, 1997; Gelman and Gallistel, 2004].

Thus, activations of occipital areas during numerosity estimation observed in this study are more in line with previous reports arguing that the numerical representation is dependent on the visual modality. Although early activation of these regions is shared across all basic visual processes, we propose that they nevertheless can index the preprocessing of quantity estimation, leading to the conversion of visual input into a number‐selective neural code.

Temporal sources within 120–290 ms

Our results also showed that in the 120–220 ms time window, the temporal lobe responded to numerosity estimation. Temporal sources are not usually reported as areas implicated in numerosity processing in the TD population, suggesting that their activation in this study may be related to perceptual processes. Supporting this view, the second group of analyses, which took into account the meaningfulness of dot patterns, showed a global meaning effect that was localized in temporal cortices from 120–180 ms until 220–290ms (Animal > Non‐Animal) in TD. This result confirmed the involvement of temporal cortices in local/global perception during numerosity processing.

Involvement of local and global perception in quantity estimation is concordant with the literature, suggesting that after extraction of visual characteristics, another processing step is needed before quantity estimation: individuation of dots. Visual enumeration of numerosity critically depends on the capacity to process multiple objects as distinct entities [Cantrell and Smith, 2013; Pagano and Mazza, 2012]. For large quantities, the perceiver may appreciate that there are many items without representing each element with its respective properties. This general individuation mechanism could be considered as a local perception of the dot pattern and is not specific to quantity estimation, but is common to other activities such as object tracking, visual search and short term memory tasks [Hyde and Wood, 2011; Piazza et al., 2011]. When dot patterns convey a global meaning (animal), recognition of the shape at the global level was enabled by the integration/grouping processes of the several distinct objects at the local level. Thus, when patterns of dots were organized to create animal shapes, more cognitive resources were required in the 120–220 ms time window to individualize the dots needed for numerosity task but also to extract the meaningfulness of the dot patterns.

Other supporting evidence of this view comes from several neuroimaging studies which have suggested the involvement of the temporal lobe in integration processes [Shafritz et al., 2002; Weissman and Woldorff, 2005], which are proposed to follow a “hierarchical axis” of object processing that extends from the analysis of local features in early visual areas to the representation of global shape in high processing areas of the ventral visual pathway [Lerner et al., 2001]. More recently, comparing intact versus disturbed global gestalt perception of hierarchically organized stimuli, Huberle and Karnath [2012] argued for a significant role of the temporo‐parietal junction in human global gestalt perception [Huberle and Karnath, 2012]. Regarding the timing of integration processes, convergent ERP evidence suggests that the major response associated with the emergence of a global shape (integration of local elements) occurs within 170 ms, in the N1 time range [Beaucousin et al., 2011; Brodeur et al., 2006; Conci et al., 2011; Herrmann and Bosch, 2001; Martinez et al., 2007; Murray et al., 2002, 2004]. MEG studies have shown that Kanizsa figures are associated with early activations in the lateral occipital complex ∼130–150ms post‐stimulus onset [Abu Bakar et al., 2008; Halgren et al., 2003]. Finally, face processing literature also confirms the integration of analytic to holistic information of faces occurs during the N170 time window [Latinus and Taylor, 2006]. The spatial and temporal localization of integration processes from locally individuated elements to global shapes are consistent with data about general visual categorisation, which clearly needs local/global perception to classify, for example in our study, animal vs. nonanimal shape. Fast decisions for basic level perceptual categories appeared to occur in occipito‐temporal brain areas: i.e., in a Go/No‐Go task, cerebral activity differs between target (animal) and nontarget trials (nonanimal) from 150 ms after stimulus onset [Macé et al., 2009; Rousselet et al., 2002]. Moreover, it has been previously shown that neurons in the human medial temporal lobe (MTL) fire selectively to images of faces, animals, objects or scenes [Kreiman et al., 2000; Quiroga et al., 2005].

Thus, temporal lobe sources in this study may be linked to both individuation/ integration abilities and associated with general visual categorisation processes. We suggest that a second process originates after sensory analyses are engaged in numerosity processing. At this level, individuation of dots requiring local perceptual abilities is completed, feeding forward to the next step of specific number estimation.

Parietal sources within 120–400 ms

As expected, from 120 until 400 ms, activation was found in the parietal sources, including the precuneus, the inferior parietal lobule (IPL) and the superior parietal lobule (SPL). Concordant with these findings, convergent results from neuroimaging and neurophysiological studies suggest that the posterior parietal brain areas, and in particular within IPL and its subdivision the IPS, are critical for numerical estimation [Cantlon et al., 2009; Dehaene et al., 2003] and are described as a part of the “core system of numbers” [Feigenson et al., 2004]. Patients with parietal lesions can be impaired in making numerical judgments (numerical computation, recognition and counting), whereas other cognitive abilities remain normal [Cipolotti et al., 1991; Dehaene and Cohen, 1997; Dehaene et al., 2003]. The IPL has been implicated with both event‐related potentials [Dehaene et al., 1996] and fMRI [Pinel et al., 2001; Stanescu‐Cosson et al., 2000] as the main source for the numerical distance and size effects that are observed behaviorally. Our findings are in accordance with these studies, revealing the involvement of the IPL in number estimation of dot patterns. Thus, the IPL could be considered as a critical brain region in the network underlying number processing.

Mostly investigating the overlap between physical and numerical size [Hubbard et al., 2005], a growing number of behavioral [de Hevia et al., 2008] and neuroimaging [Goffaux et al., 2012; Knops et al., 2009a,b; Koten et al., 2011; Rusconi et al., 2007, 2011] studies indicate that numerical representations and visuo‐spatial processes are not independent but tightly linked and rely on parietal and frontal brain regions. For example, using an ingenious multivariate classifier approach, a recent fMRI study showed that BOLD signal in parietal regions controlling visuo‐spatial orienting also plays an important role in mental arithmetic [Knops et al., 2009a,b]. Applying this view to our study, localizing dots in space and shifting attention between different locations is necessary for performing individuation of dots and correctly estimating the number of elements displayed in the observed pattern. Thus, parietal sources found activated here over large time periods could be attributed to number processing, linked with the visuo‐spatial processes engaged by this complex cognitive task.

This suggestion is relevant to recent functional imaging findings in healthy subjects which argued for a key role of the posterior parietal cortex in the implementation of a wide range of higher‐order cognitive functions [Cabeza et al., 2008; Corbetta and Shulman, 2002; Dehaene et al., 2004], suggesting that this region is highly heterogeneous [Uddin et al., 2010]. For example, although this deep cortical area has received less attention than the IPL, the precuneus [for review see Cavanna and Trimble, 2006] is described as being involved in different abilities which could be considered as a part of number estimation mechanism, including visuo‐spatial imagery [Knauff et al., 2003; Suchan et al., 2002], episodic memory retrieval [Gilboa et al., 2005; Lundstrom et al., 2005; Schmidt et al., 2002] and self‐processing operations [den Ouden et al., 2005; Lou et al., 2004]. As the precuneus is reported to be a “hub” region [e.g., Hagmann et al., 2008], its activation in our numerosity task is not unexpected. To perform the task used in this study, spatial mental representation of dots pattern is needed as well as the development of behavioural strategies to optimize efficiency. One way to proceed could be to set/memorize a standard response across the experiment and to compare it with the actual displayed pattern. Such strategy engages updating of the dots mental representation according to the remembered patterns, i.e., episodic memory is used to adapt self‐perception of the number of dots. Moreover, connectivity data revealed that the precuneus is selectively connected with other parietal areas, namely the caudal parietal operculum, the IPL, the SPL, and the IPS [Cavada and Goldman‐Rakic, 1989; Leichnetz, 2001; Selemon and Goldman‐Rakic, 1988], demonstrating a parietal network that may subserve several cognitive functions engaged in number‐related processes, especially in visuo‐spatial information processing.

Our MEG results on the timing of the parietal activity in quantity estimation are also consistent with previous ERP work, showing an extended latency of parietal area activation during number‐specific processes, from the N1‐P2 range (140–250 ms) [Hyde and Spelke, 2009; Hyde and Wood, 2011; Libertus et al., 2007; Nan et al., 2006; Pinel et al., 2001; Temple and Posner, 1998] to the P3 time window (236–360 ms) [Dehaene et al., 1996; Grune et al., 1993; Szucs and Soltesz, 2008]. However, these previous studies focused mainly on the numerical distance effect (performances decrease as the numerical distance between the numbers to compared increase), which involves numerosity estimation but is not specific to those processes.

Following the idea of an overlap between visuo‐spatial and number processing and taking into account the heterogeneity of ERP results in response to number processing tasks, the debate remains about when numerical and spatial information are mapped into a common, integrated representation, i.e., does it arise at an early processing stage [Cohen Kadosh et al., 2007; Koten et al., 2011] or only at a later stage of response activation [Cohen Kadosh et al., 2007; Swartz and Heinze, 1998]? For example, congruity between numerical and spatial size of the presented digit affected the latency of the P300 component over centro‐parietal electrodes [Swartz and Heinze, 1998]. Conversely, in a combined fMRI and ERP study using a Stroop‐like task in which numerical values and physical sizes were varied independently, Cohen‐Kabosh et al. [2007] found an interaction of numerical and physical size in parietal regions as well as in motor regions, implying late interaction at the response stage. However, the authors also found that when increasing cognitive load (using the distance effect), physical and numerical dimensions interacted earlier at the comparison stage, suggesting that the timing of space and number interactions depends on task requirements.

Thus, we argue that there is a third stage that is engaged by numerosity estimation in several regions of the parietal lobe, reflecting integration of visuo‐spatial and number‐related information and which leads to the conversion of visual input into a number‐selective neural code.

Frontal sources within 400–500 ms

Finally, from 400 to 500 ms, sources in prefrontal and frontal areas, were found in TD participants. Although much of the literature on the neural basis of numerical cognition has focused on parietal cortex, the functional roles of other brain regions engaged by numerical tasks, such as frontal cortices, have also been determined [for a review see Arsalidou and Taylor, 2011]. Frontal activations are believed to relate to the integration and management of numerical operations in working memory, response decision and execution, and error monitoring [Meintjes et al., 2010]. Thus, for example, amplitude of inferior frontal activation is directly proportional to the time pressure imposed during a number processing task rather than the complexity of the numerical calculation per se [Menon et al., 2000]. Some studies have underlined a close relation among enumeration, visual working memory and individuation [Piazza et al., 2011; Whalen et al., 1999], confirming the role of the frontal lobes in numerical processes. More specifically, a visual working memory buffer in frontal regions may be crucial in active maintenance of the individuated items during the process of mapping the set of elements onto a specific numerical value. Previous electrophysiological evidence fits the reported hierarchical timing of frontal activation highlighted in our MEG study. Some authors argued that the frontal response was preceded by activity over parietal areas, which are involved in evaluation of numerical value and its discrepancy from the expected correct solution to the equation [Berger, 2011; Tzur et al., 2010]. The authors proposed that before an error in the solution of the equation is detected, some basic parietal evaluation of the numerical value of the solution must take place and be fed forward to frontal mechanisms of evaluation and error detection [Berger, 2011].

Thus, numerosity estimation imposes demands on working memory and on more global executive functions, including error monitoring that may explain the observed activations in the frontal cortex in TD participants.

Neural Correlates and Time Course of Numerosity Estimation in ASD

The data also shed unique light on number‐related brain processing in autism spectrum disorders. Our study shows that individuals with autism exhibit widespread functional abnormalities at each step of number estimation processing from occipital (80–120 ms) to frontal sources (400–500 ms). Based on previous studies showing atypical processing in sensory and perceptual domains but also in complex cognitive functioning, the main MEG findings are interpreted as reflecting a different way of processing incoming information from occipital to frontal sources.

Occipital sources

At 80–120 ms after stimulus presentation, we found significantly reduced source activations bilaterally in ASD in lingual gyrus and cuneus, corresponding to early visual processing areas. That we found abnormal processing in these areas in autism is coherent with clinical and neurophysiological observations reporting atypical behavioural (for example, see commentary in Grandin [2009]) and cerebral responses to sensory information in individuals across the spectrum; over 96% of children with ASD are reported to have hyper‐ and hypo‐sensitivities in different modalities domains [Crane et al., 2009; Marco et al., 2011; Minshew et al., 2002]. Moreover, structural [Amaral et al., 2008; Hyde et al., 2010; Stanfield et al., 2008] and functional [Batty et al., 2011; Dinstein et al., 2012] abnormalities have been widely reported in primary visual brain areas in autism in response to a wide range of tasks [Jemel et al., 2010; Sanchez‐Marin and Padilla‐Medina, 2008; Vandenbroucke et al., 2008]. The consistency of these findings across the literature are compatible with many difficulties and/or special abilities described in autism [Happé and Frith, 2006; Markram et al., 2007; Mottron et al., 2006] and encourage a view of a cascade of events leading to impaired high‐order integrative processes during numerosity estimation in ASD. This is consistent with a model that proposed that when overloaded with sensory information, people with autism may saturate, leading to abnormal visual processing which generates other higher level disorders [Barthélémy, et al., 1995; Lelord, 1990].

Temporal sources

Between group differences in activations of temporal sources were found during numerosity processing itself and the second group of analyses highlighted that this effect may be related to differences in perceptual (i.e., local/global) processing. A global meaning effect was localized in temporal cortices (right inferior temporal cortex, right fusiform gyrus and left superior temporal gyrus) from 120 to 180 ms until 220 to 290 ms (Animal > Non‐Animal) in TD participants whereas in ASD participants, a reverse significant difference of temporal activations was observed between the two shape categories only at 290 to 350 ms (NA>A).

This result supports previous behavioural evidence showing that individuals with ASD perform atypically on a range of tasks involving integration of parts into wholes [Happé and Booth, 2008]. Organization of dots in an animal shape would be perceived by TD participants and increase the cognitive demand to ignore this global perception, leading to greater activations in temporal areas already reported to be the reflection of integration processes [Shafritz et al., 2002; Weissman and Woldorff, 2005]. On the other hand, ASD subjects may be less hindered by interference from the global animal shape of the dot patterns and hence, show fewer neural signs in response to this meaningful organization of dots in temporal areas. Accounting for these results, a recent neuroimaging study has examined global‐level interference during local processing in ASD, using a functional connectivity analysis [Liu et al., 2011]. In this study, subjects had to count coloured lines embedded in a 3D object. The study found subjects with ASD to have a lower level of activation of executive brain regions and synchronization between executive (i.e., frontal and prefrontal) and posterior visuo‐spatial (i.e., fusiform, precuneus, inferior parietal and inferior, and middle occipital) regions. The investigators concluded that subjects with ASD were less or not at all affected by the presence of a 3D figure, whereas control subjects needed to suppress automatic processing of global information. Overall, these findings are in line with the WCC and EPF psychological theories.

Parietal sources

From 120 until 400 ms, lower activation was found in the ASD group in the parietal sources, including the precuneus, the inferior parietal lobule (IPL) and the superior parietal lobule (SPL). Rare neuroimaging studies have been focused on numerosity processing when early development has been disrupted and none of them have focused on ASD. To aid in the understanding of abnormal activations observed in ASD, helpful indices can come from work in typical development [Cantlon et al., 2006; Temple and Posner, 1998]. For example, investigating neural correlates of numerical processing in adults and pre‐school children and adults, Cantlon et al. [2006] found that adults showed greater number‐related activity in the IPS than children, while children showed greater number‐related activity than adults at an adjacent SPL site [Cantlon et al., 2006]. They suggested that across development the SPL plays a role in specific number‐related processes. Our results showed differences in activations between ASD and TD participants in SPL, fitting the characterization of ASD as a developmental disorder.

Frontal sources

Finally, from 400 to 500 ms, atypical sources in prefrontal and frontal areas, including precentral gyrus, medial frontal gyrus and postcentral gyrus (BA2) and an absence of the SFG activation were found in ASD participants. In autism only, frontal activity in the right premotor cortex (BA6) was seen. In addition to sensory abnormalities and the central coherence model, autism has been variously characterized as a deficit of executive function [Hill, 2004; Ozonoff et al., 1991] and complex information processing [Minshew et al., 1997], which are processes associated with modulation of frontal brain activity during numerosity processing. Thus, our results are pertinent to these models. These brain atypicalities could be related to reduced brain functional connectivity, or underconnectivity, between frontal and posterior cortices reported in autism [Cherkassky et al., 2006; Ebisch et al., 2011; Just et al., 2004; Liu et al., 2011; Minshew et al., 1997, Liu et al., 2011].

Conclusions and Theoretical Purpose

To our knowledge, the present study is the first to directly investigate behavioural and brain representations of numerical estimation tasks in TD and ASD adults, involving different perceptual processes and their impact on the patterns of responses found. In this context, the findings need to be replicated and their interpretations tightened. Especially, we acknowledge the lack of behavioral and neurophysiological evidence of impaired numerosity estimation in ASD as a limitation.

However, to integrate our widespread observations into a more general view, we suggest a plausible four‐stage model of numerosity estimation. From 80ms, occipital activations may reflect visual preprocessing (i.e., extraction of basic visual characteristics) of quantity estimation. From 120 ms, individuation of dots in space requiring local perceptual abilities may be completed in temporal brain areas. Third, from 120 to 400 ms, integration of visuo‐spatial and number‐related information may be done in several regions of the parietal lobe and may lead to the conversion of visual input into a number‐selective neural code. Finally, after 400 ms, frontal cortex may index decisional stages about numerosity estimation, which impose demands on working memory and on more global executive functions including error monitoring. In other words, numerosity estimation may result from the serial integration of several differently weighted factors. As we suggest that the processes may be serial, the later impairments observed in ASD in parietal and frontal processes could be due to primary deficits at the sensory level. A second possibility is that atypicalities in numerosity processing in ASD may originate from overlapping difficulties as each of the processes are engaged. Finally, the hypothesis of a reduced functional connectivity between executive, number‐related and visuo‐spatial regions may also account for our results; one primary dysfunction would hence lead to an overall atypical network in ASD.

Although brain regions involved in each stage and the time course of their contribution fit with the model, it remains speculative and needs to be further investigated. For example, to specify the functional processes that underlie the differences between TD and ASD, future studies may benefit from looking at the effect of number of dots on source amplitudes. However, the current behavioural and neuroimaging data together suggest a concatenation of atypical processing in the series of cognitive operations underlying numerosity estimation in ASD.