Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2014 Feb 22;35(8):3805–3818. doi: 10.1002/hbm.22438

Reversed hierarchy in the brain for general and specific cognitive abilities: A morphometric analysis

Francisco J Román 1,2, Francisco J Abad 1, Sergio Escorial 3, Miguel Burgaleta 1,4, Kenia Martínez 1,2, Juan Álvarez‐Linera 2, María Ángeles Quiroga 3, Sherif Karama 5, Richard J Haier 6, Roberto Colom 1,2,✉
PMCID: PMC6869303  PMID: 24677433

Abstract

Intelligence is composed of a set of cognitive abilities hierarchically organized. General and specific abilities capture distinguishable, but related, facets of the intelligence construct. Here, we analyze gray matter with three morphometric indices (volume, cortical surface area, and cortical thickness) at three levels of the intelligence hierarchy (tests, first‐order factors, and a higher‐order general factor, g). A group of one hundred and four healthy young adults completed a cognitive battery and underwent high‐resolution structural MRI. Latent scores were computed for the intelligence factors and tests were also analyzed. The key finding reveals substantial variability in gray matter correlates at the test level, which is substantially reduced for the first‐order and the higher‐order factors. This supports a reversed hierarchy in the brain with respect to cognitive abilities at different psychometric levels: the greater the generality, the smaller the number of relevant gray matter clusters accounting for individual differences in intelligent performance. Hum Brain Mapp 35:3805–3818, 2014. © 2014 Wiley Periodicals, Inc.

Keywords: intelligence, Voxel‐based Morphometry (VBM), surface‐based morphometry, cortical surface area, cortical thickness

INTRODUCTION

The intelligence construct comprises a large set of mental abilities organized in a hierarchy [Carroll, 1993, 2003; Deary, 2012; Neisser et al., 1996; Nisbett et al., 2012]. At the top is the general factor (g) defined as reasoning and planning, general problem solving, and efficient learning [Gottfredson, 1997]. Next down in the hierarchy are factors such as abstract‐fluid (Gf), verbal‐crystallized (Gc), and visuospatial intelligence (Gv) [Johnson and Bouchard, 2005; McGrew, 2009]. These factors are the focus of interest for cognitive neuroscientists, mainly because of their psychometric and theoretical robustness, as well as their balance between generality and specificity [Colom et al., 2009, 2010; Colom and Thompson, 2011]. Individual tests of mental abilities are at the bottom of the hierarchy.

Although brain imaging studies of intelligence identify common areas related to intelligence assessed by different methods, especially in parietal and frontal lobes, as described by the P‐FIT model [Jung and Haier, 2007], the evidence also shows substantial variations across studies [Colom, 2007]. This might be attributed to the use of intelligence measures from different levels of the hierarchy. Colom and Thompson [2011] concluded that psychometrics and cognitive neuroscience must work in tandem to find the most likely biological correlates of individual differences in human intelligence. Following Jensen [998] they underscored the distinction between constructs (the general factor of intelligence, working memory capacity, etc.), vehicles (intelligence tests, laboratory tasks, etc.), and measurements (Raven's Progressive Matrices, Wechsler Intelligence Scales, etc.), noting that this distinction is frequently neglected in neuroscience. Using single or omnibus intelligence measures can provide largely different results. Therefore, what is needed is a clear specification of the intelligence construct relying on the framework provided by the intelligence hierarchy discovered by the psychometric approach [Barbey et al., 2012; Colom et al., 2009; Gläscher et al., 2010; Haier et al., 2009; Karama et al., 2011]. Here we adopt this approach considering three levels of this hierarchy for obtaining distinguishable but related scores.

In this regard, Voxel‐based Morphometry (VBM) and Surface‐based Morphometry (SBM) allow the quantification of different structural brain indices. Both approaches explore variations in macroscopic cortex anatomy using high resolution MRI T1‐weighted data and these have been used to study intelligence. VBM can identify differences in the local composition of brain tissue (gray matter volume (GMV)) across subjects [Ashburner and Friston, 2000; Mechelli et al., 2005] whereas SBM methods create surfaces representing structural boundaries (white matter–gray matter; gray matter–cerebrospinal fluid) by diverse meshing algorithms [Fischl and Dale, 2000; Kim et al., 2005; Thompson et al., 2004], allowing the computation of several local gray matter measures, such as cortical thickness (CTh) and cortical surface area (CSA).

Here we apply VBM and SBM to study the relationship between brain variations and intelligence performance differences. Specifically, GMV, CSA, and CTh are considered because (a) individual differences in CSA are related with the number of columns, (b) individual differences in CTh depend on the number of cells within a given column, and (c) cortical GMV combines CSA and CTh [Chklovskii et al., 2004; la Fougere et al., 2011; Rakic, 1988; Thompson et al., 2007; see Fig. 1].

Figure 1.

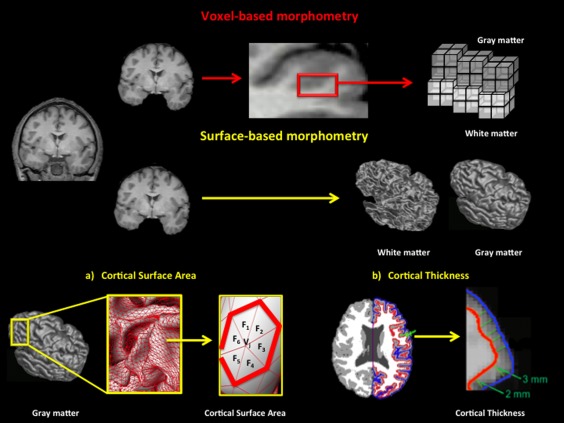
Figure 1

Open in a new tab

Steps for estimating (a) Cortical GMV using VBM and (b) CSA and CTh using SBM. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

GMV is highly correlated with CSA, whereas the correlation between GMV and CTh is substantially lower [Colom et al., 2013a]. Further, it has been suggested that CSA may be a better index than CTh for capturing the balance between local specialization and global integration in the brain [Sanabria‐Diaz et al., 2010]. Therefore, we expect more findings for GMV and CSA than for CTh when considering their relationships with individual differences in intelligence. These three structural brain indices will be systematically related with several intelligence tests, three first‐order factors (fluid, crystallized, and spatial intelligence), and a higher‐order factor (general intelligence, g). As noted by Colom and Thompson [2011] (a) performance differences on intelligence tests rely on g, groups of abilities, and specific cognitive skills, (b) psychometric estimates of performance at the level of first‐order factors capture common variance shared by their respective tests, and (c) individual differences in g capture common variance shared by all the considered first‐order factors. Therefore, it is important to keep in mind that the higher the level in the intelligence hierarchy, the lesser the amount of variance related with specificities at the measurement level (tests).

Following the latter psychometric fact, we postulate three predictions, one for each level of the intelligence hierarchy. First, given that the general factor of intelligence (g) captures the purest estimate of the intelligence construct (variance shared by all the intelligence tests and all the first‐order factors removing their specificity), we expect mainly frontal and parietal brain regions to be correlated with psychometric scores for g [Jung and Haier, 2007]. Second, because first‐order factors representing abstract‐fluid (Gf), verbal‐crystallized (Gc), and visuospatial (Gv) intelligence capture variance common to their respective measures (again removing their specificity), brain regions correlating with Gf, Gc, and Gv scores should be circumscribed to their respective common processing requirements. Thirdly, given that intelligence tests require a complex combination of g, their respective cognitive domain, and cognitive skills specifically required by each test, more widespread brain correlates are expected.

In addition to these three hypotheses, we will check and compute potential commonalities across the intelligence hierarchy. Taking into account the distinction among constructs, vehicles, and measurements, Jensen [1998] noted that not all tests estimate the intelligence construct with the same quality. Therefore, we expect distinguishable overlaps in the brain between specific tests and their respective constructs based on their g loadings quantified from a psychometric perspective: the larger the test's g loading, the greater would be the overlap in the brain with both its corresponding first‐order factor and the higher‐order factor (g).

METHOD

Participants

Four hundred five university undergraduates completed a battery of nine intelligence tests and 120 of these students, representative of the range of obtained tests' scores, were invited for MRI scanning. One hundred four agreed to participate in the study (59 females and 45 males, mean age = 19.9, SD = 1.6, age range = 18–27; 93.3% right‐handed). They completed a questionnaire asking for medical, neurological, psychiatric illness, or conditions that might preclude MRI scanning. The local ethical committee approved the study and all procedures observed the Declaration of Helsinki. Informed consent was obtained from all participants and they received a payment of 20€ for their participation.1

Intelligence Measures

Intelligence was measured by tests tapping abstract‐fluid (Gf), verbal‐crystallized (Gc), and spatial intelligence (Gv) [Horn, 1985]. The administered tests were the Raven Advance Progressive Matrices [RAPM; Raven, 1962] (screening version, even numbered items), three subtests from the Primary Mental Abilities Battery [PMA; Thurstone and Thurstone, 1968], namely, inductive reasoning (R), vocabulary (V), and mental rotation (S), four subtests from the Differential Aptitude Test Battery (DAT‐5; Bennett et al., 1990], specifically screening versions (even numbered items) for the abstract reasoning (AR), verbal reasoning (VR), spatial relations (SR), and numerical reasoning (NR) subtests, and, finally, the “Rotation of solid figures” test [Yela, 1969]. A detailed description of these tests can be found in Supporting Information Appendix 1.

Factor Analysis

A confirmatory factor analysis (CFA) was computed using AMOS 16.0.1 [Arbuckle, 2007] for testing the likelihood of the postulated measurement model: three primary factors (Gf, Gc, and Gv) defined by their three intelligence tests, and a higher‐order factor representing general intelligence (g). Maximum‐Likelihood (ML) was employed as method of estimation. The factor scores for the primary factors and for g were obtained from the AMOS program. Model fit was checked with the following indexes: CMIN/DF, RMSEA, CFI, and SRMR. Factor scores, along with the intelligence tests' scores, were submitted to imaging analyses. The g loading of each test was estimated using Schmid–Leiman transformation [Schmid and Leiman, 1957].

MRI Data Collection

MRIs were obtained with a 3 T scanner (GEHC Waukesha, WI, 3 T Excite HDX) 8‐channels coil. 3D: FSPGR with IR preparation pulse (repetition time (TR) 5.7 ms, echo time (TE) 2.4 ms inversion time (TI) 750 ms, flip angle 12). Sagital acquisition 0.8 mm thickness, full brain coverage (220 slices), matrix 266 × 266, Field of View (FOV) 24 (isotropic voxels 0.7 cm3).

VBM Analyses

OptimizedVBM was applied for identifying brain areas where regional GMVs were correlated with intelligence scores. We used Statistical Parametric Mapping software (SPM8; Wellcome Department of Imaging Neuroscience, University College London, 2009) for pre‐processing and statistical analyses. Pre‐processing involved image intensity bias correction, segmentation, and normalization. Structural data were divided into different tissue classes using the automated unified segmentation approach provided by the software [Ashburner and Friston, 2005]. The modulated gray matter partitions were then smoothed with a 12‐mm full width half maximum (FWHM) isotropic Gaussian kernel to account for slight misalignments of homologous anatomical structures and to ensure statistical validity under parametric assumptions [Burgaleta et al., 2012; Colom et al., 2009]. Each individual scan was finally fitted to a standardized SPM template specifically created for 3 T MRI scans (tissue probability map provided by the International Consortium for Brain Mapping, T1452 Atlas, John C. Mazziotta and Arthur W. Toga, http://www.loni.ucla.edu/Atlases/Atlas_Detail.jsp?atlas_id=6).

The basic design matrix for the statistical analyses was one sample t test controlling for sex, age, and handedness.

Surface‐Based Morphometry Analyses

MRIs were processed by the CIVET pipeline (version 1.1.9) developed at the MNI for fully automated structural image analysis [Ad‐Dab'bagh et al., 2006; Kim et al., 2005; MacDonald et al., 2000]. CIVET implements a surface‐based technique for estimating CTh and CSA. As noted above, CSA is mainly related to the number and spacing of mini‐columnar units of cells in the cerebral cortex, whereas CTh is influenced by the number of neurons per column, or neuron density, as well as glial support and dendritic connections [Chance et al., 2008; Lyttelton et al., 2009]. Specific stages for the analyses involve (1) registration to MNI‐Talairach space, (2) generation of high‐resolution hemispheric surfaces with 40,962 vertices each, (3) registration of surfaces to a high‐resolution template, (4) application of a reverse of step “a” allowing surface or thickness estimations in native space for each subject, and (5) smoothing using a 20‐mm kernel for CTh and 40‐mm for CSA. See Karama et al. [2009] for further details. Statistical analyses were computed using SurfStat (http://www.math.mcgill.ca/keith/surfstat/) created for MATLAB 7 (The Math‐Works, Inc.). Statistical design was based on a t test controlling for sex, age, and handedness.

Analysis With Structural Data

First, VBM and SBM analyses were made. Second, small volume correction (SVC) was used for test whether these results survived correction for multiple comparisons, using P‐FIT regions as center of the SVC [Colom et al., 2013a]. Third, using results that survived to SVCs, the index of qualitative variation (IQV) was calculated for measuring the distribution of results in the brain for each structural image [Leon‐Guerrero and Frankfort‐Nachmias, 2000]. Finally, Dice coefficients (DCs) were computed for each pair of images for quantifying their degree of similarity across the intelligence hierarchy [Barbey et al., 2013].

RESULTS

Intelligence Factors

Table 1 shows the correlations among psychometric scores along with the descriptive statistics and reliability indices (Cronbach's α).

Table 1.

Descriptive statistics and correlation matrix for the intelligence measures

1 2 3 4 5 6 7 8 9 10 11 12 13
1. RAPM (Gf) 0.398b 0.467b 0.146 0.198a 0.284b 0.236a 0.079 0.223a 0.717b 0.509b 0.393b 0.597b
2. PMA‐R (Gf) 0.371b 0.237a 0.286b 0.316b 0.130 0.108 0.275b 0.648b 0.538b 0.353b 0.568b
3. DAT‐AR (Gf) 0.208a 0.310b 0.345b 0.346b 0.193a 0.371b 0.824b 0.614b 0.550b 0.733b
4. PMA‐V (Gc) 0.296b 0.311b 0.201a 0.217a −0.010 0.348b 0.560b 0.249a 0.427b
5. DAT‐VR (Gc) 0.343b 0.114 0.081 0.241a 0.466b 0.649b 0.270b 0.511b
6. DAT‐NR (Gc) 0.200a 0.113 0.193 0.550b 0.792b 0.337b 0.619b
7. Solid Figures (Gv) 0.415b 0.408b 0.453b 0.358b 0.833b 0.606b
8. PMA‐S (Gv) 0.322b 0.293b 0.252a 0.643b 0.438b
9. DAT‐SR (Gv) 0.474b 0.333b 0.725b 0.565b
10. Fluid intelligence (Gf) 0.863b 0.721b 0.953b
11. Crystallized intelligence (Gc) 0.590b 0.905b
12. Spatial Intelligence (Gv) 0.853b
13. g factor
Mean 11.84 11.97 14.43 32.69 13.64 11.95 9.00 27.53 15.95
SD 2.36 4,49 3.52 6.57 3.00 3.23 3.89 9.67 4.79
Α 0.84+ 0.87 0.93+ 0.79 0.88+ 0.90+ 0.74 0.73 0.91+
Open in a new tab
a

P < 0.05

b

P < 0.01.

Tests: Raven Advanced Progressive Matrices test (RAPM), abstract reasoning (DAT‐AR), verbal reasoning (DAT‐VR), spatial relations (DAT‐SR) and numerical reasoning (DAT‐NR) subtests from the Differential Aptitude test (DAT‐5) Battery. Rotation of Solid Figures (Solid Figures) and from the Primary Mental Abilities Battery (PMA) the subtest: inductive reasoning (PMA‐R), vocabulary subtest (PMA‐V) and spatial subtest (PMA‐S). First‐order factors: fluid intelligence (Gf), verbal‐crystallized intelligence (Gc) and spatial intelligence (Gv) and higher‐order factor or general intelligence (g). (+) Reliability was corrected by Spearman‐Brown formula for tests in screening version.

The CFA showed a very good fit: CMIN/DF = 0.97 (values around 2.0 denote good fit), RMSEA = 0.00 [≤ 0.06 is considered a good fit; Hu and Bentler, 1999], CFI = 1.00 (≥ 0.90 is considered a good fit), and SRMR = 0.052 [≤ 0.08 is considered a good fit; Hu and Bentler, 1999]. Figure 2 depicts the structural weights for the model and the g loadings for each test.

Figure 2.

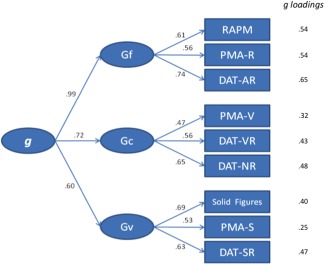
Figure 2

Open in a new tab

Confirmatory model for the considered intelligence measures (RAPM = Raven Advanced Progressive Matrices Test, PMA‐R = inductive reasoning subtests, DAT‐AR = abstract reasoning subtest, PMA‐V = vocabulary subtests, DAT‐VR = verbal reasoning subtest, DAT‐NR = numerical reasoning subtest test, PMA‐S = mental rotation subtest, DAT‐SR = spatial relations subtest and Solid Figures = Rotation of Solid Figures), the three primary factors (Gf = fluid intelligence, Gc = verbal‐crystallized intelligence and Gv = spatial intelligence), and the higher‐order factor (g). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Brain Structural Indices

Table 2 shows the relationship among the brain structural indices: cortical GMV, CSA, and CTh.

Table 2.

Descriptive statistics and correlation matrix for the structural measures

Total GMV (mm3) Total CSA (mm2) Total CTh (mm)
Total GMV (mm3) 1 0.888a 0.587a
Total CSA (mm2) 1 0.387a
Total CTh (mm) 1
M 721,903.8 179,810.3 265,206.8
SD 67,276.78 12,569.23 7438.16
Min 560,000 15,2734 247,247
Max 915,000 210,579 281,594
Skewness 0.292 0.226 −0.143
Kurtosis −0.138 −0.264 −0.373
Z Kolmogorov–Smirnov
P value 0.695 (0.719) 0.464 (0.982) 0.443 (0.989)
Open in a new tab
a

P < 0.01.

GMV, gray matter volume, CSA, cortical surface area, CTh, cortical thickness.

GMV and CSA showed the highest correlation (r = 0.89; P < 0.001) whereas the correlation between GMV and CTh was 0.59 (P < 0.001). Finally, the correlation between CSA and CTh was 0.39 (P < 0.001). All these indices were normally distributed (Z Kolmogorov–Smirnov) with P values of 0.719 (GMV), 0.982 (CSA), and 0.989 (CTh).

Brain Structural Results for the Intelligence Hierarchy

Supporting Information Appendices 2–4 show the results for GMV, CSA, and CTh respectively for (a) the specific intelligence measures (lowest level of the intelligence hierarchy), (b) first‐order factors (Gf, Gc, and Gv), and (c) the higher‐order factor (g). GMV, CSA, and CTh coordinates for each level of the hierarchy can be found in Supporting Information Appendix 5.

(a) Intelligence measures

Abstract‐Fluid intelligence subtests

For abstract reasoning (DAT‐AR), GMV showed significant findings in the right temporal lobe (uncus) and the hippocampus. No significant results were found for CSA and CTh. For inductive reasoning (PMA‐R), the insula and the right middle frontal gyrus showed GMV correlates. Also, the superior frontal gyrus was significant for CTh. No results were found for CSA. Finally, GMV results for the RAPM were significant for the middle frontal gyrus (bilateral), the caudate, and the precuneus (right parietal). For CSA, all significant results were located in the frontal lobe: superior and inferior frontal gyrus (bilateral). CTh correlated with the RAPM in the left parietal (precuneus and postcentral gyrus) and the right occipital area (middle occipital gyrus).

Crystallized intelligence subtests

For vocabulary (PMA‐V), only GMV results were significant and they were located in the middle and inferior frontal gyrus. For verbal reasoning (DAT‐VR) GMV showed significant results in the right putamen and CTh showed correlations in the left post central gyrus. For numerical reasoning (DAT‐NR), GMV results were found (1) in the middle frontal gyrus and paracentral, (2) the precuneus, postcentral gyrus, and inferior parietal lobe, (3) superior, middle, and inferior temporal lobe, (4) cuneus and superior occipital gyrus, and (5) posterior cingulate gyrus. For CSA, significant results were found in the left frontal, right parietal, and left temporal lobes. Finally, for CTh all results were found in left lobes (frontal and temporal).

Visuospatial intelligence subtests

For the rotation of solid figures test, GMV results were located in the middle frontal gyrus, CSA results were found in the right and left frontal lobes, and for CTh results were detected in the cingulate gyrus. For mental rotation (PMA‐S), GMV results were found in the frontal lobe (subcallosal gyrus), the caudate nucleus, and the cerebellum. Finally, for the spatial relations tests (DAT‐SR), GMV results were significant in the superior frontal gyrus, the fusiform and the middle temporal gyrus, the insula, and the cingulate gyrus. No results were found for PMA‐S and DAT‐SR with respect to CTh and CSA.

In summary, GMV results were observed for all this set of measures without any exception. However, SBM results (CSA and CTh) were observed mainly for just one test within constructs (RAPM for Gf, DAT‐NR for Gc, and Rotation of Solid Figures for Gv). No results were observed for CSA in six tests and this was so in four tests using CTh.

(b) First‐order factors (Gf, Gc, and Gv)

Supporting Information Appendices 2–4 depict results for the three first‐order factors. GMV results were significant in the right frontal lobe for Gf, Gc, and Gv. For Gv, the fusiform gyrus, the superior temporal gyrus, and the caudate nucleus also revealed significant GMV results. CSA findings were significant for Gf, Gc, and Gv at the frontal lobe. Finally, Gf showed significant correlations with CTh at the left parietal and right frontal lobes, Gc in the parietal lobe, and Gv in the temporal lobe.

Therefore, the frontal lobe was relevant for the three factors regarding GMV and CSA, whereas for CTh results for these three factors were more diverse (frontal and parietal for Gf, parietal for Gc, and temporal for Gv). Furthermore, observed clusters were substantially circumscribed, contrary to what was found for the specific intelligence tests, as described above.

(c) Higher‐order factor (g)

For the g factor results showed significant findings in the frontal lobe for CSA and GMV results. Specifically, the middle frontal gyrus and the precentral gyrus revealed significant GMV results. For CSA significant findings were detected bilaterally in the frontal lobe (dorsolateral prefrontal cortex). Finally, CTh showed significant results for the right parahippocampal gyrus, right occipital, and left parietal lobe. Again, observed clusters were greatly circumscribed.

Multiple Comparisons (SVCs)

We checked whether these results survive correction for multiple comparisons. As discussed by Salgado‐Pineda et al. [2003] corrections over the whole brain are very strict when they are applied to structural data. This analysis was done using SVC (FWE, P < 0.05) and the center of the spherical regions of interest for these corrections was selected independently from the data. We used the closest brodmann area (BA) of significant results included within the framework provided by the P‐FIT model [Jung and Haier, 2007] employing a radius of 20 mm. This is a stringent threshold because studies using this approach apply a radius of 15 mm [Bruno et al., 2004; Whitwell et al., 2007]; some studies even fail to report this crucial information [Kanai et al. 2010; Tricomi et al., 2010]. When the significant BA was in a relevant region for the P‐FIT model, the center for SVC was not located at the same center as that of the significant results [Colom et al., 2013a]. Specific regions surviving to SVC, and BA where the center of SVC was located can be found in Supporting Information Appendix 3.

For GMV most results survived, but some failed to pass at the test and first‐order levels. Specifically, for numerical reasoning (DAT‐NR) some findings in occipital and temporal lobes failed to pass the correction. Results for spatial relations (DAT‐SR) did not survive in the right frontal, temporal, and insula. For Gv, results for the left temporal did not survive. Note that we omitted SVCs for regions irrelevant to the P‐FIT model (e.g., caudate nucleus, uncus, hippocampus, etc).

For CSA, all results survived, whereas this was not the case for CTh. Results failing to pass the test for this latter brain index were distributed across all levels of the intelligence hierarchy. Specifically (a) parietal and occipital results did not survive for g, (b) for Gf and Gc the postcentral gyrus did not pass, (c) for Gv, the inferior temporal gyrus did not survive, (d) nothing did survive for numerical reasoning (DAT‐NR) and the postcentral gyrus failed to pass for the RAPM.

Index of Qualitative Variation

We calculated the percentage of significant results located in frontal, parietal, temporal, occipital lobes, cerebellum, and other anatomical structures (limbic lobe, subcortical structures, etc.) for the observed results but considering those surviving to SVCs only. Next, we used these regions as different categories where significant results were found (the cerebellum was not considered a category for CSA and CTh indices because CIVET excludes this brain structure). Afterwards, we computed the index of IQV [Leon‐Guerrero and Frankfort‐Nachmias, 2000] using the percentage of significant results distributed across categories: frontal, parietal, temporal, occipital, cerebellum (not for CSA and CTh indices) and other anatomical structures. IQV values range from 0 (all significant results in one category, e.g. frontal lobe) to 1 (significant results are distributed across all categories—same percentage of significant results in frontal, temporal, parietal, occipital, cerebellum, and others anatomical structures).

These calculations revealed that the general factor of intelligence (g) always showed results in one category, specifically in the frontal lobe for CSA and GMV indices, and in the limbic lobe for CTh. For the first‐order factors, results were more distributed. For example, the IQV for Gv in GMV was 0.45 (frontal, temporal, and other anatomical structures), for Gf in CTh the IQV was of 0.55 (frontal and parietal). Finally, for specific tests the results were distributed for GMV, although for some tests the results were located in one region (DAT‐AR, DAT‐VR, PMA‐V, and Solid Figures). In CSA the significant results were only found for DAT‐NR (IQV = 0.61), RAPM (IQV = 0.00), and Solid Figures (IQV = 0.00). For CTh index the results were similar, only for the RAPM the IQV was different from 0.00.

In the final stage, we calculated the mean for the IQVs at each level of the intelligence hierarchy using all indices. The results support a reversed hierarchy: (a) for the g factor, the IQV value was 0.00, (b) for the first‐order factors it was 0.14, and (c) for the specific tests the value was 0.30. Therefore, IQVs decrease ∼15% as we move upwards in the intelligence hierarchy (Table 3). A visual representation is depicted in Figure 3.

Table 3.

Index of qualitative variation (IQV) for each index

GMV CSA CTh Mean
g 0.00 0.00 0.00 0.00
Mean g factor 0.00
Gf 0.00 0.00 0.55 0.18
Gc 0.00 0.00 — 0.00
Gv 0.45 0.00 — 0.23
Mean First‐order factors 0.14
RAPM 0.68 0.00 0.62 0.43
PMA‐R 0.60 — 0.00 0.30
DAT‐AR 0.00 — — 0.00
PMA‐V 0.00 — — 0.00
DAT‐VR 0.00 — 0.00 0.00
DAT‐NR 0.75 0.61 — 0.68
Solid Fig 0.00 0.00 0.00 0.00
DAT‐SR 0.62 — — 0.62
PMA‐S 0.63 — — 0.63
Mean test level 0.30
Open in a new tab

GMV = gray matter volume; CSA = cortical surface area; CTh = cortical thickness.

IQV vary from 0 (all significant results in one category) to 1 (significant results are evenly divided across all categories). Tests: Raven Advanced Progressive Matrices test (RAPM), abstract reasoning (DAT‐AR), verbal reasoning (DAT‐VR), spatial relations (DAT‐SR) and numerical reasoning (DAT‐NR) subtests from the Differential Aptitude test (DAT‐5) Battery. Rotation of Solid Figures (Solid Figures) and from the Primary Mental Abilities Battery (PMA) the subtest: inductive reasoning (PMA‐R), vocabulary subtest (PMA‐V) and spatial subtest (PMA‐S). Primary factors: fluid intelligence (Gf), verbal‐crystallized intelligence (Gc) and spatial intelligence (Gv) and higher‐order factor or general intelligence (g). (—) No significant results.

Figure 3.

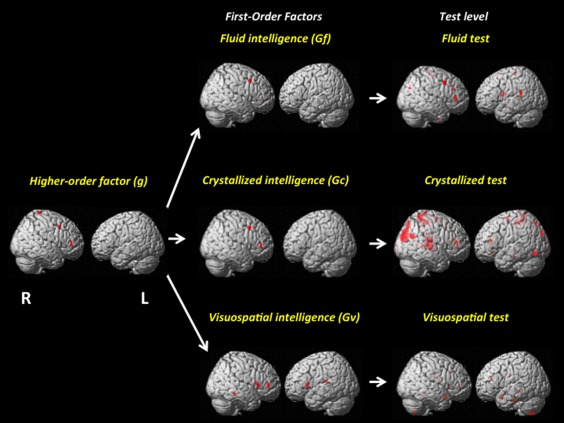
Figure 3

Open in a new tab

Visual representation of the reversed hierarchy using GMV results at P < 0.001. The test level summarizes findings for the complete set by construct (Gf, Gc, and Gv). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Note that the location of significant clusters was distributed across lobes at the test level. For the first‐order factors the majority of results were found in the frontal lobe, although Gv had significant clusters in the temporal lobe and the caudate. Finally, significant results were found in frontal lobe only for the general factor of intelligence (g).

Overlaps Across the Intelligence Hierarchy

Using xjview 8.11 (http://www.alivelearn.net/xjview8/download/) we overlapped the Statistical Parametric Maps (GMV) for each test, the first‐order factors, and the g factor. The same method was applied for CSA and CTh using SurfStat (http://www.math.mcgill.ca/keith/surfstat/).

Afterwards, DCs were computed for each pair of images for obtaining a quantification of their degree of similarity [Barbey et al., 2013; Bennett and Miller, 2010; Rombouts et al., 1997]. The DC is an index of cluster overlap. It can be interpreted as the number of voxels that will overlap between two measures divided by the sum of voxels for each measure. Values range from 0 (no similarity) to 1 (perfect similarity). DCs between g and each test are shown in Figure 4a.

Figure 4.

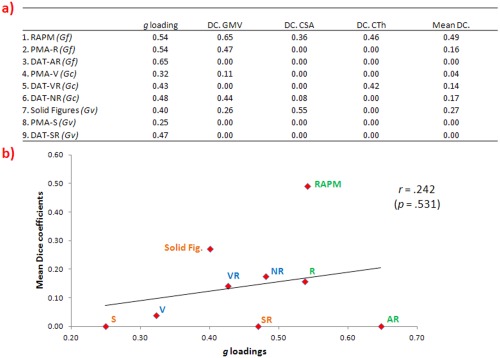
Figure 4

Open in a new tab

(a) g Loadings of each test (RAPM = Raven Advanced Progressive Matrices Test, PMA‐R = inductive reasoning subtests, DAT‐AR = abstract reasoning subtest, PMA‐V = vocabulary subtests, DAT‐VR = verbal reasoning subtest, DAT‐NR = numerical reasoning subtest test, PMA‐S = mental rotation subtest, DAT‐SR = spatial relations subtest and Solid Figures = Rotation of Solid Figures) and DCs for each brain index (GMV = gray matter volume, CSA = cortical surface area and CTh = cortical thickness). (b) Scatterplot between mean of all Dice coefficients and g loadings. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

For checking whether the g loadings of the intelligence tests are related with their degree of overlap with the g factor, the Pearson correlation between g loadings and DCs was computed (Fig. 4b). This correlation was not significant for all brain indices (r = 0.331, P = 0.385 with GMV, r = 0.020, P = 0.959 with CSA, r = 0.160, P = 0.681 with CTh, and r = 0.242, P = .531 with mean of all DCs). The scatterplot shows that the RAPM deviates from the general trend. When this test is removed, the correlation value decreases for all indices (r = 0.213, P = 0.612 with GMV, r = −0.121, P = 0.775 with CSA, r = −0.041, P = 0.924 with CTh and r = 0.043, P = 0.919 with mean of all DCs). Also, the mean of all DCs between g and the first‐order factors was of 0.76 (Gf), 0.54 (Gc), and 0.41 (Gv).

Moreover, the overlaps across all levels of the intelligence hierarchy were analyzed. Three noticeable overlaps were found: (1) RAPM, Gf, and g, (2) numerical reasoning (DAT‐NR), Gc, and g, and (3) rotation of solid figures, Gv, and g. The GMV overlap among rotation of solid figures, Gv, and g was found in right BA 10. The same coordinates were shared for the overlap among numerical reasoning (DAT‐NR), Gc, and g. Finally, for the RAPM, Gf, and g the overlap was obtained in right BA 8. For CSA, the same tests overlapped with their first order factor and the g factor in bilateral BA 46. For CTh, the overlap was only found for the RAPM, Gf and g in left BA 5. The corresponding DCs are show in Table 4.

Table 4.

Dice coefficient for all overlaps between tree levels of intelligence hierarchy [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Dice coefficient
Gf RAPM
g (0.78, 0.83, 0.68) (0.65, 0.36, 0.46)
Gf (0.56, 0.45, 0.36)
Gc DAT‐NR
g (0.75, 0.46, 0.41) (0.44, 0.08, 0.00)
Gc (0.40, 0.69, 0.00)
Gv Solid Figures
g (0.77, 0.48, 0.00) (0.26, 0.55, 0.00)
Gv (0.13, 0.70, 0.00)
Open in a new tab

In black is represented Dice coefficient for voxel‐based morphometric (VBM), in red for cortical surface area (CSA) and in blue for cortical thickness (CT). Values range from 0 (i.e., no similarity) to 1 (i.e., perfect similarity).

Note that most regions of overlap across all levels of the intelligence hierarchy survived to SVC (Supporting Information Appendix 5). However, the cluster found for the rotation of solid figures test in BA 10 was only marginally significant (P = 0.06). Also, the CTh cluster at BA 5 shared by the RAPM, Gf, and g was not significant after SVC.

Finally, as suggested by one anonymous reviewer, the analyses for the different levels of the intelligence hierarchy were computed controlling for measures within the same level (e.g., for Gf the model was: 1 + Sex + Age + Handedness + Gf + Gc + Gv; the same was done for the tests tapping the same construct). Results for GMV (P = 0.001) are depicted in Supporting Information Appendix 6. The obtained results were remarkably similar to those reported above. All lobes are involved at the test level, whereas results are much more circumscribed for upper levels of the intelligence hierarchy. Therefore, these results reinforce the main conclusion.

DISCUSSION

We have reported brain correlates of scores estimated for different levels of the intelligence hierarchy using GMV, CSA, and CTh. The sample size is large according to standards of MRI research, but we acknowledge that our sample size might be underpowered to detect effect sizes lower than r = 0.25. As noted above, each index is associated with different neuronal aspects [Chklovskii et al., 2004; la Fougere et al., 2011; Rakic, 1988; Thompson et al., 2007]. We have seen that CSA reveals more findings than CTh, which is consistent with the claim that CSA may be a better index than CTh for capturing the balance between local specialization and global integration in the brain [Sanabria‐Diaz et al., 2010]. Furthermore, CSA usually displays more variability than CTh [Winkler et al., 2010], which may impact statistical sensitivity. A further consideration is that CSA appears to be slightly more genetically determined than CTh [Panizzon et al., 2009], a pattern that fits well with the fact that neurogenesis and neuronal migration—two processes that affect CSA—are complete by the term of the gestation process [Hill et al., 2010]. Given that intelligence is known to be heritable to a certain extent [see, for instance, Nisbett et al., 2012], the association between psychometric measures and CSA might reflect those neural substrates of intelligence that are less sensitive to experience. Nevertheless, there are still other experience‐related factors that can account for CSA, such as the size and complexity of the dendritic arbors [Hill et al., 2010; Meyer, 1987; Mountcastle, 1997]. Moreover, Panizzon et al. [2009] suggest that variations in CTh could be due to differences in myelination of gray matter or the underlying white matter, rather than the number of mini‐columnar cells; and Feczko et al. [2009] proposed that CSA might be sensitive to the size of intracortical elements or to the volume of white matter adjacent to a given gyrus or sulcus. Therefore, this interpretation must be taken with caution.

The key finding of our study is a reversed hierarchy in the brain for general and specific cognitive abilities. This was supported by the fact that the level of dispersion of relevant areas across the brain decreases at the rate of ∼15% as we move upwards in the intelligence hierarchy (see Table 3). This is consistent with the psychometric fact that factors capturing variance common to both specific measures and group factors partial out the specificity present at the measurement level.

We made three predictions about the distribution of results at each level of the intelligence hierarchy using the P‐FIT model as the main framework [Jung and Haier, 2007]. The first prediction was that only parieto‐frontal regions would be correlated with latent scores estimating the general factor of intelligence (g) because it represents the common variance of the complete set of measures and first‐order factors removing their specificities. The observed results were generally consistent with this prediction regarding GMV and CSA, since only frontal regions were significant. However, results for the parietal lobe were not observed. We can suggest two likely explanations for this latter result: (a) the parietal lobe is more implicated in functional than in structural studies [Barbey et al., 2012; Colom et al., 2009, 2013a; Gläscher et al., 2010; Karama et al., 2011] and/or (b) the parietal lobe is more dependent than the frontal lobe on the considered intelligence estimate. In the present study, we employed the Raven Advanced Progressive Matrices (RAPM) as one of the measures of fluid intelligence, observing significant results in frontal and parietal clusters (Supporting Information Appendix 5). The Raven test has been administered in several studies [Gray et al., 2003; Haier et al., 1988, 1992, 2003; Larson et al., 1995; Lee et al., 2006; Neubauer et al., 1999; O'Boyle et al., 2005] but the RAPM is not g. The results observed here were more consistent with the Duncan's adaptive coding model [Duncan, 2001] than with the P‐FIT model [Jung and Haier, 2007] since results for the g factor were mainly focused on the frontal lobe. Our results for the g factor resemble those reported by Gläscher et al. [2010] in their large‐scale lesion study, who supported the substantial relevance of a very specific cluster located in the frontal BA 10 for g. Finally, the current results support the neuro‐g hypothesis when the g factor is estimated following the recommendations proposed by Haier et al. [2009]. Nevertheless, further research is strongly required to dilucidate this issue.

The second prediction stated that abstract‐fluid (Gf), verbal‐crystallized (Gc), and visuospatial intelligence (Gv) correlates would be circumscribed to their respective common processing requirements. This prediction was partly supported. Significant GMV correlates for Gf were shared with two tests of fluid intelligence (RAPM and PMA‐R) in the middle frontal gyrus. CSA results were significant bilaterally in the dorsolateral prefrontal cortex for Gf and the RAPM. CTh findings were significant in the same region for Gf, inductive reasoning (PMA‐R) and the RAPM. However, CTh results for Gf did not survive correction for multiple comparisons. Therefore, only Gf showed significant regions overlapping one of its corresponding tests, although the highest similarity was found between the RAPM and Gf. These results are consistent with Gong et al. [2005] who found that individual differences in the Cattell's Culture Fair Test (measuring Gf) are correlated with GMV in the frontal lobe only. Also, performance in reasoning tasks (highly related with Gf) is greatly affected by damage in the frontal lobes [Demakis, 2003; Duncan et al., 1995, 1996; Gray and Thompson, 2004]. The meta‐analytic review published by Demakis [2003] shows that the performance in the Wisconsin Card Sorting Test (WCST) is substantially worse for patients with frontal damage. Using fMRI, Goel and Dolan [2003] found that the frontal lobe is greatly involved in reasoning process, whereas Choi et al. [2008] found that parietal regions are also relevant for fluid intelligence. These findings are consistent with the presumption that the parietal lobe might be more relevant for functional than for structural analyses, as noted above.

Regarding Gc, all the significant GMV correlations were located in the middle frontal gyrus and they were shared with numerical reasoning (DAT‐NR) and vocabulary (PMA‐V). For CSA a significant region was detected bilaterally in the dorsolateral prefrontal cortex, although DAT‐NR only had a significant result in the left dorsolateral prefrontal cortex. CTh findings were significant in the left parietal for the verbal reasoning test (DAT‐VR), but this result did not survive to SVC. There are some reports studying the structural correlates of crystallized abilities that underline the relevance of the frontal lobe. Thus, for instance, Colom et al. [2006] found that crystallized test from the WAIS correlate mainly with the frontal lobe (Arithmetic = 100%, Similarities = 98.10%, Vocabulary = 51.2%, and Information = 28.8%). Similar results were reported by Pfleiderer et al. [2004], studying females. Geake and Hasen [2010] found frontal activation for analogy tasks with a crystallized content. However, some studies fail to find results in the frontal lobe for Verbal IQ [Choi et al., 2008; Gong et al., 2005]. Lesion studies have shown that patients with anterior temporal damages perform poorly on tests of semantic knowledge [Waltz et al., 1999]. These discrepancies might be attributed to different procedures for estimating the psychological scores of interest. Note, for instance, that we have obtained significant results in the temporal lobe for Numerical Reasoning (DAT‐NR; see Supporting Information Appendix 5).

Finally, results shared by Gv and their corresponding tests were located in the fusiform gyrus, the temporal gyrus, and the caudate for GMV, and bilaterally in the dorsolateral prefrontal cortex for CSA. The result found for CTh (right temporal) was not detected for any spatial test. The results for visuospatial intelligence were more distributed across the brain than for Gf and Gc. Studying patients, Bor et al. [2010] found that frontal lesions impair spatial performance, but there are several reports also implying the basal ganglia and the temporal lobe [Moffat et al., 2007; Olson et al., 2006; Williams‐Gray et al., 2007] which is consistent with the results reported here. Moffat et al. [2007] showed that the volume of the caudate nucleus correlates with performance in a spatial navigation task and it has been noted that the basal ganglia is connected with the dorsolateral prefrontal cortex [Burgaleta et al., in press]. Olson et al. [2006] showed that lesions in the temporal lobe impair performance on visual working memory tasks.

Taken together, the results observed for Gf, Gc, Gv and their corresponding specific measurements support the view that the first‐order factors were circumscribed mainly to one of their marker tests. Also, the reported main findings for these first‐order factors and specific intelligence measurements are generally consistent with previous research, as discussed above.

The third prediction anticipated widespread results for the specific intelligence measures. This was entirely confirmed. Indeed, significant results were found across the brain for some tests (numerical reasoning, DAT‐NR, is a perfect example with a mean IQV of 0.68) and overlaps among the nine intelligence tests were rarely observed. Of note is that this result is consistent with the report by Haier et al. [2010] who analyzed eight intelligence tests used in vocational guidance, finding that gray matter correlations were widespread for the specific intelligence tests they considered. Haier et al. [2010] suggested that scores for tests are more related to specific performance than factor scores. Also, individual tests provide measurements of more‐specific abilities than first order factors and the higher‐order factor (g). Results reported here provide an explanation for these sorts of findings.

With respect to the overlap among levels of the intelligence hierarchy, it has been suggested that using specific intelligence measures or omnibus estimates of intelligent performance may be behind the observed disparate finding across studies [Colom, 2007]. The review of brain structural studies by Jung and Haier [2007] was mainly based on the Wechsler battery (70%), 20% of the reviewed studies administered just one intelligence test, and 10% analyzed the g factor. Therefore, reaching a straightforward conclusion is difficult. The distinction among constructs, vehicles, and measurements seems necessary to refine the approach to the analysis of the biological underpinnings of intelligent performance. For that purpose, we firstly quantified the degree of overlap using DCs for each test and for the g factor. We hypothesized that the brain regions associated with tests with higher g loadings will be more closely associated to the brain regions associated with the g factor. However, we failed to find this correspondence. Computed DCs were small, a result consistent with Gläscher et al. [2010] who computed an index of overlap2 between WAIS subtest and the g factor in their study, finding that the majority of the computed values were smaller than 0.20. Our results are in further agreement with Gläscher et al. [2010] because their lesion study showed that significant regions for the g factor overlapped regions for some intelligence tests. Their results for the g factor were largely circumscribed to the frontal lobe, as noted above.

Moreover, we quantified the correspondence between first‐order factors and g finding a perfect one between g loadings and DCs. Specifically, the mean for the DCs of all indices was 0.76 (Gf), 0.54 (Gc), and 0.41 (Gv), which is completely coherent with their g loadings (Fig. 2). These DCs were similar to those reported by Barbey et al. [2013] who estimated these values for Gf and different working memory measures (all measures were latent scores) obtaining DCs ranging between −0.16 and 0.67.

Finally, significant regions shared among the three levels of the intelligence hierarchy surviving correction to multiple comparisons were found in the middle frontal gyrus and the dorsolateral prefrontal cortex (DLPFC). In this regard, Mueller et al. [2013] reported that the middle frontal gyrus and the dorsolateral prefrontal cortex are regions where intra‐subject variance is quite large. These authors suggest that it is difficult to obtain a significant result in regions where intra‐subject variance is higher, which nicely fits the findings reported here[Link]. Note that (a) the majority of our results in these regions survive to SVCs and (b) these regions were related with intelligence in several studies [Colom et al., 2006, 2009; Gong et al., 2005; Haier et al., 2004, 2009].

In summary, we have shown that the higher the level in the intelligence hierarchy, the smaller and more circumscribed the number of gray matter correlates. This supports the general conclusion that factors capturing the variance common to both specific measures and group factors partial out the specificity present at the measurement level. Interestingly, removing specific variance reveals that frontal regions in the brain are crucial for supporting human intelligence. Also, the degree of overlap among g, first order factors and specific tests was coherent with the main hypothesis, since g and first order factors showed the highest DCs, whereas the computed DCs for g and the specific tests were much smaller. Therefore, a reversed hierarchy in the brain is revealed: the higher the level, the lower the number of relevant regions required for explaining intelligence differences.

Supporting information

Supporting Information Appendix 1.

Click here for additional data file. (13.8KB, docx)

Supporting Information Appendix 2.

Click here for additional data file. (660.8KB, tif)

Supporting Information Appendix 3.

Click here for additional data file. (579.7KB, tif)

Supporting Information Appendix 4.

Click here for additional data file. (1.5MB, tiff)

Supporting Information Appendix 5.

Click here for additional data file. (155.3KB, docx)

Supporting Information Appendix 6.

Click here for additional data file. (1.5MB, tiff)

Footnotes

1

We have previously reported other results using this sample [Bruner et al, 2010, 2011, 2012; Burgaleta et al., 2012, in press; Colom et al., 2009, 2010, 2013b; Martín‐Loeches et al., 2013].

2

In the Gläscher et al study the index of overlap was: (A∩B)/(A∪B). Dice coefficient is 2*(A∩B)/(A∪B), where A and B are regions significant for the considered measures.

Note that intra‐subject variance consists mainly of variance caused by technical noise [Mueller et al., 2013].

REFERENCES

  1. Ad‐Dab'bagh Y, Lyttelton O, Muehlboeck JS, Lepage C, Einarson D, Mok K, Ivanov O, Vincent RD, Lerch J, Fombonne E, Evans AC (2006): The CIVET image processing environment: A fully automated comprehensive pipeline for anatomical neuroimaging research In: Corbetta M, editor. Proceedings of the 12th Annual Meeting of the Organization for Human Brain Mapping NeuroImage, Florence, Italy. [Google Scholar]
  2. Arbuckle JL (2007): AMOS, Version 16.0.1. Spring House, PA: Amos Development Corporation. [Google Scholar]
  3. Ashburner J, Friston KJ (2000): Voxel‐based morphometry—The methods. NeuroImage 11:805–821. [DOI] [PubMed] [Google Scholar]
  4. Ashburner J, Friston KJ (2005): Unified segmentation. NeuroImage 26:839–851. [DOI] [PubMed] [Google Scholar]
  5. Barbey AK, Colom R, Solomon J, Krueger F, Forbes C, Grafman J (2012): An integrative architecture for general intelligence and executive function revealed by lesion mapping. Brain 135:1154–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Barbey AK, Colom R, Grafman J 2013: Architecture of cognitive flexibility revealed by lesion mapping. NeuroImage 82, 547–554. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bennett CM, Miller MB (2010): How reliable are the results from functional magnetic resonance imaging? Ann NY Acad Sci 1191:133–155. [DOI] [PubMed] [Google Scholar]
  8. Bennett GK, Seashore HG, Wesman AG (1990): Differential Aptitude Test, 5th ed. Madrid: TEA.
  9. Bor D, Duncan J, Lee ACH, Parr A, Owen AM (2010): Frontal lobe involvement in spatial span: Converging studies of normal and impaired function. Neuropsychologia 44:229–237. [DOI] [PubMed] [Google Scholar]
  10. Burgaleta M, Head K, Álvarez‐Linera J, Martínez K, Escorial S, Haier R, Colom R (2012). Sex differences in brain volume are related to specific skills, not to general intelligence. Intelligence 40:60–68. [Google Scholar]
  11. Burgaleta M, MacDonald PA, Martínez K, Román FJ, Álvarez‐Linera J, Karama S, Colom R (in press): Subcortical regional morphology correlates with fluid and spatial intelligence, Human Brain Mapping. [DOI] [PMC free article] [PubMed]
  12. Bruner E, Martin‐Loeches M, Colom R (2010): Midssagital brain shape variation: Patterns, allometry, and integration. J Anat 216:589–599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Bruner E, Martín‐Loeches M, Burgaleta M, Colom R (2011): Midsaggital brain shape correlation with intelligence and cognitive performance. Intelligence 39:141–147. [Google Scholar]
  14. Bruner E, de la Cuétara JM, Colom R, Martin‐Loeches M (2012): Gender‐based differences in the shape of the human corpus callosum are associated with allometric variations. J Anat 220:417–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Bruno SD, Barker GJ, Cercignani M, Symms M, Ron MA (2004): A study of bipolar disorder using magnetization transfer imaging and Voxel‐based morphometry. Brain 127:2433–2440. [DOI] [PubMed] [Google Scholar]
  16. Carroll JB (1993): Human Cognitive Abilities. Cambridge: Cambridge University Press. [Google Scholar]
  17. Carroll JB (2003): The higher‐stratum structure of cognitive abilities: Current evidence supports g and about 10 broad factors In: H Nyborg, editor. The Scientific Study of General Intelligence: Tribute to Arthur R. Jensen. Amsterdam: Pergamon; pp 5–21. [Google Scholar]
  18. Chance SA, Casanova MF, Switala AE, Crow TJ (2008): Auditory cortex asymmetry, altered minicolumn spacing and absence of ageing effects in schizophrenia. Brain 131:3178–3192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Chklovskii DB, Mel BW, Svoboda K (2004): Cortical rewiring and information storage. Nature 431:782–788. [DOI] [PubMed] [Google Scholar]
  20. Choi YY, Shamosh NA, Cho SH, DeYoung CG, Lee MJ, Lee JM, Kim SI, Cho, Z , Kim K, Gray JR, Lee KH (2008): Multiple bases of human intelligence revealed by cortical thickness and neural activation. J Neurosci 28:10323–10329. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Colom R (2007): Intelligence? What intelligence? Behav Brain Sci 30:155–56. [Google Scholar]
  22. Colom R, Thompson PM (2011): Understanding human intelligence by imaging the brain. The Wiley‐Blackwell handbook of individual differences, 330–352.
  23. Colom R, Jung R, Haier R (2006): Distributed brain sites for the g‐factor of intelligence. NeuroImage 31:1359–1365. [DOI] [PubMed] [Google Scholar]
  24. Colom R, Haier RJ, Head K, Álvarez‐Linera J, Quiroga MA, Shih PC, Jung RE (2009): Gray matter correlates of fluid, crystallized, and spatial intelligence: Testing the P‐FIT model. Intelligence 37:124–135. [Google Scholar]
  25. Colom R, Karama S, Jung RE, Haier RJ (2010): Human intelligence and brain networks. Dialogues Clin Neurosci 12:489–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Colom R, Stein JL, Rajagopalan P, Martínez K, Hermel D, Wang Y, Álvarez‐Linera J, Burgaleta M, Quiroga MA, Shih PC, Thompson P (2013b): Hippocampal structure and human cognition: Key role of spatial processing and evidence supporting the efficiency hypothesis in females. Intelligence 41:129–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Colom R, Burgaleta M, Román FJ, Karama S, Álvarez‐Linera J, Abad FJ, Martínez K, Quiroga MA, Haier RJ (2013a): Neuroanatomic overlap between intelligence and cognitive factors: Morphometry methods provide support for the key role of the frontal lobes. NeuroImage 72:143–152. [DOI] [PubMed] [Google Scholar]
  28. Deary I (2012): 125 Years of intelligence in The American Journal of Psychology. Am J Psychol 125:145–154. [DOI] [PubMed] [Google Scholar]
  29. Demakis GJ (2003): A meta‐analytic review of the sensitivity of the Wisconsin Card Sorting Test to frontal and lateralized frontal brain damage. Neuropsychology 17:255–264. [DOI] [PubMed] [Google Scholar]
  30. Duncan J (2001): An adaptive coding model of neural function in prefrontal cortex. Nat Rev Neurosci 2:820–829. [DOI] [PubMed] [Google Scholar]
  31. Duncan J, Burgess P, Emslie H (1995): Fluid intelligence after frontal lobe lesions. Neuropsychologia 33:261–268. [DOI] [PubMed] [Google Scholar]
  32. Duncan J, Emslie H, Williams P, Johnson R, Freer C (1996): Intelligence and the frontal lobe: The organization of goal directed behavior. Cogn Psychol 30:257–303. [DOI] [PubMed] [Google Scholar]
  33. Feczko E, Augustinack JC, Fischl B, Dickerson BC (2009): An MRI‐based method for measuring volume, thickness and surface area of entorhinal, perirhinal, and posterior parahippocampal cortex. Neurobiol Aging 30:420–431. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Fischl B, Dale AM (2000): Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc Natl Acad Sci USA 97:11050–11055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Geake JG, Hasen PC (2010): Functional neural correlates of fluid and crystallized analogizing. NeuroImage 29:3489–3497. [DOI] [PubMed] [Google Scholar]
  36. Gläscher J, Rudrauf D, Colom R, Paul LK, Tranel D, Damasio H, Adolphs R (2010): The distributed neural system for general intelligence revealed by lesion mapping. Proc Natl Acad Sci USA 107:4705–4709. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Goel V, Dolan RJ (2003): Reciprocal neural response within lateral and ventral medial prefrontal cortex during hot and cold reasoning. NeuroImage 20:2314–2321. [DOI] [PubMed] [Google Scholar]
  38. Gong QY, Sluming V, Mayes A, Keller S, Barrick T, Cezayirli E, Roberts N (2005): Voxel‐based morphometry and stereology provide convergent evidence of the importance of medial prefrontal cortex for fluid intelligence in healthy adults. NeuroImage 25:1175–1186. [DOI] [PubMed] [Google Scholar]
  39. Gottfredson LS (1997): Mainstream science on intelligence: An editorial with 52 signatories, history, and bibliography. Intelligence 24:13–23. [Google Scholar]
  40. Gray JR, Thompson PM (2004): Neurobiology of intelligence: Science and ethics. Nat Rev 5:471–482. [DOI] [PubMed] [Google Scholar]
  41. Gray JR, Chabris CF, Braver TS (2003): Neural mechanisms of general fluid intelligence. Nat Neurosci 6:316–322. [DOI] [PubMed] [Google Scholar]
  42. Haier RJ, Siegel BV, Nuechterlein KH, Hazlett E, Wu JC, Paek J, Browning HL, Buchsbaum MS (1988): Cortical glucose metabolic rate correlates of abstract reasoning and attention studied with positron emission tomography. Intelligence 12:199–217. [Google Scholar]
  43. Haier RJ, Siegel BV, Tang C, Abel L, Buchsbaum MS (1992): Intelligence and changes in regional cerebral glucose metabolic rate following learning. Intelligence 16:415–426. [Google Scholar]
  44. Haier RJ, White NS, Alkire MT (2003): Individual differences in general intelligence correlate with brain function during nonreasoning tasks. Intelligence 31:429–441. [Google Scholar]
  45. Haier RJ, Jung RE, Yeo RA, Head K, Alkired MT (2004): Structural brain variation and general intelligence. Neuroimage 23:425–433. [DOI] [PubMed] [Google Scholar]
  46. Haier RJ, Colom R, Schroeder DH, Condon CA, Tang C, Eaves E, Head K (2009): Gray matter and intelligence factors: Is there a neuro‐g? Intelligence 37:136–134. [Google Scholar]
  47. Haier R, Schroeder D, Tang C, Head K, Colom R (2010): Gray matter correlates of cognitive ability tests used for vocational guidance. BMC Res Notes 3, 206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Hill J, Inder T, Neil J, Dierker D, Harwell J, Van Essen D (2010): Similar patterns of cortical expansion during human development and evolution. Proc Natl Acad Sci 107, 13135–13140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Horn J (1985): Remodeling old models of intelligence In: Wolman BB, editor. Handbook of Intelligence. In: Wolman BB, editor. Handbook of Intelligence (pp. 267–300). New York: Wiley. [Google Scholar]
  50. Hu LT, Bentler PM (1999): Cutoff criteria for fit indexes in covariance structural analysis: Conventional criteria versus new alternatives. Struct Equat Model 6:1–55. [Google Scholar]
  51. Jensen AR (1998): The g Factor: The Science of Mental Ability. Westport, CT: Praeger. [Google Scholar]
  52. Johnson W, Bouchard T (2005): The structure of human intelligence: It is verbal, perceptual, and image rotation (VPR), not fluid and crystallized. Intelligence 33:393–416. [Google Scholar]
  53. Jung RE, Haier RJ (2007): The parieto‐frontal integration theory (P‐FIT) of intelligence: Converging neuroimaging evidence. Behav Brain Sci 30:135–187. [DOI] [PubMed] [Google Scholar]
  54. Kanai R, Bahrami B, Rees G (2010): Human parietal cortex structure predicts individual differences in perceptual rivalry. Curr Biol 20:1626–1630. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Karama S, Ad‐Dab'bagh Y, Haier RJ, Deary IJ, Lyttelton OC, Lepage C, Evans AC, the Brain Development Cooperative Group (2009): Positive association between cognitive ability and cortical thickness in a representative US sample of healthy 6 to 18 year‐olds. Intelligence 37:145–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Karama S, Colom R, Jhonson W, Deary IJ, Haier R, Waber DP, Lepage C, Ganjavi H, Jung R, Evans AC, the Brain Development Cooperative Group (2011): Cortical thickness correlates of specific cognitive performance accounted for by the general factor of intelligence in healthy children aged 6 to 18. Neuroimage 55:1443–1453. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Kim JS, Singh V, Lee JK, Lerch J, Ad‐Dab'bagh Y, MacDonald D, Lee JM, Kim SI, Evans AC (2005): Automated 3‐D extraction and evaluation of the inner and outer cortical surfaces using a Laplacian map and partial volume effect classification. NeuroImage 27:210–221. [DOI] [PubMed] [Google Scholar]
  58. la Fougere C, Grant S, Kostikov A, Schirrmacher R, Gravel P, Schipper HM, Reader A, Evans A, Thiel A (2011): Where in‐vivo imaging meets cytoarchitectonics: The relationship between cortical thickness and neuronal density measured with high‐ resolution [18F]flumazenil‐PET. Neuroimage 56:951–960. [DOI] [PubMed] [Google Scholar]
  59. Larson GE, Haier RJ, Lacasse L, Hazen K (1995): Evaluation of a “Mental Effort” hypothesis for correlations between cortical metabolism and intelligence. Intelligence 21:267–278. [Google Scholar]
  60. Lee KH, Choi YY, Gray JR, Cho SH, Chae JH, Lee S, Kim K (2006): Neural correlates of superior intelligence: Stronger recruitment of posterior parietal cortex. NeuroImage 29:578–586. [DOI] [PubMed] [Google Scholar]
  61. Leon‐Guerrero A, Frankfort‐Nachmias C (2000): Social Statistics for a Diverse Society, 2nd ed Thousand Oaks, California: Pine Forge Press; pp 153–162. [Google Scholar]
  62. Lyttelton OC, Karama S, Ad‐Dab'baghm Y, Zatorre RJ, Carbonell F, Worsley K, Evans A (2009): Positional and surface area asymmetry of the human cerebral cortex. NeuroImage 46:895–903. [DOI] [PubMed] [Google Scholar]
  63. MacDonald D, Kabani N, Avis D, Evans AC (2000): Automated 3‐D extraction of inner and outer surfaces of cerebral cortex from MRI. NeuroImage 12:340–356. [DOI] [PubMed] [Google Scholar]
  64. Martin‐Loeches M, Bruner E, de la Cuétara JM, Colom R (2013): Correlation between corpus callosum shape and cognitive performance in a sample of healthy young adults. Brain Struct Funct 218, 721–731. [DOI] [PubMed] [Google Scholar]
  65. McGrew K (2009): CHC theory and the human cognitive abilities project: Standing on the shoulders of the giants of psychometric intelligence research. Intelligence 37:1–10. [Google Scholar]
  66. Mechelli A, Price CJ, Friston KJ, Ashburner J (2005): Voxel‐based morphometry of the human brain: Methods and applications. Curr Med Imaging Rev 1:105–113. [Google Scholar]
  67. Meyer G (1987): Forms and spatial arrangement of neurons in the primary motor cortex of man. J Comp Neurol 262:402–428. [DOI] [PubMed] [Google Scholar]
  68. Moffat SD, Kennedy KM, Rodrigue KM, Raz N (2007): Extrahippocampal contributions to age differences in human spatial navigation. Cereb Cortex 17:1274–1282. [DOI] [PubMed] [Google Scholar]
  69. Mountcastle VB (1997): The columnar organization of the neocortex. Brain 120:701–722. [DOI] [PubMed] [Google Scholar]
  70. Mueller W, Fox Y, Sepulcre S, Shafee L, Liu H (2013): Individual variability in functional connectivity architecture of the human brain. Neuron 77:586–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  71. Neisser U, Boodoo G, Bouchard T, Boykin A, Brody N, Ceci S, Halpern DF, Loehlin JC, Perloff R, Sternberg RJ, Urbina S (1996): Intelligence: Knowns and unknowns. Am Psychol 51:77–101. [Google Scholar]
  72. Neubauer AC, Sange G, Pfurtscheller G (1999): Psychometric intelligence and event‐related desynchronisation during performance of a letter matching task In: Pfurtscheller G, Lopes da Silva FH, editors. Event‐Related Desynchronization (ERD) and Related Oscillatory EEG‐Phenomena of the Awake Brain. Amsterdam: Elsevier; pp 219–231. [Google Scholar]
  73. Nisbett RE, Aronson J, Blair C, Dickens W, Flynn J, Halpern DF, Turkheimer E (2012): Intelligence: New findings and theoretical developments. Am Psychol 67:130–159. [DOI] [PubMed] [Google Scholar]
  74. O'Boyle MW, Cunnington R, Silk TJ, Vaughan D, Jackson G, Syngeniotis A, Egan GF (2005): Mathematically gifted male adolescents activate a unique brain network during mental rotation. Brain Res Cogn Brain Res 25:583–587. [DOI] [PubMed] [Google Scholar]
  75. Olson IR, Moore KS, Stark M, Chatterjee A (2006): Visual working memory is impaired when the medial temporal lobe is damaged. J Cogn Neurosci 18:1087–1097. [DOI] [PubMed] [Google Scholar]
  76. Panizzon MS, Fennema‐Notestine C, Eyler LT, Jernigan TL, Prom‐Wormley E, Neale M, Jacobson K, Lyons MJ, Grant MD, Franz CE, Xian H, Tsuang M, Fischl B, Seidman L, Dale A, Kremen WS (2009): Distinct genetic influences on cortical surface area and cortical thickness. Cerebral Cortex 19:2728–2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Pfleiderer B, Ohrmann P, Suslow T, Wolgast M., Gerlach AL, Heindel W, Michael N (2004): N‐Acetylaspartate levels of left frontal cortex are associated with verbal intelligence in women but not in men: A proton magnetic resonance spectroscopy study. Neuroscience 123:1053–1058. [DOI] [PubMed] [Google Scholar]
  78. Rakic P (1988): Specification of cerebral cortical areas. Science 241:170–176. [DOI] [PubMed] [Google Scholar]
  79. Raven JC (1962): Advanced Progressive Matrices. London: Lewis. [Google Scholar]
  80. Rombouts SA, Barkhof F, Hoogenraad FG., Sprenger M, Valk J, Scheltens P (1997): Test‐retest analysis with functional MR of the activated area in the human visual cortex. Am J Neuroradiol 18:1317–1322. [PMC free article] [PubMed] [Google Scholar]
  81. Salgado‐Pineda P, Baeza I, Perez‐Gomez M, Vendrell P, Junque C, Bargallo N, Bernardo M (2003): Sustained attention impairment correlates to gray matter decreases in first episode neuroleptic‐naïve schizophrenic patients. NeuroImage 19:365–375. [DOI] [PubMed] [Google Scholar]
  82. Sanabria‐Diaz G, Melie‐García L, Iturria‐Medina Y, Alemán‐Gómez Y, Hernández‐González G, Valdés‐Urrutia L, Galán L, Valdés‐Sosa P (2010): Surface area and cortical thickness descriptors reveal different attributes of the structural human brain networks. NeuroImage 50:1497–1510. [DOI] [PubMed] [Google Scholar]
  83. Schmid J, Leiman JM (1957): The development of hierarchical factor solutions. Psychometrika 22:53–61. [Google Scholar]
  84. Talairach J, Tournoux P (1988): Co‐planar Stereotaxic Atlas of the Human Brain: A 3‐Dimmensional Proportional System, an Approach to Cerebral Imaging. New York: Thieme Medical Publishers. [Google Scholar]
  85. Thompson PM, Hayashi KM, Sowell ER, Gogtay N, Giedd JN, Rapoport JL, de Zubicaray GI, Janke AL, Rose SE, Semple J, Doddrell DM, Wang YL, van Erp TGM, Cannon TD, Toga AW (2004): Mapping cortical change in Alzheimer's disease, brain development, and schizophrenia. NeuroImage 23 (Suppl 1): S2–S18. [DOI] [PubMed] [Google Scholar]
  86. Thompson PM, Hayashi KM, Dutton RA, Chiang MC, Leow AD, Sowell ER, De Zubicaray G, Becker JT, Lopez OL, Aizenstein HJ, Toga AW (2007): Tracking Alzheimer's disease. Ann NY Acad Sci 1097:183–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
  87. Thurstone LL, Thurstone Th G (1968): Aptitudes Mentales Primarias (PMA) Manual. [Examiner Manual for the SRA Primary mental Abilities Test]. Madrid, Spain: Tea Ediciones SA. [Google Scholar]
  88. Tricomi E, Rangel A, Camerer CF, O'Doherty JP (2010): Neural evidence for inequality‐averse social preferences. Nature 463:1089–1091. [DOI] [PubMed] [Google Scholar]
  89. Waltz JA, Knowlton BJ, Holyoak KJ, Boone KB, Mishkin FS, de Menezes Santos M, Thomas CR, Miller BL (1999): A system for relational reasoning in human prefrontal cortex. Psychol Sci 10:119–125. [Google Scholar]
  90. Williams‐Gray CH, Hampshire A, Robbins TW, Owen AM, Barker RA (2007): Catechol O‐methyltransferase val158met genotype influences frontoparietal activity during planning in patients with Parkinson's disease. J Neurosci 27:4832–4838. [DOI] [PMC free article] [PubMed] [Google Scholar]
  91. Winkler AM, Kochunov P, Blangero J, Almasy L, Zilles K, Fox PT, Duggirala R, Glahn DC (2010): Cortical thickness or grey matter volume? The importance of selecting the phenotype for imaging genetics studies. NeuroImage 53:1135–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
  92. Whitwell JL, Sampson EL, Loy CT, Warren JE, Rossor MN, Fox NC, Warren JD (2007): VBM signatures of abnormal eating behaviours in frontotemporal lobar degeneration. NeuroImage 35:207–213. [DOI] [PubMed] [Google Scholar]
  93. Yela M (1969): Rotación de Figuras Macizas [Rotation of Solid Figures]. Madrid: TEA. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information Appendix 1.

Click here for additional data file. (13.8KB, docx)

Supporting Information Appendix 2.

Click here for additional data file. (660.8KB, tif)

Supporting Information Appendix 3.

Click here for additional data file. (579.7KB, tif)

Supporting Information Appendix 4.

Click here for additional data file. (1.5MB, tiff)

Supporting Information Appendix 5.

Click here for additional data file. (155.3KB, docx)

Supporting Information Appendix 6.

Click here for additional data file. (1.5MB, tiff)

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES