Scale‐free brain dynamics under physical and psychological distress: Pre‐treatment effects in women diagnosed with breast cancer

Abstract

Stressful life events are related to negative outcomes, including physical and psychological manifestations of distress, and behavioral deficits. Patients diagnosed with breast cancer report impaired attention and working memory prior to adjuvant therapy, which may be induced by distress. In this article, we examine whether brain dynamics show systematic changes due to the distress associated with cancer diagnosis. We hypothesized that impaired working memory is associated with suppression of “long‐memory” neuronal dynamics; we tested this by measuring scale‐free (“fractal”) brain dynamics, quantified by the Hurst exponent (H). Fractal scaling refers to signals that do not occur at a specific time‐scale, possessing a spectral power curve $P\left(f\right)\propto f^{-\beta }$; they are “long‐memory” processes, with significant autocorrelations. In a BOLD functional magnetic resonance imaging study, we scanned three groups during a working memory task: women scheduled to receive chemotherapy or radiotherapy and aged‐matched controls. Surprisingly, patients' BOLD signal exhibited greater H with increasing intensity of anticipated treatment. However, an analysis of H and functional connectivity against self‐reported measures of psychological distress (Worry, Anxiety, Depression) and physical distress (Fatigue, Sleep problems) revealed significant interactions. The modulation of (Worry, Anxiety) versus (Fatigue, Sleep Problems, Depression) showed the strongest effect, where higher worry and lower fatigue was related to reduced H in regions involved in visuospatial search, attention, and memory processing. This is also linked to decreased functional connectivity in these brain regions. Our results indicate that the distress associated with cancer diagnosis alters BOLD scaling, and H is a sensitive measure of the interaction between psychological versus physical distress. Hum Brain Mapp 36:1077–1092, 2015. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

Stressful life events may lead to significant negative outcomes, including both physical manifestations of distress (e.g., fatigue) and psychological distress (e.g., anxiety and depression). The long‐term impacts of stress on the brain and cognition are well studied: severe stress leads to long‐term alterations in behavior and memory [Lupien et al., 1999; McEwen, 1998], neuroanatomy [Bremner, 1999; Sapolsky, 1985], and patterns of brain activity [e.g., Hull, 2002; Pechtel and Pizzagalli, 2010]. In this article, we are interested in uncovering how the dynamics of brain function are altered during the experience of stressful, real‐world events; this may prove a sensitive measure to study continuous thought processes such as psychological and physical distress. In particular, we set out to examine how different forms of physical and psychological distress jointly affect brain dynamics, which is unknown even for cognitively normal populations.

Women undergoing diagnosis and treatment for breast cancer experience significant physical and psychological distress. Worry is associated with cognitive effects in this population, as many patients with breast cancer report problems in memory and attention, which often precede chemotherapeutic treatments [Berman et al., 2014; Cimprich et al., 2010; Hermelink et al., 2007]. These changes are potentially driven by the distress that accompanies cancer diagnosis, with long‐term alterations in physiology and cognition [Brown et al., 1995; Inagaki et al., 2007; Kesler et al., 2009; Saykin et al., 2003]. However, the impact of distress and worry has not been fully characterized in the context of cancer diagnosis. For example, the effects are variable across subjects and tasks [Correa and Ahles, 2007; Hermelink et al., 2007], and the perception of cognitive decline may be primed by an expectation of negative cognitive effects [Schagen et al., 2012].

Recently, Berman et al. [2014] examined the pretreatment neurocognitive effects of cancer diagnosis using blood oxygenation level dependent functional Magnetic Resonance Imaging (BOLD fMRI) comparing women scheduled to receive either chemotherapy (PRE‐CHEMO) or radiotherapy (PRE‐RADIO), and an aged‐matched control group (CNTRL) during a working memory task. Worry was highest for the PRE‐CHEMO group, but it was significantly correlated with cognitive dysfunction across all groups. In addition, worry was correlated with task activation, particularly in the posterior cingulate and precuneus, where deactivation is associated with superior task performance [Lustig et al., 2003]. However, standard analyses of mean task activation provide limited information about the complex changes in brain function due to distress which lead to impaired memory and attention. In particular, it is unknown how the dynamics of endogenous BOLD fluctuations during working memory are disrupted by stress. This may prove critical for evaluating the neuronal impact of distress, as dynamical measures reflect changes over the whole fMRI time‐series, which are more likely to be related to persistent state‐like processes such as worry, fatigue, and depression that are not limited to trial onsets.

In this article, we hypothesized that, just as distress impairs working memory (i.e., at the behavioral level), it also disrupts long‐memory dynamics of brain regions implicated in working memory performance (i.e., at the neuronal level). We quantified long‐memory neuronal processes, by measuring the scale‐free dynamics of BOLD fMRI. Scale‐free or “fractal” scaling refers to signals that are statistically invariant over a range of timescales, and is a phenomenon that has been observed in many biophysical systems [Gisiger, 2001; Hausdorff et al., 1996; Kobayashi and Musha, 1982; Peng et al., 2002]. The power spectrum of a scale‐free signal takes the form $P\left(f\right)\propto f^{-\beta }$ (β > 0), where spectral power decreases in a power‐law fashion with greater frequency f. This implies that signal fluctuations do not predominate at any specific frequency (or time scale) as there are no “peaks” in $P\left(f\right)$. The scaling properties are quantified by exponent β, which is the negative slope of a line fitted to log(P) versus log(f), This parameter is usually referred to as the Hurst exponent (H) [Hurst, 1951] and reflects the degree of scale invariance that the signal possesses. This typically varies between H = 0.5 (white noise or scale limited) and H = 1.0 (perfectly fractal, or scale free). Signals with high H are considered “long‐memory” processes; signal changes have persistent effects in time, leading to a highly autocorrelated signal with slow, smoothly varying fluctuations.

Studies of fractal scaling have become increasingly prevalent in BOLD fMRI. Barnes et al. [2009] first established that the Hurst exponent of BOLD time series is highest at rest, and decreases in gray matter following overt tasks. He et al. [2010; He, 2011] corroborated these findings and demonstrated that H is spatially correlated with resting Glucose metabolism. In addition, Van de Ville et al. [2010] demonstrated that the BOLD signal is a function of scale‐free electroencephalography (EEG) “microstates.” Fractal scaling analysis has also been extended beyond univariate measures, as Ciuciu et al. [2014] demonstrated that inter‐regional connectivity dynamics also exhibit scale‐free behavior. Finally, there is emerging evidence that brain dynamics can be better modeled as a “multifractal” process, which comprises a spectrum of scaling exponents, instead of a single H parameter [Ciuciu et al., 2012; Shimizu et al., 2004; Wink et al., 2008]. Although not widely applied, these results demonstrate the utility of fractal scaling measures in fMRI [see He, in press for an overview of scale‐free brain function and implications]. In related work, there has also been some investigation of the link between fractal scaling and distress, as [Tolkunov et al., 2010] demonstrated that H is correlated with trait anxiety in the limbic system during emotional tasks.

In this article, we examine how fractal scaling dynamics of the BOLD signal are altered by different forms of distress. Our goal is to test the hypothesis that distress is associated with suppression of long‐memory (scale‐free) BOLD dynamics, for brain areas recruited by working memory, including the parietal cortex and prefrontal cortex. This hypothesis is supported by [Barnes et al., 2009], who showed that working memory load suppresses H. More generally, a decrease in H is a known indicator of stress and dysfunction in biological systems [Hausdorff et al., 1996; Kobayashi and Musha, 1982; Peng et al., 2002]. We compared populations of pre‐treatment breast cancer patient groups, PRE‐CHEMO and PRE‐RADIO, to healthy age‐matched CNTRL, while they performed a working memory task. This task was analyzed to determine how distress alters brain function during working memory and attention, areas of reported cognitive deficit in pretreatment breast cancer patients [Berman et al., 2014]. We also examined how BOLD scaling is related to a set of self‐reported distress measures: Worry, Anxiety, Depression, Fatigue, and Sleep Problems. In addition, we examined how distress is related to functional connectivity, to provide better insight into the potential mechanisms of distress‐related change in H.

MATERIALS AND METHODS

In the sections below, we describe the participant data, experimental task, scanning parameters, preprocessing parameters, and the procedure for estimating fractal signal. We then describe our analysis approach for assessing the hypothesis of (1) differences in fractal scaling across patient groups, as well as (2) interactions between fractal scaling in fMRI and self‐reported distress measures. We then (3) examine how functional connectivity is altered by distress, to better understand the potential causes of changes in fractal scaling. Finally, we (4) compare results across different techniques for estimating fractal scaling to determine the generalizability of our results. Subject data were originally presented in [Berman et al., 2014], including further experimental design details.

Subject Demographics

Ninety‐seven women were recruited from the University of Michigan Comprehensive Cancer Center. Sixty‐five of these women were diagnosed with localized (Stage 0 to IIIa) breast cancer and following primary surgical treatment (lumpectomy or mastectomy). These women were to be treated with adjuvant chemotherapy (n = 28) or radiation (n = 37), while thirty‐two women with negative screening mammograms served as healthy age‐matched controls. Five additional participants (four controls and one chemotherapy patient) completed study procedures but were excluded because of scan artifacts or poor performance on the Verbal Working Memory Task (VWMT; i.e., performance worse than three standard deviations away from the mean of their group). Potential participants were also excluded if they had secondary diagnosis of a neurological disorder, a psychiatric disorder or met criteria for clinical depression using the Patient Health Questionnaire (PHQ‐8). All participants were right‐handed and scored 29 or better on the Mini Mental Status Examination. All participants provided informed written consent approved by the University of Michigan Institutional Review Board for Medicine.

Behavioral Measures

Participants were assessed at baseline (pretreatment) 24 to 34 days after surgery but before adjuvant treatment (chemotherapy or radiotherapy). Subjective assessments included self‐reported measures of: Worry (TIWI) [Kelly, 2004], Anxiety (STAI) [Spielberger et al., 1983], Depression (PHQ‐8) [Kroenke et al., 2009], Fatigue (FACIT‐F) [Yellen et al., 1997], and Sleep Problems (PSQI) [Buysse et al., 1989]. Objective assessments included fMRI scanning during a VWMT, with associated behavioral measures of reaction time (RT) and accuracy (ACC). We also measured participants' hemoglobin concentration [Hb], which is inversely related to the severity of anticipated adjuvant treatment. See Supporting Information Results 1 for further information on objective non‐fMRI measures.

fMRI Task

Participants performed a VWMT during fMRI scanning. This task was analyzed to identify changes in the neural processing of working memory and attention induced by distress from a breast cancer diagnosis. The VWMT has been used extensively to assess working/short‐term memory performance in healthy younger and older adults [Badre and Wagner, 2005; Jonides et al., 2000; Nelson et al., 2003]. For each trial in the VWMT, participants were presented with a set of four letters for 1,500 ms. Following a 3,000 ms delay interval, they were presented with a “probe” letter for 1,500 and asked whether it was a member of the current memory set. Each subject was presented with 192 trials, acquired over four scanning runs of 285 repetition time (TR; 427.5 s); intertrial Intervals were jittered, ranging between 1,500 and 9,000 ms. See Supporting Information Methods 1 for further details.

fMRI Scanning Parameters

Images were acquired on a GE Signa 3 Tesla scanner, equipped with a standard quadrature head coil. Functional T2* weighted images were acquired using a spiral sequence with 25 contiguous slices with 3.75 × 3.75 × 5 mm voxels (TR = 1,500 ms; echo time [TE] = 30 ms; flip angle = 70°; field of view [FOV] = 24 cm). A T1‐weighted gradient echo anatomical overlay was acquired using the same FOV and slices (TR = 225 ms, TE = 5.7 ms, flip angle = 90°). Additionally, a 124‐slice high‐resolution T1‐weighted anatomical image was collected using spoiled‐gradient‐recalled acquisition in steady‐state imaging (TR = 9 ms, TE = 1.8 ms, flip angle = 15°, FOV = 25–26 cm, slice thickness = 1.2 mm).

fMRI Preprocessing

For each functional run, motion correction was performed with MCFLIRT (FSL ver. 5.5), slice timing correction was performed with 4‐point sinc‐interpolation, and images were spatially smoothed with a 6 mm Gaussian kernel. We identified high‐motion outlier spikes using a statistically driven procedure [Campbell et al., 2013]. Outliers were removed and interpolated from neighboring volumes using cubic splines to avoid discontinuities in BOLD signal; a median of two timepoints were replaced per run (range 0–5). We also performed linear detrending and corrected for residual motion by regressing the first two principal components (PCs) of the rigid‐body motion parameter estimates (which account for >85% of head motion variance), to provide strong control against potential head motion confounds. We obtained brain masks of the EPI and T1 data using FSL's Brain Extraction Tool (ver. 5.5), and warped subject EPI data into MNI template space using FSL's flirt package, with “avg152T1_brain.nii” as a reference volume.

Fractal Scaling Analysis

We tested for long‐memory processes in brain dynamics, by measuring the fractal scaling of BOLD time‐series; fractal scaling requires signal to be statistically identical over a range of different timescales (i.e., scale‐free). In practice, this is usually evaluated by testing whether signal variance increases in a power‐law fashion with time‐scale (or decreasing frequency f). This is “monofractal” analysis, which assumes that data are Gaussian (i.e., fully described by their second‐order moment); see Comparison with Alternative Fractal Scaling Measures below for alternative scaling analyses.

To measure monofractal scaling of BOLD signal, we used detrended fluctuations analysis (DFA) [Peng, 1995]. This was chosen as a model that is computationally efficient, insensitive to nonstationary signal, and is well established in dynamics literature. For a voxel time course x(t) (1 < t < T), we transform it into an unbounded random walk by subtracting the mean, and computing the integrated time series: $\mathit{y}\hspace{0.17em}\left(t\right)={\displaystyle {\sum }_{i=1}^t\left(\mathit{x}\left(i\right)-{\mathit{x}}_{ave}\right)}$. We then subdivide y into time windows of equal length n, and estimate a least‐squares linear fit per window. Each time point y(t) now has a fitted linear estimate ${\widehat{\mathit{y}}}_n\left(t\right)$, for window size n. Next, we computed the root‐mean‐square magnitude of fluctuations on the detrended data, which is insensitive to signal nonstationarities:

$$F\left(n\right)=\sqrt{\frac{1}{T}{\displaystyle {\sum }_{t=1}^T{\left[\mathit{y}\left(t\right)-{\widehat{\mathit{y}}}_n\left(t\right)\right]}^2}}.$$

Scale‐free signals exhibit a power‐law relationship between fluctuations and window size, defined by the equation $F\left(n\right)=C{n}^{\alpha }$, where the exponential term α defines the degree of scale invariance in the signal. The log‐transform of this equation has the linear form:

$$\log \left(\mathit{F}\left(n\right)\right)=\log \log \left(C\right)+\alpha \log \left(n\right)$$

Thus, α is given by the slope of a fitted line for log(n) versus log(F), obtained by computing F(n) for a range of window sizes n. If $0<\alpha <1$, then x(t) is a stationary signal, and the Hurst exponent H is given by α. A slope of H = 0.5 indicates highly scale‐limited signal with no long‐range correlations (e.g., white noise). Increasing slope indicates greater power‐law scaling, up to H = 1, which corresponds to a smoothly varying time‐course, with long‐range autocorrelations in the signal.

We measured the Hurst exponent of fMRI data, by applying DFA to the full voxel time series of 285 TR (427.5 s), for each preprocessed dataset. For each time series, we iteratively subdivided it into time windows of equal size, from n = 285 (full time series) down to n = 3 (the smallest window size on which detrended variance can be estimated). We then measured the slope of log(n) versus log(F) to compute H. For each subject, we obtained average H at each voxel, by computing the mean across all four task runs.

Between‐Group Differences in Fractal Scaling

The mean H voxel values were computed by averaging across subjects, for each of the CNTRL, PRE‐RADIO, and PRE‐CHEMO groups. We tested for significant, stable differences in H between the three groups at each voxel, using a nonparametric bootstrapped significance test. This test avoids any assumptions about the distribution of H and provides a direct estimate on the stability of mean differences between groups.

For each pair of groups, we performed a bootstrapped resampling of subjects (i.e., resampling with replacement) and computed the difference in mean H between the bootstrapped samples for each resampling iteration. This was repeated for 1,000 iterations, and we measured the fraction of resamples that showed a positive change in mean H at each voxel. This fraction provides the empirical P‐value for a between‐group increase in H. We similarly compute the P‐values for the between‐group decreases in H by the fraction of resamples showing negative changes in mean H. For each map of voxel P‐values, we then corrected for multiple comparisons, by identifying voxels of significant change at false‐discovery rate threshold (FDR) = 0.05, and thresholded at a minimum cluster size of three contiguous voxels.

We also examined to what degree any between‐group change in H is “global” throughout the brain. For each subject, we computed the mean H value across all gray matter voxels (using an MNI152 anatomical template), giving a single mean value for each subject. We tested for a significant difference between each pair of subject groups using the nonparametric Wilcoxon rank‐sum test, chosen to minimize any assumptions about the distribution of H. This test was performed to better characterize the overall distribution of H in the brain. For example, it is possible that changes in H are highly localized in the brain, and there is no consistent overall change in gray matter; conversely, we might observe only a few significant brain regions (due to FDR thresholding), but the mean change in H for subthreshold voxels may still be highly consistent, even if not large in magnitude.

The DFA scaling analysis procedure computes the slope on a linear fit of fluctuations F(n) versus window size n (time scale) on a log–log plot, where a slope closer to one indicates greater H. As a visualization tool, we directly plotted log(F(n)) versus log(n) curves for a set of representative regions of interest (ROIs) to demonstrate that a high H value (as computed in the above section) corresponds to a steeper slope on the log–log plot, when comparing between brain regions, and between subject groups. We took mean seed time courses from three 8‐voxel ROIs centered on: the posterior cingulate (PCC), the primary visual cortex (V1; left calcarine sulcus), and the left middle frontal lobe (LMF). We selected PCC and V1 as representative examples of brain regions with large regional differences in mean H for all subject groups (see slices 48 and 33, respectively; Fig. 1), as PCC shows consistently high mean H ≥ 0.75, whereas V1 shows consistently low mean H ≤ 0.65. We selected the LMF as a representative example of a brain region with a large cluster (36 contiguous voxels) showing significant differences between CNTRL and PRE‐CHEMO groups at a FDR = 0.05 threshold (slice 33; Fig. 1). For each of the three ROI time series, we compute mean log(F) as a function of window size n, averaged across the four runs. This was performed for all subjects. We compared mean n versus F(n) log‐scale curves for (1) PCC versus V1, averaged over all subjects and (2) in LMF, for CNTRL, PRE‐RADIO, and PRE‐CHEMO. We performed bootstrapped resampling on subjects, and computed median slope α, with 95% CIs.

Figure 1.

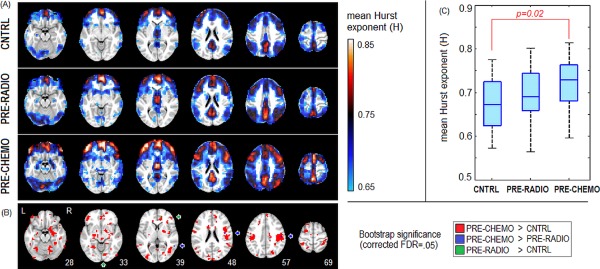
Changes in mean Hurst exponent (H) between pretreatment cancer groups. A: H maps for control (CNTRL), pre‐radiotherapy (PRE‐RADIO), and pre‐chemotherapy (PRE‐CHEMO) groups. Maps are averaged across four runs for each subject, and then averaged across all subjects. B: Bootstrap significance plot, indicating areas of significant change in mean H, for False‐Discovery Rate FDR = 0.05 threshold and minimum cluster‐size threshold of three voxels. Arrows point toward highly sparse regions of significant change for: PRE‐CHEMO > PRE‐RADIO and PRE‐RADIO > CNTRL. C: Boxplots showing distribution of subjects' average gray matter H values. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

In addition, we demonstrated that fractal scaling analysis, using standard power spectral density (PSD) estimates, produces similar trends in scaling as DFA when comparing between brain regions, and across subject groups. For the standard definition of monofractals, scale‐free signal produces a PSD curve of $P\left(f\right)\propto f^{-\beta }$, where β ≈ 2H − 1. Although our measure of fractal scaling was computed using DFA, which is robust to nonstationary signal, we also confirmed that between‐group differences in H corresponded to a systematic change in PSD curves. Using the same ROI time series, for each subject we computed the PSD per run, using a Welch estimator and standard Matlab parameters (Hamming window, eight time windows, 50% overlap), which we averaged across runs. We then plotted mean P(f) versus f log‐scale curves for the same ROIs as the previous paragraph. Bootstrapped resampling was performed on subjects, to compute the median negative slope β and the 95% CIs.

Correlations with Self‐Reported Distress Measures

We tested for systematic changes in H that are correlated with self‐reported measures of distress, including: Worry, Anxiety, Depression, Fatigue, and Sleep Problems. We first explored the relationship between these five behavioral variables, by Z‐scoring each variable across subjects, then performing principal component analysis (PCA) on the set of behavioral values, to identify the strongest covariance relationships between variables.

For behavioral data matrix X (of dimensions #subjects × 5), we obtained the Singular Value Decomposition $X=\mathit{U}\mathbf{\Lambda }{\mathit{V}}^T$, consisting of paired eigenvector matrices U = [u₁ … u₅], V = [v₁ … v₅], and diagonal matrix Λ of elements {l ₁₁, … l ₅₅}. The ith PC is represented by u _i = vector of behavioral loadings, v _i = vector of subject loadings on this PC, and $l_{\mathrm{ii}}^2$ = singular value, representing variance expressed by this PC. The PCs are the set of orthonormal factors that explain the greatest covariance between behavioral measures and are ordered by decreasing variance $l_{\mathrm{ii}}^2$. To test for the stability of PCs, we ran PCA in a Bootstrap resampling framework. For each iteration, we resampled on subjects with replacement, and reran the PCA. We plotted confidence intervals for the loadings on each behavioral variable in u _i, and the fraction of variance explained by $l_{\mathrm{ii}}^2$. We performed all analyses in this section by combining the three groups (CNTRL, PRE‐RADIO, PRE‐CHEMO), as there were no significant differences in their behavioral PCAs.

We then tested for significant correlation between behavioral PC loadings and H brain maps. For each behavioral PC vector, we performed behavioral partial least squares (bPLS) analysis (PLS) [Krishnan et al., 2011] of v _i loadings against H maps, in a split‐half subsampling framework. This multivariate procedure finds the pattern of brain voxels that shows greatest covariance between H and behavioral PC u _i. The split‐half bPLS (see [Churchill et al., 2013] for details), produces (1) a reproducible Z‐scored brain SPM, indicating brain voxels of reliable covariance with the behavioral PC, (2) a vector of latent variable scores w _i, measuring how much each subject expresses the behavioral SPM pattern, and (3) and an unbiased predictive correlation ρ = corr(w _i, v _i) of brain pattern expression versus behavior. We performed 200 resamples for bPLS analysis of each behavioral PC, to estimate an empirical 95% confidence interval on ρ. We used the bPLS model due to its stability in the presence of high‐dimensional fMRI data; many alternative multivariate models may also be used for behavioral analysis such as Canonical Correlation Analysis, see [Rosipal and Krämer, 2006] for a discussion of these models.

Effects of Distress on Functional Connectivity

To better characterize the effects of psychological distress on brain dynamics, we also examined changes in functional connectivity as a function of self‐reported measures of distress. For each subject, we segmented the whole brain using the Automated Anatomical Labelling (AAL) atlas [Tzourio‐Mazoyer et al., 2002], and down‐sampled the data to its native resolution (3.75 × 3.75 × 5 mm). For each of the 116 ROIs in the AAL atlas, we computed a mean time series, and then obtained the 116 × 116 correlation matrix between these ROIs. This produced a set of subject correlation matrices, with (116²−116)½ = 6,670 unique off‐diagonal elements.

We then examined how connectivity values changed as a function of psychological distress. We vectorized the connectivity elements, producing a (6,670 × subjects) matrix, and performed bPLS analysis of the behavioral v _i loadings from the previous section, against the matrix of functional connectivity values for each behavioral PC, using the same cross‐validation approach. In this case, bPLS analysis produces (1) a reproducible Z‐scored plot of function connectivity saliences Z _conn, indicating the change in pairwise correlations as a function of behavioral PC loading. It also produces (2) a vector of latent variable scores w _i, measuring how much each subject expresses the behavioral Z _conn pattern, and (3) and an unbiased measure of the correlation ρ = corr(w _i, v _i) between connectivity pattern expression and behavior. We performed 200 resamples for bPLS analysis of each behavioral PC, to estimate an empirical 95% confidence interval on ρ.

To summarize the connectivity changes between all 116 ROIs, we performed clustering on the Z‐scored map of changes in functional connectivity, grouping brain regions that show similar overall changes in connectivity. The 116 × 116 salience map Z _conn, was diagonalized via Singular Value Decomposition $X=U\mathbf{\Lambda }{V}^T$, and we projected the data into PC‐space coordinates: Q _conn = U ^T Z _conn. We then performed k‐means clustering on Q _conn, where the number of clusters k was determined using the variance ratio criterion [Caliński and Harabasz, 1974], which selected an optimal k = 4. We then grouped the rows and columns of Z _conn into the four clusters before plotting; the corresponding AAL brain regions are also displayed for each cluster. We then compared these results against the findings for fractal scaling obtained in the previous section.

Comparison with Alternative Fractal Scaling Measures

For this article, we used DFA to estimate the Hurst exponent for BOLD signal, due to its low computational cost, ease of interpretation, and widespread use. However, fractal‐scaling analysis is a rapidly maturing field, for which many different scaling estimators have been developed. In particular, wavelet‐based techniques have become increasingly popular [Ciuciu et al., 2012; Shimizu et al., 2004; Van de Ville et al., 2010; Veitch and Abry, 1999; Wendt and Abry, 2007; Wink et al., 2008]. Wavelets are basis functions that are compact in both time and frequency domains, and can be shifted and dilated to correspond to different delays and time scales, respectively. We measured the wavelet coefficient for a signal x(t) at time delay k and time scale a by the inner product:

$$d_x\left(a,k\right)=\frac{1}{a}\int x\left(t\right)\mathbf{\Psi }\left(\frac{t-k}{a}\right)dt$$

Wavelet‐based scaling analyses are typically performed using the discrete wavelet transform, which analyzes the signal at dyadic scales (a = 2^j for a range of j). We tested for monofractal power‐law scaling by measuring the average wavelet power at each time‐scale 2^j, which exhibits the relationship:

$$\frac{1}{K}{\displaystyle {\sum }_{\mathit{k}=1}^{\mathit{k}}{|d_x\left(2^j,k\right)|}^2}=C{2}^{j2H}$$

We can therefore estimate H by the slope of the linear fit for ${\log }_2{|{\mathit{d}}_x\left(2^j,k\right)|}^2$ versus scale j. To validate our DFA‐based results, we analyzed the data using the monofractal wavelet estimator of (http://www.cubinlab.ee.mu.oz.au/~darryl/secondorder_code.html) [Veitch and Abry, 1999].

All analyses thus far are based on monofractal scaling estimates. This formalism assumes that the data are Gaussian, and that scaling phenomena are fully defined by its variance (i.e., the second‐order moment) as a function of time scale. While this provides interpretable results, it may be an over‐simplified representation of a richer fractal scaling structure, defined across multiple statistical orders. This is the basis of multifractal analysis, which seeks to characterize the spectrum of scaling exponents present in the data. Multifractal scaling is typically defined by the following relationship:

$$\frac{1}{K}{\displaystyle {\sum }_{\mathit{k}=1}^{\mathit{k}}{|L_x\left(2^j,k\right)|}^q}=C_q{2}^{j\zeta \left(q\right)},\text{for} \text{range} \text{of} \text{scaling} \text{exponents}\left[-q_{*},q_{*}\right]$$

This is similar in form to the previous monofractal expression, but with three significant changes: first, we replaced wavelet coefficients $d_x\left(2^j,\mathit{k}\right)$ with wavelet leaders ${\mathit{L}}_x\left(2^j,k\right)$, which provide better model stability [Wendt and Abry, 2007]; second, we now measure scaling over a range of exponents q, whereas monofractal analysis was limited to q = 2; third, the constant term in the exponent H is no longer sufficient to describe the multifractal spectrum. Instead, a characteristic function $\zeta \left(q\right)$ describes scaling behavior as a function of exponent q, which is typically parameterized by the polynomial expansion $\zeta \left(q\right)={\sum }_{\mathrm{p}}{c}_{\mathrm{p}}\left(q^{\mathrm{p}}/\mathrm{p}!\right)$. Coefficients c _p (log‐cumulants) are now used to describe the scaling behavior of signal x(t). The first‐order cumulant c ₁ quantifies monofractal scaling, as c ₁ > 0.5 indicates long‐range dependence. Higher‐order log‐cumulants c _p (p > 1) indicate the presence of multifractal scaling and characterize properties of the multifractal spectrum. We examined the behavior of the first three log‐cumulants (c ₁, c ₂, c ₃), using software obtained from (http://www.irit.fr/~Herwig.Wendt/software.html).

We compared the different monofractal and multifractal scaling estimators for the pre‐treatment breast cancer dataset. Note that both monofractal and multifractal models are able to assess monofractal scaling (H or c ₁, respectively), whereas only multifractal models can quantify the spectrum of higher‐order cumulants. Due to the computational burden of computing these scaling measures, we obtain time series for each of the 116 ROIs in the AAL atlas, and apply the three scaling estimators (DFA, wavelet monofractals, wavelet multifractals), which dramatically reduces the number of time series being analyzed. Because AAL ROIs are of different sizes, we examined the mean time series of a 4‐voxel ROI, taken from the center of mass of each AAL template region. This avoids averaging different‐sized ROIs, which may create spurious regional differences in time‐series smoothness. We compared the consistency of the mean scaling parameter (H or c ₁) across brain regions, and for multifractal wavelets we also examined log‐cumulants (c ₂, c ₃). We also examined how scaling parameters vary as a function of patient group. For the wavelet models, we examined the data over seven dyadic scales (2 TR = 3 s up to 265 TR = 384 s; recommended by the monofractal wavelet diagnostics) using Daubechies wavelets with three vanishing moments (i.e., insensitive to linear and quadratic signal drifts). For multifractal analysis, we examined scaling orders of q = [−10,10].

RESULTS

Between‐Group Differences in Fractal Signal

Overall, PRE‐CHEMO patients exhibited greater fractal scaling (i.e., Hurst exponent) in their functional timeseries compared to the other groups. Figure 1A plots the average Hurst exponent (H) brain maps for CNTRL, PRE‐RADIO, and PRE‐CHEMO, where higher H indicates greater fractal scaling. Regions of peak H value are relatively consistent across groups, including inferior orbitofrontal (slice 28), middle and medial orbitofrontal lobes and anterior cingulate (slice 33, 39), inferior frontal lobes and posterior cingulate (slice 48), precuneus (slice 57, 69), and dorsal supplementary motor area (slice 69). In contrast, certain regions only show high H for PRE‐CHEMO, including cerebellum, hippocampus, amygdala (slice 28), and thalamus (slice 39). Figure 1B depicts regions of significant difference between each pair of groups. All regions of significant difference reflect an increase in H by intensity of planned adjuvant treatment. We observe widespread differences in PRE‐CHEMO > CNTRL, with large clusters in the right hippocampus, amygdala and cerebellum (slice 28), anterior cingulate and left middle orbitofrontal lobe (slice 33), middle occipital lobe (slices 39, 48) cuneus, Rolandic operculum, inferior frontal and superior temporal lobes (slice 48), postcentral and supramarginal gyri (slice 57, 69), superior parietal, and middle frontal lobes (slice 69). We observed only a few sparse regions of reliable PRE‐CHEMO > PRE‐RADIO and PRE‐RADIO > CNTRL change, limited to the anterior cingulate (PRE‐RADIO > CNTRL; slice 39), inferior temporal lobe (PRE‐CHEMO > PRE‐RADIO; slice 39), right postcentral gyrus (slice 48) and Rolandic operculum (slice 57). Figure 1C shows a similar trend in H for the global average, computed over all gray matter voxels. We observed a trend in mean H of PRE‐CHEMO > PRE‐RADIO > CNTRL, but only the PRE‐CHEMO versus CNTRL difference is significant (P = 0.02, Wilcoxon test).

Figure 2 provides sample ROIs demonstrating how higher H from DFA analysis (Fig. 1) corresponds to a steeper slope in log(F(n)) versus log(n) plots, when comparing across brain regions (Fig. 2A) and subject groups (Fig. 2B); results are shown for representative ROIs (see Methods regarding ROI selection). Figure 2A plots the average variance F(n) versus window size n on log–log scale, comparing V1 (lower H) to PCC (higher H), showing that the slope α of a linear fit is consistently higher for PCC than V1. Figure 2B shows scaling plots comparing the groups, for a single ROI in LMF, and shows that the mean slope increases with anticipated treatment severity, going from CNTRL to PRE‐RADIO to PRE‐CHEMO. Figure 2C,D show that similar scaling relationships are observed when using standard PSD‐based estimates of fractal scaling, obtained by plotting spectral power P(f) versus frequency f on a log–log scale. The negative slope β of a linear fit is higher for PCC versus V1 (Fig. 2C), and increases when going from CNTRL to PRE‐RADIO to PRE‐CHEMO (Fig. 2D). We observe relatively large deviations from linearity in PCC and V1 curves (Fig. 2C). This is absent in the log(F(n)) versus log(n) plots (Fig. 2A), which indicates that there are potential BOLD signal nonstationarities in these brain regions, which DFA corrects for.

Figure 2.

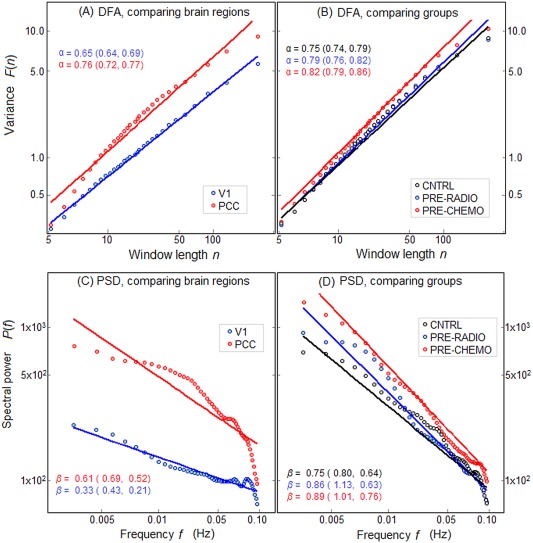
Mean power versus time‐scale plots shown on log–log scale, for different ROIs. A,B: Plot variance F(n) versus time window size n, as estimated for DFA. The slope of a linear fit α and Bootstrapped 95% CIs are also given. C,D: Plot of spectral power P(f) versus frequency f, along with the negative slope of a linear fit β and Bootstrapped 95% CIs. Left‐side plots (A,C) compare scaling behavior between different brain regions of primary visual cortex (V1) and posterior cingulate (PCC). Right‐side plots (B,D) compare scaling behavior of different patient groups, for representative left middle frontal (LMF) ROI. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Correlations with Self‐Reported Distress Measures

After assessing group differences in fractal scaling, we examined the relationship between fractal scaling and self‐reported measures of distress. We first examined the relationship between the five different behavioral measures: Worry, Anxiety, and Depression (psychological distress), Fatigue and Sleep Problems (physical distress). Note that Worry is a “trait” measure of distress, whereas Anxiety is a “state” measure [for further details, see Berman et al., 2014]. Figure 3 plots a PCA of the behavioral measures, showing PCs #1–3 (PCs #4–5 did not have a significant relationships with H maps; see below).

Figure 3.

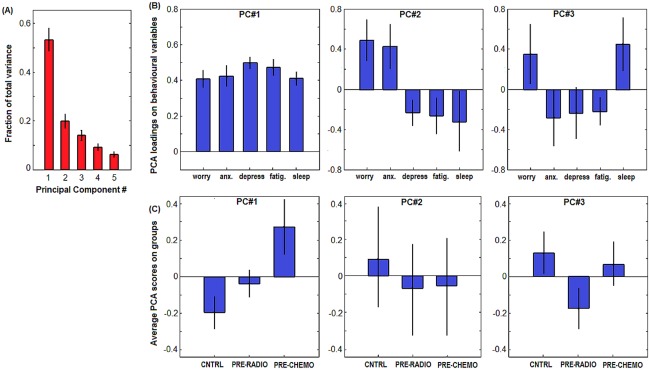
PCA of the 5 self‐report measures of stress: Worry, Anxiety (Anx.), Depression (Depress.), Fatigue (Fatig.), and Sleep problems (Sleep). A: bar plots of mean PCA eigenspectrum, indicating fraction of total variance explained by each PC, with Bootstrapped Standard Error (SE) error bars (1,000 resampling iterations). B: bar plots of mean behavioral loadings for PCs #1–3, with SE error bars. C: mean subject scores on each PC, as a function of cancer group. CNTRL = control, PRE‐RADIO = pre‐radiotherapy, PRE‐CHEMO = pre‐chemotherapy, with SE errorbars. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

In addition, we examined the relationship between distress measures and objective measures of task performance (plotted in Supporting Information Results 1). As expected, the self‐reported distress measures are all significantly related to intensity of anticipated adjuvant treatment (i.e., PRE‐CHEMO has the greatest distress loadings), and inversely related to hemoglobin concentration [Hb] (a measure of cancer stage). The distress measures are also associated with decreased performance in the working memory task, including lower accuracy and longer RT. These results also provide evidence that the change in H across groups is not caused by elevated hemoglobin levels (and thus higher BOLD dynamic range), since [Hb] declines when going from CNTRL to PRE‐CHEMO, whereas average H increases. Moreover, [Hb] is not a significant predictor of global changes in H. A PLS analysis of H maps versus [Hb] showed nonsignificant correlations at ρ = 0.03 (95%CI: −0.22 to 0.11), further demonstrating that our results are insensitive to any systematic confound caused by hemoglobin levels.

Figure 3A shows the Bootstrapped PC eigenvalues of the distress variables, and Figure 3B plots the associated behavioral loadings. PC#1 (53% of variance) shows a common effect of all five behavioral measures, indicating that they are all moderately correlated. PC#2 (20% of variance) reflects a contrast effect of high (Worry, Anxiety), anticorrelated with (Depression, Fatigue, Sleep Problems). PC#3 (14% of variance) shows a more complex contrast of (Worry, Sleep Problems) versus (Anxiety, Depression, Fatigue). Figure 3C plots the average subject loading on each PC, for each pretreatment cancer group. For PC#1, we observed a graded effect of PRE‐CHEMO > PRE‐RADIO > CNTRL (Fig. 3C), indicating that overall distress increases with anticipated severity of treatment. PC#2 reflects primarily CNTRL versus PRE‐RADIO/PRE‐CHEMO (i.e., control vs. patients), albeit with large error bars reflecting group heterogeneity, thus control and patient groups tend to have different relationships in the balance between physical and psychological distress. PC#3 expresses a CNTRL/PRE‐CHEMO versus PRE‐RADIO contrast, indicating a nonlinear relationship between distress and severity of anticipated treatment. It also demonstrates that the PRE‐RADIO group has some unique properties, that is, they tend to report high “state” anxiety relative to “trait” worry, and they report high fatigue and depression but little difficulty with sleep.

We then performed split‐half partial least squares (PLS) analysis of each behavioral PC against the Hurst exponent maps in the fMRI data. This model estimates a Z‐scored brain pattern of H expression, associated with each behavioral PC (Fig. 4) and measures the correlation between the expression of this brain pattern and the behavioral PC scores, for an independent set of subjects (producing an unbiased “predictive correlation” estimate; see Methods: Correlations with Self‐Reported Distress Measures). All 3 PCs have significant correlations (ρ) with fractal scaling: [PC#1] ρ = 0.13 (95%CI: 0.05 to 0.15); [PC#2] ρ = 0.22 (95%CI: 0.12 to 0.24); [PC#1] ρ = 0.12 (95%CI: 0.12 to 0.14). Although PC#1 explains the greatest behavioral variance, it has low correlation with H and low brain Z‐scores, indicating a relatively weak relationship with BOLD scaling. Conversely, PC#2 has the highest predictive correlation, indicating that it has the strongest brain‐behavior relationship across subjects. In addition, the higher brain Z‐scores of PC#2 and PC#3 indicate that the associated brain regions tend to be more stable than those of PC#1.

Figure 4.

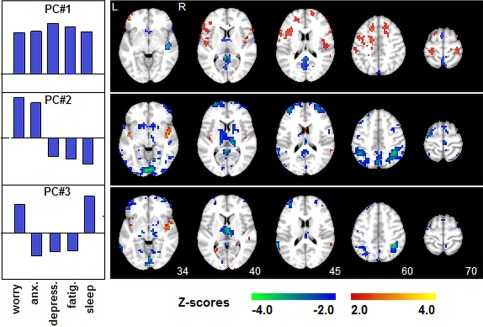
PLS analysis of distress measures versus Hurst exponent brain maps. A cross‐validated behavioral PLS is shown for subject loadings on each PC (shown in Figure 3B), against Hurst exponent brain maps (mean maps shown in Fig. 1). PCs #1–3 had significantly stable behavioral relationships. Each Z‐scored map shows regions where Hurst scaling is correlated with behavioral PC expression, displayed on the left (red = positive correlation; blue = negative correlation). Self‐reported behavioral measures include: Worry, Anxiety (Anx.), Depression (Depress.), Fatigue (Fatig.), and Sleep problems (Sleep). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

For PC#1, positive Z‐scores indicate that H is correlated with overall distress (e.g., PC#1 loadings), in inferior and superior frontal lobes (slices 45, 60) and dorsolateral prefrontal cortex (slice 60, 70); negative Z‐scores indicate that H is anticorrelated with overall distress in a sparser set of regions, including posterior cingulate and precuneus (slices 45–70). For PC#2, brain regions show decreased H when (Worry, Anxiety) are relatively high and (Depression, Fatigue, Sleep Problems) are relatively low (e.g., PC#2 loadings), in the visual cortex (slice 34), thalamus (slice 40), middle frontal (slice 45), parietal lobes, and precuneus (slice 60). PC#3 shows decreased H when (Worry, Sleep Problems) are relatively high and (Anxiety, Depression, Fatigue) are relatively low, localized to the thalamus (slice 40) and parietal lobes (slice 60).

Effects of Distress on Functional Connectivity

We also examined distress‐related changes in functional connectivity, as a complementary analysis to the Hurst exponent measures. We performed split‐half bPLS analyses of each behavioral PC against the functional connectivity values for the 116 ROIs defined by the AAL atlas. Only PC#2 showed significant behavioral correlations: [PC#1] ρ = 0.15 (95%CI: −0.23 to 0.17); [PC#2] ρ = 0.28 (95%CI: 0.09 to 0.41); [PC#1] ρ = 0.08 (95%CI: −0.13 to 0.23). Figure 5 plots the results of the PLS analysis against PC#2, showing Z‐scored changes in functional connectivity when (Worry, Anxiety) are relatively high and (Depression, Fatigue, Sleep Problems) are relatively low (Fig. 5A). We identified four significant clusters with similar functional connectivity relationships (denoted C1–4), with the corresponding AAL regions plotted in Figure 5B. The most consistent changes in functional connectivity were decreased correlation between C2 (which primarily includes the parietal and frontal regions showing significant changes in H; Fig. 4), and the more ventral regions of C3 (including fusiform and lingual gyri, amygdala, hippocampus, and parahippocampus). We also observe a general increase in functional connectivity between C4 (lower cerebellum) and all other clusters.

Figure 5.

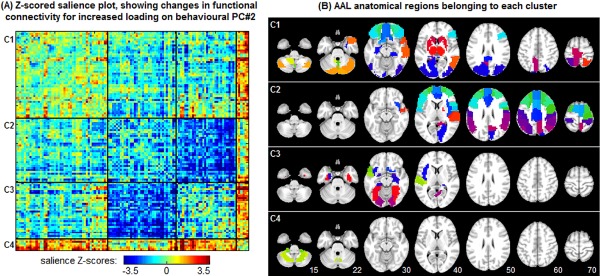
PLS analysis of distress measures versus functional connectivity. Results show PLS analysis of connectivity versus behavioral PC#2 (refer to Fig. 3), which was the only PC with a significant relationship. A: Z‐scored map of changes in connectivity between 116 AAL atlas ROIs, for increased (Worry, Anxiety) and decreased (Depression, Fatigue, Sleep Problems). The ROIs have been clustered into four groups labeled C1–4, based on k‐means clustering of connectivity relationships. B: Map showing regions of the AAL atlas associated with each functional cluster C1–4. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Comparison with Alternative Fractal Scaling Measures

In this section, we compared the results of DFA against other fractal scaling estimators, including wavelet‐based monofractal and multifractal estimators. Figure 6 plots the mean scaling exponent values of the 116 AAL template ROIs, comparing (A) DFA versus wavelet monofractals, and (B) DFA versus wavelet multifractals. Brain regions have a consistent order in scaling exponent for all estimation methods, as H values estimated by DFA are correlated with wavelet techniques at 0.96 (monofractal H) and 0.82 (multifractal c ₁). However, the three models differ in the absolute range scaling parameter values. Figure 7 displays mean scaling parameter values of the AAL ROIs as a function of patient group, along with regions showing significant differences for CHEMO > CNTRL (FDR = 0.05 threshold). Wavelet multifractals were the most sensitive (50/116 regions), followed by DFA (23/116 regions) while wavelet monofractals were the least sensitive (10/116 regions); no regions of significant CHEMO < CNTRL were identified.

Figure 6.

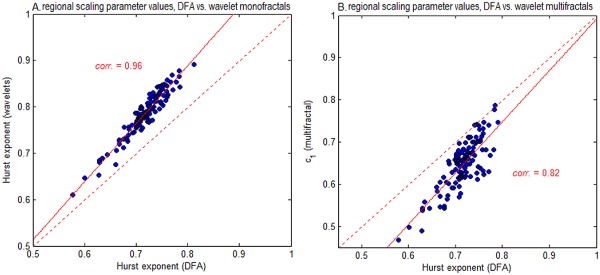
Comparing regional scaling for different fractal estimators. We plot average fractal scaling values of the 116 AAL atlas ROIs, comparing H of DFA, against (A) H of monofractal wavelet estimator, and (B) c ₁ of multifractal wavelet estimation. Each point denotes the average scaling exponent over all subjects, computed from a 4‐voxel ROI at the center of each AAL template region. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 7.

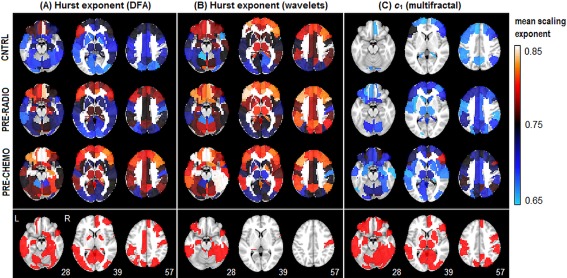
Comparing between‐group differences for different fractal estimators. We plot average fractal scaling estimates of the 116 AAL atlas ROIs for (A) DFA, (B) monofractal wavelets, and (C) multifractal wavelets. We plot (top) average scaling exponent computed on a 4‐voxel ROI at the center of each AAL template region, and (bottom) Bootstrap significance plot, indicating areas of significant difference in PRE‐CHEMO > CNTRL, for False‐Discovery Rate FDR = 0.05 threshold. No regions showed significant change in the opposite direction (i.e., PRE‐CHEMO < CNTRL). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

We also tested whether higher‐order log‐cumulants of multifractal analysis were sensitive to between‐group differences. We consistently observed c ₁ > 0.5 (median: 0.58; min: 0.40; max: 0.72) significant for 102/116 ROIs (at FDR = 0.05 threshold) indicating long‐range correlations in most brain regions. We also consistently observed c ₂ < 0 (median: −0.035; min: −0.057; max: −0.019) for 116/116 ROIs, and c ₃ < 0 (median: −0.01; min: −0.03; max: 0.01) for 111/116 ROIs. This indicated the presence of multifractal scaling in the signal. However, no regions showed significant difference in CNTRL versus PRE‐CHEMO at FDR = 0.05 for either c ₂ or c ₃. Therefore, higher‐order multifractal parameters do not appear to be sensitive to between‐group effects of distress.

DISCUSSION

This article provides the first systematic examination of fractal scaling in BOLD signal and its relationship to distress in a susceptible population, of women newly diagnosed with breast cancer awaiting adjuvant treatment. Our findings demonstrate the utility of nonlinear dynamical measures such as fractal scaling, which are sensitive to systematic changes in BOLD signal associated with patient group and behavior, without requiring overt task analyses. The measure of fractal scaling, therefore, shows potential as a sensitive biological marker of distress and its impact on brain dynamics.

Contrary to our initial hypothesis, of disrupted “long‐memory” neuronal processes in the highly distressed patient populations, the between‐group analyses showed robust increases in Hurst exponent (H) with intensity of adjuvant treatment plan. This indicates that the populations anticipating more severe adjuvant treatment have smoother, scale‐free BOLD fluctuations, with greater long‐range correlations. However, groups are highly heterogeneous, as we only observed systematic, widespread changes in PRE‐CHEMO versus CNTRL groups. This is consistent with the behavioral literature, which demonstrates heterogeneity in the severity of reported pretreatment cognitive effects for breast cancer treatment groups [Correa and Ahles, 2007; Raffa et al., 2006]. The most consistent average changes between cancer groups were not limited to regions of high or low H, as they included right hippocampus and amygdala, LMF, and anterior cingulate (all with high average H), as well as middle occipital lobes, Rolandic operculum, and supramarginal gyri (all with low average H). This confirms that the location of between‐group differences is not limited to tissues with a specific dynamic range (i.e., mean H value), and are thus unlikely to be artifacts of local tissue properties, such as vascular reactivity.

Our results also demonstrate robust overall differences in the spectral distributions for different brain regions (Fig. 2). We confirm that the spatial differences in H correspond to consistent changes in spectral power: sensorimotor regions such as the visual cortex have both less variance overall, and a “flatter” slope on the power spectral curve, compared to highly integrative regions (e.g., PCC); this is consistent with an increased need for dynamic range in highly connected “hub” regions of the brain. We also observed both an increase in total variance and a greater proportionate increase in low‐frequency spectral power with increasing intensity of adjuvant treatment plan. This further demonstrates that in high‐distress populations, BOLD fluctuations become increasingly low frequency for many brain regions, with increased dynamic range.

However, as demonstrated in Figures 3 and 4, the increase in H with intensity of cancer treatment plan is driven by a complex relationship between measures of psychological and physical distress. This demonstrates that comparing populations strictly based on patient group, or a single measure of distress, can produce misleading results that do not fully reflect the underlying cognitive processes. Moreover, distress does not consistently lead to suppressed scaling dynamics, which indicates that it cannot be simply treated as systemic brain dysfunction [Hausdorff et al., 1996; Kobayashi and Musha, 1982; Peng et al., 2002] or a cognitive load on working memory [Barnes et al., 2009].

As expected, there is a consistent increase in all self‐report measures of distress with intensity of anticipated cancer treatment, in behavioral PC#1; the correlation with fractal scaling is significant but relatively weak. We observe increased H in regions with low average fractal scaling, previously seen in between‐group analyses (Fig. 1), but also decreased H in areas of high mean H, including PCC and precuneus. These findings are complementary to the task‐based GLM analyses of [Berman et al., 2014], who found reliable increases during task engagement in PCC and precuneus for the high‐worry pretreatment cancer groups. Given that H is suppressed for more difficult exogenous tasks [Barnes et al., 2009], an increase in PCC activation and decreased H potentially indicates that higher‐worry patient groups are expending more effort to perform the task.

PC#2 shows that a (Worry, Anxiety) versus (Depression, Fatigue, Sleep Problems) interaction has the strongest relationship with fractal scaling, with the highest behavioral correlations and a reliable spatial pattern. This includes the precuneus and parietal lobes, which are implicated in visuospatial search, attentional and memory processing [Behrmann et al., 2004; Cavanna and Trimble, 2006; LaBar et al., 1999; Nee and Jonides, 2008], further demonstrating that dynamical changes are primarily localized to brain regions implicated in working memory tasks, as initially hypothesized. This also provides evidence that relatively high psychological distress (e.g., worry) but relatively low physical distress (e.g., fatigue) alters the temporal dynamics of cognitive processes implicated in visual search and attention, making them more scale‐limited, with more high‐frequency fluctuations and shorter correlations in time. How this would relate to performance on cognitive tasks is a question that we plan to pursue in the future.

Behavioral PC#3 reflects both elevated (state) Worry relative to (trait) Anxiety, and elevated Fatigue relative to Sleep problems and Depression. These effects are primarily correlated with increased fractal scaling in the thalamus, although changes are also present in the parietal lobes. The change in thalamic signal is consistent with prior neuroscience literature, as the thalamus is implicated in the regulation of anxiety [Cannistraro and Rauch, 2003] and sleep versus wakefulness [Saper et al., 2005]. This suggests that the dynamics of thalamic signal become more scale‐limited when “state” distress (Worry) is high relative to “trait distress (Anxiety),” that is, when stress levels are abnormally high for a given patient. Moreover, the BOLD signal becomes more scale‐limited when people report sleep problems but also relatively low fatigue. This suggests that the dynamics of thalamic signal may be altered, when maintaining alertness in the presence of adverse conditions such as sleep deprivation.

We may also compare our results to prior studies on trait anxiety and BOLD scaling dynamics. Comparisons between patient groups (Fig. 1) reveal a significant change in the dynamics of the amygdala, which is consistent with findings of [Tolkunov et al., 2010]. We measured an increase in H in the higher‐distress PRE‐CHEMO group; which is consistent with the moderately anxious population of [Tolkunov et al., 2010]. However, our analyses of self‐reported distress (Figs. 3 and 4) provide evidence of a more complicated relationship between trait anxiety and other sources of distress, which involve distributed brain regions beyond the limbic system.

To more fully understand interactions of H with self‐reported distress, we also examined changes in functional connectivity using the bPLS framework (Fig. 5). This allowed us to characterize how H and connectivity are jointly influenced by cognitive state. Only behavioral PC#2 evidenced significant, predictive behavioral correlations, further demonstrating that the interaction of physical versus psychological distress captured in PC#2 is the primary modulator of brain dynamics. The results of bPLS analysis demonstrated that regions showing the greatest decrease in H (e.g., middle frontal lobes, parietal lobes) were part of cluster C2, which had decreased functional connectivity with a set of ventral regions including fusiform/lingual gyri, amygdala, hippocampal, and parahippocampal gyri. This suggests (1) a potential mechanism for decreased H, which may be mediated by specific decreases in functional connectivity, and (2) as we might expect when examining distress, connectivity changes involve the amygdala, which is involved in emotion processing.

In Figures 6 and 7 we validated our DFA‐based analyses, by comparing them against wavelet‐based fractal scaling measures. Our results indicated that the scaling measures are generally robust across methods, showing a consistent ordering of brain regions in H, as well as consistent between‐group differences in mean H. The different fractal estimators have varying levels of sensitivity, with wavelet multifractals being the most sensitive and wavelet monofractals being the least sensitive to between‐group differences. However, the scale of H values varied by method, where multifractal wavelets produced the lowest c ₁ values, followed by DFA, then monofractal wavelets. Thus, while relative trends are quite robust, it may prove difficult to compare absolute scaling parameter values between studies, if they use different fractal scaling estimators. Finally, we note that although there is evidence of multifractal behavior in the BOLD time series, the additional log‐cumulants were less sensitive than the monofractal estimates to between group differences.

In this article, we analyzed fractal scaling dynamics for a VWMT. This allowed us to study dynamics of the brain‐state for which pretreatment breast cancer patients report cognitive deficits, and also allowed us to directly link results to prior task‐based analyses of Berman et al. [2014]. However, this comes at the expense of reduced generalization: it is unknown if the relationships between H, patient group and distress are stable across different cognitive states, or specifically modulated by the working memory task. Moreover, it is not yet known if these findings directly relate to other studies of scale‐free dynamics, which often focus on resting state [e.g., He, 2011; He et al., 2010; Van de Ville et al., 2010]. These issues must be investigated in future studies.

In summary, we have demonstrated significant differences in fractal scaling of BOLD signal across breast cancer preadjuvant treatment groups. However, we have also demonstrated that there is a relatively complex underlying relationship between measures of distress (Worry, Anxiety, Depression, Fatigue, Sleep Problems) and fractal scaling, with significant heterogeneity even within the individual cancer pretreatment groups (e.g., Fig. 3C). We, therefore, believe that the Hurst exponent is a useful measure to understand the neural correlates of distress, and to help quantify the relationship between physiological and psychological distress.

Supporting information

Supplementary Information

Supplementary Information