Uncertainty in visual and auditory series is coded by modality‐general and modality‐specific neural systems

Abstract

Coding for the degree of disorder in a temporally unfolding sensory input allows for optimized encoding of these inputs via information compression and predictive processing. Prior neuroimaging work has examined sensitivity to statistical regularities within single sensory modalities and has associated this function with the hippocampus, anterior cingulate, and lateral temporal cortex. Here we investigated to what extent sensitivity to input disorder, quantified by Markov entropy, is subserved by modality‐general or modality‐specific neural systems when participants are not required to monitor the input. Participants were presented with rapid (3.3 Hz) auditory and visual series varying over four levels of entropy, while monitoring an infrequently changing fixation cross. For visual series, sensitivity to the magnitude of disorder was found in early visual cortex, the anterior cingulate, and the intraparietal sulcus. For auditory series, sensitivity was found in inferior frontal, lateral temporal, and supplementary motor regions implicated in speech perception and sequencing. Ventral premotor and central cingulate cortices were identified as possible candidates for modality‐general uncertainty processing, exhibiting marginal sensitivity to disorder in both modalities. The right temporal pole differentiated the highest and lowest levels of disorder in both modalities, but did not show general sensitivity to the parametric manipulation of disorder. Our results indicate that neural sensitivity to input disorder relies largely on modality‐specific systems embedded in extended sensory cortices, though uncertainty‐related processing in frontal regions may be driven by both input modalities. Hum Brain Mapp 35:1111–1128, 2014. © 2013 Wiley Periodicals, Inc.

INTRODUCTION

Our perceptual system integrates raw sensory input from an environment that is rich in statistical regularities over both spatial and temporal scales. By exploiting these statistical properties, neural systems can significantly improve computational efficiency via information compression and predictive processing. Several studies have indicated that the brain implements these coding strategies: First, neural systems have been shown to efficiently represent structured inputs in compressed form [Borst and Theunissen, 1999; Buiatti et al., 2009; Olshausen and Field, 1996]. Second, both computational work [Friston, 2010; Grossberg, 2007; Rao and Ballard, 1999] and a number of experimental studies [e.g., Bar, 2009; Bubic et al., 2010; Friston and Kiebel, 2009; Summerfield and Egner, 2009] have advanced the hypothesis that the brain employs predictive coding strategies in perception. From this latter perspective, coding for input statistics, such as the relative frequency of different event types (their marginal distribution) or their joint co‐occurrence, is advantageous because these statistics allow for the construction of predictions regarding subsequent events. Even registering that a certain environment is highly irregular is advantageous in that it can induce a biased weighting in favor of bottom‐up information during perception [Strange et al., 2005].

More generally, statistical features of sensory data provide a basis for modeling the underlying causes of sensory states [Friston, 2010]. In theories of Bayesian surprise [Itti and Baldi, 2009], for example, the degree of subjective surprise can be quantified as the difference between an observer's probabilistic beliefs about the environment prior to and following the observation of a certain stimulus [as modeled by, e.g., the Kullback‐Leibler divergence; Kullback, 1959]. This metric effectively registers the extent to which events depart from previously observed patterns and has been shown to be a good predictor of human attention shifts [Itti and Baldi, 2009]. Representing the degree of statistical regularity within recent input also plays an important role in quantifying predictive information rate [Abdallah and Plumbey, 2009], a related metric that reflects to what extent an observer's expectations about the future are determined by the present stimulus, after partialling out whatever knowledge is provided by the recent past. This latter metric captures qualitative human judgments about the melodic qualities of music. From a processing perspective, computing statistics and uncertainty plays an important role in specific processes: these include, among others, (a) the generation of predictions, (b) evaluation of predictions against inputs, (c) the generation of error terms—all of which will more frequently take place when predictions are licensed (i.e., low entropy contexts). Regions tracking entropy may also play a central role in noticing changes in the level of disorder over time [Behrens et al., 2007; Tobia et al., 2012a]. To summarize, a precondition for engaging in these sorts of high‐level computations is the brain's capacity to extract statistical features from a temporally unfolding input stream, a capacity that appears highly developed in humans [Lewicki et al., 1992; Smithson, 1997]. Once statistical features are represented, the evaluation of incoming inputs can benefit from previously documented top‐down mechanisms that integrate prior knowledge during early stages of sensory processing [e.g., Bar et al., 2006].

Sensitivity to disorder has been studied in prior neuroimaging studies, whose results have been generally interpreted under a framework in which entropy sensitivity is taken to reflect involvement in the computation of entropy. As mentioned above, such sensitivity may alternatively indicate involvement in various processes whose mode of operation is sensitive to degree of entropy [see Tobia et al., 2012b, for in‐depth discussion) or higher‐level Bayesian computations. For this reason, when discussing prior findings it is important to consider that a relationship between activity and input entropy does not mean a given region codes for entropy, let alone that it is devoted to that function. Several studies [Bischoff‐Grethe et al., 2000; Harrison et al., 2007, 2006; Strange et al., 2005; Tobia et al., 2012b] have examined the brain's sensitivity to disorder in a continuous series of stimuli. These studies have manipulated the entropy, i.e., the relative disorder, within continuous streams of stimulus items and identified several regions as sensitive to input disorder, but with little agreement between studies. Two studies have pointed to the hippocampus as coding for the relative diversity of items [Strange et al., 2005] or the mutual information between items [Harrison et al., 2006], while a third study [Bischoff‐Grethe et al., 2000] reported lateral temporal regions as being sensitive to the strength of transition constraints among elements in an ongoing series. This body of prior work raises two questions. First, while each of these studies pursued the question of whether certain regions of the brain mediate a supramodal (i.e., general and modality‐independent) function related to coding for input disorder, all three used only visual stimuli; to date there has been no systematic evaluation of whether sensitivity to disorder in these or other regions extends across sensory modalities. Second, two of these studies [Harrison et al., 2006; Strange et al., 2005] used a decision‐making paradigm (serial reaction time [SRT] task) requiring participants to respond to each stimulus, and where strategically extracting statistical information could facilitate task performance. Requiring a response for each item may evoke activity related to response inhibition, response reassignment or response uncertainty, all of which may differ as a function of input disorder. It is therefore unknown whether the previously identified regions mediate a similar function when stimuli are rapidly presented in absence of any task orienting participants toward statistical features of the series.

Given this background, the goal of the current study was to determine the extent to which sensitivity to input entropy is mediated by modality‐general or modality‐specific systems using an experimental paradigm not conducive to strategic processing. Stimuli were presented rapidly (3.3 Hz) to reduce the opportunity for deliberate prediction or evaluation, and crucially, the task did not demand that participants attend to the stimuli whose entropy was manipulated but instead required them to monitor a separate input channel. In what follows, we briefly review prior work suggesting that input entropy may be spontaneously or automatically encoded, though in partially divergent systems for auditory and visual stimuli, then present the specific analytic framework employed in the current study. We use the terms entropy, order/disorder, and uncertainty relatively interchangeably in keeping with the terminology used in earlier work. In information theory, entropy reflects the mean uncertainty of a random variable, though in the psychological theory it has long been used as a parameter quantifying the degree of surprise, uncertainty or predictability in short sequences [Garner, 1962].

Support for Modality‐General Systems Sensitive to Input Disorder

Neural systems sensitive to input entropy independent of modality may be understood as representing or coding for the degree of disorder on an abstract or symbolic level. Additionally, these systems may mediate aforementioned modality‐general processes—such as those central to predictive coding or Bayesian updating—that are enabled by the degree of disorder in the input, rather than being devoted to entropy‐processing. Neuroimaging studies pursuing these systems have typically employed the logic of probing for brain regions exhibiting supramodal or domain‐general sensitivity to disorder, thus providing evidence for consolidated entropy processing, e.g., as shown in work probing systems mediating strategic, explicit predictions in various contexts [Schubotz and von Cramon, 2002]. Nonetheless, empirical arguments for modality‐independent systems sensitive to input entropy have been indirect. Support for these arguments has been rooted in evidence for entropy sensitivity in nonsensory regions or regions not typically associated with the stimulus presentation modality. As noted earlier, there has been no direct investigation of whether the processes underlying sensitivity to input disorder in separate stimulus modalities share a common neural substrate.

In an innovative imaging study, Bischoff‐Grethe et al. 2009 suggested that lateral temporal regions are generally implicated in extracting statistical regularities from stimulus streams. In that study, an event was defined as the coloring of one of four adjacent empty squares, events were presented at a rate of 1 Hz, and participants were instructed to monitor the stimuli for the occurrence of blue squares. The series varied over three levels of entropy, manipulated via a first‐order Markov process, and consisted of a completely deterministic sequence (i.e., entirely rule‐based with no uncertainty, Markov entropy [MH] = 0), a sequence generated by a random process (MH = 2; maximal entropy for a four‐item series), and a series with moderate statistical constraints (MH = 0.9). Entropy‐sensitive regions were defined as those differentiating between the rule‐based and random sequences, and were localized to lateral temporal regions, where higher entropy (the random condition) evoked a stronger BOLD response. Because these responses were found for spatial sequences in the visual domain, the authors suggested that these areas, commonly associated with language processing, might in fact mediate a domain‐general process involved in coding input entropy. However, in a related study [McNealy et al., 2006], where auditory streams of nonsense syllables were manipulated to study the neural mechanisms underlying online word segmentation, lateral temporal regions exhibited lower activity for random syllable streams than for structured streams consisting of repeated combinations of fixed syllable triplets (in absence of other language cues, such as syllable stress). In this latter study, stimuli were much shorter in duration (less than 300 ms) and there was no explicit task associated with listening. Thus, these findings suggest that lateral temporal regions are linked to input disorder, but that their response profiles may vary depending on the presentation modality and task demands.

The hippocampus is, in certain cases, sensitive to the probabilistic structure of visual stimulus streams. In paradigms where participants were modeled as ideal Bayesian observers, evidence was found for hippocampal sensitivity to the degree of token diversity [Strange et al., 2005] or the degree to which one item predicted the subsequent item [Harrison et al., 2006]. The possibility that the hippocampus codes for input statistics is theoretically consistent with its involvement in associative, sequential and statistical learning [Davachi and Wagner, 2002; Eichenbaum, 2004; Turk‐Browne et al., 2009], and is consistent with reports linking hippocampal activity to prediction failures [Kumaran and Maguire, 2005, 2009, 2006]; i.e., cases where unexpected events conflict with expectations derived from past experience. Yet, there is ongoing debate as to whether the hippocampus actually signals failed predictions on the basis of associative information. Recent work [Bubic et al., 2011] examining cortical responses to deviant events (i.e., failed predictions) in sequences with temporal, spatial and feature‐based structure did not detect hippocampal involvement in any of these conditions.

Harrison et al. [1962, 2007] also reported sensitivity to disorder in anterior cingulate cortex (ACC). While it may be that the ACC is involved in coding for input entropy, it is also possible that entropy‐related activity in ACC results from the fact that highly ordered inputs warrant predictive processing and are therefore associated with failed predictions. This latter account is consistent with a large body of work documenting ACC involvement in error detection and the mediation of response conflict [Botvinick et al., 2001; Carter and van Veen, 2007]. A handful of imaging studies have expanded the role of ACC to anticipatory or expectation‐related processing in the presence of informative stimulus cues [Aarts and Roelofs, 2011; Aarts et al., 2008; Bubic et al., 2011; Ursu et al., 2009]. These studies demonstrate that ACC activity is modulated by the informativeness of prior stimulus cues independent of subsequent error detection and response conflict [Aarts and Roelofs, 2011; Aarts et al., 2008], and in diverse task paradigms [Rowe et al., 2008; Shidara and Richmond, 2002]. Finally, there is evidence that the ACC is sensitive to unexpected elements in a visual series governed by an implicit learning rule independent of any response and in absence of awareness [Berns et al., 1997; Ursu et al., 2009].

Support for Modality‐Specific Systems Sensitive to Input Disorder

Another possibility is that, in addition to modality‐general systems, there exist systems responsible for computing input uncertainty that are anchored to specific domains or modalities, or even embedded within sensory systems themselves. For example, several studies have suggested that when participants are asked to monitor an input stream for targets, associatively novel events—those that induce a prediction failure—elicit responses that vary depending largely on the type of expectation violated. Bubic et al. 1999 trained participants to construct predictions based on sequential deterministic patterns, where the sequence was governed by one of three features: the spatial pattern in which stimuli were presented, the identity of the objects presented or the temporal interval between object presentations. Violations in each of these sequence types resulted in different activity patterns. Spatial patterns, which necessitate saccade reorientation, recruited middle‐frontal and premotor cortex regions more extensively than other types of violations. Importantly, all three types of visual violations were associated with increased activity in inferior parietal regions bilaterally. Using a Posner cueing paradigm [Posner, 1980], Vossel et al. [2001, 2004] examined responses to odd‐ball targets that consisted of either an object presented in an unexpected spatial location or an object whose color characteristics violated expectations. Location violations induced activity in posterior lateral temporal cortex bordering on the most inferior portion of the inferior parietal lobule (IPL), as well as the superior parietal lobule, whereas object‐feature violations evoked activity in frontal, occipito‐temporal regions and cerebellum. Both types of violations evoked activity in right IPL and intraparietal sulcus (IPS), and right inferior frontal gyrus (IFG). This suggests that, even within the visual domain, the type of predictive information conveyed by the stimuli—be it spatial, featural, or temporal—governs which neural systems participate in processing, though the IPL/IPS regions seems to be more generally responsive to multiple types of violations.

Related work [e.g., Schubotz and von Cramon, 2002] has examined brain mechanisms mediating explicit prediction using manipulations of sequence complexity in experiments where participants were trained to track regularities in sequences of stimuli and instructed to make conscious predictions about sequence‐final elements. These studies have associated the ventral premotor cortex with sensitivity to sequence complexity during the performance of these prediction tasks, and more generally in the simulation of predicted sensory outcomes [see Schubotz, 2007, for review; Schubotz and Von Cramon, 2004]. Given that premotor cortex is not typically associated with sensory processing, this may lend support to the notion of a modality‐general neural substrate for prediction. However, Schubotz and von Cramon 1999 suggest that during explicit prediction, the regions of premotor cortex sensitive to violations of prediction (1 2 1 2 1 2 → 3) differ for auditory or visual stimuli. We note that the requirement to strategically extract patterns and make predictions is known to affect activity in temporal and frontal cortices [Tobia et al., 2012a] and induce the consideration of statistical relations over longer temporal scales than found outside strategic contexts [see Sussman et al., 2002, and Bekinschtein et al., 2009 for data related to auditory sequences; see Kimura et al., 2010, for a replication in the visual domain]. In addition, sequence‐complexity manipulations in several of these studies [e.g., Schubotz and von Cramon, 2002] were operationalized via metric changes in physical features of the stimuli, e.g., the degree to which consecutive auditory tones were similar in pitch or the degree to which successive visual stimuli were similar in size, with simpler conditions containing less drastic physical transitions. Conflating symbolic entropy manipulations with the degree of metric change in a physical property makes it difficult to tease apart entropy‐sensitive regions from those sensitive to the degree of physical changes across events. The latter are regions where differential activity could be accounted for by lower‐level mechanisms related to repetition suppression or priming effects [see Overath et al., 2007, for related work when the degree of metric change was quantified via sample entropy]. Therefore, it is unclear whether ventral premotor cortex will be recruited in contexts that prompt spontaneous perceptual prediction, and in which input entropy is based on symbolic rather than metric manipulations.

Current Approach

To understand which brain regions are sensitive to input disorder in a modality‐specific or modality‐general manner, and in absence of strategic task demands, we designed an event‐related fMRI study with the following features: First, we manipulated input entropy in two presentation modalities, allowing us to directly investigate whether the neural substrate for processing disorder extends across modalities. Second, participants were not oriented toward the stimuli whose disorder were manipulated and instead performed an orthogonal task. Third, items in the auditory and visual series were presented rapidly (presentation rate = 3.3 Hz) and a single stimulus series consisted of 32 items presented within 9.6 s. By requiring participants to perform a task unrelated to the entropy manipulation, we hoped to identify systems mediating passive, spontaneous entropy processing; systems that likely provide the basis for many of the findings previously discussed. Fourth, departing from prior work that quantified responses to input disorder by examining differences in magnitude of BOLD activity for different levels of entropy, we assumed that different entropy levels will be associated not only with different activity strengths (i.e., BOLD amplitude), but also with different temporal dynamics during the presentation of the series themselves. For this reason, we separately modeled the BOLD dynamics for each entropy level and presentation modality using a Finite Impulse Response (FIR) function. This enabled us to identify regions where sensitivity to input disorder was manifested as a general magnitude difference in the BOLD signal (a main effect of Markov Entropy) or as different response dynamics over the course of series presentation (Entropy × Time interaction). Lastly, we used four levels of entropy, rather than just a random and an ordered condition as used in several prior works, because it has been shown that certain regions exhibit similar activity for high and low levels of input entropy, yet differentiate these extremes from intermediate levels [Tobia et al., 2012b].

Given that the current study forms an initial evaluation of the issue, we addressed the question of domain specificity/generality via two complementary analysis strategies whose aim was to control for family‐wise error while still affording sensitive testing. In the first analysis, we capitalized on the 2 (modality) × 4 (entropy) factorial design and conducted a whole‐brain analysis to identify brain regions that are generally sensitive to entropy or ones where sensitivity to entropy is mediated by input modality. The second method of analysis, an approach employed by several prior studies [e.g., Bubic et al., 2011; Cristescu et al., 2006; Vossel et al., 2009], separately probed for regions sensitive to disorder in each dimension; here, within the auditory or visual domain. We then defined those as functional regions of interest (fROIs), and evaluated, for each fROI, whether it demonstrated sensitivity to disorder in the other modality or overlapped with fROIs showing entropy sensitivity to the other modality. In keeping with prior work, we then focused on only the most ordered and most disordered conditions and evaluated whether there were any regions in which the Entropy × Modality interaction was reliable in response to these extremes. We expected to find regions that differentiate between ordered and disordered series in one modality, but not the other, indicating modality‐specific processing of highly ordered inputs. Finally, we conducted several analyses focused on anatomically defined regions of interest to evaluate whether sensitivity to disorder is found in the hippocampus, ACC, early visual cortex, or primary auditory cortex.

MATERIALS AND METHODS

Participants

Twenty‐one right‐handed adults (mean age = 29.9 years; SD = 9.6 years; 12 male) participated in the study. Participants reported no history of psychiatric illness, history of substance abuse, or hearing impairments, and underwent an interview with a board‐certified MD prior to scanning to evaluate other exclusion criteria. Data from one participant who completed the study were not included due to excessive movement during the scanning session. Three other participants were excluded since they only completed three of the four functional runs. Participants provided written informed consent and the human research ethics committee of the University of Trento approved the study.

Design and Materials

Stimuli consisted of brief auditory, visual and audiovisual (AV) series. Each series consisted of 32 items presented within 9.6 s at a rate of 3.3 Hz. These 32 items consisted of a repeated sampling of four tokens whose presentation order was determined by a first‐order Markov process as explained below. Within the auditory series, a token consisted of one of four pure tones (262, 294, 330, and 349 Hz; these correspond to middle “C”, “D”, “E”, “F” notes of the Western major scale). Within the visual series, a token consisted of one of four figures, each identified by a unique combination of shape, color, and location (e.g., “1” = blue triangle presented above the fixation cross). Each tone or visual element was presented for 250 ms with a 50 ms break between stimuli. We also constructed audiovisual (AV) series by combining auditory and visual series of the same entropy level. The AV series were not matched in rate of information production to the unimodal series, because unlike the single‐modality series, each of the AV series did not contain only four unique audiovisual combinations (tokens). Instead, the AV series consisted of independent auditory and visual series (matched in entropy) that were not mutually informative, and for this reason, all 16 possible combinations of the four tones and four shapes could occur. Consequently, whereas the single‐modality auditory and visual series could transmit a maximum of 6.6 bits/s (2 bits/stimulus in the random series, 3.3 stimuli/s), the audiovisual series could transmit as much as 13.2 bits/s (in the random condition; 4 bits/stimulus at 3.3 Hz given there was no mutual information between the auditory and visual channels). These audiovisual series were included in order to study the potential relation between input disorder and multisensory processing and their analysis is not reported here.

Series in the four entropy conditions were generated using a first‐order Markov process applied to four transition matrices with different levels of Markov entropy (Markov entropy = 0.81, 1.35 1.56, 2.0; Fig. 1). The random condition held no transition constraints; each item was equally likely to appear at any point independently of the previously presented item. The other three entropy conditions implemented increasing constraints. In all entropy conditions, items drawn from uniform distributions; i.e., all items occurred an equal number of times when evaluated over the entire series (the stationary distribution of the Markov process). To avoid confounding the number of self‐repetitions with the levels of disorder, the proportion of self‐repetitions in all entropy conditions (the diagonals of the transition matrices) was fixed at 25% (e.g., a transition such as 1 → 1). Controlling for self‐repetitions is crucial as these may yield neural repetition suppression effects [Hasson et al., 2006], or may be particularly salient [Endress et al., 2007; Gervain et al., 2008]. Because we fixed the proportion of self‐repetitions across conditions, it was impossible to implement a completely deterministic condition, i.e., one in which presentation n is determined solely by what was presented at n−1, since such series (e.g., 1 2 3 4 1 2 3 4…) do not contain any cases of self‐repetition, and any differential response to this condition could therefore be explained by repetition suppression mechanisms alone.

Figure 1.

Transition matrices used in current study. The four entropy conditions consisted of stimulus series constructed from four transition matrices differing in level of disorder as quantified by first‐order Markov entropy. These ranged from a “random” condition lacking any transition constraints, to an “ordered” condition with strong statistical constraints. In all cases, the marginal probabilities of all four tokens were equal (25%) when considered over the entire series. In addition, the proportion of self‐repetitions was identical across all conditions (25%).

The 3 (modality: auditory, visual, audiovisual) × 4 (entropy) design resulted in 12 experimental conditions. For each of the 12 conditions we constructed 12 stimulus series (144 series in all). These were presented in four experimental fMRI runs, with three instances of each condition per run. Each run also included six catch trials in which the fixation cross began rotating and changing color six seconds after a series had begun. Within each run were two catch trials for auditory series, two for visual series, and two for audiovisual series. Stimuli were presented in a fast event‐related fMRI design with jittered intervals and with an implicit baseline consisting of observation of the fixation cross. The optimal presentation sequence was determined by the optseq utility [Dale, 1999], which generates a trial set optimized for this type of experimental design.

Procedure

Prior to beginning the study, the sound level was adjusted for each participant so that the tone series could be clearly heard over the scanner noise generated during an EPI sequence. This calibration was done by starting a 'dummy' functional acquisition, and presenting the sample auditory series over the background noise until the participant indicated it could be comfortably heard. Scanner noise was constant over all experimental conditions. Participants were told that their task was to observe the fixation cross at the center of the display, and press a response key whenever the central fixation cross started rotating and changing color. These changes occurred six times during each run. Visual stimuli were presented 2° from the fixation cross so that they could be seen without eye movement. During each of the four experimental runs, performance was monitored online and not analyzed further; responses to catch trials were tracked by the experimenter and participants were given feedback if a response was missed in order to encourage improved performance.

Image Acquisition

A 4T Bruker/Siemens system was used to acquire high‐resolution anatomical and functional data for each participant. Structural scans were acquired with a 3D T1‐weighted MPRAGE sequence (TR/TE = 2,700/4 ms, flip angle = 7°, isotropic voxel size = 1 mm, matrix = 256 × 224; 176 sagittal slices). Two structural scans were obtained for each participant. Single‐shot EPI BOLD functional images were acquired using the point‐spread‐function distortion correction method [Zaitsev et al., 2004]. There were four experimental runs, each consisting of 285 functional scans (TR/TE = 2200/33 ms, flip angle = 75°, voxel size = 3 × 3 × 3.45 mm³, matrix = 64 × 64 mm²; 37 interleaved slices parallel to AC/PC, slice skip factor = 0.2, 428 s overall scan time per run).

Data Analysis: Single‐Subject Analysis

The first five volumes of each run were acquired to allow for T1 stabilization and removed prior to analysis of functional data. On the individual‐participant level, all four functional runs were spatially registered to a single reference time point in the first run to correct for head movement using AFNI [http://afni.nimh.nih.gov/afni/ Cox, 1996]. Time points associated with extreme movement were removed from the regression models (about 1% of the data). For each participant, the raw signal in each voxel was scaled to its mean signal during the run.

Time series were then spatially smoothed with a 6 mm kernel in the 3D volume to increase the signal‐to‐noise ratio (SNR). Data were analyzed using multiple linear regression with AFNI's 3dDeconvolve utility. The BOLD hemodynamic response function (HRF) associated with each of the 12 conditions was estimated via AFNI's Finite Impulse Response (FIR) deconvolution of the BOLD time series using tent basis functions. The FIR deconvolution returned, for each condition, an estimate of the HRF over a 17.6 s time window from the start of each series. The remaining regressors were the mean, linear and quadratic trend components of the time series (3rd‐order polynomial), and the six motion parameters for each of the functional runs.

Inter‐subject registration to common space was performed using the procedures implemented in the FreeSurfer software package [version 4.5, Fischl et al., 1999]. First, the two anatomical images of each participant were coregistered and averaged to increase image SNR. The left and right hemispheres of each participant's structural images were inflated to a surface representation and aligned to a common template using the warping procedures implemented in FreeSurfer. The automatic parcellation functionality of FreeSurfer was used to derive automatic anatomical parcellations of the cortical surface for each participant for purposes of ROI analysis; these parcellations have been shown to be similar in accuracy to manual parcellation [Fischl et al., 2004]. Beta weights estimating the BOLD HRF from 6.6–15.4 s after stimulus‐onset (five values per condition per voxel) were propagated to second‐level group analysis.

Projection of functional data to the surface domain was implemented as follows: Anatomical images were automatically aligned to the first functional run [Saad et al., 2009] and alignment was manually verified and adjusted when needed. The results of the deconvolution procedure for each condition were projected from the 3D EPI volumes onto the 2D cortical surface (imported into SUMA). It was in this 2D surface domain that all group analyses were conducted. We created a group‐level average anatomical cortical surface by averaging participants' individual cortical surfaces using FreeSurfer's make_avg_subject utility. All results were projected to this average cortical representation for display purposes.

Data Analysis: Group‐Level Analysis

To validate the analysis method, we first collapsed all levels of entropy for each modality separately and averaged the beta values in time points corresponding to the 6.6–15.4 s interval of each stimulus presentation. These mean values were contrasted against zero (the implicit baseline). These values were chosen because they reflect the time period beginning after the initial transient associated with series presentation, and ending shortly after termination of the stimulus presentation itself. Then, to evaluate the impact of entropy or its modulation by input modality, we conducted a whole‐brain, 2 (modality: auditory, visual) × 4 (entropy level) × 5 (time point [estimated HRF]) analysis on the single voxel level. To examine sensitivity to disorder separately for the auditory and visual modalities, single‐modality analyses were performed by conducting a 4 (entropy) × 5 (time point) analysis for each vertex to probe for a main effect of entropy or an entropy‐by‐time interaction.

Following Bischoff‐Grethe et al. 2009, we also directly evaluated supramodal commonalities in processing highly ordered and random series by focusing on the two extreme entropy levels. For each vertex, we conducted a 2 (modality: auditory, visual) × 2 (entropy level: high, low) repeated‐measures ANOVA on the mean beta values of activity between 6.6–15.4 s post‐stimulus onset, with participants modeled as a random factor.

All analyses were corrected for a family‐wise error (FWE) rate of P < 0.05 using cluster thresholds [Forman et al., 1995] as follows: The single voxel (surface node) threshold for the main effect of modality was set at P < 0.0001 as these should be extremely strong effects given the sampling of auditory and visual domains in the study. All other tests were similarly controlled for FWE (P < 0.05) using cluster extent, but the effects were evaluated at both a single voxel threshold of P < 0.005 and a more liberal single voxel threshold of P < 0.05. This was done to identify both relatively localized clusters where effects are highly reliable (P < 0.005 single voxel uncorrected, P < 0.05 family‐wise error cluster‐wise correction), as well as more diffuse clusters where effects may be less robust (P < 0.05 single voxel uncorrected, P < 0.05 family‐wise error cluster‐wise correction; [Hasson et al., 2007]). Clusters identified by the conservative threshold were generally subsets of those identified by the more liberal threshold.

Anatomical regions of interest were defined on the basis of FreeSurfer's anatomical parcellation, which was generated separately for each participant and returned the location of the hippocampal region, the ACC, lateral occipital complex, and transverse temporal gyrus (TTG), each bilaterally.

RESULTS

Whole‐Brain Analysis: Validation; Modality Effects

As a validation of the analysis procedure, we contrasted responses to auditory and visual stimuli with the implicit baseline that consisted of observing a fixation cross and monitoring it for possible changes. The analyses used in this study consisted of estimating the hemodynamic response profile for each condition using a Finite Impulse Response model, which is an analysis method that does not make the assumption that all conditions are associated with the same response profile differing only in amplitude [Ashby, 2011; Ollinger et al., 2001]. To evaluate modality effects, we averaged activity within 6.6–15.4 s from stimulus onset and further collapsed these values across the four auditory entropy conditions to obtain a mean auditory response and across the four visual entropy conditions to obtain a mean visual response for each voxel. These values were entered into a second‐level group random effects analysis and tested against zero. Figure 2 shows that the procedure resulted in the expected auditory and visual activation patterns at a threshold of P < 0.0001 (corrected for multiple comparisons using cluster‐extent, P < 0.05). Auditory series evoked strong bilateral activity in primary and secondary auditory areas, and visual series elicited strong activation of visual cortex and IPS as well as some deactivation of auditory cortex. These results replicate well‐established findings and are not discussed further.

Figure 2.

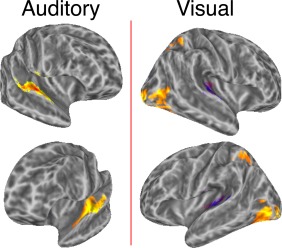
Method validation. Areas shown were highly responsive to auditory and visual series, confirming the expected main effects of modality. The significance threshold was set at P < 0.0001 (P < 0.05 corrected for FWE). Activity was estimated by using a Finite Impulse Response model that makes no a priori assumption about the shape of the hemodynamic response to each stimulus. Hemodynamic responses were estimated for each experimental condition and the mean of estimated activity between 6.6–15.4 s after series onset were averaged and tested against the implicit experimental baseline activity (fixation cross observation). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Sensitivity to Disorder and its Modulation by Modality

The whole‐brain analysis (Fig. 3, Table 1) identified several regions where the BOLD signal varied with entropy, as indicated by a statistically significant interaction between input entropy and the shape of the HRF (Entropy × Time interaction; Fig. 3A). Significant clusters were found in the left ventral and dorsal premotor cortex, left cingulate gyrus, and right supplementary motor area (SMA). Two additional regions, the right cingulate gyrus and right superior frontal sulcus (SFS) showed a similar response, but their activity was further modulated as a function of modality.

Figure 3.

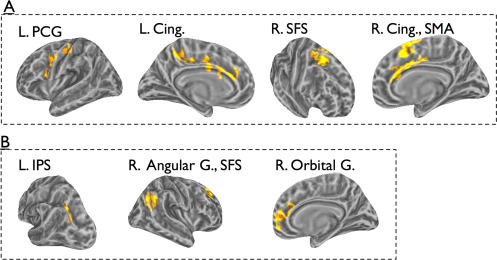
Results of omnibus ANOVA. The hemodynamic response for each of the experimental condition was estimated using a Finite Impulse Response (FIR) filter. Estimated responses in each entropy level, for the two modalities were inserted into a 2 (modality) × 4 (entropy) × 5 (time) ANOVA. Panel A: areas showing an Entropy × Time interaction. Panel B: areas showing a Modality × Entropy × Time interaction. See text for detailed analysis of response profiles. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 1.

Clusters identified in omnibus Modality × Entropy × Time analysis of variance

		Center of mass			Max	Coordinates (max F)			Location (max F)
#	Area (mm2)	x	y	z	F stat	x	y	z	Talairach location	BA
Entropy × Time interaction
1	448	−32	−26	46	3.36	−35	−25	44	L. Postcentral G.	3
2	373	−13	−39	42	3.16	−10	−23	38	L. Cingulate G.	31
3	313	−39	−5	26	4.12	−53	2	12	L. Precentral G.	6
4	267	−6	21	22	3.25	−6	21	22	L. ant. Cingulate	33
5	241	−4	−9	36	3.44	−10	−6	40	L. Cingulate G.	24
6	580	7	4	52	3.52	7	10	59	R. SFG	6
7a	560	5	6	28	2.90	7	19	21	R. ant. Cingulate	33
8a	502	22	−4	43	3.62	22	2	42	R. SFS	6
Modality × Entropy × Time interaction
1	232	−26	−56	30	3.39	−25	−58	28	L. IPS	39
2	457	15	38	8	3.34	12	44	7	R. ant. Cingulate	32
3	442	23	24	31	3.88	27	31	34	R. SFS	9
4	438	41	−71	31	3.38	45	−60	33	R. Angular G.	39

^a Entropy sensitivity in the cluster was further modulated by modality.

The regions outlined above whose entropy sensitivity was characterized by a significant Entropy × Time interaction in absence of further modulation by Modality, are not necessarily sensitive to entropy in both modalities. This statistical result could potentially be driven by strong entropy sensitivity in one modality, or may be derived from relatively weak sensitivity to disorder in each modality, which results in a statistically significant effect when data are pooled across modality. To address this issue, we considered each cluster as a functional ROI (fROI) and evaluated if it showed sensitivity to entropy in each modality. This was done by conducting a 4 (entropy) × 5 (time) ANOVA separately for each modality, collapsing across all vertices in the ROI for each condition. (Note that the clusters were defined on the basis of a significant Entropy × Time interaction that held for each surface vertex in the cluster; collapsing data across vertices may or may not reveal a significant result on the cluster level depending on the relative homogeneity of the interaction pattern in the region). In the left hemisphere, the ventral premotor cluster, and the cluster in the central cingulate gyrus showed some indication of disorder sensitivity in both modalities: ventral premotor cortex showed statistically significant sensitivity to entropy in visual series, F(5, 81) = 2.3, P = 0.05 (Greenhouse‐Geisser corrected), and marginal sensitivity to entropy in auditory series, F(12, 192) = 1.5, P =0.1. In the central cingulate, sensitivity to entropy approached statistical significance for both modalities: there was marginal Entropy × Time interaction for auditory series, F(12, 192) = 1.7, P = 0.07, and for visual series, F(12, 192) = 1.7, P = 0.07. None of the other fROIs identified by the omnibus ANOVA were characterized by sensitivity to entropy in both modalities.

Several regions, including left IPS, right ventro‐medial prefrontal cortex (vmPFC), right SFS, and the right angular gyrus exhibited modality‐dependent entropy sensitivity, as indicated by a statistically significant Modality × Entropy × Time interaction that held for all vertices in each cluster. This result could reflect modality‐specific sensitivity if it was driven by entropy sensitivity in one modality but not the other. Therefore, we treated each cluster as a fROI and evaluated for each fROI if the sensitivity held for each modality using a 4 (entropy) × 5 (time) ANOVA (we focus on main effects of entropy or its interaction with time). In left IPS, we found sensitivity to entropy only for visual series, F(12, 192) = 2.08, P = 0.02. In the right SFS, sensitivity to entropy was statistically significant for visual series, F(5, 98) = 2.51, P = 0.03, and approached significance for auditory series, F(5, 84) = 2.07, P = 0.07. In contrast, the right vmPFC (orbital gyrus) and right angular gyrus did not show statistically significant sensitivity to entropy in either modality when each modality was evaluated separately.

To summarize, the omnibus whole‐brain ANOVA revealed a number of regions sensitive to entropy, or where entropy sensitivity varied as function of modality. Of these regions, more specific conclusions could be made about three: the left ventral premotor cortex and the central extent of the cingulate gyrus appear sensitive to entropy in a relatively general, modality‐independent manner, whereas the left IPS was sensitive to entropy only within visual contexts. In the next analysis we addressed this issue from a different perspective: we separately identified regions sensitive to disorder in auditory or visual series. We then evaluated whether these overlap, as well as whether each of these regions demonstrated sensitivity to disorder in the other modality.

Sensitivity to Disorder in Auditory Series

Areas where all vertices were sensitive to the degree of disorder in brief auditory series (see Fig. 4, Table 2) consisted of lateral temporal regions along the right superior temporal sulcus (STS), the right SMA bilaterally and the anterior portion of the left IFG. Of these, sensitivity in right SMA survived a stricter single voxel threshold (P < 0.005, FWE corrected; P < 0.05 cluster‐extent threshold), and sensitivity in the other regions survived only a less‐strict single voxel threshold (P < 0.05, FWE corrected; P < 0.05 cluster‐extent threshold). Collapsing across all voxels (surface vertices), 4 (entropy) × 5 (time) ANOVAs revealed statistically significant interactions in left IFG, F(12, 192) = 2.48, P = 0.005, left SMA, F(5, 82) = 3.12, P = 0.01 (Greenhouse‐Geisser corrected), and the anterior extent of right STS/MTG, F(5, 84) = 2.43, P = 0.04 (Greenhouse‐Geisser corrected). The right SMA exhibited a marginal interaction, F(12, 192) = 1.73, P =0.06, and the posterior STS showed a marginal main effect of entropy, F(3, 48) = 2.22, P = 0.09.

Figure 4.

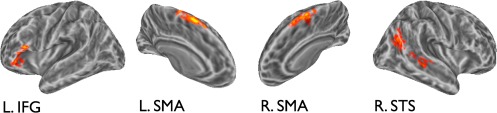
Areas where responses to auditory series varied with input entropy. BOLD time courses in these areas exhibited different temporal dynamics during series presentation as a function of input entropy, as evident in an Entropy × Time interaction. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 2.

Clusters showing sensitivity to levels of disorder in 9.6 s auditory series

		Center of Mass			Max	Coordinates (max F)			Location (max F)
#	Area (mm2)	x	y	z	F stat	x	y	z	Talairach location	BA
1	367	−46	17	8	3.35	−59	13	26	L. IFG	44
2	321	−5	4	55	3.70	−5	13	49	L. SMA	32
3	348	44	−54	18	3.26	35	−52	14	R. STG	22
4	302	9	5	49	3.47	6	19	54	R. SFG	6
	66	7	17	57	3.47	6	19	54	R. SFGa	6
5	267	44	−26	0	3.22	50	−28	−5	R. MTG	22

^aClusters where all voxels passed uncorrected threshold of p < 0.005.

Sensitivity to Disorder in Visual Series

Areas where all vertices displayed sensitivity to disorder in brief visual series consisted of a portion of the left calcarine cortex, right ACC, and IPS bilaterally (see Fig. 5, Table 3). The right ACC and left IPS clusters were identified at both the strict and lenient single voxel thresholds (both corrected for FWE), whereas the right IPS and left calcarine clusters were identified only at the less conservative single voxel threshold (P < 0.05 single voxel uncorrected; P < 0.05 cluster‐extent threshold corrected for FWE). Collapsing across all vertices, the large cluster in the left IPS exhibited a statistically significant sensitivity to entropy F(5, 85) = 2.48, P = 0.03 (Greenhouse‐Geisser corrected), as did the right IPS, F(5, 82) = 2.68, P = 0.03 (Greenhouse‐Geisser corrected), and the right ACC, F(4, 71) = 2.70, P = 0.03. In the calcarine cortex, the interaction was marginal after correction for violation of sphericity, F(5, 82) = 1.82, P = 0.11.

Figure 5.

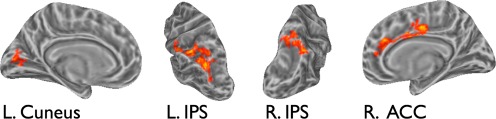
Areas where responses to visual series varied with input entropy. These areas exhibited different temporal dynamics during visual series presentation as a function of input entropy. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 3.

Clusters showing sensitivity to levels of disorder in 9.6 s visual series

		Center of mass			Max	Coordinates (max F)			Location (max F)
#	Area (mm2)	x	y	z	T stat	x	y	z	Talairach location	BA
1	1223	−29	−54	30	3.83	−22	−64	27	L. IPS	40
	121	−19	−62	30	3.83	−22	−64	27	L. IPS (posterior) **
2	86	−31	−46	38	3.81	−28	−49	38	L. IPS (anterior) **	40
3	252	−7	−72	10	2.79	−12	−78	2	L. Lingual G.	18
5	715	5	10	26	4.21	8	−8	35	R. Cingulate. G.	24
	72	5	−9	35	4.21	8	−8	35	R. Cingulate. G.a	24
6	380	26	−64	47	3.20	32	−57	41	R. IPS	7

^aClusters where all voxels passed uncorrected threshold of p < 0.005.

Evaluating Cross‐Modality Sensitivity to Input Disorder

The brain areas identified in the previous two sections represent those most sensitive to input entropy in the auditory and visual modality. As shown in the figures, none of the entropy‐sensitive clusters identified for one modality overlapped with those associated with the other modality. To further evaluate whether they exhibit a general, supramodal sensitivity to statistical regularities, we considered each of those as a fROI, and extracted activation data for the alternate modality in each fROI. A random‐effects repeated‐measures analysis with entropy and time point as factors was conducted for each ROI. This analysis did not reveal any fROI that exhibited sensitivity to disorder in the alternate modality. This is not to say that there was no cross‐modal sensitivity; all regions characterized by sensitivity to disorder in auditory series showed a response to visual stimuli (a main effect of time), but this response was not modulated by the entropy of the visual series. Thus, areas sensitive to disorder in the auditory domain were sensitive, at least, to onsets, offsets, or the temporal dynamics (e.g., presentation rate) of visual stimuli. However, there was no statistically significant sensitivity to the entropy features of visual series. Similarly, the right IPS and posterior left IPS clusters found to discriminate levels of entropy in visual series responded to auditory series, but did not differentiate the auditory series according to the entropy manipulation.

To summarize, regions highly sensitive to entropy in one modality were not sensitive to entropy features in the other. However, this does not mean these regions were differentially sensitive to entropy as function of modality (e.g., sensitivity could just exceed statistical significance for one modality and fall just short of significance for the other). To evaluate whether this sort of differentiation pattern existed in any of these regions, for each region we conducted a 2 (modality) × 4 (entropy) × 5 (time) ANOVA. Of most interest here are statistical patterns indicating differential sensitivity to entropy as function of modality (i.e., the following interactions: Modality × Entropy and/or Modality × Entropy × Time). In regions sensitive to entropy for auditory stimuli, a three‐way interaction was found in right anterior STS/MTG, F(12, 102) = 1.84, P = 0.04. In the regions sensitive to entropy for visual stimuli, a three‐way interaction was found in left IPS, F(12, 192) = 1.91, P = 0.034. For the right anterior STS/MTG the three‐way interaction was due to entropy sensitivity in the auditory condition (the criterion that defined the cluster) but not visual stimuli. For the left IPS, the three‐way interaction was due to entropy sensitivity for visual stimuli (the criterion that defined the cluster) but not auditory stimuli.

Differentiation of High and Low Entropy Conditions

The above analysis showed that areas most discriminative for input disorder in one modality did not reliably discriminate levels of disorder in the other. We now focused only on the highest‐ and lowest‐entropy conditions, which is the approach performed in prior work that compared 'random' and 'sequential' conditions [Bischoff‐Grethe et al., 2000; Schubotz and von Cramon, 2002]. We conducted a 2 (entropy: high, low) × 2 (modality: auditory, visual) ANOVA on the single voxel level, analyzing the mean estimated activity between 6.6–15.4 s poststimulus onset. We were particularly interested in identifying brain regions that differentiate between entropy levels only for one modality, since these regions could be implicated in modality‐specific predictive processing. The analysis identified several regions showing reliably different responses to entropy as function of modality (see Fig. 6, Table 4), but the interaction pattern identified in these does not directly indicate modality‐specific prediction or error propagation.

Figure 6.

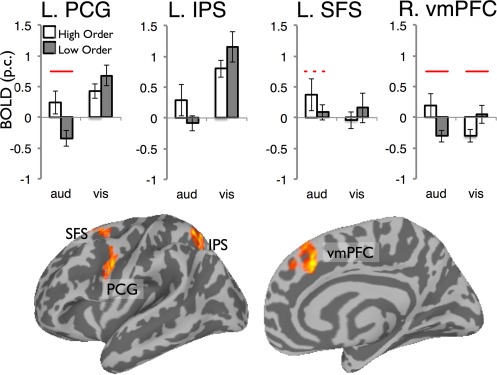
Areas where activity for the highly structured and random series varied as a function of series modality. These regions were identified by an analysis probing for a 2 (entropy: high, low) × 2 (modality) interaction on the whole‐brain level. The clusters identified were treated as functional regions of interest and the mean activity in each region is shown in bar graphs. Solid lines indicate statistically significant difference between entropy levels (P < 0.05) and the dotted line a marginally significant difference (P = 0.06). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 4.

Clusters where responses to extreme order/disorder depended on input modality

		Center of mass			Max	Coordinates (max F)			Location (max F)
#	Area (mm2)	x	y	z	F stat	x	y	z	Talairach location	BA
1	263	−53	−3	25	15.8	−50	−7	24	L. PCG	6
2	243	−32	−67	45	16.4	−26	−63	37	L. IPS	7
3	239	−21	5	43	15.4	−28	7	56	L. Med. Front. G.	6
4	337	7	12	39	16.6	12	12	32	R. Cingulate G.	24

In the left hemisphere, these effects were found in IPS, the ventral extent of precentral gyrus (PCG) and in the SFS in the vicinity of the putative human frontal eye field. To understand the nature of these interactions, we pooled participants' mean activity levels in each of the four conditions, treating each cluster as a fROI. In left PCG, there was a reliable effect of entropy for the auditory condition, but not the visual condition. In SFS, a similar trend was found, with a marginal effect of entropy for auditory inputs, but no effect of entropy for visual inputs. The right vmPFC showed a reliable effect of entropy for both visual and auditory series, though in different directions. Finally, in left IPS, the impact of input entropy was not statistically significant in either modality.

This analysis also identified a main effect of entropy in a region of the right temporal pole (Fig. 7). An examination of participants' activation values in this region revealed higher activity for ordered than disordered series in both modalities (P < 0.05 for visual, P < 0.01 for auditory).

Figure 7.

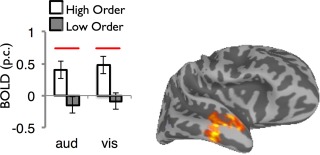
Modality‐general coding of input entropy in the right anterior temporal cortex. This region showed a main effect of entropy that was not modulated by an Entropy × Modality interaction. The center of mass of the cluster in Talairach coordinates: 54, −15, −18. Solid lines indicate statistically significant difference between entropy levels (P < 0.05). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Region of Interest Analysis

We examined sensitivity to input disorder in four regions of interest: the hippocampus, ACC, lateral occipital complex, and TTG, all of which were defined on the basis of anatomical information. For each ROI, a 2 (hemisphere) × 2 (modality) × 4 (entropy) ANOVA was conducted to evaluate sensitivity to disorder in the auditory and visual domains.

For the hippocampus, we found greater activity for auditory than visual series, F(1, 16) = 5.38, P < 0.05 (mean auditory = 0.23, SE = 0.12; mean visual = 0.08, SE = 0.10) but no main effect of entropy nor an interaction with entropy. For ACC there was lower signal for visual series, F(1, 16) = 5.81, P < 0.05 (mean auditory = 0.1, SE = 0.15; mean visual = −0.29, SE = 0.15), but similarly no main effect of entropy or higher‐level interaction with the factor.

For TTG there was the expected effect of modality, with strong activation for auditory inputs and deactivation for visual, F(1, 16) = 129.81, P < 0.001 (mean auditory = 2.75, SE = 0.29; mean visual −0.85, SE = 0.16), and a further modulation of auditory advantage by hemisphere, F(3, 48) = 26.10, P < 0.001, since the modality effect was stronger on the left. There was some impact of entropy on TTG activity, as seen in a Hemisphere × Entropy interaction, F(3, 48) = 4.35, P = 0.009. Figure S1 (Supporting Information) shows the pattern driving this interaction. Note that even though TTG is a central hub for processing auditory features, we did not find differential sensitivity to entropy as function of modality (i.e., no interaction between modality and entropy), suggesting that entropy‐related modulation of TTG activity is not strongly limited to auditory information, a finding that might indicate top‐down effects of higher‐level regions.

Finally, for visual cortex (see Figure S2 in Supporting Information) we found the expected stronger activation pattern for visual information, F(1, 15) = 86.48, P < 0.0001 (mean auditory = 0.05, SE = 0.13, mean visual 1.47, SE = 0.20), and a further modulation of visual advantage by hemisphere with stronger advantage on the right. Finally, there was a statistically significant three‐way interaction, F(3, 45) = 2.88, P = 0.046. However, a breakup of the interaction by analyzing each modality separately failed to reveal any statistically significant main effect or interaction with entropy for either modality.

DISCUSSION

Participants in the current study were presented with brief series of auditory and visual stimuli varied over four levels of uncertainty while performing an incidental cover task. We used fMRI to measure BOLD responses to these rapidly presented series, evaluating the extent to which different levels of statistical constraints drive different response dynamics in particular neural systems. The aim of this study was to examine to what extent the neural substrates sensitive to input disorder are modality‐general or modality‐specific, and if this faculty operates automatically, in the absence of task demands. Beyond probing for modality‐general systems via an omnibus ANOVA that considered both modalities conjointly, we also identified regions sensitive to entropy in auditory or visual series and searched for overlap and cross‐domain sensitivity. Although the former analysis benefited from greater statistical power due to inclusion of more data, only two of the identified regions displayed (modest) signatures of modality‐general sensitivity to entropy. Generally, our results suggest that sensitivity to input disorder is largely supported by distributed, modality‐specific systems. The systems identified in the current work are recruited spontaneously and exhibit different response dynamics over time as function of input disorder. Furthermore, due to the nature of the paradigm employed, it is clear that the regions identified here are involved in very rapid coding or differentiation of statistical features conveyed within 10 s. We first relate these findings to neurobiological models of entropy sensitivity that have focused mainly on lateral temporal regions, hippocampus and ACC. We then discuss the implications of our results for the current understanding of IPS, STS, IFG and SMA functions. We summarize with remarks about broader implications for models of processing statistical regularities.

Implications for Current Neurobiological Models of Neural Sensitivity to Input Disorder

Our results do not support the hypothesis that sensitivity to disorder is mainly subserved by a single system coding for input entropy, but that sensitivity to disorder is found both in modality‐general and modality‐specific regions. That said, regions associated with modality‐general sensitivity to entropy were characterized by statistically weaker responses than those found in regions sensitive to entropy in auditory‐only or visual‐only series.

While we identified several regions sensitive to disorder in either visual or auditory inputs, there was no overlap in these sets; that is, no region responded to the entropy manipulation across modalities. Furthermore, none of the regions characterized by modality‐specific sensitivity to disorder, when defined as fROIs, displayed cross‐modal sensitivity. In fact, the left IPS and a cluster within right anterior STS displayed a stronger signature of modality‐specific response: they were sensitive to entropy in a single modality in a manner that differed reliably from their response to entropy in the other. With respect to the specific notion that lateral temporal regions mediate general entropy processing [Bischoff‐Grethe et al., 2000], our paradigm revealed sensitivity to entropy in the auditory domain in middle and posterior right STS. However, when we confined our analysis to contrasting the most extreme levels of entropy—the random series and the highly ordered series—we found a significant effect of entropy in lateral temporal cortex, albeit located substantially anterior to that reported by Bischoff‐Grethe et al. The fact that an effect of entropy was found in the right temporal pole only in contrasting the two extreme conditions may indicate that, rather than coding for disorder per se, this region is involved in predictive processing, but only in contexts of relatively high certainty where predictions are strongly licensed and often correct. The anterior temporal lobe has also been linked to syntactic and semantic combinatorial operations during language processing [Ferstl et al., 2008].

The hippocampus has been suggested to play a central role in statistical learning and specifically, the coding of entropy [Harrison et al., 2006; Strange et al., 2005; Turk‐Browne et al., 2009]. However, hippocampal activity in the current study did not vary as function of the order manipulation. Although this may seem surprising, we suspect that the presentation rate of 3.3 Hz—compared to ∼1 Hz in work by Strange et al. 2007 and Turk‐Browne et al. 2009—is too rapid for associations between items to be encoded. Furthermore, although studies reporting hippocampal involvement [Turk‐Browne et al., 2009] manipulated statistical dependencies, this was typically done between item pairs and may therefore reflect an instantiation of associative learning rather than sensitivity to distributional statistics (i.e., entropy). Our findings are consistent with recent studies investigating the coding of entropy [Tobia et al., 2012b] or responses to violations of statistical regularities [Bubic et al., 2011], which did not implicate the hippocampus in these processes. Finally, we found effects of input disorder in the ACC. In the general ANOVA, we found nonspecific sensitivity to entropy in right cingulate, which exhibited marginal sensitivity to entropy for both visual and auditory series. Part of the right cingulate cortex was also identified when probing for regions sensitive to entropy of visual series alone, but that specific cluster did not show statistically significant sensitivity to entropy for auditory series. To summarize, manipulations of series entropy did modulate activity in cingulate cortex, with a somewhat greater response to entropy in visual series.

Sensitivity to Disorder in the Auditory Domain: Functional Implications for Superior Temporal Gyrus, Inferior Frontal Gyrus, and Supplementary Motor Area

In the auditory domain, sensitivity to disorder was found in a distributed network of regions consisting of the right STS, left IFG, and bilateral SMA, all areas implicated in various aspects of auditory processing and motor articulation. We found two clusters sensitive to disorder in auditory series along the right superior temporal sulcus (STS), a region typically associated with sensory integration and phonological processing in language [Hickok and Poeppel, 2007]. The more anterior STS cluster showed a statistical interaction pattern indicating strong differentiation between entropy sensitivity in auditory and visual series, with no sensitivity to disorder for visual series. Hickok and Poeppel 2007 have suggested that phonemic processing in language perception, although biased toward the left hemisphere for speech sounds, may be nested within a generic, nonlanguage‐specific mechanism in bilateral STS. The similarity between the presentation rate of our auditory stimuli and the syllable rate in streams of natural language may underlie STS response in the context of the current study. Furthermore, it has been suggested that STS may be sensitive to information integrated over certain temporal windows [∼5 s in Tobia et al., 2012b; ∼12 s in Hasson et al., 2008]. Our manipulation varies the amount of information presented within a 9.6 s interval, a window for temporal integration on roughly the same order as those identified in previous studies.

The left IFG also differentiated between levels of disorder in the auditory domain. This region is involved in numerous language‐related functions [Bookheimer, 2002], including phonological encoding, semantic processing, and working memory maintenance [Friederici, 2002; Makuuchi et al., 2009]. This region has also been recently linked to the acquisition of artificial grammars [Petersson et al., 2012]. Our results corroborate this latter finding for an auditory, nonspeech‐related domain and advance the hypothesis that the coding of statistical regularities during language processing may rely on more basic subfunctions within the IFG.

Robust bilateral clusters sensitive to disorder in auditory series were also found in SMA. Despite the importance of this region, as evidenced by the resulting deficits when damaged, its functional role has remained remarkably opaque [see Nachev et al., 2008, for review]. Of particular relevance to our investigation are the claims for SMA involvement in motor simulation [Cross et al., 2006], auditory orienting of attention [Mayer et al., 2006] and the implicit learning and production of motor sequences [Hikosaka et al., 1996; Tanji, 2001] including speech production [Alario et al., 2006]. Although motor simulation may play a role in conscious prediction [Schubotz, 2007], our paradigm was purely perceptual and implemented basic tone stimuli not particularly conducive to motor simulation. Nonetheless, motor simulation paradigms that activate SMA often involve the internal rehearsal of sequential motor programs. Along these lines, our results suggest that complex functions, such as sequence learning or motor production, may be subtended by a more rudimentary function responsible for encoding serial transitions in temporally extended inputs. This claim is congruent with a hypothesis outlined by Alario et al. 2009, wherein the catenation of syllables into coherent word strings for motor production relies on an abstract sequence‐encoding mechanism localized to SMA. SMA involvement was also reported in an auditory attentional orienting paradigm [Mayer et al., 2006] where valid and invalid auditory cues specified the spatial location of an upcoming auditory stimulus. Although auditory location was not manipulated in the current study, our results reinforce the general hypothesis that SMA may be sensitive to the statistical diagnosticity of auditory cues. In fact, encoding transition constraints may be an extension of the aforementioned sequencing function, since an articulatory element of a motor sequence is often partially conditioned on the preceding element, particularly in speech production.

Sensitivity to Disorder in the Visual Domain: Functional Implications for Early Visual Areas, Intraparietal Sulcus, and Anterior Cingulate Cortex

For the visual condition, left cuneus, right ACC, and three inferior parietal clusters were identified as sensitive to series entropy. This result may indicate that this peripheral sensory region computes input statistics locally. Alternatively, activity in this early visual cluster might be interpreted as an attentional modulation effect [Brefczynski and DeYoe, 1999] spurred by higher‐order areas capitalizing on the predictability of these sequences. As we noted in the Introduction, separating the representation of statistical regularities from attention‐related processes linked to input statistics, or predictions licensed by statistical structure, is quite complicated [Hesselmann et al., 2010; Summerfield and Egner, 2009; Tobia et al., 2012b].

We also found a large cluster encompassing the ACC that exhibited sensitivity to the level of disorder in visual series. This is consistent with the claim that ACC is involved in endogenous visuospatial orienting of attention [Nobre et al., 1997; Rosen et al., 1999; Thiel et al., 2004] and performs an expectancy function, particularly in the visual domain [Aarts and Roelofs, 2011; Aarts et al., 2008]. The foremost implication of the current findings for ACC function is that it performs these computations spontaneously and for rapidly presented stimuli, thus indicating a capacity for a very rapid integration.

The degree of disorder in visual series modulated neural activity in IPS. In addition, the omnibus ANOVA analysis revealed strong selectivity in this region, where sensitivity to entropy was found for visual but not auditory series, with strong differentiation between the two modalities. This region is typically thought to underlie diverse attentional functions [Nobre et al., 1997; Wojciulik and Kanwisher, 1999]. Particularly, IPS has been implicated in attentional orienting across domains. In a series of studies, IPS was identified as a common neural substrate for attentional orienting to spatial locations [Coull and Nobre, 1998; Egner et al., 2008], temporal intervals, and semantic categories [Cristescu et al., 2006]. Critically, all of these studies employed variations on Posner's [1980] cueing paradigm, where diagnostic cues elicit expectations and drive attentional orienting. It should be noted that the entropy manipulation employed here quantifies item diagnosticity in much the same way as cue validity paradigms; Markov entropy reflects the mean diagnosticity of all elements of a series, rather than discretizing item pairs into cues and targets. Recent imaging work using a similar paradigm reinforces the claim that IPS involvement in exploiting diagnostic cues spans a variety of domains. Egner et al. 1999 reported sensitivity to cue validity, for both spatial and featural cues, in many of the same regions found here, including bilateral IPS, and central ACC. In a cueing paradigm where both spatial violations and occasional oddball items occurred, Vossel et al. 2004 found that responses specific to these types of unexpected events overlapped in inferior parietal regions. In related work [Bubic et al., 2011], participants observed structured sequences of visual stimuli interspersed with deviant events violating expectations based on spatial location, temporal interval, and object identity. Bubic et al. found that, although the different types of deviants evoked partially divergent neural systems, activity in inferior parietal cortices was shared across deviant classes. These findings expand on work by Huettel et al. 2010, which demonstrated that IPS responses tracked the uncertainty derived from structured sequences of visual stimuli in the context of decision‐making under uncertainty. The involvement of this region in various domains as well as during passive perception in the current study suggests that it performs a generic expectancy function based on the informativeness of cues and endogenously deploys attention based on these cues. In the current study, the structured series implicitly conveyed predictive information, there was no response component, and the predictive information was task‐independent. Finally, the lack of IPS sensitivity to statistical regularities in auditory input suggests the region is specifically implicated in spatially or visually oriented processing, and that this does not generally extend to the auditory modality, or at least to those cases where auditory input does not convey spatial information. Prior work [Mayer et al., 2006] has shown that when auditory cues convey spatial information in an attentional orienting task, cue effects are found in numerous frontal, parietal, and temporal regions, though not the IPS specifically.

A potential limitation of the current design is that differences in sensitivity to the entropy manipulation in different modalities could be related to the relative (metric, physical) similarity of the tokens used within each modality. High similarity between tokens could make it more difficult to notice the degree of regularity and in extreme cases could result in loss of sensitivity to entropy or transition probability due to token similarity. Controlling for metric similarity across modality is difficult because similarity is defined subjectively: it necessitates equating psychological dissimilarity in the tonal domain to dissimilarity in visual features. However, we note that in the current study, there was no indication of increased sensitivity to one modality—some regions were highly sensitive to the entropy manipulation in the auditory domain, and others in the visual.

General Implications for Theories of Neural Sensitivity to Input Statistics

Beyond the implications of the above results for functions of the brain regions identified in this study, our findings also have broader implications for understanding the neural architecture underlying the brain's sensitivity to uncertainty in the sensory environment. First, when probing for areas generally sensitive to entropy without further modulatory effects of modality, we identified relatively modest signatures of domain‐general sensitivity to entropy. The relative weakness of these modality‐general effects stands in contrast to the more robust patterns found when probing for entropy sensitivity separately for each modality. Second, when separately identifying regions strongly sensitive to disorder in each modality, we did not find any region in common, which provides little support for domain‐general, consolidated accounts of this function. Instead, sensitivity to input disorder appears to be highly distributed and specific to the extended network associated with an input modality. This is theoretically consistent with the domain‐specificity of related functions, such as the evaluation of prediction violations reported previously [Bubic et al., 2011; Vossel et al., 2009], and expands this specificity to the auditory and visual sensory modalities. Another contribution of the current study is showing that input entropy is tracked not only in contexts where it provides strategic, task‐relevant information, but under relatively passive exposure conditions and at a high presentation rate. Further work will be needed to evaluate whether sensitivity to disorder is also found in the context of more demanding dual tasks where attention is strongly diverted, and to systematically evaluate the effects of presentation rate. Finally, the current findings highlight a technical consideration relevant for future investigations: in numerous regions, sensitivity to input statistics is evident in differential responses dynamics rather than in different response magnitudes.

Theoretical accounts of predictive coding [Friston, 2010] postulate that predictive mechanisms are integrated into the microcircuitry of sensory systems [see Hesselmann et al., 2010], and at each level of the processing hierarchy. Our results, which indicate that stimuli conveying predictive information evoke activity in both sensory areas and areas typically associated with higher‐order functions such as attention and language, are consistent with this claim. While our results can only inform theories of predictive coding as far as they hinge on neural sensitivity to input uncertainty, they provide a starting point by characterizing the underlying systems as modality‐specific and dispersed throughout functionally diverse regions of cortex.

Finally, our study demonstrates that regions typically engaged during complex tasks that require responses to external stimuli (e.g., IPS and ACC for attentional tasks, IFG for linguistic tasks, SMA for sequencing tasks) can be driven by a relatively basic sensory manipulation in the absence of strategic processing or explicit task demands. This suggests that the degree of uncertainty in temporally unfolding sensory data triggers endogenous attentional orienting and sequencing functions even when not required by the demands of an external task. Previously reported findings, for example, in the context of attentional orienting paradigms may reflect a specific manifestation of basic functions spontaneously performed by these regions. Future work will need to specify how sophisticated models of these higher‐level functions interface with more basic sensitivity to input uncertainty.

Supporting information

Supporting Information