Concurrent stable and unstable cortical correlates of human wrist movements

Abstract

Cortical activity has been shown to correlate with different parameters of movement. However, the dynamic properties of cortico‐motor mappings still remain unexplored in humans. Here, we show that during the repetition of simple stereotyped wrist movements both stable and unstable correlates simultaneously emerge in human sensorimotor cortex. Using visual feedback of wrist movement target inferred online from MEG, we assessed the dynamics of the tuning properties of two neuronal signals: the MEG signal below 1.6 Hz and within the 4 to 6 Hz range. We found that both components are modulated by wrist movement allowing for closed‐loop inference of movement targets. Interestingly, while tuning of 4 to 6 Hz signals remained stable over time leading to stable inference of movement target using a static classifier, the tuning of cortical signals below 1.6 Hz significantly changed resulting in steadily decreasing inference accuracy. Our findings demonstrate that non‐invasive neuronal population signals in human sensorimotor cortex can reflect a stable correlate of voluntary movements. Hence, we provide first evidence for a stable control signal in non‐invasive human brain‐machine interface research. However, as not all neuronal signals initially tuned to movement were stable across days, a careful selection of features for real‐life applications seems to be mandatory. Hum Brain Mapp 35:3867–3879, 2014. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

Previous studies on voluntary movements showed that cortical activity correlates with muscle activations and movement parameters across different spatial scales from single cells to neuronal populations [Carmena et al., 2003; Cheney and Fetz, 1980; Georgopoulos et al., 1982, 1986; Mehring et al., 2003; Schalk et al., 2008; Waldert et al., 2008]. More recent studies also inferred hand movement parameters such as speed, position, direction, velocity and grasp type in humans [Bradberry et al., 2009; Georgopoulos et al., 2005; Jerbi et al., 2007; Pistohl et al., 2008, 2011; Schalk et al., 2007; Waldert et al., 2008]. Most of these findings were obtained by analyzing recordings from single experimental sessions. The stability of neuronal correlates of movement across sessions or even days has only been investigated in non‐human primate studies, either corroborating [Chao et al., 2010; Chestek et al., 2007; Ganguly and Carmena 2009; Ince et al., 2010; Serruya et al., 2002; Stevenson et al., 2011] or questioning stability [Carmena et al., 2005; Padoa‐Schioppa et al., 2004; Rokni et al., 2007]. Whether the correlation between brain activity and motor behavior in humans shows similar inconsistencies over time has remained unexplored.

To our knowledge, this question has not yet been addressed although its answer is relevant to both basic neuroscience and brain‐machine interface research: first, the stability of a movement‐related neuronal signal may help to clarify whether natural motor control relies on a consistent relation between neuronal activity and behavior. Second, stable components could provide a robust control signal in brain‐machine interfaces where a reliable mapping of neuronal activity to external devices is needed [Nicolelis and Lebedev, 2009; Rossini, 2009]. Therefore, we assessed the temporal properties of neural correlates of wrist movement target in humans. To this end, healthy subjects performed stereotyped movements and received closed‐loop visual feedback of movement target inferred from magnetoencephalographic (MEG) signals. Movement inference over 18 sessions, spanning three days, was based on a static classification algorithm. Hence, the unchanged cortico‐motor coupling in our experiments allowed us to investigate changes in the stability of movement‐related activity across days, as indicated by the classifier's accuracy and the evolution of tuning of population activity to different targets. We demonstrate a stable correlate of motor behavior in human sensorimotor cortex that allows for closed‐loop inference.

MATERIALS AND METHODS

Recordings

Brain activity was measured using a 275‐sensor whole‐head MEG system (VSM MedTech Ltd., Vancouver, Canada) that is based on first‐order axial gradiometers (1.8 cm coil diameter; 5 cm baseline; 2.2 cm intersensor spacing) and has a noise level of 10 fT/√Hz. All experiments were carried out in an electromagnetically shielded room (constructed by Vakuum‐Schmelze Hanau, Germany). For obtaining a head position template as well as continuous monitoring of head movements three localization coils were placed on the subject's head: one at the nasion (activated at 1,423 Hz) and two at the preauricular fiducial points (left coil activated at 1,475 Hz; right coil activated at 1,526 Hz).

Electro‐oculograms (EOG) of both eyes were recorded via bipolar electrodes (impedances <5 kΩ) connected to an EEG head box (VSM MedTech) with reference on the clavicle. Horizontal EOG was recorded by placing an electrode to the outer canthi of each eye, vertical EOG by an electrode pair above/below subjects' left eye. All signals were sampled simultaneously at a rate of 1,172 Hz and low‐pass filtered at 391 Hz during acquisition.

Subject's wrist movements were detected using a custom built MEG compatible, nonmagnetic joystick. The position signals of the joystick were transmitted via optical cables and recorded as an external channel by the MEG system.

Experimental Protocol

Fourteen healthy right‐handed subjects (six males, 24 ± 2 years, handedness according to modified Oldfield score 91 ± 11, see http://www.brainmapping.org) participated in this study after giving informed consent. All experimental procedures were approved by the ethics committee of the medical faculty of the University of Tübingen and were in compliance with the Declaration of Helsinki. We randomly assigned subjects to one of two groups: in one group band‐pass (4–6 Hz) filtered signals were used for brain‐control, in the other group (six subjects) the low‐pass (<1.6 Hz) signals were used for brain‐control (for details see subsection MEG processing below). Subjects were instructed to move a non‐magnetic joystick left‐ or rightwards from a centre position by performing fast, stereotyped radial‐ulnar deviations of the wrist. The joystick could only be moved right‐ and leftwards and its maximum deflection was 3.25 cm (6.6 cm arc of a circle, 29°). To minimize movement variability due to postural changes, the forearm was gently pushed into orthopedic memory foam (AT Kunststoffe, Ahaus, Germany) and further fixed in prone position using a flexible hook‐and‐loop tape (Fig. 1A). The head's position inside the MEG device was stabilized with an inflatable air‐pillow to prevent any major head movements during task execution (mean head movement across subjects and runs was 2.9 ± 1.4 mm).

Figure 1.

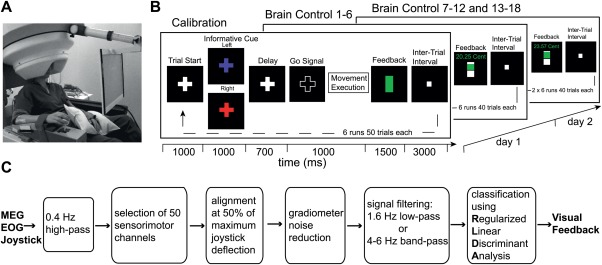
Experimental setup. (A) Subject sitting in the MEG chair with right arm resting on the non‐magnetic joystick. (B) Sequence of visual feedback within trials. Upcoming center‐out movements were cued by a colored fixation cross. During calibration sessions (CS) a vertical bar at the end of each trial indicated a correct movement execution within time constraints (green bar) or a failure trial (white bar). When switching to closed‐loop mode (brain control sessions BS) the same bar provided subjects with feedback about the static classifiers' output. (C) Schematic showing data processing steps. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

On day 1 we first recorded six calibration sessions (CS) of 50 trials each where the two movement targets were presented in a randomized and balanced way. The data of the CS were used to build a classifier which can infer wrist movement target from MEG sensor activity (see data analysis for details). After subjects took a break outside the MEG chamber for approximately 30 min they performed six brain‐control sessions (BS) of 40 trials each with visual feedback showing the classifier's output. In the BS the classifier built from the CS was held constant. This block of closed‐loop brain‐control sessions was then repeated twice (additional 12 BS) 2 days later with a break of ∼25 min between sessions 7 to 12 and 13 to 18 (Fig. 1B). Foam imprints and head positioning templates obtained during the first CS were used in all subsequent CS and BS to minimize postural sources of variability. Each trial started with the presentation of a small white fixation cross projected against a black background on a screen (42 × 32 cm, 800 × 600 pixels) approximately 60 cm in front of the subject. After 1 s the cross changed color in a randomized and balanced way indicating the upcoming movement target: red equivalent for movements to the right and purple for movements to the left. Following a delay period of 700 ms where the cross color was changed back to white, only the outline of the cross was shown to indicate a “GO” signal. Subjects had to complete the movement within 1 s after which a vertical bar appeared on the screen for providing feedback for another 1.5 s: during the CS the bar was filled with green color in case of correct timing of the movement while white color indicated wrong timing or movement to wrong target. During the BS the visual feedback was coupled to the classifiers' output: while gradual filling of the upper half of the bar showed the classifier's posterior probability of the executed movement when it was above 50% for the correct movement target, the lower half indicated less than 50% for the target. During the BS we additionally presented a monetary reward for the subject that was increased or decreased depending on the classifier's performance. Thereby, we informed subjects about the cumulative performance within a run and introduced a motivational factor. In the following 3 s intertrial interval subjects moved the joystick back to the initial center position marked by the appearance of a white square on the screen. The center position covered a range of ±7% of maximum joystick deflection.

To implement the closed‐loop visual feedback paradigm we utilized the general‐purpose platform BCI2000 [Schalk et al., 2004]. All signals sampled by VSM hardware were buffered in blocks of 82 samples (∼70 ms) and forwarded via Ethernet to a separate machine running the BCI2000 software [for details see Mellinger et al., 2007]. Here, the data blocks were stored and processed in the pipeline shown in Figure 1C.

Data Analysis

Preprocessing

During acquisition all electrophysiological signals were high‐pass filtered (0.4 Hz, first‐order IIR, zero phase shifts) to remove slow drifts. Then synthetic third‐order gradiometer formation, i.e. subtraction of a linear combination of reference MEG sensors, was applied to MEG sensor signals to reduce environmental noise and enhance low‐frequency resolution [Vrba et al., 1999]. To minimize the jitter introduced by reaction time and execution variability, single‐trial epochs were extracted from 1,120 ms before to 1,400 ms after the alignment point which was set at 50% of maximum joystick's deflection. Finally, trials with no movement, movement to the wrong target or a movement with a reaction time above five times the median absolute deviation were excluded. No further artifact rejection was performed for the closed‐loop experiments where this is commonly skipped due to constraints on time, computation and reliability in real‐time applications.

To assess potential influences of artifacts from eye and muscle activity on the stability of brain components, the classification procedure described below was repeated post hoc after excluding noisy trials. To this end, epochs of interest (see MEG processing) for all MEG sensors were band‐pass filtered 1 to 15 Hz (fourth‐order butterworth) to detect eye movements and band‐pass filtered 110 to 140 Hz (eighth‐order butterworth) to reveal muscle artifacts. Then the amplitude of each sensor (calculated using the Hilbert transform) was z‐normalized and subsequently averaged over all MEG sensors. Whenever the resulting single time series reached a threshold of z ≥ 4 and the EOG or respectively EMG signals supported the occurrence of an artifact, the affected trial was rejected. Moreover, all trials were visually inspected for signal jumps and slow drifts.

As the above procedures for artifact removal had only a very small effect on the classification accuracies (see Results section) we performed most of the offline analyses also without the artifact removal to allow for a better comparison with the results from the online, closed‐loop experiments.

MEG processing

Based on Waldert et al. [2008] showing maximum directional tuning in low‐frequency MEG signals, we decided to assess the stability of two different slow cortical components: below 1.6 Hz and 4 to 6 Hz band. The former was obtained using a Savitzky‐Golay smoothing filter (second order, 630 ms window), the latter using a 4 to 6 Hz Butterworth band‐pass filter (third order, zero phase shift). Once filtered, the signals of the first and last 490 ms of each epoch were discarded as filter transients and thus, the final epochs spanned from 630 ms before to 910 ms after the alignment point.

EOG processing

Following the procedure for MEG signals, epochs of electrical activity from EOG were obtained and low‐pass filtered with a cutoff at 30 Hz (third‐order Butterworth, zero phase shifts).

Inference of Wrist Movement Target From Electrophysiological Signals

To infer wrist movement target from both aforementioned slow MEG components we used regularized linear discriminant analysis (RLDA, see classifier description below) as classifier. The features used for classification comprised the filtered signals from the 50 MEG sensors covering bilateral sensorimotor areas (Fig. 2E) at one single time sample. For each subject, two parameters were optimized with respect to classification accuracy (CA): the time sample within the trial and the regularization parameter λ (see classifier description below). We estimated the CA across the parameter space by two means: by leave‐one‐out cross‐validation (LCV) on the first four runs of the CS, and by using the first four runs of the CS as training set and the last two as validation set (intersession validation). We finally selected the parameters that yielded maximum CA for LCV and for which the absolute difference of the CAs between both procedures was below 5%. With these criteria we accounted for both: changes between single runs and biased estimations when using LCV on non‐stationary data.

Figure 2.

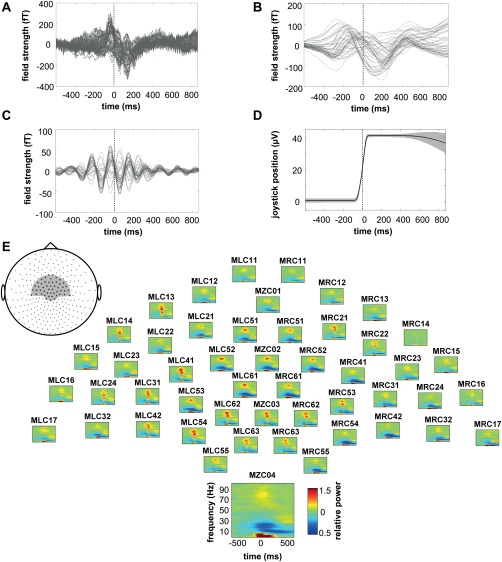
Task‐related modulation of brain activity. (A) Exemplary raw MEG signals of the 50 sensors used to build the classifier from the CS 1–6 of subject 12. Vertical line indicates point of data alignment at 50% of maximum joystick deflection. (B) Same signals after 1.6 Hz low‐pass (LP) and (C) 4–6 Hz band‐pass (BP) filtering. (D) Absolute joystick position within the same time period. (E) Corresponding topographic display of relative power spectra for the same set of MEG sensors (grey inset). Data represent the average over all CS trials of all 14 subjects; one sensor is magnified for better visualization.

To assess whether wrist movement target could be inferred from eye movements we applied the same classification procedure to the signals from vertical and horizontal EOG.

Linear Classifier

Regularized linear discriminant analysis (RLDA [Friedman, 1989]) was used to infer movement target $m\subset j=\left\{left,right\right\}$ from a signal vector of N = 50 MEG sensors. For RLDA the likelihood functions are modeled as multivariate Gaussian distributions according to

$$p(s|{\text{target}\hspace{0.17em}}_m)=\frac{1}{\sqrt{{(2\pi )}^N\left|C\right|}}{e}^{-\frac{1}{2}{(s-{\mu }_{{\text{target}\hspace{0.17em}}_m})}^T{C}^{-1}(s-{\mu }_{{\text{target}\hspace{0.17em}}_m})}$$ (1)

where s depicts the 50 dimensional signal vector comprising the filtered signals of 50 MEG sensors at a certain point in time. The common, i.e. target independent, covariance matrix C and the movement target specific mean signal vectors µ _{target m} were estimated from the data recorded during CS. To avoid singular covariance matrix estimates and poor generalization due to over‐fitting, we employed a regularization technique and used the following covariance matrix during decoding:

$$C_{reg}=(1-\lambda )C+\lambda D$$ (2)

where λ is the regularization parameter, C the full covariance matrix estimated from the training data and D represents a diagonal matrix with diagonal elements d = tr(C)/N. λ can take any value between 0 and 1, where 0 represents no regularization and 1 maximal regularization. During decoding the posterior probabilities were computed using Bayes' rule

$$p({\text{target}\hspace{0.17em}}_m|s)=\frac{p({\text{target}\hspace{0.17em}}_m)p(s|{\text{target}\hspace{0.17em}}_m)}{{\displaystyle {\sum }_j^{}p({\text{target}\hspace{0.17em}}_j)p(s|{\text{target}\hspace{0.17em}}_j)}}$$ (3)

where a uniform prior with p(target_j) = 0.5 was used. The movement target with the highest posterior probability was selected. During brain control sessions the exact value of the posterior probability was also used to generate the visual feedback (see above).

Cortical Sources of Activity

We estimated the neuronal sources of single‐trial MEG surface activity by computing Minimum Norm Estimates (MNE) on a single‐sphere head model using the Brainstorm toolbox [Tadel et al., 2011]. We used constraint dipoles (normal to cortical surface) and standard Tikhonov regularization (λ = 0.1). Localizing electromagnetic brain sources with MNE does not imply any assumptions about the underlying source currents [Hämäläinen and Ilmoniemi, 1994].

Time‐Frequency Analysis

Spectral estimation for frequencies between 0 and 100 Hz was done by time‐resolved Fourier transform using a sliding Hamming window of 400 ms. The window was shifted in steps of 17 ms. Relative power modulations were obtained by dividing the power in each frequency bin by the corresponding mean power during a baseline period (−870 to −630 ms with respect to the time point of 50% maximal joystick deflection).

Temporal Evolution of Tuning Across Sessions

To assess the tuning properties of filtered signals we calculated the signal‐to‐noise ratio (SNR) in the canonical RLDA space at the time point of inference. That is, we first projected the signal vectors s to the eigenvector F of $C_{reg}^{-1}B$ corresponding to the largest eigenvalue, where

$$B=\frac{1}{2}{\displaystyle \sum _j^{}{\left(\mu -{\mu }_{{\text{target}\hspace{0.17em}}_j}\right)}^T\left(\mu -{\mu }_{{\text{target}\hspace{0.17em}}_j}\right)}$$ (4)

is the between‐class covariance matrix and

$$\mu =\frac{1}{2}{\displaystyle \sum _j^{}{\mu }_{{\text{target}\hspace{0.17em}}_j}}$$ (5)

is the mean of the class means, yielding projected data y

$$y=s*F^T$$ (6)

Note that in the two‐class case the rank of B is equal to 1, therefore there is only one eigenvector F with nonzero eigenvalue [Fukunaga, 1990] and the canonical RLDA is one dimensional.

We then defined SNR as the distance between class means µ' in the new space in relation to the fluctuations σ' around this class means, i.e.

$$SNR=\frac{\mu {\prime }_{{\text{target}\hspace{0.17em}}_{left}}-\hspace{0.17em}\mu {\prime }_{{\text{target}\hspace{0.17em}}_{right}}}{(\sigma {\prime }_{{\text{target}\hspace{0.17em}}_{left}}+\hspace{0.17em}\sigma {\prime }_{{\text{target}\hspace{0.17em}}_{right}})/2}$$ (7)

To analyze tuning strength and tuning profile dynamics we computed SNR across blocks of sessions following two different procedures: first, to assess tuning strength, the projection to canonical space was done independently for each block of sessions (CS 1‐4, BS 1‐6, BS 7‐12, and BS 13‐18), i.e. the eigenvector F was recomputed for each block. Second, to assess changes of tuning with respect to the CS tuning profile, the eigenvector F computed from the CS was applied to the BS. In both procedures the regularization parameter λ from the original classifier of each individual subject was used.

Statistical Analysis

For all the group analyses we report results in the form of mean ± standard error of the mean (SEM). To evaluate significance of classification accuracy we used the cumulative binomial distribution to calculate the confidence level of 99% [see Mehring et al., 2003].

Differences in CA between the two independent subject groups were examined using the Wilcoxon rank‐sum test. Within group differences in CA were assessed with the Wilcoxon signed‐rank test. To test for any trends in performance over trials or over sessions we used a linear fit and assessed the significance of the slope by standard techniques [Belsley, 1980]. A two‐sided Wilcoxon rank‐sum test between pooled absolute values of the raw joystick signals of all movements to the left and to the right was applied to test for differences in movement execution. All data analyses were performed using MATLAB (The MathWorks Inc., Natick, MA).

RESULTS

Fourteen healthy subjects performed delayed radial‐ulnar wrist deviations to move a joystick left‐ or rightwards inside the MEG chamber (Fig. 1A). After a brief practicing period during which subjects could get acquainted with the setup, we recorded six runs, referred to as calibration sessions (CS, see Fig. 1B). The resulting trials of 142 ± 2 (mean ± SEM) for movements to the left and 142 ± 3 for movements to the right across the CS were used to build a linear classifier of movement target based on slow sensorimotor cortical activity: for one group of six subjects MEG signals were low‐pass filtered 1.6 Hz (LP group), while for the other group of eight subjects a 4 to 6 Hz band‐pass component was used (BP group). During subsequent brain control sessions (BS) on 2 different days the classifier provided visual feedback based on the inferred movement target. The classifier was kept constant across all BS and across both days. This closed‐loop paradigm allowed us to assess the stability of movement‐related cortical activity.

Spatiotemporal Characteristics of Cortical Activity

MEG signals exhibited clear movement‐related modulation: in the raw signals of the 50 central sensors used for building the classifiers (Fig. 2A) one can observe an early positive peak at the beginning of the movement that was followed by a negative signal deflection during continued movement execution. After applying a 1.6 Hz low‐pass filter (LP) this general time course was preserved and it became evident that single sensors did vary in peak amplitude and latency (Fig. 2B). Band‐pass filtering (BP) the same raw signals in the range 4 to 6 Hz revealed oscillatory signals with maximum signal modulation during the period of movement execution (Fig. 2C). The time‐resolved spectra are consistent with these findings (Fig. 2E). While the power increased during movement execution in frequencies below 7.5 Hz, in the ranges 37.5 to 45 Hz (low gamma) and 55 to 90 Hz (high gamma), a strong decrease in power was observed for 10 to 15 (mu) and 15 to 30 Hz (beta) within the same period. While power decrease in the mu‐band continued, the beta component in frequencies 25 to 32.5 Hz increased again after movement (beta rebound).

With regard to the topography of magnetic field strength the most salient pattern at the time point of decoding is shown in Figure 3A: a strong, dipolar magnetic activity over central to contralateral sensorimotor areas, which was, however, subject to some amount of interindividual differences. Furthermore, depending on the subject, additional weaker activity was measured at pre‐frontal or posterior parietal sites. Localizing single‐trial source currents revealed activity peaks in precentral (Brodmann area 4, Talairach coordinates x/y/z −30/−30/60 mm), postcentral (Brodmann area 3, −27/−18/−62 mm), and premotor (Brodmann area 6, −30/−10/−60 mm) areas (Fig. 3B).

Figure 3.

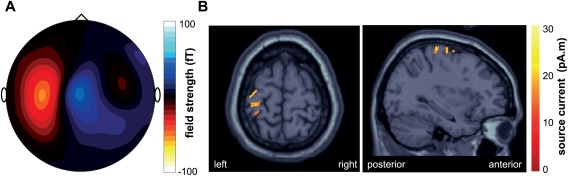
Sources of movement‐related fields. (A) Average magnetic surface activity of BP signals for the same data as in Figure 2 at the time point of movement inference (+139 ms). (B) Corresponding brain sources revealed by Minimum Norm Estimation superimposed on a template structural MRI (MNI/colin27 T1 template). Source currents were localized on a single‐trial basis and subsequently averaged over n = 284 trials.

Inference of Wrist Movement Target

Figure 4 illustrates how well movement target could be inferred during CS using 50 MEG sensors over bilateral sensorimotor areas. For the LP group we correctly classified 76 ± 4% of single trials (mean ± SEM). In comparison to this, the classification accuracy (CA) for the BP group was higher at 85 ± 3% on average (P = 0.059, Wilcoxon rank‐sum test).

Figure 4.

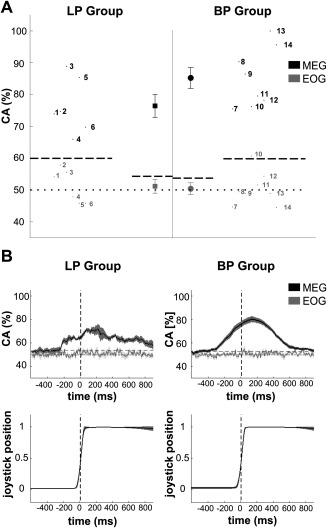
Inference of movement target in the CS. (A) Mean classification accuracy (CA) for single subjects (numbers) and average across subjects (symbols) using 50 sensors over bilateral sensorimotor areas (MEG) or eye signals (EOG). Values are obtained by training the classifier on the first four CS and applying it on the last two CS (see Methods). (B) Average of time‐resolved CA and joystick trajectory across subjects. The vertical line indicates the point of data alignment at 50% of maximum joystick deflection. In both graphs horizontal dotted and dashed lines represent chance level of 50% and the value above which CA deviates significantly (P < 0.01) from the chance level. Error bars in (A) as well as shaded areas in (B) show standard error of the mean.

We also evaluated the CA in a time‐resolved manner (Fig. 4B): for the LP group this revealed a first significant CA ∼250 ms before the trigger point of 50% maximum joystick deflection. From this point on the subject averaged CA increased monotonically, peaked around movement end and declined after movement end. This general pattern was also evident for the BP group with CA values reaching higher maximum values around 80%. Importantly, the average angular difference between the absolute joystick trajectories of both target movements was 0.8° during the movement period (i.e. from −100 ms to +100 ms relative to the alignment point) as compared to the within standard deviation of 1.1° for both rightwards and leftwards movements (range across sessions and subjects: 0.7–1.7°). Movement displacement was highly stereotyped across sessions with angular differences within each target of 0.7° on average. The time‐resolved CA of electrooculogram (EOG) signals fluctuated around chance level, suggesting that eye movements did not carry information about movement target at any moment within the window of interest (Fig. 4B, upper panel).

Temporal Evolution of Slow Cortical Components

We then assessed the temporal stability of slow cortical signals as indicated by the output of the fixed classifier during all closed‐loop sessions. Hence, Figure 5A shows the CA of wrist movement target for the BP group over 18 BS runs across three days. For all subjects movement target could be inferred with a high mean CA of 81 ± 1% across the BS. The CA during BS was not different from the CA during CS (P = 0.20, Wilcoxon signed‐rank test). Moreover, there was no change in CA between day 1 and 2 and the average CA over all sessions did not reveal a trend (linear regression: slope = −0.08%, P = 0.41). Inference from EOG signals did not yield accuracies above chance level. Altogether this indicates temporally stable correlates of movement target in 4 to 6 Hz brain activity that allowed stable inference across days.

Figure 5.

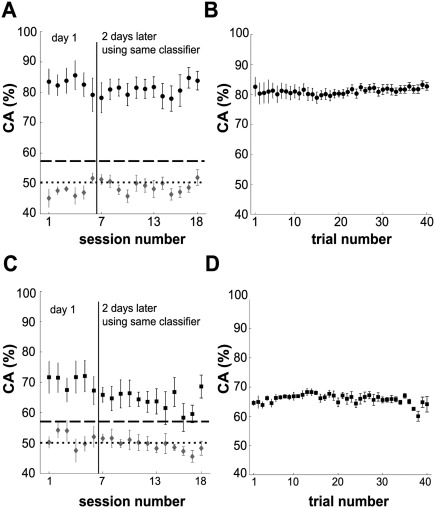
Inference of movement target in the BS. (A) Course of average CA using 4 to 6 Hz BP filtered data over 18 BS on two different days for BP group. (B) Average intra‐session performance smoothed over n = 5 trials. (C) Same as in (A) for 1.6 Hz LP filtered data of LP group and (D) corresponding intra‐session performance. Error bars in all graphs represent standard error of the mean.

The observed stability of average CA across sessions does not necessarily exclude changes within single BS. To test for such changes, we computed the CA within single BS using a moving average over five trials. We observed high accuracies from the very start of each session, with CA values fluctuating between 78% and 83%, and almost no changes of CA across trials (Fig. 5B, linear regression: slope = 0.04% per trial, P < 0.001). This shows that the signals in the 4 to 6 Hz range could be used for brain control right away from the beginning of each BS.

Applying the same analysis described above to the LP group we again obtained CAs significantly above chance level throughout the BS on both days (Fig. 5C). In contrast to the BP group the average CA across 18 BS (66 ± 1%) was significantly lower than during the CS (P < 0.05, Wilcoxon signed‐rank test). Also the CA decreased across the BS (linear regression: slope = −0.5% per session, P < 0.001). However, intra‐session CA was constant from the start to the end of each session, fluctuating between 60% and 68% with no distinct changes over trials (Fig. 5D, linear regression: slope = −0.04% per trial, P < 0.05). In summary, wrist movement to two targets was successfully inferred during the closed‐loop feedback of the LP group as well. However, in contrast to the BP group the modulation of 1.6 Hz signals between right‐ and leftward movements was not stable across time.

All results presented thus far indicate higher stability of decoding for the BP group when compared to the LP group. Is this difference attributable to the closed‐loop feedback or due to intrinsic properties of the signals? To address this question we post‐hoc built and tested classifiers using swapped pre‐processing filters, i.e. subjects from the LP group were reanalyzed off‐line using 4 to 6 Hz BP filtered signals and subjects from the BP group were reanalyzed offline with 1.6 Hz LP filtered signals. Our results show that the closed‐loop feedback had no influence on the magnitude of the CA and its evolution across sessions (Fig. 6A): the BP component yielded a high and stable CA, not only for the BP but also for the LP group. Likewise, the LP component yielded a lower and unstable CA for both groups. The CAs of each component were not different between the groups (BP component: P = 0.66, Wilcoxon rank‐sum test; LP component: P = 0.85, Wilcoxon rank‐sum test). Overall, these results suggest that the stability and instability of decoding across BS was not due to differences in the closed‐loop coupling but due to different intrinsic signal properties.

Figure 6.

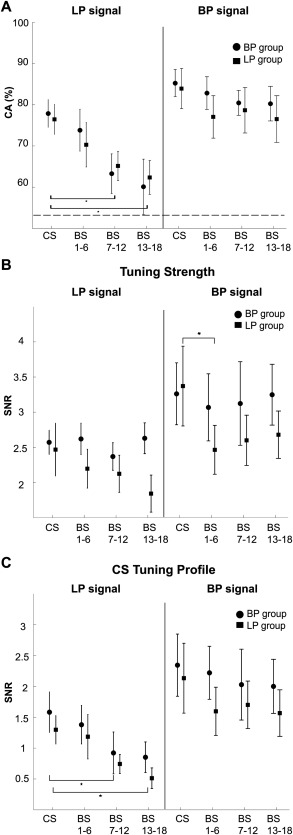
Signal component determines inference of movement. (A) Comparison of CA obtained when coupling cortical activity and motor behavior in closed‐loop mode and when evaluating CA post hoc, i.e. offline and based on the second signal component. Symbols show the resulting averages for blocks of six sessions. Error bars represent standard error of the mean; asterisks indicate statistically significant differences (P < 0.05, Wilcoxon signed‐rank test). (B) Average signal‐to‐noise ratio (SNR) when projecting all 50 MEG sensors used for classification to the individual canonical space. Calculation was based on pooled data within blocks of sessions. (C) Same as in (B) but projecting to the canonical space of the CS. Error bars represent standard error of the mean; asterisks indicate statistically significant differences (P < 0.05, Wilcoxon signed‐rank test).

What causes the instability of the LP component? One confounding variable may be that eye movements or muscular activity could have influenced this component. To address this issue, we repeated the classification procedure offline after manually removing trials that contained potential artifacts. The resulting weak changes in CA compared to the original data were not significant for either LP or BP component (all P > 0.05, Wilcoxon signed‐rank test; see Table 1). We then asked whether the instability of the LP component is caused by an attenuation of tuning across BS or by a tuning profile, which changes during BS but keeps its strength? To differentiate between these two possible explanations, we separately computed the tuning strength and a measure that quantifies the similarity of the tuning during BS to the tuning during CS (tuning profile, see Methods for details). While the tuning strength of the LP component remained constant across the BS, its tuning profile gradually changed with respect to the initial pattern found during the CS (Fig. 6B,C). This decrease of tuning similarity reached significance on the second experimental day (P < 0.05, Wilcoxon signed‐rank test). In contrast, tuning strength and profile of the BP signals remained unchanged over the BS.

Table 1.

Differences in classification accuracy between original data and data after post hoc artifact rejection

	BP component		LP component
	BP group (%)	LP group (%)	BP group (%)	LP group (%)
CS	−1.0 ± 1.2	−0.8 ± 1.0	−1.5 ± 2.5	−1.7 ± 1.5
BS	0.7 ± 3.8	0.7 ± 2.1	−0.4 ± 2.7	−0.2 ± 2.1

Means ± standard deviations across subjects. Note that negative values reflect an increase in classification accuracy after artifact rejection.

BS = brain‐control session. CS = calibration session. BP = band‐pass 4–6 Hz. LP = 1.6 Hz low‐pass.

DISCUSSION

In summary, this study demonstrates stable cortical correlates of stereotyped wrist movement across several days, which can be utilized for stable closed‐loop inference of movement targets in humans.

Concurrent Stable and Unstable Correlates of Wrist Movements

Previous studies have reported slow cortical activations that correlated with different parameters of upper limb movements [Bradberry et al., 2010, 2009; Georgopoulos et al., 2005; Jerbi et al., 2007; Rickert et al., 2005; Schalk et al., 2007; Waldert et al., 2008]. Yet, the stability of the relation between motor behavior and cortical activity remains under debate [Carmena et al., 2005; Chestek et al., 2007; Ganguly and Carmena, 2009; Padoa‐Schioppa et al., 2004; Rokni et al., 2007; Stevenson et al., 2011]. Here, we extend recent reports on stability of neuronal activity during upper limb movements in non‐human primates [Chao et al., 2010; Ince et al., 2010] to humans: by using a constant classifier that provided visual feedback of wrist movement targets inferred online from MEG, we show concurrent stable and unstable cortical signals involved in voluntary movements of humans.

Our results demonstrate that consistent with previous work [Waldert et al., 2008; Wang et al., 2010] slow MEG signals, namely below 1.6 Hz and in the 4 to 6 Hz ranges, are significantly modulated by wrist movement so that movement target could be inferred in a closed‐loop paradigm. However, modulations to the two targets evolved differently over time: while both tuning strength and tuning profile of the 4 to 6 Hz component remained stable, the tuning profile of cortical signals below 1.6 Hz significantly changed, resulting in smoothly decreasing CA. Such change in tuning profile was only noticeable across days and did not degrade the inference of movement target within single BS. Using either signal component we could infer movement targets from the very first trial of each BS suggesting that these activations did not have to be learned. Moreover, the BP component remained stable over BS even if the LP component was used to control the visual feedback. Likewise, the LP component was instable even if the BP component was used for feedback. While the feedback may have helped to assure a high level of attention and involvement in the task and thus a consistent movement execution, we conclude that our experimental design did not entail a direct feedback learning effect on cortical signals. Instead, the observed changes are attributable to the intrinsic properties of the signal components.

Differential Stability of Slow Cortical Activity

What are possible reasons for the instability of the tuning profiles of brain signals below 1.6 Hz? Undesirable influences of artifacts, mostly from eye or muscles, are an omnipresent issue. However, most brain‐machine interface studies do not describe or perform any artifact rejection [Fatourechi et al., 2007], in particular not in a real‐time fashion. As classification based on EOG signals was not informative and the pattern of stability in brain signals did not change after post hoc artifact rejection (see Table 1), an influence of artifacts is therefore very unlikely for our results. The instability could have also been caused by other experimentally uncontrolled factors correlating with cortical activity. For example kinematic variables like arm positioning [Caminiti et al., 1990; Scott and Kalaska 1997], movement speed [Churchland et al., 2006] or altered forces caused by external loads [Kalaska et al., 1989] are known to impact neuronal activity and directional tuning. However, the simplicity of the movements and our experimental setup controlling for head and arm positions as well as for movement timing make this possibility unlikely. In fact, our subjects performed highly stereotypic joystick trajectories with very low movement variability (Fig. 4). Alternatively, the level of fatigue [Tecchio et al., 2006] and fading attention could also affect the stability of cortical signals. We consider it unlikely, however, that this caused the observed instability: (i) while we would expect movement variability to increase with higher levels of fatigue or with reduced attention, the variability remained constant throughout our experiments, speaking in favor of relatively constant levels of fatigue and attention. (ii) Even if the levels of fatigue and attention did change, we would expect fatigue to increase and attention to decrease within sessions and across the first day. The initial level of both factors then should have been restored on the beginning of the second day, after subjects had an extensive break. Consequently, if fatigue or attention affected tuning, the CA should attenuate within sessions but get back to high values on the beginning of the second day, which is not what we observed (Figs. 5 and 6). Furthermore, it has been argued that measurement noise constitutes a potential confounding factor in the assessment of stability of neuronal firing per se [Stevenson et al., 2011]. Notably, the CA measure and its assessment of statistical significance we utilized here, do take measurement noise and other sources of variability into account and are therefore not prone to this problem.

Motor cortical plasticity, most often assessed during sensorimotor learning of complex movement tasks [Ganguly and Carmena, 2009; Karni et al., 1995; Sanes, 2003; Ungerleider et al., 2002], may be more likely to have caused the observed instability. In fact, previous studies demonstrated rapid cortical re‐organization during simple, repeated movements that encoded the kinematic details of the practiced movement [Classen et al., 1998; Halder et al., 2005]. In addition to changes within cortical networks, a shift of main activation from cortical to subcortical areas has been reported when movements become automated during skill learning [Floyer‐Lea and Matthews 2004; Van Der Graaf et al., 2004]. The tuning instability that we observed for the slow 1.6 Hz component may reflect use‐dependent plasticity across sessions.

On the other hand, our results also show that both tuning strength and tuning profile of the 4 to 6 Hz activity remained stable over time. As a consequence, movement target was inferred with high accuracies from this signal throughout all sessions. This component could represent efferent commands, afferent feedback, or computations involving both. Correlates of each of those signals and processes have indeed been described in slow neuromagnetic fields [Cheyne and Weinberg, 1989; Cheyne et al., 2006, 1997; Kristeva et al., 1991] and results from recordings in rat hippocampus [Bland and Oddie, 2001; Bland et al., 2006] and human cortex [Caplan et al., 2003; Cruikshank et al., 2012] generally support the view that theta (4–8 Hz) oscillations might reflect a task‐specific mechanism for sensorimotor integration.

Our choice of frequency bands was based on past studies showing maximum tuning to movement direction for slow movement‐related brain signals [Jerbi et al., 2007; Mehring et al., 2003; Rickert et al., 2005; Schalk et al., 2007; Waldert et al., 2008]. We do not exclude that other high‐frequency bands can also provide valuable movement‐related information (see our Fig. 2E, for example) and this may be investigated in the future.

In addition, it still remains an open question whether source localization can improve inference of movement parameters. A priori knowledge on the cortical regions involved and a better signal‐to‐noise ratio might indeed result in better decoding. First insights have revealed a clear coupling between oscillations localized in motor areas and movement parameters like direction [Wang et al., 2010] or hand speed [Jerbi et al., 2007]. Yet, further experiments will have to verify the feasibility of single‐trial inverse solutions in real‐time applications like brain‐machine interfaces. In particular, issues like the computational costs, biased localizations and mapping of distributed network activity still remain.

CONCLUSIONS

The results of the current study demonstrate two concurrent slow correlates of voluntary movement to targets within overlapping areas of human sensorimotor cortex. Both allowed for closed‐loop inference of movement target but showed different stability over time. We therefore conclude that slow components, although in nearby frequency bands, can reveal a highly specific relation to motor behavior.

In our view, these findings are relevant to the field of brain‐machine interface research. We demonstrate that population signals of non‐invasive recordings in humans allow for closed‐loop inference of motor behavior over days without the need for re‐calibration. As a past offline study of ours showed similar tuning in electroencephalographic signals [Waldert et al., 2008] the transfer of our approach to EEG may be possible in the future. Potential effects of higher variability, both in terms of biological noise like more variable movement behavior in natural settings and in terms of non‐biological noise, need to be evaluated. Taken together our findings might help finding stable control signals for brain‐machine interfaces in humans.