Abstract
A diffusion‐weighted (DW) template in a standard coordinate system is often necessary for the analysis of white matter (WM) structures using DW images. Although several DW templates have been constructed in the ICBM‐152 space, a template for diffusion spectrum imaging (DSI) is still lacking. In this study, we developed a DSI template in the ICBM‐152 space from 122 healthy adults. This high quality template, NTU‐DSI‐122, was built through incorporating the macroscopic anatomical information using high‐resolution T1‐weighted images and the microscopic structural information obtained from DSI datasets. Two evaluations were conducted to examine the quality of NTU‐DSI‐122. The first evaluation examined the anatomical consistency of NTU‐DSI‐122 in matching to the ICBM‐152 coordinate system. The results showed that this template matched to the ICBM‐152 templates very well across the whole brain, not only in the deep white matter regions as other DW templates but also in the superficial white matter regions. In the second evaluation, a large number of independent diffusion tensor imaging (DTI) datasets were registered to the DTI template derived from NTU‐DSI‐122. The examination was performed by quantifying the anatomical consistency among the registered DTI datasets. The results showed that using NTU‐DSI‐122 as the registration template the registered DTI datasets can achieve high anatomical alignment. Both evaluations demonstrate that NTU‐DSI‐122 is a useful high quality DW template. Therefore, NTU‐DSI‐122 can serve as a representative DSI dataset for a healthy adult population, and will be of potential value for brain research and clinical applications. The NTU‐DSI‐122 template is available at http://www.nitrc.org/projects/ntu-dsi-122/. Hum Brain Mapp 36:3528–3541, 2015. © 2015 Wiley Periodicals, Inc.
Keywords: diffusion template, diffusion spectrum imaging, white matter
INTRODUCTION
Diffusion‐weighted (DW) magnetic resonance imaging (MRI), through manipulating the diffusion‐sensitive gradients, can detect the Brownian motion of water molecules and provide the ensemble information of the complex local tissue structures by the measured diffusion probability density function (PDF) [Wedeen et al., 2005]. In particular, the capability of noninvasively revealing fiber bundle architectures makes DW‐MRI a unique technique for investigating the microscopic structures of brain white matter (WM) in vivo. Recently, many efforts have been made to construct DW templates from a large number of subjects to complement the structural information provided by the usual ICBM‐152 template, where the WM regions often exhibit homogeneous appearance [Mori et al., 2008; Peng et al., 2009; Varentsova et al., 2014; Yeh and Tseng, 2011; Zhang et al., 2011].
Mori et al. [2008] developed a template for diffusion tensor imaging (DTI) [Basser et al., 1994], ICBM‐DTI‐81, from which a white matter parcellation map (WMPM) was produced by manually delineating the regions of fiber tracts according to the color‐coded fractional anisotropy (FA) [Basser and Pierpaoli, 1996] map. Later, the IIT template [Peng et al., 2009] and its improved version, IIT2 [Zhang et al., 2011], were constructed to provide a DTI template with less distortion artifacts and better anatomical consistency than ICBM‐DTI‐81. Aside from DTI templates, other efforts were made to develop high angular resolution diffusion imaging (HARDI) [Tuch et al., 2002] templates, including NTU‐90 [Yeh and Tseng, 2011] and IIT3‐HARDI [Varentsova et al., 2014], primarily aiming at dealing with the so‐called crossing‐fiber issue, which is an inherent problem of DTI where at each voxel the diffusion PDF is modeled with a Gaussian function so that only a single fiber orientation can be estimated.
All of the aforementioned DW templates are nominally developed in the standard ICBM‐152 space and are made publicly available, hence the neuroimaging community has benefited from them. For example, the WMPM of ICBM‐DTI‐81 has been incorporated into FSL as one of the atlases, and the IIT2 template was used as a reference for reporting the findings of, for instance, psychosis [Carletti et al., 2012]. However, these DW templates still have one or more of the following limitations. First, the DW templates are all released in their final data formats, either in tensor map (ICBM‐DTI‐81, IIT, and IIT2) or in orientation distribution function (ODF) map (NTU‐90 and IIT3‐HARDI). None of the templates make their original DW images available to the public. Consequently, the users are limited to the released formats and cannot apply their own processing algorithms on the templates to create other formats which fit their needs.
The second limitation is that the current DW templates are not compatible with other diffusion techniques. Due to improvements in hardware performance and advances in parallel imaging techniques, higher order diffusion methods, such as diffusional kurtosis imaging (DKI) [Jensen et al., 2005], q‐ball imaging (QBI) [Tuch, 2004], and diffusion spectrum imaging (DSI) [Wedeen et al., 2005], are becoming feasible, leading to increasing demands of DW templates developed for the various diffusion techniques.
The third limitation, which may be the most important one, is that the anatomical consistency of the aforementioned DW templates in matching to the ICBM‐152 space is inadequate. Some anatomical locations defined through the DW templates do not match to the ICBM‐152 template, which is the ground reference for the ICBM‐152 space. In this article, we will use the IIT2 DTI template as an example to demonstrate that although the IIT2 template matches to the ICBM‐152 space well in the deep white matter (DWM) regions [Zhang et al., 2011], it fails to do so in the superficial white matter (SWM) regions. As a consequence, one would suspect that when performing registration, fiber tracking, brain parcellation, and other analyses involving the DW templates, the low anatomical consistency may lead to, for example, decreased analysis precision and/or accuracy, reduced statistical power and biased results. For instance, in the human brain connectome studies [Van Essen and Ugurbil, 2012], researchers may use the ICBM‐152 template as the reporting reference for functional connectivity results and use the IIT2 template to draw conclusions of structural connectivity. The mismatch between the two templates could introduce diverse spatial locations, leading to inconsistent results and, even worse, contradictive conclusions.
Obviously, the limitations discussed above would affect the validity of the DW templates. Therefore, building a new DW template in the ICBM‐152 space which adequately addressing these limitations would be valuable. To construct such a DW template, two points have to be considered deliberately. The first one is the format of the template. Currently, there are many diffusion techniques proposed to characterize the diffusion‐relevant structural properties, and most of them differ either in the q‐space (the Fourier reciprocal space of diffusion PDF [Wedeen et al., 2005]) sampling schemes (e.g., QBI and DSI), the diffusion models (e.g., DTI and DKI), the reconstruction algorithms (e.g., constrained spherical deconvolusion [Tournier et al., 2007] and generalized q‐sampling imaging (GQI) [Yeh et al., 2010]), or a combination of them. Ideally, it is possible to construct exhaustive DW templates for the various diffusion techniques, but the cost, including constructing the templates and verifying the anatomical consistency among the templates, would be too high to be practical. A more plausible way is to build a DW template which can accommodate the various conditions of DW datasets, and a DSI template seems to be adequate for this purpose. The rationale is based on the fact that DSI datasets usually encompass a larger amount of q‐space samples with higher maximum b‐values, and that the raw DW images of most of the diffusion techniques, such as DTI, DKI, and QBI, are actually subsets of DSI datasets. Consequently, as long as the constructed DSI template is in the raw DW format, templates for those other diffusion techniques can be readily derived from the DSI template, greatly reducing the time and cost to construct the various DW templates.
Another equally important consideration is the registration strategy, which would greatly affect the quality of the constructed DSI template in terms of anatomical matching. A common registration approach used in previous studies is to register the images of the DW datasets (e.g., the images without applying diffusion‐sensitive gradients [the b0 images]) and/or quantitative maps derived from the DW datasets (e.g., FA maps) to the ICBM‐152 template [Mori et al., 2008; Peng et al., 2009; Varentsova et al., 2014; Zhang et al., 2011]. However, the role of the structural images in the previous studies for developing the DW templates in the ICBM‐152 space may be overlooked. We know that the ICBM‐152 template comprises structural images such as T1‐weighted image (ICBM‐152‐T1) and T2‐weighted image (ICBM‐152‐T2). Compared to DW images, the ICBM‐152 template not only has different image contrasts but also has significantly higher resolution and higher signal‐to‐noise ratio (SNR). Therefore, when registering the DW related images to the ICBM‐152 template directly, the discrepancy between the anatomical information (e.g., image contrasts, resolution, SNR) contained in the two image modalities would lead to less accurate registration in, for example, the SWM regions. For this reason, it is essential that the structural images (e.g., T1‐weighted images) should be incorporated in the procedure of registering the individual DSI datasets to the ICBM‐152 template, to achieve a higher anatomical consistency in matching to the ICBM‐152 space. Notice that the incorporation of the structural images does not preclude the value of the DSI images in the registration. The structural images usually have relatively homogeneous appearance in the WM regions, and so are insufficient to achieve an adequate WM alignment. Instead, it has been shown that explicitly using the entire DSI datasets in the registration process could give a better WM alignment among the registered DSI datasets [Hsu et al., 2012]. Therefore, it is necessary to seek a strategy which combines the structural images and the DSI images to drive the construction of the DSI template. One of the plausible ways is the two‐step strategy suggested by Hsu et al. [2012], with slight modifications. In the first step, the structural images are used to drive the registration in matching to the ICBM‐152 space, and the resultant deformation maps are applied to the DSI datasets to construct an intermediate DSI template. In the second step, methods which use the DSI information to drive the registration are used to further transform the registered DSI datasets in the first step to the intermediate DSI template, and subsequently the final DSI template is constructed. This construction strategy has an advantage that the current registration methods can be readily used. For example, the Shoot [Ashburner and Friston, 2011] or the DARTEL [Ashburner, 2007] algorithms can be used to register the structural images in the first step, and the LDDMM‐DSI method [Hsu et al., 2012], which is designed for registering between DSI datasets, can be used in the second step.
The aim of this study was to construct a high quality DW template in the ICBM‐152 space which: (1) used DSI as the q‐space sampling scheme, and (2) used a two‐step registration strategy which combined both structural images and DSI images to drive the construction of the template. This would result in a DSI template developed in the ICBM‐152 space, named NTU‐DSI‐122. The article was organized as follow. The inclusion criteria of participants, acquisition parameters, construction procedures, and evaluation metrics of the quality of NTU‐DSI‐122 were detailed in the Materials and Methods section. The constructed template and evaluation results were shown in the Results section. Finally, the pros and cons of NTU‐DSI‐122 were presented in the Discussion section.
MATERIALS AND METHODS
Participants
A total of 122 healthy adults (age 27.97 ± 5.25 years, 19 − 40 years) with right handiness were recruited in the study. The participant population comprised 61 males (age 27.92 ± 5.08 years, 19–40 years) and 61 females (age 28.02 ± 5.47 years, 19–40 years), with no statistically significant age difference between sexes (P = 0.9182, two‐sided two sample t‐test). Equal numbers of males and females were recruited to reduce potential sex‐related bias of the constructed template. To ensure that the template represents a healthy adult population, all participants did not report any history of neurological or mental disorders, nor were these subjects currently taking psychotropic medication. The study was approved through the research ethics committee of the institute. All participants underwent MRI experiments and the purpose and relevant information regarding the study were clearly explained to the participants. Written informed consent was obtained from each participant.
Data Acquisition
The MRI experiment was conducted on a 3T MRI scanner (Tim Trio, Siemens, Erlangen, Germany) with a 32‐channel phased‐array head coil. In addition to instructing the participants to lie still during the entire experiment, potential head movement was further reduced by restricting the head using a vacuum sponge. Following localizer scans, the T1‐weighted images, DSI images, and phase images (for susceptibility‐induced distortion correction) were obtained from each participant.
A volume of T1‐weighted images was acquired using a three‐dimensional (3D) magnetization‐prepared rapid acquisition gradient echo sequence, where TR/TI/TE = 2000/900/2.98 ms and flip angle = 9°. The acquisition matrix was 256 × 192 × 208 with a 1.0 mm isotropic resolution.
A DSI dataset comprised 101 DW volume images with variable b‐values (bmax = 4,000 sec/mm2) and a b0 volume image. The volume images in the DSI dataset corresponded to 102 isotropic grid points in the q‐space. This DSI acquisition scheme (DSI102) was a modified version of the DSI203 scheme of Kuo et al. [Kuo et al., 2008], which was an optimal protocol balancing the acquisition time and angular resolution on a 3T scanner. While DSI203 acquired data in a full‐sphere in the q‐space, the DSI102 scheme only collected data in a half‐sphere. The DSI102 scheme assumed that the diffusion signals are real and antipodal symmetric around the origin of the q‐space. Therefore, if projecting the acquired half‐sphere diffusion signals to fill the other half, the resulted full‐sphere data would fit in a 7 × 7 × 7 q‐space cube. A single‐shot spin‐echo echo‐planar imaging (EPI) sequence, embedded with twice‐refocused diffusion‐sensitive gradients for reducing the eddy‐current induced distortions [Reese et al., 2003], was used for DSI acquisition. The scanning parameters were identical for all of the volume images in the DSI dataset, except that the amplitudes and orientations of the diffusion‐sensitive gradients varied according to the q‐space positions. Each volume image covered the entire brain and comprised 56 interleaved transverse slices which were 2.5‐mm thick with no gap. The field of view (FoV) and matrix size for each slice were 200 × 200 mm2 and 80 × 80, respectively, resulting in a 2.5 × 2.5 mm2 in‐plane resolution. The volume images were acquired using a TE of 130 ms and a TR of 9,600 ms, thus the acquisition duration of a complete DSI dataset was approximately 16.5 min.
To correct for susceptibility‐induced distortions in the DSI datasets, we acquired 10 TE‐offset volume images of gradient‐echo EPI, where the TE values varied from 37 to 46 ms with a step of 1 ms. The raw data (k‐space data) of the 10 TE‐offset EPI volume images were collected to calculate the field maps [Hsu et al., 2009]. The imaging position, FoV and resolution of the TE‐offset EPI volume images were the same as those of the volume images in the DSI datasets.
Quality Assurance on DSI Datasets
Variable amounts of head motion might occur during DSI acquisition due to a long scanning time. In the presence of strong diffusion‐sensitive gradients, jerky head motion typically induces signal loss in the DW images, and DW images acquired at higher b‐values tend to be more susceptible to signal loss. For the DSI datasets with severe signal loss, the diffusion signals cannot be completely restored through post‐processing methods and these datasets should be excluded from the template construction. To ensure the quality of the constructed DSI template, all of the acquired DSI datasets were scrutinized carefully. For each DSI dataset, every axial slice was assessed through visual inspection, and the number of slices with visually‐detectable signal loss was counted. DSI datasets with more than two slices showing signal loss were excluded. In addition to the assessment of motion‐induced signal loss, other visually apparent artifacts, such as stripes, were inspected, and DSI datasets affected by these artifacts were also excluded. From those passing the quality assurance, 122 DSI datasets were chosen to construct the DSI template.
Image Preprocessing
Before template construction, three preprocessing steps were performed on the acquired images for every subject . It has been reported that correction for susceptibility‐induced distortions of DTI datasets could significantly improve the consistency and accuracy of tractography [Irfanoglu et al., 2012]. The conclusion obviously applies to DSI datasets. Therefore, in the first step, we used an in‐house algorithm [Hsu et al., 2009] along with the field maps derived from the TE‐offset EPI volume images to correct for the susceptibility‐induced distortions of the DSI datasets. Hereafter, referred to the native DSI dataset of subject after distortion correction. In the second step, the T1‐weighted image of subject , , was segmented using SPM12 [Ashburner and Friston, 2005] to produce tissue probability map (TPM). By this step, the TPM of subject ( ) was rigidly aligned in the MNI space and associated with through , so and were in the same space, where denoted function composition. Lastly, the b0 image of ( ) was, via SPM12, rigidly registered to the skull‐striped (masked according to ) by minimizing the cost function of normalized mutual information. Therefore, the deformation map made aligned with . Note that and were actually rigid‐body deformation maps, so they can be expressed as six parameter transformation matrixes.
DSI Template Construction
To construct a DSI template in the ICBM‐152 space, we slightly modified the two‐step registration strategy as suggested by Hsu et al. [2012]. Briefly, in the first step, the T1‐weighted images (more specifically, the TPM) were registered to the ICBM‐152 template, and the estimated deformation maps were applied on the individual DSI datasets so that they were temporarily registered to the ICBM‐152 space. The intermediate DSI template was produced by averaging these temporarily registered DSI datasets. In the second step, the LDDMM‐DSI algorithm was used to transform the registered DSI datasets in the first step to the intermediate DSI template to construct the final DSI template, NTU‐DSI‐122. The construction steps were summarized in Figure 1 and the details were described below.
Estimating the mean of TPMs (Fig. 1a): This step used SPM12 to estimate the average TPM [Ashburner and Friston, 2009, 2011], , which could represent the mean shape and mean value of the TPMs of all participants. In the meanwhile, the deformation map associated with , , was also estimated, rendering aligned in the space of .
Normalizing the mean TPM to the ICBM‐152 space (Fig. 1a): In this step, was normalized to the ICBM‐152 TPM template, , using the DARTEL algorithm [Ashburner, 2007]. The resultant deformation map, , led to be in the ICBM‐152 space.
Constructing the intermediate DSI template (Fig. 1b,c): To register to the ICBM‐152 space, not only the image space transformation ( ) but also the q‐space transformation ( ) should be considered [Hsu et al., 2012]. Therefore, the overall transformation applied on was , and the registered DSI dataset was . Here, was introduced through a combination of the aforementioned deformation maps to generate a single deformation map, , and was produced using the finite strain method [Alexander et al., 2001; Hsu et al., 2012], , where and were the image space and q‐space coordinates, respectively, and was the operator extracting the rotation components from the local Jacobian matrixes of the image space deformation maps. The intermediate DSI template ( ) was constructed by averaging all of the registered DSI datasets, that is, .
Constructing the final DSI template (Fig. 1d,e): The LDDMM‐DSI algorithm [Hsu et al., 2012] was used to transform to , resulting in the deformation map . All of the registered DSI datasets, , , were used to construct the final DSI template, .
Figure 1.
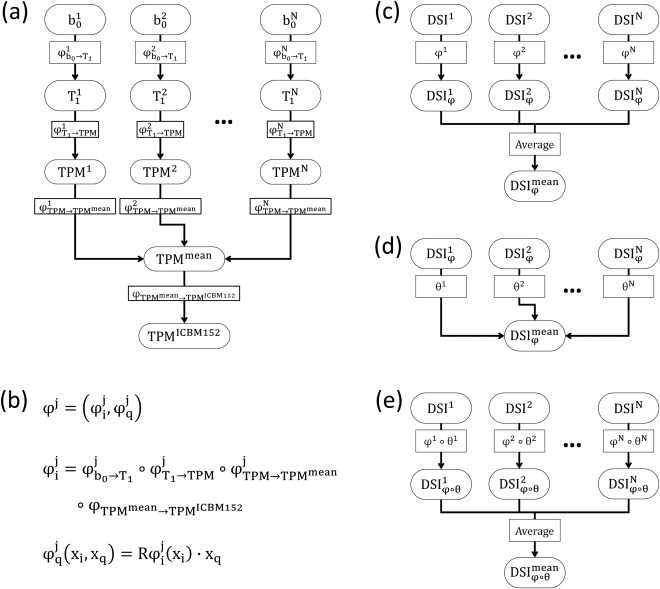
Processing flow for constructing the NTU‐DSI‐122 template.
EVALUATION
Evaluation of the Anatomical Consistency of NTU‐DSI‐122 in Matching to the ICBM‐152 Space
ICBM‐152 is one of the most popular coordinate systems in the neuroimaging community. Therefore, it is essential to examine the anatomical consistency of NTU‐DI‐122 in matching to the ICBM‐152 space to ensure that the template is a reliable reporting system for neuroimaging studies. Because there is no publicly available DSI template constructed in the ICBM‐152 space, the evaluation was conducted by comparing NTU‐DSI‐122 with the IIT2 DTI template [Zhang et al., 2011], particularly in terms of anatomical consistency. Both templates were nominally constructed in the ICBM‐152 space, hence we used the ICBM‐152 template as the comparison standard. For a fair comparison, the NTU‐DSI‐122 template was reduced to a DTI dataset (NTU‐DSI‐122‐DTI), where all of the volume images in NTU‐DSI‐122 were processed using linear fitting to generate the tensor map. The FA map of NTU‐DSI‐122 (NTU‐DSI‐122‐FA) was derived from NTU‐DSI‐122‐DTI.
In the evaluation, we used two assessments to examine the anatomical consistencies of the two templates in matching to the ICBM‐152 space. The first assessment was conducted through quantifying local spatial correlations. Specifically, for each voxel, a window of 11 × 11 × 11 voxels in size with the center at that voxel was defined, and in the window we calculated the Spearman's rank correlation coefficient (SCC) value between the WM TPM of the ICBM‐152 template (ICBM‐152‐WM) and NTU‐DSI‐122‐FA and that between ICBM‐152‐WM and the FA map of IIT2 (IIT2‐FA). Similarly, we also calculated the SCC values between ICBM‐152‐T2 and the b0 images of NTU‐DSI‐122 (NTU‐DSI‐122‐b0) and between ICBM‐152‐T2 and the b0 images of IIT2 (IIT2‐b0). In the study, SCC values larger than 0.65 were considered as high correlation, between 0.65 and 0.35 were moderate correlation, between 0.35 and 0 were low correlation, and smaller than 0 were negative correlation. We expected that in regions with high anatomical consistencies (with respect to ICBM‐152‐WM or ICBM‐152‐T2), they would present high SCC values. One of the limitations of using SCC values in assessing anatomical consistency was the ceiling effect, that is, in regions with relatively homogeneous intensities, the SCC values can no longer fairly reflect the spatial correlations. To address this limitation, we took the spatial homogeneity into account using the coefficient of variation (CV), which was defined as the ratio of the standard deviation to the mean. The CV map was produced for ICBM‐152‐WM, where at each voxel the CV value was calculated within the same window as the one used in producing the SCC values. Besides the issue of spatial homogeneity, we restricted the assessment within the WM regions. Therefore, we defined a mask which included those voxels with the CV values of ICBM‐152‐WM greater than 0.4 and the intensities of ICBM‐152‐WM greater than 0.33. This mask was applied to the SCC maps to eliminate those regions that did not belong to the mask. To summarize the assessment, the cumulative distribution function (CDF) was calculated within the mask for each SCC map.
As fiber‐tracking is one of the most important applications of DW images, this method was used in the second assessment. Specifically, a deterministic fiber‐tracking algorithm [Basser et al., 2000] was performed on NTU‐DSI‐122‐DTI and IIT2 using DSI Studio1 with whole brain seeding and without specifying the passing regions of interest (ROIs). For each template, a total of 100,000 streamlines were produced as the estimation of the whole brain fiber tracts, and then a binary map representing the endpoints of the streamlines was created. The endpoints of the streamlines would be expected to locate around the boundaries of gray matter (GM) and WM, thus the endpoint maps were used to qualitatively inspect the anatomical consistencies of the two templates in matching to the ICBM‐152 space. As the FA thresholds are usually used in fiber‐tracking algorithms as one of the streamline termination criteria, the thresholds would greatly affect the location of the endpoints. For a fair comparison, the FA threshold for NTU‐DSI‐122‐DTI and that for IIT2 were manually adjusted such that the endpoint maps of the two templates had approximately the same voxel numbers. In the study, FA thresholds of NTU‐DSI‐122‐DTI and IIT2 were 0.16 and 0.12, respectively. Other tracking parameters were the same for both templates.
Evaluation of the Anatomical Consistency Among the Registered DTI Datasets Using NTU‐DSI‐122 as the Registration Template
It has been shown that the choice of a template is one of the leading factors affecting the quality of registration in a DTI registration task [Van Hecke et al., 2011]. Therefore, we used NTU‐DSI‐122‐DTI as the template, and registered a set of independent DTI samples to it. The registered DTI datasets were evaluated to quantify the registration quality. In the evaluation, the IIT2 DTI template was also used as the template for comparison. To control factors that might confound the comparison, we used the same variables in registration procedures including registration algorithm, registration parameters, testing DTI samples, and quantification indexes.
A total of 183 DTI datasets, selected from the Hammersmith Hospital cohort of the IXI database2 (IXI‐HH), were used as the testing samples. The tensor maps of the DTI datasets were estimated through linear fitting. The FA maps were linearly registered to NTU‐DSI‐122‐FA via affine transformation (12 parameters) [Friston et al., 1995]. The estimated affine transformation matrixes were then applied to spatially transform the tensor maps and reorient the tensors using the preservation of principal direction (PPD) strategy [Alexander et al., 2001]. Subsequently, a nonlinear registration algorithm, LDDMM‐DTI [Cao et al., 2006], was performed to further register the linearly aligned DTI datasets to NTU‐DSI‐122‐DTI. The LDDMM‐DTI algorithm, a method using the whole tensor in the cost function, was designed to diffeomorphically transform DTI datasets by searching for the geodesics between the individual DTI datasets and the DTI template. LDDMM‐DTI has been shown to be superior to the conventional 3D LDDMM in transforming DTI datasets [Cao et al., 2006]. Different from the reproducing kernel Hilbert space formulation in Cao et al. [Cao et al., 2006], we used the differential operator [Beg et al., 2005] to construct the Hilbert smoothing space for velocity fields. During LDDMM‐DTI registration, the tensors were reoriented according to the PPD strategy [Alexander et al., 2001]. In this study, the LDDMM‐DTI algorithm used the steepest gradient descent method to estimate the solution and was implemented with in‐house software written in C++. To speed up the estimation and avoid the solution to be trapped in local minima, a multiresolution estimation scheme was used, where the results from the lower resolution level were upsampled and served as the initial estimation for the next finer resolution level. In the registration, the geodesics were divided into 10 steps and .
One approach to evaluate the registration quality is to assess the anatomical consistency among the registered images; however, it is a difficult task because we do not know the true answer. Usually, one expect that good alignment corresponds to high overlapping of the transformed ROIs, which have been predefined in the native images [Klein et al., 2009], and assessment in this way is conventionally regarded as a standard approach for assessing the anatomical consistency among the registered images. However, this method requires experts with prior knowledge about the specified anatomical ROIs, making this approach labor intensive and inevitably subject to inter‐ or intra‐rater variations. Moreover, when evaluating the anatomical consistency of registered DTI datasets, this method could only assess the image space consistency, neglecting the tensor consistency. Therefore, rather than predefining ROIs in the native images, we quantified the anatomical consistency among the registered DTI datasets by measuring four indexes on a voxel‐by‐voxel basis. For a given voxel, let be the diffusion tensors of the registered DTI datasets, and the principal eigenvector of . The first index used to evaluate the anatomical consistency was the tensor version of CV (CV‐TEN) [Jones et al., 2002], defined as
where was the element‐wise average of , and was the Forbenius norm of tensor . The second index was the orientation incoherence (ICOH) [Basser and Pajevic, 2000] for principal eigenvectors. It was defined as
where , , and were, respectively, the principal, secondary, and tertiary eigenvalues of the mean dyadic matrix,
For the other two indexes, we used the CV of two commonly‐used diffusion quantities, FA and mean diffusivity (MD), to quantify the anatomical consistency among the registered DTI datasets. For each voxel, the CV of FA (CV ‐ FA) was calculated by dividing the standard deviation of FA by the mean of FA, and so did the CV of MD (CV ‐ MD). To restrict the assessment within the WM regions, only voxels with the intensities of ICBM‐152‐WM greater than 0.33 were taken into account. All of the four quantification indexes were used to measure the deviations among the registered DTI datasets in different properties of the diffusion tensor. CV‐TEN measured the deviation of the whole tensor, ICOH evaluated the deviation of the principal eigenvectors, and CV‐FA and CV‐MD measured the deviations of diffusional anisotropy and overall diffusivity, respectively. Although the indexes to be compared cannot fully represent the anatomical consistency, their values indicate a tendency such that lower index values represent better anatomical consistency. To summarize the tendency across the whole WM, the CDFs of both the NTU‐DSI‐122 and IIT2 templates were calculated for each index.
RESULTS
The Constructed DSI Template, NTU‐DSI‐122
Figure 2 shows the general fractional anisotropy (GFA) map of NTU‐DSI‐122 which is color‐coded by the primary orientations (the orientations corresponding to the maximal ODF values). The WM skeletons of NTU‐DSI‐122 were determined as the regions with GFA greater than 0.1 and were shown overlaid on top of ICBM‐152‐T1. We can see that the overall WM skeletons of NTU‐DSI‐122 align well with the WM regions of ICBM‐152‐T1. In the SWM regions, the contour of the WM skeletons of NTU‐DSI‐122 highly conform to the gyrus‐sulcus patterns of ICBM‐152‐T1, and in the DWM regions, the fiber orientations indicated by the colors also coincide well with known anatomy. However, by referencing to ICBM‐152‐T1, we observe slight mismatch in part of the brain stem, part of the cerebellar and part of the temporal lobe regions (see red arrows in Fig. 2).
Figure 2.
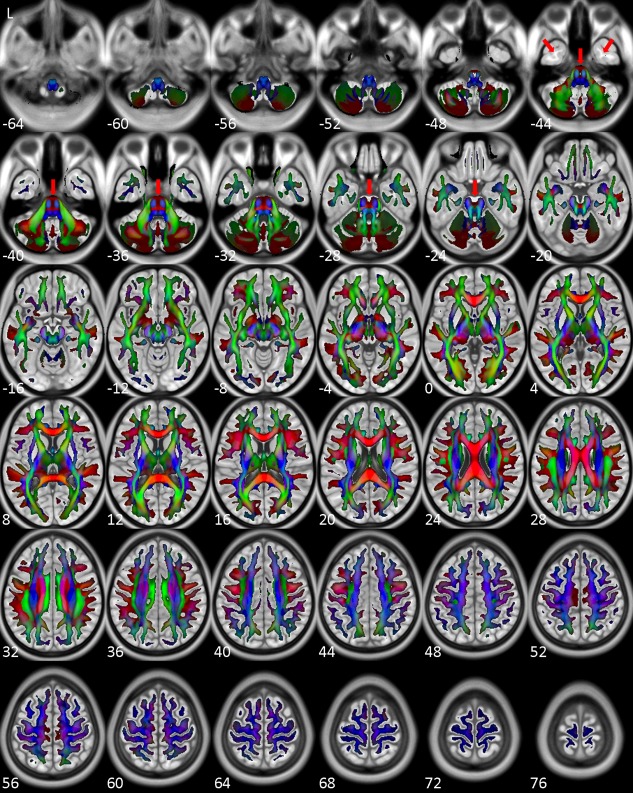
Directionally color‐coded (by the orientations corresponding to the maximal ODF values) GFA map of NTU‐DSI‐122. Regions shown here are those with GFA values greater than 0.1. The background is ICBM‐152‐T1 indexed by the z coordinates (in millimeter) in the ICBM‐152 space. Red arrows indicate slight mismatch between the GFA map and ICBM‐152‐T1. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Evaluation
Evaluation of the anatomical consistency of NTU‐DSI‐122 in matching to the ICBM‐152 space
Figure 3 shows the results of quantifying the anatomical consistencies of NTU‐DSI‐122 and IIT2 in matching to the ICBM‐152 space, including the SCC maps, the difference maps and the corresponding CDF plots. As those regions with high homogeneity are masked out, the regions under consideration includes most of the SWM, part of the DWM, part of the brain stem and part of the cerebellar regions. From the SCC maps of NTU‐DSI‐122, we can see that most of the regions under consideration (83.4% of voxels of NTU‐DSI‐122‐b0 and 88.8% of voxels of NTU‐DSI‐122‐FA, with respective to the total number of voxels within the mask) show high spatial correlations with respect to the ICBM‐152 templates. In contrast, only 50.7% voxels of IIT2‐b0 and 51.9% voxels of IIT2‐FA achieve high correlations. We also observe that there is a small portion of voxels of the IIT2 template (6.2% for IIT2‐b0 and 4.4% for IIT2‐FA), primarily in the SWM and cerebellar regions, showing negative correlations, which is not observed in NTU‐DSI‐122. The difference maps show that the regions with SCC values which are higher in NTU‐DSI‐122 than in IIT2 are primarily in the SWM and the cerebellar regions.
Figure 3.
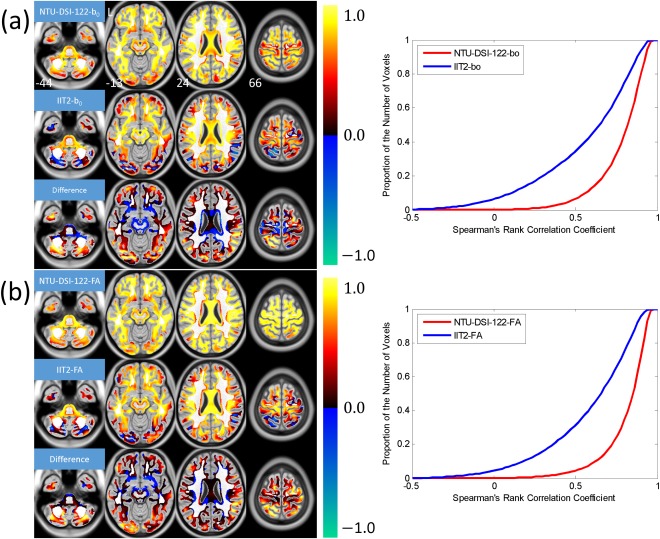
Results of using Spearman's rank correlation coefficient (SCC) to evaluate the anatomical consistencies of the NTU‐DSI‐122 and IIT2 templates in matching to the ICBM‐152 space. The SCC maps were calculated for (a) b0 images (NTU‐DSI‐122‐b0 and IIT2‐b0) with respect to ICBM‐152‐T2 and (b) FA maps (NTU‐DSI‐122‐FA and IIT2‐FA) with respect to ICBM‐152‐WM. The difference maps shown in (a) and (b) are the SCC map of NTU‐DSI‐122‐b0 minus that of IIT2‐b0 and the SCC map of NTU‐DSI‐122‐FA minus that of IIT2‐FA, respectively. Only those voxels with the intensities of ICBM‐152‐WM greater than 0.33 and the coefficient of variation (CV) of ICBM‐152‐WM greater than 0.4 are taken into account. The background is ICBM‐152‐T1 indexed by the z coordinates (in millimeter) in the ICBM‐152 space. The cumulative distribution functions for NTU‐DSI‐122 and IIT2 are plotted in the right panels of (a) and (b). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 4 displays selective transverse sections of (a) ICBM‐152‐T2, (b) NTU‐DSI‐122‐b0, (c) IIT2‐b0, (d) ICBM‐152‐WM, (e) NTU‐DSI‐122‐FA, and (f) IIT2‐FA. Comparing NTU‐DSI‐122‐b0 and IIT2‐b0, the image contrast of IIT2‐b0 appears closer to that of ICBM‐152‐T2, however, in terms of locations of gyri and sulci, NTU‐DSI‐122‐b0 looks more similar to ICBM‐152‐T2. For the FA maps, although IIT2‐FA appears slightly sharper than NTU‐DSI‐122‐FA, we can see that the delineation of the GM and WM in NTU‐DSI‐122‐FA matches ICBM‐152‐WM better than that of IIT2‐FA, particularly in the regions near the cortex, that is, the SWM regions (see examples indicated by the red arrows).
Figure 4.
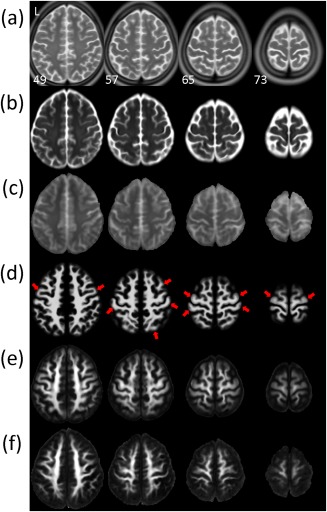
Visual comparison of the anatomical consistencies of the NTU‐DSI‐122 and IIT2 templates in matching to the ICBM‐152 space. Multiple transverse sections near the cortex are displayed for (a) ICBM‐152‐T2, (b) NTU‐DSI‐122‐b0, (c) IIT2‐b0, (d) ICBM‐152‐WM, (e) NTU‐DSI‐122‐FA, and (f) IIT2‐FA. Red arrows indicate the regions where the delineation of the gray matter and white matter in NTU‐DSI‐122‐FA is closer to ICBM‐152‐WM than that of IIT2‐FA. The images are indexed by the z coordinates (in millimeter) in the ICBM‐152 space. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Figure 5 shows the endpoint maps of NTU‐DSI‐122‐DTI (blue) and IIT2 (green), and ICBM‐152‐T1 (the background) is used for inspection reference. We can see that some of the endpoints of IIT2 are located in the sulcus regions (see red arrows for example), which are outside of the brain. In contrast, the endpoints of NTU‐DSI‐122‐DTI are found primarily around the boundaries of GM and WM.
Figure 5.
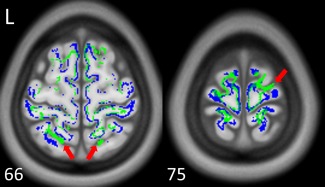
The endpoint maps of the whole brain tracking of NTU‐DSI‐122‐DTI (blue) and IIT2 (green). Red arrows indicate that the endpoints of IIT2 are located in the sulcus regions, which are outside of the brain and anatomically implausible. The background is ICBM‐152‐T1 indexed by the z coordinates (in millimeter) in the ICBM‐152 space. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
Evaluation of the anatomical consistency among the registered DTI datasets using NTU‐DSI‐122 as the registration template
The quantification maps and the corresponding CDF plots for assessing the anatomical consistency among the 183 registered DTI datasets, in matching to either the NTU‐DSI‐122 template or the IIT2 template, are shown in Figure 6 with (a) CV‐TEN, (b) ICOH, (c) CV‐FA, and (d) CV‐MD. Although the four indexes represent four different diffusional properties, they illustrate the same trend. First, we observe that for both the NTU‐DSI‐122 and IIT2 templates, the deviations among the registered DTI datasets in the SWM regions are larger than those in the DWM regions. Second, by comparing the quantification maps and the CDF plots of NTU‐DSI‐122 with those of IIT2, we find that deviations of NTU‐DSI‐122 are generally lower than those of IIT2 in the SWM, DWM, brain stem and cerebellar regions.
Figure 6.
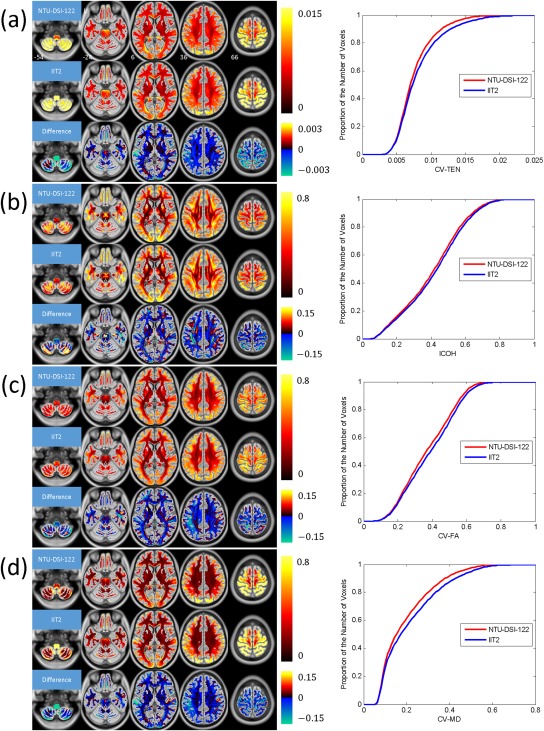
Results of using quantification indexes to evaluate the anatomical consistencies among the registered DTI datasets when using NTU‐DSI‐122‐DTI or IIT2 as the registration template. The indexes include (a) CV‐TEN, (b) ICOH, (c) CV‐FA, and (d) CV‐MD. The difference maps in these subfigures, respectively, represent the maps of NTU‐DSI‐122 minus the maps of IIT2. Only the white matter regions are considered, which is defined as the regions with the intensities of ICBM‐152‐WM greater than 0.33. The background is ICBM‐152‐T1 indexed by the z coordinates (in millimeter) in the ICBM‐152 space. The cumulative distribution functions for NTU‐DSI‐122 and IIT2 are plotted in the right panels of subfigures from (a) to (d). [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]
DISCUSSION
This is the first study to present a high quality DSI template, NTU‐DSI‐122. The evaluation results show that NTU‐DSI‐122 matches to the ICBM‐152 coordinate system very well, not only in the DWM regions but also in the SWM regions. Moreover, high accuracy of alignment among registered DTI datasets can be achieved when NTU‐DSI‐122 is used as the registration template. Therefore, NTU‐DSI‐122 can serve as a representative DSI dataset in the ICBM‐152 space for the healthy adult population.
The high quality of the NTU‐DSI‐122 template can be attributed to the novel two‐step construction strategy and state‐of‐the‐art registration methods. The two‐step construction strategy, as described in the Materials and Methods section, accommodates both the anatomical information provided by the T1‐weighted images and microstructural information provided by the DSI datasets, and hence allowing the construction of the high‐definition DSI template in the ICBM‐152 space. In the first step, a unified segmentation method [Ashburner and Friston, 2005] is applied to estimate the TPM of each subject. A geodesic shooting method [Ashburner and Friston, 2009, 2011; Miller et al., 2006] is subsequently used to estimate the mean TPM of the subjects and the associated deformation maps, and the DARTEL toolbox [Ashburner, 2007], a high‐dimensional diffeomorphic transformation method, is used to estimate the deformation map driving the mean TPM to the ICBM‐152 space. Each individual DSI dataset is temporarily registered to the ICBM‐152 space through the sequentially combined deformation maps. This is an essential step, because the registered DSI datasets would adequately match to the ICBM‐152 space by this step. Having constructed an intermediate DSI template in the first step, the second step, which involves a novel transformation method designed for DSI datasets, LDDMM‐DSI [Hsu et al., 2012], further transforms the registered DSI datasets in the first step to the intermediate DSI template to construct the final DSI template. Therefore, one can consider the first step as a transformation emphasizing on conforming brain morphology to the ICBM‐152 space, and the second step as a transformation emphasizing the q‐space signals convergence across subjects.
In the qualitative results, the NTU‐DSI‐122 template shows slight mismatch with respect to the ICBM‐152‐T1 template in part of the brain stem, part of the cerebellar and part of the temporal lobe regions (Fig. 2), where EPI images conventionally present strong susceptibility‐induced distortions. In addition, the NTU‐DSI‐122‐FA looks less sharp than IIT2‐FA. Both results likely reflect the residual susceptibility‐induced distortions of the DSI datasets, even after applying distortion correction. Another possibility is that the b0 images might not perfectly align with the T1‐weighted images. Because of the imperfect correction and alignment, the DSI datasets might not align with the ICBM‐152 space across the whole brain perfectly. Nevertheless, the NTU‐DSI‐122 template has at least two merits. First, NTU‐DSI‐122 has high anatomical consistency in matching to the ICBM‐152 space, which can be evidenced by both visual inspections and quantitative assessments. For visual inspections, we can see that in the SWM regions, NTU‐DSI‐122‐b0 and NTU‐DSI‐122‐FA, respectively, matches very well to ICBM‐152‐T2 and ICBM‐152‐WM (Fig. 4); in the DWM regions, the principal orientations of NTU‐DSI‐122 coincide well with known anatomy by referencing to ICBM‐152‐T1 (Fig. 2). We also observe that by simply setting a threshold on the GFA map of NTU‐DSI‐122, high conformation between the contour of the drawn WM skeleton and the gyrus‐sulcus patterns of ICBM‐152‐T1 can be obtained (Fig. 2). Furthermore, the endpoint map of whole brain tracking of NTU‐DSI‐122 shows that the streamline endpoints are primarily located around the boundaries between GM and WM (Fig. 5), which obey the anatomical constraint; whereas the results of IIT2 show that some of the endpoints are located in the sulcus regions (Fig. 5), which is anatomically implausible. The good anatomical matching observed from the endpoint map also indicates that, even after a series of processing procedures, the derivatives of NTU‐DSI‐122 still retain high anatomical consistency with the ICBM‐152 space. For quantitative assessments, NTU‐DSI‐122 shows high spatial correlations with respect to the ICBM‐152 templates in most of the SWM, part of the DWM, part of the brain stem and part of the cerebellar regions (Fig. 3), whereas IIT2 fails to achieve, particularly in some of the SWM and the cerebellar regions (Fig. 3). All of these results suggest that high anatomical consistency of NTU‐DSI‐122 in matching to the ICBM‐152 space is true across the whole brain; it is true not only for the DWM regions as other DW templates but also for other brain regions.
The second merit of NTU‐DSI‐122 is that it can serve as a useful registration template according to the results of second evaluation. In the evaluation, a set of independent DTI samples are registered to either NTU‐DSI‐122‐DTI or IIT2, and four indexes are used to quantify the registration quality. Although the four indexes quantify different diffusion properties, from the whole tensor, orientation, to scalar summary measures, they illustrate the same trend, that is, higher anatomical consistency among the registered DTI datasets can be achieved using NTU‐DSI‐122‐DTI as the registration template than using IIT2 (Fig. 6). This trend should be convincing because the number of testing samples (a total of 183 DTI datasets are used) is relatively large. Note that the evaluation also shows a limitation of using NTU‐DSI‐122 as the registration template, that is, the anatomical deviations among the registered DTI datasets in the SWM regions are relatively larger than those in the DWM regions (Fig. 6). This may be explained by the fact that some of the SWM regions exhibit relatively greater anatomical variations among the human beings, so the deviations in these regions after registration are inevitably larger. Another possibility is that the tensors near the GM–WM boundary are relatively more isotropic than those in the DWM regions, making the transformation methods that merely rely on DTI datasets difficult to achieve adequate registrations in the SWM regions due to limited information about microstructural orientation. For the mismatches caused by the latter, they may be ameliorated by incorporating the structural images into the registration procedure.
The two merits mentioned above would make NTU‐DSI‐122 valuable to a wide range of studies. For example, for studies requiring a clear definition of the boundary between GM and WM, such as human brain connectome studies [Van Essen and Ugurbil, 2012] which involve both functional connectivity and structural connectivity, NTU‐DSI‐122 may serve as a reference template.
The construction procedure proposed in this study is used to develop a DSI template in a standard space (ICBM‐152); however, with slight modifications, this procedure can be applied to develop a population‐specific DSI template. This is readily achieved by eliminating the “Normalizing mean TPM to the ICBM‐152 space” step from the construction flow, in other words, enforcing to be an identity transformation. According to the evaluation results of NTU‐DSI‐122, we believe that the population‐specific DSI templates constructed in this manner (i.e., combining both anatomical information provided by the high definition structural images and the DSI datasets) would achieve higher anatomical consistency than those constructed using either the structural images or the DSI datasets. Also, the same arguments should be applicable to other DW datasets for the construction of population‐specific templates. Take DTI as an example, following our proposed two‐step strategy, we can (1) construct an intermediate DTI template by registering the T1‐weighted images altogether, and then (2) further transform the registered DTI datasets in the first step to the intermediate DTI template to construct the final template. Note that in the second step, a transformation method for DTI, for example LDDMM‐DTI [Cao et al., 2006], is required.
In conclusion, the NTU‐DSI‐122 template constructed in this work has high anatomical consistency in matching to the ICBM‐152 space and can be a useful registration template. We believe that NTU‐DSI‐122 can serve as a representative DSI dataset for a healthy adult population and will be of potential value for brain research and clinical applications. NTU‐DSI‐122 is released in the original DW image format with an isotropic resolution of 1 × 1 × 1 mm3, providing the flexibility of using the template. The NTU‐DSI‐122 template is available at http://www.nitrc.org/projects/ntu-dsi-122/.
Footnotes
Available at http://dsi-studio.labsolver.org.
Available at http://biomedic.doc.ic.ac.uk/brain-development/.
REFERENCES
- Alexander DC, Pierpaoli C, Basser PJ, Gee JC (2001): Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans Med Imaging 20:1131–1139. [DOI] [PubMed] [Google Scholar]
- Ashburner J (2007): A fast diffeomorphic image registration algorithm. Neuroimage 38:95–113. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ (2005): Unified segmentation. Neuroimage 26:839–851. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ (2009): Computing average shaped tissue probability templates. Neuroimage 45:333–341. [DOI] [PubMed] [Google Scholar]
- Ashburner J, Friston KJ (2011): Diffeomorphic registration using geodesic shooting and Gauss‐newton optimisation. Neuroimage 55:954–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S (2000): Statistical artifacts in diffusion tensor MRI (DT‐MRI) caused by background noise. Magn Reson Med 44:41–50. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C (1996): Microstructural and physiological features of tissues elucidated by quantitative‐diffusion‐tensor MRI. J Magn Reson B 111:209–219. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D (1994): Estimation of the effective self‐diffusion tensor from the NMR spin echo. J Magn Reson B 103:247–254. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A (2000): In vivo fiber tractography using DT‐MRI data. Magn Reson Med 44:625–632. [DOI] [PubMed] [Google Scholar]
- Beg MF, Miller MI, Trouve A, Younes L (2005): Computing large deformation metric mapping via geodesic flows of diffeomorphisms. Int J Comput Vis 61:139–157. [Google Scholar]
- Cao Y, Miller MI, Mori S, Winslow RL, Younes L (2006): Diffeomorphic matching of diffusion tensor images. Proc IEEE Comput Soc Conf Comput Vis Pattern Recognit 2006:67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carletti F, Woolley JB, Bhattacharyya S, Perez‐Iglesias R, Fusar Poli P, Valmaggia L, Broome MR, Bramon E, Johns L, Giampietro V, Williams SC, Barker GJ, McGuire PK (2012): Alterations in white matter evident before the onset of psychosis. Schizophr Bull 38:1170–1179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Ashburner J, Frith CD, Poline JB, Heather JD, Frackowiak RSJ (1995): Spatial registration and normalization of images. Hum Brain Mapp 3:165–189. [Google Scholar]
- Hsu YC, Hsu CH, Tseng WY (2009): Correction for susceptibility‐induced distortion in echo‐planar imaging using field maps and model‐based point spread function. IEEE Trans Med Imaging 28:1850–1857. [DOI] [PubMed] [Google Scholar]
- Hsu YC, Hsu CH, Tseng WY (2012): A large deformation diffeomorphic metric mapping solution for diffusion spectrum imaging datasets. Neuroimage 63:818–834. [DOI] [PubMed] [Google Scholar]
- Irfanoglu MO, Walker L, Sarlls J, Marenco S, Pierpaoli C (2012): Effects of image distortions originating from susceptibility variations and concomitant fields on diffusion MRI tractography results. Neuroimage 61:275–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K (2005): Diffusional kurtosis imaging: The quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 53:1432–1440. [DOI] [PubMed] [Google Scholar]
- Jones DK, Griffin LD, Alexander DC, Catani M, Horsfield MA, Howard R, Williams SC (2002): Spatial normalization and averaging of diffusion tensor MRI data sets. Neuroimage 17:592–617. [PubMed] [Google Scholar]
- Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang MC, Christensen GE, Collins DL, Gee J, Hellier P, Song JH, Jenkinson M, Lepage C, Rueckert D, Thompson P, Vercauteren T, Woods RP, Mann JJ, Parsey RV (2009): Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage 46:786–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuo LW, Chen JH, Wedeen VJ, Tseng WY (2008): Optimization of diffusion spectrum imaging and q‐ball imaging on clinical MRI system. Neuroimage 41:7–18. [DOI] [PubMed] [Google Scholar]
- Miller A, Trouve A, Younes L (2006): Geodesic shooting for computational anatomy. J Math Imaging Vis 24:209–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S, Oishi K, Jiang H, Jiang L, Li X, Akhter K, Hua K, Faria AV, Mahmood A, Woods R, Toga AW, Pike GB, Neto PR, Evans A, Zhang J, Huang H, Miller MI, van Zijl P, Mazziotta J (2008): Stereotaxic white matter atlas based on diffusion tensor imaging in an ICBM template. Neuroimage 40:570–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng H, Orlichenko A, Dawe RJ, Agam G, Zhang S, Arfanakis K (2009): Development of a human brain diffusion tensor template. Neuroimage 46:967–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reese TG, Heid O, Weisskoff RM, Wedeen VJ (2003): Reduction of eddy‐current‐induced distortion in diffusion MRI using a twice‐refocused spin echo. Magn Reson Med 49:177–182. [DOI] [PubMed] [Google Scholar]
- Tournier JD, Calamante F, Connelly A (2007): Robust determination of the fibre orientation distribution in diffusion MRI: Non‐negativity constrained super‐resolved spherical deconvolution. Neuroimage 35:1459–1472. [DOI] [PubMed] [Google Scholar]
- Tuch DS (2004): Q‐ball imaging. Magn Reson Med 52:1358–1372. [DOI] [PubMed] [Google Scholar]
- Tuch DS, Reese TG, Wiegell MR, Makris N, Belliveau JW, Wedeen VJ (2002): High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn Reson Med 48:577–582. [DOI] [PubMed] [Google Scholar]
- Van Essen DC, Ugurbil K (2012): The future of the human connectome. Neuroimage 62:1299–1310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Hecke W, Leemans A, Sage CA, Emsell L, Veraart J, Sijbers J, Sunaert S, Parizel PM (2011): The effect of template selection on diffusion tensor voxel‐based analysis results. Neuroimage 55:566–573. [DOI] [PubMed] [Google Scholar]
- Varentsova A, Zhang S, Arfanakis K (2014): Development of a high angular resolution diffusion imaging human brain template. Neuroimage 91:177–186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weisskoff RM (2005): Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med 54:1377–1386. [DOI] [PubMed] [Google Scholar]
- Yeh FC, Tseng WY (2011): NTU‐90: A high angular resolution brain atlas constructed by q‐space diffeomorphic reconstruction. Neuroimage 58:91–99. [DOI] [PubMed] [Google Scholar]
- Yeh FC, Wedeen VJ, Tseng WY (2010): Generalized q‐sampling imaging. IEEE Trans Med Imaging 29:1626–1635. [DOI] [PubMed] [Google Scholar]
- Zhang S, Peng H, Dawe RJ, Arfanakis K (2011): Enhanced ICBM diffusion tensor template of the human brain. Neuroimage 54:974–984. [DOI] [PMC free article] [PubMed] [Google Scholar]


