In vivo normative atlas of the hippocampal subfields using multi‐echo susceptibility imaging at 7 Tesla

Abstract

Objectives: To generate a high‐resolution atlas of the hippocampal subfields using images acquired from 7 T, multi‐echo, gradient‐echo MRI for the evaluation of epilepsy and neurodegenerative disorders as well as investigating ${\mathit{R}}_2^{*}$ (apparent transverse relaxation rate) and quantitative volume magnetic susceptibility (QS) of the subfields. Experimental Design: Healthy control subjects (n = 17) were scanned at 7 T using a multi‐echo gradient‐echo sequence and susceptibility‐weighted magnitude images, ${\mathit{R}}_2^{*}$ and QS maps were reconstructed. We defined a hippocampal subfield labeling protocol for the magnitude image produced from the average of all echoes and assessed reproducibility through volume and shape metrics. A group‐wise diffeomorphic registration procedure was used to generate an average atlas of the subfields for the whole subject cohort. The quantitative MRI maps and subfield labels were then warped to the average atlas space and used to measure mean values of ${\mathit{R}}_2^{*}$ and QS characterizing each subfield. Principal Observations: We were able to reliably label hippocampal subfields on the multi‐echo susceptibility images. The group‐averaged atlas accurately aligns these structures to produce a high‐resolution depiction of the subfields, allowing assessment of both quantitative susceptibility and ${\mathit{R}}_2^{*}$ across subjects. Our analysis of variance demonstrates that there are more apparent differences between the subfields on these quantitative maps than the normalized magnitude images. Conclusion: We constructed a high‐resolution atlas of the hippocampal subfields for use in voxel‐based studies and demonstrated in vivo quantification of susceptibility and ${\mathit{R}}_2^{*}$ in the subfields. This work is the first in vivo quantification of susceptibility values within the hippocampal subfields at 7 T. Hum Brain Mapp 35:3588–3601, 2014. © 2013 Wiley Periodicals, Inc.

INTRODUCTION

The human hippocampus is the most frequently studied structure in the temporal lobe, due to its role in formation of memory and learning, among other functions. Structural abnormalities of the whole hippocampus, as assessed by volume measurements, have been studied extensively in diseases such as epilepsy [Bernasconi et al., 2005], Alzheimer's disease (AD) [Barnes et al., 2009], schizophrenia [Steen et al., 2006], depression [Bergouignan et al., 2009], and post‐traumatic disorder [Karl et al., 2006].

The hippocampal formation is a compound structure, comprising the dentate gyrus (fascia dentata), the hippocampus proper, and the subiculum (parahippocampal gyrus), located in the temporal lobe of the brain [Duvernoy et al., 2005]. The hippocampus proper is further divided into three subfields, Cornu Ammonis (CA) 1–3, with the fourth CA subfield or the hilus frequently considered as part of the dentate gyrus. Both pre‐clinical and postmortem studies suggest that these morphologically and functionally distinct subfields are selectively affected throughout the progression of different neurological diseases. West et al. [1994] for instance, demonstrated that the most distinctive neuronal loss associated with Alzheimer's disease (AD) was seen in CA1. Comparatively, Rössler et al. [2002] showed that CA1 and the subiculum (SUB) are both involved in the stage‐dependent neuronal loss of the disease. Pathologic stress has also been associated with atrophy in the CA3 [Sapolsky et al., 1990].

Changes in the hippocampal subfields have also been linked to temporal lobe epilepsy (TLE). For instance, mesial temporal sclerosis (MTS), the most common underlying pathology in TLE, can be characterized according to changes in the hippocampal subfields. According to the existing literature, three types of changes can occur: type 1 (associated with sclerosis in CA1 and CA4), type 2 (defined by CA1 sclerosis), and type 3 (associated with end folium sclerosis) [Blümcke et al., 2007]. Since epilepsy surgical outcomes differ significantly for each of these MTS types, and because of the clear importance of the subfields in epilepsy monitoring and surgical planning, we believe that analysis of each subfield independently will lead to more accurate TLE diagnosis and improved surgical planning.

Imaging the hippocampal subfields in vivo at 1.5 or 3.0 T is challenging due to the limited spatial resolution and signal‐to‐noise afforded by clinical 1.5 or 3.0 T scanners [Thomas et al., 2008]. However, recent advances in ultra‐high‐field imaging have provided the opportunity to study the hippocampal internal architecture in vivo at high resolution. Previous studies at 3–4.7 T [Malykhin et al., 2010; Mueller et al., 2009; Van Leemput et al., 2009] or 7 T [Wisse et al., 2012] have focused on standard T ₂‐weighted sequences to attain the necessary contrast and resolution to delineate the hippocampal subfields and investigate morphometric properties. Gradient‐echo MRI sequences, such as those used for quantitative susceptibility mapping (QSM) [de Rochefort et al., 2008] may offer improved delineation of the hippocampus and its associated subfields. Specifically, multi‐echo gradient echo sequences have the added benefit of providing additional information, such as $T_2^{*}$ relaxation time and quantitative volume magnetic susceptibility. These quantitative metrics can be used to better characterize structures of interest while still permitting the use of traditional volumetric and morphometric analyses.

For example, $T_2^{*}$ imaging has been used at 7 T in multiple previous reports to study the normal anatomy of the hippocampus [Cho et al., 2010a; Prudent et al., 2010; Thomas et al., 2008]. It has also been used to analyze diseased populations as in temporal lobe epilepsy [Breyer et al., 2010] or Alzheimer's disease [Kerchner et al., 2010; Theysohn et al., 2009].

Quantitative susceptibility mapping (QSM) and qualitative susceptibility weighted imaging (SWI) have demonstrated enhanced contrast and sensitivity compared to traditional T ₂‐weighted imaging in several clinical applications, including imaging of vascular malformations, calcifications, and iron deposition [Chavhan et al., 2009; Rauscher et al., 2005]. Furthermore, susceptibility‐weighted contrast has demonstrated clinical potential in the assessment of epilepsy [Saini et al., 2009] and Alzheimer's disease [Nakada et al., 2008]. Moreover, QSM can detect cerebral microbleeds with a higher sensitivity than gradient echo (GRE) magnitude imaging [Klohs et al., 2011] and can be used to accurately quantify iron content in deep gray matter nuclei [Langkammer et al., 2012]. For these reasons, in this study we investigated the potential of the high‐field, susceptibility related contrast to better characterize the subfields of the hippocampus. Presently, there are no reports of QS values in the hippocampal subfields at higher fields in vivo, and only one study quantifying ${\mathit{R}}_2^{*}$ at 7 T [Cho et al., 2010b]. This study presents the first attempt at in vivo quantification of susceptibility values within the subfields at 7 T, and our quantitative MRI measurements provide a useful starting point for more advanced analyses of subfield composition in both healthy control and diseased populations.

Neuroanatomical atlases derived from group‐wise registration of a cohort of subjects can provide enhanced localization and visualization for structural and functional imaging studies, as well as enable voxel‐based or morphometric analysis in a broad set of applications. The objective of the work reported here was to enhance our understanding of the hippocampal subfields through the development of a high resolution normative atlas using 7 T quantitative susceptibility imaging. To this end, we first developed and validated a manual labeling protocol for the hippocampal subfields to assess how well they could be identified with our proposed imaging sequence. We then applied a group‐wise registration technique to align images from seventeen healthy subjects and generated a neuroanatomical atlas of the hippocampus and its subfields, assessing accuracy of the alignment using the manually labeled subfields. ${\mathit{R}}_2^{*}$ and QS maps from each subject were subsequently warped to generate ${\mathit{R}}_2^{*}$ and QS atlases, and we evaluated these quantitative metrics both within the hippocampal subfields and in the basal ganglia for comparative purposes.

METHODS

Materials and Imaging

The subject cohort enrolled in this study included 17 healthy controls (10 Males, 7 Females, mean age 31.3 ± 8.7). All data were acquired on a 7 T neuroimaging optimized MRI scanner (Agilent, Santa Clara, CA, USA/Siemens, Erlangen, Germany) using a 16‐channel transmit‐receive head coil array constructed in‐house. The imaging sequence used for this study was a multi‐echo gradient‐echo sequence with six echoes acquired with a 0.5 mm in‐plane resolution (TR = 40 ms, TE₁ = 4.57 ms, echo spacing = 4.89 ms, flip angle = 13°, N = 1, matrix = 256 × 360 × 80, slice thickness = 1.5 mm, FOV = 128 × 180 × 120 mm, total time = 12 min), with slices acquired perpendicular to the long axis of the hippocampus in a coronal oblique orientation. Quantitative maps of the apparent transverse relaxation rate, ${\mathit{R}}_2^{*}$ = 1/ $T_2^{*}$, were calculated using a Levenberg–Marquardt, least‐squares fitting routine for non‐linear equations. Specifically, the following mono‐exponential decay function:

$$S(\text{TE}\hspace{0.17em})=S_0\cdot \exp (-\text{TE}\hspace{0.17em}\cdot {\mathit{R}}_2^{*})$$ (1)

was fit to the magnitude data on a voxel‐by voxel basis. In Eq. (1), TE represents the echo time in ms and S ₀ the signal intensity at TE = 0. A magnitude image derived from the average of all six echoes was used for subfield labeling and group‐wise registration for atlas building.

This study has been approved by the office of research and ethics of Western University, and informed consent was obtained from all volunteers prior to their recruitment in the study.

MRI Phase Processing

From the gradient echo data, susceptibility‐weighted images (SWI), local frequency shift (LFS) and quantitative susceptibility (QS) maps were reconstructed using the following multi‐step procedure. Removal of channel dependent phase offsets and channel combination was performed simultaneously by calculating the Hermitian inner product between all later echoes and the first, then summing the complex data across channels. This is a customary approach for simultaneously removing the influence of channel specific and $B_1^{-}$‐induced phase errors and combining multi‐channel MRI data [Robinson et al., 2011]. The resulting raw phase images were then unwrapped in three‐dimensions using a region‐growing algorithm [Abdul‐Rahman et al., 2007]. The phase image for each echo was then divided by its corresponding echo time to produce a local frequency shift maps and a weighted average local frequency shift map was calculated using the phase noise variances as the weights. To remove slowly varying background field caused by tissue‐air interfaces, we have implemented and applied the projection onto dipole fields (PDF) [Liu et al., 2011], as well as the sophisticated harmonic artifact reduction on phase data (SHARP) filtering technique [Schweser et al., 2011] to the Fourier transform of the unwrapped phase data. We tried a variety of multiple kernel sizes to acquire the optimal results for our application, and we obtained the best results by applying a SHARP filter with a spherical convolution kernel of size 3 mm. For edge pixels, binary erosion using a spherical structuring element with the same size as the convolution kernel was performed prior to the SHARP deconvolution operation to eliminate artifacts at the edge of the brain volume. The SHARP filter size was chosen to minimize artifacts in the hippocampal region and may not be ideal for maximizing contrast in other areas of the brain such as the basal ganglia.

Susceptibility Weighted Image Calculation

Susceptibility weighted images (SWI), which are preferentially sensitive to subtle tissue boundaries arising from differences in the $T_2^{*}$ and frequency, were generated using a frequency mask (FM) derived from the MR phase information. Specifically, the unwrapped phase image was filtered using the Fourier‐domain, Gaussian high‐pass filter described in the previous section. The filtered phase images (one for each echo) were then combined into a single local frequency shift (LFS) map using a weighted linear regression [Kressler et al., 2010]. The resulting LFS map was used to calculate a frequency mask (FM) according to the following non‐linear, Hann window function:

$$\begin{array}{c}\\ \text{FM}\left(x\right) = \begin{array}{ccc}0& \text{if} x < -\mathrm{X}& \\ \frac{1}{2}[1+\cos \left(\frac{\pi x}{\mathrm{X}}\right)]& \text{if} -\mathrm{X}\le x \le 0& \\ 1& \text{if} x > 0& \end{array},\end{array}$$ (2)

where x denotes the frequency shift of a voxel in the LFS map and X is the cutoff frequency of the Hann window function. The cutoff frequency was set to 20 Hz for this work. To acquire a susceptibility weighted contrast, the magnitude image must be multiplied by the frequency mask, an effect that is accentuated by repeated this multiplication sever times. We multiplied the frequency mask into the magnitude image four times to generate the SWI maps.

Quantitative Susceptibility Maps

Quantitative susceptibility mapping measures the apparent magnetic susceptibility of the tissue using MR phase images, which unfortunately is an ill‐conditioned inverse problem (i.e., one that does not necessarily have a unique solution). Recent research suggests that the incorporation of spatial prior information, generated from the magnitude image data, can be used to identify a meaningful solution to this problem [de Rochefort et al., 2010]. In their work, computation of quantitative susceptibility from local Larmor frequency shift maps was performed using quadratic minimization of a regularized least‐squares objective function. The QS minimization problem can be written in a weighted least‐squares form with spatial priors as described by de Rochefort et al. [2010]:

$${\min }_X{\left|\right|W(CX-\delta )\left|\right|}_2^2+{\alpha }^2{\left|\right|W_{0}X\left|\right|}_2^2+{\beta }^2{\left|\right|W_{1}GX\left|\right|}_2^2,$$ (3)

where δ denotes the k‐space local frequency shift, C the Fourier domain dipole convolution kernel, and X the Fourier domain susceptibility distribution of interest. W, W ₀, and W ₁ are weighting matrices (spatial prior information) defined as: the magnitude image itself (W), a binary mask of the brain of the magnitude image (W ₀), and the gradient norm of the magnitude image (W ₁). The matrix $G$ denotes the gradient operator, while $\alpha$ and $\beta$ are the associated regularization constants. In our numerical implementation of QSM, a minimum quadratic form of Eq. (3) was solved using the conjugate gradient normal residual (CGNR) method [de Rochefort et al., 2010]:

$$C^{*}{W}^{*}W C X + {\alpha }^2 W_0{}^{*} W_0 X + {\beta }^2 G^{*} W_1{}^{*} W_1 G_{ }X = C^{*} W^{*} W \delta .$$ (4)

In principal, a compromise must be selected for the values of α ² and β ² to achieve low streaking artifact, while preserving accuracy of the maps [de Rochefort et al., 2010; Kressler et al., 2010]. We have chosen values of α ² and β ² equal to 1 × 10⁴, since they resulted in the smallest log residual at the transition point in the L‐curve (log–log plot of the norm of a regularized solution and the norm of the corresponding residual norm) and produced realistic values of susceptibility over a range of iterative steps in the CGNR algorithm. Larger values resulted in increased smoothing and reduced streaking artifact. The CGNR algorithm outlined above was implemented in Matlab (R2012b, The MathWorks, Natwick, MA).

To ensure reproducibility, values of quantitative magnetic susceptibility must be reported relative to a common reference structure. Previous studies have used either cerebrospinal fluid (CSF) [Li et al., 2011] or frontal white matter [Wharton et al., 2010] as a reference. In this study, we used a bilateral region of interest (ROI) in the frontal white matter, to avoid phase‐related artifacts due to flow and partial volume related effects relating to reference ROIs within the CSF. All QS values in this study are reported relative to the reference susceptibility of the bilateral frontal white matter ROI.

Subfield Labeling

A magnitude image derived from the average of all six echoes was used to perform the subfield labeling using the ITKsnap software [Yushkevich et al., 2006]. The hippocampus, including the hippocampus proper and subiculum, was outlined and subdivided into different fields of cornu ammonis (CA) and dentate gyrus (DG) based on an adaptation of the manual delineation protocol proposed by Mueller et al. [2007] as well as the Duvernoy et al. [2005] atlas. The Mueller et al. [2007] protocol at 4 T was extended, using the higher field advantage; by including anatomical definitions obtained from the protocol described by Wisse et al. [2012] at 7 T. We did not include the entorhinal cortex (ERC), alveus, and fimbria. The hippocampus was partitioned into anterior (head), posterior (tail), and mid‐region (body) segments, with no further subdivision of the head and tail since the additional folds (digitations of the head) from medial bending of the hippocampus in these regions caused differentiation between subfields to be unreliable. The partitioning of hippocampal head and tail followed definitions by Yushkevich et al. [2010] and the remaining slices between them were defined as the hippocampal body and subject to further subfield delineation.

For the body of the hippocampus, the following sub‐regions were segmented; subiculum (SUB), Ammon's horn (CA1, CA2 + CA3), and CA4+dentate gyrus (DG). The border between the SUB and ERC was formed following the uncal sulcus from its fundus to the medial surface [Wisse et al., 2012]. As the ERC can be found in the hippocampal fissure [Insausti et al., 1987], our SUB label may have sometimes incorporated part of the ERC. The border of the SUB with CA1 was defined as a vertical line at the edge of the SUB touching the most medial border of the DG + CA4 region, in imitation to the protocol by Mueller et al. [2007]. The CA1/CA2 boundary was designated as the point at which a noticeable decrease in width of the CA1 subfield was observed, following the most lateral point of the DG. No distinction was made between CA2 and CA3 since our images showed no visible boundary between them. Similarly, in line with the debate in histological literature as to whether CA4 belongs to the CA [Duvernoy et al., 2005] or the DG [Amaral et al., 2004] CA4 and DG were combined. The opening of subfields into the globular region of the hippocampal formation formed the CA2 + CA3/DG + CA4 border, which was specifically identified by the continuation of a clear consistent hypointense line representing the stratum lacunosum‐moleculare of CA and dendrites of the molecular layer of DG, as described by Wisse et al. [2012]. The remaining globular region of the hippocampal formation was marked as CA4 + DG.

A single rater applied the described manual segmentation protocol to the set of seventeen subjects. To assess the accuracy and reproducibility of our segmentation protocol, images from five volunteers were segmented a second time by an additional operator, and the resulting labels compared to the first segmentation using the dice similarity coefficient (DSC), defined as: $DSC=\frac{2({\mathit{R}}_A\cap {\mathit{R}}_B)}{{\mathit{R}}_A+{\mathit{R}}_B}$ as well as the absolute percentage volume error $(\left|\delta V_p\right|)$, defined as: $|\delta V_p|=\frac{|(V_A-V_B)|}{V_B}\times 100\%$. The intraclass correlation coefficient (ICC) was also computed for inter‐rater reliability analysis with values near unity indicating consistent volume measurements. Reported subfield volumes were normalized by the intracranial volume (ICV) as estimated by the Freesurfer software [Buckner, 2004], using the formula: normalized volume = (raw volume/ICV) × 1,000 mm³.

Average Atlas Construction

To construct an atlas of the hippocampal subfields, we used an iterative group‐wise diffeomorphic registration as implemented in the ANTS software [Avants and Gee, 2004]. The atlas was created using the iterative procedure of (1) registering each image to an estimate of the average, then (2) updating the average estimate using the warped images. All images were first corrected for bias field inhomogeneities using the non‐uniform intensity normalization (N3) algorithm [Sled et al., 1998] and each registration step involved affine registration followed by diffeomorphic registration. The affine initialization used a histogram matched mutual information similarity metric to align all images to one subject of the dataset, which was chosen arbitrary. The diffeomorphic registration was performed using a cross correlation similarity metric with a window radius of 5 voxels and used a greedy symmetric transformation (greedy SyN) with Gaussian regularization (sigma = 3). Each optimization was performed over three resolutions with a maximum of 30 iterations at the coarsest level (one quarter of the full resolution), 90 at the next coarsest (one half of the full resolution), and 20 at the full resolution. The average atlas construction, alternating between the registration phase and average update phase, was performed in four iterations, with a shape update performed at each iteration to maintain stability of the average. This shape update consisted of warping the atlas a small step size (epsilon = 0.25) towards the mean of the inverse warps. After the template construction, the ${\mathit{R}}_2^{*}$, SWI and QS maps were warped to the atlas space, upsampled to 0.5 mm isotropic resolution and averaged. The segmented labels of each subject were warped in the same manner and fused using a majority vote (for each voxel the label that appeared the most across subjects was chosen).

To validate accuracy of the group‐wise registration, we evaluated the alignment of the whole hippocampus for all subjects in the average atlas space by computing the pair‐wise Dice similarity metric between the warped hippocampus labels for every pair of subjects in atlas space.

${\mathit{R}}_2^{*}$ V alidation

To validate our ${\mathit{R}}_2^{*}$ values, we performed an ex vivo scan on a resected hippocampal specimen after a surgical operation: anterior temporal lobectomy. The specimen was part of an ongoing temporal lobe epilepsy study at our centre, and the hippocampus was confirmed as sclerotic by both clinical imaging and histology. The scanning was performed on a ultra‐high‐field 9.4 T MRI scanner (Varian, Palo Alto, CA, USA) using a millipede birdcage coil (Agilent, Santa Clara, CA ,USA) with a multi‐echo gradient‐echo sequence. The specimen was imaged at a resolution of 0.1 mm isotropic. The resulting ${\mathit{R}}_2^{*}$ values were compared with the ${\mathit{R}}_2^{*}$ values from the patient's 7 T pre‐operative scan within the subfields. The subfields were delineated on a representative coronal slice of the ex vivo scan, shown in Figure 3. This figure summarizes the pre‐op, ex vivo comparison. To further evaluate our ${\mathit{R}}_2^{*}$ maps we compared values of the basal ganglia structures with those reported in Deistung et al. [2013] at 7 T. Manual ROI labels for the thalamus, putamen, caudate nucleus, and globus pallidus were delineated on a representative coronal slice of our atlas.

Figure 3.

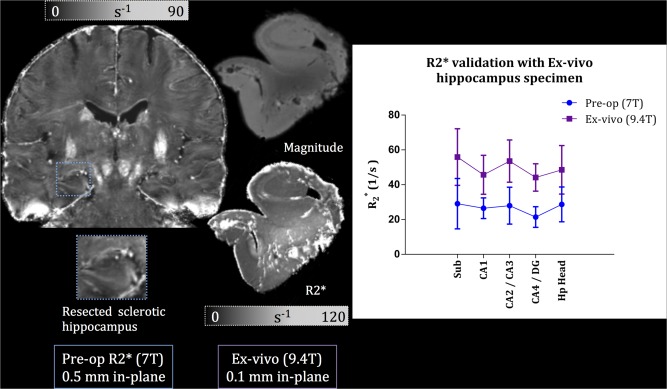
Validation of pre‐operative ${\mathit{R}}_2^{*}$ with 9.4 T ex vivo imaging of a resected hippocampus. Left: coronal slice of the pre‐op ${\mathit{R}}_2^{*}$ at 7 T with a zoomed‐in view of the sclerotic hippocampus before epilepsy surgery excision. Middle: magnitude image of the patient's resected hippocampus imaged at 9.4 T resulting in a 0.1 mm isotropic resolution (top); ${\mathit{R}}_2^{*}$ image of the hippocampus, where the subfield delineation was performed (bottom). Right: graph of comparison between pre‐op (blue) and ex vivo (purple) ${\mathit{R}}_2^{*}$ values within the subfields. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Quantitative Susceptibility Validation

Since QS values of the hippocampal subfields have not been previously reported at 7 T, to evaluate our quantitative maps, we compared values of the basal ganglia structures with those reported in Deistung et al. [2013] and Wharton and Bowtell [2010] at 7 T. Five normal controls were scanned according to the previously described imaging protocol, with the in‐plane orientation being axial instead of coronal. The phase images were filtered using SHARP with a 7 mm kernel size, otherwise the processing and susceptibility quantification was identical to our previous cohort. Manual ROI labels for the thalamus, putamen, caudate nucleus, and globus pallidus were delineated on a representative axial slice of each subject. Manual segmentation was preferred to atlas‐based segmentation, to avoid miss registration and partial voluming effects. The validation experiment is summarized in Figure 4.

Figure 4.

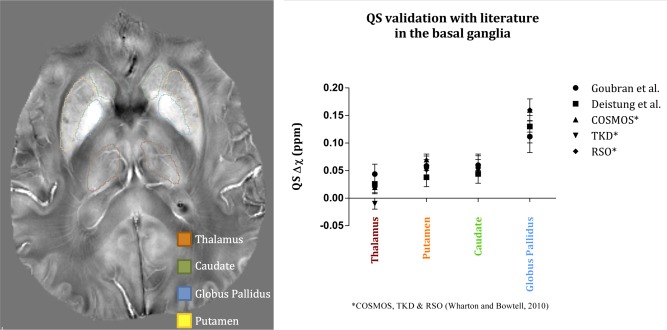
Validation of our QS values in the basal ganglia with Deistung et al. [2013] and Wharton and Bowtell [2010]. Left: axial slice of a QS map from a single subject showing the outlines of the basal ganglia structures. Right: graph demonstrating QS values within the basal ganglia for three papers. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Statistical Comparison

To investigate the differences between magnitude, ${\mathit{R}}_2^{*}$ and QS maps, we performed a one‐way analysis of variance (ANOVA) using the mean value over each subfield label in each subject's native‐space scan. These tests were corrected using Tukey's multiple comparisons method and the alpha (P) value was set to 0.05. The magnitude images were intensity normalized with 100 being the mean intensity. The statistical analysis was performed using Prism (GraphPad, La Jolla) statistical software. Table 3 summarizes the significant results found between subfields for the three different imaging techniques.

Table 3.

One‐way analysis of variance (ANOVA) between all subfields for ${\mathit{R}}_2^{*}$ and QS maps

Imaging	Subfields	Mean diff.	95% CI of diff.	Level of significance
${\mathit{R}}_2^{*}$	CA4‐DG versus CA1	5.152	3.043–7.260	P ≤ 0.0001
	CA4‐DG versus Hp tail	2.376	0.2673–4.485	P ≤ 0.05
	CA4‐DG versus Hp head	2.556	0.4472–4.665	P ≤ 0.01
	Sub versus CA1	6.806	4.697–8.914	P ≤ 0.0001
	Sub versus Hp tail	4.03	1.921–6.139	P ≤ 0.0001
	Sub versus Hp head	4.21	2.101–6.319	P ≤ 0.0001
	CA1 versus CA2‐CA3	−4.774	−6.882 to −2.665	P ≤ 0.0001
	CA1 versus Hp tail	−2.776	−4.884 to −0.6671	P ≤ 0.01
	CA1 versus Hp head	−2.596	−4.705 to −0.4872	P ≤ 0.01
	CA2‐CA3 versus Hp head	2.178	0.06928–4.287	P ≤ 0.05
QS map	CA4‐DG versus CA2‐CA3	0.01383	0.004786–0.02288	P ≤ 0.001
	CA4‐DG versus Hp tail	−0.01031	−0.01936 to −0.001263	P ≤ 0.05
	Sub versus CA2‐CA3	0.01601	0.006958–0.02505	P ≤ 0.0001
	CA1 versus CA2‐CA3	0.01887	0.009818–0.02791	P ≤ 0.0001
	CA2‐CA3 versus Hp tail	−0.02414	−0.03319 to −0.01510	P ≤ 0.0001
	CA2‐CA3 versus Hp head	−0.02118	−0.03022 to −0.01213	P ≤ 0.0001

RESULTS

Figure 1 displays representative coronal slices of our atlas‐based maps for (i) the average magnitude image across all echoes (top left), (ii) ${\mathit{R}}_2^{*}$ (top right), (iii) SWI (bottom left), and (iv) QS (bottom right). As well, the average magnitude image for all echoes for a single subject is displayed in the center of Figure 1 to illustrate the difference between the atlas‐based images and the single subject case. Magnified representations of the left hippocampus are shown for visual comparison and assessment of the contrast and sharpness of the average maps. Since inter‐subject anatomical variability was accounted for using a deformable registration, it was possible to generate these group‐averaged atlases (average of all 17 subjects) which serve to effectively increase the signal to noise ratio and contrast to noise ratio in the hippocampal subfields. The sharp anatomical definition in these images is evidence of the accuracy of the group‐wise registration within the hippocampus and in the subcortical regions. The cortical regions do not possess the same level of alignment because of the higher variability in cortical folding patterns, which is expected and difficult to account for with image‐based registration.

Figure 1.

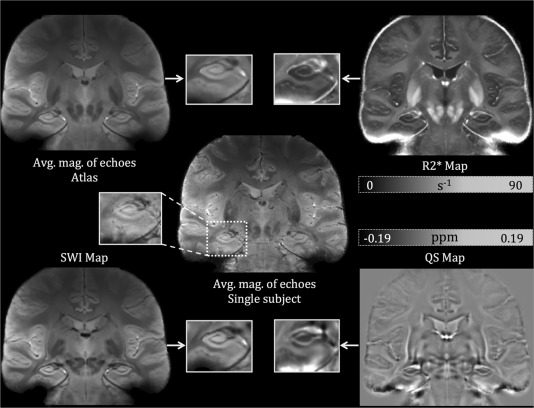
Single subject (middle) as well as atlas‐based images of average magnitude across echoes (top left), ${\mathit{R}}_2^{*}$ (top right), qualitative SWI (bottom left), and QS maps (bottom right). The adjacent image to each map shows a zoomed‐in representation of a hippocampal slice in the coronal view. The same slice is chosen for all maps to compare CNR and SNR across the different maps.

The inter‐rater reliability results measured by the Dice similarity metric and volume difference (in mm³) between the labels are summarized in Table 1. The Dice metric demonstrates good agreement between both raters across the subfields, with the Dice coefficient for the total hippocampus being 0.844 for the right side and 0.839 for the left side. The highest Dice coefficient between all subfields was 0.847 for the right side and 0.801 for the left, both representing the CA4 + DG label, while the lowest was for the CA2 + CA3 label, being 0.682 and 0.638 for the right and left sides, respectively. Similarly, the volume difference measures outlined in Table 1 showed good agreement, on average, which validates the repeatability of our protocol. The volume of the CA1 label had showed the most agreement between the raters with a volume percentage difference of 6%. In addition, Table 1 also displays the intraclass correlation (ICC) analysis for inter and intra‐rater reliability. High consistency was observed between our raters for most of the subfields (ICC > 0.75) as well as for the repeated datasets our first rater which demonstrates the reliability of our protocol. Segmentation of the CA2 + CA3 label was the least reliable with an ICC between raters of 0.624. The volumes of the subfields resulting from our manual delineation protocol were reported in Table 2.

Table 1.

Dice similarity coefficient, absolute percentage volume error, and intra‐class correlation coefficient metrics in conducted patient space

	Sub	CA1	CA2+CA3	CA4+DG	Hp tail	Hp head	Total
DSC
L	0.605	0.714	0.638	0.801	0.692	0.768	0.839
R	0.734	0.796	0.682	0.847	0.706	0.814	0.844
$\left|\delta V_p\right|$	9.6	6.0	11.3	11.2	15.4	6.7	6.5
ICC Rater 1	0.949	0.973	0.781	0.966	0.813	0.984	—
ICC (between raters)	0.833	0.834	0.624	0.881	0.727	0.906	—

Table 2.

Hippocampal subfield volumes normalized by intracranial volume (ICV), reported in mm³

	Sub	CA1	CA2 + CA3	CA4 + DG	Hp tail	Hp head	Total Hp
Left	222.5	249.2	71.9	214.2	428.9	1263.8	2450.3
Right	233.0	248.4	73.4	216.5	469.8	1312.1	2553.2
Mean (sd)	227.8 (61.2)	248.8 (54.2)	72.7 (7.9)	215.3 (47.2)	449.3 (146.3)	1287.9 (196.3)	2501.8 (251.2)

Figure 2 displays coronal views of selected slices running through hippocampal body for the three major image contrasts used in this study: the magnitude image averaged across echoes, ${\mathit{R}}_2^{*}$ and quantitative susceptibility maps. Two sets of three consecutive slices (Fig. 2a,b) are shown. The segmentation labels for the subfields are overlaid on the images. The segmentation protocol was performed using the magnitude images only. For the slices corresponding to Figure 2a (the left side of the figure), both ${\mathit{R}}_2^{*}$ and QS showed improved delineation of the subiculum/CA1 and CA1/(CA2 + CA3) boundaries compared to the magnitude image. Furthermore, the QS map defined the (CA2 + CA3) subfield more clearly compared both the ${\mathit{R}}_2^{*}$ and magnitude images based on the reduced susceptibility in this region of the hippocampus. Accuracy of the group‐wise registration and the resulting average atlas was evaluated both qualitatively and quantitatively. The mean Dice metric between the hippocampus labels in the atlas space was 0.69 ± 0.03 and ranged from 0.69 to 0.77.

Figure 2.

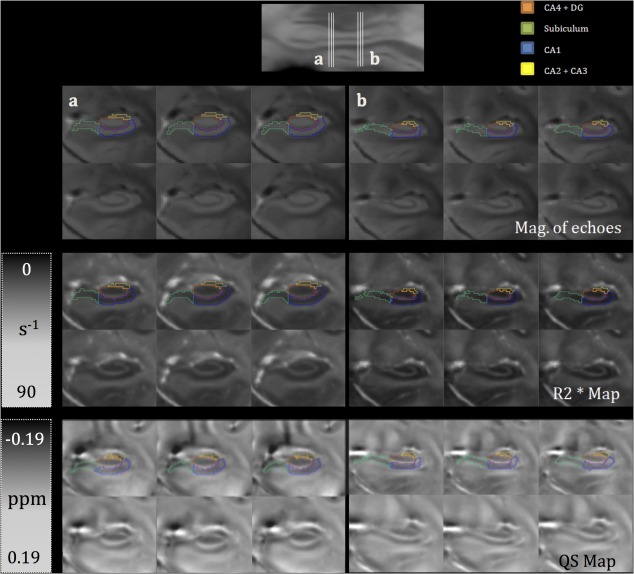
Two sets of three consecutive coronal slices as seen in atlas space in the magnitude across echoes, ${\mathit{R}}_2^{*}$ and QS maps, with the top row of each block showing segmentation labels overlaid on the images. The location of the slices is indicated on a sagittal view of the hippocampus at the top of the figure. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 4 summarizes the quantitative, intrinsic MRI measures of the hippocampal subfields, specifically ${\mathit{R}}_2^{*}$ and quantitative susceptibility (QS). The values in Table 4 represent mean values averaged across all subjects. QS values demonstrated relatively high standard deviations within each subfield, which did not correlate with the size of the subfield. As for our ${\mathit{R}}_2^{*}$ ex vivo validation using a resected hippocampus from epilepsy surgery, Figure 3 shows a very good agreement within the subfields between the pre‐operative 7 T scan and the 9.4 T image. In addition, the ${\mathit{R}}_2^{*}$ values for basal ganglia structures in our study are as follows (in units of s⁻¹): thalamus (38.8), putamen (49.5), caudate nucleus (43.1), and globus pallidus (72.7). Comparatively, Deistung et al. [2013] reported the following values: thalamus (41.4), putamen (49.4), caudate nucleus (42.3), and globus pallidus (83.4). Similarly, the QS validation on five normal volunteers scanned axially showed that our values (in parts‐per‐million of the main magnetic field, ppm) for these structures (0.0395, 0.0586, 0.0599, and 0.117) are within range of those reported in Deistung's study (0.0261, 0.0380, 0.0440, and 0.131) and those reported in Wharton and Bowtell [2010] at 7 T (0.020, 0.060, 0.060, and 0.160). These values are graphed in Figure 4 to demonstrate the agreement between our values and those reported in the literature. The ANOVA analysis showed that ${\mathit{R}}_2^{*}$ resulted in the highest number of significant comparisons between the subfields, followed by QS; and that normalized magnitude images showed no significance for all subfield comparisons. Table 3 summarizes all the significant comparisons for ${\mathit{R}}_2^{*}$ and QS.

Table 4.

Subfield volumes, ${\mathit{R}}_2^{*}$, and QS values as a mean across all subject in subject space

		Sub	CA1	CA2 + CA3	CA4 + DG	Hp tail	Hp head
Volume of region (mm3)	µ (σ)	227.8 (61.2)	248.8 (54.2)	72.7 (7.9)	215.3 (47.2)	449.3 (146.3)	1287.9 (196.3)
${\mathit{R}}_2^{*}$ (1/s)	µ (σ)	32.2 (2.3)	25.5 (2.0)	30.0 (4.2)	30.4 (3.3)	28.2 (1.9)	28.1 (2.1)
QS Δχ (ppm)	µ (σ)	−0.0216 (0.013)	−0.0187 (0.008)	−0.0376 (0.016)	−0.0237 (0.009)	−0.0134 (0.005)	−0.0164 (0.011)

DISCUSSION

Quantitative ${\mathit{R}}_2^{*}$ maps have shown great potential as a diagnostic tool for numerous diseases affecting the hippocampus both because of the improved contrast, and through the use of voxel‐based studies. Similarly, the quantitative atlas‐based QS map demonstrates a unique contrast driven by the underlying magnetic susceptibility of the tissue and vasculature, which cannot be obtained using standard GRE/ $T_2^{*}$ weighted images. In vivo susceptibility mapping can also resolve substructures of deep gray matter (GM) nuclei consistent with histological sections of post mortem brains [Deistung et al., 2013]. The low variability of the ${\mathit{R}}_2^{*}$ values within small structures as the subfields (8.5% of the mean on average across all reported subfields) demonstrates the sensitivity of this quantitative measure to local magnetic changes. The reported QS values show higher variability within each small hippocampal substructure, which could be due to phase variations from the sinus interface or reconstruction artifacts.

The ANOVA analysis suggests that there are more apparent differences between the subfields on the maps than the magnitude images. These differences between subfields can be caused by many factors, one of which may be different iron distribution within the CA1–CA3 region as compared to the CA4‐DG region. Antharam et al. [2012] mapped iron distribution, R ₂ and ${\mathit{R}}_2^{*}$ for the subfields in three unfixed post‐mortem control cases and five Alzheimer's disease (AD) specimens. They have validated the relationship between R ₂, ${\mathit{R}}_2^{*}$, and tissue iron content of the hippocampal subfields and reported higher mean R ₂ and ${\mathit{R}}_2^{*}$ in the CA4‐DG region as compared to the CA1–CA3 region in both groups; which is consistent with our R ₂ values, if CA1 through CA3 are combined. Their evidence demonstrates that regions of increasing ${\mathit{R}}_2^{*}$ correspond to regions of higher iron content, which is consistent with literature [Yao et al., 2009] and the hypothesis that iron concentration affects ${\mathit{R}}_2^{*}$ contrast. This work is the first in vivo quantification susceptibility values within the hippocampal subfields at 7 T.

It is evident at this detailed level of segmentation that the contrast cannot be attributed solely to varying iron concentrations. Other parameters affecting water diffusion and susceptibility, including the variation in compartmentalization due to cell dimensions and density of packing, and differences in hydration between gray and white matter, are also presumed relevant [Antharam et al., 2012]. The changes in QS may also be due to the subependymal intrahippocampal veins and the sulcual intrahippocampal veins, which are manifested as susceptibility changes within the CA1 and the CA2/3 transition, respectively.

Yushkevich et al. [2009] developed a normalized atlas of the subfields using five post‐mortem specimens at 9.4 T. In this publication we focused on the quantification of ${\mathit{R}}_2^{*}$ and QS values in the subfields. This quantification requires in vivo scanning since fixation affects metal ions [Gellein et al., 2008], protein cross‐linking [Dawe et al., 2009], and water diffusion properties [Thelwall et al., 2006]. Shepherd et al. [2009] have shown, as well, that fixation in 4% formaldehyde results in a reduction of up to 80% in estimated T₂ values. Hence, we were constrained by the requirement of imaging in vivo unfixed tissue, with which achieving a sufficient SNR for subfield segmentation is more challenging than postmortem imaging. Figure 3 demonstrates an example ex vivo scan at 9.4 T of a resected hippocampal specimen after anterior temporal lobectomy. This specimen represents the potential of ex vivo imaging of excised hippocampal specimens. Previous reports have identified concerns with $T_2^{*}$ imaging of the hippocampus. In our imaging protocol we do see loss of signal at the gyrus rectus within the medial frontal lobe due to susceptibility artifact from the sinuses; however this is only anterior to the optic chiasm and does not affect the amygdala or anterior region of the hippocampus, as shown by the sagittal slice in Figure 2. Similarly, we experienced some signal loss within the inferior region of the fusiform gyrus but this is only contained in the neocortex and does not extend past the collateral sulcus.

Cho et al. [2010b] reported ${\mathit{R}}_2^{*}$ values within the subfields at 7 T, as follows: Sub = 34.3, CA1 = 42.59, CA2 + CA3 = 39.2 (combining both subfields), CA4 = 43.66. Our values for these subfields were 32.2, 25.5, 30.0, and 30.4, respectively. Both the values reported by Cho et al. [2010b] and our values follow the trend of increased ${\mathit{R}}_2^{*}$ in the CA4‐DG label as compared to the combined CA1–CA3 label, demonstrated by Antharam et al. [2012] on unfixed ex vivo specimens at 14 T.

However, their method suffers from some limitations such as the use of only one ROI composed of 21 pixels, taken on a single coronal slice, to represent a subfield. That is pixels within the ROI may not represent the entire subfield due to the limited sampling. Another limitation may be the use of a dual echo, instead of a multi‐echo, sequence in their imaging protocol which is less effective to compute ${\mathit{R}}_2^{*}$ values. It should also be noted, that Cho et al. [2010b] obtained a consistently higher standard deviation per subfield than our study. We have demonstrated, as well, the reliability of our ${\mathit{R}}_2^{*}$ values in the basal ganglia comparison with Deistung et al. [2013] and our ex vivo 9.4 T validation.

The results of our reliability analysis are presented in Table 1 and they validate repeatability of our manual segmentation protocol. One potential source of error leading to inter‐rater differences is the learning curve in segmentation as Rater 2 only segmented five subjects of the dataset. As expected, the Dice coefficient was lower for the smaller subfields due to the bias of the measure towards bigger structures. It is, however, difficult to objectively assess the volumes of subfields across protocols, due to the underlying differences in the protocols, the different imaging parameters and the combination of certain subfields into a singular label depending on the protocol. For instance, Mueller et al. [2009] combined CA3 with DG in a single label while Malykhin et al. [2010] combined CA1, CA2, and CA3 in a single label. Similarly, some protocols restrict subfield delineation to the body of the hippocampus [Mueller et al., 2007, 2009] and others [Malykhin et al., 2010; Wisse et al., 2012] claim that approach insufficient for detection of disease progression and instead segment the subfields along the whole length of the hippocampus. Several boundaries such as that between the CA4/DG are not agreed upon and might require definitions based on histological detail to be resolved. Since an in‐plane resolution of 0.5 mm is insufficient to resolve small detail between the subfields, we therefore decided to combine the CA4/DG label, and applied the same rational to the CA2/CA3 boundary. Of those protocols used as comparators in this article, only two of them attempted to resolve CA2 as a distinct subfield [Mueller et al., 2009; Wisse et al., 2012], by defining the border between CA2 and CA3 as the medial side of a virtual square or define a CA1‐CA2 “transition zone” to account of the overlap of the dorsomedial part of CA1 into CA2 label.

Our average Dice values between the hippocampus labels in the atlas space, with a mean of 0.69 ± 0.03, are comparable to the best performing methods reported in a recent evaluation of nonlinear brain registration [Klein et al., 2009], which reported Dice overlaps with the SyN registration algorithm on two different datasets, CUMC (Columbia University Medical Centre) and LPBA (LONI Probabilistic Brain Atlas), made up of 12 and 40 subjects, respectively. The hippocampal Dice overlaps were 0.68 and 0.75 for the CUMC12 and LPBA40 datasets, respectively.

Several techniques have been presented for solving the field‐to‐source inverse problem for quantitative susceptibility mapping, most notably the calculation of susceptibility through multiple orientation sampling (COSMOS), truncated k‐space division (TKD), and morphology enabled dipole inversion (MEDI). Although maps obtained using COSMOS demonstrate high agreement with post‐mortem measurements of brain iron, the method relies on multiple acquisitions with different head orientations which limits the technique for use in a clinical setting. The available single head orientation algorithms suffer to varying degrees from non‐local artifacts, instability or underestimation of susceptibility values [Deistung et al., 2013]. We used the Bayesian regularized solution developed by de Rochefort et al. [2010], which makes use of spatial priors from the magnitude images, and provided accurate delineation of both anatomical structure and volume magnetic susceptibility in the brain. Phase shifts induced by eddy currents, $B_1^{+}$ non‐uniformity, or flow can introduce errors in the QS maps. However, these errors were minimized in our QS pipeline since the first echo was subtracted from all subsequent echoes using the Hermitian product method. Such subtraction removes the influence of temporally invariant background phase offsets caused by external field inhomogeneities. Flow‐related errors in QS, however, are not temporally invariant. When blood flow through veins is present, the accrual of phase as a function of echo time may become non‐linear [Yamada et al., 1997]. Under this condition, performing a linear fit of the phase to the echo time will not yield accurate estimates of the frequency shift. However, close inspection of our LFS and QS maps registered to the template space does not reveal significant presence of large vessels in the hippocampal subfields. For this reason, we believe the effects of venous flow artifacts in our data are minimal.

One application of the atlas‐based approach presented here would be the study of quantitative intrinsic MR measures in the subfields in neurological diseases. The significant differences found in the ANOVA analysis of ${\mathit{R}}_2^{*}$ and QS across adjacent subfields (Table 3) reveals that these quantitative maps may be superior in sensitivity to detect abnormalities in specific subfields than magnitude images. The subfield labels, presented in Table 2, could also be used for volumetric or morphometric analysis. Evaluation of neurological disorders which affect the hippocampal subfields, such as temporal lobe epilepsy or Alzheimer's disease, would benefit greatly from the use of these techniques. Another application could be in targeting for deep brain stimulation (DBS), since quantitative $T_2^{*}$ [Elolf et al., 2007] and susceptibility contrast [Schäfer et al., 2012] allow for improved visualization of commonly targeted deep GM structures. For these stereotactic neurosurgical applications, subject‐atlas registration could be used to improve accuracy of electrode placement in deep GM nuclei to alleviate motoric disorders due to tremor as Parkinson's disease or dystonia.

CONCLUSION

We have constructed a normative atlas of the hippocampal subfields from in vivo susceptibility‐weighted images of 17 healthy volunteers acquired using 7 T MRI. Using our reliable manual delineation protocol of the subfields, we demonstrated the feasibility of subfield specific analyses of the hippocampus. The average atlas accurately aligns the subtle anatomical features of the hippocampus, producing high‐resolution maps of quantitative susceptibility and ${\mathit{R}}_2^{*}$. This work represents the first in vivo quantification of susceptibility values within the hippocampal subfields at ultra‐high‐field strengths. It can be further complemented by investigation of these quantitative MRI parameters in patient populations where hippocampal subfields are known to be selectively affected, such as temporal lobe epilepsy or Alzheimer's disease.