Skip to main content
PMC home page
Human Brain Mapping logoLink to Human Brain Mapping
. 2015 Jun 9;36(8):3064–3075. doi: 10.1002/hbm.22828

Comparison of diffusion tractography and tract‐tracing measures of connectivity strength in rhesus macaque connectome

Martijn P van den Heuvel 1,2,✉, Marcel A de Reus 1,2, Lisa Feldman Barrett 3,4, Lianne H Scholtens 1,2, Fraukje MT Coopmans 1,2, Ruben Schmidt 2,5, Todd M Preuss 6,7, James K Rilling 7,8,9,10, Longchuan Li 11,12
PMCID: PMC6869766  PMID: 26058702

Abstract

With the mapping of macroscale connectomes by means of in vivo diffusion‐weighted MR Imaging (DWI) rapidly gaining in popularity, one of the necessary steps is the examination of metrics of connectivity strength derived from these reconstructions. In the field of human macroconnectomics the number of reconstructed fiber streamlines (NOS) is more and more used as a metric of cortico‐cortical interareal connectivity strength, but the link between DWI NOS and in vivo animal tract‐tracing measurements of anatomical connectivity strength remains poorly understood. In this technical report, we communicate on a comparison between DWI derived metrics and tract‐tracing metrics of projection strength. Tract‐tracing information on projection strength of interareal pathways was extracted from two commonly used macaque connectome datasets, including (1) the CoCoMac database of collated tract‐tracing experiments of the macaque brain and (2) the high‐resolution tract‐tracing dataset of Markov and Kennedy and coworkers. NOS and density of reconstructed fiber pathways derived from DWI data acquired across 10 rhesus macaques was found to positively correlate to tract‐tracing based measurements of connectivity strength across both the CoCoMac and Markov dataset (both P < 0.001), suggesting DWI NOS to form a valid method of assessment of the projection strength of white matter pathways. Our findings provide confidence of in vivo DWI connectome reconstructions to represent fairly realistic estimates of the wiring strength of white matter projections. Our cross‐modal comparison supports the notion of in vivo DWI to be a valid methodology for robust description and interpretation of brain wiring. Hum Brain Mapp 36:3064–3075, 2015. © 2015 Wiley Periodicals, Inc.

Keywords: connectome, macaque, diffusion imaging, tract tracing, connectivity, white matter, connectomics

INTRODUCTION

Ever increasingly detailed reconstructions of macroscale connections have revealed the mammalian brain to include a complex network of structurally and functionally interacting regions (e.g., [Hagmann et al., 2008; Kotter et al., 2007; Markov et al., 2013a; Markov et al., 2012; Oh et al., 2014; Scannell et al., 1995; Stephan et al., 2001]). In non‐human mammalian species, tract‐tracing experiments have revealed an elaborate wiring pattern of the brain, argued to be organized according to a putative cost‐effective, hierarchical and small‐world modular topology (e.g. [Bullmore and Sporns, 2009, 2012; Shen et al., 2012; Sporns, 2011]). Earlier as well as contemporary studies using invasive tract‐tracing as a method for pathway reconstruction have led to highly detailed wiring diagrams of the rhesus macaque [Markov et al., 2012; Stephan et al., 2001], cat [Scannell et al., 1995], mouse [Oh et al., 2014], and rat brain [Bota and Swanson, 2007], establishing tract‐tracing as a powerful method for assessing white matter connectivity. Furthermore, advances in MR diffusion imaging have made it increasingly feasible to map the connections of the human brain in vivo, resulting in detailed maps of the white matter pathways constituting the “human macroscale connectome” [Hagmann et al., 2008; Sporns et al., 2005]. The possibility of mapping white matter axonal pathways in the human brain in vivo using MR imaging has fueled the investigation of brain connectivity and network organization in many cognitive, translational, and clinical neuroscience studies [Bassett et al., 2009; Bullmore and Sporns, 2012; Filippi et al., 2013; Fornito et al., 2012; Honey et al., 2009; van den Heuvel and Fornito, 2014; van den Heuvel et al., 2009]).

Besides measuring the qualitative presence of an anatomical pathway, both tract‐tracing and MR tractography allow for an assessment of the connectivity “quality” or “strength” of the reconstructed pathways. Tract‐tracing techniques allow for a mapping of connectivity by means of measurement of the density of labeling [Shen et al., 2012]; an often used metric of connectivity strength derived from diffusion MR techniques is the number of reconstructed tractography streamlines [Hagmann et al., 2008; van den Heuvel et al., 2012]. In particular, the latter metric appears to be of growing interest to the MRI community in the examination of connectome changes in psychiatric and neurological disorders (e.g. [Bullmore and Sporns, 2012; Filippi et al., 2013; Fornito et al., 2012; van den Heuvel and Fornito, 2014]). However, how this introduced metric of weight relates to properties of bundles of axonal projections and thus how DWI derived number of streamlines should be interpreted in the context of connectivity strength at the axonal level, remains poorly understood (e.g., [Hagmann et al., 2008; Jones, 2010; Sporns, 2012; van den Heuvel et al., 2012]). Important work has been performed to validate the binary layout and anatomical accuracy of diffusion MR reconstructions of tracts in both the human and primate brain by means of post‐mortem examinations (e.g., [Catani et al., 2013; Li et al., 2012]) and by means of comparisons to tract‐tracing results (e.g., [Azadbakht et al., in press; Dauguet et al., 2006; Dyrby et al., 2007; Schmahmann et al., 2007; Thomas et al., 2014]), but examinations of MR‐derived metrics of connectivity strength in context of tract‐tracing findings are sparse. In this study, we thus particularly focused on the examination of DWI derived NOS as a metric of connectivity strength in comparison to tract‐tracing derived metrics of projection strength.

Here, we report on a macroscale connectome‐perspective examination of diffusion MR metrics and tract‐tracing based metrics of projection strength in the rhesus macaque brain. Tract‐tracing information on the connection strength of cortico‐cortical anatomical pathways was extracted from (1) the CoCoMac database of collated tract‐tracing experiments reporting on connectivity strength of cortico‐cortical pathways from weak to strong [Stephan et al., 2001] and (2) the high‐quality dataset of Markov and Kennedy and coworkers documenting quantitative measurements of projection strength of a large number of interareal axonal pathways of the macaque cerebral cortex [Markov et al., 2012]. Combining these datasets with DWI data acquired in vivo in 10 rhesus macaques, we show evidence of DWI NOS to positively correlate to tract‐tracing derived measurements of connectivity strength.

MATERIALS AND METHODS

In what follows, we first describe the acquisition, reconstruction, and derivation of connectivity strength of pathways of the macaque cerebral connectome based on in vivo DWI data as acquired in 10 adult rhesus macaque monkeys. This is followed by a description of the reconstruction and derivation of connectivity and connectivity strength of interareal pathways between the same set of cortical regions of the macaque connectome as extracted from the CoCoMac database of collated tract‐tracing experiments [Stephan et al., 2001] and from the high‐quality dataset of Markov and Kennedy and coworkers reporting on quantitative measurements of connectivity strength of interareal pathways in the macaque brain [Markov et al. 2012].

MRI Acquisition

Anatomical diffusion‐weighted imaging (DWI) was acquired in 10 adult macaque specimens. The demographics (10 female, Macaque mulatta, age 14 ± 6.7 years) and acquisition procedure of the animal DWI data are described in detail as part of a previous study on connectome reconstruction and analysis of the macaque cortical brain network [Li et al., 2013]. Briefly, data acquisition included the acquisition of high‐resolution T1 images and of diffusion‐weighted images. Scanning parameters included, T1w: TR/TI/TE = 2600/900/3.37 ms, resolution = 0.5 × 0.5 × 0.5 mm3, FOV = 160 × 160 × 88, matrix = 320 × 320 × 176, GRAPPA = 2, 3 averages, total scan time of 25 min; DWI: TR/TE = 7000/108 ms, resolution = 1.1 × 1.1 × 1.1 mm3, FOV = 141 × 132, matrix = 128 × 120, 43 slices, GRAPPA = 3, 60 diffusion directions (acquired with b = 1000 s/mm2), 10 averages with half of the averages having opposite phase encoding directions [Andersson et al., 2003], in total including 600 diffusion directions with a scan time of 86 min.

Data preprocessing

As described in [Li et al., 2013], the T1 image was used to perform automated gray matter, white matter, and CSF segmentation. For each individual dataset, the T1 reconstructed cortical mantle was initially segmented into 300 equal‐sized, randomly distributed parcels (150 parcels per hemisphere), creating an initial parcellation of the cortex into small brain regions to serve as cortical areas in the reconstructions of cortical‐to‐cortical pathways (see below) [de Reus et al., 2014; Hagmann et al., 2008; Li et al., 2013; van den Heuvel and Sporns, 2011]. The intermediate 300 parcel resolution segmentation was used to enable accurate surface‐based parcellation segmentations incorporating information on individual cortical folding patterns of the macaque cortex while still ensuring good anatomical overlap of cortical regions between the 10 specimens [Li et al., 2013]. DWI data preprocessing included correction for susceptibility, eddy current distortions, and motion [Andersson et al., 2003] and realignment of the b = 0 image to the anatomical T1 image for anatomical reference. Next, following a common procedure for human and non‐human primate in vivo DWI connectome studies, the diffusion profile within each voxel was assessed using generalized q‐sampling imaging (GQI, regularization parameter sigma 1.25) [Yeh et al., 2010], allowing for the reconstruction of multi‐orientation fiber configurations (e.g., crossing fibers) [de Reus et al., 2014; Yeh et al., 2010]. White matter pathways were reconstructed by means of deterministic fiber tracking allowing for complex fiber orientations [de Reus et al., 2014], starting eight streamline seeds in all voxels classified as white matter. Pathways were reconstructed by following the best fitting diffusion direction from voxel to voxel, with fiber reconstruction continuing until a streamline either (1) reached a voxel of low generalized FA (equivalent to FA < 0.1), (2) exited the brain mask (i.e., gray/white matter mask), or (3) made a sharp turn of >45 degrees.

DWI connectome reconstruction

From the total collection of reconstructed tractography streamlines, for each region pair i and j of the initial individually mapped 300 cortical parcels it was determined whether a reconstructed streamline touched both region i and j. A pathway was said to be present when one or more streamlines were observed, and indicated by the number of reconstructed fiber streamlines NOS in a 300 × 300 connectivity matrix. When no streamlines were observed between a region pair a 0 was included in the connectivity matrix. The initial, individual mapping to a 300 × 300 matrix (based on the individual cortical segmentations into 300 parcels, see atlas description above) was applied to incorporate effects of individual variation in cortical structure on connectome formation [Li et al., 2013]. Next, to be able to make a one‐to‐one comparison to the tract‐tracing datasets (see below), each individual 300 × 300 reconstructed matrix was sampled to the combined Walker‐von Bonin & Bailey (WBB47) parcellation atlas of the macaque cortex, dividing the cortical mantle of a single hemisphere into 39 distinct cortical regions [von Bonin and Bailey, 1947; Walker, 1940]. The WBB47 atlas was used as it covers the entire macaque cortex, is included in the CoCoMac database (see below), and ensures (due to its relatively large region sizes) a relative good spatial overlap across specimens. The WBB47 atlas (see Fig. 1 and also the tract‐tracing description below) was used before for the examination of connectivity in the macaque cortex [Stephan et al., 2000], as well as for a recent study examining the network topology of the macaque connectome [Scholtens et al., 2014]. Using the procedure of Hagmann et al. [Hagmann et al., 2008], resampling of the connectivity matrix was performed by determining for each of the distinct parcels their level of overlap with the 39 cortical regions, after which for each 39 × (39 − 1)/2 connection pairs their level of reconstructed streamlines NOS was determined. We note that the WBB47 parcellation atlas does not include a distinction between the left and right hemisphere. Combined with the notion that the CoCoMac database in most cases does not describe the examined hemisphere, and the notion that the Markov–Kennedy dataset describes injection sites in both the left and right hemisphere, the DWI NOS connectivity matrix was formed for one hemisphere only (chosen to be the left in the DWI data including 150 cortical parcels). In addition, to make sure that the initial high‐to‐low spatial mapping step of our analysis (i.e., the mapping of the initial parcellation to the WBB47 atlas) did not affect our results, an additional analysis was performed in which the WBB47 atlas was directly used to reconstruct the connectivity matrix (thus not involving the 300‐to‐39 resampling step of the DWI NOS data). This analysis showed consistent results with our main analysis (see Supporting Information for the results of this additional analysis).

Figure 1.

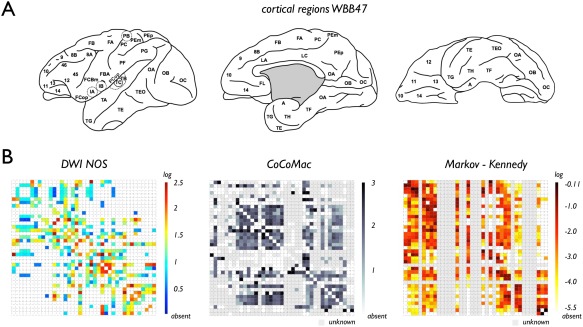
Figure 1

Open in a new tab

(A) Thirty‐nine cortical regions of the WBB47 macaque atlas. (B) Panels show the macaque connectome map of the 39 WBB47 cortical regions and their cortico‐cortical pathways as reconstructed by DWI (left), as reconstructed from the CoCoMac database (middle) and as reconstructed from the Markov–Kennedy data (right). Cells of region pairs that were found not to be connected are indicated by white (i.e., zero) entries in all three matrices. Cells of region pairs of which no information on connectivity strength was present (i.e., connectivity between region pairs not examined) in the CoCoMac and Markov–Kennedy dataset are depicted in gray. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Next, across the sampled 39 × 39 individual WBB47 connectivity matrices a group consensus matrix was formed by taking the non‐zero mean of the structural connectivity (SC) matrices across the 10 macaque datasets. To reduce the number of false positive reconstructions, pathways that were consistently observed in 60% or more of the individual datasets were included [de Reus and van den Heuvel, 2013]. For the resulting DWI group‐connectivity matrix (SCdwi) the connectivity strength of each reconstructed pathway was computed as the average number of observed reconstructed streamlines between i and j, resulting in the weighted connectivity matrix SCdwi‐NOS. Due to the log‐normal distribution of NOS, log‐transformed values (log10) were used in the correlation analysis.

In addition to raw NOS count, several studies have noted the potential influence of the volume of the cortical regions on the NOS count of a region's pathways. With the volume of the segmented regions not being uniformly distributed, it is argued that regions with a higher volume are more likely to touch streamlines, therefore obtaining a—potentially artifactual—higher NOS count [Hagmann et al., 2008; Iturria‐Medina et al., 2008; van den Heuvel et al., 2013]. To control for this effect, studies have proposed to correct for the volume of the two connecting regions, defining the connectivity strength of a reconstructed pathway between region A and region B as the observed NOS count divided by the average of the volumes of region A and region B, resulting in volume‐corrected NOS count, a weight metric often referred to in DWI connectome literature as “streamline density” [Hagmann et al., 2008; van den Heuvel and Sporns, 2011]. Indeed, also in this dataset a positive correlation was observed between regional raw NOS count and regional volume (P < 0.0001, r = 0.7194). This while measurements of connectivity strength as derived from tract‐tracing experiments are (much) less influenced by this effect (indeed, no association was observed between tract‐tracing strength and regional volume, P = 0.21). Thus, in addition to raw NOS count, we also examined the relationship between streamline density of the group‐averaged weighted connectivity matrix SCdwi‐streamline‐density (computed by dividing raw NOS count by the mean volume of the interconnected cortical regions) and projection strength as derived from macaque tract‐tracing.

In addition to the NOS count for each DWI reconstructed pathway, also the average fractional anisotropy (diffusion tensor imaging derived FA), mean diffusivity (MD), and radial diffusivity (RD, i.e., the amount of diffusivity transverse to the main diffusion direction, a metric often interpreted to be inversely related to tract myelination) was computed, taken as the weighted average over all voxels traversed by the streamlines interconnecting i and j. FA, MD, and RD were all computed on the basis of traditional diffusion tensor fit, reconstructed alongside the GQI diffusion estimates.

CoCoMac Connectome Reconstruction and Tract‐Tracing Projection Strength

Information on macroscale cortico‐cortical white matter axonal projections between regions of the macaque cortex was obtained from the Collations of Connectivity data on the Macaque brain database (CoCoMac, RRID: nif‐0000‐00022), an open‐access database describing a large collection of collated data from published macaque anatomical tracer studies [Stephan et al., 2000, 2001; Rembrandt et al., 2011]. Similar to the DWI data, cortical regions were defined by means of the WBB47 parcellation atlas, dividing the cortical surface into 39 nonoverlapping cortical regions (see Fig. 1). The WBB47 parcellation scheme, the accompanied CoCoMac extraction and the graph theoretical examination of the derived connectome map are described in detail in a recent publication [Scholtens et al., 2014]. The CoCoMac database was queried for all possible combinations of 39 regions in the WBB47 atlas reporting on the specific presence (i.e., examined and observed anatomical tract) as well as the specific absence (i.e., examined, but not found tract) of anatomical projections between brain regions across all studies included in the database, resulting in the inclusion of data of 126 studies. From these reports a 39 × 39 binary SC matrix was constructed, including an anatomical tract between region i and region j if at least three or more studies in the CoCoMac database examined this pathway and the number of positive reports across these studies was at least 60% (referred to as prevalence, reducing the inclusion of potential false positive reports [Scholtens et al., 2014]; Other settings of the number of studies and prevalence resulted in similar findings). The (consistent) presence of a connection was marked as a 1 between i and j in the adjacency matrix SCcocomac, an absence was marked as a 0 [Shen et al., 2012]. If information on the connectivity between two regions was not present in the CoCoMac database, the connection was deemed to be absent and presented as “not a number” (NaN) in the connectivity matrix (and as a result not included in our examination of connectivity strength) [Shen et al., 2012]. CoCoMac provides limited information on demographics of the specimens included in the reported studies, with of 6% (8 out of 126) of studies included in the examined WBB47 extraction reporting information on age (age range of reported studies 1–25 years) and 10% reporting on gender (12 out of 126 studies, 86% males/14% females). CoCoMac includes information on connectivity of the species macaca fascicularis, macacafuscata, macaca mulatta, and macaca nemestrina.

The CoCoMac database classifies the strength of observed anatomical pathways based on the original descriptions of the level of tracer density/strength [Shen et al., 2012]. As described in one of the original papers accompanying the CoCoMac database pathways are categorized into three strength classes: 1 (weak), 2 (intermediate), and 3 (strong) (Stephan et al., 2001); pathways of which no information on connectivity is present are labeled as a NaN and accordingly not taken into account in our weight comparison analysis. Using this extracted information, for each of the reconstructed tracts in the connectivity matrix SC two types of connectivity strength values were examined: (A) as a majority vote across the study reports, resulting in a ordinal value of 1 (weak), 2 (moderate), or 3 (strong) forming a weighted connectivity matrix SCtract‐CCM‐majority, and (B) as the non‐zero, non‐NaN mean of the ordinal strength values reported by the studies reporting levels of strength, resulting in a 39 × 39 weighted connectivity matrix (SCtract‐CCM) with cell entries reflecting the connection strengths as a continuous value ranging from 1 to 3.

Connectome Reconstruction from Markov–Kennedy Dataset of Quantitative Measurements of Connectivity Strength

As mentioned, the CoCoMac database is limited in that it contains collated, categorical information on connectivity strength, classifying pathways into “weak,” ”moderate,” and “strong.” Recent detailed tract‐tracing studies of Markov and Kennedy and coworkers have reported quantitative measures of connectivity strength in the macaque brain [Markov et al., 2012, 2013a, 2013b]. Furthermore, the Markov–Kennedy data were acquired in consistent experimental settings, using one single parcellation scheme of the macaque cortex and using one type of tract‐tracing methodology. In contrast to CoCoMac database extractions, the Markov–Kennedy dataset does not (yet) include a full coverage of the macaque cortex describing 29 target regions (32%) of the 91 cortical regions defined in the cortex parcellation atlas, but it nevertheless provides one of the most detailed maps of cortico‐cortical pathways of the macaque cortex. From the 29 injection sites across 28 macaques, the Markov–Kennedy dataset describes a 29 × 29 mapping of all existing pathways between these regions, reporting a connectivity matrix of 66% density [Markov et al., 2012]; of the 91 recording regions it provides information on efferent pathways to the 29 injection sites. As documented, the Markov–Kennedy dataset describes connectivity data of 28 specimens, including M. fascicularis (27) and M. mulatta (1) [Markov et al., 2012], with the majority of samples referred to as “adult” (13 adults, two 6‐month old and one 12‐month old, rest not explicitly reported) and with three documented reports of inclusion of male specimens and 13 of female specimens (rest not explicitly reported) [Markov et al., 2014].

The Markov–Kennedy dataset provides quantitative information on the projection strength of the reported interareal pathways, reported as the weight index of extrinsic fraction of labeled neurons (FLNe) [Markov et al., 2013a]. Repeated injections in a number of primary visual regions across specimens revealed modest inter‐subject variation in FLNe [Markov et al., 2012]. In this study, the FLNe weight index as documented in the Markov–Kennedy dataset and as used by Markov et al. for macaque connectome analysis [Markov et al., 2013a, 2013b] was used for comparison to DWI NOS. The FLNe 91 × 29 data as described in [Markov et al., 2012] and as presented at http://core-nets.org/index.php was used. Next, to allow overlap with the reconstructed DWI NOS connectivity matrix, the 91 cortical regions as used by Markov et al. were (manually) mapped to the WBB47 cortical atlas; Supporting Information Table 1 describes the 91‐to‐WBB47 region‐to‐region mapping. Next, using this region‐to‐region mapping a WBB47‐based FLNe connectivity matrix (SCtract‐FLNe) was formed: in those cases in which the cortical areas of a WBB47 region‐pair overlapped multiple regions of the 91‐region atlas, FLNe scores of the connecting interareal tracts were averaged; in those cases in which information on connectivity strength was missing from the Markov–Kennedy dataset (i.e., information on efferent connectivity of regions outside the 29 injection sites) a NaN was included in SCtract‐FLNe, and these connections were not taken into account in the tract‐tracing to diffusion MRI‐based comparison; this resulted in a SCtract‐FLNe, connectivity matrix of 76% density. For the correlation analysis, log (log10) transformed values were used [Markov et al. 2013a].

Statistical Comparison between Connectivity Strength as Measured by tract‐Tracing and Diffusion MRI

For the main topic of investigation of this study, connectivity strength of reconstructed tracts derived from tract‐tracing (variants SCtract and SCtract‐FLNe) and from DWI analysis (SCdwi‐NOS) were compared by means of correlation analysis, comparing levels of connectivity strength of pathways mutually observed in both reconstructions. First, for the analysis in which the tract‐tracing connectivity strength was determined as a majority vote of the reports in the CoCoMac database (i.e., SCtract‐CCM‐majority), for each class of strength (i.e., s = 1, s = 2, and s = 3) the weights of the existing corresponding connections in the (raw and log‐transformed) SCdwi‐NOS matrix were selected and differences in DWI‐based connectivity strength between the three classes s = 1, s = 2, and s = 3 were tested using the Jonckheere–Terpstra test, a statistical test allowing for the evaluation of an ordering effect in the presented data (i.e., here s = 1 < s = 2 < = 3). Second, the more continuous SCtract‐CCM weights were compared to (log transformed) SCdwi‐NOS by means of linear regression analysis. Third, a correlation procedure was performed for the weights derived from the Markov–Kennedy data, correlating (log transformed) SCtract‐FLNe values with (log transformed) SCdwi‐NOS values for tracts observed in both reconstructions.

RESULTS

Comparison of Connectivity Strength Derived from DWI‐NOS and CoCoMac

Figure 1 illustrates the WBB47 DWI NOS, CoCoMac and Markov–Kennedy reconstructed macaque connectome maps. A positive significant relationship between tract‐tracing strength and NOS was observed in the SCtract‐majority data, with tract‐tracing connectivity strength defined as a majority vote across reports in the CoCoMac database, revealing a significant positive ordering in DWI NOS strength across the three categories of tract‐tracing strength (raw NOS: P = 0.0063; log‐transformed NOS: P = 0.0013, Fig. 2B, Jonckheere–Terpstra).

Figure 2.

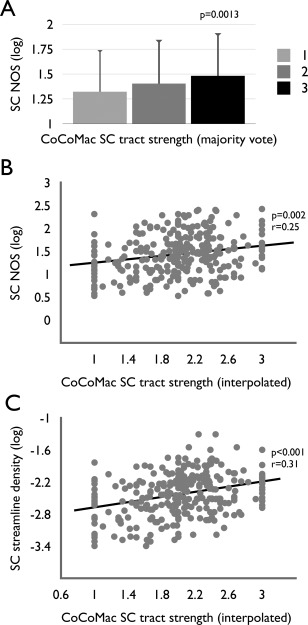
Figure 2

Open in a new tab

(A) A positive relationship (P < 0.05, linear regression) between CoCoMac derived connectivity strength and DWI derived connectivity strength was verified in the analysis in which axon density strength from CoCoMac was taken as a majority vote (resulting in three strength categories of connections of 1 [weak], 2 [moderate], and 3 [strong] projections, see Methods). A significant increasing staircase pattern of NOS connectivity strength was observed across the three CoCoMac strength categories (Jonckheere–Terpstra test, P = 0.0013). (B) Correlation analysis revealed a positive correlation between connection strength as derived from DWI (weights reflecting log of NOS) and as derived from CoCoMac (estimation of continuous values derived from averaging of ordinal strength values across reported studies). (C) Correlation analysis between NOS density values and CoCoMac strength values similarly revealed a significant, positive association.

Additional regression analysis between strength values SCtract‐CCM and SCdwi‐NOS confirmed a positive relationship between DWI and tract‐tracing metrics of connectivity strength, revealing a significant positive relationship (NOS log transformed, p = 1.6 × 10−3, r = 0.2481, Fig. 2A, linear regression, surviving Bonferroni correction for multiple testing; including spatial distance as a covariate revealed a similar positive correlation (p = 1.5 × 10−4, r = 0.22). (Note: as other studies have used a redistribution of the raw NOS count to a Gaussian distribution rather than a log transform [e.g. Hagmann et al., 2008; van den Heuvel et al., 2012], we also tested this type of connection strength in relationship to SCtract‐CCM, resulting in a similar positive relationship [see Supporting Information Figure 1].) Furthermore, taking streamline density SCdwi‐ streamline‐density as a DWI metric of connection strength (dividing off the volume of the connected regions [see Methods]) revealed a similar—even slightly stronger—positive relationship between SCdwi‐ streamline‐density and SCtract‐CCM (log transformed, P = 1.011 × 10−6, r = 0.3133, Fig. 2C). As an additional test, categorizing NOS density into three categories (weak [lowest 33% of SCdwi‐ streamline‐density], moderate [middle 33%] and strong [top 33%]) similar to the three classes of strength in the CoCoMac database, again revealed a positive relationship between DWI and CoCoMac connectivity strength (chi‐squared: 22.24, P = 1.8 × 10−4).

Comparison of Connectivity Strength Derived from DWI‐NOS and Markov–Kennedy

Comparing connectivity strength derived from macaque diffusion MRI to the Markov–Kennedy quantitative information on projection strength also revealed a positive relationship, showing a significant correlation between SCdwi‐ streamline‐density and SCtract‐FLNe (log transformed, P = 2.4407 × 10−05, r = 0.2620, Fig. 3). Furthermore, similar to the analysis of the CoCoMac data, taking streamline density SCdwi‐ streamline‐density (dividing off volume of the connected regions from raw NOS count) as a metric of DWI connectivity strength again revealed a positive (and again slightly stronger) association (SCdwi‐ streamline‐density versus SCtract‐FLNe, log transformed, P = 8.28 × 10−07, r = 0.3040, Fig. 3, Including spatial distance as a covariate: p = 2.4 × 10−6, r = 0.29).

Figure 3.

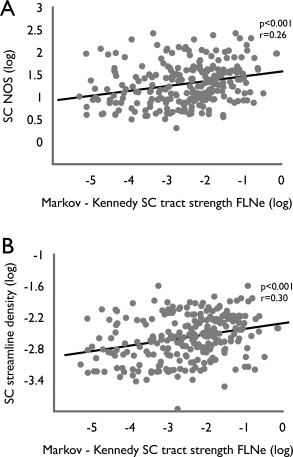
Figure 3

Open in a new tab

(A) Correlation analysis between DWI‐derived and tract‐tracing derived metrics of projection strength of interareal white matter connections as provided by the high‐quality quantitative dataset of Markov and Kennedy and coworkers [Markov et al., 2012]; (see Methods), revealed a positive correlation between DWI number of streamlines NOS and tract‐tracing metrics of connectivity strength FLNe (P = 2.4407 × 10−05, r = 0.2620, both values log10 transformed). (B) Correlation analysis between streamline density and FLNe strength similarly revealed a positive, significant association.

Association between Metrics of White Matter Complexity and tract‐Tracing Strength

As a post hoc examination of the specificity of the observed effect between SCtract and SCdwi‐NOS values a comparison between tract‐tracing strength (SCtract‐CCM‐majority, SCtract‐CCM, SCtract‐FLNe) and metrics of white matter integrity (FA, MD, and RD) of the reconstructed tracts was performed. In contrast to the evaluation of NOS, correlation analysis revealed no associations between tract‐tracing strength and FA (FA to SCtract‐CCM P = 0.8448, Jonckheere–Terpstra | FA to SCtract‐CCM P = 0.3203 linear regression; FA to SCtract‐FLN P = 0.0302 linear regression). Interestingly, a negative correlation was observed between CoCoMac connectivity strength and DWI derived MD (P = 0.0056, r = 0.1661) and RD (P = 0.0062, r = 0.1642; see Supporting Information Figure 3), an effect also observed between FLNe weights of the Markov–Kennedy data and DWI MD (P = 0.0004, r = 0.2198) and DWI RD (P = 0.0018, r = 0.1957; Supporting Information Figure 4). These findings suggest strong connections to display a relatively lower MD/RD (reflecting a higher white matter complexity) than weak pathways. With no clear correlation between NOS and RD or MD values (P = 0.77) present in the DWI data, this effect suggests a relative unique contribution to the explained variance of tract‐tracing weights.

Indeed, a multilinear model with both SCdwi‐NOS and SCdwi‐RD as independent variables, explained more variance in both the CoCoMac and Markov–Kennedy datasets: the total amount of explained variance in the CoCoMac data increased by a factor of 1.39 as compared to SCdwi‐NOS alone, with both SCdwi‐NOS (P = 0.0002) and SCdwi‐RD (P = 0.0132) as significant unique predictors [1.29 in a SCdwi‐NOS + SCdwi‐MD model, with SCdwi‐NOS (p = 5.0 × 10−4) and SCdwi‐MD (P = 0.0327)]. Similarly, the total amount of explained variance in the Markov–Kennedy FLNe data increased by a factor of 1.83 as compared to SCdwi‐NOS alone, with both SCdwi‐NOS (P < 0.001) and SCdwi‐RD (P = 0.0151) as significant unique predictors [1.42 in a SCdwi‐NOS + SCdwi‐MD model, with SCdwi‐NOS (P < 0.0001) and SCdwi‐MD (P = 0.0202)].

Edge Classes

The association between DWI NOS and tract‐tracing strength was found to be relatively consistent across different types of selected subsets of edges across the network. Examining the SCdwi‐streamline‐density–SCtract‐CCM association for short‐range (shortest 33%), mid‐range (33–66%) and long‐range (top 33%) connections in a post hoc analysis again revealed positive correlations, with mid‐range tracts (p = 7.5 × 10−4, r = 0.46) showing the strongest effect (short: p = 3.6 × 10−4, r = 0.35; long: P = 0.065 ns, r = 0.20; data shown in Supporting Information Figure 2). Similar results were found with the Markov–Kennedy data, with mid‐range tracts again showing the strongest effect (short‐range: r = 0.18, P = 0.0747 ns; mid‐range: r = 0.38, p = 2.9 × 10−4; long‐range: r = 0.28, P = 0.0211).

In addition, examining the association between SCdwi and SCtract‐CCM for intramodular connections (describing edges spanning between nodes of the same node communities) versus intermodular connections (describing edges spanning between nodes of different modules) both revealed a positive correlation (p = 2.9 × 10−4, r = 0.34, and p = 7.3 × 10−4, r = 0.26 respectively). Overlapping results were observed for intramodular connections in the Markov–Kennedy data (p = 1.2 × 10−5, r = 0.34), but the relationship SCdwi‐streamline‐density–SCtract‐FLNe did not reach significance for intermodular connections (P = 0.15 ns, r = 0.15; data shown in Supporting Information Figure 6).

DISCUSSION

This study reports on a positive association between DWI‐derived number of reconstructed fiber streamlines (NOS) and connectivity strength of interareal pathways as derived from tract‐tracing data in the macaque brain. Extending previous studies focusing on the spatial overlap between DWI and tract‐tracing derived connectome maps our findings show a positive association between connectivity strength of anatomical pathways as measured by DWI and as measured by tract‐tracing. Our study suggests that MR derived pathways with a higher NOS count reflect ‐to some level‐ pathways with a higher fiber density and/or axonal tract volume.

The observed association with tract‐tracing connectivity strength was found to be the strongest for the number of reconstructed streamlines NOS, with RD or MD explaining additional variance in a combined model; no clear association was found between FA and tract‐tracing strength. This suggests that NOS provides information about connectivity strength not provided by FA, information that is above and beyond information provided by RD and MD. Findings suggest DWI NOS and streamline density to be fairly accurate markers for in vivo assessment connectivity strength. The clearest relationships between DWI derived and tract‐tracing derived data were observed for log transformed data, and although the biological underpinnings of this type of distribution in context of connectivity data remains unclear, this is in support of a suggested lognormal distributions of connectivity strength in the mammalian brain [Bota et al., 2015; Hagmann et al., 2008; Markov et al., 2012; Oh et al., 2014; van den Heuvel and de Reus, 2014; van den Heuvel et al., 2015]. Taken together, our observations suggest that reconstructed number of tractography streamlines may include a useful approximation for axonal number in in vivo DWI connectome studies. Future studies further examining this potential validation of DWI NOS and streamline density using other connectome datasets (as for example the highly detailed connectome maps of the mouse [Oh et al., 2014] and rat brain [Bota and Swanson, 2007; Bota et al., 2015]) would be of high interest.

Our findings are encouraging for DWI derived metrics of connectivity strength to be considered as a valid marker for in vivo assessment of white matter connectivity strength. However, for a fair discussion, a number of technological issues on both methodologies have to be considered when interpreting the results of our cross‐modality comparison. First, our study is limited to the evaluation of cortical tracts only and does thus not include information on DWI and tract‐tracing strength of subcortical–cortical tracts. The current study builds on our previous work [Li et al. 2013] in which detailed cortical surface meshes of the macaque cortex were reconstructed, which were then used (in this study) as initial network nodes in the reconstruction of the connectivity networks. Reconstruction of white matter pathways around subcortical regions are known to be particular challenging (and thus more sensitive to making incorrect reconstructions) as many white matter fiber bundles (such as spino‐thalamic cortical tracts) pass through a series of nuclei with touching boundaries, making the correct reconstruction of the complex wiring architecture around subcortical regions even more difficult. In addition to this, information on tract‐tracing data between sub‐cortical structures and between sub‐cortical and cortical structures is sparse for the CoCoMac database and absent in the case of the Markov–Kennedy data. To avoid the inclusion of any additional variation by including only sparsely and noisy sampled data we limited our evaluation to cortico‐cortical tracts in this study.

In this context, it is generally noted that the analysis of DWI data may lead to false positive and false negative reconstructions of pathways [de Reus and van den Heuvel, 2013; Johansen‐Berg and Rushworth, 2009]. Current local modeling algorithms (still) have difficulty reconstructing the correct diffusion/fiber directions in white matter voxels of complex fiber architecture and in voxels near cortical gray matter areas. It has been mentioned that the nature of (deterministic) fiber tracking—starting seeds in each part of the white matter and using hard evaluation and stopping criteria—has been suggested to lead towards a possible overestimation of weights on long‐range tracts [Hagmann et al., 2008], as well as an increasing difficulty of correctly completing long‐range tracts [Jbabdi and Johansen‐Berg, 2011; Johansen‐Berg and Rushworth, 2009; Jones, 2008; van den Heuvel et al., 2012]. As a result, DWI approaches have been reported to result in consistent connectome reconstructions in test–retest examinations, but also ones in which certain classes of connections are systematically underrepresented and others overrepresented [Bassett et al., 2011; Zalesky et al., 2010]. In this study, high‐quality DWI data (in total 600 directions) combined with a GQI (see Methods) [Yeh et al., 2010] was used to allow for the reconstruction of multi‐orientation fiber configurations. This to provide (some) resolving power in voxels where the diffusion signal is complex, for example in places of spraying, kissing or bending fibers [Yeh et al., 2010]. Several other methods to resolve complex diffusion orientations and to reconstruct fiber pathways have of course been proposed and would be equally promising to examine in context of tract‐tracing connectivity strength. Although a comparison between different diffusion reconstruction and tractography methods is not the main topic of our study, an examination of the class of (also often‐used) probabilistic reconstruction methods for DWI data with respect to tract‐tracing strength would be of interest. In a previous publication of our group [Li et al., 2013], probabilistic tractography as implemented in the FMRIB's Diffusion Toolbox (FDT, http://www.fmrib.ox.ac.uk/fsl/) [Behrens et al., 2003, 2007] was used to reconstruct white‐matter cortico‐cortical connections of the macaque macroscale connectome. FDT was used to reconstruct the diffusion probability density functions in each brain voxel, combined with tractography starting 1000 streamline seeds per cortical vertex in each of the 300 starting regions on the cortical sheet (being the same 300 starting regions as used in this study, see Methods). Next, per specimen a connectome map was formed using the derived “probabilistic streamlines” [Li et al., 2013], with probabilistic streamline count taken as weights for the reconstructed interareal pathways. Here, in an additional analysis we translated these computed probabilistically weighted connectome maps to the WBB47 39 × 39 cortical atlas (using the same procedure as in our deterministic approach) and correlation analysis again revealed a significant, positive correlation between DWI derived connectivity strength and tract‐tracing measurements of connectivity strength, in both the CoCoMac dataset (P = 1.5657 × 10−04, r = 0.1715) and the Markov–Kennedy dataset (P = 3.3702 × 10−09, r = 0.2442; data shown in Supporting Information Figure 5).

Second, it should be considered that (collated) tract‐tracing datasets also have their limitations, further complicating a direct comparison of tract‐tracing to DWI. Tract‐tracing methodology, similar to DWI analysis, is also sensitive to producing false‐positive and false‐negative tract reconstructions [Oh et al., 2014]. Indeed, for some tracts, studies in CoCoMac explicitly report their presence, while others explicitly report their absence. In this study, we minimized the effects of false positives (i.e., reported tracts that are not truly anatomically present) by including only those tracts that were found present in the majority of study reports and/or specimens, and by focusing our analysis on tracts consistently observed in both DWI and tract‐tracing reconstructions. In this context, it is important to note that—as being the case in many tract‐tracing based connectome reconstructions—both the CoCoMac and Markov–Kennedy reconstructed macaque connectome maps are based on a collation of data across a large number of specimens, combining data into one single connectome map, thus largely ignoring inter‐subject variability and hemispheric asymmetry. As a result, collated tract‐tracing connectome maps do not take into account individual variation in connectivity layout and strength. Moreover, in particular the CoCoMac database includes data from a wide range of types of experiments, combining data across anterograde or retrograde viral tracer techniques, multiple parcellation atlases, multiple macaque species and varying experimental settings. As a result, notwithstanding CoCoMac being a well‐respected and often used database for assessing information on macaque brain connectivity (e.g. [Harriger et al., 2012; Modha and Singh, 2010; Shen et al., 2012; Sporns, 2011; Stephan et al., 2001]), it has to be kept in mind that the database contains a somewhat “potpourri” of information on interareal connectivity of the macaque brain. The Markov–Kennedy tract‐tracing dataset contains data from (mostly) a single macaque species and has been acquired in as consistent experimental settings as possible. In addition, considering that our performed DWI versus tract‐tracing comparison involves a cross‐correlation between independently acquired datasets—with a comparison between tract‐tracing and DWI in the same specimens perhaps including a more optimal (but very difficult to perform in a connectome perspective) approach—no correction regarding potential differences in demographics between the datasets is/can be performed. MRI acquisition involved data of 10 macaques (all macaca mulatta, mean age 14 years), but information on demographics of the tract‐tracing datasets is sparse. As mentioned, CoCoMac includes a collation of data across a large number of studies, with information on age‐range and gender being present in only a small percentage of studies (<10%). The majority of the Markov–Kennedy data is reported to include adult specimens, with some samples in developing stages. With development and aging reported to have a clear effect on white matter integrity in both human and primate species (e.g. [Bennett et al., 2010; Betzel et al., 2014; Chen et al., 2013; Sexton et al., 2014]) this is a limiting factor of our DWI versus tract‐tracing comparison. However, to give a complete picture, it is worth to note that the far majority of these DWI studies that report on development and aging to have a modulating effect on white matter microstructure (in diffusion MRI approximated by FA and/or MD/RD), rather than on NOS. It is for the latter that we find the most clear relationship with tract‐tracing metrics of connectivity strength.

As a general third methodological remark, it is important to realize that both connectome reconstructions are likely to include false positive and false negative reconstructions. Indeed, although not the focus of our investigation (as binary overlap has been the topic of other studies, e.g., [Azadbakht et al., in press; Dauguet et al., 2006; Dauguet et al., 2007; Dyrby et al., 2007; Thomas et al., 2014]), we note that the reconstructed DWI and tract‐tracing connectome maps are far from perfectly aligned. Some connections were only observed in the tract‐tracing data and others only observed in the DWI reconstructions. Computing the level of binary overlap did reveal significant overlap between the tract‐tracing and DWI derived connectome maps (SCtract‐CCM and SCdwi‐NOS: 59.3% Matthew's correlation coefficient (MCC) = 0.24, P = 1.0202 × 10−09 | SCtract‐FLNe and SCdwi‐NOS: 52.6%, MCC = 0.2305, P = 7.9696 × 10−11), but the total level of overlap is modest (see Supporting Information for computation of overlap and additional analysis). In this context, we report that (as previously noted [Markov et al., 2012]) the level of overlap between macaque connectome maps derived from CoCoMac and Markov–Kennedy was significant, but relatively low (overlap of 63.1%, MCC = 0.30, P < 0.001), with the Markov–Kennedy data identifying previously unobserved interareal tracts (see [Markov et al., 2012]). Nevertheless, testing Markov–Kennedy strength across the three different CoCoMac classes in a post hoc analysis revealed a clear significant staircase pattern (with group average Markov–Kennedy weights of CoCoMac Class 3 being 2.3 times higher than Class 2, and Class 2 being 2.06 times higher than values of Class 1, Jonckheere–Terpstra test, P < 0.0001) and correlation analysis between CoCoMac interpolated connectivity strength values and Markov–Kennedy weights across tracts observed in both datasets also revealed a significant, positive association (SCtract‐CCM versus log transformed SCtract‐FLNe, P = 2.6221 × 10−07, r = 0.3310).

In this technical note, we report on a simple but potentially important correlation between in vivo diffusion MRI derived number of tractography streamlines and tract‐tracing projection strength. Our findings provide evidence of the number and density of tractography streamlines of DWI reconstructions of macroscale connectome pathways to form a valid in vivo approximation of white matter tract strength. Our comparison of tract‐tracing to DWI‐derived NOS may thus provide confidence for a growing number of studies that use DWI techniques to map connectome changes in disease, reporting alterations of reconstructed number of streamlines and accompanying brain network alterations in a wide variety of neurological and psychiatric disorders.

Supporting information

Supporting Information and Legends

Click here for additional data file. (529.5KB, docx)

Supplemental Figure 1

Click here for additional data file. (359.4KB, tiff)

Supplemental Figure 2

Click here for additional data file. (1.3MB, tiff)

Supplemental Figure 3

Click here for additional data file. (462KB, tiff)

Supplemental Figure 4

Click here for additional data file. (451KB, tiff)

Supplemental Figure 5

Click here for additional data file. (1.6MB, tiff)

Supplemental Figure 6

Click here for additional data file. (1.6MB, tiff)

REFERENCES

  1. Andersson JL, Skare S, Ashburner J (2003): How to correct susceptibility distortions in spin‐echo echo‐planar images: Application to diffusion tensor imaging. NeuroImage 20:870–888. [DOI] [PubMed] [Google Scholar]
  2. Azadbakht, H , Parkes, LM , Haroon, HA , Augath, M , Logothetis, NK , de Crespigny, A, D'Arceuil, HE , Parker, GJ : Validation of High‐resolution tractography against in vivo tracing in the macaque visual cortex. Cereb Cortex (in press). Epub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bassett DS, Bullmore ET, Meyer‐Lindenberg A, Apud JA, Weinberger DR, Coppola R (2009): Cognitive fitness of cost‐efficient brain functional networks. Proc Natl Acad Sci USA 106:11747–11752. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bassett DS, Brown JA, Deshpande V, Carlson JM, Grafton ST (2011): Conserved and variable architecture of human white matter connectivity. NeuroImage 54:1262–1279. [DOI] [PubMed] [Google Scholar]
  5. Behrens TE, Woolrich MW, Jenkinson M, Johansen‐Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM (2003): Characterization and propagation of uncertainty in diffusion‐weighted MR imaging. Magn Reson Med 50:1077–1088. [DOI] [PubMed] [Google Scholar]
  6. Behrens TE, Berg HJ, Jbabdi S, Rushworth MF, Woolrich MW (2007): Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? NeuroImage 34:144–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bennett IJ, Madden DJ, Vaidya CJ, Howard DV, Howard JH Jr (2010): Age‐related differences in multiple measures of white matter integrity: A diffusion tensor imaging study of healthy aging. Hum Brain Mapp 31:378–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Betzel RF, Byrge L, He Y, Goni J, Zuo XN, Sporns O (2014): Changes in structural and functional connectivity among resting‐state networks across the human lifespan. NeuroImage 102(Pt 2):345–357. [DOI] [PubMed] [Google Scholar]
  9. Bota M, Swanson LW (2007): Online workbenches for neural network connections. J Comp Neurol 500:807–814. [DOI] [PubMed] [Google Scholar]
  10. Bota M, Sporns O, Swanson, LW (2015): Architecture of the cerebral cortical association connectome underlying cognition. Proc Natl Acad Sci USA 112: E2093–E2101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Bullmore E, Sporns O (2009): Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat Rev 10:186–198. [DOI] [PubMed] [Google Scholar]
  12. Bullmore E, Sporns O (2012): The economy of brain network organization. Nat Rev 13:336–349. [DOI] [PubMed] [Google Scholar]
  13. Catani M, Thiebaut de Schotten M, Slater D, Dell'Acqua F (2013): Connectomic approaches before the connectome. NeuroImage 80:2–13. [DOI] [PubMed] [Google Scholar]
  14. Chen X, Errangi B, Li L, Glasser MF, Westlye LT, Fjell AM, Walhovd KB, Hu X, Herndon JG, Preuss TM, Rilling JK (2013): Brain aging in humans, chimpanzees (pan troglodytes), and rhesus macaques (macaca mulatta): Magnetic resonance imaging studies of macro‐ and microstructural changes. Neurobiol Aging 34:2248–2260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dauguet J, Peled S, Berezovskii V, Delzescaux T, Warfield SK, Born R, Westin CF (2006): 3D histological reconstruction of fiber tracts and direct comparison with diffusion tensor MRI tractography. Medical image computing and computer‐assisted intervention: MICCAI. International Conference on Medical Image Computing and Computer‐Assisted Intervention, Vol. 9. pp 109–116. [DOI] [PubMed]
  16. Dauguet J, Peled S, Berezovskii V, Delzescaux T, Warfield SK, Born R, Westin CF (2007): Comparison of fiber tracts derived from in‐vivo DTI tractography with 3D histological neural tract tracer reconstruction on a macaque brain. NeuroImage 37:530−538. [DOI] [PubMed] [Google Scholar]
  17. de Reus MA, van den Heuvel MP (2013): Estimating false positives and negatives in brain networks. NeuroImage 70:402–409. [DOI] [PubMed] [Google Scholar]
  18. de Reus MA, Saenger VM, Kahn RS, van den Heuvel MP (2014): An edge‐centric perspective on the human connectome: Link communities in the brain. Philos Trans R Soc Lond B Biol Sci. 2014 Oct 5;369. pii: 20130527. doi: 10.1098/rstb.2013.0527. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dyrby TB, Sogaard LV, Parker GJ, Alexander DC, Lind NM, Baare WF, Hay‐Schmidt A, Eriksen N, Pakkenberg B, Paulson OB, Jelsing J (2007): Validation of in vitro probabilistic tractography. NeuroImage 37:1267–1277. [DOI] [PubMed] [Google Scholar]
  20. Filippi M, van den Heuvel MP, Fornito A, He Y, Hulshoff Pol HE, Agosta F, Comi G, Rocca MA (2013): Assessment of system dysfunction in the brain through MRI‐based connectomics. Lancet Neurol 12:1189–1199. [DOI] [PubMed] [Google Scholar]
  21. Fornito A, Zalesky A, Pantelis C, Bullmore ET (2012): Schizophrenia, neuroimaging and connectomics. NeuroImage 62:2296–2314. [DOI] [PubMed] [Google Scholar]
  22. Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O (2008): Mapping the structural core of human cerebral cortex. PLoS Biol 6:e159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Harriger L, van den Heuvel MP, Sporns O (2012): Rich club organization of macaque cerebral cortex and its role in network communication. PloS One 7:e46497. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P (2009): Predicting human resting‐state functional connectivity from structural connectivity. Proc Natl Acad Sci USA 106:2035–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Iturria‐Medina Y, Sotero RC, Canales‐Rodriguez EJ, Aleman‐Gomez Y, Melie‐Garcia L (2008): Studying the human brain anatomical network via diffusion‐weighted MRI and graph theory. NeuroImage 40:1064–1076. [DOI] [PubMed] [Google Scholar]
  26. Jbabdi S, Johansen‐Berg H (2011): Tractography: Where do we go from here? Brain Connect 1:169–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Johansen‐Berg H, Rushworth MF (2009): Using diffusion imaging to study human connectional anatomy. Annu Rev Neurosci 32:75–94. [DOI] [PubMed] [Google Scholar]
  28. Jones DK (2008): Studying connections in the living human brain with diffusion MRI. Cortex 44:936–952. [DOI] [PubMed] [Google Scholar]
  29. Jones DK (2010): Challenges and limitations of quantifying brain connectivity in vivo with diffusion MRI. Imaging Med 2:14. [Google Scholar]
  30. Kotter R, Maier J, Margas W, Zilles K, Schleicher A, Bozkurt A (2007): Databasing receptor distributions in the brain. Methods Mol Biol 401:267–284. [DOI] [PubMed] [Google Scholar]
  31. Li L, Rilling JK, Preuss TM, Glasser MF, Damen FW, Hu X (2012): Quantitative assessment of a framework for creating anatomical brain networks via global tractography. NeuroImage 61:1017–1030. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Li L, Hu X, Preuss TM, Glasser MF, Damen FW, Qiu Y, Rilling J (2013): Mapping putative hubs in human, chimpanzee and rhesus macaque connectomes via diffusion tractography. NeuroImage 80:462–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Markov NT, Ercsey‐Ravasz MM, Ribeiro Gomes AR, Lamy C, Magrou L, Vezoli J, Misery P, Falchier A, Quilodran R, Gariel MA, Sallet J, Gamanut R, Huissoud C, Clavagnier S, Giroud P, Sappey‐Marinier D, Barone P, Dehay C, Toroczkai Z, Knoblauch K, Van Essen DC, Kennedy H (2012): A weighted and directed interareal connectivity matrix for macaque cerebral cortex. Cereb Cortex 24:17–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Markov NT, Ercsey‐Ravasz M, Lamy C, Ribeiro Gomes AR, Magrou L, Misery P, Giroud P, Barone P, Dehay C, Toroczkai Z, Knoblauch K, Van Essen DC, Kennedy H (2013a): The role of long‐range connections on the specificity of the macaque interareal cortical network. Proc Natl Acad Sci USA 110:5187–5192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Markov NT, Ercsey‐Ravasz M, Van Essen DC, Knoblauch K, Toroczkai Z, Kennedy H (2013b): Cortical high‐density counterstream architectures. Science 342:1238406. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. NT Markov, J Vezoli, P Chameau, A Falchier, R Quilodran, C Huissoud, C Lamy, P Misery, P Giroud, S Ullman, P Barone, C Dehay, K Knoblauch, H Kennedy (2014): Anatomy of hierarchy: feedforward and feedback pathways in macaque visual cortex. J Comp Neurol 522:225–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Modha DS, Singh R (2010): Network architecture of the long‐distance pathways in the macaque brain. Proc Natl Acad Sci USA 107:13485–13490. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, Mortrud MT, Ouellette B, Nguyen TN, Sorensen SA, Slaughterbeck CR, Wakeman W, Li Y, Feng D, Ho A, Nicholas E, Hirokawa KE, Bohn P, Joines KM, Peng H, Hawrylycz MJ, Phillips JW, Hohmann JG, Wohnoutka P, Gerfen CR, Koch C, Bernard A, Dang C, Jones AR, Zeng H (2014): A mesoscale connectome of the mouse brain. Nature 508:207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. B Rembrandt, CP Tobias, W Thomas, D Markus (2011): Macaque structural connectivity revisited: CoCoMac 2.0. BMC Neurosci 12(Suppl 1):P72. doi: 10.1186/1471-2202-12-S1-P72. [DOI] [Google Scholar]
  40. Scannell JW, Blakemore C, Young MP (1995): Analysis of connectivity in the cat cerebral cortex. J Neurosci 15:1463–1483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Schmahmann JD, Pandya DN, Wang R, Dai G, D'Arceuil HE, de Crespigny AJ, Wedeen VJ (2007): Association fibre pathways of the brain: Parallel observations from diffusion spectrum imaging and autoradiography. Brain 130:630–653. [DOI] [PubMed] [Google Scholar]
  42. Scholtens LH, Schmidt R, de Reus MA, van den Heuvel MP (2014): Linking macroscale graph analytical organization to microscale neuroarchitectonics in the macaque connectome. J Neurosci 34:12192–12205. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Sexton CE, Walhovd KB, Storsve AB, Tamnes CK, Westlye LT, Johansen‐Berg H, Fjell AM (2014): Accelerated changes in white matter microstructure during aging: A longitudinal diffusion tensor imaging study. J Neurosci 34:15425–15436. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Shen K, Bezgin G, Hutchison RM, Gati JS, Menon RS, Everling S, McIntosh AR (2012): Information processing architecture of functionally defined clusters in the macaque cortex. J Neurosci 32:17465–17476. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Sporns O (2011): Networks of the Brain. Cambridge: MIT Press. [Google Scholar]
  46. Sporns, O (2012): Discovering the Human Connectome. Cambridge: MIT Press. [Google Scholar]
  47. Sporns O, Tononi G, Kotter R (2005): The human connectome: A structural description of the human brain. PLoS Comput Biol 1:e42. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Stephan KE, Hilgetag CC, Burns GA, O'Neill MA, Young MP, Kotter R (2000): Computational analysis of functional connectivity between areas of primate cerebral cortex. Philos Trans R Soc London 355:111–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Stephan KE, Kamper L, Bozkurt A, Burns GA, Young MP, Kotter R (2001): Advanced database methodology for the collation of connectivity data on the macaque brain (CoCoMac). Philos Trans R Soc London 356:1159–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Thomas C, Ye FQ, Irfanoglu MO, Modi P, Saleem KS, Leopold DA, Pierpaoli C (2014): Anatomical accuracy of brain connections derived from diffusion MRI tractography is inherently limited. Proc Natl Acad Sci USA 111:16574–16579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. van den Heuvel MP, de Reus MA (2014): Chasing the dreams of early connectionists. ACS Chem Neurosci 5:491–493. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. van den Heuvel MP, Fornito A (2014): Brain networks in schizophrenia. Neuropsychol Rev 24:32–48. [DOI] [PubMed] [Google Scholar]
  53. van den Heuvel MP, Stam CJ, Kahn RS, Hulshoff Pol HE (2009): Efficiency of functional brain networks and intellectual performance. J Neurosci 29:7619–7624. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. van den Heuvel MP, Kahn RS, Goni J, Sporns O (2012): High‐cost, high‐capacity backbone for global brain communication. Proc Natl Acad Sci USA 109:11372–11377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. van den Heuvel MP, Sporns O, Collin G, Scheewe T, Mandl RC, Cahn W, Goni J, Hulshoff Pol HE, Kahn RS (2013): Abnormal rich club organization and functional brain dynamics in schizophrenia. JAMA Psychiatry 70:783–792. [DOI] [PubMed] [Google Scholar]
  56. van den Heuvel MP, Sporns O (2011): Rich‐club organization of the human connectome. J Neurosci 31:15775–15786. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. van den Heuvel, MP, Scholtens, LH , de Reus, MA: Topological organization of connectivity strength in the rat connectome. Brain Struct Funct (in press). [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. von Bonin, G , Bailey, P (1947): The neocortex of Macaca mulatta. Urbana: University of Illinois Press. [Google Scholar]
  59. Walker A (1940): Cytoarchitectural study of the prefrontal area of the macaque monkey. J Comp Neurol 73:27. [Google Scholar]
  60. Yeh FC, Wedeen VJ, Tseng WY (2010): Generalized q‐sampling imaging. IEEE Trans Med Imaging 29:1626–1635. [DOI] [PubMed] [Google Scholar]
  61. Zalesky A, Fornito A, Harding IH, Cocchi L, Yucel M, Pantelis C, Bullmore ET (2010): Whole‐brain anatomical networks: Does the choice of nodes matter? NeuroImage 50:970–983. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information and Legends

Click here for additional data file. (529.5KB, docx)

Supplemental Figure 1

Click here for additional data file. (359.4KB, tiff)

Supplemental Figure 2

Click here for additional data file. (1.3MB, tiff)

Supplemental Figure 3

Click here for additional data file. (462KB, tiff)

Supplemental Figure 4

Click here for additional data file. (451KB, tiff)

Supplemental Figure 5

Click here for additional data file. (1.6MB, tiff)

Supplemental Figure 6

Click here for additional data file. (1.6MB, tiff)

Articles from Human Brain Mapping are provided here courtesy of Wiley

RESOURCES