Qualitatively different coding of symbolic and nonsymbolic numbers in the human brain

Abstract

Are symbolic and nonsymbolic numbers coded differently in the brain? Neuronal data indicate that overlap in numerical tuning curves is a hallmark of the approximate, analogue nature of nonsymbolic number representation. Consequently, patterns of fMRI activity should be more correlated when the representational overlap between two numbers is relatively high. In bilateral intraparietal sulci (IPS), for nonsymbolic numbers, the pattern of voxelwise correlations between pairs of numbers mirrored the amount of overlap in their tuning curves under the assumption of approximate, analogue coding. In contrast, symbolic numbers showed a flat field of modest correlations more consistent with discrete, categorical representation (no systematic overlap between numbers). Directly correlating activity patterns for a given number across formats (e.g., the numeral “6” with six dots) showed no evidence of shared symbolic and nonsymbolic number‐specific representations. Overall (univariate) activity in bilateral IPS was well fit by the log of the number being processed for both nonsymbolic and symbolic numbers. IPS activity is thus sensitive to numerosity regardless of format; however, the nature in which symbolic and nonsymbolic numbers are encoded is fundamentally different. Hum Brain Mapp 36:475–488, 2015. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

An approximate sense of quantity is shared across many species and human cultures [Nieder and Dehaene, 2009], and it is thought to develop very early in human infants [Libertus and Brannon, 2009]. It is thus not surprising that many have hypothesized that symbolic numbers (e.g., Indo‐Arabic numerals) are initially derived from this more evolutionarily and developmentally basic, nonsymbolic approximate number system [ANS; e.g., Dehaene, 1997; Eger et al., 2009; Feigenson et al., 2004; Fias et al., 2003; Libertus and Brannon, 2009; Lyons and Ansari, 2009; Lyons and Beilock, 2009; Nieder and Dehaene, 2009; Piazza et al., 2007; Verguts and Fias, 2004]. One implication of this view is that symbolic numbers should inherit, at least in part, their representational structure from their nonsymbolic counterparts [e.g., Dehaene, 2008; Dehaene and Cohen, 2007]. Recent evidence suggests that symbolic and nonsymbolic numbers are more distinct than previously assumed [Bulthé et al., 2014; Cohen Kadosh et al., 2010; Damarla and Just, 2013; Lyons et al., 2012], but the possibility of parallel underlying neural representational structures remains open and untested.

By representational structure, we mean how the different representations within a given system relate to one another. Single‐cell recordings in monkeys [see Nieder, 2005, for a review] and behavioral evidence in humans [e.g., Merten and Nieder, 2009] have provided a clear picture of the representational structure of nonsymbolic numbers. Populations of neurons in monkey parietal cortex are tuned to specific nonsymbolic numbers, and the neuronal tuning curves increase in width (i.e., decrease in precision) as the tuned‐for number in question increases [Nieder, 2005]. A model of number representation based on these observations is an excellent predictor of behavior in both humans and monkeys [Merten and Nieder, 2009]. Figure 1a shows a simulated example using human performance data from Merten and Nieder as a basis for this scaling function. A heretofore untested implication of this model is that the tuning curves for different pairs of numbers overlap to different degrees. That is, the representations of different numbers overlap one another, but, crucially, they do so in a systematic manner that depends on the ratio between the numbers in question. The pairwise proportion of overlap for the Numbers 1–9 is shown in Figure 1b. Two neurons' responses (in terms of net firing rate), regardless of their tuning preference, are expected to be very similar for the Numbers 8 and 9 because the curves for these numbers strongly overlap. We assessed similarity of neural patterns for different numbers via representational similarity analysis [RSA; Kriegeskorte et al., 2008]: distributed, voxelwise correlations between brain responses, in this case to the Numbers 1–9, presented as either symbolic (Arabic numerals) or nonsymbolic (dot‐arrays). We assessed activity patterns in bilateral intraparietal sulci (IPS), regions known to be important for both symbolic and nonsymbolic number representation in humans and monkeys [Eger et al., 2009; Fias et al., 2003; Piazza et al., 2007]. In this way, we examined whether the observed patterns of similarity relations between pairs of number match the degree of representational overlap predicted by the model of nonsymbolic numbers depicted in Figure 1.

Figure 1.

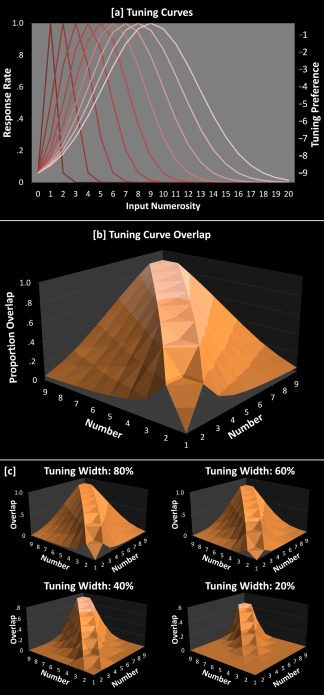
a: Simulated neuronal tuning curves. Curves are Gaussian functions computed with the width of each curve increasing linearly with numerosity in keeping with human behavioral data [Merten and Nieder, 2009] and are similar to actual neuronal results reviewed in Nieder [2005]. b: For each pair of tuning curves, this shows the proportion of those curves that overlap with one another. Note that as the ratio between two numbers approaches 1, the overlap increases. Note also that the main diagonal should yield values of exactly 1 because a number will overlap perfectly with itself. The diagonal has been interpolated here simply for visualization purposes. c: This shows the reduction in degree of overlap as the width of the tuning curves is reduced (width is computed as a percentage of the width of curves in Fig. 1a). Notice that the structure of the pattern in Figure 1b is preserved—even where tuning width is reduced to 20% of that in Figure 1a.

The overall patterns of activity in a section of cortex seen for two highly overlapping numbers should be correlated more so than for two numbers with minimally overlapping curves. We can thus capitalize on the fact that functional magnetic resonance imaging (fMRI) measures neural responses at the level of large populations of neurons to directly test whether the correlation between the distributed patterns of activity seen for two numbers is indeed predicted by the degree to which the curves for those two numbers are expected to overlap. Plotting the correlations between each pair of numbers should yield a graph highly similar to that in Figure 1b. Note that this is a more direct and quantitatively precise test of the hypothesized underlying structure of nonsymbolic number representation—that neural tuning for different numbers shows systematic overlap as a function of numerosity—than has previously been shown by more traditional, univariate analyses of fMRI data [e.g., Piazza et al., 2004]. Furthermore, in this study, we isolated neural activity that corresponds to a single number, independent of response‐demands, so that activity patterns of two different numbers can be correlated in a manner not contaminated by the presence of still other numbers. Paradigms that rely on activity when comparing two numbers or the change in activity when a one number switches to another render it nearly impossible to determine if a given pattern of activity corresponds to one of the numbers, both numbers, the comparison process itself, or some combination of all three.

Eger et al. [2009] and Damarla and Just [2013] used experimental paradigms similar to that employed here to examine whether distributed neural patterns of activity for numbers [{4 8 16 32} and {2 4 6 8} in Eger et al.; {1 3 5} in Damarla and Just] presented in symbolic and nonsymbolic formats could be distinguished from one another. Here, we instead ask (1) about similarity between numbers and (2) test this across a larger set of Numbers (1–9). Taken together, this approach yields a complete snapshot of the representational similarity across all numbers in the dataset; that is, we can build a clear picture of the underlying numerical structure with respect to systematic representational overlap as a function of numerosity. We can then test whether the observed representation structure—how the representations of different numbers in a system relate to one another—matches that predicted by the model in Figure 1. Because this model is derived from neuronal and behavioral data, one can thus draw a direct line between those data and ours in a manner that incorporates the predictions made by an explicit model of how an entire system of (nonsymbolic) numbers is represented.

The critical question that follows is whether symbolic numbers are also characterized by the same—or at least a similar—representational structure. Does the pattern of similarity between numbers resemble that predicted by the model in Figure 1? If the pairwise pattern of correlations for symbolic numbers is similar to that seen for their nonsymbolic counterparts, this would be consistent with the view that symbolic numbers inherit and retain the underlying representational structure from the approximate, nonsymbolic number system. It is important to note here that symbolic numbers tend to be more precise than their ANS counterparts [e.g., Buckley and Gillman, 1974], and so one might not expect an exact match between the two formats. For instance, one widely held assumption is that symbolic numbers simply operate with narrower tuning curves [thus, accounting for their improved precision; Nieder and Dehaene, 2009; Piazza et al., 2007; Verguts and Fias, 2004], which would result in an attenuated but nevertheless similar pattern of relations. Four examples are shown in Figure 1c, each adopting an ever more precise tuning function (80% down to 20% the width of that in Fig. 1a,b), but nevertheless retaining the same numerosity‐dependent scaling as in Figure 1a,b. The crucial thing to note is that the underlying structure of pairwise relations is preserved: the correlations between pairwise overlap values in Figure 1b and assuming functions of 80%, 60%, 40%, and 20% the width of that in Figure 1a (as shown in Fig. 1c) are 0.995, 0.971, 0.889, and 0.662, respectively. In other words, a more precise but otherwise qualitatively similar representational structure for symbolic and nonsymbolic numbers predicts that the pairwise RSA correlation patterns for the two formats should be correlated.

An alternative view is that symbolic numbers form a representational system whose structure is qualitatively distinct from the ANS [e.g., Carey, 2011; Zorzi and Butterworth, 1999]. For instance, one may notice from the previous paragraph that as tuning width decreased (Fig. 1c), the correlation with the pattern of overlap in Figure 1b decreased as well (from 0.995 at 80% as wide to 0.662 at 20% as wide). If the tuning curves were to become infinitely precise, the overlap between pairs of numbers would go to zero, and hence the correlation with the pattern of overlap in Figure 1b should also go to 0. Notice that infinitely precise tuning curves would essentially correspond to discrete, categorical representations. In this way, one could argue that the representational structure of symbolic numbers no longer retains any of the analogue qualities of their ANS counterparts (at least in the literate, adult subjects tested in the current study). Here, we test whether the observed patterns of correlations seen between pairs of symbolic numbers is reliably related (i.e., statistically above 0, across subjects) to the patterns of correlations seen between patterns of nonsymbolic numbers.

Finally, it is worth noting that there is a potential middle way. It may be that symbolic and nonsymbolic numbers differ in their respective representational structures but the representations for a given number derive from a common source. In this view, one would predict that the cross‐format correlations between the same number (e.g., the numeral “6” with six dots) should be higher than cross‐format correlations between different numbers (e.g., the numeral “3” and six dots). Here, we test this prediction. Thus, combined with the analyses described earlier, we test both whether symbolic and nonsymbolic numbers share a similar representational structure, and, independently, whether they share common representations per se.

MATERIALS AND METHODS

Data from 33 University of Chicago undergraduate and graduate students were collected on a 3T Philips Achieva scanner using an 8‐channel Philips SENSE head‐coil. The data analyzed here were taken from a larger data collection project spanning multiple scanning sessions (all data reported here were taken from the same scanning session; results here are not reported elsewhere and address a unique set of hypotheses). Thirty six descending interleaved slices were collected at a TR of 2sec (TE = 25 msec), with a slice‐thickness of 3.0 mm (0.25 mm skip), an in‐plane resolution of 2.875 × 2.875 mm (80 × 80 matrix), and a flip‐angle of 80°. Prior to analysis, time‐series were corrected for slice‐timing and subject motion, and then subjected to a high‐pass temporal filter [general linear model (GLM) Fourier basis set]. No spatial smoothing was used. Data were next submitted to a random‐effects GLM [Friston et al., 1994] convolved using a standard 2‐gamma HRF model. Large, bilateral IPS regions (Fig. 3a) were identified via the main effect of all dot numerosities greater than baseline, thresholded first voxelwise at P < 0.005, and subsequently cluster‐level corrected for multiple‐comparisons using a Monte‐Carlo simulation procedure [Forman et al., 1995] at α < 0.01. Preprocessing and RFX contrast analyses were conducted using BrainVoyager QX (version 2.4.1); RSA was conducted using MATLAB (version 2012a). Left and right IPS regions were localized via the main effect of nonsymbolic numbers > baseline, and comprised 392 and 308 functional voxels, respectively (baseline was estimated as the model intercept for a given subject in a given voxel).

Figure 3.

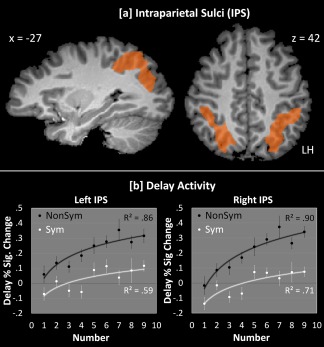
a: Bilateral IPS regions were identified via the main effect of nonsymbolic numbers > baseline at P < 0.005 (cluster‐corrected at α = 0.01). All parietal areas identified for symbolic numbers > baseline were subsumed by the nonsymbolic IPS areas shown above. b: IPS activity (from the regions shown in Fig. 3a) for symbolic and nonsymbolic numbers during the delay period, plotted as a function of Number (1–9). Log fit was high for both formats, indicating that the IPS was sensitive to number in both formats. Note that linear fit was also high in each case (left‐nonsymbolic: R ² = 0.85; left‐symbolic: R ² = 0.63; right‐nonsymbolic: R ² = 0.86; left‐nonsymbolic: R ² = 0.69).

While in the scanner, subjects completed six runs of a delayed match‐to‐sample task adapted from single‐cell studies with monkeys that have been successful in detailing numerical tuning curves for individual neurons [see Nieder, 2005; Fig. 2c]. In the current version, subjects first saw a number for 500 msec followed by a jittered delay (1.5–5.5 sec). A second number was then presented for 500 msec, after which the screen went blank for 2,500 msec or until the subject responded. Fixation time between response on a given trial and the initial stimulus onset for the subsequent trial was also jittered (1.9–8.4 sec). Subjects' task was to determine if the two numbers were numerically equal or different by pressing one of two buttons with their two index fingers. Which button meant same or different was randomized across participants. The two numbers were numerically equal on 50% of trials (match); the second number was greater than the first on 25% of trials (nonmatch); the second number was lesser than the first on 25% of trials (nonmatch). Numbers were either presented symbolically (Indo‐Arabic numerals) or nonsymbolically (dot‐arrays). Font style was randomized for symbolic trials to reduce the efficacy of visual pattern‐matching. Note that the short presentation time of both stimuli reduced the likelihood that participants counted the dots in the dot‐arrays. Continuous parameters (dot‐size, array contour, density, aggregate area) were balanced across nonsymbolic trials, such that each parameter was correlated with numerosity on half the trials, and anticorrelated on the remaining half. This was intended to reduce the efficacy of relying on any one of these to compare numerosities in the nonsymbolic task.

Figure 2.

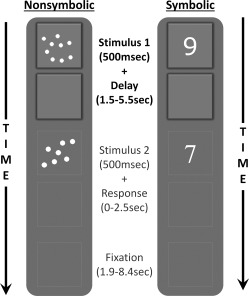
Example trials for symbolic and nonsymbolic numbers. Participants' task was to decide whether the second stimulus matched the first in terms of quantity. The focus of this study was on the period corresponding to presentation of the first stimulus and the delay as they held the number in mind (prior to seeing the second stimulus or being able to prepare a specific response). The program moved on to the fixation period between trials after detecting a response; no feedback was given.

The quantities to be held in mind during the delay period (between the first and second numbers) were the integers 1–9. Subjects saw 18 trials for each quantity; in nine of these trials, numbers were presented symbolically; in the other nine, numbers were presented nonsymbolically. To increase the precision of our estimate for a given voxel's activity for a given number, activity across the nine trials (for each subject) was averaged together. Our focus was on activity during the first stimulus and the delay before the onset of the second stimulus (activity during the second stimulus and response was modeled to remove accompanying variance but was treated as a covariate of no interest in the model). This allowed for a measure of neural activity during representation of a single quantity, independent of activation related to preparation and execution of a specific motor response.

Single‐cell recordings [see Nieder, 2005, for a review] and human behavioral data [Merten and Nieder, 2009] converge to show that nonsymbolic number representation can be well modeled by assuming a Gaussian distribution centered on each number (Fig. 1a). The width of this distribution is assumed to increase linearly as number increases. The scaling parameter we adopted here was 0.421, as Merten and Nieder [2009] showed that this value yielded very good fit for human nonsymbolic number estimation performance. Representations can be simulated to be more “precise” by narrowing the width—that is, by decreasing the scaling parameter. Figure 1c shows examples of the reduction in predicted pairwise overlap with reduced scaling parameters, with the original 0.421 value reduced to 0.337, 0.252, 0.168, and 0.084. Finally, there is some debate in the literature over whether distribution widths increase linearly with number, or if number is actually represented on a log scale with fixed distribution widths. Part of the debate is that both version of the model tend to predict very similar neuronal and behavioral curves [indeed, both models yielded similarly good fit of behavioral data in Merten and Nieder, 2009]. This debate is beyond the scope of this article; however, it is worth noting that the degree of pairwise overlap (e.g., Fig. 1b) is extremely similar whether one adopts the linear or log version of the model: the predicted overlap proportions (Fig. 1b, x‐axis of Fig. 6) are correlated at r = 0.996. Hence, it is perhaps unsurprising that our results are highly similar whether one opts for the log or linear version of the model.

Figure 6.

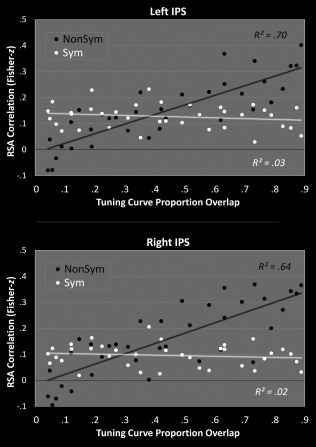
The average Fisher‐z values (across 33 subjects) was plotted for each pair of numbers (Fig. 5) against the proportion of tuning curve overlap for those two numbers (assuming an analogue representation, see Fig. 1). Note that a log‐fit was similar for both formats (nonsymbolic: left: R ² = 0.68, right: R ² = 0.64; symbolic: left: R ² = 0. 01, right: R ² = 0.01).

RESULTS

Univariate Results

Figure 3b shows delay activity for symbolic and nonsymbolic numbers in each hemisphere of the IPS plotted as a function of the number being held in mind. In both hemispheres, data were well fit by a log model, which is highly consistent with previous work [Nieder and Dehaene, 2009]. Further, this indicates that the IPS is sensitive to number represented both symbolically and nonsymbolically—consistent with this, the 2(Format: symbolic, nonsymbolic) × 9(Number: 1–9) interaction was not significant in either hemisphere, whether number was modeled linearly or as a log function. In other words, activity during the delay varied systematically with the quantity of the number being held in mind, whether that number was presented symbolically or nonsymbolically—a result highly consistent with previous work [Eger et al., 2009; Fias et al., 2003; Piazza et al., 2007]. However, this analysis—as with previous studies—cannot distinguish the underlying type of numerical coding. To see why this is may be a problem, we turn next to the behavioral results.

Behavioral Results

Figure 4 shows behavioral results plotted as a function of the number held in mind during the delay period (akin to Fig. 3b). For nonsymbolic numbers, as in Figure 3b, both behavioral measures (response‐times and error‐rates) varied systematically as a function of number (whether modeled linearly or as a log‐function), such that, as number increased, both response‐times (RTs) and error‐rates (ERs) increased. This was true even after controlling for the ratio between the delay number and the match number (Stimuli 1 and 2, respectively, in Fig. 2). In other words, the complete pattern of behavioral results in Figure 4 can be attributed to the magnitude of Stimulus 1. Results were markedly different for symbolic numbers, however: Performance on neither measure varied significantly as a function of number.

Figure 4.

Behavioral curves plotted as a function of the number held in mind (during the delay period). Linear fit was very high for nonsymbolic numbers but not for symbolic numbers. Note that results were similar for log fit (RT‐nonsymbolic: R ² = 0.81; RT‐symbolic: R ² = 0.02; ER‐nonsymbolic: R ² = 0.71; ER‐symbolic: R ² = 0.11).

Interestingly, these results partially contrast with the overall mean‐activity results from the previous section (Fig. 3b). Although the nonsymbolic behavioral and fMRI results are highly consistent with one another, the symbolic results are quite different. One explanation is symbolic and nonsymbolic numbers are represented in qualitatively different ways. That is, while the results in Figure 3b [as well as considerable previous work: e.g., Eger et al., 2009; Fias et al., 2003; Piazza et al., 2007] indicate that the IPS is sensitive to numerosity for both symbolic and nonsymbolic numbers, the nature of the underlying neural representations may be fundamentally different.

Specifically, the behavioral data suggest that nonsymbolic numbers are represented in approximate fashion, while symbolic numbers are represented in a much more precise, categorical fashion. For nonsymbolic numbers, if the width of neuronal tuning curves increases (and precision of representation decreases) as nonsymbolic quantity increases [as has been demonstrated in numerically tuned neurons in monkeys: Nieder, 2005; see also Fig. 1a), then one would expect to see systematically degraded performance as a function of increasing quantity. This is exactly what we see for nonsymbolic numbers in Figure 4. By contrast, if symbolic numbers are represented in a more categorical fashion, then the Numbers 1–9 should be represented with equally high precision, and so performance should not vary with the number held in mind during the delay.

At the neural level, the above accounts imply that there should be very little (if any) overlap between tuning curves for symbolic numbers. If true, then one would expect there to be minimal correlations between neural representations of different numbers at the population level (as we will measure with RSA in the next section). Most importantly, these correlations should not vary systematically as a function of number. The overlap between tuning curves for nonsymbolic numbers should be overall higher and should vary systematically with number (as in Fig. 1a,b).

RSA

For RSA, for each voxel in each subject, we extracted 19 different values from the RFX GLM. These were activity levels for the symbolic and nonsymbolic quantities 1–9, and a measure of baseline activity (average activity for that subject and that voxel ). In all RSA analyses, baseline activity was included as a covariate (hence, all reported values are partial‐correlations). Adjacent voxels will share vascular, neural, and imaging elements (e.g., field strength) that may create the appearance of very high correlations across voxels due largely to sources unrelated to the functional elements of interest here (numerical representation). Covarying out baseline activity is a statistical means of reducing the influence of those elements of no interest.

RSA was computed for each hemisphere of the IPS separately. The left hemispheric IPS activation comprised 392 functional voxels (Talairach center‐of‐gravity: −30, −52, 38); right hemisphere comprised 308 functional voxels (Talairach center‐of‐gravity: 29, −55, 38). A partial‐r was computed for each pair of numbers. This was done separately for each of the 33 subjects. Because r‐values are non‐normally distributed, r‐values were next transformed using Fisher's z‐transformation: z = arctanh(r). The z for each number‐pair was then averaged over all subjects; averages are plotted as a function of number‐pair in Figure 5 (see also Tables 1–2). Note that the maps are symmetrical over the main‐diagonal. Also, the main diagonal corresponds to autocorrelations (r = 1), but for visualization purposes, these were interpolated with surrounding cells. A z of 0.10 is associated with an r‐value of 0.0997 and P‐values of 0.0245 and 0.0406, in the left and right hemispheres, respectively; a z of 0.20 is associated an r‐value of 0.1974 and ps of <0.0001 and 0.0003. Significance bands in Figure 5 are computed in this manner. An alternative means of testing for significance is a one‐sample t‐test of zs in a cell against 0 (N = 33). As a rule of thumb, average z‐values in Figure 5 of 0.07 or greater were significantly greater than 0 at P < 0.05 (two‐tailed), and significance increased on average by roughly an order of magnitude for each increase in z‐value of 0.04 (e.g., z of 0.39 roughly corresponds to P = 5 E−10).

Figure 5.

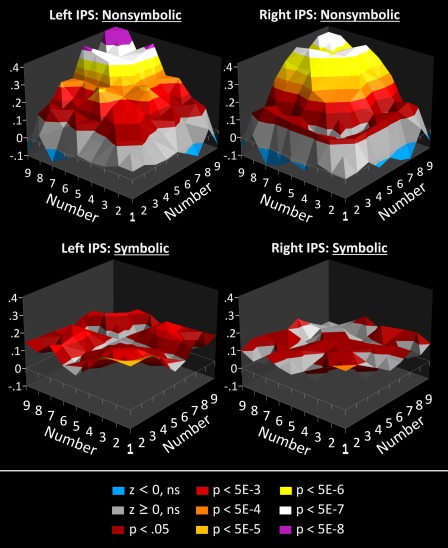
RSA results were shown by plotting the average Fisher‐z values (across 33 subjects) relating the patterns of activity for each pair of numbers in each hemisphere of the IPS, and for nonsymbolic (top) and symbolic (bottom) numbers. Z‐axes plot Fisher‐z values. Different color bands distinguish z‐values that meet increasingly strict significance criteria (which vary across hemispheres due to the different numbers of voxels in each ROI). Note that the main‐diagonal of each map should contain values of 1, but to avoid occluding other values, these are instead interpolated with their nearest neighbors.

From Figure 5 (see also Tables 1–2), one can see that the pattern of correlations for nonsymbolic numbers is highly similar to that predicted by the degree of overlap between analogue tuning curves in Figure 1b. By contrast, RSA results for symbolic numbers show a flat field of near‐zero correlations, which is more consistent with independent, non‐overlapping representations of each symbolic number (i.e., a discrete, categorical representation).

Figure 6 shows these correlations plotted against the degree of tuning curve overlap from Figure 1b (as the matrices in Fig. 5 are symmetrical, only the 36 off‐diagonal values from one half of each map are used). In this manner, one can statistically quantify the degree to which correlations across numbers in each format match the degree of overlap predicted from an approximate, analogue representation. This relation was significant for nonsymbolic (Left: r ₃₄ = 0.839, P < 0.001; Right: r ₃₄ = 0.800, P < 0.001) but not symbolic numbers (Left: r ₃₄ = −0.177, P = 0.302; Right: r ₃₄ = −0.131, P = 0.445). The difference in slopes across formats was also significant in both hemispheres (Left: F _1,68 = 62.75, P < 0.001; Right: F _1,68 = 51.93, P < 0.001). Note that the main effect of format was significant in both hemispheres as well (Left: F _1,68 = 35.29, P < 0.001; Right: F _1,68 = 17.01, P < 0.001), with the overall degree of correlations between numbers higher for nonsymbolic numbers. Finally, if one directly relates RSA correlation values for symbolic with nonsymbolic numbers (as a function of each of the 36 number pairs), the relation was in fact slightly negative (Left: r ₃₄ = −0.406, P = 0.014; Right: r ₃₄ = −0.326, P = 0.053), indicating, if anything, opposing patterns of similarity for symbolic and nonsymbolic number‐pairs. Notice that the upper bounds of the 95% confidence intervals on these correlations are below or essentially equal to 0 (Left: CI_95(upper) = −0.090; Right: CI_95(upper) = 0.002.This indicates that the representational structure of symbolic numbers is not merely a more precise version of that seen for nonsymbolic numbers. Instead, taken together with the analyses discussed above, the overall pattern of results is highly consistent with the notion that nonsymbolic numbers are analogue‐coded and symbolic numbers are coded in a qualitatively distinct, perhaps categorical manner.

Note that the theoretical perspective adopted in the preceding paragraph and in Figure 6 treats individual variation as idiosyncratic deviation from a central tendency—that is, noise in one's estimate that can be reduced by averaging across observations from individual humans to obtain a clearer picture of the hypothesized underlying central principle [for a similar approach to fitting model predictions with group averages of fMRI data, see, e.g., Piazza et al., 2004]. An alternative view concerns the likelihood of agreement between a model and what is observed in a specific individual (e.g., the patient seated across one's desk). In the current dataset, one can assess this by computing the correlation between predicted overlap from the model in Figure 1b and the pattern of (transformed) partial‐rs for each subject individually (i.e., repeat the analysis in Fig. 6 separately for each individual subject). By comparing average model fit, one can assess whether the model in Figure 1b is, on average, more capable of predicting an individual's RSA results (partial‐rs) for nonsymbolic relative to symbolic numbers. Average correlations between the model and RSA results were significantly greater than 0 for nonsymbolic (Left: mean = 0.438, se = 0.050, t ₃₂ = 8.73, P < 0.001, d = 3.09; Right: mean = 0.461, se = 0.057, t ₃₂ = 8.07, P < 0.001, d = 2.85) but not symbolic numbers (Left: mean = −0.049, se = 0.029, t ₃₂ = −1.72, P = 0.095, d = −0.61; Right: mean = −0.038, se = 0.031, t ₃₂ = −1.23, P = 0.229, d = −0.43). Average correlations between the model and RSA results were significantly greater for nonsymbolic than symbolic numbers (Left: t ₃₂ = 7.57, P < 0.001, d = 2.68; Right: t ₃₂ = 7.87, P < 0.001, d = 2.78). Finally, if one directly relates correlation values for symbolic with nonsymbolic numbers (as a function of each of the 36 number pairs), the average relation was slightly negative (Left: mean = −0.089, se = 0.029, t ₃₂ = −3.02, P = 0.005, d = −1.07; Right: mean = −0.075, se = 0.029, t ₃₂ = −2.60, P = 0.014, d = −0.92).

Rather than the amount of overlap predicted by a hypothetical model, another way to think about the data in Figures 5 and 6 is in terms of the ratio between two numbers. It has long been recognized that the ratio between two numbers is a strong determinant of how well individuals are able to compare the two numbers in terms of their relative quantity [e.g., Dehaene, 2008]—an effect that is especially striking for nonsymbolic numbers [e.g., Buckley and Gillman, 1974]. This is thought to be driven by the fact that there is increasing overlap in the approximate representations of two numbers as the ratio between them approaches 1. Thus, if indeed nonsymbolic numbers are represented in an analogue fashion, then the correlation in neural activity between two numbers should be directly related to the ratio between those numbers. According to our view that symbolic numbers are represented in a more discrete fashion—with little or no overlap between numbers—we should not see such a relation for symbolic numbers. In keeping with these predictions, the relation between ratio and correlation coefficients (plotted as a function of 36 possible number‐pairs) was significant for nonsymbolic (Left: r ₃₄ = 0.837, P < 0.001; Right: r ₃₄ = .796, P < 0.001) but not symbolic numbers (Left: r ₃₄ = −0.152, P = 0.377; Right: r ₃₄ = −0.106, P = 0.537). The difference in slopes was also significant in both hemispheres (Left: F _1,68 = 60.58, P < 0.001; Right: F _1,68 = 49.71, P < 0.001). Interestingly, this (non)result for symbolic numbers (along with the behavioral results in Fig. 4) is consistent with previous behavioral and neuroimaging work indicating that ratio‐effects in symbolic number comparison tasks are driven less by numerical representations per se, but perhaps by more general processes related to response generation [Göbel et al., 2004; Maloney et al., 2010; Van Opstal et al., 2008; Verguts and Van Opstal, 2005]. In sum, our RSA results hold whether one considers neural correlations between numbers as a function of the modeled overlap between pairs of tuning curves, or simply as the ratio between two numbers.

Number Specificity and Cross‐Format Representation

Given null results for symbolic numbers discussed earlier and shown in Figures 5 and 6, one may wonder whether this was driven by failure to elicit reliable activation patterns for each symbolic number. To test this, we conducted a split‐half analysis. Trials were arbitrarily divided into even and odd instances of a given number in a given format, and activity estimates were obtained via an RFX GLM as above. For each subject, we were then able to examine the correlations between a given number symbol (say, 3) in one half of the dataset and that same number (in the same format) in the other half of the dataset. As before, this could also be done for different number‐pairs. If the activity pattern for a given number symbol (3) is reliably activated, then same‐number correlations (e.g., 3 with 3) should be higher than different‐number correlations (e.g., 3 with 2, 3 with 4, etc.). In this way, for each subject, we computed average same‐number correlations and average different‐number correlations (this was done separately for symbolic and nonsymbolic numbers and are shown in Fig. 7—white and black bars, respectively). In both hemispheres, for symbols, same‐number correlations (converted here to Fisher‐z values) were indeed significantly greater than different‐number correlations. Left: same>different: t ₃₂ = 20.56, P < 0.001, d = 7.27. Right: same>different: t ₃₂ = 14.09, P < 0.001, d = 4.98. The same was true for nonsymbolic numbers. Left: same>different: t ₃₂ = 21.79, P<0.001, d = 7.71. Right: same>different: t ₃₂ = 20.56, P<0.001, d = 6.26. Hence, the null results for symbols in Figures 5 and 6 (no systematic correlations between different symbolic numbers) cannot be attributed to a failure to reliably evoke consistent patterns across instances of a given number.

Figure 7.

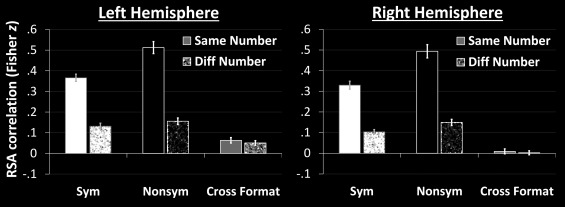
Same‐number and different‐number correlations for symbolic (white) and nonsymbolic (black) stimuli is given in this figure. Gray bars indicate cross‐format correlations. Correlation values have been Fisher‐z transformed. Error‐bars indicate standard errors of the mean (across 33 subjects).

Next, we assessed numerical specificity across formats. That is, we tested whether same number correlations across formats (e.g., the numeral “6” with six dots) were greater than different number correlations across formats (e.g., the numeral “3” with six dots). This allowed us to assess whether, in spite of comprising different representational structures, a given number in one format nevertheless shares a core representation with its counterpart in the other format. Note that testing same‐number against different‐number correlations is an important check to ensure that cross‐format correlations are indeed number‐specific. Statistics were computed as in the previous paragraph (including transformation to Fisher z‐values), with the exception that there was no need to first split the dataset into even and odd instances; results are depicted in Figure 7 (gray bars). In the left hemisphere, same‐number cross‐format correlations were significantly greater than zero (t ₃₂ = 4.71, P < 0.001, d = 1.67); however, these correlations were not indicative of shared number‐specific representation, as same‐number correlations were not any greater than different‐number correlations (t ₃₂ = 1.00, P = 0.324, d = 0.35). In the right hemisphere, same‐number cross‐format correlations were neither greater than zero (t ₃₂ = 0.76, P = 0.451, d = 0.27) nor greater than different‐number correlations (t ₃₂ = 0.60, P = 0.550, d = 0.21). Consistent with previous work [Bulthé et al., 2014; Damarla and Just, 2013; Lyons and Beilock, 2012], these results do not support the claim that numbers in symbolic and nonsymbolic formats overlap in their representations.

Discussion

Here, we test whether symbolic numbers inherit the representational structure of their nonsymbolic counterparts, and our results strongly indicate that they do not. Bilateral IPS showed activity during the delay that varied systematically with the quantity of the number being held in mind, whether that number was presented symbolically or nonsymbolically. This result is consistent with previous work [Eger et al., 2009; Fias et al., 2003; Piazza et al., 2007], and it indicates that the IPS is sensitive to numerosity in both formats. Behavioral results, however, showed that the quantity of a number held in mind predicts the speed and accuracy with which one matches said number with another number only in the nonsymbolic case (Fig. 4). This suggested that, while parietal cortex appears to code for number in both formats, the manner in which it does so depends on format. RSA neural results confirmed this prediction: the degree to which patterns of voxelwise activity correlated for a pair of numbers was directly predicted by the amount of hypothesized—under the assumption of an approximate, analogue representation—neuronal tuning‐curve overlap for those two numbers but only for nonsymbolic numbers (Figs. 5 and 6). Symbolic numbers showed overall significantly reduced correlations between numbers (compared to their nonsymbolic counterparts), and these correlations did not vary systematically as a function of either ratio or predicted overlap (Figure 1b–c). These three lines of evidence (traditional mean‐based fMRI data, behavioral results, and RSA) converge to show that parietal cortex is important for representing both symbolic and nonsymbolic numbers, but the former are represented in a more discrete fashion (with little to no overlap between numbers), while the latter are represented in a more analogue fashion (with overlap increasing systematically with increasing numerosity). Our results are consistent with evidence suggesting that symbolic and nonsymbolic numbers are more distinct than previously thought [e.g., Cohen Kadosh et al., 2011; Lyons et al., 2012; Shuman and Kanwisher, 2004]. Specifically, our results indicate that symbolic numbers form a system of discrete, categorical representations qualitatively distinct from the approximate, nonsymbolic number system.

It is worth distinguishing here between representational structure—how elements (i.e., numbers) within a representational system relate to one another—and the representations themselves. The RSA results in Figures 5 and 6 (and Tables 1 and 2) indicate that the structure of how symbolic numbers relate to one another is qualitatively different than the structure of how nonsymbolic numbers relate to one another. Importantly, this distinction does not appear to be driven simply by narrower tuning curves for symbolic numbers. As Figure 1c shows, narrower curves still preserve the overall structure of the representational overlap, and hence yield similar RSA predictions—that is, the RSA patterns for symbolic and nonsymbolic numbers (plotted as a function of each number pair, as in Fig. 6) should still be correlated. However, the RSA results for each pair of symbolic numbers were unrelated (or in fact perhaps slightly negatively related) to both the RSA results for nonsymbolic numbers and the predictions from the model in Figure 1. Thus, a narrowed tuning curve account would need to postulate essentially infinitely narrow curves—or, discrete, categorical representations. It is on this basis that we argue that the representational structures of symbolic and nonsymbolic numbers are qualitatively different.

Table 1.

RSA correlations (from Figure 5) for each nonsymbolic number pair (Fisher z‐transformed)

Left	9	8	7	6	5	4	3	2	1
9	—	0.402	0.262	0.368	0.212	0.220	0.134	0.105	−0.080
8	0.052	—	0.323	0.341	0.222	0.155	0.123	0.152	0.039
7	0.048	0.057	—	0.321	0.215	0.169	0.145	0.078	−0.078
6	0.047	0.048	0.063	—	0.233	0.252	0.123	0.121	−0.033
5	0.046	0.038	0.040	0.038	—	0.181	0.130	0.073	0.012
4	0.033	0.038	0.042	0.036	0.036	—	0.154	0.080	0.004
3	0.040	0.037	0.036	0.031	0.039	0.038	—	0.114	0.011
2	0.043	0.034	0.042	0.037	0.033	0.034	0.035	—	0.045
1	0.036	0.051	0.027	0.027	0.031	0.032	0.043	0.036	—
Right	9	8	7	6	5	4	3	2	1
9	—	0.366	0.314	0.355	0.305	0.227	0.090	0.105	−0.062
8	0.047	—	0.334	0.369	0.290	0.228	0.138	0.159	0.037
7	0.040	0.056	—	0.343	0.302	0.212	0.077	0.139	−0.095
6	0.039	0.047	0.058	—	0.271	0.241	0.130	0.132	−0.070
5	0.038	0.048	0.043	0.049	—	0.200	0.073	0.129	−0.022
4	0.037	0.042	0.037	0.046	0.041	—	0.070	0.124	−0.042
3	0.039	0.039	0.036	0.039	0.041	0.038	—	0.117	0.021
2	0.034	0.036	0.038	0.041	0.033	0.034	0.036	—	0.002
1	0.036	0.045	0.033	0.038	0.032	0.033	0.036	0.032	—

Values above the diagonal are averages (across 33 subjects); values below the diagonal are corresponding standard‐errors of the mean.

Table 2.

RSA correlations (from Figure 5) for each symbolic number pair (Fisher z‐transformed)

Left	9	8	7	6	5	4	3	2	1
9	—	0.053	0.152	0.147	0.104	0.046	0.139	0.142	0.148
8	0.042	—	0.161	0.030	0.077	0.183	0.145	0.075	0.119
7	0.045	0.041	—	0.083	0.134	0.173	0.172	0.156	0.184
6	0.041	0.043	0.039	—	0.090	0.085	0.110	0.084	0.098
5	0.041	0.041	0.040	0.034	—	0.133	0.134	0.122	0.072
4	0.041	0.037	0.034	0.048	0.041	—	0.173	0.108	0.137
3	0.048	0.048	0.040	0.046	0.041	0.035	—	0.163	0.229
2	0.048	0.039	0.039	0.045	0.046	0.042	0.045	—	0.233
1	0.044	0.054	0.034	0.047	0.052	0.039	0.049	0.040	—
Right	9	8	7	6	5	4	3	2	1
9	—	0.032	0.083	0.136	0.098	0.030	0.131	0.139	0.102
8	0.043	—	0.072	0.037	0.039	0.158	0.116	0.019	0.066
7	0.050	0.045	—	0.102	0.056	0.088	0.100	0.122	0.123
6	0.041	0.039	0.040	—	0.119	0.120	0.116	0.094	0.088
5	0.035	0.041	0.041	0.030	—	0.105	0.048	0.058	0.076
4	0.035	0.031	0.040	0.037	0.038	—	0.160	0.026	0.121
3	0.044	0.045	0.040	0.037	0.036	0.036	—	0.122	0.163
2	0.047	0.043	0.034	0.046	0.036	0.042	0.036	—	0.206
1	0.048	0.050	0.034	0.042	0.038	0.042	0.037	0.039	—

Values above the diagonal are averages (across 33 subjects); values below the diagonal are corresponding standard‐errors of the mean.

Turning to the representations themselves, it remains possible that the representation for a given symbolic number (e.g., the numeral “6”) and its direct nonsymbolic counterpart (e.g., six dots) are linked, even if the respective symbolic and nonsymbolic systems are unrelated. To draw a loose analogy, a train station and an airport in a given city may by physically adjacent or even occupy the same building, but the respective locomotive and aerial networks to which each belongs may be entirely unrelated. To test this possibility, we examined whether the cross‐format correlations were number‐specific—for example, is the correlation between “6” and six dots, greater than that between “3” and six dots? Figure 7 (gray bars) indicate that they were not. In other words, consistent with recent work [Bulthé et al., 2014; Damarla and Just, 2013; Lyons et al., 2012], our results show that symbolic and nonsymbolic numbers differ not only in terms of their representational structure but also in terms of the representations themselves.

On a broader note, our results provide an example of how, even though a given region represents two types of stimuli, this does not mean that the underlying neural codes for these stimuli are the same. Our argument parallels one made from behavioral evidence. Distance effects (better performance when comparing two numerically distant versus two numerically close numbers) are regularly observed for both symbolic and nonsymbolic numbers [e.g., Buckley and Gillman, 1974], leading to the conclusion that their underlying representations operate according to similar principles [e.g., Dehaene, 2008]. However, further evidence suggests there are distinct sources driving the distance effects observed for symbolic and nonsymbolic numbers [Göbel et al., 2004; Maloney et al., 2010; Van Opstal et al., 2008; Verguts and Van Opstal, 2005]. In other words, though outward behavior is similar (distance effects), the underlying causes may be different. Our RSA analyses indicate that, while the IPS is sensitive to number in both formats, the underlying nature of symbolic and nonsymbolic processing is nevertheless quite distinct.

In this respect, it is important to emphasize that we are not attempting to argue against a considerable body of literature indicating that parietal cortex is important for processing symbolic numbers [Ansari, 2008; Bugden et al., 2012; Cohen Kadosh et al., 2010; Dehaene et al., 2003; Eger et al., 2009; Fias et al., 2003; Holloway et al., 2013; Lyons and Ansari, 2009; Nieder and Dehaene, 2009; Notebaert et al., 2011; Piazza et al., 2007; Pinel et al., 2001; Sandrini et al., 2004; Santens et al., 2010]. Indeed, Figure 3b shows numerically sensitive responses (i.e., good fit between delay activity and the log of the number being held in mind) in bilateral IPS for symbolic and nonsymbolic numbers, in keeping with previous predictions about the nature of number representation in the brain [see Nieder and Dehaene, 2009, for a review]. IPS activity is thus sensitive to numerosity regardless of format, but RSA results show that the nature of this sensitivity depends fundamentally on whether numbers are represented symbolically or nonsymbolically.

It is worth considering that regions were localized via the main effect of nonsymbolic numbers > baseline. With respect to RSA, correlations between each nonsymbolic number and baseline activity (due to the within‐subjects nature of the contrast) will be inflated due to this localizer contrast. We included baseline activity as a covariate for both symbolic and nonsymbolic RSA; thus, if anything, the localizer contrast may have deflated the overall strength of correlations between nonsymbolic numbers. Furthermore, because the localizer was an unweighted main effect, it does not bias one to find greater number–number correlations for any one pair of nonsymbolic numbers over another (which was the primary focus of the RSA results).

With respect to symbolic numbers, one may object to the nature of the localizer on theoretical as opposed to statistical grounds because the nonsymbolic localizer may have biased us to find numerical tuning for nonsymbolic as opposed to symbolic numbers. The whole‐brain main‐effect of symbolic numbers > baseline yielded a significant result only at a more liberal P < 0.05 (cluster‐corrected at α = 0.05) threshold, and even then only in a subset of 33 functional voxels in left IPS (which were subsumed by the larger left IPS region found for nonsymbolic > baseline). It may be that symbolic numbers are processed only in this subset of IPS voxels. If so, then including the other 359 left IPS voxels in the RSA may have unnecessarily suppressed the apparent correlations between symbolic numbers in this region. First, we chose to analyze the larger IPS regions (392 and 308 voxels) in the main analyses because the larger number of observations increases our power to detect subtle differences in correlations between pairs of numbers. Second, we do not find the above argument convincing on the grounds that—as will be seen in the next section—the canonical (mean‐based) results shown in Figure 3 indicated IPS sensitivity to increasing number in symbolic numbers even when including all voxels in the larger IPS regions. Nevertheless, we re‐ran the RSA analyses on only the 33 left IPS voxels that also showed a significant main effect of symbolic > baseline. Results were highly similar, with the exception that overall correlations were reduced, as one would expect given the inclusion of roughly a tenth the number of observations. Crucially, the central conclusions remain unchanged; complete results can be found in Supporting Information.

Another potential objection is that subjects may have relied entirely on matching of perceptual features, and so did not actually activate numerosity. First, both symbolic and nonsymbolic stimuli were varied so as to discourage such a strategy. Second, all fMRI analyses focused on activity during the delay, prior to onset of the matching decision. From Figure 3b, bilateral IPS showed systematic increase in activity as a function of the number being held in mind during the delay period, indicating that subjects did indeed activate the quantity associated with the stimulus. Third, several studies have demonstrated that, when a number precedes a second number in time, the (numerical) meaning of the first influences processing of the second, indicating that, even though the quantity of the first may be irrelevant to processing the second, the numerical meaning of the first is nevertheless activated [Bahrami et al., 2010; Naccache and Dehaene, 2001; Roggeman et al., 2007; Van Opstal et al., 2008]. Note also that these studies typically involve very brief presentations of the first number; here, we required subjects to explicitly hold the first number in mind, making activation of said number's numerical meaning still more likely. Taken together, these lines of evidence—stimulus design, evidence in Figure 3b, and previous literature—converge to make it clear that subjects did in fact activate numerosity during the delay period for both symbolic and nonsymbolic numbers. This point is particularly salient when considering the null RSA result for symbolic numbers, and reinforces the conclusion that the IPS does process symbolic numbers, but it does so in a manner qualitatively different than for their nonsymbolic counterparts.

With respect to the nonsymbolic task, given that we measured activity during a delay period that was several seconds long in some cases, one might imagine that subjects may have converted dot‐arrays into a verbal code, and so we would not be measuring nonsymbolic number activity at that point. We do not think this is the case however, because a verbal code, being symbolic, would have yielded RSA results akin to those seen for symbolic numbers. This was of course not the case (Fig. 5), which makes this explanation less plausible. In a similar vein, it is difficult to proffer an alternative explanation based on “task difficulty” or working memory load that accounts for all of our results. While these explanations could certainly explain the behavioral results in Figure 4, it is then unclear how they account for the divergent nature of the mean‐based results in Figure 3 and the RSA results in Figure 5. In sum, while various alternative explanations might account for this or that part of the results, we maintain that the simplest single explanation that accounts for all aspects of the data is that the IPS processes both symbolic and nonsymbolic numbers, but it does so in a manner that varies qualitatively across formats.

Conclusion

We provide the first neural evidence that symbolic and nonsymbolic numbers are coded in fundamentally different ways in the human IPS. Our results are also consistent with evidence suggesting that symbolic and nonsymbolic numbers may be more distinct than previously thought [Bulthé et al., 2014; Cohen Kadosh et al., 2011; Lyons et al., 2012; Shuman and Kanwisher, 2004]. On the one hand, we show that the IPS is sensitive to numerosity whether presented symbolically or nonsymbolically. On the other hand, we provide converging behavioral and neural evidence that nonsymbolic numbers are coded according to an analogue principle of overlapping, approximate tuning curves. Crucially, we find no evidence that symbolic numbers are coded in this manner. Instead, both behavioral and neural results indicate that symbolic numbers are each coded independently of one another, with little or no representational overlap between numbers. A long line of behavioral evidence indicates that symbolic number processing is more precise than nonsymbolic number processing [e.g., Buckley and Gillman, 1974; Dehaene, 2008]. Our data provide a potential neural mechanism for this: while the precision of nonsymbolic number representation becomes steadily less precise as the number being represented increases, the complete lack of overlap in symbolic numerical tuning curves (indicating essentially infinitely precise or categorical representation) may be extended to explain how symbolic numbers can retain representational precision even at extremely large values (e.g., one can numerically differentiate 1,000,000 from 1,000,001 using number symbols but not arrays of dots).

Supporting information

Supplementary Information