Hemispheric lateralization of topological organization in structural brain networks

Abstract

The study on structural brain asymmetries in healthy individuals plays an important role in our understanding of the factors that modulate cognitive specialization in the brain. Here, we used fiber tractography to reconstruct the left and right hemispheric networks of a large cohort of 346 healthy participants (20–86 years) and performed a graph theoretical analysis to investigate this brain laterality from a network perspective. Findings revealed that the left hemisphere is significantly more “efficient” than the right hemisphere, whereas the right hemisphere showed higher values of “betweenness centrality” and “small‐worldness.” In particular, left‐hemispheric networks displayed increased nodal efficiency in brain regions related to language and motor actions, whereas the right hemisphere showed an increase in nodal efficiency in brain regions involved in memory and visuospatial attention. In addition, we found that hemispheric networks decrease in efficiency with age. Finally, we observed significant gender differences in measures of global connectivity. By analyzing the structural hemispheric brain networks, we have provided new insights into understanding the neuroanatomical basis of lateralized brain functions. Hum Brain Mapp 35:4944–4957, 2014. © 2014 Wiley Periodicals, Inc.

INTRODUCTION

Hemispheric lateralization in the human brain has been a constant focus of interest in different fields of neurosciences. The hemispheres of the human brain are functionally and structurally asymmetric. The study of such asymmetries provides important clues to the neuroanatomical basis of lateralized brain functions [see for review, Toga and Thompson, 2003]. Diffusion tensor imaging (DTI) [Basser et al., 1994; Jones and Leemans, 2011; Tournier et al., 2011] provides a validated and sensitive way of identifying hemispheric changes in brain white matter (WM). In that context, WM asymmetries have been observed, mainly focusing on the arcuate fasciculus because of its relationship to hemispheric specialization of language [e.g., Buchel et al., 2004; Catani et al., 2007; Nucifora et al., 2005; Rodrigo et al., 2007; Takao et al., 2011; Thiebaut de Schotten et al., 2011; Vernooij et al., 2007]. Other DTI studies have explored fractional anisotropy asymmetry in the cingulum [e.g., Gong et al., 2005; Kubicki et al., 2003; Takao et al., 2011], corticospinal tract [e.g., Park et al., 2004; Westerhausen et al., 2007], and uncinate fasciculus [Kubicki et al., 2002]. Our understanding of structural asymmetries is still largely limited to the level of individual structures. In the present study, we decided not to focus on these regional asymmetries, but instead concentrate on the capacity of information flow within and between regions of a hemisphere, by investigating the hemispheric structural network with a graph theoretical approach [Hagmann et al., 2008].

It has been suggested that some aspects of brain asymmetries also interact with gender. For example, gender differences have been reported in the structural asymmetry of the planum temporale, with greater asymmetries in males [Jancke et al., 1994; Kulynych et al., 1994]. These gender differences in brain asymmetries have been proposed as the underlying origin of gender differences in lateralized behaviors, such as motor and visuospatial skills, and linguistic performance. Furthermore, hemispheric asymmetry reduction in older adults (known as the HAROLD effect), interpreted as a compensatory neural mechanism to counteract age‐related efficiency decline, has been frequently reported in studies of functional brain aging [Cabeza 2002; Cabeza et al., 1997, 2004; Morcom et al., 2003; Reuter‐Lorenz et al., 2000]. To date, very scant data is available regarding WM asymmetries and its potential changes with age [Ardekani et al., 2007; Hsu et al., 2008, 2010; Kovalev et al., 2003; Lebel et al., 2008]. For example, Ardekani et al. [2007] found that hemispherical anisotropy decreases with age. It has been suggested that this loss of asymmetry is associated with a loss of myelinated nerve fibers. Despite these advances in brain asymmetry research, however, little is known about whether there are differences in the topological organization of brain networks between the hemispheres and whether those differences are related to age and gender.

In the present study, the structural network dissimilarities will be characterized by means of a graph theoretical analysis [for review, see Bullmore and Sporns, 2009], which provides a novel way to explore topological and geometrical properties of brain networks, such as clustering coefficient, small‐worldness, efficiency, and path length [Rubinov and Sporns, 2010]. To date, only a few studies have examined hemisphere‐related differences in the topological organization of brain networks. Iturria‐Medina et al. [2011] used diffusion‐weighted MR tractography in 11 healthy subjects (23–38 years); it was found that the right hemisphere is more efficient and interconnected than the left hemisphere [Iturria‐Medina et al., 2011]. Another study [Tian et al., 2011] reported a gender‐hemisphere interaction in functional brain networks of 86 young, healthy adults (17–25 years) using resting‐state functional MRI. Specifically, they found that compared with females, males have a higher normalized clustering coefficient in the right hemispheric network but a lower clustering coefficient in the left hemispheric network.

However, to our knowledge, no study currently exists in which structural network dissimilarities between hemispheres and their associations with both gender and age have been investigated. In the present study, we analyzed the left and right hemispheric networks of a large cohort of 346 healthy participants (20–86 years) with a graph theoretical approach. After constructing hemispheric networks for each participant, we further calculated topological parameters, such as small‐worldness, local efficiency, and betweenness centrality and investigated their associations with gender and age.

MATERIALS AND METHODS

Participants and MRI Data Acquisition

The present study included data from 346 normal subjects and were separated into three age groups, defined by the 33rd and 66th percentile to obtain an equal distribution of the number of subjects across the three age groups: (a) 20.17–42.21 years (young adults, 112 subjects, 63 males, 49 females), (b) 42.22–60.92 years (middle‐aged adults, 116 subjects, 54 males, 62 females), and (c) 60.93–86.20 years (older adults, 118 subjects, 52 males, 66 females). The data of all subjects are part of the Information eXtraction from Images data base, which is made publically available by the Imperial College London (http://biomedic.doc.ic.ac.uk/brain-development/index.php?n=Main.Datasets). All subjects that participated in this study had no history of neurological and psychiatric disorders. Informed consent was obtained from each subject, and Ethical approval was granted by the Thames Valley MREC. Diffusion tensor images were acquired with a Phillips 3T system using the following parameters: single shot spin‐echo; TR 12,000 ms; TE 51 ms; slice thickness 2 mm; voxel size = 1.75 × 1.75 × 2 mm³. Diffusion gradients were applied along 14 noncollinear directions with a b‐value of 1000 s/mm². Additionally, one nondiffusion weighted image (b = 0 s/mm²) was acquired.

DTI Preprocessing

The DTI data were preprocessed in ExploreDTI [Leemans et al., 2009] and consisted of the following steps: (a) the diffusion data were corrected for subject motion and eddy‐current induced geometrical distortions [Leemans and Jones, 2009] and (b) the diffusion tensors were calculated using the RESTORE approach [Chang et al., 2005]. More detailed descriptions of these steps can be found elsewhere [Caeyenberghs et al., 2010a, 2010b, 2011].

WM Tractography

For each individual dataset, WM tracts of the brain network were reconstructed (Fig. 2A) as described previously [Basser et al., 2000]. Fiber pathways were generated by starting seed points sampled uniformly throughout the data at 2‐mm isotropic resolution. Trajectory propagation was terminated if fractional anisotropy (FA) < 0.2 or if the angle between consecutive steps exceeded 45 degrees. The step size was set at 1 mm.

Figure 2.

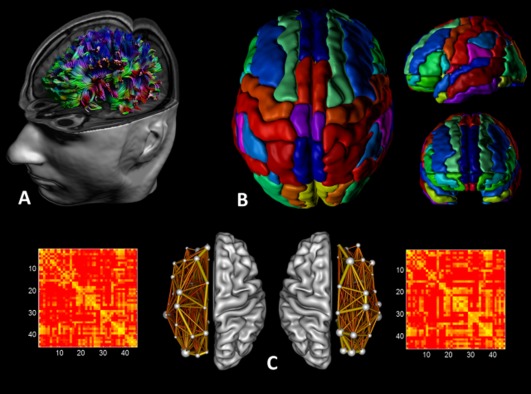
Structural networks were explored using graph theory through the following steps: (A) First, for each DTI dataset a whole‐brain tractography was performed using ExploreDTI. (B) Then, we defined the network nodes as the regions of the AAL template for each hemisphere. Each hemispheric network contained the same number of homologous regions of the AAL, that is, 45 regions. (C) We next determined a continuous measure of association between nodes. This was the percentage of tracts between each pair of regions of the AAL template, resulting in two 45 × 45 connectivity matrices for each subject, one for the left hemisphere and the other for the right hemisphere. Finally, from the hemispheric networks, measures of local and global connectivity were computed. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Construction of the Left and Right Hemispheric Networks

The whole‐brain fiber tract reconstructions of the previous step were segmented into left and right hemispheric networks, each containing the same number of homologous regions of the automated anatomical labeling atlas [Fig. 2B, AAL, Tzourio‐Mazoyer et al. 2002]. Using this procedure, we obtained 45 cortical and subcortical regions for each hemisphere, each region of interest (ROI) representing a node of a hemispheric network (see Figs. 1 and 2C), and the edges between two nodes reflecting a reconstructed WM tract. Important to note, all reconstructed data were visually checked for registration accuracy for each subject. We reinspected the data in three orthogonal planes to ensure that the registration has been performed correctly and that no additional artifacts have been introduced into the data.

Figure 1.

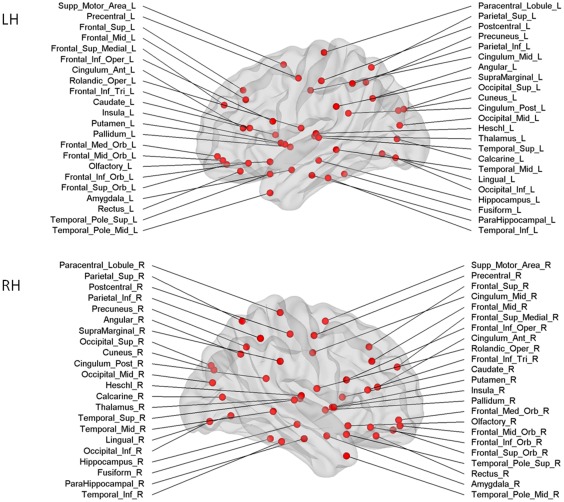
Cortical and subcortical regions for each hemisphere (upper panel left hemisphere, lower panel right hemisphere, 45 nodes in each hemisphere) as anatomically defined by a prior template image in standard stereotaxic space. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Interregional connectivity was then examined by determining the percentage of tracts (number of fiber connections normalized for the total number of tracts—so that results were not skewed by raw fiber count) between any two labels (i.e., any two regions of the AAL template within a hemisphere) [Hagmann et al., 2008]. This value became the edge weight in the connectivity matrix. Besides these weighted graph analyses, a binary network analysis was performed, whereby we only considered the existence/absence of fiber pathways. More specifically, the network edges were defined as 1 if there was at least one connection between both regions and as 0 otherwise [Hagmann et al., 2008; Shu et al. 2009]. As a result, for each participant, there were four connectivity matrices: for both hemispheres the “percentage of tracts” and “binary” (each represented by a symmetric 45 × 45 matrix, Fig. 2C).

Graph Theory Analysis

We used the Brain Connectivity Toolbox [Rubinov and Sporns, 2010; https://sites.google.com/site/bctnet/] to compute several network metrics including measures of network segregation (e.g., clustering coefficient), integration (e.g., path length and efficiency), and centrality (e.g., betweenness centrality). These metrics were quantified at both the network and regional levels. The equations to calculate each of these measures can be found in Rubinov and Sporns [2010]. We only provide brief definitions for each of the network properties used in this study.

The small‐worldness of a structural network has two key metrics: the clustering coefficient C and the characteristic path length L of the network. The clustering coefficient of a node represents the number of edges that exist between its nearest neighbors. The clustering coefficient of a network is thus the average of clustering coefficients across nodes and is a measure of network segregation. The characteristic path length of a network is the average shortest path length between all pairs of nodes in the network and is the most commonly used measure of network integration [Rubinov and Sporns, 2010]. Global efficiency is inversely related to characteristic path length: networks with a small average characteristic path length are generally more efficient than those with large average characteristic path length. We also calculated regional efficiency as a standard nodal connectivity measures. Regional efficiency is the global efficiency computed for each node [Sporns and Zwi, 2004].

To evaluate the topology of the constructed hemispheric networks, these parameters were compared to the corresponding mean values of a benchmark random graph [Maslov and Sneppen, 2002]. Thus, the small‐worldness index of each hemispheric network was obtained as [C/C _rand]/[L/L _rand], where C _rand and L _rand are the mean clustering coefficient and the characteristic path length of random networks [Bassett and Bullmore, 2006]. In a small‐world network, the clustering coefficient is significantly higher than that of random networks (C/C _rand ratio greater than 1), whereas the characteristic path length is comparable to random networks (L/L _rand ratio close to 1).

Finally, betweenness centrality was calculated as measure of centrality, which is based on the idea that central nodes participate in many short paths within a network and consequently act as important controls of information flow [Rubinov and Sporns, 2010].

Statistical Analysis

To determine whether there were significant differences in any of the global network parameters, the general linear model procedure was used to perform a three‐way repeated‐measures analysis of variance (ANOVA) with gender (male, female) and age group (young adults, middle‐aged, elderly) as a between‐subject factor, and hemisphere (right, left) as a repeated‐measures factor. Significant main and interaction effects were further explored by post hoc tests using Tukey correction.

The statistical analyses for the regional nodal parameters were similar to those for global network parameters. In brief, a three‐way repeated‐measures ANOVA was used to determine the significant differences in the three regional nodal parameters. If the hemisphere main effect survived the threshold, a paired t‐test was performed to identify which brain regions exhibited rightward of leftward asymmetries. Bonferroni corrections for multiple comparisons were made (hence P < 0.001 was considered significant following correction for the node‐specific analyses regarding the 45 regions). If the main effect of age group or gender survived the statistical threshold, further t‐tests were performed. The threshold for all these tests was set at P < 0.0005 (90 regions). All statistical analyses were performed with the Statistica software (StatSoft).

RESULTS

Overall Organization of the WM Networks

In this study, we constructed structural networks based on separate hemispheres rather than on the whole brain. We found that the normalized clustering coefficients γ were larger than one (i.e., the clustering coefficients for these networks were larger than those of their matched random networks) and the normalized path lengths λ were nearly one (i.e., the path lengths of these networks were comparable to those of their matched random networks) for 12 subgroups (3 age groups × 2 hemispheres × 2 genders) of structural networks. When evaluating the global network parameters using a summary parameter “small‐worldness” σ = γ/λ, we observed that σ was larger than one in our 12 subgroups of structural networks. Thus, these hemispheric networks exhibited prominent small‐world properties, consistent with previous whole‐brain structural network studies [Gong et al., 2009; Hagmann et al., 2007, 2008; Iturria‐Medina et al., 2008].

Furthermore, using the three‐way repeated‐measures ANOVA, we found that the overall normalized clustering coefficient γ, normalized path length λ, and the small‐worldness σ, showed significant differences between age groups and hemispheres (see Table 1). More specifically, we found increased values of γ, λ, and σ in the structural networks of the right hemisphere as compared to the left hemisphere. Using post hoc (Tukey) testing, we observed that the older adults (age group 3) showed increased values of γ, λ, and σ in their networks as compared to the young adults (age group 1) (all corrected P's < 0.05).

Table 1.

Hemispheric, age group, and gender effect on global and local network parameters revealed by a three‐way repeated‐measures ANOVA

		γ	λ	σ	E glob	Bc	E loc
Hemisphere effect	F‐value	255	253	223	71.69	277	271
	P‐value	<0.001	<0.001	<0.001	<0.001	<0.001	<0.001
Age group effect	F‐value	6.07	3.95	6.65	15.54	4.94	6.27
	P‐value	<0.001	<0.05	<0.001	<0.001	<0.01	<0.001
Gender effect	F‐value				16.13
	P‐value				<0.001
Interaction	F‐value				3.63a
	P‐value				<0.05

^aOnly one interaction was significant, that is, the hemisphere by age group for global efficiency.

Global Efficiency of the Structural Networks

Our results showed that the global efficiency of structural networks using binary networks of the brain was affected by gender, hemisphere, and age group (see Table 1). We found that males had greater global efficiencies than females. Moreover, there was an interaction between hemisphere and age group (Table 1, indicated by a). Post hoc Tukey revealed that the global efficiency was the highest for the left hemisphere of the young adults (all P's < 0.001). The global efficiency of the right hemisphere of the young adults demonstrated also a higher global efficiency than the right hemisphere of the elderly (P < 0.001). Tukey post hoc tests showed that the global efficiency of the left hemisphere of middle‐aged adults was higher than for the right hemisphere of the middle‐aged adults (P < 0.001) and both hemispheres of older adults (right: P < 0.001; left: P < 0.01). Finally, the left hemisphere of the group of the elderly revealed a higher global efficiency than the right hemisphere (P < 0.001).

Betweenness Centrality of the Structural Networks

First, a three‐way repeated‐measures ANOVA demonstrated a significant main effect of hemisphere and age group on the betweenness centrality (as shown in Table 1). We found that betweenness centrality of the right hemispheric networks was higher than for the left hemispheric networks. Compared with young adults, elderly showed significant greater betweenness centrality (P < 0.01).

Regional Nodal Properties of the Hemispheric Networks

For regional measurements, local efficiency was computed using the binary networks. We considered only local efficiency as network property in these analyses to reduce Type I errors and it has been suggested to be the most important measure of network analysis [Rubinov and Sporns, 2010].

Two‐way repeated‐measures ANOVA revealed a significant age effect and hemisphere effect on local efficiency (as indicated in Table 1). The left hemisphere was significantly more efficient than the right hemisphere. Furthermore, post hoc Tukey testing revealed that the young adults revealed higher values of local efficiency than the elderly (all P < 0.001). No significant main effect of gender or significant interaction effects were found.

Paired t‐tests for the hemisphere effect were performed to further determine the regional differences. Bonferroni corrections for multiple comparisons were made, hence P < 0.001 was considered significant following correction for the node‐specific analyses regarding the 45 regions. Twenty eight brain regions exhibited significant left‐greater‐than‐right asymmetries (Fig. 3 and listed in Table 2) mainly involving regions of the heteromodal or unimodal association cortex. To investigate the interregional changes in topological properties and connectivity, we used the functional brain divisions described by Mesulam [1998]. The 28 brain regions were grouped into five major divisions: association, paralimbic, limbic, primary, and subcortical. Association division consisted of 14 brain regions, paralimbic had six, limbic one region, four subcortical regions, and primary had three brain regions.

Figure 3.

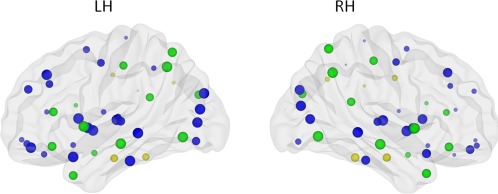
Image depicting significant main effect of hemisphere on efficiency. Size of the ROIs (spheres) represents value of the nodal efficiency for the right and left hemispheric network, collapsed across age groups. The colors of the nodes refer to: blue: regions with significant left‐greater‐than‐right asymmetries (P < 0.001), yellow: regions with significant right‐greater‐than‐left asymmetries (P < 0.001), green: not significant. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 2.

Significant hemisphere effects on local efficiency revealed by paired t‐tests (P < 0.001)

Region	Classification
Left > Right
Precentral gyrus	Primary
Superior frontal gyrus (dorsal)	Association
Orbitofrontal cortex (superior)	Paralimbic
Middle frontal gyrus	Association
Orbitofrontal cortex (middle)	Paralimbic
Inferior frontal gyrus (triangular)	Association
Rolandic operculum	Association
Supplementary motor area	Association
Olfactory	Limbic
Superior frontal gyrus (medial)	Association
Orbitofrontal cortex (medial)	Paralimbic
Rectus gyrus	Paralimbic
Anterior cingulate gyrus	Paralimbic
Calcarine fissure	Primary
Superior occipital gyrus	Association
Middle occipital gyrus	Association
Inferior occipital gyrus	Association
Inferior parietal lobule	Association
Paracentral lobule	Association
Caudate	Subcortical
Putamen	Subcortical
Pallidum	Subcortical
Thalamus	Subcortical
Heschl gyrus	Primary
Superior temporal gyrus	Association
Temporal pole of the superior temporal gyrus	Paralimbic
Middle temporal gyrus	Association
Inferior temporal gyrus	Association
Right > Left
Middle cingulate gyrus	Paralimbic
Parahippocampal gyrus	Paralimbic
Fusiform gyrus	Association
Supramarginal gyrus	Association
Angular gyrus	Association

Regions including two paralimbic regions (middle cingulate gyrus and parahippocampal gyrus), and three regions of the association cortex (the fusiform gyrus, supramarginal gyrus, and angular gyrus) were identified as regions with significant right‐greater‐than‐left asymmetries, as shown in Table 2.

In addition, t‐tests for the age effect were also performed for each region to evaluate the differences between young and old adults at the regional level. The threshold for all tests was set at P < 0.0005 (90 regions). Both negative (young adults > old adults) and positive (young adults < old adults) age effects were found on the regional efficiency in the individual regions across both hemispheres (see Fig. 4 and Table 3). Lower nodal efficiency in older adults as compared to young adults was located in 11 regions of the heteromodal or unimodal association cortex (bilateral middle frontal gyrus, bilateral triangular part of the inferior frontal gyrus, bilateral middle occipital gyrus, bilateral inferior occipital gyrus, right superior occipital gyrus, left inferior parietal gyrus, and left angular gyrus), 4 subcortical regions (bilateral caudate nuclei and bilateral thalamus), 1 paralimbic region (right orbital part of the middle frontal gyrus), and 1 limbic region (olfactory cortex). By contrast, higher regional efficiency in old adults as compared to young adults was observed in four paralimbic regions (bilateral middle cingulate gyrus, bilateral posterior cingulate gyrus) and one region of the association cortex (left precuneus).

Figure 4.

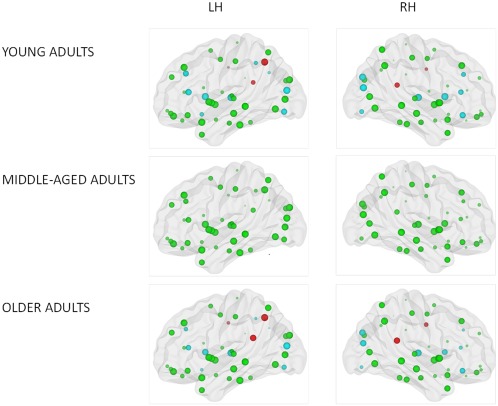
Figure illustrating significant main effect of age group on local efficiency. Size of the ROIs (spheres) represents value of the nodal efficiency for the right and left hemispheric network for each age group. The colors of the nodes refer to: red: higher nodal efficiency in older adults as compared to young adults (positive age effect) (P < 0.0005); blue: higher nodal efficiency in young adults as compared to older adults (negative age effect) (P < 0.0005), green: not significant. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table 3.

Significant age group effects on local efficiency revealed by post hoc t‐tests (P < 0.0005)

Region	Side	Classification
Young > Elderly
Middle frontal gyrus	R/L	Association
Orbitofrontal cortex (middle)	R	Paralimbic
Inferior frontal gyrus (triangular)	R/L	Association
Olfactory cortex	L	Limbic
Superior occipital gyrus	R	Association
Middle occipital gyrus	R/L	Association
Inferior occipital gyrus	R/L	Association
Inferior parietal lobule	L	Association
Angular gyrus	L	Association
Caudate	R/L	Subcortical
Thalamus	R/L	Subcortical
Elderly > Young
Middle cingulate gyrus	R/L	Paralimbic
Posterior cingulate gyrus	R/L	Paralimbic
Precuneus	L	Association

DISCUSSION

In the present study, we analyzed the left and right hemispheric networks of a large cohort of 346 healthy participants (20–86 years) with a graph theoretical approach. The principal goal was to determine the differences in the topological organization of brain networks between the hemispheres. Additionally, interactions between age and gender were also explored, as discussed next.

Small‐Worldness of the Hemispherical Networks

A small‐worldness topology is responsible for a high efficiency with a low wiring cost, and this kind of organization is actually shared by many networks in social, technological, information, or biological domains [Barabasi and Albert, 1999]. This kind of network organization is also highly suitable for human brain networks, allowing both segregation and integration of information [Bullmore and Sporns, 2009; Guye et al., 2010]. Our results have shown the “small‐worldness” for the 12 subgroups (3 age groups × 2 hemispheres × 2 genders) of structural networks. This finding is consistent with previous whole‐brain structural network studies using diffusion tractography in normal adults [Gong et al., 2009; Hagmann et al., 2007, 2008; Iturria‐Medina et al., 2008] and in patient populations [Lo et al.; 2010; Shu et al., 2009, 2011; van den Heuvel et al., 2010; Wen et al., 2011].

However, compared with the small‐world properties of matched random networks, an increased normalized path length and clustering coefficient (along with an increase in small‐worldness) was observed in the networks of the older adults and right‐hemisphere networks. Given that the small‐world topology is an optimal balance between local specialization and global integration as networks evolved over time to cope with high complexity of dynamic behavior [Bullmore and Sporns, 2009], our findings of increased normalized path length/clustering coefficient and small‐worldness in these networks indicate a shift away from an optimal “small‐world” network organization toward an imbalanced structural architecture with a more random configuration, in which all nodes have roughly the same number of connections.

Right‐Hemispheric Networks are Less Efficient

A significant leftward asymmetry on measures of efficiency and interconnectivity was found. Interestingly, we observed that the right hemisphere presents a higher betweennes centrality than the left hemisphere. When considered in combination with the small‐world characteristics, efficiency, and betweenness centrality results of the right hemisphere, this induces us to think that the configuration in the right hemispheric network is less optimal for information processing. Small‐world characteristics were different between the two cerebral hemispheres. Compared to the left hemisphere, the right hemisphere showed greater normalized clustering coefficient and larger normalized path length that led to a significant larger small‐world index. In other words, right‐hemispheric networks tend to have a more random configuration relative to left hemispheric networks. Moreover, the left hemisphere showed increased efficiency at both global and local levels in the left hemisphere as compared to the right hemisphere, suggesting that the brain regions in the left hemisphere interconnect in better integration compared to the right hemisphere. The increase in betweenness centrality indicates a putative compensation mechanism of the right hemisphere for the reduced efficiency of parallel information transfer. Our results are contrary to those of Iturria‐Medina et al. [2011], who found higher global efficiency in the right hemisphere. However, it is questionable whether their sample size (N = 11) would be sufficiently large to make a reliable inference. Consistent with our results, conversely, left‐greater‐than‐right‐asymmetries were found in healthy adolescents [Dennis et al., 2013] as well as in neonates brains [Ratnarajah et al., 2013].

The hemispheric effect was further localized in terms of regional efficiency. Specifically, brain regions involved in motor actions and language played crucial roles in efficient communication in the left hemisphere, while brain regions involved in memory and visuospatial attention played crucial roles in efficient communication in the left hemisphere. Previous studies reporting structural asymmetries of the human brain have been described in terms of gyrification, regional volumes, or WM microstructure differences using a variety of techniques, that is, MRI morphometry, neuropsychological investigation of patients with brain lesions, tachistoscopic/dichotic investigations [for a comprehensive review, see Toga and Thompson, 2003], whereas our regional asymmetry analysis is based on the fiber connectivity pattern of each region in terms of its nodal efficiency. Despite the differences between the measures and procedures used in different studies, we found a considerable regional correspondence between previous studies, and our asymmetry findings [Lerch et al., 2006].

Hemispheric lateralization for language is one of the most robust findings of cognitive neuroscience [Josse and Tzourio‐Mazoyer, 2004]. We observed significant leftward asymmetries in language‐relevant temporal regions of the AAL template, including the superior temporal gyrus, superior temporal pole, Heschl gyrus, Rolandic operculum, and inferior frontal regions, such as the triangular part of the inferior frontal gyrus which comprises Broca's region. These findings agree well with many structural reports [e.g., Good et al., 2001; Luders et al., 2006; Watkins et al., 2001] and the documented left hemispheric dominance for language [Price, 2000].

Beyond language, motor function plays an important role for the discussion of connectivity and hemispheric lateralization. In correspondence with previous human studies, leftward asymmetries for the precentral gyrus and supplementary motor area, regions associated with motor control actions, have been well recognized for right‐handed subjects [Dadda et al., 2006; Luders et al., 2006; Rogers et al., 2004]. In addition, a leftward asymmetry was found in several basal ganglia of our AAL atlas, such as caudate nucleus, putamen, and pallidum. Their role has been implicated in a number of important motor functions [Coghill et al., 1994; Jones et al., 1991], in particular in the initiation of motor responses [Coxon et al., 2010; Toxopeus et al., 2007]. Unfortunately, previous structural network analyses were limited to cortical regions without including subcortical regions in their parcelation schemes. In the future, it might be more meaningful to use advanced integrative atlases including basal ganglia to explore how connectivity of these basal ganglia regions could be related to asymmetries. Moreover, leftward asymmetries in language‐ and motor‐related fibers, including the parieto‐premotor part of the superior longitudinal fasciculus, the corticospinal tract, and the arcuate fasciculus, have been observed in healthy adults [Stephan et al., 2007], and infants [Dubois et al., 2009].

The cingulate gyrus of our AAL atlas gave mixed results. Leftward asymmetry was found for the anterior cingulate, whereas rightward symmetry was demonstrated in the middle cingulate. Previous reports on cingulate asymmetry have been inconsistent, depending on the used methodology. Leftward asymmetries for the cingulate have been found in cortical thickness [Luders et al., 2006] and DTI studies [Gong et al., 2005]. Rightward asymmetries are previously reported using volumetric and voxel‐based measures [Watkins et al., 2001]. For the first time, in our study we were not limited to the whole cingulate region without making distinction between its anterior, middle, and posterior parts, using the AAL template.

Beyond language and motor functions, memory and visuospatial attention play also an important role for the discussion of connectivity and lateralization. First of all, we found a rightward asymmetry in terms of efficiency in the parahippocampal gyrus of the AAL template, which is thought to be involved in memory encoding and retrieval, and is consistent with the widely reported right‐sides asymmetries for the hippocampal regions [Bigler et al., 1997; Good et al., 2001; Pegues et al., 2003]. The other right‐lateralized regions, that is, fusiform gyrus, supramarginal gyrus, and angular gyrus of our parcelation scheme, are compatible with the specialization of right visual and parietal cortices for visuospatial attention. For example, Tuch et al. [2005] found a lateralization of correlations between behavioral reaction time performance on a speeded visuospatial attention task and fractional anisotropy values to right visual and parietal WM pathways, including the right optic radiation, right posterior thalamus, and right medial precuneus WM.

All these nodal analyses appear to support the fact that the left hemisphere has a leading role for language and motor control, whereas right hemispheric areas play a dominant role in the implementation of memory and visuospatial functions.

Structural Networks are Less Efficient in Older Adults

Although WM networks of old adults showed prominent small‐world properties, the underlying organization of the WM networks was altered in older adults, resulting in a decreased overall global efficiency and reduced regional local efficiency. In other words, the aging network becomes less connected. This decrease may be related to morphomolecular changes in neurons, axons, dendrites, and synapses, as well as the accumulation of neuropathologies that occur with age [Hof and Morrison, 2004]. This decreased structural connectivity of the older adults appears consistent with previous functional [Achard and Bullmore, 2007] and structural [Gong et al., 2009] network studies of aging on one hand, and previous studies reporting alterations in DTI‐based metrics with age, on the other hand [Hsu et al., 2008, 2010; Lebel et al., 2008]. The regional efficiency showed extensive changes across the cerebral cortex in aging. As shown in Figure 4, reduced efficiency was found in 17 regions predominantly in the frontal, occipital, parietal, and subcortical regions. Hence, our findings support the notion of aging as a “disconnection syndrome” from a network perspective. In contrast, five regions localized in cingulate gyrus and precuneus showed increased efficiency, indicating a putative compensation mechanism of network reorganization in aging.

Structural Networks are Less Efficient in Women

In addition to the age‐related network changes, we found a significant difference in global network connectivity between males and females. Specifically, females displayed a significantly increased characteristic shortest path length. The path length of a node expresses how close it is connected globally to other nodes of the network, with shorter path lengths reflecting higher levels of efficient access to information [Rubinov and Sporns, 2010]. The average inverse shortest path length is a related measure known as the global efficiency [Latora and Marchiori, 2001], which is the most commonly used measure of functional integration [Achard and Bullmore, 2007]. Females showed strong decreases in global efficiency. However, the absence of gender effects on local efficiency marks the fact that gender does not strongly affect the local connectivity or local organization of the brain networks, indicating that the effects on global efficiency and shortest path length are likely to be related to organizational effects rather than just reduced local connectivity. This finding of an affected global organization in females does not overlap with previous studies [Gong et al., 2009; Tian et al., 2011], where they showed that females had a denser local clustering and higher local network efficiency. Possible explanations for these conflicting results are the used tractography methods [e.g., Behrens et al., 2007; Jeurissen et al. 2011] and diffusion MRI sequences [Bassett et al., 2011]. Nevertheless, recent studies on the effects of different acquisition schemes [Bassett et al., 2011; Vaessen et al., 2010] and tractography algorithms [Bastiani et al., 2012] on graph metrics revealed that the effect was small in healthy volunteers. With the structural network‐based approach still in its infancy years, it is clear that further studies are necessary to identify gender differences in structural WM networks, which may play an important role in explaining differences in cognitive function or in resilience to disease.

LIMITATIONS

Several issues need to be addressed. First, we used a DTI‐based streamline tractography approach [Basser et al., 2000; Mori et al., 1999] to define the edges of the structural network. This is by far the most widely applied tractography method, mainly for its simplicity, robustness, and speed [Cheng et al., 2012; Griffa et al., 2013]. Such a tractography method, however, is not able to resolve crossing fiber bundles [Jones et al., 2013; Mori and van Zijl, 2002; Tournier et al., 2011]. Many other algorithms could be used to develop the structural network, but choosing one is not a trivial matter, because different tractography algorithms for analysis of the same imaging data can lead to subtly different graph theoretical results [Bastiani et al., 2012]. Further studies should reconstruct anatomical networks with diffusion tractography methods that have the advantages of overcoming fiber crossings and being robust to image noise [e.g., Behrens et al., 2007; Dell'acqua and Catani, 2012; Dell'acqua et al., 2007, 2010, 2013; Descoteaux et al., 2009; Hess et al., 2006; Jbabdi and Johansen‐Berg, 2011; Jeurissen et al., 2011, 2013; Tournier et al., 2004, 2007, 2008, 2013; Tuch, 2004; Wedeen et al., 2005, 2008]. Importantly, despite of its advantages over more conventional tractography approaches, these methods still present important limitations as well, such as a the difficulty to separate real from false connections and the ambiguity in modeling [Parker et al., 2013; Tax et al., 2014; Jones and Cercignani, 2010]. Related to this issue, more recent acquisition sequences have been shown to generate networks with a higher probability of long‐distance connections than the classical DTI sequences [Bassett et al., 2011; Zalesky et al., 2010a, 2010b]. Nevertheless, recent studies on the effects of different acquisition schemes on graph metrics [Bassett et al., 2011; Vaessen et al., 2010] revealed that the effect was small in healthy volunteers.

Moreover, we adopted the AAL template as parcelation scheme, which is based on a sulcal patterns from only one subject. The main advantage of using the AAL template for nodal parcelation is that it can support direct comparison of results to prior connectome studies using the same AAL template in healthy adults [e.g., Gong et al., 2009; Li et al., 2009] and patient populations [e.g., Lo et al., 2010; van den Heuvel et al., 2010; Zalesky et al., 2011]. It is important to consider that although the atlas that we used was carefully checked for registration errors, in the future it might be more meaningful to apply a probabilistic atlas of human brain to regional parcelation or define individual brain regions through a combination of DTI with fMRI given the interindividual variability of anatomical structures [Thompson et al., 1996, Sporns et al., 2005].

Moreover, future studies should include information on the level of education of the participants and a formal assessment scale of handedness, such as the Edinburgh Handedness Inventory [Oldfield, 1971]. These two factors may be considered important confounders of the described differences in the topological organization of brain networks between the hemispheres. The interactions with handedness and level of education should be explored in further studies.

Finally, other currently available MRI sequences have further improved the detection of WM damage in elderly, such as T2‐weighted imaging and fluid‐attenuated inversion recovery (FLAIR) scans [for a review, see Gunning‐Dixon et al., 2009]. Because FLAIR and T2 scans can be very sensitive in detecting WM hyperintensities, a more complete evaluation can be obtained to objectively assess WM lesions in the older adults' group by integrating these modalities. The extent of detected WM damage can provide long‐term neurological and behavioral prognostic information. Further studies correlating the abnormalities seen on FLAIR with graph metrics need to be done to better define the age‐related changes in the organization of the WM networks.

CONCLUSIONS

Despite the present findings, this study on structural network dissimilarities between hemispheres and their associations with gender and age is still preliminary, and further studies are needed. First, we observed that small‐world properties were present for the structural hemispheric networks across age groups and gender. Further studies, simultaneously evaluating the small‐world characteristics of functional and structural hemispheric networks, are needed. Second, we observed that the topological architecture of the hemispheres was different. Specifically, the left hemisphere was significantly more efficient and interconnected than the right hemisphere. As has been mentioned, brain asymmetries are closely related to lateralized processes like language, memory, visuospatial attention, and motor control. Thus, further analysis of the relationship between hemispheric asymmetries and performance on behavioral parameters should be carried out. Investigating hemispheric lateralization is not only important for our general understanding of human brain function, but also with regard to the many clinical disorders that implicate hemispheric asymmetries, such as schizophrenia, autism, and stroke. Graph theoretical analyses might be able to understand how brain asymmetries in brain disorders are caused and how they can be influenced.